Response of Single Cells to Shock Waves and Numerically Optimized Waveforms for Cancer Therapy

Abstract

Shock waves are used clinically for breaking kidney stones and treating musculoskeletal indications. The mechanisms by which shock waves interact with tissue are still not well understood. Here, ultra-high-speed imaging was used to visualize the deformation of individual cells embedded in a tissue-mimicking phantom when subject to shock-wave exposure from a clinical source. Three kidney epithelial cell lines were considered to represent normal healthy (human renal epithelial), cancer (CAKI-2), and virus-transformed (HK-2) cells. The experimental results showed that during the compressive phase of the shock waves, there was a small ($<$2%) decrease in the projected cell area, but during the tensile phase, there was a relatively large (∼10%) increase in the projected cell area. The experimental observations were captured by a numerical model with a constitutive material framework consisting of an equation of state for the volumetric response and hyper-viscoelasticity for the deviatoric response. To model the volumetric cell response, it was necessary to change from a higher bulk modulus during the compression to a lower bulk modulus during the tensile shock loading. It was discovered that cancer cells showed a smaller deformation but faster response to the shock-wave tensile phase compared to their noncancerous counterparts. Cell viability experiments, however, showed that cancer cells suffered more damage than other cell types. These data suggest that the cell response to shock waves is specific to the type of cell and waveforms that could be tailored to an application. For example, the model predicts that a shock wave with a tensile stress of 4.59 MPa would increase cell membrane permeability for cancer cells with minimal impact on normal cells.

Introduction

A shock wave is a type of acoustic wave characterized by the presence of a rapid-pressure jump governed by the interaction of nonlinear effects that steepen the waveform and attenuation mechanisms that smooth the waveform (1). Shock waves have been medically used for decades in a procedure called lithotripsy, in which shock waves fragment kidney stones. Although lithotripsy is a mature technology, there are concerns about bioeffects, including renal hemorrhage and scarring with a permanent loss of functional renal volume (2, 3). Although damage is predominantly thought to be induced by cavitation (4, 5) even in environments where cavitation is minimized, damage has been reported in cells (6) and tissues (7), suggesting a direct impact of shock waves on cells.

Shock waves have also been employed for orthotripsy, which is the treatment of musculoskeletal disorders, such as plantar fasciitis, tendon pain, and nonunions or delayed unions of long-bone fractures (8). The mechanism by which shock waves have an effect on musculoskeletal conditions is not understood. One of the hypotheses is that the disruption of the tissue by shock waves results in “microtrauma,” which then induces neovascularization that is believed to improve blood supply and tissue regeneration. The increased permeability of the vessel wall may also promote the healing process (8).

Cancer therapy is another field in which shock waves have been investigated (9, 10, 11). It has been reported that besides mechanically rupturing cells, shock waves may enhance the sonoporation effect that temporarily increases the membrane permeability to allow molecules in the surrounding medium to diffuse into cells (9). This provides a mechanism for shock-wave-mediated therapeutic drug delivery and gene transfer. Furthermore, some experimental results have shown a positive influence of shock waves on suppressing tumor growth and selectively killing malignant cells (10, 11). The mechanisms by which shock waves affect cancer cells are not well understood.

All of these applications motivate the need for a better understanding of the interaction between shock waves and cells. The goal of this work is to develop a numerical model for the response of a single cell to shock waves that is calibrated and validated against ultra-high-speed imaging of single-cell deformation under the action of shock waves. The differences in cell response to shock waves due to cell type is also examined. The numerical model employs a three-dimensional (3D) continuum model of an individual cell modeled with a combined equation of state (EoS) and hyper-viscoelastic material framework. The validated numerical model was then used to analyze the development of the stress and strain fields under the compressive and tensile phases of the shock wave, from which insights into the mechanisms of cell destruction and sonoporation were obtained. Two shock-wave profiles are proposed to specifically target cancer cells for enhanced sonoporation or rupture while minimizing impact on normal healthy cells.

Materials and Methods

The experimental rig consisted of a shock-wave source coupled to a tissue-mimicking gel in which cells were embedded. The gel contained cell media to maintain cell viability. Three kidney epithelial cell lines representing cancer cells, normal healthy cells, and virus-transformed cells were studied. An ultra-high-speed camera (SIMX 16; Specialised Imaging, Tring, United Kingdom) with a 20$\times$ objective (UMPLFLN20XW; Olympus, Tokyo, Japan) was used to image individual cells. Before the cell experiments, the camera and shock source were coaligned with a needle hydrophone.

For each experiment, the camera was focused onto a cell in the focal region of the shock waves. A reference image was taken before the delivery of shock waves. A shock wave was delivered, and the camera was triggered to capture 16 frames at a rate of 3.3 Mfps (interframe time of 300 ns with an exposure time of 200 ns). Each cell was imaged with three different shock-wave energy settings. The imaging experiment was repeated on eight different target cells for each of the three cell lines investigated. Further details of the experimental system are described in the Supporting Material.

The high-speed images were filtered and then processed to extract the boundary of the cells from the images using methods described in the Supporting Material. The deformation of the cell was determined by comparing the cell boundary during shock-wave passage to the cell boundary in the reference image; we note that a separate reference image was used for each camera channel to avoid channel-to-channel differences. Quantitative analysis of the perimeter and area change was performed based on the extracted cell boundaries.

Shock-wave pressure profiles

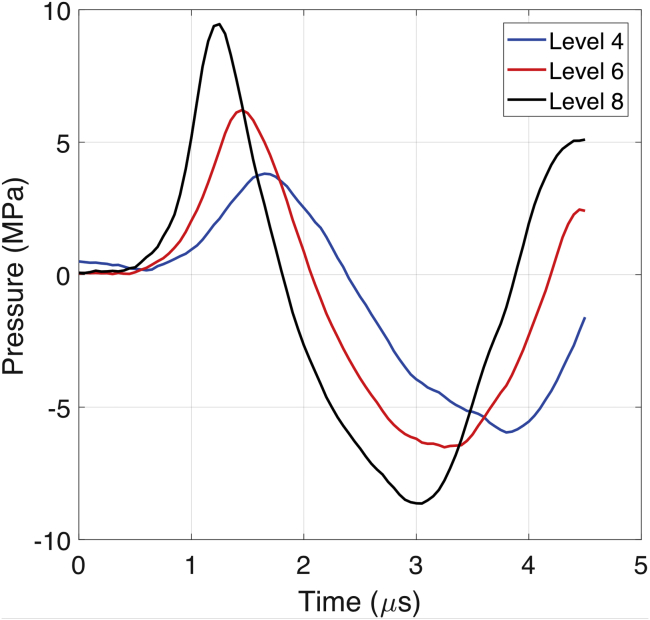
Fig. 1 shows pressure waveforms measured at the focus of a clinical shock-wave source (Minilith SL1-0G; STORZ, Tuttlingen, Germany) at three different energy settings (levels 4, 6, and 8) using a bespoke fiber-optic probe hydrophone embedded in a tissue-mimicking phantom (12). In each case, the shock wave consists of a compressive phase (duration around 1.5 μs) followed by a tensile phase (duration around 2.1 μs). As the energy level increased, three effects were observed: an increase in the peak positive pressure, a decrease in the shock-rise time (time duration for the shock front pressure to rise from 10 to 90% of the maximal shock pressure), and a gradual increase in the peak negative pressure. These are characteristic behaviors of a focused nonlinear acoustic wave (13).

Figure 1.

Measured focal shock waves in a tissue-mimicking phantom for source energy level 4 (blue), level 6 (red), and level 8 (black). To see this figure in color, go online.

Single-cell deformation under a shock wave

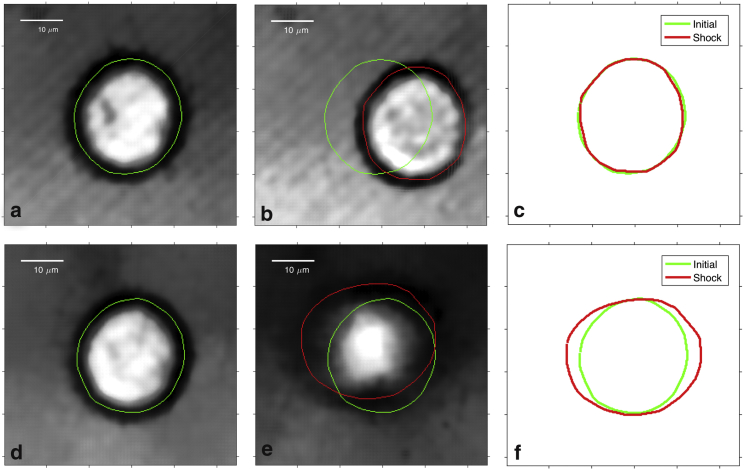
Fig. 2, a–c show representative images of an individual healthy human kidney (human renal epithelial (HRE); Lonza, Basel, Switzerland) cell during the compressive phase of a shock wave at energy level 8. The cell boundary was extracted, as described in the Supporting Material, and it can be seen that the cell is translated and the contour is slightly compressed in this phase of the shock wave. Fig. 2, d–f show the cell during the tensile phase, and it can be seen that the boundary has expanded and also become more diffuse in the image. As described in the Supporting Material, the effects of variability in the imaging, segmentation, and acousto-optic interactions were analyzed and found not to mask the cell deformation under shock waves.

Figure 2.

Deformation of a healthy HRE cell during the compression phase (a–c) and tension phase (d–f) at energy level 8. (a) and (d) depict the cell before the shock wave, (b) and (e) depict the cell during the shock wave interaction, and (c) shows a cell contour comparison before (green) and during (red) shock wave exposure. To see this figure in color, go online.

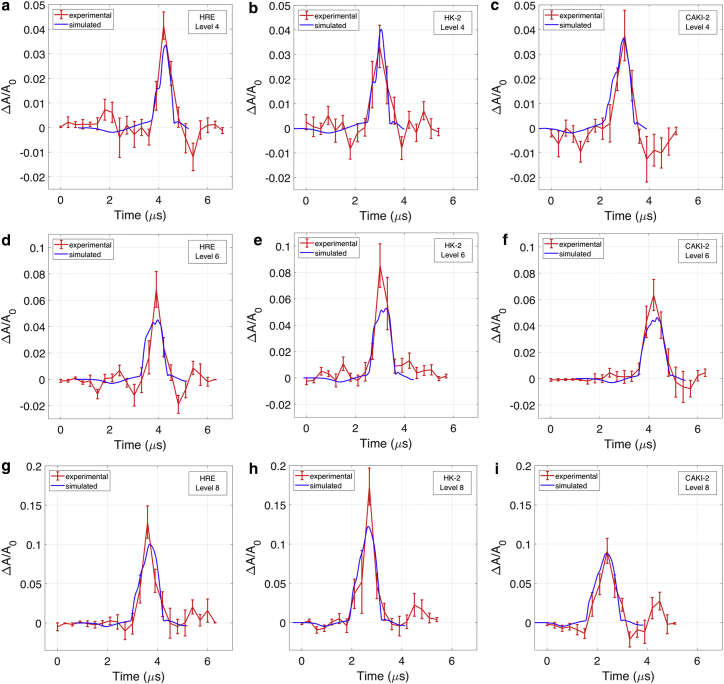
The projected cell area inside the cell boundary was calculated for every image, and Fig. 3, a, d, and g show the relative area change-time curve (see Eq. 10 in the Supporting Material) for HRE cells for the three shock wave energy settings. It can be seen that the cells initially undergo a small compression ($<$2% area decrease) followed by a large expansion that increases with the increase of shock-wave energy levels (up to 13% area increase at shock-wave energy level 8). The timing of cell deformation was found to be consistent with the compressive phase and tensile phase of the shock wave; however, the sixfold increase in cell area changes between tension and compression was not consistent with the fact that the magnitude of the tensile stress was comparable to that of compression with similar loading rates. These data suggest that the cells are stiffer during compression than under tension.

Figure 3.

Experimental (red) and simulation (blue) results of cell-area change in response to shock waves. The cell deformation is shown at the following shock-wave energy levels: (a–c) level 4, (d–f) level 6, (g–i) level 8 for HRE (a, d, and g), HK-2 (b, e, and h), and CAKI-2 cells (c, f, and i). The error bar shows the SE based on nine individual cells for each case. To see this figure in color, go online.

The experiments were repeated with virus-transformed immortalized kidney cells (HK-2; ATCC, Manassas, Virginia) (Fig. 3, b, e, and h) and kidney cancer cells (CAKI-2; ATCC, Manassas, Virginia) (Fig. 3, c, f, and i). Both the cancer cells and immortalized cells exhibited the same qualitative behavior as that of the healthy cells (a small response to the compressive phase and a large response to the tensile phase of the shock wave). Further, the cell-area change increased with the shock-wave energy level setting, and the difference in the maximal area increase among the three cell types also became more distinguishable; see Supporting Material. At energy level 8, the maximal area increase was 13% in HRE cells (Fig. 3 g), 17% in the HK-2 cells (Fig. 3 h), and 9% in CAKI-2 cells (Fig. 3 i). The difference was statistically significant for HK-2 and CAKI-2 cells with a p-value of less than 0.05 in the Mann-Whitney U test. Furthermore, the duration of cell-area expansion was longer for the CAKI-2 cells (∼1.8 μs) than for the HRE and HK-2 cells (∼1.5 μs). These results indicate that the CAKI-2 cells exhibit stiffer mechanical characteristics during tension than those of normal or virus-transformed cells. We note that the duration of the tensile deformation of cells was slightly shorter than the 2.1 μs duration of the shock-wave tensile phase, which suggests that there may be a hysteresis effect present in the transition from compression to expansion.

The projected cell area can be thought as a proxy for the volumetric deformation of the cell and the cell perimeter for assessing its deviatoric response. It was found that the ratio of the projected area change to perimeter change for all three cell types at the three different energy-level settings remained between 1.5 and 2, which results in less than a 10% variation from a circular shape (analysis presented in the Supporting Material) and therefore suggests that the cells did not undergo substantial shear deformation during the shock-wave exposure. A measure of shear-related perimeter change was calculated by factoring out the volumetric contribution. It was found that the shear-related perimeter change for all three cell types remained less than 0.5%, further suggesting a small shearing effect in the experiment. More details are provided in the Supporting Material.

Cell viability test

To investigate the difference in cell response to shock waves for different cell types embedded in the agarose gel, a cell viability test was performed using a lactate dehydrogenase assay (ThermoFisher Scientific, Pierce, Waltham, Massachusetts) after shock-wave exposure. Cell viability is determined by light absorbance; to measure a detectable signal, ∼500,000 cells were concentrated to the shock-wave focal zone and exposed to 500 shock waves at energy levels 4 and 8. The detailed experimental protocol is explained in the Supporting Material.

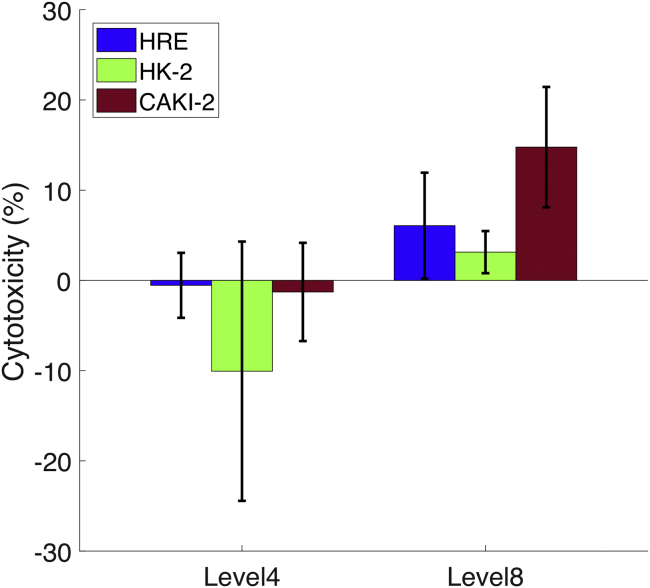
Fig. 4 shows the results of cell cytotoxicity after shock-wave exposure at energy levels 4 and 8. It can be seen that at energy level 4, no shock-wave-induced cytotoxicity was observed. The negative values indicate that shock-wave-treated cell samples presented higher cell viability than that of the nontreated sham samples. This effect has been found in previous studies in which lower-amplitude shock waves enhanced cell proliferation (14, 15). At energy level 8, all three cell lines exhibited cell cytotoxicity after shock-wave exposure, and the cancer cell line (CAKI-2) suffered higher cytotoxicity compared to the other two normal cell lines (HK-2 and HRE).

Figure 4.

Cell cytotoxicity of different cell lines at shock-wave energy levels 4 and 8. The error bar represents the SD calculated from six experimental repeats for each cell line and shock-wave condition. Welch’s t-tests showed a statistically significant difference between CAKI-2 and HK-2 or HRE (p$<$ 0.05). To see this figure in color, go online.

Numerical study

The 3D finite element model employed here consisted of a cell surrounded by an extracellular matrix. The deformation was decomposed into a deviatoric response and a volumetric response. The deviatoric response was described by the first-order generalized Maxwell viscoelasticity, which consists of a long-term shear modulus $\left({\mu }_{\infty }\right)$, a viscous shear modulus $\left({\mu }_1\right)$, and a viscosity $\left({\eta }_1\right)$ (16). The volumetric response was modeled by a bilinear acoustic EoS that employed different bulk moduli for the compressive and tensile phases of the shock wave with a transition at the early stage of the tensile wave. The surrounding matrix was modeled by nonlinear elasticity in combination with an acoustic EoS.

The measured shock waves (see Fig. 1) were used as boundary conditions for the top surface of the model and propagated as a plane wave through the computational domain. Further details are presented in the Supporting Material.

Numerical model calibration and validation

The mechanical properties of the numerical model under ultra-high strain-rate-loading were calibrated against the experimental measurements of the cell-area change.

Based on the larger deformation observed in the tensile phase than in the compressive phase, a bilinear EoS was proposed to model the volumetric change of a single-cell subject to shock waves. This EoS employs a high bulk modulus in compression and a lower bulk modulus in tension with a transition-pressure threshold to govern the transition between them. The compressive bulk modulus was estimated to be 2 GPa because of the small cell deformation under compression as well as the high water content of the cell (pure water has a bulk modulus of 2.2 GPa (17)). The other two material parameters (i.e., tensile bulk modulus and transition pressure threshold) were calibrated for each cell line by minimizing the least-square error of cell-area change between the simulation and experimental results. The final mechanical properties of the model calibrated across all three shock-wave energy levels are presented in Table 1.

Table 1.

Mechanical Properties for Different Cell Types

	Compressive	Tensile	Transition
	Bulk Modulus (GPa)	Bulk Modulus (MPa)	Pressure (MPa)
CAKI-2	2	34	−4
HK-2	2	20	−4.6
HRE	2	25	−4.6

The bulk moduli and transition pressure for HK-2 and HRE cells are similar, whereas the CAKI-2 cells exhibit a higher modulus in tension and a lower transition pressure. The mechanical properties suggest that even though the cancer cells have the largest bulk modulus, the lower transition pressure threshold makes them the first to undergo large deformation during tension.

The simulation results of the cross-sectional area change (which is equivalent to the projected cell area from the experiments) for each cell line using the optimized material parameters are presented in blue in Fig. 3. It can be seen that the simulations capture the response across all three energy levels with one unique set of material properties for each cell line. During the calibration process, the influence of the deviatoric material properties (shear moduli and viscosity) on the cell-area change was found to be insignificant (a factor of 10⁶ in the deviatoric properties resulted in $<$0.01% of area change). This is consistent with the experimental observations that the cell response is dominated by its volumetric deformation. The deviatoric properties used in the study were obtained from the literature (${\mu }_0$ = 3.1 kPa, ${\mu }_1$ = 0.34 kPa, η = 69.6 Pa.s) (18, 19).

Quantification of stress and strain evolution of cells

The numerical model quantifies the cell response in terms of stress and strain evolutions in 3D, which provides insights into shock-wave interactions with cells. The shock-wave propagation was found not to be strongly influenced by the difference in mechanical properties between the cell types. The von Mises stress, which quantifies the amount of shearing in the model, was found to be of the order of 100 Pa using the deviatoric mechanical properties from the literature. The overall cell membrane strain ΔS/S₀, which describes the area change of the cell membrane (see Eq. 21 in the Supporting Material), was also analyzed as an indicator of cell-membrane permeability showing the maximal values of 10% in HRE, 12% in HK-2, and 8.5% in CAKI-2 cells at shock-wave energy level 8. More details are provided in the Supporting Material.

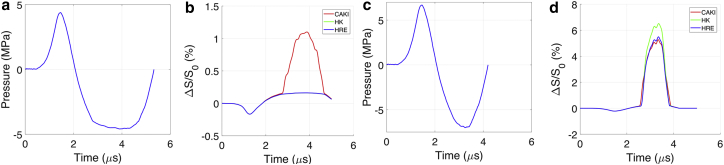
Optimization of shock-wave loading

The validated numerical model allows for the testing of designed shock-wave profiles to elicit a specific cell response. For example, a shock wave with a tensile stress of the order of 4.5 MPa will exceed the transition threshold of cancer cells, but not healthy cells, and therefore, it could sonoporate or even rupture cancer cells without damaging normal cells. Fig. 5, a and b present a proposed shock-wave profile with a peak negative pressure of 4.59 MPa and the predicted membrane strain for each cell type. The difference in the threshold for CAKI-2 and HRE (HK-2) cells resulted in 1.1% of membrane strain in CAKI-2 cells at the maximal tensile pressure, whereas the membrane strain of HK-2 and HRE cells remained less than 0.2%. The rupture-strain threshold for cancer cells has been reported to be around 5% (20, 21); therefore, with 1.1% of tensile membrane strain, increased cell membrane permeability may be expected even though permanent damage may not occur.

Figure 5.

(a) First proposed shock loading with a maximal tensile pressure of 4.59 MPa. (b) The resultant cell membrane strain is shown in three cell types. (c) The second proposed shock loading has a maximal tensile pressure of 7 MPa. (d) The resultant cell membrane strain is shown in three cell types. To see this figure in color, go online.

Research studies have also shown that the rupture strain threshold is 40% or higher for normal cells (22, 23). Therefore, another shock loading with a peak negative pressure of 7 MPa was proposed (see Fig. 5 c), and it is expected to result in rupture of cancer cells ($>$5% membrane-area increase). In this case, the noncancerous cells (HK-2 and HRE cells) showed relatively large deformation during tension (∼5.5 and 6.5%, respectively); however, this is still well below the reported rupture threshold for normal cells. In addition, the expansion in cancer cells was longer in duration compared to that of their noncancerous counterparts (HK-2 and HRE cells), which may lead to higher energy deposition for damaging cancer cells.

Results and Discussion

The key result in this work is that cells subject to shock waves were stiffer under compression (compressive deformation $<$2%) than under tension (tensile deformation ∼10%) even though the compressive phase of the shock wave was comparable to the tensile phase. This phenomenon was captured in the simulation by use of a bilinear model for the bulk modulus in the EoS with a high modulus for compression and a lower modulus for tension with a transition-pressure threshold.

Differences in cell deformation under compression and tension have been reported at lower strain rates and are related to the cytoskeletal network, which consists of actin filaments, intermediate filaments, and microtubules bathed in a fluid environment (the cytosol) (24). It has been suggested that actin filaments and intermediate filaments provide resistance to tension (acting like springs), whereas microtubules are resistant to compression (acting like rods) (25). It is thus expected that cells behave differently under different external loadings (e.g., compression versus tension). Furthermore, the observed cell deformation is also consistent with the idea that under compression, the presence of water in the cells results in a bulk modulus similar to that of water. Under tension, the decrease in bulk modulus beyond a critical tensile stress suggests that some combination of mechanical structure failure and fluid cavitation may be at play within the cell. However, in the data shown in Fig. 3, no macroscopic failure or cavitation was directly observed. Possible mechanisms for microrupture include intracellular cavitation in the cytoplasm (26), intramembrane cavitation in which rupture occurs between the layers of the lipids that make up the cell membrane (27), or phase transition of the lipids in the cell membrane from a gel state to a fluid state (28). The presence of large deformation under tension indicates that both cell damage and increased membrane permeability are likely to occur during this stage of the shock loading.

Fitting of the numerical models to the measured cell deformation suggested that CAKI-2 cells have a greater tensile stiffness than that of HK-2 and HRE cells. This contrasts with the general consensus that cancers cells have lower stiffness than normal cells (29, 30), although there are also reports of cancer cells having greater stiffness than normal cells (31, 32). Additionally, previously reported stiffness values refer to the Young’s modulus measured at slow strain rates ($<$10 s^-1), whereas we report the bulk modulus at a very high strain rate ($>$10⁴ s^-1), at which a strong strain rate effect is expected. Note also that the bulk modulus and Young’s modulus will not be strongly correlated, particularly when the Poisson’s ratio is close to 0.5, as is expected for cells.

The cell viability experiments indicate that shock waves at energy level 4 did not result in cell death for any of the cell types. The simulations predicted that the maximal tensile membrane strains of both cancerous and normal healthy cell lines at energy level 4 are less than 4% (Fig. S19 a). Previous work has reported that the rupture strain threshold for cancer cells is around 5% (20, 21), whereas that of normal cells has been reported to be 40% or higher (22, 23). The predicted strains induced by energy level 4 are less than these values (with the caveat that these reports are at low strain rates); therefore, the lack of cell death is consistent with the strains being below the damage threshold. For the experiments at energy level 8, CAKI-2 cells exhibited greater cell toxicity than that of normal cells; this was despite the fact that the larger bulk modulus of the cancerous cells meant that the simulations predicted that the CAKI-2 cells should experience a peak tensile membrane strain (8%, Fig. S19 c) that is smaller than that of normal cells ($>$10%, Fig. S19 a). The difference is consistent with the reports that cancerous cells are more fragile than normal cells and that this effect is more important than the change in the bulk modulus.

These results motivated the design of shock-wave profiles to specifically target cancer cells for therapy without affecting normal cells. The first was designed to facilitate sonoporation into cancer cells by employing a shock wave with a peak tensile pressure of −4.59 MPa, which should exceed the transition pressure threshold of cancer cells (−4 MPa), but not that of normal cells (−4.6 MPa). The results from the simulations, depicted in Fig. 5, a and b, predicted a 1.1% membrane strain increase for CAKI-2 cells as opposed to 0.2% found for the HK-2 and HRE cells. The strain in the CAKI-2 cells should be sufficient to result in cell membrane permeability without inducing cell death and without any effect on healthy cells. The second designed shock-wave profile employed a higher tensile pressure and resulted in $>$5% membrane strain in cancer cells (Fig. 5, c and d) for cancer-cell rupture, whereas the predicted membrane stretch was of ∼5% in normal cells; these strains should result in cell death for CAKI-2 cells (which are more fragile) while leaving normal cells intact.

We acknowledge that the experimental setup employed here does not fully capture in vivo conditions. Embedding cells in transparent gel allowed for the visualization and study of single-cell deformation under shock waves in the presence of a scaffold that captures the bulk mechanical properties of tissue. Ideally, the cells under investigation would be in contact with their surroundings; however, this setup is crucial to study cell behavior at the cellular and subcellular levels (e.g., therapeutic molecules permeating cell membranes).

In conclusion, to our knowledge, this work reports the first quantitative combination of experimental measurements and numerical simulations of the deformation of single cells in response to shock waves. The experimental results showed that the dominant response of the cells was during the tensile phase of the shock waves with a tensile strain of ∼10% for a peak tensile pressure around −8 MPa. A bilinear bulk modulus with tensile transition stress was used to capture the observed asymmetry between compression and tension. The experiments and simulations suggest that cell damage or sonoporation effects occur during the tensile phase even though the pressure magnitude is greater during compression. The numerical model was then used to identify shock-wave profiles that can differentiate the tensile responses between cancer cells and noncancerous cells to achieve cancer-cell-specific therapy: sonoporation and cell damage.

Editor: Philip LeDuc.