Gaussian Curvature Directs Stress Fiber Orientation and Cell Migration

Abstract

We show that substrates with nonzero Gaussian curvature influence the organization of stress fibers and direct the migration of cells. To study the role of Gaussian curvature, we developed a sphere-with-skirt surface in which a positive Gaussian curvature spherical cap is seamlessly surrounded by a negative Gaussian curvature draping skirt, both with principal radii similar to cell-length scales. We find significant reconfiguration of two subpopulations of stress fibers when fibroblasts are exposed to these curvatures. Apical stress fibers in cells on skirts align in the radial direction and avoid bending by forming chords across the concave gap, whereas basal stress fibers bend along the convex direction. Cell migration is also strongly influenced by the Gaussian curvature. Real-time imaging shows that cells migrating on skirts repolarize to establish a leading edge in the azimuthal direction. Thereafter, they migrate in that direction. This behavior is notably different from migration on planar surfaces, in which cells typically migrate in the same direction as the apical stress fiber orientation. Thus, this platform reveals that nonzero Gaussian curvature not only affects the positioning of cells and alignment of stress fiber subpopulations but also directs migration in a manner fundamentally distinct from that of migration on planar surfaces.

Introduction

Proper organization of the actin cytoskeleton is crucial for a wide range of important cell behaviors, including division (1), migration (2), and endocytosis (3). In addition to being affected by soluble chemical signals, actin organization is influenced by the physical characteristics of a cell’s surroundings. For example, high substrate stiffness induces the formation of thick actin bundles called stress fibers (SFs) (4) and cell spreading (5).

On rigid planar surfaces, fibroblast-like cells tend to migrate in the direction in which their primary contractile SFs are oriented (6). The contraction of these SFs, which contain nonmuscle myosin II, contributes to forward locomotion of the cell body and retraction of the trailing edge (7, 8, 9). These SFs are present at the basal surface of the cell (often called “ventral SFs”) (10, 11, 12) and above the nucleus (called apical or “perinuclear actin cap fibers”) (6, 13).

Although planar surfaces have historically been used to study cell cytoskeletal organization and motility, physiological environments have more complex geometries. It is well known that geometric cues on subcellular length scales can pattern the arrangement of the actin cytoskeleton. For example, nano- (14, 15) and micropatterned (13, 16) adhesive ligands guide the alignment of SFs. We and others have found that geometric cues on the order of a cell-length scale can also guide SF organization. For example, on cylindrical substrates, SF subpopulations align along the principal directions of the surface (17, 18, 19, 20). One population of SFs on top of the nucleus aligns in the axial direction, whereas a subpopulation of SFs below the nucleus aligns in the circumferential direction. These SF subpopulations, termed apical and basal SFs, respectively, align in these preferred directions in a manner that depends on the curvature magnitude.

Although the cylinder is a common geometry in the body that appears in the form of vessels and ducts, surfaces with more complex curvature fields are also present. A saddle-like region exists in which one blood vessel branches from another, for example. Many types of glands, including sebaceous and sweat glands, are capped by epithelial surfaces that resemble a sphere. These surfaces have distinct Gaussian curvatures; a cylinder has zero Gaussian curvature, a saddle’s is negative, and a spherical cap has positive Gaussian curvature. In vivo, the radii of curvature of these surfaces vary from tens of microns (e.g., arterioles (21) and ducts of eccrine sweat glands (22)) to hundreds of microns and millimeters (e.g., arteries (21) and intestinal villi (23)). Despite their widespread appearance in biology, the effect of these geometries on cell behavior is largely unknown.

We used fibroblasts as a model cell type to understand how such nonzero Gaussian curvature fields influence SF organization and migration. We cultured cells on a radially symmetric surface developed for this study that we call a sphere-with-skirt (SWS) surface. This surface seamlessly connects a spherical cap of positive Gaussian curvature to a saddle-like skirt of negative Gaussian curvature. The radii of curvature of the SWS surface (roughly 80–500 μm) are on the order of a cell-length scale (roughly 60–150 μm). Use of this platform reveals significant effects of geometry on cell positioning, SF alignment, and cell migration and shows that cell behavior on physiologically relevant Gaussian-curved surfaces is fundamentally distinct from that seen on more commonly studied planar substrates.

Materials and Methods

Preparation of SWS substrates

Master arrays of SWS substrates were prepared by first-spin coating a thin film of liquid polydimethylsiloxane (PDMS) (Dow Corning, Midland, MI) onto a solid slab of PDMS (Fig. S1). All PDMS was prepared with a 1:10 ratio of cross-linker to elastomer base. Then, spheres made of PDMS (∼170 μm in diameter for small SWSs) or glass (∼450 μm in diameter for large SWSs) were placed in the film in a regular array. The PDMS spheres were made using a microfluidic device (24), and the glass spheres were obtained from Polysciences (Warrington, PA). The liquid PDMS rose via capillarity around the bases of the spheres to form the skirts. The substrate was then cured on a hot plate.

Once cured, the surface was plasma etched, and trichloro(1H,1H,2H,2H-tridecafluoro-n-octyl) silane (Tokyo Chemical Industry, Portland, OR) was vapor deposited on the surface. Liquid PDMS was poured around the silanized master array and baked on a hot plate. Once solidified, the freshly poured PDMS was separated from the master array to yield an array of SWS holes. This array of holes was then silanized, and SWS substrates were cast from the silanized hole array. To ensure that the surface of the SWS substrate was smooth, a thin film of liquid PDMS was spin coated onto the surface. The substrate was then baked overnight at 65°C.

Surface characterization

The SWS surfaces were visualized using a Quanta 600 field emission gun environmental scanning electron microscope (Singh Center for Nanotechnology, University of Pennsylvania, Philadelphia, PA). The PDMS surfaces were sputtered with either chromium or gold/palladium to reduce charging. Surface roughness was characterized using a KLA Tencor P7 profilometer (Quattrone Nanofabrication Facility at the Singh Center for Nanotechnology, University of Pennsylvania) with a scan rate of 50 μm/s.

Cell culture

Spontaneously immortalized mouse embryonic fibroblasts (MEFs) were cultured in Dulbecco’s modified eagle medium containing 10% by volume fetal bovine serum, 2 mM L-glutamine, 2.5 μM HEPES, and 50 μg/mL gentamicin. Primary MEFs were isolated from Lifeact-GFP mice (25) in collaboration with the Burkhardt Laboratory at the Children’s Hospital of Philadelphia and were cultured in the same medium. These cells were maintained at 37°C and 10% CO₂. Human aortic vascular smooth muscle cells were cultured as described previously (17). Cells were fixed in 4% paraformaldehyde, permeabilized in 0.05% by volume Triton X-100, and stained with phalloidin:tetramethylrhodamine isothiocyanate (ECM Biosciences, Versailles, KY).

To prepare the surface for cell culture, it was functionalized with the extracellular matrix protein fibronectin (FN). The PDMS substrate was placed in a 35 mm dish and treated with ultraviolet ozone before a sessile drop of ∼50 μg/mL bovine plasma FN was added to the surface. The FN solution contained three parts of unlabeled bovine plasma FN (EMD, Burlington, MA) and one part of bovine plasma FN that had been labeled with either Alexa Fluor 488 or Alexa Fluor 647 succinimidyl ester (Thermo Fisher Scientific, Waltham, MA), according to the manufacturer’s protocol. The substrate was incubated at 37°C and 10% CO₂ for 30 min. Then, the surface was rinsed with phosphate-buffered saline and cell culture medium before the suspended cells were seeded in a sessile drop. The cells and substrate were incubated at 37°C and 10% CO₂ for 30 min, and then 4 mL of medium was added to the dish to submerge the substrate. Immortalized MEFs were cultured overnight before being fixed. Lifeact-GFP MEFs were cultured for ∼10 h before imaging.

Imaging

Fixed MEFs and their FN-labeled surfaces were imaged using a 25× magnification/0.95 NA water immersion objective on a Leica TCS-SP5 laser scanning confocal microscope (Bioengineering Microscopy Core, University of Pennsylvania, Philadelphia, PA). Live imaging of Lifeact-GFP MEFs was performed on a Leica SP8 laser scanning confocal microscope (Cell and Developmental Biology Microscopy Core, University of Pennsylvania, Philadelphia, PA). A 10× magnification/0.4 NA air objective and an incubation stage were used to image for ∼12 h per experiment. Images were collected every ∼13 min.

Image analysis

To analyze SF orientation, the image stacks of phalloidin and FN signals from confocal scans were rotated so that the viewing direction was normal to the surface at the center of the cell (Fig. S2). A series of custom ImageJ macros and MATLAB (The MathWorks, Natwick, MA) scripts were used to reslice the FN channel along a radius through the center of the cell, fit a parabola to the surface profile, and rotate the FN and phalloidin stacks to achieve the normal view. In the rotated stack, radially oriented SFs point in the vertical direction, and azimuthally oriented SFs point in the horizontal direction. Once the phalloidin stack was rotated, lines were drawn in Fiji (ImageJ; National Institutes of Health, Bethesda, MD) over each apical and basal SF. The maximal intensity projection of the rotated phalloidin stack was used as an initial guide for SF characterization. However, final characterization was performed by scanning through the rotated phalloidin stack slice-by-slice and following individual SFs.

Once the SF lines were drawn, a custom ImageJ macro performed a radial reslice of the FN channel about each SF. Additional details are available in Fig. S3. Briefly, a 50-μm-long line was drawn that shared the same center position and orientation angle as that of an SF of interest. Then, the rotated FN channel was sliced along this line to obtain the surface profile directly beneath the SF. The brightness and contrast of the profile image were enhanced using Fiji’s automatic brightness and contrast function, which alters the histogram of gray values so that a small fraction (typically <1%) of pixels become saturated. Then, Fiji’s despeckle function was used to reduce noise. A threshold was then applied. Inclusion of the brightest ∼1% of pixels yielded points at the center of the FN signal and minimized noise that distorted curve fitting. A parabola of the form h = a₁x² + a₂x + a₃ was fit to the remaining points in MATLAB, and the curvature of the contour was calculated at the center point. Subsequently, the reslice line was rotated about its center by a total of 170° in 10° increments in the clockwise direction, and the reslicing of the FN channel was performed for each rotation. The principal curvatures of the surface at the point directly beneath the center of the SF are equal to the maximal (i.e., largest positive), c_max, and minimal (i.e., largest negative), c_min, curvatures calculated from the radial reslicing procedure. The deviatoric curvature of the surface, δc, is defined as the difference between these two curvatures; i.e., δc = c_max − c_min.

The Automated Detection and Analysis of ProTrusions (ADAPT) plugin for Fiji was used to capture cell trajectories and measure the boundaries of migrating Lifeact-GFP MEFs (26). Maximal projections of the phalloidin stacks were generated, and their brightness and contrast were adjusted. Then, the ADAPT plugin was used to outline the cells at each time point. The cell centers of mass, boundary positions, and edge velocities were measured by ADAPT and postprocessed in custom MATLAB scripts. The topographical maps were generated by a custom ImageJ macro that used ImageJ’s fit circle function to fit a circle to FN slices at regular intervals and then plotted the circles on maximal projections of the phalloidin stacks. All three-dimensional models were created in Blender (Blender Foundation, Amsterdam, the Netherlands).

Results

SF subpopulations align along principal directions on a negative Gaussian curvature surface

To study how SF organization is affected by nonzero Gaussian curvature, we designed and fabricated a surface that we call an SWS (Fig. 1 A). An initial master array of features was created by spin coating a thin layer of PDMS onto a solid PDMS slab, placing PDMS spheres into the film, and baking the substrate to capture the “skirt” that forms as a result of capillary rise around the spheres. This master array was used to make negative molds from which the substrates were cast (Fig. S1). The SWS has a unique curvature field that is useful for studying the effects of nonzero Gaussian curvature on cell behaviors. Each unit possesses a spherical cap that has positive Gaussian curvature that smoothly transitions to a negative Gaussian curvature skirt. Additionally, the magnitude of the skirt’s Gaussian curvature decreases with distance from the feature’s symmetry axis, making this a useful platform for studying the effects of not only the sign but also the magnitude of Gaussian curvature.

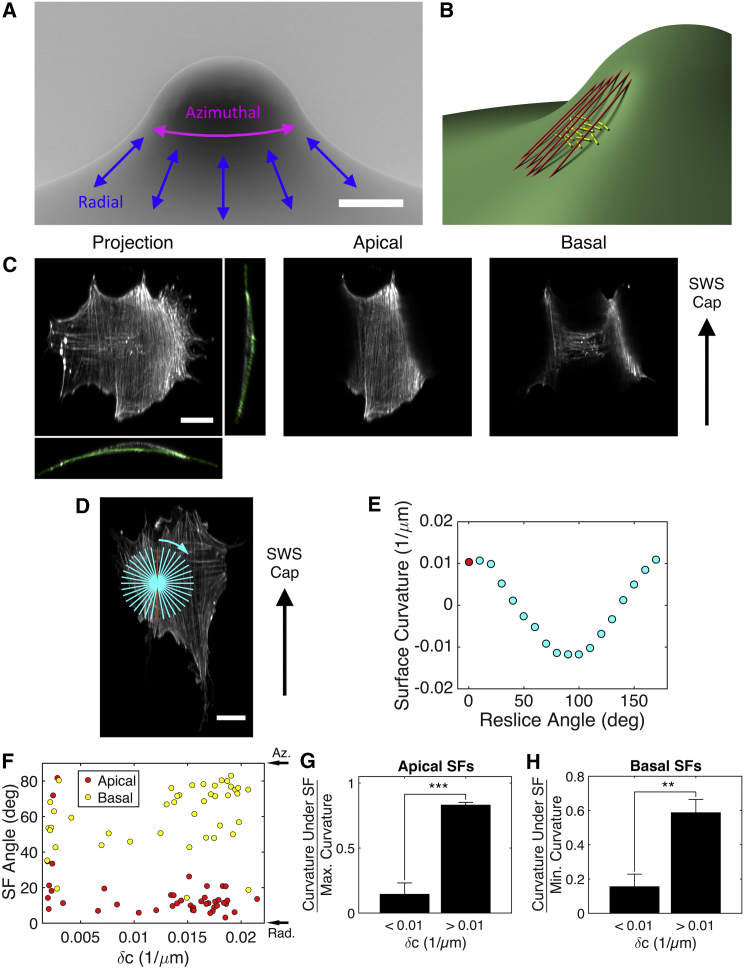
Figure 1.

SF subpopulations align along principal curvature directions on a surface with negative Gaussian curvature. (A) A scanning electron micrograph of SWS surface is shown. Scale bar, 50 μm. (B) This diagram shows the alignment of apical (red) and basal (yellow) SFs on an SWS skirt. (C) A representative MEF is shown on an SWS skirt. Orthogonal sections reveal chords formed by apical SFs. The apical SF image is a projection of 16 slices. The basal SF image is a single slice. Gray coloring represents phalloidin, and green coloring represents FNs. Scale bar, 20 μm. (D) A projection of phalloidin staining of another MEF on a different SWS skirt is shown. The red line is a 50-μm-long reslice line oriented along and centered at an apical SF. Cyan lines are radial reslice lines. Scale bar, 20 μm. (E) The curvature of the surface based on FN signals beneath the cell in (D) is shown. Red and cyan dots correspond to the radial reslice lines in (D). (F) SF subpopulation orientation angles are shown as a function of δc. The values are the average for each cell. (G) The average curvature under apical SFs divided by the average maximal curvature for radially resliced apical SFs is shown. (H) The average curvature under basal SFs divided by the average minimal curvature for radially resliced basal SFs is shown. 13 cells are shown on small δc surfaces, and 31 cells are shown on large δc surfaces. The results in (G) and (H) are the mean and SE, ^∗∗p ≤ 0.01, ^∗∗∗p ≤ 0.001 (Student’s t-test). Az., azimuthal; deg, degree; Max., maximal; Min., minimal; Rad., radial. To see this figure in color, go online.

Once an array of SWSs was fabricated, the surface was functionalized with fluorophore-conjugated FN, and MEFs were seeded on the surface. Then, a laser scanning confocal microscope was used to image the F-actin cytoskeletons of cells on the features. To examine SF orientation, the cells were stained with phalloidin:tetramethylrhodamine isothiocyanate, a fluorescent marker of polymerized actin. The phalloidin and FN channels were rotated so that the viewing plane was tangent to the surface at the center of the cell; once so oriented, the scans were resliced (Fig. S2). This analytical approach provided a representation of the SFs that facilitates analysis because in this rotated view, many of the SFs lay in the slicing planes.

A scan through the rotated phalloidin stacks revealed two distinct subpopulations of SFs, each aligned in distinct directions in cells on the highly curved regions of the skirts (Fig. 1, B and C; Movie S1). The apical SFs, primarily located above the nucleus, aligned in the radial direction. A separate population of basal SFs located beneath the nucleus aligned largely in the azimuthal direction. Although some of the basal SFs were visible in a maximal projection of the rotated phalloidin stack, many were hidden beneath the bright apical SFs and were only revealed by carefully scanning through the stack. A similar pattern of SF alignment was seen in vascular smooth muscle cells (Fig. S4). We previously observed a similar SF subpopulation orientation pattern in cells on surfaces with zero Gaussian curvature; when cultured on cylinders, MEFs and human vascular smooth muscle cells had apical SFs aligned in the axial direction and basal SFs aligned in the circumferential direction (17).

We next probed how these alignment patterns depend on curvature magnitude. On the simple cylindrical surface, the SF subpopulations became more strongly aligned in their preferred directions as the magnitude of the nonzero principal curvature increased. Unlike the cylinder, however, the SWS surface has two nonzero principal curvatures at every point. To measure these principal curvatures, a radial reslicing algorithm was employed (see Figs. 1 D, S2, and S3; Materials and Methods) that revealed contours of the surface in slices beneath the SFs at various angles. This method allows for direct measurement of the local curvature field around each SF (Fig. 1 E).

We used the surface curvature values calculated from the radial reslicing to calculate the difference in principal curvatures for each SF. This difference, also known as the deviatoric curvature (δc), is a convenient metric of the “curvature challenge” experienced by each cell. A cell on a saddle-like region of the SWS with large δc was challenged by large curvatures pointing in different directions. For each cell, the average orientation angles of the apical and basal SFs as well as the mean δc were calculated (Fig. 1 F). On regions of the surface with small δc (i.e., more planar regions), basal and apical SFs had no preferential orientation. On portions of the surface with δc > ∼0.01 μm⁻¹, apical SFs aligned strongly in the radial direction. Basal SFs aligned preferentially in the azimuthal direction but with a slightly broader distribution of angles than that of the apical SFs.

To quantify the extent to which SF subpopulations aligned along principal directions of the surface, the curvatures of surface contours directly beneath the SFs were divided by the principal curvatures. By this normalization, SFs aligned along principal directions have a ratio equal to unity. For example, the curvature of the surface directly beneath an apical SF aligned perfectly in the radial direction would be equal to the maximal (i.e., largest positive) principal curvature. Normalizing this curvature by the maximal principal curvature yields unity. Any apical SFs that deviate from perfect radial alignment have normalized curvatures less than unity. The apical SF data are reported in Fig. 1 G. Surface curvatures beneath basal SFs were normalized by the minimal (i.e., largest negative) principal curvature to show how strongly those SFs aligned along that convex principal curvature (Fig. 1 H). We find that SFs aligned strongly in cells that experienced large δc > 0.01 μm⁻¹. Therefore, cells were divided into two groups: those that experienced large and small (i.e., <0.01 μm⁻¹) δc. Apical SFs in cells challenged by large δc aligned preferentially along the concave principal curvature (Fig. 1 G). Basal SFs in cells challenged by large δc aligned along the convex principal curvature (Fig. 1 H). However, for the latter case, the ratio of contour curvatures was ∼0.6. Thus, basal SF alignment was less pronounced than that of apical SFs.

On cylinders, the alignment of apical SFs has been attributed to their resistance to bending; when oriented in the axial direction, these long SFs can remain nearly straight and avoid the energetic penalty associated with bending (17, 19, 20, 27). Although the long, apical SFs on the SWS align along the direction of maximal curvature, they also remain unbent. Instead of following the surface curvature closely, these SFs lift away from the surface and form chords over the concave portion of the surface (see Fig. 1 B and cross sections in Fig. 1 C). Thus, much like on cylindrical surfaces, apical SFs in cells on a surface with negative Gaussian curvature align in a manner that minimizes their bending. Basal SFs, on the other hand, preferentially align in the direction in which they are most bent on the SWS surface. This is similar to the basal SF alignment pattern on cylinders in which this subpopulation aligns along the circumference of the cylinder (17).

Cells avoid spherical caps unless the curvature is weak

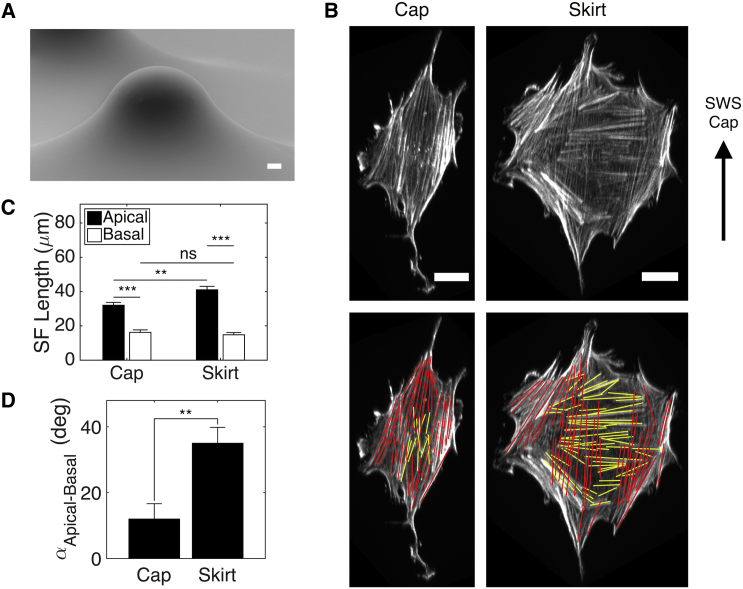
Isolated MEFs were never observed on the positive Gaussian curvature cap of the SWS. We reasoned that the absence of cells on the SWS cap may be a result of the SF-bending argument described above. On the positive Gaussian curvature surface, there is no configuration in which the long, apical SFs could avoid bending. Thus, cells are unable to migrate onto the spherical cap because they are unable to form and maintain this SF subpopulation. Consistent with this hypothesis, we found that MEFs were able to attach and spread on the spherical cap of a larger SWS surface with similar overall geometry but smaller principal curvatures (Fig. 2, A and B). The apical SFs in these cells were ∼22% shorter than those in cells on the skirts of this surface (Fig. 2 C), a finding that also supports the resistance-to-bending argument because the total energetic penalty for SF-bending scales with the length of the SF. On the positive Gaussian curvature surface, the SFs, forced to bend, may reduce the energetic cost associated with bending by limiting their length.

Figure 2.

Negative Gaussian curvature drives SF subpopulations to align in different directions. (A) A scanning electron micrograph of a large SWS surface is shown. Scale bar, 50 μm. (B) Projections of phalloidin signals (gray) in cells on a spherical cap and skirt are shown. Red and yellow lines indicate apical and basal SFs, respectively. Scale bars, 20 μm. (C) SF subpopulation lengths on caps and skirts are shown. (D) The angle between average SF subpopulation orientation angles in cells on caps and skirts is shown. n_cap = 11 cells; n_skirt = 15 cells. The results are the mean and SE, ^∗∗p ≤ 0.01, ^∗∗∗p ≤ 0.001 (Student’s t-test). deg, degree; ns, nonsignificant. To see this figure in color, go online.

SF alignment on caps differs from that on skirts. Despite the smaller curvature magnitudes relative to the small SWS, the apical and basal SF subpopulations in cells on the skirt still aligned in distinct directions. However, cells on the spherical cap of the large SWS had a significantly smaller average angle separating the two SF subpopulations (Fig. 2 D). Thus, in addition to curvature magnitude, the sign of the Gaussian curvature influences the relative orientation of SF subpopulations.

Negative Gaussian curvature establishes cell polarity and directs migration

Cell motility is intimately connected to actin dynamics, and the direction of cell motion has been linked to the orientation of apical SFs on planar surfaces (6, 28, 29). To understand how curvature influences cell motility, we used real-time imaging to study cell migration on SWSs. Primary MEFs expressing Lifeact-GFP, a fluorescent F-actin-binding protein, were cultured on small SWSs and imaged for ∼12 h with a laser scanning confocal microscope (Fig. 3 A; Movie S2).

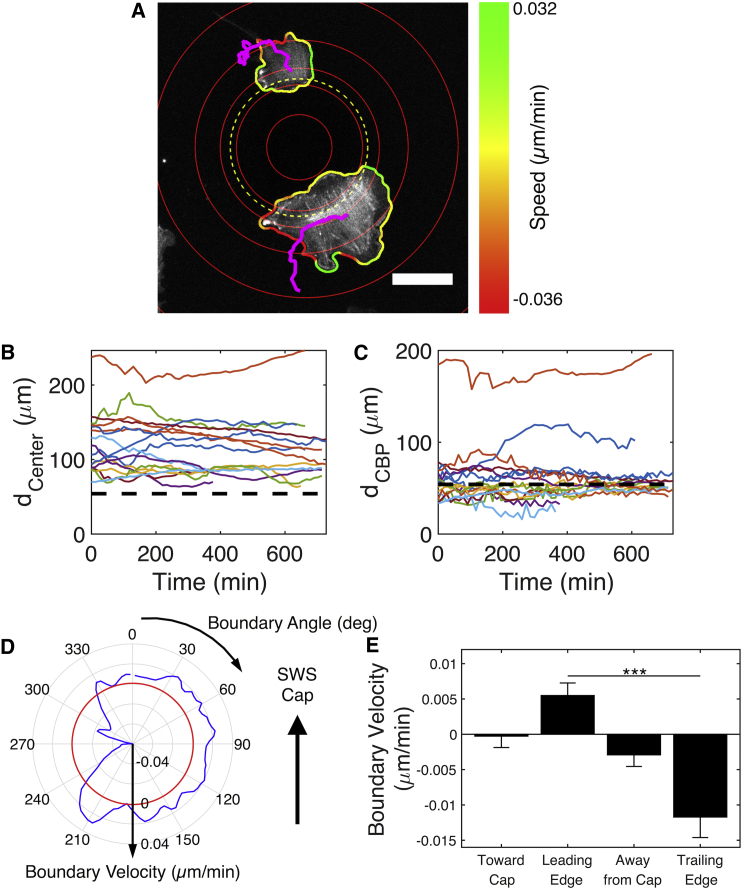
Figure 3.

Negative Gaussian curvature guides cell polarization and migration. (A) A projection of Lifeact-GFP signals of two cells on an SWS skirt is shown. Red concentric circles indicate rings of common height separated by 18 μm in height. The yellow dashed ring indicates the approximate location of the line of inflection. Magenta lines indicate trajectories of centers of mass. Cell outline colors indicate boundary velocities. Scale bar, 50 μm. (B) The radial distance of cell centers from the SWS symmetry axis is shown. The dashed line indicates the position of the line of inflection. (C) The radial distance of the boundary position closest to the SWS symmetry axis is shown. CBP, closest boundary point. The dashed line indicates the position of the line of inflection. n = 16 cells from three experiments. (D) The boundary velocity averaged over all time points for the bottom cell in (A) is shown. The red circle indicates zero velocity. (E) The average boundary velocities in different directions are shown. Boundaries toward cap include angles from 315 to 45°, leading edge from 45 to 135°, away from cap from 135 to 225°, and trailing edge from 225 to 315°. n = 13 cells from three experiments. The results are the mean and SE, ^∗∗∗p ≤ 0.001 (Student’s t-test). deg, degree. To see this figure in color, go online.

Trajectories based on the cell’s centers of mass were found using the ADAPT plugin for Fiji (26). The positions of cell centers, converted to polar coordinates with the symmetry axis of the feature as the origin, are shown as a function of time (d_Center, Fig. 3 B). Cells near the skirts of SWSs remained in these regions and migrated around the feature in the azimuthal direction. The large distribution in radial positions at any time point is due to the large range of cell sizes (∼1200 μm² < projected area < 28,000 μm²; see Fig. S5). Additionally, none of the cells migrated onto the spherical cap. The cells did extend lamellipodia onto the cap, but the apical SFs terminated near the line of inflection (i.e., the line where the spherical cap transitions to the skirt) (Movie S2). We posit that the cells are using these lamellipodia to probe their environment and find that they are unable to form adhesions to support the SFs that would allow radial migration onto the cap. Additionally, these live imaging results further support the idea that the magnitude of the curvature of the spherical cap on the small SWS is too large to support SF formation and acts as a barrier to migration. We found no evidence of topographical features, change in roughness, or gradient in FN concentration near the line of inflection that might have caused these observed behaviors (Fig. S6). We do not believe there are gradients in substrate stiffness along the SWS surface because it is made of a single piece of PDMS. Additionally, the PDMS composition used in these experiments is very stiff (∼3 MPa (30)) compared to the ranges of stiffness in which durotaxis is typically observed (∼10³–10⁴ Pa) (31, 32).

In addition to providing information about the centers of mass, the ADAPT analysis also identified the cell boundaries at each time point. Plotting the position of the cell boundary closest to the SWS symmetry axis, d_{closest boundary point}, at each time point revealed that the cells protruded past the line of inflection with short-lived lamellipodia, but no protrusion reached onto the top of the spherical cap (Fig. 3 C).

We next examined the velocities of cell boundaries captured by the ADAPT analysis and found that cells on skirts establish leading and trailing edges that polarize the cell in the azimuthal direction. The ADAPT analysis calculated the instantaneous velocity of the cell boundaries at each time point and generated a visualization showing regions of the cell that were protruding (i.e., have a positive velocity; green) or retracting (i.e., have a negative velocity; red) (Fig. 3 A). By taking the average velocity at each boundary point, we observed that cells on skirts established one protruding edge that was opposite a retracting edge. An example average boundary velocity plot is shown in Fig. 3 D for the bottom cell in Fig. 3 A. This plot is centered on the cell; horizontal displacements of the contour indicate azimuthal motion, and upward displacements indicate motion toward the spherical cap. This cell is polarized in the counterclockwise azimuthal direction with a leading edge on the right side of the plot and a retracting edge on the left side. On average, cell boundaries protruded little in the directions toward or away from the cap (Fig. 3 E). The cells established a leading edge in an azimuthal direction with a positive boundary velocity of ∼0.007 μm/min that was on the opposite side of the retracting edge that had an average boundary velocity of approximately −0.01 μm/min. Thus, the negative Gaussian curvature skirt of the small SWS enforces a cell polarity that establishes a robust azimuthal migration pattern.

Directional migration deviates from apical SF orientation on a negative Gaussian curvature surface

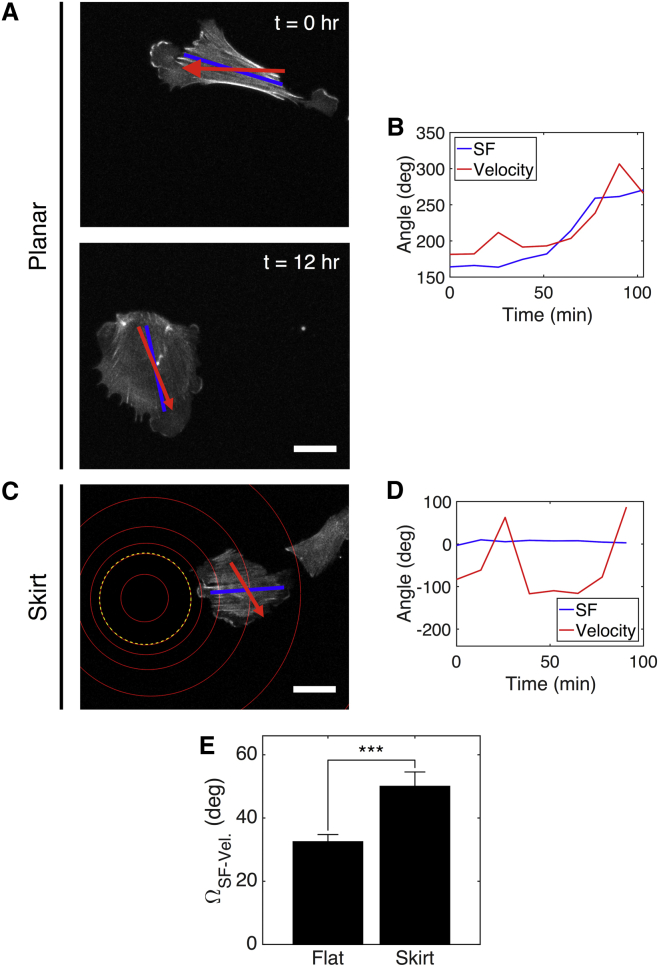
Previous work on planar surfaces indicates that the direction of cell migration coincides with the orientation direction of apical SFs (6, 28, 29). The primary lamellipodium explores the environment immediately ahead of the cell, and the SFs provide the force necessary for forward locomotion. We indeed found that Lifeact-GFP MEFs tended to migrate in this way on the nearly flat regions between SWS features. Fig. 4 A and Movie S3 show a representative cell migrating on a near-planar region of the SWS substrate. The cell initially has its primary lamellipodium and apical SFs pointed toward the left of the field of view. At that moment, the cell is migrating in nearly the same direction. Approximately 12 h later, this cell has turned more than 90° in the counterclockwise direction. Its SFs and migration vector are pointed in the downward direction. Over the entire time period in which the cell was imaged and throughout the turning process, the SF orientation and migration vectors pointed in nearly the same direction (Fig. 4 B).

Figure 4.

Negative Gaussian curvature alters migration direction relative to SF orientation. (A) A projected Lifeact-GFP signal of a representative cell on a planar region of an SWS substrate is shown. At t = 0 h, the cell’s SFs are oriented in the horizontal direction (blue), and it migrates to the left (red). At t = 12 h, the same cell’s SFs are oriented in the vertical direction, and it migrates downward. (B) The SF and velocity angles for the cell shown in (A) are displayed. (C) A cell on an SWS skirt has SFs oriented in the horizontal direction (blue), but it migrates down and to the right (red). Red concentric circles indicate rings of common height separated by 18 μm in height. The yellow dashed circle indicates the approximate location of the line of inflection. (D) The SF and velocity angles for the cell shown in (C) are displayed. (E) The angle between SF and velocity vectors for cells on flat regions versus skirts is shown. n_flat = 19 cells from two experiments; n_skirt = 14 cells from three experiments. Scale bars, 50 μm. The results are the mean and SE, ^∗∗∗p ≤ 0.001 (Student’s t-test). deg, degree; hr, hour; Vel., velocity. To see this figure in color, go online.

In contrast, the migration direction of cells on skirts differs from the orientation direction of their apical SFs. Fig. 4 C shows a representative cell on a skirt that has SFs oriented in the radial direction but migrates in the azimuthal direction. For the duration of observation, the angle between these two directions, Ω_SF-Velocity., was ∼50° (Fig. 4 D); this value is significantly greater for cells on skirts than for cells on the nearly planar surfaces (Fig. 4 E). Thus, negative Gaussian curvature alters the relationship between apical SF orientation and migration direction.

Discussion

An SWS platform reveals effects of Gaussian curvature on SF alignment

Using a microfabricated substrate we call an SWS, we show that macroscale curvature fields with nonzero Gaussian curvature template the organization of SF subpopulations. The negative Gaussian curvature skirt portion of the SWS drives radial alignment of apical SFs and azimuthal alignment of basal SFs. These directions correspond to the maximal and minimal principal curvature directions, respectively. This effect is dependent on the magnitude of the principal curvatures; no preferential alignment occurs when the curvature field is weak. This subpopulation alignment pattern is reminiscent of the pattern observed when cells are cultured on cylindrical substrates. When cells are cultured on cylinders with sufficiently large curvature, the two SF subpopulations align along the principal directions of the surface: the apical SFs align along the axial direction, and the basal SFs align along the circumferential direction.

It has been suggested that the apical SFs align along the axial direction on cylinders with small radii to minimize their bending; that is, bending of these long, thick fibers is thought to be energetically costly, so they align along the direction in which they are least bent (19, 20, 27). On the cylindrical surface, the apical SFs align along this principal direction presumably because the curvature in this direction is zero. We were therefore surprised to find that long apical SFs also align along one of the principal directions (the radial direction) on the skirt of the SWS; unlike on the cylinder, the principal curvature in this direction is large. We suspect that these SFs align this way because they can form straight chords across the concave gap (Fig. 1, B and C). That is, instead of lying tangent to the surface at all points, these SFs form straight bridges from focal adhesions at one end to the nucleus or to focal adhesions at the other end. By separating themselves from the surface, the apical SFs can remain largely unbent.

At each point on the skirt, there are two directions tangent to the surface along which the curvature is zero locally (Fig. 1 E). If the apical SFs orient to remain as straight as possible, why do they form radial chords instead of aligning along these zero curvature directions? The contours of zero curvature on the surface are not straight lines over lengths comparable to the SFs in Euclidean three-dimensional space. Thus, the radial chord pattern may be preferred because the apical SFs can remain straight and span the length of the cell.

Although substrate curvature plays a role in establishing distinct SF subpopulation orientation, it is not sufficient to explain the alignment patterns. A separate requirement appears to precede the minimization of apical SF bending: these SFs must sit on top of the nucleus. On planar surfaces and cylinders, a subpopulation of SFs resides above the nucleus and is slightly bent; these SFs compress the nucleus and are slightly arced because of the presence of the short nucleus underneath (13). If long SFs were preferentially aligned to remain as straight as possible, they would sit beneath the nucleus, directly tangent to planar surfaces and aligned in the axial direction directly on the surface of cylinders. Minimization of bending may drive the alignment of apical SFs, but only after the requirement for localization above the nucleus is met. By escaping the surface on SWS skirts, apical SFs may relieve compression of the nucleus that is observed on planar surfaces (13). Thus, substrate curvature may alter nuclear shape and size, which are events that are thought to influence gene expression and are disturbed in various types of cancers (33, 34, 35, 36, 37, 38, 39). The linker of nucleoskeleton and cytoskeleton (LINC) complex connects SFs to the nucleus; future analysis of components from the LINC complex on the SWS might provide new insight into the role of nuclear contact in curvature alignment of SFs.

MEFs do not migrate onto the spherical cap portion of the SWS surface that has large, positive Gaussian curvature. This observation of cell-scale curvature repulsion complements observations in the literature of geometric responses at other scales. For example, nanoscale features can repel migrating cells by limiting the formation of mature focal adhesions (40, 41). On the cell-scale SWS, we hypothesize that the SFs may inhibit migration onto the spherical cap via the bending argument presented above: there is no direction in which the apical SFs could be oriented to avoid bending significantly, so the cells do not spread or migrate onto this region of the substrate. Live-imaging experiments showed that cells extend lamellipodia onto the cap but do not form SFs there. MEFs were able to spread on the positive Gaussian curvature cap of a large SWS substrate, suggesting that there is a threshold curvature magnitude at which cells can form and maintain long SFs. On the large SWS substrate, the sign of the Gaussian curvature guided the relative alignment of SF subpopulations. Apical and basal SFs in cells on skirts aligned in distinct directions from each other, whereas the subpopulations aligned nearly in the same direction in cells on the caps. Future work will explore the dependence of SF subpopulation alignment on the magnitudes of the principal curvatures of a positive Gaussian curvature surface. By culturing cells on an ellipsoidal cap, we can understand if positive Gaussian curvature guides SF alignment in a manner similar to that observed on surfaces with negative Gaussian curvature. We suspect that the SF subpopulations will align along the principal directions; apical SFs might preferentially align along the smallest principal curvature, whereas basal SFs might align along the largest.

In addition to patterning SFs in a model MEF system, we found that skirts also oriented SF subpopulations in vascular smooth muscle cells. These cells are recruited to and interact with surfaces with pronounced negative Gaussian curvature in vivo, such as surfaces formed by endothelial cells in which one blood vessel branches from another (42). Endothelial cells also experience these curvature fields and may be influenced by macroscale geometric factors. This result suggests that nonzero Gaussian curvature may be an important cue for cell patterning in vivo.

Effects of Gaussian curvature on cell migration

Ventral SFs are implicated in cell migration. Ventral SFs contain myosin II, are pinned at both ends by focal adhesions, and are thought to be responsible for generating the traction forces necessary for translocation of the cell body and retraction of the trailing edge during cell migration (7, 8, 9, 10, 11, 12). Although ventral SFs are canonically thought to be near the rear and at the basal surface of the cell, recent work has suggested that both basal and apical SFs are subclasses of ventral SFs (28, 43).

On planar and near-planar surfaces, we and others find that apical SFs align in the direction in which the cell is migrating (Fig. 4 A; Movie S3; (6, 28, 29)). It has further been suggested that the large focal adhesions attached to the ends of apical SFs may establish and maintain cell polarity by stabilizing the primary lamellipodium (28, 29). Although apical SFs are oriented in the direction in which cells migrate while moving up skirts, cells on skirts eventually reestablish a primary lamellipodium in the azimuthal direction and migrate in the direction nearly perpendicular to the direction in which their apical SFs are oriented. Thus, the curvature of the skirt may cause the basal SFs to become the subclass of ventral SFs that establishes cell polarity and migration direction instead of the subclass of apical SFs. Perhaps the hindrance to migration imposed by the positive Gaussian curvature cap slows cell movement and allows time for the observed reorganization of SFs and primary lamellipodium. It is also possible that the radially-aligned apical SFs contribute to azimuthal movement of the nucleus as others have observed that the force of actin cables in the direction perpendicular to migration may be harnessed to propel the nucleus forward via transmembrane actin-associated nuclear lines (44). Thus, on a negative Gaussian curvature surface, basal SFs may drive translocation of the cell body, and apical SFs may serve to move the nucleus in the azimuthal direction. Closer examination of nuclear movement in live cells will reveal the relationship between SF subpopulations and translocation of the nucleus.

Conclusions

Nonzero Gaussian curvature is a prominent stimulus that patterns cytoskeletal organization and migration. Negative Gaussian curvature surfaces with length scales on the order of a cell length drive SFs to align along principal directions. Cells tend to avoid positive Gaussian surfaces unless the curvature is weak. The restructuring of SFs in cells in response to negative Gaussian curvature precedes repolarization and directs migration along the surface. These results emphasize the importance of studying cellular responses to nonplanar surfaces and reveal a critical role for curvature in directing actin organization and the directionality of migration.

Author Contributions

N.D.B., R.D.K., R.K.A., and K.J.S. designed the research, analyzed the data, and wrote the manuscript. N.D.B. performed the experiments. T.X. isolated the primary Lifeact-GFP MEFs.

Editor: David Odde.