Integrated Structural Biology for Alpha-Helical Membrane Protein Structure Determination

Abstract

While great progress has been made, only 10% of the nearly one thousand integral, α-helical, multi-span membrane protein families are represented by at least one experimentally determined structure in the protein data bank. Previously, we developed the algorithm BCL::MP-Fold, that samples the large conformational space of membrane proteins de novo by assembling predicted secondary structure elements guided by knowledge-based potentials. Here, we present a case study of rhodopsin fold determination by integrating sparse and/or low-resolution restraints from multiple experimental techniques including Electron Microscopy, Electron Paramagnetic Resonance spectroscopy, and Nuclear Magnetic Resonance spectroscopy. Simultaneous incorporation of orthogonal experimental restraints not only significantly improved the sampling accuracy, but also allowed identification of the correct fold, which is demonstrated by a protein size-normalized trans-membrane RMSD as low as 1.2Å. The protocol developed in this case study can be used for the determination of unknown membrane protein folds when limited experimental restraints are available.

eTOC blurb

Xia et al. developed a computational structure prediction pipeline to utilize multiple experimental restraints to fold membrane proteins in BCL and Rosetta. The pipeline described in the manuscript could determine structures to an accuracy of 1.2Å RMSD relative to the experimentally determined structural model.

Introduction

Integral membrane proteins remain a formidable challenge for structure determination methods

Alpha-helical integral membrane proteins (IMPs) are important players in many cellular functions; specifically, they orchestrate the communication between the cell and external stimuli by transferring signals and chemicals across the plasma membrane. Roughly 20–35% of a genome’s proteins are IMPs and yet only around 2–3% of the experimentally determined structures in the protein data bank (PDB) are IMPs (Bill et al., 2011). Around 80% of all protein structures currently deposited in the PDB (Berman et al., 2002) have been determined by X-ray crystallography. The particular challenge for IMP crystallization arises as crystals are inherently three-dimensional while IMPs naturally assemble into membranes that extend in two dimensions. It remains difficult to provide realistic membrane mimics in the context of a stable three-dimensional crystal, although impressive progress has been made using lipidic cubic phases (Sanders and Sonnichsen, 2006, Wiener, 2004, Loll, 2003, White, 2004, Landau and Rosenbusch, 1996). Even if MP structure determination through crystallization is feasible, biological relevance of the resulting models needs to be verified using orthogonal experimental techniques to exclude artifacts introduced by crystallization aides such as thermo-stabilizing mutations, helper proteins integrated into MP loop regions, or the non-native membrane mimic.

Experimentally determined structures of IMPs cover a small variety of folds

Interestingly, IMPs in the PDB cluster into only about 100 distinct IMP folds with more than one transmembrane helix (TMH). This number is small compared to the fold space of soluble proteins and small with respect to the number of IMP sequence families (read below). Multiple factors could contribute to this finding: the fold space of IMPs might be smaller than the fold space for soluble proteins as structure might be better conserved than sequence in IMPs with IMPs of very low sequence identity adopting the same fold (Grant et al., 2004). This seems to be the case for G-Protein Coupled Receptors (GPCRs) or in the LeuT transporter family. In addition, it is possible that once the experimental procedures have been refined to crystallize one particular class of IMPs, many members of the same fold family are experimentally studied rather than discovering new folds (Stevens et al., 2013), resulting in a non-representative fold representation in the PDB.

A vast sequence space for IMPs remains to be represented with experimentally determined structures

Oberai and colleagues have estimated that between 700 and 1700 families of IMPs would cover 90% of the IMP sequence space (Oberai et al., 2006). By the end of 2011, structural genomic efforts have increased structural coverage of IMPs to ~28%. It was estimated that without significant structural genomic investment it would take up to 25 years to achieve a structural coverage of 50% of IMPs (Khafizov et al., 2014). Accelerating fold determination for particularly important IMPs would therefore be of great relevance to biology. It is estimated that 3305 human membrane proteins exist in the Homo sapiens proteome (Uniprot), with 90% of the sequences mapping to one Pfam family. In particular, of all the Pfam-mapped human IMPs, only 10% (around 50) have an experimentally determined structural representative that is a human protein or a sequence related non-human protein (Kloppmann et al., 2012). It was calculated that with the best theoretical prediction, an additional 100 protein families need to be structurally characterized to cover the human α-helical IMP proteome to 58% of all sequences (Pieper et al., 2013).

Current experimental and computational methods to determine IMP structures suffer from limitations

The large theoretical fold space is contrasted by experimental datasets that – if available at all – are often limited by crystals that fail to defract to high resolution (X-ray crystallography), medium resolution of electron microscopy (EM) density maps, or the limited number of structural restraints from complementary experimental techniques such as nuclear magnetic resonance (NMR), site-directed spin labeling-electron paramagnetic resonance (SDSL-EPR) spectroscopy, or cross-linking coupled with mass spectrometry (XLMS). Those experimental datasets are limited in a sense that they provide insufficient information to determine a structure at atomic detail. Ideally, computational methods could be used to fill those information gaps (Lindert et al., 2012, Alexander et al., 2014, Barth et al., 2009). However, de novo prediction of an IMP’s fold from its primary sequence remains a challenging problem (Koehler Leman et al., 2015). The vast size of the theoretical fold space makes exhaustive sampling of an IMP’s potential conformations prohibitive. In addition, necessary simplification when approximating a conformation’s free energy frequently results in problems distinguishing accurate from inaccurate models.

BCL::MP-Fold and Rosetta predict membrane protein structural ensembles using experimental data

BCL::MP-Fold (Weiner et al., 2013) was developed for de novo protein structure prediction. We demonstrated in previous studies that BCL::Fold is able to efficiently sample the fold of large IMP (DiMaio et al., 2009). To achieve sufficient coverage of the fold space, the algorithm simplifies the sampling by assembling predicted secondary structure elements (SSEs) in a virtual membrane using a Monte Carlo Metropolis algorithm, while the loops connecting the SSEs are modeled implicitly (Karakas et al., 2012). After each Monte Carlo step, the free energy of the intermediate model is approximated using knowledge-based scoring functions that were specifically developed for IMPs (Weiner et al., 2013). Incorporation of limited experimental data can compensate for the simplified representation of IMPs during sampling and energy evaluation. Incorporation of individual experimental data has been established and benchmarked for EM (Lindert et al., 2012, Lindert et al., 2009), NMR (Weiner et al., 2014), EPR (Fischer et al., 2015), and XLMS (Hofmann et al., 2015). The BCL::MP-Fold algorithm outputs a simplified fold consisting of SSEs that exhibit only limited deviations from idealized dihedral angles. These models are then input for further optimization to atomic detail using the Rosetta modeling suite (Yarov-Yarovoy et al., 2006, Mandell et al., 2009, Leaver-Fay et al., 2011). Similar to BCL::MP-Fold, incorporation of individual experimental restraints into Rosetta been successful for EM (DiMaio et al., 2009), NMR (Bowers et al., 2000, Schmitz et al., 2012) and EPR (Alexander et al., 2008) data. The membrane environment was simulated implicitly during the structural refinement.

Considering the theoretical fold space for IMPs, we estimate that billions of folds are possible, a number increasing sharply with an increasing number of trans-membrane spans. The number of IMP sequence is large as well, though most IMP families have relatively few trans-membrane spans. We hypothesize that simultaneous integration of experimental data from multiple sources can allow for accurate prediction of IMP structures at atomic detail. Here we test this hypothesis by using BCL and Rosetta to incorporate a combination of EM, EPR, and NMR data to predict the fold of Rhodopsin. The proposed computation structure prediction pipeline is not limited to the prediction of new folds. BCL::MP-Fold and Rosetta were developed to allow simulations from a given starting structure and leverage sparse experimental data to derive a model for alternative states.

Result

The Result section is divided into subsections discussing the fold space and sequence space for IMPs, followed by the results of the Rhodopsin fold prediction experiment. Results from BCL::MP-Fold and Rosetta refinement are divided into subsections describing in detail the sampling accuracy, fold discrimination and the effects of combining hybrid experimental data on protein fold prediction.

Estimation of the fold space for α-helical IMPs from theoretical arrangements of TMHs

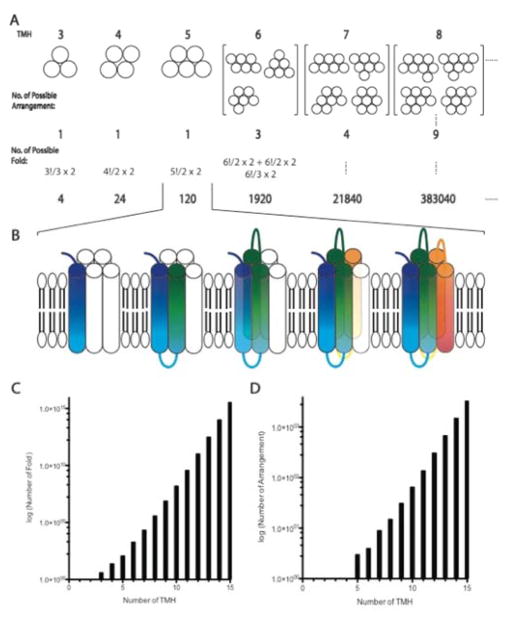
To estimate a lower boundary for the theoretical size of the IMP fold space we first simplify the problem by considering only helices that actually span the membrane. We further assume that these helices are perfectly parallel and arranged on a hexagonal grid to maximize packing density. Under these assumptions we can compute the number of TMH arrangements, which is the general relative placement of trans-membrane spans. From the number of arrangements, we can infer the number of folds, which are the distinct, compact units of protein structure that differ in specific topological order of trans-membrane spans including the order of the TMH insertion and extra-/intra-cellular location of the N-terminus. Thus, the number of unique folds for a theoretical protein with X number of TMHs will be the number of its possible arrangements with all possible helices insertion in a particular arrangement times two from whether its N-terminal being inside/outside divided by the symmetry operators under a particular arrangement (Figure 1A). An example of a Five-TMH protein’s fold defined by our criteria is demonstrated here (Figure 1B). For proteins with less than five TMHs, there is only one unique arrangement, but up to 120 unique folds. As one might expect, the number of TMH arrangements and folds increases exponentially with the number of trans-membrane spans (Figure 1C,D). For example, an IMP with nine TMHs can adopt about one million distinct folds. Consequently, exhaustive sampling of all possible folds is prohibitive for larger IMPs even if one considers that some folds might be forbidden because loops might be too short to connect trans-membrane spans distant in the fold. Next we will look at the sequence space for the number of IMP families that exist.

Figure 1. The theoretical fold space for IMP.

The theoretical fold space of α-helical MPs is computed through the arrangement of helices (A) and the topological insertion of TMHs (B). The theoretical fold (C) and arrangement (D) numbers scale with the number of TMHs. The computed hexagonal grid and the TMHs are represented as circles from a top view (A): systems with more than three TMHs start to have more than one arrangement. The non-redundant arrangement and fold is computed for each number of TMH. An example fold of a five TMH IMP is illustrated in the rainbow diagram (B). The number of folds (C) and TMH arrangements (D) computed for different numbers of TMHs is plotted on a logarithmic scale.

Sequence space for α-helical MPs

An analysis of protein sequence families documented by Pfam (pfam27.0) and crosschecked by Uniprot annotation (Figure 2A) revealed 895 IMP families consisting of α-helical TMHs. For 108 of these IMP families, at least one structure has been determined experimentally based on a cross check with the MPtopo database. Since the complexity of IMP folds grows exponentially with an increasing number of TMHs, we collected TMH statistics over the 895 families from sequence space. The family counts were plotted against the TMH number: more than 70% of the IMP families have less than 7 TMHs, few have more than 12 TMHs.

Figure 2. The sequence space for IMPs.

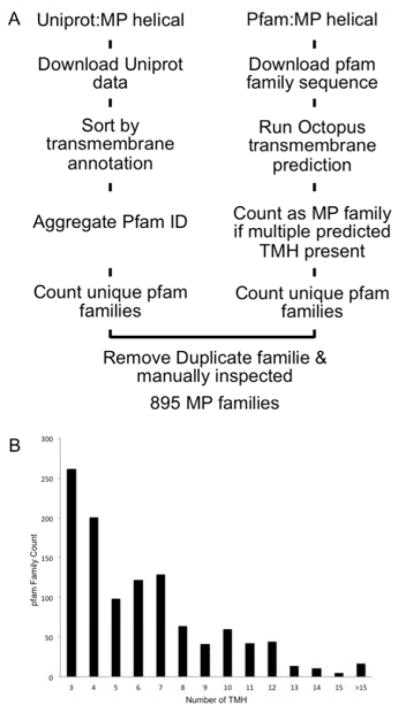
A survey of the protein sequence database was performed to map the unique membrane protein families separated by sequence homology (A). Taking statistics about the average TMH numbers of each IMP family and counting the occurrences of families with average TMH numbers, a histogram (B) of families with different number of TMHs was illustrated.

The IMP sequence space is large, though most of the IMP families fall in the lower complexity regions of the fold space, i.e. the simplified fold space is limited to 10⁵. Computational structure prediction methods such as BCL::MP-Fold are suitable for sampling such fold spaces, though distinguishing accurate from inaccurate folds would remain an obstacle for de novo methods without assistance from experimental data (Karakas et al., 2012).

BCL::MP-Fold assembly of TMHs using hybrid experimental data

BCL:MP-Fold was used to simultaneously incorporate experimental data from multiple sources like EM density maps, EPR distance restraints from DEER experiments, NOE distance restraints from NMR experiments, and chemical shift information during structure prediction. In the following subsections, we present our results for α-helical IMP fold prediction from hybrid experimental data for Rhodopsin.

In addition to pure de novo structure prediction, predictions were performed from limited experimental data using a single dataset (NMR, EPR, or EM), integrating two data sets (NMR_EPR, EM_NMR, or EM_EPR – double-hybrid) or integrating all three experimental data sets (EM_EPR_NMR – triple-hybrid). Predicted structural models were evaluated by computing the RMSD100 (Carugo and Pongor, 2001) of the sampled models relative to the experimentally determined structure and their respective energy scores in the BCL. Note that the RMSD100 calculation was performed over aligned regions of the structure: since BCL::MP-Fold assembles only the TMHs in the three-dimensional space, the RMSD100 values presented here only relate to the TM helices of the IMP.

In each case, BCL::MP-Fold was able to sample the native-like fold (Table 1). However, although the de novo sampled structures were structurally similar to the experimentally determined structure (RMSD100 = 4.5 Å) (PDB ID 1GZM (Li et al., 2004)), the scoring function lacked the discriminative power to identify the most accurate models. The models with the most favorable score often exhibited large structural deviations from the experimentally determined structure. Incorporation of experimental restraints improved the sampling accuracy and discriminative power of the scoring function. Prediction using a single set of experimental data (Table 1 and Figure 3A,C) improved sampling and scoring slightly. Notably, NMR data improved model discrimination and sampling density around the experimentally determined structure (Figure S1B), where the best scoring models achieved an RMSD100 of 5.1 Å. EM data helped in positioning the TMHs in the EM density rods, resulting in more accurate sampling of the native fold (RMSD100 = 2.9 Å). However, the medium resolution density map, combined with our simplified energy evaluation, was unable to unambiguously identify the most accurate models by score. EPR data suffered from the limited number of restraints leading to a moderate 1 Å improvement in sampling accuracy (RMSD100 = 3.5 Å). Again, the scoring function was unable to identify these improved models. Both, NMR- and EM-assisted models included low RMSD100 folds in the top scoring models and were further refined in next stage under the assumption that an all atom representation of the protein structure combined with higher resolution energy evaluation would allow to identify and refine the most accurate models.

Table 1. Structure prediction results from hybrid experimental data.

The RMSD100 metric is used to quantify model quality. RMSD100: RMSD100 of models ranked by RMSD100 to native model; Score: RMSD100 of models ranked by either BCL score or Rosetta score; Top5%: Averaged RMSD100 over top 5% models ranked by the respective metric. RMSD100_TM: RMSD100 value calculated from TMH regions of the models that ranked by total RMSD100. Score (TM_RMSD): RMSD100 value calculated from TMH regions of the models that ranked by Rosetta score.

Restraints BCL			RMSD100		Score
			Best	Top 5%	Best	Top 5%
No Restraints			4.5	5.4	9.4	9.2
NMR			3.1	3.8	5.1	6.1
	EPR		3.5	4.5	8.5	7.5
		EM	2.9	4.8	8.3	8.1
NMR	EPR		2.7	3.7	3.6	4.0
NMR		EM	3.0	4.0	4.0	5.5
	EPR	EM	1.9	4.1	8.4	7.4
NMR	EPR	EM	1.4	2.9	2.5	3.9

Restraints Rosetta			RMSD100		RMSD100_TM		Score		Score (RMSD100_TM)
			Best	Top 5%	Best	Top 5%	Best	Top 5%	Best	Top 5%
NMR			4.0	4.4	1.7	3.0	5.3	6.4	2.1	1.8
		EM	4.0	4.2	3.0	3.0	5.4	4.9	4.6	3.7
NMR	EPR		3.9	4.1	1.5	1.8	8.2	5.8	1.5	1.6
	EPR	EM	3.3	3.7	1.9	2.1	4.4	4.2	2.0	2.1
NMR		EM	3.3	3.5	1.6	1.3	3.8	4.1	1.1	1.1
NMR	EPR	EM	2.9	3.0	1.3	1.2	3.8	3.6	1.2	1.1

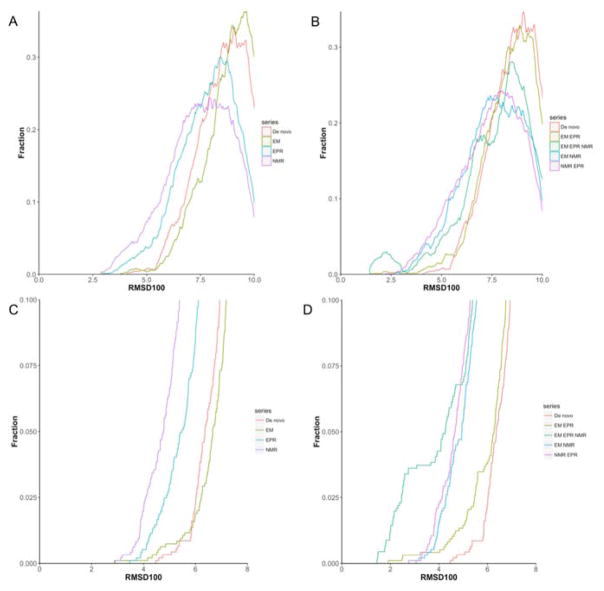
Figure 3. Prediction accuracy of low-resolution SSE assembly using hybrid experimental data.

Density distributions of structure prediction accuracies using single experimental dataset (A,C) and hybrid experimental dataset (B,D). The fraction of models versus the predicted models’ RMSD100 to the native crystal structure is shown. (A) A comparison is drawn between the sampling density for native-like models using de novo structure prediction (orange), EM (light green), EPR (blue) and NMR (purple). (C) Cumulative fraction of models that falls within 8Å RMSD, the y-axis is cut off at 0.1. (B) A comparison is drawn between the sampling density for native-like models using de novo structure prediction (orange), NMR_EPR (light green), EM_EPR (green), EM_NMR (blue) and EM_EPR_NMR (Purple). (D) Cumulative fraction of models that falls within 8Å RMSD, the y-axis is cut off at 0.1.

Before we proceeded to the refinement step, we combined two or three experimental data sets to test if integrating data from multiple sources improved sampling accuracy and/or discriminative power. Substantial improvements were observed over de novo prediction or the single-experimental data prediction. The NMR_EPR, EM_NMR sets improved sampling density near the native-like folds to below 3 Å RMSD100 (Table 1 and Figure 3B). The best models ranked by score are among the 5% most accurate models. EM_EPR prediction also improved the RMSD100 of the most accurate folds sampled to 1.9 Å but had an accurate model ranked only second by score (RMSD100 = 2.2 Å). The improvement in sampling density was less compared to tests that included NMR restraints (Figure 3B), possibly due to the limited distance information in experimental data and alternative folds fulfilling the 27 EPR distance restraints.

Unsurprisingly, the EM_EPR_NMR set performed best. The most accurate model had an RMSD100 of 1.4 Å and an average RMSD100 of 2.9 Å among the top 5% sampled folds. The sampling density was also significantly larger as seen in the peak centered near 2 Å in Figure 3B,D. Models ranked by score in EM_EPR_NMR also had the best agreement with the crystal structure, which is demonstrated by an RMSD100 of 2.5 Å and an average RMSD100 of 3.9 Å among the top 5% scoring models. The top scoring models using two or three datasets were further processed for all-atom refinement.

Loop modeling and structural refinement using hybrid experimental data

The BCL::MP-Fold models consist of simplified helices with only limited deviations from idealized dihedral angles. The models don’t contain loops and side-chain components. The top scoring models sampled in the BCL::MP-Fold stage using EM, NMR, EM_NMR, EM_EPR, NMR_EPR and EM_NMR_EPR datasets were refined in Rosetta using their corresponding restraint sets. In each case, except EM and EM_EPR, the top scoring BCL models used as inputs in this stage were within reasonable accuracy to the experimentally determined 1GZM structure. The single restraint set (EM and NMR) was successful in refinement and finding native-like models among the best scoring models. However, using two or three experimental data sets, added additional layers of accuracy in refinement (Figure 4A,B and Table 1).

Figure 4. Prediction accuracy of Rosetta refinement using hybrid experimental data.

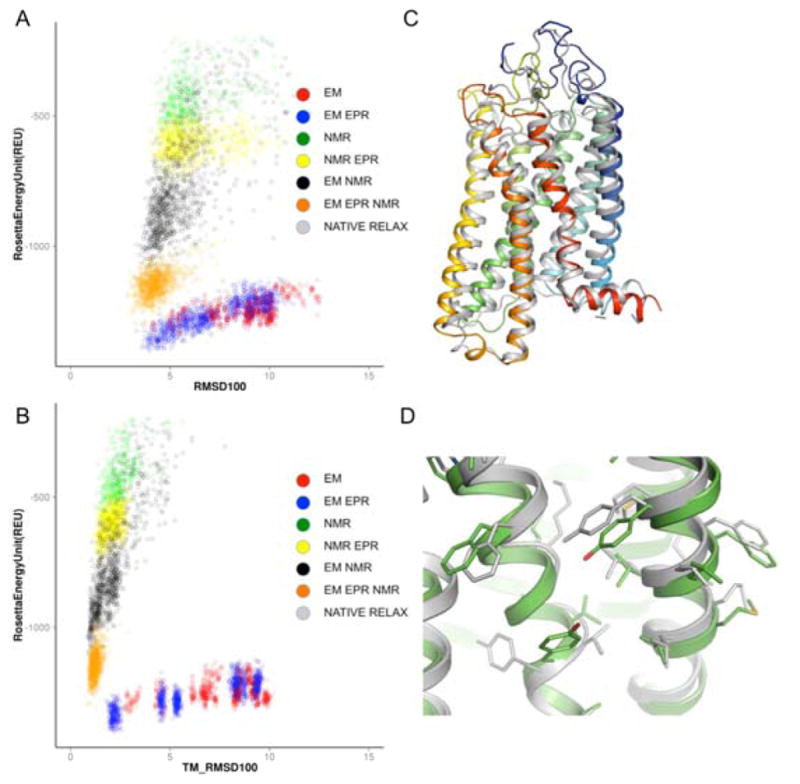
The scatter plot for model quality in terms of sampling and scoring of rhodopsin models to atomic detail using Rosetta modeling suite and representative predicted models of low energy. The resulting models are plotted with their respective Rosetta score against their RMSD relative sto the experimentally determined 1GZM structure (A), or TMH RMSD to the TMH region of 1GZM (B). The scatter plot is color coded with the respective dataset used for the refinement: NMR (Green), EM (Red), NMR_EPR (Yellow), EM_EPR (Blue), EM_NMR (Black) and EM_EPR_NMR (Orange). The best scoring model from EM_EPR_NMR experiment is depicted in rainbow diagram, with the experimental structure show in grey (C). The side chain rotational conformer of the predicted structure matched the experimental structure with high accuracy (D).

The energy landscape of the rhodopsin fold, visualized by plotting the RMSD100 of each model with its respective Rosetta energy score, shows that native-like models are strongly favored by the inclusion of experimental data during the refinement stage (Figure 4A,B). The use of hybrid experimental data improved the prediction accuracy in the core of the protein. The RMSD100_TM, which quantifies the RMSD100 of the trans-membrane region, for the top 5% sampled models using hybrid restraint data improved by at least 1 Å improvement over that of the top 5% sampled models using single restraint (Table 1, RMSD100_TM).

With EM data alone, which is not able to generate an unambiguous answer to the correct fold using the low-resolution scoring functions in BCL::MP-Fold, the Rosetta refinement successfully sampled the core of the protein with a high accuracy of 3 Å RMSD100_TM. Although input models contained models with incorrect folds that extend to an RMSD100_TM above 8 Å, the native-like folds were strongly favored by the EM density scoring function. EM_EPR and EM_NMR both showed improvements when EM data was incorporated.

Overall, whereas the inclusion of the EM density map resulted in an improvement of the total RMSD100 of the best scoring model to below 6 Å, distance type restraints (NMR, NMR_EPR) were unable to refine the best scoring models to below 6 Å (Figure 4A and Table 1). The EM data restrains loop conformations to the boundary of the density map. NMR information could improve modeling the correct contacts between the TMHs, as seen in the improvement in TM_RMSD100 to below 2 Å in the best scoring models. The models that were refined using NMR data also had less favorable scores to our surprise. To break down the cause of the worse scores, rescoring using only the built-in Rosetta scoring function was performed to investigate the behavior of the membrane scoring function (see discussion).

Refinement using EM_NMR_EPR resulted in the most accurate models (RMSD100 = 2.9 Å). The total RMSD100 approached a limit of 4 Å while the RMSD100 of the core helical TM region was close to 1 Å. In our prediction pipeline, the retinal molecule is not modeled. Accurate modeling of the extra-cellular loop 2 (ECL2) that interacts with the retinal molecule and the 30 amino acids long N-terminus remains challenging using the Rosetta loop modeling algorithm.

The refinement protocol using hybrid experimental data could recapitulate backbone conformation features observed in the crystal structures such as kinks in TMHs. For example, the best scoring model from the EM_NMR_EPR dataset reproduced the backbone contacts and loop conformation similar to the native structure (Figure 4C). Even when input models were idealized helices, the kinks in helices six and seven could be observed after the refinement. The side chain conformers from the model could be modeled to high accuracy (Figure 4D).

Discussion

The fold and sequence space of α-helical MPs is vast, but computational modeling provides promising results

Structural representatives remain to be determined for about seven hundred more IMP families to allow for comprehensive comparative modeling of all IMPs. At an average rate of six new folds per year (average over the last 5 years), experimentally determining the remaining IMP folds would take approximately 110 years. Our survey also showed that a large number of IMP families have a relatively low theoretical fold complexity. The fold space of these IMPs can be comprehensively searched with the current computational algorithms. Therefore, integrating limited experimental data into these computational algorithms should accelerate fold determination for such IMP families. For larger proteins, such as 7-TM Rhodopsin, which has a theoretical fold space of around one hundred thousand representations, additional restraints will be required to achieve high prediction accuracy.

In this survey, we also found that within a single IMP family, there are members containing different numbers of predicted TMHs, further increasing complexity for accurate homology modeling, which requires a template structure that contains most of the structural elements. Modeling such IMPs would require a combination of template-based modeling methods and de novo structure prediction in order to sample the additional fold space.

Recent developments in co-evolution contact prediction offer alternative information for IMP structure determination (Tang et al., 2015, Marks et al., 2011, Kamisetty et al., 2013, Morcos et al., 2011). With large enough sequence databases, residue-residue contacts can be inferred from residues that co-evolve. Such restraints have been used to improve structure prediction accuracy for IMPs by restricting the sampling space in Rosetta (Ovchinnikov et al., 2015). Combining sparse experimental restraints from NMR with evolutionary constraints allows for accurate prediction of soluble protein structure in many cases (Tang et al., 2015). Evolutionary Coupling-NMR developed by Tang et al. incorporates evolutionary contacts during and after the NMR data interpretation and NOE assignment. In a more recent publication by Ovchinnikov et al, 206 unknown IMP folds were predicted using integrated metagenome data and co-evolutionary analysis (Ovchinnikov et al., 2017). The sizes of the proteins involved in this study are below 300 amino acids. With the expansion of genomic databases coupled with computational prediction algorithms, evolutionary constraints provide viable orthogonal structural information to guide protein structure prediction.

Available experimental data for Rhodopsin are suboptimal for IMP structure determination

Although the use of actual experimental data would be preferred in demonstrating our algorithm’s capability in application, this proved difficult in the present case: The DEER restraints published by Hubbell et al(Altenbach et al., 2008). are centered on the intra-cellular side of rhodopsin to monitor the conformational changes upon receptor activation. The amino acid pairs for labeling were selected for that purpose alone and are not suited to determine the fold. In our previous studies using a single restraint type, incorporating these 16 restraints resulted in an RMSD100 improvement from 5Å to 4.5Å (Fischer et al., 2015). In our study using simulated DEER restraints, the RMSD100 of the most accurate model arrived at 3.5 Å. The additional improvement by 1Å is a direct result of selecting restraints that restrict the overall fold of the protein. There is a complete NMR dataset available for sensory Rhodopsin from bacteria (Gautier and Nietlispach, 2012), however the NMR restraints for bovine rhodopsin are sparse and affiliated with a higher uncertainty due to experimental limitations. In the experimental paper where the bovine rhodopsin NMR structure was described, only secondary structure restraints stem from NMR. In addition, 17 long-range constraints from EPR experiments and 58 inter-helical constraints from low resolution electron diffraction experiments are used (pdb ID: 1JFP) (Yeagle et al., 2001). The experimental procedure was also based on resolving overlapping peptide constructs of bovine rhodopsin solubilized in DMSO, which is not expected to stabilize a biologically relevant conformation of a membrane protein. As a result, the limited availability of actual NMR-derived distance data prompted us to use simulated NMR restraints. For our simulated NMR distances, the lower bound of distances is 0 Å, the upper bound of the distances is below 6Å.

Experimental data overcomes the limitations of simplified representation of IMPs during de novo structure prediction

Due to the simplified representation of IMPs in the BCL and in Rosetta, the depth of the native energy minimum is reduced. As a consequence, energy differences between the native-like folds and non-native-like folds are small and unambiguous identification of the correct native fold becomes often difficult or impossible. Further, by virtue of their respective sampling algorithms, not all IMP conformations are easily accessible or accessible at all. Therefore, the optimal native conformation might be missed as the algorithm fails to sample it.

In the Rosetta stage, we observed that models predicted from EM and EM_EPR datasets had more favorable scores compared to models predicted from NMR data. To confirm that those discrepancies were not caused by the experimental data, the models were re-evaluated using the original Rosetta membrane scores. Notably, the Rosetta score of the crystal structures was substantially lower than the Rosetta score of the computational models (Figure S2), suggesting that the Rosetta energy function can correctly distinguish non-native states from native states. Since the overall RMSDs of the computational models are above 3 Å, the energy gap could be explained by inaccurate loop conformations that arise from insufficient sampling of the long N-terminal loop and ECL2. An energy gap is observed between models predicted from EM, EM_EPR and other datasets where NMR data were included. Analysis of the individual score components showed that EM and EM_EPR models, although exhibiting a larger deviation in the core of the protein, have less unfavorable energy contributions from fa_rep (Lennard-Jones repulsive energy between atoms in different residues(Rohl et al., 2004, Leaver-Fay et al., 2013)), and fa_dun (Internal energy of sidechain rotamers as derived from Dunbrack’s statistics (Shapovalov and Dunbrack, 2011)). At the same time, models predicted from triple-hybrid experimental data exhibited lower Rosetta scores compared to that of EM_NMR, NMR_EPR, and NMR. The experimental data leveraged in the prediction constrained the model to sample conformations in a fold space close to the experimentally determined structural model and was able to correct the deviations in the scoring function used by Rosetta. The reason for such observations is perhaps the richness in the side-chain contact information provided by NMR distance data, that forces side-chain contact that are otherwise hard to be sampled due to the simplified representation of the IMPs.

Structure determination from limited experimental data will be important to determine alternative conformational states of integral membrane proteins

Many IMPs function through shifting ensembles of numerous conformations. Structural models of IMPs could be obtained through X-ray crystallography: in many cases, disruptive experimental technologies are used to stabilize and alter the energy landscape of the native IMP via thermo-stabilizing mutations, chimeric protein engineering, or the non-native-like membrane mimics. Biophysical methods observe ensembles of molecules in their native-like dynamic equilibrium to complement or correct observations in crystal structures.

The best examples are perhaps GPCRs. GPCRs exist in a dynamic conformational equilibrium of basal, activated, inactivated, G-protein coupling, and arrestin binding states as demonstrated by many recent biophysical studies (Manglik et al., 2015, Kaiser et al., 2015, Kim et al., 2013, Dror et al., 2015, Shukla et al., 2014, Manglik and Kobilka, 2014, Alexander et al., 2014, Nygaard et al., 2013, Altenbach et al., 2008, El Moustaine et al., 2012, Xue et al., 2015). Solution NMR experiments using ¹⁹F probes conjugated to specific amino acids (Kim et al., 2013) and ¹³C methionine side chain labels (Nygaard et al., 2013) capture β2 adrenergic receptor in distinct population of structural states aside from observed crystal structures. The shift of the conformational equilibrium of GPCRs during signal transduction is accompanied by major structural changes, as revealed by SDSL-EPR in β2 adrenergic receptor (Manglik et al., 2015) and rhodopsin (Altenbach et al., 2008, Alexander et al., 2014). The architecture of the molecular assembly of GPCR and heterotrimeric G-protein and arrestin in a dynamic state could also be visualized using cross-linking mass spectrometry (XLMS) and EM (Shukla et al., 2014). While the homo-dimeric metabotropic glutamate receptor 1 (mGluR1) is crystalized in an inactive state dimer(Wu et al., 2014), a later study using fluorescence resonance transfer and crosslinking displayed a deviating dimer interface in the biological sample. Conformational rearrangement in an oligomerized state has also been observed, where the activated receptor dimers undergo conformational change in individual subunits as well as the dimer interface (El Moustaine et al., 2012, Xue et al., 2015). Molecular dynamics simulations and Monte Carlo simulations utilizing these experimental data were also successful in generating structural models that match the observed conformational states (Shukla et al., 2014, Alexander et al., 2014, Nygaard et al., 2013).

Transporters also exist in multiple conformations with respect to their transport cycle. The small multidrug resistance transporter EmrE ultilizes the proton gradient to export cytotoxic molecules against their chemical gradient out of the cell and protect the bacteria. Whereas the crystal structure is limited to its substrate bound state (Chen et al., 2007), the transport cycle needs to adopt the intermediate proton-bound state to complete a cycle. A systematic SDSL-EPR study on EmrE has revealed rotation and tilting of TM helices 1 – 3 in response to the change of the protonation state (Dastvan et al., 2016), which in turn results in the change of substrate entry and binding site. The distance distribution from the SDSL-EPR study, combined with computational modeling was successful in producing an intermediate structural ensemble that fills the knowledge gap of the crystal structures.

NMR, EPR, cryo-EM data, albeit samples are at high temperature or flash-frozen, are expected to reflect native-like conditions when different conformations of the protein exist in the equilibrium. SDSL-EPR spectroscopy can observe such ensemble states as a probability distribution of a distance within an ensemble is observed. NMR spectroscopy can observe ensemble averages of conformations or distinct conformational states depending on the time-scale of motion in the exchange process. With improvements in direct electron detection and image averaging, EM can also distinguish diverse conformational states in the sample(Zhou et al., 2015).

BCL::MP-Fold and Rosetta algorithms can also be used to optimize a given starting structure. Thus, from any given starting structural model or crystal structure we can derive a model for an alternate state of an MP by fitting it to sparse experimental data observed for this state (Dastvan et al., 2016).. By combining experimental data from different sources and excluding the likely outlier populations due to artifacts in the disruptive experimental methods, one can model the entire conformational ensemble of the IMP. Such ensemble models along with the statistic inference could be used to provide further molecular mechanistical insight on protein function, and possibly guide small molecule modulator development against intermediate states.

Conclusion

The existing abundance of sequence data of IMPs are expected to challenge the limit of experimental structural determination pipelines in the near future. Hybrid approaches combining experimental and computational techniques could accelerate determination of protein structures and refine existing knowledge of protein structural functions. We demonstrated that using a combination of computational structure prediction methods and sparse experimental data enables accurate fold determination for large IMPs to atomic detail. Although combining orthogonal experimental data improved the prediction accuracy, future applications should always consider the source of the experimental data on whether they can be used complementarily since not all combinations yield results of comparable quality. Future development of the proposed structural prediction pipeline will be focused on the prediction of structural ensembles.

STAR Methods

Contact for Reagents and Resource Sharing

Further information and request for computational resources may be directed to, and will be fulfilled by the Lead Author, Dr. Jens Meiler (jens.meiler@vanderbilt.edu).

Method Details

Enumerating the theoretical α-helical integral membrane protein fold space

The theoretical calculation was done using Mathematica (Wolfram). We simplified the TMH fold space by defining the position of α-helices on a two-dimensional grid, where the arrangements for a given number of TMHs was plotted. For each unique TMH arrangement, we inserted the TMHs into the arrangement to generate all possible folds. A particular fold was accepted when each TMH had two direct contacts with other TMHs and every TMH was connected in a single fold. When internal symmetry was detected for an arrangement of TMHs, the number of folds was divided by the symmetry operator. Assuming each TMH in the neighboring sequence adopts anti-parallel insertion in membrane, to account for topology of N-terminal facing extracellular or intracellular environment, we multiplied the number of folds by two. For each number of TMHs, the number of possible arrangements of TMHs and the number of possible folds were computed.

Enumerating the sequence space of α-helical integral membrane protein

The database search for all α-helical IMPs was performed using UniProt and pfam (Figure 2A). We used the UniProt server to retrieve the sequence information of α-helical IMPs by searching for the annotated keyword ‘Transmembrane helix’. The TMH annotation and the pfam family id associated with each Uniprot entry was downloaded as a tab delimited table. Around 75 thousand entries were pulled and entries containing less than three TMHs were filtered out. The unique pfam families and their number of TMHs were then compiled by clustering all UniProt entries based on their pfam id. We also directly used the pfam server to download all 2100 families that were annotated as IMPs. The sequences in each pfam family were then subjected to transmembrane span prediction using SPOCTOPUS(Viklund et al., 2008) until multiple sequences were predicted to have more than two TMHs. The IMP family list mined from the two methods were then combined and cleaned for duplicates and manually inspected. The XML representation of the MPtopo database (Jayasinghe et al., 2001) was downloaded to search for IMP families with a known structural fold.

Integral membrane protein structure prediction using combined experimental restraints and BCL::MP-Fold

All detailed computational protocol and command documentations should be referred to Methods S1. The test dataset of bovine rhodopsin (PDB entry 1GZM) (Li et al., 2004) was downloaded from the PDB and considered the ‘native’ structure. An experimentally determined electron density map for rhodopsin (Ruprecht et al., 2004) at 5.5 Å resolution was used for the EM data. At this resolution, TMH density could be distinguished but the connectivities between density rods could not be observed directly. The NMR data was simulated in the form of backbone chemical shift (CS) using SPARTA+ (Shen and Bax, 2010), and ten sets of randomly selected sparse side chain Nuclear Overhauser effect (NOE)-derived distances at a 1 restraint per residue level (a total of 326 distances) using BCL with simulated uncertainties dereived from the NMR knowledge-based potential (Weiner et al., 2014). Ten sets of distance data from EPR double electron-electron resonance (DEER) spectroscopy was simulated with a distance uncertainty model (Alexander et al., 2008). Each set consisted of at least 3 restraints per TMH (a total of 27 distances). A sample restraint file containing simulated NOE and DEER distances was included in Table.S1 & S2.

The protocol was based on the protein structure prediction protocols of BCL::MP-Fold (Weiner et al., 2013) and BCL::EM-Fold (Lindert et al., 2012). The SSEs were first predicted from the primary structure of Rhodopsin using the consensus of two secondary structure prediction methods, JUFO9D (Koehler et al., 2009) and SPOCTOPUS (Viklund et al., 2008). When limited NMR data was included, the backbone CS was used to generate SSEs definitions from the primary structure. The SSEs were then assembled in a multi-stage approach and intermediate and final models were evaluated using a membrane-specific knowledge-based potential and the Metropolis criterion. During the assembly process, the protein model was randomly perturbed by one of over 100 MC moves belonging to one of six categories: (1) adding SSEs, (2) removing SSEs, (3) swapping SSEs, (4) single SSE moves, (5) SSE-pair moves, and (6) moving domains. The energy function contained terms for evaluating amino acid pairwise distances, amino acid environment, loop closure, radius of gyration, contact order, secondary structure prediction agreement, environment prediction agreement, TM topology, and steric interferences. A static membrane object was utilized in conjunction with the environment-specific potentials. If experimental data were used, the scoring function was extended by the appropriate scoring terms to account for density rod agreement with experimental density map in the case of EM (Lindert et al., 2012), and a knowledge-based distance agreement evaluation in the case of EPR (Alexander et al., 2008) and NMR (Weiner et al., 2014). The scores were linearly combined to a sum score with weighted score components.

1000 models were sampled in each prediction experiment with hybrid data. The models were evaluated through the RMSD100 (Carugo and Pongor, 2001) metric: $\mathit{RMSD}100=\frac{\mathit{RMSD}}{1+ln\sqrt{N/100}}$, where the root-mean-square deviation (RMSD) of the Cα-coordinates between the predicted model and the crystal structure model is normalized by the number of amino acid (N) of the protein. When the prediction was performed from single/multi sets of experimental data and native-like models could be identifies by their score rank, the top 1% scoring models (10) were selected for the subsequent Rosetta refinement – regardless of the selected set included non-native-like models. When the prediction was performed from EM data only, the top 10 folds were selected.

Integral membrane protein structure refinement using combined experimental restraints and Rosetta

Rosetta was used to add loop regions and side chains to the model, and refine with a high-resolution scoring function. The protocol for the Rosetta refinement was modified to incorporate multiple experimental data. All computational protocol and command documentation mentioned in this section are referred to in Methods S1.

As Rosetta uses fragments from a structural database to model local sequence bias, the fragment search excluded fragments from structures that are homologous to Rhodopsin. In the case of NMR data incorporation, fragment search was performed using backbone CS information to select for fragment with preferable backbone torsion angles (Vernon et al., 2013). For each of the models from the previous BCL stage, 500 models were sampled using Rosetta’s cyclic coordinate descent algorithm (Canutescu and Dunbrack, 2003) to build loops and remodel TMHs. Further atomic detail refinement was carried out using Rosetta’s “relax” application (Leaver-Fay et al., 2011) once for each of the 500 model. A TMH definition file is used for the placement of a virtual membrane encompassing each input model for membrane environment evaluations. When EM experimental data was used, additional electron density scoring terms were turned on (DiMaio et al., 2009). In the case of distance restraints from NMR, a bounded penalty potential f(x) was used to discourage sampling of conformations that are inconsistent with the experimental data. For each distance restraint, an upper (ub) and a lower boundary (lb) are provided by the user (Table S1). If the measured distance of xÅ fulfills the criterion lb≤x≤ub, if x is outside the boundary, a score penalty would be given: if x ≤ lb, $f(x)={(\frac{x-lb}{sd})}^2$; if ub ≤ x ≤ ub + rswitch * sd, $f(x)={(\frac{x-ub}{sd})}^2$; if ub + rswitch * sd ≤ x, $f(x)=\frac{1}{sd}{\left(x-(ub+\mathit{rswitch}\ast sd))+(\frac{\mathit{rswitch}\ast sd}{sd}\right)}^2$, where the rswitch term is set to default of 0.5. The distance restraints from EPR DEER measurements (Table S2) are treated with a knowledge-based potential as detailed in (Hirst et al., 2011). The score terms were linearly combined with respective weighting to compute the total Rosetta energy score. The RMSD100 relative to the ‘native’ 1GZM structure was used to quantify the prediction accuracy. The RMSD100 specific to the TMH region was computed by limiting the comparison of Cα-coordinates to residues in the predicted TMHs. Inspection of the models and their depiction was performed using Pymol (Schrodinger, 2015).

Highlights.

• A computational prediction pipeline was developed to utilize EM, NMR, EPR data.

• At least 800 integral membrane protein families remain to be structurally elucidated.

• Hybrid experimental data improves membrane protein structure prediction accuracy.

Abbreviations

NMR

Nulcear Magnetic Resonance

EPR

Electron Paramagnetic Resonance

EM

Electron Microscopy

BCL

BioChemical Library

IMP

Integral Membrane Protein