Bayesian Multiresolution Variable Selection for Ultra-High Dimensional Neuroimaging Data

Abstract

Ultra-high dimensional variable selection has become increasingly important in analysis of neuroimaging data. For example, in the Autism Brain Imaging Data Exchange (ABIDE) study, neuroscientists are interested in identifying important biomarkers for early detection of the autism spectrum disorder (ASD) using high resolution brain images that include hundreds of thousands voxels. However, most existing methods are not feasible for solving this problem due to their extensive computational costs. In this work, we propose a novel multiresolution variable selection procedure under a Bayesian probit regression framework. It recursively uses posterior samples for coarser-scale variable selection to guide the posterior inference on finer-scale variable selection, leading to very efficient Markov chain Monte Carlo (MCMC) algorithms. The proposed algorithms are computationally feasible for ultra-high dimensional data. Also, our model incorporates two levels of structural information into variable selection using Ising priors: the spatial dependence between voxels and the functional connectivity between anatomical brain regions. Applied to the resting state functional magnetic resonance imaging (R-fMRI) data in the ABIDE study, our methods identify voxel-level imaging biomarkers highly predictive of the ASD, which are biologically meaningful and interpretable. Extensive simulations also show that our methods achieve better performance in variable selection compared to existing methods.

1 INTRODUCTION

Rapid advances in neuroimaging technologies have generated a large amount of high resolution imaging data, facilitating cutting-edge research in relevant areas. This presents new challenges for data scientists to develop efficient statistical methods for analysis of such ultra-high dimensional imaging data. Our work is primarily motivated by the Autism Brain Imaging Data Exchange (ABIDE) study [1].

1.1 Autism Brain Imaging Data Exchange (ABIDE) Study

The major goal of the ABIDE study is to explore association of brain activity with the autism spectrum disorder (ASD), a widely recognized disease due to its high prevalence and substantial heterogeneity in children [2]. The ABIDE study aggregated 20 resting-state functional magnetic resonance imaging (R-fMRI) data sets from 17 different sites including 539 ASDs and 573 age-matched typical controls. The R-fMRI is a popular non-invasive imaging technique that measures the blood oxygen level to reflect the resting brain activity. For each subject, the R-fMRI signal was recorded for each voxel in the brain over multiple time points (multiple scans). Several standard imaging preprocessing steps [1] including motion corrections, slice-timing correction, and spatial smoothing have been applied to the R-fMRI data, which were registered into the standard Montreal Neurological Institute (MNI) space consisting of 228,483 voxels. To characterize the localized spontaneous brain activity, we focus on the fractional amplitude of low-frequency fluctuations (fALFF) [3] based on the R-fMRI time series at each voxel for each subject. The fALFF is defined as the ratio of the power spectrum of low frequency (0.01–0.08Hz) to the entire frequency range and has been widely used as a voxel-wise measure of the intrinsic functional brain architecture derived from R-fMRI data [4]. In this work, we analyze the voxel-wise fALLF values over 116 regions in the brain involving 185,405 voxels in total, where regions are defined according to the Automated Anatomical Labeling (AAL) system [5]. Besides the imaging data and the clinical diagnosis of the ASD, demographical variables were also collected, such as age at scan, sex and intelligence quotient (IQ).

One question of interest in this study is to identify imaging biomarkers, i.e., voxel-wise fALFF values over 116 regions, for detecting the ASD risk. In particular, our goal is to perform two levels of variable selection: at the first level, important regions are selected in relation to the ASD risk; at the second level, a set of important voxels within the selected regions are selected and are referred to as ASD imaging risk factors. Correspondingly, two levels of structural information – functional connectivity among regions and spatial dependence among voxels – can be incorporated to facilitate variable selection and produce biologically more interpretable results. To achieve this goal, we use a Bayesian probit regression model for spatial variable selection, where the binary outcome is the ASD disease status and the predictors include all voxel-level imaging biomarkers from multiple regions. We use Ising prior models to incorporate structural information for the two levels of variable selection. However, it is extremely challenging to perform spatial variable selection in such ultra-high dimensional structured feature space (185,405 voxels within 116 regions) under our modeling framework.

1.2 Variable Selection in High-Dimensional Feature Space

Regularization methods [6], [7], [8], [9], [10] have been developed to conduct variable selection and extended to handle high-dimensional feature spaces and allow for incorporation of structural information. Alternatively, Bayesian methods also play a prominent role in solving the variable selection problem. O’Hara and Sillanpää [11] provides a review of several commonly used Bayesian variable selection methods and posterior simulation algorithms, such as the Gibbs variable selection (GVS) [12] and the stochastic search variable selection (SSVS) [13]. They usually specify a positive prior probability for each model parameter being exactly zero (i.e., the corresponding variable is not included in the model) and compute the posterior probability of each regression parameter being nonzero, which are often referred to as the posterior inclusion probability and can be used to quantify the uncertainty of variable selection – one advantage of Bayesian methods over existing regularization methods. Subsequently, important variables are identified by whether the posterior inclusion probabilities are greater than a threshold value. To incorporate the structural information and capture the dependence among variables, Ising or binary Markov random field (MRF) priors are frequently used for Bayesian variable selection [14], [15], [16], [17]. In particular, Smith et al. [16] and Smith and Fahrmeir [17] developed Bayesian spatial variable selection to identify active regions in fMRI studies. To improve efficiency of posterior simulations for Bayesian variable selection, transdimensional sampling algorithms [18] and adaptive Monte Carlo methods [19], [20], [21] have been proposed.

Although the aforementioned regularization and Bayesian methods have been successful for variable selection in relatively high-dimensional feature space (e.g., the number of predictors is on the order of thousands), these methods become infeasible due to their prohibitive computational costs when faced with a problem such as our motivating study involving hundreds of thousands or even millions of predictors. This has stimulated the development of variable selection techniques for ultra-high dimensional problems. Fan and Lv [22] proposed the Sure Independence Screening (SIS) approach often used in conjunction with regularization methods. This method does not require intensive computations and has good theoretical properties. Although it is applicable to a probit regression model, the SIS does not explicitly model the dependence among variables and cannot assess the uncertainty of variable selection. In a Bayesian modeling framework, Bottolo and Richardson [23] developed a powerful sampling scheme to accommodate the high-dimensional multimodal model space based on the evolutionary Monte Carlo. This method has been shown to be able to handle up to 10,000 predictors, but it is still computationally inefficient when applied to our motivating study with almost 200,000 predictors. More recently, by assigning nonlocal priors to model parameters, Johnson and Rossell [24] proposed a novel Bayesian model selection method that possesses the posterior selection consistency when the number of predictors is smaller than the sample size. Johnson [25] demonstrated that it can achieve high selection accuracy in ultra high-dimensional problems, comparable to the SIS combined with regularization methods. However, their method is not directly applicable to our problem in that it was developed for a linear regression model without incorporating any structural information in the covariate space. Goldsmith et al. [26] and Huang et al. [27] developed a single-site Gibbs sampler for Bayesian spatial variable selection using Ising priors with application to neuroimaging studies. This algorithm is able to fit linear regression models with ultra-high dimensional imaging biomarkers, i.e. “scalar-on-image regression” models, however, the single-site updating scheme leads to a very slow mixing of the Markov chain in the posterior computation for a probit regression model [18], [21]. Thus, there are needs for developing more efficient posterior computation algorithms that can be applied to our motivating problem. Particularly, we resort to a multiresolution approach.

1.3 Multiresolution Approach

The idea of multiresolution, which facilitates the information transition through a construction of coarse-and-fine-scale model parameters, has been adopted to optimize algorithms successfully in data mining and machine learning. The pioneer work of utilizing the multiresolution idea for Bayesian computation traces back to a multi-grid MCMC method proposed by Liu and Sabatti [28]. This approach was originally adopted by Goodman and Sokal [29] to solve a problem in statistical physics. Motivated by image denoising problems, Higdon et al. [30] proposed a coupled MCMC algorithm with the coarsened-scale Markov chains serving as a guide to the original fine-scale chains. The coupled Markov chains can better explore the entire sample space and avoid getting trapped at local maxima of the posterior distribution. Holloman et al. [31] further proposed a multiresolution genetic algorithm to reduce computational burden, provide more accurate solution of maximization problem, and improve mixing of the MCMC sampling. Similarly, Koutsourelakis [32] adopted a multiresolution idea to estimate spatially-varying parameters in PDE-based models with the salient features detected by the coarse solvers. From the computational perspective, Giles [33] showed that the computational complexity for estimating the expected value from a stochastic differential equation could be reduced by a multiresolution Monte Carlo simulation. More recently, Kou et al. [34] applied a multiresolution method to diffusion process models for discrete data and showed that their approach improves computational efficiency and estimation accuracy. From the perspective of model construction, Fox and Dunson [35] adopted the multiresolution idea in Gaussian process models to capture both long-range dependencies and abrupt discontinuities.

In this work, we develop efficient multiresolution MCMC algorithms for variable selection in the ultra-high dimensional feature space of imaging data. In contrast to the coupled Markov chain methods [30], [31], [34] that alternate between different resolutions in posterior simulation, we construct and conduct posterior computations for a sequence of nested auxiliary models for variable selection from the coarsest scale to the finest scale. Our goal is to conduct variable selection at the finest scale – the resolution in the observed data. The MCMC algorithm for the model at each resolution depends on the posterior inclusion probabilities obtained from fitting the auxiliary model at the previous, coarser resolution through the use of a “smart” proposal distribution that allows the algorithm to explore the entire sample space more efficiently. This avoids the complication of alternating between resolutions for a large number of selection indicators in our problem.

Our major contributions in this work are severalfold. First, we are among the very first to develop a multiresolution approach for Bayesian variable selection in a ultra-high dimensional feature space involving hundreds of thousands or millions of voxels (predictors). Second, the proposed MCMC algorithm leads to fast convergence and good mixing of Markov chains. For example, the posterior computation can be completed within hours for a variable selection problem involving 200,000 predictors. Third, our approach is able to incorporate multi-level structural information into variable selection, e.g., the functional connectivity between ROIs and the spatial dependence between voxels in the motivating study, leading to biologically more meaningful and interpretable results and improving accuracy in variable selection and prediction. To the best of our knowledge, no existing methods can be directly applied to our motivating problem and achieve similar performance. Lastly, using the motivating data our method identifies highly predictive voxel-level imaging risk factors of the ASD. It provides valuable insights for neuroscientists and epidemiologists to understand the ASD etiology that is essential for the development of effective treatments.

The remainder of the paper is organized as follows. In Section 2, we present the Bayesian spatial probit regression model for variable selection with incorporation of structural information. We present the prior specifications in Section 2.2 and the standard posterior computation algorithm in Section 2.3. In Section 3, we propose our multiresolution approach for variable selection in a ultra-high dimensional feature space and describe two efficient sequential resolution sampling schemes. In Section 4, we apply the proposed method to the R-fMRI data in the ABIDE study to identify important voxel-level fALFF biomarkers that are predictive of the ASD risk. In Section 5 we conduct simulation studies to demonstrate the superiority of our proposed approach. Finally, we conclude with a discussion in Section 6.

2 MODEL FORMULATION

2.1 A Probit Regression Model for Variable Selection

Suppose there are n subjects in the data. For i = 1, …, n, let y_i ∈ {0, 1} be the binary outcome representing the disease status of subject i (disease = 1, control = 0). Assume that the whole brain 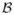consists of R regions and region r contains V_r voxels, for r = 1, …, R, with $V={\sum }_{r=1}^R{V}_r$ representing the total number of voxels in the brain. Let x_irv denote the imaging biomarker at voxel v within region r for subject i and s_ij denote clinical variable j for subject i (j = 1, …, p). We consider a probit regression model for variable selection

$$\begin{array}{lll}{y}_i\hfill & =\hfill & I[z_i\ge 0],\hfill \\ z_i\hfill & =\hfill & {\alpha }_0+\sum _{j=1}^p{\alpha }_j{s}_{ij}+\sum _{r=1}^R{c}_r\sum _{v=1}^{V_r}{\gamma }_{rv}{\beta }_{rv}{x}_{\mathit{irv}}+{\epsilon }_i,\hfill \end{array}$$ (1)

where ε_i ~ N(0, 1), indicator function I( 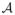) = 1 if event 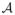occurs and 0 otherwise, α_j and β_rv are coefficients of clinical variable s_ij and imaging biomarker x_irv, respectively, c_r ∈ {0, 1} is the selection indicator for region r, and γ_rv ∈ {0, 1} is the selection indicator for voxel v in region r. Thus, the imaging biomarker x_irv is excluded from the model if at least one of c_r and γ_rv is zero.

We further denote by e_mk = (0, …, 0, 1, 0, …, 0)^⊤ an m × 1 vector with the kth element of 1 and all other elements of 0, by 0_m = (0, …, 0)^⊤ an all-zero vector of dimension m×1, by ${\mathbf{1}}_m={\sum }_{k=1}^m{\mathbf{e}}_{mk}$ an all-one vector, and by ${\mathbf{I}}_m={\sum }_{k=1}^m{\mathbf{e}}_{mk}{\mathbf{e}}_{mk}^{\top }$ an m × m identity matrix. Define ${\mathbf{M}}_r={({\mathbf{0}}_{{\underset{\_}{V}}_r}^{\top },{\mathbf{1}}_{V_r}^{\top },{\mathbf{0}}_{{\overline{V}}_r}^{\top })}^{\top }$ (of dimension V × 1) and M = (M₁, ···, M_R) (of dimension V × R), where ${\underset{\_}{V}}_r={\sum }_{r^{\prime }=1}^{r-1}{V}_{r^{\prime }}$ and ${\overline{V}}_r={\sum }_{r^{\prime }=r+1}^R{V}_{r^{\prime }}$. It follows that M represents an index map between voxels and regions; and model (1) can be rewritten in a compact form,

$$\mathbf{y}=I[\mathbf{z}\ge {\mathbf{0}}_n],\mathbf{z}=\mathbf{S}\mathit{\alpha }+\mathbf{X}(\mathit{\lambda }\circ \mathit{\beta })+\mathit{\epsilon },$$ (2)

with ε ~ N(0_n, I_n). Here y = (y₁, …, y_n)^⊤, z = (z₁, …, z_n)^⊤, ε = (ε₁, …, ε_n)^⊤, x_rv = (x_1rv, …, x_nrv)^⊤, X_r = (x_r1, …, xr_Vr), X = (X₁, …, X_R), s_j = (s_1j, …, s_nj)^⊤, S = (1_n, s₁, …, s_p), α = (α₀, α₁, …, α_p)^⊤, β_r = (β_r1, …, β_rVr)^⊤, $\mathit{\beta }={({\mathit{\beta }}_1^{\top },\dots ,{\mathit{\beta }}_R^{\top })}^{\top }$, c = (c₁, …, c_R)^⊤, γ_r = (γ_r1, …, γ_rVr)^⊤, $\mathit{\gamma }={({\mathit{\gamma }}_1^{\top },\dots ,{\mathit{\gamma }}_R^{\top })}^{\top }$, and λ = (Mc) ∘ γ with “∘” representing the Hadamard product (or entry-wise product) [36]. It is worth noting that λ, the V dimensional binary vector, defines the set of important voxels.

2.2 Prior Specifications

We assign the Gaussian priors to the regression coefficients in model (2),

$$\mathit{\alpha }~\mathrm{N}({\mathbf{0}}_{p+1},{\sigma }_{\alpha }^2{\mathbf{I}}_{p+1}),\mathit{\beta }~\mathrm{N}({\mathbf{0}}_V,{\sigma }_{\beta }^2{\mathbf{I}}_V),$$ (3)

where ${\sigma }_{\alpha }^2$ and ${\sigma }_{\beta }^2$ are the prior variances of the regression coefficients. Given a network configuration matrix W = {w_ij} for a multivariate binary random variable d = (d₁, …, d_m)^⊤ ∈ {0, 1}^m, we denote by d ~ Ising(a, b, W) an Ising distribution with a sparsity parameter a and a smoothness parameter b and the probability mass function of d is proportional to $exp\left(a{\sum }_{i=1}^{m}I[d_i=0]+b{\sum }_{i=1}^m{\sum }_{j=1}^m{w}_{ij}I[d_i=d_j]\right)$. The prior specifications for c and γ_r are

$$\begin{array}{lll}\hfill \mathbf{c}& \sim \hfill & \text{Ising}({\eta }_1,{\xi }_1,\mathbf{F}),\hfill \\ \hfill {\mathit{\gamma }}_r& \stackrel{\text{iid}}{\sim }\hfill & \text{Ising}({\eta }_2,{\xi }_2,{\mathbf{L}}_r),\text{for}r=1,\dots ,R,\hfill \end{array}$$ (4)

where F = {f_r′r} with f_r′r ∈ ℝ representing the population-level functional connectivity between region r′ and region r and L_r = {l_rv′v} with l_rv′v ∈ {0, 1} indicating whether voxels v′ and v are neighbors in region r. In our case, F can be estimated separately from the R-fMRI time series [37] or obtained from existing literature. For the hyper-prior specifications in (3) and (4), we have

$$\begin{array}{r}{\sigma }_{\beta }^2~\text{IG}(a_{\beta },b_{\beta }),{\eta }_k~\mathrm{U}(a_{\eta },b_{\eta }),\\ {\xi }_k~\mathrm{U}(a_{\xi },b_{\xi }),\text{for}k=1,2,\end{array}$$ (5)

where IG(a, b) denotes an inverse gamma distribution with shape a and rate b, and U(a, b) represents a uniform distribution on region [a, b].

2.3 Standard Posterior Computation

In a standard MCMC algorithm for posterior computation of models (2)–(5), each parameter in z, c, γ, α and ${\sigma }_{\beta }^2$ can be directly sampled from its full conditional. The sparsity and smoothness parameters in the Ising priors, η_k and ξ_k for k = 1, 2, can be updated using the auxiliary variable method by Møller et al. [38]. The details of the MCMC algorithm are provided in the supplementary materials.

In the case of high or ultra-high dimensional data, we suggest a block update of β. The full conditional of β is

$$\pi (\mathit{\beta }\mid \mathbf{z},\mathit{\alpha },\mathbf{c},\mathit{\gamma },{\sigma }_{\beta }^2,\mathbf{S},\mathbf{X})\propto \prod _{r=1}^R\prod _{v=1}^{V_r}\varphi ({\beta }_{rv}/{\sigma }_{\beta })exp\left\{-\frac{1}{2}{\Vert \mathbf{z}-\mathbf{S}\mathit{\alpha }-\mathbf{X}\{\mathit{\lambda }\circ \mathit{\beta }\}\Vert }^2\right\},$$ (6)

where ϕ(·) is the standard normal density function and ||·|| denotes the Euclidean vector norm. Given λ, the block update entails drawing β₁ (the coefficients corresponding to the selected predictors with λ = 1) and β₀ (the coefficients corresponding to the unselected predictors with λ = 0) separately from

$${\mathit{\beta }}_1~\mathrm{N}\left({\mathit{\mu }}_{{\mathit{\beta }}_1},{\mathbf{\sum }}_{{\mathit{\beta }}_1}\right),{\mathit{\beta }}_0~\mathrm{N}({\mathbf{0}}_{m_0},{\sigma }_{\beta }^2{\mathbf{I}}_{m_0}),$$ (7)

where ${\mathbf{\sum }}_{{\mathit{\beta }}_1}={\left({\sigma }_{\beta }^{-2}{\mathbf{I}}_{m_1}+{\mathbf{X}}_{\mathit{\lambda }}^{\top }{\mathbf{X}}_{\mathit{\lambda }}\right)}^{-1},{\mathit{\mu }}_{{\mathit{\beta }}_1}={\mathbf{\sum }}_{\beta }{\mathbf{X}}_{\mathit{\lambda }}^{\top }(\mathbf{z}-\mathbf{S}\mathit{\alpha })$, m₁ = ||λ||², m₀ = V − m₁, and X_λ includes the columns of X corresponding to the important voxels defined by λ. The computational complexity of computing Σ_β1 is $O(n{m}_1^2)$. While m₁ changes from one MCMC iteration to another, the posterior samples of m₁ are likely concentrated on values substantially smaller than V when the true model is sparese, i.e., the number of important voxels is small. Of note, in practice, we can divide β₁ and β₀ into smaller pieces and updated each part individually.

Compared with the single-site Gibbs sampling approach [26], [27], the block update of β reduces the computational costs and improves Markov chains mixing and hence is more appealing for high-dimensional problems where the number of predictors is on the order of thousands. However, for ultra-high dimensional problems such as imaging data in a standard brain space with around 200,000 voxels, this algorithm is still very inefficient. To address this challenge, we propose a novel multiresolution posterior computation approach.

3 MULTIRESOLUTION APPROACH

The basic steps of our multiresolution approach include first carefully constructing a sequence of brain region partitions from the pre-defined coarsest scale to the finest scale – the resolution in the observed data – and subsequently defining and fitting a sequence of auxiliary models for variable selection from the coarsest scale to the finest scale. The key idea is that the posterior samples on coarse scale variable selection are used to create a “smart” proposal for the MCMC posterior computation for the model in the next, finer scale, allowing the MCMC algorithm to explore the entire sample space for model selection more efficiently.

3.1 Partition and Auxiliary Models

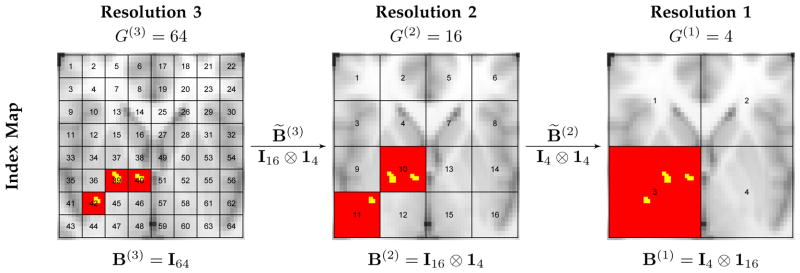
Suppose that we define K resolutions with resolution K being the target resolution in the observed data. At resolution k, the R brain regions are grouped into G^(k) mutually exclusive partitions with 1 = G⁽⁰⁾ < G⁽¹⁾ < G⁽²⁾ < ··· < G^(K) = R, where each partition is a collection of regions based on functional connectivity or spatial contiguity. The partitions at resolution k are nested within the partitions at resolution k−1. Let ${\mathbf{B}}^{(k)}=(b_{rg}^{(k)})$ be an R × G^(k) matrix with $b_{rg}^{(k)}\in \{0,1\}$ indicating whether region r is located in partition g at resolution k, and ${\stackrel{\sim }{\mathbf{B}}}^{(k)}=({\stackrel{\sim }{b}}_{g{g}^{\prime }}^{(k)})$ be a G^(k) × G^(k−1) matrix with ${\stackrel{\sim }{b}}_{g{g}^{\prime }}^{(k)}\in \{0,1\}$ indicating whether partition g at resolution k is located in partition g′ at resolution k−1. We have B^(k) 1_G^(k) = 1_R due to mutually exclusive partitions at each resolution and B^(k−1) = B^(k)B̃^(k) due to nested partitions across resolutions. In addition, B^(K) =I_R B̃⁽¹⁾ =1_G⁽¹⁾, B̃^(k) 1_G^(k−1) = 1_G^(k) and ${\{{\mathbf{B}}^{(k)}\}}_{k=1}^K$ is uniquely determined by ${\{{\stackrel{\sim }{\mathbf{B}}}^{(k)}\}}_{k=1}^K$. Figure 1 provides a detailed illustration on the partitions of a two-dimensional rectangle area in one slice of brain at three resolutions. Of note, B^(k) defines the partitions at resolution k.

Fig. 1.

An example of multiresolution partitions and variable selection. Suppose a rectangle area in one axial slice cutting through brain that contains 64 regions (R = 64) is of interest. We consider three resolutions (K = 3). Three images in the right, middle, and left panels are labeled with the partition indices for the nested partitions at resolutions 3, 2 and 1 respectively. At the highest resolution (Resolution 3) there are 64 partitions (G⁽³⁾ = 64) with each partition including only one region and the partition indices are the same as the region indices, thus B⁽³⁾ = I₆₄. Resolution 2 has 16 partitions (G⁽²⁾ = 16) where each partition g contains four regions indexed by 4g − 3, 4g − 2, 4g − 1 and 4g, for g = 1, …, 16, indicating B̃⁽³⁾ = B⁽²⁾ = I₁₆ ⊗ 1₄, where ⊗ is Kronecker product. Resolution 1 has four partitions (G⁽¹⁾ = 4) where each partition g′ contains four finer-scale partitions at resolution 2 indexed by 4g′ − 3, 4g′ − 2, 4g′ − 1 and 4g′, for g′ = 1, …, 4, resulting in B̃⁽²⁾ = I₄ ⊗ 1₄; thus it contains 16 regions indexed by 16g′ − 15, 16g′ − 14, …, 16g′, for g′ = 1, …, 16, leading to B⁽¹⁾ = I₄ ⊗ 1₁₆. Suppose the true important voxels (yellow) are located in regions 39, 40 and 41. Valid posterior inferences for models at different resolutions produce high posterior inclusion probabilities of imaging biomarkers in the corresponding partitions (red) at all resolutions.

In a similar fashion, at resolution k, we divide region r with a total of V_r voxels into $H_r^{(k)}$ mutually exclusive subregions with $1=H_r^{(0)}<H_r^{(1)}<H_r^{(2)}<\dots <H_r^{(K)}=V_r$, where each subregion is a collection of contiguous voxels. The subregions in resolution k are nested within the subregions in resolution k−1. Let ${\mathbf{A}}_r^{(k)}=(a_{\mathit{rvh}}^{(k)})$ denote a $V_r\times H_r^{(k)}$ matrix with $a_{\mathit{rvh}}^{(k)}\in \{0,1\}$ indicating whether voxel v is located in subregion h at resolution k and let ${\stackrel{\sim }{\mathbf{A}}}_r^{(k)}=({\stackrel{\sim }{a}}_{rh{h}^{\prime }}^{(k)})$ denote an $H_r^{(k)}\times H_r^{(k-1)}$ matrix with ${\stackrel{\sim }{a}}_{rh{h}^{\prime }}^{(k)}\in \{0,1\}$ indicating whether subregion h at resolution k is located in subregion h′ at resolution k−1. Similarly, we have ${\mathbf{A}}_r^{(k)}{\mathbf{1}}_{H_r^{(k)}}={\mathbf{1}}_{V_r}$ due to mutually exclusive subregions at each resolution and ${\mathbf{A}}_r^{(k-1)}={\mathbf{A}}_r^{(k)}{\stackrel{\sim }{\mathbf{A}}}_r^{(k)}$ due to subregions nested across resolutions. In addition, ${\mathbf{A}}_r^{(K)}={\mathbf{I}}_{V_r},{\stackrel{\sim }{\mathbf{A}}}_r^{(1)}={\mathbf{1}}_{H_r^{(1)}},{\stackrel{\sim }{\mathbf{A}}}_r^{(k)}{\mathbf{1}}_{H_r^{(k-1)}}={\mathbf{1}}_{H_r^{(k)}}$, and ${\{{\mathbf{A}}_r^{(k)}\}}_{k=1}^K$ is uniquely determined by ${\{{\stackrel{\sim }{\mathbf{A}}}_r^{(k)}\}}_{k=1}^K$. It follows that ${\mathbf{A}}^{(k)}=\text{diag}\{{\mathbf{A}}_1^{(k)},\dots ,{\mathbf{A}}_R^{(k)}\}$ defines the subregions at resolution k.

Given the partitions defined by B^(k) and the subregions defined by A^(k), denoted , which is given by

$$\begin{array}{lll}\hfill \mathbf{y}& =\hfill & I[{\mathbf{z}}^{(k)}\ge {\mathbf{0}}_n],\hfill \\ \hfill {\mathbf{z}}^{(k)}& =\hfill & \mathbf{S}{\mathit{\alpha }}^{(k)}+\mathbf{X}\left\{{\mathit{\lambda }}^{(k)}\circ {\mathit{\beta }}^{(k)}\right\}+{\mathit{\epsilon }}^{(k)},\hfill \end{array}$$ (8)

where z^(k), α^(k), β^(k) and ε^(k) have the same definitions and dimensions as z, α, β and ε in the target model (2). The binary indictor vector λ^(k) = (MB^(k)c^(k)) ∘ (A^(k) γ^(k)), where ${\mathbf{c}}^{(k)}=(c_g^{(k)})$ is of dimension G^(k) × 1 with $c_g^{(k)}$ denoting the selection indicator for partition g; ${\mathit{\gamma }}_r^{(k)}=({\gamma }_{rh}^{(k)})$ is of dimension $H_r^{(k)}\times 1$ with ${\gamma }_{rh}^{(k)}$ representing the selection indicator for subregion h; and ${\mathit{\gamma }}^{(k)}={({\mathit{\gamma }}_1^{{(k)}^{\top }},\dots ,{\mathit{\gamma }}_R^{{(k)}^{\top }})}^{\top }$ is of dimension H^(k) × 1 with $H^{(k)}={\sum }_{r=1}^R{H}_r^{(k)}$. By this definition, 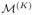is equivalent to model (2) including the prior specifications in Section 2.2. The main difference between (k < K) and 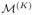is that variable selection is conducted at the partition level and the subregion level in as opposed to the region level and the voxel level in 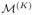, reflected by the definitions of the selection indicators in , i.e. {c^(k), γ^(k)}.

The dimensions of c^(k) and γ^(k) increase as the resolution k increases and eventually become equal to the dimensions of c and γ in the target model (2). In other words, the large number of latent indicators c and γ in the target model 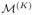, are replaced by a smaller number of latent indicators c^(k), γ^(k) (k < K) in the auxiliary model particularly in the initial resolutions. In ultra-high dimensional problems, this dimension reduction can be very significant and is exploited in our proposed sampling schemes in Sections 3.2 and 3.3 to allow for efficient posterior computations for the sequence of auxiliary models (k < K) and the target model .

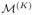For prior specifications of (k < K), we assign the same priors to α^(k) and β^(k) in (8) as α and β in (2). Denote by ${\sigma }_{\beta }^{2(k)}$ the prior variance for β^(k). We assign independent identically distributed Bernoulli priors with a probability 0.5 to c^(k) and γ^(k). Given the above prior specifications, the posterior inclusion probability for each voxel or region is always positive in each auxiliary model.

3.2 Sequential Resolution Sampling

In the analysis of ultra-high dimensional imaging data, it is reasonable to assume that the signals (i.e., important voxels and regions) are sparse and the vast majority of voxels in the brain are not associated with the outcome. Typically, many of the unimportant voxels/regions, providing little information on prediction of disease risk, are included in the model at each iteration of a standard MCMC algorithm such as the one in Section 2.3, resulting in potentially intractable posterior computations and poor mixing. To construct an efficient and computationally feasible MCMC algorithm, one solution is to specify a good proposal distribution in the Metropolis–Hastings (M–H) step for voxel/region selection. Ideally, this proposal distribution should possess two properties:

• P1: It assigns large probabilities for excluding unimportant voxels and including important voxels, which substantially reduces the number of selected voxels and simplifies computations in most MCMC iterations.

• P2: It still assigns a positive probability for including each voxel in the model, ensuring that the simulated Markov chain is able to explore the entire sample space of the voxel selection.

In other words, we want to construct a “smart” proposal distribution that mimics the true posterior distribution, likely concentrating on a neighborhood of the true model with sparse signals and hence improving efficiency and mixing. To this end, we resort to the multiresolution auxiliary models defined in Section 3.1, and develop a sequential resolution sampling (SRS) procedure. Specifically, we conduct the posterior computations for each auxiliary model sequentially from resolution 1 to resolution K. At resolution 1, we use the standard MCMC algorithm for posterior simulation on model 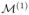. At resolution k, for k = 2, …, K, we propose a resolution dependent MCMC algorithm for posterior simulation on model , referred to as the SRS–MCMC. The essential step is an M–H step for sampling selection indicators {c^(k), γ^(k)}, where the “smart” proposal distribution is constructed using the posterior distribution (samples) of {c^(k−1), γ^(k−1)} in 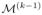at resolution k − 1. Of note, using the SRS procedure, at resolution K, we can obtain posterior samples on voxel/region selection at the finest scale, i.e. our target resolution.

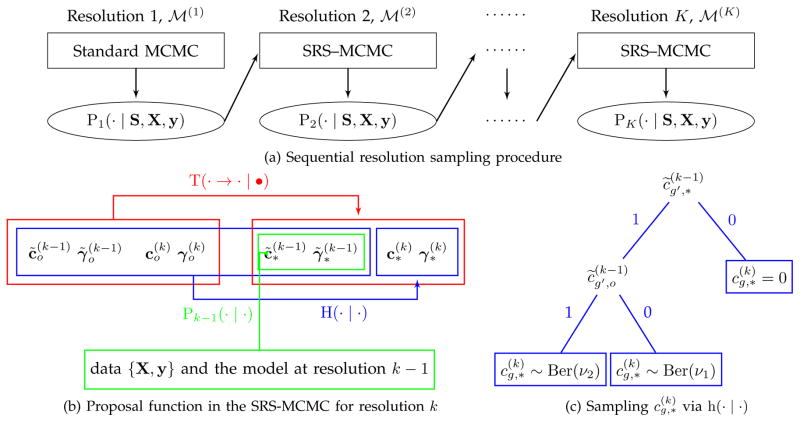
The SRS procedure is illustrated in Figures 1 and 2. Figure 1 presents an example where the location information of the important voxels is passed along from resolution 1 to resolution 3, becoming more and more accurate. Figure 2 provides the details of the SRS procedure. Specifically, to construct the “smart” proposal distributions in the M–H step of the SRS– MCMC, we first introduce auxiliary variable selection indicators c̃^(k−1) and γ̃^(k−1) in at resolution k,

Fig. 2.

Illustration of sequential resolution sampling. (a) Initially, we utilize the standard MCMC algorithm to produce the posterior distribution of the selection indicators in 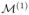at resolution 1, i.e. P₁(· | S, X, y), which is then used to guide the construction of the proposal function in the SRS-MCMC algorithm to produce P₂(· | S, X, y) for 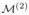at resolution 2. This procedure is performed sequentially until resolution K to generate the posterior distribution P_K(· | S, X, y) for our target model 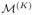. (b) Decomposition of the proposal function T(· → · | •) (red) includes two steps for drawing a proposed sample. Step 1 (green): draw { ${\stackrel{\sim }{\mathbf{c}}}_{\ast }^{(k-1)},{\stackrel{\sim }{\mathit{\gamma }}}_{\ast }^{(k-1)}$} from the posterior distribution P_k−1(· | ·) under the model 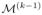at resolution k−1. Step 2 (blue): sample { ${\mathbf{c}}_{\ast }^{(k-1)},{\mathit{\gamma }}_{\ast }^{(k-1)}$} given { ${\stackrel{\sim }{\mathbf{c}}}_{\ast }^{(k-1)},{\stackrel{\sim }{\mathit{\gamma }}}_{\ast }^{(k-1)}$} in step 1 and the current state of the Markov chain using H(· | ·). (c) A binary tree represents the sampling scheme for $c_{g,\ast }^{(k)}$ based on the probability mass function h(· | ·). It is determined by $c_{g^{\prime },\ast }^{(k)}$ and ${\stackrel{\sim }{c}}_{g^{\prime },o}^{(k)}$ for g′ satisfying ${\stackrel{\sim }{b}}_{g{g}^{\prime }}^{(k)}=1$, and $c_{g,o}^{(k)}$.

$$\begin{array}{lll}{\stackrel{\sim }{c}}_{g^{\prime }}^{(k-1)}\hfill & =\hfill & max\left\{c_g^{(k)}:{\stackrel{\sim }{b}}_{g{g}^{\prime }}^{(k)}=1\right\},\hfill \\ {\stackrel{\sim }{\gamma }}_{r{h}^{\prime }}^{(k-1)}\hfill & =\hfill & max\left\{{\gamma }_{rh}^{(k)}:{\stackrel{\sim }{a}}_{rh{h}^{\prime }}^{(k)}=1\right\},\hfill \end{array}$$ (9)

for g′= 1, …, G^(k−1), r = 1, …, R and $h^{\prime }=1,\dots ,H_r^{(k-1)}$. {c̃^(k−1), γ̃^(k−1)} are completely determined by {c^(k), γ^(k)} and can be considered as a “coarse-scale summary” of the variable selection indicators in . In particular, {c̃^(k−1), γ̃^(k−1)} in are of the same dimension and structure as the variable selection indicators {c^(k−1), γ^(k−1)} in 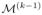. The key idea is to use the posterior distribution of {c^(k−1), γ^(k−1)} in 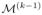as the proposal distribution for {c̃^(k−1), γ̃^(k−1)} in , which subsequently is used to guide to the construction of the proposal distribution for {c^(k), γ^(k)} in . For the ease of illustration, we denote 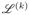= {c^(k), γ^(k), c̃^(k−1), γ̃^(k−1)} for all the latent indicators at resolution k.

The posterior distribution of the parameters and latent quantities in is

$$\pi ({\mathbf{z}}^{(k)},{\mathit{\alpha }}^{(k)},{\mathit{\beta }}^{(k)},{\sigma }_{\beta }^{2(k)},{\mathbf{c}}^{(k)},{\mathit{\gamma }}^{(k)},{\stackrel{\sim }{\mathbf{c}}}^{(k-1)},{\stackrel{\sim }{\mathit{\gamma }}}^{(k-1)}\mid \mathbf{S},\mathbf{X},\mathbf{y})=\pi ({\mathbf{z}}^{(k)},{\mathit{\alpha }}^{(k)},{\mathit{\beta }}^{(k)},{\sigma }_{\beta }^{2(k)},{\mathbf{c}}^{(k)},{\mathit{\gamma }}^{(k)}\mid \mathbf{S},\mathbf{X},\mathbf{y})·\pi ({\stackrel{\sim }{\mathbf{c}}}^{(k-1)}\mid {\mathbf{c}}^{(k)})\pi ({\stackrel{\sim }{\mathit{\gamma }}}^{(k-1)}\mid {\mathit{\gamma }}^{(k)}),$$ (10)

where π(c̃^(k−1) | c^(k)) and π(γ̃^(k−1) | γ ^(k)) are equal to 1 if (9) holds and 0 otherwise. In the SRS–MCMC, the updating scheme for {z^(k), α^(k), β^(k), ${\sigma }_{\beta }^{2(k)}$} given all other parameters is the same as the Gibbs sampling scheme for {z, α, β, ${\sigma }_{\beta }^2$} for model (2); see the supplementary materials for details. However, the updating scheme for 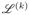is more elaborate and is described in detail as follows.

In the M-H step of the SRS-MCMC, we introduce the subscripts “*” and “o” to represent the proposed and current values of the corresponding parameters, respectively. Denote by “•” all other parameters {z^(k), α^(k), β^(k)} and data {S, X, y}. A proposal distribution for updating ${\mathcal{L}}_o^{(k)}$ is given by

$$\mathrm{T}({\mathcal{L}}_o^{(k)}\to {\mathcal{L}}_{\ast }^{(k)}\mid •)=\mathrm{H}({\mathbf{c}}_{\ast }^{(k)},{\mathit{\gamma }}_{\ast }^{(k)}\mid {\mathbf{c}}_o^{(k)},{\mathit{\gamma }}_o^{(k)},{\stackrel{\sim }{\mathbf{c}}}_o^{(k-1)},{\stackrel{\sim }{\mathit{\gamma }}}_o^{(k-1)},{\stackrel{\sim }{\mathbf{c}}}_{\ast }^{(k-1)},{\stackrel{\sim }{\mathit{\gamma }}}_{\ast }^{(k-1)})·{\mathrm{P}}_{k-1}({\stackrel{\sim }{\mathbf{c}}}_{\ast }^{(k-1)},{\stackrel{\sim }{\mathit{\gamma }}}_{\ast }^{(k-1)}\mid \mathbf{S},\mathbf{X},\mathbf{y}).$$ (11)

Here P_k−1(· | ·), specifying the sampling scheme for { ${\stackrel{\sim }{\mathbf{c}}}_{\ast }^{(k-1)},{\stackrel{\sim }{\mathit{\gamma }}}_{\ast }^{(k-1)}$}, is the posterior distribution of the variable selection indicators {c^(k−1), γ^(k−1)} in 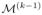at resolution k−1, and H(· | ·) specifies the sampling scheme for { ${\mathbf{c}}_{\ast }^{(k)},{\mathit{\gamma }}_{\ast }^{(k)}$} given the sampled { ${\stackrel{\sim }{\mathbf{c}}}_{\ast }^{(k-1)},{\stackrel{\sim }{\mathit{\gamma }}}_{\ast }^{(k-1)}$} from P_k−1(· | ·) and the current state of the Markov chain, i.e., 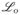. The sampling scheme based on decomposition (11) is illustrated in Figure 2b. One choice of H(· | ·) that has performed well in our numerical studies is

$$\begin{array}{l}\mathrm{H}({\mathbf{c}}_{\ast }^{(k)},{\mathit{\gamma }}_{\ast }^{(k)}\mid {\mathbf{c}}_o^{(k)},{\mathit{\gamma }}_o^{(k)},{\stackrel{\sim }{\mathbf{c}}}_o^{(k-1)},{\stackrel{\sim }{\mathit{\gamma }}}_o^{(k-1)},{\stackrel{\sim }{\mathbf{c}}}_{\ast }^{(k-1)},{\stackrel{\sim }{\mathit{\gamma }}}_{\ast }^{(k-1)})\\ =\prod _{{\stackrel{\sim }{b}}_{g{g}^{\prime }}^{(k)}=1}\mathrm{h}(c_{g,\ast }^{(k)}\mid c_{g,o}^{(k)},{\stackrel{\sim }{c}}_{g^{\prime },\ast }^{(k-1)},{\stackrel{\sim }{c}}_{g^{\prime },o}^{(k-1)},{\nu }_c)\\ ·\prod _{r=1}^R\prod _{{\stackrel{\sim }{a}}_{rh{h}^{\prime }}^{(k)}=1}\mathrm{h}({\gamma }_{rh,\ast }^{(k)}\mid {\gamma }_{rh,o}^{(k)},{\gamma }_{r{h}^{\prime },\ast }^{(k-1)},{\gamma }_{r{h}^{\prime },o}^{(k-1)},{\nu }_{\gamma })\end{array}$$ (12)

where h(· | ·) is a probability mass function for binary random variable defined as $\mathrm{h}(x\mid y,a,b,\nu )=(1-a){\delta }_0(x)+a[(1-b){\nu }_1^x{(1-{\nu }_1)}^{1-x}+b{\nu }_2^x{(1-{\nu }_2)}^{1-x}]$ for x ∈ {0, 1} with ν₁, ν₂ ∈ (0, 1) and a, b ∈ {0, 1}. In practice, we can choose a large value of ν₂ to speed up the convergence, and in our numerical studies, we set ν₁ = 0.5, ν₂ = 1. Figure 2c presents a binary tree to illustrate the sampling scheme for $c_{g,\ast }^{(k)}$ based on the h(· | ·) function and the sampling scheme for ${\gamma }_{rh,\ast }^{(k)}$ according to h(· | ·) is along the same lines.

In addition to the above M-H step, we suggest a moving step with full conditional updates for each element of {c^(k), γ^(k)} given {c̃^(k−1), γ̃^(k−1)} and all other parameters using Gibbs sampling. In this step, we merely need to update the selection for the fine-scale partitions/subregions that are nested within the selected coarse-scale partitions/subregions. Thus, this step does not require extensive computations and it improves the mixing of the entire Markov chain. To recapitulate, the updating scheme in SRS-MCMC is as follows.

Updating Scheme for {c^(k), γ^(k)} in SRS-MCMC

M-H Step

Set ${\mathcal{L}}_o^{(k)}={\mathcal{L}}_{\ast }^{(k)}$

• Draw $({\stackrel{\sim }{\mathbf{c}}}_{\ast }^{(k-1)},{\stackrel{\sim }{\mathit{\gamma }}}_{\ast }^{(k-1)})~{\mathrm{P}}_{k-1}(·\mid \mathbf{S},\mathbf{X},\mathbf{y})$;

• Draw $({\mathbf{c}}_{\ast }^{(k)},{\mathit{\gamma }}_{\ast }^{(k)})~\mathrm{H}(·\mid {\mathbf{c}}_o^{(k)},{\mathit{\gamma }}_o^{(k)},{\stackrel{\sim }{\mathbf{c}}}_o^{(k-1)},{\stackrel{\sim }{\mathit{\gamma }}}_o^{(k-1)},{\stackrel{\sim }{\mathbf{c}}}_{\ast }^{(k-1)},{\stackrel{\sim }{\mathit{\gamma }}}_{\ast }^{(k-1)})$;

• Draw r ~ U[0, 1]. Set ${\mathcal{L}}^{(k)}={\mathcal{L}}_{\ast }^{(k)}$ if r < R, where

  $$R=\frac{\pi ({\mathcal{L}}_{\ast }^{(k)}\mid •)}{\pi ({\mathcal{L}}_o^{(k)}\mid •)}\frac{\mathrm{T}({\mathcal{L}}_{\ast }^{(k)}\to {\mathcal{L}}_o^{(k)}\mid •)}{T({\mathcal{L}}_o^{(k)}\to {\mathcal{L}}_{\ast }^{(k)}\mid •)}.$$

Moving Step

Full conditional updates of { $c_g^{(k)},{\gamma }_{rh}^{(k)}$} via Gibbs sampling.

• For g′ with ${\stackrel{\sim }{c}}_{g^{\prime }}^{(k-1)}=1$ and g with ${\stackrel{\sim }{b}}_{g{g}^{\prime }}^{(k)}=1$,

• if ${\mathbf{c}}_{[-g]}^{(k)}\ne {\mathbf{0}}_{G^{(k)}-1}$ then draw $c_g^{(k)}~\pi (·\mid {\mathbf{c}}_{[-g]}^{(k)},{\mathit{\gamma }}^{(k)},•)$, else set $c_g^{(k)}=1$;

• for r with $b_{rg}^{(k)}=1$, h′ with ${\stackrel{\sim }{\gamma }}_{r{h}^{\prime }}^{(k-1)}=1$ and h with ${\stackrel{\sim }{a}}_{rh{h}^{\prime }}^{(k)}=1$,

• if ${\mathit{\gamma }}_{r[-h]}^{(k)}\ne {\mathbf{0}}_{H_r^{(k)}-1}$, then draw ${\gamma }_{rh}^{(k)}~\pi (·\mid {\mathit{\gamma }}_{r[-h]}^{(k)},{\mathit{\gamma }}_{[-r]}^{(k)},{\mathbf{c}}^{(k)},•)$, else set ${\gamma }_{rh}^{(k)}=1$.

  where ${\mathbf{c}}_{[-g]}^{(k)}={(c_1^{(k)},\dots ,c_{g-1}^{(k)},c_{g+1}^{(k)},\dots ,c_{G^{(k)}}^{(k)})}^{\top },{\mathit{\gamma }}_{r[-h]}^{(k)}={({\gamma }_{r,1}^{(k)},\dots ,{\gamma }_{r,h-1}^{(k)},{\gamma }_{r,h+1}^{(k)},\dots {\gamma }_{r,H^{(k)}}^{(k)})}^{\top }$, and ${\mathit{\gamma }}_{[-r]}^{(k)}={({\mathit{\gamma }}_1^{(k)\top },\dots ,{\mathit{\gamma }}_{r-1}^{(k)\top },{\mathit{\gamma }}_{r+1}^{(k)\top },\dots ,{\mathit{\gamma }}_R^{(k)\top })}^{\top }$.

3.3 Fast Sequential Resolution Sampling

The SRS procedure in Section 3.2 provides a general framework for posterior computations for variable selection in a ultra-high dimensional feature space. The choice of auxiliary models over resolutions and the corresponding MCMC algorithms can be flexible as long as they reduce the total computational cost and improve the mixing of the Markov chains. As an example, we consider two modifications that can potentially further improve computation efficiency: 1) Gaussian quadrature approximation in the auxiliary models (k < K) that further reduces the number of parameters in the models and 2) a joint updating scheme for the regression coefficients and the selection indicators in . Combining both, we develop a fast sequential resolution sampling (fastSRS) algorithm.

3.3.0.1 Gaussian Quadrature Approximation in Auxiliary Models

The element-wise representation of auxiliary model (8) at resolution k is given by

$$z_i^{(k)}={\alpha }_0^{(k)}+\sum _{j=1}^p{\alpha }_j^{(k)}{s}_{ij}+\sum _{g=1}^{G^{(k)}}\left[c_g^{(k)}\sum _{r=1}^R\left\{b_{rg}^{(k)}\sum _{h=1}^{H_r^{(k)}}\left({\gamma }_{rh}^{(k)}\sum _{v=1}^{V_r}{a}_{\mathit{rvh}}^{(k)}{\beta }_{rv}^{(k)}{x}_{\mathit{irv}}\right)\right\}\right]+{\epsilon }_i^{(k)}.$$ (13)

To introduce an approximation to summation ${\sum }_{v=1}^{V_r}{a}_{\mathit{rvh}}^{(k)}{\beta }_{rv}^{(k)}{x}_{\mathit{irv}}$, we first define two integrable functions ${\beta }_r^{(k)}(·)$ and x_ir(·) defined on 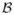with constraints that ${\beta }_r^{(k)}({\mathbf{s}}_v)={\beta }_{rv}^{(k)}$ and ${\mathrm{x}}_{ir}^{(k)}({\mathbf{s}}_v)=x_{\mathit{irv}}$, where the coordinate s_v ∈ 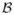represents the location of voxel v. Denote by ${\mathcal{S}}_{rh}^{(k)}$ the compact domain of subregion h in region r. Let δs represent the volume of a voxel in the brain. Based on the definition of the Riemann integral, we have

$${\int }_{{\mathcal{S}}_{rh}^{(k)}}{\beta }_r^{(k)}(\mathbf{s}){\mathrm{x}}_{ir}(\mathbf{s})d\mathbf{s}\approx \delta \mathbf{s}\sum _{v=1}^{V_r}{a}_{\mathit{rvh}}^{(k)}{\beta }_{rv}^{(k)}{x}_{\mathit{irv}}.$$ (14)

When δs is small, this approximation is accurate. If both ${\beta }_r^{(k)}(·)$ and x_ir(·) are smooth over 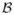, we can further approximate the integral using Gaussian quadrature on a set of sparse grids given by

$$\begin{array}{lll}{\int }_{{\mathcal{S}}_{r,h}^{(k)}}{\beta }_r^{(k)}(\mathbf{s}){\mathrm{x}}_{ir}(\mathbf{s})d\mathbf{s}\hfill & \approx \hfill & \sum _{v\in {\mathcal{Q}}_{r,h}^{(k)}}{w}_{\mathit{rvh}}^{(k)}{\beta }_{rv}^{(k)}{x}_{\mathit{irv}},\hfill \\ \sum _{v\in {\mathcal{Q}}_{rh}^{(k)}}{w}_{\mathit{rvh}}^{(k)}{\beta }_{rv}^{(k)}{x}_{\mathit{irv}}\hfill & =\hfill & \delta \mathbf{s}\sum _{v=1}^{V_r}{q}_{\mathit{rvh}}^{(k)}{\beta }_{rv}^{(k)}{x}_{\mathit{irv}}\hfill \end{array}$$ (15)

where $w_{\mathit{rvh}}^{(k)}$ is the weight and ${\mathcal{Q}}_{rh}^{(k)}$ is a set of voxel indices of the sparse grid points on ${\mathcal{S}}_{rh}^{(k)}$ based on the Smolyak’s construction rule [39]. The term $q_{\mathit{rvh}}^{(k)}=w_{\mathit{rvh}}^{(k)}/\delta \mathbf{s}$ if $v\in {\mathcal{Q}}_{rh}^{(k)},q_{\mathit{rvh}}^{(k)}=0$, otherwise. Combining (14) and (15), we can replace $a_{\mathit{rvh}}^{(k)}$ by $q_{\mathit{rvh}}^{(k)}$ in (13) to construct auxiliary models based on Gaussian quadrature approximation.

Of note, we only need to conduct such approximation at coarse scale resolutions to reduce computation when each subregion contains a large number of voxels. With ${\sum }_{r=1}^R{\sum }_{h=1}^{H_r^{(k)}}{\mathcal{Q}}_{rh}^{(k)}$ approaching V as the resolution increases, the saving in computational costs vanishes and it is recommended to use the original model (8) for fine scale resolutions. Since the auxiliary models are only used to guide the construction of the proposal distributions and our target model 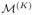remains unchanged, such an approximation is still valid.

3.3.0.2 Joint Updating Scheme

We introduce an auxiliary variable defined as

$${\stackrel{\sim }{\beta }}_{rv}^{(k)}={\gamma }_{rh}^{(k)}{\beta }_{rv}^{(k)},$$ (16)

for r = 1, …, R, and v, h with $a_{\mathit{rvh}}^{(k)}=1$. Define ${\stackrel{\sim }{\mathit{\beta }}}_{rh}^{(k)}={({\stackrel{\sim }{\beta }}_{rv}^{(k)},a_{\mathit{rvh}}^{(k)}=1)}^{\top },{\stackrel{\sim }{\mathit{\beta }}}_r^{(k)}={({\stackrel{\sim }{\mathit{\beta }}}_{r1}^{(k)\top },\dots ,{\stackrel{\sim }{\mathit{\beta }}}_{r{H}_r^{(k)}}^{(k)\top })}^{\top }$ and ${\stackrel{\sim }{\mathit{\beta }}}^{(k)}={({\stackrel{\sim }{\mathit{\beta }}}_1^{(k)\top },\dots ,{\stackrel{\sim }{\mathit{\beta }}}_R^{(k)\top })}^{\top }$. It follows that β̃^(k) is completely determined by γ^(k) and β^(k) and the joint posterior distribution of all parameters is given by

$$\begin{array}{l}\pi ({\mathbf{z}}^{(k)},{\mathit{\alpha }}^{(k)},{\mathit{\beta }}^{(k)},{\sigma }_{\beta }^{2(k)},{\mathcal{L}}^{(k)},{\stackrel{\sim }{\mathit{\beta }}}^{(k)}\mid \mathbf{S},\mathbf{X},\mathbf{y})\\ =\pi ({\mathbf{z}}^{(k)},{\mathit{\alpha }}^{(k)},{\mathit{\beta }}^{(k)},{\sigma }_{\beta }^{2(k)},{\mathbf{c}}^{(k)},{\mathit{\gamma }}^{(k)}\mid \mathbf{S},\mathbf{X},\mathbf{y})\\ \pi ({\stackrel{\sim }{\mathbf{c}}}^{(k-1)}\mid {\mathbf{c}}^{(k)})\pi ({\stackrel{\sim }{\mathit{\beta }}}^{(k)}\mid {\mathit{\gamma }}^{(k)},{\mathit{\beta }}^{(k)})\pi ({\stackrel{\sim }{\mathit{\gamma }}}^{(k-1)}\mid {\mathit{\gamma }}^{(k)}),\end{array}$$ (17)

where π(β̃^(k) | γ^(k), β^(k)) = 1 if (16) holds and zero otherwise. Furthermore, for r = 1, …, R and $h=1,\dots ,H_r^{(k)},\pi ({\mathit{\beta }}_{rh}^{(k)}\mid {\gamma }_{rh}^{(k)}=1,\mathbf{S},\mathbf{X},\mathbf{y})=\pi ({\stackrel{\sim }{\mathit{\beta }}}_{rh}^{(k)}\mid {\gamma }_{rh}^{(k)}=1,\mathbf{S},\mathbf{X},\mathbf{y})$ and $\pi ({\mathit{\beta }}_{rh}^{(k)}\mid {\gamma }_{rh}^{(k)}=0,\mathbf{S},\mathbf{X},\mathbf{y})=\pi ({\mathit{\beta }}_{rh}^{(k)})$, implying that the marginal posterior distribution of β^(k) is determined by the marginal posterior distribution of {β̃^(k), γ^(k)} and its prior. Thus, we integrate out β^(k) in (17) and focus on $\pi ({\mathbf{z}}^{(k)},{\mathit{\alpha }}^{(k)},{\sigma }_{\beta }^{2(k)},{\mathcal{L}}^{(k)},{\stackrel{\sim }{\mathit{\beta }}}^{(k)}\mid \mathbf{S},\mathbf{X},\mathbf{y})$, leading to the target distribution of the fastSRS-MCMC algorithm. Compared to the SRS-MCMC algorithm, the updating scheme for {z^(k), α^(k), ${\sigma }_{\beta }^{2(k)}$} is the same but the sampling scheme for 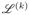and β̃^(k) needs to be modified. For an M-H step, we choose the following proposal distribution

$$\stackrel{\sim }{\mathrm{T}}[\{{\stackrel{\sim }{\mathit{\beta }}}_o^{(k)},{\mathcal{L}}_o^{(k)}\}\to \{{\stackrel{\sim }{\mathit{\beta }}}_{\ast }^{(k)},{\mathcal{L}}_{\ast }^{(k)}\}\mid •]=\mathrm{T}({\mathcal{L}}_o^{(k)}\to {\mathcal{L}}_{\ast }^{(k)}\mid •)\stackrel{\sim }{\mathrm{H}}({\stackrel{\sim }{\mathit{\beta }}}_{\ast }^{(k)}\mid {\stackrel{\sim }{\mathit{\beta }}}_o^{(k)},{\mathit{\gamma }}_{\ast }^{(k)},{\mathit{\gamma }}_o^{(k)}),$$ (18)

where T(· → · | •) is the proposal distribution in SRS-MCMC in Section 3.2. The function H̃(· | ·) is decomposed as

$$\stackrel{\sim }{\mathrm{H}}({\stackrel{\sim }{\mathit{\beta }}}_{\ast }^{(k)}\mid {\stackrel{\sim }{\mathit{\beta }}}_o^{(k)},{\mathit{\gamma }}_{\ast }^{(k)},{\mathit{\gamma }}_o^{(k)}=\prod _{r=1}^R\prod _{h=1}^{H_r^{(k)}}\stackrel{\sim }{\mathrm{h}}({\stackrel{\sim }{\mathit{\beta }}}_{rh\ast }^{(k)}\mid {\stackrel{\sim }{\mathit{\beta }}}_{rh,o}^{(k)},{\gamma }_{rh,\ast }^{(k)},{\gamma }_{rh,o}^{(k)},{\sigma }_{\beta }^{2(k)}),$$ (19)

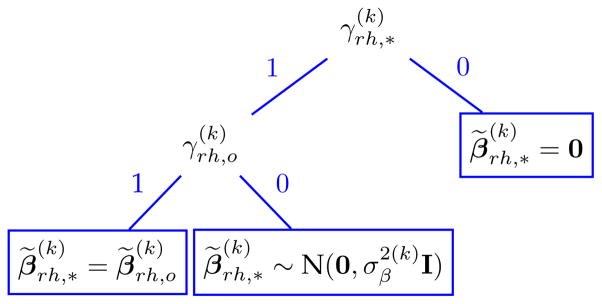
Here, h̃(· | ·) is a probability density function for a d-dimensional random vector h̃(u | v, a, b, σ²) = (1 − a)δ₀(u)+a[(1 − b)ϕ(u; 0, σ²I)+bδ_v(u)], where u, v ∈ ℝ^d (d > 1), a, b ∈ {0, 1}, σ² > 0, and ϕ(·; μ, Σ) denotes a normal density function with mean μ and covariance Σ. Figure 3 illustrates the sampling scheme for ${\stackrel{\sim }{\mathit{\beta }}}_{rh,\ast }^{(k)}$ based on h̃(· | ·), which depends on ${\mathit{\beta }}_{rh,o}^{(k)},{\gamma }_{rh,\ast }^{(k)},{\gamma }_{rh,o}^{(k)},$ and ${\sigma }_{\beta }^{2(k)}$.

Fig. 3.

A binary tree to illustrate the sampling scheme of ${\stackrel{\sim }{\mathit{\beta }}}_{rh,\ast }^{(k)}$ via h̃(· | ·).

In addition to the M-H step, we suggest a moving step to improve the mixing by updating {c^(k), γ^(k), β̃^(k)} given c̃^(k−1) and γ̃^(k−1). The moving step for c^(k) is the same as the SRS-MCMC in Section 3.2. For {β̃^(k), γ^(k)}, we consider a block updating scheme. For h′ with ${\stackrel{\sim }{\gamma }}_{r{h}^{\prime }}^{(k-1)}=1$, denote by ${\stackrel{\sim }{\mathit{\beta }}}_{r{h}^{\prime }}^{(k)}={({\stackrel{\sim }{\mathit{\beta }}}_{rh}^{(k)\top }:{\stackrel{\sim }{a}}_{rh{h}^{\prime }}^{(k)}=1)}^{\top }$ and ${\mathit{\gamma }}_{r{h}^{\prime }}^{(k)}={({\gamma }_{rh}^{(k)\top }:{\stackrel{\sim }{a}}_{rh{h}^{\prime }}^{(k)}=1)}^{\top }$ the collection of the regression coefficients and the collection of the selection indicators in for subregion h′ at resolution k − 1, respectively. Similarly, define ${\stackrel{\sim }{\mathit{\beta }}}_{r{h}^{\prime }1}^{(k)}={({\stackrel{\sim }{\mathit{\beta }}}_{rh}^{(k)\top }:{\gamma }_{rh}^{(k)}=1,{\stackrel{\sim }{a}}_{rh{h}^{\prime }}^{(k)}=1)}^{\top }$ and ${\stackrel{\sim }{\mathit{\beta }}}_{r{h}^{\prime }0}^{(k)}={({\stackrel{\sim }{\mathit{\beta }}}_{rh}^{(k)\top }:{\gamma }_{rh}^{(k)}=0,{\stackrel{\sim }{a}}_{rh{h}^{\prime }}^{(k)}=1)}^{\top }$. The updating scheme for { ${\stackrel{\sim }{\mathit{\beta }}}_{r{h}^{\prime }}^{(k)},{\mathit{\gamma }}_{r{h}^{\prime }}^{(k)}$} is based on the following decomposition of the joint full conditional distributions:

$$\pi ({\stackrel{\sim }{\mathit{\beta }}}_{r{h}^{\prime }}^{(k)},{\mathit{\gamma }}_{r{h}^{\prime }}^{(k)}\mid •)=\pi ({\gamma }_{r{h}^{\prime }}^{(k)}\mid •)\pi ({\stackrel{\sim }{\mathit{\beta }}}_{r{h}^{\prime }1}^{(k)}\mid {\mathit{\gamma }}_{r{h}^{\prime }}^{(k)},•)\pi ({\stackrel{\sim }{\mathit{\beta }}}_{r{h}^{\prime }0}^{(k)}\mid {\mathit{\gamma }}_{r{h}^{\prime }}^{(k)},•),$$ (20)

The details of (20) are provided in the supplementary materials. The updating scheme for the fastSRS-MCMC is summarized as follows.

Updating Scheme for {c^(k), γ^(k), β̃^(k)} in fastSRS-MCMC

M-H Step

Set $\{{\mathcal{L}}_o^{(k)},{\stackrel{\sim }{\mathit{\beta }}}_o^{(k)}\}=\{{\mathcal{L}}^{(k)},{\stackrel{\sim }{\mathit{\beta }}}^{(k)}\}$

• Draw ${\mathcal{L}}_{\ast }^{(k)}~\mathrm{T}({\mathcal{L}}_o^{(k)}\to ·\mid •)$;

• Draw ${\stackrel{\sim }{\mathit{\beta }}}_{\ast }^{(k)}~\stackrel{\sim }{\mathrm{H}}(·\mid {\stackrel{\sim }{\mathit{\beta }}}_o^{(k)},{\mathit{\gamma }}_{\ast }^{(k)},{\mathit{\gamma }}_o^{(k)})$;

• Draw r ~ U[0, 1]. Set $\{{\mathcal{L}}^{(k)},{\stackrel{\sim }{\mathit{\beta }}}^{(k-1)}\}=\{{\mathcal{L}}_{\ast }^{(k)},{\stackrel{\sim }{\mathit{\beta }}}_{\ast }^{(k-1)}\}$ if r < R, where

  $$R=\frac{\pi ({\mathcal{L}}_{\ast }^{(k)},{\stackrel{\sim }{\mathit{\beta }}}_{\ast }^{(k)}\mid •)}{\pi ({\mathcal{L}}_o^{(k)},{\stackrel{\sim }{\mathit{\beta }}}_o^{(k)}\mid •)}·\frac{\stackrel{\sim }{\mathrm{T}}[\{{\mathcal{L}}_{\ast }^{(k)},{\stackrel{\sim }{\mathit{\beta }}}_{\ast }^{(k)}\}\to \{{\mathcal{L}}_o^{(k)},{\stackrel{\sim }{\mathit{\beta }}}_o^{(k)}\}\mid •]}{\stackrel{\sim }{\mathrm{T}}[\{{\mathcal{L}}_o^{(k)},{\stackrel{\sim }{\mathit{\beta }}}_o^{(k)}\}\to \{{\mathcal{L}}_{\ast }^{(k)},{\stackrel{\sim }{\mathit{\beta }}}_{\ast }^{(k)}\}\mid •]}.$$

Moving Step

Full conditional updates of { $c_g^{(k)},{\mathit{\gamma }}_{r{h}^{\prime }}^{(k)},{\stackrel{\sim }{\mathit{\beta }}}_{r{h}^{\prime }}^{(k)}$} via Gibbs sampling.

• For g′ with ${\stackrel{\sim }{c}}_{g^{\prime }}^{(k-1)}=1$ and g with ${\stackrel{\sim }{b}}_{g{g}^{\prime }}^{(k)}=1$,

• if ${\mathbf{c}}_{[-g]}^{(k)}\ne {\mathbf{0}}_{G^{(k)}-1}$ then draw $c_g^{(k)}~\pi (·\mid {\mathbf{c}}_{[-g]}^{(k)},{\mathit{\gamma }}^{(k)},•)$, else set $c_g^{(k)}=1$;

• for r with $b_{rg}^{(k)}=1$, h′ with ${\stackrel{\sim }{\gamma }}_{r{h}^{\prime }}^{(k-1)}=1$, draw { ${\stackrel{\sim }{\mathit{\beta }}}_{r{h}^{\prime }}^{(k)},{\mathit{\gamma }}_{r{h}^{\prime }}^{(k)}$} based on (20).

4 APPLICATION

We analyze the motivating ABIDE study introduced in Section 1.1 using the SRS procedure. Our goal is to identify important voxel-wise image biomarkers that are predictive of the ASD risk. After removing missing observations, our analysis includes 831 subjects aggregated from 14 different sites. For each subject, the voxel-wise fALFF values are computed for each of 185,405 voxels over 116 regions in the brain. In addition, three clinical variables, age at scan, sex and IQ, are included in the analysis. Since we observe no substantial differences in the fALFF values and the number of ASDs/TDs between different study sites, site is not included in our analysis, consistent with a previous analysis of the data [1].

A region-wise functional connectivity network is constructed based on the correlations between the regional R-fMRI time series that are summarized from voxel-wise R-fMRI time series using a singular value decomposition approach [37]. The neighborhood of each voxel is defined as the set of closest voxels from six different directions (top, bottom, front, back, left, and right) in terms of the Euclidean distance; voxels are connected to their neighbors in the spatial dependence network. These two levels of structural information are incorporated using the Ising priors for selection indicators c and γ. For other prior specifications, we set ${\sigma }_{\alpha }^2=20$, leading to a fairly flat prior on α, and set a_β = 5 and b_β = 10, leading to a less-informative prior on ${\sigma }_{\beta }^2$; we specify the range of the uniform distribution priors for the sparsity parameters in the two levels of Ising model as [a_η, b_η] = [−5, 5] and for the smoothness parameters as [a_ξ, b_ξ] = [0, 5].

In light of the brain anatomy, brain partitions and corresponding subregions at eleven resolutions are used to construct auxiliary multiresolution models, { : k = 1, …, 11}. We utilize the fastSRS-MCMC in Section 3.3 to conduct the posterior inference. For each resolution, we run five MCMC chains with random initial values for 2,000 iterations with 1,000 burnin. The MCMC convergence is assessed by the GR method [40]. For all resolutions, the potential scale reduction factors (PSRF) for the log-likelihood over 1,000 iterations after burn-in are less than 1.1, suggesting convergence.

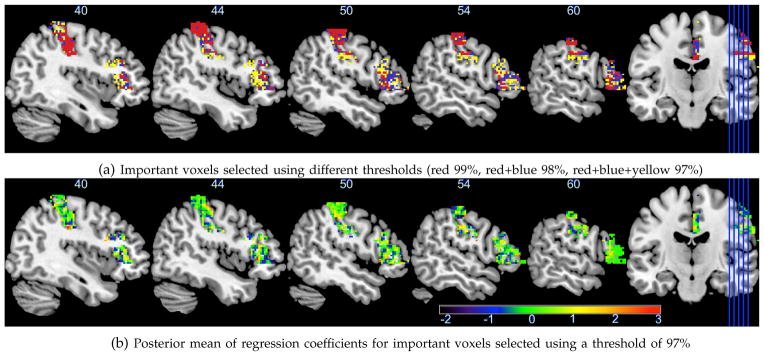
Similar to other works in imaging data analysis, we assume that the true signals are sparse. After obtaining the posterior samples of the model at the finest scale resolution, the threshold for variable selection is set to 99%, 98% or 97% quantiles of the posterior inclusion probabilities (ranging from 0.000 to 0.380) for all voxels, equivalent to selecting top 1%, 2% and 3% voxels. The selection results based on different thresholds are summarized in Table 1. For all thresholds, the selected voxels are mainly located in two regions: the right postcentral gyrus (PoCG-R) and the right inferior frontal gyrus (triangular part) (IFGtriang-R). With a threshold of 97%, our approach selects 2, 381 and 1, 424 voxels in the PoCG-R and the IFGtriang-R, respectively. Most of them are spatially clustered and contiguous within a region, as shown in Figure 4a. The PoCG is known as the center of the brain for sending and receiving the message and its volume has been shown significantly larger in autism patients compared with controls [41]. The IFGtriang is well known for its dominant roles in the cognitive control of language and memory [42], [43]. More recently, several recent task-related fMRI studies [44] showed that autism patients exhibited reduced brain activities in the IFGtriang-R. Our results further suggest that the resting state brain activities (reflected by the fALFF) in the PoCG-R and the IFGTriang-R along with other four regions are highly predictive of the ASD risk. Figure 4b presents the posterior means of the regression coefficients for the selected voxels, interestingly, showing both large positive values (red voxels) and large negative values (blue voxels) in the selected regions, especially the IFGtriang-R. Di Martino et al. [1] reported a negative association of the fALFF in a similar region (the right middle frontal gyrus) with the ASD, suggesting that there may be an anti-correlated brain network [45] located in this region that is predictive of the ASD risk. The posterior means with 95% credible intervals of regression coefficients for age, sex and IQ are respectively −0.132 (−0.580, 0.352), −0.956 (−2.048, −0.004) and −1.504 (−1.848, −1.133), indicating that age is not significantly associated with the ASD, while patients with low IQ and males have a relatively high ASD risk. These findings have the potential to help neuroscientists and epidemiologists better understand the autism etiology.

TABLE 1.

Selection results and prediction accuracy for the ASD risk. The six selected AAL regions are the right postcentral gyrus (PoCG-R), the right inferior frontal gyrus triangular part (IFGtriang- R), the right median cingulate and paracingulate gyri (DCG-R), the right superior frontal gyrus (SFGmed-R), the supplementary motor area (SMA-R) and the right heschl gyrus (HES-R). N_voxel is the total number of selected voxels. P-Sens and P-Spec represent sensitivity and specificity in prediction of the ASD risk via a ten-fold cross validation

Threshold	Selected AAL Regions	Nvoxel	P-Sens	P-Spec
99%	IFGtriang-R, PoCG-R, DCG-R,	1,779	0.938	0.918
98%	IFGtriang-R, PoCG-R, DCG-R,	3,494	0.927	0.921
97%	IFGtriang-R, PoCG-R, DCG-R, SFGmed-R, SMA-R, HES-R	5,160	0.901	0.932

Fig. 4.

Five real brain Sagittal (right) slices (X = 40, 44, 50; 54, 60 mm) cutting through two regions: IFGtriang-R and PoCG-R.

To evaluate the goodness of fit of our model, we perform a posterior predictive assessment [46] based on the χ² discrepancy and obtain a posterior predictive p-value of 0.850, indicating a good fit. To assess the performance on the ASD risk prediction, we use a tenfold cross-validation approach based on the important sampling method [47]. Table 1 shows that both sensitivity and specificity are greater than 0.9 for all three thresholds, indicating a strong predictive power of our method.

As a comparison, we also analyze the ABIDE data using an alternative approach, namely, SIS+LASSO, implemented by R packages SIS and gl1ce. This approach first identifies a set of potentially important voxels via the SIS method [48] for a probit regression model, and then applies the LASSO [6] to the same model using only the voxels selected in the first step. This approach selects only 99 important voxels, most of which are not located in the regions identified by our method. More notably, when evaluated via a ten-fold cross-validation, the SIS+LASSO approach achieves a considerably lower prediction sensitivity (0.705) and specificity (0.701) compared to our method, suggesting the superiority of our method in the prediction of the ASD risk.

5 SIMULATION STUDIES

We conduct simulation studies to evaluate the variable selection performance of the proposed methods compared with other methods for high and ultrahigh dimensional problem. In Section 5.1, focusing on a high dimensional case (1,600 voxels), we compare three posterior computation algorithms: the standard sampling method (SS) described Section 2.3 and the two proposed approaches (SRS and fastSRS) in terms of selection accuracy, computational time and ESS. To assess the effect of ν₂, for the SRS approach, we consider both cases ν₂ = 0.9 and ν₂ = 1. In Sections 5.2 and 5.3, we simulate ultra-high dimensional imaging data in light of the ABIDE data in Section 4; and we compare the proposed method with a widely used method, SIS+LASSO, as described in Section 4 for the setting when the number of true important voxels is smaller than the sample size (Simulation 2).

All the hyper-prior specifications follow those in Section 4. Similarly, all the MCMC simulations are performed under multiple chains with random initials. The convergence is confirmed by the GR method, where the PSRF is close to one for each of the simulations. All algorithms are implemented in Matlab. All the simulations are run on a PC with 3.4 GHz CPU, 8GB Memory and Windows System.

5.1 Simulation 1

We focus on a 40 × 40 two-dimensional square with 1,600 voxels (Figure 5). It consists of four regions (regions 1 – 4) each of which contains 400 voxels, i.e. R = 4, V_r = 400, for r = 1, …, 4. We set n = 100 and jointly simulate imaging biomarkers ${{\{x_{\mathit{irv}}\}}_{r=1}^R}_{v=1}^{V_r}$ from a zero mean Gaussian process with an exponential kernel (variance 0.5, correlation 36). We further set 35 and 50 voxels in regions 1 and 4 to be the true signals (red voxels in Figure 5) with the coefficients drawn from Gaussian processes with mean 5 and −6 (variance 0.2, correlation parameter 50). For each of the three algorithms, we run 3,000 iterations with 1,000 burn-in.

Fig. 5.

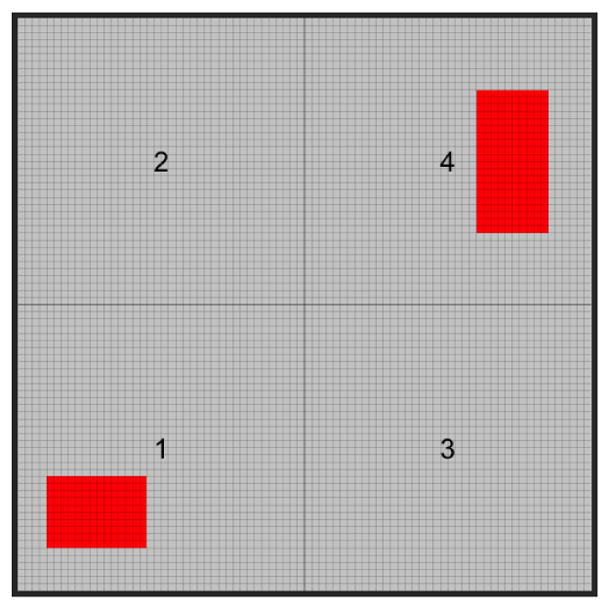
Simulation 1 design: two-dimensional square with four regions labeled with texts. Important voxels (red) are located in regions 1 and 4.

Table 2 presents the variable selection sensitivity and specificity under different thresholds, the area under the curve (AUC), the effective computing time, the resolution related computing time, and the ESS per minute for each algorithm. Comparing among different algorithms, while showing a similar performance of feature selection accuracy, the proposed algorithms (SRS and fastSRS) require a substantially lower computational cost compared to the standard method and this difference is expected to become more pronounced as the number of variables increases. In addition, as shown in Table 2, the ESS per minute for the fastSRS algorithm is around 60 times and 680 times greater than that of the algorithms SRS and SS respectively, consistent with our expectation that the fastSRS substantially improves the mixing of the Markov chains compared with the other two methods. The comparison between the SRS algorithm under different ν₂ values suggests the satisfactory performance by setting ν₂ = 1, which is adopted in the fastSRS algorithm.

TABLE 2.

Variable selection performance by three different algorithms in Simulation 1

	Threshold	SS	SRS (ν2 = 0.9)	SRS (ν2 = 1)	fastSRS
Sensitivity/Specificity	95%	0.659/0.984	0.600/0.978	0.625/0.982	0.671/0.985
	90%	0.847/0.941	0.729/0.934	0.753/0.936	0.847/0.941
	85%	0.941/0.889	0.941/0.888	0.953/0.895	0.965/0.895
	80%	0.977/0.838	1.000/0.842	1.000/0.846	1.000/0.844
AUC		0.973	0.966	0.970	0.979
Effective Time (mins)1		13.100	1.710	1.600	2.600
Resolution related Time (mins)2		0.000	5.342	5.033	7.233
ESS/min		0.669	7.458	8.381	454.004

¹Computational time for resolution K (highest resolution) for the SRS and the fastSRS.

²Computational time for resolutions 1, …, K − 1 for the SRS and the fastSRS.

To study the impact of Ising priors (4) on the variable selection results, we also implement the fastSRS algorithm with Ising priors replaced by the independent Bernoulli priors, and the results are shown in Table 3 belonging to the “Strong Signal”. From the results, we can see that the benefit of Ising priors is marginal based on current simulation setting. Therefore, we decrease the signal strength by changing the means of the coefficients of true signals to 2 and −3, and the results based on the new simulated data are listed below the “Weak Signal” in Table 3. As we can see, when signal gets weaker, adding Ising priors improves the variable selection accuracy, which is expected due to the incorporation biological and structural information.

TABLE 3.

Variable selection accuracy for the Ising prior model and independent Bernoulli prior model

	Threshold	fastSRS (With Ising Prior)	fastSRS (Without Ising Prior)
Strong Signal
Sensitivity/Specificity	95%	0.671/0.985	0.600/0.981
	90%	0.847/0.941	0.824/0.940
	85%	0.965/0.895	0.953/0.895
	80%	1.000/0.844	1.000/0.845
AUC		0.979	0.972
Weak Signal
Sensitivity/Specificity	95%	0.188/0.958	0.282/0.963
	90%	0.388/0.926	0.353/0.914
	85%	0.824/0.888	0.706/0.882
	80%	1.000/0.846	0.824/0.835
AUC		0.938	0.901

The comparable feature selection performance of the three algorithms indicates that our multiresolution approach is a useful tool to improve computational efficiency and accelerate the MCMC convergence. When the data dimension is very high, the standard sampling suffers from intensive or even intractable computation. In contrast, both the SRS and the fastSRS are still computationally feasible and have a good performance on feature selection, while the fastSRS provides a more appealing ESS. Thus, in the subsequent simulations, we only conduct posterior inference using the fastSRS, similar to Section 4.

5.2 Simulation 2

We consider an ultra-high dimensional case in simulation 2 and compare the proposed fastSRS method with the SIS+LASSO approach in terms of variable selection accuracy. We simulate 50 data sets with a sample size of 831 based on the ABIDE data. In each data set, the imaging biomarkers are generated by permuting the original ABIDE data (X) over regions, i.e., $X_{\mathit{irv}}^{\ast }=X_{{\zeta }_{ir}rv}$ for r = 1, …, R and v = 1, …, V_r, where $X_{\mathit{irv}}^{\ast }$ are the observed imaging biomarkers in a data set and (ζ_1r, …, ζ_nr) is one permutation of (1, …, n). As such, we maintain the correlations of fALFF values between voxels within each region. We choose 371 and 241 spatially contiguous voxels in two regions (IFGtriang-R and PoCG-R) that are detected in Section 4 as the true signals. The voxel-wise regression coefficients are drawn from N(7, 0.1) and N(5, 0.1) for the important voxels in the IFGtriang-R and the PoCG-R respectively, and are set to be zero for all other voxels. The fastSRS is run for 2,000 iterations with 1,000 burn-in. The SIS and the LASSO are implemented by R packages SIS and gl1ce.

Table 4 summarizes the number of true positives (TP), the number of true negatives (TN), sensitivity and specificity for different variable selection methods. Without pre-specifying the number of selected variables for SIS, the SIS function in the SIS package selects a small number of voxels (around 30), which is far smaller than the number of important voxels. To improve the performance of the SIS+LASSO, we specify the number of selected variables in SIS to be 700 for all simulations – larger than the number of true important voxels – and then apply the LASSO based on these 700 pre-selected variables. From Table 4, our methods show a substantially better performance compared to the SIS+LASSO approach in terms of the variable selection accuracy.

TABLE 4.

Variable selection performance over 50 simulated data sets by the fastSRS algorithm and the SIS+LASSO approach in Simulation 2

Method	Threshold	TP (sd)	TN (sd)	Sensitivity	Specificity
fastSRS	99%	586 (19.54)	183,528 (19.42)	0.958	0.993
	98%	612 (0.00)	181,701 (4.95)	1.000	0.983
	97%	612 (0.00)	180,002 (212.43)	1.000	0.974
SIS+LASSO		65 (5.86)	184,777 (4.84)	0.106	1.000

5.3 Simulation 3

In this simulation, we directly use the voxel-wise fALFF values over the whole brain (116 regions and 185,405 voxels) from the ABIDE data for all 831 subjects as well as the region-wise functional connectivity and voxel-wise spatial correlation information. Similar to simulation 2, the true important voxels are set to be located in the two regions (IFGtriang-R and PoCG-R) as detected in Section 4, containing 852 and 1,090 spatially contiguous voxels, respectively. The voxel-wise regression coefficients are drawn from N(3, 0.1) and N(2, 0.1) for the signals in IFGtriang-R and PoCG-R, respectively, and are set to be zero for all other voxels. The fastSRS-MCMC is run for 2,000 iterations with 1,000 burn-in. Of note, different from simulation 2, the number of important voxels is larger than the sample size in this simulation.

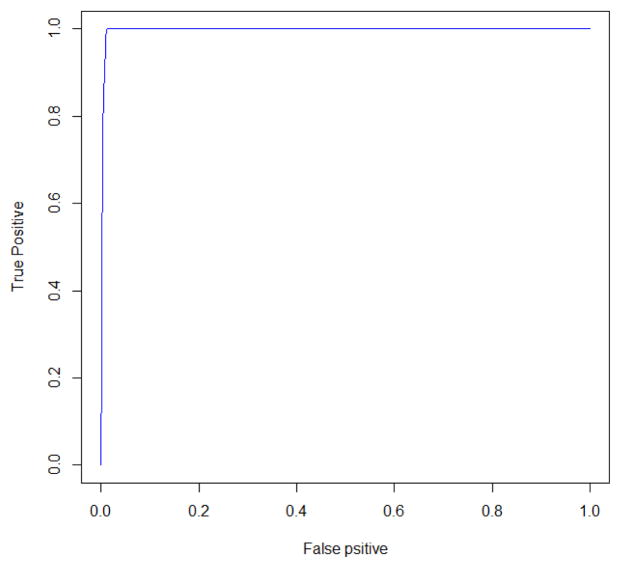
The variable selection accuracy under three thresholds are summarized in Table 5. The results suggest that our method achieves very high variable selection accuracy: both sensitivity and specificity are close to one for thresholds of 97% and 98%. Also, we obtain a very good receiver operating characteristic (ROC) curve by varying the threshold between 1% and 99% as shown in Figure 6. Such satisfactory performance not only shows the feasibility of the proposed method in an ultra-high dimensional case, but also lends credence to the selection results in the data application as the setting in the current simulation mimics the setting in the real data. The computational time for the whole posterior simulation is 2.77 hours, which is remarkable for such ultra-high dimensional data.

TABLE 5.

Variable selection accuracy for different thresholds using fastSRS-MCMC in simulation 3

Threshold	Sensitivity	Specificity
99%	0.696	0.997
98%	0.986	0.990
97%	1.000	0.982

Fig. 6.

Receiver operating characteristic (ROC) curve for variable selection using fastSRS-MCMC in simulation 3

6 Discussion

In this work, motivated by the analysis of imaging data, we present a novel Bayesian multiresolution approach for variable selection in an ultra-high dimensional feature space. Our approach is computationally feasible and efficient; and it can incorporate multi-level structural information into feature selection, leading to biologically more interpretable results and improved performance. As shown in our numerical studies, it works especially well when the true important voxels are sparse and spatially clustered.

Our approach performs variable selection by applying a threshold to the estimated posterior inclusion probabilities. We show that the selection accuracy can be very high for a set of different thresholds that are determined by the quantiles of the estimated inclusion probabilities. One interesting question would be a principled approach on how to choose an optimal threshold to obtain the highest variable selection accuracy. Liang et al. [49] has developed a multiple test-based sure variable screening procedure using marginal posterior inclusion probabilities for the generalized linear models. This approach enjoys good theoretical properties and potentially can be extended to our approach for determining an optimal threshold.

The current multiresolution approach is developed based on the commonly used latent indicator approach in a Bayesian modeling framework. The bottleneck of its posterior computation lies in the inefficiency in sampling multi-level high dimensional latent selection indicators. One direction of extending our work that may further reduce computational time is to develop parallel computing algorithms for jointly updating high dimensional latent indicators and implement them using the popular General-Purpose computation on Graphics Process Unit (GPGPU) technique [50]. Also, the Bayesian shrinkage approach as a different strategy for variable selection has also attracted much attention recently [51], [52], [53], [54], [55]. This method is closely related to penalized likelihood approaches and it imposes a “weak” sparsity prior assumption that ensures a high probability on the model parameters being close to zero rather than a positive probability of being exactly zero. It avoids introducing latent indictors and the aforementioned complication in posterior computations. Thus, another potentially interesting extension of our work is to develop a multiresolution variable selection procedure using Bayesian shrinkage methods.

The Matlab code is available at https://sites.google.com/site/yizezhaoweb/ or by request from the authors.

Biographies

Yize Zhao received her BSc degree in Statistics from Zhejiang University, China in 2010 and her PhD degree in Biostatistics from Emory University in 2014. She is now a post-doctoral research at Statistical and Applied Mathematical Sciences Institute (SAMSI) and Biostatistics Department at University of North Carolina at Chapel Hill. Her research interests include Bayesian modeling, high-dimensional data analysis and functional data analysis.

Jian Kang is an Assistant Professor in the Department of Biostatistics and Bioinformatics and the Department of Radiology and Imaging Sciences. He received his Ph.D. in Biostatistics from the University of Michigan in 2011, under the advising of Professor Timothy D. Johnson and Professor Thomas E. Nichols. His methodological research focuses on the development of statistical methods and theory for the analysis of large-scale complex biomedical data, such as imaging data, genetics data and clinical data. Dr. Kang is particularly interested in Bayesian methods and computational algorithms for the ultra-high dimensional problem.

Qi Long received the PhD degree in biostatistics from the University of Michigan, Ann Arbor, in 2005. He is an associate professor in the Department of Biostatistics and Bioinformatics at Emory University. His research interests include analysis of big data with applications to electronic health records data, omics data, and imaging data, missing data, causal inference and Bayesian methods.