Estimating Time to the Common Ancestor for a Beneficial Allele

Abstract

The haplotypes of a beneficial allele carry information about its history that can shed light on its age and the putative cause for its increase in frequency. Specifically, the signature of an allele’s age is contained in the pattern of variation that mutation and recombination impose on its haplotypic background. We provide a method to exploit this pattern and infer the time to the common ancestor of a positively selected allele following a rapid increase in frequency. We do so using a hidden Markov model which leverages the length distribution of the shared ancestral haplotype, the accumulation of derived mutations on the ancestral background, and the surrounding background haplotype diversity. Using simulations, we demonstrate how the inclusion of information from both mutation and recombination events increases accuracy relative to approaches that only consider a single type of event. We also show the behavior of the estimator in cases where data do not conform to model assumptions, and provide some diagnostics for assessing and improving inference. Using the method, we analyze population-specific patterns in the 1000 Genomes Project data to estimate the timing of adaptation for several variants which show evidence of recent selection and functional relevance to diet, skin pigmentation, and morphology in humans.

Introduction

A complete understanding of adaptation depends on a description of the genetic mechanisms and selective history that underly heritable traits (Radwan and Babik 2012). Once a genetic variant underlying a putatively adaptive trait has been identified, several questions remain: What is the molecular mechanism by which the variant affects organismal traits and fitness (Dalziel et al. 2009)?; what is the selective mechanism responsible for allelic differences in fitness?; did the variant arise by mutation more than once (Elmer and Meyer 2011)?; and when did each unique instance of the variant arise and spread (Slatkin and Rannala 2000)? Addressing these questions for numerous case studies of beneficial variants across multiple species will be necessary to gain insight into general properties of adaptation (Stinchcombe and Hoekstra 2008).

Here, our focus is on the last of the questions given above; that is, when did a mutation arise and spread? Understanding these dates can give indirect evidence regarding the selective pressure that may underlie the adaptation. This is especially useful in cases where it is logistically infeasible to assess fitness consequences of a variant in the field directly (Barrett and Hoekstra 2011). In humans, for example, dispersal across the globe has resulted in the occupation of a wide variety of habitats, and in several cases, selection in response to specific ecological pressures appears to have taken place. There are well-documented cases of loci showing evidence of recent selection in addition to being functionally relevant to known phenotypes of interest (Jeong and Di Rienzo 2014). Nakagome et al. (2016) specify time intervals defined by the human dispersal out-of-Africa and the spread of agriculture to show the relative concordance among allele ages for several loci associated with autoimmune protection and risk, skin pigmentation, hair and eye color, and lactase persistence.

When a putative variant is identified as the selected site, the nonrandom association of surrounding variants on a chromosome can be used to understand its history. This combination of surrounding variants is called a haplotype, and the nonrandom association between any pair of variants is called linkage disequilibrium (LD). Due to recombination, LD between the focal mutation and its initial background of surrounding variants follows a per-generation rate of decay. New mutations also occur on this haplotype at an average rate per generation. The focal mutation’s frequency follows a trajectory determined by the stochastic outcome of survival, mating success, and offspring number. If the allele’s selective benefit increases its frequency at a rate faster than the rate at which LD decays, the resulting signature is one of high LD and a reduction of polymorphism near the selected mutation (Smith and Haigh 1974). Many methods to exploit this pattern have been developed in an effort to identify loci under recent positive selection (reviewed in Nielsen [2005]). A parallel effort has focused on quantifying specific properties of the signature to infer the age of the selected allele.

The most commonly used methods to estimate allele age rely on summary statistics. These approaches can be further classified as either heuristic or model-based methods. Heuristic approximations rely on a point estimate of the mean length of the selected haplotype (using the decay of homozygosity around the selected locus), or a count of derived mutations within an arbitrary cutoff distance from the selected site (Thomson et al. 2000; Tang et al. 2002; Meligkotsidou and Fearnhead 2005; Hudson 2007; Coop et al. 2008). These approaches ignore uncertainty in the extent of the selected haplotype on each chromosome, which can lead to inflated confidence in the point estimates.

Alternative model-based approaches that also use summary statistics employ an Approximate Bayesian Computation (ABC) framework. These methods use an explicit model for simulation to identify a distribution of ages that are consistent with the observed data (Tavaré et al. 1997; Pritchard et al. 1999; Beaumont et al. 2002; Przeworski 2003; Voight et al. 2006; Tishkoff et al. 2007; Peter et al. 2012; Beleza, Santos, et al. 2013; Nakagome et al. 2016; Ormond et al. 2016). This provides a measure of uncertainy induced by the randomness of recombination, mutation, and genealogical history and produces an approximate posterior distribution on allele age. Despite these advantages, ABC approaches suffer from an inability to capture all relevant features of the sample due to their reliance on summary statistics.

As full-sequencing data become more readily available, defining the summary statistics which capture the complex LD among sites and the subtle differences between haplotypes will be increasingly challenging. For this reason, efficiently computable likelihood functions that leverage the full sequence data, rather than low dimensional summaries of the data, are increasingly favorable.

Several approaches attempt to compute the full likelihood of the data using an importance sampling framework (Slatkin 2001; Coop and Griffiths 2004; Slatkin 2008; Chen and Slatkin 2013). Conditioning on the current frequency of the selected allele, frequency trajectories and genealogies are simulated and given weight proportional to the probability of their occurrence under a population genetic model. While these approaches aim to account for uncertainty in the allele’s frequency trajectory and genealogy, they remain computationally infeasible for large samples or do not consider recombination across numerous loci.

In a related problem, early likelihood-based methods for disease mapping have modelled recombination around the ancestral haplotype, providing information for the time to the common ancestor (TMRCA) rather than time of mutation (Rannala and Reeve 2001, 2002; McPeek and Strahs 1999; Morris et al. 2000, 2002). These models allowed for the treatment of unknown genealogies and background haplotype diversity before access to large data sets made computation at the genome-wide scale too costly. Inference is performed under Markov chain Monte Carlo (MCMC) to sample over the unknown genealogy while ignoring LD on the background haplotypes, or approximating it using a first-order Markov chain. In a similar spirit, Chen et al. (2015) revisit this class of models to estimate the strength of selection and time of mutation for an allele under positive selection using a hidden Markov model (HMM).

HMMs have become a routine tool for inference in population genetics. The Markov assumption allows for fast computation and has proven an effective approximation for inferring the population-scaled recombination rate, the demographic history of population size changes, and the timing and magnitude of admixture events among genetically distinct populations (Li and Stephens 2003; Price et al. 2009; Hinch et al. 2011; Li and Durbin 2011; Wegmann et al. 2011). The approach taken by Chen et al. (2015) is a special case of two hidden states—the ancestral and background haplotypes. The ancestral haplotype represents the linked background that the focal allele arose on, while the background haplotypes represent some combination of alleles that recombine with the ancestral haplotype during its increase in frequency. Chen et al. (2015) compute maximum-likelihood estimates for the length of the ancestral haplotype on each chromosome carrying the selected allele. Inference for the time of mutation is performed on these fixed estimates assuming that they are known. The authors condition the probability of an ancestry switch event on a logistic frequency trajectory for the selected allele and assume independence among haplotypes leading to the common ancestor. The likelihood for background haplotypes is approximated using a first-order Markov chain to account for nonindependence among linked sites.

Here, we present an HMM that leverages both the length of the ancestral haplotype on each chromosome as well as derived mutations that have accumulated on the ancestral haplotype. Our method implements an MCMC which samples over the unknown ancestral haplotype to generate a sample of the posterior distribution for the TMRCA. Our emission probabilities account for the LD structure among background haplotypes using the Li and Stephens (2003) haplotype copying model and a reference panel of haplotypes without the selected allele (fig. 1b and c). In contrast to the first-order Markov chain employed by Chen et al. (2015), the Li and Stephens (2003) model provides an approximation to the coalescent with recombination by modelling a focal haplotype as an imperfect mosaic of haplotypes in the reference panel.

Fig. 1.

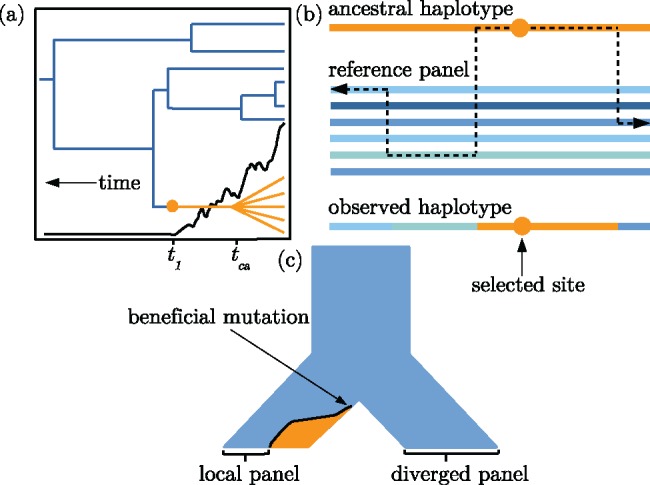
Visual descriptions of the model. (a) An idealized illustration of the effect of a selectively favored mutation’s frequency trajectory (black line) on the shape of a genealogy at the selected locus. The orange lineages are chromosomes with the selected allele. The blue lineages indicate chromosomes that do not have the selected allele. Note the distinction between the time to the common ancestor of chromosomes with the selected allele, t_ca, and the time at which the mutation arose, t₁. (b) The copying model follows the ancestral haplotype (orange) moving away from the selected site until recombination events within the reference panel lead to a mosaic of nonselected haplotypes surrounding the ancestral haplotype. (c) A demographic history with two choices for the reference panel: Local and diverged. After the ancestral population at the top of the figure splits into two sister populations, a beneficial mutation arises and begins increasing in frequency. The orange and blue colors indicate frequency of the selected and nonselected alleles, respectively.

While Chen et al. (2015) use a mutation parameter in their HMM, the count of derived mutations on the background haplotype does not directly influence their estimation of time since mutation. The probability of observing a mutation on the selected haplotypes of beneficial allele carriers depends on two parameters: The per-generation mutation rate and the time to the common ancestor (TMRCA). The Chen et al. model uses a compound parameter for these such that the observed mutations do not directly inform their estimates of timing. In our model, we separately include the TMRCA and mutation rate as parameters and thus incorporate information from mutations directly into our inference of the TMRCA.

Our approach also differs in that we do not presume to know the true extent of the ancestral haplotype, and instead treat it as a latent variable to be marginalized over. This allows our estimation of the TMRCA to reflect uncertainty in the precise switch point off of the ancestral haplotype, which in many cases will be difficult to distinguish from the background haplotypes. Another significant difference is that our model does not make assumptions about the frequency trajectory apart from that a sufficiently hard sweep occurred to incur a star-shaped genealogy. Below, we use simulations to show the sensitivity of our model to these simplified assumptions for varying strengths of selection, final allele frequencies, and sampling regimes for the choice of reference panel. An R package is available to implement this method on github (https://github.com/jhavsmith/startmrca; last accessed January 23, 2018).

New Approaches

Model Description

In general, the TMRCA for a sample of haplotypes carrying the advantageous allele (hereafter referred to as t_ca) will be more recent than the time of mutation (Kaplan et al. 1989). We aim to estimate t_ca in the case where a selectively advantageous mutation occurred in an ancestor of our sample t₁ generations ago (fig. 1a in main text). Viewed backwards in time, the selected variant decreases in frequency at a rate proportional to the selection strength. During a rapid drop in allele frequency, the coalescent rate among haplotypes carrying the selected variant is amplified. The same effect would be observed for population growth from a small initial size forward in time (Hudson 1990; Slatkin and Hudson 1991). As a result, the genealogy of a sample having undergone selection and/or population growth becomes more “star-shaped.” This offers some convenience, as it becomes more appropriate to invoke an assumption of independence among lineages when selection is strong. We would like to emphasize that this assumption necessarily implies that the beneficial allele has a single ancestral haplotype that has increased in frequency. This is in contrast to a scenario in which the beneficial allele has been present in the population for some time prior to selection. For that case, multiple ancestral haplotypes would increase in frequency simultaneously resulting in a genealogy that is not star-shaped.

We assume no crossover interference between recombination events within a haplotype, and therefore treat each side flanking the focal allele separately. We define one side of the selected site, within a window of some predetermined length, to have L segregating sites, such that an individual’s sequence will be indexed from site $s=\{1,\mathrm{\dots },L\}$, where s = 1 refers to the selected site (a notation reference is provided in table 1). To simplify notation, this description will be written for a window on one side flanking the selected site. Note that the opposing side of the selected site is modelled in an identical fashion after redefining L.

Table 1.

Notation Used to Describe the Model.

n	Number of haplotypes with the selected allele
m	Number of haplotypes without the selected allele
L	Number of SNPs flanking the selected site (one side considered at a time)
X	n × L matrix of haplotypes with the selected allele
H	m × L matrix of haplotypes without the selected allele
Xij	Allele in haplotype i at SNP j, where $i\in \{1,\mathrm{\dots },n\}$, and $j\in \{1,\mathrm{\dots },L\}$
Hzj	Allele in haplotype z at SNP j, where $z\in \{1,\mathrm{\dots },m\}$, and $j\in \{1,\mathrm{\dots },L\}$
Aj	Allele at site j on the ancestral haplotype
Zij	The reference panel haplotype from which Xi copies at site j
tca	Time to the most recent common ancestor (TMRCA)
Wi	The location of the first recombination event off of the ancestral haplotype
r	Recombination rate per basepair per generation
μ	Mutation rate per basepair per generation
θ	Haplotype miscopying rate, or population-scaled mutation rate $(4N\mu )$
ρ	Haplotype switching rate, or population-scaled recombination rate $(4Nr)$
dw	Physical distance of site w from the selected site, where $w\in \{1,\mathrm{\dots },L\}$
cj	Number of basepairs between sites j and j + 1
αiw	Likelihood of haplotype i for sites $1,\mathrm{\dots },w$
βiw	Likelihood of haplotype i for SNPs $(w+1),\mathrm{\dots },L$

Let X denote an n × L data matrix for a sample of n chromosomes with the selected variant. X_ij is the observed allelic type in chromosome i at variant site j, and is assumed to be biallelic where $X_{ij}\in \{1,0\}$. Let H denote an m × L matrix comprising m chromosomes that do not have the selected variant where $H_{ij}\in \{1,0\}$. Let A denote the ancestral haplotype as a vector of length L where A_j is the allelic type on the ancestral selected haplotype at segregating site j and $A_j\in \{1,0\}$. We assume independence among lineages leading to the most recent common ancestor of the selected haplotype. This is equivalent to assuming a star-shaped genealogy which, as noted above, is a reasonable assumption for sites linked to a favorable variant under strong selection. We can then write the likelihood as

$$\mathrm{Pr}(X|t_{\text{ca}},A,H)=\prod _i^n\mathrm{Pr}(X_i|t_{\text{ca}},A,H).$$ (1)

In each individual haplotype, X_i, we assume the ancestral haplotype extends from the selected allele until a recombination event switches ancestry to a different genetic background. Let W = w indicate that the location of the first recombination event occurs between sites w and w + 1, where $W\in \{1,\mathrm{\dots },L\}$ (w = L indicates no recombination up to site L). We can then condition the probability of the data on the interval where the first recombination event occurs and sum over all possible intervals to express the likelihood as

$$\mathrm{Pr}(X_i|t_{\text{ca}},A,H)=\sum _{w=1}^L\mathrm{Pr}(X_i|t_{\text{ca}},A,H,W_i=w)\mathrm{Pr}(W_i=w|t_{\text{ca}}).$$ (2)

Assuming haplotype lengths are independent and identically distributed draws from an exponential distribution, the transition probabilities for a recombination event off of the ancestral haplotype are

$$\mathrm{Pr}(W_i=w|t_{\text{ca}})=\{\begin{array}{cc}{\mathrm{e}}^{-r{t}_{\text{ca}}{d}_w}(1-{\mathrm{e}}^{-r{t}_{\text{ca}}(d_{w+1}-d_w)})\hfill & \text{if}w=\{1,\mathrm{\dots },(L-1)\};\hfill \\ {\mathrm{e}}^{-r{t}_{\text{ca}}{d}_L}\hfill & \text{if}w=L\hfill \end{array}$$ (3)

where d_w is the distance, in base pairs, of site w from the selected site and r is the local recombination rate per base pair, per generation. The data for each individual, X_i, can be divided into two parts: One indicating the portion of an individual’s sequence residing on the ancestral haplotype (before recombining between sites w and w + 1), $X_{i(j\le w)}$, and that portion residing off of the ancestral haplotype after a recombination event, $X_{i(j>w)}$. We denote a separate likelihood for each portion:

$${\alpha }_{iw}=\mathrm{Pr}(X_{i(j\le w)}|t_{\text{ca}},A,W_i=w),$$ (4)

$${\beta }_{iw}=\mathrm{Pr}(X_{i(j>w)}|H_{(j>w)},W_i=w).$$ (5)

Because the focal allele is on the selected haplotype, ${\alpha }_{i1}=1$. Conversely, we assume a recombination event occurs at some point beyond locus L such that ${\beta }_{iL}=1$. We assume the waiting time to mutation at each site on the ancestral haplotype is exponentially distributed with no reverse mutations and express the likelihood as

$${\alpha }_{iw}=\mathrm{Pr}(X_{i(j\le w)}|t_{\text{ca}},A,W_i=w)={\mathrm{e}}^{-t_{\text{ca}}\mu (d_w-w)}\prod _{j=2}^w\mathrm{Pr}(X_{ij}=a|t_{\text{ca}},A),$$ (6)

$$\mathrm{Pr}(X_{ij}=a|t_{\text{ca}},A)=\{\begin{array}{cc}{\mathrm{e}}^{-t_{\mathrm{c}\mathrm{a}}\mu }\hfill & \text{if}a=A_j;\hfill \\ 1-{\mathrm{e}}^{-t_{\mathrm{c}\mathrm{a}}\mu }\hfill & \text{if}a\cancel{=}{A}_j\hfill \end{array}.$$ (7)

The term, ${\mathrm{e}}^{-t_{\text{ca}}\mu (d_w-w)}$, on the right side of equation (6) captures the lack of mutation at invariant sites between each segregating site. Assuming $t_{\text{ca}}\mu$ is small, equation (6) is equivalent to assuming a Poisson number of mutations (with mean $t_{\text{ca}}\mu$) occurring on the ancestral haplotype.

For β_iw, the probability of observing a particular sequence after recombining off of the ancestral haplotype is dependent on standing variation in background haplotype diversity. The Li and Stephens (2003) haplotype copying model allows for fast computation of an approximation to the probability of observing a sample of chromosomes related by a genealogy with recombination. Given a sample of m haplotypes, $H\in \{h_1,\mathrm{\dots },h_{\mathrm{m}}\}$, a population scaled recombination rate ρ and mutation rate θ, an observed sequence of alleles is modeled as an imperfect copy of any one haplotype in the reference panel at each SNP. Let Z_ij denote the reference panel haplotype which X_i copies at the jth SNP, and c_j denote the number of base pairs between SNPs j and j + 1. Z_ij follows a Markov process with transition probabilities

$$\mathrm{Pr}(Z_{i(j+1)}=z\prime |Z_{ij}=z)=\{\begin{array}{cc}{\mathrm{e}}^{-{\rho }_j{c}_j/m}+(1-{\mathrm{e}}^{-{\rho }_j{c}_j/m})(1/m)\hfill & \text{if}z\prime =z;\hfill \\ (1-{\mathrm{e}}^{-{\rho }_j{c}_j/m})(1/m)\hfill & \text{if}z\prime \cancel{=}z.\hfill \end{array}$$ (8)

To include mutation, the probability that the sampled haplotype matches a haplotype in the reference panel is $m/(m+\theta )$, and the probability of a mismatch (or mutation event) is $\theta /(m+\theta )$. Letting a refer to an allele where $a\in \{1,0\}$, the matching and mismatching probabilities are

$$\mathrm{Pr}(X_{ij}=a|Z_{ij}=z,h_1,\mathrm{\dots },h_m)=\{\begin{array}{cc}m/(m+\theta )+(1/2)(\theta /(m+\theta ))\hfill & \text{if}{h}_{z,j}=a;\hfill \\ (1/2)(\theta /(m+\theta ))\hfill & \text{if}{h}_{z,j}\cancel{=}a.\hfill \end{array}$$ (9)

Equation (5) requires a sum over the probabilities of all possible values of Z_j using equations (8) and (9). This is computed using the forward algorithm as described in Rabiner (1989) and Appendix A of Li and Stephens (2003). It should be noted that this formulation does not model the observation of an invariant site among the background haplotypes. We tried an approach to model these sites, but saw no improvement in model performance (see supplementary appendix S2, Supplementary Material online).

The complete likelihood for our problem can then be expressed as:

$$\mathrm{Pr}(X|t_{\text{ca}},A,H)=\prod _{i=1}^n\sum _{w=1}^L{\alpha }_{iw}{\beta }_{iw}\mathrm{Pr}(W_i=w|t_{\text{ca}},A).$$ (10)

This computation is on the order $2Ln{m}^2$, and in practice for m = 20, n = 100 and L = 4,000 takes approximately 3.027 s to compute on an Intel Core i7-4750HQ CPU at 2.00 GHz × 8 with 15.6 GB RAM.

Inference

Performing inference on t_ca requires addressing the latent variables w and A in the model. Marginalizing over possible values of w is a natural summation per haplotype that is linear in L as shown above. For A, the number of possible values is large ($2^L$), and so we employ a Metropolis–Hastings algorithm to jointly sample the posterior of A and t_ca, and then we take marginal samples of t_ca for inference. We assign a uniform prior density for both A and t_ca, such that $\mathrm{Pr}(A)=1/2^L$ and $\mathrm{Pr}(t_{\text{ca}})=1/(t_{\text{max}}-t_{\text{min}})$ where t_max and t_min are user-specified maximum and minimum values for t_ca. Proposed MCMC updates of the ancestral haplotype, $A\prime$, are generated by randomly selecting a site in A and flipping to the alternative allele. For t_ca, proposed values are generated by adding a normally distributed random variable centered at 0: $t_{\text{ca}}\prime =t_{\text{ca}}+N(0,{\sigma }^2)$. To start the Metropolis–Hastings algorithm, an initial value of t_ca is uniformly drawn from a user-specified range of values (10–2,000 in the applications here). To initialize the ancestral haplotype to a reasonable value, we use a heuristic algorithm which exploits the characteristic decrease in variation near a selected site (see supplementary appendix S2, Supplementary Material online).

For each haplotype in the sample of beneficial allele carriers, the Li and Stephens (2003) model uses a haplotype miscopying rate θ, and switching rate ρ, to compute a likelihood term for loci following the recombination event off of the ancestral haplotype. For our analyses, we set $\rho =4.4\times {10}^{-4}$ using our simulated values of $r=1.1\times {10}^{-8}$ per bp per generation and N = 10,000, where $\rho =4Nr$. Following Li and Stephens (2003) we fix $\theta ={(\sum _{m=1}^{n}1/m)}^{-1}$; as derived from the expected number of mutation events on a genealogy relating n chromosomes at a particular site. We found no discernible effects on estimate accuracy when specifying different values of ρ (supplementary fig. 1, Supplementary Material online).

Results

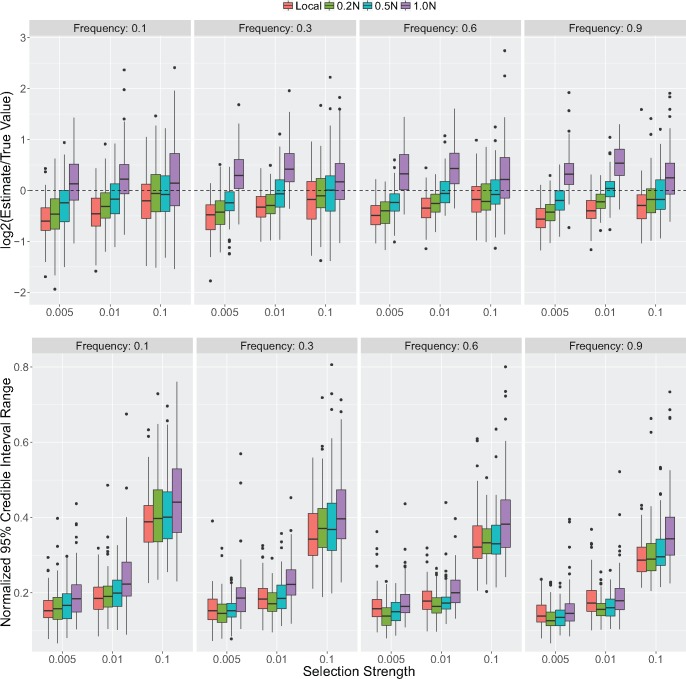
Because our model requires a sample (or “panel”) of reference haplotypes without the selected allele, we tested our method for cases in which the reference panel is chosen from the local population in which the selected allele is found, as well as cases where the panel is from a diverged population where the selected haplotype is absent (fig. 1c). Regardless of scenario, the estimates are on average within a factor of 2 of the true value, and often much closer. When using a local reference panel, point estimates of t_ca increasingly underestimate the true value (TMRCA) as selection becomes weaker and the final allele frequency increases (fig. 2). Put differently, the age of older TMRCAs tends to be underestimated with local reference panels. Using the mean posteriors as point estimates, mean values of log₂(estimate/true value) range from −0.62 to −0.14. Simulations using a diverged population for the reference panel removed the bias, though only in cases where the divergence time was not large. For a reference panel diverged by $0.5N$ generations, mean log₂(estimate/true value) values range from −0.21 to −0.18. As the reference panel becomes too far diverged from the selected population, estimates become older than the true value (0.36 to 0.94 log₂(estimate/true value)). In these cases, the HMM is unlikely to infer a close match between background haplotypes in the sample and the reference panel, leading to many more mismatches being inferred as mutation events on the ancestral haplotype and an older estimate of t_ca.

Fig. 2.

Accuracy results from simulated data. Accuracy of TMRCA point estimates and 95% credible interval ranges from posteriors inferred from simulated data under different strengths of selection, final allele frequencies and choice of reference panel. Credible interval range sizes are in units of generations and are normalized by the true TMRCA for each simulated data set. See Materials and Methods below for simulation details.

The bottom panel of figure 2 shows the effect of selection strength and final allele frequency on the size of the 95% credible interval around point estimates normalized by the true TMRCA for each simulated data set. Before normalizing, credible interval sizes using a local reference panel range from 73 to 213 generations for $2Ns=100$, versus 18 to 22 generations when $2Ns=2000$. Using local and diverged reference panels, we found a minimal effect of the sample size on point estimates (supplementary figs. 2 and 3, Supplementary Material online). As expected, larger sample sizes for the carrier panel improve estimate accuracy. However, higher allele frequencies and weak selection are likely to induce more uncertainty due to the ancestral haplotype tracts recombining within the sample. We find this effect more pronounced with large sample sizes for the reference panel. We speculate that a large sample of reference haplotypes leads the focal selected haplotype to have increased probability of copying from the reference panel leading to a shorter selected haplotype and slight overestimate of the TMRCA.

We also performed simulations under varying degrees of mutation and recombination rate misspecification (supplementary fig. 4, Supplementary Material online). In most cases, mean values of log₂(estimate/true value) stay within an order of magnitude of 0. As expected, when both the mutation and recombination rate are misspecified, we find the most discrepancy. To assess the convergence properties of the MCMC, five replicate chains were run for each of 20 simulated data sets produced under three 2Ns values (100, 200, and 2,000) for frequency trajectories ending at 0.1 (supplementary fig. 5, Supplementary Material online). While care is always warranted with MCMC approaches, we find in practice that convergence among our replicate chains is attained relatively quickly ($\approx 3,000$ iterations for simulated data and 3,000–9,000 iterations for applied cases; see supplementary fig. 9, Supplementary Material online).

We compared the performance of our estimator with three other model-based approaches for allele age estimation by matching the simulation scheme performed by Chen et al. (2015) (supplementary table 5, Supplementary Material online). Our method shows improvement in accuracy (RMSE) and/or lower bias for simulations with lower frequencies of the beneficial allele (40%) regardless of the reference panel used. In cases where the final beneficial allele frequency is higher (80%), our method’s accuracy remains as good or better than the other methods when using a diverged reference panel, with a two-orders-of-magnitude improvement of bias under strong selection (s = 0.05). Estimates when using a local reference panel and a high final beneficial allele frequency remain comparable to the other methods for strong selection, but tend to have more bias and decreased accuracy as selection strength decreases.

Assuming a star-genealogy among beneficial allele carriers may result in underestimating the variance for the posterior distribution when there is nonindependence in our sample. To measure this affect, we computed TMRCA estimates on 100 bootstrap replicates for 4 simulated data sets under 2 selection strengths and 2 final allele frequencies (supplementary table 7, Supplementary Material online). We find close agreement between the 95% posterior credible intervals of the original data and the 95% confidence intervals computed on the bootstrap estimates for a selection strength of 0.1. for both final allele frequencies of 0.4 and 0.8. As expected, older TMRCAs are likely to violate the star-genealogy assumption, and in these cases we find that estimates from our original data are more narrow than the bootstrap confidence intervals.

Recombination versus Mutation as a Source of Information

We compared our model-based inference with simpler estimates of the TMRCA using the number of derived mutations on the ancestral haplotype, and the mean length of the ancestral haplotype. In addition to quantifying the improvement our method has over these calculations, this also serves as an ad-hoc way to understand how the relative weight of information from mutation and recombination affects the performance of our method. One can model the haplotype lengths as independent and exponentially distributed to derive a recombination-based estimator, ${\widehat{t}}_{\mathrm{r}}$, as

$${\widehat{t}}_{\mathrm{r}}=\frac{1}{{\overline{w}}_{o}r},$$ (11)

where r is the recombination rate and ${\overline{w}}_o$ is the observed mean ancestral haplotype length. To leverage the count of derived mutations on the ancestral haplotype, we use the Thomson et al. (2000) estimator. In a sample of n haplotypes with the selected allele, a mutation-based estimator, ${\widehat{t}}_{\mathrm{m}}$, can be calculated as

$${\widehat{t}}_{\mathrm{m}}=\frac{1}{n}\sum _i^n\frac{y_i}{w_i\mu },$$ (12)

where y_i is the number of derived mutations on the ith haplotype which has length w_i basepairs. See Hudson (2007) for a derivation of the estimate for the variance of the Thomson estimator.

When using derived mutations, uncertainty in both the ancestral haplotype sequence and the length of the ancestral haplotype on each chromosome (w_i) can lead to poor estimation. To improve inference, researchers typically define a restricted “nonrecombining” region that may reliably contain derived mutations on the ancestral haplotype. This has two disadvantages: 1) There is more information available in the data which cannot be used because excess caution is necessary to prevent overcounting of derived mutations; and 2) there may still be unobserved recombination events in this restricted locus. To minimize the use of heuristics for a derived mutation approach, we used our model to find maximum-likelihood estimates of the ancestral haplotype breakpoints using equation (2) in the model description. We also used the mean posterior estimate of the ancestral haplotype from our model to identify derived mutations. To calculate a recombination-based estimator of the TMRCA, we calculated ${\overline{w}}_o$ using the same maximum-likelihood estimates of the ancestral haplotype lengths inferred for the mutation estimator.

When using a local reference panel, the simple mutation estimator ${\widehat{t}}_{\mathrm{m}}$ consistently underestimates the true TMRCA. The recombination estimate, however, remains accurate (supplementary fig. 6, Supplementary Material online). We suspect this to be a result of poor estimation of the ancestral haplotype and violation of the star-genealogy assumption. In cases where selection is weaker and the genealogy is not star-shaped, derived mutations occurring early in the genealogy will be overrepresented and incorrectly inferred to be the ancestral allele. In this way, high-frequency-derived alleles will not be counted. As predicted, increasing selection strength improves mutation estimator accuracy. The recombination estimator appears robust to this effect as long as selection is not too strong. For very strong selection, and young TMRCA values, maximum-likelihood estimates of the haplotype lengths become constrained by the size of the locus studied. For example, in simulations with a selection strength of 0.05 and frequency of 0.1, the mean TMRCA is around 100 generations. Using equation (11) above, the mean length of the ancestral haplotype for a TMRCA of 100 generations is 2 Mb, which is twice as large as the window size we use to make computation for our simulations feasible. Using a larger window around the selected locus would ameliorate this effect.

When using a diverged reference panel we find an opposite effect. In this case, the count of derived mutations results in an overestimate and the haplotype lengths yield an underestimate. We suspect this to be driven by poor matching between the reference panel and the background haplotypes among beneficial allele carriers. The low probability of matching between the reference and background haplotypes means that the lengths of the ancestral haplotype are inferred to extend further than their true lengths. This also leads to an overestimate for the mutation estimator because differences between the ancestral and background haplotypes are incorrectly inferred as derived mutations on the ancestral haplotype.

Application to 1000 Genomes Data

We applied our method to five variants previously identified as targets of recent selection in various human populations (fig. 3). Using phased data from the 1000 Genomes Project, we focused on variants that are not completely fixed in any one population so that we could use a local reference panel. The Li and Stephens (2003) haplotype copying model is appropriate in cases where ancestry switches occur among chromosomes within a single population, so we excluded populations in the Americas for which high levels of admixture are known to exist.

Fig. 3.

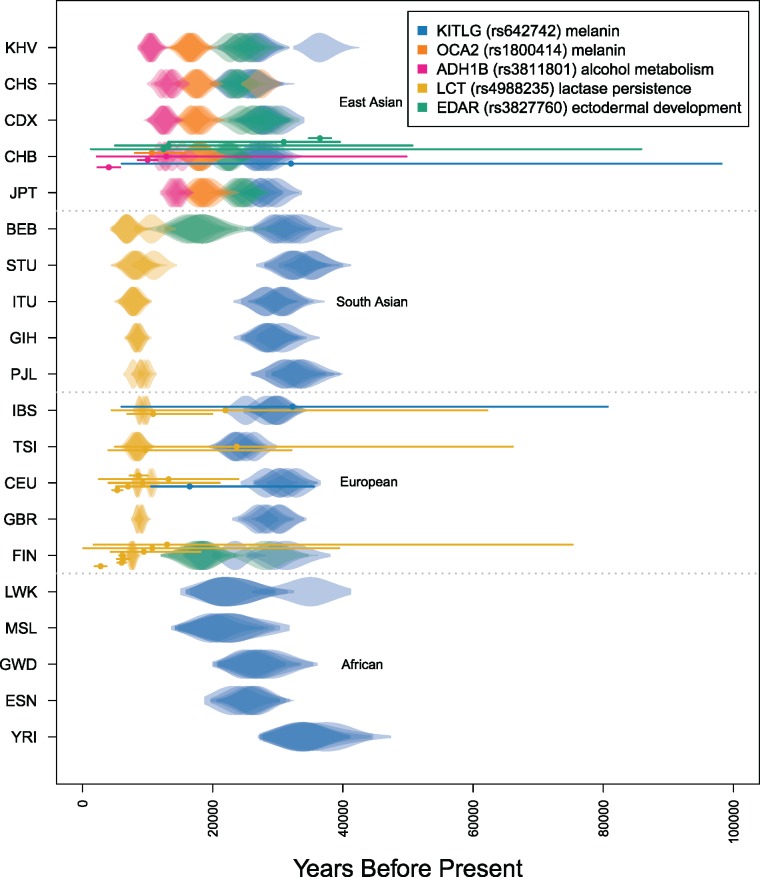
Comparison of TMRCA estimates with previous results. Violin plots of posterior distributions for the complete set of estimated TMRCA values for the five variants indicated in the legend scaled to a generation time of 29 years. Each row indicates a population sample from the 1000 Genomes Project panel. Replicate MCMCs are plotted with transparency. Points and lines overlaying the violins are previous point estimates and 95% confidence intervals for each of the variants indicated by a color and rs number in the legend (see supplementary tables 3 and 4, Supplementary Material online). The population sample abbreviations are defined in text.

While the simulation results described above provide some intuition for the effects of selection strength, final allele frequency, and choice of reference panel, we also performed simulations using the demographic history inferred by Tennessen et al. (2012) to explore the effects of nonequilibrium demographic history on our estimation accuracy (supplementary fig. 10, Supplementary Material online). We find subtle differences in accuracy between the two demographic histories, where the nonequilibrium histories lead to negligible differences in mean values for log₂(estimate/true value) and larger credible interval ranges.

ADH1B

A derived allele at high frequency among East Asians at the ADH1B gene (rs3811801) has been shown to be functionally relevant for alcohol metabolism (Osier et al. 2002; Eng et al. 2007). Previous age estimates are consistent with the timing of rice domestication and fermentation approximately 10,000 years ago (Li et al. 2007; Peng et al. 2010; Peter et al. 2012). However, a more recent estimate by Peter et al. (2012) pushes this time back several thousand years to 12,876 (2,204–49,764) years ago. Our results are consistent with an older timing of selection, as our CHB sample (Han Chinese in Beijing, China) TMRCA estimate is 15,377 (13,763–17,281) years. Replicate chains of the MCMC are generally consistent, with the oldest estimates in the CHB sample showing the most variation among resampled data sets and the youngest estimate of 10,841 (9,720–12,147) in the KHV sample showing the least. When using a fine-scale recombination map, all of the ADH1B TMRCAs are inferred to be slightly older (supplementary fig. 7, Supplementary Material online).

EDAR

Population genomic studies have repeatedly identified the gene EDAR to be under recent selection in East Asians (Akey et al. 2004; Williamson et al. 2005; Voight et al. 2006) with a particular site (rs3827760) showing strong evidence for being the putative target. Functional assays and allele specific expression differences at this position show phenotypic associations to a variety of phenotypes including hair thickness and dental morphology (Bryk et al. 2008; Fujimoto et al. 2008; Kimura et al. 2009; Kamberov et al. 2013).

Our estimate of 22,192 (19,683–25,736) years for the EDAR allele in the CHB sample is older than ABC-based estimates of 12,458 (1,314–85,835) and 13,224 (4,899–50,692) years made by Bryk et al. (2008) and Peter et al. (2012), respectively. Kamberov et al. (2013) use spatially explicit ABC and maximum likelihood approaches to compute older estimates of 30,925 (13,175–39,575) and 36,490 (34,775–38,204). We included all populations for which the variant is present including the FIN and BEB samples where it exists at low frequency. Our results for the youngest TMRCAs are found in these two low frequency populations, where the estimate in FIN is 17,386 (13,887–20,794) and the estimate in BEB is 18,370 (14,325–22,872). Among East Asian populations, the oldest and youngest TMRCA estimates are found in the KHV sample (25,683; 23,169–28,380) and CHB sample (22,192; 19,683–25,736).

LCT

Arguably the best-studied signature of selection in humans is for an allele at the LCT gene (rs4988235) which confers lactase persistence into adulthood—a trait unique among mammals and which is thought to be a result of cattle domestication and the incorporation of milk into the adult diets of several human populations (Enattah et al. 2002; Bersaglieri et al. 2004; Tishkoff et al. 2007). There are multiple alleles that show association with lactase persistence (Tishkoff et al. 2007). We focused on estimating the age of the T-13910 allele, primarily found at high frequency among Northern Europeans, but which is also found in South Asian populations. In addition to association with the lactase persistence phenotype, this allele has been functionally verified by in vitro experiments (Olds and Sibley 2003; Troelsen et al. 2003; Kuokkanen et al. 2006).

Mathieson et al. (2015) use ancient DNA collected from 83 human samples to get a better understanding of the frequency trajectory for several adaptive alleles spanning a time scale of 8,000 years. For the LCT persistence allele (rs4988235), they find a sharp increase in frequency in the past 4,000 years ago. While this is more recent than previous estimates, an earlier TMRCA or time of mutation is still compatible with this scenario.

Our estimates using European and South Asian samples fall between the range from 5,000 to 10,000 years ago, which is broadly consistent with age estimates from modern data. The credible intervals for estimates in all of the samples have substantial overlap which makes any ranking on the basis of point estimates difficult. We infer the PJL (Punjabi from Lahore, Pakistan) sample to have the oldest TMRCA estimate of 9,514 (8,596–10,383) years. Itan et al. (2009) use spatial modelling to infer the geographic spread of lactase allele from northern to southern Europe. Consistent with their results, the youngest estimate among European populations is found in the IBS sample at 9,341 (8,688–9,989) years. Among all samples, the youngest estimate was found in BEB at 6,869 (5,143–8,809).

KITLG and OCA2

The genetic basis and natural history of human skin pigmentation is a well-studied system with several alleles of major effect showing signatures consistent with being targets of recent selection (Jablonski and Chaplin 2012; Beleza, Santos, et al. 2013; Wilde et al. 2014; Eaton et al. 2015). We focused on an allele found at high-frequency world-wide among non-African populations at the KITLG locus (rs642742) which shows significant effects on skin pigmentation differences between Europeans and Africans (Miller et al. 2007); although more recent work fails to find any contribution of KITLG toward variation in skin pigmentation in a Cape Verde African-European admixed population (Beleza, Johnson, et al. 2013). We also estimated the TMRCA for a melanin-associated allele at the OCA2 locus (rs1800414) which is only found among East Asian populations at high frequency (Edwards et al. 2010).

For the KITLG variant, our estimates among different populations vary from 18,000 to 34,000 years ago, with the oldest age being in the YRI (Yoruba in Ibadan, Nigeria) sample (33,948; 28,861–39,099). The youngest TMRCA is found in FIN at 18,733 years (16,675–20,816). The next two youngest estimates are also found in Africa with the TMRCA in the MSL (Mende in Sierra Leone) sample being 22,340 (15,723–28,950) years old, and that for LWK (Luhya in Webuye, Kenya) being 22,784 (17,922–28,012) years old, suggesting a more complex history than a model of a simple allele frequency increase outside of Africa due to pigmentation related selection pressures. Previous point estimates using rejection sampling approaches on a Portuguese sample (32,277; 6,003–80,683) and East Asian sample (32,045; 6,032–98,165) are again most consistent with our own results on the IBS (29,731; 26,170–32,813) and CHB samples (26,773; 24,297–30,141) (Beleza, Santos, et al. 2013; Chen et al. 2015). Among East Asians, the oldest and youngest estimates are again found in the JPT (28,637; 24,297–30,141) and KHV (24,544; 21,643–27,193) samples, respectively. The TMRCA for OCA2 alleles in the JPT (18,599; 16,110–20,786) and KHV (16,370; 14,439–18,102) samples are also the oldest and youngest, respectively.

Discussion

Our method improves estimation for the timing of selection on a beneficial allele using a tractable model of haplotype evolution. This approach leverages detailed information in the data while remaining amenable to large sample sizes. Using both carriers and noncarriers of the allele, we can more effectively account for uncertainty in the extent of the ancestral haplotype and derived mutations. We show the performance of our method using simulations of different selection strengths, beneficial allele frequencies, and choices of reference panel. By applying our method to five variants previously identified as targets of selection in human populations, we provide a comparison among population-specific TMRCAs. This gives a more detailed account of the order in which populations may have acquired the variant and/or experienced selection for the trait it underlies.

In that regard, it is hypothesized that local selection pressures and a cultural shift toward agrarian societies have induced adaptive responses among human populations around the globe. The data associated with some variants seem to indicate more recent selective events than others. Our results for variants associated with dietary traits at the LCT and ADH1B genes both imply relatively recent TMRCAs ($<15,000$ years ago), consistent with hypotheses that selection on these mutations results from recent changes in human diet following the spread of agriculture (Simoons 1970; Peng et al. 2010). In contrast, the inferred TMRCAs for EDAR, KITLG, and OCA2 imply older adaptive events which may have coincided more closely with the habitation of new environments or other cultural changes.

Several hypotheses have been suggested to describe the selective drivers of skin pigmentation differences among human populations, including reduced UV radiation at high latitudes and vitamin D deficiency (Loomis 1967; Jablonski and Chaplin 2000). Estimated TMRCAs for the variants at the OCA2 and EDAR loci among East Asians appear to be as young or younger than the KITLG variant, but older than the LCT and ADH1B locus. This suggests a selective history in East Asian populations leading to adaptive responses for these traits occurring after an initial colonization. In some cases, the dispersion of replicate MCMC estimates makes it difficult to describe the historical significance of an observed order for TMRCA values. However, the consistency of estimates among different populations for particular variants adds some confidence to our model’s ability to reproduce the ages which are relevant to those loci or certain geographic regions.

To assess the relative concordance of our estimates with those from previous approaches, we compared our results with a compilation of previously published estimates based on the time of mutation, time since fixation, or TMRCA of variants associated with the genes studied here (supplementary fig. 8, Supplementary Material online). The range of confidence intervals for these studies is largely a reflection of the assumptions invoked or relaxed for any one method, as well as the sample size and quality of the data used. In principle, our method extracts more information than approaches that use summary statistics such as ABC. In our empirical application, we found that our method provides a gain in accuracy while accounting for uncertainty in both the ancestral haplotype and its length on each chromosome. Notably, our method provides narrower credible intervals by incorporating the full information from ancestral haplotype lengths, derived mutations, and a reference panel of noncarrier haplotypes.

Another caveat of our method is its dependence on the reference panel, which is intended to serve as a representative sample of nonancestral haplotypes in the population during the selected allele’s increase in frequency. Four possible challenges can arise: 1) Segments of the ancestral selected haplotype may be present in the reference panel due to recombination, (this is more likely for alleles that have reached higher frequency); 2) the reference panel may contain haplotypes that are similar to the ancestral haplotype due to low levels of genetic diversity; 3) the reference panel may be too diverged from the focal population; and 4) population connectivity and turnover may lead the “local” reference panel to be largely composed of migrant haplotypes which were not present during the selected allele’s initial increase in frequency.

Under scenarios 1 and 2, the background haplotypes will be too similar to the ancestral haplotype and it may be difficult for the model to discern a specific ancestry switch location. This leads to fewer differences (mutations) than expected between the ancestral haplotype and each beneficial allele carrier. The simulation results are consistent with this scenario: Our method tends to underestimate the true age across a range of selection intensities and allele frequencies when using a local reference panel.

Conversely, under scenarios 3 and 4 the model will fail to describe a recombinant haplotype in the sample of beneficial allele carriers as a mosaic of haplotypes in the reference panel. As a result, the model will infer more mutation events to explain observed differences from the ancestral haplotype. Our simulation results show this to be the case with reference panels diverged by N generations: Posterior mean estimates are consistently older than their true value. Our simulations are perhaps pessimistic though—we chose reference panel divergence times of N and $0.5N$ generations, approximately corresponding to F_ST values of 0.4 and 0.2, respectively. For the smaller F_ST values observed in humans, we expect results for diverged panels to be closer to those obtained with the local reference panel. Nonetheless, future extensions to incorporate multiple populations within the reference panel would be helpful and possible by modifying the approach of Price et al. (2009). Such an approach would also enable the analysis of admixed populations (we excluded admixed samples from our analysis of the 1000 Genomes data above).

Aside from the challenges imposed by the choice of reference panel, another potential source of bias lies in our transition probabilities, which are not conditioned on the frequency of the selected variant. In reality, recombination events at some distance away from the selected site will only result in a switch from the ancestral to background haplotypes at a rate proportional to $1-p_l$, where p_l is the frequency of the ancestral haplotype alleles at locus l. In this way, some recombination events may go unobserved—as the beneficial allele goes to high frequency the probability of a recombination event leading to an observable ancestral to background haplotype transition decreases. One solution may be to include the frequency-dependent transition probabilities derived by Chen et al. (2015). Under their model, the mutation time is estimated by assuming a deterministic, logistic frequency trajectory starting at $\frac{1}{2N}$. An additional benefit of using frequency trajectories would be the ability to infer posterior distributions on selection coefficients. While the selection coefficient is typically assumed to be related to the time since mutation by $t_1=\hspace{0.17em}\text{log}(Ns)/s$, we do not have an equivalent expression for time to the common ancestor. Rather than the initial frequency being $\frac{1}{2N}$ for a new mutation, our initial frequency must correspond to the frequency at which the TMRCA occurs. Griffiths and Tavare (1994) derive a framework to model a genealogy under arbitrary population size trajectories, which should be analogous to the problem of an allele frequency trajectory, and additional theory on intra-allelic genealogies may be useful here as well (Griffiths and Tavare 1994; Wiuf and Donnelly 1999; Wiuf 2000; Slatkin and Rannala 2000).

Our model also assumes independence among all haplotypes in the sample in a composite-likelihood framework, which is equivalent to assuming a star-genealogy (Larribe and Fearnhead 2011; Varin et al. 2011). This is unlikely to be the case when sample sizes are large or the TMRCA is old. It is also unlikely to be true if the beneficial allele existed on multiple haplotypes preceding the onset of selection, was introduced by multiple migrant haplotypes from other populations, or occurred by multiple independent mutation events (Innan and Kim 2004; Hermisson and Pennings 2005; Przeworski et al. 2005; Pritchard et al. 2010; Berg and Coop 2015). Methods for distinguishing selection from standing variation versus de novo mutation are available that should make it easier distinguish these cases (Messer and Neher 2012; Peter et al. 2012; Messer and Petrov 2013; Garud et al. 2015).

If the underlying allelic genealogy is not star-like, one can expect different estimates of the TMRCA for different subsets of the data. Here, we performed multiple MCMCs on resampled subsets of the data to informally diagnose whether there are violations from the star-shape genealogy assumption. We speculate that exactly how the TMRCAs vary may provide insight to the underlying history. In cases where the TMRCA estimates for a particular population are old and more variable than other populations, the results may be explained by structure in the genealogy, whereby recent coalescent events have occurred among the same ancestral haplotype before the common ancestor. When estimates are dispersed among resampled data sets the presence of multiple ancestral haplotypes prior to the variant’s increase in frequency may be a better explanation. Further support for this explanation might come from comparisons to other population samples which show little to no dispersion of estimates from resampled data sets. Future work might make it possible to formalize this inference process.

A final caveat regards the misspecification of mutation and recombination rates. TMRCA estimates are largely determined by the use of accurate measures for these two parameters. In a way, this provides some robustness to our method. Our age estimates depend on mutation and recombination rates, so accurate specification for one of the values can compensate for slight misspecification in the other. In cases where a fine-scale recombination map is unavailable we suggest using a uniform recombination rate specific to the locus of interest (see Materials and Methods and supplementary fig. 7, Supplementary Material online). Choosing an appropriate mutation rate will continue to depend on current and future work which tries to resolve discrepancies in published mutation rate estimates inferred by various approaches (Ségurel et al. 2014).

One future direction for our method may be to explicitly incorporate the possibility of multiple ancestral haplotypes within the sample. Under a disease mapping framework, Morris et al. (2002) implement a similar idea in the case where independent disease causing mutations arise at the same locus leading to independent genealogies, for which they coin the term “shattered coalescent.” For our case, beneficial mutations may also be independently derived on different haplotypes. Alternatively, a single mutation may be old enough to reside on different haplotypes due to a sufficient amount of linked variation existing prior to the onset of selection. Berg and Coop (2015) model selection from standing variation to derive the distribution of haplotypes that the selected allele is present on.

While we have treated the TMRCA as a parameter of interest, our method also produces a sample of the posterior distribution on the ancestral haplotype. This could provide useful information to estimate the frequency spectrum of derived mutations on the ancestral haplotype. Similarly, the frequency of shared recombination breakpoints could shed light on the genealogy and how well it conforms to the star-shape assumption. The extent of the ancestral haplotype in each individual may also prove useful for identifying deleterious alleles that have increased in frequency as a result of strong positive selection on linked beneficial alleles (Chun and Fay 2011; Hartfield and Otto 2011). For example, Huff et al. (2012) describe a risk allele for Crohn’s disease at high frequency in European populations which they suggest is linked to a beneficial allele under recent selection. Similar to an admixture mapping approach, our method could be used to identify risk loci by testing for an association between the ancestral haplotype and disease status. As another application, identifying the ancestral haplotype may be useful in the context of identifying a source population (or species) for a beneficial allele prior to its introduction and subsequent increase in frequency in the recipient population.

In many cases, the specific site under selection may be unknown or restricted to some set of putative sites. While our method requires the position of the selected site to be specified, future extensions could treat the selected site as a random variable to be estimated under the same MCMC framework. This framework would also be amenable to marginalizing over uncertainty on the selected site.

While we focus here on inference from modern DNA data, the increased accessibility of ancient DNA has added a new dimension to population genetic data sets (Lazaridis et al. 2014; Skoglund et al. 2014; Allentoft et al. 2015; Haak et al. 2015; Mathieson et al. 2015). Because it will remain difficult to use ancient DNA approaches in many species with poor sample preservation, we believe methods based on modern DNA will continue to be useful going forward. That said, ancient DNA is providing an interesting avenue for comparative work between inference from modern and ancient samples. For example, Nakagome et al. (2016) use simulations to assess the fit of this ancient DNA polymorphism to data simulated under their inferred parameter values for allele age and selection intensity and they find reasonable agreement. Much work still remains to fully leverage ancient samples into population genetic inference while accounting for new sources of uncertainty and potential for sampling bias.

Despite these challenges, it is clear that our understanding of adaptive history will continue to benefit from new computational tools which extract insightful information from a diverse set of data sources.

Materials and Methods

We generated data using the software mssel (Hudson R, personal communication), which simulates a sample of haplotypes conditioned on the frequency trajectory of a selected variant under the structured coalescent (Hudson and Kaplan 1988; Kaplan et al. 1988). Trajectories were first simulated forwards in time under a Wright–Fisher model for an additive locus with varying strengths of selection and different ending frequencies of the selected variant. Trajectories were then truncated to end at the first time the allele reaches a specified frequency. See supplementary table 1, Supplementary Material online, for relative ages of simulated TMRCA values for different end frequencies and selection strengths. For the results in figure 2, 100 simulations were performed for each parameter combination. MCMCs were run for 5,000 iterations with a burn-in excluding the first 3,000 iterations. A standard deviation of 10 was used for the proposal distribution of t_ca. The red boxplots indicate local reference panels. The blue and green boxplots indicate reference panels diverged by .5N generations and 1N generations, respectively. Each data set was simulated for a 1-Mb locus with a mutation rate of $1\times {10}^{-8}$, recombination rate of $1\times {10}^{-8}$_, and population size of 10,000. Sample sizes for the selected and reference panels were 100 and 20, respectively.

For more efficient run times of the MCMC, we set a maximum number of individuals to include in the selected and reference panels to be 100 and 20, respectively. In cases where the true number of haplotypes for either panel was greater than this in the full data set, we resampled a subset of haplotypes from each population for a total of five replicates per population. For simulation results supporting the use of this resampling strategy, see supplementary figure 5, Supplementary Material online. The MCMCs were run for 15,000 iterations with a standard deviation of 20 for the TMRCA proposal distribution. The first 9,000 iterations were removed as a burn-in, leading to 6,000 iterations for a sample of the posterior. Convergence was assessed by comparison of MCMC replicates. Figure 3 and supplementary figure 8, Supplementary Material online, show the results for all five variants along with previous point estimates and 95% confidence intervals assuming a generation time of 29 years (Fenner 2005). Supplementary table 3, Supplementary Material online, lists the mean and 95% credible intervals for estimates with the highest mean posterior probability which we refer to in the text below. Supplementary table 4, Supplementary Material online, lists the previous estimates and confidence intervals with additional details of the different approaches taken.

To model recombination rate variation, we used recombination rates from the Decode sex-averaged recombination map inferred from pedigrees among families in Iceland (Kong et al. 2010). Because some populations may have recombination maps which differ from the Decode map at fine scales, we used a mean uniform recombination rate inferred from the 1-Mb region surrounding each variant. The motivation for this arises from how recombination rates have been previously shown to remain relatively consistent among recombination maps inferred for different populations at the megabase-scale (Broman et al. 1998; Baudat et al. 2010; Kong et al. 2010; Auton and McVean 2012). Further, we found our estimates depend mostly on having the megabase-scale recombination rate appropriately set, with little difference in most cases for estimates obtained by modeling fine-scale recombination at each locus (supplementary fig. 7, Supplementary Material online). We specify the switching rate among background haplotypes after recombining off of the ancestral haplotype to be 4Nr, where N = 10,000 and r is the mean recombination rate for the 1-Mb locus.

For modeling mutation, a challenge is that previous mutation rate estimates vary depending on the approach used (Ségurel et al. 2014). Estimates using the neutral substitution rate between humans and chimps are more than $2\times {10}^{-8}$ per bp per generation, while estimates using whole-genome sequencing are closer to $1\times {10}^{-8}$. As a compromise, we specify a mutation rate of $1.6\times {10}^{-8}$.

Supplementary Material

Supplementary data are available at Molecular Biology and Evolution online.