Partition-based ultrahigh-dimensional variable screening

Summary

Traditional variable selection methods are compromised by overlooking useful information on covariates with similar functionality or spatial proximity, and by treating each covariate independently. Leveraging prior grouping information on covariates, we propose partition-based screening methods for ultrahigh-dimensional variables in the framework of generalized linear models. We show that partition-based screening exhibits the sure screening property with a vanishing false selection rate, and we propose a data-driven partition screening framework with unavailable or unreliable prior knowledge on covariate grouping and investigate its theoretical properties. We consider two special cases: correlation-guided partitioning and spatial location- guided partitioning. In the absence of a single partition, we propose a theoretically justified strategy for combining statistics from various partitioning methods. The utility of the proposed methods is demonstrated via simulation and analysis of functional neuroimaging data.

1. Introduction

Biotechnological advances have resulted in an explosion of ultrahigh-dimensional data, where the dimension of the data can be of exponential order in the sample size. Because of high computational cost and poor numerical stability, ultrahigh-dimensional data have long defied existing regularization approaches designed for high-dimensional data analysis (Tibshirani, 1996; Fan & Li, 2001; Zou & Hastie, 2005; Meinshausen & Bühlmann, 2006; Yuan & Lin, 2006; Zhao & Yu, 2006; Zou, 2006; Candès & Tao, 2007; Zhang & Lu, 2007; Huang et al., 2008; Zou & Zhang, 2009; Meinshausen & Bühlmann, 2010; Wang & Leng, 2012). An overarching goal of ultrahigh-dimensional data analytics is to effectively reduce the dimension of covariates.

Sure independence screening (Fan & Lv, 2008) has been extended to generalized linear models (Fan & Fan, 2008; Fan et al., 2009; Fan & Song, 2010), generalized additive models (Fan et al., 2012) and proportional hazards models (Zhao & Li, 2012; Gorst-Rasmussen & Scheike, 2013; Hong et al., 2016a; Li et al., 2016). By extending screening criteria that are solely based on marginal correlations between the outcome and predictors, a variety of statistics that account for dependence between predictors have been proposed to improve screening accuracy and robustness (Hall & Miller, 2009; Zhu et al., 2011; Cho & Fryzlewicz, 2012; Li et al., 2012; Cui et al., 2015). In particular, high-dimensional ordinary least squares projection (Wang & Leng, 2016), which uses the generalized inverse of the design matrix in lieu of marginal correlations, has good theoretical properties and high computational efficiency.

In many cases, scientists have knowledge about important predictors from previous research. For example, neuroimaging studies have identified voxel-level imaging predictors clustered in certain brain regions that are linked to brain functions or diseases. Genome-wide association studies have detected single nucleotide polymorphisms that are strongly associated with clinical outcomes. However, most variable screening approaches are not designed to make use of such information.

As an alternative to marginal screening approaches, conditional sure independence screening methods have been developed for generalized linear models (Barut et al., 2016) and proportional hazards models (Hong et al., 2016a). By including important predictors, conditional screening ranks the marginal utility of each variable after adjusting for variables in the conditioning set.

Partitioning biomarkers into smaller groups according to biological knowledge or other useful information may facilitate variable selection. In biological studies, leveraging information about groups of weak predictors is often useful because such predictors may have a nontrivial impact on outcomes as a group, and without considering the group structure these features might be missed. We exemplify the merit of using the grouping structure with a simple example.

Suppose that we want to identify the important associations between the outcome Y and X₁,…, X₁₀₀₀, where Y = 0.5X₁ − X₂ + ε with ε ~ N(0, 1.6) and (X₁,…, X₁₀₀₀) follows a multivariate normal distribution with mean zero, unit marginal variance and correlation corr (X_j, X_k) = 0.5 for any j ⧧ k ∈{1,…, 1000}. To screen for important variables, marginal screening would fit 1000 variate regression models, $Y=X_j{\beta }_j+\stackrel{\sim }{\epsilon }$ for j = 1, …, 1000, and use ${\widehat{\beta }}_j$, the estimate of β_j, as the screening statistic. Suppose that we partition these 1000 predictors into 200 groups such that the group membership index sets are ${\mathcal{S}}_1=(1,\dots ,5),\dots ,{\mathcal{S}}_{200}=(996,\dots ,1000)$. An alternative screening approach would fit 200 multivariate regression models along the group partition, $Y={\displaystyle {\sum }_{j\in {\mathcal{S}}_g}{X}_j{\beta }_j}+\stackrel{\sim }{\epsilon }$, and use the corresponding ${\widehat{\beta }}_j$ as the screening statistic. We examine the performances of the two approaches based on 300 samples and 400 replicates. Figure 1 shows plots of the densities of ${\widehat{\beta }}_1$ and ${\widehat{\beta }}_2$ and the mixture density of ${\widehat{\beta }}_3,\dots ,{\widehat{\beta }}_{1000}$ for both approaches. Due to signal cancellation, the univariate regression introduces large biases in estimating β₁ and β₂, causing considerable overlap between the distribution of ${\widehat{\beta }}_1$ or ${\widehat{\beta }}_2$ and those of the estimates for the noise variables, whereas groupwise multivariate regression separates the distribution of ${\widehat{\beta }}_1$ or ${\widehat{\beta }}_2$ from the distributions of the others.

Fig. 1.

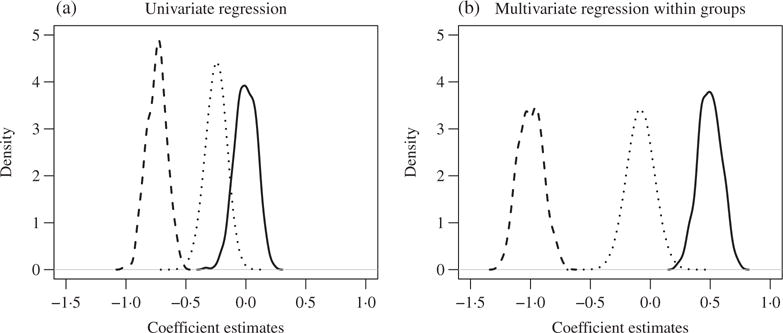
Simple example simulations: (a) summary distributions of 400 replicates of coefficient estimates in 1000 univariate regression model fits; (b) summary of 200 group-specific multivariate regression model fits. Plotted are the estimated densities of ${\widehat{\beta }}_1$ (solid) and ${\widehat{\beta }}_2$ (dashed) and the estimated mixture densities of ${\widehat{\beta }}_3,\dots ,{\widehat{\beta }}_{1000}$ (dotted); true coefficients are β₁ = 0.5, β₂ = − 1 and β₃ = ⋯ = β₁₀₀₀ = 0.

This example motivates partition-based screening, which is based on a partition of covariates using prior knowledge. Our work generalizes the univariate framework of sure independence screening (Fan & Lv, 2008) and its group version (Niu et al., 2011). Under mild conditions, partition-based screening exhibits good theoretical properties. A new functional operator, generalized linear conditional expectation, is introduced to help establish sure screening properties. When prior grouping information is available, we show that the screening accuracy of partition-based screening is superior to that of competing methods. In the absence of prior grouping information, we propose correlation-based screening and spatial partition-based screening, which make the proposed methods applicable to a wide range of problems.

2. Partition-based variable screening

Suppose that we have n independent samples D = {(X_i, Y_i), i = 1, …, n}, where Y_i is an outcome and X_i = (X_i,1,…, X_i,_p)^T is a collection of p predictors for the ith sample. Assume without loss of generality that all the covariates have been standardized so that E(X_i,_j) = 0 and $E(X_{i,j}^2)=1$. We consider a class of generalized linear models by assuming that the conditional density of Y_i given X_i belongs to a linear exponential family,

$$\pi (Y_i|X_i)=\exp \{Y_i({\beta }_0+X_i^{\mathrm{T}}\beta )-b({\beta }_0+X_i^{\mathrm{T}}\beta )+A(Y_i,X_i)\}$$ (1)

where A(·, ·) and b(·) are known functions, β = (β₁,…, β_p)^T represent the coefficients of the predictors, and β₀ is an intercept, regarded as a nuisance parameter. Let $\mathrm{ℳ}=\{j:{\beta }_j⧧0\}$. We assume that b(·) is twice continuously differentiable, with a nonnegative second derivative b″(·). For a nonrandom function f (·) and a sequence of independent random variables ξ_i (i = 1,…, n), let $E_n\{f(\xi )\}=n^{-1}{\displaystyle {\sum }_{i=1}^{n}f({\xi }_i)}$ be the empirical mean of ${\{f({\xi }_i)\}}_{i=1}^n$, which are independent replicates of f (ξ). The loglikelihood function is

$$\mathrm{\ell }({\beta }_0,\beta ;D)=\frac{1}{n}{\displaystyle \sum _{i=1}^{n}l({\beta }_0+X_i^{\mathrm{T}}\beta ,Y_i)=E_n\{l({\beta }_0+X^{\mathrm{T}}\beta ,Y)\}}$$ (2)

where l(θ, y) = yθ − b(θ). We assume that {X_ij, X_i, Y_i} are independently and identically distributed copies of {X_j, X, Y}. When p < n, the maximum likelihood estimator of β, denoted by ${\widehat{\beta }}_{\text{MLE}}$, can be obtained by maximizing ℓ(β₀, β; D). When p ⩾ n, regularization estimation is often performed under an assumption of sparsity among predictors. When p is of exponential order in n, a popular approach for reducing the dimensionality is screening.

First, we consider a simple case where the covariates can be partitioned into G disjoint groups in accordance with known information. Denote by g_j the group membership of variable X_j. Let $X_g^{\ast }=\{X_j:g_j=g\}$ be the collection of predictors in group g, where g ∈ {1,…, G}. Additionally, let ${\beta }_g^{\ast }=\{{\beta }_j:g_j=g\}$ represent the corresponding coefficients and let β_g,0 be the group-specific intercept in the model. Denote their estimates by ${\widehat{\beta }}_g^{\ast }=\{{\widehat{\beta }}_j:g_j=g\}$ and ${\widehat{\beta }}_{g,0}^{\ast }$, respectively. For predictor j with g_j = g, the partition-based screening statistic is defined as

$$({\widehat{\beta }}_{g,0}^{\ast },{\widehat{\beta }}_g^{\ast })=\underset{({\beta }_{g,0},{\beta }_g^{\ast })}{\arg max}{E}_n\{l({\beta }_{g,0}+X_g^{\ast \mathrm{T}}{\beta }_g^{\ast },Y)\}.$$

We call ${\widehat{\beta }}_g^{\ast }$ the partition-based screening statistic. Then, for a chosen thresholding parameter γ, the set of indices selected by our proposed partition-based screening is ${\widehat{\mathrm{ℳ}}}_{\gamma }=\{j:|{\widehat{\beta }}_j|⩾\gamma \}$.

When g_j = j (j = 1,…, p), partition-based screening encompasses sure independence screening as a special case.

3. Sure screening properties

Let (Ω, ℱ, pr) be the probability space for all random variables considered in this paper. Let ℝ^d be a d-dimensional Euclidean vector space for some positive integer d. Denote by E(·), var(·) and cov(·, ·) the expectation, variance and covariance operators associated with (Ω, ℱ, pr). For any vector $a=(a_1,\dots ,a_p)\in {\mathrm{ℝ}}^p$, let $a_c={(a_j,j\in \mathcal{C})}^{\mathrm{T}}$ be the subvector with elements indexed by $\mathcal{C}$. Let ${\Vert a\Vert }_d={({\displaystyle {\sum }_{j=1}^p|a{|}_j^d})}^{1/d}$ be the L_d-norm for any vector a ∈ℝ^p, and denote the Euclidean norm by ||a|| when no confusion is likely to arise. Let λ_min(M) and λ_max(M) be the smallest and largest eigenvalues of the matrix M, respectively.

We start with population-level parameters for the discussion of sure screening properties. Let

$$({\overline{\beta }}_{g,0}^{\ast },{\overline{\beta }}_g^{\ast })=\underset{({\beta }_{g,0},{\beta }_g^{\ast })}{\arg max}E\{l({\beta }_{g,0}+X_g^{\ast \mathrm{T}}{\beta }_g^{\ast },Y)\}$$ (3)

where ${\overline{\beta }}_g^{\ast }=\{{\overline{\beta }}_j:g_j=g\}$ is the population version of ${\widehat{\overline{\beta }}}_g^{\ast }$. We first establish conditions to ensure that if |β_j| exceeds a threshold, then $|{\overline{\beta }}_j|$ will exceed a certain constant. Write ${\beta }_{-j}^{\ast }={\{{\beta }_l:g_l=g_j,l⧧j\}}^{\mathrm{T}}$ and $X_{-j}^{\ast }={\{X_l:g_l=g_j,l⧧j\}}^{\mathrm{T}}$. With (2), ${\overline{\beta }}_j$ satisfies the score equations

$$E\{b\prime ({\overline{\beta }}_{g,0}^{\ast }+X_{-j}^{\ast \mathrm{T}}{\overline{\beta }}_{-j}^{\ast }+X_j{\overline{\beta }}_j){(1,X_g^{\ast \mathrm{T}})}^{\mathrm{T}}\}=E\{Y{(1,X_g^{\ast \mathrm{T}})}^{\mathrm{T}}\}.$$ (4)

To derive the theoretical properties of the proposed methods, we introduce a functional operator on random variables.

Definition 1

For two random variables ζ : Ω → ℝ and ξ : Ω → ℝ^p, let h : ℝ → ℝ be a continuous link function. The generalized linear conditional expectation of ζ given ξ is

$$E_h(\zeta |\xi )=h({\alpha }_0+{\alpha }^{\mathrm{T}}\xi ),$$ (5)

where (α₀, α^T)^T is the solution to the equation E[{ζ − h(α₀ + α^Tξ)}(1, ξ^T)^T] = 0.

The generalized linear conditional expectation measures how ξ can explain ζ through a generalized linear model, where ζ is regarded as the outcome variable and ξ as the predictors. It can also be interpreted as the best prediction of ζ using ξ based on a generalized linear model, leading to an alternative measure of the dependence between ζ and ξ. The generalized linear conditional expectation may depend on the choice of link functions, and it is equivalent to the conditional expectation if the true conditional distribution of ζ given ξ is specified by the corresponding generalized linear model. The introduction of (5) facilitates the development of partition-based screening and its theoretical properties, and extends the linear conditional expectation proposed by Barut et al. (2016) and Hong et al. (2016a). Some basic properties are summarized below.

Lemma 1

Let ζ and ξ be random variables in (Ω, ℱ, pr).

1. When h(x) = 1(x) = x, E_h(ζ | ξ) is unique and has a closed-form expression. Moreover, E₁(ζ | ξ) = E(ζ) + cov(ζ,ξ)var(ξ)⁻¹{ξ −E(ξ)} and E{E₁(ζ | ξ)ξ} = E(ζξ).

2. When the conditional distribution of ζ given ξ belongs to a linear exponential family, i.e., f(ζ | ξ) = exp{ζ(γ₀ + γ^Tξ) − b(γ₀ + γ^Tξ) + A(ζ, ξ)}, then h(x) = b'(x) and $E_{b\prime }(\zeta |\xi )=E(\zeta |\xi )=b\prime ({\gamma }_0+{\gamma }^T\xi )$.

3. For any h, we have E{E_h(ζ | ξ)} = E(ζ).

These properties immediately imply the following result.

Theorem 1

Suppose that the solution to (4) is unique. For j = 1,…,p, the partition-based regression parameter ${\overline{\beta }}_j$ equals 0 if and only if $E_{b\prime }(Y|X_{-j}^{\ast })=E_{b\prime }(Y|X_{-j}^{\ast },X_j)$.

The sufficient part of Theorem 1 implies that if the generalized linear conditional expectation of the response given all the predictors within group g_j does not involve X_j, then the regression coefficient β_j will be vanishing, implying that unimportant variables would have smaller fitted coefficients.

To ensure the sure screening property at the population level, the important variables $\{X_j,j\in \mathrm{ℳ}\}$ should be conditionally associated with Y given other variables within the same group $\{X_{-j}^{\ast },j\in \mathrm{ℳ}\}$. The following conditions are required.

Condition 1

For $j\in \mathrm{ℳ}$, there exist c₀ > 0 and κ < 1/2 such that

$$|E[X_j\{E_{b\prime }(Y|X_{-j}^{\ast },X_j)-E_{b\prime }(Y|X_{-j}^{\ast })\}]|>c_0{n}^{-\kappa }.$$

Condition 2

The derivative b′(θ) satisfies a Lipschitz condition, i.e., there exists an L > 0 such that |b′(θ₁) − b′(θ₂)| < L|(θ₁) − (θ₂)|for all θ₁,θ₂ ∈ ℝ.

Condition 3

There exists a constant M > 0 such that $E(X_j^2)\le M$ for all j.

Condition 1 provides a lower bound on the generalized linear dependence between each active covariate X_j and Y conditional on other covariates within the same group, justifying the use of group partitions to retain true signals. Linear regression, logistic regression and probit regression all satisfy Condition 2.

Theorem 2

If Conditions 1–3 hold, then there exists c₂ > 0 such that ${min}_{j\in \mathrm{ℳ}}|{\overline{\beta }}_j|>c_2{n}^{-\kappa }$.

To establish sure screening properties, we need regularity conditions (Fan & Song, 2010; Barut et al., 2016); see Conditions A.1–A.6 in the Supplementary Material.

Theorem 3

Let $S_g={\displaystyle {\sum }_{j=1}^{p}I(g_j=g)}$ be the size of group g. Assume that Conditions A.1–A.6 in the Supplementary Material hold and that $Q_{g,n}=n^{1-2\kappa }{(R_n{r}_{g,n})}^{-2}\to \mathrm{\infty }$ as n → ∞ for all g = 1,…, G.

1. With c₂ as in Theorem 2, there exists a positive constant c₃ such that

   $$pr\left(\underset{1\le j\le p}{max}|{\widehat{\beta }}_j-{\overline{\beta }}_j|⩾c_2{n}^{-\kappa }/2\right)\le {\displaystyle \sum _{g=1}^G{S}_g\exp (-c_3{Q}_{g,n})+n{r}_2\exp (-r_0{R}_n^{\alpha }),}$$

   where $r_2={\displaystyle {\sum }_{g=1}^G{S}_g(S_g{r}_1+s_1)}$.
2. If Conditions 1–3 hold, then with γ = c₄n^−κ and c₄ ≤ c₂/2, we have

   $$\text{pr}\left(\mathrm{ℳ}\subset {\widehat{\mathrm{ℳ}}}_{\gamma }\right)⩾1-{\displaystyle \sum _{j\in \mathrm{ℳ}}\exp (-c_3{Q}_{g_j,n})-n{r}_3\exp (-r_0{R}_n^{\alpha }),}$$

   where $r_3={\displaystyle {\sum }_{j\in \mathrm{ℳ}}(S_{g_j}{r}_1+s_1)}$.

For logistic regression, the Lipschitz constant r_g,n is bounded. Therefore, the optimal rate for R_n is of order n^{(1−2κ)/(2+α)}, ensuring that Q_g,_n is of the same order as $R_n^{\alpha }$. This also implies that the partition-based screening method can handle group sizes of order log S_g = o(n^{(1−2κ)α/(α+2)}) (g = 1,…, G). The same optimal rate and a similar order of dimensionality can be achieved for logistic regression by sure independence screening (Fan & Song, 2010) and conditional sure independence screening (Barut et al., 2016).

To provide an upper bound on the number of selected variables, we need the following additional conditions:

Condition 4

${\displaystyle {\sum }_{j=1}^p\mathrm{var}(X_j{\beta }_j)}$ and b″(θ) are both bounded for all θ and β.

Condition 5

Let g = g_j and ${\mathrm{\Omega }}_j=E[{\delta }_j{(1,X_g^{\ast \mathrm{T}})}^{\mathrm{T}}(1,X_g^{\ast \mathrm{T}})]$ with

$${\delta }_j=\frac{b\prime ({\overline{\beta }}_{g,0}^{\ast }+X_{-j}^{\ast \mathrm{T}}{\overline{\beta }}_{-j}^{\ast }+X_j{\overline{\beta }}_j^{\ast })-b\prime ({\stackrel{\sim }{\beta }}_{g,0}^{\ast }+X_{-j}^{\ast \mathrm{T}}{\stackrel{\sim }{\beta }}_{-j}^{\ast })}{{\overline{\beta }}_{g,0}^{\ast }-{\stackrel{\sim }{\beta }}_{g,0}^{\ast }+X_{-j}^{\ast \mathrm{T}}({\overline{\beta }}_{-j}^{\ast }-{\stackrel{\sim }{\beta }}_{-j}^{\ast })+X_j{\overline{\beta }}_j^{\ast }},$$

where $({\stackrel{\sim }{\beta }}_{g,0}^{\ast },{\stackrel{\sim }{\beta }}_{-j}^{\ast })=\arg {max}_{({\beta }_0,{\beta }_{-j}^{\ast })}E\{l({\beta }_0+X_{-j}^{\ast \mathrm{T}}{\beta }_{-j}^{\ast },Y)\}$. Then there exists a K₁ > 0 such that ${\lambda }_{min}({\mathrm{\Omega }}_j)>K_1$ for all j = 1,…, p.

Condition 6

Assume that ║U║² = o(V) where U = (U₁,…, U_p)^T with

$$U_j=E\{E_1(X_j|X_{-j}^{\ast },X_g^{\ast },g⧧g_j)({\beta }_0-{\stackrel{\sim }{\beta }}_{g_j,0}^{\ast }+X^{\mathrm{T}}\beta -X_{-j}^{\ast \mathrm{T}}{\stackrel{\sim }{\beta }}_{-j}^{\ast })\}$$

and $V={\sup }_{1\le j\le p}E[{\{X_j-E_1(X_{-j}^{\ast },X_g^{\ast },g⧧g_j)\}}^2]$. Here (β₀, β^T)^T are the parameters that generate the data.

For a linear model, Condition 5 becomes ${\lambda }_{min}[E\{{(1,X_g^{\ast \mathrm{T}})}^{\mathrm{T}}{(1,X_g^{\ast \mathrm{T}})}^{\mathrm{T}}(1,X_g^{\ast \mathrm{T}})\}]>K_1$ for all g, which is a mild condition. In Condition 6, U_j = 0 for the linear model when cov(X) has a block-diagonal structure over a group partition, i.e., $\mathrm{cov}(X_g^{\ast },X_{g\prime }^{\ast })=0$ for g ⧧ g′, because $E_1(X_j|X_{-j}^{\ast },X_g^{\ast },g⧧g_j)=E_1(X_j|X_{-j}^{\ast })$ and $E_1\{X_{-j}^{\ast }({\beta }_0-{\stackrel{\sim }{\beta }}_{g_j,0}^{\ast }+X^{\mathrm{T}}\beta -X_{-j}^{\ast \mathrm{T}}{\stackrel{\sim }{\beta }}_{-j}^{\ast })\}=E[X_{-j}^{\ast }\{b\prime ({\beta }_0+X^{\mathrm{T}}\beta )-b\prime ({\stackrel{\sim }{\beta }}_{g_j,0}^{\ast }+X_{-j}^{\ast T}{\stackrel{\sim }{\beta }}_{-j}^{\ast })\}]=0$.

Condition 6, which requires ||U|| to be bounded, may be restrictive. This condition holds if the number of nonzero coefficients is finite or if the correlations among different partitions shrink as p → ∞. Condition 6 can be viewed as rigid, even though the group structure is natural in many biomedical applications. To overcome this difficulty, one could first perform a principal component analysis on X, and then apply the proposed procedures to the residuals of X after projecting them to a set of variables with the largest loadings on the leading eigenvectors (Hong et al., 2016a). See the Supplementary Material for more details.

Theorem 4

With γ, c₃ and r₂ as in Theorem 3, if Conditions 4–6 and A. 1–A.6 hold, then as n →∞,

$$\text{pr}\{|{\widehat{\mathrm{ℳ}}}_{\gamma }|\le O(n^{2\kappa }V)\}⩾1-{\displaystyle \sum _{g=1}^G{S}_g\exp (-c_3{Q}_{g,n})-n{r}_2\exp (-r_0{R}_n^{\alpha }).}$$

4. Extensions of partition-based screening

4.1. Goodness-of-fit adjustment

One difficulty in the proposed partition-based screening is that the coefficient estimates from group-specific models may not be comparable because different models may have various degrees of goodness-of-fit. Under the generalized linear model framework, we propose to adjust for the goodness-of-fit by weighting the screening statistics using the deviance ratio Ψ_g ∈ (0,1) (Friedman et al., 2010), which is the fraction of null deviance explained by the covariates in group g and is equal to R² in the linear model. In other words, we weight the partition-based screening statistic as ${\widehat{\beta }}_j^a={\mathrm{\psi }}_{g_j}{\widehat{\beta }}_j$ for predictor j and redefine the selected index set as ${\widehat{\mathrm{ℳ}}}_{\gamma }^a=\{j:|{\widehat{\beta }}_j^a|>\gamma \}$. However, the performance of such a procedure may be sensitive to grouping. For instance, in the example in § 1, goodness-of-fit adjustment can improve the model selection accuracy when all the true predictors are in the same group, as in Fig. 2(a). In contrast, when the true predictors are in separate groups, there is no improvement; see Fig. 2(b) and the Supplementary Material.

Fig. 2.

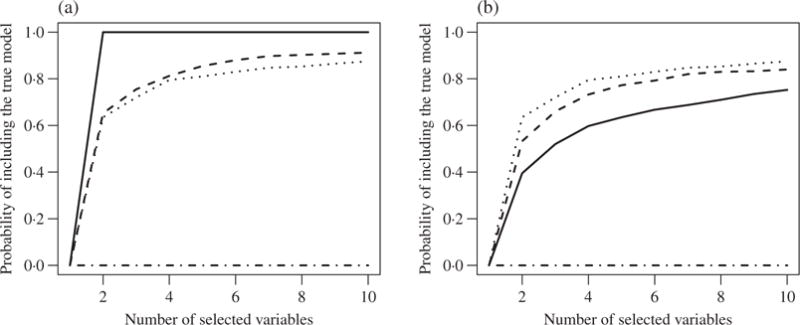
Variable screening accuracy in the example in § 1 by sure independence screening (dot-dash), high-dimensional ordinary least squares projection (dotted), partition-based screening without goodness-of-fit adjustment (dashed) and partition-based screening with goodness-of-fit adjustment (solid). Panel (a) shows results with the group partitions defined in § 1 where group 1 includes the two true predictors; panel (b) displays results with a random group partition where the two true predictors are not in the same group.

4.2. Data-driven partition

When prior partitioning information is unavailable, we may use information from the data, including correlations between predictors and the spatial locations. Let us denote the data-driven partition by $\widehat{\mathcal{G}}$. We derive two procedures for determining $\widehat{\mathcal{G}}$ based on such information.

The data-driven partition can be determined by the covariance or correlation structure of the design matrix. We propose a simple correlation-guided partition procedure. We use the correlation between covariates to define a p × p distance matrix, denoted by Δ = (d_j,_k), where d_j,_k = 1 − |corr(X_k, X_j)| (1 ≤ k,j ≤ p). We apply the nearest-neighbour chain algorithm (Murtagh, 1983), a standard hierarchical clustering algorithm, to Δ to obtain an estimate of $\widehat{\mathcal{G}}$, where the number of groups, $\widehat{G}$, can be determined by controlling the corresponding maximum group size ${max}_g{\widehat{S}}_g$ for the generalized linear model fitting. Based on our experience, choosing ${max}_g{\widehat{S}}_g\propto n^{1/2}$ can lead to good performance. When the correlation matrix has a block-diagonal structure and the correlations within each block are high, this procedure can correctly identify the block structure. Covariate-assisted variable screening (Ke et al., 2014) and graphlet screening (Jin et al., 2014) are also based on the covariance structure of covariates, but these procedures focus on linear regression.

Spatial regression models have often been used in environmental health and neuroimaging studies, where a spatial location is attached to each covariate. For example, in the scalar-on-image regression problem for brain imaging, where the spatial location of each voxel is in a standard three-dimensional brain template, the imaging intensities at different voxels are usually considered as potential predictors for clinical outcomes. It is generally believed that spatially close predictors tend to have stronger correlations and may have more similar effects on the outcome (Wang et al., 2017). Therefore spatial location information can be useful in determining the partition for variable screening. Specifically, model-based clustering (Fraley & Raftery, 2002) and k-means clustering (Jain, 2010) can be used to assign each predictor to a fixed number of clusters or spatial locations, typically determined by controlling the corresponding maximum group size in a similar fashion to correlation-guided partitioning.

Using a partition $\widehat{\mathcal{G}}$ determined by data, we can also establish the following theoretical results for data-driven partition-based screening, which can be proved by conditioning on the event $\{\widehat{\mathcal{G}}=\mathcal{G}\}$ and using Theorems 1–4.

Theorem 5

Suppose that $\widehat{\mathcal{G}}$ is a consistent estimator of $\mathcal{G}$ satisfying Conditions 1–6 and A.1–A.6; that is, ${\lim }_{n\to \mathrm{\infty }}\text{pr}(\widehat{\mathcal{G}}=\mathcal{G})=1$. With the same γ, c₃, r₂ and r₃ as in Theorem 3, as n → ∞ we have

$$\text{pr}\left(\mathrm{ℳ}\subset {\widehat{\mathrm{ℳ}}}_{\gamma }\right)⩾\text{pr}(\widehat{\mathcal{G}}=\mathcal{G})-{\displaystyle \sum _{j\in \mathrm{ℳ}}\exp (-c_3{Q}_{g_j,n})}-n{r}_3(-r_0{R}_n^{\alpha }),$$

$$\text{pr}\left\{|{\widehat{\mathrm{ℳ}}}_{\gamma }|\le O(n^{2\kappa }V)\right\}⩾\text{pr}(\widehat{\mathcal{G}}=\mathcal{G})-{\displaystyle \sum _{g=1}^G{S}_g\exp (-c_3{Q}_{g,n})}-n{r}_2(-r_0{R}_n^{\alpha }).$$

4.3. Combined partition-based screening

Several partitioning rules for covariates may exist, but none is clearly superior. For example, in neuroimaging, brain atlases, such as Talairach–Tournoux, Harvard–Oxford, Eickoff–Zilles and automatic anatomical labelling, have variable partitioning of brain regions. In genome-wide association studies, different sources of information, including the locations of genes that harbour single nucleotide polymorphisms and linkage disequilibrium between single nucleotide polymorphisms, can be integrated to determine the groups. Using multiple sources of partitioning, we propose a strategy for combining screening statistics from different partitions and establish its theoretical properties.

Definition 2

Suppose that we have K < ∞ partitions and that partition k has G^(k) groups and group indices ${\mathcal{G}}^{(k)}={(g_1^{(k)},\dots ,g_p^{(k)})}^{\mathrm{T}}$. Let $S_g^{(k)}={\displaystyle {\sum }_{j=1}^{p}I(g_j^{(k)}=g)}$ and let ${\widehat{\beta }}^{(k)}={({\widehat{\beta }}_1^{(k)},\dots ,{\widehat{\beta }}_p^{(k)})}^{\mathrm{T}}$ be the screening statistics for partition k. The combined partition-based screening statistic is $\stackrel{\sim }{\beta }={({\stackrel{\sim }{\beta }}_1,\dots ,{\stackrel{\sim }{\beta }}_p)}^{\mathrm{T}}$ with ${\stackrel{\sim }{\beta }}_j={max}_{1\le k\le K}|{\widehat{\beta }}_j^{(k)}|$. Given a thresholding parameter γ, the selected index set is ${\stackrel{\sim }{\mathrm{ℳ}}}_{\gamma }=\{j:{\stackrel{\sim }{\beta }}_j⩾\gamma \}$, which is referred to as combined partition-based screening selection.

Theorem 6

Suppose that Conditions 4–6 and A.1–A.6 hold for all partitions k (k = 1, …, K), and take γ = c₅n^−κ for some constant c₅.

1. If there exists an l ∈ {1, …, K} such that ${\mathcal{G}}^{(l)}$ satisfies Conditions 1–3, then ${\lim }_{n\to \mathrm{\infty }}\text{pr}(\mathrm{ℳ}\subset {\stackrel{\sim }{\mathrm{ℳ}}}_{\gamma })=1$.

2. Let V^(k) be the V term in Condition 6 for ${\mathcal{G}}^{(k)}$. Then combined partition-based screening controls the false positive rates; that is,

   $$\underset{n\to \mathrm{\infty }}{\lim }\text{pr}\left\{|{\stackrel{\sim }{\mathrm{ℳ}}}_{\gamma }|\le O\left(n^{2\kappa }{\displaystyle \sum _{k=1}^K{V}^{(k)}}\right)\right\}=1.$$

Theorem 6 suggests that combined partition-based screening has sure screening properties, even when some partition-based screening procedures do not satisfy Conditions 1–3, which are in general difficult to verify. Moreover, Conditions 4–6 and A.1–A.6 are true for many generalized linear models. Thus, combined partition-based screening can extract useful prior knowledge about partitions and maintain good theoretical properties.

4.4. Choice of thresholding parameters

The thresholding parameter γ is critical to the performance of the variable screening procedure. Overestimating γ will inflate false positive rates and underestimating γ will hinder sure screening. We define the expected false positive rate ${\text{EFPR}}_{\gamma }=E(|{\stackrel{\sim }{\mathrm{ℳ}}}_{\gamma }\cap {\mathrm{ℳ}}^c|/|{\mathrm{ℳ}}^c|)$, where ${\mathrm{ℳ}}^c=\{j:j\notin \mathrm{ℳ}\}$. To control EFPR_γ, we resort to higher-criticism t statistics (Zhao & Li, 2012; Barut et al., 2016; Hong et al., 2016a). We introduce ${\widehat{\mathrm{ℳ}}}_{\tau }^{\#}=\{j:I_j{({\widehat{\beta }}_j)}^{1/2}|{\widehat{\beta }}_j|⩾\tau \}$, where $I_j({\widehat{\beta }}_j)$ is the element that corresponds to β_j in the information matrix $I_{g_j}({\overline{\beta }}_{g_j}^{\ast })$. The key idea is to select γ such that ${\widehat{\mathrm{ℳ}}}_{\gamma }$ of the same size as ${\widehat{\mathrm{ℳ}}}_{\tau }^{\#}$, where τ is chosen to control the expected false positive rate. Under Conditions 4 and 5 and Conditions A.1–A.6 and B in the Supplementary Material, we have the following theorem.

Theorem 7

For a given false positive number q, take τ = Φ⁻¹ {1 − q/(2p)}, where Φ denotes the standard normal distribution function. Set $\gamma =|{\widehat{\beta }}_{(s)}|$, where $s=|{\widehat{\mathrm{ℳ}}}_{\tau }^{\#}|$ and {(1), …, (p)} is a permutation of {1, …, p} such that $|{\widehat{\beta }}_{(1)}|>\cdots >|{\widehat{\beta }}_{(p)}|$. Then there exist N₇ > 0 and c₇ > 0 such that for any n > N₇, EFPR_γ ≤ q/p + c₇n^−1/2.

For ${\widehat{\mathrm{ℳ}}}_{\gamma }$, the set of indices selected by combined partition-based screening in § 4.3, we choose $\gamma =|{\widehat{\beta }}_{(s)}|$ with s = min_1≤k≤K s^(k). Here s^(k) is the size of the higher-criticism t-tests for partition k.

5. Simulation studies

We conducted simulation studies to compare the model selection accuracy of partition-based screening with that of existing variable screening methods. We generated the covariates X from multivariate normal distributions and specified the true coefficient β with four different settings.

• Setting 1: (n, p) = (200, 5000) and $\beta ={(3,3,3,3,3,-7.5,0_{p-6}^{\mathrm{T}})}^{\mathrm{T}}$. Thus $\mathrm{ℳ}=\{1,\dots ,6\}$. The covariance structure of X is compound symmetric with unit variance and correlation 0.5, i.e., $\mathrm{cov}(X)=0.5I_p+{0.51}_p{1}_p^{\mathrm{T}}$.

• Setting 2: (n, p) = (200, 5000) and β_j = 3(−1)^jI (j ≤ 10) for j ∈ {1, …, p}. Thus $\mathrm{ℳ}=\{1,\dots ,10\}$. The covariance structure of X is that of a block first-order autoregression model with unit variance and correlation 0.9, i.e., cov(X_j, X_j′) = 0.9^|j−j′| for any $j⧧j^{\prime }\in {\mathrm{ℬ}}_k$, where ${\mathrm{ℬ}}_k=\{j\in \mathrm{\mathbb{Z}}:100k-99\le j\le 100k\}$ for k = 1,…, 50, and cov(X_j, X_j′) otherwise.

• Setting 3: (n, p) = (200, 5000) and β_j = (−1)^jI (j ≤ 10) for j ∈ {1,…, p}. Thus $\mathrm{ℳ}=\{1,\dots ,10\}$. The covariance structure of X is block compound symmetric with unit variance and correlation 0.9, i.e., cov(X_j, X_j′) = 0.9 for any $j⧧j^{\prime }\in {\mathrm{ℬ}}_k$, where ${\mathrm{ℬ}}_k=\{j\in \mathrm{\mathbb{Z}}:100(k-1)+1\le j\le 100k\}$ for k = 1,…, 50, and cov(X_j, X_j′) = 0 otherwise.

• Setting 4: (n, p) = (500, 10 000). We first define $\mathcal{S}$ as a collection of 100 × 100 equally spaced grid points on [0, 1]². Specifically, set $\mathcal{S}={\{s_j\}}_{j=1}^p$ with s_j = 0.01 (l, k), j = (100 − 0.5l)(l − 1) + k − l for 1 ≤ l, k ≤ 100, and $\mathcal{S}={\cup }_{g=1}^{100}{\mathcal{S}}_g$, where ${\mathcal{S}}_g\cap {\mathcal{S}}_{g^{\prime }}=\varphi$ for any g ⧧ g′ ∈ {1,…, G}. All the s_j were clustered into 100 exclusive spatially contiguous regions using a k-means clustering algorithm. Set β_j = 3(−1)^j if $s_j\in {\mathcal{S}}_1$ and β_j = 0 otherwise. The covariance structure of X is exponentially decaying over space, cov(X_j, X_j′) = exp(−10‖s_j − s_j′‖₂) for any $j⧧j^{\prime }\in \mathcal{S}$. For example, cov(X_j, X_j′) = 0.9 when ‖s_j − s_j′‖₂ = 0.01 and cov(X_j, X_j′) < 0.05 when ‖s_j − s_j′‖₂ > 0.3. This configuration was designed to mimic the spatial data with an active set $\mathrm{ℳ}=\{j:s_j\in {\mathcal{S}}_1\}$.

Given X and β generated from each of the above settings, we generated Y from a linear regression model and a logistic regression model. For the linear regression model, we set the variance of random errors so that the theoretical R² is equal to 0.9. We replicated our simulation 200 times and evaluated the performance using the following criteria: probability of including the true model, minimum model size, and true positive rate.

Definition 3

Every partition $\mathcal{G}$ belongs to at least one of the following types:

1. a size-reduced partition if there exists a group $g\in \mathcal{G}$ that contains all active covariates, which means $\mathrm{ℳ}\in \{j:g_j=g\}$;

2. an optimal partition if there exists a group $g\in \mathcal{G}$ that is a collection of all active covariates, which means $\mathrm{ℳ}\in \{j:g_j=g\}$;

3. a misspecified partition if there does not exist a group $g\in \mathcal{G}$ such that $\mathrm{ℳ}\subset \{j:g_j=g\}$.

Each partition is either a size-reduced partition or a misspecified partition. An optimal partition must be a size-reduced partition. Neither the misspecified partition, the size-reduced partition, nor the optimal partition, is unique in general. For each non-optimal reduced partition, there exists at least a group containing $\mathrm{ℳ}$ that can be further reduced in size while containing $\mathrm{ℳ}$.

We assessed the performance of the proposed methods under various partition types. In Setting 1, the size-reduced partition ${\mathcal{G}}^{\text{red}}=(g_1^{\text{red}},\dots ,g_{357}^{\text{red}})$ was specified with 357 groups and each group had 14 members except for group 357 which had 16 members; the group size was approximately n^1/2. For covariate j ∈ {1, …, 4998}, its group label was assigned to be $g_j^{\text{red}}={\displaystyle {\sum }_{g=1}^{357}gI(14g-13\le j\le 14g)}$, and for j = 4999 or 5000, $g_j^{\text{red}}=357$, where $\mathrm{ℳ}\subset \{j:g_j^{\text{red}}=1\}$ for each setting. The misspecified partitions ${\mathcal{G}}^{{\text{mis}}_1}={(g_1^{{\text{mis}}_1},\dots ,g_p^{{\text{mis}}_1})}^{\mathrm{T}}$ and ${\mathcal{G}}^{{\text{mis}}_2}={(g_1^{{\text{mis}}_2},\dots ,g_p^{{\text{mis}}_2})}^{\mathrm{T}}$ were respectively sampled from $\text{pr}(g_j^{{\text{mis}}_1}=g)=1/178(g=1,\dots ,178)$ and $\text{pr}(g_j^{{\text{mis}}_2}=g)=1/357(g=1,\dots ,357)$. In this setting, variable X₆ is marginally unimportant but conditionally important. Some studies (Barut et al., 2016; Hong et al., 2016a,b) have shown that conditional sure independence screening performs much better than sure independence screening in terms of retaining X₆. In Settings 2 and 3, where the correlation matrix for covariates is block diagonal, we focused primarily on the performance of partition-based screening under reduced partitions and correlation-guided partition-based screening with the same specifications as in Setting 1. The partition determined by the estimated correlation structure is denoted by ${\mathcal{G}}^{\text{cor}}$. In Setting 4, the optimal partition ${\mathcal{G}}^{\text{opt}}$ was designed as follows. For each covariate j, $g_j^{\text{opt}}={\displaystyle {\sum }_{g=1}^{100}gI(s_j\in {\mathcal{S}}_g)}$, where $\mathrm{ℳ}=\{j:g_j^{\text{opt}}=1\}={\mathcal{S}}_1$. To generate ${\mathcal{G}}^{\text{red}}$, we combined groups 1 and 2 while keeping other groups intact, i.e., for each covariate j, $g_j^{\text{red}}=I(s_j\in {\mathcal{S}}_1\cup {\mathcal{S}}_2)+{\displaystyle {\sum }_{g=2}^{99}gI(s_j\in {\mathcal{S}}_{g+1})}$, where $\mathrm{ℳ}\subset \{j:g_j^{\text{opt}}=1\}={\mathcal{S}}_1\cup {\mathcal{S}}_2$. To form the misspecified partitions in Setting 4, we split ${\mathcal{S}}_1$ into two adjacent but mutually exclusive subregions ${\mathcal{S}}_{1,1}$ and ${\mathcal{S}}_{1,2}$ such that ${\mathcal{S}}_1={\mathcal{S}}_{1,1}\cup {\mathcal{S}}_{1,2}$. We considered two different misspecified partitions, denoted by ${\mathcal{G}}^{{\text{mis}}_1}$ and ${\mathcal{G}}^{{\text{mis}}_2}$, where $g_j^{{\text{mis}}_1}={\displaystyle {\sum }_{g=1}^{2}gI(s_j\in {\mathcal{S}}_{1,g})}+{\displaystyle {\sum }_{g=3}^{101}gI(s_j\in {\mathcal{S}}_{g-1})}$ and $g_j^{{\text{mis}}_2}=I(s_j\in {\mathcal{S}}_{1,g})+2I(s_j\in {\mathcal{S}}_{1,2}\cup {\mathcal{S}}_2)+{\displaystyle {\sum }_{g=3}^{100}g(s_j\in {\mathcal{S}}_g)}$. Figure 3 is a graphical representation of Setting 4.

Fig. 3.

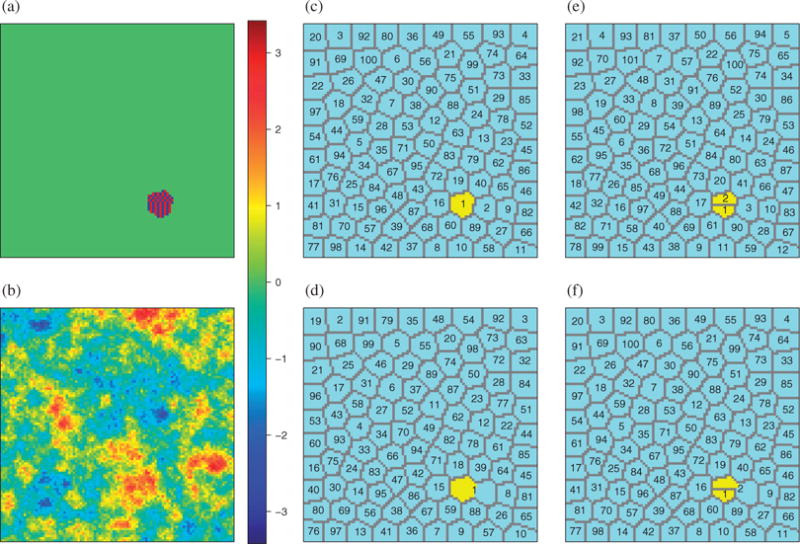
Model designs and configurations of different partitions on $\mathcal{S}$, the 100 × 100 equally spaced grid points in two-dimensional space [0, 1]², in Setting 4 of the simulation study for spatial variable screening: (a) the true coefficient β_j, which takes only three possible values, −3 in blue, 3 in red and 0 in green; (b) one set of simulated predictors X_j over space from a Gaussian random field on $\mathcal{S}$ with covariance kernel exp(−10||s − s′||₂) for s, s′ ∈ $\mathcal{S}$; (c) the partition ${\{{\mathcal{S}}_g\}}_{g=1}^{100}$ in Setting 4 to define the true nonzero coefficients, with β_j ⧧ 0 if and only if $s_j\in {\mathcal{S}}_1$, in yellow. Panels (c), (d), (e) and (f) respectively represent the optimal partition ${\mathcal{G}}^{\text{opt}}$, the size-reduced partition ${\mathcal{G}}^{\text{red}}$, and two misspecified partitions, ${\mathcal{G}}^{{\text{mis}}_1}$ and ${\mathcal{G}}^{{\text{mis}}_2}$, for the corresponding partition-based screening for selecting variables in Setting 4; in panels (c)–(f), ${\mathcal{S}}_1$ is coloured yellow.

For further comparison, we investigated the performance of sure independence screening (Fan & Lv, 2008) and high-dimensional ordinary least squares projection (Wang & Leng, 2016) in Settings 1–4. In addition, conditional sure independence screening (Barut et al., 2016) with a conditioning variable X₁ was considered for Settings 1–3. To evaluate the performance of high-dimensional ordinary least squares projection for logistic regression, we modified it to accommodate generalized linear models with a ridge penalty by specifying the tuning parameter to be 1. Sure and conditional sure independence screening results were obtained using the R (R Development Core Team, 2017) package SIS, while high-dimensional ordinary least squares projection was implemented using the R package screening. To make different methods comparable, we chose γ so that the number of selected indices was equal to the sample size and computed the true positive rate and the probability that the selected indices include the true model, following Fan & Lv (2008).

Table 1 summarizes the simulation results. In Settings 1–3, partition-based screening performs best for linear and logistic regression. In Setting 4, the performance of spatial-oriented reduced partition screening is almost the same as spatial-oriented optimal partition screening in linear regression, and is close to spatial-oriented optimal partition screening in logistic regression. This indicates that even when an optimal partition is not available, a size-reduced partition is a good alternative. In Settings 2 and 3, correlation-guided partition screening produces better selection accuracy than all three existing methods, and is comparable to partition-based screening. Thus, when there is insufficient prior knowledge to determine a size-reduced partition but the covariate variables have a block-diagonal correlation structure up to permutations, data-driven partition-based screening can yield improved selection accuracy. In Setting 1, where the covariance structure of covariates is compound symmetric, correlation-guided partition screening does not yield more accurate selection than high-dimensional ordinary least squares projection and conditional sure independence screening. In this case we examined the performance of partition-based screening with randomly generated misspecified partitions, as well as combined partition-based screening that combines five or ten different random partition-based screening statistics. The results indicate that combined partition-based screening with ten random ${\mathcal{G}}^{{\text{mis}}_2}$ is slightly better than combined partition-based screening with five random ${\mathcal{G}}^{{\text{mis}}_2}$ and outperforms partition-based screening with ${\mathcal{G}}^{{\text{mis}}_1}$ only or with ${\mathcal{G}}^{{\text{mis}}_2}$ only. Therefore, in the absence of an optimal partition, combining multiple partitions for variable screening fares better than relying on a single partition. Moreover, it produces better results than high-dimensional ordinary least squares projection and sure independence screening in Setting 1. The advantages of combined partition-based screening are obvious in Setting 4, where the accuracy of spatial-oriented partition screening with ${\mathcal{G}}^{\text{red}}$ can be improved by combining it with two misspecified partition-based screening statistics. Thus, combining various screening statistics from multiple sources of partitions, even though they may have been misspecified, appears to be a useful strategy.

Table 1.

Model selection accuracy of variable screening methods for linear and logistic regression in Settings 1–4

Setting 1	Linear regression			Logistic regression
	PIT (%)	MMS	TPR (%)	PIT (%)	MMS	TPR (%)
SIS	10	2273	84	12	2590	80
HOLP	91	24	98	53	173	90
CSIS	97	11	100	73	62	95
PartS ( ${\mathcal{G}}^{\text{red}}$)	100	7	100	100	6	100
PartS ( ${\mathcal{G}}^{{\text{mis}}_1}$)	84	36	97	46	226	88
PartS ( ${\mathcal{G}}^{{\text{mis}}_2}$)	87	34	98	60	145	91
CombPartS (5 ${\mathcal{G}}^{{\text{mis}}_2}$)	93	25	99	64	115	93
CombPartS (l0 ${\mathcal{G}}^{{\text{mis}}_2}$)	96	22	99	74	105	96
CorrPartS ( ${\mathcal{G}}^{\text{cor}}$)	78	64	96	47	219	88
Setting 2	Linear regression			Logistic regression
	PIT (%)	MMS	TPR (%)	PIT (%)	MMS	TPR (%)
SIS	0	3982	56	0	4243	41
HOLP	0	3721	59	0	4231	43
CSIS	69	52	96	0	311	90
PartS ( ${\mathcal{G}}^{\text{red}}$)	100	10	100	100	10	100
CorrPartS ( ${\mathcal{G}}^{\text{cor}}$)	91	10	98	88	10	98
Setting 3	Linear regression			Logistic regression
	PIT (%)	MMS	TPR (%)	PIT (%)	MMS	TPR (%)
SIS	0	3671	20	100	1367	60
HOLP	65	110	100	16	560	90
CSIS	6	3033	70	6	2265	70
PartS ( ${\mathcal{G}}^{\text{red}}$)	100	11	100	100	10	100
CorrPartS ( ${\mathcal{G}}^{\text{cor}}$)	62	101	100	18	426	80
Setting 4	Linear regression			Logistic regression
	PIT (%)	MMS	TPR (%)	PIT (%)	MMS	TPR (%)
SIS	0	9890	17	0	9860	26
HOLP	0	9886	18	0	9876	27
SpatPartS ( ${\mathcal{G}}^{\text{opt}}$)	100	100	100	100	100	100
SpatPartS ( ${\mathcal{G}}^{\text{red}}$)	100	100	100	73	174	100
SpatPartS ( ${\mathcal{G}}^{{\text{mis}}_1}$)	0	8232	65	0	9033	65
SpatPartS ( ${\mathcal{G}}^{{\text{mis}}_2}$)	0	9190	55	0	9269	74
CombPartS ( ${\mathcal{G}}^{\text{red}}$, ${\mathcal{G}}^{{\text{mis}}_1}$, ${\mathcal{G}}^{{\text{mis}}_2}$)	100	100	100	80	174	100

SIS, sure independence screening; HOLP, high-dimensional ordinary least squares projection; CSIS, conditional sure independence screening; PartS, partition-based screening; CombPartS, combined partition-based screening; CorrPartS, correlation-guided partition screening; SpatPartS, spatial-oriented partition screening; MMS, median minimum size of the selected models that are required to have a sure screening; TPR, average true positive rate; PIT, estimated probability of including all true predictors in the top n selected predictors.

6. Application

We applied the proposed methods to analyse resting-state functional magnetic resonance imaging data from the Autism Brain Imaging Data Exchange study (Di Martino et al., 2014). The primary goal of this study was to understand how brain activity is associated with autism spectrum disorder, a disease with substantial heterogeneities among children. Functional magnetic resonance imaging measures blood oxygen levels linked to neural activity, and resting-state functional magnetic resonance imaging measures brain activity only when the brain is not performing any tasks. This study aggregated 20 resting-state functional magnetic resonance imaging datasets from 17 experiment sites. For each subject, the resting-state functional magnetic resonance imaging signal was recorded for each voxel in the brain over multiple time-points. Standard imaging pre-processing steps (Di Martino et al., 2014) included motion correction, slice-timing correction, and spatial smoothing. The entire brain was registered into the 3 mm standard Montreal Neurological Institute space, which consists of 38 547 voxels in 90 brain regions defined by the automated anatomical labelling system (Hervé et al., 2012). After removal of missing values, the complete dataset included 819 subjects, consisting of 378 patients and 441 age-matched controls. To select imaging biomarkers for autism spectrum disorder risk prediction, we considered the fractional amplitude of low-frequency fluctuations (Zou et al., 2008), defined as the ratio of the power spectrum for frequencies 0.01–0.08 Hz to the entire frequency range. This measure has been widely used as a voxel-wise measure of the intrinsic functional brain architecture derived from resting-state functional magnetic resonance imaging data (Zuo et al., 2010).

We constructed a spatial logistic regression model that has clinical diagnosis of autism spectrum disorder as the outcome and the voxel-wise fractional amplitudes of frequency fluctuations as imaging predictors, adjusting for age at scan, sex and intelligence quotient. Because imaging predictors on the risk of autism spectrum disorder are spatially clustered and sparse (Liu & Calhoun, 2014), the primary aim of this study is to identify imaging biomarkers among 38 547 voxel-level fractional amplitudes of low-frequency fluctuations that predict the autism spectrum disorder risk. We applied partition-based screening by using anatomical information, correlation among imaging predictors and spatial information. Specifically, we considered the following methods: brain region partition-based screening on 90 brain regions; correlation-guided partition screening, which partitions the 38 547 voxels into G groups using the clustering algorithm introduced in § 4–2, where G is taken to be 256, 128, 64, 32, 16 or 8; spatial-oriented partition screening, which partitions the 38 547 voxels into 1024 equal-sized regions where the voxels are spatially contiguous within each region; and combined partition-based screening that combines all of the above. We also applied high-dimensional ordinary least squares projection for logistic regression with the ridge penalty, as implemented in the R package screening.

To assess the performance of the different methods, we used ten-fold crossvalidation, randomly splitting the data into ten equal-sized subsets. We applied the variable screening methods to the training dataset and obtained a set of selected voxels, based on which we made a prediction about the disease status in the testing dataset using logistic regression with the elastic net penalty, as implemented in the R package glmnet. We repeated this ten times and computed the crossvalidation accuracy. Among all the methods, combined partition-based screening achieved the smallest crossvalidation prediction error, 37%, and high-dimensional ordinary least squares projection had the largest crossvalidation prediction error, 48%. All the other partition-based screening methods achieved a prediction error of approximately 40%. More details and the receiver operating characteristic curves are given in the Supplementary Material.

Next, we applied combined partition-based screening to the entire dataset, using the method in § 4–4 to determine the threshold by taking an upper bound on the expected false positive rate to be 0.20. A total of 6142 important voxels were selected. Eight regions with more than 60 selected voxels are reported in Table 2, along with the median rank of voxel-specific screening statistics within each region. These regions are known to be involved in specific brain functions related to autism (Friederici et al., 2003; Japee et al., 2015).

Table 2.

Eight automated anatomical labelling regions with more than 60 voxels that are selected by combined partition-based screening

Selected region	Voxel counts	Median rank	Selected region	Voxel counts	Median rank
Frontal_Mid_R	95	5	Frontal_Sup_L	71	14
Temporal_Mid_R	78	27	Frontal_Mid_L	71	47
Temporal_Mid_L	75	154	Frontal_Sup_R	66	35
Precuneus_L	73	56	Precuneus_R	65	41

7. Discussion

The method proposed in this paper can be improved. First, our framework requires that the size of each partition group be less than the sample size to make (3) sensible. If this condition is not met, penalized likelihood methods such as the lasso can be applied, though these approaches may involve the selection of tuning parameters and the correction of biases due to penalization. A simple but efficient remedy would be to further refine the groups randomly. This refining procedure can be performed multiple times, and the resulting screening statistics can be combined using the rule in § 4.3. Second, although this paper has focused on non-overlapping partitions for ease of theoretical development, our screening framework can accommodate overlapping partitions. According to the combination rule in § 4.3, for each predictor that is covered by more than one partition, we can simply choose the screening statistic with larger value. Third, the time complexity of correlation-guided partition screening is O(p²), mainly due to the need to compute the correlation matrix and clustering predictors. To compute the correlations among ultrahigh-dimensional predictors more efficiently, we suggest adopting parallel computing techniques. To speed up the clustering of predictors, we propose to threshold the correlation matrix and generate a binary matrix, regarded as the adjacency matrix of an undirected graph. The connected components corresponding to group partitions can be obtained by using the breadth-first or depth-first search algorithms with time complexity between O(p) and O(p²).