DisTeam: A decision support tool for surgical team selection

Abstract

Objective

Surgical service providers play a crucial role in the healthcare system. Amongst all the influencing factors, surgical team selection might affect the patients’ outcome significantly. The performance of a surgical team not only can depend on the individual members, but it can also depend on the synergy among team members, and could possibly influence patient outcome such as surgical complications. In this paper, we propose a tool for facilitating decision making in surgical team selection based on considering history of the surgical team, as well as the specific characteristics of each patient.

Methods

DisTeam (a decision support tool for surgical team selection) is a metaheuristic framework for objective evaluation of surgical teams and finding the optimal team for a given patient, in terms of number of complications. It identifies a ranked list of surgical teams personalized for each patient, based on prior performance of the surgical teams. DisTeam takes into account the surgical complications associated with teams and their members, their teamwork history, as well as patient’s specific characteristics such as age, body mass index (BMI) and Charlson comorbidity index score.

Results

We tested DisTeam using intra-operative data from 6065 unique orthopedic surgery cases. Our results suggest high effectiveness of the proposed system in a health-care setting. The proposed framework converges quickly to the optimal solution and provides two sets of answers: a) The best surgical team over all the generations, and b) The best population which consists of different teams that can be used as an alternative solution. This increases the flexibility of the system as a complementary decision support tool.

Conclusion

DisTeam is a decision support tool for assisting in surgical team selection. It can facilitate the job of scheduling personnel in the hospital which involves an overwhelming number of factors pertaining to patients, individual team members, and team dynamics and can be used to compose patient-personalized surgical teams with minimum (potential) surgical complications.

1. Introduction

Surgical service providers’ capabilities, skills, and interactions can highly affect patient outcome. Among all the influencing factors, such as pre-operative deviation [1], the success of a surgical team highly depends on the individual surgical service providers in the team. Ideally, the expertise of individual team members complements each other, and team members effectively communicate with each other. An optimal team selection might lead to reduced conflicts, better coordination [2], and ultimately better patient outcome. Thus, selecting the right providers for a surgical team is crucial for optimizing patient outcome, e.g. in terms of number of complications or shorter recovery period. Despite the obvious benefits, selecting the optimal team yet remains a difficult task [3].

Much of the prior work in this domain has focused on measuring the performance of individual healthcare providers. Such efforts are fraught with challenges, including the need to control for patient factors, procedural/diagnostic complexity, effects stemming from the practice environment itself, lack of details on outcomes of interest, relative rarity of bad outcomes, and difficulty with inferring causality between modifiable healthcare provider actions and adverse outcomes. For example, a recent attempt to measure anesthesiologist performance in patient pain intensity on arrival to the recovery room instead discovered an overriding confounding variable in the identity of the recovery room nurse [4]. Worse, recent examinations stemming from an evaluation of cardiac anesthesiologists’ impact on patient outcomes, its retraction and subsequent revised republication, revealed incredible sensitivity to debatable assumptions on the correlation of healthcare providers to their practice environment, assumptions which easily lead to multiple reversals in the interpretation of results [5].

Effective functionality of surgical teams is regarded as one of the principles of creating safe health care delivery systems [6,7]. Health care settings are high-risk work environments especially in surgical settings [8,9]. Improving patient outcome and safety is one of the top priorities of hospitals and surgical service providers [9]. The majority of surgical adverse events occur in intra-operative settings [10]. Several studies have performed human factor analysis in the operating rooms (OR), as a complex and high-risk system, and analyzed the relationship between the performance of OR and surgical outcomes [6,11]. In addition, several studies have focused on intraoperative complications and used various methodologies such as malpractice claim analysis [12,13], root cause analysis [14,15], or prospective analysis [16–18]. Despite all the efforts in analyzing the relationships between key factors in OR and patient outcome, the relative contribution of the influencing factors is still unknown [10].

The relation between effective team function and system’s outcome has been also studied in various domains, e.g. team work and safety in airline industry, where a significant relation was observed between teamwork and safety.¹ Several studies have reported the impact of effective teamwork and communication among the team members on patient outcome, e.g. in trauma care [19,20] and intensive care [21]. Several studies also specifically focused on teamwork in the OR [17,22–24]. This all indicates the importance of team selection and human factors. Surgical services, as one of the major care services, are inherently precarious. Thus, a high level of coordination is required among the surgical members with different expertise and experience levels. The time and resource limitations, availability of providers, and the uncertainty which might exist in complex hospital systems [10], can add to the intricacy of the team arrangement and selection procedure.

Team selection in surgery procedures is a crucial task [26] as it might affect patient outcome. It involves assigning individuals to tasks that change frequently over time [27]. This multi-period assignment augments the complexity of the task. The scheduling becomes even more complicated when the scheduler aims to match the staff capabilities with the tasks, considering the operational timing requirements and limitations [27]. One can imagine that finding the best fitted staffs for a task and assigning them to a team can be extremely difficult in this context. Current commercially available scheduling software (e.g. Snap Schedule,² ScheduleAnywhere³) consider several factors such as personnel preferences for days, shifts, units; and regulatory and union requirements. Despite obvious advantages such as accessibility and customization, they do not consider the team structure and history, as well as patient’s specific characteristics including previous patient outcomes.

In this paper, we will provide a framework for facilitating decision making in team selection based on considering history of teams and their members in terms of surgical complications, as well as by considering patient’s characteristics such as age, body mass index (BMI) and comorbidity scores. The main contribution of this paper is in using metaheuristic approaches for identifying a ranked list of surgical teams personalized for each patient, based on prior performance of the surgical teams. To the best of our knowledge, no study thus far considers prior interactions with resulting patient outcomes. It should be noted that our focus in this paper will be on developing a decision support tool for assisting in team selection, and we thus will not discuss other related aspects such as scheduling algorithms.⁴ This will facilitate the job of scheduling personnel in the hospital which involves an overwhelming number of factors pertaining to patients, individual team members, and team dynamics. In the rest of the paper, we will first provide an overview of the existing literature in Section 2, and then we will discuss our approach in more detail in Section 3. The performance of the proposed framework is evaluated in the Section 4, finally in the last section we will discuss limitations of current work and will point to future directions.

2. Related work

The availability of large-scale datasets and the complex nature of real world problems have resulted in development of various intelligent and heuristic approaches in different domains [28]. Genetic algorithm (GA), developed by John Holland at the University of Michigan in 1960’s and 1970’s [29], is a search metaheuristic which belongs to the larger class of evolutionary algorithms and is widely used in the field of artificial intelligence. GA aims to find the optimal solution among a set of possible solutions by considering each solution as an individual in a population, and by generating better solutions from these individuals via applying a selection process similar to natural evolution [30]. That is, if an intermediate solution (individual) is a better fit to a problem, it will be more likely to be considered for the reproduction. One should note that the genetic algorithm approach differs from the derivative-based optimization (DBO, e.g. Newton’s method in optimization) algorithms in at least two ways: 1) GA searches a population of potential solutions in each iteration whereas DBO quests only a single point, and 2) DBO techniques employ deterministic transition rules for finding the next (better) solution while GA uses probabilistic transition rules and random selections to form the next population of the solutions [33,34].

GA has been widely used in various domains, e.g. finance [35], engineering [36], and economics [37]. GA has been also reported as the most popular meta-heuristic approach [38]. In addition, GA has been successfully applied in similar (optimal) team selection problems in other domains [39–41]. Some examples are: using genetic algorithm and a multi-criteria decision making approach for selecting the line-up for a cricket team [42], a fuzzy-genetic analytical model for project team formation problem [43], or using GA and social network measures for finding the team formation for a research and development (R&D) department [44].

Optimization and the genetic algorithm, in particular, have recently attracted more attention in the healthcare field. GA has been applied in a wide range of healthcare sub-domains such as cancer detection using GA partial least square discriminant analysis [45], vascular soft issue elasticity estimation using the combined finite element modeling and GA [46], selecting the most relevant genes that are associated with a disease [47], and healthcare management and patient admission scheduling [48]. One notable study in healthcare domain is [30] which employed genetic algorithm to develop a framework for multi-objective optimization for searching large design spaces and determining the optimal resource levels in surgical services. They showed that the framework is able to identify the efficient design points. In another study, Steiner et al. [49] focused on partitioning the healthcare system of Parana State in Brazil and used multi-objective genetic algorithm for optimizing the system. They showed that their proposed approach can be helpful for decision making in health management. Du et al. [50] focused on optimizing the scheduling of clinical pathways aiming to improve the management standard in hospitals. They combined the genetic algorithm with particle swarm optimization and proposed a hybrid model that can improve the scheduling of patients’ treatments.⁵ As evident from literature, researchers have used GA in various problems in the healthcare domain, however, to the best of our knowledge, no study has so far used GA for facilitating the surgical team selection. Furthermore, there is no system or algorithm that considers surgical team structure, cooperation history, and patient characteristics in forming (optimal) surgical teams.

3. Data and methodology

3.1. Data

This study was approved by the University of Florida institutional review board. The data was collected from University of Florida’s integrated data repository (IDR) after obtaining a confidentiality agreement from the IDR. It contained de-identified intra-operative data for adult patients (age ≥21) who received non-ambulatory/nonobstetric Orthopedics surgery at Shands at the University of Florida between June 1, 2011 and November 1, 2014. The de-identified surgery dates indicated the number of days elapsed from a common undisclosed original date prior to the study period. Subjects who did not receive a surgical procedure, or who were discharged on the same day as their surgery, were excluded from the dataset. Those cases whose de-identified surgery start date and/or end date were missing were excluded as well. We also removed any invalid, generic or placeholder provider entries (e.g. providers whose ids were missing). A list of patient socio-demographics is given in Table 1. Providers were considered from intraoperative phases of care. In the intraoperative phase, providers were those individuals who were documented as having participated in a patient’s surgery. The majority of these roles were surgeons (and surgical assistants), anesthesiologists and anesthetists, and circulating nurses. As a teaching hospital where trainees may rotate to different services, trainees were included using their denoted roles within the given surgery. The intra-operative dataset, named as the original intra-operative data in rest of the paper, contained 6065 unique cases of orthopedics surgery. These surgeries were operated by 60 distinct surgeons, 157 anesthesiologists, and 223 circulators.

Table 1.

List of variables, their types, and description.

No	Variable	Type	Description
1	Age	Numeric	Patient age at hospital encounter (set as 90, if age 90 or older)
2	BMI	Numeric	Patient’s body mass index
3	Comorbidity	Numeric	Patient’s Charlson comorbidity index (ver. 2011)
4	LOS	Numeric	Length of stay (inpatient/observation in days or in hours)
5	Complication count	Numeric	Derived from diagnosis1-diagnosis50 and complication codeset
6	Service	Character	Type of surgical service
7	Principal Dx	Character	Primary diagnosis code and description
8	Principal Px	Character	Primary procedure code and description
9	Race	Character	Patient’s race
10	Ethnicity	Character	Patient’s ethnicity
11	Gender	Character	Patient’s gender
12	Marital status	Character	Patient’s marital status at hospital encounter

Surgical complication codes were defined as the codeset of a list of ICD9-CM codes, denoting various surgical complications. The complication ICD9-CM codeset is listed in Appendix A. The diagnoses are coded during an abstraction of the medical record which occurs at the conclusion of the hospitalization. The ICD9-CM complication codeset contains codes from 996 through 999, along with their corresponding subclasses. We scanned through each of 50 diagnosis codes to check if any of the complication codes matches. The complication outcome, which is used in DisTeam, is the sum of all detected complication codes for a hospital encounter. Surgical complications do not necessarily denote any error in the surgical process, as several complications are outcomes which may be unavoidable given the nature of the patient’s comorbidity status and/or the nature of the procedure itself.

3.2. Methodology

The proposed solution for selecting optimal surgical team(s) is composed of two modes: 1) Training mode, and 2) Operational mode, as shown in Fig. 1. The training mode consists of two separate modules: patient clustering module, and extracting existing teams module. Patient clustering allows us to tailor the surgical team selection procedure to patient characteristics. The extracting existing teams module fetches distinct surgical service providers that will be further used in forming the intermediate solutions (individuals). The optimization procedure is performed in the operational mode using the genetic algorithm. The training and operational modes are explained in more details.

Fig. 1.

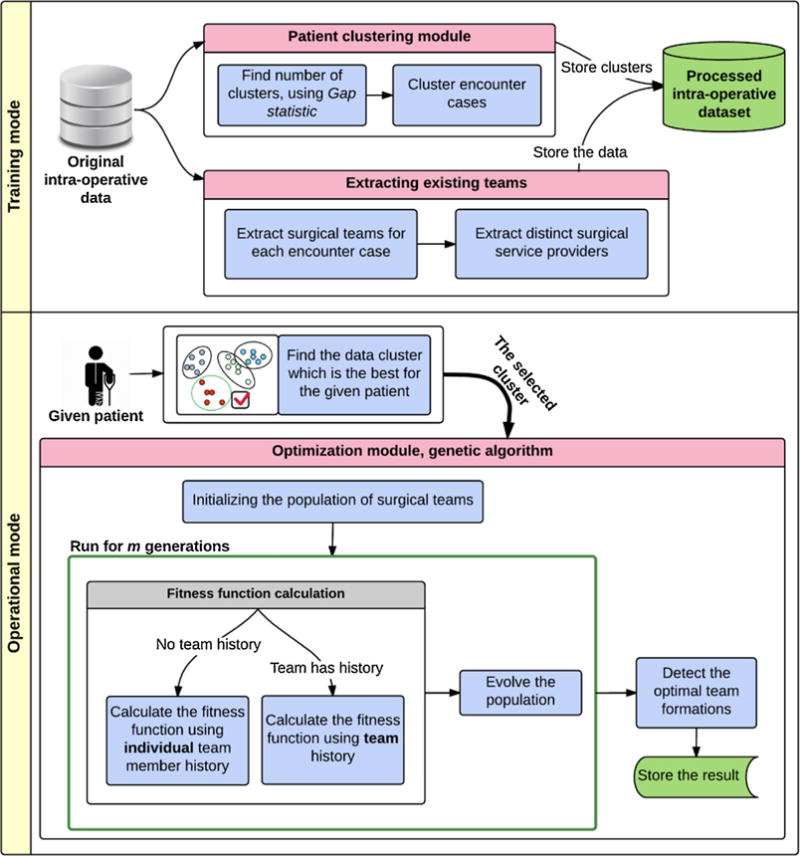
The surgical team selection framework has two modes: 1) Training mode, and 2) Operational mode. In the training mode, the original intra-operative data is first clustered based on the patients’ features and the data is preprocessed to extract the surgical teams for each orthopedics encounter case, based on the intra-operative data. Next, the distinct surgical providers are extracted from the teams. The extracted information along with case complementary information such as number of complications are integrated into the processed intra-operative dataset. In the operational mode, the proper subset of data for the given patient is first selected. And, using the genetic algorithm, the optimal surgical team selections for the given patient are detected and stored.

3.2.1. Training mode

3.2.1.1. Patient clustering module

First, in the training mode, we used a retrospective dataset of patients to form groups of similar patients based on several features including age, ethnicity and race, Charlson comorbidity index, and body mass index (BMI). This allowed us to identify the most representative cluster for a new patient. We used a variation of K-Means clustering approach [51], due to its speed and ease of implementation, named K-Prototypes [52] which can handle both numerical and categorical features.

In K-Prototypes algorithm, data points are clustered against k prototypes.⁶ K-Prototypes algorithm uses decision tree induction algorithms to generate rules for clusters, which helps to increase the interpretability of the algorithm and to detect the clusters of interest more accurately [52]. In K-Prototypes, number of prototypes (k) should be provided by the user. We used the Gap statistic [53] for estimating the best k. The Gap statistic⁶ considers an appropriate reference null distribution and compares the change in within-cluster dispersion. Fig. 2a shows the Gap statistic graph versus various numbers of clusters. As seen, the Gap statistic peaks at k = 2 with the value of ~2.4. We further investigated the issue by plotting DG_k = Gap (k) − (Gap (k + 1) − S_k+1). The results are depicted in Fig. 2b. In Fig. 2b, the optimal k is the smallest k for which DG_k becomes positive. As observed, the existence of 2 clusters is confirmed. Thus, from Fig. 2a and b, number of clusters was set to 2 in K-Prototypes clustering algorithm. The 6065 Orthopedics surgery cases were clustered in two groups with 2238 and 3827 surgical providers, respectively.

Fig. 2.

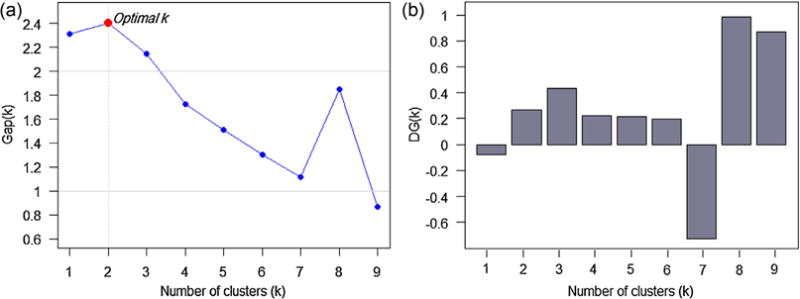
a) Gap statistic vs. number of clusters. The statistic is peaked at k = 2, indicating the best estimated number of clusters, b) Trend of DG_k = Gap (k) − (Gap (k + 1) − S_k+1) vs. numbers of clusters. DG_k becomes positive for the first time at k = 2, confirming that the data has 2 clusters.

3.2.1.2. Extracting existing teams module

The input to this module is the original intra-operative data. In this step, the surgical team associated with each patient is extracted. Each surgical team consists of a number of team members, i.e. surgical service providers (>1), who provided care to the patient, e.g. a surgeon, an anesthesiologist, a nurse, etc. For each team, the corresponding information of all team members (surgical service providers) is also extracted from the integrated data repository and they are tagged based on their roles (surgeon, anesthesiologist, or circulator). The collected information is stored in an intermediary dataset, named as the processed intra-operative dataset in Fig. 1.

3.2.2. Operational mode

In the operational mode, whenever a new patient’s information is entered into the system, the best possible team is suggested (Fig. 1). To do this, the following steps are taken: 1) finding the most similar patient cluster, 2) extracting candidate teams, and finally 3) selecting the best candidate. In the clustering module, we determine which cluster best represents the new patient by computing the distance between the patient and cluster centroids, and then selecting the closest (most similar) centroid as the target cluster.⁷ The target cluster is then used in the optimization module to select the best surgical team.

3.2.2.1. Optimization module

Genetic algorithm (GA) is the core of our optimization module. The idea in genetic algorithm is to mimic the process of natural selection⁸ in order to find the optimal solution for a problem [54]. In other words, GA artificially implements the natural evolution procedure by mimicking inheritance, selection, mutation, and crossover.

A candidate solution is called an individual in genetic algorithm. A population of individuals is evolved to find the optimal solution. Each individual possesses a number of characteristics, called as chromosomes, which can be altered [55]. In our case, each individual represents a surgical team configuration (i.e. a team candidate). The team contains three chromosomes representing team members, i.e. surgeon, anesthesiologist, and circulator of the surgical team, denoted by S, A, and C respectively in Fig. 3. A population contains several surgical team candidates (Fig. 3).

Fig. 3.

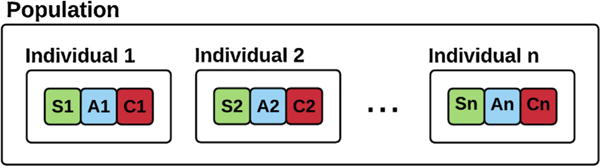
A population of intra-operative surgical teams. Individuals refer to a surgical team candidate. Each team consists of three members indicating the surgeon, the anesthesiologist, and the circulator of the team.

Each team candidate has three members. In our existing dataset, there are 60 distinct surgeons, 157 anesthesiologists, and 223 circulators. Thus, there are $\left(\begin{array}{c}60\\ 1\end{array}\right)\left(\begin{array}{c}157\\ 1\end{array}\right)\left(\begin{array}{c}223\\ 1\end{array}\right)=60\ast 157\ast 223=2,100,660$ different possible team configurations, which proves prohibitive for a brute force search. This shows the complexity of finding the optimal team.

The optimization module starts by initializing a population, via randomizing the possible combination of individuals to create a set of distinct individuals. We used the stochastic initialization procedure, i.e. the initializer generates different populations if it is provided with different initial seeds.⁹ In particular, an individual is created by generating a random index for each provider role, i.e. surgeon, anesthesiologist, and circulator. A random population is then created as a set of random individuals. The population generation is an iterative process, where each population in each iteration is referred to as a generation. In each generation, we evaluate the fitness of each individual in the population as well as the fitness of the entire population. The fitness function is the core of the optimization module which acts as the objective function in the optimization procedure.

In this study, we used a fitness function that reflects individual and team’s complication history. Historically, patient morbidity and severe outcome have been mainly associated with the factors in intra-operative period [57]. Several factors can influence patient safety and outcome, e.g. surgical team members’ expertise, level of coordination, and communication. One way to quantify the patient outcome is counting the number of complications that are associated with the surgical encounter. Thus, we formulated the individual fitness function based on the number of complications that have occurred during the surgery. In our formulation, fitness score ranges from 0 to 1, and a lower fitness score indicates a potentially better team configuration. We associated surgical complications with providers at three different levels: collective (any past surgical case involving “all” current team members), pairwise (any past surgical case involving any “two” current team members), and individual (any past surgical case involving any current team member). This accounts for individual performance, and captures the collective and pairwise cooperation history. We denote the number of collective, pairwise, and individual case involving complications by C^C, C^P, and C^I, respectively. The same notation is used to denote the total number of collective, pairwise, and individual cases (including with/without complications): N^C, N^P, and N^I, respectively.

We first consider past collective surgical cases of the given candidate team. If there are no collective surgical cases, then we check for pairwise surgical cases of any members of the candidate team. And, if no pairwise cooperation is found, we consider the individual provider’s performance. That is, our fitness function was designed to consider past cooperation among the members (either collective or pairwise). We compute the ratio of complications, as in Eq. (1). If no cooperation history is available, the ratio of complications is computed separately for each provider in the team. Average individual complications will be higher than collective and past complication ratios, thus the overall fitness value will be slightly higher for teams with no past cooperation.¹⁰ For a given candidate team t, we compute complication ratio and the ratio of no-complication cases, C_t and $N_t^0$ respectively, in Eq. (1).

$$\begin{gathered} C_t=\left\{\begin{array}{c}\mathit{Collective}\mathit{team}\mathit{history},\frac{{\displaystyle \sum C^C}}{\left({\displaystyle \sum N^C}\right)C_{max}^C}\\ \mathit{Pairwise}\mathit{team}\mathit{history},\frac{{\displaystyle \sum C^P}}{\left({\displaystyle \sum N^P}\right)C_{max}^P}\\ \mathit{No}\mathit{team}\mathit{history},\frac{{\displaystyle {\sum }_{i\in t}{C}^I}}{\left({\displaystyle {\sum }_{i\in t}{N}^I}\right)C_{max}^I}\end{array}\right\} \\ {N}_t^0=\left\{\begin{array}{c}\mathit{Collective}\mathit{team}\mathit{history},\frac{{\displaystyle \sum N_0^C}}{{\displaystyle \sum N^C}}\\ \mathit{Pairwise}\mathit{team}\mathit{history},\frac{{\displaystyle \sum N_0^P}}{{\displaystyle \sum N^P}}\\ \mathit{No}\mathit{team}\mathit{history},\frac{{\displaystyle {\sum }_{i\in t}{N}_0^I}}{{\displaystyle {\sum }_{i\in t}{N}^I}}\end{array}\right\}. \end{gathered}$$ (1)

In Eq. (1), i refers to the provider i in team t, $C_{max}^C$, $C_{max}^P$ and $C_{max}^I$ are the maximum complications ratio for collective cooperation, pairwise, and individual, respectively. And, $N_0^C$, $N_0^P$, and $N_0^I$ are the number of collaborative, pairwise, and individual surgeries with no complications, respectively. The fitness function is defined as a linear combination of the complications ratio and no-complication ratio, as stated in Eq. (2). Since in health-care the patient outcome is of the highest importance, we also included the ratio of cases with no complication in the function, setting higher weights on performing a surgery with no complication at all.

$$F_t=\alpha C_t+\left(1-\alpha \right)\left(1-N_t^0\right).$$ (2)

In Eq. (2), the ratio of cases with no complication $N_t^0$ is subtracted from 1, as lower F_t values are representing better fit.

The extreme conditions were treated exclusively in the code. For example, if a team has no cases, a division by zero error is raised. But, the system assigns a large fitness value (i.e. 99) for such extreme conditions thus excluding them from the optimization process. More specifically, if the denominator in Eq. (1) is zero the division by zero exception is raised in the code for which we set the fitness function to a large arbitrary number, i.e. 99. Since DisTeam fitness function converges to 0, a solution with large fitness function equal to 99 would be automatically excluded from the optimization process. After calculating the fitness value for the surgical teams (F_t), the fitness of the population is calculated by averaging over the team fitness values, as indicated in Eq. (3). In each generation, the fitness of the population is used in the optimization procedure in which DisTeam makes the fitness function to converge to zero.

$$F=\frac{1}{n}{\displaystyle \sum _{t=1}^n{F}_t}.$$ (3)

The team fitness score values are compared to find the best team configurations. The potentially more suitable teams with lower fitness function values are selected from the population. Next, we evolve the population (i.e. teams) over generations to find more optimal solutions. In the evolution procedure, in each generation, a proportion of the teams who are more fit are retained (survived) for the next generation. These teams are considered as parents in the next generation and are used to generate better children (new teams). In other words, we select high performing teams and create new teams from them to minimize the number of complications. This operation is called crossover, i.e. the process of taking more than one parent solutions and producing a (better) child from them. An example is shown in Fig. 4.

Fig. 4.

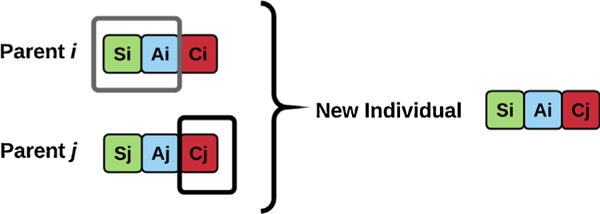
An example of the crossover operation. Generating new individuals (teams) from more fit parents, i.e. teams with lower average number of complications.

In addition, a few individuals are randomly selected from the current population and are passed to the next generation to assure the chromosomes variety in the next generation. Finally, the chromosomes of a very few individuals are manipulated to simulate the mutation. To perform the mutation, we randomly select a provider in a team, mutate its index to obtain a new provider, and replace the selected provider with the new provider in the team (Fig. 5). The mutation proportion is kept at a very low level (<5%) to prevent unexpected and large evolutions that might harm the optimization process and convergence speed.

Fig. 5.

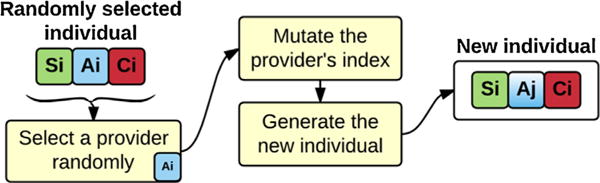
An example of mutation operation. Generating new individuals (teams) through random selection and mutation.

The new generation of the individuals is then used in the next iteration of the algorithm and the procedure is repeated until we reach the maximum number of generations.¹¹ The proposed system has two different outputs: 1) the selected best performing surgical team from the entire generations, i.e. the team with the minimum F_i, and 2) the optimal population, i.e. the population with the minimum F, containing a set of individuals. The population with the minimum average number of complications over its individuals can be helpful since it provides the hospital with a set of different team selections which perform relatively close to each other. This is extremely helpful in scheduling and brings more flexibility, since even if the best performing individual (team) is not available, there will be other options to use.

4. Case study

4.1. Optimization module, parameter setting

As a case study, we tested DisTeam performance on the intraoperative data, including 6065 unique cases of Orthopedics surgery, that was introduced in the Data and Methodology section. The data contain patient socio-demographics as listed in Table 1, surgical teams’ data, and the outcomes. Different parameters of the genetic algorithm including the convergence rate and diversity of the optimal populations were evaluated. Fig. 6 shows the trends of the fitness value of the population, as defined in Eq. (3), and its convergence rate against generations for 4 different best performing setups. As discussed earlier, the optimization module uses genetic algorithm, which needs to be provided with 3 main parameters: retain (survival) rate, random selection rate, and mutation. Retain rate indicates the proportion of individuals that survive and move to the next generation. Random selection guarantees the diversity of the individuals in the next generation by selecting some random individuals from the current generation. And, mutation mimics the genetic mutation concept by changing one of the chromosomes (surgical service providers) randomly.

Fig. 6.

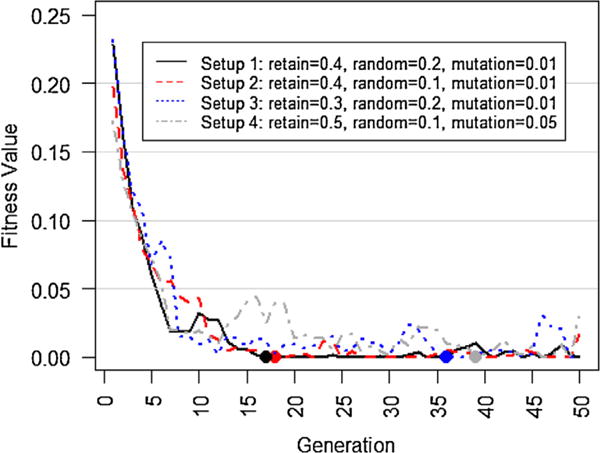
Fitness value trends in various setups (α = 0.5). Filled circles represent the first time (generation) when the optimal team is found. As seen, Setups 1 and 2 converge to the optimal solution faster than the other two setups. The results for Setup 4 suggests that high retain rate slows down the optimization procedure. Setups 3 and 4 provide approximately optimal team selections, although they converge slower.

Although setting different optimization parameters affects the convergence rate, DisTeam is able to quickly converge to the optimal population, i.e. the one with fitness value of 0, amongst 2,100,660 total number of possible surgical team formations (Fig. 6). As seen, setups 1 and 2 converge faster than the other two. Other setups can be also beneficial as they provide more population diversity around the optimal solution through the slower converge rate. Thus, based on the needs of the healthcare setting, DisTeam parameters can be set to find the optimal solution quickly, or to find the optimal solution along with a variety of approximately optimal solutions. The latter will be specifically useful if there are availability concerns about specific surgical service providers, which is almost the case in real-life situations. In an actual setting, DisTeam can be easily adjusted for workforce availability by including a filtering module that initially filters out unavailable surgical service providers for the given date and time, and according to the workload. The weighting parameter, i.e. α, equals to 0.5 in Fig. 6. Using different weighting rates can be useful in some healthcare settings, e.g. putting more weights on the number of complications rather than the number of cases with zero complication. However, different weights can slightly affect the convergence of the fitness function. We set α to different values and checked the trend of the fitness value for setup 1 that was the fastest converging setup as observed in Fig. 6. The results are depicted in Fig. 7. As seen, although using different values impact the convergence rate of DisTeam, it still finds the optimal solution in less than 40 generations.

Fig. 7.

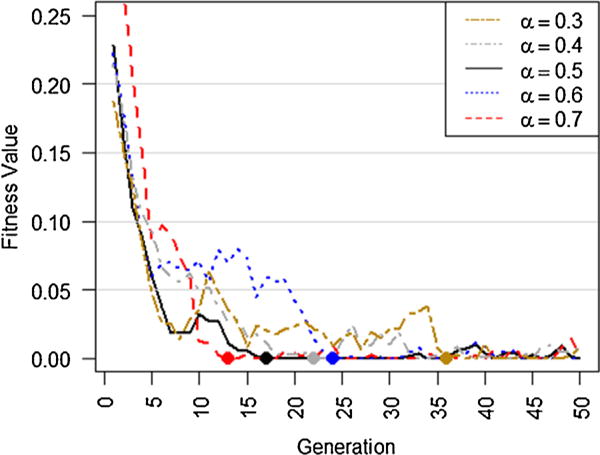
Fitness value trends using different weightings (a). Higher a puts more weights on the number of complications rather than the number of cases with zero complications. As seen, DisTeam converges to the optimal solution in less than 40 generations in all scenarios.

4.2. Setup 1, results

In this section, we present a practical example of the team selection procedure for Setup 1 to demonstrate the usability of DisTeam. The objective is to find the optimal surgical team for a given patient. Without loss of generality, let us suppose we have a new patient presented to the system, 57 years old, white, non-Hispanic, with a BMI of 27.8, and comorbidity index of 6. As a first step, the cluster whose centroid is the closest to the given patient’s data features is selected. In this given example, cluster 1 was selected that contained 3827 distinct surgical cases in which 52 surgeons, 151 anesthesiologists, and 207 circulators were involved.

We then provided the system with the selected cluster dataset of surgical service providers to find the optimal surgical team for the given patient. As seen in Fig. 8, DisTeam converges to the first optimal solution in the 15^th generation, which is considerably fast. After the 15^th generation, the fitness value fluctuates around the optimal solution due to the parameter settings that were used in Setup 1. One may note that the heuristic approaches do not necessarily converge to the same solution in different runs. That means if we re-run the same experiment, we might obtain slightly different results. Another point is that, after surgery, the data should be updated for the involved providers in the surgery to keep the data updated and thus the process dynamic. This might affect the optimal solution in the upcoming time events.

Fig. 8.

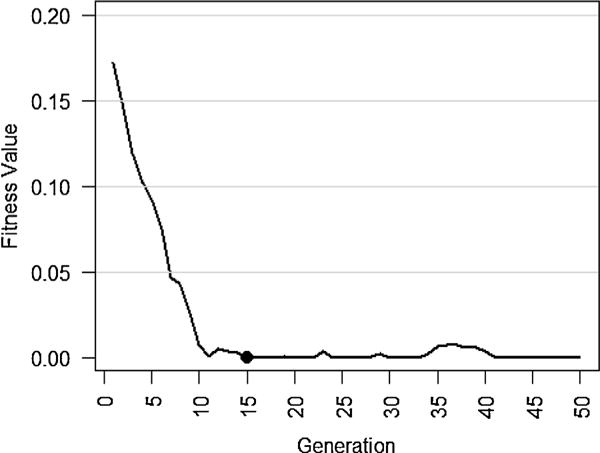
Fitness value trend in the optimal surgical team selection procedure for the given patient. The filled circle represents the first time (generation) in which the optimal team is found. As seen, the first optimal solution is found in the 15^th generation.

Table 2 shows the optimal surgery team selection that was detected for the given patient. As it is observed, the selected surgical providers have had a promising performance in doing the Orthopedics operation, comparing their average rate of complications with the role-specific averages. In addition, the results show that DisTeams successfully considered the past co-operations, if available, amongst the selected surgical service providers.

Table 2.

The optimal surgical team selection for the given patient obtained by DisTeam.

De-identified surgical provider ID	Role	No. cases	No. complications	Average complication rate	Average complication rate (role specific)
1	Surgeon	114	123	1.08	1.83
106	Anesthesiologist	123	115	0.93	1.92
140	Circulator	9	0	0	2.03
Past cooperation
1 and 106		1	0	0

5. Discussion and future work

In this paper, we proposed DisTeam which is a metaheuristic framework for objective evaluation of surgical teams and finding the optimal team for a given patient, in terms of number of complications. We followed two main goals: 1) adding surgical team performance history dimension to the model, 2) providing personalized solutions for patients. The team selection in surgery procedures can affect the patient outcome. DisTeam considers patients’ characteristics by using a clustering technique, in order to find a personalized solution for the given patient. The clustering module provides the personalization, otherwise it does not affect the system complexity if it is removed from DisTeam. We tested the system without clustering and almost the same convergence rate was observed. The clustering module, can be easily updated or modified based on the requirements of the target hospital. Number of complications has been considered as the main target variable where the system aims to minimize it through the optimization procedure. Other factors, such as surgical team’s total number of cases and cases with zero complications, have been also considered in the optimization procedure. Past collaboration experience among the surgical providers is another influencing factor which we considered it in our proposed system. We used metaheuristic approach due to several reasons: 1) The ability of the program to quickly provide a set of multiple local optima which brings more flexibility by listing alternative teams, 2) its high performance on noisy data, 3) ease of distribution and parallelization, 4) simplicity and ease of interpretation [28,58]. The results show the usability and the great potential of DisTeam in forming surgical teams. DisTeam can be extended to include more influencing factors. In this paper, we used a simple surgical team selection that included 1 surgeon, 1 anesthesiologist, and 1 circulator. DisTeam can be easily extended to cover more complicated team selections. DisTeam can be employed for any surgical team selection procedure in a health-care setting through modifying the population and individual generation procedures and defining the best-tuned fitness function, according to the specific characteristics of the given problem/surgery.

We draw reader’s attention to the fact that the genetic algorithm is a meta heuristic optimization search approach and is different from the conventional statistical approaches where the (cross) validation is applied on disjoint training and test datasets. In the training phase of DisTeam, we performed clustering and the surgical providers’ information were retrieved. This is different from training of the model as the model is not trained on the data, but it searches over the data. One should note that DisTeam, in its current version, can act as a decision support system, but it cannot be considered as a replacement for the scheduling and resource allocation unit in a hospital, due to complexities present in healthcare settings. In practice, it needs to be closely integrated with the scheduling software to provide team selection suggestions based on the availability and work hours of the providers. In a real setting, the scheduling system is preferred to be used in advance, providing DisTeam with the list of potentially available individuals. This can reduce the search space, increase the convergence speed, create surgical team alternatives that are fully available. Another issue that might have an impact on the performance of DisTeam is that new surgical team members will possibly have fewer complications reported compared to a senior provider. We computed the average number of complications to account for this effect, but still further refinement can be taken into the consideration. Moreover, the current version of DisTeam contains a relatively small number of patient characteristics and outcomes of interest. As each of these facets may increase the interest in personalized medicine, we consider it prudent to keep an eye towards extensibility.

Another important thing to note is that DisTeam may not choose the same team with the lowest score within the cluster. This is because: 1) There would not be a single “the best” team in each cluster since the data are updated according to the performance of the teams and providers, thus, the best team might change, and 2) The built-in randomization procedure in the algorithm as well as GA functions characteristics cause variety in the solutions. Another property of DisTeam is that it provides two sets of answers: a) The best team over all the generations, and b) The best population which might consists of different teams and can be used as an alternative solution. This increases the flexibility of the system as a complementary decision support tool. One should note that in real setting the clustering process is not suggested to be updated as a new data point is added to the system, however, it would be better to perform the clustering on a longer period basis, such a weekly or monthly, based on the decisions of the operating hospital. Further increases in speed may be also attainable via pooling of recent solutions, which would be especially prudent in a dynamic approach.

In summary, DisTeam can provide a complimentary perspective besides considering only the work hours and availability when scheduling surgical cases. It can support the decision-making process through providing a list of the most suitable surgical teams in terms of the patients’ outcome. While not optimal, it can definitely add a complementary perspective to the decision space, rather than just considering surgical service providers’ availability. The patient clustering approach that is used in DisTeam allows it to propose teams that are personalized to the characteristics of the given patient. This advantage along with the consideration of team cooperation history are the two unique properties that distinguish DisTeam from other simple approaches that solely rank the top role-specific providers and recommend them as a team.

Appendix A

See Table A1.

Table A1.

Complication ICD9-CM codeset.

No	Code	Code definition
1	996.0	Mechanical complication of cardiac device, implant, and graft
2	996.1	Mechanical complication of other vascular device, implant, and graft
3	996.2	Mechanical complication of nervous system device, implant, and graft
4	996.3	Mechanical complication of genitourinary device, implant, and graft
5	996.4	Mechanical complication of internal orthopedic device, implant, and graft
6	996.5	Mechanical complication of other specified prosthetic device, implant, and graft
7	996.6	Infection and inflammatory reaction due to internal prosthetic device, implant, and graft
8	996.7	Other complications of internal (biological) (synthetic) prosthetic device, implant, and graft
9	996.8	Complications of transplanted organ
10	996.9	Complications of reattached extremity or body part
11	997.0	Nervous system complications
12	997.1	Cardiac complications
13	997.2	Peripheral vascular complications
14	997.3	Respiratory complications
15	997.4	Digestive system complications
16	997.5	Urinary complications
17	997.6	Amputation stump complication
18	997.7	Vascular complications of other vessels
19	997.9	Complications affecting other specified body systems, not elsewhere classified
20	998.0	Postoperative shock
21	998.1	Hemorrhage or hematoma or seroma complicating a procedure
22	998.2	Accidental puncture or laceration during a procedure
23	998.3	Disruption of wound
24	9984	Foreign body accidentally left during a procedure
25	998.5	Postoperative infection
26	998.6	Persistent postoperative fistula
27	998.7	Acute reaction to foreign substance accidentally left during a procedure
28	998.8	Other specified complications of procedures, not elsewhere classified
29	998.9	Unspecified complication of procedure, not elsewhere classified
30	999.0	Generalized vaccinia
31	999.1	Air embolism
32	999.2	Other vascular complications
33	999.3	Other infection
34	999.4	Anaphylactic shock due to serum
35	999.5	Other serum reaction
36	999.6	ABO incompatibility reaction
37	999.7	Rh incompatibility reaction
38	999.8	Other infusion and transfusion reaction
39	999.9	Other and unspecified complications of medical care, not elsewhere classified

Appendix B

K–prototypes algorithm

Suppose we have a set of n data points, D = {D₁, D₂, …, D_n}, where each data point has m features, i.e. D_i = [d_i1, d_i2,…, d_im]. The goal is to partition D into k disjoint clusters such that the inter-cluster distance of the data points is minimized while maximizing the intra-clusters distance. The distance measure is thus defined in K-Prototypes algorithm [52] as in Eq. (B1).

$$E={\displaystyle \sum _{i=1}^k\left(E_i^r+E_i^c\right)}={\displaystyle \sum _{i=1}^k{E}_i^r}+{\displaystyle \sum _{i=1}^k{E}_i^c}=E^r+E^c.$$ (B1)

In Eq. (B1), E is the total distance function for clustering n data points with numerical and categorical features. E^r is the sum of the distance for the numerical features over all the k clusters and E^c is the sum for the categorical attributes. Both E^r and E^c are non-negative, thus E is minimized through minimizing E^r and E^c. The squared Euclidean distance is used for calculating the distance function for numerical values. And, the distance function for categorical features is based on the number of mismatches between the data points and the cluster prototypes. The overall procedure of K-Prototypes algorithm is presented in Fig. B1.

Gap statistic

Theoretically, the Gap statistic approach is a way to standardize the comparison of log W_k with a null reference distribution of data with no clear clustering, where W_k is the within-cluster dispersion. Suppose, x_i, and x_j are two given data points in a given cluster C_k, which contains n_k data points. Then, the sum of intra-cluster distances between the points in C_k is defined as in Eq. (B2).

$$D_k={\displaystyle \sum _{x_i\in C_k}{\displaystyle \sum _{x_j\in C_k}{\Vert x_i-x_j\Vert }^2}}=2n_k{\displaystyle \sum _{x_i\in C_k}{\Vert x_i-{\mu }_k\Vert }^2}.$$ (B2)

Fig. B1.

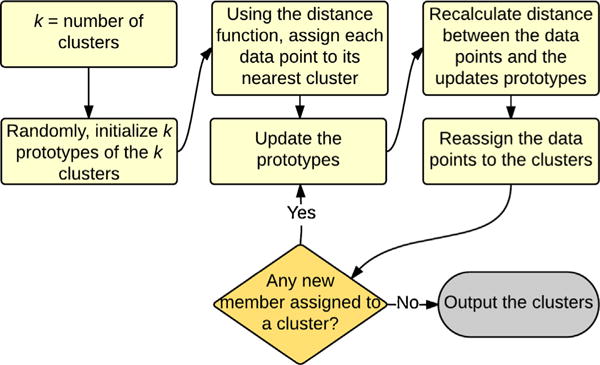
K–Prototypes clustering algorithm. The algorithm is similar to K-Means but it works with both numerical and categorical features. K prototypes are first randomly initiated and using a distance function, data points are placed in the nearest prototype. The prototypes are then updated, and the procedure is repeated until no further movement of data points between the clusters is possible.

In Eq. (B2), μ_k is the centroid of C_k. Through summing up the normalized values of D_k over the K clusters, as stated in Eq. (B3), W_k is obtained which can be regarded as a measure of the compactness of the clustering approach.

$$W_k={\displaystyle \sum _{k=1}^k\frac{1}{2n_k}{D}_k}.$$ (B3)

Now, the estimated optimal number of clusters, i.e. K, is detected by the Gap statistic, where K is optimal, if log W_k places the farthest below the curve of the reference distribution. Eq. (B4) defines the Gap statistic.

$$Ga{p}_n\left(k\right)=E_n^{\ast }\left\{\log W_k\right\}-\log W_k.$$ (B4)

In Eq. (B4), $E_n^{\ast }$ is the expectation under a sample size n from the reference distribution. We generated the reference dataset by sampling uniformly from the original intra-operative data. Next, 10 different replicates were generated from the reference distribution using the Monte Carlo sampling method,¹² and the average of log W_k was considered as the estimation of $E_n^{\ast }\left\{\log W_k\right\}$. Finally, S_k is defined based on the standard deviation of the obtained log W_k from 10 Monte Carlo replicates, i.e. SD_k. This measure accounts for the simulation error, and is defined as in Eq. (B5).

$$S_k=\sqrt{1+\frac{1}{10}S{D}_k}.$$ (B5)

The optimal number of clusters (K) is the smallest k for which Eq. (B6) holds [53].

$$\mathit{Gap}\left(k\right)\ge \mathit{Gap}\left(k+1\right)-S_{k+1}.$$ (B6)