Computational Models for Calcium-Mediated Astrocyte Functions

Abstract

The computational neuroscience field has heavily concentrated on the modeling of neuronal functions, largely ignoring other brain cells, including one type of glial cell, the astrocytes. Despite the short history of modeling astrocytic functions, we were delighted about the hundreds of models developed so far to study the role of astrocytes, most often in calcium dynamics, synchronization, information transfer, and plasticity in vitro, but also in vascular events, hyperexcitability, and homeostasis. Our goal here is to present the state-of-the-art in computational modeling of astrocytes in order to facilitate better understanding of the functions and dynamics of astrocytes in the brain. Due to the large number of models, we concentrated on a hundred models that include biophysical descriptions for calcium signaling and dynamics in astrocytes. We categorized the models into four groups: single astrocyte models, astrocyte network models, neuron-astrocyte synapse models, and neuron-astrocyte network models to ease their use in future modeling projects. We characterized the models based on which earlier models were used for building the models and which type of biological entities were described in the astrocyte models. Features of the models were compared and contrasted so that similarities and differences were more readily apparent. We discovered that most of the models were basically generated from a small set of previously published models with small variations. However, neither citations to all the previous models with similar core structure nor explanations of what was built on top of the previous models were provided, which made it possible, in some cases, to have the same models published several times without an explicit intention to make new predictions about the roles of astrocytes in brain functions. Furthermore, only a few of the models are available online which makes it difficult to reproduce the simulation results and further develop the models. Thus, we would like to emphasize that only via reproducible research are we able to build better computational models for astrocytes, which truly advance science. Our study is the first to characterize in detail the biophysical and biochemical mechanisms that have been modeled for astrocytes.

1. Introduction

Astrocytes have traditionally been regarded as glial cells responsible for the homeostasis and metabolic support for neurons (Carmignoto and Gómez-Gonzalo, 2010). Current evidence indicates that astrocytes support neuronal functions also in many other ways. Astrocytes are in a close proximity to a large number of brain synapses (Bushong et al., 2002; Fellin et al., 2006; Halassa et al., 2007; Oberheim et al., 2009; Freeman, 2010; Volterra et al., 2014; Olude et al., 2015; Cali et al., 2016), and the astrocytes together with pre- and postsynaptic neurons have been proposed to form functional tripartite synapses (Araque et al., 1999). Astrocytes can thus broadly sense and regulate synaptic activity. A growing body of evidence also suggests that astrocytes modulate neural circuits and are involved in many brain functions, perhaps also in cognitive functions and behavior (Perea et al., 2009; Wang et al., 2009; Halassa and Haydon, 2010; Henneberger et al., 2010; Suzuki et al., 2011; Araque et al., 2014; Sibille et al., 2014; Khakh and Sofroniew, 2015; Poskanzer and Yuste, 2016). Although more and more evidence is accumulating on the astrocytic modulation of neurotransmission and synaptic plasticity, in vivo evidence to support that astrocytes are directly activated by neurotransmission and signal back to neurons to modulate neurons' output remains unclear. Particularly, how this modulation occurs in time and space is unresolved.

Since the 1990s a variety of experimental techniques and organisms have been used to study astrocytes. Until 2010 most of the studies were performed using in vitro cell cultures and slice preparations. Recently, studies addressing astrocytes' roles in brain functions in vivo have accumulated. In short, one could identify three waves of astrocyte research over the past three decades, as proposed by Bazargani and Attwell (2016). The first wave of evidence revealed that neurotransmitter glutamate increases the astrocytic calcium (Ca²⁺) concentration in vitro and this yields to Ca²⁺ wave propagation between astrocytes (Cornell-Bell et al., 1990; Charles et al., 1991; Dani et al., 1992; Newman and Zahs, 1997), which could lead to Ca²⁺ increase in the nearby neurons (Nedergaard, 1994; Parpura et al., 1994). The second wave of evidence showed that pharmacological tools used to separate astrocytic and neuronal components are not selective (Parri et al., 2001; Agulhon et al., 2010; Hamilton and Attwell, 2010). Furthermore, it was speculated that astrocytic processes close to synapses do not have endoplasmic reticulum (ER) present and that blocking the inositol trisphosphate (IP₃) receptors (IP₃Rs) in the astrocytes has an effect on the astrocytic Ca²⁺ but not on the synaptic events (Fiacco et al., 2007; Petravicz et al., 2008; Agulhon et al., 2010; Patrushev et al., 2013). The third wave of evidence (Bazargani and Attwell, 2016) led to the conclusion that the Ca²⁺ transients in the astrocytic processes near vascular capillaries (Otsu et al., 2015) and neuronal synapses (Nimmerjahn et al., 2009) and not in the soma are the key that needs to be addressed in more detail. In summary, the challenges in astrocyte research have been the lack of selective pharmacological tools and the partially contradictory results obtained in in vivo in contrast to various in vitro preparations.

Although there is partial controversy, which hinders attempts to explain all findings on astrocytes' roles in the central nervous system in an unambiguous way, the majority of data collected over the past decades strongly suggests that fluctuations in Ca²⁺ concentrations in both soma and processes are important measures of astrocytic activities. Then astrocytic Ca²⁺ activity is utilized, in one way or another, by neurons to sense ongoing neural activity in closeby or more distant networks. The dynamic, far-reaching fluctuations, or transients, in astrocytic Ca²⁺ concentration were also recently recorded in awake behaving mice in vivo by several independent studies (Ding et al., 2013; Paukert et al., 2014; Srinivasan et al., 2015). Moreover, astrocytes, similarly to any other cell in the mammalian body, are known to express an overwhelming complexity of molecular and cell-level signaling. The full complexity of the signaling pathways which control Ca²⁺ transients and exert their effects in astrocytes is poorly understood, and the question about their relevance in awake behaving animals remains unanswered. It is essential that the research community seeks to systematically characterize the key signaling mechanisms in astrocytes to understand the interactions between different systems, including neuronal, glial, and vascular, in brain circuitry. Astrocytic signaling may provide a potential, widespread mechanism for regulating brain functions and states (Yang et al., 2014; Haim and Rowitch, 2017).

Several factors might be important in orchestrating how astrocytes exert their functional consequences in the brain. These include (a) different receptors or other mechanisms that trigger an increase in Ca²⁺ concentration in astrocytes, (b) Ca²⁺-dependent signaling pathways or other mechanisms that govern the production and release of different mediators from astrocytes, and (c) released substances that target other glial cells, the vascular system, and the neuronal system. The listed three factors (a–c) operate at different temporal and spatial scales and depend on the developmental stage of an animal and on the location of astrocytes. Namely, a substantial amount of data on a diverse array of receptors to detect neuromodulatory substances in astrocytes in vitro has been gathered (Backus et al., 1989; Kimelberg, 1995; Jalonen et al., 1997), and accumulating evidence is becoming available for in vivo organisms as well (Beltrán-Castillo et al., 2017). Neuromodulators have previously been expected to act directly on neurons to alter neural activity and animal behavior. It is, however, possible that at least part of the neuromodulation is directed through astrocytes, thus contributing to the global effects of neurotransmitters (see e.g., Ma et al., 2016). Experimental manipulation of astrocytic Ca²⁺ concentration is not a straightforward practice and can produce different results depending on the approach and context (for more detailed discussion, see e.g., Agulhon et al., 2010; Fujita et al., 2014; Sloan and Barres, 2014). Additional tools, both experimental and computational, are required to understand the vast complexity of astrocytic Ca²⁺ signaling and how it is decoded to advance functional consequences in the brain.

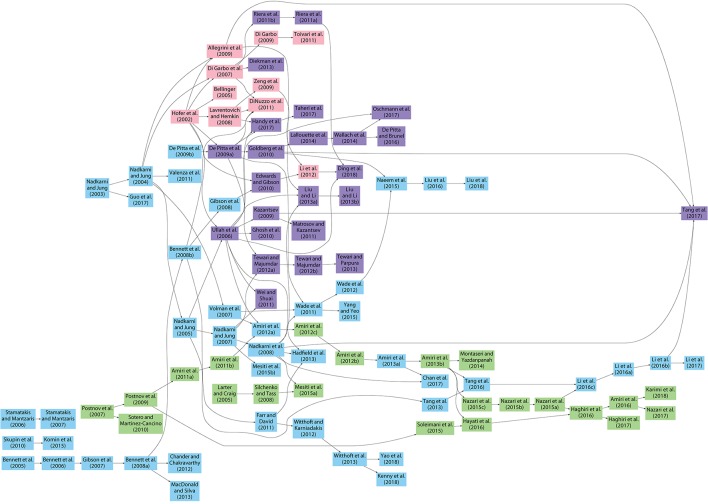
Several reviews of theoretical and computational models have already been presented (for a review, see e.g., Jolivet et al., 2010; Mangia et al., 2011; De Pittà et al., 2012; Fellin et al., 2012; Min et al., 2012; Volman et al., 2012; Wade et al., 2013; Linne and Jalonen, 2014; Tewari and Parpura, 2014; De Pittà et al., 2016; Manninen et al., 2018). We found out in our previous study (Manninen et al., 2018) that most astrocyte models are based on the models by De Young and Keizer (1992), Li and Rinzel (1994), and Höfer et al. (2002), of which the model by Höfer et al. (2002) is the only one built specifically to describe astrocytic functions and data obtained from astrocytes. Some of the other computational astrocyte models that steered the field are the models by Nadkarni and Jung (2003), Bennett et al. (2005), Volman et al. (2007), De Pittà et al. (2009a), Postnov et al. (2009), and Lallouette et al. (2014). However, irreproducible science, as we have reported in our other studies, is a considerable problem also among the developers of the astrocyte models (Manninen et al., 2017, 2018; Rougier et al., 2017). Several other review, opinion, and commentary articles have addressed the same issue as well (see e.g., Cannon et al., 2007; De Schutter, 2008; Nordlie et al., 2009; Crook et al., 2013; Topalidou et al., 2015; McDougal et al., 2016). We believe that only via reproducible science are we able to build better computational models for astrocytes and truly advance science.

This study presents an overview of computational models for astrocytic functions. We only cover the models that describe astrocytic Ca²⁺ signaling by biophysical means. We first categorize the existing models based on whether they are describing astrocytes or neuron-astrocyte interactions. We have previously described some aspects of the astrocyte and neuron-astrocyte models in our related study (Manninen et al., 2018), where we listed the details of both the astrocyte and neuron models in a simplistic, educational manner. In this review, we characterize in detail the existing models based on what kind of astrocytic mechanisms have been taken into account. Our study is expected to help guide future computational studies addressing the cross-talk between astrocytes and other systems in the brain and help researchers select suitable models for their research questions.

2. Materials and methods

In this section, we first outline the basics of astrocyte biology. The mechanisms presented here are not typically included in computational neuroscience models and one of our aims is to carefully assess which of the mechanisms are presently modeled and how realistically. We then list the computational astrocyte models, developed by the end of 2017, for our detailed evaluation. At the end of the section, we give the details how we characterized the models.

2.1. Astrocyte biophysics and biochemistry for modeling of astroglial functions

Astrocytes are the most diverse glial cells in the central nervous system. Astrocytes from different brain regions differ in morphology, physiology, and expression of genes encoding the most fundamental proteins responsible for astroglial function. In general, astrocytes can have a soma, perisynaptic processes which engulf neuronal synapses and also enclose some extracellular space, called perisynaptic or extrasynaptic (or sometimes periastrocytic) space within, and perivascular processes which connect the astrocyte with blood vessels and enclose some extracellular space called perivascular space. Below we present a generic view of some of the most important biophysical and cellular mechanisms that are shown to underlie important astrocytic functions (for more information, see also Kettenmann and Ransom, 2013; Verkhratsky and Butt, 2013).

2.1.1. Ion distribution and ion channels for basic membrane excitability

Astroglial cells express all major ion channel types, including potassium (K⁺), sodium (Na⁺), and Ca²⁺ channels, and also various types of anion and chloride (Cl⁻) channels, water channels (aquaporins), transient receptor potential (TRP) channels, and non-selective channels. The ion distribution is also somewhat different from neurons: intracellular concentrations of K⁺ and Ca²⁺ are similar to neurons, but the concentrations of Na⁺ and especially Cl⁻ are higher compared to neurons. Astrocytes have a rather negative resting membrane potential (around −80 to −90 mV) because of the predominance of K⁺ conductance. Electrical depolarization of astroglia does not produce regenerative action potentials as in neurons.

Ca²⁺-mediated signals have been proposed to be the main mediator of communication between astrocytes and other cellular elements in the brain (Nimmerjahn, 2009; Volterra et al., 2014; Bazargani and Attwell, 2016). Transient Ca²⁺ increases restricted to single cells are called Ca²⁺ oscillations. In isolated astrocytes, intracellular Ca²⁺ oscillations have been shown to depend mainly on the Ca²⁺-induced Ca²⁺ release (CICR) via IP₃Rs from the ER to the cytosol (see e.g., Agulhon et al., 2008). CICR has been shown to depend on Ca²⁺ with or without the influence of IP₃. Ca²⁺ influx via voltage-gated Ca²⁺ channels (VGCCs) and other types of Ca²⁺ influxes from the extracellular space have been linked with Ca²⁺ oscillations as well (Aguado et al., 2002).

2.1.2. Membrane transporters for uptake and homeostatic control of ions, neurotransmitters, and other substances

The membrane transporters are particularly important for astroglia because they control movements of various substances, including ions, neurotransmitters, and metabolic substrates. Astroglial transporters include adenosine and adenosine triphosphate (ATP)-dependent transporters such as the Na⁺/K⁺-ATPase (NKA, also called Na⁺/K⁺ pump) and Ca²⁺-ATPase [also called Ca²⁺ pump or plasma membrane Ca²⁺-ATPase (PMCA)] on the plasma membrane, in addition to sarco/ER Ca²⁺-ATPase (SERCA) located on the ER membrane. They also contain so-called secondary transporters, such as glutamate transporters [excitatory amino acid transporters (EAATs)], gamma-aminobutyric acid (GABA) transporters, glycine transporters, Na⁺/Ca²⁺ exchangers (NCXs), Na⁺/hydrogen (H⁺) exchangers, Na⁺/bicarbonate (${\text{HCO}}_3^{-}$) cotransporters, Na⁺/K⁺/Cl⁻ cotransporters (NKCC1), and some others. Although, for example, glutamate transporters are expressed by all cell types in the brain, astrocytes are the main cell type responsible for glutamate uptake. Astrocytes have enzymes that convert both glutamate and GABA into glutamine. Glutamine is then released into the extracellular space and taken up by the presynaptic terminal, and can be converted to glutamate or GABA.

The NKCC1 cotransporter specifically contributes to the regulation of extracellular K⁺ homeostasis in the central nervous system. During excessive neuronal firing, the local extracellular K⁺ concentration can increase markedly and lead to neural dysfunction. Uptaking extracellular K⁺, transporting it intracellularly and releasing to areas with lower concentration are some of the most important functions of astrocytes. This process of intracellularly transporting K⁺ from extracellular areas of high concentration to areas of low concentration, via active uptake and release, is called spatial K⁺ buffering. K⁺ can also diffuse in extracellular space which also helps in lowering the local high concentration. Furthermore, astrocytes also buffer other ions than K⁺.

2.1.3. Ionotropic and metabotropic receptors for sensing the environment

Astrocytes are able to sense with the help of their receptors local and more distant environments, including the neural activity and the synaptically released neurotransmitters, both in in vitro cell cultures and brain slices as well as in in vivo (Glaum et al., 1990; Dani et al., 1992; Porter and McCarthy, 1996; Hirase et al., 2004). Astroglial cells can express the same variety of receptors as neurons, both ionotropic and metabotropic. These include glutamate, GABA, glycine, acetylcholine, adrenergic, serotonin, histamine, cannabinoid, and neuropeptide receptors, and purinoceptors for adenosine and ATP. For example, extracellular ATP can bind to astroglial purinergic G-protein receptors, resulting in IP₃-mediated CICR, and, eventually, release of ATP to the extracellular space.

2.1.4. Release of transmitters and modulators

As described above, astroglia are capable of receiving signals from neurons via membrane receptors and converting the received information into Ca²⁺ excitability. The fact that astrocytes could release extracellular signaling molecules, regulated by this Ca²⁺ excitability, not only to the vascular system but also to the neuronal one implies a very active role for astroglia in the brain. The concept of regulated transmitter/modulator release from astrocytes to neurons is generally known as gliotransmission (Parpura et al., 1994; Bezzi and Volterra, 2001), and the released substances are referred to as gliotransmitters. Most common gliotransmitters are glutamate, D-serine, and ATP (Parpura et al., 1994; Parri et al., 2001). Astrocytes are, in general, thought to release transmitters, and probably also modulators, by several different mechanisms, which can be broadly divided into exocytotic release, diffusional release through membrane pores, and transporter mediated release. It is, however, not known which of these mechanisms are used in certain astroglial functions.

These terms “gliotransmission” and “gliotransmitter” may be somewhat misleading as the very same transmitters are also released by neurons. Moreover, it is assumed that a mechanism similar to vesicular release from neuronal synaptic terminals exists also in astrocytes. Some studies have indeed detected vesicle-type structures in astrocytes in vitro, and thus it has been proposed that gliotransmitter release might be purely vesicular. It is, however, important to bear in mind that the existence of molecular machinery for packing gliotransmitters into vesicles and for arranging the vesicles into a readily releasable pool has not so far been supported by experimental evidence in vivo (see e.g., Fujita et al., 2014; Sloan and Barres, 2014). More evidence on the release mechanism, using improved experimental model systems and techniques that allow studies at deeper resolution in physiological conditions, is required (Li et al., 2013; Bazargani and Attwell, 2016; Fiacco and McCarthy, 2018; Savtchouk and Volterra, 2018).

In our evaluation of models, we use the term “gliotransmission” for all biophysical and phenomenological mechanisms that were modeled to take into account the release of substances from astrocytes and targeting neurons. The reason for this is that the term “gliotransmission” is often used in the original modeling publications.

In addition, glutamate released from astrocytes can activate extrasynaptic N-methyl-D-aspartate receptor (NMDAR)-dependent currents, often called NMDAR-dependent slow inward current (SIC). In modeling studies, SIC is many times modeled similarly to, for example, the modulating current (I_astro) presented by Nadkarni and Jung (2003).

2.1.5. Connexin-based gap junction hemichannels

It is not just neurons that form networks but also astrocytes. A fundamental difference between neuronal and astroglial networks is that astrocytes are connected, through gap junctions composed mainly of connexin 43 hemichannels, to form a functional cellular syncytium in the central nervous system. In their open state, these channels are permeable to large hydrophilic solutes with molecular mass of several hundred Daltons, and are permeable to small solutes in their closed state (see e.g., Bao et al., 2007). The gap junction connectivity is instrumental for astrocytes' functions, including generation of Ca²⁺ waves, water transport, K⁺ buffering, and control of vascular system, and is one of the most important mechanisms to be modeled in astrocyte networks.

Three different pathways have been discovered so far to induce Ca²⁺ waves in astroglial networks. The first route depends on the transfer of IP₃ via gap junctions (Giaume and Venance, 1998). Transported IP₃ via gap junctions triggers CICR in the coupled astrocytes and induces Ca²⁺ wave propagation in astroglial syncytium. The second route to induce Ca²⁺ waves depends on the extracellular diffusion of ATP (see e.g., Newman and Zahs, 1997; Guthrie et al., 1999 and section 2.1.4). The third route has been shown to depend on extracellularly applied potassium chloride, causing, among others, a pathophysiological phenomenon called cortical spreading depression (Peters et al., 2003). The regulation of gap junction communication within the astroglial syncytium is a complex process and is intensively studied.

Most of the above described biophysical and biochemical mechanisms have been modeled in some detail in astrocytes. Below we address altogether 106 models developed until the end of 2017 and describe their capacity to represent the dynamics of astrocyte biophysics and biochemistry.

2.2. Selection of models

The number of computational astrocyte models has increased over the past couple of years. This increase in the number of models does not, however, solely reflect the vast amount of experimental data that is currently presented for astrocytes and for their roles in brain functions and the regulation of the neuronal system. Several focused reviews of computational astrocyte and neuron-astrocyte models have appeared during the last few years (see e.g., Jolivet et al., 2010; Mangia et al., 2011; De Pittà et al., 2012; Fellin et al., 2012; Min et al., 2012; Volman et al., 2012; Wade et al., 2013; Linne and Jalonen, 2014; Tewari and Parpura, 2014; De Pittà et al., 2016; Manninen et al., 2018); of which our study (Manninen et al., 2018) is the most comprehensive evaluation of more than 60 models published by the end of 2014. In the present study, we characterize in more detail the biophysical and biochemical components of astrocytes that were taken into account in the astrocyte and neuron-astrocyte interaction models published by the end of 2017.

Table 1 presents altogether 106 astrocyte models. As in our other study (Manninen et al., 2018), we here limited our evaluation of models to astrocytic signal transduction pathways that were defined using several characteristics. First, models were able to include pre- and postsynaptic neuron models as part of the whole models. Second, part of intracellular signaling in the astrocytes was explicitly modeled, thus models were required to include (biophysical) mechanisms for astrocytic Ca²⁺ dynamics. We considered in the present study only models where astrocytic Ca²⁺ signaling was described by a differential equation that was a function of time and at least one of the other astrocytic variables, for example IP₃. Third, astrocytic Ca²⁺ affected some signaling variables or other intracellular signals in the astrocytes. Models which described Ca²⁺ dynamics but were not explicitly made for astrocytes were excluded from the present study. Moreover, models that mainly concentrated on describing ionic homeostasis, such as regulation of extracellular K⁺ ions, were also excluded from the evaluation unless they incorporated astrocytic Ca²⁺ signaling. These strict criteria were needed because of the large number of models.

Table 1.

List of astrocyte and neuron-astrocyte models published each year.

Year	Models	No.
1995	Roth et al., 1995	1
2002	Höfer et al., 2002	1
2003	Nadkarni and Jung, 2003	1
2004	Goto et al., 2004; Nadkarni and Jung, 2004	2
2005	Bellinger, 2005; Bennett et al., 2005; Larter and Craig, 2005; Nadkarni and Jung, 2005	4
2006	Bennett et al., 2006; Iacobas et al., 2006; Stamatakis and Mantzaris, 2006; Ullah et al., 2006	4
2007	Di Garbo et al., 2007; Gibson et al., 2007; Nadkarni and Jung, 2007; Postnov et al., 2007; Stamatakis and Mantzaris, 2007; Volman et al., 2007	6
2008	Bennett et al., 2008a,b; Gibson et al., 2008; Lavrentovich and Hemkin, 2008; Nadkarni et al., 2008; Silchenko and Tass, 2008	6
2009	Allegrini et al., 2009; De Pittà et al., 2009a,b; Di Garbo, 2009; Kang and Othmer, 2009; Kazantsev, 2009; Postnov et al., 2009; Zeng et al., 2009	8
2010	Edwards and Gibson, 2010; Ghosh et al., 2010; Goldberg et al., 2010; Skupin et al., 2010; Sotero and Martínez-Cancino, 2010	5
2011	Amiri et al., 2011a,b; DiNuzzo et al., 2011; Dupont et al., 2011; Farr and David, 2011; Matrosov and Kazantsev, 2011; Riera et al., 2011a,b; Toivari et al., 2011; Valenza et al., 2011; Wade et al., 2011; Wei and Shuai, 2011	12
2012	Amiri et al., 2012a,b,c; Chander and Chakravarthy, 2012; Li et al., 2012; Tewari and Majumdar, 2012a,b; Wade et al., 2012; Witthoft and Karniadakis, 2012	9
2013	Amiri et al., 2013a,b; Diekman et al., 2013; Hadfield et al., 2013; Liu and Li, 2013a,b; MacDonald and Silva, 2013; Tang et al., 2013; Tewari and Parpura, 2013; Witthoft et al., 2013	10
2014	Lallouette et al., 2014; López-Caamal et al., 2014; Montaseri and Yazdanpanah, 2014; Wallach et al., 2014	4
2015	Komin et al., 2015; Mesiti et al., 2015a,b; Naeem et al., 2015; Nazari et al., 2015a,b,c; Soleimani et al., 2015; Yang and Yeo, 2015	9
2016	Amiri et al., 2016; De Pittà and Brunel, 2016; Haghiri et al., 2016; Hayati et al., 2016; Li et al., 2016a,b,c; Liu et al., 2016; Oku et al., 2016; Tang et al., 2016	10
2017	Chan et al., 2017; Guo et al., 2017; Haghiri et al., 2017; Handy et al., 2017; Li et al., 2017; Nazari et al., 2017; Oschmann et al., 2017; Taheri et al., 2017; Tang et al., 2017	9
2018	Ding et al., 2018; Karimi et al., 2018; Kenny et al., 2018; Liu et al., 2018; Yao et al., 2018	5
All		106

Models are ordered alphabetically for each year of publication. Altogether 106 models have been published by the end of 2017. For chosen criteria, see section 2.2.

2.3. Characteristics of models

We first categorized and tabulated the existing models based on whether they were describing single astrocytes, astrocyte networks, neuron-astrocyte synapses, or neuron-astrocyte networks. Next, we categorized the models further to see which older models were used as references. Most of the astrocyte models utilized the Ca²⁺ dynamics models by De Young and Keizer (1992) and Li and Rinzel (1994), or a modification of them, even though these two models were not made to describe astrocytic behavior (Manninen et al., 2018). Thus, the details of these models (De Young and Keizer, 1992; Li and Rinzel, 1994) were not listed. Models are in alphabetical order, first are models that used the models by De Young and Keizer (1992) and Li and Rinzel (1994) as references, second are the models that used the model by Höfer et al. (2002) as reference, third are the models that combined all three models (De Young and Keizer, 1992; Li and Rinzel, 1994; Höfer et al., 2002), and last are models that were based on some other models, such as the models by Sneyd et al. (1994), Keener and Sneyd (1998, 2009), and Houart et al. (1999) (see section 3). It is worth noting that most of the above-mentioned models have adapted CICR model presented by Bezprozvanny et al. (1991) as basis of their models.

Next, we characterized the models based on what type of signaling events were modeled in astrocytes. We listed for each model the number of astrocytes modeled, input used for the astrocytic module, astrocytic variables described by differential equations, and astrocytic Ca²⁺ fluxes related to cytosolic Ca²⁺. It is important to note that neurotransmitters were not named here as astrocytic variables but in some models they were used as inputs to the astrocyte models [e.g., synaptic glutamate ([Glu]_syn) or neurotransmitter (NT)]. By contrast, we listed gliotransmitters as astrocytic variables if they were modeled with a differential equation. As the exact mechanisms of astrocytic signaling that regulate exocytosis and release of molecular substances from astrocytes are still largely unknown, most of the models used phenomenological descriptions of gliotransmitters or other substances released. Proposed gliotransmitters included, for example, glutamate ([Glu]_ext) and ATP ([ATP]_ext). Note the difference between [Glu]_syn and [Glu]_ext, the former meaning the neurotransmitter glutamate released from the presynaptic neuron and the latter meaning the gliotransmitter glutamate released from the astrocyte. Other examples of strategies for modeling gliotransmission or similar exocytotic or modulating signaling mechanisms from astrocytes to neurons included modeling currents depending on astrocytic Ca²⁺ (I_astro, Nadkarni and Jung, 2003) and several other types of currents depending, for example, on astrocytic mediator (G_m, I_ast, Postnov et al., 2007, 2009), or modeling phenomenological gating variable (f, Volman et al., 2007). In addition, we listed diffusion of astrocytic variables either in the cytosol, ER, or extracellular space. In the present study, we did not catalog the transfer of molecules or ions between intracellular space and extracellular space under the attribute “diffusion,” but we listed, for example, different Ca²⁺ related fluxes over the plasma membrane under “Ca²⁺ fluxes.” We chose to list gap junction signaling between astrocytes which is an important, fundamental form of intercellular signaling directly from the intracellular space of one cell to the intracellular space of another cell. We did not incorporate gap junctions under the attribute “diffusion,” but only included it in the attribute “gap junction.” IP₃ and Ca²⁺ are examples of second messengers that are able to pass through gap junctions. The last items we listed were the output of the astrocytic module and experimentally shown event that the model was finetuned to capture [Ca²⁺ dynamics (Ca²⁺), homeostasis (Home.), vascular (Vasc.), synchronization (Synch.), information transfer (Inf.), plasticity (Plast.), and hyperexcitability (Hyper.)] for each model. To get a general idea of how these different mechanisms can be modeled, see, for example, books by Keener and Sneyd (2009) and Dupont et al. (2016).

Sometimes the authors of the publications used incorrect terminology when explaining their model components. As an example, Silchenko and Tass (2008), Zeng et al. (2009), Sotero and Martínez-Cancino (2010), Dupont et al. (2011), Li et al. (2012), and Ding et al. (2018) presented one Ca²⁺ flux as a leak from cytosol into extracellular space in their study. We named it here as Ca²⁺ efflux because Ca²⁺ leak flux via astrocytic cell membrane is normally used for a flux from extracellular space into cytosol, thus from the larger Ca²⁺ concentration in the extracellular space toward the smaller Ca²⁺ concentration in the cytosol. Goto et al. (2004) named the direction of fluxes incorrectly for CICR, ER leak flux, and ER pump (that we assumed to be SERCA) in their text, but in their equations the direction of fluxes were marked correctly for CICR and leak and again incorrectly for ER pump. Yao et al. (2018) also marked the signs incorrectly for some of the fluxes. Directions of the CICR and ER leak flux should be from the ER to the cytosol, and SERCA pump from the cytosol to the ER. Often the authors of the modeling publications did not name their Ca²⁺ pump on the membrane of ER as SERCA pump, but since the very same equation was used for SERCA pump by other authors, we marked it as SERCA pump for all the authors, except for the model by Guo et al. (2017) because they pointed out that their pump was ATP-independent. Naming of the variable h, taken from the model by Li and Rinzel (1994), was also presented in a contradictory manner by several authors. The very same variable h was given alternative explanations, some of them having completely opposite meanings, or no explanation at all. We decided to name h in this work as active fraction of IP₃Rs. Authors did not always state clearly how many astrocytes were modeled. In these cases we marked it as n/a. Some authors named gliotransmitters in their work as neurotransmitters (see e.g., Stamatakis and Mantzaris, 2006). We tried our best to give as correct a view of the models as possible.

Most of the astrocyte models presented here are based on ordinary differential equations (ODEs), modeling well-stirred astrocytes (see e.g., Nadkarni and Jung, 2003; Ullah et al., 2006; Volman et al., 2007; De Pittà et al., 2009a; Goldberg et al., 2010; Dupont et al., 2011; Valenza et al., 2011; Amiri et al., 2012a; Wade et al., 2012; Hadfield et al., 2013; Tang et al., 2013; Lallouette et al., 2014; Wallach et al., 2014; Li et al., 2016a; Chan et al., 2017; Guo et al., 2017; Handy et al., 2017; Taheri et al., 2017). These models make the assumption that chemical species have the same concentrations throughout the entire volume of the astrocyte, which can also be called as average concentrations. However, it has been shown that the concentration of certain chemical species, such as Ca²⁺, can vary drastically in different parts of the cell (see e.g., Thul, 2014; Dupont et al., 2016), and several models took into account the spatiality by modeling diffusion of at least some of the chemical species in astrocytes using partial differential equations (PDEs, see e.g., Roth et al., 1995; Höfer et al., 2002; Bennett et al., 2008a; Gibson et al., 2008; Allegrini et al., 2009; Kang and Othmer, 2009; Edwards and Gibson, 2010; Wei and Shuai, 2011; Li et al., 2012; López-Caamal et al., 2014; Mesiti et al., 2015a; Yao et al., 2018). Some models took a simpler approach to spatiality by modeling ODEs combined with fluxes between different astrocytic compartments, such as cytosol and ER (see e.g., Larter and Craig, 2005; Di Garbo et al., 2007; Postnov et al., 2007; Lavrentovich and Hemkin, 2008; Di Garbo, 2009; Zeng et al., 2009; Amiri et al., 2011a; DiNuzzo et al., 2011; Farr and David, 2011; Oschmann et al., 2017; Kenny et al., 2018). In addition of modeling Ca²⁺ fluxes between ER and cytosol, Silchenko and Tass (2008) modeled free diffusion of extracellular glutamate as a flux. It seems that most of the authors implemented their ODE and PDE models using some programming language, but a few times, for example, XPPAUT (Ermentrout, 2002) was named as the simulation tool used. Because of the stochastic nature of cellular processes (see e.g., Rao et al., 2002; Raser and O'Shea, 2005; Ribrault et al., 2011) and oscillations (see e.g., Perc et al., 2008; Skupin et al., 2008), different stochastic methods have been developed for both reaction and reaction-diffusion systems. These stochastic methods can be divided into discrete and continuous-state stochastic methods. Some discrete-state reaction-diffusion simulation tools can track each molecule individually in a certain volume with Brownian dynamics combined with a Monte Carlo procedure for reaction events (see e.g., Stiles and Bartol, 2001; Kerr et al., 2008; Andrews et al., 2010). On the other hand, the discrete-state Gillespie stochastic simulation algorithm (Gillespie, 1976, 1977) and τ-leap method (Gillespie, 2001) can be used to model both reaction and reaction-diffusion systems. A few simulation tools already exist for reaction-diffusion systems using these methods (see e.g., Wils and De Schutter, 2009; Oliveira et al., 2010; Hepburn et al., 2012). In addition, continuous-state chemical Langevin equation (Gillespie, 2000) and several other stochastic differential equations (SDEs, see e.g., Shuai and Jung, 2002; Manninen et al., 2006a,b) have been developed for reactions to ease the computational burden of discrete-state stochastic methods. A few simulation tools providing hybrid approaches also exist and they combine either deterministic and stochastic methods or different stochastic methods (see e.g., Salis et al., 2006; Lecca et al., 2017). Of the above-named methods, most realistic simulations are provided by the discrete-state stochastic reaction-diffusion methods, but none of the covered astrocyte models used these stochastic methods or available simulation tools for both reactions and diffusion for the same variable. However, four models combined stochastic reactions with deterministic diffusion in the astrocytes. Skupin et al. (2010) and Komin et al. (2015) modeled with the Gillespie algorithm the detailed IP₃R model by De Young and Keizer (1992), had PDEs for Ca²⁺ and mobile buffers, and ODEs for immobile buffers. Postnov et al. (2009) modeled diffusion of extracellular glutamate and ATP as fluxes, had an SDE for astrocytic Ca²⁺ with fluxes between ER and cytosol, and ODEs for the rest. MacDonald and Silva (2013) had a PDE for extracellular ATP, an SDE for astrocytic IP₃, and ODEs for the rest. In addition, a few studies modeling just reactions and not diffusion used stochastic methods (SDEs or Gillespie algorithm) at least for some of the variables (see e.g., Nadkarni et al., 2008; Postnov et al., 2009; Sotero and Martínez-Cancino, 2010; Riera et al., 2011a,b; Toivari et al., 2011; Tewari and Majumdar, 2012a,b; Liu and Li, 2013a; Tang et al., 2016; Ding et al., 2018).

3. Results

Previous studies in experimental and computational cell biology fields have guided the development of computational models for astrocytes and their interactions with neurons. Most of the firstly developed astrocyte models were relatively simplistic but they were gradually expanded to cover astrocytic regulation of a variety of phenomena and cells in the nervous system. Next, we will present the computational models for astrocytes in section 3.1 and the computational models that include bidirectional signaling between neurons and astrocytes in section 3.2.

3.1. Computational astrocyte models

The early phase of model development concentrated more on single astrocytes and astrocyte-astrocyte communication. We will go through the single astrocyte models in section 3.1.1 and the astrocyte network models in section 3.1.2.

3.1.1. Single astrocyte models

Half of the single astrocyte models were so-called generic, meaning that they did not describe astrocytes in any specific anatomical brain location. Others, however, were specified to model astrocytes in the cerebrum (Farr and David, 2011; Witthoft and Karniadakis, 2012), cerebral cortex (Diekman et al., 2013; Witthoft et al., 2013; Mesiti et al., 2015b; Kenny et al., 2018), cortex (De Pittà et al., 2009b; Toivari et al., 2011), hippocampus (Riera et al., 2011a,b; Chander and Chakravarthy, 2012), as well as the visual cortex (Gibson et al., 2007; Bennett et al., 2008b) and somatosensory cortex (Bennett et al., 2008b; Taheri et al., 2017). One third of the single astrocyte models took into account neurotransmitters in a simplistic way just as a stimulus, having either the neurotransmitter as a constant, step function, or something similar (see e.g., Larter and Craig, 2005; Gibson et al., 2007; Bennett et al., 2008b; De Pittà et al., 2009a; Dupont et al., 2011; Toivari et al., 2011; Witthoft and Karniadakis, 2012; Hadfield et al., 2013; Witthoft et al., 2013; Kenny et al., 2018). Only two models (Chander and Chakravarthy, 2012; Oschmann et al., 2017) actually modeled the amount of neurotransmitter with a differential equation. The stimulus to the astrocyte model by Oschmann et al. (2017) was taken from the model by Tsodyks and Markram (1997). In addition, Mesiti et al. (2015b) modeled the presynaptic neuron. We included these three models (Chander and Chakravarthy, 2012; Mesiti et al., 2015b; Oschmann et al., 2017) under single astrocyte models, because these models did not have bidirectional communication between astrocytes and neurons. The characteristics of single astrocyte models can be found in Table 2.

Table 2.

Characteristics of single astrocyte models.

Model	No.	Input	Variables	Ca2+ fluxes	Diffusion	GJ	Output	Event
De Young and Keizer (1992) and Li and Rinzel (1994) -TYPE MODELS
Bennett et al., 2008b	1	[Glu]syn	[Ca2+], [EET]ext, h, [IP3]	CICR, endogenous buffer, leak from ER into cyt, SERCA	Dcyt: [IP3],Dext: [EET]ext	No	[EET]ext	Vasc.
Chander and Chakravarthy, 2012	1	Current, [Glu]syn	[Ca2+], [EET]ext, [GLC], h, [IP3], [LAC]	CICR, endogenous buffer, leak from ER into cyt, SERCA	No	No	[EET]ext	Vasc.
De Pittà et al., 2009b	1	[IP3]	[Ca2+], h	CICR, leak from ER into cyt, SERCA	No	No	[Ca2+]	Ca2+
Farr and David, 2011	1	ρ, [K+]N	[Ca2+], [Ca2+]ER, [EET], h, [IP3], [K+]ext, nBK, Vm	CICR, endogenous buffer, leak from ER into cyt, SERCA	No	No	[K+]ext	Vasc.
Gibson et al., 2007	1	[Glu]syn	χ, [ATP]ext, [Ca2+], G, h, [IP3], PIP2	CICR, endogenous and exogenous buffers, leak from ER into cyt, SERCA	Dext: [ATP]ext	No	[ATP]ext	Vasc.
Hadfield et al., 2013	1	[Glu]syn	[20-HETE], [Ca2+], [EET], h, [IP3]	CICR, endogenous buffer, leak from ER into cyt, SERCA	No	No	[20-HETE], [EET]	Vasc.
Kenny et al., 2018	1	[Glu]syn, [K+]N, [NO]N	[Ca2+], [Ca2+]ER, [EET], h, [${\text{HCO}}_3^{-}$], [IP3], [K+], [K+]ext, mTRPV, nBK, [Na+], [NO], Rvol/area	CICR, endogenous and exogenous buffers, leak from ER into cyt, SERCA, TRPV4	No	No	[K+]ext	Vasc.
Komin et al., 2015	1	Spon.	Bi, Bi,ER, Bm, Bm,ER, [Ca2+], [Ca2+]ER, detailed IP3R	CICR, immobile and mobile buffers, leak from ER into cyt, SERCA	Dcyt: [Ca2+], Bm,DER: [Ca2+]ER, Bm,ER	No	[Ca2+]	Ca2+
	1	Spon.	[Ca2+], [Ca2+]ER	CICR, influx, leak from ER into cyt, MCU, mitochondrial NCX, PMCA, SERCA	No	No	[Ca2+]	Ca2+
Mesiti et al., 2015b	1	Vin,N → [IP3]	[Ca2+], [IP3]	CICR, leak from ER into cyt, SERCA	No	No	[Ca2+]	Ca2+
Roth et al., 1995	1	[IP3]	[Ca2+], [Ca2+]ER, h	CICR, leak from ER into cyt, SERCA	Dcyt: [Ca2+],DER: [Ca2+]ER	No	[Ca2+]	Ca2+
Skupin et al., 2010	1	Spon.	Bi, Bm, [Ca2+], detailed IP3R	CICR, immobile and mobile exogenous buffers, leak from ER into cyt, SERCA	Dcyt: [Ca2+], Bm	No	[Ca2+]	Ca2+
Witthoft and Karniadakis, 2012	1	[Glu]syn, [K+]N	[Ca2+], [EET], h, [IP3], [K+]ext, mTRPV, nBK, Vm	CICR, endogenous buffer, leak from ER into cyt, SERCA, TRPV4	No	No	[K+]ext	Vasc.
Witthoft et al., 2013	1	[Glu]syn, [K+]N	[Ca2+], [EET], h, [IP3], [K+], [K+]ext, mTRPV, nBK, [Na+], Vm	CICR, endogenous buffer, leak from ER into cyt, SERCA, TRPV4	No	No	[K+]ext	Vasc.
Höfer et al. (2002) -TYPE MODELS
Lavrentovich and Hemkin, 2008	1	Spon.	[Ca2+], [Ca2+]ER, [IP3]	CICR, efflux, influx, leak from ER into cyt, SERCA	No	No	[Ca2+]	Ca2+
Toivari et al., 2011	1	[5-HT]syn	[Ca2+], [Ca2+]ER, [IP3], R	CCE, CICR, efflux, leak from ER into cyt, leak from ext into cyt, P2XR, SERCA	No	No	[Ca2+]	Ca2+
Zeng et al., 2009	1	Spon.	[Ca2+], [Ca2+]ER, H-H channel kinetics, [IP3]	CICR, efflux, leak from ER into cyt, SERCA, 4 types of VGCCs	No	No	[Ca2+]	Ca2+
De Young and Keizer (1992), Li and Rinzel (1994), and Höfer et al. (2002) -TYPE MODELS
De Pittà et al., 2009a	1	[IP3]	[Ca2+], h	CICR, leak from ER into cyt, SERCA	No	No	[Ca2+]	Ca2+
	1	[IP3]	[Ca2+], h, [IP3]	CICR, leak from ER into cyt, SERCA	No	No	[Ca2+]	Ca2+
	1	[Glu]syn	[Ca2+], h, [IP3]	CICR, leak from ER into cyt, SERCA	No	No	[Ca2+]	Ca2+
Diekman et al., 2013	1	GLC, O2,out	ΔΨ, [ADP], [ADP]mito, [Ca2+]ER, [Ca2+]mito, [Ca2+]ps, h, [H+]mito, [IP3], K+, Na+, [NADH]mito, O2,mito, PTP	Buffer, CICR, leak from ER into cyt, MCU, mitochondrial NCX, SERCA	No	No	[ATP]mito	Home.
	1	O2,mito, Pyr	ΔΨ, [ADP]mito, [Ca2+]mito, [NADH]mito	MCU, mitochondrial NCX	No	No	[ATP]mito	Home.
Ding et al., 2018	1	Spon.	[Ca2+], [Ca2+]ER, H-H channel kinetics, [IP3], detailed IP3R	CCE, CICR, efflux, leak from ER into cyt, SERCA, 2 types of VGCCs, contribution of DAG/PKC to VGCCs	No	No	[Ca2+]	Ca2+
Handy et al., 2017	1	[IP3]	[Ca2+], [Ca2+]free, h	CCE, CICR, efflux, leak from ER into cyt, leak from ext into cyt, PMCA, SERCA	No	No	[Ca2+]	Ca2+
Oschmann et al., 2017	1	Glusyn	[Ca2+], [Ca2+]ER, h, [IP3], [K+], [Na+], Vm	CICR, leak from ER into cyt, NCX, SERCA	No	No	[Ca2+]	Ca2+
Riera et al., 2011a	1	Spon.	[Ca2+], [Ca2+]free, h, [IP3]	CCE, CICR, efflux, influx via channels, leak from ER into cyt, SERCA	No	No	[Ca2+]	Ca2+
Riera et al., 2011b	1	Spon.	[Ca2+], [Ca2+]free, h, [IP3]	CCE, CICR, efflux, influx via channels, leak from ER into cyt, SERCA	No	No	[Ca2+]	Ca2+
Taheri et al., 2017	1	[IP3]	[Ca2+], [Ca2+]free, h	CCE, CICR, efflux, leak from ER into cyt, leak from ext into cyt, PMCA, SERCA	No	No	[Ca2+]	Ca2+
OTHER TYPES OF MODELS
Dupont et al., 2011	1	[Glu]syn	[Ca2+], [DAG], [DIM], fPKC, [IP3], Rinact	CICR, efflux, influx, leak from ER into cyt, SERCA	No	No	[Ca2+]	Ca2+
Karimi et al., 2018	1	Ca2+	Ca2+, ${\text{Ca}}_{\text{ER}}^{2+}$	CICR, efflux, leak from ER into cyt, SERCA	No	No	Ca2+	Ca2+
Larter and Craig, 2005	1	[Glu]syn	[Ca2+], [Ca2+]ER, [Glu]ext, [IP3]	CICR, efflux, Glu-dependent influx, influx, leak from ER into cyt, SERCA	No	No	[Glu]ext	Ca2+
López-Caamal et al., 2014	1	[Ca2+]	Bi, [Ca2+], [Ca2+]ER	CICR, immobile endogenous and exogenous buffers, efflux via pump, influx via IP3-dependent channel, perturbation flux, RyR, SERCA	Dcyt: [Ca2+],DER: [Ca2+]ER	No	[Ca2+]	Ca2+
Montaseri and Yazdanpanah, 2014	1	Syn. act.	Ca2+, Sm=IP3	Efflux, influx, IP3-dependent influx	No	No	Ca2+	Ca2+

This table shows the following: model, number (No.) of astrocytes modeled, input for the astrocytes, astrocytic variables described by differential equations, astrocytic Ca²⁺ fluxes related to cytosolic Ca²⁺, diffusion of astrocytic variables either in the cytosol, ER, or extracellular space, not between these spaces, gap junction signaling (GJ) between astrocytes, output of the astrocytes, and experimentally shown event that the model was finetuned to capture [Ca²⁺ dynamics (Ca²⁺), homeostasis (Home.), and vascular (Vasc.)]. Compartment is cytosol (cyt) if not otherwise stated. Amounts modeled in concentrations are given inside square brackets. In addition to astrocytes, Gibson et al. (2007), Bennett et al. (2008b), Farr and David (2011), Chander and Chakravarthy (2012), Witthoft and Karniadakis (2012), Witthoft et al. (2013), and Kenny et al. (2018) modeled smooth muscle cells. Gibson et al. (2007) and Kenny et al. (2018) modeled also an endothelial cell, and Kenny et al. (2018) included K⁺, glutamate, and nitric oxide (NO) release from neurons. However, Gibson et al. (2007) did not provide a detailed explanation of their model, but only cited previous models. Chander and Chakravarthy (2012) modeled also neuronal membrane potential and neuronal glutamate release. The stimulus for the model by Oschmann et al. (2017) came from the model by Tsodyks and Markram (1997). Mesiti et al. (2015b) modeled also the presynaptic neuron. Diekman et al. (2013) modeled also aspects of mitochondrial signaling, cell volume, and membrane potential in the astrocyte. Zeng et al. (2009) and Ding et al. (2018) modeled Hodgkin-Huxley (H-H) type channel gating kinetics (Hodgkin and Huxley, 1952). In addition, Ding et al. (2018) simulated two models, with and without detailed IP₃R model modified from De Young and Keizer (1992). Komin et al. (2015) presented two models, a reaction-diffusion model and a reaction model. De Pittà et al. (2009a) simulated three models, of which the simplest one is the model by Li and Rinzel (1994). However, the details of all three models are given together in the table under De Young and Keizer (1992), Li and Rinzel (1994), and Höfer et al. (2002) -type models. Diekman et al. (2013), Mesiti et al. (2015b), and Karimi et al. (2018) presented two models, the others were simplified versions of the main model. However, the simpler model by Mesiti et al. (2015b) was not detailed enough based on our criteria in section 2.2.

Most of the single astrocyte models studied Ca²⁺ oscillations, of which a few models specifically focused on modeling only spontaneous Ca²⁺ oscillations (see Table 2). All the other models had components for CICR and SERCA pump except the model by Montaseri and Yazdanpanah (2014). Furthermore, all the other models except the models by López-Caamal et al. (2014) and Montaseri and Yazdanpanah (2014) modeled leak from the ER into the cytosol. Half of the models had influx of Ca²⁺ from outside of the astrocyte or efflux of Ca²⁺ to outside of the astrocyte. About one third of the models took into account Ca²⁺ buffers and astrocytic release of signaling molecules. None of the models had gap junctions, because these were single astrocyte models. Thus, these models had similar core structure with small variations. As an example, six modeled capacitive Ca²⁺ entry (CCE) which is mediated via store-operated Ca²⁺ (SOC) channels (Riera et al., 2011a,b; Toivari et al., 2011; Handy et al., 2017; Taheri et al., 2017; Ding et al., 2018) and two modeled VGCCs (Zeng et al., 2009; Ding et al., 2018), as well as one had Ca²⁺ flux via ryanodine receptors (RyRs) (López-Caamal et al., 2014) and three had Ca²⁺ influx via TRP vanilloid-related channel 4 (TRPV4) (Witthoft and Karniadakis, 2012; Witthoft et al., 2013; Kenny et al., 2018). Only Diekman et al. (2013) and Komin et al. (2015) modeled mitochondrial Ca²⁺ unitransporters (MCUs). Two modeled mitochondrial NCX (Diekman et al., 2013; Komin et al., 2015) and one modeled NCX via plasma membrane (Oschmann et al., 2017). Skupin et al. (2010), Komin et al. (2015), and Ding et al. (2018) used detailed IP₃R model by De Young and Keizer (1992). Six models had diffusion either in the cytosol, in the ER, or in the extracellular space (Roth et al., 1995; Gibson et al., 2007; Bennett et al., 2008b; Skupin et al., 2010; López-Caamal et al., 2014; Komin et al., 2015).

The first models developed in this category were the models by Roth et al. (1995) and Larter and Craig (2005). Roth et al. (1995) extended the model by Li and Rinzel (1994) by adding Ca²⁺ diffusion in the cytosol and ER. They also divided their cell to alternating active and passive compartments. In passive compartments, Ca²⁺ signal propagated by diffusion, whereas in active compartments there were also additional Ca²⁺ fluxes propagating the signal. Roth et al. (1995) showed with their model that different parts of the astrocyte, such as the ER membrane, produced different frequencies of Ca²⁺ oscillations if the diffusion constant had a value close to the physiological range. If the diffusion constant had unphysiologically high value, then the different parts of the astrocyte all oscillated with the same frequency.

Larter and Craig (2005) presented the only model in this category that included a differential equation for extracellular glutamate ([Glu]_ext). Their equation for extracellular glutamate included the rate of glutamate vesicle release from the astrocyte, the input glutamate rate arriving from nearly synapses, and two terms describing the rates of glutamate uptake by neurons and astrocytes. Larter and Craig (2005) tested their model by setting the extracellular glutamate to zero during the simulations (meaning both glutamate release from the astrocyte and glutamate arriving from the nearby synapses were zero) and showed that the astrocytic Ca²⁺ was not oscillating in this case. They further tested their model when the astrocyte was not releasing glutamate, but they still had the input glutamate rate arriving from nearly synapses. In this case, the astrocytic Ca²⁺ was oscillating. They also tested how the number of glutamate in the astrocytic vesicles affected the model behavior. They showed that when increasing the number of glutamate in the astrocytic vesicles, the Ca²⁺ oscillations transformed into Ca²⁺ bursting oscillations. Thus, their message was that the presence of glutamate, but not the positive astrocytic glutamate feedback, was required for astrocytic Ca²⁺ oscillations. In addition, the positive glutamate feedback process made it possible for the astrocyte to have bursting oscillations when the input glutamate rate arriving from nearby synapses had low values.

Only six of the single astrocyte models had K⁺ concentration modeled in the perisynaptic space, perivascular space [in Table 2 called as extracellular space (ext)], or intracellular space of the astrocyte. These are marked in Table 2 as [K⁺]_N, [K⁺]_ext, and [K⁺], respectively. The model by Diekman et al. (2013) had the most simple K⁺ model, they modeled only astrocytic K⁺ that depended on NKA. Oschmann et al. (2017) modeled both the astrocytic and extracellular K⁺ concentrations. The astrocytic K⁺ concentration depended on three transmembrane transporters; glutamate transporter, NKA, and NCX. The extracellular K⁺ concentration was a function of astrocytic K⁺ concentration. Farr and David (2011) and Witthoft and Karniadakis (2012) modeled the K⁺ concentration both in the perisynaptic space [named as synaptic cleft and synaptic space by Farr and David (2011) and Witthoft and Karniadakis (2012)] and in the perivascular space. They both used the same simple model for the K⁺ concentration in the perisynaptic space. K⁺ was released from the neurons into the perisynaptic space and removed from the perisynaptic space via the astrocytic NKA (Farr and David, 2011). However, Witthoft and Karniadakis (2012) named the removal so that it included both astrocytic NKA and astrocytic inwardly rectifying K⁺- and voltage-gated K⁺ (KIR) channel. Farr and David (2011) and Witthoft and Karniadakis (2012) also used the same simple model for the K⁺ concentration in the perivascular space. The K⁺ concentration in the perivascular space depended on astrocytic voltage- and Ca²⁺-operated K⁺ (BK) channels and smooth muscle cell's KIR channels. They also had a K⁺-dependent decay term in the perivascular space. Witthoft et al. (2013) modeled in more detail the K⁺ concentration in the perisynaptic space (named as synaptic space by Witthoft et al., 2013), intracellular space of the astrocyte, and perivascular space. In the model by Witthoft et al. (2013), the K⁺ concentration in the perisynaptic space depended on K⁺ released from the neurons and removed via the astrocytic NKCC1 and NKA, in addition to (bidirectional) astrocytic KIR channels and a decay term. The astrocytic K⁺ concentration depended on K⁺ entering from the perisynaptic space via NKA and NKCC1, in addition to astrocytic KIR channels on the perisynaptic side as well as astrocytic BK and KIR channels on the perivascular side of the astrocyte. The equation also had a decay term. The K⁺ concentration in the perivascular space depended on astrocytic BK and KIR channels as well as arteriolar KIR channels and a decay term. Kenny et al. (2018) modeled the K⁺ concentration in the perisynaptic space (named as synaptic cleft by Kenny et al., 2018), intracellular space of the astrocyte, perivascular space, intracellular space of the smooth muscle cell, and extracellular space. In the model by Kenny et al. (2018), the K⁺ concentration in the perisynaptic space depended on K⁺ released from the neuron and removed via the astrocytic K⁺/Cl⁻ cotransporter (KCC1), NKCC1, and NKA, in addition to K⁺ diffusion between extracellular space and perisynaptic space as well as astrocytic K⁺ channels. The astrocytic K⁺ concentration depended on K⁺ entering from the perisynaptic space via KCC1, NKCC1, and NKA, in addition to K⁺ channels on the perisynaptic side and BK channels on the perivascular side of the astrocyte. The K⁺ concentration in the perivascular space depended on astrocytic BK channels and smooth muscle cell's KIR channels. In conclusion, only the model by Witthoft et al. (2013) took into account spatial K⁺ buffering.

Some of the most recent models developed in this category were the models by Komin et al. (2015), Handy et al. (2017), and Taheri et al. (2017). Komin et al. (2015) presented two models, a reaction-diffusion model and a reaction model. With both models they tested if the temperature-dependent SERCA activity was the reason for the differences in Ca²⁺ activity. They showed that their reaction-diffusion model behaved similarly to the experimental data, thus increased SERCA activity (higher temperature) led to decreased Ca²⁺ activity. On the other hand, their reaction model showed the opposite. Thus, they claimed that spatiality was needed to be taken into account to get biologically correct results. However, since the core models were different in the reaction-diffusion and reaction models, it would be interesting to see how the results would look like if the same core model was tested with and without diffusion.

Handy et al. (2017) and Taheri et al. (2017) used the same model but explored somewhat different parameter spaces. They studied the role of SOC channels as well as the PMCA and SERCA pumps in Ca²⁺ activity. They specifically tested which form the Ca²⁺ response had with different parameter values of the channel and pumps (single peak, multiple peaks, plateau, or long-lasting response). They found out that SOC channels were necessary for plateau and long-lasting responses as well as for stable oscillations with multiple peaks. Stable oscillations disappeared when the SERCA pump was partially blocked, but plateau and long-lasting responses were still present. The likelihood of having multiple peaks increased when the PMCA pump was blocked. Taheri et al. (2017) also did Ca²⁺ imaging on cortical astrocytes in mice. They applied ATP on acute brain slices and recorded the Ca²⁺ responses from different subcompartments of the astrocytes, from soma as well as from large and short processes, and categorized the results into four different types of responses named above. Their conclusion was that the variability mainly stemmed from differences in IP₃ dynamics and Ca²⁺ fluxes via SOC channels. To take into account the experimental variability between the different subcompartments, Taheri et al. (2017) ran simulations with different parameter values of the SOC channel and the PMCA and SERCA pumps together with the input IP₃ kinetics. Next, they chose the parameter subspaces that matched their experimental data the best. Their simulations suggested that the soma had higher PMCA and lower SERCA flux rates as well as shorter rise duration for the IP₃ transient than the small and large processes.

3.1.2. Astrocyte network models

Half of the astrocyte network models were so-called generic. Others, however, were specified to model astrocytes in the cerebrum (Iacobas et al., 2006; Ghosh et al., 2010), cortex (Goldberg et al., 2010; Wallach et al., 2014), neocortex (Li et al., 2012), visual cortex and somatosensory cortex (Bennett et al., 2008a), hippocampus (Goto et al., 2004; Ullah et al., 2006), retina (Edwards and Gibson, 2010), spinal cord (Bennett et al., 2006; Gibson et al., 2008), as well as the striatum (Höfer et al., 2002). One fourth of the astrocyte network models took into account neurotransmitters in a simplistic way just as a stimulus, having either the glutamate as a constant, step function, or something similar (see e.g., Goto et al., 2004; Ullah et al., 2006; Bennett et al., 2008a; Kang and Othmer, 2009; MacDonald and Silva, 2013). Only Wallach et al. (2014) actually modeled the amount of neurotransmitter glutamate with a differential equation. The stimulus to the astrocyte model by Wallach et al. (2014) was taken from the model by Tsodyks and Markram (1997). We included this model under astrocyte models because this model was not bidirectional between astrocytes and neurons. The characteristics of astrocyte network models can be found in Table 3.

Table 3.

Characteristics of astrocyte network models.

Model	No.	Input	Variables	Ca2+ fluxes	Diffusion	GJ	Output	Event
De Young and Keizer (1992) and Li and Rinzel (1994) -TYPE MODELS
Bennett et al., 2005	19–57	[ATP]ext	χ, [ATP]ext, [Ca2+], h, [IP3]	CICR, endogenous buffer, leak from ER into cyt, SERCA	Dcyt: [IP3], Dext: [ATP]ext	No	[ATP]ext	Ca2+
Bennett et al., 2006	19–95	[ATP]ext	χ, [ATP]ext, [Ca2+], h, [IP3]	CICR, endogenous buffer, leak from ER into cyt, SERCA	Dcyt: [IP3], Dext: [ATP]ext	No	[ATP]ext	Ca2+
Bennett et al., 2008a	1–7	[Glu]syn	[Ca2+], [EET]ext, h, [IP3]	CICR, endogenous buffer, leak from ER into cyt, SERCA	Dcyt: [IP3], Dext: [EET]ext	No	[EET]ext	Vasc.
Gibson et al., 2008	3–n/a	[ATP]ext	χ, [ATP]ext, [Ca2+], h, [IP3]	CICR, endogenous buffer, leak from ER into cyt, SERCA	Dcyt: [IP3], Dext: [ATP]ext	No	[ATP]ext	Ca2+
Goto et al., 2004	200	[Glu]syn	[Ca2+], [IP3], detailed IP3R	CICR, leak from ER into cyt, SERCA	No	Ca2+, IP3	[Ca2+]	Ca2+
MacDonald and Silva, 2013	1–200	[Glu]syn	[ATP]ext, [Ca2+], [Ca2+]ER, h, [IP3]	CICR, endogenous buffer, leak from ER into cyt, leak from ext into cyt, PMCA, SERCA	Dext: [ATP]ext	No	[ATP]ext	Ca2+
Stamatakis and Mantzaris, 2006	1–n/a	[ATP]ext	[ATP]ext, [Ca2+], h, [IP3]	CICR, leak from ER into cyt, SERCA	Dcyt: [IP3], Dext: [ATP]ext	No	[ATP]ext	Ca2+
Stamatakis and Mantzaris, 2007	1–n/a	[ATP]ext	[ATP]ext, [Ca2+], h, [IP3]	CICR, leak from ER into cyt, SERCA	Dext: [ATP]ext	No	[ATP]ext	Ca2+
Höfer et al. (2002) -TYPE MODELS
Bellinger, 2005	9	[IP3]	[ATP]ext, [Ca2+], [Ca2+]ER, [Glu]ext, [IP3], R	CCE, CICR, efflux via pump, Glu-dependent ER release, Glu-dependent influx, leak from ER into cyt, leak from ext into cyt, P2XR, SERCA	No	Ca2+, IP3	[ATP]ext, [Glu]ext	Ca2+
Höfer et al., 2002	1–361	Rate of [PLCβ]	[Ca2+], [Ca2+]ER, [IP3], R	CCE, CICR, efflux via pump, leak from ER into cyt, leak from ext into cyt, SERCA	Dcyt: [Ca2+], [IP3]	Ca2+, IP3	[Ca2+]	Ca2+
Li et al., 2012	3–300	Spon.	[Ca2+], [Ca2+]ER, [Ca2+]ext, H-H channel kinetics, [IP3], [K+], [K+]ext, P, Rk	CICR, efflux, efflux via pump, leak from ER into cyt, SERCA, VGCC	Dcyt: [Ca2+], [IP3],Dext: [Ca2+]ext, [K+]ext,	IP3	[Ca2+]	Ca2+
De Young and Keizer (1992), Li and Rinzel (1994), and Höfer et al. (2002) -TYPE MODELS
Edwards and Gibson, 2010	361	[ATP]ext	χ, [ATP]ext, [Ca2+], h, [IP3]	CICR, endogenous and exogenous buffers, leak from ER into cyt, SERCA	Dcyt: [Ca2+], [IP3],Dext: [ATP]ext	IP3	[ATP]ext	Ca2+
Ghosh et al., 2010	2	[GLC]ext, [Gln]ext, [Glu]ext	[Ca2+], h, [IP3]	CCE, CICR, efflux, leak from ER into cyt, leak from ext into cyt, SERCA	No	IP3	[LAC]	Vasc.
Goldberg et al., 2010	1–100	[IP3]	[Ca2+], h, [IP3]	CICR, leak from ER into cyt, SERCA	No	IP3	[Ca2+]	Ca2+
Kazantsev, 2009	30	Spon.	[Ca2+], h, [IP3]	CCE, CICR, efflux, leak from ER into cyt, leak from ext into cyt, SERCA	No	IP3	[Ca2+]	Ca2+
Lallouette et al., 2014	1,331	[IP3]	[Ca2+], h, [IP3]	CICR, leak from ER into cyt, SERCA	No	IP3	[Ca2+]	Ca2+
Matrosov and Kazantsev, 2011	1–10	Spon.	[Ca2+], h, [IP3]	CCE, CICR, efflux, leak from ER into cyt, leak from ext into cyt, SERCA	No	IP3	[Ca2+]	Ca2+
Ullah et al., 2006	1–3	[Glu]syn	[Ca2+], h, [IP3]	CCE, CICR, efflux, leak from ER into cyt, leak from ext into cyt, SERCA	No	IP3	[Ca2+]	Ca2+
Wallach et al., 2014	130	[Glu]syn	[Ca2+], h, [IP3]	CICR, leak from ER into cyt, SERCA	No	IP3	[Ca2+]	Ca2+
Wei and Shuai, 2011	169	[IP3]	[Ca2+], h, [IP3]	CICR, leak from ER into cyt, SERCA	Dcyt: [Ca2+], [IP3]	IP3	[Ca2+]	Ca2+
OTHER TYPES OF MODELS
Iacobas et al., 2006	625	[ATP]ext, [UTP]ext	[ATP]ext, [Ca2+], [IP3], [UTP]ext	CICR, efflux via pump, P2XR, sequestration flux	Dext: [ATP]ext, [UTP]ext	IP3	[ATP]ext, [UTP]ext	Ca2+
Kang and Othmer, 2009	11	Glusyn	[ATP]ext, [Ca2+], [CaPKC], [IP3], [IP3R]	CICR, leak from ER into cyt, SERCA	Dcyt: [Ca2+], [CaPKC], [IP3], Dext: [ATP]ext	IP3	[ATP]ext	Ca2+

This table shows the following: model, number (No.) of astrocytes modeled, input for the astrocytes, astrocytic variables described by differential equations, astrocytic Ca²⁺ fluxes related to cytosolic Ca²⁺, diffusion of astrocytic variables either in the cytosol, ER, or extracellular space, not between these spaces, gap junction signaling (GJ) between astrocytes, output of the astrocytes, and experimentally shown event that the model was finetuned to capture [Ca²⁺ dynamics (Ca²⁺) and vascular (Vasc.)]. Compartment is cytosol (cyt) if not otherwise stated. Amounts modeled in concentrations are given inside square brackets. In addition to astrocytes, Bennett et al. (2008a) modeled also smooth muscle cells and Edwards and Gibson (2010) modeled also Müller cells. Edwards and Gibson (2010) simulated their system both with and without diffusion. The stimulus for the model by Wallach et al. (2014) came from the model by Tsodyks and Markram (1997).

All the astrocyte network models studied Ca²⁺ waves and few models specifically addressed spontaneous Ca²⁺ waves and vascular events (see Table 3). All the models except the model by Iacobas et al. (2006) had the components for all three; CICR, leak from the ER into the cytosol, and the SERCA pump. About one fourth of the models took into account Ca²⁺ buffering. About one third of the models had either influx of Ca²⁺ from outside of the astrocyte or efflux of Ca²⁺ to outside of the astrocyte, or both. About half of the models took into account astrocytic release of signaling molecules. Thus, the models had equations mostly for extracellular ATP, but one considered equations for extracellular glutamate (Bellinger, 2005). However, none of the models presented a detailed mechanistic description of how the release occurs. More than half of the models took into account diffusion, and, especially, almost half of the models studied the ATP diffusion in the extracellular space. Three quarters of the astrocyte network models had gap junctions for IP₃ but some models had them also for Ca²⁺. Thus, these models had similar core structure with small variations. As an example, Li et al. (2012) were the only ones that modeled K⁺ concentration, both in astrocytic and extracellular spaces, and VGCCs. Goto et al. (2004) were the only ones to use the detailed IP₃R model by De Young and Keizer (1992). Höfer et al. (2002), Bellinger (2005), Ullah et al. (2006), Kazantsev (2009), Ghosh et al. (2010), and Matrosov and Kazantsev (2011) modeled CCE.

The first model developed in this category was the model by Höfer et al. (2002). Höfer et al. (2002) showed with their two-dimensional (19 × 19) astrocyte network model that IP₃ permeability in gap junctions was a more important factor in intercellular Ca²⁺ waves than Ca²⁺ permeability. When blocking the IP₃ permeability, intercellular Ca²⁺ wave propagation was prevented. However, intercellular Ca²⁺ wave propagation was not prevented when the Ca²⁺ permeability was blocked. In the model by Höfer et al. (2002), the IP₃ concentration depended on two distinct production terms via phospholipase C (PLC), one corresponding to PLC isotype β (PLCβ) and the other to PLC isotype δ (PLCδ). Höfer et al. (2002) showed that PLCδ was needed to be modeled to get the downstream cells to respond to the stimulus with a Ca²⁺ increase.

Two of the newest models developed in this category were the models by Lallouette et al. (2014) and Wallach et al. (2014). Lallouette et al. (2014) simplified the astrocyte network model by Goldberg et al. (2010) to be able to simulate the function of a three-dimensional (11 × 11 × 11) astrocyte network. With this network of more than a thousand astrocytes, Lallouette et al. (2014) studied how the variability in the topology of gap-junction coupled astrocytes affected the intercellular Ca²⁺ wave propagation. They tested five different coupling rules and found out that these different coupling rules can be used to reproduce the variation in the experimental data. They showed that dense connectivity or having long-distance gap-junction coupled astrocytes reduced the intercellular Ca²⁺ wave propagation. Wallach et al. (2014) continued the previous study by stimulating astrocyte network by Tsodyks and Markram (1997) model. In the present study, the model by Wallach et al. (2014) is listed in the category of astrocyte network models because the astrocytes did not have an effect on the neuron. Wallach et al. (2014) demonstrated through experimental and simulation studies that there was a threshold stimulation frequency when astrocytes started to respond with Ca²⁺ oscillations. However, this threshold frequency was different for different astrocytes and it increased with the number of astrocytes coupled.

3.2. Computational neuron-astrocyte models

In recent years, bidirectional neuron-astrocyte communication has been the focus of much research in the field of neuroscience. Most of the existing neuron-astrocyte models concentrated on astrocytic Ca²⁺ dynamics affected by glutamate in the synaptic cleft, and reciprocal neuron-astrocyte signaling. Many of the models were presented without a specific biological or disease-related question, and the focus was on combining existing models into a new construction, or adding the authors' own model components to previously published models. Next, we will go through neuron-astrocyte synapse models in section 3.2.1 and neuron-astrocyte network models in section 3.2.2.

3.2.1. Neuron-astrocyte synapse models

Neuron-astrocyte synapse models include models which have only one astrocyte and one to multiple synapses. Of the models covered in our study, about half of the neuron-astrocyte synapse models were found to be so-called generic models, in other words they were developed with no specific brain area or cell in mind. Others, however, were specified to model neuron-astrocyte synapses in the cortex or neocortex (Nadkarni and Jung, 2003, 2004; Di Garbo et al., 2007; Volman et al., 2007; DiNuzzo et al., 2011; Valenza et al., 2011; Nazari et al., 2015b, 2017; Amiri et al., 2016; Li et al., 2017), hippocampus (Nadkarni and Jung, 2005, 2007; Nadkarni et al., 2008; Tewari and Majumdar, 2012a,b; Tang et al., 2013, 2016; Tewari and Parpura, 2013; Li et al., 2016b), thalamocortical networks (Amiri et al., 2011a), or brainstem (Oku et al., 2016).

The modeling approaches for neurons varied depending on the author. Half of the studied publications utilized relatively complex biophysical neuron models, namely Hodgkin and Huxley (1952) model (Nadkarni and Jung, 2003; Sotero and Martínez-Cancino, 2010; Tewari and Majumdar, 2012a,b; Tang et al., 2013, 2016; Guo et al., 2017; Li et al., 2017), Traub et al. (1991) model or its derivative Pinsky and Rinzel (1994) model (Nadkarni and Jung, 2004, 2005, 2007; Silchenko and Tass, 2008; Tewari and Parpura, 2013; Li et al., 2016a,b), or Olufsen et al. (2003) model (Di Garbo et al., 2007; Di Garbo, 2009). Simpler phenomenological models used in the studied publications were the FitzHugh-Nagumo (FitzHugh, 1961) model (Postnov et al., 2007), leaky integrate-and-fire (LIF, Gerstner and Kistler, 2002) model (Wade et al., 2011, 2012; Amiri et al., 2016; De Pittà and Brunel, 2016; Nazari et al., 2017; Liu et al., 2018), Izhikevich (2007) model (Valenza et al., 2011; Nazari et al., 2015a,b,c), Morris and Lecar (1981) model or its derivatives (Volman et al., 2007; Amiri et al., 2011b, 2013b), and Suffczynski et al. (2004) neuronal population model (Amiri et al., 2011a). The released neurotransmitter was modeled explicitly by Nadkarni and Jung (2005, 2007), Volman et al. (2007), Nadkarni et al. (2008), Silchenko and Tass (2008), Amiri et al. (2011b, 2013b), Wade et al. (2011), Tewari and Majumdar (2012a,b), Tang et al. (2013, 2016), Tewari and Parpura (2013), Nazari et al. (2015a,b,c), De Pittà and Brunel (2016), and Li et al. (2017), however not necessarily with a differential equation. Other models utilized, for example, phenomenological transfer functions between neuronal events and astrocytic IP₃ concentration. Several models had increased astrocytic IP₃ concentration after the neuronal membrane potential increased over some threshold (marked in Table 4 as V_m,N → [IP₃]). The details of the neuron-astrocyte synapse models can be found in Table 4.

Table 4.

Characteristics of neuron-astrocyte synapse models.

Model	No.	Input	Variables	Ca2+ fluxes	Diffusion	GJ	Output	Event
De Young and Keizer (1992) and Li and Rinzel (1994) -TYPE MODELS
Guo et al., 2017	1	Vm,N → [IP3]	[Ca2+], h, [IP3]	CICR, leak from ER into cyt, ATP-independent ER pump	No	No	Iastro	Ca2+
Li et al., 2016a	1	Vm,N → [IP3]	[Ca2+], [Glu]ext, h, [IP3]	CICR, leak from ER into cyt, SERCA	No	No	Iast = c[Glu]ext	Ca2+
Li et al., 2016b	1	Vm,N → [IP3]	[Ca2+], f=Gluext, h, [IP3]	CICR, leak from ER into cyt, SERCA	No	No	Iast = cf	Ca2+
Li et al., 2017	1	[GABA]syn	[Ca2+], [Glu]ext, h, [IP3]	CICR, leak from ER into cyt, SERCA	No	No	Iast = c[Glu]ext	Ca2+
Liu et al., 2018	1	[2-AG]post	[Ca2+], [Glu]ext, h, [IP3]	CICR, leak from ER into cyt, SERCA	No	No	[Glu]ext	Plast.
Nadkarni and Jung, 2003	1	Vm,N → [IP3]	[Ca2+], h, [IP3]	CICR, leak from ER into cyt, SERCA	No	No	Iastro	Ca2+
Nadkarni and Jung, 2004	1	Vm,N → [IP3]	[Ca2+], h, [IP3]	CICR, leak from ER into cyt, SERCA	No	No	Iastro	Ca2+
Nadkarni and Jung, 2005	1	[Glu]syn	[Ca2+], h, [IP3]	CICR, leak from ER into cyt, SERCA	No	No	Iastro	Hyper.
Nadkarni and Jung, 2007	1	[Glu]syn	[Ca2+], h, [IP3]	CICR, leak from ER into cyt, SERCA	No	No	[Ca2+]	Plast.
Nadkarni et al., 2008	1	[Glu]syn	[Ca2+], h, [IP3]	CICR, leak from ER into cyt, SERCA	No	No	[Ca2+]	Inf.
Tang et al., 2013	1	NT	[Ca2+], h, [IP3]	CICR, leak from ER into cyt, SERCA	No	No	Iastro	Inf.
Tang et al., 2016	1	NT	[Ca2+], h, [IP3]	CICR, leak from ER into cyt, SERCA	No	No	Iastro	Inf.
Valenza et al., 2011	1	Vm,N → [IP3]	[Ca2+], h, [IP3]	CICR, leak from ER into cyt, SERCA	No	No	Iastro	Ca2+
Volman et al., 2007	1	y=Glusyn	[Ca2+], f=Gluext, h, [IP3]	CICR, leak from ER into cyt, SERCA	No	No	f	Inf.
Wade et al., 2011	1	y=Glusyn	[Ca2+], f=Gluext, h, [IP3]	CICR, leak from ER into cyt, SERCA	No	No	Ca2+, f	Plast.
Wade et al., 2012	1	[2-AG]post	[Ca2+], [Glu]ext, h, [IP3]	CICR, leak from ER into cyt, SERCA	No	No	[Glu]ext	Plast.
Höfer et al. (2002) -TYPE MODELS
Di Garbo et al., 2007	1	Vm,N → [IP3]	[Ca2+], [Ca2+]ER, [IP3], R	CCE, CICR, efflux, leak from ER into cyt, leak from ext into cyt, P2XR, SERCA	No	No	Iastro	Ca2+
Di Garbo, 2009	1	Vm,N → [IP3]	[Ca2+], [Ca2+]ER, [IP3], R	CCE, CICR, efflux, leak from ER into cyt, leak from ext into cyt, P2XR, SERCA	No	No	Iastro	Ca2+
DiNuzzo et al., 2011	1	[Na+]	[ATP], [Ca2+], [Ca2+]ER, [G6P], [GAP], [GLC], [Gly], [IP3], [LAC], [Na+], [NADH],[O2], [PCr], [PEP], [Pyr]	CICR, leak from ER into cyt, leak from ext into cyt, NCX, PMCA, SERCA	No	No	Iastro	Vasc.
De Young and Keizer (1992), Li and Rinzel (1994), and Höfer et al. (2002) -TYPE MODELS
De Pittà and Brunel, 2016	1	[Glu]syn	γ, [Ca2+], [Glu]ext, h, [IP3], x	CICR, leak from ER into cyt, SERCA	No	No	[Glu]ext	Plast.
Tewari and Majumdar, 2012a	1	[Glu]syn	[Ca2+], E, [Glu]ext, h, [IP3], O1, O2, O3, Rf	CICR, leak from ER into cyt, SERCA	No	No	[Glu]ext	Plast.
Tewari and Majumdar, 2012b	1	[Glu]syn	[Ca2+], E, [Glu]ext, h, [IP3], O1, O2, O3, Rf	CICR, leak from ER into cyt, SERCA	No	No	[Glu]ext	Plast.
Tewari and Parpura, 2013	1	[Glu]syn	[Ca2+], E, [Glu]ext, h, [IP3], O1, O2, O3, Rf	CICR, leak from ER into cyt, SERCA	No	No	[Glu]ext	Synch.
OTHER TYPES OF MODELS
Amiri et al., 2011a	1	Syn. act.	Ca2+, ${\text{Ca}}_{\text{ER}}^{2+}$, Gm, Sm=IP3	CICR, efflux, influx, IP3-dependent influx, leak from ER into cyt, SERCA	No	No	Gm	Synch.
Amiri et al., 2011b	1	NT	Ca2+, ${\text{Ca}}_{\text{ER}}^{2+}$, Gm, Sm=IP3	CICR, efflux, influx, IP3-dependent influx, leak from ER into cyt, SERCA	No	No	Iast = cGm	Synch.
Amiri et al., 2013b	1	NT	Ca2+, ${\text{Ca}}_{\text{ER}}^{2+}$, Gm, Sm=IP3	CICR, efflux, influx, IP3-dependent influx, leak from ER into cyt, SERCA	No	No	$I_{\text{ast}}=c\text{C}{\text{a}}^{2+}$	Inf.
Amiri et al., 2016	1	Syn. act.	Ca2+, ${\text{Ca}}_{\text{ER}}^{2+}$, Gm, Sm=IP3	CICR, efflux, influx, IP3-dependent influx, leak from ER into cyt, SERCA	No	No	Iast = cGmexp(−E2)	Synch.
Nazari et al., 2015a	1	NT	Ca2+, ${\text{Ca}}_{\text{ER}}^{2+}$, Gm, Sm=IP3	CICR, efflux, influx, IP3-dependent influx, leak from ER into cyt, SERCA	No	No	$I_{\text{ast}}=c\text{C}{\text{a}}^{2+}$	Inf.
	1	NT	Ca2+, Gm, Sm=IP3	Efflux, influx, IP3-dependent influx	No	No	$I_{\text{ast}}=c\text{C}{\text{a}}^{2+}$	Inf.
Nazari et al., 2015b	1	NT	Ca2+, ${\text{Ca}}_{\text{ER}}^{2+}$, Gm, Sm=IP3	CICR, efflux, influx, IP3-dependent influx, leak from ER into cyt, SERCA	No	No	Iast = cGm	Inf.
Nazari et al., 2015c	1	NT	Ca2+, ${\text{Ca}}_{\text{ER}}^{2+}$, Gm, Sm=IP3	CICR, efflux, influx, IP3-dependent influx, leak from ER into cyt, SERCA	No	No	$I_{\text{ast}}=c\text{C}{\text{a}}^{2+}$	Inf.
Nazari et al., 2017	1	Syn. act.	Ca2+, ${\text{Ca}}_{\text{ER}}^{2+}$, Gm=Gluext, Sm=IP3	CICR, efflux, influx, IP3-dependent influx, leak from ER into cyt, SERCA	No	No	Iast = cGmexp(−kE2)	Synch.
	1	Syn. act.	Ca2+, IP3	Efflux, influx, IP3-dependent influx	No	No	$I_{\text{ast}}=c\text{C}{\text{a}}^{2+}exp(-k{E}_2)$	Synch.
Oku et al., 2016	1	Syn. act.	Ca2+, 2 variables	Not specified	No	No	Variable	Ca2+
Postnov et al., 2007	1	Syn. act.	Ca2+, ${\text{Ca}}_{\text{ER}}^{2+}$, Gm, Sm=IP3	CICR, efflux, influx, IP3-dependent influx, leak from ER into cyt, SERCA, Vm,N-dependent influx	No	No	Iast = cGm	Plast.
Silchenko and Tass, 2008	1	[Glu]syn	[Ca2+], ${\left[C{a}^{2+}\right]}_{\text{ER}}$, [Glu]ext, [IP3], R1, R2, R3, R4	CICR, efflux, Glu-dependent influx, influx, leak from ER into cyt, SERCA	Dext: [Glu]ext	No	[Glu]ext	Ca2+
Sotero and Martínez-Cancino, 2010	1	Syn. act.	[Ca2+], ${\left[C{a}^{2+}\right]}_{\text{ER}}$, Gm=Gluext, Sm=IP3	CICR, efflux, influx, IP3-dependent influx (depends also on IP3 in neighboring astrocytic microdomains), leak from ER into cyt, SERCA	No	No	Iast = cGm	Synch.

This table shows the following: model, number (No.) of astrocytes modeled, input for the astrocytes, astrocytic variables described by differential equations, astrocytic Ca²⁺ fluxes related to cytosolic Ca²⁺, diffusion of astrocytic variables either in the cytosol, ER, or extracellular space, not between these spaces, gap junction signaling (GJ) between astrocytes, output of the astrocytes, and experimentally shown event that the model was finetuned to capture [Ca²⁺ dynamics (Ca²⁺), vascular (Vasc.), synchronization (Synch.), information transfer (Inf.), plasticity (Plast.), and hyperexcitability (Hyper.)]. Compartment is cytosol (cyt) if not otherwise stated. Amounts modeled in concentrations are given inside square brackets. DiNuzzo et al. (2011) modeled also smooth muscle cells. Thalamocortical neural population model was used by Amiri et al. (2011a). Cortical spiking neural population model, which is based on the LIF model, was used by Amiri et al. (2016). Sotero and Martínez-Cancino (2010) used the dynamical mean field approximation to the system of 500,000 synapses with 13 equations per synapse. They reduced the number of differential equations to 13 (13 + 2) = 195. Nazari et al. (2015a) presented two different astrocyte models, with or without ${\text{Ca}}_{\text{ER}}^{\mathit{\text{2}}+}$ and fluxes via ER membrane. Amiri et al. (2016) and Nazari et al. (2017) presented three different models, one was the original and the other two were reductions of the original model. However, the details of the two reduction models by Amiri et al. (2016) were given in such a way that they did not fulfill our criteria given in section 2.2. Li et al. (2017) simulated two single astrocytes models, and also combined the more complex astrocyte model with a neuronal seizure model. Di Garbo et al. (2007) and Di Garbo (2009) simulated also just the astrocyte models with ATP stimuli, in addition to the neuron-astrocyte synapse models. $I_{astro}=\mathit{\text{2.11}}\mathcal{H}(\mathit{\text{ln}}(\Delta Ca))ln(\Delta Ca)$, where $\mathcal{H}$ is the heaviside function and ΔCa = [Ca²⁺]−196.69(nM) (Nadkarni and Jung, 2003).

The neuron-astrocyte synapse models were developed to explain many different biological events as can be seen in Table 4. Examples of the studied phenomena included Ca²⁺ dynamics, plasticity, hyperexcitability, information transfer, synchronization, and vascular events. All the other models except the models by Oku et al. (2016) and Guo et al. (2017) had all astrocytic components for CICR, leak from the ER into the cytosol, and the SERCA pump. About one third of the models had influx of Ca²⁺ from outside of the astrocyte and efflux of Ca²⁺ to outside of the astrocyte. The models had neither gap junction signaling because these models had only one astrocyte nor buffers. Thus, these models had similar core structure with small variations. As an example, two modeled CCE (Di Garbo et al., 2007; Di Garbo, 2009) and one modeled efflux via the PMCA pump and NCX (DiNuzzo et al., 2011) as well as diffusion (Silchenko and Tass, 2008).

The first model developed in this category was the model by Nadkarni and Jung (2003). Nadkarni and Jung (2003) studied Ca²⁺ oscillations with a model consisting of a single astrocyte and single Hodgkin-Huxley type neuron. The astrocyte model was based on the model by Li and Rinzel (1994) but they added a differential equation for IP₃. When the membrane potential of the neuron was higher than certain threshold, IP₃ concentration was increased in the astrocyte. The model also included a degradation of IP₃. The membrane potential of the neuron depended on additional inward current (I_astro) that depended on astrocytic Ca²⁺. Nadkarni and Jung (2003) showed that with higher rate of IP₃ production, the astrocytic Ca²⁺ concentration was higher. In addition, with large enough rate of IP₃ production, the neuron oscillated spontaneously without any external stimulus. Their hypothesis was that a higher expression of metabotropic glutamate receptors (mGluRs) and the resulting spontaneous oscillations caused epilepsy.

As the exact mechanisms of signaling from astrocytes to neurons are still largely unknown or controversial, most of the models had phenomenological descriptions of gliotransmitter release. About one third of the models took into account gliotransmitter release with equations for extracellular glutamate (see Table 4). Other models used phenomenological transfer functions to relay the effect of gliotransmission to the target synaptic terminal (I_astro, part of I_ast, f, and G_m). Only a few of the studied models had detailed astrocytic vesicle release model, namely the models by Silchenko and Tass (2008), Tewari and Majumdar (2012a,b), and Tewari and Parpura (2013). Silchenko and Tass (2008) modeled five vesicle states which represented different stages in the transmitter vesicle cycle. The rate of prefusion complex formation depended on astrocytic Ca²⁺ concentration which was modeled by two steps. In the first step, they simplified the equation where Ca²⁺ activated Ca²⁺-binding soluble N-ethylmaleimide-sensitive factor attachment protein receptor (SNARE) proteins by assuming that the concentration of activated SNARE-proteins was considered stationary. In the second step, they simplified the equation for the fusion of vesicles leading to an irreversible exocytosis of glutamate. However, Silchenko and Tass (2008) did not provide all the details of the model which makes the reuse of the model difficult. The models by Tewari and Majumdar (2012a,b) and Tewari and Parpura (2013) assumed, based on experimental data on cultured hippocampal astrocytes, that the binding of three Ca²⁺ ions was required for gliotransmitter release. The fusion and recycling process of the synaptic-like micro-vesicle was modeled using two differential equations that both depended on the probability that the synaptic-like micro-vesicle was ready to be released. In addition to these more detailed vesicle release models, De Pittà and Brunel (2016) modeled astrocytic glutamate exocytosis in a phenomenological way with just a few equations. They assumed that a fraction of gliotransmitter resources was available for release at any time. Then, every time astrocytic Ca²⁺ increased beyond a certain threshold, the fraction of readily releasable astrocytic glutamate resources was released into the periastrocytic space.

Two of the newest models were provided by Li et al. (2016a, 2017). However, these studies contained, to the best of our understanding, fundamental errors in the biological terminology. Basically, the model by Li et al. (2016a) was the same as presented by Nadkarni and Jung (2004), but the neuronal membrane potential depended on astrocytic glutamate, as presented by Postnov et al. (2009), instead of astrocytic Ca²⁺, as presented by Nadkarni and Jung (2004). Li et al. (2017) developed a GABA-activated astrocyte model (which they, misleadingly, termed GABAergic). The model by Li et al. (2017) is similar to the model by Li et al. (2016a), but Li et al. (2017) added a more complex differential equation for IP₃ by taking into account both the GABA released by the interneuron and glutamate released by the astrocyte, somewhat similarly to Ullah et al. (2006), Nadkarni and Jung (2005), Volman et al. (2007), and others. The differential equations for the extracellular glutamate released by the astrocyte had similar forms as the IP₃ equations and were somewhat similar to the equation by Wade et al. (2012). Li et al. (2016a) showed how a higher equilibrium concentration of extracellular glutamate or glutamate degradation time constant predicted a higher neuronal firing frequency and existence of epileptic seizures. Li et al. (2017), on the other hand, presented using their GABA-activated astrocyte model (misleadingly termed GABAergic) that after a 0.5 s long GABA stimulation, astrocytic Ca²⁺ oscillations were long-lasting. After combining the GABA-activated astrocyte model (misleadingly termed GABAergic) and a neuronal seizure model, they concluded that in this model, the astrocyte, through stimulating pyramidal neurons and thus increasing excitatory activity, prevented the transition from seizure activity into a normal firing activity state, which GABA alone was capable of inducing by inhibiting pyramidal neuron activity.

3.2.2. Neuron-astrocyte network models

Neuron-astrocyte network models include models that have several astrocytes in addition to neurons. Half of the neuron-astrocyte network models were so-called generic models. Others, however, were specified to model neuron-astrocyte interactions in the cortex (Allegrini et al., 2009; Liu and Li, 2013a; Chan et al., 2017; Tang et al., 2017; Yao et al., 2018), hippocampus (Amiri et al., 2012a, 2013a; Mesiti et al., 2015a; Li et al., 2016c), spinal cord (Yang and Yeo, 2015), or thalamocortical networks (Amiri et al., 2012b,c).

The modeling strategies for neurons varied depending on the author. Three of the studied publications utilized Hodgkin and Huxley (1952) model (Liu and Li, 2013b; Li et al., 2016c; Yao et al., 2018) and one utilized Traub et al. (1991) model's derivative Pinsky and Rinzel (1994) model (Mesiti et al., 2015a). Simpler phenomenological models used in the studied publications were the FitzHugh-Nagumo (FitzHugh, 1961) model (Postnov et al., 2009; Hayati et al., 2016), LIF (Gerstner and Kistler, 2002) model (Liu and Li, 2013a; Naeem et al., 2015), Izhikevich (2007) model (Allegrini et al., 2009; Haghiri et al., 2016, 2017; Tang et al., 2017), Morris and Lecar (1981) model or its derivatives (Amiri et al., 2012a, 2013a; Chan et al., 2017), and Suffczynski et al. (2004) neuronal population model (Amiri et al., 2012b,c). The released neurotransmitter was modeled explicitly by Amiri et al. (2012a, 2013a), Liu and Li (2013a), Yang and Yeo (2015), Li et al. (2016c), and Yao et al. (2018). Other models utilized phenomenological transfer functions between the neurotransmitter and astrocytic IP₃ concentration. The details of the neuron-astrocyte network models can be found in Table 5.

Table 5.

Characteristics of neuron-astrocyte network models.

Model	No.	Input	Variables	Ca2+ fluxes	Diffusion	GJ	Output	Event
De Young and Keizer (1992) and Li and Rinzel (1994) -TYPE MODELS
Amiri et al., 2012a	1–5	NT	[Ca2+], f, h, [IP3]	CICR, leak from ER into cyt, SERCA	No	IP3	Iast = cf	Synch.
Amiri et al., 2013a	1–50	NT	[Ca2+], f, h, [IP3]	CICR, leak from ER into cyt, SERCA	No	IP3	Iast = cf	Synch.
Chan et al., 2017	10,000	Vm,N → [IP3]	[Ca2+], f, h, [IP3]	CICR, leak from ER into cyt, SERCA	No	IP3	Iast = cf	Synch.
Li et al., 2016c	50	NT	[ATP]ext, [Ca2+], [Glu]ext, h, [IP3]	CICR, leak from ER into cyt, SERCA	Dext: [ATP]ext, [Glu]ext	IP3	Iast,ATP = c[ATP]ext, Iast,Glu = c[Glu]ext	Inf.
Liu et al., 2016	1–25,000	[2-AG]post	[Ca2+], [Glu]ext, h, [IP3]	CICR, leak from ER into cyt, SERCA	No	IP3	[Glu]ext	Plast.
Naeem et al., 2015	1–5	[2-AG]post	[Ca2+], [Glu]ext, h, [IP3]	CICR, leak from ER into cyt, SERCA	No	IP3	[Glu]ext	Plast.
Yang and Yeo, 2015	28	[Glu]syn	[ATP]ext, [Ca2+], [Glu]ext, h, [IP3]	CICR, leak from ER into cyt, SERCA	Dext: [ATP]ext, [Glu]ext	IP3	[ATP]ext, [Glu]ext	Inf.
Yao et al., 2018	1–6	[ATP]ext, [Glu]syn, [Glu]ext	χ, [ATP]ext, [Ca2+], [Ca2+]ER, G, [Glu]ext, h, [IP3], [K+], [K+]ext, [Na+], [Na+]ext	Buffer, CICR, leak from ER into cyt, leak from ext into cyt, PMCA, SERCA	Dext: [ATP]ext, [K+]ext, [Na+]ext	No	[ATP]ext, [Glu]ext	Hyper.
Höfer et al. (2002) -TYPE MODELS
Allegrini et al., 2009	400	Vm,N → [IP3]	[Ca2+], [IP3], Rin	CICR, efflux via pump, SERCA	Dcyt: [Ca2+], [IP3]	Ca2+, IP3	Iastro	Synch.
De Young and Keizer (1992), Li and Rinzel (1994), and Höfer et al. (2002) -TYPE MODELS
Liu and Li, 2013a	n/a	[Glu]syn	[Ca2+], [IP3], Rac	CICR, efflux via pump, leak from ER into cyt, SERCA	No	Ca2+, IP3	Iastro	Inf.
Liu and Li, 2013b	6	Vm,N → [IP3]	[Ca2+], [IP3], Rac	CICR, efflux via pump, leak from ER into cyt, SERCA	No	Ca2+, IP3	Iastro	Inf.
Tang et al., 2017	100	Vm,N → [IP3]	[Ca2+], h, [IP3]	CICR, leak from ER into cyt, SERCA	No	IP3	Iastro	Hyper.
OTHER TYPES OF MODELS
Amiri et al., 2012b	2	Syn. act.	Ca2+, ${\text{Ca}}_{\text{ER}}^{2+}$, Gm, Sm=IP3	CICR, efflux, influx, IP3-dependent influx, leak from ER into cyt, SERCA	No	IP3	Gm	Hyper.
Amiri et al., 2012c	2	Syn. act.	Ca2+, ${\text{Ca}}_{\text{ER}}^{2+}$, Gm, Sm=IP3	CICR, efflux, influx, IP3-dependent influx, leak from ER into cyt, SERCA	No	IP3	Gm	Synch.
Haghiri et al., 2016	1–99	Syn. act.	Ca2+, ${\text{Ca}}_{\text{ER}}^{2+}$, Gm, Sm=IP3	CICR, efflux, influx, IP3-dependent influx, leak from ER into cyt, SERCA, Vm,N-dependent influx	No	No	Iast = cGm, Isyn = (k−cGm)(z−z0)	Synch.
	1–99	Syn. act.	Ca2+, ${\text{Ca}}_{\text{ER}}^{2+}$, Sm=IP3	CICR, efflux, influx, IP3-dependent influx, leak from ER into cyt, SERCA, Vm,N-dependent influx	No	No	Iast = cGm	Synch.
Haghiri et al., 2017	1–500	Syn. act.	Ca2+, ${\text{Ca}}_{\text{ER}}^{2+}$, Ga=ATPext, Gm=Gluext, Sm=IP3	CICR, efflux, influx, IP3-dependent influx, leak from ER into cyt, SERCA, Vm,N-dependent influx	No	No	Iast = c1Ga+c2Gm = Iast,ATP+Iast,Glu, Isyn = (k−cGm)(z−z0)	Synch.
Hayati et al., 2016	1-n/a	Syn. act.	Ca2+, ${\text{Ca}}_{\text{ER}}^{2+}$, Gm, Sm=IP3	CICR, efflux, influx, IP3-dependent influx, leak from ER into cyt, SERCA, Vm,N-dependent influx	No	No	Iast = cGm	Synch.
	1-n/a	Syn. act.	Ca2+, Gm, Sm=IP3	Efflux, influx, IP3-dependent influx, Vm,N-dependent influx	No	No	Isyn = (k−cGm)(z−z0)+c1Gm	Synch.
Mesiti et al., 2015a	1–20	[Ca2+], Vm,N → [IP3]	[Ca2+], [Ca2+]ER, [IP3]	CICR, efflux, influx, IP3-dependent influx, leak from ER into cyt, SERCA	Dcyt: [Ca2+], [IP3]	IP3	Iastro	Ca2+
Postnov et al., 2009	1–10	Syn. act.	Ca2+, ${\text{Ca}}_{\text{ER}}^{2+}$, Ga=ATPext, Gm=Gluext, Sm=IP3	CICR, efflux, influx, IP3-dependent influx, leak from ER into cyt, SERCA, Vm,N-dependent influx	Dext: ATPext, Gluext	Ca2+, IP3	Iast,ATP = cGa, Iast,Glu = cGm	Ca2+
Soleimani et al., 2015	1–24	Syn. act.	Ca2+, ${\text{Ca}}_{\text{ER}}^{2+}$, Gm, Sm=IP3	CICR, efflux, influx, IP3-dependent influx, leak from ER into cyt, SERCA	No	No	Iast	Synch.

This table shows the following: model, number (No.) of astrocytes modeled, input for the astrocytes, astrocytic variables described by differential equations, astrocytic Ca²⁺ fluxes related to cytosolic Ca²⁺, diffusion of astrocytic variables either in the cytosol, ER, or extracellular space, not between these spaces, gap junction signaling (GJ) between astrocytes, output of the astrocytes, and experimentally shown event that the model was finetuned to capture [Ca²⁺ dynamics (Ca²⁺), synchronization (Synch.), information transfer (Inf.), plasticity (Plast.), and hyperexcitability (Hyper.)]. Compartment is cytosol (cyt) if not otherwise stated. Amounts modeled in concentrations are given inside square brackets. Liu and Li (2013b) modeled a triple-neuron feedforward-loop neuronal network. Thalamocortical neural population model was used by Amiri et al. (2012b,c). The presentation of the model by Mesiti et al. (2015a) was confusing. They seemed to present several models but the details were not given clearly. They seemed to have variables that were not used in the equations. Thus, it was difficult to know the actual model components. They simulated their model both with and without diffusion. Amiri et al. (2013a) simulated two models, the one was similar to their earlier neuron-astrocyte synapse model (Amiri et al., 2011b), and thus the details are not given here. Soleimani et al. (2015) and Haghiri et al. (2016, 2017) presented two different models, the other ones were reductions of the main ones. However, the simplified models by Soleimani et al. (2015) and Haghiri et al. (2017) were not detailed enough based on our criteria in section 2.2. Hayati et al. (2016) presented three different models, of which two models were detailed enough. A few models did not detail the mechanisms by which astrocytes communicated with each other (Haghiri et al., 2016, 2017; Hayati et al., 2016; Soleimani et al., 2015), thus it is possible that in some of these models each astrocyte is only connected to neurons (see e.g., Haghiri et al., 2017; Soleimani et al., 2015). $I_{astro}=\mathit{\text{2.11}}\mathcal{H}(\mathit{\text{ln}}(\Delta Ca))ln(\Delta Ca)$, where $\mathcal{H}$ is the heaviside function and ΔCa = [Ca²⁺]−196.69(nM) (Nadkarni and Jung, 2003).

The neuron-astrocyte network models were developed to explain many different biological events as can be seen in Table 5. Examples included Ca²⁺ dynamics, synchronization, information transfer, plasticity, and hyperexcitability. All the other models except the model by Allegrini et al. (2009) had components for all three; CICR, leak from the ER into the cytosol, and the SERCA pump. More than half of the models had influx of Ca²⁺ from outside of the astrocyte and efflux of Ca²⁺ to outside of the astrocyte. About one third of the models took into account gliotransmitter release by modeling extracellular glutamate, and few were also modeling extracellular ATP. Other models used phenomenological transfer functions to relay the effect of gliotransmission to the target synaptic terminal (I_astro, I_syn, part of I_ast, and G_m). None of the studied models had a detailed astrocytic vesicle release model. Most of the models had gap junction signaling for IP₃, and some also for Ca²⁺. Thus, these models had a similar core structure with small variations. As an example, only Yao et al. (2018) modeled buffering as well as astrocytic and extracellular K⁺. Diffusion was taken into account in the models by Allegrini et al. (2009), Postnov et al. (2009), Mesiti et al. (2015a), Yang and Yeo (2015), Li et al. (2016c), and Yao et al. (2018). Yao et al. (2018) presented one of the available models for cortical spreading depression.

One of the first models developed in this category was the two-dimensional model by Postnov et al. (2009). They studied how different lengths of stimulus affected astrocytic Ca²⁺ and showed how short stimulus of less than 100 s did not induce Ca²⁺ wave propagation. However, a longer stimulus of 320 s showed Ca²⁺ wave propagation for a short distance and a stimulus of about 2,000 s showed Ca²⁺ wave propagation along the astrocyte network. They also tested how Ca²⁺ wave propagation was affected by different noise levels added to the model. They found out that the stronger the noise, the more accelerated was the Ca²⁺ wave propagation. With the largest noise level they tested, they found out that the spatially synchronized behavior was destroyed, and the model started to behave irregularly.

A few publications presented simplification of model complexity. Simplification is, in general, used to reduce the model order to allow cost-effective computation yet preserving the major, key dynamical behavior of the model. Soleimani et al. (2015), Haghiri et al. (2016, 2017), and Hayati et al. (2016) presented the original and simplified versions of the earlier published models by Postnov et al. (2007, 2009). However, most of the reduced astrocyte models were not detailed enough based on our criteria in section 2.2. In the future, it is important to put more emphasis on the model order reduction of the complex neuron-astrocyte interaction models to be able to simulate the behavior of large networks biologically more accurately (see e.g., Lehtimäki et al., 2017).

One of the newest models was the model by Chan et al. (2017). Their neuron-astrocyte network model was able to generate ultra-slow neuronal oscillatory activity patterns with frequencies less than 0.01 Hz, recorded by high-density microelectrode arrays and examined using methods reflecting conventional EEG analysis rather than conventional microelectrode array analysis. Their model showed that the frequency of these neuronal oscillations depended on the astrocytic Ca²⁺ oscillations. These astrocytic Ca²⁺ oscillations depended on the properties of IP₃Rs and lasted from a few seconds to minutes. The results of Chan et al. (2017) also suggested that astrocytes preferred asynchronous neuronal firing to synchronous neuronal firing.

3.3. Model evolution

Figure 1 shows how the computational astrocyte and neuron-astrocyte models have evolved from each other (see also, Manninen et al., 2018). We realized that several similar or exactly the same models have been published without clearly explaining the similarity and without including citations to the other, earlier published similar models. This is both negligent and unethical. The very rules of science should be that every publication includes a description of what has been done before and what has been done now on top of the previously published publications. We have tried our best to give here as complete a picture as possible. The starting point of an arrow represents the model which was used as a reference by the latter model indicated as the arrowhead. We minimized the number of arrows so that the minimum number of arrows are pointing to the arrowheads. This means basically that all the previous models in the same chain of arrows might have been used to built the model in the arrowheads, but of course not all of them probably were necessary. Models are excluded from Figure 1 if there was no clear evidence that the authors had used any other models presented in this study as a reference and their model was not used as a reference by any other models presented in this study. The models by De Young and Keizer (1992), Li and Rinzel (1994), and Höfer et al. (2002) were most often used as a starting point when developing new models (Manninen et al., 2018). In addition, the other models that have helped to steer the field are the models by Nadkarni and Jung (2003), Bennett et al. (2005), Volman et al. (2007), De Pittà et al. (2009a), Postnov et al. (2009), and Lallouette et al. (2014).

Figure 1.

Evolution of astrocyte and neuron-astrocyte models published from 1995 to 2017. The starting point of an arrow represents the model which was used as a reference by the latter model indicated as the arrowhead. The number of arrows was minimized so that the minimum number of arrows are pointing to the arrowheads. This means basically that all the previous models in the same chain of arrows might have been used to built the model in the arrowhead, but of course not all of them probably were necessary. With blue, we presented De Young and Keizer (1992) and Li and Rinzel (1994) -type models. With pink, we presented Höfer et al. (2002) -type models. With purple, we presented De Young and Keizer (1992), Li and Rinzel (1994), and Höfer et al. (2002) -type models. All the other types of models appear green.

4. Discussion and conclusions

In this review, we present the state-of-the-art in the computational modeling of astrocytes and the interactions astrocytes have with vascular and neuronal systems. We were delighted to see the number of researchers presently interested in modeling astrocytic functions. Due to the large number of models, we concentrated on about a hundred models that included biophysical descriptions for Ca²⁺ signaling and dynamics in astrocytes. The models were categorized into four groups: single astrocyte models, astrocyte network models, neuron-astrocyte synapse models, and neuron-astrocyte network models. We characterized the components of the models in detail, contrasted and compared the models with one another, and evaluated their usability in future work. Selecting the best models to be utilized in one's own research can be very tedious and time-consuming due to the large number of available models. We therefore wish to provide practical help and guidelines in choosing the proper astrocyte models for future modeling projects. Our work also promotes the transparency of scientific work and recommends actions to establish good practices in computational modeling and the presentation of results.

One of the fundamental questions in neuroscience is how different mechanisms of astrocytes and neuron-astrocyte interactions are linked with cognitive functions and behavior in mammals. A variety of evidence is accumulating on the roles of astrocytes in neuronal excitability, synaptic transmission, plasticity, and in higher cognitive functions, including the initiation, maintenance and consolidation of memories (Volterra et al., 2014; Magistretti and Allaman, 2015; Bazargani and Attwell, 2016). Most of the evidence stems from in vitro experimental studies, but also from in vivo studies. Experimental wet-lab work on astrocytes has given rise to a variety of studies to computationally address astrocytes' Ca²⁺ excitability and its putative role in neural functions in a variety of conditions (Manninen et al., 2018). Although there is partial controversy and ongoing debate on the existence of gliotransmission in vitro and in vivo (see Fiacco and McCarthy, 2018; Savtchouk and Volterra, 2018, and section 2.1.4), recent attempts to model the astrocytes' roles in synaptic and network dynamics are a welcome and useful additional tool to help testing various hypotheses. This is indeed a good sign: astrocytes, the important but mostly neglected glial cells, are gradually being taken into account in efforts to understand the roles of astrocytes in neural network dynamics. Based on our evaluation, we found out that in silico models have been presented for many of the above-mentioned, experimentally observed neural phenomena. However, it was not always clear which of the models were based on cell culture and which ones on slice studies. Very few of the models were constructed using in vivo data. According to our evaluation of 106 models, 53 models were constructed to study Ca²⁺ dynamics and 15 models were constructed to study neural synchronization. In addition, 12 models were used to study information transfer, 11 models were used to study vascular events, 10 models were used to study plasticity, four models were used to study hyperexcitability, and one model was used to study homeostasis. However, the models often described a limited set of molecular mechanisms which sometimes led us to doubt if the models were detailed enough to answer the questions asked.

Even though some promising studies on the modeling of glial functions exist (see e.g., Höfer et al., 2002; Nadkarni et al., 2008; De Pittà et al., 2009a; Lallouette et al., 2014; Taheri et al., 2017), the actual value of the models can only be assessed with time and the reimplementation and resimulation of published models. Astrocytic mechanisms, such as astrocytic Ca²⁺ fluxes related to cytosolic Ca²⁺, diffusion of astrocytic variables either in the cytosol, ER, or extracellular space, and gap junction signaling between astrocytes, were characterized in more detail here than in our other, educational study (Manninen et al., 2018) to facilitate the viewing of the similarities and differences of the models, as well as to support the utilization of the models in future work. In the present study, a careful review of the details of the published models revealed that several publications gave inaccurate descriptions of the models. Examples include misleading or completely missing graphical illustrations of the models, incorrect mathematical equations, biologically incorrectly or sometimes misleadingly named variables, unclear or non-existent statements of the number of cells modeled, and non-existent description of the applicability of the selected model components (see also, Manninen et al., 2018). Moreover, our detailed evaluation revealed that most models were generated making slight variations to a small set of older models that did not originally represent data obtained for astrocytes. However, neither citations to previous models with similar core structure nor explanations about what exactly was added to the previous models were provided. This made it possible, in some cases, to publish the same or a very similar model several times. Very few models provided a detailed sensitivity analysis, that is, an analysis of the robustness of the model against changes in parameter values. We therefore conclude that most of the models published thus far do not serve the scientific community in their best potential and the simulation results of the models are very difficult to reproduce. A proper validation of the simulation results against experimental findings and a careful review process of manuscripts are needed to promote the transparency and utility of in silico models. Large-scale neuroscience projects, such as presented by Markram et al. (2015), Amunts et al. (2016), and Grillner et al. (2016), are seeking to solve these challenges by providing sophisticated informatics tools for the construction, estimation and validation of models.

Our study highlights the need for reproducible research, which is an enormous challenge in all areas of science (Baker, 2016; Munafò et al., 2017; Rougier et al., 2017). In our other studies, we have shown how tedious and difficult it is to reproduce and replicate the simulation results of published astrocyte models (Manninen et al., 2017, 2018). We have shown that it is often impossible to reproduce the results without first carefully assessing and verifying all equations or contacting the authors for more details of the published model. In our previous studies, we have reimplemented altogether seven astrocyte models and were able to reproduce the simulation results of only two of the publications completely, based on the information in the original publications and corrigenda (Manninen et al., 2017, 2018). After fixing the observed errors in the original equations, we were able to reproduce the original results of one more model completely (Manninen et al., 2017). One of the goals of the present study is to show how many similar models have already been developed and how emphasis should be put on making the developed models usable for other researchers by publishing the model codes online. Furthermore, reviewers should be able to verify that the implementation and equations presented in the manuscript match. One solution would be to submit all the details of the model, such as equations, parameter values, initial values, and stimuli, in table format with the manuscript, similarly to what was presented in our previous studies (see e.g., Manninen et al., 2017). It would also be helpful to present the outline of the model in a table (see e.g., Tables 2–5 and Manninen et al., 2010, 2018). Reproducible models can truly advance the computational fields of neuroscience and glioscience.

It seems increasingly evident that astrocytes modulate a variety of events in the brain. Astrocytes are fully integrated into the brain cellular circuitry and are an essential part of the neural networks. Future mathematical and computational models of brain functions should better take into account the hidden capacity of astrocytes and other glial cells, as also pointed out by Sompolinsky (2014), and available methodologies (see e.g., Stiles and Bartol, 2001; Kerr et al., 2008; Skupin et al., 2008; Wils and De Schutter, 2009; Andrews et al., 2010; Oliveira et al., 2010; Hepburn et al., 2012; Tilūnaitė et al., 2017). Such comprehensive models will help us detail the complex interactions between different types of glial cells and other systems in the brain, including the vascular and neuronal systems, and may lead to a better understanding of the roles astrocytes have in the brain. Most urgently, in silico modeling in neuroscience should strive to incorporate state-of-the-art wet-lab data on glial cells to advance the construction and validation of models. In this process, more emphasis should be put on the selection of the animal species, the developmental stage of an organism, and the type of wet-lab preparation. Future work should also include the development of theory, based on constraints of physics and chemistry, to provide a linkage between the phenomena measured at different levels and scales in the brain. In conclusion, the description of the state-of-the-art in neuron-glia modeling and the constructive criticism presented in this work will be useful in setting new goals and guidelines for future modeling in neuroscience.

Author contributions

TM designed the study, acquired the in silico models, characterized and evaluated the models in detail, tabulated the details of the models, drafted the first version of the manuscript, and coordinated the production of the final version. RH contributed to the design of the study, interpreted biological terminology used in in silico models, evaluated some of the models, as well as contributed to the drafting and critical revision of the manuscript. M-LL conceived and designed the study, acquired funding, interpreted concepts in in silico models, contributed to the drafting and critical revision of the manuscript, and supervised the study. All approved the final version of the manuscript.

Conflict of interest statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Glossary

Abbreviations

2-AG

2-arachidonoylglycerol

5-HT

5-hydroxytryptamine

20-HETE

20-hydroxyeicosatetraenoic acid

ΔΨ

Electrochemical gradient

γ

Fraction of ligand-bound mGluRs

ρ

Ratio of bound to total Glu receptors

χ

Depletion of ATP stores

ADP

Adenosine diphosphate

ATP

Adenosine triphosphate

B_i

Immobile buffer concentration

B_m

Mobile buffer concentration

BK

Voltage and Ca²⁺-operated K⁺ channel

c

Constant

c₁

Constant

c₂

Constant

Ca²⁺

Calcium ion

[Ca²⁺]_free

Total free Ca²⁺ concentration

CaPKC

Ca²⁺-PKC complex

CCE

Capacitive Ca²⁺ entry

CICR

Ca²⁺-induced Ca²⁺ release

Cl⁻

Chloride ion

cyt

Cytosol

D_cyt

Diffusion in cyt

D_ER

Diffusion in ER

D_ext

Diffusion in ext

DAG

Diacylglycerol

DIM

Ligand-bound mGluR dimer

E

Fraction of effective synaptic-like micro-vesicles in extrasynaptic space

E₂

Euclidean distance between the stimulating electrode and individual neuron

EAAT

Excitatory amino acid transporter

EET

Epoxyeicosatrienoic acid

ER

Endoplasmic reticulum

ext

Extracellular space (can be also periastrocytic, perisynaptic, extrasynaptic, or perivascular space)

f

Phenomenological variable modeling events from Ca²⁺ rise to vesicle release

f_PKC

Fraction of active PKC

G

G protein

G_a

Astrocytic mediator

G_m

Astrocytic mediator

G6P

GLC 6-phosphate

GABA

Gamma-aminobutyric acid

GAP

Glyceraldehyde 3-phosphate

GJ

Gap junction

GLC

Glucose

Gln

Glutamine

Glu

Glutamate

Gly

Glycogen

h

Active fraction of IP₃Rs (Li and Rinzel, 1994)

H⁺

Hydrogen ion

${\text{HCO}}_3^{-}$

Bicarbonate ion

H-H

Hodgkin-Huxley

Home.

Homeostasis

Hyper.

Hyperexcitability

I_ast

Modulating current from the astrocyte to the neuron

I_ast,ATP

Modulating current from the astrocyte to the neuron

I_ast,Glu

Modulating current from the astrocyte to the neuron

I_astro

Modulating current from the astrocyte to the neuron depending on astrocytic Ca²⁺ (Nadkarni and Jung, 2003)

I_syn

Synaptic current

Inf.

Information transfer

IP₃

Inositol trisphosphate

IP₃R

IP₃ receptor

k

Constant

K⁺

Potassium ion

KCC1

K⁺/Cl⁻ cotransporter

KIR

Inwardly rectifying K⁺- and voltage-gated K⁺ channel

LAC

Lactate

LIF

Leaky integrate-and-fire

mito

Mitochondrial component

m_TRPV

Open probability of TRPV4 channel

MCU

Mitochondrial Ca²⁺ unitransporter

mGluR

Metabotropic Glu receptor

N

Neuron

n_BK

Open BK channel probability

Na⁺

Sodium ion

NADH

Nicotinamide adenine dinucleotide hydrogen

NCX

Na⁺/Ca²⁺ exchanger

NKA

Na⁺/K⁺-ATPase

NKCC1

Na⁺/K⁺/Cl⁻ cotransporter

NMDAR

N-methyl-D-aspartate receptor

NO

Nitric oxide

No.

Number

NT

Neurotransmitter

O₁–O₃

Opening probabilities of three gates related to gliotransmitter release

O₂

Oxygen

O_2,out

O₂ level outside the mitochondrion

ODE

Ordinary differential equation

P

Recovery for K⁺ in cyt

P2XR

Ionotropic purinergic ATP receptor

PCr

Phosphocreatine

PDE

Partial differential equation

PEP

Phosphoenolpyruvate

PIP₂

Phosphatidylinositol 4,5-bisphosphate

PKC

Protein kinace C

Plast.

Plasticity

PLC

Phospholipase C

PLCβ

PLC isotype β

PLCδ

PLC isotype δ

PMCA

Plasma membrane Ca²⁺-ATPase

post

Postsynaptic

ps

Pore-space

PTP

Permeability transition pore

Pyr

Pyruvate

R

Active fraction of IP₃Rs (Höfer et al., 2002)

R₁–R₅

Concentrations of five vesicle states

R_ac

Fraction of IP₃Rs that are not inactivated by Ca²⁺ [marked as h by Liu and Li (2013a) and q by Liu and Li (2013b), and same equation as by Allegrini et al. (2009), modified from Li and Rinzel (1994) and Höfer et al. (2002)]

R_f

Fraction of the readily releasable synaptic-like micro-vesicles inside the astrocyte

R_in

Fraction of IP₃Rs that are not activated by Ca²⁺ [marked as h by (Allegrini et al., 2009) and same equation as by Liu and Li (2013a, b), modified from Li and Rinzel (1994) and Höfer et al. (2002)]

R_inact

Fraction of Ca²⁺-inhibited IP₃Rs (Dupont et al., 2011)

R_k

Recovery for [K⁺]_ext (variable that restores [K⁺]_ext to the normal level)

R_vol/area

Volume-area ratio

RyR

Ryanodine receptor

S_m

Secondary messenger

SDE

Stochastic differential equation

SERCA

Sarco/ER Ca²⁺-ATPase

SIC

NMDAR-dependent slow inward current

SNARE

Soluble N-ethylmaleimide-sensitive factor attachment protein receptor

SOC

Store-operated Ca²⁺ channel

Spon.

Spontaneous

syn

Synaptic cleft

Syn. act.

Synaptic activity

Synch.

Synchronization

TRP

Transient receptor potential channel

TRPV4

TRP vanilloid-related channel 4

UTP

Uridine-5′-triphosphate

V_in

Pulse membrane voltage

V_m

Membrane voltage

Vasc.

Vascular

VGCC

Voltage-gated Ca²⁺ channel

x

Fraction of gliotransmitter resources

y

Fraction of synaptic resources in the active states

z

Synaptic activation variable

z₀

Reference level of z.