Using machine learning techniques to develop forecasting algorithms for postoperative complications: protocol for a retrospective study

Abstract

Introduction

Mortality and morbidity following surgery are pressing public health concerns in the USA. Traditional prediction models for postoperative adverse outcomes demonstrate good discrimination at the population level, but the ability to forecast an individual patient’s trajectory in real time remains poor. We propose to apply machine learning techniques to perioperative time-series data to develop algorithms for predicting adverse perioperative outcomes.

Methods and analysis

This study will include all adult patients who had surgery at our tertiary care hospital over a 4-year period. Patient history, laboratory values, minute-by-minute intraoperative vital signs and medications administered will be extracted from the electronic medical record. Outcomes will include in-hospital mortality, postoperative acute kidney injury and postoperative respiratory failure. Forecasting algorithms for each of these outcomes will be constructed using density-based logistic regression after employing a Nadaraya-Watson kernel density estimator. Time-series variables will be analysed using first and second-order feature extraction, shapelet methods and convolutional neural networks. The algorithms will be validated through measurement of precision and recall.

Ethics and dissemination

This study has been approved by the Human Research Protection Office at Washington University in St Louis. The successful development of these forecasting algorithms will allow perioperative healthcare clinicians to predict more accurately an individual patient’s risk for specific adverse perioperative outcomes in real time. Knowledge of a patient’s dynamic risk profile may allow clinicians to make targeted changes in the care plan that will alter the patient’s outcome trajectory. This hypothesis will be tested in a future randomised controlled trial.

Strengths and limitations of this study.

• Will use modelling techniques that take advantage of the rich time-series data that are available, rather than data from a single time point.

• Will use efficient modelling techniques that can process large amounts of data quickly.

• Will use group-based learning to increase model accuracy by separating groups of patients who likely have different relationship between underlying features and predicted outcomes.

• Dissemination to other healthcare facilities may be limited by the availability of high-quality preoperative and intraoperative input data in a usable format.

Introduction

An estimated 40 million people undergo surgery every year in the USA. Postoperative mortality rate at 1 year for surgical inpatients is between 5% and 10%^{1 2} and an estimated 10% of surgical patients suffer major in-hospital morbidity.^3–8 Perioperative morbidity and mortality are therefore pressing public health concerns. Many patient characteristics, including comorbid medical conditions, associate strongly and independently with perioperative mortality and major morbidity.1 2 9–11 While many of these characteristics are not modifiable, some perioperative risk factors, such as intraoperative blood pressures and anaesthetic concentrations,1 2 9 10 can be modified in real time. Although the association between perioperative variables and postoperative outcomes has been well established at the population level using approaches such as standard logistic regression,1 2 9 10 12 the ability to use deviations in physiological parameters in real time to dynamically forecast the trajectory of each individual patient remains poor.

There is a gap in the field with an opportunity to assess the potential utility of machine learning-based forecasting algorithms to anticipate adverse perioperative outcomes, guide interventions and improve overall quality of care. Standard forecasting models, such as logistic regression, linear regression and other statistical modelling procedures, have long been used to identify and prioritise risk factors for adverse outcomes. Although most of these statistical techniques have been shown to have moderate predictive values, they are limited in their prognostic ability and practical use.1 2 6 9 10 In contrast to standard forecasting models, we have demonstrated machine learning and data mining approaches for patients on intensive care units that generate markedly superior prediction for outcomes such as mortality.¹³ Our methods differ from standard statistical techniques in their ability to effectively incorporate time-series data. Most standard modelling techniques for surgical patients are based on a snapshot scheme, which only considers the data values at a given moment. They are not competent in extracting features from time-series data, especially in real-time fashion, such as temporal trends and shapes. Therefore, the objective of this study is to use machine-learning techniques to build forecasting algorithms that use patient characteristics and high-fidelity intraoperative time-series data to predict adverse perioperative outcomes.

Methods and analysis

Study design

Our central hypothesis is that with sufficient knowledge of patient characteristics coupled with repeated, high-fidelity time-series data from the perioperative electronic medical record, advanced models can be constructed for individual patients that will forecast adverse perioperative outcomes. To test this hypothesis, we will conduct an observational cohort study of adult patients who undergo surgery at Barnes-Jewish Hospital in St Louis, Missouri. First, we plan to develop forecasting algorithms for specific adverse perioperative outcomes using historical data. Next, we plan to validate these algorithms by determining whether they can be used to reliably forecast individual adverse perioperative outcomes.

Patient population and sample size

This study will include all adult patients who had surgery in the 48 operating rooms at Barnes-Jewish Hospital in St Louis, Missouri between 1 June 2012 and 31 August 2016. Patients who receive anaesthesia care in areas outside the main operating rooms, such as the obstetric suite or the outpatient surgery suite, will not be included. Barnes-Jewish Hospital is a 1252-bed academic university-affiliated adult tertiary care hospital, performing approximately 19 000 surgeries a year. We therefore anticipate that gathering data from a 4.25-year period will lead to a total sample size of approximately 80 000–81 000 surgeries for algorithm development and validation.

The Human Research Protection Office at Washington University in St Louis has granted a waiver of informed consent for all subjects enrolled in this study. This study has been determined to involve no more than minimal risk to participants, as no additional data will be collected beyond that already contained in the electronic record. For the same reason, the waiver of consent will not adversely affect the participants’ rights and welfare. It is impracticable to conduct this research without a waiver of consent because 100% participation from the patients is imperative to obtain scientifically sound data.

Data acquisition

For this project, we will use a variety of electronic medical record sources to cover the entire perioperative period. Much of the relevant information will be imported from MetaVision (iMDsoft, Wakefield, Massachusettes), an anaesthesiology information management software system that is the perioperative electronic clinical documentation system currently use by the Department of Anesthesiology. MetaVision captures comprehensive clinical data beginning with the preoperative assessment and continuing throughout the duration of the perioperative period. Information captured preoperatively includes patients’ medical and surgical histories, chronic medical issues, medications used and functional capacity. Intraoperatively, minute-by-minute vital signs are captured, in addition to fluid balances, ventilator parameters and anaesthetic medications administered. Blood pressure measurements are available at intervals ranging from once per min to once every 5 min, while other vital signs are captured once per min. Thus, a 3-hour procedure would have about 180 measurements for each vital sign. All data fields are alphanumeric and are captured in a uniform and granular manner allowing for easy coding and data analysis. Reports from MetaVision are commonly used to support many patient safety and quality improvement initiatives in addition to numerous research studies.

Postoperative outcome data will be obtained from Sunrise Clinical Manager (Allscripts, Chicago, Illinois), the electronic medical record currently used for inpatient care at Barnes-Jewish Hospital. Data will also be obtained from several registries, including the Systematic Assessment and Targeted Improvement of Services Following Yearlong Surgical Outcomes Surveys patient-reported outcomes registry (NCT02032030), the National Surgical Quality Improvement Program database, the Society of Thoracic Surgeons database. Preoperative and postoperative laboratory values will be obtained from the Center for Biomedical Informatics at Washington University, which hosts the data repository where these data are stored once they are processed by the laboratory. In general, a preoperative complete blood count is available if the patient is undergoing major surgery with potential significant blood loss or if other clinical reasons are present. Electrolytes and renal function are available if there is clinical reason to suspect an abnormality (including, but not limited to, patients with hypertension, diabetes mellitus or chronic kidney disease). Additional tests, such as hepatic function and coagulation studies, are available on smaller sets of patients in whom the tests are clinically indicated. A data dictionary has been included (online supplementary tables 1-4) detailing all the data elements that will be captured for this study.

The specific outcomes that will be predicted by the forecasting algorithms will include in-hospital mortality, postoperative acute kidney injury and postoperative respiratory failure. In-hospital mortality will be ascertained from Sunrise Clinical Manager. Postoperative acute renal failure will be defined according to the Kidney Disease: Improving Global Outcomes (KDIGO) criteria¹⁴: an increase in serum creatinine of 0.3 mg/dL, increase in serum creatinine to 1.5 times the baseline value or initiation of renal replacement therapy within 48 hours of surgery end time. Patients receiving renal replacement therapy prior to surgery, patients with no baseline creatinine available within 30 days prior to surgery and patients undergoing kidney transplant or dialysis access procedures will be excluded from analysis of this outcome. Postoperative respiratory failure will be defined as mechanical ventilation for greater than 48 hours or unplanned postoperative intubation within 48 hours. These events will be extracted from clinical documentation recorded by respiratory therapists in Sunrise Clinical Manager. Patients receiving mechanical ventilation prior to surgery will be excluded from analysis of this outcome.

Data analysis, part 1—forecasting algorithm development

We will develop hybrid learning techniques to combine the strength of generative models such as histogram and kernel density estimation and discriminative models such as support vector machines, logistic regressions and kernel machines to improve predictions of adverse perioperative outcomes (in-hospital mortality, postoperative acute renal failure, postoperative respiratory failure). The goal is to deliver superior prediction quality with good interpretability and high computational efficiency that supports fast processing of big data. Based on our preliminary work using density-based logistic regression (DLR) to develop an early clinical deterioration warning system for patients in the general wards of Barnes-Jewish Hospital,^{15 16} we propose to develop novel hybrid data mining/machine learning algorithms that exploit both non-parametric and parametric techniques. For each target outcome, we plan to develop a model that will predict the likelihood of the postoperative outcome in real time using preoperative features and time-series data from the preceding 60 min.

DLR first applies a Nadaraya-Watson kernel density estimator, a non-parametric transformation, on the input data to extract features that conform best to the true distribution of data and then applies the parametric logistic regression model on the transformed features. The resulting model exhibits five desirable properties: non-linear separation ability, high efficiency, good interpretability, ability to handle mixed data types including numerical and categorical ones and support for multiway classification. Our previous results using Barnes-Jewish Hospital clinical data showed that DLR achieves better classification accuracy than state-of-the-art non-linear classifiers such as support vector machines and kernel logistic regression but is also much more efficient than non-linear models.¹⁷ In fact, DLR has the same asymptotic complexity as linear classifiers and can scale up to very large datasets in practice.¹⁷

To analyse the collected time-series data, we need to extract features that capture temporal patterns, such as a rapid temperature increases or abnormal heart rate fluctuations. To make predictions at a given point in time, time-series values from the preceding 60 min will be used. Missing values will be handled using linear interpolation. We will first extract a large pool of time-series features including: first-order features such as variance, skewness and kurtosis, and second-order features such as energy, entropy, correlation, inertia and local homogeneity.^{18 19} The second-order features are known to be robust under noises.^{20 21} Self-similarity is widely observed in human physiological signs. Detrended fluctuation analysis²² measures the degree of self-similarity in time series and has been applied to analyse heartbeat and oxygen levels.²³ Approximate entropy measures the degree of unpredictability in a time series.²⁴ Spectral analysis has also been used to analyse clinical time series.²² We will also consider cross-sign features including correlation,²⁵ coherence,²⁵ lagged regression, non-linear regression¹⁹ and the synchronisation index.²⁶ We will also extract features based on the bag-of-patterns approach^27–29 and autocorrelation.^30–32 In addition, we will also generate features based on shapelets.³³ A shapelet is a subseries that is used to compare against each time series. For a shapelet with length l and a time series T, the shapelet gives a feature value which is the minimum Euclidean distance between the shapelet and any subseries of T with length l. Efficient methods have been developed to find good shapelets, based on length estimation and optimised search.^34–36

We will also develop a novel deep learning method to extract more robust features from time series. A leading method for feature selection from time series has been the shapelet method. However, we have shown that deep learning methods can significantly improve over shapelet. Deep learning methods, especially those using convolutional neural networks (CNNs),³⁷ have achieved great success in learning useful representations (features) from images.^{38 39} However, its uses in time-series classification are very limited. We plan to apply CNNs to time-series data to generate good representations. We note that the convolutional layers in CNNs can be viewed as a collection of local filters over the input space; the filters' weights are learnt through back propagation. The filters in CNNs regulate the time series in different frequency bands and the dot product operations in the CNNs measure distances between two subseries. Thus, CNNs can be viewed as a more general framework than shapelet learning which can adaptively find the suitable down-sampling rates and scales of the shapelets.

Our preliminary work has shown that it is beneficial to use a large feature set: the modelling accuracy increases as more features are used and the top features in the final model include features from different categories.²³ With the above features, we will address overfitting. An overfit model will generally have poor predictive performance and interpretability. We will investigate three schemes to avoid overfitting including: (1) using feature selection methods, such as forward feature selection based on F-score or area under curve score,⁴⁰ to find the most discriminative features; (2) adding regularisation terms (such as L1,⁴¹ L2,⁴² Akaike information criterion, Bayesian information criterion,⁴³ minimum description length⁴⁴ or a probabilistic prior) to the optimisation objective and (3) using metatechniques such as bootstrap aggregation⁴⁵ and exploratory undersampling⁴⁶ to further address overfitting and class imbalance.

We plan to use bin-based kernel density estimation, another non-parametric technique, to process the input features in each dimension. In previously described DLR, we use the Nadaraya-Watson kernel density estimator for each data point in each dimension, which has time complexity of O(mN²) where m is the number of dimensions and N is the number of data points. Therefore, it is still slow for big datasets with a large N. Bin-based kernel density estimation differs from the Nadaraya-Watson kernel density estimator in that we divide each dimension into equal-sized bins and estimate the density for each bin instead of each data point. This will reduce the time into O(mB²) where B<<N is the number of bins. Note that instead of using a simple histogram count for each bin, we will use a Gaussian kernel function to smooth the density estimation across bins. The time complexity can be further reduced to O(mB) using techniques such as Gauss transformation.⁴⁷ Such dramatic reduction of computing time will enable us to process large datasets and perform quick model building. We will also combine the kernel density estimator-based features with other parametric models such as Cox regression.

We will leverage a hierarchical optimisation algorithm for training DLR,¹⁷ which automatically learns free parameters in the model under a maximum likelihood framework. This optimisation formulation learns the coefficients in the model and provides a way to automatically select the kernel bandwidth in the Nadaraya-Watson estimator or the bin size in the bin-based kernel density estimation, which is absent in previous work. We will also employ techniques including stochastic gradient descent⁴⁸ and its parallelised implementation⁴⁹ to further enhance the scalability of the training algorithm.

Our algorithm will use group-based modelling. The idea is to first use a few key features to divide the patients into some major categories, and then train a separate classifier for each category. The intuition is that from clinical knowledge, we know that some different groups of patients have drastically different behaviours and should correspond to different statistical models. Mixing such vastly different groups together to train a single model may not give the best result. Therefore, it is instrumental to identify important subpopulations of patients before we use sophisticated hybrid algorithms to accurately model the patients in each group. For a simple example, we can group the patients into a few age ranges, for example, <45, 45–55, 56–65 and so on. Although age can be used as a feature in a single classifier for all patients, such explicit division leads to multiple, more specific classifiers. It can be viewed as a hybrid algorithm combining a decision tree with other classifiers. We may also use metrics defined on multiple attributes to group the patients. Features that will be used as classifiers will include age, sex and surgery type (cardiac vs non-cardiac). To systematically integrate such clinical knowledge into modelling, we plan to study hybrid models that are mixture of two or more classifiers. For example, we can construct a global decision tree whose nodes denote patient groups, where each group is modelled by a local classifier such as DLR. Different nodes may use different types of classifiers. Previous work on a similar idea has demonstrated improved performance⁵⁰ in an intensive care prognosis application.

Data analysis, part 2—forecasting algorithm validation

After algorithm development, the forecasting algorithms will be tested for accuracy of their predictive performances in two ways. First, algorithm validity will be tested within the historical database by dividing the database into training, validation and testing datasets. Second, the performance of the developed algorithms will be additionally validated prospectively (out-of-sample performance), using precision and recall.

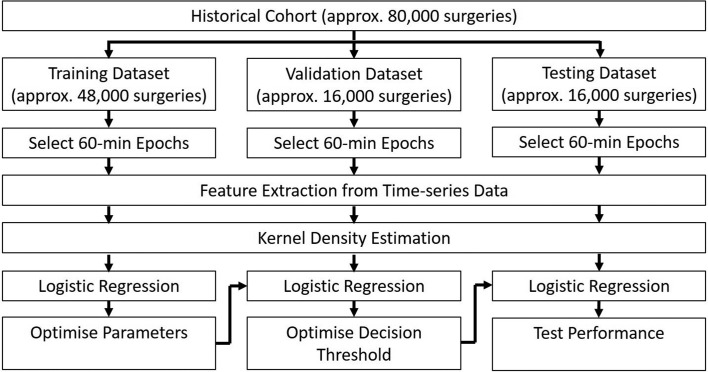
For initial model training and validation, the historical database will be divided into a training dataset (60% of the database), a validation dataset (20% of the database) and a testing dataset (20% of the database). Each training, validation or testing example will be a 60 min epoch randomly selected from a single surgery. More than one epoch from the same surgery may be included if the surgery lasted long enough to generate more than one distinct 60 min epoch. However, all epochs from the same surgery will be included either all in the training dataset, all in the validation dataset or all in the testing dataset. Because we expect that our target outcomes will be relatively rare events, overall classification accuracy is not likely to be a useful measure of model performance. Instead, we will use precision (true positives/(true positives+false positives)) and recall (true positives/(true positives+false negatives)). We will optimise model parameters using the training dataset. Then we will prespecify our desired recall and use the validation dataset to select the decision threshold that leads to the highest precision without sacrificing our desired recall. Then we will apply our model to the testing dataset and report the observed precision and recall. The overall flow of algorithm training and validation is outlined in figure 1.

Figure 1.

Data flow for algorithm training and validation using the historical database.

Additionally, we propose to perform a validation test of the predictive performance of the developed algorithms prospectively, using patient records that did not belong to the learning database. For this evaluation, we will apply our model to the prospectively collected data. We will report the observed precision and recall as measures of model performance.

Prespecified secondary analyses

In addition to the primary algorithms described above (in-hospital mortality, postoperative acute kidney injury and postoperative respiratory failure), we anticipate using the acquired data to develop prediction algorithms for additional outcomes. These outcomes are outlined in table 1.

Table 1.

Prespecified secondary outcomes

Data source	Outcome
Sunrise clinical manager	30-day hospital readmission Intensive care unit admission Postoperative delirium
NSQIP database	30-day mortality 30-day hospital readmission Unplanned intubation Postoperative sepsis Postoperative myocardial infarction Postoperative cerebrovascular accident Postoperative pulmonary embolism Postoperative deep vein thrombosis Postoperative cardiac arrest requiring cardiopulmonary resuscitation
Society of thoracic surgeons database	30-day mortality 30-day hospital readmission Postoperative atrial fibrillation Postoperative venous thromboembolism Postoperative acute respiratory distress syndrome
SATISFY-SOS registry	Patient-reported 30-day readmission Patient-reported postoperative myocardial infarction Patient-reported postoperative cardiac arrest Patient-reported postoperative heart failure Patient-reported postoperative cerebrovascular accident Patient-reported postoperative venous thromboembolism Patient-reported postoperative respiratory arrest Patient-reported postoperative pneumonia Patient-reported severe postoperative pain lasting greater than 1 day Patient-reported severe postoperative nausea and vomiting lasting greater than 1 day Return to work 30 days after surgery Quality of life 30 days after surgery Ability to perform activities of daily living 30 days after surgery

NSQIP, National Surgical Quality Improvement Program; SATISFY-SOS, Systematic Assessment and Targeted Improvement of Services Following Yearlong Surgical Outcomes Surveys.

Discussion

Implications and future directions

We anticipate that the successful development of machine learning-based algorithms for predicting adverse postoperative outcomes will impact the perioperative care of surgical patients in important ways. Because our algorithms will use time-series data, we expect to be able to use them in real time to provide perioperative healthcare clinicians with dynamic predictions of their patients’ risks for specific adverse outcomes. Because the features in our models will include modifiable risk factors such as blood pressure and concentrations of anaesthetic agents, we believe clinicians will be able to make changes that may alter their patients’ risk trajectories. The models may also help clinicians make decisions regarding their patients’ postoperative disposition (intensive care unit vs hospital ward; inpatient admission vs discharge). To be feasible and efficient, we suggest that the forecasting algorithms could be incorporated into a telemedicine paradigm, such as an anaesthesiology control tower for a perioperative suite. Once the forecasting algorithms are developed, we intend to conduct a randomised controlled trial to investigate whether implementation of the algorithms in the operating rooms leads to a reduction in the incidence of adverse postoperative outcomes. The incorporation of machine-learning forecasting algorithms into perioperative care will complement the expertise of clinicians and has the potential to increase both safety and efficiency.

Strengths and limitations

One of the greatest strengths of this project is the novel use of machine learning techniques to harness the abundant data in the perioperative electronic medical record. Unlike traditional risk prediction models, which use data from a single time point and therefore incorporate only a small fraction of the available information about the patient, our algorithms will take advantage of the rich time-series data generated in the operating rooms and, more broadly, in perioperative settings (eg, preoperative assessment clinic, postoperative recovery area). Another strength is the efficiency of the proposed modelling techniques, which will need to quickly process large amounts of data. The use of group-based learning will increase the accuracy of the derived models by separating groups of patients who likely have different relationships between underlying features and the predicted outcomes.

This project does have limitations that should be noted. Because the forecasting algorithms will use large quantities of data, generalisability of the results and implementation of the algorithms at other healthcare facilities will depend on the availability of high-quality input data. In particular, the preoperative evaluation and medical history may not be documented in an electronic format with discrete analysable fields at some other institutions. Even when such data are available, differences in formatting will require caution during implementation at other hospitals.

Ethics and dissemination

Once the investigation has been completed, we intend to publish the results in a peer-reviewed publication. We also intend to present the results of this work at professional conferences for both the anaesthesiology and computer science communities. In accordance with the recent proposal from the International Committee of Medical Journal Editors, patient-level data will be made available within 6 months after publication of the primary manuscript.⁵¹ Data will be provided to researchers who submit a methodologically sound research proposal including a protocol and statistical analysis plan. No patient-identifying fields (including dates) will be included in the shared dataset. Age will be provided in years, unless the patient is older than 89 years. In this case, age will be reported as ‘>89 years.’ Any dates will be presented as ‘number of days since index surgery.’