Significance
The ubiquity of scale-free mobility in nature, as observed in systems ranging from microorganisms to fishing boats, has stimulated a number of foraging theories and individual-based random search models. Here, we unveil an essential yet unexplored property of multiple-scale motion, which relates to the stability of entire populations. We use Lotka–Volterra models to predict that foragers diffusing normally tend to go extinct in fragile fragmented ecosystems, whereas their populations become resilient to degraded conditions and have maximized abundances when individuals perform scale-free Lévy flights. Our analytical and simulated results shift the scope of multiple-scale foraging from the individual level to the scales of collective phenomena that are of primary interest in conservation biology.
Keywords: Lotka–Volterra, foraging, Lévy flights, ecological modeling, metapopulations
Abstract
Multiple-scale mobility is ubiquitous in nature and has become instrumental for understanding and modeling animal foraging behavior. However, the impact of individual movements on the long-term stability of populations remains largely unexplored. We analyze deterministic and stochastic Lotka–Volterra systems, where mobile predators consume scarce resources (prey) confined in patches. In fragile systems (that is, those unfavorable to species coexistence), the predator species has a maximized abundance and is resilient to degraded prey conditions when individual mobility is multiple scaled. Within the Lévy flight model, highly superdiffusive foragers rarely encounter prey patches and go extinct, whereas normally diffusing foragers tend to proliferate within patches, causing extinctions by overexploitation. Lévy flights of intermediate index allow a sustainable balance between patch exploitation and regeneration over wide ranges of demographic rates. Our analytical and simulated results can explain field observations and suggest that scale-free random movements are an important mechanism by which entire populations adapt to scarcity in fragmented ecosystems.
Species extinction, population loss, and biodiversity decline represent real dangers for the continuity of life on earth (1). Current extinction rates are several orders of magnitude above normal background rates (2–4). Halting and reversing this trend are formidable challenges that require a better understanding of how ecosystems operate and where interdisciplinary approaches can play an essential role. Over the years, physical and mathematical concepts have provided valuable tools for studying a range of ecological phenomena, such as nonlinear and chaotic dynamics in population biology (5), nonequilibrium phase transitions (6), or the structure and resilience of ecological networks (7).
Fragile ecosystems are often fragmented, namely composed of populations separated in space, either because of a natural tendency of individuals to aggregate in patches or because of human perturbations (8–10). Within small areas, populations are more exposed to local extinctions due to demographic stochasticity or when the growth of an invasive species leads to the overexploitation of slowly recovering resources (11–13). In systems of fragments (metapopulations), the ability of the organisms to move from one fragment to another has been identified as a crucial stabilizing factor that can prevent irreversible decline (8, 14, 15).
Interacting species in uniform (16–20) or fragmented (6, 13, 21) landscapes have been extensively explored with Lotka–Volterra (LV) models, a paradigmatic framework in population dynamics (22–25). Individual mobility is a key aspect in this approach, and it is usually modeled by standard random walks without long-range displacements (but see ref. 26). In recent years, thanks to the improvement of tracking devices, data analyses have yet revealed that single-animal trajectories often contain multiple characteristic scales, calling for new theories of mobility beyond simple diffusion (27–31).
A body of observations in a variety of animal taxa has reported evidence of mobility patterns well-described by Lévy flights or Lévy walks, two parsimonious multiple-scale diffusion models involving essentially one parameter (32–42). A widely discussed interpretation of such movements relies on the efficiency of random search strategies in unpredictable environments, when prey are scarce and distributed in patches (32, 43, 44). For a predator having no information on prey locations, the rate of prey capture can be maximized by performing Lévy walks with exponent , a value often observed in the field (33, 34, 37, 39). From a more general point of view, foraging success under environmental uncertainty can be a generative mechanism of multiscale movement, allowing information gathering and optimal exploratory behavior (45). Some studies have also examined multiscale movements as being emergent from interactions between a forager and heterogeneities in the environment (35, 46).
The consequences of Lévy mobility on collective properties in systems of interacting individuals remain elusive (47). A distinction exists a priori between the reproductive interest of an individual and the survival of entire populations, referred to as “organic” and “biotic” adaptations, respectively, in ref. 48. Following the latter viewpoint, we address here how multiple-scale foraging allows populations to respond to changes in resource availability. Notably, Lévy walks were shown to be evolutionary stable in mussels colonies by achieving a compromise between reducing the risk of predation and minimizing intraspecific competition for food (40). In ants, individual variability in searching behaviors across scales can provide to the colony a functional advantage for foraging compared with colonies containing different behavioral stereotypes, like single-scale foragers (49). In some cases, a seemingly optimal individual foraging strategy may lead to severe resource depletion due to feedback effects (50, 51). The movement strategies considered as efficient for an individual immersed in a sea of static prey (a common theoretical setting) need to be reexamined for large populations and longer timescales.
Here, we show by means of previously unexplored analytical arguments and computer simulations that multiscaled random walks have a significant impact on the stability of metapopulations close to extinction thresholds. We consider both deterministic and stochastic lattice LV models (18–20), where the resources are fragmented into areas distant from each other and predators can perform Lévy flights instead of nearest neighbor (NN) random walks.
Analytical Population Model in Patchy Landscapes
We start with a solvable rate equation model defined on a 2D space, where prey are restricted to occupy patches and predators diffuse according to a power law mobility kernel. Space is made of a regular lattice of square cells, each of length . Some cells can contain prey and thus, represent “patches” of area . These patches form a periodic square array for simplicity, the separation distance between neighboring patches being , where is an integer. No prey can be present outside of the patches. The predator and prey densities in cell at time , where , are denoted as and , respectively. Outside the prey patches, , but can be. Assuming that occupied cells contain many individuals and fluctuations are negligible, we write the LV equations (20)
| [1] |
| [2] |
where , , , and are the predator movement, reproduction, mortality, and predation rates, respectively. is the patch carrying capacity, and is the prey reproduction rate. SI Text has more details. The cell-to-cell predator jump distribution is given for simplicity by the product of two 1D scale-free distributions with integer argument and exponent :
| [3] |
where , for , is the normalization constant, and or is the Kronecker symbol. We use the product of two power laws because of the lattice symmetry, but other choices lead to similar results (see below). The foragers are normally diffusive (Brownian) for and superdiffusive (Lévy) for . In the case of , extremely long steps are taken, equivalent in practice to random relocations in space. Large displacements are not penalized by any time cost. SI Text discusses the biological relevance and limitations of this latter assumption.
The quantity represents the probability that a predator remains in the same cell after a movement step, when the latter is too small to bring the predator outside its current cell. Approximate arguments allow us to relate to the patch size: one assumes that predators actually perform continuous steps, inside or across patches, of minimal length , which is set to unity in the following. For patches with , one obtains (SI Text).
In the absence of movement ( or ), the prey and predator abundances are zero at large times everywhere except in prey cells, where Eqs. 1 and 2 reduce to two ordinary differential equations for a single patch. They admit two simple stationary fixed points, and , corresponding to total extinction (by overexploitation) and predator extinction (by underexploitation), respectively. A third globally stable coexistence fixed point exists for (20):
| [4] |
and . If , predators go extinct, and . Oscillatory solutions do not exist (20).
With mobile individuals (), the cells are no longer isolated. A quantity of particular interest in this case is the spatially averaged number of predators per unit area: . We look for nonzero stationary solutions of Eqs. 1 and 2. The steady-state takes the form (SI Text)
| [5] |
with being the predator density in the prey patches:
| [6] |
where is the Fourier transform of and is the first Brillouin zone defined by .
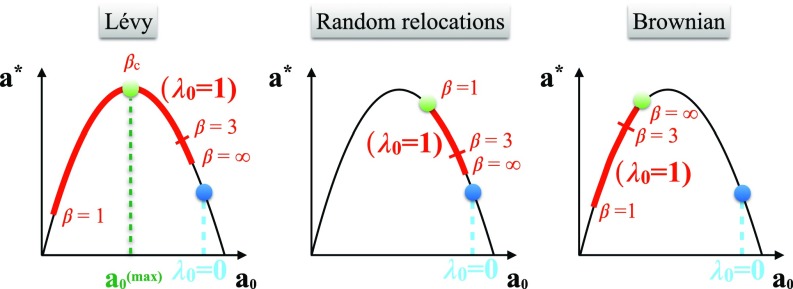
Notably, in Eq. 5, the mean predator density for the whole system obeys a logistic relation with respect to , the predator density in one prey patch (Fig. 1). Thus, is maximal when and vanishes at and . [At and above, the only acceptable stationary solution is .] In the low-density regime, , predators underexploit prey: any increase in produces an increase of . Whereas at high density, , foragers overexploit the patches: any increase in decreases the total abundance. The demographic parameters being fixed, the largest is always obtained in the absence of movement (). Therefore, some amount of movement will be beneficial (increase ) if is located in the overexploitation regime, , implying that . We set this condition in the following, as it is relevant to fragile systems.
Fig. 1.
When immobile predators () overexploit prey patches [], incorporating mobility () usually increases the total predator abundance . The strategy maximizing (green circle) can be Lévy, random, or Brownian. The Lévy strategy is an advantageous response in the most fragile systems, since there, may otherwise reach low values from two sides. For , the foragers practically perform NN random walks ( limit), and varies little.
We define the optimal movement strategy as the one maximizing the predator abundance . Keeping all of the parameters fixed except , the density given by Eq. 6 can be varied, giving rise to three possibilities. (i) for an exponent , such that (Fig. 1, Left) (where without loss of generality). The value satisfies
| [7] |
with and . Recall that the dependence in is contained in the term . (ii) If Eq. 7 does not admit any solutions in the interval , may still reach a maximum for the lowest possible value , the movement mode that less overexploits resources (Fig. 1, Center). (iii) In the third case (Fig. 1, Right), Brownian movement () provides the optimal strategy, namely the best way of exploiting in conditions of underexploitation.
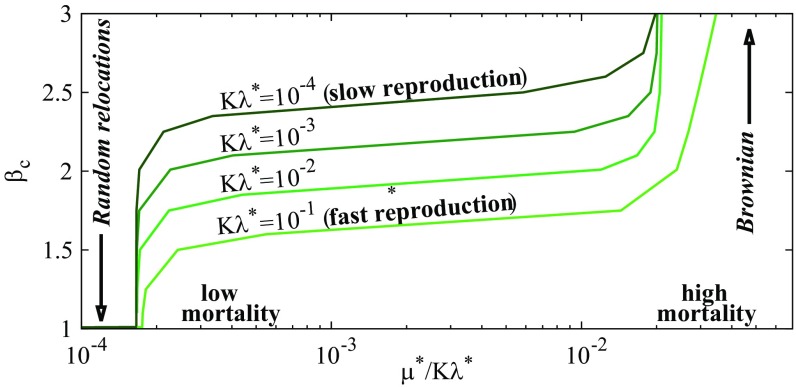
We explore a realistic ecological situation, where predators are mobile, slowly reproducing, and long lived (i.e., ; note that all of the demographic rates may be scaled by the movement scale ). For an environment of low patch density, Fig. 2 shows that the optimal obtained from solving Eq. 7 can be in the Lévy range and depends little on and over wide intervals. For a fixed predator reproduction rate , the strategy leading to the largest rapidly switches to Brownian or to random relocations at very high and low , respectively: high predator mortality rates reduce prey overexploitation and promote Brownian strategies (predators stay close to the prey patch where they were born). Random relocations, in contrast, allow patch regeneration if predators are long lived. Similarly, low values of the predator reproduction rate reduce the predation pressure and slowly move upward toward Brownian motion. In the following, we drop the superscript ∗ and set the movement rate to .
Fig. 2.
Lévy exponent maximizing predator abundance as a function of the reduced mortality rate for various reproduction rates as given by Eq. 7. , and the patch volume fraction is 0.04 (). At very large (low) , the optimal strategy is Brownian (with random relocations or , respectively). Fast (slow) predator reproduction favors more (less) superdiffusive strategies.
Stochastic Lattice LV Model
The foregoing analytical results show the importance of Lévy movements at the population level. What is more, Fig. 1, Left allows us to clarify the notion of “fragility” from a movement ecology point of view: a system is most fragile when markedly different ranging modes (here, or ) bring the system close to distinct zero-abundance fixed points [ and above]. We focus below on this generic situation and proceed to verify our predictions with simulations in a few representative numerical examples. We also incorporate the effects of fluctuations in the description by building a stochastic model inspired in ref. 20.
Rules.
Space is a 2D lattice of sites of unit area with periodic boundary conditions. Each site can be empty (), with a predator (), with a predator reproducing (), or with a prey (). Double occupation of a site is forbidden (except for the reproductive state). The prey is confined to limited areas: circular patches of radius are randomly distributed, inside which the sites are initially set to state . (We choose , so that patches have the same area as in the analytical model.) Prey cannot occupy sites that are outside the patches. Monte Carlo simulations are performed over many landscapes with initial predators (other numbers do not affect the results).
At each elementary step, an occupied site is chosen randomly and updated as follows:
-
Predator death. If a predator is selected, it dies with probability .
-
Predator movement and reproduction. A selected surviving predator randomly chooses a site at a distance , where is drawn from a power law distribution , with as an exponent and as the normalization constant. If another predator is present at the new position, the selected predator does not move; otherwise, it occupies the new site (only one predator moves at a time). If a prey is present there, the predator eats it and reproduces.
-
Prey reproduction. If a prey is selected, one of its NN sites (within the patch) is chosen randomly. If that site is empty, a prey offspring is produced there with probability . In other cases, nothing happens.
In these rules, , and . In the stochastic lattice Lotka–Volterra model (SLLVM) of ref. 20, all agents were mobile with NN hopping, and the carrying capacity was uniform. Here, prey are static, and for the sites belonging to the patches ( elsewhere). The fraction of area covered by the patches is ( in the analytic model). A mean field (MF) solution of our SLLVM can be obtained when the predators are well-mixed in the system (i.e., in the random relocations regime or close to one). Neglecting spatiotemporal fluctuations, we show in SI Text that the predator abundance is given by Eq. 4 but with substituted by .
We consider two scenarios. In the first one, prey are scarce, and , such that predators go extinct in the above MF approximation (i.e., ). Given a predator mortality rate , we choose , which is achieved by setting the patch radius to
| [8] |
where is fixed. In the second scenario, the predator mortality rate is held fixed, and prey abundance varied through the parameters and .
Results.
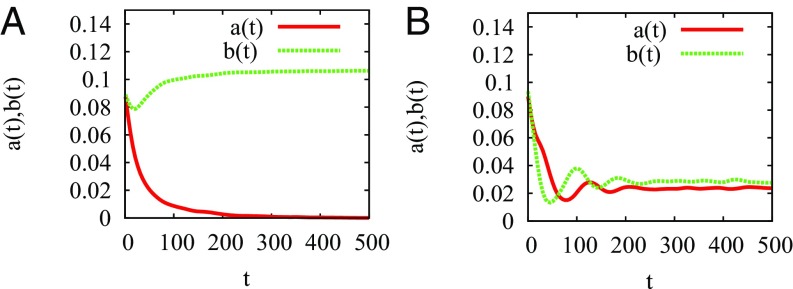
Highly superdiffusive predators () randomly sample space and therefore, poorly exploit the patches. In the first scenario, their spatially average density is zero at large time as expected from the MF analysis, whereas prey reach their maximum capacity in the patches (Fig. 3A). This situation corresponds to extinction by underexploitation (Movie S1). With the same parameter values but Brownian mobility (), in contrast, long-lived quasistationary states of predator–prey coexistence settle (Fig. 3B). Predator populations concentrate in the patches as shown in a typical configuration (Fig. 4A): due to its slow diffusion, a Brownian predator located in a patch has a high probability to stay in its vicinity before dying, like its offspring.
Fig. 3.
Evolution of the spatially averaged densities and toward quasistationary states for a single run in the case of (A) highly superdiffusive () and (B) Brownian predators; the other parameters are , , , and . A Monte Carlo time step corresponds to selecting all individuals once on average.
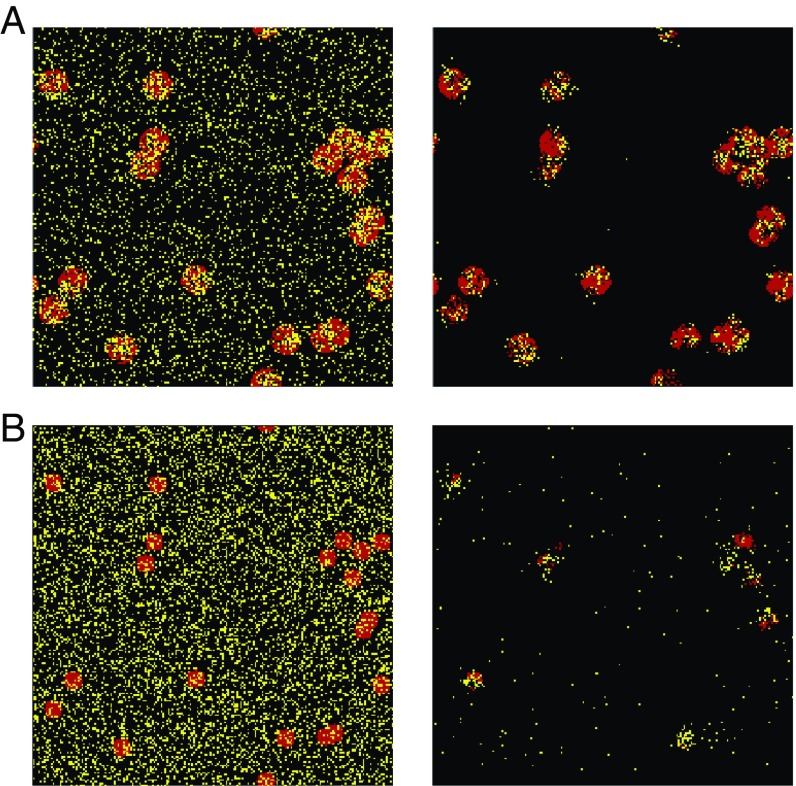
Fig. 4.
Initial (Left) and large (Right) time configurations of a metapopulation of Brownian predators (yellow dots) and randomly placed prey patches (prey are in red). (A) Same parameters as in Fig. 3B (survival); (B) and smaller patch radii (global extinction by overexploitation) (Movie S2). The patches in the cases in A and B have the same locations for easier comparison. .
The foregoing results suggest that Brownian motion in scarce and patchy environments stabilizes coexistence compared with the MF expectation. However, such systems are not necessarily resilient in front of less favorable conditions. Fig. 4B illustrates a configuration where the predator mortality rate and the patch radius , given by Eq. 8, are lower than in Fig. 4A. Predators live longer and their number rapidly grows inside the patches, not letting the time for the prey to regenerate (Movie S2). The patches are thus overexploited and irreversibly disappear after some unfavorable fluctuation (the empty patch is an absorbing state for the prey). Since the predators are left with no surrounding resources, they also go extinct. Fig. 5, Upper shows that the average large time density of normally diffusive predators (regime ) declines as decreases and even vanishes when becomes too small. This important cause of extinction is not predicted by the analytic theory, which neglects temporal fluctuations.
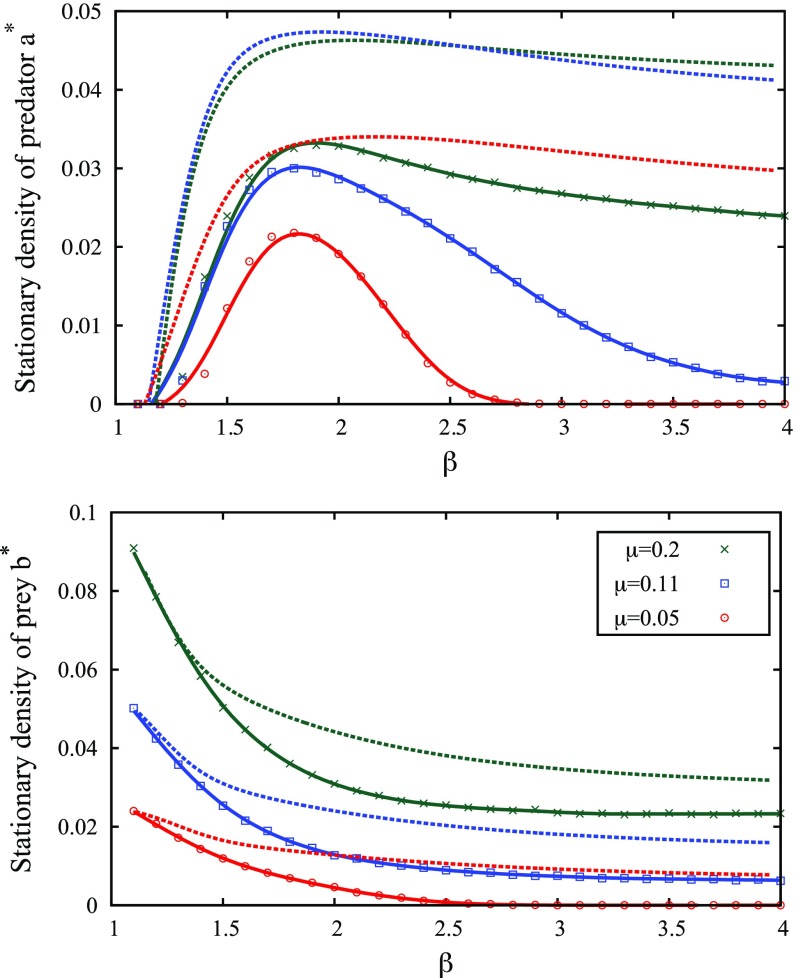
Fig. 5.
(Upper) Average predator density after Monte Carlo steps as a function of and for three values of the mortality rate in the first scenario (solid lines with symbols). , and the other parameters are the same as those in Fig. 3. At low (open red circles), is nonzero only in a relatively narrow region centered around . Dashed lines show the corresponding analytical calculations (Eqs. 5 and 6). (Lower) Average prey density obtained with the same parameters. SI Text has more details.
Fig. 5, Upper shows that predators maximize their abundance when performing Lévy flights with a particular exponent value given by , with all of the other parameters being fixed (first scenario) (Movie S3). The location of the maximum depends little on the mortality rate as expected from the “flat” aspect of the theoretical curves of Fig. 2. In addition, less favorable conditions (lower mortality rate and smaller patches) mildly affect the average number of predators in the system when is around or below. In the Brownian case (), however, the same changes cause dramatic population declines as mentioned above. The predator population is not only maximal at but also persists if conditions are altered, a feature that ref. 52 calls structural stability (the meaning of “resilience” here). The movement strategy becomes crucial for the most fragile ecosystems (smallest values of in Fig. 5, Upper): predators face extinction due to underexploitation or overexploitation depending on , two situations that are avoided by adopting intermediate Lévy flight strategies in a relatively narrow range around . In such situations, Lévy flights achieve a sustainable balance between exploitation and exploration and are advantageous for stability and resilience.
As shown in Fig. 5, abundances and given by the analytic theory (Fig. 5, dashed lines) are in qualitative agreement with simulations. There are no adjustable parameters. Note, however, that theory significantly overestimates and , which do not vanish in the Brownian/low-mortality regime. This is because local extinctions in the SLLVM are driven by fluctuations in finite size patches (where is an absorbing state), whereas noise is absent in the deterministic LV approach. Although less pronounced, the maximum of predicted by theory is in good agreement with simulations: from Eq. 7, we find (), (), and ().
Fig. 5, Lower displays the corresponding prey densities. Unlike , decays monotonically with and is practically constant for . Fig. 5 illustrates the aforementioned resilience of predator populations with respect to changes in prey abundance: at , the prey population decays by a factor of two due to the change , whereas the predator population varies by less than , therefore exhibiting a remarkable collective adaptation to the scarcer environment. Comparatively, for the same perturbation at , where the number of prey is reduced by a factor of about three, the predator population is divided by eight.
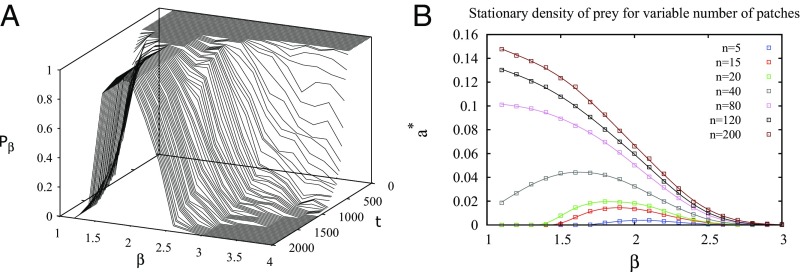
Another useful quantity in population dynamics is the joint survival probability, the probability that at least one individual of each species is alive at time , which is denoted as . It is depicted in Fig. 6A. The parameters in this example are chosen such that the system is subject to particularly unfavorable conditions for prey survival: small patches, low predator mortality rate, and a lower prey recovering rate than in Fig. 5. At large times, only a narrow range of value of around exhibits two-species coexistence ().
Fig. 6.
(A) Evolution of the joint survival probability up to in unfavorable ecological conditions (, , , , given by Eq. 8). At large times, values of larger than 2.3 and lower than 1.5 result in a survival probability smaller than 0.5 due to overexploitation and underexploitation, respectively. (B) Predator density as a function of the scaling exponent at fixed mortality rate () and patch radius () for different numbers of patches (). Eq. 7 predicts without any adjustable parameters maximum values at , , and for , and , respectively, close to the simulation results (, , and ).
We next vary the resource availability by means of the patch density or , keeping and fixed (scenario 2). When the mortality rate is low and prey is abundant ( in Fig. 6B), one could expect the predator abundance to be high, close to the MF fixed point , and to depend little on the movement strategy. However, Fig. 6B shows an example where no populations survive in the Brownian regime, while is nonvanishing in the Lévy range.
The exponent that maximizes the predator population depends on the patch density. At small patch numbers, is in the vicinity of two in this example, and predators do not survive if they perform other types of movements. As the patch density increases, the range of values of allowing predator survival increases, and the optimal moves to the left until reaching unity. Importantly, the analytic expression [7] predicts this decrease of with patch density (see caption of Fig. 6B). These results indicate that, at low mortality, foraging strategies can be more flexible when resources are abundant as long as predators avoid Brownian strategies. This fact could have profound evolutionary consequences.
Discussion
In summary, population models with LV interactions reveal that the stochastic movement strategies adopted by individuals searching for scarce resources have important consequences on the evolution of systems near extinction thresholds. These collective aspects cannot be directly inferred from single-forager random search models, which have been extensively studied (30, 32, 43, 44, 53). When resources are fragmented and regenerate slowly, predator metapopulations can avoid extinctions and maximize their abundance by means of Lévy flights. For a wide range of demographic parameters (Fig. 2), the multiple-scale structure of Lévy mobility allows both local exploitation and long-range exploratory relocations that reduce the predation pressure on depleted zones. Lévy populations are also resilient: a reduction of resources mildly affects their abundances, whereas it can produces rapid declines or extinctions when monoscaled (standard) random walk displacements are used. In some cases, the range of random strategies allowing long-lived coexistence states becomes very narrow around the Lévy exponent as the patch density decreases.
Step length distributions with exponents around two have been reported in many animal species (33, 34, 37) and also, hunter-gatherers (38) or fishing boats (54). Our approach is useful for understanding aspects of human–environment interactions, such as the multiple-scale displacements of fishing boats on the open ocean, where fish density is patchy and highly nonuniform (55). These movements may result in a sustainable exploitation of fragile resources by giving profitable zones time to regenerate. Similar considerations apply to the nomadic hunter-gatherers discussed in ref. 38 who lived in resource-scarce lands. Future tests of our theory could also be performed in controlled laboratory experiments with microorganisms, like dinoflagellates, which are predators known to exhibit Lévy patterns with exponent at low prey concentrations (33).
More generally, our results establish a connection between random search problems and the theory of metapopulations (8), where a set of populations isolated in space becomes stabilized by fluxes between them. Lévy random motion effectively allows individuals born in a patch to visit other patches during their lifespan, as also suggested in ref. 15. In a similar vein, power law dispersal is known to increase asynchrony in metapopulations with cyclic Rosenzweig–MacArthur or LV dynamics, making them less vulnerable (56). Additional developments to many-species systems with realistic networks of trophic interactions (57) and including heterogeneous patch size distributions are needed to study the effects of scale-free mobility on stability, sustainability, and diversity.
Our scope extends the notion of optimality in foraging by investigating the movement strategies that bring populations away from extinction thresholds. This is an essential step for developing movement-based ecological theories and concepts that could impact urgent problems in conservation biology.
Supplementary Material
Acknowledgments
We thank M. Benitez for fruitful discussions. This work was supported by Programa de Apoyo a Proyectos de Investigación e Innovación Tecnológica Grant IN105015 and Instituto de Física (Universidad Nacional Autónoma de México).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1719889115/-/DCSupplemental.
References
- 1.Valiente-Banuet A, et al. Beyond species loss: The extinction of ecological interactions in a changing world. Funct Ecol. 2015;29:299–307. [Google Scholar]
- 2.Pimm S, Raven P, Peterson A, Sekercioglu CH, Ehrlich PR. Human impacts on the rates of recent, present, and future bird extinctions. Proc Natl Acad Sci USA. 2006;103:10941–10946. doi: 10.1073/pnas.0604181103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Barnosky AD, et al. Has the earth’s sixth mass extinction already arrived? Nature. 2011;471:51–57. doi: 10.1038/nature09678. [DOI] [PubMed] [Google Scholar]
- 4.De Vos JM, Joppa LN, Gittleman JL, Stephens PR, Pimm SL. Estimating the normal background rate of species extinction. Conserv Biol. 2015;29:452–462. doi: 10.1111/cobi.12380. [DOI] [PubMed] [Google Scholar]
- 5.May RM. Stability and Complexity in Model Ecosystems. Vol 6 Princeton Univ Press; Princeton: 2001. [Google Scholar]
- 6.Bascompte J, Solé RV. Habitat fragmentation and extinction thresholds in spatially explicit models. J Anim Ecol. 1996;65:465–473. [Google Scholar]
- 7.Bastolla U, et al. The architecture of mutualistic networks minimizes competition and increases biodiversity. Nature. 2009;458:1018–1020. doi: 10.1038/nature07950. [DOI] [PubMed] [Google Scholar]
- 8.Levins R. Some demographic and genetic consequences of environmental heterogeneity for biological control. Bull Entomol Soc Am. 1969;15:237–240. [Google Scholar]
- 9.Taylor L, Woiwod I, Perry J. The density-dependence of spatial behaviour and the rarity of randomness. J Anim Ecol. 1978;47:383–406. [Google Scholar]
- 10.Ritchie ME. Scale-dependent foraging and patch choice in fractal environments. Evol Ecol. 1998;12:309–330. [Google Scholar]
- 11.Hamilton WJ, Gilbert WM, Heppner FH, Planck RJ. Starling roost dispersal and a hypothetical mechanism regulating rhthmical animal movement to and from dispersal centers. Ecology. 1967;48:825–833. doi: 10.2307/1933740. [DOI] [PubMed] [Google Scholar]
- 12.Hamilton WJ, Gilbert WM. Starling dispersal from a winter roost. Ecology. 1969;50:886–898. [Google Scholar]
- 13.Okubo A, Levin SA. Diffusion and Ecological Problems: Modern Perspectives. Vol 14 Springer Science & Business Media; Berlin: 2013. [Google Scholar]
- 14.Hanski I, Gaggiotti OE. Ecology, Genetics, and Evolution of Metapopulations. Academic; London: 2004. [Google Scholar]
- 15.Niebuhr BB, et al. Survival in patchy landscapes: The interplay between dispersal, habitat loss and fragmentation. Sci Rep. 2015;5:11898. doi: 10.1038/srep11898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Hassell M, Miramontes O, Rohani P, May R. Appropriate formulations for dispersal in spatially structured models: Comments on bascompte & solé. J Anim Ecol. 1995;64:662–664. [Google Scholar]
- 17.Rohani P, Miramontes O. Host-parasitoid metapopulations: The consequences of parasitoid aggregation on spatial dynamics and searching efficiency. Proc R Soc Lond B Biol Sci. 1995;260:335–342. [Google Scholar]
- 18.Tainaka K, Itoh Y. Topological phase transition in biological ecosystems. Europhys Lett. 1991;15:399–404. [Google Scholar]
- 19.Matsuda H, Ogita N, Sasaki A, Satō K. Statistical mechanics of population: The lattice lotka-volterra model. Prog Theor Phys. 1992;88:1035–1049. [Google Scholar]
- 20.Mobilia M, Georgiev IT, Tauber UC. Phase transitions and spatio-temporal fluctuations in stochastic lattice lotka-volterra models. J Stat Phys. 2007;128:447–483. [Google Scholar]
- 21.Rocha RP, Figueiredo W, Suweis S, Maritan A. Species survival and scaling laws in hostile and disordered environments. Phys Rev E. 2016;94:042404. doi: 10.1103/PhysRevE.94.042404. [DOI] [PubMed] [Google Scholar]
- 22.Lotka AJ. Analytical note on certain rhythmic relations in organic systems. Proc Natl Acad Sci USA. 1920;6:410–415. doi: 10.1073/pnas.6.7.410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Volterra V. Leçons sur la Théorie Mathématique de la lutte pour la vie. Gauthier-Villars; Paris: 1936. [Google Scholar]
- 24.Bashan A, et al. Universality of human microbial dynamics. Nature. 2016;534:259–262. doi: 10.1038/nature18301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Perhar G, et al. Using daphnia physiology to drive food web dynamics: A theoretical revisit of Lotka-Volterra models. Ecol Inf. 2016;35:29–42. [Google Scholar]
- 26.Hanert E. Front dynamics in a two-species competition model driven by lévy flights. J Theor Biol. 2012;300:134–142. doi: 10.1016/j.jtbi.2012.01.022. [DOI] [PubMed] [Google Scholar]
- 27.Morales JM, Haydon DT, Frair J, Holsinger KE, Fryxell JM. Extracting more out of relocation data: Building movement models as mixtures of random walks. Ecology. 2004;85:2436–2445. [Google Scholar]
- 28.Nathan R, et al. A movement ecology paradigm for unifying organismal movement research. Proc Natl Acad Sci USA. 2008;105:19052–19059. doi: 10.1073/pnas.0800375105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Revilla E, Wiegand T. Individual movement behavior, matrix heterogeneity, and the dynamics of spatially structured populations. Proc Natl Acad Sci USA. 2008;105:19120–19125. doi: 10.1073/pnas.0801725105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Bénichou O, Loverdo C, Moreau M, Voituriez R. Intermittent search strategies. Rev Mod Phys. 2011;83:81–129. doi: 10.1103/PhysRevE.80.031146. [DOI] [PubMed] [Google Scholar]
- 31.Benhamou S. Of scales and stationarity in animal movements. Ecol Lett. 2014;17:261–272. doi: 10.1111/ele.12225. [DOI] [PubMed] [Google Scholar]
- 32.Viswanathan GM, Da Luz MG, Raposo EP, Stanley HE. The Physics of Foraging: An Introduction to Random Searches and Biological Encounters. Cambridge Univ Press; Cambridge, UK: 2011. [Google Scholar]
- 33.Bartumeus F, Peters F, Pueyo S, Marrasé C, Catalan J. Helical lévy walks: Adjusting searching statistics to resource availability in microzooplankton. Proc Natl Acad Sci USA. 2003;100:12771–12775. doi: 10.1073/pnas.2137243100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Ramos-Fernández G, et al. Lévy walk patterns in the foraging movements of spider monkeys (Ateles Geoffroyi) Behav Ecol Sociobiol. 2004;55:223–230. [Google Scholar]
- 35.Boyer D, et al. Scale-free foraging by primates emerges from their interaction with a complex environment. Proc R Soc Lond B Biol Sci. 2006;273:1743–1750. doi: 10.1098/rspb.2005.3462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Atkinson R, Rhodes C, Macdonald D, Anderson R. Scale-free dynamics in the movement patterns of jackals. Oikos. 2002;98:134–140. [Google Scholar]
- 37.Reynolds AM, et al. Displaced honey bees perform optimal scale-free search flights. Ecology. 2007;88:1955–1961. doi: 10.1890/06-1916.1. [DOI] [PubMed] [Google Scholar]
- 38.Brown CT, Liebovitch LS, Glendon R. Lévy flights in dobe ju/’hoansi foraging patterns. Hum Ecol. 2007;35:129–138. [Google Scholar]
- 39.Sims DW, et al. Scaling laws of marine predator search behaviour. Nature. 2008;451:1098–1102. doi: 10.1038/nature06518. [DOI] [PubMed] [Google Scholar]
- 40.de Jager M, Weissing FJ, Herman PM, Nolet BA, van de Koppel J. Lévy walks evolve through interaction between movement and environmental complexity. Science. 2011;332:1551–1553. doi: 10.1126/science.1201187. [DOI] [PubMed] [Google Scholar]
- 41.Miramontes O, Boyer D, Bartumeus F. The effects of spatially heterogeneous prey distributions on detection patterns in foraging seabirds. PLoS One. 2012;7:e34317. doi: 10.1371/journal.pone.0034317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Humphries NE, Weimerskirch H, Queiroz N, Southall EJ, Sims DW. Foraging success of biological lévy flights recorded in situ. Proc Natl Acad Sci USA. 2012;109:7169–7174. doi: 10.1073/pnas.1121201109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Bartumeus F, Catalan J. Optimal search behavior and classic foraging theory. J Phys A Math Theor. 2009;42:434002. [Google Scholar]
- 44.Bartumeus F, Levin SA. Fractal reorientation clocks: Linking animal behavior to statistical patterns of search. Proc Natl Acad Sci USA. 2008;105:19072–19077. doi: 10.1073/pnas.0801926105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Bartumeus F, et al. Foraging success under uncertainty: Search tradeoffs and optimal space use. Ecol Lett. 2016;19:1299–1313. doi: 10.1111/ele.12660. [DOI] [PubMed] [Google Scholar]
- 46.Reynolds A. Liberating lévy walk research from the shackles of optimal foraging. Phys Life Rev. 2015;14:59–83. doi: 10.1016/j.plrev.2015.03.002. [DOI] [PubMed] [Google Scholar]
- 47.Heinsalu E, Hernández-Garcia E, López C. Clustering determines who survives for competing brownian and lévy walkers. Phys Rev Lett. 2013;110:258101. doi: 10.1103/PhysRevLett.110.258101. [DOI] [PubMed] [Google Scholar]
- 48.Williams GC. Natural selection, the costs of reproduction, and a refinement of lack’s principle. Am Nat. 1966;100:687–690. [Google Scholar]
- 49.Campos D, Bartumeus F, Méndez V, Andrade JS, Espadaler X. Variability in individual activity bursts improves ant foraging success. J R Soc Interface. 2016;13:20160856. doi: 10.1098/rsif.2016.0856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Boyer D, López-Corona O. Self-organization, scaling and collapse in a coupled automaton model of foragers and vegetation resources with seed dispersal. J Phys A Math Theor. 2009;42:434014. [Google Scholar]
- 51.Bhat U, Redner S, Bénichou O. Does greed help a forager survive? Phys Rev E. 2017;95:062119. doi: 10.1103/PhysRevE.95.062119. [DOI] [PubMed] [Google Scholar]
- 52.Arnoldi JF, Haegeman B. Unifying dynamical and structural stability of equilibria. Proc Math Phys Eng Sci. 2016;472:20150874. doi: 10.1098/rspa.2015.0874. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Humphries NE, Sims DW. Optimal foraging strategies: Lévy walks balance searching and patch exploitation under a very broad range of conditions. J Theor Biol. 2014;358:179–193. doi: 10.1016/j.jtbi.2014.05.032. [DOI] [PubMed] [Google Scholar]
- 54.Bertrand S, Burgos JM, Gerlotto F, Atiquipa J. Lévy trajectories of peruvian purse-seiners as an indicator of the spatial distribution of anchovy (Engraulis Ringens) ICES J Mar Sci. 2005;62:477–482. [Google Scholar]
- 55.Makris NC, et al. Fish population and behavior revealed by instantaneous continental shelf-scale imaging. Science. 2006;311:660–663. doi: 10.1126/science.1121756. [DOI] [PubMed] [Google Scholar]
- 56.Gupta A, Banerjee T, Dutta PS. Increased persistence via asynchrony in oscillating ecological populations with long-range interaction. Phys Rev E. 2017;96:042202. doi: 10.1103/PhysRevE.96.042202. [DOI] [PubMed] [Google Scholar]
- 57.González C, López Martínez R, Hernández López S, Benítez M. A dynamical model to study the effect of landscape agricultural management on the conservation of native ecological networks. Agroecol Sust Food Syst. 2016;40:922–940. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.