Molecular dynamics correctly models the unusual major conformation of the GAGU RNA internal loop and with NMR reveals an unusual minor conformation

Abstract

The RNA “GAGU” duplex, (5′GACGAGUGUCA)₂, contains the internal loop (5′-GAGU-3′)₂ , which has two conformations in solution as determined by NMR spectroscopy. The major conformation has a loop structure consisting of trans-Watson–Crick/Hoogsteen GG pairs, A residues stacked on each other, U residues bulged outside the helix, and all sugars with a C2′-endo conformation. This differs markedly from the internal loops, (5′-GAGC-3′)₂, (5′-AAGU-3′)₂, and (5′-UAGG-3′)₂, which all have cis-Watson–Crick/Watson–Crick AG “imino” pairs flanked by cis-Watson–Crick/Watson–Crick canonical pairs resulting in maximal hydrogen bonding. Here, molecular dynamics was used to test whether the Amber force field (ff99 + bsc0 + OL3) approximates molecular interactions well enough to keep stable the unexpected conformation of the GAGU major duplex structure and the NMR structures of the duplexes containing (5′-GAGC-3′)₂, (5′-AAGU-3′)₂, and (5′-UAGG-3′)₂ internal loops. One-microsecond simulations were repeated four times for each of the duplexes starting in their NMR conformations. With the exception of (5′-UAGG-3′)₂, equivalent simulations were also run starting with alternative conformations. Results indicate that the Amber force field keeps the NMR conformations of the duplexes stable for at least 1 µsec. They also demonstrate an unexpected minor conformation for the (5′-GAGU-3′)₂ loop that is consistent with newly measured NMR spectra of duplexes with natural and modified nucleotides. Thus, unrestrained simulations led to the determination of the previously unknown minor conformation. The stability of the native (5′-GAGU-3′)₂ internal loop as compared to other loops can be explained by changes in hydrogen bonding and stacking as the flanking bases are changed.

INTRODUCTION

RNA performs many important roles, such as storing genetic information, catalysis, and regulating gene expression (Eddy 2001; Doudna and Cech 2002; Altman 2007; Serganov and Patel 2007; Wu and Belasco 2008; Atkins et al. 2011). Many families of RNA have a conserved 3D structure that dictates function (Pley et al. 1994; Cate et al. 1996; Verschoor et al. 1998; Ban et al. 2000; Yusupov et al. 2001; Adams et al. 2004; Amunts et al. 2014). Therefore, understanding and being able to model the interactions that stabilize structure is important. Blind tests of prediction of 3D structure from sequence have revealed that local structure in loops is difficult to predict accurately (Miao et al. 2015, 2017). In principle, given a secondary structure, molecular dynamics (MD) with an accurate force field should be able to predict the 3D structures of component loops. Here, we test the ability of the Amber force field ff99 + bsc0 + OL3 (Cornell et al. 1995; Cheatham et al. 1999; Pérez et al. 2007; Zgarbová et al. 2011; Case et al. 2012) (see Table 1 for a list of abbreviations) to model known structures of 2 × 2 nt internal loops with tandem AG pairs.

TABLE 1.

List of abbreviations

The internal loop motif, (5′-GA-3′)₂, comprises 20% of 2 × 2 nt internal loops in a database of 1899 secondary structures (Christiansen and Znosko 2008). NMR structures of such loops symmetrically closed by GC, CG, AU, UA, or GU pairs have also been determined (Santa Lucia and Turner 1993; Wu and Turner 1996; Heus et al. 1997; Tolbert et al. 2007). When both closing base pairs are CG, AU, UA, UG, or GU, e.g., (5′-GGAU-3′)₂, trans-Hoogsteen/sugar edge GA (sheared) pairs form. The internal loop, (5′-GGAC-3′)₂, however, has cis-Watson–Crick/Watson–Crick GC and GA (imino) pairs. Computational studies on these systems (Yildirim et al. 2009; Morgado et al. 2012; Aytenfisu et al. 2014) pointed toward stacking and out-of-plane G amino group H-bonds as stabilizing the cis-Watson–Crick/Watson–Crick GA pairs.

The internal loop motif, (5′-AG-3′)₂, comprises <0.5% of the 2 × 2 nt loop database (Christiansen and Znosko 2008) and is not found in the RNA FRABASE of crystal structures (Popenda et al. 2010). It is proposed, however, in the context of 5′UAGG/3′AGAC, in a Group II ribozyme (Marcia and Pyle 2012; Chan et al. 2012; Zhao et al. 2015) and in 5′GAGU/3′CGAG in the SOLE element of oskar mRNA (Simon et al. 2015). To better understand the interactions providing thermodynamic stabilities of RNA duplexes containing 2 × 2 nt tandem symmetrical internal loops, NMR structures of six sequences with (5′-AG-3′)₂ internal loops flanked by different base pairs have been determined (Wu et al. 1997; Hammond et al. 2010; Kennedy et al. 2012). The (5′-GAGC-3′)₂, (5′-AAGU-3′)₂, (5′-UAGG-3′)₂, (5′-UAGA-3′)₂, and (5′-CAGG-3′)₂ internal loops each form a conformation where hydrogen bonding is maximized, i.e., cis-Watson–Crick/Watson–Crick AG (imino) noncanonical pairs are formed and flanked by Watson–Crick or wobble GU base pairs. Surprisingly, the (5′-GAGU-3′)₂ internal loop forms two conformations of which the major one has two trans-Watson–Crick/Hoogsteen GG pairs, two A residues stacked on each other, U residues bulged outside the helix and all sugars in a C2′-endo conformation (Table 2; Figs. 1–3).

TABLE 2.

Structural characteristics of sequences used in this study

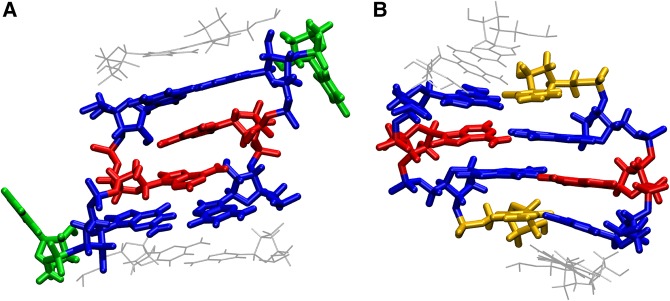
FIGURE 1.

Structure of loop and closing base pair of the two types of conformations studied in this work. (A) GAGU major NMR conformation and (B) GAGC NMR conformation (AAGU and UAGG have the same loop structure as GAGC). The types of hydrogen bonding are listed in Table 2. Guanines are colored in blue, adenines in red, uracil in green, and cytosine in yellow.

FIGURE 3.

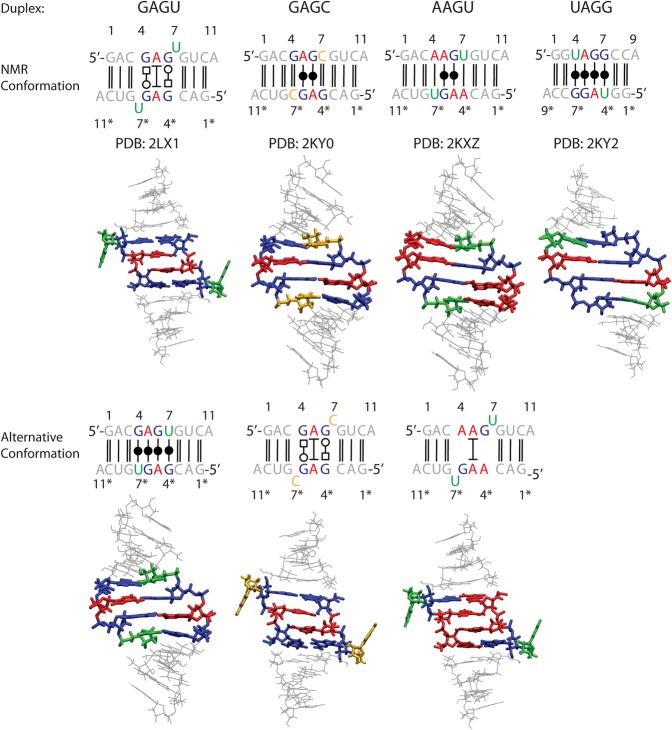
Sequences (top) and starting conformations of simulated duplexes. Upper and lower conformations, respectively, correspond to NMR determined structures and structures of alternative conformations created using the procedure outlined in Materials and Methods. Guanine residues are colored blue, adenine red, uracil green, and cytosine yellow. Nucleotides in the sequences of complementary strands are labeled with (*).

To our knowledge, no molecular mechanics analysis has been performed for the (5′-AG-3′)₂ internal loops. In this work, MD simulations were used to compare the simulated stabilities of NMR structures of the (5′-AG-3′)₂ internal loop flanked by four different closing pairs (Fig. 3). There were two initial goals. First, to test the ability of Amber force field ff99 (Cornell et al. 1995; Cheatham et al. 1999) and current Amber force field (ff99 + bsc0 + OL3) (Cornell et al. 1995; Cheatham et al. 1999; Pérez et al. 2007; Zgarbová et al. 2011; Case et al. 2012) to properly model the interactions responsible for stability of these structures. Second, to provide reasons for the unusual conformational preference of the (5′-GAGU-3′)₂ internal loop. An unexpected result was prediction of details of the minor conformation(s) of the (5′-GAGU-3′)₂ internal loop that inspired new measurements and interpretation of NMR spectra of the unmodified GAGU duplex and of several modified with inosine, or purine, or LNA, or 2′F sugars.

To accomplish the above goals, alternative conformations for three duplexes were also created (Fig. 3) and studied along with the NMR conformations. Specifically, a (5′-GAGC-3′)₂-like conformation that maximizes hydrogen bonding was created for the GAGU duplex, and a (5′-GAGU-3′)₂-like bulged conformation was created for the GAGC and AAGU duplexes (see Table 1; Fig. 3 for abbreviations). The UAGG duplex was only studied in its NMR conformation (Fig. 3) because of its different length and the difficulty of manually transforming a purine into a pyrimidine nucleotide. The upper panel of Figure 3 depicts the NMR conformations and the lower panel depicts alternative conformations. Alternative conformations provide insight into atomic features that favor the unusual (5′-GAGU-3′)₂ major conformation. The modeled (5′-GAGU-3′)₂-like conformation of the duplex with the GAGC sequence differs from the GAGU duplex only in that it has cytosine residues bulged out instead of uracils. On the other hand, the modeled (5′-GAGU-3′)₂-like (bulged) conformation of the duplex with the AAGU sequence has uracils bulged out, but the duplex requires an AG pair instead of a GG pair. Four 1-µsec-long simulations were run for each starting conformation of each sequence. The simulations reveal that the current Amber force field correctly reproduces the experimental observations that the NMR conformations are more stable than the alternative conformations. Further analysis suggests that the unusual conformational preference for (5′-GAGU-3′)₂ lies in the combination of steric, hydrogen bonding, and stacking interactions. Additionally, simulations starting with the maximally H-bonded conformation for (5′-GAGU-3′)₂ suggest an unusual minor conformation that is consistent with newly measured NMR spectra.

RESULTS

The original Amber ff99 does not adequately model the helixes flanking the (5′-GAGU-3′)₂ loop

The original ff99 force field (Cornell et al. 1995; Cheatham et al. 1999) does not include corrections to α, γ (Pérez et al. 2007), and glycosidic dihedrals (Zgarbová et al. 2011). It was tested by running two 1-µsec simulations starting with either the major NMR or an alternative “maximally H-bonded” conformation of the GAGU duplex (Fig. 3). Graphs of 1D and 2D root-mean-square deviations (RMSD) as a function of time with respect to starting structure of the whole duplex, loop, and helical regions separately are given in Supplemental Figure S1 in the Supplemental Material. Simulations with Amber ff99 are characterized by extensive fraying of the duplex terminal base pairs in both NMR (bulged) and alternative (maximally H-bonded) conformations even though those base pairs are stabilized by a 3′ dangling A. In the NMR conformation, the loop remained relatively stable with an RMSD of ∼2 Å from the starting structure while the alternative conformation underwent partial unfolding with RMSD rising to about 5 and 6 Å from the starting structure in both simulations. In simulations of both conformations, the formation of “ladder like” conformation occurs, as previously observed when simulating other sequences with ff99 (Banáš et al. 2010; Zgarbová et al. 2011). Thus ff99 + bsc0 + OL3, which introduced improvements for α, γ, and glycosidic dihedrals, was subsequently tested.

NMR structures of GAGU, GAGC, AAGU, and UAGG duplexes are stable during 1-µsec simulations

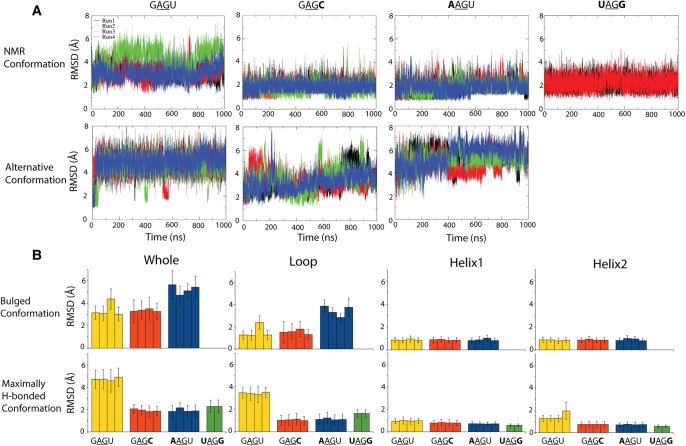
Figure 4 shows the mass-weighted RMSD and average RMSD compared to starting structure for simulations run with Amber ff99 + bsc0 + OL3 (Cornell et al. 1995; Cheatham et al. 1999; Pérez et al. 2007; Zgarbová et al. 2011; Case et al. 2012). Panel (A) gives the RMSD as a function of time while panel (B) gives the average RMSD and the standard deviation as a function of a specific subset of nucleotides in the structure. In addition, the RMSD of structural elements (loop and helical regions) are given in Supplemental Figure S2 in the Supplemental Material. With one exception, the NMR conformation is more stable for all duplexes than the alternative conformation when measured by RMSD to starting structure. The exception is trajectory 3 of the GAGU duplex NMR (bulged) conformation, which has an RMSD similar to GAGU trajectories for the alternative (maximally H-bonded) starting structure. In this trajectory there is transient hydrogen bonding between A5 and A5* nts, which are stacked in the starting conformation, where (*) refers to opposite strand (Table 1). This is reflected in a higher RMSD of the loop region, but the closing helices remain stable. Figure 4B demonstrates that the main source of instability in all simulations is the loop region, as expected. With one exception, the helical regions have average RMSD to starting structure below 1 Å. The exception is trajectory 4 of the GAGU alternative conformation where helix 2 has an average RMSD around 2 Å from the starting structure.

FIGURE 4.

(A) RMSD to starting structure of studied duplexes as a function of simulation time with Amber ff99 + bsc0 + OL3. Upper and lower panels show simulations starting with NMR and alternative conformations, respectively. Results for different trajectories are given in different colors. RMSD was mass-weighted and calculated for all atoms. Note the same y-axis bounds in all graphs. (B) Average RMSD to starting structure of studied duplexes. Error bars are standard deviations. Upper panel corresponds to the GAGU-like major conformation for all sequences and the lower panel corresponds to the AAGU or GAGC-like, “maximally H-bonded,” conformations. Average RMSD is given for the whole molecule, loop region (excluding bulged nucleotides), and the 5′-end and 3′-end helix regions. Note that the y-axis bounds are the same in lower and upper panels.

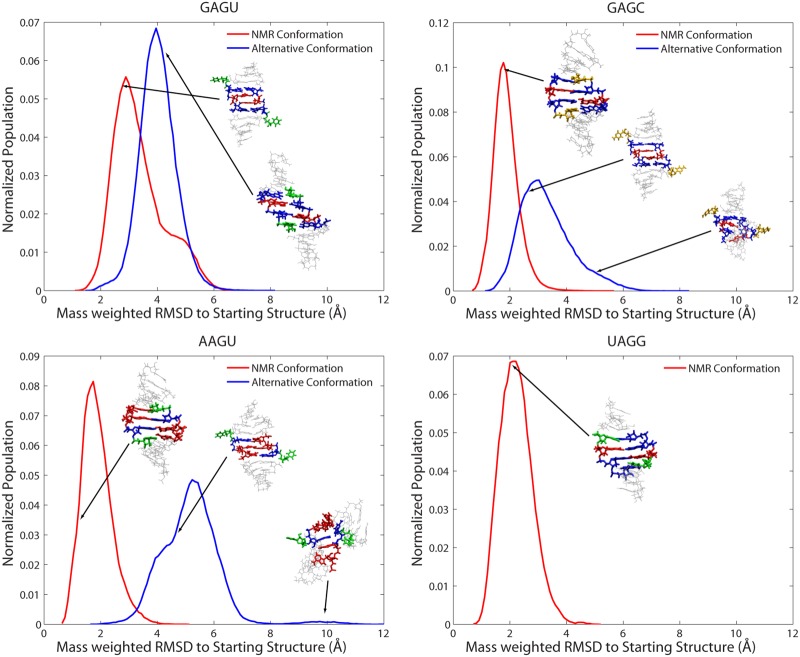
Figure 5 shows histograms of normalized populations of conformations as a function of mass-weighted RMSD to respective starting structures (Fig. 3) calculated over all four runs with Amber ff99 + bsc0 + OL3. The presence of single, relatively narrow peaks for all duplexes and conformations indicates a homogenous population of conformations across all simulations for a specific duplex and starting conformation. Positions of peaks of populations in simulations starting from NMR conformations are closer to their starting conformation than in simulations starting from alternative conformations. Evidently, the NMR conformations are more stable in the simulations. In GAGU and GAGC duplexes, the peak of population of simulations starting from the NMR structure is about 1 Å lower than the peak of simulations starting from an alternative conformation. In the AAGU duplex this difference is about 3.5 Å.

FIGURE 5.

Histograms of normalized populations from MD simulations starting with NMR and alternative conformations. Conformations and positions of cluster centroids are indicated. RMSD was mass-weighted to respective starting structure. The results given are the sum of all four (or two for UAGG) Amber ff99 + bsc0 + OL3 runs.

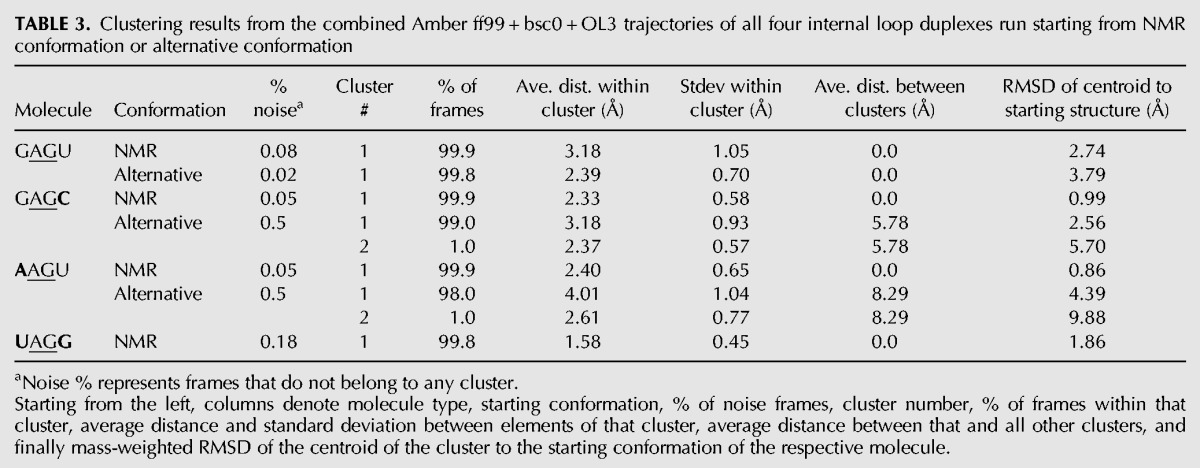
Further information about the ensemble of conformations produced during the simulations was obtained by clustering analysis as described in Materials and Methods. Table 3 shows the Amber ff99 + bsc0 + OL3 results of clustering performed on the combined trajectories for all duplexes and starting structures. Similar to the findings in Figure 5, the results indicate a strongly homogeneous population of states with at least 98% of frames belonging to one cluster in all simulations of duplexes and starting structures. Furthermore, in all but one case, the average distance between elements within a cluster is between 1.6 and 3.2 Å. The exception is the alternative (bulged) conformation of the AAGU duplex, which has a broader distribution with an average distance between elements of about 4 Å. The centroids of clusters (last column of Table 3) correspond roughly to the peaks of histograms of distribution with respect to mass-weighted RMSD and are shown in Figure 5, where the positions of centroids on the RMSD scale are marked with arrows.

TABLE 3.

Clustering results from the combined Amber ff99 + bsc0 + OL3 trajectories of all four internal loop duplexes run starting from NMR conformation or alternative conformation

Analysis of 2D RMSD plots of frames in Amber ff99 + bsc0 + OL3 trajectories provides more information about the changes in conformation during the simulations. Inspection of 2D RMSD plots (Supplemental Fig. S3 in the Supplemental Material) indicated relative stability of NMR conformations for all sequences. In all but one of the trajectories starting with NMR conformations, a collection of several similar long-lived conformations in each trajectory is separated by no more than 1–2 Å in RMSD. The exception was simulation 3 of the NMR (bulged) GAGU structure where separation between clusters is between 2–3 Å.

Alternative (bulged) structures for GAGC and AAGU duplexes are less stable than the alternative (maximally H-bonded) structure for the GAGU duplexes

Inspection of 2D RMSD plots of the simulations of the alternative conformations (Fig. 3) indicated a relatively stable GAGU duplex structure in the alternative (maximally H-bonded) conformation with changes in RMSD generally between 1 and 2 Å along the trajectories. Alternative (bulged) conformations of GAGC and AAGU duplexes are less stable than their NMR (maximally H-bonded) conformations. The AAGU duplex alternative (bulged) conformation especially had more defined clusters of different structures and a 2–3 Å change in RMSD along the trajectory (Supplemental Fig. S3 panel C). Transitions between the NMR and alternative conformations, measured by calculating RMSD between frames in trajectories starting with NMR or alternative structure, were not observed for any of the sequences in any of their trajectories (data not shown). This is expected for the GAGU duplex as 2D NOESY, i.e., 2D EXSY (Jeener et al. 1979) NMR experiments indicate a transition time between major and minor conformations on the order of 25 msec at 1°C (Supplemental Fig. S4). Thus, the likelihood of a transition within the four 1-µsec simulations is low if the force field is accurate.

Amber ff99 + bsc0 + OL3 largely preserves contacts present in the NMR structure of the GAGU duplex

Table 4 shows the percentage of NMR determined structural features (as defined in Table 2) that are preserved during the simulations of the NMR (bulged) conformation of the GAGU duplex for all four simulations. The GG trans-WC/Hoogsteen base pair between G4 and G6* was considered preserved if the distance between all hydrogen bonded atoms (4N7–6*N1, 4O6–6*N2, 4*N7–6N1, and 4*O6–6N2) was between 2.5 Å and 3.5 Å. The AA stack was deemed preserved if the distance between 3 pairs of atoms in the stacking adenines (5AC6–5*AC6, 5AN3–5*AN3, and 5AC8–5*AC8) were all within 25% of their NMR model value (3.65 Å, 6.03 Å, and 5.10 Å, respectively). In the NMR models, the puckers of loop nucleotides (residues 4–7 and 4*–7*) are centered around 140° (Kennedy et al. 2012), i.e., close to the lower bound of C2′-endo conformation. Because of that, C2′-endo conformation was defined as having pucker phase between 120° and 180°. For the G residues forming the GG trans-WC/Hoogsteen base pairs, glycosidic dihedrals with a maximum centered on the syn orientation (between 270° and 90°) were reported in Table 4 as preserved. Only G6 in simulation 3 populated primarily the anti glycosidic dihedral. The G6 sugar pucker, however, never visits the C3′-endo conformation and the G6-G15 hydrogen bonding remains trans-WC/Hoogsteen throughout the simulation. For all types of NMR contacts, the average value of all measured quantities was reported for each simulation independently. The results indicate that the NMR contacts are well preserved with typical averages of over 90% preserved distance-related NMR contacts. The only exception was simulation 3, where only 34.8% of the frames have the stacking between A residues and 81.9% of frames have the GG pairs. NMR-detected C2′-endo sugar puckers were also well preserved, with the exception of all G6/G6* puckers and G4 pucker in simulation 3, which were primarily C3′-endo. Carbon-13 chemical shifts of G6/G6* C1′ atoms are downfield from other C1′ atoms in the loop and may indicate less preference of that residue for the C2′-endo sugar pucker (Supplemental Table S2).

TABLE 4.

Percentage of NMR contacts preserved during simulations starting with the NMR conformation of (5′-GAGU-3′)₂ duplex

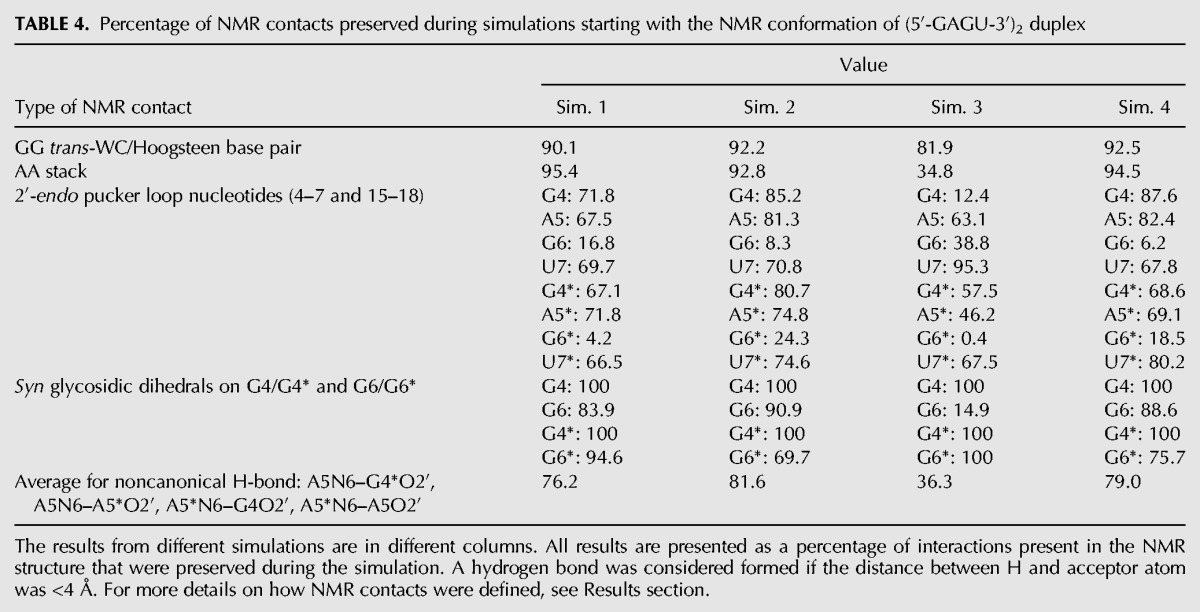
In addition to the contacts described above, the NMR (bulged) model of the GAGU duplex contains H-bonds between the amino group of A5 and O2′ atoms from G4* and A5* on the opposite strand and the equivalent interactions between A5* and G4 and A5 (Fig. 6). Table 4 lists the percentage of these interactions that are preserved in all four simulations starting with the NMR (bulged) conformation of the GAGU sequence. The H-bonds were deemed present if the distance between the corresponding heavy atoms was <4 Å. As Table 4 shows, the stabilizing H-bonds are preserved in over 75% of the frames in all but simulation 3 where it was only about 36%.

FIGURE 6.

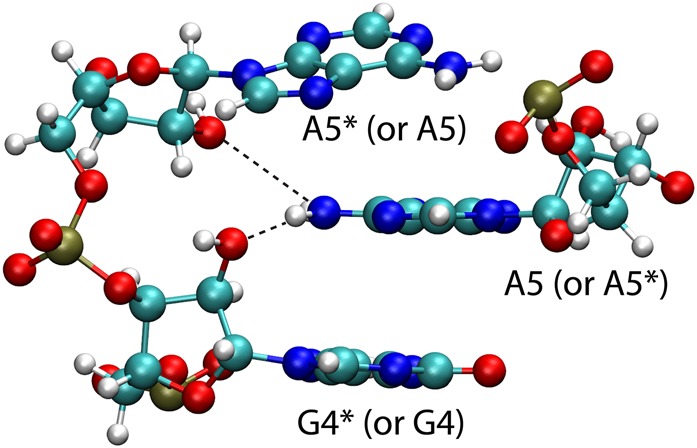
Two stabilizing interactions in the (5′-GAGU-3′)₂ NMR major structure. Hydrogen bonding between A5 amino group and 2′-oxygen on G4* and A5* residues on the complementary strand.

NMR spectra for a construct with the amino group of A5 replaced by a hydrogen reveal that the H-bonds involving that amino group are not essential for formation of the GAGU NMR (bulged) structure

As described above, both NMR and MD simulations of the GAGU duplex contain H-bonds between the amino group of A5 and cross-strand O2′ atoms (Fig. 6). To test if these interactions are essential for formation of the GAGU NMR (bulged) structure, A5 was replaced by purine to substitute hydrogen for the amino group of A5. Based on 1D spectra (Supplemental Fig. S5A,B), purine substitution apparently causes the stability of the duplex to decrease relative to hairpin. However, 2D spectra of the modified and unmodified duplexes are similar (Supplemental Fig. S5C), indicating that the structures of the duplexes are essentially the same. In particular, NOEs G6H1–G4*H8, G6H8–H1′, and G4H8–H1′, and others are found in both spectra. Moreover, there is a new NOE from the purine H6 to the cross-strand G4*H2′, which places the purine H6 at the spatial position of the A5 amino group in the 3D model of the unmodified duplex. Evidently, the A5 amino group is positioned to allow H-bonding to cross-strand 2′OH groups, but these H-bonds are not essential for stabilizing the GAGU NMR (bulged) structure.

MD simulations starting with the maximally H-bonded alternative conformation for the (5′-GAGU-3′)₂ internal loop suggest an unusual minor conformation

NMR experiments indicate that a minor conformation is present for the GAGU duplex, but no detailed structure has been proposed other than to note that G4/4* and G6/6* residues are in the anti conformation and that U7/7* residues are stacked instead of bulged out (Hammond et al. 2010). Because the maximally H-bonded alternative conformation in Figure 3 is a plausible minor conformation, MD simulations starting with this structure were run. Figures 4 and 5 and Table 3 indicate that the alternative conformation of the (5′-GAGU-3′)₂ internal loop maintains an essentially single conformation during all four simulations at around 4 Å distance from the maximally H-bonded starting structure. The centroid structure of the single cluster produced from clustering all trajectories starting with the alternative (maximally H-bonded) conformation of the GAGU duplex is given in Figure 7. In this structure, helices remain relatively stable with only about 1 Å RMSD distance from the starting conformation, but the loop region undergoes significant reorganization resulting in about 4.5 Å RMSD difference from the starting structure. The closing GU pairs are changed from GU wobble to GU cis-Watson–Crick/sugar edge type (Leontis et al. 2002) where O2 from uracil forms a shared H-bond with both amino and imino groups from guanine and the amino group of G4 also forms a H-bond with O2′ from ribose (Fig. 7C). These H-bonds are preserved throughout all four simulations. The average and standard deviations for 4O6–7*N3, 4N1–7*O2, and 4N2–7*O2′ bonds between G4 and U7* are 3.1 ± 0.4 Å, 3.0 ± 0.3 Å, and 3.9 ± 0.7 Å; and for the 7N3–4*O6, 7O2–4*N1, and 7O2′–4*N2 bonds between U7 and G4*, the values are 3.1 ± 0.5 Å, 3.0 ± 0.3 Å, and 3.9 ± 0.8 Å.

FIGURE 7.

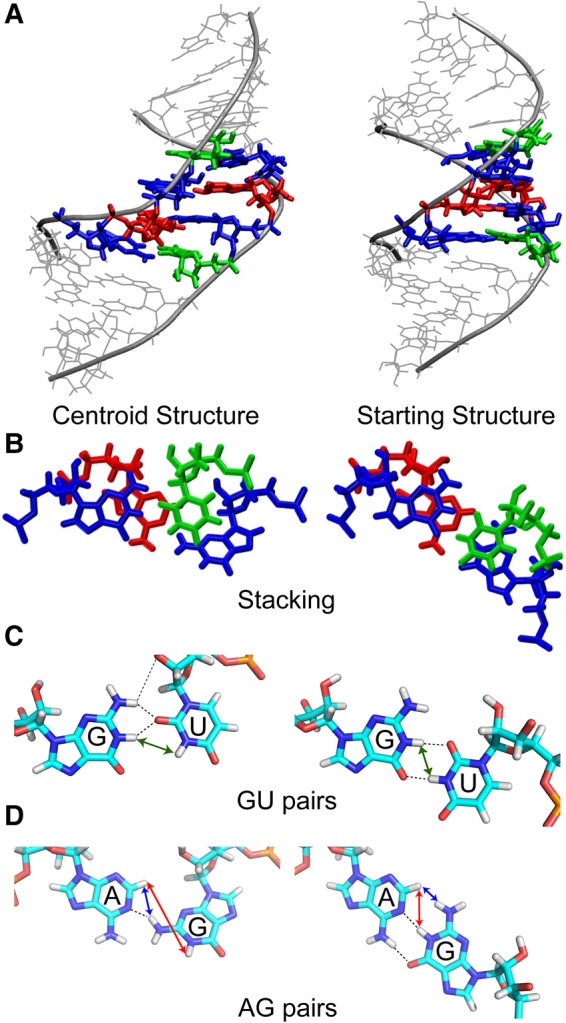
(Left column) Structure of the centroid of the only cluster from the simulations of the alternative (maximally H-bonded) conformation of GAGU duplex. (Right column) Starting structure of the GAGU (maximally H-bonded) alternative simulations. We call the centroid structure G4&G6 NH₂ H-bonded conformation. Panel A shows the overall structures emphasizing the difference in the minor grooves. Panel B shows the difference in stacking. Panels C and D show the hydrogen bonding (dashed lines) in the (C) GU pairs and (D) AG pairs. Blue, red, and green arrows in the AG and GU pairs correspond to NOESY cross-peaks (or lack of them) indicated with circles of corresponding color in Figures 8, 10A, 11, and Supplemental Figure S6.

AG imino H-bonds from the initial GAGU maximally H-bonded starting structure are changed as well, with only a single H-bond between N1 of adenine and the amino group of guanine. These H-bonds remain throughout all simulations with an average distance and standard deviations of 3.1 ± 0.3 Å for the bonds in A5–G6* and G6–A5* base pairs. The stacking between G4–U7* and A5–G6* base pairs is reduced as well (Fig. 7B). According to the clustering procedure in Table 3, the centroid conformation is stable. It encompasses 99.8% of all frames in all trajectories with standard deviation between them of only 0.7 Å. The sequence does visit the starting maximally H-bonded conformation as can be seen from the transient excursions to RMSD of around 2 Å in Figure 4, although this behavior is not captured in a separate cluster by the clustering procedure. Thus, trajectories starting with the alternative (maximally H-bonded) conformation, of the GAGU duplex provide models for minor conformations. We call the MD-generated internal loop structure a G4&G6 NH₂ H-bonded conformation.

NMR spectra are consistent with the G4&G6 NH₂ H-bonded minor conformation of (5′-GAGU-3′)₂ generated by MD simulations

Multiple lines of NMR evidence suggest that the G4&G6 NH₂ H-bonded conformation modeled by MD and represented in Figure 7 (left column) is a more accurate representation of the minor conformation of the (5′-GAGU-3′)₂ internal loop than is the maximally H-bonded starting structure. Minor conformation resonances for H1, H3, H2, H8, H6, and H1′ atoms are assigned through intense exchange cross-peaks to major conformation resonances and are listed in Supplemental Table S1. As previously observed (Hammond et al. 2010), the upfield shift of U7H5 and U7H6 in the minor conformation relative to their values in the major conformation suggest that U7 is stacked in the helix. Drastically reduced H1′–H8 NOESY cross-peaks for G4 and G6 indicate these bases are in the anti conformation (Hammond et al. 2010). In addition, none of the minor-conformation H1′ resonances exhibit scalar-coupling to H2′ resonances greater than 2 Hz, indicating that all sugar residues are primarily in the C3′-endo conformation (Hammond et al. 2010). However, the observations that sugar residues are all C3′-endo, all bases are in the anti conformation, and U7 is stacked in the helix, do not distinguish between the G4&G6 NH₂ H-bonded and maximally H-bonded starting structure.

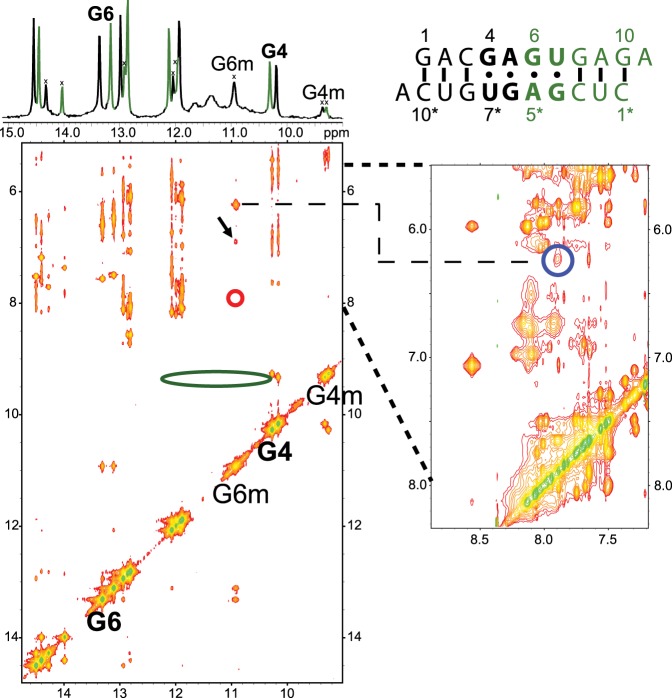
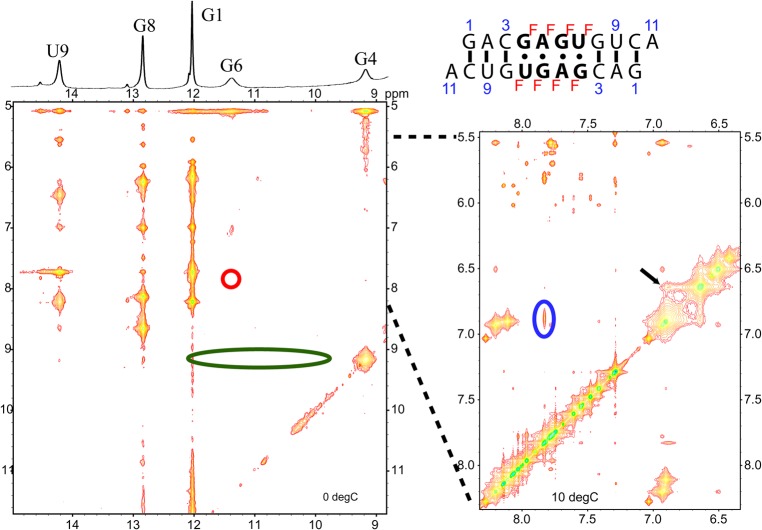
Figure 8 shows a 2D NOESY spectrum of the non-self-complementary duplex 5′GACGAGUGAGA/3′ACUGUGAGCUC. This sequence was used to solve the structure of the major GAGU duplex conformation (Kennedy et al. 2012). A NOESY cross-peak between G6m amino protons and A5*mH2 in the minor (m) conformation (Fig. 8, blue circle) could indicate an AG imino pair (Fig. 7D, right). This cross-peak, however, is also consistent with the G6 NH₂ H-bonded AG pair observed in the MD simulation (Fig. 7D, left). In an AG imino pair, the GH22-AH2 distance is ∼2.0–2.2 Å, while in the G6 NH₂ H-bonded AG pair the GH21-AH2 distance is ∼2.6–2.8 Å. On the other hand, no NOESY cross-peak is observed between G6mH1 and A5*mH2 (Fig. 8, red circle). This peak is typically observed in AG imino pairs (Peterson et al. 1994; Wu and Turner 1996; Hammond et al. 2010), but should be much weaker or missing in the G6 NH₂ H-bonded AG pair (Fig. 7D, left). Consequently, the NOESY pattern is most consistent with the G6 NH₂ H-bonded AG pair, unless the missing G6mH1-A5*mH2 cross-peak is a consequence of imino proton water exchange. Water exchange is likely ruled out, however, because there is a reasonably sized G6mH1–G6mNH₂ peak and at least one other cross-peak to G6mH1 (Fig. 8; black arrow). By process of elimination, this peak can only be from G6mH1 to A5* amino or a 2′OH. In either an AG imino pair or a G6 NH₂ H-bonded pair, the NOE from G6H1 to an A5* amino or a 2′OH (both of which are exchangeable protons) will be substantially weaker than to the nonexchangeable A5*H2 in an AG imino pair. Thus, water exchange cannot explain the absence of a G6mH1-A5*mH2 cross-peak if it were an AG imino pair. Distances between protons in Figure 7D, however, show that a G6mH1-A5*mNH₂ cross-peak is consistent with spin diffusion through G6mNH₂ in a G6 NH₂ H-bonded AG pair.

FIGURE 8.

2D NOESY spectrum (mixing time 50 msec; −3°C; 0.9 mM strands) of non-self-complementary duplex, 5′GACGAGUGAGA/3′ACUGUGAGCUC. G6 and G4 H1 (imino) signals of both strands are labeled on the diagonal and on the 1D spectrum (top); “m” refers to the minor conformation. The strong cross-peak from G6m imino at 11 ppm to 6.25 ppm is due to G6m amino protons (H21 and H22), which also have a cross-peak (blue circle) to A5*H2. The red circle highlights the lack of a cross-peak between G6m imino and A5*H2 that is typically observed in an AG imino pair. The green ellipse at G4m (9.4 ppm) indicates the lack of cross-peaks to U7H3 as might be observed in a GU wobble pair. The black arrow indicates an unassigned cross-peak to G6m H1. NOESY cross-peaks (or lack of them) indicated by blue, red, and green circles correspond to interproton distances indicated by colored arrows in Figure 7C and D.

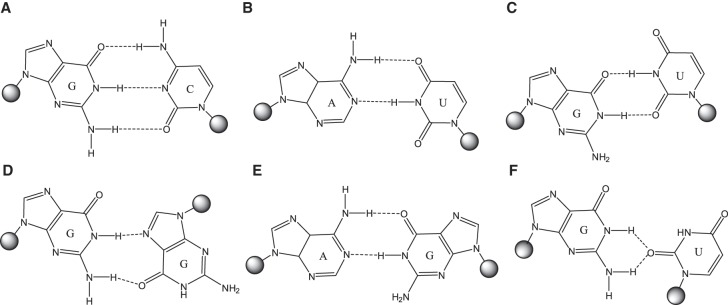
In a canonical AG imino pair (Fig. 2), the GH1 proton is involved in a H-bond to AN1, resulting in GH1 chemical shifts typically greater than 12 ppm (Peterson et al. 1994; Wu and Turner 1996; Wu et al. 1997; Hammond et al. 2010; Chen et al. 2015). An exception is the loop (5′-UAGA-3′)₂, where GH1 is stacked between two six-membered purine rings which cause an upfield shift to 11.6 ppm (Hammond et al. 2010). The signal for G6mH1 (minor conformation) of (5′-GAGU-3′)₂ is relatively upfield at 10.9 ppm in the spectrum of the non-self-complementary duplex (Fig. 8). This region is typically associated with G imino protons H-bonded to carbonyl oxygen atoms, or not hydrogen bonded at all. It would be an unusual shift for a H-bond to nitrogen. This upfield shift might be consistent with the G6 NH₂ H-bonded AG pair where GH1 is not involved in a H-bond, or perhaps a rapidly exchanging mixture of imino and G6 NH₂ H-bonded AG pairs.

FIGURE 2.

Base-pairings of studied sequences. (A) Canonical cis-Watson–Crick/Watson–Crick GC pair closing the NMR conformation of (5′-GAGC-3′)₂ internal loop. (B) Canonical cis-Watson–Crick/Watson–Crick AU pair closing the NMR conformation of (5′-AAGU-3′)₂ internal loop. (C) Canonical cis-Watson–Crick/Watson–Crick (wobble) GU pair closing the NMR conformation of (5′-UAGG-3′)₂ internal loop and alternative maximally H-bonded conformation of (5′-GAGU-3′)₂. (D) trans-Watson–Crick/Hoogsteen GG pair in the loop of (5′-GAGU-3′)₂ NMR (bulged) conformation; both G′s are syn. (E) cis-Watson–Crick/Watson–Crick (imino) AG pair in the loop of alternative (maximally H-bonded) conformation of (5′-GAGU-3′)₂ and NMR conformations of (5′-GAGC-3′)₂, (5′-AAGU-3′)₂, and (5′-UAGG-3′)₂. (F) cis-Watson–Crick/Sugar edge GU pair stabilizing the centroid of simulation observed starting with (5′-GAGU-3′)₂ alternative (maximally H-bonded) structure.

No evidence of any G4mH1-U7*mH3 (or G4*mH1-U7mH3) cross-peak is found in 2D NOESY spectra of unmodified GAGU duplex. This strong peak is expected if a GU wobble pair was formed in minor conformations (Fig. 8; green oval at G4mH1). However, this is not surprising as U7H3 peaks are very broad or not observed in the 1D spectrum, perhaps due to rapid water exchange or dynamics. Rapid exchange of U7H3 with water is more consistent with a G4 NH₂ H-bonded GU pair where U7H3 would be solvent exposed in contrast to a GU wobble pair where U7H3 would be protected by a H-bond.

In order to further characterize the minor conformation, including the MD-modeled unusual GU and AG pairs, structural properties of constructs containing chemically modified nucleotides were investigated. These include guanosine to inosine modifications which examine the significance of G amino group interactions, and sugar modifications which stabilize the C3′-endo conformation observed in the minor conformation.

Guanosine to inosine substitutions

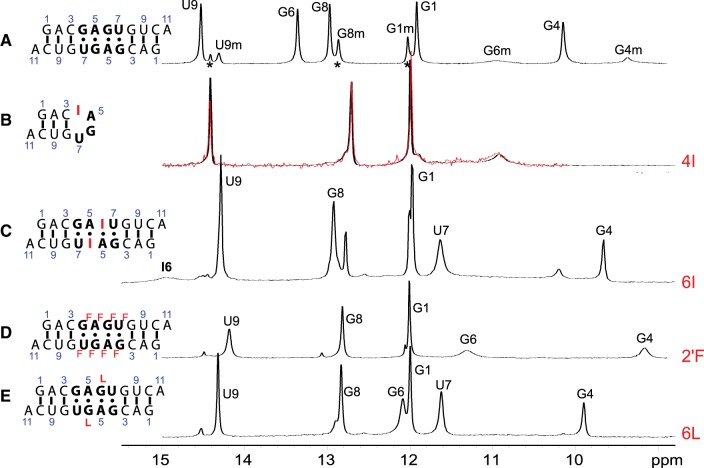
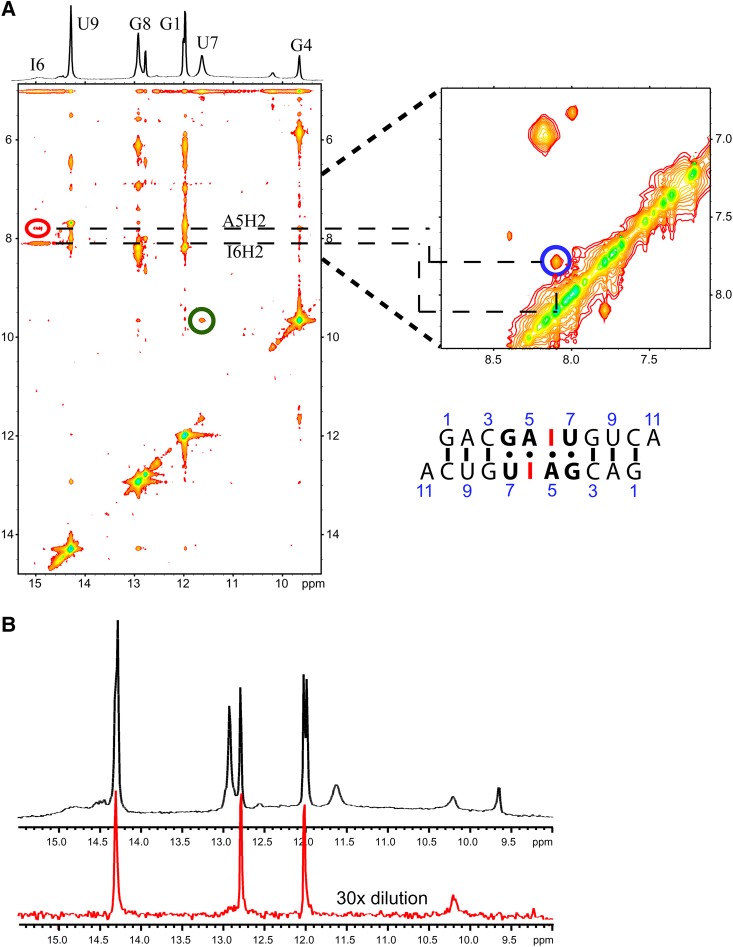
The NMR model of the major (bulged) conformation of the (5′-GAGU-3′)₂ internal loop has a H-bond between the amino group of G4 and an intranucleotide nonbridging phosphate oxygen. There is also an amino proton of G6 H-bonded to the carbonyl oxygen of G4* on the other strand (Fig. 2D). The minor (G4&G6 NH₂ H-bonded) conformation generated by MD simulations (Fig. 7, left) has interstrand H-bonds formed by the amino groups of both G4 and G6. In contrast, no internucleotide hydrogen bonding is expected for the amino protons of G in GU wobble and AG imino pairs (Fig. 7C,D, right). Inosine (I) differs from guanosine in that the guanosine NH₂ group is replaced by a hydrogen. Thus, if either G4 or G6 is replaced by inosine, the (5′-GAGU-3′)₂ internal loop NMR major (bulged) and minor (G4&G6 NH₂ H-bonded) conformations are expected to be destabilized while a minor conformation consisting of GU wobble and AG imino pairs would be relatively unaffected. NMR spectra (Fig. 9B,C) for rGACIAGUGUCA (4I) and rGACGAIUGUCA (6I) indicate that the (5′-GAGU-3′)₂ major (bulged) conformation is not formed by either 4I or 6I. The 6I sequence forms a duplex with IA imino and GU wobble pairs as indicated by NOE cross-peaks (Fig. 10A) and a population of a hairpin conformation as indicated by the concentration dependence of resonance areas (Fig. 10B). In contrast, spectra of 4I do not suggest formation of AG imino or IU wobble pairs. Rather, the 4I spectra indicate formation of a hairpin conformation despite a slightly higher RNA concentration than for the 6I sample. The hairpin conformation is consistent with lack of imino proton spectral changes in response to 50-fold dilution of the sample (Fig. 9B). Evidently, the amino group of G4 is required for formation of a duplex. The bifurcated GU H-bond in the G4 NH₂ H-bonded conformation of MD simulations (Fig. 7) that were started with the (5′-GAGU-3′)₂ maximally H-bonded conformation is consistent with involvement of the G4 amino, but a wobble conformation is not. Also, the bifurcated H-bond is consistent with lack of a U7H3 resonance as this proton is exposed to solvent without protection by a H-bond. In contrast, a wobble GU pair would generate a U7H3 resonance (Johnston and Redfield 1981). Thus, the NMR spectra for 4I are consistent with the MD prediction of an unexpected G4&G6 NH₂ H-bonded minor structure for the GAGU duplex.

FIGURE 9.

NMR spectra of the imino region of (A) unmodified self-complementary duplex, (5′GACGAGUGUCA)₂, (2.0 mM strands) (Hammond et al. 2010); (B) guanosine to inosine substitution at position 4 (4I); black and red indicate 1.2 mM and 24 µM RNA strands, respectively; (C) guanosine to inosine substitution at position 6 (6I) (1.1 mM strands); (D) 2′OH to 2′F substitution at positions 4–7 (2F) (2.4 mM strands); and (E) guanosine to G locked nucleic acid (LNA) substitution at position 6 (6L) (1.3 mM strands). Asterisks identify peaks from hairpin conformation. All spectra at 1°C except (C) which is at −2°C.

FIGURE 10.

(A) 2D NOESY and 1D spectrum of r(GACGAIUGUCA)₂ (6I) at 1.1 mM strand. Temperature is −2°C with 50 msec mixing time. Blue, red, and green circles correspond to NOESY cross-peaks between protons indicated by colored arrows in Figure 7C and D. (B) Imino proton spectrum at 1°C of 6I at 1.1 mM strand (top) and diluted 30-fold (bottom, 15-fold vertical expansion). Peaks remaining at low concentration belong to a hairpin conformation.

It is somewhat surprising that the 4I sequence forms a hairpin with no indication of a duplex. IU pairs are known to form (Pan et al. 1998) and at the NMR temperature of 1°C, the free energy increment for the 5′CI/3′GU nearest neighbor in a potential duplex is −2.1 kcal/mol (Wright et al. 2007), which is more favorable than the −1.7 kcal/mol for a 5′CG/3′GU nearest neighbor (Chen et al. 2012). The relative stabilities of 5′GA/3′UG and 5′IA/3′UG nearest neighbors, however, are unknown. Moreover, the hairpin structure may be stabilized by the presence of a 3′ dangling I in the loop. At 1°C, that would provide a favorable increment of −2.8 kcal/mol (Turner et al. 1987). This interaction may explain the dominant hairpin structure of 4I. That is, the flexibility of inosine as a 3′ dangling end at the beginning of a hairpin loop may provide a more favorable free energy than a constrained IU pair with a CG pair on one side and unfavorable stacking on an AG pair on the other side.

Chemical modifications that restrain the sugar conformation to C3′-endo

Replacement of loop residues with nucleotides having “locked” (LNA) (Vester and Wengel 2004) or 2′F sugars (Manoharan et al. 2011) to favor C3′-endo sugar pucker largely eliminates the major NMR (bulged) conformation of the GAGU duplex, where all loop residues are C2′-endo. The resulting conformations are more similar to all-Watson–Crick duplexes (Figs. 9D,E, 11; Supplemental Fig. S6). When G6 is replaced with LNA-G, a GH1-UH3 cross-peak indicative of a GU wobble pair is found in 2D NOESY spectra (Supplemental Fig. S6), although U7H3 is rapidly exchanging with solvent (note the weak U7H3 diagonal-peak in 2D NOESY spectrum of duplex 6L). Also, the LNA-G6H1 resonance is farther downfield at 12.1 ppm than in the minor structure of the unmodified GAGU duplex or in the 2′F duplex (Fig. 9D,E; Supplemental Table S1). Moreover, a weak cross-peak from LNA-G6H1 to A5*H2 is observed in a 2D NOESY spectrum of duplex 6L (Supplemental Fig. S6). Thus, duplex 6L appears to have a significant population of the maximally H-bonded AG imino/GU wobble conformation.

FIGURE 11.

2D NOESY spectra of 2′F: Residues 4–7 have 2′-OH replaced with 2′F. Temperature is 0°C with 50 msec mixing time in imino region spectrum (left) and 10°C with 100 msec mixing time in aromatic region spectrum (right). Blue, red, and green circles correspond to NOE cross-peaks between protons indicated by arrows in Figure 7C and D. The black arrow indicates a strong cross-peak between G6 amino and A5* amino protons (see Fig. 7D).

The 2D NOESY spectra of duplex 2′F show a strong cross-peak between G6 amino and a peak identified by process of elimination as A5 amino (Fig. 11, black arrow). This cross-peak is expected in the G4&G6 NH₂ H-bonded conformation, but should be missing or weak in the maximally H-bonded starting conformation (Fig. 7). Further, the U7H3 signal is missing, as would be expected for the solvent-exposed U7H3 of the G4&G6 NH₂ H-bonded conformation. Evidently, duplex 2′F primarily exhibits the G4&G6 NH₂ H-bonded conformation of Figure 7. Based on NOE and chemical shift patterns, duplex 2′F appears most similar to the unmodified, minor conformation (Figs. 9D, 11; Supplemental Table S1).

DISCUSSION

There is a prolonged time lag between determination of RNA sequence and structure. Accurate force fields can help fill this gap by reducing the amount of experimental data required to develop realistic structural models. Moreover, many RNAs are dynamic and simulations can provide predictions of dynamics. Because there are many parameters in a force field, confidence in simulations requires benchmarking against experimental characteristics of a wide variety of RNAs.

In this work, the unusual major NMR (bulged) conformation (Fig. 3) of the RNA duplex with the (5′-GAGU-3′)₂ internal loop (Kennedy et al. 2012) provided a novel test of the Amber ff99 + bsc0 + OL3 force field (Cornell et al. 1995; Cheatham et al. 1999; Pérez et al. 2007; Zgarbová et al. 2011; Case et al. 2012). This internal loop structure has stacked A′s, GG H-bonded pairs, U′s bulged out of the helix, and all sugars in a C2′-endo conformation (Figs. 1–3; Table 2). This structure differs from NMR structures of internal loops, (5′-GAGC-3′)₂, (5′-AAGU-3′)₂, and (5′-UAGG-3′)₂, which have imino AG pairs flanked by canonical pairs and are maximally H-bonded as shown in Figures 1–3 (Hammond et al. 2010). The internal loops studied here are therefore good tests of force fields because they explore performance on RNAs with different combinations of motifs that critically depend on a subtle balance of interactions.

Four 1-µsec-long MD simulations were run on each of three duplexes in two starting conformations for a total of 24 simulations. Additionally, two 1-µsec simulations were run on the UAGG duplex starting with its NMR (maximally H-bonded) conformation. RMSD and 2D RMSD (Fig. 4; Supplemental Figs. S1–S3 in the Supplemental Material) were calculated to examine the predicted stability of different conformations. Clustering analysis (Table 3) and distribution of frames with respect to starting structures (Fig. 5) were also computed to determine the homogeneity of simulated structures. Additionally, interactions likely to stabilize the NMR conformation of the GAGU duplex (Tables 3, 4) were examined in detail.

For all four systems, Amber ff99 + bsc0 + OL3 accurately models the conformational preferences of all four loops, always giving lower average RMSD to the starting point for simulations starting from the NMR structure (Figs. 4, 5). Interactions in the NMR-derived model of the major (bulged) conformation of the (5′-GAGU-3′)₂ loop were generally well preserved with the exception of the sugar pucker for G6/6* and the appearance of AA pairs in one simulation (Tables 3, 4). Likewise, duplexes with (5′-GAGC-3′)₂, (5′-AAGU-3′)₂, and (5′-UAGG-3′)₂ loops are stable in their NMR (maximally H-bonded) conformations (Table 4). The AAGU duplex showed a clear preference toward its NMR conformation as evidenced by an approximate 3 Å higher RMSD to the starting structure when started in the alternative (bulged) conformation and by the set of multiple stable structures observed in the 2D RMSD plots (Fig. 4, panel B; Supplemental Fig. S3, panel C). The GAGC duplex showed a relatively stable alternative (bulged) conformation with RMSD about 1 Å higher to the bulged starting structure as compared to when the simulation was started in the NMR (maximally paired) conformation. Evidently the identity of the bulged out base (C in GAGC vs. U in GAGU) does not play a part in short time stability of the bulged conformation (Figs. 4, 5). Either C or U could be locked into a bulged conformation. At equilibrium, however, NMR reveals that (5′-GAGC-3′)₂ does not form a bulged structure. Presumably, this reflects the extra stability of a GC over a GU pair (see below).

While 1-µsec simulations are too short for convergence, the stability of the (GACGAGUGUCA)₂ duplex′s NMR structure is in sharp contrast to the instability of duplex terminal base pairs and helical structure observed with Amber ff99 simulations. Evidently, the α/γ and χ revisions of ff99 have improved the approximations of the forces driving RNA structure.

When simulations for the GAGU duplex were started with an alternative (maximally H-bonded) internal loop structure of wobble GU and imino GA pairs, the loop rapidly switched to have reduced stacking overlap, changed AG and GU H-bonds, and a narrow minor groove (Fig. 7). NMR data of the GAGU duplex minor conformation and of chemically modified sequences provide experimental evidence suggesting that this G4&G6 NH₂ H-bonded loop is the dominant minor conformation of the GAGU duplex. Properties of this loop, specifically the bifurcated H-bond in the GU pair, the narrow minor groove, and all anti χ dihedrals with C3′-endo sugars are found in the ribosome (G1002 and U966 in PDB ID: 1JJ2) in the context of a GU pair adjacent to a UU pair in an internal loop (Klein et al. 2001). Essentially the same H-bonding pattern has also been modeled for NMR structures of the GU pairs in (GGCGUGCC)₂ (Chen et al. 2000).

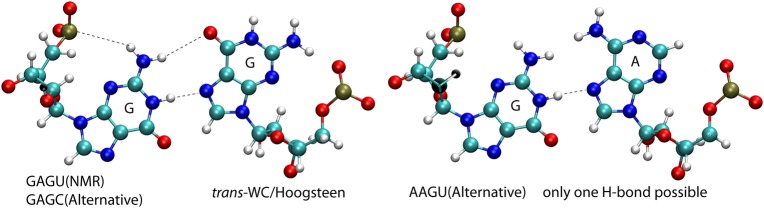
The secondary and NMR structures along with the MD simulations provide insight into reasons why the GAGU duplex has a unique shape. The GAGU duplex in its stable NMR (bulged) conformation and the GAGC and AAGU duplexes in unstable alternative (bulged) conformations have the same loop 3D shape. In the (5′-GAGU-3′)₂ loop, a GG trans-WC/Hoogsteen base pair stabilizes this bulged conformation. On the basis of NMR, however, the duplexes with the (5′-GAGC-3′)₂ and (5′-AAGU-3′)₂ loops never form the bulged structure. Moreover, NMR and MD show that the tandem AG pairs of (5′-GAGC-3′)₂ and (5′-AAGU-3′)₂ are flanked by stable Watson–Crick pairs. In each case, the closing pair of the internal loop is preceded by a CG pair (see top of Fig. 3). At 0°C, nearest neighbor ΔG° parameters for 5′CG/3′GU, 5′CG/3′GC, and 5′CA/3′GU are, respectively, −1.8 ± 0.3, −3.3 ± 0.3, and −3.1 ± 0.2 kcal/mol (Xia et al. 1998; Chen et al. 2012). Because there are two such nearest neighbors in each duplex, these interactions for 5′CG/3′GU loop closure are 3.0 ± 0.8 and 2.6 ± 0.8 kcal/mol, respectively, less favorable than closure by 5′CG/3′GC and 5′CA/3′GU. Thus, it costs more to break the GC and AU pairs of (5′-CGAGCG-3′)₂ and (5′-CAAGUG-3′)₂ to extrude the C or U bases into solvent than to extrude the U of (5′-CGAGUG-3′)₂. In both the GAGU and AAGU duplexes, the U is in a GUG part of the sequence (Fig. 3). In 5′-GUG-3′ single stranded trimer, the U is bulged out (Lee and Tinoco 1980; Lee 1983), similar to the U in the NMR structure for the GAGU duplex (Fig. 3). However, in the (5′-GAGU-3′)₂ internal loop, a GG trans-WC/Hoogsteen base pair with two H-bonds stabilizes the bulged conformation. In contrast, as illustrated in Figure 12, the unstable AAGU bulged conformation replaces the GG pair with an AG pair that can form only a single H-bond if pairing is isosteric with the GG pair (Leontis et al. 2002). This is reflected in higher RMSDs for simulations starting with the AAGU alternative (bulged) conformation (Fig. 4).

FIGURE 12.

Comparison of nucleotides in the loop region. In the GAGU NMR and GAGC alternative conformation (which both have the same loop region), two structure stabilizing trans-Watson–Crick/Hoogsteen H-bonds are formed (left base pair). In the AAGU alternative conformation, G is replaced with A and only one hydrogen bond is possible.

Given the range of hydrogen bonding and stacking interactions involved in the structures studied here, it is encouraging that the Amber ff99 + bsc0 + OL3 force field simulations agree with the structures previously determined by NMR. For example, the simulations reproduce the two GG pairs with all Gs in a syn conformation as found in the NMR (bulged) structure of the GAGU duplex (Kennedy et al. 2012). Known structures rarely contain base pairs formed by two syn bases (Leontis and Westhof 2001). Additionally, the simulations predicted an unexpected minor conformation for (5′-GAGU-3′)₂ that is consistent with new NMR spectra. Simulations on other systems, however, have sometimes been successful (Spasic et al. 2012; Aytenfisu et al. 2014) and sometimes not (Banáš et al. 2010; Bergonzo et al. 2014, 2015; Condon et al. 2015; Zgarbová et al. 2017). In general, recent progress (Smith et al. 2017; Šponer et al. 2017) reinforces the promise of physics-based approaches for development of force fields for RNA and other polymers.

MATERIALS AND METHODS

Starting structures

Atomic coordinates for the duplexes with internal closing base pair/loop combinations, (5′-GAGU-3′)₂, (5′-GAGC-3′)₂, (5′-AAGU-3′)₂, and (5′-UAGG-3′)₂, were taken from their respective NMR structures, 2LX1 (Kennedy et al. 2012), 2KY0, 2KXZ, and 2KY2 (Hammond et al. 2010). In each case, the conformation with the least NMR restraint violations, as indicated in the coordinate files, was used in simulations.

Creating alternative conformations

Alternative conformations (Fig. 3) were created for GAGU, GAGC, and AAGU duplexes. Because they all have a central 5′AG3′ sequence, the alternative conformations were created (in silico) by mutating the closing nucleotides. For example, the alternative conformation for the GAGU sequence was created from the AAGU sequence by mutating the 5′-end loop-closing A into G on both strands. Similarly, the alternative conformation for the GAGC duplex was obtained from the major GAGU duplex structure (2LX1) by mutating the 3′-end loop-closing U to C. Because mutating purine to purine and pyrimidine to pyrimidine involved changing only a few atoms, the effect on the conformation of the molecule is minimal. The duplex with the UAGG sequence had a shorter total strand length and different base pair composition in addition to having pyrimidines replacing the purines and vice versa at the base pairs closing the helix. Therefore, the duplex with the UAGG sequence was simulated only starting in its NMR conformation.

MD simulations

All MD simulations were run with the same protocol. First, a duplex was immersed in a truncated octahedron box filled with TIP3P water models (Jorgensen et al. 1983) such that there is at least 10 Å of water from each side of the molecule. Enough Na⁺ ions were added to neutralize the RNA charge. Based on the volume of the water box, enough Na⁺ and Cl⁻ ions were then added to obtain a 0.1 M NaCl concentration, which is similar to NMR conditions. Systems were then energy minimized in two 1000 step stages. First, the solute molecule was held fixed and only water molecules were minimized.

Second, the whole system was allowed to equilibrate. The system was then heated from 0 to 300 K over 50 psec using a Langevin thermostat (Chandrasekhar 1943) with 1 psec⁻¹ frequency of collision. In the final stage of equilibration, Berendsen pressure regulation (Berendsen et al. 1984) with isotropic position scaling was turned on and the system equilibrated for 1 nsec at pressure of 1 atm. Finally, production simulations were run at 300 K and 1 atm (NPT ensemble). Bonds to hydrogens were constrained with the SHAKE algorithm (Ryckaert et al. 1977), which allowed for a 2 fsec time step. Simulations were run with the graphical card implementation (Salomon-Ferrer et al. 2013) of the molecular dynamics engine of the Amber 12 software package (Case et al. 2012). All molecules were modeled with the Amber ff99 + bsc0 + OL3 force field for RNAs. This force field contains the original parameters from force fields ff94 (Cornell et al. 1995) and ff99 (Cheatham et al. 1999; Wang et al. 2000) along with corrections for α and γ backbone dihedrals (Pérez et al. 2007) and glycosidic dihedrals for all four bases (Zgarbová et al. 2011). Each duplex was simulated in four independent simulations for 1 µsec, except for the UAGG duplex for which two simulations were run. In addition, two 1-µsec simulations were run for the GAGU duplex in its NMR (bulged) and alternative conformation using the older ff99 force field. The total simulation time for all duplexes was 30 µsec.

Analysis of MD results

Distances, angles, dihedrals, root-mean-square displacement (RMSD), and two-dimensional RMSD were calculated using the cpptraj module of the Amber software package (Roe and Cheatham 2013). When calculating the RMSD of the loop region of bulged conformations, the bulged nucleotides (U7 and U7* in GAGU and AAGU duplexes and C7 and C7* in GAGC duplex) were left out.

Clustering of trajectories

Clustering was performed on the combined trajectories of all four internal loop duplexes run starting from NMR conformation or alternative conformation. The dbscan clustering algorithm (Ester et al. 1996) was used as implemented in the cpptraj module (Roe and Cheatham 2013) of Amber. Clustering was performed such that the minimum distance between points required for forming a cluster was 1.8 Å and the minimum number of points required for forming a cluster was 40. Dbscan also reports the percentage of noise frames, i.e., frames that do not belong to any of the clusters. This quantity is in the third column of Table 3.

NMR experiments and modeling

NMR spectra of modified RNAs were acquired with Varian Inova 600 and 500 MHz spectrometers as previously described for unmodified RNA (Hammond et al. 2010; Kennedy et al. 2012). RNA strand concentrations ranged from about 0.9 to 2.4 mM. All samples were in the same buffer: 20 mM sodium phosphate, 0.5 mM Na₂EDTA, 80 mM NaCl, pH 6.1. Previously published structures were modeled from spectra taken at 270 to 288 K. Imino proton spectra, however, showed little or no change in chemical shifts up to 288 K for (GACGAGUGUCA)₂, 293 K for (GACAAGUGUCA)₂, and 303 K for (GACGAGCGUCA)₂ (Hammond et al. 2010; Kennedy et al. 2012).

Chemical synthesis of oligonucleotides

Oligonucleotides with inosine or LNA were synthesized using standard phosphoramidite chemistry (Beaucage and Caruthers 1981) with commercially available RNA and LNA phosphoramidites (GenePharma, Exiqon). Oligonucleotides were deprotected and purified as described previously (Xia et al. 1998; Kierzek and Kierzek 2003) and characterized using MALDI-TOF mass spectrometry. The 2′F oligonucleotide was synthesized with a previously reported method (Manoharan et al. 2011).

SUPPLEMENTAL MATERIAL

Supplemental material is available for this article.