Robust light harvesting by a noisy antenna

Ultrafast bulk and single-molecule spectroscopy experiments described by a single theoretical model show how protein fluctuations influence photosynthetic light harvesting.

Abstract

Photosynthetic light harvesting can be very efficient in solar energy conversion while taking place in a highly disordered and noisy physiological environment. This efficiency is achieved by the ultrafast speed of the primary photosynthetic processes, which is enabled by a delicate interplay of quantum effects, thermodynamics and environmental noise. The primary processes take place in light-harvesting antennas built from pigments bound to a fluctuating protein scaffold. Here, we employ ultrafast single-molecule spectroscopy to follow fluctuations of the femtosecond energy transfer times in individual LH2 antenna complexes of purple bacteria. By combining single molecule results with ensemble spectroscopy through a unified theoretical description of both, we show how the protein fluctuations alter the excitation energy transfer dynamics. We find that from the thirteen orders of magnitude of possible timescales from picoseconds to minutes, the relevant fluctuations occur predominantly on a biological timescale of seconds, i.e. in the domain of slow protein motion. The measured spectra and dynamics can be explained by the protein modulating pigment excitation energies only. Moreover, we find that the small spread of pigment mean energies allows for excitation delocalization between the coupled pigments to survive. These unique features provide fast energy transport even in the presence of disorder. We conclude that this is the mechanism that enables LH2 to operate as a robust light-harvester, in spite of its intrinsically noisy biological environment.

1. Introduction

Natural photosynthesis begins with the absorption of sunlight, followed by a rapid energy transfer and charge separation. These primary photosynthetic processes lead to a highly efficient conversion of solar energy into an electrochemical potential gradient across the photosynthetic membrane. The solar energy is thus stored in a form that can later be used to drive cellular processes. The key to the remarkable quantum efficiency of the primary processes of photosynthesis (nearly all absorbed photons can result in charge separation) is the ultrafast speed with which they proceed, outcompeting all the adverse recombination mechanisms.1–3 In recent years, the events following photoexcitation were investigated in great detail by nonlinear ultrafast spectroscopy. It was found that the key to their speed is a delicate interplay of quantum effects, such as delocalization, thermodynamics and environmental noise.4 All these events take place in specially synthesized light-harvesting complexes (LHCs) made out of pigments and proteins. In this work, we will focus on a typical LHC, light-harvesting complex 2 (LH2) from purple bacteria. Thanks to cryogenic electron microscopy and X-ray crystallography, the structure of many of these complexes, including LH2, is known.5–8 Pigments such as chlorophylls and carotenoids interact with sunlight and carry out the light harvesting function. The protein, on the other hand, acts as a scaffold, binding the pigments and thus fixing their positions and orientations. Moreover, the protein has a specific and unavoidable role in modulating the electronic properties of the pigments, e.g. by hydrogen bonding and/or by electrostatic interaction.9–11 Crucially, the protein scaffold itself is not static, but, being submerged in a highly disordered and fluctuating physiological environment, exhibits dynamics over many timescales, from ultrafast vibrations to slow motion on a timescale of seconds. How this scaffold motion influences the function of the pigments is to a large extent unknown. Are photosynthetic antennas robust under environmental fluctuations? Or are they rapidly switching between good and poor light-harvesting regimes? The high average efficiency suggests the former, but how is this achieved? In the following work, we address these questions.

The fast excitation dynamics can be very well studied by the methods of ultrafast nonlinear spectroscopy. These allow one to probe the LHC's excited state manifold, and to closely follow the fate of the electronic excitation after a photon is absorbed by the LHC.3,12 Such a close monitoring is possible because the relevant ultrafast dynamics of the LHC is naturally triggered by its interaction with light. In a pulsed-spectroscopy sequence, one or more pulses can be used to initiate the dynamics, while other pulses can probe/modify the evolution. In this way, a whole ensemble of complexes can be synchronized and probed. With respect to the probed properties, the LHCs act as an ensemble of nearly identical units, all of them exhibiting a similar response. The complex to complex variation manifests merely as the inhomogeneous broadening of the measured spectra, and the measured dynamics are averaged over the whole disordered ensemble. The nature and origin of the variations between the individual LHCs cannot be directly observed. Questions regarding the origin of the disorder, and whether it is dynamically sampled, on what time scale, or whether the ensemble is heterogeneous cannot be answered by traditional ensemble spectroscopy.

The ensemble synchronization, so crucial in observing the ultrafast bulk response, is not generally possible when observing the natural protein motion, because it is (at least to a large extent) not directly photo-induced. As a result, one is limited to the observation of the average properties of inhomogeneous ensembles only. The only way to observe the protein dynamics is then to observe the complexes on an individual basis. This is possible by single-molecule (or single-complex) spectroscopy (SMS).13–15 Using a microscope and an ultrasensitive detector, light emission from single LHCs is monitored in SMS. By recording spectral or intensity variations of its signal, a LHC protein can thus be observed while slowly changing its state. Due to the slow timescale of measurement, the observed changes can be ascribed to the conformational dynamics of individual LHC proteins.13–18 Also, the above-mentioned questions regarding the heterogeneity of the ensemble can be addressed. However, because of this low time resolution, limited by the weak signal of single complexes, traditional SMS does not resolve the excitation dynamics within the complexes, and it cannot aid in judging the influence of slow protein motion on ultrafast excitation energy transfer. In order to investigate the influence of the slow protein motion on ultrafast dynamics, the ultrafast and single-complex approaches have to be unified into a single framework. This enables the simultaneous measurement of the characteristics of ultrafast processes relevant to efficient light-harvesting and their slow variations due to the protein motion. This is precisely what we have achieved in this work.

Our LHC of study is the LH2 antenna complex of the purple bacterium Rhodopseudomonas acidophila.5,19 It is a typical LHC with a high density of pigments, demonstrating strong, intermediate and weak inter-pigment interactions. Its energy transfer quantum efficiency reaches practically unity.20 It was subjected to intensive study already way before, and has been studied much more since, its structure was elucidated.5,6 Correspondingly, there is a vast body of spectroscopic information available about this particular system.14 As determined by nonlinear ensemble spectroscopy, its excitation dynamics proceeds on an ultrafast timescale of fs to ps.3,21–26 Hole-burning, fluorescence-narrowing and photon-echo peak shift spectroscopies have led to observations of energetic disorder within LH2 ensembles.27–29 Single molecule spectroscopy has shown a significant level of protein conformational fluctuations.16–18,30–36 LH2 was also the subject of a study on the first coherent ultrafast SMS on LHCs, in which coherent beatings in single complexes were observed.37 The LH2 of Rps. acidophila has a highly symmetrical ring structure, with a 9-fold rotational symmetry. This significantly reduces the number of free parameters in our model. Last but not least, the LH2 antenna exhibits excellent stability under SMS conditions,16,31 which enables us to measure the ultrafast relaxation in a single LH2 repeatedly for minutes.

We have recently reported on an experiment of ultrafast two-pulse SMS, which allows for the observation of ultrafast energy relaxation in individual LHCs.38 In this work, we extend this experiment to measure the distribution of energy relaxation times across the excited state manifold. Furthermore, we develop a theoretical description of the experiment within the framework of the Frenkel exciton model (FEM), which is commonly used to describe ultrafast bulk spectroscopy on photosynthetic systems.11,39,40 In order to characterize the light-harvesting of the LH2 complexes, we measure their absorption (initial state), fluorescence (final state), broadband transient absorption (ultrafast, 100 fs dynamics) and narrowband transient absorption (fast, ps dynamics) spectra. By quantitatively and simultaneously describing all these experiments, we construct a FEM with very strict constraints. In fact, the model describes far more experimental data than is the number of its parameters. In this model, the ensemble spectra are calculated by averaging over individual realizations of the static disorder of the pigment energies. The same model is applied to model the ultrafast SMS experiment. Individual energetic disorder realizations, used for the calculation of ensemble spectra, correspond to individual LHCs at specific times in the SMS technique, and they yield the individually measured relaxation times. In this way, the ‘static’ disorder of the ensemble of complexes measured by the ultrafast techniques becomes dynamic on the timescale of the slow protein motion observed in SMS. We demonstrate that the full range of expected relaxation time changes is observed by our SMS measurement. This means that the measured times are not significantly averaged by fluctuations on faster timescales, and that we truly observe the intrinsic timescale of these changes. The slow protein motion dynamically modifies the energy landscape on which the excitation relaxes. By this, the protein determines the excitation dynamics and therefore the light harvesting function of the complexes. We conclude that the LH2 antenna is designed in such a way that the intrinsic spread of site energies is ‘controlled’. As a consequence, the excitation remains delocalized between several pigments even in the presence of the fluctuations. This delocalization enables fast energy transfer, a prerequisite for efficient light harvesting.

2. Materials and methods

2.1. Experimental methods

The LH2 complexes from Rps. acidophila were isolated and purified as previously described.41 The isolated LH2 antennas of Rps. acidophila were suspended in a buffer, 25 mM Tris, pH 8, 0.03% β-DM, and measured at room temperature. The linear ensemble absorption spectrum was measured by using a commercial machine (Lambda 40, Perkin Elmer). The ensemble fluorescence spectrum was measured by the same microscopy setup that was used to collect the single-molecule spectroscopy signals, by increasing the LH2 concentration and focusing in the volume. The broadband pump–probe spectrum was measured by Marco Ferretti using the 2DES setup42,43 as a side product of a 2DES measurement, where it is used for phasing the 2D spectrum. A home-built NOPA produced broadband pulses from 800 nm to 900 nm (Fig. S6 in the ESI†), which were used for the acquisition of the pump–probe signal. The narrowband pump–probe spectrum was measured using the transient absorption setup in LaserLab Amsterdam.12,44 A fundamental of the laser (Legend, Coherent) was used as a narrowband (24 nm FWHM) pump at 804 nm (Fig. S7A in the ESI†). As a probe, a sapphire-generated continuum was used (Fig. S7B in the ESI†), and a tilted 850 nm long-pass filter was used to select the near-IR wavelengths. A low pump intensity (300 nJ per pulse) was used to avoid annihilation. The OD of the sample was 0.5 at the B850 peak.

Ultrafast two-pulse single-molecule spectroscopy was measured and analyzed as described before.38 Briefly, the complexes are diluted to a concentration of ∼10 pM and immobilized on a poly-l-lysine (PLL, Sigma) coated glass surface. For better LH2 stability, samples frozen only once were used. The buffer is deoxygenated by the oxygen-scavenging enzyme system PCA/PCD (2.5 mM protocatechuic acid, 25 nM protocatechuate-3,4-dioxygenase, Sigma) to increase the survival time of the complexes by preventing singlet oxygen formation. The LH2 complexes are imaged by a confocal microscope and excited by two pulses produced by a home-built Michelson interferometer. The pulse source is a 76 MHz pulsed Ti:Sapphire laser (Mira 900F, Coherent), the wavelength is changed by tuning the laser cavity. The pulse repetition rate was decreased to 2 MHz by a pulse picker (PulseSelect, APE) to increase the survival time of the complexes and eliminate long-lived excited species such as triplet states. The excitation polarization is adjusted to near-circular by a Berek compensator (New Focus). The pulse length entering the microscope (Eclipse TE300, Nikon) was about 200 fs, measured by the fringe-resolved autocorrelation (FRAC) for each excitation wavelength. As discussed before, for such a long pulse, the dispersion by the microscope objective is less than 5% and therefore negligible. The fluorescence emission is separated from the excitation by a dichroic filter (815DCLP, Chroma Tech) and a long-pass interference filter (FELH850, Thorlabs) and recorded by an avalanche photodiode (PerkinElmer). At 800 nm, an excitation power of about 1 pJ per pulse was used, and adjusted to compensate for absorption dependence (see Fig. 1B). By scanning the pulse delay (delay line, Newport), a modulation of the observed fluorescence intensity is achieved. The measurement is controlled by a custom-made LabView environment. The resulting dips are fitted with an effective model with relaxation from a resonant to an off-resonant state. The fitted fluorescence intensity dependence on the pulse delay τ is

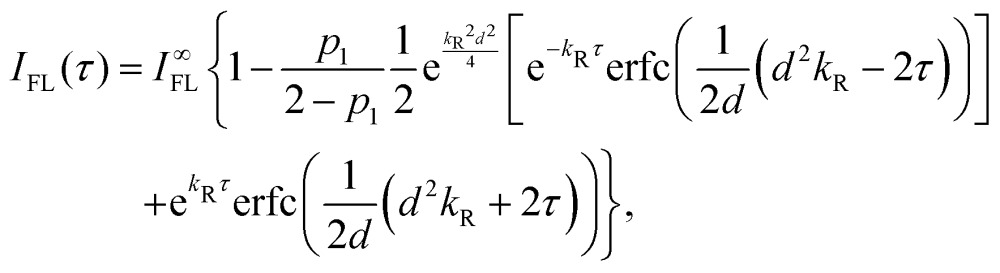1

where k_R = 1/τ_R is the relaxation rate, I∞FL is the baseline intensity at large delay, p₁ is the one-pulse excitation probability (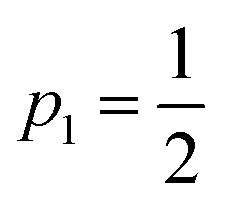 for full saturation) and d is an effective pulse width related to the pulse FWHM by 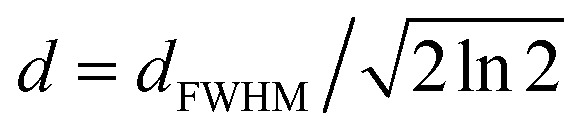. This formula is derived from the kinetic equations for the effective three-state model, which can be found in the supporting information to ref. 38, where the dependence on its parameters and the achievable time resolution are also discussed in detail.

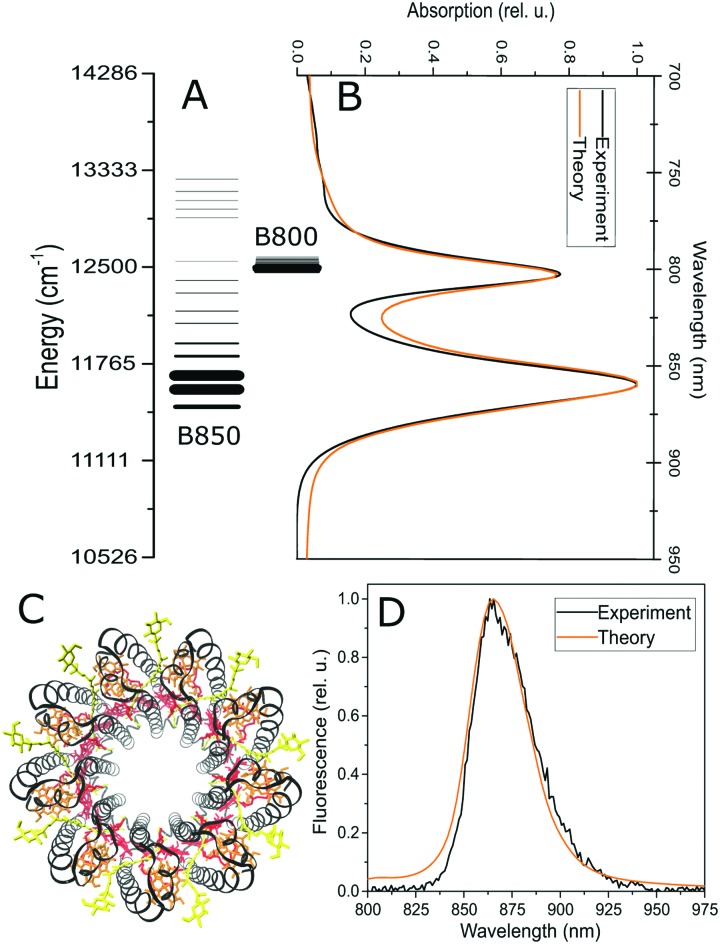
Fig. 1. Structure of the excited state manifold in the LH2 antenna complex. (A) The lines represent individual excitonic states, with energies (position) and oscillator strength (line thickness) averaged over the static pigment energetic disorder. Initial (B) and final (D) light harvesting states in LH2, measured by absorption and fluorescence, respectively. Experimental data (black) are compared to the theoretical model (orange). (C) The structure of the LH2 antenna, with the B850 (red) and B800 (orange) bacteriochlorophyll rings. Black: protein helices, yellow: carotenoids. The picture was rendered in VMD47 based on the ; 2FKW structure used for calculations.8.

2.2. General parameters and dynamics

The pigment dipole moment orientations are taken from the crystal structure of the Rps. acidophila in the RCSB protein databank, structure (; 2FKW).8 The couplings are calculated in the dipole–dipole approximation, taking the value of 6.3 D for the effective BChl transition dipole moment.21,40 The screening factor is adjusted, taking 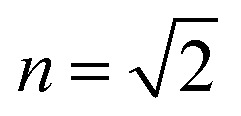, to match the literature values.26,45,46 Note that the results are not very sensitive to the exact scaling of the couplings. The site energies (vertical transitions) are taken to be 12 320 cm^–1 and 12 520 cm^–1 for the B850 BChl dimers and 12 520 cm^–1 for the B800 ring. The full Hamiltonian, including the separation into the B850 and B800 blocks, can be found in Fig. S5 in the ESI.† The bath is described by a multi-component spectral density composed from three Brownian oscillators, as in previous work.45 The parameters of the Brownian oscillators are: reorganization energies {λ₁, λ₂, λ₃} = {30, 27, 330}  cm^–1, and damping factors {γ₁, γ₂, γ₃} = {30, 400, 1200}  cm^–1. The spectral density is scaled by different factors for the B800 and B850 ring pigments, ν₈₅₀ = 0.52 andν₈₀₀ = 0.27. The protein fluctuations in the SM2P and static disorder in the ensemble measurements are modelled by an uncorrelated Gaussian disorder, σ₈₅₀ = 650 cm^–1 and σ₈₀₀ = 71.5 cm^–1. (Note the agreement with the narrower FL excitation lines in the B800 band compared to B850 at 1.2 K ref. 36.) The ensemble spectra were averaged over this disorder, and the single-molecule distributions were generated by sampling this distribution.

The couplings between pigments were fixed and not used as a fitting parameter. The average site energies were taken from the literature45,46 and slightly adjusted in the beginning of the simulations to provide the correct position of the absorption peaks (B800 and B850 can be adjusted independently). The details of the spectral density were taken from ref. 45 and not changed. Overall, the only parameters used for the fitting were the scaling factors ν₈₀₀ and ν₈₅₀ of the coupling to the bath, different for the B800 and B850 rings, and the widths σ₈₀₀ and σ₈₅₀ of the energetic disorder, also different for the two rings. That is, the whole fit was achieved by varying only four parameters (apart from the choice of the model, which can also be viewed as a parameter).

The pure dephasing of the optical coherences is described by a cumulant expansion, which is exact for the employed spectral density. The dynamics within the one- and two-exciton manifold is described by a time-independent Redfield theory. Additionally, the system Hamiltonian is separated into two blocks, the B800 and B850 rings. Between these blocks, the exciton population transfer is calculated by a generalized Förster theory. The Redfield transfer rates are calculated as usual,

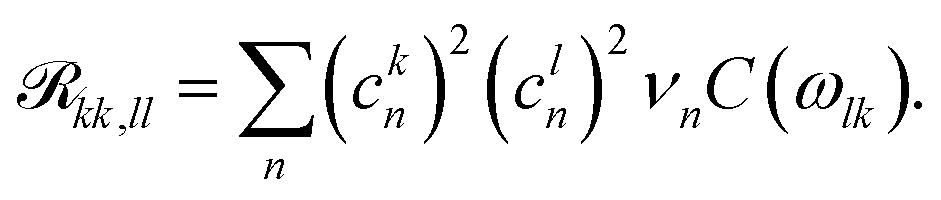2

Here, ckn are the transformation coefficients between the site (n) and exciton (k) basis, and C(ω) is the spectral density. The generalized Förster rates between cluster c₁ and c₂ are calculated as

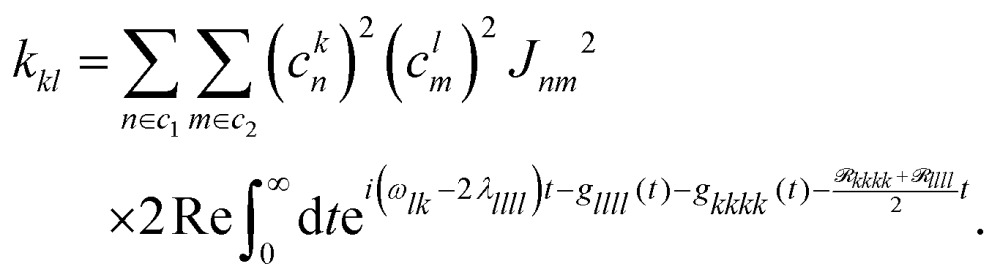3

Here, 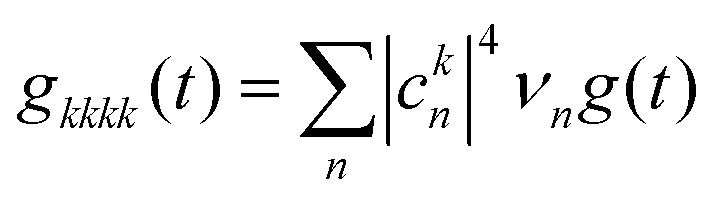is the transformed lineshape function (ν_n is the coupling of site n to the bath) and 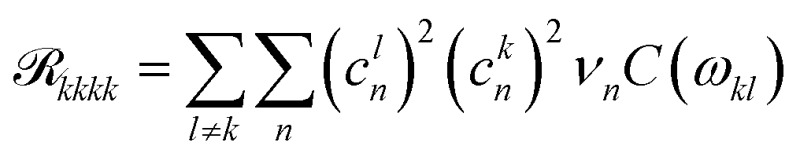is the population decay of the k-th exciton. The reorganization energy λ transforms in the same way as the lineshape function. The lineshape function is given by the spectral density as usual, 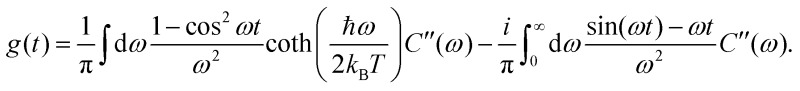The total spectral density is 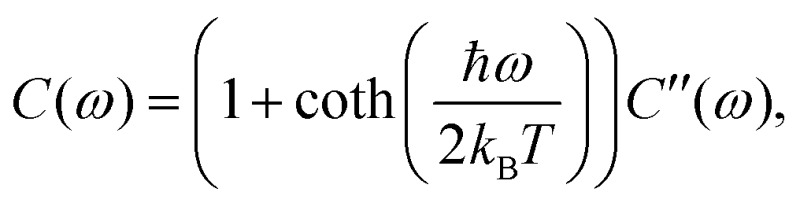where C′′(ω) is the Fourier transform of the imaginary part of the bath correlation function.

2.3. Ultrafast single-molecule spectroscopy

In this section, we develop a connection between the excitonic dynamics, observed by time-resolved spectroscopy, and the relaxation times observed by the SM2P technique. To this end, we have to consider the relevant processes taking place in the near-saturating two-pulse excitation regime. We will suppose that for the processes occurring during and after photoexcitation, the separation of timescales holds in the following order: absorption (tens of fs), energy transfer (around 100 fs), annihilation (units of ps23), and emission (units of ns). We can therefore treat these effects independently, in this order.

Let us first consider the saturating excitation regime. When exciting the dense manifold of states, either of localized or delocalized nature, and observing the subsequent equilibrated fluorescence emission, two kinds of saturation take place. First, each of the transitions gets saturated with increasing intensity:

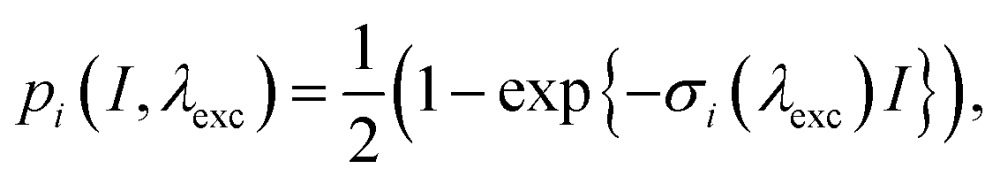4

where p_i is the probability of excitation of the i-th state by a pulse with intensity I, σ_i(λ_exc) is the (generalized to include pulse overlap and duration) i-th state absorption, and λ_exc is the excitation wavelength. At low intensity, the excitation is proportional to the intensity, while at high intensity, it becomes saturated below 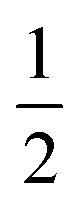. Second, the phenomenon of singlet–singlet annihilation occurs, which is much faster than the excited state lifetime. Singlet–singlet annihilation ensures that if more than one excitation is present in the system, all but one of them are quickly dissipated.1 The probability of having an excitation in the system available for emission is thus

p_exc(I,λ_exc) = 1 – p₀(I,λ_exc) = 1 – Π_i(1 – p_i(I,λ_exc)). 5

The observed fluorescence intensity, proportional to p_exc, thus saturates faster than the individual transitions. The maximum possible excitation probability is 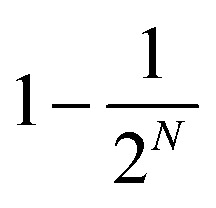, where N is the number of states reachable by the laser. For the dense excitonic manifold, this reaches almost 1. It is the combined annihilation and absorption saturation that we observe when increasing the excitation intensity.

In the experiment, the intensity was set to operate in the saturation regime, i.e. p_exc ≈ 0.95 (p_exc can be set as a fitting parameter, although the results are not very sensitive to its particular value). In order to calculate the saturation levels of the individual states p_i, we first calculate their absorption σ_i. This is done by using their transition dipole moment μ_i0² and the overlap of their lineshape α_i(λ,λ0i) with the pulse spectrum pulse(λ,λ_exc),

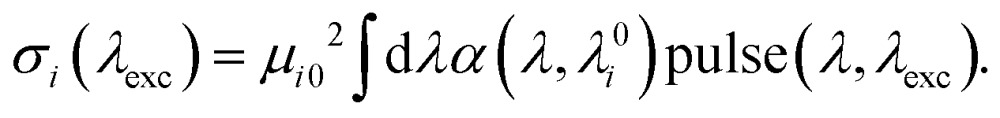6

Next, we set the desired level of saturation p_exc(I,λ_exc) and increase the intensity I in eqn (5) until this saturation is reached. By this approach, the probabilities of excitation of all the states by one pulse, p_i(λ_exc), are obtained.

Now that we have determined how much the individual states are excited by the pulses, we have to connect the observed relaxation times, obtained by fitting with the effective saturated three-level model, to the actual excitation dynamics. As mentioned before,38 due to the separation of timescales discussed above, the singlet–singlet annihilation plays in our favor, effectively enabling us to restrict our model to the one-exciton manifold. The restriction can be justified as follows. There are two situations in which multiple excitations can be present in the LH2 (let us consider two excitations, while the reasoning can be straightforwardly extended to more). First, two excitations can be created by the two pulses of the excitation sequence, and one excitation by each. Annihilation then results in one excitation present for emission, and this case was accounted for in our description of the saturation above. Second, two excitations can be created by a single pulse. They then undergo independent ultrafast relaxation, resulting in two excitations present in the relaxed state (effectively forming a higher-excited state). These then undergo annihilation (relaxation to one-exciton manifold) on a sub-ps timescale. The contribution from the multiply-excited states is therefore not visible in the pulse delay dependence, which enables us to stay within the one-exciton manifold. The contributions from the individual states can then be treated independently.

In deriving the effective transfer rate, there are two limiting situations that need to be taken into account. First, energy relaxation from one resonant state to more than one off-resonant state. In this case, the effective rate is simply the sum of the out-going rates. Second, the contributions from more resonant states. This case is less straightforward as the dip resulting from two independent dips cannot be obtained by, e.g., averaging these two. We thus proceed in a different way, where we construct the effective states and rate from the actual states and rates. To this end, let us define the effective relaxation rate from the i-th state as

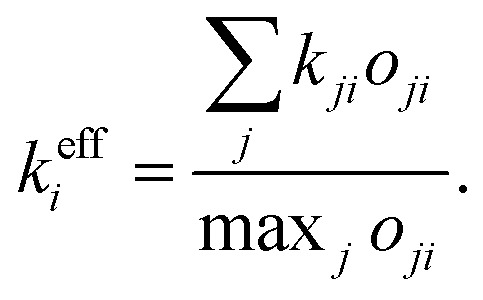7

Here, k_ji is the population transfer rate from state j to state i, and o_ji is the “visibility” of the dip resulting from relaxation from state i to state j. We define this “visibility” by the depth of the dip,

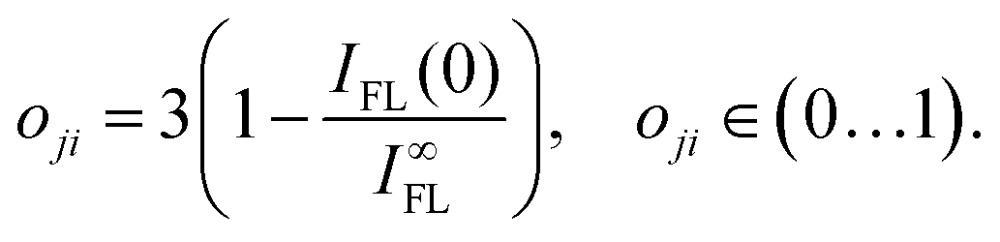8

For short pulses, it can be shown by solving the kinetic equations for the three-state model (eqn (S1) in supporting information to ref. 38) that the visibility can be expressed analytically as

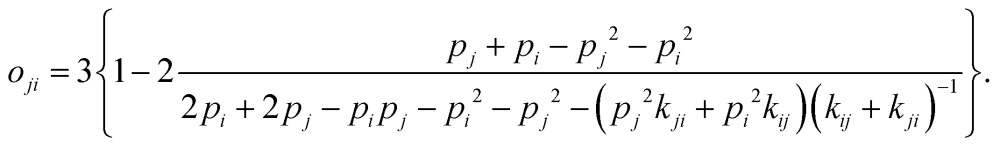9

To check that the construction makes sense in a familiar limit, let us consider one-directional transfer from the partially saturated state 2 to an off-resonant state 1. We get 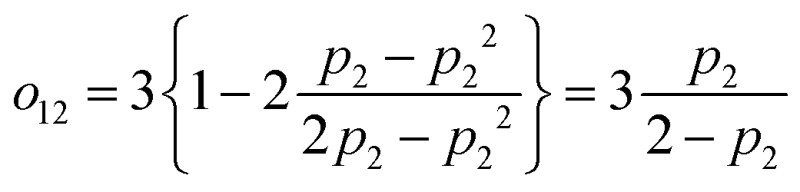, which vanishes for no excitation of state 2 and approaches 1 for the full saturation p₂ → 0.5. For the case of two fully saturated states, p₁ = p₂ = 0.5, we get o₁₂ = o₂₁ = 0, as expected. In the effective relaxation rate defined by eqn (7), the rates are additive, weighted by a fraction of the visibility of their dip to the most visible one. Such an approach keeps both the rate additivity and assumed full saturation of the effective state. Let us now construct the resonant state, which is assumed to be fully saturated in the model. The contribution of the individual states to this state should be weighted by their contribution to the overall signal, which is given by their excitation probability p_i. The effective observed rate is then

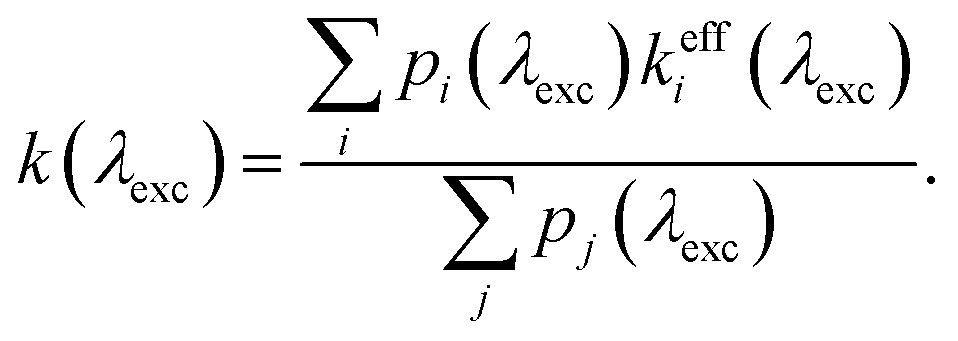10

As a check, let us consider the relaxation from two fully saturated states 1, 2 to two off-resonant states 3, 4. We obtain 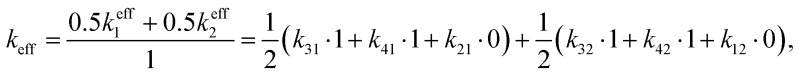which is the average of the rates from the two resonant states, which consist of the added rates of the off-resonant states.

It should be mentioned that in the case of incomplete saturation under the given experimental conditions, the extracted relaxation rate can be underestimated. This can be seen from the fact that a lower intensity yields a smaller dip visibility (shallower dip). In the fitting formula (1), the depth of the dip decreases both with longer relaxation time and lower excitation intensity. Therefore, fitting with a fully-saturated model results in a compensation by longer lifetime. This was probably the case with the 780 nm-excitation measurement in ref. 38. The same distribution measured in this work at a fully-saturating intensity presents a somewhat faster relaxation, in agreement with the theoretical prediction.

2.4. Statistical analysis

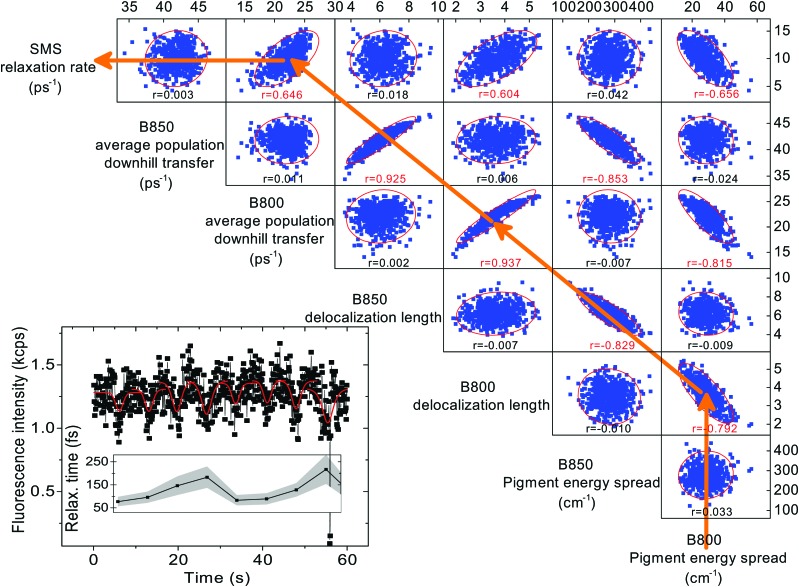
For each excitation wavelength between 100 and 200, measured relaxation times obtained from about 20 different complexes were analyzed. Their distributions were plotted in the form of histograms. Correspondingly, the theoretical calculations were repeated for 200 realizations of energetic disorder. Adding more realizations did not result in further changes of the calculated quantities. For the experimental histograms, the errors were estimated from the number of counts per bin assuming independent measurements. For the statistics presented in Fig. 5 and Fig. S2 (ESI†) 500 realizations of disorder were used. Pearson linear correlations were calculated between the relevant quantities in the data processing program Origin. For each pair of variables, the Pearson correlation coefficient is given, and p = 0.05 significant correlations are highlighted. Also, 95% confidence ellipses are drawn. The quantities are calculated for every disorder realization in the following way. The SMS relaxation rate is given by eqn (10) and averaged over all the excitation wavelengths used for measurement. The average downhill population transfer is calculated as an average overall transfer between the excitons in the respective ring of pigments, kdowni_{i∈B850/B800}, where 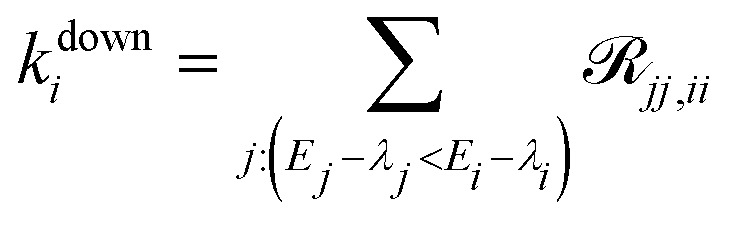. The delocalization length is calculated in the standard way, as an average of inverse participation ratios, 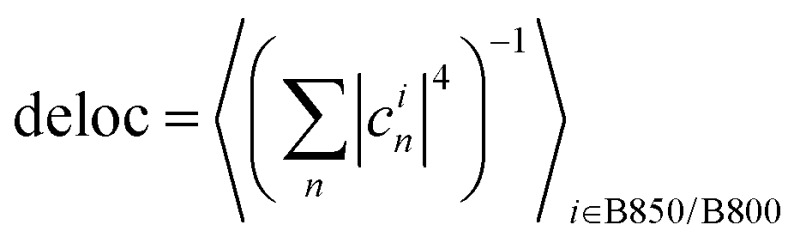. The pigment energy spread is the square root of variance of the pigment energies.

Fig. 5. Correlation matrix of various calculated quantities. Blue points: individual disorder realizations, corresponding to measured relaxation times. Red ellipses: 95% confidence ellipse. Under each correlation plot, the Pearson's correlation coefficient r is given, red values represent p = 0.05 significant correlations. The orange arrows represent the causality of our reasoning: a smaller B800 pigment energy spread leads to larger B800 delocalization, which leads to a faster overall B800 downhill transfer, which corresponds to a faster observed SMS relaxation rate. The definition of the calculated quantities can be found in the Materials and methods section. Inset: An example of a measured ultrafast SMS fluorescence trace of a single LH2 complex, excited at 800 nm, with extracted relaxation times (data from ref. 38, obtained by recording the intensity and varying the delay between the pulses). Red dips: three-state effective description fits by eqn (1); shaded area: standard error of the fits. This trace demonstrates how the individual realizations are sampled on the slow timescale of seconds.

3. Results

3.1. The structure of the excitonic states

The LH2 complex consists of two rings of pigments, which give rise to its two characteristic well-separated absorption bands, see Fig. 1C. Reflecting the structure of the complex8 and the resulting interpigment couplings, we divide the LH2 into the B850 ring (18 pigments arranged as 9 dimers) and the B800 ring (9 pigments) in our model. The bright states of the former ring are mainly responsible for the absorption band at 850 nm, while the latter ring is almost exclusively responsible for the absorption at 800 nm, hence the standard naming scheme of the rings. It has been shown previously that there is an appreciable exciton delocalization within both of the rings.26,48–50 To capture this aspect, we treat the rings as strongly-coupled excitonic blocks, and we describe their dynamics on the basis of their energy eigenstates (excitonic states) by the standard Redfield theory.39,51 This approach has been previously successfully used to describe the ultrafast intra-ring transfer.17,45 The energy transfer between the strongly coupled blocks of pigments, i.e. between the B800 and B850 rings, is well described by the generalized multi-chromophoric Förster theory.52–54 Previous theoretical26,45 and experimental25,28,43 studies indicate that the low-frequency part of the bath spectral density (i.e. protein and slow pigment vibrations) has the strongest influence on the pigment excitation dynamics. We therefore model the pigment environment by a three-component low-frequency spectral density of modes, taken from ref. 45 and 55. The energetic disorder of the pigments is described by a Gaussian distribution of the transition energies of individual pigments. The model has only a very small number of fitting parameters: three transition energies (two for the B850 dimers and one for B800), two couplings of the pigments to the vibrational bath ν_800/850 (different for the B800 and B850 pigments) and two widths of the energetic disorder σ_800/850 (again different for the two rings). Moreover, since the couplings, being calculated based on the crystal structure of the LH2 (see section Materials and methods), are not varied, the pigment energies are fixed by the steady state absorption and fluorescence spectra. All four remaining parameters influence spectral line shapes in a similar way (they make them broader), however, their influence on the dynamics measured by time resolved spectroscopy is profoundly different. Within the Redfield theory, the couplings ν_800/850 of the pigments to the bath increase energy relaxation rates, while increased disorder disrupts the regular energy landscape, widens the energy gaps and leads to an overall slowing down of the population transfer within the rings. In generalized Förster theory, the parameter influence is entangled by the interplay of delocalization, energy gaps and linewidths. Overall, we are therefore left with only four parameters to describe all the time-resolved spectroscopy experiments, and these parameters have sufficiently independent influences on the spectra and dynamics to allow for a unique fit. The steady state and transient absorption spectra are calculated in a standard way, using the response function formalism and the doorway-window picture.45,46,56 All details can be found in the Methods section and in the ESI.†

3.2. Linear absorption and fluorescence

In order to characterize the initial and final states in the excited state manifold, we measured the steady state absorption and fluorescence spectra. In the absorption spectrum, Fig. 1B, we can see the two characteristic peaks corresponding to the absorption of the B800 and B850 rings of pigments. The fluorescence emission, shown in Fig. 1D, occurs from the lowest-energy states (corresponding to the canonical quasi-equilibrium in the excited state) and it is Stokes-shifted to the red from the absorption. These two types of spectra provide a strong constraint on the structure of the excitonic manifold, which is depicted in Fig. 1A. The widths of the observed bands arise from a combination of both the homogeneous linewidth (determined by the interaction with the environment and lifetime broadening due to energy transfer, see eqn (1) in the ESI†) and the inhomogeneous broadening resulting from the pigment energy disorder. Next to fixing the average pigment site energies, the linear absorption and fluorescence spectra thus present important constraints on the width of the energetic disorder and on the strength of the coupling to the phonon bath. An equivalent model has been used in the past to reproduce not only the ensemble, but also the single-molecule fluorescence spectra of LH2.16 The lineshapes are calculated using a cumulant expansion for pure dephasing and including the lifetime broadening, see the ESI† for more details.

3.3. Broad- and narrow-band transient absorption

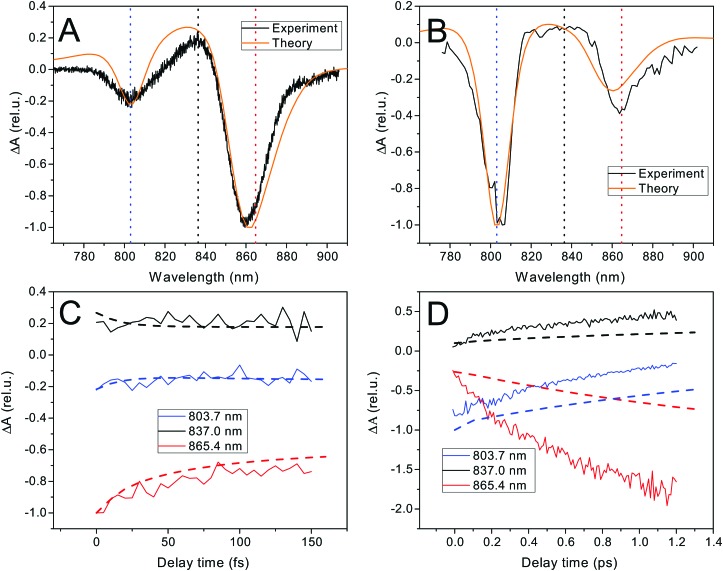
The fast excitation dynamics in LH2 proceeds on two timescales. First, an ultrafast energy relaxation within each of the rings, and also between the B800 states and the hot B850 states, occurs within tens to hundreds of femtoseconds.20,25 This initial dynamics can be well studied by transient absorption (TA) with ultrashort i.e. broadband pulses. We use an all-parallel polarization scheme in order to include the anisotropy decay induced by the exciton dynamics. The time zero spectrum, shown in Fig. 2A, has two negative peaks corresponding to the ground state bleach (GSB) and stimulated emission (SE) of the B800 and B850 rings, and a positive excited state absorption (ESA) from the B850 ring (the ESA of the B800 ring overlaps with the negative peak because of the narrow distribution of the excitonic energies). The dynamics within the first 100 fs, shown in Fig. 2B, is dominated by the decay of the B850 peak. (After subtraction of the decay dynamics, a Fourier transform reveals low-frequency oscillations.) The theoretical spectrum and kinetics fit extremely well, indicating that the excitonic state structure and the Redfield theory description of ultrafast dynamics are appropriate. On a ten times slower timescale of picoseconds, the transfer between the rings takes place. This can be monitored by narrowband TA, where we predominantly excite the B800 ring and observe the energy transfer to the B850 ring. We use a magic angle polarization configuration, which ensures an isotropic signal, yielding only population transfer signatures. As expected, the amplitude of the B800 peak is much higher at the initial time, Fig. 2B. The appreciable amplitude of the B850 peak is given by the presence of high-exciton components of the B850 states in the B800 region. In the kinetics, shown in Fig. 2D, the transfer between rings is apparent in the decay of the B800 peak and the rise of the B850 peak and its ESA. The time zero theoretical spectrum fits again very well, reflecting the correct exciton composition. The theoretical energy transfer between the rings, here described by generalized Förster theory, is somewhat slower than in the measurement, where the transfer time is 0.7–0.8 ps (extracted by an exponential fit), in agreement with ref. 22 and 23. This inter-ring transfer in LH2 is notoriously difficult to describe, as the relevant pigment coupling is in the intermediate regime between the well-understood weak and strong coupling limits (see Hamiltonian in the ESI,† Fig. S5). The currently employed theory neglects the partial initial delocalization between the rings, which probably speeds up the initial transfer.21,22,37,57 There is also possibly some room for improvement of the fit by altering the model parameters. This, however, is at the expense of the accuracy in describing the ultrafast transfer. We ultimately need to calculate the ultrafast single-LH2 energy relaxation rates that depend only weakly on the transfer between the rings. For this purpose, the current model is sufficiently adequate, see also the Discussion section below. The full measured TA spectra can be found in the ESI,† Fig. S3. The strong constraints they put on our FEM make sure that it describes the fast excitation dynamics well.

Fig. 2. Ultrafast and fast excitation dynamics in LH2. (A and C) Broadband TA spectrum, T = 0 spectrum (orange: theory, black: experiment) and kinetics at three peak wavelengths (dashed: theory, full: experiment). The decay is caused by intraband relaxation and anisotropy decay. (B and D) Narrowband TA spectrum excited at 805 nm, T = 0 spectrum (orange: theory, black: experiment) and kinetics at three peak wavelengths (dashed: theory, full: experiment). The decay of the 803.7 nm peak and rise of the other two components reflects the transfer between the B800 → B850 rings.

3.4. Ultrafast single-molecule spectroscopy

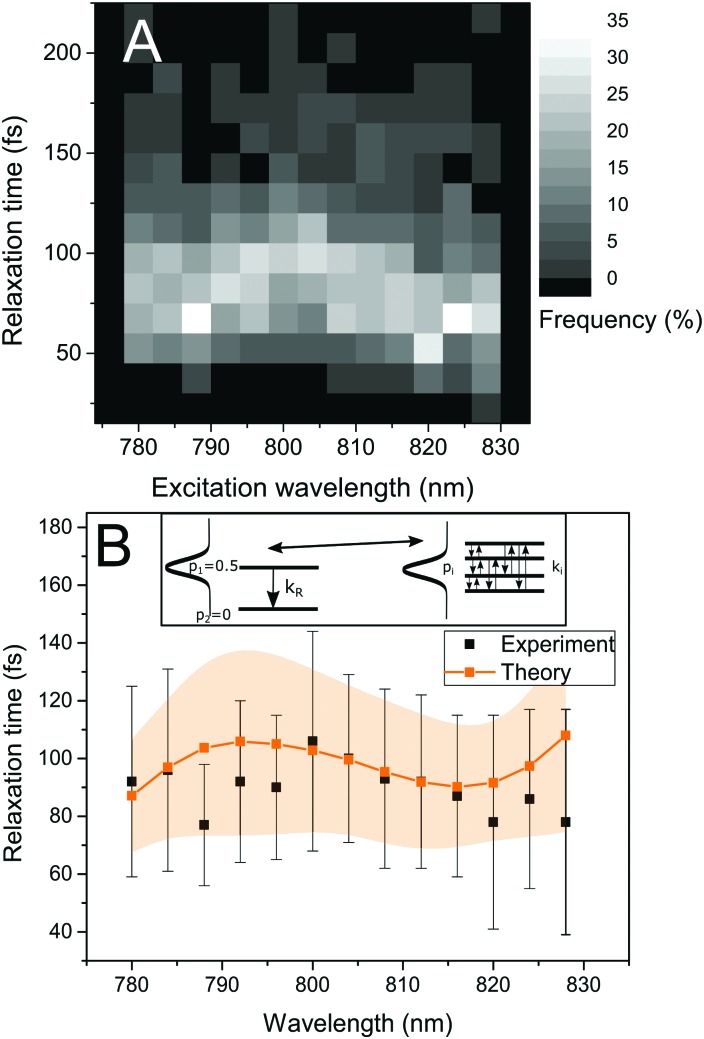
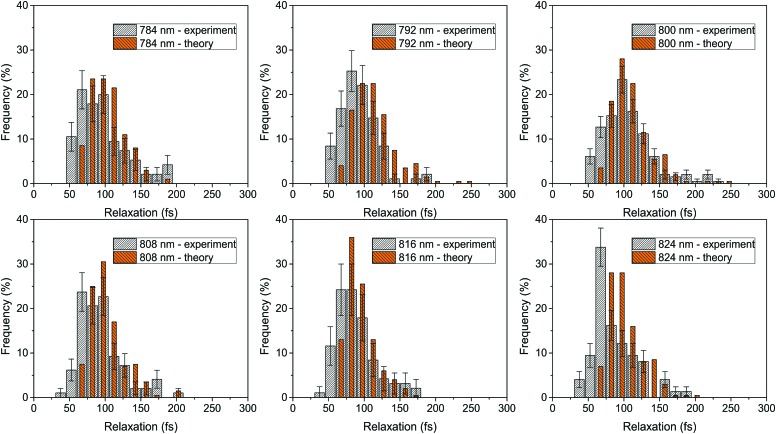
To observe the ultrafast energy relaxation in individual LH2s, we employ incoherent two-pulse SMS, one of the few recently-emerging ultrafast single-molecule techniques.58 As described previously,38,59 this technique measures the effective energy relaxation time away from the spectral region of excitation. Employing pulse pairs, this approach is not directly limited by the pulse duration and we can observe down to about 40 fs relaxation times with 200 fs pulses (which can have about 5 nm narrow bandwidth).38 We scanned the excitation wavelength across the B800 band, and, for all measured excitation wavelengths, we recorded a distribution of relaxation times, shown in Fig. 3A. We can see that both the distribution widths and mean positions vary across the excitonic manifold. The depicted relaxation times are extracted by fitting the experimental results with an effective three-state model. This model includes a ground state, a state resonant with the laser, and an off-resonant state, (see inset in Fig. 3B left, where the resonant and off-resonant states are depicted). Due to the amount of noise in the data (intrinsic photon-counting shot noise), fitting by a more elaborate model would not be unique. Instead, we have chosen to construct an effective state description from the common Frenkel exciton model of our LHC. The construction is done by the following procedure. First, we select the contributing excitonic states of LH2 by the overlap of their absorption line with the laser pulse. Next, as the experiment is done under near-saturating conditions, we combine the saturation of the two-level transition with the fact that at these intensities very effective singlet–singlet annihilation occurs,23 and increase the light intensity until reaching the desired fluorescence saturation point. This yields the probabilities of the excitonic states to be excited. Then, we calculate the effective excitation escape rate for every excitonic state by weighing the outward population transfer rates with the visibility of the intensity dip they would produce. Finally, the effective energy relaxation rate is given by the sum of the effective rates weighted by the excitonic excitation probabilities. The mathematical description of the procedure is straightforward, and it can be found in the Materials and methods section. As a result of this construction, we can calculate the single-LH2 effective energy relaxation times from the excitonic model by considering particular realizations of the energetic disorder. The mean energy relaxation times across the excitonic manifold obtained by this procedure can be found in Fig. 3B. As can be seen, the correspondence between the theory and measurement is satisfactory. Moreover, for every point in Fig. 3B, we have the whole distribution of relaxation times at our disposal. In Fig. 4, the measured and calculated distributions for six excitation wavelengths are presented, showing a fine agreement both in distribution shape and positions. This is the sought connection between the static disorder in the ensemble spectroscopy and the slow dynamic fluctuations of the single complexes. The relaxation time distributions are quite sensitive to the model parameters. As the ultrafast relaxation is well-described by the Redfield theory, the average relaxation rates scale with the strength of coupling to the bath ν_850,800. The relaxation time distribution shape and width change with the interpigment coupling J and the energetic disorder width σ_850/800. This sensitivity is demonstrated in Fig. S1 in the ESI.†

Fig. 3. Ultrafast energy relaxation in single LH2 complexes. (A) Experimental relaxation time distributions measured at various excitation wavelengths. The shades of gray correspond to the frequency of occurrence. (B) Mean relaxation time as a function of the excitation wavelength, experiment (black points) compared with theory (orange). The vertical marks for the experimental points and the shaded area for the theoretical data represent the standard deviation. Inset: Schematic of the transformation connecting the effective two-level description used for fitting the data and the realistic exciton states in FEM.

Fig. 4. Relaxation time distributions for six excitation wavelengths across the B800 band. The experiment (white) is compared with theory (orange). The error bars denote the errors of the experimental histograms, estimated as described in the Materials and methods section.

4. Discussion

By explaining all our experimental results within a single theoretical framework, we have managed to connect the ultrafast excitation dynamics with the slow protein motion. The ‘static’ energetic disorder of the pigments in the ultrafast ensemble measurement is sampled by the slow protein motion, as it moves on its potential energy surface. The fact that the full extent of the energetic disorder is sampled on the biological timescale of seconds brings the potential control over light harvesting into the domain of protein motion. To investigate this further, we evaluate the correlation between various quantities in our FEM. In Fig. 5, the correlation matrix of the pigment energies, exciton delocalization length, energy transfer rate and observed ultrafast SMS rate is presented. The process of how the protein fluctuations influence the light harvesting is indicated by orange arrows and proceeds as follows. The protein determines the energy landscape of the pigments. We find that the smaller the spread of the pigment energies, the larger the excitation delocalization between the pigments. Larger delocalization then leads to faster population transfer, and faster population transfer corresponds to faster observed energy relaxation. We observed this change in the effective delocalization of states in the antenna when repeatedly measuring the ultrafast relaxation time in a single LH2 complex, as shown in the inset in Fig. 5.

As seen from Fig. 2D, apart from the ultrafast predominantly intra-ring transfer, there is also a slower transfer from the B800 to the B850 ring, occurring on a ps timescale. Because our ultrafast SMS technique is sensitive to the ultrafast energy relaxation, we do not directly observe the transfer between the rings. However, this transfer is strongly influenced by the excitonic effects within the rings.21,54 As such, it should be affected by the very same fluctuations that alter the ultrafast rate. To test this hypothesis, we have calculated the correlation of the thermally averaged B800 → B850 transfer rate with the quantities of our FEM presented in Fig. 5. The results, presented in Fig. S2 in the ESI,† show that the fast transfer between the rings correlates with the ultrafast SMS rate. Interestingly, this demonstrates that the ultrafast intra-ring and fast inter-ring transfers are not independent but are controlled by the same parameters. Observation of the ultrafast relaxation then also provides information about the overall energy transfer in the LH2 complex.

Our model fully recovers the observed dynamics by assuming that the protein modulates only the electronic transition energies of the antenna pigments. Importantly, the timescale of this modulation is slower than the time resolution of our SMS experiment (seconds). In the opposite case, we would observe (at least partial) averaging of the measured times, which would then exhibit a narrower distribution than that predicted by theory. It should be mentioned that, as we have shown before, due to the intrinsic photon counting shot noise, a complex with a constant relaxation time will yield a Gaussian distribution about 30 fs wide.38 This fact results in a slight broadening of the measured distributions, giving room for a small amount of fluctuations in the sub-second range. We note that the protein conformation in principle could (and to some extent probably does) cause many more changes than that of the pigment transition energies. Other possibly fluctuating quantities include the inter-pigment couplings, with the possible formation of states with charge-transfer character, and the strength of the interaction of the pigments with their environment. In the ensemble spectroscopy of LH2, such variations are not observed, as the measured inhomogeneous broadening can be fully accounted for by assuming a distribution of pigment energies. Strikingly, we find that this holds also when following the fluctuations of a single LH2 protein. This leaves us with two options: either the other quantities are not as susceptible to protein conformational change, or their variation does not have such a profound influence on the excitation dynamics. In both cases, we conclude that the protein-motion-induced pigment energy landscape variations play a decisive role in modifying the light-harvesting function of single LH2 complexes. This is in agreement with the SMS measurements of the distribution of spectral peaks of single LH2 complexes.16,30,31,36

Another issue that needs consideration is that all pigment transition energies in a single LH2 can in principle be modulated by their local (membrane) environment. This leads to an additional ‘intercomplex’ energy disorder.29,50 However, as was demonstrated in ref. 29, this disorder is decreased when all complexes feel a similar detergent environment, which is also the case for our measurement. Furthermore, for the energy transfer, only the energy difference between the states matters. The energy shift of the whole LH2 then only results in an effectively displaced excitation wavelength. Single-molecule measurement demonstrated only a small 2 nm shift of the whole B850 band between the native membrane and the detergent environment.35 Also, the proposed intercomplex disorder width of about 60 cm^–1 (≈3.8 nm)29,50 is smaller than our pulse width in the SMS measurement, and the relaxation time wavelength dependence, shown in Fig. 3B, is a slowly-varying function. Our SMS measurement is therefore sensitive only to the disorder within the LHCs. This agrees well with the observation in ref. 38 that a single LH2 can sample the whole ensemble distribution of relaxation times.

Looking carefully at the relaxation time distributions in Fig. 4, we find that the shortest observed relaxation times around 50 fs are absent in the theoretical simulations. One possible reason is the absence of intramolecular vibrational relaxation in our Redfield model description, which would add a possible relaxation path, even though the bacteriochlorophylls in LH2 have a small Stokes' shift (about 5 nm),28 which by itself is not enough to escape the excitation pulse of comparable width. Another possibility is the already mentioned slower transfer between the B800 and B850 rings, the speedup of which could add to the observed rate. Yet another possible explanation of the narrower theoretical distributions is a slight underestimation of the B800 ring disorder width: increasing this disorder leads to broader distributions but also too slow ultrafast excitation dynamics. This could, however, be an artifact of the Redfield theory, which is slightly slower in describing the intra-B800 transfer.55 In order to investigate such discrepancies further, a more elaborate model for the excitation dynamics is needed. However, at the more detailed level of description, apart from the bath memory and dynamic reorganization, the driving by the strong excitation light and the interaction of the resulting multiple excitations should also be included. We feel that the increased complexity would not provide new insights, especially when considering the accompanying increase in the number of fitting parameters and the experimental error of the single-molecule measurements.

There is an ongoing debate regarding the origin of the energetic disorder. Some temperature dependent measurements suggest a heterogeneity/anharmonicity of the protein potential energy surface (PES).17,60 At the same time, for most of the ambient temperature experiments, including the SMS studies, the disorder was successfully described by a normal distribution.16,31,32,36 The argument for this description is based on many relevant protein degrees of freedom, leading to a Gaussian distribution of the energies thanks to the central limit theorem. Our work, where we observe not only disorder-caused broadening, but also the actual distributions, supports the harmonic disorder description, at least in the room temperature case. In a recent work, an electrostatic mechanism was proposed that may produce non-Gaussian energetic disorder.61 It would be of interest to test whether an excitonic model with such an energetic disorder can also reproduce our experimental relaxation time distributions. This would provide even more information on the details of the protein influence on the excitation dynamics. However, as recent work suggests, the site energy variation of the chlorophylls mainly results from the macrocycle deformation.11,30,62,63 Also, in the crystal structure of LH2 from Rps. acidophila, such a deformation of the BChl macrocycle was seen.7 In reality, we expect many contributing factors to the energetic disorder, which would result in the Gaussian disorder employed in our description. The observed timescale of the relaxation time fluctuations poses a particular challenge for a theoretical or computational explanation as the changes occur in seconds. Such a timescale is very difficult to study with current computer models of protein dynamics, although the latest molecular dynamics simulations of protein dynamics are reaching the millisecond range.64 In this work, we have shown how protein fluctuations influence the light harvesting in single LHCs by changing the pigment energy landscape. The precise mechanism of the pigment energy modulation (for instance, through the macrocycle deformation) remains to be elucidated, e.g., by quantum chemistry calculations similar to ref. 57. It would be very interesting to investigate what kind and what magnitude of protein conformational change are needed to account for the pigment energy variability observed here. At the same time, the variation in other quantities could also be tested and its relative magnitude compared to the energetic disorder.

One possible way to influence the extent of the protein fluctuations is to perform the ultrafast SMS measurement at low temperature. By substantially lowering the temperature, the LH2 proteins could be frozen in their configurations. As a result, the ensemble ergodicity would not apply anymore, the relaxation time distribution obtained from one complex would be a narrow part of the ensemble one. Also, the timescale of relaxation time fluctuations can be expected to be slower. Furthermore, previous work has shown that at cryogenic temperatures, the protein fluctuations become anharmonic, adopting multiple possible configurations.17,60 Comparison of low ambient and low temperature measurement could therefore provide interesting information on the nature of the protein fluctuations and the related pigment energetic disorder.

As also observed by SMS, in LHCs of higher plants and algae, the protein controls their light harvesting state. Pronounced changes in the protein conformation were found to completely switch the state of these complexes. In the case of the Lhca antennas associated with photosystem I, the protein switching leads to the formation of states with charge-transfer character.65 These states have low energy (red forms) and may act as excitation traps, but in reality contribute to light harvesting by absorbing photons in the >700 nm spectral region that can still be used effectively for charge separation.66 In the case of the Lhcb antennas associated with photosystem II, the protein conformation change can switch the whole complex from a bright, light-harvesting state to a dark, highly dissipative state.67–69 This enables the plants and algae to rapidly dissipate otherwise harmful excess excitation energy. In contrast, the purple bacteria typically live in low-light, near-anoxygenic conditions. They therefore do not have such a photoprotective mechanism. Interestingly, at high illumination intensities33 or when immobilized inside a thin polymer film,18 LH2 can also dwell in quenched states. These results showed that in LH2, the protein conformational dynamics can also significantly switch the state of the complexes. However, under low illumination and in a detergent, that is, closer to in vivo conditions, the dark states are only very briefly visited, see a typical ‘blinking’ trace in Fig. S4 in the ESI.† They therefore do not seem to have functional significance. Also, as seen in the previous SMS measurement of the spectral dynamics of single LH2 antennas from Rps. acidophila, there are only mildly red-shifted states present, and they can be fully described by the FEM without mixing with charge transfer states.16 Finally, the observed energy relaxation time distributions are relatively narrow and, importantly, no complexes with drastically slowed down dynamics were observed. The desired function of the LH2 complexes is to absorb light and transfer the excitation energy as efficiently as possible at all times. At the same time, being part of a living organism at ambient temperature, some fluctuations of the protein are inevitable. Therefore, we propose that the LH2 complex is designed as a robust, efficient light-harvesting antenna. This is achieved by constructing the protein scaffold in such a way that the excitation remains delocalized between several pigments even in the presence of physiological fluctuations. In order to support this hypothesis, we calculated the energy relaxation in case the coupling is reduced by half or the B800 ring energetic disorder is doubled. The results can be found in Fig. S1 in the ESI.† In both cases, we find that the average energy relaxation slows down and the relaxation time distribution becomes wider. The natural LH2 is therefore constructed to robustly withstand environmental fluctuations and efficiently harvest sunlight.

5. Conclusions

In this work, we combine ultrafast ensemble and single-molecule spectroscopy measurements on LH2, the light harvesting antenna of purple bacteria. We describe all of the experimental data by a Frenkel exciton model with combined Redfield/generalized Förster dynamics. We derive the theoretical description of the ultrafast SMS, bringing it one step closer to becoming a standard technique. The combination of spectroscopic techniques allows us to assess the influence of slow environmental fluctuations on the ultrafast light-harvesting function. We find that of all the potentially important noise timescales, the slow fluctuations on a timescale of seconds have a decisive influence on the ultrafast energy transfer within the antenna. In agreement with previous work, we find that these fluctuations predominantly alter the energies of the pigments. In future work, it would be very interesting to determine what kind and magnitude of protein conformational changes are needed to produce such variations. Based on the theoretical model, we propose that the LH2 protein scaffold is constructed in such a way that the excitation remains delocalized between several pigments, even in the presence of physiological fluctuations. As a result, LH2 functions as a robust, efficient light-harvesting antenna. As such, it offers an interesting blueprint for understanding natural light-harvesters and the design of artificial ones.

Conflicts of interest

There are no conflicts to declare.