Abstract
Models of the representation of numerosity information used in discrimination tasks are integrated with a diffusion decision model. The representation models assume distributions of numerosity either with means and standard deviation that increase linearly with numerosity or with means that increase logarithmically with constant standard deviation. The models produce coefficients that are applied to differences between two numerosities to produce drift rates and these drive the decision process. The linear and log models make differential predictions about how response time (RT) distributions and accuracy change with numerosity and which model is successful depends on the task. When the task is to decide which of two side-by-side arrays of dots has more dots, the log model fits decreasing accuracy and increasing RT as numerosity increases. When the task is to decide, for dots of two colors mixed in a single array, which color has more dots, the linear model fits decreasing accuracy and decreasing RT as numerosity increases. For both tasks, variables such as the areas covered by the dots affect performance, but if the task is changed to one in which the subject has to decide whether the number of dots in a single array is more or less than a standard, the variables have little effect on performance. Model parameters correlate across tasks suggesting commonalities in the abilities to perform them. Overall, results show that the representation used depends on the task and no single representation can account for the data from the different paradigms.
Keywords: Diffusion model, approximate number system, response time and accuracy, integrated models, individual differences
What is the mental representation of numerosity? This is a classic question in psychophysics and also a topical one because it has been claimed that scores on simple, non-symbolic numerosity tasks are predictive of math development in childhood and math achievement later in life (Halberda et al., 2008; Park & Brannon, 2013). For instance, for a large internet sample, Halberda et al. (2012) found that performance on a nonsymbolic task was related to numeracy ability across the life span (to age 85). Currently, numerosity knowledge is said to be represented in an Approximate Number System (ANS) in which numerosities are represented by distributions around their central values (Dehaene, 2003), a system which might be present in animals as well as humans (Gallistel & Gelman, 1992). There is also a body of work in which research using animals and human neurophysiological measurements has been used to identify neural structures that are involved in numerosity judgments (e.g., Hyde & Spelke, 2008, Nieder & Miller, 2003; Piazza et al., 2004). We review these in the discussion.
It has also been asserted that the ability to perform non-symbolic tasks forms a scaffold on which symbolic mathematical skills are built (Gallistel & Gelman, 1992, 2000). This was expressed explicitly by Park and Brannon (2013): “Humans and nonhuman animals share an approximate number system (ANS) that permits estimation and rough calculation of quantities without symbols. Recent studies show a correlation between the acuity of the ANS and performance in symbolic math throughout development and into adulthood, which suggests that the ANS may serve as a cognitive foundation for the uniquely human capacity for symbolic math.” In accord with this, Park and Brannon (2013, 2014; also Hyde, Khanum, & Spelke, 2014) found that repeated training on nonsymbolic arithmetic improved symbolic arithmetic, but repeated training on other tasks (a visuo-spatial short-term memory task and a numerical ordering task) did not. However, it has also been argued that symbolic and nonsymbolic magnitude knowledge have separate effects on mathematics achievement (Fazio et al., 2014) and that the relation between nonsymbolic performance and achievement is currently not clear (De Smedt et al., 2013).
There are currently two, competing, ANS models that have roots in Weber and Fechner’s work in the 1800’s. In one, numerosity in the ANS is represented on a linear scale and variability around numerosities increases as numerosity increases. In the other, numerosity in the ANS is represented on a decreasing logarithmic scale with equal variability around all numerosities (Figure 1). In both, the distributions of variability are Gaussian (Dehaene & Changeux, 1993; Gallistel & Gelman, 1992; see Zorzi et al., 2005, for a review). Both models explain two standard findings (cf., Weber’s law) - why it is easier to discriminate 10 from 20 objects than 18 from 20 (accuracy decreases as the difference in two numerosities decreases, the distance effect) and why it is easier to discriminate 20 objects from 30 than 60 objects from 70 (accuracy decreases as numerosities increase; the size effect). It has been claimed that the two models are not discriminable (Dehaene, 2003) but that argument is based solely on the accuracy with which numerosity tasks are performed. Here we show that they are, in fact, discriminable when response times (RTs) are considered.
Figure 1.
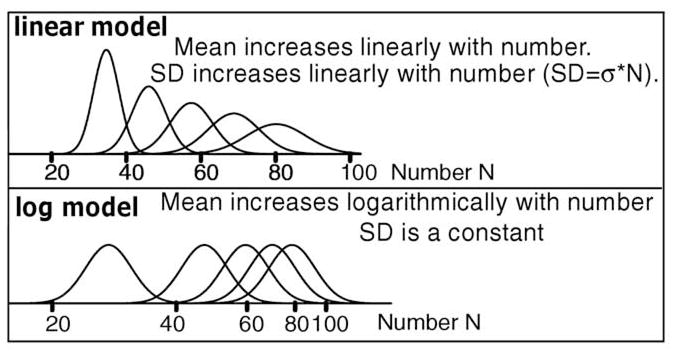
Models of numerosity representation.
In this article, we present a model for numerosity discrimination, a fundamental numeracy skill. Typical tasks include deciding whether the number of blue dots in a display is greater or less than some specified number, deciding whether there are more blue dots in a display than yellow dots, and deciding whether there are more dots in one versus another array that are spatially separated. We model RTs and their full distributions for both correct responses and errors jointly with accuracy. We test the representations of numerosity that the ANS models predict by mapping them to accuracy and RT data via the diffusion decision-making model (Ratcliff, 1978; Ratcliff & McKoon, 2008). When the ANS models are integrated with the diffusion model, they make strong differential predictions because they must account for RTs as well as accuracy.
One reason an approach that explains the decision-making process is needed is that the field of numerical cognition has been unable to settle on empirical measures to be used in individual-difference analyses. Considerable controversy has arisen about the presence or absence of correlations among dependent variables and between them and individual differences such as IQ and math ability. In the diffusion model and other sequential-sampling models (Ratcliff & McKoon, 2008; Ratcliff & Smith, 2004), accuracy and RTs arise from the same underlying components of processing but in the numeracy literature, some hypotheses have been based on RTs, some on accuracy, and some on the slope of a function that relates accuracy or RTs to the difficulty of a test item. Many studies in numeracy have used RTs alone and many have used accuracy alone, and this has led to inconsistent findings about how individual differences affect performance. For example, sometimes correlations are found between symbolic tasks (“is 5 greater than 2”) and nonsymbolic tasks (“is the number of dots in one array greater than in another array”), and sometimes not (e.g., Price, et al., 2012; Sasanguie, et al., 2011; Maloney et al., 2010; Holloway & Ansari, 2009; De Smedt et al., 2009). Sometimes correlations are found between non-symbolic number tasks and math ability, and sometimes not (e.g., Lyons & Beilock, 2011; Libertus et al., 2011; Gilmore et al., 2010; Halberda et al., 2008, 2012; Inglis, et al., 2011; Holloway & Ansari, 2009; Mundy & Gilmore, 2009; Price, et al., 2012).
In a comprehensive study, Gilmore et al. (2011) found little correlation between all combinations of accuracy and RT across a range of symbolic and nonsymbolic tasks. A recent meta-analysis by Chen and Li (2014) further illustrated the extent of the problem. For 36 recent studies, they found 21 used overall accuracy, 9 used mean RT, 17 used the Weber fraction (an accuracy-based measure), and 8 used a numerical distance effect based on RT. Other analyses of individual differences confirm this diversity by reviewing studies that use a range of different dependent variables (De Smedt at al., 2013; Fazio et al., 2014). In the face of such inconsistencies, and their finding that RTs and Weber fractions were largely uncorrelated in an experiment they conducted, Halberda et al. (2012, p. 11116) suggested that the two dependent variables might index independent abilities. Price et al. (2012, p. 54) concurred, saying that “the relationship between RT slope and the Weber fraction is not very strong, which might be explained by the fact that one is a measure of RT while the other is a measure of accuracy.”
In many numeracy studies, including most of those just cited and the studies we present in this article, the response required of a subject is a decision between two alternatives. Whatever the quality of a subject’s numerosity information, a response must be chosen and the choice will take some amount of time. Accuracy and speed can trade off, and the trade-off is under a subject’s control. A subject might decide to respond as quickly as possible, sacrificing accuracy, or as accurately as possible, sacrificing speed. In consequence, the quality of the numeracy information on which an individual bases his or her decision can be obscured by the speed/accuracy setting he or she chooses. This means that neither accuracy by itself nor RTs by themselves can provide a direct measure of an individual’s numeracy knowledge.
In the diffusion model (and other sequential sampling models, Ratcliff & Smith, 2004), joint consideration of accuracy and RTs allows an individual’s speed/accuracy setting to be separated from the quality of the information upon which decisions are based. The central mechanism in the model (Ratcliff, 1978; Ratcliff & McKoon, 2008) is the noisy accumulation of information from a stimulus representation over time. A response is made when the amount of accumulated information reaches one or the other of two criteria, or boundaries, one for each of the two possible choices (e.g., deciding whether the number of dots in a display is larger or smaller than 25). The rate of accumulation, called drift rate, is determined by the quality of the information encoded from a stimulus. The distance between the two boundaries is determined by the speed/accuracy setting-- faster, less accurate responses if the distance is small, slower, more accurate responses if the distance is large. The independence of drift rate and the distances to the boundaries means that information quality is separated from speed/accuracy settings and so can be independently observed.
In the diffusion model, accuracy and RTs must be explained by the same mechanism. This is required in order to account for the locations of RT distributions (longer RTs for more difficult decisions than easier ones) and the characteristic, right-skewed, shape of the distributions. It is also required to account for the inverted U-shaped function that typically results when RTs are plotted against accuracy (a latency-probability function, Ratcliff, Smith, & McKoon, 2015, which is discussed in detail later.)
For all the experiments in this article we compared the two ANS models, each integrated with the diffusion model. Recently there has been concern about the lack of replicability of studies in psychology. Less prominently, there has been concern that models or empirical results apply only to the specific design of a single experiment. We addressed these concerns with 11 experiments and 5 tasks. Each major empirical and modeling result was replicated at least once. In three experiments, subjects were tested on more than one task to examine correlations among an individual’s numeracy abilities across tasks.
Three tasks used displays of dots. Two are common in numeracy research, one in which blue and yellow dots are intermingled in a single array and subjects decide whether there are more blue dots or more yellow dots, and one in which there are two side-by-side arrays of dots all of the same color and subjects decide which of them has more dots. For the third task, subjects decided whether the number of dots of one of two colors, intermingled in a single array, is larger or smaller than a criterion number (e.g., 25). The fourth task used X’s and O’s in a single array and subjects decided which had the greater number. The fifth task used asterisks in a single array and subjects decided whether the number of asterisks was larger or smaller than a criterion number.
There were five independent variables, all replicated in at least two experiments, and numerosity (number of dots, X’s and O’s, or asterisks) was manipulated in all 11 experiments. In most of the experiments with dots, either the summed areas of the two sets of dots (e.g., the blue and yellow ones) were the same or they were proportional to their number (i.e., a larger total area for a larger numerosity). In some experiments, the dots were all relatively large, averaging about 13 pixels in diameter, or small, averaging about 4.5 pixels in diameter. When subjects decided whether the number of dots of one color was larger or smaller than a criterion number, the number of dots of the other color was manipulated.
Preview
To preview the results, we summarize the most salient of them here. The first was highly counter-intuitive. As mentioned above, it is almost always found that as decisions become more difficult and accuracy goes down, responses become slower. This is the pattern that was obtained with two of the tasks we used, deciding which of two side by side arrays has the greater number of dots and deciding whether the number of dots in a single array is larger or smaller than a standard. However, when the task was to decide which of two colors of dots in a single array had the greater number, we found a highly unusual and counter-intuitive pattern: as difficulty increased and accuracy decreased, responses became faster.
The second result was that, when the linear and log ANS models were integrated with the diffusion model, they could be discriminated (because accuracy and RT data must be explained jointly), something that has not been possible in the past, as we pointed out above.
The third result was that which model could account for the data was different for different tasks. The linear ANS-diffusion model did well for the first pattern of data (the counter-intuitive one) but the log ANS-model failed in clear qualitative ways. The log ANS-diffusion model did well for the second pattern of data (the usual one) but the linear model failed in clear qualitative ways.
Fourth, whichever ANS-diffusion model was successful for a given task, it fit the data well. It captured the data for accuracy, mean RTs for correct responses and errors, the shapes and locations of the RT distributions, and the ways these all changed across experimental conditions that varied in difficulty.
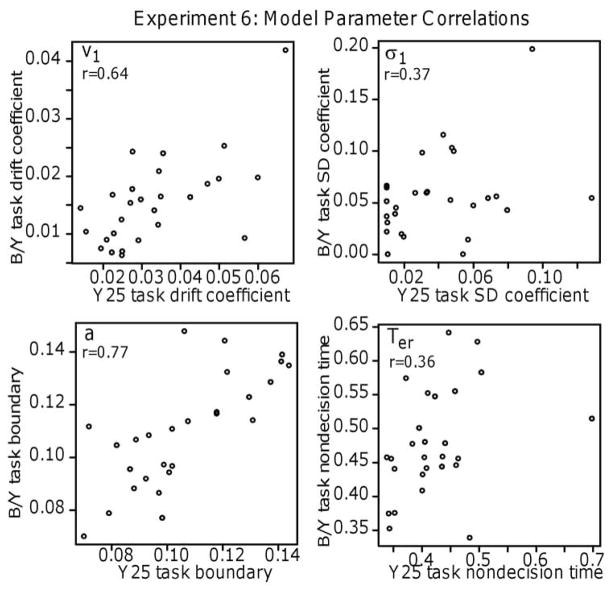
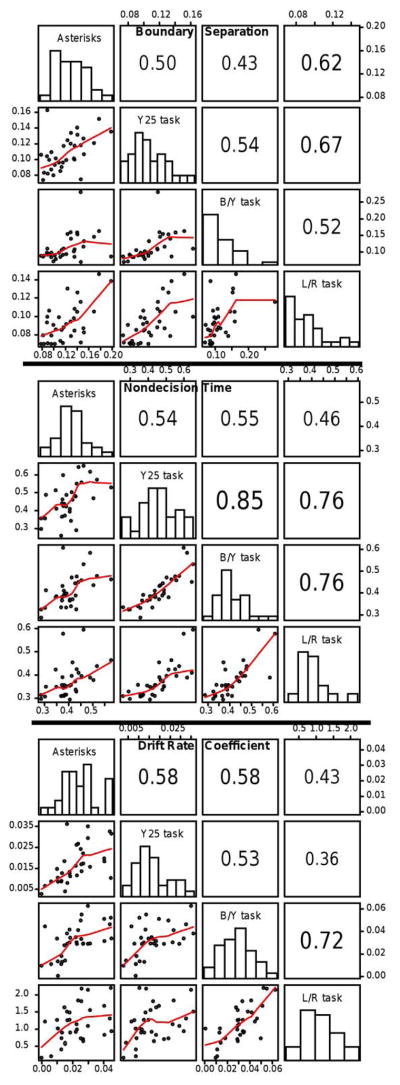
Fifth, we found large correlations among the tasks in drift rates, which suggests that individuals bring similar numeracy skills to all the tasks we used.
The sixth result was a solution for an issue that has bedeviled research on numerosity discrimination-- it has been difficult to divorce confounding variables from judgments of numerosity (DeWind et al., 2015; DeWind & Brannon, 2012; Feigenson et al., 2002; Gebuis & Gevers, 2011; Gebius & Reynvoet, 2012a, 2012b, 2013; Mix et al., 2002). For example, if all the dots in an array of dots of two colors have the same size, then the total area of the dots of the larger-numerosity color will be larger than the total area of the dots of the smaller-numerosity color. But if the totals are equated, then the totals of the circumferences of the dots will be larger for the larger-numerosity color. With any manipulations designed to control one variable, some other variable will be confounded with numerosity. With the ANS-diffusion models, the contributions of individual variables can be measured.
The seventh result was that, when we examined the effects of confounding variables on our tasks, we found variables that affected performance on some numerosity tasks but not others.
The Two-Choice Diffusion Model
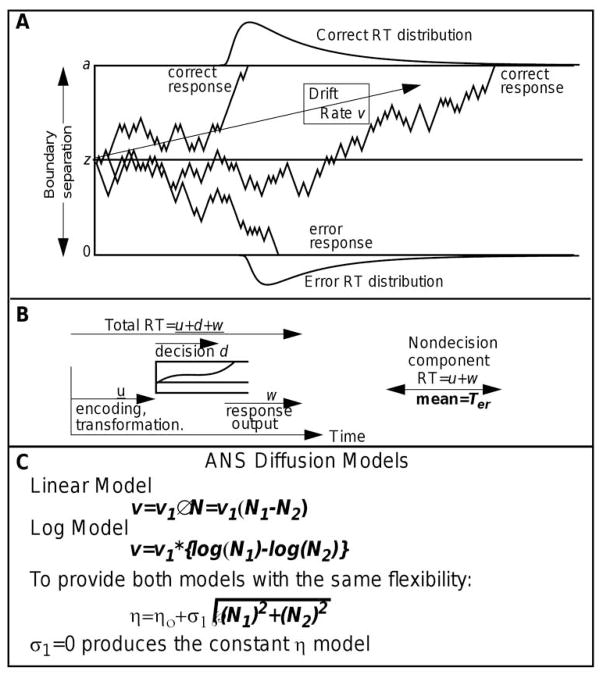
The model is designed to explain the cognitive processes that make simple two-choice decisions that take place in under a second or two. The model has been applied in a wide range of domains including clinical applications and applications in neuroeconomics and neuroscience in humans, monkeys, rodents, and even insect swarms (Forstmann, Ratcliff, & Wagenmakers, 2016; Ratcliff, Smith, Brown, & McKoon, 2016). Figure 2A illustrates the model. Information is accumulated from a starting point, z, toward one or the other of two boundaries, a or 0. The zig-zag lines indicate noise in the accumulation process. For the example in the figure, the mean rate of accumulation, drift rate (v), is positive. Drift rate is determined by the quality of the information extracted from the stimulus in perceptual tasks and the quality of the match between a test item and memory in, for example, lexical decision and memory tasks. Processes outside the decision process such as stimulus encoding and response execution are combined into one component of the model, nondecision time, with mean Ter. Total RT (Figure 2B) is the sum of the time to reach a boundary and nondecision time. The noise in the accumulation of information (Gaussian distributed) results in decision processes with the same mean drift rate terminating at different times, producing RT distributions, and sometimes at the wrong boundary, producing errors.
Figure 2.
A illustrates the diffusion decision model. B shows the additional components of the decision model that produce the total RT. C shows the standard assumption about drift rate and its variability across trials. D shows equations for drift rates and across trial SD in drift rate for the two ANS-diffusion models.
The values of the components of processing are assumed to vary from trial to trial, under the assumption that subjects cannot accurately set the same parameter values from one trial to another (e.g., Laming, 1968; Ratcliff, 1978). Across-trial variability in drift rate is normally distributed with SD η, across-trial variability in starting point (equivalent to across-trial variability in the boundaries) is uniformly distributed with range sz, and across-trial variability in the nondecision component is uniformly distributed with range st. In signal detection theory, which deals only with accuracy, all sources of across-trial variability are collapsed into one parameter, the variability in information across trials. In contrast, with the diffusion model, the separate sources of across-trial variability are identified (Ratcliff & Tuerlinckx, 2002; Ratcliff & Childers, 2015).
For experiments in which subjects compare a stimulus to a standard, there is one more component of processing, the drift-rate criterion (Ratcliff, 1985). For example, when asked to decide whether the number of dots in an array is more or less than 25, then drift rates should be such that their mean is toward the “large” boundary when there are more than 25 dots and toward the “small” value when there are fewer than 25. That is, the drift-rate criterion should be set at 25. However, subjects do not always behave in this way. They may set their criterion at 24 or 26 or some other number. It is to accommodate shifts like this that the drift-rate criterion is a free parameter when a discrimination task involves comparison to a standard.
Boundary settings, nondecision time, starting point, drift rates for each condition in an experiment that varies in difficulty, the drift-rate criterion, and the across-trial variabilities in drift rate, nondecision time, and starting point are all identifiable. When data are simulated from the model (with numbers of observations approximately equal to those that would be obtained in real experiments) and the model is fit to the simulated data, the parameters used to generate the data are well recovered (Ratcliff & Tuerlinckx, 2002). The success of parameter identifiability comes in part from the tight constraint that the model account for the full distributions of RTs for correct and error responses (Ratcliff, 2002).
Integrating the Diffusion Model and the ANS Models
When the diffusion model is combined with a model for how information is represented in cognitive structures, the representation model must produce a value, drift rate (and in some models, SD in drift rate across trials), that when taken through the decision process accounts for all the data. In other words, the diffusion model provides a meeting point between data and models of representation.
The ANS linear and log models (Figure 1) have their roots in research tracing back to Weber’s and Fechner’s research in the 1800’s (e.g., Woodworth, 1938). Weber’s law states that as stimulus intensity increases, the size of the just-noticeable difference between stimuli increases so that the ratio of the difference in intensity to intensity (ΔS/S) remains constant. Fechner derived a logarithmic representation from this: the intensity of a stimulus is proportional to the logarithm of the physical intensity and the psychological difference between two stimulus intensities is the difference in the logarithms of their intensities. Thus as intensity grows, the psychological difference between equally spaced stimuli decreases (e.g., log(10)-log(5) = 0.69 while log(20)-log(15) = 0.29). In this model, the SD around mean numerosity values has to be constant as intensity grows to explain Weber’s law. Weber’s law can also be explained by the linear model: the psychological difference between two intensities is linear with the intensity values and the SD in the psychological representation also increases linearly thus leading to decreasing discriminability as intensity grows. These alternatives have had extensive discussion in numerosity research (e.g., Gallistel & Gelman, 1992; Dehaene & Changeux, 1993) with the conclusion mentioned above, that they cannot be discriminated (Dehaene, 2003). ROGER
In the integrated models, drift rate and the SD in drift rate are both provided by the ANS representation model, and boundary settings, nondecision times, and the ranges in starting point and nondecision time come from the diffusion model. Figure 2C shows how drift rate for the two models is computed. For the linear model, drift rate (v) is the difference between the two numerosities multiplied by a coefficient (v1) and for the log model, drift rate is the difference in the logs of two numerosities multiplied by a coefficient (v1). It is the coefficient of drift rate that separates individuals; a larger coefficient gives better performance.
Figure 2C also shows how across-trial variability (the SD, η in the models) in drift rate is computed. For the linear model, (η) is a constant (η0) plus a coefficient (σ1) multiplied by the square root of the sum of squares of the two numerosities (the square root of the sum of squares is how standard deviations are combined - variances are added). For the log model, we might assume that η remains constant as numerosity increases, just as for traditional models based on accuracy measures. However, there is no guarantee that a diffusion model will behave in the same way and so we gave our log model the same flexibility in accounting for data as the linear model: η could either stay constant as numerosity increases or increase with numerosity with the same expression for η as for the linear model. This also has the advantage of giving the linear and log models the same number of parameters which makes model selection less ambiguous because different measures such as AIC and BIC give the same results. Thus, the only difference between the linear and log models was that the drift rate assumption was different: linear versus log.
The integrated models are severely constrained. Without a representation (i.e., ANS) model, drift rates are usually estimated separately for each condition of an experiment when the diffusion model is applied to data. Instead, for the integrated models, drift rates are set by the representation model and cannot be adjusted to, for example, produce a better fit for one data point without affecting predictions for all the other data. There is only one coefficient for drift rates for all values of numerosity for each condition (e.g., a condition with large dots or one with small dots) and only two coefficients for η for all conditions of the experiment. If the model failed to fit even one value of accuracy or one RT distribution from the numerosity conditions, modifying the parameters to accommodate that one miss would make the fit worse for all the other conditions.
When the linear and log models are integrated with the diffusion model, there are no more than eight free parameters plus one drift-rate coefficient for each independent variable (excluding numerosity). From the diffusion model, there are always the distance between the boundaries, nondecision time, and the ranges in the starting point and nondecision time. When the task is to compare stimuli against a standard there is also the drift-rate criterion. For some tasks, the starting point is a free parameter. For others, it can be set to half the distance between the boundaries and so is not a free parameter; this occurs when the RT distributions at one of the two boundaries are symmetric with those at the other. From the ANS models, there are the drift-rate coefficients for each independent variable except numerosity, the constant component of SD across-trials, and the coefficient for SD. (If the SD coefficient is close to zero, the model is one with constant SD in drift rate.)
For the experiments in which the task was to compare the number of dots of a color or the number of asterisks to a standard value, there was only one value of numerosity, so we set N1 in the computation of drift rate and its SD (Figure 2C) to that numerosity value and N2 to the standard (e.g., 25).
Fitting the Integrated Diffusion Models to Data
The values of all the parameters are estimated together by fitting the model to the data from all the conditions in an experiment simultaneously using a standard method of fitting. The data for each subject is fit individually and the model parameters presented in the tables are the means across subjects. RT distributions are represented by 5 quantiles, the .1, .3, .5, .7, and .9 quantiles. The quantiles and the response proportions for each condition are entered into a minimization routine and the diffusion model is used to generate the predicted cumulative probability of a response occurring by that quantile RT. Subtracting the cumulative probabilities for each successive quantile from the next higher quantile gives the proportion of responses between adjacent quantiles. For a G-square computation, these are the expected proportions, to be compared to the observed proportions of responses between the quantiles (i.e., the proportions between 0, .1, .3, .5, .7, .9, and 1.0, which are .1, .2, .2, .2, .2, and .1). The proportions for the observed (po) and expected (pe) frequencies and summing over 2Npolog(po/pe) for all conditions gives a single G-square (log multinomial likelihood) value to be minimized (where N is the number of observations for the condition).
The number of degrees of freedom in the data is computed as follows: there are 6 proportions (bins) between the quantiles and outside the .1 and .9 quantiles. These proportions are multiplied by the proportion of responses for that condition and across correct and error responses; these 12 proportions must add to 1 so there are 11 degrees of freedom in the data for each condition of the experiment. For example, if there were 10 numerosity conditions crossed with a variable that has two levels, then there would be 220 degrees of freedom in the data. When the models are fit to data, the number of degrees of freedom is the number in the data minus the number of the model’s free parameters.
Usually in fits of the diffusion model to data, there are no models of stimulus representation like those the ANS models provide and so there is a separate drift rate for each condition of an experiment. For Experiment 1, for example, this would lead to a model with 26 parameters whereas for the ANS-diffusion models, the number of parameters is greatly reduced, to only eight.
The model was fit to the data using the G-square statistic in the same way as fitting the chi-square method described by Ratcliff and Tuerlinckx (2002; see also Ratcliff & Childers, 2015; Ratcliff & Smith, 2004). G-square statistics are asymptotically chi-square and so critical chi-square values can be used to assess goodness of fit. In many applications we have found that if the value of the chi-square (or G-square) is below 2 times the critical value, the fit is good (Ratcliff, Thapar, Gomez, & McKoon, 2004; Ratcliff, Thapar, & McKoon, 2010) even in the less constrained case in which the diffusion model is applied without a representation model and so each condition has its own drift rate.
In the results sections for the experiments, the mean values of the model parameters and the G-square statistic across subjects are reported. For the plots in the figures for the experiments, the quantile RTs and response proportions in the data are averaged across subjects. The predictions from the models are generated from the best-fitting parameters for each subject and then these predictions are averaged across subjects in exactly the same way as the data are averaged.
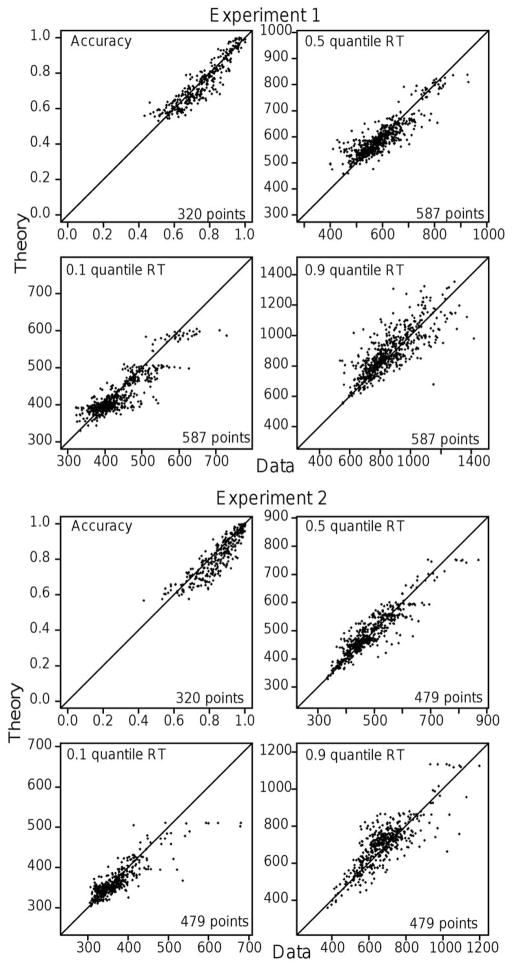
Because the fits are presented as averages over subjects, it may be that there are some very bad fits for some individuals. Appendix A shows plots of the experimental and predicted response proportions and 0.1, 0.5, and 0.9 quantile RTs plotted against each other for Experiments 1 and 2. These show a visual representation of the quality of the fits for each condition for each subject and so allow an assessment of how good or bad fits are for each condition and subject.
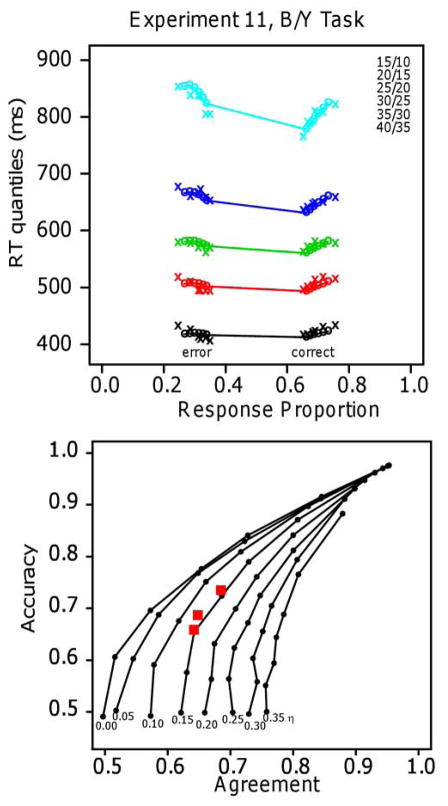
The difference in G-square values between the log and linear models provides a numerical goodness of fit measure from which the models can be compared. As noted above, because the number of parameters for the two models was the same, G-squares provide the same results for comparisons of models as do the AIC and BIC values (because these measures are G-square plus a penalty term based on the number of parameters - which is the same for the pairs of models). However, in our view, small numerical differences are not enough to be sure that one model should be preferred over another. We prefer to see qualitative differences in predictions between the models as well as numerical differences that are not small. Furthermore, for each experiment we report the number of subjects that favor each model from the G-square value. By a binomial test, if 22 (or more) out of 32 subjects or 12 (or more) out of 16 subjects support one model over the other model, then the result is significant. This provides another measure of support at an individual subject level for one model over the other model.
Displaying the match between data and model
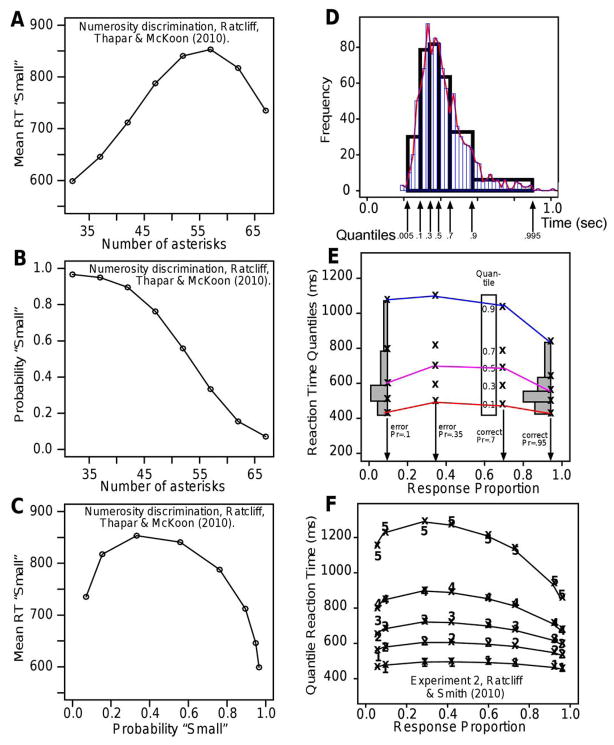
The match can be displayed in latency-probability functions and quantile-probability functions (Ratcliff, 2001; Ratcliff, Van Zandt, & McKoon, 1999). To illustrate latency probability functions (termed a parametric plot), data from a numerosity discrimination task (Ratcliff, Thapar, & McKoon, 2010) are plotted in Figures 3A–3C. The stimuli were arrays of asterisks mixed with empty spaces and subjects decided whether the number of asterisks was larger or small than 50. Figure 3A shows mean RTs (in ms) for “small” responses as a function of the number of asterisks for eight conditions that vary in difficulty (responses were grouped: 30–34, 35–39, 40–44, …, 65–69, for means 32, 37, 42, ..., 67). “Small” is the correct response for numbers smaller than 50 (on the left side of the function) and the incorrect response for numbers larger than 50 (on the right side of the function). RTs are shorter for the easier conditions for both correct and incorrect responses (the outer data points) and longer for the more difficult conditions (the nearer-center data points). Figure 3B shows the probabilities of “small” responses, fewer of them as the number of asterisks increases. The bottom panel shows the inverted U-shaped latency-probability function derived from plotting the RTs against the response probabilities. As the probability of a correct response decreases from right to left, RTs first increase and then decrease (and for “large” responses, the functions are similar). Predictions from the model can be plotted in the same way (e.g., Ratcliff & McKoon, 2008, Figure 6). Often in experiments with symmetric responses for the two choices, conditions are combined, for example, in Figure 3A, mean RT for “large” responses might be the left to right mirror image of those for “small” responses. Then correct “small” responses to the 32 asterisk condition would be combined with correct “large” responses to the 67 asterisk condition to produce one of four levels of difficulty from the eight conditions. Errors would be combined in the same way so that the four levels of difficulty would produce eight data points as in Figure 3F (the error RTs on the left correspond to the symmetric correct responses on the right).
Figure 3.
Construction of latency-probability functions and quantile probability functions.
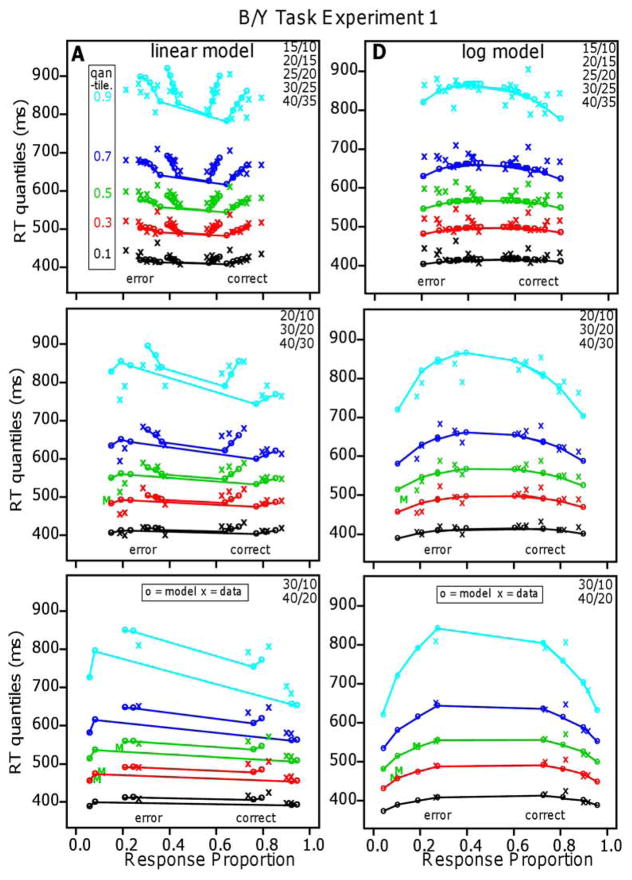
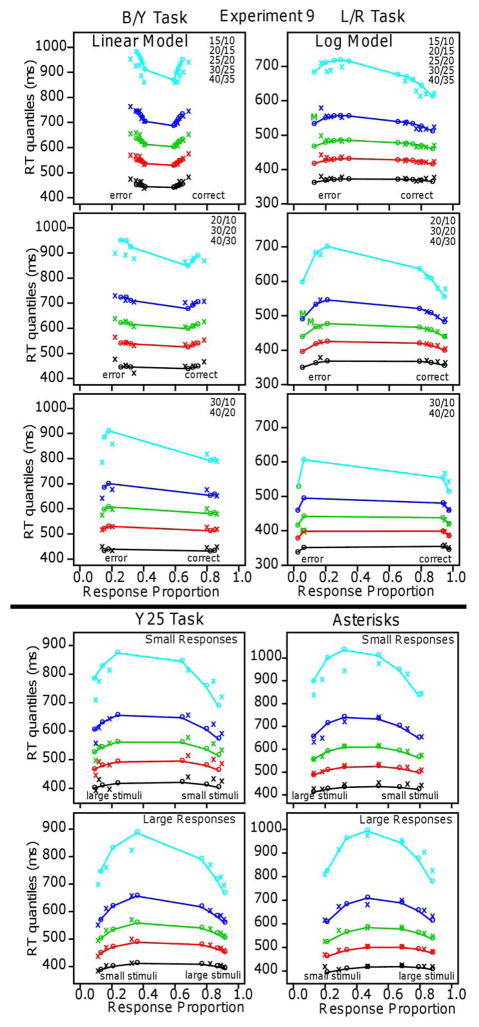
Figure 6.
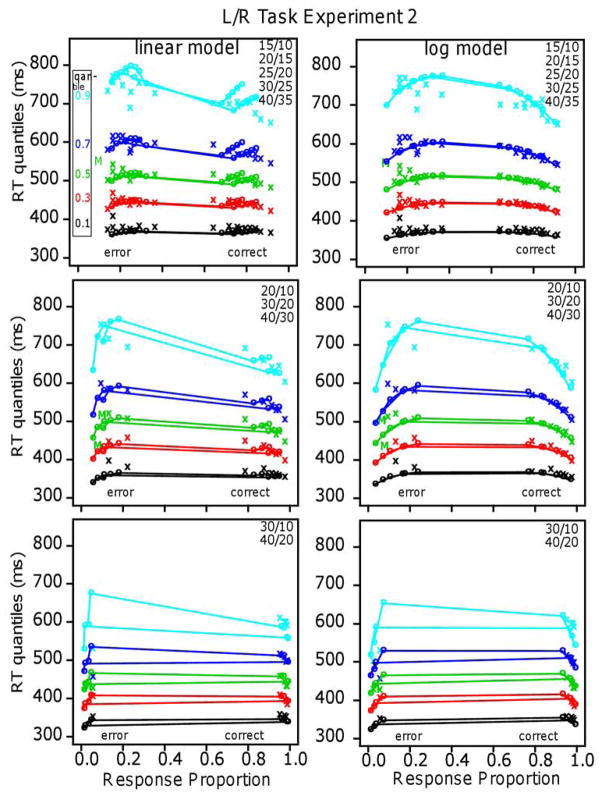
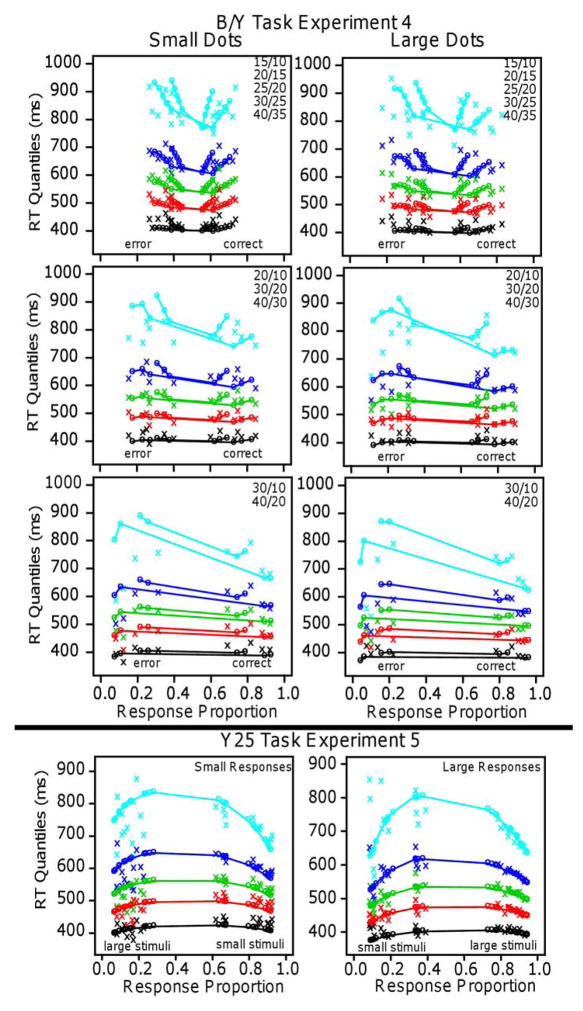
Quantile-probability functions for Experiment 1 for the linear and log models. These plot RT quantiles against response proportions (correct responses to the right of 0.5 and errors to the left). The green/central lines are the median RTs. The number of dots in the conditions in the plots are shown in the top right corner and the more extreme functions are for proportional-area conditions and the less extreme for equal-area conditions.
For most of the experiments described in this article, we display the data and model predictions in quantile probability plots. Figure 3D shows how they are constructed. The top panel shows a histogram of the data (thin narrow bars and red line) overlaid with rectangles derived from the 0.1, 0.3, 0.5, 0.7, and 0.9 RT quantiles. The rectangles represent equal areas of 0.2 probability mass between each pair of middle quantiles and 0.1 probability mass outside of the 0.1 and 0.9 quantiles. The quantile rectangles capture the main features of the RT distribution (as can be seen in the figure) and therefore provide a reasonable summary of the overall distribution shape. Figure 3E shows a quantile-probability plot. Quantile RTs for the 0.1, 0.3, 0.5, 0.7, and 0.9 quantiles (stacked vertically) are plotted against the proportions of responses that were made for each condition for four experimental conditions different in difficulty. Correct responses for two conditions are on the right, errors for two conditions are on the left. For the more difficult condition, the proportion of correct responses is 0.7 and for the easier condition, the proportion of correct responses is 0.95. Errors for the other two conditions are plotted on the left with error probabilities 0.1 and 0.35. Figure 3F shows an example of the fit between model and data for an experiment with four conditions, with the numbers representing the data for the five quantiles and the x’s and lines representing the model predictions (from Ratcliff & Smith, 2010, Experiment 2). The latency-probability function for the median RT instead of the mean RT is the middle line in Figure 3F.
Quantile-probability plots make it easy to see changes in RT distribution locations and spread as a function of response probabilities and how model and data compare. In Figure 3F, as response probability changes from about 0.6 (the most difficult condition) to near 1.0 (the easiest condition), the 0.1 quantile (leading edge) changes little, but the 0.9 quantile changes by as much as 400 ms. Thus, the change in mean RT is mainly in the tail; the whole distribution does not shift. Also, error responses are slower than correct responses mainly because of their spread, not the location of the leading edge. In these ways, quantile-probability plots allow all the important aspects of both the accuracy and RT data to be read from a single plot.
Experiments: Stimuli, Subjects, and Procedures
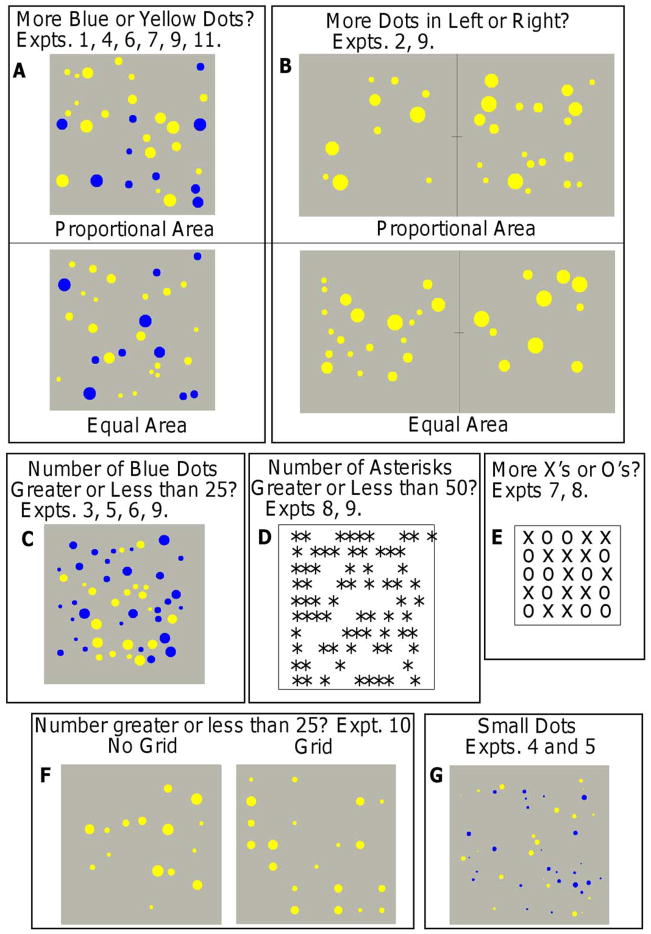
Figure 4 illustrates the displays that were used in the experiments. We list all of them here to provide a summary and then describe them again in the discussion of each experiment. In Figure 4A, blue and yellow dots are intermingled in a single array and the question was for which color is the number of dots larger. In Figure 4B, there are two arrays side by side with dots all of the same color and the question was which array has more dots.
Figure 4.
Examples of stimuli for the experiments.
In many of the experiments, there was an area manipulation, equal versus proportional. For blue and yellow dots mixed in a single array, the summed areas of the dots of the two colors were either equal or proportional (larger summed area for the larger numerosity color). At the same time, the summed areas of dots of different numerosities were either equal or proportional. For example, consider two conditions: 10 blue dots intermingled with 15 yellow dots and 35 blue dots intermingled with 40 yellow dots. For equal area, the sum of the areas of the 10 blue dots would be the same as the sum of the areas of the 15 yellow dots, the 35 blue dots, and the 40 yellow dots. For proportional area, the sums would be larger for larger numerosities than smaller ones. For dots of the same color in two arrays, the area manipulation is the same: the sums of the areas of the dots in the two arrays were equal or proportional and the sums were equal from one numerosity to another, or they were all proportional to their number. Figures 4A and 4B illustrate the area manipulation.
In Figure 4C, blue and yellow dots are intermingled in a single array and the question was whether the number of dots of one of the colors was greater or less than 25. In Figure 4D, asterisks are intermingled with white spaces and the question was whether the number of asterisks was greater or less than 50. In Figure 4E, X’s and O’s are intermingled and the question was whether there were more X’s or more O’s. In Figure 4F, there was one array of dots presented and for some of the displays, the dots were positioned randomly (the left example) or positioned on a grid (the right example); in both cases, the question was whether the number of dots was greater or less than 25. Finally, Figure 4G shows small dots which were tested along with regular-size dots in different stimulus arrays. These experiments used single arrays of intermingled blue and yellow dots; in Experiment 4, the question was for which color is the number of dots greater, and in Experiment 5, it was whether the number of dots of one of the colors is greater or less than 25.
For the single-array stimuli with dots (Figures 4A, 4C, 4G, and 4F), the dots were displayed on a 17-inch diagonal CRT monitor with a width of 32 cm and a height of 24 cm and with a 4×3 screen set to 1280×960 pixels (with 256 colors). The background was gray to control luminance (Halberda et al., 2008). The dots were presented in a 640×640 gray array in the middle of the screen that was 17.3 × 17.3 degrees of visual angle when viewed from a distance of 53 cm. For all but Experiments 4 and 5, the dots had radii of 6, 8, 10, 12, 14, or 16 pixels subtending angles of 0.324, 0.432, 0.540, 0.648, 0.756, and 0.864 degrees in diameter, respectively. For Experiments 4 and 5, the smaller dots’ radii were 2, 3, 4, 5, 6, or 7 pixels.
For each trial of a single-array experiment, either dot sizes were selected randomly but constrained so that the summed areas of the two colors of dots in an array (and the areas across all the numerosities, as described above) were equal, or they were selected randomly without any other constraint and so the areas were proportional to the number of dots. We constrained the positions of the dots so that the maximum horizontal/vertical distance dot centers could be separated by was 360 pixels (10.58 degrees) and the minimum spacing between dot edges was 5 pixels (0.135 degrees).
For the stimuli with two side-by-side arrays of dots, the same CRTs were used with the same settings as for the single-array experiments. The gray background within which the two arrays of dots were presented was 640 pixels high x 1160 pixels wide which is 17.3 by 31.3 degrees of visual angle. The minimum spacing between dot edges was 5 pixels and between the two arrays, there was an 80 pixel separation between dot centers. There was a thin vertical line between the two arrays (Figure 4B) within which stimulus arrays were presented. There was also a small fixation cross between the two arrays and subjects were instructed to look at that on the beginning of each trial. The radii of the dots were the same as the larger ones listed above.
Stimuli in most of the experiments with dots were presented for 250 or 300 ms and then the screen returned to the background color. This was done to reduce the possibility that subjects used slow strategic search processes to perform the task. Subjects were instructed to respond as quickly and accurately as possible. Responses were collected by key presses on a PC keyboard, usually the/and z keys, one for each choice. For all the tasks, there were several practice trials (e.g., 4) and for these, the correct response was given on each trial so that subjects would be certain to understand the instructions (e.g., it would say “an example of more blue dots” when the decision was about which color had the more dots). Subjects initiated each block by pressing the space bar on the keyboard.
For most of the experiments, the subjects were students in an introductory psychology class who participated for class credit. As is typical in our pool, some of them were not cooperative and began, from the beginning or in the middle of the experiment, to respond with fast guesses. For this reason, about 20% of the subjects were eliminated in each experiment. We identified the non-cooperative subjects by placing an upper cutoff at 300 ms and lower cutoff at 0 and examining the proportion of responses in this range and their accuracy. If there were more than 5% and accuracy was at or near chance for these responses, we eliminated the subject (based only on these aspects of the data, without examining other results). We also eliminated one or two subjects from a few of the experiments who were not fast guessing but responded with chance accuracy. For data analyses for all the experiments, we placed a lower RT cutoff at 300 ms and an upper cutoff at 2000 ms. This eliminated less than 5% of the responses in each experiment.
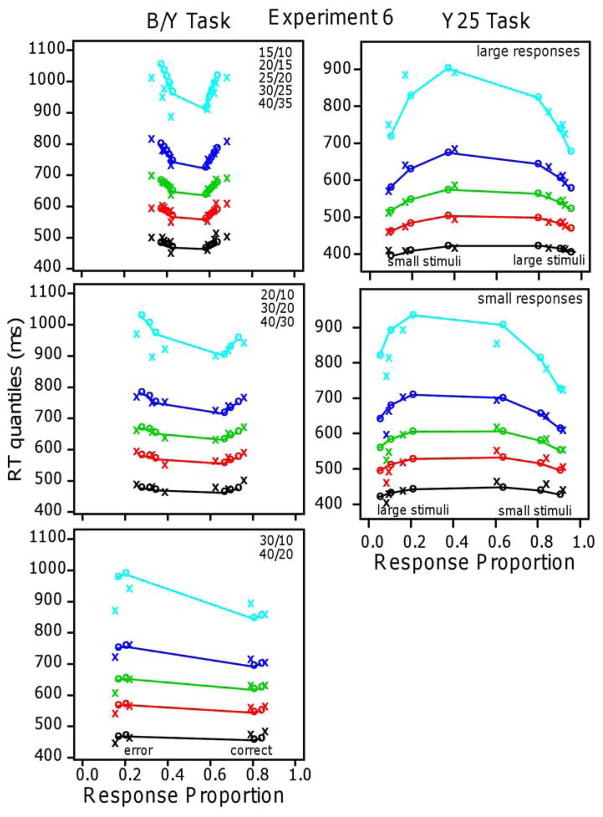
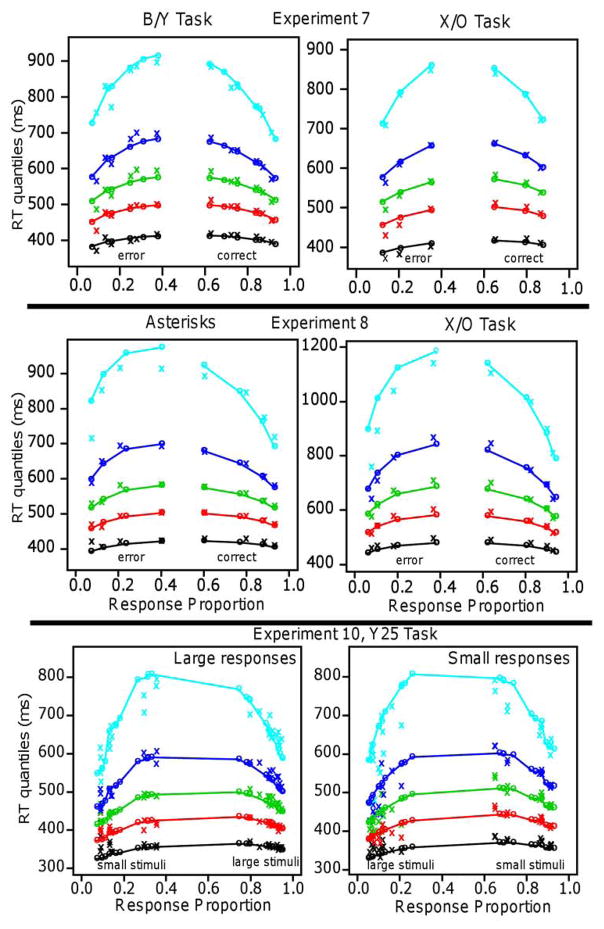
For experiments with one task, there were typically 20 blocks of 96 or 100 trials giving about 2000 observations per subject and for experiments with two or more tasks, two tasks were tested per session with about 1000 trials per session. We aimed for 16 subjects in the experiments with one task and 32 for the experiments with two or more tasks. Because of the fast-guessing subjects, we usually tested a few extra subjects and this led to larger numbers in some of the experiments. Experiments 1–5 had 16 subjects, Experiment 6 had 35, Experiments 7, 8, and 9 had 32, Experiment 10 had 15 (because classes ended before we could get the 16th), and Experiment 11 had 18.
Experiment 1
The stimuli in Experiment 1 were blue and yellow dots intermingled in a single array (Figure 4A) and subjects decided whether there were more blue or more yellow dots. We label this task the B/Y task. It is in this experiment that we first found the counter-intuitive result that as accuracy decreases, responses speed up.
To manipulate numerosity, the numbers of the blue and yellow dots differed in their numerosities and the differences between their numerosities. There were 10 combinations of the numbers of blue and yellow dots; 15/10, 20/15, 25/20, 30/25, and 40/35 for differences of 5; 20/10, 30/20, and 40/30 for differences of 10; and 30/10 and 40/20 for differences of 20. The sums of the dot areas were equal or proportional.
Accuracy and RT Results
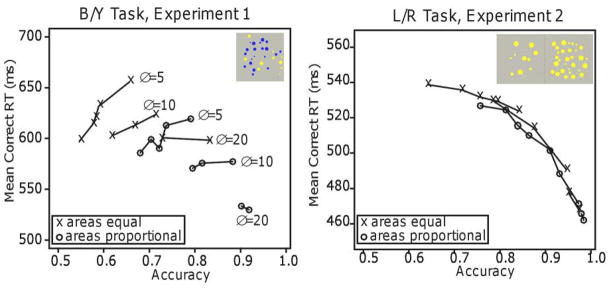
The data for “blue” and “yellow” responses were symmetric so correct responses for blue and yellow dots were combined and errors for blue and yellow dots were combined. Table 1 shows accuracy and mean correct RTs as a function of the area manipulation with the data averaged over the 10 proportional-area and 10 equal-area conditions. The left panel of Figure 5 shows mean RTs plotted against accuracy with the x’s for equal-area conditions and the o’s for proportional-area conditions. Lines were drawn between conditions with the same numerosity difference (5, 10, and 20) for the two area conditions separately.
Table 1.
Experiments 1 and 2: accuracy and correct mean RTs
| Experiment | measure | proportional area | equal area |
|---|---|---|---|
| 1 | accuracy | 0.817 | 0.675 |
| 1 | RT | 601 | 638 |
| 2 | accuracy | 0.900 | 0.824 |
| 2 | RT | 495 | 513 |
Figure 5.
Plots of mean RT against accuracy for Experiments 1 and 2. The x’s are for equal-area conditions and the o’s are for proportional-area conditions. Δ represents the difference in numerosity between the two stimuli.
As expected, accuracy decreased as the difficulty of the discrimination increased. Specifically, accuracy decreased both as the numerosity of the dots increased and as the difference between the numerosities of the dots of the two colors decreased, the standard result with these manipulations. Also as expected, equal-area discriminations were more difficult than proportional-area discriminations, with accuracy higher and RTs shorter with proportional areas.
The RT data show the unexpected finding and demonstrate why RTs must be considered in data analyses. For numerosity differences of 5 and 10, as accuracy decreased, RTs also decreased (for differences of 20, RTs changed little). For example, for the top function in the figure, as the probability of a correct response decreases from around 0.68 to around 0.55, RTs speed up from around 660 ms to around 600 ms. It is this joint consideration of accuracy and RTs that gives the counter-intuitive result.
Analyses of variance with two factors, the two area conditions and the 10 combinations of numbers of blue and yellow dots, showed significant effects on accuracy (F(1,15)=203.6, p<.05; F(9,135)=116.7, p<.05) and on mean RTs (F(1,15)=68.1, p<.05; F(9,135)=27.6, p<.05, respectively). The interaction was not significant for accuracy (F(9,135)=1.6, p>.05) but it was for RTs (F(9,135)=5.5, p<.05). We were not concerned with power in the statistical tests because it is qualitative patterns along with model fits to the sizes of the effects that are most relevant, not the size relative to the variability in the data. While a 2% effect on accuracy, for example, might be significant and have a high effect size, it might have no practical effect on performance in the context of the modeling.
Experiment 2
In Experiment 1, accuracy decreased as difficulty increased and RTs decreased. In Experiment 2, accuracy decreased as difficulty increased and RTs increased (as opposed to decreasing as occurred in Experiment 1). The stimuli were side-by-side arrays (Figure 4B) and the dots were always yellow for both arrays. Subjects decided which of the two arrays had more dots, the left or the right. We call this the L/R task. Summed areas were either equal or proportional. There were the same 10 combinations of numbers of dots as for Experiment 1.
Accuracy and RT Results
The data for “left” and “right” responses were symmetric so correct responses for left and right dots were grouped and errors for left and right dots were grouped as for Experiment 1. Table 1 shows the accuracy and mean correct RT results as a function of the area manipulation with the data averaged over the 10 proportional-area and 10 equal-area conditions. The right panel of Figure 5 shows plots constructed like those of Experiment 1. Accuracy decreased as the difference in numerosity between the two arrays decreased and as the numerosity of the two arrays increased, and it was lower for the equal-area conditions than the proportional-area ones. The result for RTs was the typical one, that RTs increased as accuracy decreased. Unlike Experiment 1, the data from all the equal-area conditions and all the proportional-area conditions fell on a single parametric plot.
Analyses of variance showed significant differences in accuracy among the 10 combinations of numerosity and the two area conditions, F(9,135)=151.7, p<.05, and F(1,15)=68.2, p<.05, respectively, and their interaction was significant, F(9,135)=8.0, p<.05. There were also significant differences in RTs among the numerosity conditions and the area conditions, F(9,135)=25.7, p<.05 and F(1,15)=38.7, p<.05, and their interaction was not significant, F(9,135)=1.3. These results show that both the area and numerosity manipulations affected performance on this task. In following analyses for later experiments, we average over the numerosity conditions (because the numerosity effect is always large) to simplify the ANOVAs and t-tests.
Fitting the Integrated Models to the Results of Experiments 1 and 2
Quantile-probability plots (Figures 6 and 7) show accuracy and the full distributions of RTs for correct and error responses and how these change across conditions. As illustrated in Figure 3, the 0.1, 0.3, 0.5 (median), 0.7, and 0.9 quantiles of the RT distribution for each condition are plotted vertically on the y-axis and the proportions of responses are plotted on the x-axis. Because the probability of a correct response is larger than .5, quantiles for correct responses are on the right of .5 and quantiles for errors on the left (the two probabilities sum to 1.0). The difficulty of the stimuli in each condition determines the probabilities of correct and error responses, that is, the location of the stacks of quantiles on the x-axis.
Figure 7.
Quantile-probability functions for Experiment 2.
For the models, nondecision time determines the placement of the functions vertically. The shapes of the functions are determined by just three values (Ratcliff & McKoon, 2008): the distance between the boundaries, the range across trials in the starting point (which is equivalent to across-trial variability in the settings of the boundaries), and the SD across trials in drift rates (η). The drift rates for the different levels of difficulty (i.e., the different conditions) sweep out functions across response probabilities.
Figures 6 and 7 show the quantile probability functions for Experiments 1 and 2, respectively, and the fits of the models to them. The x’s are the data and the o’s and lines joining them are the predictions of the models. The proportional-area conditions are farther to the left and right because they have higher accuracy than the equal-area conditions, which are nearer the center. The horizontal lines that connect correct and error responses across 0.5 are not meaningful; they are there only to show which correct responses correspond to which error responses.
The quantile-probability functions for Experiment 1 (Figure 6) show the unexpected result for the five quantiles. They decrease sharply from their left and right ends (error responses and correct responses, respectively) toward the center, showing the decrease in RTs as accuracy decreases. This is true for the equal-area conditions and the proportional-area conditions. In contrast, the functions for Experiment 2 (Figure 7) show the typical inverted U shaped functions bending up from their left and right ends with RTs increasing as accuracy decreases.
To fit the models to the data, there were four parameters from the diffusion model: the distance between the boundaries, across-trial range in the starting point and across-trial range in nondecision time. There were four parameters from the ANS models: a drift-rate coefficient (v1) for the equal-area conditions, a drift-rate coefficient for the proportional-area conditions (v2), the SD coefficient (σ1), and the constant component of the across-trial SD in drift rate (η0). The number of degrees of freedom was 212: the number of conditions multiplied by the 11 degrees of freedom for the proportions of responses between and outside the .1, .3, .5, .7, and .9 bins for correct and error responses minus 1 because the proportions add to 1 and minus the number of parameters.
The results for the linear model for Experiment 1 show a remarkable qualitative and quantitative match between theory and data. The model produces the decreases in RT quantiles as accuracy decreases, the larger and sharper decreases for the equal-area conditions than the proportional-area conditions, and the larger decreases for the higher than the lower quantiles. It also produces the flattening of the functions as the difference in numerosities between the blue and yellow dots increases (from 5 to 10 to 20). (Accuracy for the easiest condition, 15/10 dots, was a little higher than the model’s predictions but this could be accommodated by allowing drift rate to increase a little more quickly than linearly as numerosities decrease.)
The critical difference in the predictions between the linear and log models is the counterintuitive result that for the linear model, for a constant numerosity difference, as the total number of dots increases, RT decreases. In our data, this effect is largest for differences in numerosity of 5. In order to provide another measure of which qualitative pattern of results was obtained for individual subjects, we fit median RTs as a function of the number of dots for differences of 5 with linear regression. We examined this qualitative effect in the data from the experiments with the B/Y task and the L/R task and we report how many subjects had a slope less than zero. For the counterintuitive result (decreasing RT with decreasing accuracy), the slope is less than zero, and for the standard result and log model, the slope is greater than zero.
Tables 2 and 3 show the parameter values of the linear model that best fit the data. The mean G-square value for the linear model was 261 and the critical value of the chi-square for 212 degrees of freedom is 246.0. The mean G-square over subjects is just above the critical value, which indicates a good fit of the model to data. For individuals, G-square values were lower for the linear model for 13 out of 16 subjects and the slope of the median RT versus overall numerosity function for differences of 5 was less than 0 for 28 out of 32 comparisons (equal and proportional area for 16 subjects). Both of these support the linear model for individual subject data.
Table 2.
Diffusion model parameters
| Experiment and task | Model | a | Ter | η0 | 10σ1 | sz | st | z |
|---|---|---|---|---|---|---|---|---|
| 1, B/Y | linear | 0.114 | 0.446 | 0.010 | 0.066 | 0.083 | 0.266 | a/2 |
| 1, B/Y | log | 0.103 | 0.425 | 0.038 | 0.021 | 0.043 | 0.254 | a/2 |
| 2, L/R | linear | 0.098 | 0.398 | 0.032 | 0.071 | 0.073 | 0.237 | a/2 |
| 2, L/R | log | 0.092 | 0.390 | 0.152 | 0.005 | 0.057 | 0.224 | a/2 |
| 3, Y25 | linear | 0.102 | 0.386 | 0.026 | 0.027 | 0.076 | 0.203 | 0.054 |
| 3, Y25 | log | 0.093 | 0.389 | 0.022 | 0.002 | 0.064 | 0.215 | 0.052 |
| 4, B/Y | linear | 0.113 | 0.421 | 0.027 | 0.078 | 0.087 | 0.235 | a/2 |
| 4, B/Y | log | 0.103 | 0.406 | 0.024 | 0.045 | 0.055 | 0.227 | a/2 |
| 5, Y25 | linear | 0.098 | 0.419 | 0.028 | 0.038 | 0.068 | 0.201 | 0.045 |
| 5, Y25 | log | 0.091 | 0.412 | 0.030 | 0.012 | 0.049 | 0.199 | 0.040 |
| 6, Y25 | linear | 0.109 | 0.433 | 0.027 | 0.038 | 0.066 | 0.222 | 0.059 |
| 6, Y25 | log | 0.102 | 0.427 | 0.037 | 0.017 | 0.051 | 0.220 | 0.058 |
| 6, B/Y | linear | 0.111 | 0.485 | 0.030 | 0.053 | 0.064 | 0.297 | a/2 |
| 6, B/Y | log | 0.108 | 0.481 | 0.053 | 0.020 | 0.058 | 0.291 | a/2 |
| 7, B/Y | linear | 0.107 | 0.403 | 0.019 | 0.063 | 0.061 | 0.220 | a/2 |
| 7, B/Y | log | 0.109 | 0.413 | 0.069 | 0.050 | 0.077 | 0.227 | a/2 |
| 7, X/O | linear | 0.099 | 0.425 | 0.037 | 0.035 | 0.072 | 0.235 | a/2 |
| 7, X/O | log | 0.099 | 0.427 | 0.033 | 0.036 | 0.073 | 0.236 | a/2 |
| 8, asterisks | linear | 0.121 | 0.409 | 0.068 | 0.019 | 0.090 | 0.185 | a/2 |
| 8, asterisks | log | 0.113 | 0.396 | 0.039 | 0.012 | 0.065 | 0.171 | a/2 |
| 8, X/O | linear | 0.129 | 0.431 | 0.015 | 0.052 | 0.059 | 0.203 | a/2 |
| 8, X/O | log | 0.129 | 0.429 | 0.009 | 0.052 | 0.069 | 0.199 | a/2 |
| 10, Y25 | linear | 0.105 | 0.364 | 0.036 | 0.024 | 0.080 | 0.177 | 0.054 |
| 10, Y25 | log | 0.096 | 0.357 | 0.033 | 0.005 | 0.047 | 0.191 | 0.051 |
Table 3.
Diffusion model drift rate coefficients and individual fit measures
| Experiment and task | Model | v1 | v2 | v3 | v4 | vc | Number preferred | Number slopes<0 | G2 | df |
|---|---|---|---|---|---|---|---|---|---|---|
| 1, B/Y | linear | 0.037 | 0.016 | 13/16 | 28/32 | 261 | 212 | |||
| 1, B/Y | log | 0.501 | 0.225 | 3/16 | 287 | 212 | ||||
| 2, L/R | linear | 0.066 | 0.048 | 6/16 | 11/32 | 303 | 212 | |||
| 2, L/R | log | 1.067 | 0.784 | 10/16 | 280 | 212 | ||||
| 3, Y25 | linear | 0.033 | 0.033 | 0.029 | 0.030 | −0.004 | 13/16 | 301 | 252 | |
| 3, Y25 | log | 0.634 | 0.629 | 0.581 | 0.571 | −0.029 | 3/16 | 312 | 252 | |
| 4, B/Y | linear | 0.030 | 0.016 | 0.040 | 0.020 | 11/16 | 56/64 | 475 | 430 | |
| 4, B/Y | log | 0.436 | 0.229 | 0.566 | 0.268 | 5/16 | 494 | 430 | ||
| 5, Y25 | linear | 0.032 | 0.030 | 0.037 | 0.035 | −0.032 | 12/16 | 328 | 252 | |
| 5, Y25 | log | 0.559 | 0.531 | 0.643 | 0.592 | −0.050 | 4/16 | 348 | 252 | |
| 6, Y25 | linear | 0.033 | −0.045 | 15/35 | 95 | 57 | ||||
| 6, Y25 | log | 0.607 | −0.071 | 20/35 | 98 | 57 | ||||
| 6, B/Y | linear | 0.015 | 21/35 | 32/35 | 136 | 103 | ||||
| 6, B/Y | log | 0.275 | 14/35 | 138 | 103 | |||||
| 7, B/Y | linear | 0.040 | 0.025 | 24/32 | 90.6 | 58 | ||||
| 7, B/Y | log | 0.534 | 0.321 | 8/32 | 95.0 | 58 | ||||
| 7, X/O | linear | 0.031 | 16/32 | 43.2 | 26 | |||||
| 7, X/O | log | 0.386 | 16/32 | 42.6 | 26 | |||||
| 8, asterisks | linear | 0.015 | 24/32 | 41.2 | 37 | |||||
| 8, asterisks | log | 0.557 | 8/32 | 41.7 | 37 | |||||
| 8, X/O | linear | 0.029 | 24/32 | 45.4 | 37 | |||||
| 8, X/O | log | 0.355 | 8/32 | 47.6 | 37 | |||||
| 10, Y25 | linear | 0.035 | 0.033 | 0.036 | 0.036 | −0.041 | 10/15 | 338 | 252 | |
| 10, Y25 | log | 0.627 | 0.608 | 0.638 | 0.628 | −0.069 | 5/15 | 342 | 252 |
Note: For Experiments 1, 2, and 7, v1 proportional area, v2 equal area. For Experiments 3 and 5, v1 small dots few distrac-tors, v2 small dots many distractors, v3 large dots few distractors, v4 large dots many distractors. For Experiment 4, v1 small dots proportional area, v2 small dots equal area, v3 large dots proportional area, v4 large dots equal area. For Experiment 10, v1 random arrangement proportional area, v2 random arrangement equal area, v3 grid arrangement proportional area, v4 grid arrangement equal area.
The proportional-area and equal-area drift-rate coefficients were significantly different, 0.037 and 0.016, a difference of over a factor of 2 (t(15)=8.1, p<.05). We discuss these coefficients below.
The fit of the linear model to the data is impressive for several reasons. First, there is only one drift-rate coefficient for the 10 equal-area conditions and only one for the 10 proportional-area conditions-- drift rate is determined by the coefficient and the two numerosities being compared. Second, the values of the four parameters from the diffusion model and the constant component of the across-trial SD in drift rate are fixed across all 20 conditions. There is no model freedom with which to alter a single parameter to accommodate, for example, a miss in one data point.
The fit is also impressive in relation to the number of parameters that would usually be used to fit the diffusion model to data, as mentioned above. For Experiments 1 and 2, there would be 20 drift-rate parameters and possibly 20 parameters for across-trial SD in drift rates (because the SD in drift rates increases with numerosity in order to fit the data). Integrating the linear model with the diffusion model reduces this to 2 drift-rate coefficients and 2 SD coefficients, the constant SD coefficient i(η0) and the one that specifies how the SD changes with numerosity (σ1).
The log model completely and qualitatively misses the decreases in RTs with decreasing accuracy. It does, however, produce predictions that go through the middles of the quantile-probability functions and so the G-square value is not markedly different from that for the linear model.
For Experiment 2, the results were the opposite: The log model fit the data well, the linear model did not, and the functions in Figure 7 show the result that would be expected intuitively: as accuracy decreased, RTs increased. The results are also different from Experiment 1 in that the quantile data from the equal-area and proportional-area conditions fall on the same function (if they were plotted together) as they do for the means in Figure 5. The fit of the log model to the data was good: It produced predicted values that match the quantile-probability functions with the mean G-square value a little above the critical value, 246.0. The number of parameters, the number of conditions, and the number of degrees of freedom were the same as for Experiment 1. There was one drift-rate coefficient for the 10 equal-area conditions, one for the 10 proportional-area conditions, the four diffusion-model parameters, the constant component of the SD in drift-rate across trials, and two parameters for the SD coefficients. The linear model missed the data qualitatively but its predictions go through the middles of the quantile-probability functions and so its G-square value is not a great deal larger than that of the log model. For individuals, G-square values were lower for the log model for 10 out of 16 subjects and the slope of the RT versus overall numerosity function for differences of 5 was greater than 0 for 21 out of 32 comparisons (equal and proportional area for 32 subjects). Both of these support the log model for individual subject data, but not as strongly as the linear model is supported for Experiment 1. The results for Experiment 2 are consistent with those obtained for a side-by-side task by Park and Starns (2015). They found that, for constant differences in numerosity, as overall numerosity increased (12/9 vs. 21/18 and 14/12 vs. 20/18), mean RT increased (12 ms and 5 ms effects, respectively, supporting the log model.
In fits of the standard model to other experimental paradigms, across-trial variability in drift rate has been a free parameter that is equated across conditions and its value typically varies between .08 and .3. We report SD coefficient values (σ1) and the constant values (η0). The values of across-trial SD in drift rate can be computed from these using the equation in Figure 2C. For comparison with other fits of the model to data in other articles, we present values of η for Experiments 1 and 2 below. (Note that the SD coefficients are labeled 10σ1 because the values in the table are multiplied by 10). For Experiment 1, the smallest and largest values of η are 0.13 and 0.36 (for the 15/10 and 40/35 numerosity conditions) and for Experiment 2, the smallest and largest values of η are 0.16 and 0.18. Thus, there are large differences in η for Experiment 1 across conditions while for Experiment 2, the values of η are almost constant across conditions.
Estimating the Contributions of Confounding Variables
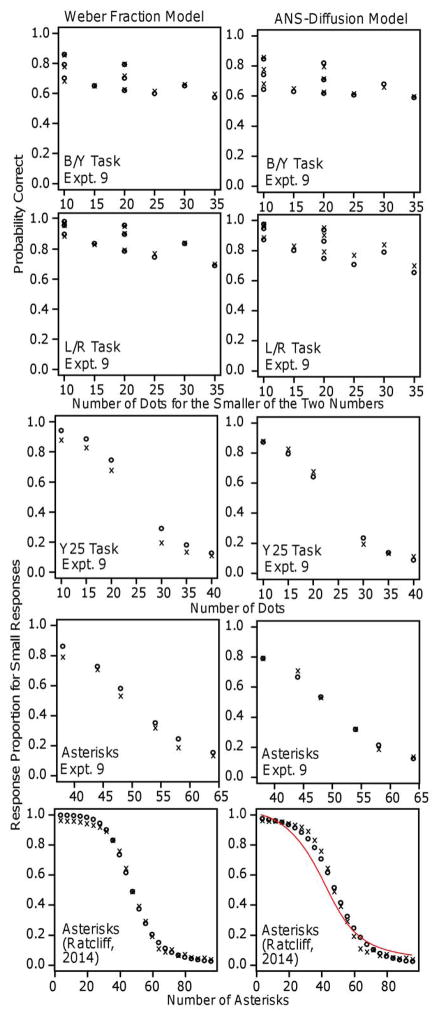
As mentioned above, research on numeracy has been concerned with whether experimental results can be explained by numerosity alone, without some confounding variable such as area, the length of a line drawn around the dots, or their density (e.g., DeWind et al., 2015; DeWind & Brannon, 2012; Feigenson et al., 2002; Gebuis, Cohen Kadosh, & Gevers, 2016; Gebuis & Gevers, 2011; Gebius & Reynvoet, 2012a, 2012b, 2013; Leibovich, Katzin, Harel, Henik, 2016; Mix et al., 2002). Efforts to control for such variables face the problem that controlling for one leaves another confounded with numerosity.
Our results show that the ANS-diffusion models can provide a way of measuring the effects of these variables. As Experiments 1 and 2 versus Experiment 3 (presented next) demonstrate, some confounded variables affect performance for some tasks but not others. In Experiments 1 and 2, the summed areas of the dots were either equal or proportional to the number. To the extent that area contributed to decisions, the drift-rate coefficient should be larger for proportional-area conditions and, if it is, then the difference in the equal- and proportional-area coefficients provides an estimate of the relative contributions of area and numerosity. In Experiment 1, the difference in the drift-rate coefficients from the linear model was 0.21 (means 0.37 minus 0.16), i.e., the effect of area was over double that for the equal-area condition. In Experiment 2, the difference in the coefficients from the log model was 0.29 (1.07 minus 0.78) and so the effect of area was about 35% over the value for the equal-area condition.
Our results argue against the notion that effects that have been attributed to representations of numerosity can be explained instead completely by non-numerical cues (Gebius, Gevers, & Cohen-Kadosh, 2014; Tibber et al., 2013). For example, Gebius and Reynvoet (2013) argued that numerosity information is not extracted automatically from visual stimuli in either an active task (subjects had to monitor numerosity and occasionally make a judgment) or a passive task (subjects viewed sequences of arrays of dots and neurophysiological measures were collected).
DeWind et al. (2015) have recently proposed a different method for measuring the effects of confounding variables. They used a linear combination of the logs of the ratios of the differences in independent variables between two sets of stimuli (e.g., their areas, numerosities, etc.) to produce a decision variable (cf., signal strength in signal detection theory). The inverse z-transformation of this combination was used to predict accuracy and the coefficients of the linear combination were used as estimates of the contributions of the independent variables. However, this method is only about accuracy, not RTs. Ratcliff (2014) found that z-transforms of accuracy can sometimes match drift rates, but whether that applies with DeWind et al.’s method and for numerosity discrimination tasks will require further research.
Why Does the Linear Model Produce Shorter RTs as Accuracy Decreases?
To illustrate, we use the simple case for which the boundaries of the diffusion process are equidistant from the starting point (although the logic is the same if they are not equidistant). Incidentally, with equidistant boundaries (Figure 8A), the correct and error RT distributions for a single drift rate (i.e., no trial-to-trial variability in starting point or drift rate) are identical except that there is lower probability mass in the error distribution.
Figure 8.
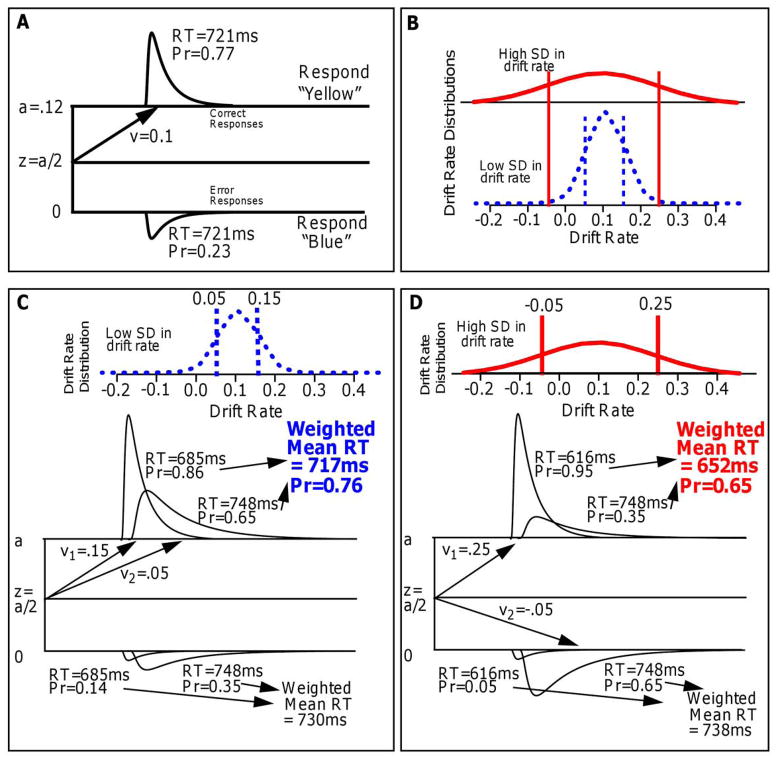
An illustration of how the predictions of the linear model arise. A illustrates a single diffusion process with a single drift rate (with no across trial variability in drift rate). RT distributions for correct and error responses are equal if the starting point is equidistant from the boundaries. B shows distributions of drift rate (across trials) for high numerosity (wide red solid distribution) and low numerosity (narrow blue dashed distribution). To represent these distributions for illustration, two drift rates are chosen (v1 and v2 and accuracy is the average of the two accuracy values and mean RT is a weighted sum of the two RTs. C shows the averages for the low-SD condition and D shows the averages for the high-SD condition with the averages for correct responses shown in green. For completeness, error responses are also shown; note that for boundaries equidistant from the starting point, for a single drift rate, correct and error RTs are the same.
Figure 8B shows trial-to-trial variability in drift rate with two normal distributions both centered on a drift rate of 0.1. The red solid function represents a larger numerosity, which has a larger SD, and the blue dashed function represents a smaller numerosity, which has a smaller SD. For illustration, two values of drift rate were selected from each function, at about plus and minus one SD, −0.05 and 0.25 for the larger numerosity and 0.05 and 0.15 for the smaller.
Figures 8C and 8D show the RT distributions for correct and error responses from 8A, with the two values of v for the smaller numerosity (7C) and the two values for the larger numerosity (7D). For the smaller numerosity, the 0.15 and 0.05 drift rates produce accuracy values of 0.86 and 0.65, respectively, which average to 0.76, and they produce RTs of 685 ms and 748 ms for correct responses which, when weighted by their probabilities (0.86 and 0.65), average to 717 ms. For the larger numerosity, the 0.25 and −0.05 drift rates produce accuracy values of 0.95 and 0.35, which average to 0.65. They produce RTs of 616 ms and 748 ms for correct responses which, when weighted by their probabilities (0.95 and 0.35), average to 652 ms. Thus, accuracy is lower for the larger numerosity, 0.65, than the smaller, 0.76, and-- the counterintuitive result-- RTs are shorter, 652 ms and 717 ms. The computations for RTs for errors are shown at the bottom boundary in the figures.
To explain this more generally: when the distribution of drift rates has a large SD, then drift rates in the left tail are negative. They are slower than responses in the right tail but they have lower probabilities of correct responses (because their drift rate is toward the error boundary). This means that fast correct responses in the right tail are weighted more heavily (there are more of them) than slower responses in the left tail, which leads to overall faster responses. As numerosity increases, the SD increases which leads to the lower probability and faster responses.
There is an alternative hypothesis that has been suggested to explain counter-intuitive results similar to those obtained in Experiment 1 but in different perceptual tasks. The assumption is that within-trial variability increases with stimulus strength, or in our case, numerosity (e.g., Donkin, Brown, & Heathcote, 2009; Smith & Ratcliff, 2009; Teodorescu, Moran, & Usher, 2016; Teodorescu & Usher, 2013). In the diffusion model, usually the variability in the accumulation of information from the starting point to the boundaries is constant across levels of difficulty. If within-trial variability increases with numerosity, processes hit the boundaries faster because of increased variability, which leads to the decrease in RTs with decreasing accuracy. However, there is a major problem with this within-trial variability account: it cannot explain why the decrease in RT with decreasing accuracy only occurs for intermingled blue/yellow dot displays and not side-by-side displays (and in the experiments described below, not for single arrays matched against a standard). An increase in within-trial variability with numerosity would be expected to be a general property of numerosity decisions, not a property of a particular stimulus configuration and task.
Experiment 3
In Experiment 1, accuracy decreased as difficulty increased and RTs decreased. In this experiment, like Experiment 2, accuracy decreased as difficulty increased and RTs increased. In Experiments 1 and 2, the proportional-area conditions were easier than the equal-area ones; in this experiment, performance was about the same.
The stimuli were single arrays of intermingled blue and yellow dots (Figure 4A). Subjects decided whether the number of yellow dots (or the number of blue dots) was larger or smaller than 25; we call this the Y25 task. There were three variables: the number of dots for the target color (the dots to be compared to 25) was 10, 15, 20, 30, 35, or 40, there were either 15 or 35 dots of the other color, and areas were either equal or proportional, for a total of 24 conditions, collapsing over whether the target color was blue or yellow. The target color alternated from one block to the next.
Results
Table 4 shows accuracy and mean RTs. Correct responses for 10, 15, and 20 dots were combined with correct responses for 30, 35, and 40 dots and then averaged. The data show the standard result that RTs increase as accuracy decreases. The data were not collapsed over “larger” responses to larger-than-25 stimuli and “smaller” responses to smaller-than-25 stimuli because the two sets of data were not symmetric.
Table 4.
Experiment 3: accuracy and correct mean RTs collapsed over stimulus difficulty
| measure | 15 non-target dots | 35 non-target dots | ||
|---|---|---|---|---|
| proportional area | equal area | proportional area | equal area | |
| accuracy | 0.856 | 0.858 | 0.837 | 0.841 |
| mean RT | 537 | 528 | 537 | 534 |
Analyses of variance were conducted with two factors, area and the number of non-target dots. The data were averaged over the numerosity conditions for these analyses. The difference in accuracy between the equal- and proportional-area conditions was only 0.2% and the difference in correct mean RTs was only 1 ms and neither was significant, F(1,15)=1.0 for accuracy and F(1,15)=0.4 for RTs. The differences in accuracy and correct mean RTs between the two numbers of non-target dots were small, 1.8% in accuracy and 8 ms in RTs, but they were significant, F(1,15)=12.7, p<.05 for accuracy and F(1,15)=12.7, p<.05 for RTs. The interactions were not significant, F(1,15)=0.1 and F(1,15)=1.2 for accuracy and RTs, respectively.
To fit the models, drift rates were calculated with the drift-rate coefficient multiplying the difference between the number of target dots and 25 for the linear model and the difference between the logs of the number of target dots and 25 for the log model. The SD coefficient was also calculated using the number of target dots and 25.
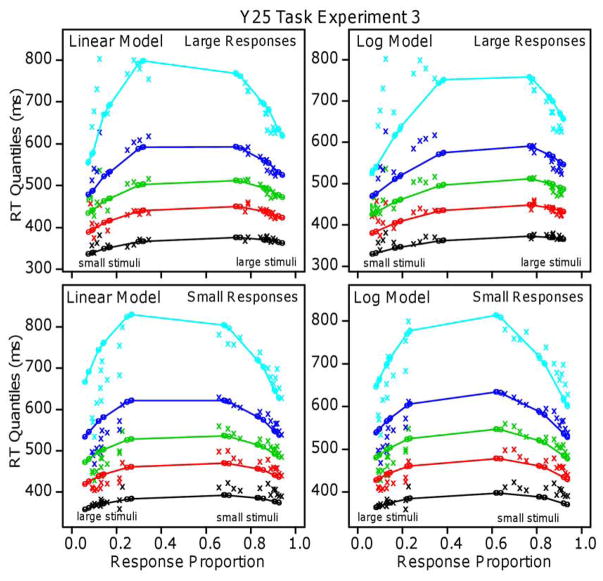
Figure 9 shows the quantile-probability plots for the data and the models’ predictions, with the x’s for the data and the o’s and lines that connect them for the predictions. The top two panels are for “larger” responses and the bottom two are for “smaller” responses. For each plot, there are 12 sets of quantile data points for correct responses and 12 for errors, where the 12 are made up of the combinations of the area variable, the number of non-target dots, and three numerosities, 10, 15, and 20 target dots for “smaller” stimuli or 30, 35, and 40 dots for “larger” stimuli. The best-fitting values of the parameters and mean G-square measures are shown in Tables 2 and 3.
Figure 9.
Quantile probability plots for Experiment 3 for the log and linear models for large and small responses separately.
There were six numerosity values, two area conditions, and two numbers of non-target dots, giving 264 (24 times 11) degrees of freedom in the data. There were twelve parameters, so the number of degrees of freedom for fitting the models was 252. The twelve parameters were the usual four for the diffusion model, the starting point of the diffusion process, a drift-rate criterion, a drift-rate coefficient for each of the four combinations of area and number of non-targets, and 2 SD coefficients (one constant and one specifying how the SD changes with numerosity). A drift-rate criterion (this was subtracted from all the drift rates produced from the expressions for drift rates in Figure 2C) was needed because some of the subjects did not set the zero point of drift rate exactly at 25.
The mean G-square value was a little lower for the linear model than for the log model and 13 out 16 G-square values for individual subjects were smaller for the linear as opposed to the log model, thus supporting the linear model. However, the linear and log models fit the data qualitatively about equally well. There were larger differences in accuracy for small stimuli than large stimuli and both models predict this. Both models miss slightly the leading edges of the RT distributions for “smaller” responses to small stimuli.
We conducted analyses of variance on the drift-rate coefficients. The effect of the area variable was not significant for either model, F(1,15)=1.5 and F(1,15)=1.2 for the linear and log models, respectively; the effect of the number of non-targets was significant, F(1,15)=27.1, p<.05, and F(1,15)=12.5, p<.05, respectively; and the interactions were not significant (F(1,15)=1.3 and F(1,15)=0.1). The area variable had less than a 2% effect and the difference between 15 and 35 non-target dots was only about 10%, notably small relative to the 100% and 30% effects of the area variable on the drift rate coefficient in Experiments 1 and 2, respectively.
Comparison of Parameter Values for Experiments 1, 2, and 3
There were no large or systematic differences across the experiments in the best-fitting values for the parameters of the diffusion model. The distance between the boundaries was about the same for the three experiments and nondecision time was a modest 50 ms longer for Experiment 1 than for Experiments 2 and 3. The across-trial ranges in nondecision time and starting point were similar across the experiments (note that they are estimated less well than the other parameters with larger SD’s in their estimates, Ratcliff & Tuerklinckx, 2002; Ratcliff & Chiilders, 2015).
Drift-rate coefficients can be compared within the linear or within the log model across conditions of an experiment, but not between them because the log and linear models place numerosity on different scales. However, drift rates track difficulty in both models and the relative sizes of the differences among conditions can be used to understand how manipulations affected the quality of encoded representations of stimuli. The main results were that the area manipulation affected the drift-rate coefficients most in the B/Y task, next in the L/R task, and almost not at all in the Y25 task. Proportional-area stimuli increased drift-rate coefficients by 100% for the B/Y task, 30% for the L/R task, and less than 10% for the Y25 task.
SD coefficients can be also be compared. For Experiments 1 and 3, the SD coefficients for the linear model were 2.5 times larger for the B/Y task than the Y25 task (t(28.5)=4.4, p<.05). This suggests that there is a lot more variability in extracting numerosity information from two intermixed stimuli than extracting numerosity information from one stimulus.
When the linear model was successful, the SDs in drift rate η (derived from the SD coefficients) should have increased with numerosity and they did, although only modestly: the minimum and maximum values of η were 0.10 and 0.15 (compared with 0.13 and 0.36 for Experiment 1). When the log model was successful, the SDs should have been approximately constant and they were: constant at 0.03 (compared with 0.16 and 0.18 for Experiment 2).
Experiment 4
Experiments 4 and 5 are two of the experiments we conducted to replicate results from the context of one set of independent variables to another set. The task for Experiment 4 was the B/Y task from Experiment 1: the arrays were intermingled blue and yellow dots and subjects decided which had the greater number. The new variable was dot size: the dots were either about the same sizes as for Experiments 1, 2, and 3 or they were very small (Figure 4G). The results replicated those of Experiment 1 for both sizes: RTs decreased as accuracy decreased, the area variable affected performance, and the linear model fit the data better than the log model.
The stimuli for Experiment 4 were constructed in the same way as for Experiment 1 except for the manipulation of dot size. The manipulation of area was the same as for Experiment 1 and the numeracy conditions were the same, 15/10, 20/15, 25/20, 30/25, 40/35, 20/10, 30/20, 40/30, 30/10, and 40/20. The radii of the dots were either 8, 10, 12, 14, 16, or 18 pixels or 2, 3, 4, 5, 6, or 7 pixels.
RT and Accuracy Results
Responses to blue dots were combined with responses to yellow dots in the appropriate way. The effects of size and the area variable averaged over numerosity are shown in Table 5. Responses were less accurate and slower for the equal-area conditions than the proportional-area conditions, F(1,15)=124.4, p<.05, for accuracy and F(1,15)=74.2, p<.05, for RTs. They were less accurate and slower for the small dots than the regular-sized ones, F(1,15)=45.3, p<.05, for accuracy and F(1,15)=9.1, p<.05, for RTs. The interactions were also significant, F(1,15)=6.9, p<.05, for accuracy and F(1,15)=13.7, p<.05), for RTs. The effects of area on accuracy and RTs were larger than those of dot size, 11% and 4%, respectively, for accuracy and 29 ms and 15 ms, respectively, for RTs.
Table 5.
Experiment 4: accuracy and correct mean RT collapsed over stimulus difficulty
| measure | small-size dots | large-size dots | ||
|---|---|---|---|---|
| proportional area | equal area | proportional area | equal area | |
| accuracy | 0.751 | 0.652 | 0.809 | 0.682 |
| mean RT | 578 | 600 | 557 | 592 |
Figure 10 shows quantile-probability plots for small dot sizes on the left panel and the larger ones on the right, x’s the data and o’s the predictions of the linear model. Difficulty increased from the ends of the functions toward the middle and accuracy and RTs decreased, replicating Experiment 1. Fits of the models to the data are described after Experiment 5.
Figure 10.
Quantile probability plots for Experiments 4 and 5. For Experiment 4, the inner functions are for equal-area conditions, the outer functions for proportional are conditions.
Experiment 5
This experiment was a replication of the Y25 task from Experiment 3 with the added manipulation of dot size. Blue and yellow dots were intermingled in single arrays and subjects decided whether the number of dots of one of the colors was larger or smaller than 25. There were 10, 15, 20, 30, 35, or 40 of the target-color dots in each array, 15 or 35 dots of the other color, and the summed areas of the dots were equal or proportional. The sizes of the small and regular-sized dots were the same as for Experiment 4.
Results
Table 6 shows the data for correct responses collapsed over the three numbers of dots smaller than 25 and the three numbers of dots larger than 25. As difficulty increased from the ends of the functions toward the middle, accuracy decreased and RTs increased, replicating Experiment 3.
Table 6.
Experiment 5: accuracy and correct mean RT collapsed over stimulus difficulty
| measure | area | small-size dots | large-size dots | ||
|---|---|---|---|---|---|
| 15 non-target dots | 35 non-target dots | 15 non-target dots | 35 non-target dots | ||
| accuracy | proportional | 0.827 | 0.813 | 0.835 | 0.840 |
| equal | 0.821 | 0.813 | 0.847 | 0.840 | |
| mean RT | proportional | 558 | 566 | 544 | 556 |
| equal | 555 | 561 | 548 | 551 | |
The areas of the dots did not significantly affect accuracy or mean correct RTs (F’s less than 0.8). The number of non-target dots did not significantly affect accuracy, F(1,15)=0.8, but it did significantly affect RTs, F(1,15)=8.9, p<.05, although the effect was only 7 ms. The size of the dots had a significant effect on accuracy, about 2%, F(1,15)=16.6, p<.05, and on RTs, about 10 ms, F(1,15)=20.7. The interactions were not significant; F’s were less than 2.4 for accuracy and less than 2.2 for RTs.
Figure 10 shows quantile-probability plots for the larger and smaller dot sizes all in the same plot, x’s the data and o’s the predictions of the linear model (the log model predictions were indistinguishable). As difficulty increased from the ends of the functions toward the middle, accuracy and RTs decreased, replicating Experiment 3.
Fitting the Models to the Data for Experiments 4 and 5
Tables 2 and 3 show the best-fitting parameter and mean G-square values and Figure 10 shows the quantile-probability plots with predictions from the linear model. The shapes of the plots are the same as those for Experiments 1 and Experiment 3. The log model failed to fit the data for Experiment 4, as it did for Experiment 1, and it fit the data about as well as the linear model for Experiment 5, as it did for Experiment 3.
For Experiment 4, as difficulty increased and accuracy decreased, RTs decreased for differences in numerosity of 5, the effect was smaller for differences of 10, and the functions flattened out for differences of 20, the same pattern as for Experiment 1.
To fit the linear model to the data, there were the usual four parameters for the diffusion model plus the constant component of the across-trial SD in drift rate, four drift-rate coefficients, one for each of the area by dot-size conditions, and the SD coefficient. There were 430 degrees of freedom (11 times 40 conditions minus the ten parameters) for a critical chi-square of 479.3. The mean G-square value was 474, a little below the critical value.
The linear model separated the effects of confounded variables, as it did for Experiments 1, 2, and 3, by estimating the relative sizes of them in the drift-rate coefficients. For Experiment 4, for the linear model, the area manipulation doubled the drift-rate coefficient, from 0.018 for equal areas to 0.035 for proportional areas (F(1,15)=101.8, p<.05) and the dot-size manipulation had a 30% effect, the drift-rate coefficient was 0.023 for small dots and 0.030 for regular-size dots (F(1,15)=61.2, p<.05). The interaction was also significant (F(1,15)=10.2, p<.05). These drift-rate coefficients provide measures of the effects of the manipulations and dot size on numerosity discrimination. Although there is an interaction, the effects of the two variables appear to be proportional or multiplicative rather than additive (see Table 3).
For individuals, G-square values were lower for the linear model for 11 out of 16 subjects and the slope of the RT versus overall numerosity function for differences of 5 was less than 0 for 56 out of 64 comparisons (equal and proportional area crossed with dot size for 16 subjects). Both of these support the linear model for individual subject data.
For Experiment 5, dividing the data by the two area conditions, the number of non-target dots and dot size gave too few errors for many of the high-accuracy conditions (i.e., less than the 5 needed to produce error RT quantiles). Furthermore, the differences between the equal- and proportional-area conditions was only 0.2% in accuracy and 2 ms in mean RT, so we combined the two conditions. This reduced the number of conditions to 24. There were the usual four parameters for the diffusion model, the constant component of the across-trial SD in drift rate, the coefficient for across-trial SD in drift rate, a drift-rate criterion (because subjects did not set the zero point of drift exactly at 25), the starting point of the diffusion process, and four drift-rate coefficients. Note that the drift-rate criterion for the linear model in Experiment 5 seems large relative to the drift-rate coefficients, but the drift rates are derived from the coefficients by multiplying them by the number of dots minus 25 (so the drift rates for the coefficient 0.032 in Table 3 are 0.16, 0.32, and 0.48 which are larger than the drift rate criterion of −0.032). There were 252 degrees of freedom (11 times 24 conditions minus 12 parameters) and the critical value was 290.0. The mean G-square from the fits to the data was a little larger than this, 328, showing a good fit to the data. For individuals, G-square values were lower for the linear model for 12 out of 16 subjects which supports the linear model for individual subject data.
The effects of the confounded variables were small. The effect of the number of non-target dots, 0.035 vs. 0.033 for 15 non-target dots compared to 35, was significant (F(1,15)=4.2, p<.05) but the size was only 6%, which is comparable to the 10% effect in Experiment 3. The effect of the size of the dots was also significant (F(1,15)=28.8, p<.05), but the effect was not large, about a 15% effect, with the drift-rate coefficient for large stimuli 0.036 and the coefficient for small stimuli 0.031. The interaction was not significant (F(1,15)=0.6).
The results of the area manipulation for Experiments 4 and 5 replicated the effects of the confounded variables in Experiments 1 and 3. For the B/Y task (Experiment 4), the area conditions had large effects on accuracy, RTs, and drift-rate coefficients but for the Y25 task (Experiment 5), area had non-measurable effects.
The SD coefficients differed significantly between the two experiments, with the coefficient for Experiment 4 larger than the one for Experiment 5 (t(23.4)=3.4, p<.05). As for Experiments 1 and 3, this is likely because extracting information about the relative number of two stimuli from an intermingled array produces more variability than comparing one array to a standard. The SD coefficients are used to produce across-trial SDs in drift rate (η) using the numerosity values for each condition in the experiments (using the equation in Figure 2C). For linear models, for Experiment 4, the smallest value was 0.17 and the largest 0.44 and for Experiment 5, the smallest was 0.13 and the largest 0.21. These results are similar to those from Experiments 1 and 3.
The other model parameters were similar to those from Experiments 1 and 3, respectively. The values of boundary separation and nondecision time differed little between Experiments 4 and 5 and, although the differences in the range of starting point and the range in nondecision time appear larger, the large variability associated with those parameters means that they do not differ in a meaningful way.
Correlational/Individual Differences Analyses
Experiments 1 through 5 have shown that numerosity discriminations are not based on exactly the same aspects of stimuli across tasks. When the task was to compare the numerosity of blue and yellow dots intermingled in a single array (the B/Y task) or dots of the same color in two side-by-side arrays (the L/R task), area and dot size had large effects on performance; discrimination was easier for proportional- than equal-areas and easier for larger dots than smaller ones. But when the task was to compare the numerosity of one array of dots against a standard (the Y25 task), area and dot size had small or nonexistent effects.
The findings just enumerated are complex and this brings up two questions: are the numerosity skills an individual brings to a numerosity discrimination task the same from one level of a dimension to another and are they the same from one task to another?
Within a task, for Experiments 1 and 2, there were two levels of the area variable. The correlations between subjects’ drift-rate coefficients for the equal- and proportional-area conditions were high, 0.83 in Experiment 1 and 0.85 in Experiment 2. For Experiment 3, there were two dimensions, area and number of non-target dots, each with two levels, giving six correlations; the average of them was 0.93. For Experiment 4, the dimensions were area and dot size and the average of the six correlations was 0.97. For Experiment 5, the dimensions were area, dot size, and number of non-target dots. Collapsing over area, the average of the six pairs of correlations was 0.88. Altogether, these correlations show that subjects who were good at one level of a dimension or combination of dimensions were good at the others, indicating that the numerosity skills that a subject used were about the same for all the conditions in the experiments.
The second question was whether the B/Y, L/R, and Y25 tasks assess the same numerosity abilities? In other words, are drift-rate coefficients highly correlated across tasks? These are critical questions for research in numerical cognition; if the skills an individual brings to one numerosity discrimination task are not correlated with those of another task, then choices about what tasks to use to measure and investigate the abilities that might underlie math achievement are compromised. It would be difficult to argue that numerosity in general is predictive of or related to achievement. We addressed this issue with Experiments 6 through 9, for which subjects were each tested on two or more tasks.
Experiment 6
Subjects were tested on the B/Y task, deciding whether there were more blue or yellow dots in a single array and the Y25 task, deciding whether the number of blue dots or the number of yellow dots in a single array was larger or smaller than 25. The two tasks were tested in a single 50-min. session so in order to keep the number of observations per condition large, only equal-area arrays were used.
For the B/Y task, there were the same ten numerosity conditions as for Experiment 1, which varied levels of numerosity and differences between the levels. For the Y25 task, there were the same six levels of numerosity and the same two numbers of non-target dots, 15 and 35 as for Experiment 3. Which task was presented first alternated across subjects.
Results
Responses to blue dots were combined with responses to yellow dots in the appropriate way for the B/Y task. For analyses for the Y25 task, there was only a 2.5% difference in accuracy and only a 3 ms difference in correct mean RTs between the 15 and 35 numbers of non-target dots, so the data were averaged over them to give more observations (because in many of the conditions there were too few errors to provide quantile RTs for fitting).
Figure 11, left panel, shows the quantile-probability plots for the B/Y task and the predictions of the linear model: RTs decrease as accuracy decreases for constant differences in numerosity just as in Experiments 1 and 4. The right panel shows the quantile-probability plots for the Y25 task and the predictions of the linear model: RTs increase as accuracy decreases, just as in Experiments 3 and 5. The best-fitting parameter values and the mean G-square values are shown in Tables 2 and 3.
Figure 11.
Quantile probability plots for Experiment 6.
The linear model fit the data reasonably well for both tasks. For the B/Y task, the number of degrees of freedom was 103 (10 conditions and seven model parameters, boundary distance, across-trial range in starting point, nondecision time, across-trial range in nondecision time, the constant component of the SD coefficient, the SD coefficient, and a drift-rate coefficient, Tables 2 and 3). The critical chi-square value was 132.1 and the mean G-square value was a little larger than this, showing a good fit to the data. For the Y25 task, the number of degrees of freedom was 57 (six conditions and nine parameters, the same six parameters that were listed first for the B/Y task plus a drift-rate criterion, the starting point of the diffusion process, z, and one drift-rate coefficient). The critical chi-square value was 75.6. The mean G-square value was a little larger than the critical value, showing reasonable fits.
The log model also fit both tasks reasonably well, and the numerical mean G-square value was only a little larger for the log model than the linear model. For the B/Y task, G-square values were lower for the linear model than the log model for 21 out of 35 subjects and the slope of the RT versus overall numerosity function for differences of 5 was less than 0 for 32 out of 35 comparisons. This shows that the overall fit was quite similar for the two models, but the qualitative pattern of data (decreasing RT with increasing numerosity function for differences of 5) clearly supported the linear model. For the Y25 task, G-square values were lower for the linear model for 15 out of 35 subjects, which shows similar amounts of support for both models.
Figure 12 shows scatter plots and correlations among the distance between the boundaries, a, nondecision time, Ter, the SD coefficient, σ1, and the drift-rate coefficient v1 for the two tasks. The critical value of the correlation coefficient for 32 observations (32 subjects) is 0.35 with 30 degrees of freedom.
Figure 12.
Scatter plots and correlation coefficients for ANS-diffusion model parameters between the B/Y discrimination task and the Y25 task in Experiment 6.
The main aim of this experiment was to examine whether a subject brought the same numerosity skills to the two tasks. Skill is measured by the drift-rate coefficient, v1, and it was significantly correlated between the two tasks (top left panel of Figure 12). The SD coefficients were also significantly correlated (top right panel). The distances between the boundaries correlated strongly (bottom left panel); subjects who responded more slowly and more carefully in one task also did so in the other task. Nondecision times were significantly correlated but less strongly (Figure 12, bottom right panel), although the small correlation might be due to outliers (the correlation was larger in Experiments 7, 8, and 9).
Experiment 7
Subjects were tested on two tasks. One was the B/Y task from Experiments 1, 4, and 6. The other was new: the stimuli were 5×5 arrays of X’s and O’s and subjects decided whether there were more X’s or O’s (we call this the X/O task). The total number of X’s and O’s was always 25 (Figure 4E). To make the two tasks as similar as possible, we made the number of dots in the B/Y task sum to 25 and we made the combinations of the numbers of blue and yellow dots match the combinations of X’s and O’s. The combinations were 18/7 and 7/18 for the easiest conditions, 16/9 and 9/16 for the medium difficulty conditions, and 14/11 and 11/14 for the most difficult conditions. For the dots, the areas were either equal or proportional.
In this experiment, the differences in numerosity were not constant as numerosity increased as they were in Experiment 1 (for example, the differences between 10 and 15, 15 and 20, and 20 and 25 were all 5). This excluded the conditions that led to Experiment 1’s counter-intuitive result. Thus, the linear and log models both fit the data reasonably well and so we examined correlations between model parameters for the two tasks for both models.
The two tasks were tested in a single 50-min. session. All the blocks of one task were completed before all the blocks of the other task and the order was switched for successive subjects. The X’s and O’s were white characters on a black background (the inverse of Figure 4E), presented in a square that was 235 pixels per side (6.3 degrees of visual angle) in the center of the screen. The X’s were 30 pixels wide and 35 pixels high and the O’s were 33 pixels wide and 35 pixels high (subtending angles of 0.81 by 0.95 degrees and 0.89 by 0.95 degrees, respectively). The X’s and O’s were spaced 50 pixels apart vertically and horizontally.
Results
The data for “blue” and “yellow” responses were symmetric and so were “X” and “O” responses, so they were each combined in the appropriate way (e.g., correct responses for X’s for the easy condition were combined with correct responses for O’s for the easy condition, error responses for X’s for the easy condition were combined with error responses for O’s for the easy condition, and so on for the other conditions). The linear and log models both fit the data well and we plot results only for the linear one (parameter values for both are shown in Tables 2 and 3). The quantile-probability plots for the linear model are shown in Figure 13. They show that the quantile RTs for all the conditions for each experiment fall on a single quantile-probability function.
Figure 13.
Quantile probability plots for Experiments 7, 8, and 10.
For the B/Y task, accuracy averaged over the numerosity conditions was better with proportional than equal areas, 0.83 and 0.74 correct responses, and mean RT for correct responses was shorter (569 ms and 604 ms). The differences were significant, t(31)=13.4, p<.05, for accuracy and t(31)=8.7, p<.05, for mean RT. For the X/O task, accuracy averaged over the numerosity conditions was 0.77 correct responses and correct mean RT averaged over the numerosity conditions was 585 ms, thus the two tasks showed comparable performance. (Median RTs and accuracy values can be read off the quantile probability plots in Figure 13 - median RTs are the middle one of the five horizontal lines).
There were 58 degrees of freedom for the B/Y task (six conditions and eight parameters, boundary separation, across-trial range in starting point, nondecision time, across-trial range in nondecision time, the constant component of the SD coefficient, the SD coefficient, and two drift-rate coefficients, one for the equal-area conditions and one for the proportional-area ones. Because the data were symmetric, the starting points in the models could be set to half the distance between the boundaries. Similarly, there were 26 degrees of freedom for the X/O task (three conditions and seven parameters). The critical chi-square value was 76.8 for the B/Y task and 38.0 for the X/O task. The mean G-square values for both tasks were a little higher than their critical values, showing reasonably good fits, and the G-square values for the B/Y task supported the linear model, but the G-square values for the linear and log models for the X/O task were close to the same (Table 3). The two drift-rate coefficients for the B/Y task were significantly different, t(31)=15.1, p<.05, for the linear model and t(31)=13.1, p<.05, for the log model (as for Experiment 1).
For the B/Y task for individuals, G-square values were lower for the linear model for 24 out of 32 subjects while for the X/O task, there were equal numbers for each model (16 out of 32). These provide support for the linear model for individual subject data but no differential support for the X/O task.
The correlations between the model parameters for the two tasks are shown in Table 7. The critical value for the correlation coefficient is 0.35 with 30 degrees of freedom. The drift-rate coefficients were significantly correlated between the two tasks, indicating that common numerosity skills are used. The distance between the boundaries and nondecision time were also significantly correlated (as in Experiment 6).
Table 7.
Experiment 7, correlations between and within tasks
| B/Y vs. X/O | B/Y | ||||||
|---|---|---|---|---|---|---|---|
| Model | a | Ter | sz | st | σ1 | (v1+v2) vs. v1 | v1 vs. v2 |
| Linear | 0.68 | 0.71 | −0.05 | 0.49 | −0.13 | 0.71 | 0.72 |
| Log | 0.60 | 0.71 | 0.43 | 0.49 | 0.15 | 0.58 | 0.90 |
The SD coefficient σ1 was not significantly correlated between the tasks (unlike Experiment 6). This is because the value of the across-trial SD in drift rate differed little across numerosity conditions and so produced little constraint on the value of σ1. The SD coefficient produces the values of the SD in drift rate across trials, η, for each condition in an experiment using the coefficients and the numerosities for the two stimuli as in the bottom equation in Figure 2C. The numbers of blue and yellow dots and of X’s and O’s were 18 and 7, 16 and 9, or 14 and 11. The values of η for the linear model for the X/O task were 0.101, 0.103, and 0.106 and for the B/Y task they were 0.131, 0.134, and 0.141. These are indistinguishable from constant values which, along with high estimation variability (Ratcliff & Tuerlinckx, 2002), means that they are relatively poorly estimated and this explains why they do not correlate significantly across the tasks.
The most important result from this is that the drift coefficients, boundary settings, and nondecision time parameters correlate across these two tasks. This suggests that processes and representation are related across tasks and especially that the two tasks are tapping into the same numerosity aptitude. Later we discuss a way of manipulating many possible confounding variables and estimating drift rate coefficients for each variable to see which ones carry discriminative power.
Experiment 8
One of the tasks for this experiment was an X/O task like that used in Experiment 7, with subjects deciding whether there were more X’s or O’s in a 5×5 display. The other task was an asterisks task, with subjects deciding whether the number of asterisks in a 10×10 array was larger than 50 or not.
We have used this asterisks task in a number of other studies because it provides a way to map accuracy from near chance to near ceiling. This range of accuracy and RT distributions for correct and error responses provides significant constraints with which to test the diffusion model (Leite & Ratcliff, 2011; Ratcliff, 2006, 2014; Ratcliff et al., 1999, 2001, 2007, 2010, 2012, 2015, 2016). Drift rates for this task correlate positively with drift rates for recognition memory and lexical decision tasks (Ratcliff et al., 2010), suggesting future research to investigate whether other numerosity discrimination tasks produce correlations with those tasks. Significant correlations have also been found with symbolic number discrimination and memory for numbers (Ratcliff, Thompson, and McKoon, 2015; Thompson, Ratcliff, & McKoon, 2016).
When the diffusion model has been fit to the data for this asterisks task, there has been no representation model and so drift rates are estimated from the data with a different drift rate for each level of numerosity (e.g., Ratcliff, 2014; Ratcliff, Thompson, & McKoon, 2015). In these earlier applications, it has been assumed that the SD in drift rate across trials (η) is constant. When drift rates were plotted against number of asterisks, the functions appeared linear (Ratcliff, 2014, Figure 2). This is a puzzle because in ANS models, the difference in drift rates between 15 and 20 asterisks would be expected to be larger than the difference between 80 and 85, just as the difference between 15 and 20 dots was larger than the difference between 30 and 35 dots in the Y25 task in Experiment 3. For the Y25 task, the linear model fit well, but it required that η increase with numerosity.
There are two possible resolutions to this puzzle. One is that subjects treat the asterisks task not as one in which the number of asterisks is compared to a standard (50), but instead as one in which the number of asterisks in a display is compared to the number of blank spaces. This makes the task like the B/Y and L/R tasks. The second is that the arrangement of asterisks in a regular grid with all characters of the same size may allow a much better assessment of numerosity relative to a criterion than dots of random sizes in random positions. The difference between these two schemes is what enters the calculation of η. In the first scheme, N2=100-N1 whereas in the second N2=50.
When the range of asterisks is 31–70, the means of the extreme bins are 33 and 68. For N1=33, 50, and 68 asterisks, the value of sqrt(N12+N22) for the first scheme is 75, 71, and 75, while for the second it is 60, 71, and 84. If the constant η0 were half the average value of η, then the differences in η across conditions would be quite small and impossible to detect.
If subjects are judging whether there are more or fewer spaces or asterisks then we can use the linear model as implemented for the X/O task in Experiment 7. Thus we can determine whether the models fit in the same way for the two tasks and to determine if individual differences are the same across the two tasks.
The asterisks were presented in 10 × 10 arrays 4.0 cm wide by 8.8 cm high, subtending 4.3 by 9.5 degrees of visual angle. The numbers of asterisks in the displays ranged from 31 to 70 in steps of 1 (always adding to 100). The displays of X’s and O’s were constructed in the same way (not the same as in Experiment 7) such that the size and visual angles were half of those for the asterisks stimuli. The numbers of X’s and O’s ranged from 5 to 20 in steps of 1, always adding to 25. All the blocks of one task were completed before all the blocks of the other task and the order of the tasks was switched for successive subjects.
Results
We grouped the number of asterisks into eight conditions, 31–35, 36–40, .. 66–70 and the number of X’s and O’s into eight conditions, 5–6 X’s and 19–20 O’s, 7–8 X’s and 17–18 O’s, and so on. Responses were symmetric for both experiments, so the data were also grouped over above or below 50 and above or below 12.5 in the appropriate way to form four conditions. (For the asterisks task, the accuracy values for the four groups for small stimuli were 0.93, 0.88, 0.80, and 0.58 and for large responses, the values were 0.92, 0.88, 0.81, and 0.61 which shows no accuracy compression for large numbers of asterisks and shows why combining small and large numbers is valid). Full psychometric functions for this task are examined in Experiment 9 and the Weber fraction analysis later.
To compare the tasks, for the asterisks task we assumed that subjects were deciding whether an array of asterisks contained more asterisks or more blank spaces (i.e., not comparing the number of asterisks to 50), just the same as deciding whether there were more X’s or O’s. This means that N1/N2 were 32/68, 37/63, 42/58, and 47/53. (We also fit the scheme in which N2=50 and found fits and parameter values that were almost identical.)
The linear and log models were applied in the same way as in Experiment 7 with the same parameters (shown in Tables 2 and 3) and they fit the data indistinguishably well, as in Experiment 7. The quantile-probability plots are shown in Figure 8 (middle) with the predictions of the linear model. There were 44 degrees of freedom (four conditions and the same seven parameters as for Experiment 6) with a critical chi-square value of 52.5 for both tasks. The mean G-square from the fits were below the critical value for each model and task, showing good fits. There was support for the linear model in individual fits with 24/32 subjects better fit by the linear model by G-square (the mean G-squares were quite similar for the log and linear models, Table 3).
The application of the models used the assumption that the numbers of asterisks and spaces (just like the numbers of X’s and O’s in the X/O task) enter the computation for the SD in drift rate across trials. We can compute how much η changes across conditions using the expression in Figure 2C. For the middle and the most extreme numbers of asterisks, 50 and 70, η is 0.20 and 0.21, which means that the SD in drift rate across trials in the model for the hardest to the easiest condition was essentially constant. This is consistent with all the prior applications of the diffusion model to this task for which it was always assumed that η was a constant across conditions.
The correlations between the tasks for the linear and log models are shown in Table 8. The drift-rate coefficients correlated across tasks (0.52 and 0.60), as they did for Experiments 6 and 7. There were strong correlations between the boundary separations (0.55 and 0.54) and the nondecision times (0.72 and 0.67) for the linear and log models respectively. The SD coefficients correlated 0.56 and −0.03 for the X/O and asterisks tasks, respectively. As for Experiment 7 and as discussed above, the data are fit with approximately constant values of across-trial SD in drift rate and this explains the lack of correlation between the SD parameters.
Table 8.
Experiment 8, correlations between and within tasks
| Asterisks vs. X/O | ||||||
|---|---|---|---|---|---|---|
| Model | a | Ter | sz | st | σ1 | v1 |
| Linear | 0.55 | 0.72 | 0.27 | 0.47 | 0.35 | 0.52 |
| Log | 0.54 | 0.67 | 0.12 | 0.53 | −0.12 | 0.60 |
As for Experiment 7, the drift coefficients, boundary settings, and nondecision time parameters correlated across the two tasks. This suggests that processes and representation are related across tasks and that the two tasks are tapping into the same numerosity aptitude.
Experiment 9
At this point, we have shown significant correlations in drift-rate coefficients from one task to another for three pairs of tasks. In this experiment, we confirm and extend these results by testing each subject on four tasks, the B/Y, Y25, L/R, and asterisks tasks. These were the tasks from Experiments 1, 2, 3, and 8.
There were two sessions of the experiment, each with two tasks, 25 min. each, always tested in the same order (B/Y, Y25, L/R, and asterisks). The independent variables for the B/Y and L/R tasks were the 10 numerosity combinations from Experiments 1 and 2 and for the Y25 task they were the six numerosity conditions from Experiment 3. The areas of the dots were always equal (to produce more observations per condition because there was only half a session for each task). The asterisks task was the same as for Experiment 8 except that the range of the numbers of asterisks was reduced to between 36 and 65. For each experiment, we collapsed across conditions in the same way as for the previous experiments, giving 10 conditions for the B/Y and L/R tasks and 6 for the Y25 and asterisks tasks.
Results
The linear and log models were fit to the data and the one that best fit the data for each task was the same as for the earlier experiments. These best-fitting models were used in the correlational analyses below.
The B/Y task showed the decrease in RT as accuracy decreased (Figure 14; Table 9) and the linear but not the log model fit the data well. The mean G-square value for the linear model (133) was close to the critical value, 127.7 for 103 degrees of freedom. The L/R discrimination task showed the increase in RTs as accuracy decreased. (This was less apparent with numerosity differences of 5 than with 10 and 20.) The log model fit the data better than the linear model with the mean G-square value for the log model (133) a little larger than the critical value of 127.7.
Figure 14.
Quantile probability plots for the four tasks in Experiment 9.
Table 9.
Model parameters for Experiments 9 and 11 and Experiment 1, Ratcliff (2013)
| Exp. and model | Task | a | Ter | η0 | 10σ1 | sz | st | z | v1 | vc | G2 | df | No. pref. | slope <0 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 9 linear | Aster | 0.121 | 0.402 | 0.038 | 0.016 | 0.082 | 0.184 | 0.057 | 0.023 | 0.011 | 77 | 57 | 22/32 | |
| 9 log | Aster | 0.115 | 0.397 | 0.045 | 0.011 | 0.062 | 0.184 | 0.054 | 1.000 | 0.021 | 80 | 57 | 10/32 | |
| 9 linear | Y25 | 0.112 | 0.410 | 0.072 | 0.036 | 0.065 | 0.195 | 0.051 | 0.033 | 0.045 | 104 | 57 | 17/32 | |
| 9 log | Y25 | 0.104 | 0.408 | 0.092 | 0.015 | 0.052 | 0.199 | 0.046 | 0.657 | 0.070 | 122 | 57 | 15/32 | |
| 9 linear | B/Y | 0.108 | 0.461 | 0.040 | 0.053 | 0.065 | 0.271 | a/2 | 0.018 | 133 | 103 | 29/32 | 26/32 | |
| 9 log | B/Y | 0.106 | 0.456 | 0.091 | 0.026 | 0.062 | 0.267 | a/2 | 0.333 | 139 | 103 | 3/32 | ||
| 9 linear | R/L | 0.097 | 0.375 | 0.055 | 0.090 | 0.063 | 0.158 | a/2 | 0.066 | 144 | 103 | 14/32 | 11/32 | |
| 9 log | R/L | 0.092 | 0.367 | 0.239 | 0.015 | 0.060 | 0.150 | a/2 | 1.175 | 133 | 103 | 18/32 | ||
| 11 linear | B/Y | 0.097 | 0.441 | 0.036 | 0.051 | 0.057 | 0.267 | a/2 | 0.033 | 94 | 60 | |||
| R (2014, E. 1) linear | Aster | 0.125 | 0.368 | 0.056 | 0.008 | 0.068 | 0.168 | 0.056 | 0.013 | 0.011 | 245 | 255 | 19/19 | |
| R (2014, E. 1) log | Aster | 0.115 | 0.400 | 0.021 | 0.013 | 0.068 | 0.235 | 0.045 | 0.543 | 0.034 | 405 | 255 | 0/19 |
For the B/Y task, there is support for the linear model over the log model with G-square values lower for the linear model for 29/32 subjects and slope of the median RT versus numerosity function less than 0 for 26/32 subjects (for a numerosity difference of 5). For the L/R task, the log model had 18/32 subjects with lower G-square values than for the linear model and 21/32 slopes of the median RT versus numerosity function greater than 0.
For the Y25 task, the number of distractors was manipulated, but we collapsed over these two sets of conditions to obtain more observations per condition. This is justified because there was less than a 1% difference in accuracy and a 10 ms difference in mean RT for few distractors versus many distractors. The linear model fit better than the log model. The critical value of G-square was 75.6 for 57 degrees of freedom and the mean G-square from the linear model was about a third larger than the critical value indicating a good fit of the model to data. The linear model fit the data better than the log model and the difference in goodness of fit is larger here than for Experiment 3. The critical value of G-square was 75.6 for 57 degrees of freedom and the mean G-square from the linear model was about a third larger than the critical value indicating a good fit of the model to data. As before, the model underestimated the RT quantiles for “small” stimuli by a modest but consistent amount.
For the asterisks task, the linear model fit a little better than the log model. The mean G-square value (76.6) was close to the critical value (75.6) which indicates a good fit. There appears to be compression in large stimuli relative to small stimuli, but this is mainly a bias in drift rate in which small stimuli for all the conditions are more likely to be called large and this is captured by the drift criterion (Table 9).
For the asterisks and the Y25 tasks, there is little decisive support for either the linear or log models from G-square values for individual subjects. The number of subjects with mean G-square values support the linear model, for the asterisks task was 22 out of 32 and for the Y25 task, 17 out of 32.
As for the asterisks task in Experiment 8, we can check whether the linear model is consistent with a constant value of across-trial SD in drift rate. Using the equation in Figure 2C and the parameter values from Table 9, the SD drift rate across trials for 38 and 63 asterisks (means of the two extreme ranges) were 0.12 to 0.14 and these are not discriminable from a constant value of the SD. In contrast, for the Y25 discrimination task and the linear model, for the extreme numerosity values of 20 and 40, the SD drift rate across trials values were 0.17 and 0.24. For the B/Y task and linear model, for 10 vs. 15 dots and 35 vs. 40 dots, the SD drift rate across trials values were 0.14 and 0.32, and for the L/R task and the log model, the SD drift rate across trials values were 0.27 and 0.32. These values in the SD in drift rate across trials are consistent with constant values for the asterisks and L/R tasks and are consistent with the linear model with increasing SD for the B/Y task and Y25 task.
The correlations between all the pairs of tasks (Figure 15) for the drift-rate coefficients, the distances between the boundaries, and nondecision times were all significant (critical value of 0.34) as they were in Experiments 7 and 8. The results are consistent with the hypothesis that the four tasks tap into common numerosity abilities. However, the number of subjects was not large for an individual differences study and the data could not be used, for example, to determine whether the correlation between one task and a second was larger or smaller than the correlation between that task and a third task.
Figure 15.
Scatter plots, histograms, and correlations for boundary separation (top panel), nondecision time (middle panel), and drift rate coefficient (bottom panel) for the four tasks. Each dot represents an individual subject. The identity of the comparison in each off-diagonal plot or correlation is obtained from the task labels in the corresponding horizontal and vertical diagonal plots. The lines in the bottom left of the plots are lowess smoothers (from the R package).
Experiment 10
This experiment had the goal of examining two new manipulations while replicating results from earlier experiments. Subjects judged whether the number of dots in a display was larger or smaller than 25, but unlike the Y25 task used in the earlier experiments, the dots were all of the same color (i.e., there were no non-target dots). Second, the dots in the arrays were located in random positions, as in all the earlier experiments with dots, or positioned on a grid like that used for X’s and O’s and asterisks. Examples of the stimuli are shown in Figure 4F. The question was whether or not the presence of the non-target dots was in some way responsible for the finding that area had no effect on performance. To anticipate, results were just the same as for the earlier Y25 experiments.
There were six numerosity conditions, 10, 15, 20, 30, 35, or 40 dots. Areas were either equal or proportional. For half the trials, the dots were displayed in random positions and for the other half, positions on a 8 × 8 grid.
Results
Accuracy and correct mean RT were collapsed over the numerosity conditions and results are shown in Table 10. As for all the other Y25 experiments, area had no significant effect on accuracy, about 1% (F(1,14)=4.3), and its effect on RTs was 0 ms (F(1,14)=0.0). The effects of random vs. grid positions were also not significant. The effect on accuracy was about 1.5% (F(1,14)=4.6) and the effect on RTs was 3 ms, (F(1,14)=2.0).
Table 10.
Experiment 10: accuracy and correct mean RT collapsed over stimulus difficulty
| measure | random arrangement | grid arrangement | ||
|---|---|---|---|---|
| proportional area | equal area | proportional area | equal area | |
| accuracy | 0.858 | 0.838 | 0.861 | 0.860 |
| mean RT | 505 | 507 | 502 | 500 |
Figure 13 (bottom) shows the quantile-probability plots and the predictions of the linear model (the log model’s fits to the data were not distinguishably different). The data points from all the conditions fell on the same quantile-probability function. There were 252 degrees of freedom (24 conditions and 12 model parameters, the same as for Experiments 3 and 5 except the four drift rate coefficients were for area crossed with grid vs. no grid). The critical chi-square value was 290.0 and the mean G-square values for the linear and log models were both a little larger than the critical value, showing good fits. For individual subjects, there was support for the linear model, with 10 out of 15 G-square values supporting the linear model, but little other compelling evidence for one model over the other. The manipulations of the area and random vs. grid variables had no more than a 6% effect on the drift-rate coefficients and their main effects and interaction were not significant (the three F values were less than 0.2).
Neither the presence of non-target dots nor the grid arrangement affected the pattern of results for the Y25 task and so neither was responsible for the linear model fitting data a little better than the log model in Experiment 3.
Experiment 11
For all the experiments in this paper, when the log or linear model fit the data well, it did so with across-trial variability in drift rates; that is, the value the model produced for a single stimulus’s drift rate was not identical from one presentation of it to another presentation of it. However, it has been claimed that this is not correct, that there is no such across-trial variability in drift rates in applications to perceptual decision-making (Churchland et al., 2008; Kira, Yang, & Shadlen, 2015; Ditterich, 2006a, 2006b; Drugowitsch et al., 2012; Kiani et al., 2014; Palmer et al., 2005; Zhang et al., 2014; see the discussion in Ratcliff, Smith, Brown, & McKoon, 2016). Here, we use a double-pass procedure to show that there is in fact across-trial variability. We do this with the B/Y task because the assumption of across-trial variability is most critical for this task; it is required for the linear model to account for the counter-intuitive pattern of data.
With the double-pass procedure, an exact copy of a stimulus is repeated from one block of trials to another (Burgess, & Colborne, 1988; Cabrera, Lu, & Dosher, 2015; Gold et al., 1999; Green, 1964; Lu & Dosher, 2008). The logic is that if there is no across-trial variability in drift rates, then the only variability comes from variability within each trial, which means that the probability that the response on the second presentation is the same as on the first will be at chance. If instead there is across-trial variability in drift rate, then the probability can be greater than chance. For example, if for all stimuli, a subject tends to attend more to the middle of a display and a particular stimulus has more blue dots than yellow in the middle, the subject might be biased to respond “blue” and this bias would hold for the second presentation as well, making the probability of the same, “blue,” response greater than chance. Ratcliff, Voskuilen, & McKoon (submitted) used the double-pass procedure with four perceptual tasks and the asterisks task and for all of them found greater-than-chance probabilities that responses were the same from one presentation of a stimulus to the second.
The numbers of blue and yellow dots in the displays were 15/10, 20/15, 25/20, 30/25, 35/30, and 40/35 and the areas were always proportional. There were 18 blocks of 96 trials and each second successive block was identical to the one before it so that there were 96 trials intervening between a stimulus and its exact repetition.
Results
Responses for blue and yellow dots were symmetric so the data were grouped in the appropriate way and the starting point for the diffusion model was set halfway between the boundaries. The linear model fit the data well, with both RTs and accuracy decreasing with increasing numerosity. The top panel of Figure 16 shows the quantile-probability plots, which replicate those from Experiments 1, 4, 6, and 9. The mean G-square value was 96.8 with a critical chi-square value of 77.9 with 59 degrees of freedom (six conditions with seven parameters, the distance between the boundaries, across-trial range in the starting point, nondecision time, across-trial range in nondecision time, the constant component of the across-trial SD in drift rate, the SD coefficient, and one drift-rate coefficient).
Figure 16.
Quantile probability plots for Experiment 11 (top panel) and a plot of accuracy against agreement between the two responses in the double pass procedure. Seven values of drift rate were used to produce each function (shown as the small dots on the lines) and 8 values of the standard deviation in drift rate across trials (η) were used to generate each function. The other model parameters were the means from the fits to the data. The red squares are values of accuracy plotted against agreement for the conditions of the experiment.
The bottom panel of Figure 16 illustrates how double-pass data can be displayed. Accuracy is plotted against the probability that the two responses to a stimulus are the same (the “agreement” probability). We generated simulated data to give the eight curves in the figure. There were seven levels of drift rate (which gave seven levels of accuracy) and eight levels of across-trial SD in drift rate (η). The data were simulated using these drift rates and across-trial variabilities in drift rate, η (not ones derived from the drift rate coefficients), plus the best-fitting values of boundary separation, nondecision time, across-trial range in starting point, and across-trial range in nondecision time from to fits to accuracy and RT data. The seven drift rates were 0.0, 0.05, 0.1, 0.15, 0.2, 0.3, and 0.5 and the seven SDs varied from 0.0–0.3 in steps of 0.05.
For the first presentation of a stimulus, for each condition in the plot, that is, each drift rate and each across-trial SD in drift rate, a random drift rate was generated from that distribution. The starting point and nondecision time values were chosen randomly from their across-trial distributions. For the second presentation, the same value of drift rate was used. New values for the starting point and nondecision time were chosen from their distributions. For each combination of drift rate and across-trial variability in drift rate, we generated 20,000 simulated choices and RTs (using the random walk method for generating simulated choices from the diffusion model, Tuerlinckx et al., 2001) and plotted accuracy against agreement probability for Figure 16. Each line in the figure joins points that have the same value of across-trial SD in drift rate, with drift rate varying along the line.
The red squares are the mean values of agreement from the data with groupings of pairs of conditions (15/10 and 20/15, 25/20 and 30/25, 35/30 and 40/35). The values of probability and agreement fall close to the line for which η=0.15. The standard errors in the values of agreement are 0.019, 0.015, and 0.017 for the data groups corresponding to low, medium, and high numerosity values (in other words, the agreement probabilities are significantly different from those in the zero η line). The values of the SD in drift rate across trials corresponding to the same three conditions were 0.15, 0.22, and 0.29. Thus, in the relationship between the model and data, the SD in drift rate that is common between the two presentations as estimated from the double pass procedure did not appear to increase with numerosity. Furthermore, the value of the SD in drift rate across trials read off of Figure 16 was about the same size as the value of η for the lowest value of numerosity from fits of the linear model to data. This suggests that with larger numerosity there is more random variability that is added to the drift rate, variability that is not common across repeated presentations. The model also predicted a low correlation between RTs on the two trials (0.06) and the data showed such a low correlation (0.10).
The data and model predictions from this task show that there is variability in drift rate from trial to trial and some of this variability represents consistent differences in encoding the stimuli from one to another presentation. This provides direct evidence for variability from trial to trial in drift rate, variability that is crucial in order to fit the linear model to the data from this kind of task.
Weber Fraction
In perception, the Weber fraction (w) is the difference in stimulus intensity needed to produce a certain level of accuracy divided by the intensity; it is usually a constant. The Weber fraction is used extensively as an index of numerical acuity or ability (e.g., Halberda et al., 2012; but see Inglis & Gilmore, 2014), where it is defined as the amount the mean value of a numerosity, N, must be multiplied by to give the SD of the distribution around that numerosity, i.e., SD=N*w (i.e., the coefficient of variation). In the standard model, evidence is represented by normal distributions as in signal detection theory as in Figure 1.
The Weber fraction is not just a measure that summarizes data like mean accuracy and mean RT do. Instead, it is derived from a model that is fit to data. This means that its validity can be assessed by a standard chi-square goodness-of-fit statistic. It is an accuracy-based model with numerosities represented on a linear scale and variability around numerosities increasing as numerosity increases, the same assumptions as for the linear model used here. The log model cannot provide the same estimate of the Weber fraction because if distributions that are normal on a log scale are transformed to a linear scale (to be consistent with the Weber-fraction computation), the transformed distribution would not be normally distributed and so the computations would not be the same as those for the linear model. Simple numerical methods might be used to assess whether the two models produce similar estimates of the Weber-fraction (which they might). But the important point is that anyone using or promoting the log model cannot validly use the Weber fraction without further investigation because the Weber fraction is computed from a different model, namely, the linear model with normal distributions of numerosity around their central values.
We compared the Weber-fraction model’s predictions of accuracy to the linear-diffusion model’s using a chi-square statistic. The linear model’s predictions came from fitting the model to accuracy and RT data as usual. We used the data from Experiment 9 which includes four of the main tasks for this article. We also used the data from the asterisks task in Ratcliff (2014, Experiment 1) which varied the number of asterisks across a large range (from 2–98) and which provided a strong test of the Weber model as well as providing a strong test of the linear and log models as applied to the asterisks task. To give accuracy predictions for each task of Experiment 9, we used whichever of the linear or log models gave the best fit to the data. For the asterisks task, we used the linear model because it fit the data better than the log model.
The Weber fraction plays a similar role to the drift-rate coefficient in the ANS-diffusion models because drift rate is most related to accuracy. But it is important to note that acuity in the Weber-fraction model is related to the SDs in the distributions whereas acuity in the ANS-diffusion models is measured by the drift rate coefficients (which are related to the means, not the SDs). We can compute correlations between them to see if they vary in the same ways across individuals. In terms of the fits of the models to data, we expected the diffusion model to fit data worse than the Weber-fraction model because the diffusion model is constrained by RTs as well as accuracy. Park and Starns (2015) also present a detailed analysis of the relationship between drift rate and Weber fraction. They showed that the Weber fraction is contaminated by speed-accuracy tradeoffs and that drift rate is a better predictor of math ability.
Table 11 shows Weber fractions, drift-rate coefficients, SD coefficients (σ1), the mean chi-square values for the two models for accuracy, the number of subjects with non-significant chi-square values, and the correlations between the Weber-fraction and the appropriate linear or log model. The degrees of freedom for the chi-square in the data from Experiment 9 were 10 for the B/Y and L/R tasks and 6 for the Y25 and asterisks tasks, because there were 10 or 6 pairs of correct and error responses, respectively, and the probabilities for each pair add to 1, giving 1 degree of freedom per condition (accuracy value).
Table 11.
Mean Weber fractions, mean diffusion model drift and SD coefficients, mean chi-square goodness of fit, numbers of chi-squares for individuals less than the critical value, and parameter correlations.
| Experiment and model | Task | w | v1 | 10σ1 | χ2 Weber | χ2 diffus. | N<crit Weber | N<crit diffus. | correl. w,v1 | correl. w,σ1 |
|---|---|---|---|---|---|---|---|---|---|---|
| 9, linear | B/Y | 0.647 | 0.0180 | 0.0538 | 10.5 | 12.7 | 29 | 25 | −0.67 | −0.02 |
| 9, log | L/R | 0.223 | 1.194 | 0.0130 | 6.7 | 14.7 | 31 | 23 | −0.54 | 0.29 |
| 9, linear | Y25 | 0.341 | 0.0327 | 0.0364 | 57.2 | 13.9 | 6 | 16 | −0.70 | −0.35 |
| 9, linear | Asterisks | 0.211 | 0.0231 | 0.0160 | 30.9 | 6.3 | 14 | 28 | −0.67 | −0.16 |
| R (2014, Exp. 1), linear | Asterisks | 0.206 | 0.0129 | 0.0082 | 54.5 | 29.6 | 6 | 13 | −0.58 | −0.21 |
We subtracted 1 from the degrees of freedom for the data for the one parameter in the Weber-fraction model. It is difficult to perform an equivalent comparison for the diffusion model because it used more parameters to fit data and it is fit to quantile RTs and response proportions which have many more degrees of freedom. So for the comparison here, we computed chi-square for the model fit to accuracy data alone and we used the same critical value for the chi-square. For the experiment from Ratcliff (2014), the data were grouped into 24 conditions so the degrees of freedom were 23.
Figure 17 shows plots of predictions from the appropriate ANS diffusion model and the Weber-fraction model averaged over subjects, the o’s the predicted values and the x’s the data. For the B/Y and L/R tasks, the top four panels, the probabilities of correct responses are plotted against the smaller of the two numbers for each condition (e.g., 10 is the smaller of the two numbers for the 15/10, 20/10, and 30/10 conditions so there are three points in the vertical line above 10). The Weber-fraction model fit these data a little better than the ANS diffusion model, as expected (because it was also fit to RT quantile). The number of subjects with non-significant chi-square values was larger for the Weber models than the diffusion model (Table 11).
Figure 17.
Plot of accuracy against numerosity for the four tasks in Experiment 9 and the asterisks task in Ratcliff (2014, Experiment 1). The x’s are the data and the o’s are the predictions from the Weber fraction model (left column) and the diffusion model (right column). The red/thin line in the bottom right plot is from the log model fit.
For the Y25 task, third row in Figure 17, the proportions of responses that were “smaller” are plotted against the number of dots. The linear diffusion model fit the data better than the Weber model with chi-square values 4 times larger for the Weber model. Half the subjects showed non-significant chi-square values for the diffusion model and only six for the Weber model. For the asterisks task for Experiment 9, the diffusion model again fit the data better with the mean chi-square value about 5 times larger for the Weber model and 28 subjects with non-significant chi-square values for the diffusion model as opposed to 14 for the Weber model. Figure 16 (third and fourth rows) shows how the Weber model misfit the data for the Y25 and asterisks tasks. The data for both tasks are roughly symmetric about the mid point and the functions are consistent with asymptotes less extreme than 0 or 1. The Weber model for both tasks produces a function that approaches 1 with the lower values of numerosity and approaches 0 more slowly than the data (though appears about to cross over at the largest numerosity. In contrast, the deviations between diffusion model predictions and the data are much less systematic.
To do the same analysis for the asterisks task from Ratcliff (2014, Experiment 1), we fit both linear models to the data and found they were indistinguishable. For the linear model with N2=50, the value of G-square was 245 (Table 9) and values of η for N1=4, 50, and 96, were 0.19, 0.15, and 0.19. For the scheme with N2=100-N1, the value of G-square was 243 (the values of the other parameters were within a few percent of each other). For this model, η0=0.056 and σ1=0.00082 which gave values of η for N1=4, 50, and 96 of 0.10, 0.11, and 0.14. The values of η from both models are not distinguishable from constant values.
We then generated predictions, and compared the predicted accuracy values to those from the fit of the Weber-fraction model to the accuracy data. The model was fit to the RT quantiles and response proportions as in the earlier experiments. The mean G-square (245) was less than the critical value (293.2 with 255 degrees of freedom) and only 1 out of 19 subjects had a significant value above the critical value. We also fit the log model to these data and the fit was much worse than the linear model. The mean G-square was 404 and all subjects had G-square values larger than the critical value. The values of the parameters are shown in the bottom two rows of Table 9.
Table 9 and Figure 17 (bottom panels) show predictions from the Weber model, the predictions from the linear model, and proportion of “small” responses plotted against the number of asterisks. The diffusion model fits to the choice proportions missed the data slightly at around 60 asterisks (the thin solid/red line shows the values for the log model). The value of chi-square from the response proportions was 29.6 with a critical value of 36.4 with 24 degrees of freedom and 14 out of 19 subjects had chi-square values less than the critical value. The Weber fraction model missed at the low numbers of asterisks; it predicted values that were at ceiling (approaching 1) while the data had values near 96% correct. The chi-square value was 54.5 and only 6 of the subjects had chi-square values less than the critical value. The values of the drift coefficient parameters shown in Table 9 are comparable with those from the fits to the asterisks task in Experiment 8 but with the drift rate and SD in drift coefficients about half the values of those from Experiment 8.
In the literature, the Weber fraction seems to be treated as a property of an individual rather than a property of a task and an individual. However, the mean values of the Weber fraction across individuals for the four tasks from Experiment 9 differed considerably. The values (in Table 11) ranged from 0.22 to 0.65 and for the asterisk task from Ratcliff (2014), the value was 0.21. For Experiments 1 and 3, the values were 0.643 (0.277 for the proportional-area condition) and 0.269 (0.165 for the proportional-area condition), respectively. These results show that the Weber fraction depended not only on the experimental task, but also on the independent variable.
The large variability in the Weber fraction as a function of tasks and variables suggests it has limited use as a measure of an individual’s numerical acuity. On the other hand, if Weber fractions correlate across tasks, then they might provide relative measures of individuals’ acuity. In fact, Weber fractions did correlate with each other across the four tasks; the mean was 0.58 for the six pairwise combinations and the range was 0.38–0.76. The analog from the diffusion model is the drift-rate coefficient and its mean correlation across tasks was 0.53 (from the values in Figure 15).
We also examined the correlations between the Weber fractions and the drift-rate coefficients within tasks. The mean of the four correlations in Table 11 was 0.65. This suggests that the drift-rate coefficients and Weber fractions can provide similar measures of individual differences. (The correlation of the Weber fractions and the SD in drift coefficient was small and inconsistent, showing that this measure was not related to the Weber fraction).
These analyses suggest further exploration of the possibility that the Weber fraction model might, for some purposes, provide an account of accuracy data as good as that of the ANS-diffusion models. For the two-array stimulus tasks, it gave slightly better fits than the diffusion model, but for the one-array tasks, the diffusion model gave fits that were several times better. However, the numbers of subjects in our experiments were small for individual differences studies, so any conclusions that could be drawn about differences in the sizes of correlations among tasks would be tentative.
There are two main conceptual problems with the Weber fraction model. First, the numerosity distributions are normal and because the distribution spans minus to plus infinity (Figure 1 top), there is some probability that a number will be perceived as negative. For example, the large value for the Weber fraction for the B/Y task with equal-area dots (0.65) produces an estimate of negative values with probability 6.2% of the time for 5 dots. This means that the Weber fraction model should be modified to have a lower limit on the distributions. However, for most other empirically obtained Weber fractions, the probability of negative values will be small (perhaps vanishingly small), but it is still non-zero. The spread of the distributions into negative values is not a problem for the integrated models because drift rates can be negative (as in Figure 8). The second problem is that, because the behavior of numerosity appears to be qualitatively different for numbers less than 5 compared with numbers higher, we might not want to apply the Weber (or any of the models) uniformly across all the range of non-zero numbers.
This then leads to the issue of what is the basis for estimation of numerosity in this task with these stimuli? The results from the B/Y task in Experiments 1 and 9 suggest that the effect of area cannot be separated from numerosity, in fact, in the B/Y task with intermingled dots, area and numerosity appear to be integral stimuli in the Garner (1974) sense. We take this up in the general discussion.
Discussion
A key point our results make is that measures of numerosity skills and abilities are context dependent. The pattern of RTs against accuracy depends on the task, the cognitive processes by which numerosity judgments are made depends on the task, the cognitive representations of numerosities on which performance is based depend on the task, and whether a confounding variable affects performance depends on the task. This represents remarkable flexibility in how the cognitive system deals with numerosity information. It can encode numerosities on a linear scale or a log scale; it can encode them with larger variability in their representations or smaller variability, and it can include information other than number (e.g., area) in the representations or not. Decision-making processes for numerosity discrimination must accommodate all of these possibilities.
These conclusions about context dependency were made possible by the integrated ANS-diffusion models because the interpretations of data that the models give are constrained simultaneously by accuracy and RTs. For the tasks to which they were applied, they must, and did, explain data in full-- accuracy, the distributions of RTs for correct responses and for errors, and how these change as a function of independent variables.
The diffusion model breaks performance apart into components of decision-making processes. These are the information (drift rate) that drives the decision process, the criteria (boundaries) that determine how much information must be accumulated from a stimulus in order to make a decision, and processes outside the decision process itself (nondecision time). These components are independent of each other (or nearly so in many fits of the model to data) and that means that drift rates provide a direct view of the information driving a decision; it is not obscured by the speed/accuracy settings an individual adopts or the time taken by nondecision processes.
In almost all previous applications of the diffusion model, drift rates have not been determined by a model of the cognitive representations of stimuli that drive decisions (but see Nosofsky & Palmeri, 1997; Nosofsky et al., 2011; Ratcliff, 1981; Smith & Ratcliff, 2009; White et al., 2011, for exceptions in which diffusion and random walk models are matched or integrated with models of representation). In the numerical cognition domain, independently, Park and Starns (2015) and Reike and Schwarz (2016) implemented the log model. In most other earlier applications, the drift rates and the across-trial SD in them (a constant across drift rates) have been free parameters and as such they have been estimated by fitting the model to data with a different drift rate for each condition that varies in difficulty. Instead, the ANS models provide representations of stimuli and so provide the decision process with drift rates and their across-trial SDs. From the point of view of a representation model, the diffusion model allows it to predict accuracy and RT data, which it could not do on its own. From the point of view of the diffusion model, a representation model constrains drift rates and their SDs. The combination of the diffusion model and a representation model reduces the degrees of freedom for fitting data considerably, for example, from 44 parameters for fitting 220 degrees of freedom in the data to 8 parameters for the linear and log models for Experiments 1 and 2 (44 parameters are needed for the standard diffusion model because different drift rates and different values of SD are needed for each condition). One way to think about the combination is that the diffusion model provides a meeting ground between models of representations and RT and accuracy data.
To determine drift rates, the ANS models produce a coefficient that multiplies the difference between two numerosities for the linear model and the difference between the logs of the two numerosities for the log model. These assumptions set the means of the Gaussian distributions around each numerosity (Figure 2C). As we showed, the representations are subject to confounding variables. Equal-area stimuli were more difficult than proportional ones for experiments that required judgments about two stimuli and so the coefficient for equal areas was smaller. This made the differences between the means of the distributions smaller; in other words, the difference between 30 and 40 on the x axis in Figure 1 shrank compared to proportional-area stimuli.
The SDs in the drift rates are produced by a coefficient that multiplies the square root of the sum of squares of the two numerosity values (Figure 2C), plus a constant. The SD coefficient for the linear model must increase with numerosity in order for the model to explain why both accuracy and RT decrease as numerosity increases with a constant difference between two numerosities. The usual assumption for the log model is that the SD is constant but we allowed it to change with numerosity in the same way as for the linear model in order to give it the same flexibility as the linear model. Thus, there were four possible models, the linear model and the log model each with a constant SD or with increasing SD. Applying the linear and log models allowed us to examine whether the scale on drift rate (the log model) or the variability in drift rate (the linear model) is responsible for changes in discriminability with numerosity. The interesting result was that it depends on the paradigm.
Evidence for stimulus- and decision-related signals in EEG
Philiastides et al. (2006) applied multivariate pattern analysis to EEG activity from an array of electrodes in a face/car discrimination task. The analysis produced a single regressor value for each trial that indicated how strongly the stimulus represented a face or a car. An early (170 ms) and a late (300 ms) event-related potential (ERP) component were predictive of decision accuracy. Ratcliff, Philiastides, and Sajda (2009) examined the data on a trial-by-trial basis and found that a higher late-component amplitude on a trial was associated with a higher drift rate for that trial; this was not true for the earlier component. Thus, for nominally identical stimuli, the amplitude of the late ERP component predicted the quality of information processing. Ratcliff, Sederberg, Smith, and Childers (2016) conducted a similar analysis of EEG data from a recognition memory task. They showed that higher late parietal signals were associated with higher drift rates, again on a trial-by-trial basis, but higher earlier frontal signals were not.
These results are consistent with the view that a perceptual representation is built for a stimulus and then decision-relevant information is extracted from it to drive the decision process. The EEG results are consistent with this view: amplitudes of EEG measures for the initial representation are not predictive of evidence used in the decision process but the amplitudes of later measures are.
Our results for the numerosity tasks in the experiments described here fit within this framework. For intermingled blue and yellow dots, a stimulus representation is built and, depending on the task, either relative evidence for blue versus yellow is extracted (the B/Y task) or evidence about one of the colors is extracted (the Y25 task). For the B/Y task, relative numerosity information cannot be extracted independently of other variables such as the areas of the two stimulus classes. This description in terms of representations does not require a strong commitment to the assumption of stimulus and decision representations per se. It is easily possible to describe this view in terms of processing and evidence extracted at different points in the process rather than representations and still be consistent with the modeling.
Speculations
One can speculate about why the log and linear models apply to the tasks that they do. It may be that Fechner’s log representation is restricted to whole objects and possibly only to comparisons between whole objects (as opposed to comparisons with a standard). For Experiment 2, the stimuli were two side-by-side arrays and so they could each be considered as wholes and so the log model applied. For Experiment 1, the stimuli were single arrays. If the log model applies only to whole arrays, then separate log representations for the two stimulus types cannot be extracted from an array with intermingled elements of two types and so a log representation cannot be used to decide whether there are more of one type than the other. For Experiment 3, the linear model fit a little better than the log model, but there were no qualitative differences between predictions that allowed the two to be unambiguously discriminated. It may be that a somewhat different representation is used in comparing an array to a standard, but the data show that a representation of one of the stimuli can be extracted from a display with two types of stimuli intermingled. One can also speculate about why area is sometimes relevant to decisions and sometimes not. The results can be re-described in terms of Garner’s (1974) integral versus separable dimensions: When two arrays of dots are compared, extraneous dimensions like area are integral and so cannot be dissociated from numerosity, but when one array is compared with a standard, the other dimensions have minimal impact on performances.
Correlations among tasks
With the separation of drift rates, boundary settings, and nondecision times, we asked about relationships across tasks. The most important question was whether the numerosity skills that an individual brought to a task were generally the same as those for other tasks. The answer was yes. The correlations between the drift-rate coefficients for all the pairs of tasks that we tested had a mean of 0.55. The same was true of boundary settings (mean 0.56) and nondecision times (mean 0.67); if an individual was conservative in one task (i.e., set boundaries farther apart), he or she was conservative in the others; if he or she was slow on encoding and/or response execution processes, he or she was slow on the others. Ratcliff, Thompson, and McKoon (2015) showed further correlations among numerosity discrimination, symbolic number discrimination, and memory for numbers. All of these results suggest that the numeracy skills used for one task are strongly related to those used for other tasks. However, such a conclusion is somewhat premature because the numbers of subjects in our experiments and Ratcliff et al.’s were only around 32. Studies with larger numbers of subjects should be conducted to investigate whether, for example, some pairs of tasks are less related than others. Nevertheless, our studies show the feasibility of correlational studies and their potential for new understandings of relationships among different ways of encoding and making decisions about numeracy.
Difficulties in numerosity research: Failures to replicate
The ANS-diffusion models may also offer opportunities for resolving the seemingly inconsistent results in numeracy research that we enumerated in the Introduction. First, the effect of some particular independent variable on performance has been different from one study to another and this may arise, at least in part, because the studies used different empirical measures (usually only one), sometimes RTs, sometimes accuracy, sometimes the Weber fraction, and so on. Second, the correlations among tasks have also been different from one study to another, with performance on symbolic tasks sometimes correlated with performance on non-symbolic tasks and sometimes not. Again, one issue with some of the studies is the use of different dependent variables. Third, it has often been found that accuracy and RTs are not correlated, which has led to proposals that they measure different skills. The ANS-diffusion models explain how the two measures can rely on the same skills while being themselves uncorrelated. We believe that the ANS-diffusion model approach will allow some rationalization of the current practice whereby different researchers choose differently from four or five dependent variables, often based on particular laboratory traditions.
Difficulties in numerosity research: confounding variables
Another persistent problem has been that it has not been possible to separate whether numerosity decisions are based on numerosity information alone, some other confounding variable alone (e.g., area), or both. We showed that the ANS-diffusion models provide a way of measuring contributions from these different sources of information. The models translate stimulus information into decision-relevant drift-rate coefficients, where the coefficients may or may not reflect a particular aspect of a stimulus. If the coefficients are different for two equal-area sets of dots than two proportional-area sets of dots, then area is decision-relevant; if there is no difference between the coefficients, then area is not decision-relevant. If the coefficients are different for mixtures of red and green dots than mixtures of blue and yellow dots, then color is decision-relevant; if not, it is not. If only area, not numerosity, is relevant, then coefficients would multiply differences in area instead of differences in numerosity. More specifically, in the B/Y task with proportional areas, the amounts of blueness and yellowness plus numerosity contribute to performance. With equal areas, only numerosity contributes and the drift-rate coefficient is much smaller. Thus it seems that it is not possible for the processing system to extract an estimate of numerosity separate from area in this task. For the L/R task, area still affects performance even though there are two separate arrays. For the Y25 task, the estimate is relative to a criterion value and area (and likely other perceptual variables) is not a reliable predictor and it does not affect performance.
Perhaps one way to look at this is that in tasks with mixed elements (blue and yellow dots), usually the number of elements and other perceptual variables are correlated and so the processing system has learned to use all of these variables (or it just came that way!) in estimates of relative numerosity. But in tasks in which the task is to judge the numerosity relative to standard (our Y25 task), area and other perceptual variables are not predictive of numerosity. For example, seeing an array of blue M&M’s close up with large visual area does not make it seem that there are more than if they are seen further away with a smaller visual area. More generally, our results show that the effects of confounding variables on the information used in decisions about numerosity are task dependent.
To this point, we have used the ANS models to measure the effects of possibly confounding variables by assuming that each level of a variable can have a different drift-rate coefficient. These drift-rate coefficients are defined by the ANS model, linear or log. Another way of estimating the contributions of variables is simply to enter them into a linear regression where drift rate is determined by a combination of the variables. Experimentally, stimuli could be generated with different combinations of variables, for example, randomly selected values or values that maximize the differences among them (e.g., with combinations such as large numerosity and small dots versus large numerosity and large dots).
Linear and log models can be implemented with drift rate a linear combination of measurements of the various independent (confounding) variables. For example, in the linear model with two arrays of dots intermingled, v1=a1(N1-N2)+a2(area1-area2)+a3(dotsize1-dotsize2)+a4(convexhullsize1-convexhullsize2)+... In the log model for two separate arrays, the equation would have logs of the variables (cf. DeWind et al., 2015). The expression for SDs would have to be explored. The most obvious expression would be sqrt(b1(N12+N22)+b2(area12+area22)+...), but it might be better to have the SD a combination of numerosity values only.
With this regression approach it would be possible to examine correlations among the coefficients to see whether two factors are measuring the same property of the stimulus and whether the coefficients are different from zero, i.e., whether that physical property affects performance. In order to use this approach, a maximum likelihood fitting method would need to be used in which each individual RT, choice, and all the independent variables were used for each response (Ratcliff & Tuerlinckx, 2002; Ratcliff & Childers, 2015). Because the maximum likelihood method is sensitive to outliers, care would have to be taken to use cooperative subjects. Ratcliff, Sederberg, Smith, and Childers (2016) used this exact approach with single-trial EEG regressors as the independent variables in a diffusion model analysis. They found coefficients different from zero which means that the EEG regressor measured the same evidence used in the decision process as drift rate in the diffusion model. This regression proposal differs from the ANS-diffusion analyses because it would not control some of the variables and it would require a large experiment and a detailed analysis of the method because it is not guaranteed to work as might be expected. If successful, it would be complementary to the ANS-diffusion models because it would allow the effects of several variables to be examined in one experiment with a random combination of the variables.
Replications
In the Introduction, we mentioned our concern to demonstrate the replicability of our results. Toward that end, we conducted several experiments that are not reported in this article. Four were variations of Experiment 2. The task for Experiment 2 was to decide which of two side-by-side arrays with dots of the same color was more numerous. For two variations, the dots for the two arrays were different colors (blue and yellow; which side was which color switched sides randomly). Either subjects decided which array had more dots, left or right, or they decided which color had more dots. Both patterns of results matched those from Experiment 2 closely. This means that the difference between Experiments 1 and 2 is not the result of the difference in the colors of the two arrays and not the result of the decision being based on left/right versus blue/yellow responses. For a third variation, stimuli stayed on the screen for 750 ms (Park & Starns, 2015) instead of 250 ms. Results showed an attenuation of RT differences relative to those in Experiment 2 (Figure 5 right panel), which might have been due to subjects comparing the arrays sequentially with eye movements between them (cf., Krajbich, Armel, & Rangel, 2010). For a fourth variation, we masked stimuli after 250 ms and obtained the same results as in Experiment 2. All together, the results of Experiment 2 were robust with respect to these variations. We also conducted a variation of Experiment 1 in which the arrays stayed on the screen until a response was made, instead of a 300 ms presentation duration. The data replicated those from Experiment 1 and showed the results robust to the availability of stimulus information. The results from these experiments also illustrate a different kind of file drawer problem than is usually discussed, namely a file drawer full of replications instead of one full of failures to replicate.
Neurophysiological studies
There have been a number of neurophysiological studies of numeracy. The procedures and measures cannot be directly compared to the tasks we have used here, but they do suggest that there might be possible connections in the future.
There is evidence from single-cell recording studies in monkeys and neuroimaging studies in humans that numerosity is represented topographically in areas such the parietal and prefrontal cortex. Experiments with monkeys have used small numerosities that are in the range of subitizing in humans. For example, Nieder and Miller (2003; see also Roitman, Brannon, & Platt, 2007) used a matching task in which arrays of dots were presented successively and the monkey had to release a lever if the number of dots matched. They found cells in the lateral prefrontal cortex that responded to different values of numerosity (in the range 2–6) so that their peak firing rate was at a specific numerosity and firing rates declined with increasing numerical distance from the preferred numerosity. Nieder and Merten (2007) extended this to the range 1–30 and found similar results.
In many of the studies with humans using fMRI and EEG, dots stimuli are presented in a sequence and viewing is often passive, requiring no overt response (except sometimes on catch trials). The manipulation to assess numerosity is to change stimulus properties but keep numerosity constant up to some point at which numerosity changes so as to separate numerosity from other variables. Piazza et al. (2004) measured the neural response after the numerosity change as a function of the numerosity of the stimulus before the change. The difference showed activation curves with increased activity as a function of the difference between the two numerosities (see also, Hyde & Spelke, 2008, 2012). Harvey et al. (2013) presented stimuli with 1 to 7 dots in ascending and descending order and found the peak BOLD signal varied over the posterior parietal cortex to form a topographical representation of numerosity. Park et al. (2016) presented EEG data that showed changes in activity in early visual processing (75 to 180 ms after stimulus presentation) as a function of changes in numerosity that were larger than changes in other visual properties of the stimulus. They argued that this provided evidence for rapid and early extraction of numerosity information in the visual pathways. In contrast, Gebuis and Reynvoet (2013) argued that results from their EEG data showed no automatic extraction of numerosity from a visual stimulus and that numerosity judgments are based on sensory properties of stimuli. Piazza et al. (2012) argued that representations of exact numbers evolved from parietal coding schemes for approximate numeracy.
In most of the neurophysiological studies above, the variability in the neural response increased with numerosity and the difference in the peak activity between adjacent numerosities decreased with increasing numerosity. When these were plotted on a log scale, the spread of the distributions of activity was about the same, which is consistent with the log model we used here. However, there are few if any neurophysiological studies with stimuli like those in Experiment 1 (intermixed arrays of dots of different colors, Halberda et al., 2008) and so data are not available to test the linear model. Furthermore, most of the studies had slow presentation of stimuli and did not require any explicit decision because they recorded brain activity from passive viewing. The differences between such neurophysiological studies and the procedures we used with fast explicit decisions are large enough to make it difficult to see how they could relate to each other.
Conclusions
The results of the studies we have reported have a number of implications for cognitive numeracy research. One is that they provide a solution, or at least the beginning of a solution, to the problem that it has not been possible to decide whether cognitive representations of numerosity are linear or logarithmic. There are two interconnected reasons for this, one that tests of representation models have been based only on accuracy and the other that the models have not been tied to a model of decision processes. With both RT and accuracy data and the diffusion model for two-choice decisions, we showed instances for which the two models were significantly and qualitatively different in their accounts of experimental data.
Our results also suggest an agenda for numeracy research. Studies are needed to observe the effects of independent variables (possibly confounding variables) through the lens of an ANS-diffusion model (or some other model that uses RT and accuracy data jointly) so that numeracy skills, as measured by drift-rate coefficients, can be more directly observed, not obscured by an individual’s boundary settings or nondecision time. The same kinds of studies are needed to measure correlations between tasks, between independent variables, and between the skills employed in different tasks.
The results of the individual difference studies suggest that it might be worth considering using a single-stimulus task to measure numerosity skill instead of the two-stimulus tasks. The former has the advantage of being insensitive to the other variables such as area and density and so might provide a more pure measure of numerosity skill.
In two-stimulus tasks, when the effects of the other variables are measured, it might be that they are all correlated across individuals which means that confounding variables might be less of a problem (because they all tell the same story about ability). However, some researchers believe that numerosity discrimination is largely or totally performed with discrimination based on non-numeric variables. If the single-stimulus task is largely insensitive to these variables, it is more difficult to argue this point.
Another agenda item is to use the ANS-diffusion models to help understand the development of numeracy skills in children. It may or may not be that different tasks show identical developmental paths and which tasks do this may or may not be the same from one age to another or one point in development to another.
Still another agenda item is to use the ANS-diffusion models to help understand how simple numeracy abilities are related to performance on tests of math abilities. The models’ more direct measures of abilities than those used previously may lead to new research on, for example, whether abilities in symbolic and/or nonsymbolic discrimination tasks support performance on achievement tests and whether they do so in the same or different ways, whether non-symbolic abilities are the basis for development of symbolic abilities, and whether symbolic and non-symbolic abilities have the same or different developmental trajectories. However, we reiterate the caveat that answers to questions like these may be different when different tasks are used to address them.
Overall, the analyses we have presented demonstrate the power of quantitative models to understand data and the power of combining models for the cognitive representations of stimuli with decision-making models. We hope that further research with such models will eventually lead to advances in the ways children are taught numerosity skills and the ways numerosity skills can be supported for populations for which they are problematic such as older adults.
Acknowledgments
Preparation of this article was supported by NIA grant R01-AG041176. Aspects of this work were presented at the Annual Summer Interdisciplinary Conference in Mammoth Lakes, July 2015 and in the Psychonomic Society meeting in Chicago, November 2015. We thank two reviewers who did a lot to improve this article.
Appendix A
A different way of showing the quality of fit of the models to data is to plot predicted values of accuracy and RT quantiles for the model predictions against data (e.g., Ratcliff et al., 2010). Figure A1 shows these plots for each individual condition for each subject for Experiments 1 and 2. The plots show quite good correspondence between theory and data and the few points that show relatively poor fits should be considered in the context of the number of points in the plots (shown in the bottom right corner of each panel) and the fact that an eight parameter model produced all these fits.
Figure A1.
Plots model predictions plotted against data for response proportions and the 0.1, 0.5 (median) and 0.9 quantile RTs for all the conditions for data from each individual subject.
References
- Burgess AE, Colborne B. Visual signal detection. IV. Observer inconsistency. Journal of the Optical Society of America A. 1988;5(4):617–627. doi: 10.1364/josaa.5.000617. [DOI] [PubMed] [Google Scholar]
- Cabrera CA, Lu Z-L, Dosher BA. Separating decision and encoding noise in signal detection tasks. Psychological Review. 2015;122(3):429–460. doi: 10.1037/a0039348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Q, Li J. Association between individual differences in non-symbolic number acuity and math performance: A meta-analysis. Acta Psychologica. 2014;148:163–172. doi: 10.1016/j.actpsy.2014.01.016. [DOI] [PubMed] [Google Scholar]
- Churchland AK, Kiani R, Shadlen MN. Decision-making with multiple alternatives. Nature Neuroscience. 2008;11:693–702. doi: 10.1038/nn.2123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dehaene S. The neural basis of Weber-Fechner’s law: Neuronal recordings reveal a logarithmic scale for number. Trends in Cognitive Science. 2003;7:145–147. doi: 10.1016/s1364-6613(03)00055-x. [DOI] [PubMed] [Google Scholar]
- Dehaene S, Changeux JP. Development of elementary numerical abilities: A neuronal model. Journal of Cognitive Neuroscience. 1993;5:390–407. doi: 10.1162/jocn.1993.5.4.390. [DOI] [PubMed] [Google Scholar]
- De Smedt B, Noel MP, Gilmore C, Ansari D. How do symbolic and non-symbolic numerical magnitude processing skills relate to individual differences in children’s mathematical skills? A review of evidence from brain and behavior. Trends in Neuroscience and Education. 2013;2:48–55. [Google Scholar]
- De Smedt B, Verschaffel L, Ghesquiere P. The predictive value of numerical magnitude comparison for individual differences in mathematics achievement. Journal of Experimental Child Psychology. 2009;103:469–479. doi: 10.1016/j.jecp.2009.01.010. [DOI] [PubMed] [Google Scholar]
- DeWind NK, Adams GK, Platt ML, Brannon EM. Modeling the approximate number system to quantify the contribution of visual stimulus features. Cognition. 2015;142:247–265. doi: 10.1016/j.cognition.2015.05.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeWind NK, Brannon EM. Malleability of the approximate number system: effects of feedback and training. Frontiers in Human Neuroscience. 2012 Apr; doi: 10.3389/fnhum.2012.00068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ditterich J. Computational approaches to visual decision making. In: Chadwick DJ, Diamond M, Goode J, editors. Percept, decision, action: Bridging the gaps. Chichester, U.K: Wiley; 2006a. p. 114. [Google Scholar]
- Ditterich J. Stochastic models of decisions about motion direction: Behavior and physiology. Neural Networks. 2006b;19:981–1012. doi: 10.1016/j.neunet.2006.05.042. [DOI] [PubMed] [Google Scholar]
- Donkin C, Brown S, Heathcote A. The over-constraint of response time models: Rethinking the scaling problem. Psychonomic Bulletin & Review. 2009;16:1129–1135. doi: 10.3758/PBR.16.6.1129. [DOI] [PubMed] [Google Scholar]
- Drugowitsch J, Moreno-Bote R, Churchland AK, Shadlen MN, Pouget A. The cost of accumulating evidence in perceptual decision making. The Journal of Neuroscience. 2012;32:3612–3628. doi: 10.1523/JNEUROSCI.4010-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fazio LK, Bailey DH, Thompson CA, Siegler RS. Relations of different types of numerical magnitude representations to each other and to mathematics achievement. Journal of Experimental Child Psychology. 2014;123:53–72. doi: 10.1016/j.jecp.2014.01.013. [DOI] [PubMed] [Google Scholar]
- Feigenson L, Carey S, Hauser M. The representations underlying infants’ choice of more: object files versus analog magnitudes. Psychological Science. 2002;13:150–156. doi: 10.1111/1467-9280.00427. [DOI] [PubMed] [Google Scholar]
- Forstmann BU, Ratcliff R, Wagenmakers EJ. Sequential sampling models in cognitive neuroscience: Advantages, applications, and extensions. Annual Review of Psychology. 2016;67:641–666. doi: 10.1146/annurev-psych-122414-033645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gallistel CR, Gelman R. Preverbal and verbal counting and computation. Cognition. 1992;44:43–74. doi: 10.1016/0010-0277(92)90050-r. [DOI] [PubMed] [Google Scholar]
- Gallistel CR, Gelman R. Non-verbal numerical cognition: From reals to integers. Trends in Cognitive Sciences. 2000;4:59–65. doi: 10.1016/s1364-6613(99)01424-2. [DOI] [PubMed] [Google Scholar]
- Garner WR. The processing of information and structure. Potomac, MD: Lawrence Erlbaum Associates; 1974. [Google Scholar]
- Gebuis T, Cohen Kadosh R, Gevers W. Sensory-integration system rather than approximate number system underlies numerosity processing: A critical review. Acta Psychologica. 2016;171:17–35. doi: 10.1016/j.actpsy.2016.09.003. [DOI] [PubMed] [Google Scholar]
- Gebuis T, Gevers W. Numerosities and space; indeed a cognitive illusion! A reply to de Hevia and Spelke (2009) Cognition. 2011;121:248–252. doi: 10.1016/j.cognition.2010.09.008. [DOI] [PubMed] [Google Scholar]
- Gebuis T, Gevers W, Cohen Kadosh R. Topographic representation of high-level cognition: numerosity or sensory processing? Trends in Cognitive Science. 2014;18:1–3. doi: 10.1016/j.tics.2013.10.002. [DOI] [PubMed] [Google Scholar]
- Gebuis T, Reynvoet B. Continuous visual properties explain neural responses to nonsymbolic number. Psychophysiology. 2012a;49:1649–1659. doi: 10.1111/j.1469-8986.2012.01461.x. [DOI] [PubMed] [Google Scholar]
- Gebuis T, Reynvoet B. The role of visual information in numerosity estimation. PLoS One. 2012b;7:e37426. doi: 10.1371/journal.pone.0037426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gebuis T, Reynvoet B. The neural mechanisms underlying passive and active processing of numerosity. NeuroImage. 2013;70:301–307. doi: 10.1016/j.neuroimage.2012.12.048. [DOI] [PubMed] [Google Scholar]
- Gilmore C, Attridge N, Inglis M. Measuring the approximate number system. Quarterly Journal Of Experimental Psychology. 2011;64:2099–2109. doi: 10.1080/17470218.2011.574710. [DOI] [PubMed] [Google Scholar]
- Gilmore CK, McCarthy SE, Spelke ES. Non-symbolic arithmetic abilities and mathematics achievement in the first year of formal schooling. Cognition. 2010;115:394–406. doi: 10.1016/j.cognition.2010.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gold JM, Bennett PJ, Sekuler AB. Signal but not noise changes with perceptual learning. Nature. 1999;402:176–178. doi: 10.1038/46027. [DOI] [PubMed] [Google Scholar]
- Green DM. Consistency of auditory detection judgments. Psychological Review. 1964;71:392–407. doi: 10.1037/h0044520. [DOI] [PubMed] [Google Scholar]
- Halberda J, Ly R, Wilmer JB, Naiman DQ, Germine L. Number sense across lifespan as revealed by a massive Internet-based sample. Proceedings of the National Academy of Sciences. 2012;109:11116–11120. doi: 10.1073/pnas.1200196109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halberda J, Mazzocco MMM, Feigenson L. Individual differences in nonverbal number acuity predict maths achievement. Nature. 2008;455:665–668. doi: 10.1038/nature07246. [DOI] [PubMed] [Google Scholar]
- Harvey BM, Klein BP, Petridou N, Dumoulin SO. Topographic representation of numerosity in the human parietal cortex. Science. 2013;341:1123–1126. doi: 10.1126/science.1239052. [DOI] [PubMed] [Google Scholar]
- Holloway ID, Ansari D. Mapping numerical magnitudes onto symbols: The numerical distance effect and individual differences in children’s math achievement. Journal of Experimental Child Psychology. 2009;103:17–29. doi: 10.1016/j.jecp.2008.04.001. [DOI] [PubMed] [Google Scholar]
- Hyde DC, Khanum S, Spelke ES. Brief non-symbolic, approximate number practice enhances subsequent exact symbolic arithmetic in children. Cognition. 2014;131:92–107. doi: 10.1016/j.cognition.2013.12.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hyde DC, Spelke ES. All numbers are not equal: an electrophysiological investigation of small and large number representations. Journal of Cognitive Neuroscience. 2008;21:1039–1053. doi: 10.1162/jocn.2009.21090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hyde DC, Spelke ES. Spatiotemporal dynamics of processing nonsymbolic number: An event-related potential source localization study. Human Brain Mapping. 2012;33:2189–2203. doi: 10.1002/hbm.21352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Inglis M, Attridge N, Batchelor S, Gilmore CK. Non-verbal number acuity correlates with symbolic mathematics achievement: but only in children. Psychonomic Bulletin and Review. 2011;18:1222–1229. doi: 10.3758/s13423-011-0154-1. [DOI] [PubMed] [Google Scholar]
- Inglis M, Gilmore C. Indexing the Approximate Number System. Acta Psychologica. 2014;145:147–155. doi: 10.1016/j.actpsy.2013.11.009. [DOI] [PubMed] [Google Scholar]
- Kiani R, Corthell L, Shadlen MN. Choice certainty is informed by both evidence and decision time. Neuron. 2014;84:1329–1342. doi: 10.1016/j.neuron.2014.12.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kira S, Yang T, Shadlen MN. A neural implementation of Wald’s Sequential Probability Ratio Test. Neuron. 2015;85(4):861–873. doi: 10.1016/j.neuron.2015.01.007. http://doi.org/10.1016/j.neuron.2015.01.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krajbich I, Armel C, Rangel A. Visual fixations and the computation and comparison of value in simple choice. Nature Neuroscience. 2010;13:1292–1298. doi: 10.1038/nn.2635. [DOI] [PubMed] [Google Scholar]
- Laming DRJ. Information theory of choice reaction time. New York: Wiley; 1968. [Google Scholar]
- Leite FP, Ratcliff R. What cognitive processes drive response biases? A diffusion model analysis. Judgment and Decision Making. 2011;6:651–687. [Google Scholar]
- Libertus ME, Feigenson L, Halberda J. Preschool acuity of the approximate number system correlates with school math ability. Developmental Science. 2011;14:1292–1300. doi: 10.1111/j.1467-7687.2011.01080.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leibovich T, Katzin N, Harel M, Henik A. From “sense of number” to “sense of magnitude”: The role of continuous magnitudes in numerical cognition. Behavioral and Brain Sciences. 2016;39:1–62. doi: 10.1017/S0140525X16000960. [DOI] [PubMed] [Google Scholar]
- Lu ZL, Dosher BA. Characterizing observer states using external noise and observer models: Assessing internal representations with external noise. Psychological Review. 2008;115:44–82. doi: 10.1037/0033-295X.115.1.44. [DOI] [PubMed] [Google Scholar]
- Lyons IM, Beilock SL. Numerical ordering ability mediates the relation between number-sense and arithmetic competence. Cognition. 2011;121:256–261. doi: 10.1016/j.cognition.2011.07.009. [DOI] [PubMed] [Google Scholar]
- Maloney E, Risko E, Preston F, Ansari D, Fugelsang J. Challenging the reliability and validity of cognitive measures: The case of the numerical distance effect. Acta Pyschologica. 2010;134:154–161. doi: 10.1016/j.actpsy.2010.01.006. [DOI] [PubMed] [Google Scholar]
- Mix K, Huttenlocher J, Levine SC. Quantitative development in infancy and early childhood. New York: Oxford University Press; 2002. [Google Scholar]
- Mundy E, Gilmore CK. Children’s mapping between symbolic and nonsymbolic representations of number. Journal of Experimental Child Psychology. 2009;103:490–502. doi: 10.1016/j.jecp.2009.02.003. [DOI] [PubMed] [Google Scholar]
- Nieder A, Merten K. A labeled-line code for small and large numerosities in the monkey prefrontal cortex. Journal of Neuroscience. 2007;27:5986–5993. doi: 10.1523/JNEUROSCI.1056-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nieder A, Miller E. Coding of cognitive magnitude: Compressed scaling of numerical information in the primate prefrontal cortex. Neuron. 2003;37:149–157. doi: 10.1016/s0896-6273(02)01144-3. [DOI] [PubMed] [Google Scholar]
- Nosofsky RM, Little DR, Donkin C, Fific M. Short-term memory scanning viewed as exemplar-based categorization. Psychological Review. 2011;118:280–315. doi: 10.1037/a0022494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nosofsky RM, Palmeri TJ. An exemplar based random walk model of speeded classification. Psychological Review. 1997;104:266–300. doi: 10.1037/0033-295x.104.2.266. [DOI] [PubMed] [Google Scholar]
- Palmer J, Huk AC, Shadlen MN. The effect of stimulus strength on the speed and accuracy of a perceptual decision. Journal of Vision. 2005;5:376–404. doi: 10.1167/5.5.1. [DOI] [PubMed] [Google Scholar]
- Park J, Brannon EM. Training the approximate number system improves math proficiency. Psychological Science. 2013;24:2013–2019. doi: 10.1177/0956797613482944. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park J, Brannon EM. Improving arithmetic performance with number sense training: An investigation of underlying mechanism. Cognition. 2014;133:188–200. doi: 10.1016/j.cognition.2014.06.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park J, DeWind NK, Woldorff MG, Brannon EM. Rapid and direct encoding of numerosity in the visual stream. Cerebral Cortex. 2016;26:748–763. doi: 10.1093/cercor/bhv017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park J, Starns JJ. The approximate number system acuity redefined: A diffusion model approach. Frontiers in Psychology. 2015;6:1955. doi: 10.3389/fpsyg.2015.01955. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Philiastides MG, Ratcliff R, Sajda P. Neural representation of task difficulty and decision making during perceptual categorization: A timing diagram. Journal of Neuroscience. 2006;26:8965–8975. doi: 10.1523/JNEUROSCI.1655-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piazza M, Izard V, Pinel P, Le Bihan D, Dehaene S. Tuning curves for approximate numerosity in the human intraparietal sulcus. Neuron. 2004;44:547–555. doi: 10.1016/j.neuron.2004.10.014. [DOI] [PubMed] [Google Scholar]
- Price G, Palmer D, Battista C, Ansari D. Nonsymbolic numerical magnitude comparison: reliability and validity of different task variants and outcome measures, and their relationship to arithmetic achievement in adults. Acta Psychologica. 2012;140:50–57. doi: 10.1016/j.actpsy.2012.02.008. [DOI] [PubMed] [Google Scholar]
- Ratcliff R. A theory of memory retrieval. Psychological Review. 1978;85:59–108. [Google Scholar]
- Ratcliff R. A theory of order relations in perceptual matching. Psychological Review. 1981;88:552–572. [Google Scholar]
- Ratcliff R. Theoretical interpretations of speed and accuracy of positive and negative responses. Psychological Review. 1985;92:212–225. [PubMed] [Google Scholar]
- Ratcliff R. International encyclopedia of the social and behavioral sciences. Vol. 6. Oxford, England: Elsevier; 2001. Diffusion and random walk processes; pp. 3668–3673. [Google Scholar]
- Ratcliff R. A diffusion model account of reaction time and accuracy in a two choice brightness discrimination task: Fitting real data and failing to fit fake but plausible data. Psychonomic Bulletin and Review. 2002;9:278–291. doi: 10.3758/bf03196283. [DOI] [PubMed] [Google Scholar]
- Ratcliff R. Modeling response signal and response time data. Cognitive Psychology. 2006;53:195–237. doi: 10.1016/j.cogpsych.2005.10.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R. Measuring psychometric functions with the diffusion model. Journal of Experimental Psychology: Human Perception and Performance. 2014;40:870–888. doi: 10.1037/a0034954. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Childers R. Individual differences and fitting methods for the two-choice diffusion model. Decision. 2015;2:237–279. doi: 10.1037/dec0000030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Love J, Thompson CA, Opfer J. Children are not like older adults: A diffusion model analysis of developmental changes in speeded responses. Child Development. 2012;83:367–381. doi: 10.1111/j.1467-8624.2011.01683.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, McKoon G. The diffusion decision model: Theory and data for two-choice decision tasks. Neural Computation. 2008;20:873–922. doi: 10.1162/neco.2008.12-06-420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Philiastides MG, Sajda P. Quality of evidence for perceptual decision making is indexed by trial-to-trial variability of the EEG. Proceedings of the National Academy of Sciences. 2009;106:6539–6544. doi: 10.1073/pnas.0812589106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Sederberg P, Smith T, Childers R. A single trial analysis of EEG in recognition memory: Tracking the neural correlates of memory strength. Neuropsychologia. 2016;93:128–141. doi: 10.1016/j.neuropsychologia.2016.09.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Smith PL. A comparison of sequential sampling models for two-choice reaction time. Psychological Review. 2004;111:333–367. doi: 10.1037/0033-295X.111.2.333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Smith PL. Perceptual discrimination in static and dynamic noise: the temporal relation between perceptual encoding and decision making. Journal of Experimental Psychology: General. 2010;139:70–94. doi: 10.1037/a0018128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Smith PL, Brown SD, McKoon G. Diffusion decision model: Current issues and history. Trends in Cognitive Science. 2016;20:260–281. doi: 10.1016/j.tics.2016.01.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Smith PL, McKoon G. Modeling regularities in response time and accuracy data with the diffusion model. Current Directions in Psychological Science. 2015;24:458–470. doi: 10.1177/0963721415596228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Thapar A, Gomez P, McKoon G. A diffusion model analysis of the effects of aging in the lexical-decision task. Psychology and Aging. 2004;19:278–289. doi: 10.1037/0882-7974.19.2.278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Thapar A, McKoon G. The effects of aging on reaction time in a signal detection task. Psychology and Aging. 2001;16:323–341. [PubMed] [Google Scholar]
- Ratcliff R, Thapar A, McKoon G. Application of the diffusion model to two-choice tasks for adults 75–90 years old. Psychology and Aging. 2007;22:56–66. doi: 10.1037/0882-7974.22.1.56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Thapar A, McKoon G. Individual differences, aging, and IQ in two-choice tasks. Cognitive Psychology. 2010;60:127–157. doi: 10.1016/j.cogpsych.2009.09.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Thompson CA, McKoon G. Modeling individual differences in response time and accuracy in numeracy. Cognition. 2015;137:115–136. doi: 10.1016/j.cognition.2014.12.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Tuerlinckx F. Estimating the parameters of the diffusion model: Approaches to dealing with contaminant reaction times and parameter variability. Psychonomic Bulletin and Review. 2002;9:438–481. doi: 10.3758/bf03196302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Van Zandt T, McKoon G. Connectionist and diffusion models of reaction time. Psychological Review. 1999;106:261–300. doi: 10.1037/0033-295x.106.2.261. [DOI] [PubMed] [Google Scholar]
- Ratcliff R, Voskuilen C, McKoon G. Internal and external variability in perceptual decision making. doi: 10.1037/rev0000080. (submitted) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reike D, Schwarz W. One model fits all: Explaining many aspects of number comparison within a single coherent model -- A random walk account. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2016;42:1957–1971. doi: 10.1037/xlm0000287. [DOI] [PubMed] [Google Scholar]
- Roitman JD, Brannon EM, Platt ML. Monotonic coding of numerosity in macaque lateral intraparietal area. PLoS Biology. 2007;5:1672–1682. doi: 10.1371/journal.pbio.0050208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sasanguie D, Defever E, Van den Bussche E, Reynvoet B. The reliability of and the relation between non-symbolic numerical distance effects in comparison, same-different judgments and priming. Acta Psychologica. 2011;136:73–80. doi: 10.1016/j.actpsy.2010.10.004. [DOI] [PubMed] [Google Scholar]
- Smith PL, Ratcliff R. An integrated theory of attention and decision making in visual signal detection. Psychological Review. 2009;116:283–317. doi: 10.1037/a0015156. [DOI] [PubMed] [Google Scholar]
- Teodorescu AR, Moran R, Usher M. Absolutely relative or relatively absolute: violations of value invariance in human decision making. Psychonomic Bulletin and Review. 2016;23:22–38. doi: 10.3758/s13423-015-0858-8. [DOI] [PubMed] [Google Scholar]
- Teodorescu AR, Usher M. Disentangling decision models: From independence to competition. Psychological Review. 2013;120:1–38. doi: 10.1037/a0030776. [DOI] [PubMed] [Google Scholar]
- Thompson CA, Ratcliff R, McKoon G. Individual differences in the components of children’s and adults’ information processing for simple symbolic and non-symbolic numeric decisions. Journal of Experimental Child Psychology. 2016;150:48–71. doi: 10.1016/j.jecp.2016.04.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tibber MS, Manasseh GSL, Clarke RC, Gagin G, Swanbeck SN, Butterworth Lotto RB, Dakin SC. Sensitivity to numerosity is not a unique visuospatial psychophysical predictor of mathematical ability. Vision Research. 2013;89:1–9. doi: 10.1016/j.visres.2013.06.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tuerlinckx F, Maris E, Ratcliff R, De Boeck P. A comparison of four methods for simulating the diffusion process. Behavior, Research, Instruments, and Computers. 2001;33:443–456. doi: 10.3758/bf03195402. [DOI] [PubMed] [Google Scholar]
- White CN, Ratcliff R, Starns JJ. Diffusion models of the flanker task: Discrete versus gradual attentional selection. Cognitive Psychology. 2011;63:210–238. doi: 10.1016/j.cogpsych.2011.08.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woodworth RS. Experimental Psychology. New York: Henry Holt & Company; 1938. [Google Scholar]
- Zhang S, Lee MD, Vandekerckhove J, Gunter M, Wagenmakers EJ. Time-varying boundaries for diffusion models of decision making and response time. Frontiers in Quantitative Psychology and Measurement. 2014;5:1364. doi: 10.3389/fpsyg.2014.01364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zorzi M, Stoianov I, Umilta C. Computational modeling of numerical cognition. In: Campbell JID, editor. Handbook of mathematical cognition. New York: Psychology Press; 2005. pp. 67–84. [Google Scholar]