Flexibility vs Preorganization: Direct Comparison of Binding Kinetics for a Disordered Peptide and Its Exact Preorganized Analogues

Abstract

Many intrinsically disordered proteins, which are prevalent in nature, fold only upon binding their structured partner proteins. Such proteins have been hypothesized to have a kinetic advantage over their folded, preorganized analogues in binding their partner proteins. Here we determined the effects of ligand preorganization on the k_on for a biomedically important system: an intrinsically disordered p53 peptide ligand and the MDM2 protein receptor. Based on direct simulations of binding pathways, computed k_on values for fully disordered and preorganized p53 peptide analogues were within error of each other, indicating little if any kinetic advantage to being disordered or preorganized for binding the MDM2 protein. We also examined the effects of increasing the concentration of MDM2 on the extent to which its mechanism of binding to the p53 peptide is induced fit vs conformational selection. Results predict that the mechanism is solely induced fit if the unfolded state of the peptide is more stable than its folded state; otherwise, the mechanism shifts from being dominated by conformational selection at low MDM2 concentration to induced fit at high MDM2 concentration. Taken together, our results are relevant to any protein binding process that involves a disordered peptide of a similar length that forms a single α-helix upon binding a partner protein. Such disorder-to-helix transitions are common among protein interactions of disordered proteins and are therefore of fundamental biological interest.

Graphical Abstract

INTRODUCTION

Many proteins that are either partially or completely unfolded in their unbound states^1,2 fold only upon binding their structured partner proteins. Such “intrinsically disordered” proteins (IDPs) have been proposed to have a kinetic advantage over their preorganized, folded analogues for binding their partners,^3,4 which challenges the long-standing assumption that the preorganization of a ligand to its receptor-bound conformation results in a faster association rate constant (k_on). Potential mechanisms by which this kinetic advantage might be achieved are (i) the “fly-casting” mechanism, in which the IDP collides more rapidly with the partner receptor due to a larger “capture” radius,³ and (ii) the “dock-and-coalesce” mechanism for IDPs with two or more segments in which the initial docking of one segment results in a more rapid, pseudointramolecular docking of the remaining segments.⁴ Throughout this work, the term “ligand” refers to a molecule (e.g., small molecule, peptide, or protein) that binds to a larger molecule that serves as the target receptor.

While experimental studies have provided informative insights about the effects of preorganization on the binding kinetics of IDP ligands,^5–10 these studies have not been able to provide definitive proof of a kinetic advantage (or lack thereof) to being disordered vs preorganized. Existing experimental studies indicate differing results on the effect of ligand preorganization on binding kinetics. For example, preorganization has resulted in faster binding for certain IDPs (ACTR and Y507A mutant of the E3 rRNase domain),^5,6 and no significant effect on the binding kinetics for other IDPs (PUMA and c-Myb).^7,8 In addition, an unfolded variant of the Fyn SH3 domain that was engineered via truncation of only four residues has achieved the same k_on as the full-length, folded domain for a high-affinity peptide,⁹ and the preorganization of the disordered monomers of an engineered GCN4-p1 leucine zipper variant has resulted in slower dimerization.¹⁰ Ideally, the effect of ligand preorganization on binding kinetics would be assessed by engineering peptide analogues that differ only in their degree of preorganization without altering the chemical structures, which is not possible in experiments.

Molecular simulations provide the only practical means to compute k_on values for both IDPs and their exact preorganized analogues—which have been engineered in silico—by directly generating the corresponding binding pathways. Furthermore, while experiments can typically measure only the k_on, simulations can be used to directly compute the rate constants of individual steps. However, due to the relatively long time scales of protein binding processes, only one simulation study has reported atomistic binding pathways along with the k_on for an IDP ligand (p53 peptide) and its protein receptor (MDM2), and these simulations did not sample fully disordered analogues of the ligand.¹¹ Both atomistic and residue-level models have been used to characterize solely the late stages of binding, i.e., after the IDPs have collided with their partner proteins.^12–14 Residue-level simulation studies of binding pathways for IDPs have been reported,^15,16 including the only study that has determined the effects of preorganization on the binding kinetics of an IDP, focusing on the intrinsically disordered, phosphorylated KID (pKID) domain and its folding into a pair of linked-together α-helices upon binding the KIX protein.¹⁶

Here, we focused on an IDP ligand that adopts a single α-helix upon binding its folded protein receptor: the intrinsically disordered, N-terminal peptide fragment of tumor suppressor p53 and MDM2 protein. We determined the effects of ligand preorganization on the k_on by directly simulating binding pathways of the disordered p53 peptide and several of its exact analogues with various extents of preorganization. In addition, we used the computed k_on values to predict the effect of increasing the concentration of MDM2 on the extent to which the binding mechanism proceeds through induced fit and conformational selection. Based on atomistic simulations, the binding mechanism of the MDM2 receptor and p53 peptide ligand is predicted to shift from being dominated by conformational selection at low receptor concentration to induced fit at high receptor concentration.¹⁷ Likewise, based on experimental rate constants, this shift in mechanism is expected to occur upon increasing the ligand concentration for systems involving disordered protein receptors and their small organic ligands.^18,19 Given the prevalence of single α-helix binding motifs among protein–ligand interactions,²⁰ the mechanism of MDM2–p53 binding is not only of biomedical importance²¹ but fundamental to biology.

METHODS

Key features of our simulation strategy are the following. First, we employed minimal residue-level models (C_α models) along with a Gō-type potential energy function,^22,23 which enables tuning of the extent of preorganization of the IDP (in our case, the p53 peptide) from fully disordered to fully preorganized. Second, dynamics were propagated using a Brownian dynamics algorithm with the inclusion of appropriately parametrized hydrodynamic interactions (HIs) between protein residues to yield realistic diffusion properties.²⁴ Third, we applied the weighted ensemble (WE) path sampling strategy,^25–27 which has been demonstrated to be orders of magnitude more efficient than standard Brownian dynamics simulations in generating pathways and rate constants for protein binding processes.²⁸ Full details of the protein model, simulations, and analysis are below.

The Protein Model

Residue-level protein models were used in which each residue was represented by a single pseudoatom at its C_α position, yielding 85 pseudoatoms for the MDM2 protein (residues 25–109) and 13 pseudoatoms for the p53 peptide (residues 17–29). Coordinates for the unbound and bound conformations of MDM2 and p53 peptide were taken from the crystal structure of the MDM2–p53 peptide complex (PDB code: 1YCR).²⁹

A Gō-type potential energy function^22,23 was used to govern the conformational dynamics of the protein model. In this energy function, bonded interactions between pseudoatoms are modeled by standard molecular mechanics terms for bonds, angles, and dihedrals; and nonbonded interactions between pseudoresidues separated by four or more pseudobonds were treated as either native or non-native contacts. A native contact was defined as a residue–residue contact in which the heavy atoms of the two residues are within 5.5 Å of each other in the crystal structure of the native complex. In addition to 57 intermolecular native contacts between p53 and MDM2, the p53 peptide and MDM2 consisted of 10 and 266 intramolecular contacts, respectively.

The protein model was parametrized by focusing separately on the following three contributions to the total energy function:

$$E_{\text{total}}=E_{\mathrm{p}53}+E_{\text{MDM}2}+E_{\text{MDM}2/\mathrm{p}53}$$ (1)

where E_p53 and E_MDM2 correspond to intramolecular contributions from p53 and MDM2, respectively, and E_MDM2/p53 corresponds to the intermolecular MDM2/p53 contributions.

As others have done,³⁰ we tuned the degree of structure and backbone flexibility of the IDP (in our case, the p53 peptide) by applying a single scaling factor α to the pseudoangle, pseudodihedral, and intramolecular nonbonded terms of the energy function involving solely the IDP:

$$\begin{gathered} E_{\mathrm{p}53}=\sum _{\text{bonds}}{k}_{\text{bond}}{(r-r_{\text{eq}})}^2 \\ +\alpha \{\sum _{\text{angles}}{k}_{\text{angle}}{(\theta -{\theta }_{\text{eq}})}^2 \\ +\sum _{\text{dihedrals}}{V}_1[1+cos(\phi -{\phi }_1)]+V_3[1+cos(3\phi -{\phi }_3)] \\ +\sum _{i<j-4,\text{non-native}}^{p53}{\epsilon }^{\text{non-native}}{\left(\frac{{\sigma }_{ij}^{\text{non-native}}}{r_{ij}}\right)}^{12} \\ +\sum _{i<j-4,\text{native}}^{\mathrm{p}53}{\epsilon }^{\text{native}}\left[5{\left(\frac{{\sigma }_{ij}^{\text{native}}}{r_{ij}}\right)}^{12}-6{\left(\frac{{\sigma }_{ij}^{\text{native}}}{r_{ij}}\right)}^6\right]\} \end{gathered}$$ (2)

where r, θ, φ are pseudo bond lengths, pseudoangles, and pseudodihedrals, respectively; V₁ and V₃ are potential barriers for the dihedral terms; ε^native is the energy well depth for native contacts, r_ij is interatomic distance between pseudoatoms i and j during simulation, and ${\sigma }_{ij}^{\text{native}}$ is the corresponding distance in the crystal structure; ${\sigma }_{ij}^{\text{non-native}}$ and ε^non-native for non-native contacts were set to 4.0 Å and 1 kcal/mol, respectively. Equilibrium bond lengths (r_eq), angles (θ_eq), and dihedral phase angles (φ₁ and φ₃) were taken from the crystal structure. The force constants, k_bond and k_angle, were set to 100 kcal/mol/Å and 20 kcal/mol/rad, respectively, and V₁ and V₃ were set to 1 and 0.5 kcal/mol, respectively. The scaling factor α was set to 0.1, 0.5, 1.0, and 2.0 to model analogues of the p53 peptide that exhibit, on average, a fraction of native contacts (Q_p53) of 0.25, 0.5, 0.85, and 0.99, respectively, based on 10 μs standard simulations of the isolated peptide (Figures S1 and S2). Thus, α values of 0.1 and 2.0 represent the fully disordered and fully preorganized versions of the p53 peptide, respectively.

The same potential function was used for MDM2 (E_MDM2) and nonbonded MDM2–p53 interactions (E_MDM2/p53), except for the omission of the scaling factor α. An ε^native of 1.0 kcal/mol was used for intramolecular native contacts of MDM2, yielding a fraction of native contacts Q_MDM2 > 0.8 based on five 10 μs simulations. To ensure that the fully disordered p53 peptide folds upon binding MDM2, the ε^native for native MDM2–p53 interactions was set to the minimum value (2.0 kcal/mol) required to ensure that the peptide folds upon binding MDM2 (Q_p53 > 0.7 throughout a 10 μs standard simulation (no WE sampling); Figure S3). Following others,¹⁶ the same ε^native value for intermolecular contacts (in our case, MDM2–p53 contacts) was used for all analogues of the IDP (the p53 peptide). The same ε^native was also used for native contacts within the fully preorganized p53 peptide.

Weighted Ensemble (WE) Simulations

To generate MDM2–p53 peptide binding pathways, we applied the WE path sampling strategy,³¹ as implemented in the WESTPA software package (https://westpa.github.io/westpa),³² to orchestrate a large set of Brownian dynamics trajectories that were carried out using the framework of the Northrup–Allison–McCammon (NAM) method.³³ In this hybrid WE/NAM approach, two concentric spherical surfaces are first defined with radii b and q that correspond to separation distances between MDM2 and the p53 peptide. The inner sphere, or b surface, represents the initial unbound state, and the outer sphere, or q surface, represents a much larger separation distance (q ≫ b) at which trajectories are terminated to avoid wasting computing time sampling any indefinite drifting apart of the binding partners. The next step of the WE/NAM approach is to define a progress coordinate between the unbound and bound states and to divide this coordinate into bins with the goal of populating each bin with N trajectories, each of which is assigned a statistical weight. Starting from N trajectories in the initial unbound state, the dynamics of each trajectory are simultaneously propagated in parallel and occasionally coupled by replication and combination events at fixed time intervals τ based on their progress toward the target state (e.g., the bound state), splitting and combining the statistical weights, respectively, such that no bias is introduced into the dynamics.³¹ To maintain steady-state conditions, any trajectory that reaches the q surface is “recycled” by terminating the trajectory and starting a new trajectory from an initial, unbound state with the same statistical weight.

In our WE simulations, the radii b and q were set to 35 and 50 Å, respectively; as required for the WE/NAM approach, b is sufficiently large such that the intermolecular forces between the binding partners can be assumed to be isotropic (as mentioned above, only short-range residue–residue interactions were modeled in our simulations). Initial unbound states were generated by randomly reorienting the binding partners with respect to each other at a separation of 35 Å using their corresponding conformations from the crystal structure of MDM2–p53 complex.²⁹ For the progress coordinate, we used the C_α RMSD of the p53 peptide after alignment of MDM2 ranging from 0 to 100 Å. This progress coordinate was evenly divided into 29 bins with a target number of 6 trajectories/bin, yielding a maximum total of 390 trajectories at any point in the WE simulation. The fixed time interval τ for each WE iteration was set to 100 ps, which allowed for at least one trajectory to advance to the next bin after each WE iteration.

For each p53 peptide analogue (each α value), 10 independent WE simulations of the MDM2–p53 binding process were carried out under pseudoequilibrium conditions in which trajectories were recycled at the q surface, but not the bound state, to allow for refinement of the bound-state definition after completion of the simulations. Once this was refined, we effectively recycled trajectories that reached the refined definition of the bound state by removing the trajectories from subsequent analysis with proper renormalization of the remaining probabilities. This renormalization was straightforward given that no trajectories in the reverse, unbinding direction were generated in our Gō-type simulations. Each WE simulation was carried out for a maximum trajectory length of 200 ns (2000 WE iterations), which was sufficiently long for obtaining converged estimates of the k_on (Figure S5). Conformations were sampled every 1 ps for analysis.

Propagation of Dynamics

The dynamics of our WE simulations were propagated using a standard Brownian dynamics algorithm³⁴ with the inclusion of hydrodynamic interactions (HI),²⁴ as implemented in the UIOWA_BD software.^24,35 Hydrodynamic radii were set to 5.3 Å, which has been found to reproduce the translational and rotational diffusion coefficients of all-atom models of folded proteins when using the residue-level models of this study.²⁴ The solvent viscosity was set to 0.89 cP to represent water at 25 °C. To enable the use of a 50 fs time step, all pseudobonds between residues were constrained to their native bond lengths by applying the LINCS algorithm.³⁶

Calculation of Bimolecular Rate Constants

All bimolecular rate constants k were calculated using the Northrup–Allison–McCammon (NAM) equation:³³

$$k=\frac{k_{\mathrm{D}}(b)\beta }{1-(1-\beta )k_{\mathrm{D}}(b)/k_{\mathrm{D}}(q)}$$ (3)

where k_D(r) is the diffusion rate constant for the two binding partners achieving a separation distance r, and β is the probability that a simulation starting from the unbound state with a separation distance of b (35 Å) reaches the target state before drifting apart to a separation distance of q (50 Å). To calculate the rate constant k₁, the target state is the encounter complex; likewise, to calculate k_on, the target state is the native, bound state (see definitions in Results).

Assuming that the motions of the two binding partners are isotropic, the diffusion rate constants were calculated using the Smoluchowski equation: k_D = 4πDr, where D is the relative translational diffusion coefficient of the two partners (i.e., the sum of their corresponding diffusion coefficients). Therefore, eq 3 reduces to

$$k=\frac{4\pi Db\beta }{1-(1-\beta )b/q}$$ (4)

The translational diffusion coefficient of MDM2 was calculated using five 10 μs standard simulations of isolated MDM2, and the translational diffusion coefficient for each analogue of the p53 peptide was calculated using conformations sampled every 100 ps from a single 10 μs standard simulation of the corresponding isolated p53 peptide. The β value was estimated using the following equation:³⁷

$$\beta =\frac{f_{\text{SS}}^{\text{target}}}{f_{\text{SS}}^{\text{target}}+f_{\text{SS}}^{\text{qsurf}}}$$ (5)

where $f_{\text{SS}}^{\text{target}}$ is the steady-state flux into the target state (encounter complex or bound state) and $f_{\text{SS}}^{\text{qsurf}}$ is the steady-state flux across the q surface in the WE simulation. All rate constants were calculated from each of 10 independent WE simulations, and then averaged. Uncertainties in the averaged rate constants represent two standard errors of the mean (SEM).

Calculation of the Percentage of Productive Collisions

The percentage of productive collisions (i.e., encounter complexes that succeed in rearranging to the bound state) was calculated according to the following equation:

$$\%\text{productive}\text{collisions}=\frac{f_{\text{SS}}^{\text{native}}}{f_{\text{SS}}^{\text{encounter}}}$$ (6)

where $f_{\text{SS}}^{\text{native}}$ is the steady-state flux into the native, bound state and $f_{\text{SS}}^{\text{encounter}}$ is the steady-state flux into the encounter complex; both fluxes were evaluated only after an approximate steady state was achieved (Figure S5). Reported percentages of productive collisions are averages over 10 independent WE simulations with uncertainties representing two SEM.

RESULTS

The goals of this study were to determine (i) the effects of preorganizing the p53 peptide ligand on its k_on for binding the MDM2 protein receptor and (ii) the effect of increasing the concentration of the MDM2 receptor on the binding mechanism. As shown in Figure 1A, the extent of preorganization in the p53 peptide was tuned by applying a scaling factor α to the components of the energy function that involve solely the p53 peptide (see Methods) and setting the α values to 0.1 (fully disordered), 0.5, 1.0, and 2.0 (fully preorganized). To enable the calculation of statistically robust rate constants, we applied the WE path sampling strategy^25,26 in conjunction with molecular simulations to enhance the sampling of binding events while maintaining rigorous kinetics. For each p53 peptide analogue (i.e., each α value), a set of 10 independent WE simulations were carried out, yielding >3000 binding events per simulation to achieve highly precise rate constants with relative errors of ≤16%, which amounts to a ≤ 0.1 kcal/mol difference in the corresponding free energy barrier at 25 °C as estimated by −RT ln(1/1.16). The simulations required one month to complete using 128 CPU cores of 2.3 GHz AMD Interlagos processors.

Figure 1.

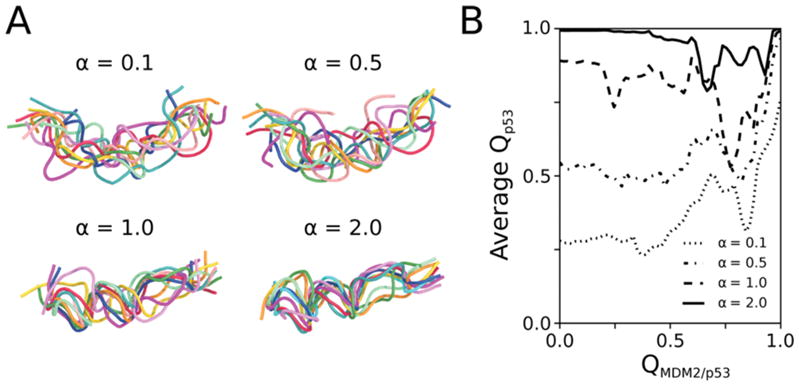
Tuning of the protein model to yield p53 peptide analogues with varying extents of preorganization. (A) Representative conformations of p53 peptide analogues that range from fully disordered (α = 0.1) to fully preorganized (α = 2.0). Conformations were sampled every 1 μs from 10 μs BF simulations of the corresponding unbound p53 peptide. (B) The fully disordered p53 analogue folds only upon binding the MDM2 protein as revealed by monitoring the average fraction of native contacts in the p53 peptide (Q_p53) as a function of the fraction of native contacts between MDM2 and p53 peptide (Q_MDM2/p53) for all of the p53 peptide analogues. Data shown for each p53 peptide analogue is based on 10 independent WE simulations.

Is There a Kinetic Advantage to Being Disordered vs Preorganized?

To directly compare the binding kinetics of the fully disordered p53 peptide relative to the other more preorganized analogues, it was essential to ensure that the fully disordered peptide was able to fold into an α-helical conformation upon binding MDM2. As shown by Figure 1B, all of the p53 peptide analogues are folded when bound to the MDM2 protein. By construction, our model of the fully disordered peptide (α = 0.1) results in an induced fit (folding-after-binding) mechanism³⁸ in which the peptide folds only upon binding MDM2 in our simulations; likewise, the fully preorganized peptide (α = 2.0) results in a conformational selection (binding-after-folding) mechanism in which the peptide is fully folded before binding MDM2 in our simulations (Figure 1B).

For all of the p53 peptide analogues, ranging from fully disordered to fully preorganized, our simulations reveal that the mechanism of binding to the MDM2 receptor involves a two-step process in which diffusive collisions of the binding partners first form a metastable “encounter” complex followed by rearrangement of the encounter complex to the native, bound state (Figure 1; Figure S3):

$$\mathrm{p}53\text{peptide}+\text{MDM}2\underset{k_{-1}}{\overset{k_1}{\rightleftharpoons }}\text{encounter}\text{complex}\underset{k_{-2}}{\overset{k_2}{\rightleftharpoons }}\text{bound}\text{state}$$

where k₁ is the rate constant for formation of the encounter complex, k₋₁ is the rate constant for the dissociation of the encounter complex to the unbound state, k₂ is the rate constant for rearrangement of the encounter complex to the bound state, and k₋₂ is the rate constant for rearrangement of the bound state to the encounter complex.

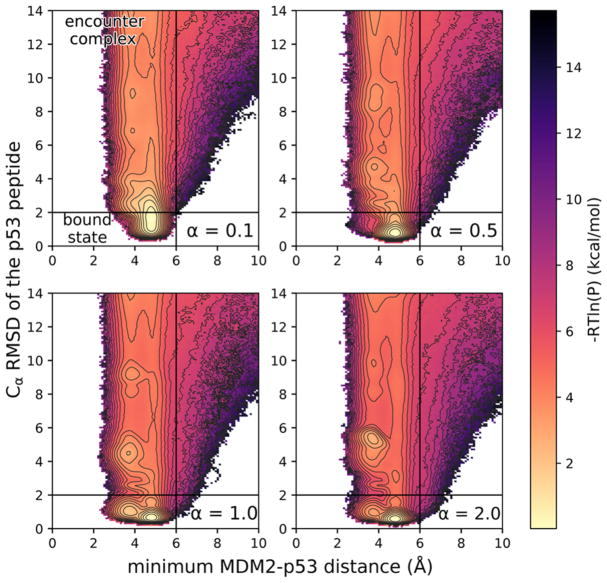
For our calculations of rate constants, we used the most stringent definitions of the encounter complex and bound state that encompassed the corresponding basins in the probability distributions of both the fully disordered and preorganized p53 peptides in Figure 2. The encounter complex was defined as those conformations satisfying the following criteria: (i) the binding partners are within van der Waals contact (<6 Å), (ii) the C_α RMSD for the p53 peptide after alignment of MDM2 is >2 Å, and (iii) at least one MDM2–p53 native contact is formed. The bound state was defined as having the binding partners within van der Waals contact and a C_α RMSD ≤ 2 Å of the p53 peptide after alignment of MDM2.

Figure 2.

Zoomed-in views of probability distributions over the WE progress coordinate for various extents of structure in the p53 peptide, ranging from fully disordered (α = 0.1) to fully preorganized (α = 2.0) (for a representative full view of the probability distribution, see Figure S4). The progress coordinate consisted of the C_α RMSD of the p53 peptide after alignment of MDM2 from the crystal structure of the MDM2–p53 peptide complex²⁹ and minimum MDM2–p53 distance. Definitions of the encounter complex and bound state are delineated by the solid black lines (for a representative full view of the probability distribution, see Figure S4). The color scale represents –RT ln P where P is the pseudoequilibrium probability density based on trajectory weights from each of 10 independent WE simulations that were carried out for the corresponding MDM2– p53 system (see Methods). Contour lines represent intervals of 0.5 kcal/mol.

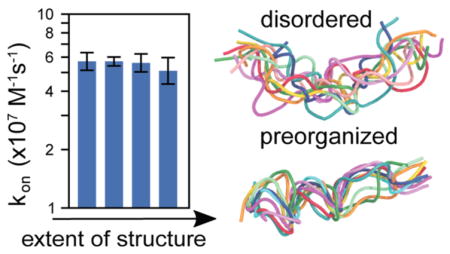
To assess whether there is a kinetic advantage to the peptide ligand being disordered or preorganized, we computed the k_on values of the exact ordered and disordered analogues using the NAM framework in conjunction with WE simulations (see Methods). As shown in Table 1, the ratio of the k_on for the fully disordered peptide relative to that of the fully preorganized peptide is 0.9 ± 0.2 (uncertainties represent two SEM), with a percent uncertainty that amounts to only a 0.1 kcal/mol difference in the corresponding free energy barrier as estimated by $-RTln(k_{\text{on}}^{\alpha =2.0}/k_{\text{on}}^{\alpha =0.1})$. Thus, given the high precision of these computed values, any kinetic advantage to being disordered (or preorganized) is very small.

Table 1.

Computed k_on, k₁ for Formation of the Encounter Complex, Lifetime of the Encounter Complex, % Productive Collisions, and Relative Translational Diffusion Coefficients D for the MDM2–p53 Binding Process and p53 Peptide Analogues Ranging from Fully Disordered (α = 0.1) to Fully Preorganized (α = 2.0) in the Presence of Hydrodynamic Interactions (HIs)^a

	α = 0.1	α = 0.5	α = 1.0	α = 2.0	relative to α = 0.1
					α = 0.5	α = 1.0	α = 2.0
kon (107 M−1 s−1)	5.7 ± 0.6	5.7 ± 0.3	5.6 ± 0.6	5.1 ± 0.8	1.0 ± 0.1	1.0 ± 0.2	0.9 ± 0.2
k1 (107 M−1 s−1)	6.1 ± 0.5	6.1 ± 0.3	6.2 ± 0.6	5.9 ± 0.6	1.0 ± 0.1	1.0 ± 0.1	1.0 ± 0.1
lifetime of the encounter complex (ps)	80 ± 20	90 ± 30	130 ± 50	80 ± 20	1.1 ± 0.5	1.6 ± 0.8	1.0 ± 0.4
% productive collisions	65 ± 3	64 ± 6	68 ± 3	66 ± 2	1.0 ± 0.1	1.1 ± 0.1	1.0 ± 0.1
D (10−6 cm2/s)	4.2 ± 0.7	3.9 ± 0.4	3.9 ± 0.5	4.0 ± 0.4	0.9 ± 0.2	0.9 ± 0.2	1.0 ± 0.2

^aData shown are averages from 10 independent WE simulations; uncertainties represent two SEM.

We next examined the extent to which ligand preorganization influences the individual steps of the binding process. The computed bimolecular rate constant for formation of the encounter complex, k₁, of the fully disordered p53 peptide is within error of that of its fully preorganized analogue with a ratio of 1.0 ± 0.1, indicating that being disordered (or preorganized) did not enable more rapid initial collisions. Given that native contacts are rewarded and non-native contacts are penalized in our simulation model (a Gō-type model), k₋₂ ≪ k₂ such that the expression for the overall association rate constant is k_on = (k₁k₂/(k₋₁ + k₂). Since k_on and k₁ are within error of each other for all of the peptide analogues [e.g., for the fully disordered peptide, the k_on and k₁ are (5.7 ± 0.6) × 10⁷ M⁻¹ s⁻¹ and (6.1 ± 0.5) × 10⁷ M⁻¹ s⁻¹, respectively], the kinetics of the binding processes must be close to the limiting case where k₋₁ ≪ k₂, such that k_on = (k₁k₂/(k₋₁ + k₂) ≅ k₁.³⁸ The formation of the encounter complex is therefore rate-limiting for all of the p53 peptide analogues (k₂ was not computed since the hybrid WE/NAM approach permits calculation of bimolecular rate constants, but not unimolecular rate constants). Interestingly, the most preorganized peptide analogues (α = 1.0 and α = 2.0) undergo partial loss of structure upon forming the encounter complex (Figure 1B). This result suggests that the MDM2 receptor might aid the process of binding by disrupting preformed interactions within the p53 peptide that hinder rearrangement of the encounter complex to the bound state.

To gain further insight into the similarity in the k_on values among all of the p53 peptide analogues, we calculated the percentage of productive collisions (i.e., those collisions that eventually reach the bound state) and the lifetime of the encounter complex. As shown in Table 1, the percentage of productive collisions for the fully disordered and fully preorganized p53 peptides are within error of each other (a ratio of 1.0 ± 0.1 for the percentage of productive collisions of the fully disordered peptide relative to that of the fully preorganized peptide) as are the lifetimes of the encounter complex (ratio of 1.0 ± 0.4). The high percentages of productive collisions (65 ± 3% and 66 ± 2% for the fully disordered and fully preorganized peptides, respectively) are consistent with our conclusion above that k₋₁ ≪ k₂. Given that our simulations were carried out under steady-state conditions, generating pathways in only the binding direction, it was possible to obtain statistically robust estimates of non-equilibrium observables (e.g., rate constants and percentage of productive collisions), but not equilibrium observables (e.g., populations and lifetimes of the encounter complex), which would require sampling of unbinding as well as binding pathways. Nonetheless, since both the percentage productive collisions and lifetimes of the encounter complex are similar for the fully disordered and fully preorganized peptides, k₋₁ as well as k₂ must be similar for the peptides. Thus, the folding of the fully disordered p53 peptide upon binding MDM2 does not appear to affect k₂ relative to that of the fully preorganized peptide. It is worth noting that the k₂ step may be slower in all-atom simulations due to attractive non-native interactions that are missing in our Gō-type simulations and that such nonnative interactions would likely result in additional benefits to the p53 peptide being preorganized relative to being disordered.

Our computed k_on values are within error of the computed k_on from atomistic simulations [(7 ± 4) × 10⁷ M⁻¹ s⁻¹]¹¹ and 6× faster than the experimental value (9.2 × 10⁶ M⁻¹ s⁻¹).³⁹ Thus, while the use of the Gō-type potential energy function^22,23 would be expected to artificially accelerate the dynamics,^40,41 the inclusion of appropriately parametrized HIs yields realistic rate constants.²⁴ In particular, the computed relative translational diffusion coefficients for MDM2 and the p53 peptide for all of the peptide analogues are in excellent agreement with that predicted for the corresponding all-atom models by the hydrodynamics program HYDROPRO,⁴² 3.7 × 10⁻⁶ cm²/s. As others have shown,²⁴ the translational diffusion coefficients of proteins are underestimated in molecular simulations that neglect HIs—in our case, by 10× (Table 1; Table S1)—underscoring the importance of including HIs in simulations that lack explicit solvent.²⁴ Interestingly, the extent of structure in the p53 peptide has no significant effect on the relative translational diffusion coefficient for the p53 peptide and MDM2 protein.

Effect of Including Hydrodynamic Interactions (HIs)

The inclusion of HIs in our simulations increased the k_on by 30× (Table 1; Table S1). This result may appear at odds with previous simulation studies of protein–protein associations in which the inclusion of HIs was found to slow down the approach of the proteins.^28,43 However, our results are in fact consistent with these studies since the effect of including HIs on the k_on depends on the extent to which the intramolecular and intermolecular HIs have opposing effects on the diffusion of the binding partners. Whereas intramolecular HIs speed up the diffusion of binding partners that have no interactions with each other, yielding larger translational diffusion coefficients, intermolecular HIs slow down the diffusion of the binding partners when they are close to one another and have the tendency to move together. Our results involving the MDM2–p53 system reveal that the net effect of including both intramolecular and intermolecular HIs is a faster k₁ as well as slower dissociation of the encounter complex (k₋₁), the latter being evident from longer lifetimes of the encounter complex and a greater percentage of productive collisions.

Effect of Increasing Receptor Concentration

As demonstrated by previous experimental studies, the mechanism by which a small organic ligand binds a disordered protein receptor shifts from conformational selection to induced fit with increasing ligand concentration.^18,19 Here, we examined the effects of increasing the concentration of a protein receptor (MDM2) on its mechanism of binding to a disordered peptide (p53 peptide), i.e., the relative fluxes through conformational selection and induced-fit mechanisms (Figure 3A).

Figure 3.

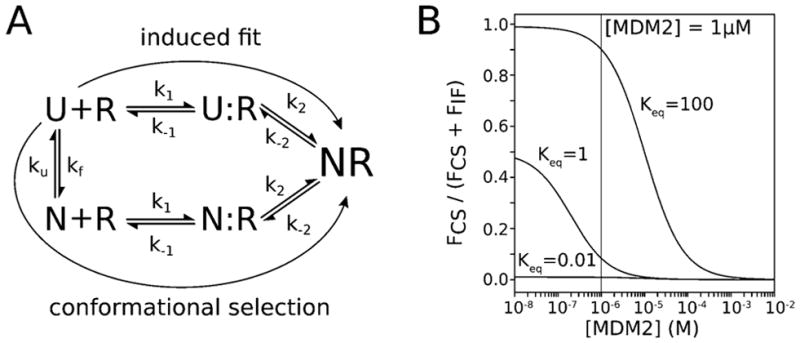
Conformational selection and induced-fit mechanisms of binding, and the effects of increasing receptor concentration. (A) Conformational selection and induced fit mechanism of binding for an IDP ligand and its folded receptor. N is the folded (fully preorganized) state of the IDP, U is the unfolded (fully disordered) state of the IDP, and R is the receptor, U:R and N:R are the encounter complexes resulting from diffusional collisions of the unfolded and folded states, respectively, with the receptor, and NR is the native, bound conformation. (B) Fractional flux through conformational selection (CS) for the binding process as a function of receptor (MDM2) concentration. Given that the equilibrium constant K_eq of the IDP (K_eq = k_f/k_u) is not known, the fractional flux is estimated for three K_eq values (0.01, 1, and 100). The black line represents the [MDM2] used in an experimental study of the MDM2–p53 peptide binding mechanism.³⁹

Given that the computed k_on ≅ k₁ for all of the p53 peptide analogues in this study, the binding mechanism for the MDM2/p53 peptide system can be approximated as a two-step mechanism with a very fast second step (the k₂ step; Figure S6) such that the fractional flux can be calculated using the following equation:

$$\frac{F_{\text{CS}}}{F_{\text{CS}}+F_{\text{IF}}}\cong \frac{k_{\mathrm{f}}}{(k_{\mathrm{u}}+k_{\mathrm{f}})+k_{\text{on}}[\mathrm{R}]}$$ (7)

where k_on is set to an order-of-magnitude estimate (10⁷ M⁻¹ s⁻¹) since the computed k_on values are essentially the same for the fully disordered and fully preorganized p53 peptides; F_CS and F_IF are the fluxes through the conformational selection and induced-fit mechanisms, respectively; [R] is concentration of the folded receptor (MDM2); as shown in Figure 3A, k_f is the rate constant for folding of the ligand (p53 peptide) from the fully disordered, unfolded (U) state, and k_u is the rate constant for unfolding of the ligand from the fully preorganized, native folded (N) state. Thus, in this scenario, the fractional flux through conformational selection depends only on the concentration of the receptor and is therefore independent of ligand concentration. A detailed derivation of eq 7 can be found in the Supporting Information.

Since the equilibrium constant K_eq (ratio of k_f/k_u) for the folding of the isolated p53 peptide is not known, we tested three different scenarios: (i) K_eq = 1 for equally stable unfolded and folded states, (ii) K_eq = 100 for an unfolded state that is much less stable than the folded state, and (iii) K_eq = 0.01 for an unfolded state that is much more stable than the folded state (Figure 3B). When the folded state is much less stable than the unfolded state (K_eq = 0.01), the mechanism of binding would be solely induced fit, regardless of MDM2 concentration. Substantial flux through conformational selection would be expected only when the folded state is equal or greater in stability to the unfolded state (K_eq ≥ 1). For example, if K_eq = 1, ~10% flux through conformational selection would be expected at the MDM2 concentration (1 μM) in binding kinetics experiments.³⁹ In the regime where K_eq ≥ 1, the mechanism of binding is predicted to shift from being dominated by conformational selection to induced fit with increasing MDM2 concentration (Figure 3B). These results are consistent with those from atomistic simulations in which a Markov state model^44,45 was constructed to estimate rate constants for the MDM2–p53 peptide binding process and relative fluxes through conformational selection and induced fit were estimated (i) using a mechanism consisting of four instead of the three states used here and (ii) for various extent of helical content of the p53 peptide, which is analogous to varying K_eq values for the unfolding/folding equilibrium of the peptide.¹⁷ In particular, the dominant binding mechanism becomes induced fit as the concentration of MDM2 increases and the extent of helical content decreases (or K_eq decreases).

DISCUSSION

To our knowledge, the only other study that has directly compared the binding kinetics of an IDP relative to its exact preorganized analogue is a simulation study that focused on the binding of the disordered pKID domain to its partner protein, KIX.¹⁶ In this study, the disordered pKID domain was found to have a modest kinetic advantage (~2.5×) for binding relative to the preorganized analogue due to a more rapid k₂ step, which corresponds to the rearrangement of the encounter complex to the native, bound state. In contrast, our study yielded similar computed k_on values for the disordered and preorganized analogues of the p53 peptide in binding the MDM2 protein, revealing that the folding of the disordered p53 peptide upon binding MDM2 is very fast such that the k₂ step is just as rapid as that of the preorganized analogue.

As noted above, the pKID domain is significantly larger than the p53 peptide: upon binding its partner protein, the pKID domain adopts two α-helices while the p53 peptide adopts only a single α-helix. Given its larger size, the folding of the fully disordered pKID domain is slower and may therefore have a more significant influence on k₂. In particular, since the fully disordered pKID consists of two segments, the folding of the domain can take advantage of a dock-and-coalesce mechanism⁴ in which the docking of one segment facilitates the folding process in the k₂ step.

The fact that our computed k₁ values for the formation of the encounter complex are the same for the disordered and preorganized p53 peptides indicates that the MDM2–p53 binding process does not involve the “fly-casting” mechanism in which the disordered peptide would be predicted to collide more rapidly with its partner protein due to a greater capture radius.³ The lack of a fly-casting effect in our molecular simulations is underscored by our use of a Gō-type potential, which creates the optimal scenario for capturing the effect, i.e., the fully disordered p53 peptide folds only upon binding (forming ≥70% of intramolecular p53 native contacts only upon forming ≥98% of intermolecular MDM2–p53 native contacts; Figure 1B). Furthermore, we observed no differences in the capture radius of the fully disordered p53 peptide relative to its fully preorganized analogue as quantified by the radius of gyration R_g (most probable values of 7.7 and 7.3 Å, respectively) as well as a more sensitive metric, the maximum principal axis radius R_M (6.6 and 6.9 Å, respectively; see Figure S5), despite the fact that the disordered conformations were generated with no rewarding of native contacts. The lack of differences in the capture radius and therefore the hydrodynamic radius is consistent with the fact that the computed translational diffusion coefficients of the fully disordered and fully preorganized p53 peptides are indistinguishable from each other (Table 1). Regardless, based on the Stokes–Einstein equation in which the translational diffusion coefficient is inversely proportional to the hydrodynamics radius, any kinetic advantage that could result from a larger capture radius (and therefore hydrodynamics radius) of the disordered peptide relative to its preorganized analogue might be canceled out by the effects of a slower translational diffusion coefficient.

CONCLUSIONS

We have determined the effects of preorganization of the intrinsically disordered, N-terminal p53 peptide on the kinetics of binding its partner protein, MDM2, using molecular simulations. In particular, our application of the WE strategy enabled the generation of >3000 of binding events, yielding statistically robust k_on values for the fully disordered p53 peptide and exact analogues of the peptide that have been preorganized to various extents.

The resulting computed k_on values are in reasonable agreement with experiment. Notably, the k_on for the fully disordered p53 peptide is within error of that for its fully preorganized analogue, indicating no kinetic advantage to being disordered or preorganized for binding MDM2. Given that the rate constant k₁ for formation of the encounter complex is essentially the same for the fully disordered and fully preorganized peptides, fly-casting is not a significant effect in our simulations of the MDM2–p53 peptide system, even though the ideal scenario for this effect was modeled, i.e., using a Gō-type potential that ensured folding of the fully disordered peptide only upon binding MDM2. Furthermore, since the percentages of productive collisions and lifetimes of the encounter complex are similar for the fully disordered and preorganized p53 peptides, the rate constant k₂ for rearrangement of the encounter complex to the bound state must also be similar. Thus, folding of the fully disordered p53 peptide upon binding MDM2 during the k₂ step must be very rapid. In contrast, the slower folding of larger IDPs may have a more significant effect on k₂ relative to that for their fully preorganized analogues, as predicted for the pKID domain¹⁶ and by the dock-and-coalesce mechanism.⁴ Interestingly, the two most preorganized p53 peptide analogues undergo partial loss of structure upon forming the encounter complex, implying that the MDM2 receptor might “erase” preformed interactions within the p53 peptide that hamper the k₂ step.

Finally, based on our k_on values, we determined the effect of increasing the concentration of MDM2 on its mechanism of binding to the disordered p53 peptide ligand. When the unfolded state is much less stable than the folded state of the isolated p53 peptide, the mechanism for the binding of the MDM2 receptor to the disordered p53 peptide is predicted to switch from being dominated by conformational selection to induced-fit with increasing concentration of MDM2. On the other hand, when the unfolded state is either equal to or much greater in stability than the folded state, the mechanism of binding is solely induced fit, regardless of the MDM2 concentration. These results are consistent with those from recent atomistic simulations of the binding process involving the MDM2 receptor and p53 peptide ligand.¹⁷

Given the general features of our residue-level simulation models, results from our molecular simulations are relevant to any protein binding process involving a disordered peptide of a similar length to the p53 peptide that folds into a single α-helix upon binding its partner protein. Such disorder-to-helix transitions are common among molecular recognition events, including protein interactions of IDPs that play crucial cellular roles.^2,20,46 Our results provide a valuable set of simulation data for testing future hypotheses that might be proposed for the binding mechanisms of IDPs and their preorganized analogues.

Supplementary Material

SI file

FIGURE S1 Probability distributions of the fraction of native contacts of the p53 peptide (Q_p53) in the absence of MDM2, ranging from fully disordered (α = 0.1) to fully preorganized (α = 2.0). Distributions for each value of the scaling factor α were generated using conformations sampled every 100 ps from a single 10-μs standard simulation starting from the MDM2-bound conformation.

FIGURE S2 Average fraction of native contacts in p53 (Q_p53) as a function of the ε^native for MDM2-p53 native contacts. For each ε^native value, the average Q_p53 was calculated using conformations sampled every 100 ps from a single 10-μs standard simulation of the MDM2-p53 peptide complex with the fully disordered peptide (α = 0.1) starting from the MDM2-bound conformation.

FIGURE S3 Full view of the free energy landscape of the MDM2-p53 binding process as a function of the C_α RMSD of the p53 peptide after alignment of MDM2 from the crystal structure of the MDM2-p53 peptide complex ¹ and the minimum MDM2-p53 distance for the fully disordered p53 peptide (α = 0.1). Data shown is based on conformations sampled every 1 ps from 10 independent WE simulations under steady-state conditions. Contour lines represent intervals of 0.5 kcal/mol.

FIGURE S4 Computed k_on as a function of WE iteration for p53 peptide analogues with various extents of structure, ranging from fully disordered (α = 0.1) to fully preorganized (α = 2.0). The molecular time is defined as Nτ where N is the number of WE iterations and τ is the fixed time interval of each iteration.

FIGURE S5 Probability distributions of the “capture” radius for the p53 peptide with various extents of structure, ranging from fully disordered (α = 0.1) to fully preorganized (α = 2.0), as monitored by the radius of gyration R_g, and maximum principal axis radius R_M. For each α value, the probability distribution was calculated from a 10-μs BF simulation of the isolated peptide. Based on the R_g metric, it may appear that the fully disordered p53 peptide achieves a significantly larger maximum value than that of the fully preorganized peptide (11.6 Å vs. 8.0 Å). However, the more sensitive R_M metric reveals that the fully disordered p53 peptide not only assumes more expanded conformations (maximum value of 10.2 Å), but also more contracted conformations (minimum value of 3.3 Å).

Figure S6: Approximation of the binding mechanism of the disordered p53 peptide ligand to the folded MDM2 protein receptor when k_on ≅ k₁. States are defined as in Fig. 3A.

Table S1. Computed k_on, k₁ for formation of the encounter complex, lifetime of the encounter complex, % productive collisions, and relative translational diffusion coefficients for the MDM2-p53 binding process and various analogues of the p53 peptide, ranging from fully disordered (α = 0.1) to fully preorganized (α = 2.0) in the absence of hydrodynamic interactions (HIs). Data shown are averages from 10 independent WE simulations; uncertainties represent 95% confidence intervals.