Pressure induced superconductivity bordering a charge-density-wave state in NbTe₄ with strong spin-orbit coupling

Abstract

Transition-metal chalcogenides host various phases of matter, such as charge-density wave (CDW), superconductors, and topological insulators or semimetals. Superconductivity and its competition with CDW in low-dimensional compounds have attracted much interest and stimulated considerable research. Here we report pressure induced superconductivity in a strong spin-orbit (SO) coupled quasi-one-dimensional (1D) transition-metal chalcogenide NbTe₄, which is a CDW material under ambient pressure. With increasing pressure, the CDW transition temperature is gradually suppressed, and superconducting transition, which is fingerprinted by a steep resistivity drop, emerges at pressures above 12.4 GPa. Under pressure p = 69 GPa, zero resistance is detected with a transition temperature T_c = 2.2 K and an upper critical field μ₀H_c2 = 2 T. We also find large magnetoresistance (MR) up to 102% at low temperatures, which is a distinct feature differentiating NbTe₄ from other conventional CDW materials.

Introduction

Transition-metal chalcogenides possess rich structural chemistry and a wide variety of unusual physical properties^1–3. The latter includes, for instance, charge density wave (CDW)³, superconductivity^4–7 and recently reported extremely large magnetoresistance in WTe₂^8–13. Among chalcogenides, tellurides are usually different from sulfides and selenides in crystal structures, electronic structures and physical properties, due to the diffusive nature of the tellurium valence orbitals¹⁴ and thus more covalent character of tellurium¹. While sulfides and selenides, such as NbS₂, NbSe₂ and NbSe₃, were intensively studied in the context of CDW and/or superconductivity^3,4,15, tellurides have not received much attention until recently^8–13. One import feature of tellurides is that the atomic number of Te is very large, resulting in a strong spin-orbital (SO) coupling. Nowadays, topological materials with strong SO coupling have been drawing plenty of attention in condensed matter physics¹⁶. It is highly desirable to discover noval superconductors with strong SO coupling for understanding the nature of topological superconductivity. On the other hand, low dimensionality is accompanied by strong lattice instability. Additional interest for pursuing a quasi-1D material with itinerant electrons comes from the possible realization of Luttinger liquid, in which an exotic spin-charge separation is expected¹⁷. Thus, it should be of great interest to study superconductivity in quasi-1D tellurides with large atomic number^14,18, where competing interactions might give rise to interacting ground states.

The magnetoresistance (MR) in ordinary non-magnetic metals is a relatively weak effect and usually at the level of a few percent^19,20. Materials exhibiting large MR are not only utilized to enlarge the sensitivity of read/write heads of magnetic storage devices, e.g., magnetic memory²¹ and hard drives²², but also stimulating many fundamental researches^8,23. Typically, large negative MR occurs in thin-film metals²⁴, manganese based perovskites^25,26 and some disordered systems^27,28, while large positive MR has been observed in semiconductors²⁹ and semimetals^8,30. In general, there exists only a few of CDW materials, which show large positive MR^31–33. The origin of the huge positive MR effect in the CDW state is still under debate. Exploring more CDW materials with large MR may help to clarify the controversial explanations.

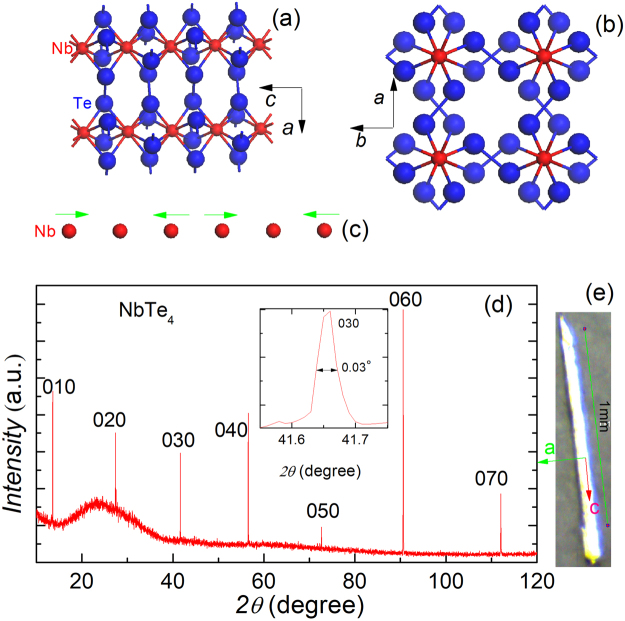
NbTe₄ and TaTe₄ belong to the same group of quasi-1D CDW materials (space group P4/mcc). The structure of NbTe₄ was first determined by Selte and Kjekshus in 1964³⁴. The metal atoms Nb form linear chains along the tetragonal c-axis and the Te atoms form square antiprismatic formulae in which the metal atoms confined (Fig. 1(a,b)). Superlattice reflections indicate that the a-axis is doubled and the c-axis is tripled, leading to an enlarged unit cell 2a* × 2a* × 3c* ^34,35. NbTe₄ undergoes a strong lattice distortion around room temperature to form an incommensurate charge density wave (CDW) phase^35–37. The resulting CDW superstructure in NbTe₄ was visualized by scanning tunneling microscopy (STM)³⁷. Intriguingly, the CDW ordering in NbTe₄ is highly anisotropic due to the quasi-1D chain structure. Strikingly, there exist three CDW orders in NbTe₄, two are incommensurate with wave vectors ${\overrightarrow{q}}_1$ = (0, 0, 0.311c*) and ${\overrightarrow{q}}_2$ = (0.5a*, 0.5b*, 0.344c*), respectively, and the third is commensurate with ${\overrightarrow{q}}_3$ = (0.5a*, 0, $\frac{1}{3}$c*)³⁵. The crystal structure of NbTe₄ is depicted in Fig. 1(a,b). The displacements of Nb ion in a single column for the commensurate phase are shown in Fig. 1c, which can also be found in previous literature³⁸. Indeed, NbTe₄ and TaTe₄ are the only two reported crystals in which three CDWs coexist³⁵. In this paper, we report large magneto-resistance and high pressure induced superconductivity in NbTe₄. The CDW transition temperature is strongly suppressed by applied pressure, and superconductivity fingerprint of steep resistivity drop emerges when pressure exceeds 12.4 GPa. Under pressure p = 69 GPa, zero resistance is reached with a transition temperature T_c = 2.2 K and an upper critical field of 2 T. We also observed large magnetoresistance (MR) up to 102% at low temperatures in NbTe₄, which is rarely observed in conventional CDW systems.

Figure 1.

Structural characterization by x-ray diffractions for NbTe₄. (a,b) The basic crystal structure of NbTe₄ projected along the [010] (a) and [001] (b) directions. (c) The red solid circles represent equidistant Nb ions on the axis of a single column of the basic structure; the arrows show the displacements and resultant trimerizations of the Nb ions in the commensurate phase. (d) XRD structure characterization of a NbTe₄ single crystal. Only (0 l 0) peaks can be observed. The inset: The enlarged XRD curve of (030) peak. (e) A typical crystal of NbTe₄, with crystallographic directions marked.

Results and Discussions

Figure 1d displays the X-ray diffraction pattern of NbTe₄ single crystal. Only multiple reflections of the (0 l 0) planes can be detected, consistent with the quasi-one-dimensional crystal structure depicted in Fig. 1(a,b). The interplane spacing is determined to be 6.499 $\mathrm{\AA }$, agreeing with the previous reported value of the NbTe₄ phase³⁴. For the (030) peak, the full width at half-maximum is only 0.03°, indicating high quality of the crystals.

The temperature dependence of resistivity under various applied magnetic fields (μ₀H up to 15 T) is summarized in Fig. 2a. In zero field, the room temperature resistivity is 59.2 $\mu \mathrm{\Omega }\cdot \mathrm{cm}$ and decreases to 9.4 $\mu \mathrm{\Omega }\cdot \mathrm{cm}$ at T = 2 K, yielding a residual resistivity ratio (RRR) of 6.3. Low RRR in NbTe₄ single crystals has been commonly reported, which is irrespective of growth conditions^39,40. To understand the origin of the poor RRR, we performed the measurements of energy dispersive X-ray spectroscopy (EDXS). The chemical composition determined by EDXS gives the atomic ratio Nb:Te = 0.8:4, with a measurement error of ±3.5% depending on the elements measured. This result indicates that there exists significant deficiency for Nb, which may be responsible for the poor RRR. To get further insight into the resistivity data, we take the partial derivative of resistivity with respect to temperature, as shown in the inset of Fig. 2a. At T^* = 200 K a cusp is observed, consistent with the previous reports^39,40. It is known that the two incommensurate superlattices with ${\overrightarrow{q}}_1$ = (0, 0,0.311c*) and ${\overrightarrow{q}}_2$ = (0.5a*, 0.5b*, 0.344c*) are stable at room temperature in NbTe₄. Below room temperature, additional superlattice ordering with ${\overrightarrow{q}}_3$ = (0.5a*, 0, $\frac{1}{3}$c*) ermerges at about 200 K. The change of the slope in the temperature dependence of resistivity at 200 K should be due to the appearance of the ${\overrightarrow{q}}_3$ superlattice^39,40. Usually, more drastic anomalies in resistivity should be observed at the CDW transition temperatures. For example, two sharp increases in resistivity were observed in NbSe₃ at 145 and 59 K¹⁵, corresponding to about 20% and 48% of conduction electrons condensating into the CDW states, respectively^15,33. The observed small change of resistivity around 200 K in NbTe₄ is indicative of a finite but slight decrease of free carrier density associated with the reconstruction of the Fermi surface by Brillouin zone refolding. The anomaly at around T_L = 50 K may be due to the lock-in transition into the 2a* × 2a* × 3c* superstructure, which is worthy of further clarification⁴⁰. The anomies at T^* = 200 K and T_L = 50 K, which were also observed in previous reports^39,40, further confirm the CDW features observed in NbTe₄.

Figure 2.

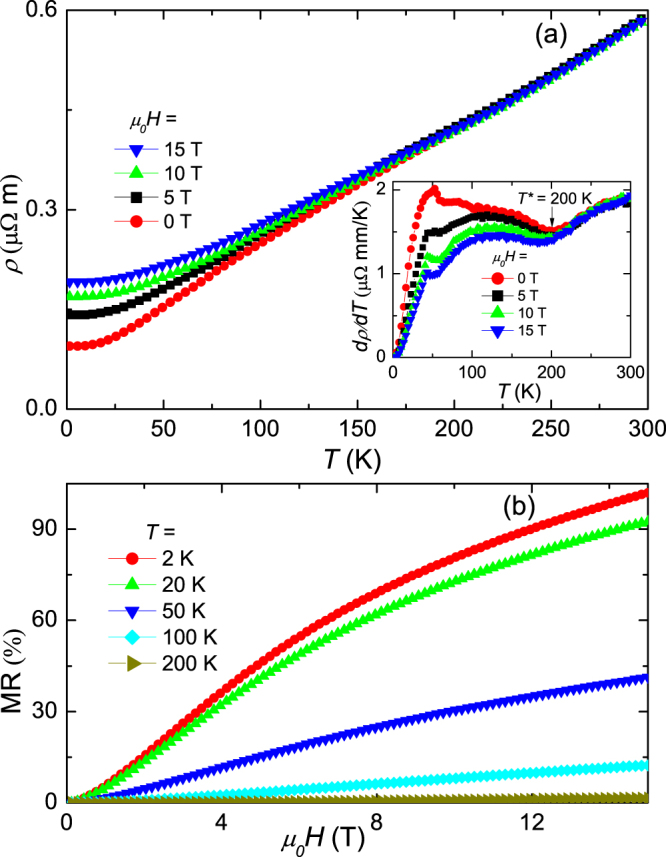
Transport properties of NbTe₄ at ambient pressure. (a) Plots of resistivity against temperature under μ₀H = 0, 5, 10, and 15 T. The current is along the c-axis, and the field is along the b-axis. Inset: Plots of dρ/dT versus temperature. (b) Field dependence of $\mathrm{MR}=[\rho (H)-\rho \mathrm{(0)]/}\rho \mathrm{(0)}$ under various temperatures.

The field (H//b) dependence of resistance (I//c) at various temperatures is shown in Fig. 2b. The magneto-resistance (MR), which is defined as $\mathrm{MR}=[\rho \mathrm{(15}T)-\rho \mathrm{(0)]/}\rho \mathrm{(0)}$, rises up to 102% under a magnetic field of 15 T at T = 2 K. Although the MR value of NbTe₄ is orders of magnitude smaller than that of WTe₂⁸ and Bi³⁰, it is much larger than that of a usual single-band weakly interacting electron system, in which the MR is usually at the level of a few percent^8,20. For a single-band noninteracting electron system, the Hall field exactly balances the Lorentz force, and the electron moves as if in zero field without being deflected; thus, there is no remarkable magnetoresistance^20,41.

Figure 3 displays the field (H//b) dependence of Hall resistivity (I//c) ρ_yx at various temperatures. At 2 K, ρ_yx is positive under low fields but switches to negative sign in higher fields. With increasing temperature, the required field where ρ_yx changes its sign decreases. The curvature and sign reversal in the Hall resistivity indicate the coexistence of hole-type minority carriers with high mobility and electron-type majority carriers with low mobility^42,43. The multiband nature of NbTe₄ is also manifested in the breakdown of the Kohler’s rule, as plotted in the inset of Fig. 3. According to the Kohler’s rule, if only one relaxation time τ exists in metals, then MR can be characterized by a function of ${\mu }_{0}H/\rho \mathrm{(0)}$, and the results for different temperatures should collapse into a single curve^41,44. As shown clearly in the inset of Fig. 3, the Kohler’s rule is violated in NbTe₄, as evident by the non-overlapping of the MR curves at different temperatures. The observeation indicates more than one relaxation time τ exist, supporting the multiband result obtained by the Hall measurements.

Figure 3.

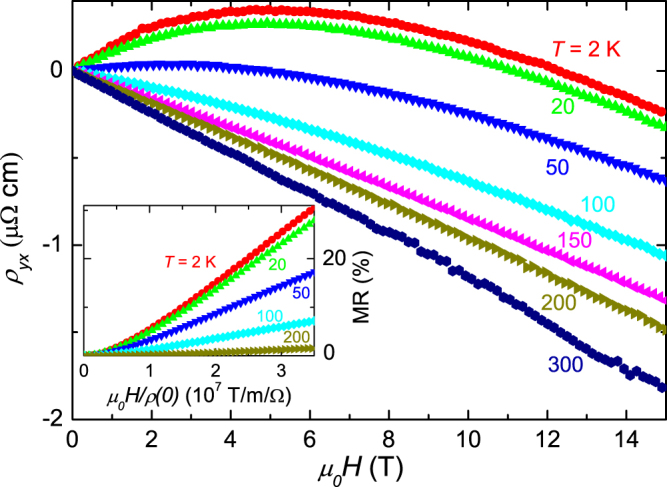
Hall resistivity and Kohler plot for NbTe₄. Field dependence of Hall resistivity (ρ_yx) under various temperatures. The current is along the c-axis, and the field is along the b-axis. The inset: Kohler’s rule by plotting the MR vs. ${\mu }_{0}H/\rho \mathrm{(0)}$ from 2 K to 200 K.

Materials exhibiting a large magneto-resistance have potential device applications and thus have been attracting researchers’ interest⁴⁵. The most well-known examples are the giant magnetoresistance in magnetic multilayers²⁴ and colossal magnetoresistance in manganites²⁶, both of them rely on the coupling between spin configuration and charge transport. However, even among nonmagnetic materials, extremely large magnetoresistance (MR) may arise in semimetals with electron-hole Fermi surface (FS) compensation^46–49.

As a discussion of the multiband effects in NbTe₄, we define the direction of the current (Hall voltage) as the x-axis (y-axis). Even though no net current should exist in the y-direction, the currents in the y-direction by one particular type of carriers may be non-zero in a multiband system. When we applied magnetic field, the y-direction currents should be affected by the Lorentz force which is antiparallel to the x-direction⁵⁰. The back flow of carriers provides a substantial source of the large magnetoresistance in metals with multiple bands like MgB₂⁴¹ and semimetals like Bi⁴⁸ and WTe₂⁸. Owing to the coexistence of both electron- and hole-type carriers, the large MR in NbTe₄ may be attributed to multiband effects. We employed a two band mode to fit the ρ_xx and ρ_yx data simultaneously in the low field region (See supplementary material for a simultaneous fitting of ρ_xx and ρ_xx data by the two band semiclassical model). The values of n_e and n_h are close to each other at all the measured temperatures, which suggests that the large MR should result from the electron-hole compensation effect. The mobilities μ_e and μ_h increase with decreasing temperatures as the usual metals. Meanwhile, the carrier concentrations decrease significantly at low temperatures, which occurs commonly in a CDW system. At T = 2 K, μ_e is 0.22 m²V⁻¹s⁻¹, while μ_h is 0.29 m²V⁻¹s⁻¹. Actually large magnetoresistance was also observed in the CDW materials NbSe₃^31,33 and AMo₆O₁₇ (A = Na, K, and Tl)³². It has been proposed that the large MR in these CDW systems may result from the magnetic-field-induced enhancement of the CDW gap³¹, but a study by Tritt et al.⁵¹ presented negative results on such a claim. Until now, the nature of the huge positive MR effect in the CDW state is still ambiguous. Actually, only a few CDW materials show large positive MR^31–33. The origin of the large MR in NbTe₄ deserves further investigation.

Superconductivity often occurs in the proximity of other competing ordered states. Both high-T_c cuprates and Fe-based superconductors are close to antiferromagnetic (AFM) ordered states^52,53. The AFM order in Fe-based superconductor is of a spin density wave (SDW)-type. For CDW materials, high pressure or chemical doping can continuously suppress the CDW order, and then superconducting transition temperature is enhanced or superconducting state emerges after the suppression of CDW state^54,55. The weakening of competing orders normally favors superconductivity⁵⁶. The CDW order of NbTe₄ survives up to very high temperatures. Thus it is interesting to investigate whether superconductivity can be induced by pressure.

Figure 4a shows the evolution of resistance (I//c) as a function of temperature of the NbTe₄ single crystal at various pressures from 5 GPa to 69 GPa. The samples used in high pressure and ambient pressure measurements are two different ones, but they are from the same batch. Under an applied pressure of p = 5 GPa, the cusp associated with the appearance of the ${\overrightarrow{q}}_3$-superlattice CDW transition is suppressed to T^* = 173 K, as shown in Fig. 4b. The MR decreases to less than 10% with an applied pressure of 5 GPa, and becomes smaller and smaller with an increasing pressure, as shown in Fig. 4c. When the pressure increases up to 12.4 GPa, the cusp associated with the CDW transition is suppressed and becomes too weak to be distinguished in the resistivity curve, instead, a sudden resistivity decrease presents at T~2.4 K, which could be a fingerprint of superconductivity. So we keep increasing the pressure to trace the superconducting transition. Upon further increasing pressure, at T = 1.7 K, which is the base temperature of our high pressure measurement system, the resistance drops to very small. Finally, under p = 69 GPa, which is the highest pressure we can apply, zero resistance has been detected. The low-T resistance appears to increase monotonically with pressure. In contrast, the room-temperature resistance keeps increasing up to 12.4 GPa, and then steadily decreases, which coincides with the disappearance of the CDW phase. Whether the variation in room-temperature resistance is correlated with the CDW order deserves further clarification. T_c around 2.2 K is stabilized for the pressure range from 10 to 69 GPa. Such a wide stabilization pressure range could be a result of heavy doping due to Nb deficiency up to 0.2. Figure 4d shows the suppression of superconductivity under magnetic fields (H//b). The inset gives the temperature dependence of the upper critical field ${\mu }_0{H}_{c2}(T)$, determined by using 90% normal state resistivity criterion. The temperature dependence of ${\mu }_0{H}_{c2}(T)$ is nearly linear in the investigated temperature range. According to the Ginzburg-Landau theory, the upper critical field H_c2 evolves with temperature following the formula $H_{c2}(T)=H_{c2}\mathrm{(0)}\left(1-t^2\right)/(1+t^2)$, where t is the renormalized temperature T/T_c. It is found that the experimental upper critical field ${\mu }_0{H}_{c2}(T)$ can be well fitted by this model and its zero-temperature limit is extracted to be 2.0 T. Due to the limited temperature range, the estimated ${\mu }_0{H}_{c2}\mathrm{(0)}$ by this way may be of considerable error.

Figure 4.

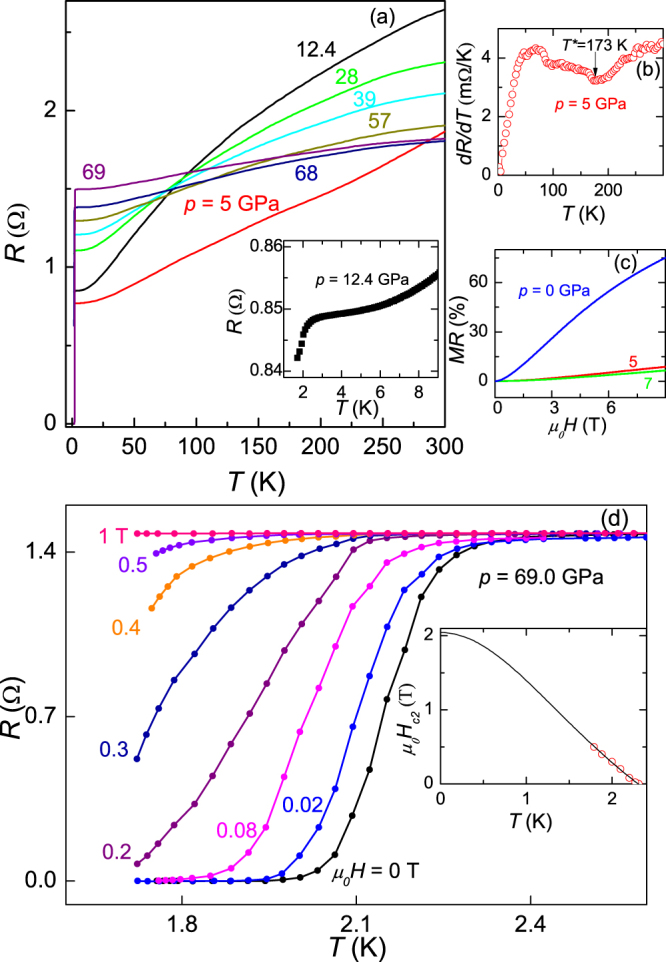
Transport properties for single crystal NbTe₄ under pressure. (a) The plot of resistance versus temperature for the pressure ranging from 5 GPa to 69 GPa. The current is along the c-axis. The inset: The enlarged plot of resistance at low temperatures under p = 12.4 GPa. (b) Plots of d R/d T versus temperature under p = 5 GPa. (c) Field dependence of MR under p = 0, 5 and 7 GPa. (d) Temperature dependence of resistance for several different magnetic fields under p = 69 GPa. The inset displays the upper critical fields as a function of temperatures.

The temperature-pressure phase diagram is summarized in Fig. 5. The CDW transition temperature in NbTe₄ is strongly suppressed with an applied high pressure. Accompanying the suppression of the CDW order, superconductivity fingerprint appears. Such superconducting phase diagrams, where superconductivity may compete with different kind of orders, have been observed in many systems, including high-T_c cuprates, Fe-based superconductors, NbSe₂ and Cu_xTiSe₂^52–55. Barath et al. proposed that the superconducting paring mechanism in Cu_xTiSe₂ could be associated with the quantum criticality, stemming from the fluctuations of CDW order⁵⁷. There are also many theoretical works on the superconducting dome in transition metal dichalcogenides (TMDCs), and pursuing the nature of the observed superconducting states is still on-going^58,59. High temperature high pressure treatment could induce phase transformation in NbTe₄⁶⁰, which may be relevant to the occurrence of superconductivity. Further investigation on this issue is of potential interest. Since the physical properties of NbTe₄ and TaTe₄ show numerous similar features, the further research on pressure effect of TaTe₄ should be gainful⁶¹. As a low dimensional chalcogenide, it could be fascinating to explore whether intercalation or doping could induce superconductivity, or at least decrease the critical superconducting pressure, as the case in Cu_xTiSe₂⁵⁷, Cu_xBi₂Se₃⁶², Ir_1−x Pd_xTe₂¹⁶, (NbSe₄)_3.33I⁶³. Primarily because of the strong SO coupling, the appealing Majorana surface state has been suggested to exist in Cu_xBi₂Se₃ superconductor^62,64. Due to the large atom number in NbTe₄, it is expected to own strong SO coupling. Furthermore, a recent theoretical work has proposed monolayer hole-doped TMDCs as candidates for topological superconductors⁶⁵, which makes transition metal chalcogenide systems more fascinating. Thus it becomes quite interesting to explore the possible presence of nonconventional quantum states in NbTe₄. Our work may provide another promising system for exploring novel topological superconductors.

Figure 5.

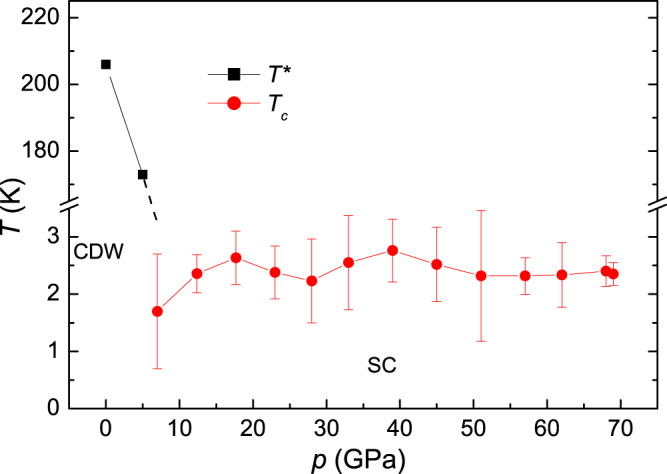
Temperature versus pressure phase diagram of NbTe₄. T^* and T_c denote the resistivity anomaly temperature and the superconducting transition temperature, respectively.

Summary

In conclusion, we discovered unusually large magnetoresistance(MR) and pressure induced superconductivity with a maximum T_c of 2.2 K in a quasi-one-dimensional (1D) transition-metal chalcogenide NbTe₄ with strong spin-orbit coupling. Superconductivity appears when the CDW order is suppressed by high pressure. Although T_c is relatively low, the large MR and strong SO coupling make NbTe₄ a promising candidate for the exploration of novel superconductors.

Methods

Sample synthesis and characterization

The NbTe₄ crystals were grown by a self-flux method. Powders of the elements Nb (99.97%) and Te (99.99%), all from Alfa Aesar, in an atomic ratio of Nb:Te = 1:8 were thoroughly mixed together, loaded, and sealed into an evacuated quartz ampule. The ampule was slowly heated up to 1273 K and held for 25 h. After that, it was slowly cooled to 873 K at a rate of 3 K/h, followed by furnace cooling down to room temperature. Shiny, gray-black soft crystals in flattened needle shapes were harvested with a typical dimension of 1.2 × 0.02 × 0.02 mm³, as shown in Fig. 1(e). Single crystal X-ray diffraction (XRD) was performed at room temperature using a PANalytical X-ray diffractometer (Model EMPYREAN) with a monochromatic CuK_α1 radiation. Energy-dispersive x-ray spectroscopy (EDXS) was collected by an Octane Plus Detector (AMETEX EDAX), equipped in a field-emitting scanning electron microscope (SEM, Hitachi S-4800).

Measurements

The resistance data was collected using standard four-probe method in a screw-pressure-type diamond anvil cell (DAC), which is made of non-magnetic Cu-Be alloy. The diamond culet was about 300 μm in diameter. A T301 stainless steel gasket was pre-indented from a thickness of 250 μm to 35 μm, leaving a pit inside the gasket. A hole with diameter of 300 μm was drilled in the center of the pit by laser ablation. The pit of the indented gasket was then covered with a mixture of epoxy and fine cubic boron nitride (c-BN) powder and compressed tightly to insulate the electrode leads from the metallic gasket. Next, the c-BN-covered pit served as the sample chamber, where a NbTe₄ single crystal in dimension of 200 μm × 35 μm × 5 μm was inserted without the pressure-transmitting medium, together with a ruby ball served as a pressure marker at the top of the sample. The value of the pressure was determined by the ruby fluorescence method. Platinum (Pt) foil with a thickness of 5 μm was used as electrodes. The gasket surface outside the pit was insulated from the electrode leads by a layer of Scotch tape. The DAC was put inside a home-made multifunctional measurement system (1.8–300 K, JANIS Research Company Inc.; 0–9 T, Cryomagnetics Inc.) with helium (He) as the medium for heat conduction to obtain high efficiency of heat transfer and good precision of temperature control. Two Cernox resistors (CX-1050-CU-HT-1.4 L) located near the DAC were employed to ensure the accuracy of temperature in the presence of magnetic field. The ambient-pressure electrical transport measurements were carried out in a Oxford cryostat system with magnetic field up to 15 T and temperature down to 1.5 K. Ohmic contacts were made with gold wires and silver paste.

Author Contributions

Zhu-an Xu and Xiaojun Yang designed the research. Zhu-an Xu administered the experiment. Xiaojun Yang synthesized the samples. Xiaojun Yang and Yonghui Zhou performed the measurements. Mengmeng Wang, Hua Bai, Xuliang Chen, Chao An, Ying Zhou, Qian Chen, Yupeng Li, Zhen Wang, Jian Chen, Chao Cao, Yuke Li, Yi Zhou and Zhaorong Yang presented helpful suggestions in the measurements and in the data analysis. Zhu-an Xu, Xiaojun Yang and Zhaorong Yang analyzed the data, interpreted the results, and wrote the paper.

Competing Interests

The authors declare no competing interests.