Mapping Population-based Structural Connectomes

Abstract

Advances in understanding the structural connectomes of human brain require improved approaches for the construction, comparison and integration of high-dimensional whole-brain tractography data from a large number of individuals. This article develops a population-based structural connectome (PSC) mapping framework to address these challenges. PSC simultaneously characterizes a large number of white matter bundles within and across different subjects by registering different subjects’ brains based on coarse cortical parcellations, compressing the bundles of each connection, and extracting novel connection weights. A robust tractography algorithm and and streamline post-processing techniques, including dilation of gray matter regions, streamline cutting, and outlier streamline removal are applied to improve the robustness of the extracted structural connectomes. The developed PSC framework can be used to reproducibly extract binary networks, weighted networks and streamline-based brain connectomes. We apply the PSC to Human Connectome Project data to illustrate its application in characterizing normal variations and heritability of structural connectomes in healthy subjects.

1. Introduction

With recent advances in imaging technologies, large biomedical studies, such as the UK Biobank (Miller et al., 2016) and Human Connectome Project (HCP) (Sotiropoulos et al., 2013; Van Essen et al., 2013), have collected multimodal imaging data (e.g., structural magnetic resonance imaging (sMRI) and diffusion MRI (dMRI)), and other associated data, such as clinical and genetic information. Mapping the brain’s structural connectome on the system level is critically important for understanding brain physiology, pathology and structural connectivity in both clinical and research-oriented applications. The structural connectome consists of grouped white matter (WM) trajectories that connect different brain regions, representing a comprehensive diagram of neural connections. To date, dMRI is the only noninvasive technique useful for estimating WM trajectories and water diffusivity along these trajectories in vivo. It has been widely used to quantify WM integrity and WM abnormalities associated with brain disorders.

At the population level, to quantify variations in the diffusion connectomes and local WM changes of healthy and diseased brains, there are roughly three broad analytical methods, including (i) standard region-based analysis (Lee et al., 2009; Alexander et al., 2007), (ii) voxel-based analysis (Smith et al., 2006; Schwarz et al., 2014; Snook et al., 2007), and (iii) tract-specific analysis (Fornito et al., 2013; Zhu et al., 2011; Yeatman et al., 2012; Cousineau et al., 2017; Jin et al., 2014; Heiervang et al., 2006; Ciccarelli et al., 2003; Wang et al., 2016a; Wassermann et al., 2010; Garyfallidis et al., 2017; Olivetti et al., 2017; Sharmin et al., 2016). The region-based method often parcellates the brain into regions of interest (ROIs) that have anatomical meaning and studies the statistical properties of each region (Lee et al., 2009; Alexander et al., 2007). Although it is convenient to focus on specific regions, it suffers from the difficulty in identifying meaningful regions in WM, particularly among the long curved structures common in fiber tracts. The voxel-based analysis spatially normalizes brain images across subjects and performs statistical analysis at each voxel. One of the most popular voxel-based methods is the Tract-Based Spatial Statistics (TBSS) (Smith et al., 2006), which is based on the projection of fractional anisotropy (FA) maps of individual subjects onto a common mean FA tract skeleton. The voxel-based methods are limited due to their reliance on existing registration methods that lack the ability to explicitly model the underlying architecture of WM fibers, including the neural systems and circuits affected, in the registration process (Zalesky et al., 2010; Yeatman et al., 2012).

Compared to the region- and voxel-based methods, tract-specific analysis provides several desirable outputs. It can visualize specific WM bundles, quantitatively analyze the geometry of WM bundles, and analyze the diffusion properties along WM bundles. One of the most challenging tasks in this approach is to efficiently use the whole-brain tractography data to construct reproducible population-based structural connectome maps, while effectively accounting for variation across subjects within and between populations. The tract-specific approaches can be naturally grouped into two categories: fiber clustering-based (O’Donnell et al., 2013; Guevara et al., 2017; Jin et al., 2014; Guevara et al., 2011; Garyfallidis et al., 2017) WM analysis and parcellation-based connectome analysis (O’Donnell et al., 2013; de Reus and van den Heuvel, 2013; Zalesky et al., 2010). Although both method types perform segmentation of the WM bundles, they have different goals.

The advantage of methods based on fiber clustering is that they can use the shape, size and location of streamlines (also referred to as fiber curves or fiber tracts) to identify anatomically defined WM tracts, and study the WM integrity along these tracts (Jin et al., 2011, 2014; Kochunov et al., 2015; O’Donnell et al., 2013). However, such methods heavily depend on the choice of clustering method and that of the similarity metric for comparing streamlines (Zhang et al., 2014). Also, they usually consider only part of the whole-brain fiber curves and may result in the loss of valuable information. In contrast, parcellation-based methods (O’Donnell et al., 2013; de Reus and van den Heuvel, 2013) can utilize the whole-brain fiber curves and produce an adjacency V × V matrix A_i, where V is the number of ROIs and can vary from tens to hundreds according to the cortical parcellation methods used in (Desikan et al., 2006; Destrieux et al., 2010; Glasser et al., 2016; Cammoun et al., 2012). The (u, υ)–th element of A_i represents a measure of the strength of connection between regions u and υ (de Reus and van den Heuvel, 2013; Fornito et al., 2013; Durante et al., 2017; Durante and Dunson, 2016; Cheng et al., 2012a; Zalesky et al., 2010). For a specific pair of ROIs, the most popular connectivity strength is an indicator (range of 0–1) of whether there is any streamline connecting them so that standard graph analysis may be applied. However, the use of such a binary connectivity matrix leads to an enormous loss of information such that all geometric and diffusivity information along the WM bundles is discarded.

In this paper, we develop a hybrid method (O’Donnell et al., 2013; Guevara et al., 2017) that can utilize the geometric information of streamlines, including shape, size and location, for a better parcellation-based connectome analysis. This approach allows us to increase the robustness of extracted WM bundles between two ROIs and extract discriminative and reproducible geometric features for network-based connectome analysis. Such robustness and reproducibility are critical for down-stream statistical analyses. Furthermore, we use a newly defined reproducibility measure and a test-retest dataset to optimize various tuning parameters in the construction of the structural connectome. This optimization procedure and the proposed global reproducibility measure distinguish this work from the existing reproducibility studies (Bastiani et al., 2012; Cheng et al., 2012b; Buchanan et al., 2014; Cousineau et al., 2017).

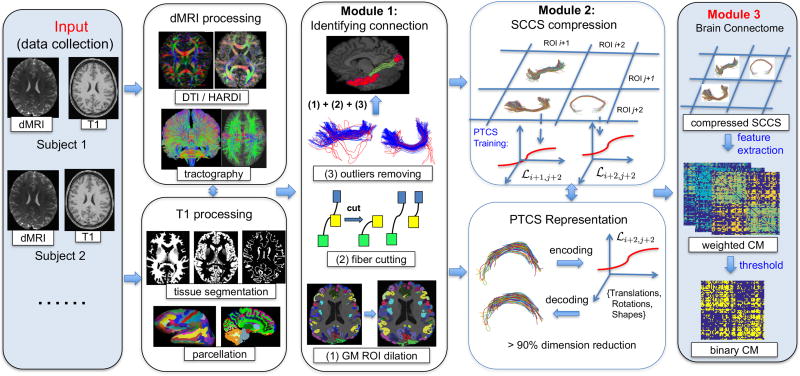
The comprehensive framework developed in this paper is termed population-based structural connectome (PSC) mapping, which is designed to reproducibly construct structural connectomes across subjects within and between populations. Figure 1 demonstrates a schematic overview of the PSC framework. Five major methodological contributions of this paper relative to the current approaches for analyzing tractograms are summarized as follows

• Most current techniques transform the full brain tractogram into a simplified adjacency matrix for groupwise network analysis. In contrast, the proposed PSC pipeline preserves the geometric information, which is crucial for quantifying brain connectivity and understanding its variation across subjects. The PSC constructs a structural connectome across three different levels, from simple to complex, including the binary network, the weighted networks and the streamline-based connectome. Such a multi-level representation allows to perform brain network analysis at different levels of detail, inspect the brain connectome from different perspectives, and validate the findings in the space of WM bundles..

• One of our objectives is to increase the robustness and reproducibility of the of the reconstructed structural connectome. A test-retest dataset is used to select the tuning parameters in the PSC to optimize its reproducibility and preserve useful information in the connectome maps.

• We use a nonlinear spatial normalization method to decompose the variation of WM tracts into different components. More specifically, the shape component is separated from its confounding variables for the analysis of the shapes of tracts. Such a decomposition minimizes the variability across individual streamlines, while allowing us to efficiently compress streamlines in each connection.

• We use the PSC framework to perform comprehensive analyses of 856 subjects with high-resolution dMRI and T1 images in the HCP dataset. In contrast, as reviewed in Table 1 of Guevara et al. (2017), most existing methods were applied to whole-brain tractography datasets of fewer than 200 subjects.

• The open-source software and documentation for the PSC framework will be freely available online at http://www.nitrc.org/ and https://github.com/BIG-S2.

Figure 1.

A systematic overview of the population-based structural connectome mapping framework. GM: gray matter, CM: connectivity matrix, ROI: region of interest, SCCS: streamline connectivity cell structure, PTCS: parcellation-based tractography common space, and PSC: population-based structural connectome.

Table 1.

ICC score of selected topological features on the test-retest dataset.

Scale	Density	Characteristic Path Length	Local Efficiency	Clustering Coefficient
V = 68, θr = 10	0.925	0.745	0.789	0.800
V = 68, θr = 20	0.890	0.814	0.802	0.791
V = 68, θr = 50	0.877	0.679	0.791	0.793
V = 148, θr = 10	0.933	0.911	0.887	0.803
V = 148, θr = 20	0.908	0.874	0.908	0.767
V = 148, θr = 50	0.893	0.759	0.861	0.824

2. Materials and Methods

2.1. Overview

Let us focus on dMRI and sMRI data acquired for Q subjects. For each subject, we can use one of the state-of-the-art tractography algorithms (Girard et al., 2014; Smith et al., 2013) to reconstruct a tractography dataset F_i for i = 1, …, Q. Each F_i = {f_i,1, …, f_i,Ni} consists of N_i three-dimensional (3D) streamlines, where each f_i,j is represented by an ordered sequence of 3D points {p_i,j,k = (x_i,j,k, y_i,j,k, z_i,j,k)^T ∈ ℝ³ : k = 1, …, m_i,j} for j = 1, …, N_i. In most cases, to fully characterize the structural connectivity pattern of an individual human brain, N_i is larger than one million and m_i,j can be hundreds. Mathematically, each streamline also can be represented as a parameterized curve in ℝ³ through spline fitting or simply connecting the sequence of points using piecewise linear functions. Let us denote this parameterized curve as f_i,j : [0, 1] → ℝ³, where each f_i,j(s) represents a point f_i,j(s) = (x_i,j(s), y_i,j(s), z_i,j(s))^T ∈ ℝ³ for s ∈ [0, 1].

The proposed PSC framework has three major components, as illustrated in the three rightmost columns in Figure 1. These are (i) reliable construction of the structural connectome for the whole brain; (ii) low-dimensional representation of streamlines in each connection; and (iii) multi-level connectome analysis. In Sections 2.2–2.4, we introduce each of these modules in detail. Section 2.5 introduces the quantitative evaluation of reproducibility. Section 2.6 describes two real datasets, a test-retest dataset and the HCP dataset.

2.2. Reliable Construction of the Structural Connectome

HARDI tractography with anatomical priors

One of the key steps of the PSC framework is to reliably reconstruct the whole-brain structural connectome through state-of-the-art tractography algorithms. A reliable reconstruction of the structural connectome is challenging because of the various positions, shapes, sizes, and lengths of the WM bundles (Fornito et al., 2013; Girard et al., 2014; Yeh et al., 2013; Basser et al., 2000; Smith et al., 2012, 2013). For instance, homogeneously initiating streamlines in the WM induces over-reconstruction for long streamlines, yet this is the most commonly used seeding strategy. It is crucial to carefully design the seeding procedure, stopping and masking criteria, and optimal parameters for tractography to reduce bias in the reconstruction of streamlines.

In this paper, we use the tractography algorithm presented by Girard et al. (2014). This method has reduced bias in streamline reconstruction because it borrows anatomical information from high-resolution T1-weighted image. The T1-weighted image is first softly segmented into different parts based on the tissue type, e.g., WM, gray matter (GM), and cerebrospinal fluid. This segmentation assigns a probability for each voxel being a certain type of tissue and thus provides a soft criterion for guiding the growth and termination of streamlines. For instance, WM bundles are expected to stop in the GM region and should not reach the cerebrospinal fluid. Moreover, streamlines are initialized from the interface between GM and WM to compensate for the streamline density bias that may be caused by the length of fiber bundles. Starting from these regions, in-house implementation of a state-of-the-art probabilistic algorithm based on the fiber orientation distribution function (Descoteaux et al., 2009; Tournier et al., 2012) is used to propagate the streamlines. Also, a technique called particle filtering tractography is adapted (Girard et al., 2014) to reduce the number of streamlines that prematurely stop in the WM or cerebrospinal fluid. This technique stops most of the streamlines in the GM and at the GM-WM interface which, in turn, significantly improves the percentage of valid streamlines in the reconstruction. The parameters in our tractography algorithm, such as the maximum deviation angle, fiber orientation distribution function (ODF) threshold, and parameters for particle filtering, are carefully selected based on the evaluation of the global connectivity metrics in the Tractometer (Girard et al., 2014; Côté et al., 2013).

In our analysis of real data, on average, 1.15 × 10⁵(±12, 219) voxels were identified as the seeding region (about 14 ~ 15% of the total brain volume) for each individual in the HCP dataset (with isotropic voxel size of 1.25 mm). The final tractography dataset for each subject contains approximately 1 million streamlines, and each streamline has a step size of 0.2 mm.

Coarse brain parcellation and connectome extraction

We use an atlas with known parcellation to define the nodes of the structural connectivity network. Here, we consider two popular parcellation atlases, the Desikan-Killiany (Desikan et al., 2006) and Destrieux (Destrieux et al., 2010) atlases, at two resolutions. The Desikan-Killiany parcellation has 68 cortical surface regions with 34 nodes in each hemisphere, whereas Destrieux has 148 cortical regions with 74 nodes in each hemisphere. In addition, we include 17 subcortical regions, such as the hippocampus, caudate, putamen, pallidum, amygdala, nucleus accumbens, and brainstem, among others. Freesurfer (Fischl, 2012) is used to perform the brain parcellation.

Given the parcellation of an individual brain, the streamline data are then grouped according to the regions that they connect. We process the T1-weighted image, the dMRI image and the tractography dataset using the following three steps to extract streamlines connecting any pair of regions: (i) Co-register the T1-weighted image to the b₀ and FA images extracted from dMRI within each subject: A linear registration obtained using FLIRT (Jenkinson et al., 2002) is first applied and a non-linear registration using advanced normalization tools (ANTs) (Avants et al., 2011) is used to refine the registration. (ii) Warp Desikan-Killiany (or Destrieux) parcellation to an individual T1-weighted image using Freesurfer. (iii) Group each tractography dataset F_i into different bundles depending on the regions that each streamline connects.

Step iii is not as frequently used in the current literature as are steps i and ii. Most existing approaches use the endpoints of a streamline to identify the regions that it connects (Hagmann et al., 2008; Zalesky et al., 2010). However, the tractography algorithm may prematurely stop streamlines in WM (Girard et al., 2014). Moreover, streamlines can pass through multiple ROIs, especially for the subcortical regions. These issues can result in incomplete and false connections, leading to bias in the subsequent analysis. To overcome these issues, we develop three procedures in the PSC framework, cortex surface dilation, streamline cutting, and outlier streamline removing. The third column in Figure 1 illustrates these procedures.

2.2.1. Cortical surface dilation

We dilate each GM cortical region into WM in ψ voxels, where ψ is the parameter for controlling the amount of dilation. The tractography algorithm can prematurely stop the streamlines in the WM regions or at the GM-WM interface. However, the cortical ROIs extracted by Freesurfer only include the GM ROIs. Dilation of the cortical ROIs to include the GM-WM interface enables us to extract a complete set of WM pathways for each connection.

Similar dilation procedures have been used in the literature (Reveley et al., 2015; Donahue et al., 2016; Shadi et al., 2016b; Finger et al., 2012). As pointed out by Thomas et al. (2014), even though it may decrease the specificity (e.g., ability to avoid false connections), including some WM regions in the GM ROIs can increase the sensitivity (e.g., ability to detect true connections). Donahue et al. (2016) used the nearby WM voxels to decide whether two GM ROIs are connected, which improved the results by two times with respect to the study of van den Heuvel et al. (2015). These findings and the apparent limitations of the current tractography algorithm encourage us to explore the effect of dilation on the reproducibility and robustness of the extracted connectomes. The detailed algorithm for the dilation procedure is presented in the Supplementary Material, Section 1. Supplementary Figure 1 illustrates the effect of the dilation for an image with 1 mm isotropic resolution.

2.2.2. Streamline cutting

A key idea behind streamline cutting is to account for the possible passage of streamlines through multiple ROIs. Most tractography algorithms stop the propagation of streamlines based on certain pre-set stopping criteria; otherwise, the streamline will grow continuously. It is common to have streamlines connecting multiple ROIs, especially subcortical ROIs. To extract a connection for any pair of ROIs on the path of a tract, we cut the tract into $\left(\begin{array}{c}\hfill n\hfill \\ \hfill 2\hfill \end{array}\right)$ line segments if it passes n (n > 2) ROIs. A similar cutting operation has been proposed by Ziyan et al. (2009) in order to remove the erroneous part of the tract that deviates from a major fiber bundle.

Using the tractography algorithm by (Girard et al., 2014), it is very rare for the middle ROI(s) to be a cortical ROI because when a streamline reaches the cortical region, it triggers one of the stopping criteria with high probability. Thus, for streamlines that pass through multiple ROIs, most of the middle ROIs are subcortical regions. Therefore, this cutting procedure has a greater effect on subcortical-cortical connections than on cortical-cortical connections. It allows us to extract the parts of streamlines that connect two given regions, regardless of whether these streamlines start, end or pass through those two regions.

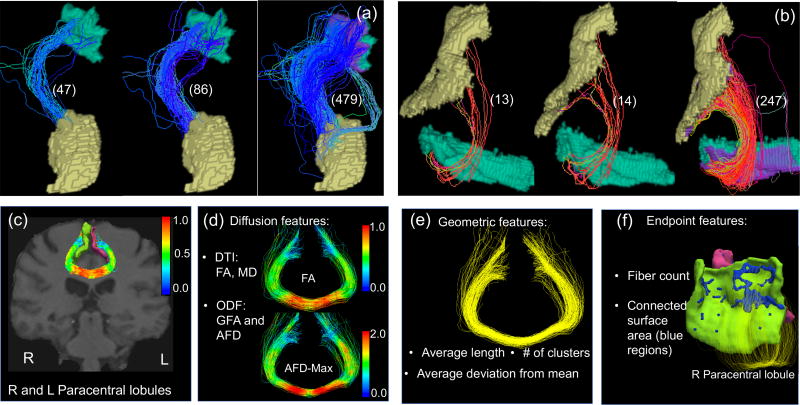
The combination of dilation and streamline cutting enables us to faithfully extract more complete and reliable WM pathways between two ROIs. Panel (a) and (b) of Figure 2 compare the streamlines before and after applying streamline cutting and dilation for two selected pairs of ROIs. For the two examples in Figure 2, we identified about 10 times more streamlines after applying dilation and streamline cutting. Similar phenomena were observed for most pairs of ROIs, indicating that the procedures developed in the PSC framework can extract rich fiber bundles.

Figure 2.

The top row shows the effect of using streamline cutting and dilation. In panels (a) and (b), we show the identified streamlines between two ROIs without streamline cutting and dilation, with only streamline cutting and with both streamline cutting and dilation, respectively, from left to right. The numbers the parentheses represent the number of fiber tracts. The dilated regions are marked in purple in each ROI. The bottom row shows the extracted features in PSC that describe the WM connectivity pattern between any ROI pair: panel (c) is an example of streamlines connecting the right and left paracentral lobules; panels (d)–(f) show different features extracted from the connection.

2.2.3. Removing outlier streamlines

In this step, our goal is to identify streamlines that do not follow major WM pathways as outliers in each connection. Almost all tractography algorithms (Girard et al., 2014) can produce false fiber tracts for various reasons, such as the accumulation of errors for streamline propagation, low resolution of dMRI, or the stopping criteria of streamline propagation. Removing these outliers can improve either the estimation of fiber bundles or the connection between two ROIs (Côté et al., 2015; Khatami et al., 2017). In Figure 1, item (3) in module 1 illustrates some apparent outlying streamlines in red for two randomly selected connections.

We choose a scalable outlier detection method based on the QuickBundle method (Garyfallidis et al., 2012) to rapidly remove outliers (Côté et al., 2015). The key idea of QuickBundle is to use the minimum average direct-flip (MDF) distance to classify streamlines based on a pre-set distance threshold θ_t. In PSC, streamlines in each connection have the same orientation, i.e., they all start from one region and end at the same other region. Utilizing this property, we replace the MDF distance by the simple 𝕃² distance, $d(f_1,f_2)=\Vert f_1-f_2\Vert =\sqrt{\int {(f_1(s)-f_2(s))}^2\mathit{\text{ds}}}$, for two streamlines f₁ and f₂ in a specific connection. Letting m be the number of sample points on each streamline, the computational complexity of computing such 𝕃² distance is O(m), making the outlier removal step computationally efficient. Given a fixed θ_t, a streamline is assigned to a cluster if its 𝕃² distance to the cluster center is smaller than θ_t. The outliers then are the singleton clusters with very few streamlines inside.

2.3. Efficient Representation and Analysis of Streamlines

After the preprocessing steps in Section 2.2, for a pair of ROIs, we obtain the streamlines that connect them. This streamline-based connectivity structure is illustrated in Figure 1, module 2. We refer to this special connectivity structure as the streamline connectivity cell structure (SCCS), where each cell contains streamlines that connect the corresponding ROIs. In most parcellation-based connectivity analysis pipelines, the streamlines are discarded because of the data size, since each SCCS may contain thousands of streamlines. However, the SCCS contains rich geometric information and enables tract-based analysis (O’Donnell et al., 2009; Prasad et al., 2014; Wang et al., 2016a; Wassermann et al., 2010), which is more discriminative than some summary statistics (Colby et al., 2012).

In this section, our goal is to develop an efficient representation system to enable us to compress and compare the SCCSs extracted from a large-scale neuroimaging dataset. To achieve this goal, this part of PSC includes two components: (i) a shape analysis framework to separate the variation of streamlines in each cell of the SCCS, and (ii) an encoding and decoding procedure to efficiently compress the SCCS.

2.3.1. Streamline variation decomposition

In each cell of the SCCS (e.g., first row of Figure 2), streamlines have very similar shape and are smooth. The shape here refers as the streamline after removing some shape confounding variables, e.g., translations, rotations, scaling and re-parameterization (Srivastava et al., 2011). Our idea for compression is to use a shape analysis framework (Srivastava et al., 2011; Corouge et al., 2004) to decompose all streamlines into different components and then represent the aligned shape component using a low-dimensional structure. All other components, such as rotation and translation, can be preserved by using a few parameters. Finally, the original streamlines can be recovered by recombining these components.

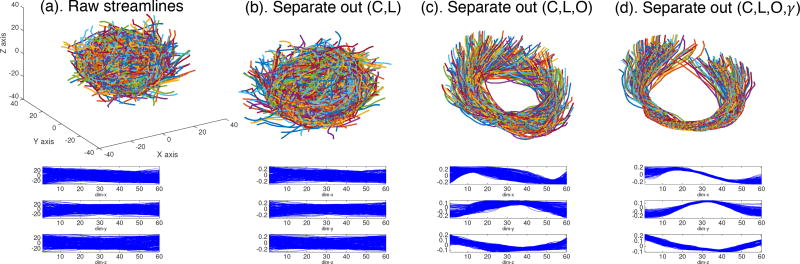
Let Ω_(a,b) be the functional space of all WM bundles that connect ROIs a and b, and a smooth streamline f ∈ Ω_(a,b) is a function f : [0, 1] → ℝ³. According to Srivastava et al. (2011), we can decompose the variation of streamlines in Ω_(a,b) into translations, rotations, scalings, re-parameterizations, and shapes. This decomposition is quite flexible. For instance, we can merge some shape-confounding components into the shape component to simplify the decomposition. In Figure 3, we illustrate the remaining shape part of the simulated streamlines after separating different shape confounding components. As more shape-confounding components are separated and removed, the remaining shapes are more consistent across different streamlines.

Figure 3.

The remaining shape component after separating different shape-preserving transformations in a simulated example. The first row shows the 3D curves; the second row shows the x, y, z coordinates. C: translation, L: scaling, O: rotation, and γ: re-parameterization.

We adapt an elastic shape analysis framework (Srivastava et al., 2011) to separate the translations, rotations, scalings and re-parameterizations from the shapes. It is assumed that we have a template streamline μ_(a,b) (such template can be learned from the data) for each connection (a, b) in one SCCS. The template μ_(a,b) is usually a centered 3D curve with a unit length, representing the shared geometric structure of streamlines in this connection. We can align streamlines {f₁(·), …, f_n(a,b) (·)} ∈ Ω_(a,b) to this template to perform the decomposition. It is easy to separate the translation and scaling (Srivastava et al., 2011; Corouge et al., 2004), respectively denoted as C and L, by centering and normalizing each streamline. Without specifically stating otherwise, hereafter, we consider all streamlines to have been centered and normalized.

To separate rotation and re-parameterization, we represent each streamline as its square root velocity function (SRVF) $q(s)=\dot{f}(s)/\sqrt{|\dot{f}(s)|}$. A rotation of f by O ∈ SO(3) is denoted as O * f and its SRVF becomes O * q. Re-parameterization is represented as γ ∈ Γ, where Γ is the set of all orientation-preserving diffeomorphisms of [0, 1], γ : [0, 1] → [0, 1]. Re-parameterization of f by γ is denoted as f(γ(s)), and its SRVF is denoted as $(q,\gamma )=(q◦\gamma )\sqrt{\dot{\gamma }}$, where ◦ denotes the composition of two functions. The following optimization is used to separate the translation and re-parameterization from a streamline f_k with respect to the template μ_(a,b):

$$(O_k,{\gamma }_k)=\underset{O\in \mathit{\text{SO}}(3),\gamma \in \mathrm{\Gamma }}{\text{argmin}}\Vert q_{{\mu }_{(a,b)}}-O\ast (q_k,\gamma )\Vert ,$$ (1)

where q_k is the SRVF of f_k and q_μ(a,b) is the SRVF of μ_(a,b). When the template μ_(a,b) is unknown, or in the case that we need to learn a template from some training data, we can formulate the estimation of rotations, re-parameterizations and μ_(a,b) as a joint optimization problem as follows:

$$(O_k,{\gamma }_k)=\underset{O\in \mathit{\text{SO}}(3),\gamma \in \mathrm{\Gamma }}{\text{argmin}}\Vert q_{{\mu }_{(a,b)}}-O\ast (q_k,\gamma )\Vert ,$$ (2)

$$q_{{\mu }_{(a,b)}}=n_{(a,b)}^{-1}\sum _{k=1}^{n_{(a,b)}}{O}_k\ast (q_k,{\gamma }_k)\text{ for }k=1,\dots ,n_{(a,b)},$$

where n_(a,b) is the total number of streamlines in the training data. The optimization of Eqn. (2) is done through an iterative procedure until convergence. We optimize O_k through Procrustes analysis (Corouge et al., 2004) and γ_k through dynamic programming (Srivastava et al., 2011). Finally, as illustrated in the last column of Figure 3, we obtain a collection of tightly aligned fiber tracts as the shape component, denoted as $\{\stackrel{\sim }{f_k}|\stackrel{\sim }{f_k}=O_k\ast (f_k◦{\gamma }_k)\text{ for }k=1,\dots ,n_{a,b}\}$.

2.3.2. Encoding and decoding streamlines

Due to the variation decomposition, the cross-sectional variance of the remaining shape components $\stackrel{\sim }{f_k}(s)$ for any s ∈ [0, 1] is much smaller than that of the original streamlines. This phenomenon allows us to represent the shape component using a low-dimensional structure, which is the component that takes the most space to save. For each cell of the SCCS, we use a training dataset to learn a template streamline and a set of basis functions for efficiently representing the shapes of streamlines. Specifically, for each connection (a, b), we pool the streamlines from a set of representative subjects, extract the template streamline and shape component, and learn a set of basis functions using functional principal component analysis (fPCA) to represent the functional space of the aligned streamlines. Let ${\varphi }_l^i:[0,1]\to ℝ$ be a basis function for i = 1, 2, and 3 and $l=1,\dots ,M_{(a,b)}^i$, where $M_{(a,b)}^i$ is the number of basis functions learned for the i-th coordinate, in which i = 1, 2, and 3 represent the x, y and z coordinates, respectively. We denote this representation coordinate as follows:

$${ℒ}_{(a,b)}=\{{\mu }_{(a,b)},\{{\varphi }_l^i:i=1,2,3;l=1,\dots ,M_{(a,b)}^i\}\},$$ (3)

in which the template fiber μ_(a,b) is the origin of this coordinate system.

For a given streamline f in connection (a, b), we align it to μ_(a,b) to extract the shape component f̃(·) after separating the rotation O, translation C, scaling L and re-parameterization γ. We then encode the shape part as

$$\stackrel{\sim }{f}(s)=\left(\begin{array}{c}\hfill {\mu }_{(a,b)}^1(s)+{\sum }_{l=1}^{{\hat{M}}_{(a,b)}^1}{c}_l^1{\varphi }_l^1(s)\hfill \\ \hfill {\mu }_{(a,b)}^2(s)+{\sum }_{l=1}^{{\hat{M}}_{(a,b)}^2}{c}_l^2{\varphi }_l^2(s)\hfill \\ \hfill {\mu }_{(a,b)}^3(s)+{\sum }_{l=1}^{{\hat{M}}_{(a,b)}^3}{c}_l^3{\varphi }_l^3(s)\hfill \end{array}\right)+\left(\begin{array}{c}\hfill {\epsilon }^1(s)\hfill \\ \hfill {\epsilon }^2(s)\hfill \\ \hfill {\epsilon }^3(s)\hfill \end{array}\right),$$ (4)

where ε is the error term, $c_l^i$ is the coefficient corresponding to the basis function ${\varphi }_l^i$ and ${\hat{M}}_{(a,b)}^i$ represents the total number of basis functions for i = 1, 2, and 3 that are used to approximate f̃(s) up to the error of ε(s) = (ε¹(s), ε²(s), ε³(s))^T.

Through this encoding procedure, we represent the streamline f as $\{C,O,L,\gamma ,c_l^i:i=1,2,3;l=1,\dots ,{\hat{M}}_{(a,b)}^i\}$. The re-parameterization γ does not alter the streamline path (Srivastava et al., 2011) since it is only used to align streamlines to the template to reduce the cross-sectional variance. Thus, we can discard γ for the purpose of compression. The original streamline path can be recovered from $\{C,O,L,c_l^i:i=1,2,3;l=1,\dots ,{\hat{M}}_{(a,b)}^i\}$, which is a decoding procedure:

$$\hat{f}=O^T\ast L\ast \stackrel{\sim }{f}+C.$$ (5)

Let ‖·‖² be the 𝕃² norm of a vector or matrix. A smaller ‖ε‖ corresponds to a more accurate representation of f, which requires more coefficients. We define a measure, called the compression ratio, as

$$\rho =100(1-N_c/N_r),$$ (6)

for evaluating the representation efficiency, where N_r is the number of parameters used to represent the raw streamline f and N_c is the number of parameters used to represent f̂ after compression.

The proposed encoding procedure is a learning-based approach. For each cell of the SCCS, we learn the common geometry of the streamlines (the template) and a set of basis functions to efficiently represent the deviation of an individual streamline from the template. To represent different data, such as tractography data associated with neurodegenerative disease, a new training process would be necessary. However, we emphasize that the proposed compression method is robust. The alignment process separates the shape from other shape-preserving transformations and the compression is conducted on the shape part. Given new tractography data, as long as the streamline shapes remain similar to those in the training dataset, the designed compression method should work well. In our PSC pipeline, for each connection based on the Desikan-Killiany and Destrieux parcellations, we provide a template streamline and a set of basis functions learned from HCP subjects. If a new subject has streamlines that cannot be precisely represented by the provided coordinate systems, a warning will be given and a new training procedure is recommended.

2.4. Multi-level Groupwise Connectome Analysis

We now obtain a parcellation-based tractography common space (PTCS) for each connection, which is given by $\text{PTCS}={\cup }_{a,b=1}^V(a,b)\otimes {ℒ}_{(a,b)}$. To the best of our knowledge, PTCS is the first common space of its kind to efficiently represent streamlines for parcellation-based connectome analysis. For any new subject, in PTSC, we can use (4) to transform all tractography data from the original 3D measurement space onto the coordinate system of PTCS, which is a compression process of the SCCS. Based on the saved (compressed) SCCS, we can carry out the groupwise connectome analysis at three different levels, from complex to simple: (i) the streamline level; (ii) the weighted network level; and (iii) the binary network level. See the illustration of multi-level groupwise connectome analysis in the rightmost column of Figure 1.

At the streamline level, our PSC framework saves the object SCCS, in which each cell contains the streamlines that connect the corresponding pair of regions. The geometric information of each streamline is well preserved in the SCCS. Since the streamlines in each cell of the SCCS are aligned to a template, we can directly compare their shapes without the misalignment issue. We also can calculate the WM integrity measures, such as FA and generalized FA (GFA), along all streamlines in each cell of the SCCS and perform statistical analysis for these diffusion measurements. The diffusion profile along with these tracts integrate both the geometric and diffusion properties of a connection.

At the weighted network level, the object of the SCCS is turned into an adjacency matrix, representing how different brain regions are connected. The scalar in each cell often represents the coupling strength between two ROIs. For example, the commonly used metric is the count of streamlines (Smith et al., 2012, 2013). However, that count is not considered to be reliable when measuring the coupling strength (Fornito et al., 2013; Smith et al., 2013; Jones et al., 2013). Instead of only using the count as the “connection strength”, we propose to include multiple features of a connection to generate a tensor network for each brain. The tensor network has a dimension of V × V × P, where P represents the number of features and V represents the number of nodes. Each of the P matrices is a weighted network and describes one aspect of the connection. As illustrated in the bottom row of Figure 2, the following features are included in our PSC package.

1. Diffusion-related features. Diffusion properties along streamlines characterize the water diffusivity along WM streamlines for each ROI pair. For each streamline, our PSC package provides eight different diffusion-related features, the mean of FA, max FA, the mean of the mean diffusivity (MD), max MD, the mean of GFA, max GFA, the mean of the apparent fiber density (AFD) and max AFD. More diffusion-related features can be included in the PSC package in the future.

2. Geometry-related features. The average length, shape, and cluster configuration characterize the geometric information of streamlines for each ROI pair. The average length of streamlines in a connection reflects the intrinsic spatial distance between two regions. In the PTCS, the coefficients $\{c_l^i\}$, i = 1, 2, 3 of streamlines are natural shape information. We calculate the averages of $\{c_1^i,\dots ,c_n^i\}$ for i = 1, 2 and 3, and use them as three different shape features. In addition, we calculate the number of clusters using the Quickbundle method with a fixed θ_t, which is more robust to some confounding effects in the tractography reconstruction, such as the seeding strategy.

3. Endpoint-related features. We consider the features generated from the end points of streamlines for each ROI pair. We first extract the number of end points as a feature, which is the same as the count of streamlines. We also calculate the total connected surface area (CSA) for each ROI pair. Specifically, we treat each ROI as a 3D surface, as illustrated in Figure 2 (f). At each intersection between the surface and a streamline, we calculate the area covered by all small circles generated by streamlines. In the Supplementary Section 2, we present the detailed procedure to calculate the CSA feature. Note that the CSA feature is similar to the continuous connectivity feature proposed by Moyer et al. (2017), with both having the effect of smoothing the count matrix. However, the extracted weight in Moyer et al. (2017) depends on the density of the streamlines, whereas the CSA depends on the touching area. A weighted version of the CSA is also calculated by dividing the CSA by the total surface area of the two ROIs.

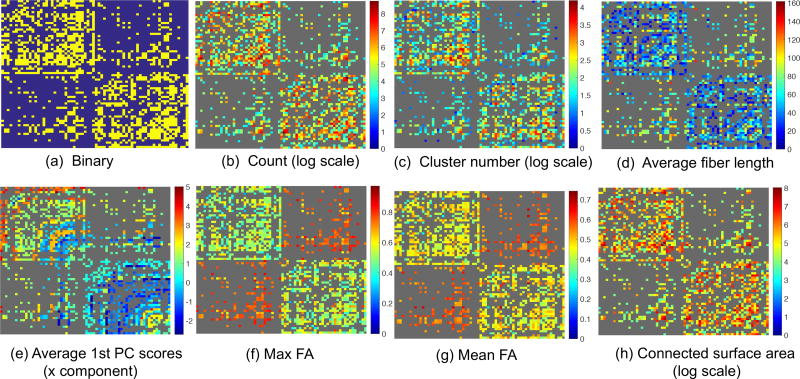
At the binary network level, we threshold the streamline count matrix into a binary matrix. Each element of the binary matrix indicates the presence or absence of a connection for a specific ROI pair. Statistical analysis of such binary networks (Durante and Dunson, 2016; Durante et al., 2017) and the inference of the network change with different phenotypes (Wang et al., 2016b) suggests that this type of data contains rich information. However, defining a proper threshold is not trivial at all (Shadi et al., 2016a). With a novel reproducibility evaluation metric and a test-retest dataset (introduced in Sections 2.5 and 2.6, respectively), we are able to find a proper threshold for our PSC framework in order to turn the streamline count matrix into a binary network. Figure 4 presents some representative binary networks and weighted networks on the scale of V = 68 based on the cortical ROIs in the Desikan-Killiany atlas from a randomly selected subject in the HCP dataset.

Figure 4.

Examples of extracted brain networks using PSC calculated for a randomly selected HCP subject.

2.5. Quantitative Evaluation of Reproducibility

Robustness and reproducibility are critical for a good structural connectome mapping pipeline. Based on a test-retest dataset (introduced in Section 2.6), we develop different quantitative metrics to evaluate the robustness and reproducibility of PSC under different preprocessing parameters. Currently, the reproducibility of the brain structural connectome is mainly evaluated through the intraclass correlation coefficient (ICC) (Prckovska et al., 2016; Welton et al., 2015), which is defined as $\text{ICC}={\sigma }_{\mathit{\text{bs}}}^2/({\sigma }_{\mathit{\text{bs}}}^2+{\sigma }_{\mathit{\text{ws}}}^2)$, and its extensions, where ${\sigma }_{\mathit{\text{bs}}}^2$ represents the between-subject variance and ${\sigma }_{\mathit{\text{ws}}}^2$ represents the within-subject variance under an analysis of variance (ANOVA) model. Since the ICC is limited to univariate variables (Shrout and Fleiss, 1979), we propose a distance-based ICC (dICC) to evaluate the reproducibility of complex connectivity representations, such as weighted networks. Specifically, the dICC is defined as $\text{dICC}=({\overline{d}}_{\mathit{\text{bs}}}^2-{\overline{d}}_{\mathit{\text{ws}}}^2)/{\overline{d}}_{\mathit{\text{bs}}}^2$, where ${\overline{d}}_{\mathit{\text{bs}}}^2$ and ${\overline{d}}_{\mathit{\text{ws}}}^2$ respectively represent the average squared distance between subjects and within multiple scans of a subject. Here, ${\overline{d}}_{\mathit{\text{bs}}}^2$ is analogous to the “total variance”, ${\overline{d}}_{\mathit{\text{ws}}}^2$ to the “within-subject variance”, and ${\overline{d}}_{\mathit{\text{bs}}}^2-{\overline{d}}_{\mathit{\text{ws}}}^2$ to “between-subject variance”.

We need to define the distances for different representations of the structural connectome to calculate the dICC. We first consider the binary and weighted networks. For any two binary networks B₁ and B₂, we define their distance as d_b = |B₁ − B₂|, where |·| represents the 𝕃¹ metric. For two weighted networks A₁ and A₂, we use the 𝕃² metric to calculate their distance d_w1 = ‖A₁ − A₂‖. Note that it is possible to use other metrics to calculate the dICC, e.g., we first log-transform each weighted matrix and then calculate their 𝕃² distances. These options are explored in the Supplementary Material, Section 3.

At the streamline level, it is not trivial to define a good metric to compare two SCCSs due to the complex structure of SCCSs. Specifically, each cell in the SCCS contains streamlines in the native subject space, and there are different numbers of streamlines for the same connection across subjects. Instead of directly comparing SCCSs, we extract and compare the mean diffusion profiles along streamlines, which depend on the spatial location of streamlines and the diffusivities along them. Subsequently, for each ROI pair, we calculate the 𝕃² distance between their mean FA curves in order to calculate the associated dICC score for SCCSs.

2.6. Real Datasets

We use two real datasets, a test-retest dataset and the HCP dataset, to evaluate three different aspects of the developed PSC framework: robustness and reproducibility, representation efficiency, and the heritability of various extracted connectivity features.

Test-Retest Dataset

The test-retest dataset represents a clinical acquisition. It consists of 11 healthy subjects, each of whom has 3 repeated acquisitions with an approximate two-week interval between two consecutive acquisitions. A total of 33 acquisitions comprise this dataset. The average age of all subjects is 26 ± 2.4 years. The diffusion space (q-space) was acquired along 64 uniformly distributed directions with a b-value of b = 1000 s/mm² and a single b₀ (=0 s/mm²) image. The scan was done by using the single-shot echo-planar imaging sequence on a 1.5 Tesla Siemens MAGNE-TOM (128 × 1 28 matrix, 2 mm isotropic resolution, TR/TE 11000/98 ms and GRAPPA factor 2). An anatomical T1-weighted 1 × 1 × 1 mm³ MPRAGE (TR/TE 6.57/2.52 ms) image was also acquired. The diffusion data were upsampled to 1 × 1 × 1 mm³ resolution using a trilinear interpolation and the T1-weighted image was registered on the upsampled b₀ image. Quality control by manual inspection was used to verify the registration (Girard et al., 2014).

Human Connectome Project (HCP) Dataset

The HCP datasets represents a high-resolution dMRI acquisition. A full dMRI session for the HCP data includes 6 runs (each approximately 10 minutes), representing 3 different gradient tables, with each table acquired once with right-to-left and left-to-right phase encoding polarities, respectively. Each gradient table includes approximately 90 diffusion weighting directions plus 6 b₀ acquisitions interspersed throughout each run. Within each run, there are three shells of b = 1000, 2000, and 3000 s/mm² interspersed with an approximately equal number of acquisitions on each shell. See Van Essen et al. (2012) and Sotiropoulos et al. (2013) for more details about the data acquisition and preprocessing. We have used all 3 shells for fiber ODF estimation. Only the b = 1000 data were used for diffusion tensor estimation and the calculation of diffusion tensor metrics, such as FA and MD. We extracted 856 subjects with both preprocessed dMRI and anatomical T1-weighted MRI data from the 900-subject release of the HCP dataset.

3. Experimental Results

In the experimental section, we evaluate the following four aspects of the PSC framework.

1. Choice of optimal parameters in PSC: There are several tuning parameters in PSC that are important for generating reproducible connectomes. The test-retest dataset together with the quantitative reproducibility measures enable us to select these parameters.

2. Validation of reproducibility: We are interested in validating and comparing the robustness and reproducibility of various connectomes extracted by PSC.

3. Evolution of the proposed compression method: We want to evaluate and compare the compression ratio of the SCCS with that of existing methods.

4. Demonstration of groupwise analyses: The HCP dataset was processed using PSC. Using these data, we illustrate the potential applications of PSC in characterizing normal variations and heritability of structural connectomes in healthy subjects.

3.1. Choosing the Parameters of PSC

There are several tuning parameters in PSC that are critical for generating robust structural connectomes. We use the test-retest dataset and the defined reproducibility metrics to select these tuning parameters.

Dilation parameter ψ

As described in Section 2.2, we dilate the GM cortical region into the WM area with ψ voxels. A proper choice of ψ is important. As ψ increases, each GM ROI contains a small portion of WM and thus, streamlines that stop at the GM-WM interface will be included in the extracted connections. However, a large ψ can increase the number of false positive connections.

Length filtering parameters

Most local tractography algorithms (Girard et al., 2014) are likely to generate short erroneous streamlines. Initialized from the WM-GM interface, most streamlines rapidly stop propagating since they immediately enter the GM region. It is routine to filter streamlines based on their length. Specifically, we filtered out streamlines with lengths outside of an interval [L_len, U_len]. We set the upper bound U_len to be 240 mm, since streamlines with lengths larger than 240 mm are deemed to be outliers. However, the effect of L_len on constructing structural connectomes is unknown.

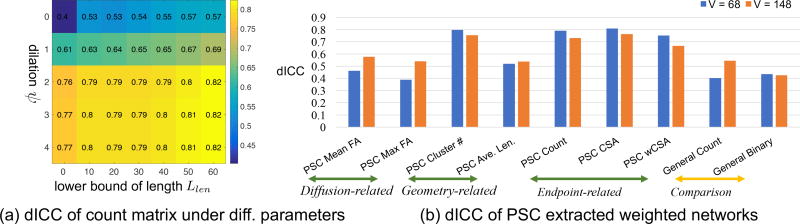
We used the sub-network that consists of the nodes of cortical regions to determine the optimal values of ψ and L_len, since the dilation was done solely for the cortical region. Specifically, we considered the reproducibility of streamline count matrix under the Desikan-Killiany parcellation (V = 68 for cortical regions) on the test-retest dataset with different choices of (ψ, L_len). The reproducibility scores (dICC) are shown in Figure 5 (a). This reveals that ψ is a crucial parameter for reproducibility. By increasing ψ from 0 to 2, the reproducibility of the count matrices dramatically improves, whereas for ψ > 2, the improvement is negligible. Therefore, we set ψ = 2 (dilate 2 mm into WM since we have the isotropic 1 mm image resolution in the test-retest dataset). We also observe that filtering out short streamlines improves the reproducibility of the extracted count matrices. However, a large L_len can filter out a large portion of relatively short streamlines, making the structural connectome very sparse. We set L_len = 20 throughout this paper.

Figure 5.

Reproducibility study of the weighted networks. (a) Effect of parameters ψ and L_len on the reproducibility (measured by dICC) of streamline count matrix under the Desikan-Killiany parcellation. (b) Reproducibility score (dICC) of the final PSC extracted weighted networks based on ψ = 2, L_len = 20 and θ_t = 8 mm. A comparison of PSC with a general weighted network extraction framework is also shown.

Outlier threshold

The clustering threshold θ_t in QuickBundle affects the outlier detection and feature extraction for each connection. We selected a set of candidate θ_ts in (1, 20) (mm) and then calculated the number of outliers identified for each θ_t. For θ_t > 10 mm, QuickBundle barely detected any outliers, whereas for θ_t < 5 mm, QuickBundle identified too many outliers. Since we focus on these apparent outlying streamlines that do not follow any major WM pathways, we conservatively set θ_t = 8 mm; the manual inspection validated our choice.

3.2. Reproducibility of Connectomes Produced by PSC

Since the structural connectome of a normal adult brain is temporally stable, a good PSC framework must produce similar structural connectomes based on different scans of the same person acquired within a few weeks. In this section, we evaluated and compared the reproducibility of structural connectomes at three different levels ranging from the binary network and the weighted network to the whole-brain streamline data (saved in the SCCS) under two different cortical surface parcellations. The two parcellations are Desikan-Killiany (Desikan et al., 2006) with V = 68 cortical surface nodes and Destrieux (Destrieux et al., 2010) with V = 148. The optimal parameters for dilation (ψ = 2 mm), streamline length filtering (L_len = 20 mm, U_len = 240 mm) and outlier removal (θ_t = 8 mm)) were used in PSC to process the test-retest dataset.

3.2.1. Reproducibility at the binary network level

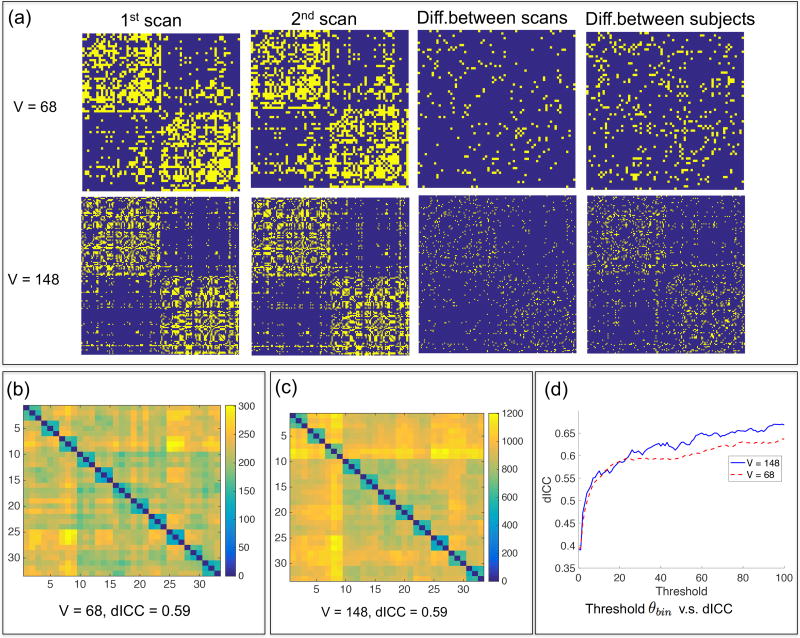
We considered the structural connectomes generated by PSC for all 33 scans in the test-retest dataset and thresholded each count adjacency matrix to obtain a binary network matrix B_i = Φ(A_i, θ_bin), where Φ is a threshold function defined as Φ(A_i(a, b), θ_bin) = 1(A_i(a, b) > θ_bin), in which 1(·) is an indicator function of an event. Finding a good threshold θ_bin is an important problem for brain network analysis (Li et al., 2012; Shadi et al., 2016a). Figure 6 presents the results of the reproducibility analysis. We observe only a small number of non-zero edges in the difference matrix of two scans of the same subject. In contrast, there are many more non-zero edges in the difference matrix of two different subjects. For both parcellations, the dICC increases from 0.40 to around 0.64 as the threshold θ_bin increases from 0 to 100. Since the increasing rate in the range of (0, 20) is much higher than that in the range of (20, 100), we recommend to set θ_bin = 20 in PSC, where the dICC value is close to 0.59. Moreover, we observe that increasing V does not increase the dICC, which is consistent with the findings in the literature (Prckovska et al., 2016; Welton et al., 2015).

Figure 6.

Reproducibility study at the binary network level. (a) The leftmost two columns show two binary network matrices from two different scans of the same subject. Column 3 shows the difference between the scans, and column 4 shows the difference between the 1st scan and that from a different subject. (b)–(c) Pairwise distance matrices between 33 binary networks extracted from the test-retest dataset. (d) Relationship between the threshold θ_bin and the dICC score.

We also used the ICC to evaluate the reproducibility of topological features of the binary network and compared them with those in the existing literature (Prckovska et al., 2016; Welton et al., 2015; Zhao et al., 2015; Cheng et al., 2012a). Four selected topological features were calculated, the network density, characteristic path length, local efficiency, and clustering coefficient (Watts and Strogatz, 1998). The ICC(1,1), introduced by (Shrout and Fleiss, 1979), was calculated using all 33 binary networks obtained by using θ_bin = 20. Table 1 summarizes the results. The ICC scores of these topological features are significantly higher than those in the literature (Cheng et al., 2012a; Welton et al., 2015). For instance, Cheng et al. (2012a) reported ICC scores in the range of 0.2 ~ 0.7 and Welton et al. (2015) reported ICC scores < 0.6. These results suggest that the proposed PSC can produce more robust binary networks.

3.2.2. Reproducibility at the weighted network level

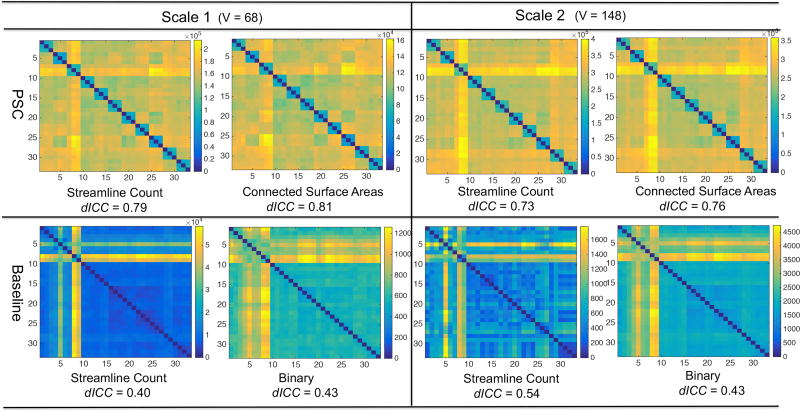
Various weighted networks defined in Section 2.4 were extracted from the test-retest dataset by using PSC with the optimal parameters. We used the defined 𝕃² distance to calculate the dICC scores under the two parcellations. Figure 5 (b) shows the dICC scores of different weighted networks. Among all network features, the mean FA, max FA and average length have relatively lower dICC scores, indicating that these three features are less discriminative or reproducible. The new CSA feature has the highest dICC scores under different parcellations. We consider CSA as a robust feature that may be better related to the “amount” of neurons connecting a pair of regions. In addition, we can see that the endpoint-related features have higher dICC scores than all other features, indicating that the endpoint-related features are very robust and reproducible under the PSC framework. By comparing the two resolutions of the endpoint-related features, we observe that the dICC scores are higher at V = 68 than V = 148.

We compared the proposed PSC framework with a general method from the literature (e.g. Roncal et al. (2013)) without using the GM ROI dilation, streamline cutting and outlier removal procedures. The streamline count matrix was extracted and then the binary matrix was generated by setting θ_bin = 0 to threshold the streamline count matrix. The reproducibility results for the count and binary matrices are presented in the last two columns of the bar chart in Figure 5 (b). Figure 7 compares the pairwise distance matrices of different features extracted from PSC and this general method. With the weighted networks generated by PSC, we observe a subject-specific block pattern along the diagonal, indicating strong reproducibility of weighted networks. The dICC scores are around 0.8 under both resolutions. In contrast, the corresponding pairwise distance matrices for the general method do not have such a clear block pattern and their dICC scores are much smaller. This indicates that the proposed PSC framework can extract much more reliable weighted networks compared with the standard method.

Figure 7.

Comparison of PSC with a routine procedure of extracting the connectivity matrices from tractography data. The test-retest dataset is used here. The top row shows the pairwise distance matrices of the streamline count and the CSA matrices produced by PSC. The bottom row shows pairwise distance matrices of the streamline count matrices and the binary network matrices produced by the routine procedure. To compare with the binary networks produced by PSC, readers can refer to Figure 6.

3.2.3. Reproducibility at the streamline level

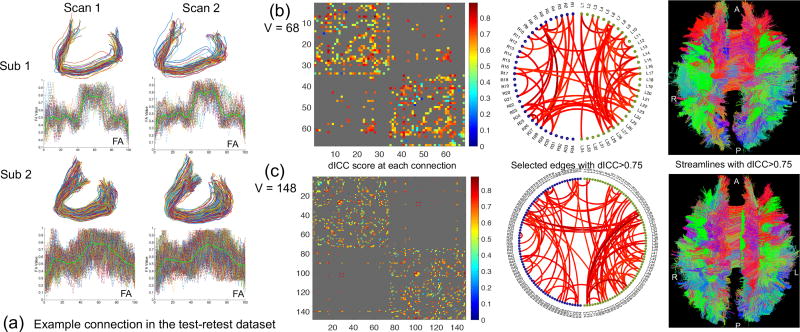
Each cell of the SCCS contains the original streamlines for each connection extracted using PSC. At this stage, the streamlines have not been compressed yet. To perform the streamline-based analysis, we extracted the FA values along each streamline, treated them as a function from [0, 1] to ℝ, and calculated an average FA curve for each connection (or each cell of the SCCS). The 𝕃² distance between mean FA curves is used to calculate the dICC score at each connection. In our experiment, the dICC scores were only evaluated at the connections that have at least 20 streamlines in all subjects in the test-retest dataset. Figure 8 presents the results.

Figure 8.

Reproducibility analysis of PSC at the streamline level. (a) Extracted streamlines connecting left and right frontal sulci from two subjects in the test-retest dataset. The FA value along each streamline and the mean FA curves (in solid green) are also plotted; (b) and (c) Reproducibility analysis based on the mean FA curves at the scale V = 68 and V = 148, respectively. In each panel, we show the dICC score matrix, selected edges with the dICC > 0.75, and the streamlines corresponding to the selected edges, from left to right, respectively. A: anterior; P: posterior; R: right; and L: left.

In Figure 8 panel (a), we show the streamlines connecting the left and right frontal sulci and the FA values along them from two scans of two randomly selected subjects in the test-retest dataset. These streamlines are part of the corpus callosum bundle. We observe that the streamlines and the FA values along them are different across subjects, but are very similar across multiple scans of the same subject. In Figure 8 (b) and (c), from left to right, we show the calculated dICC scores using the 𝕃² distance between mean FA curves, the selected edges with dICC > 0.75, and the streamlines in a randomly selected subject corresponding to the selected edges with dICC> 0.75, respectively. The dICC scores for most connections are higher than 0.6, indicating good reproducibility of PSC at the streamline level. There are 144 connections at the scale of V = 68 and 202 connections at that of V = 148 with dICC> 0.75. Since the PSC framework preserves both the networks (binary and weighted) and the streamlines (SCCS), we can readily map the connections with dICC> 0.75 back to the streamline space. From the mapped back streamlines, we see that the WM bundles that have high values of reproducibility are similar across different parcellations.

3.3. Connectome Representation Efficiency

In this section, we examine the representation efficiency of the proposed PTCS. Due to the flexibility of the proposed decomposition, we can separate different shape-preserving transformations and remove specific transformations from the shape component. In a simulation study presented in the Supplementary Material, Section 4.1, we examine three different scenarios: extracting the shape component by separating (i) translations only, (ii) rotations and translations, and (iii) rotations, translations and re-parameterizations (scaling is preserved in the shape component since it does not help with the compression). It has been shown that by removing more shape-confounding parameters, we can achieve better representation efficiency (compression ratio). However, separating the re-parameterization parameters can be computationally expensive with naive implementations (Huang et al., 2016; Srivastava et al., 2011). To speed up the alignment process, we can either use a fast alignment procedure (Huang et al., 2016) (a simulation study indicates that it is more than three times faster than the current dynamic programming implementation) or assume an identity re-parameterization for all streamlines (similar to scenario ii). In the following experiments, we used the latter approach for simplicity: the streamlines in each connection are only decomposed into rotation, translation and shape components.

Representation efficiency for streamlines in connections

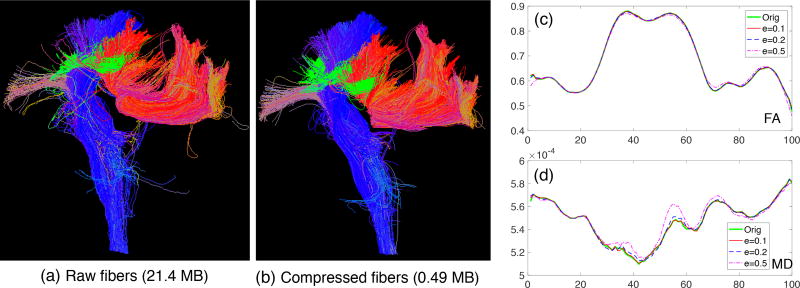
We used the defined compression ratio to evaluate the representation efficiency of the PTCS. We considered streamlines in three representative connections under the Desikan-Killiany parcellation: (i) those connecting the left and right superior parietal lobule, which is part of the corpus callosum bundle, indexed as connection (L28, R28); (ii) those connecting the left caudal middle frontal gyrus and left superior parietal lobule, indexed as connection (L3, R28); and (iii) those connecting the brain stem and the left precentral gyrus as part of the corticospinal tracts, indexed as connection (LS9, R23). Figure 9 (a) presents those example bundles. To learn a PTCS for each connection, 20 subjects from HCP were used as the training set. Another 20 subjects were used as the test set for calculating the average compression ratio. The compression ratio was evaluated under different values of ε. The proposed method was compared with the classical cubic spline method and the linearization compression method in Presseau et al. (2015). Table 2 presents the comparison results. The PTCS outperforms the cubic spline and linearization compression methods in all cases. At the precision of ‖ε‖ = 0.2 mm, we have ρ ≈ 98%. That is, with around 2% of parameters, we can almost perfectly recover the streamlines with the original image resolution of 1.25 × 1.25 × 1.25 mm³. The size of the whole HCP tractography dataset can be reduced from a few terabytes to dozens of gigabytes.

Figure 9.

Evaluation of the proposed compression method. (a) Raw streamlines in connections (L28, R28), (L3, R28) and (LS9, R23) in a subject from the HCP dataset, which require 21.4 MB disk space. (b) Reconstructed compressed streamlines from PSC with ‖ε‖ = 0.2 mm which require only 0.49 MB disk space. (c–d) Mean FA and MD curves along the streamlines in (L28, R28) when the streamlines are compressed with different values of ‖ε‖.

Table 2.

Compression ratio of streamlines connecting some representative ROI pairs

Error ‖ε‖ (mm)	Connection (LS9, R23)				Connection (L3, R28)				Connection (L28, R28)
	0.1	0.2	0.5	2.0	0.1	0.2	0.5	2.0	0.1	0.2	0.5	2.0
PTCS	.961	.976	.987	.992	.959	.974	.984	.988	.961	.977	.988	.992
Linearization	.865	.930	.969	.981	.867	.930	.966	.978	.867	.933	.969	.980
Cubic Spline	.783	.873	.935	.960	.770	.864	.925	.951	.779	.872	.934	.959

To further test the robustness of the PTCS learned from HCP subjects, we applied our PSC pipeline to three other datasets that have relatively low image quality. The detailed compression results are presented in the Supplementary Material, Section 4.2. Although there is a slight decrease in the compression ratios, we can still achieve comparable compression ratios in these datasets using the PTCS trained from the HCP data, indicating that the proposed compression method is very robust. The slight decrease in the compression ratio may be due to the low image resolution.

Impact of diffusion measures along bundles

Since tract-based studies often use dMRI diffusivity metrics, such as FA and MD, along WM bundles, we performed additional experiments to explore how our compression can impact the integrity of diffusivity information along WM bundles that connect two ROIs. Supplementary Table 3 shows that the percentages of the mean FA and MD change. The mean FA and MD values along these tracts barely change when ‖ε‖ is smaller than 0.5. Figure 9 panel (c) and (d) present the mean FA and MD curves along streamlines in (L28, R28) when the tracts are compressed with different ‖ε‖ (a randomly selected HCP subject). Figure 9 indicates that PSC not only removes outliers and compresses streamlines, but also preserves the diffusion properties along the reconstructed streamlines after compression.

3.4. Groupwise Connectome Analysis

In this section, we demonstrate the use of PSC for groupwise analysis in a large cohort study. The whole HCP dataset was processed using PSC, and various representations of connectomes were extracted for future statistical analysis.

Heritability of the weighted network

Given the weighted networks extracted by PSC, we examined the heritability of the weighted structural networks of different cortical ROIs. Among 856 subjects in the HCP dataset, we identified 86 monozygotic twin pairs, 83 dizygotic twin pairs, and 207 singleton subjects. In our heritability analysis, we used the 68 × 68 mean FA weight matrix (under the Desikan-Killiany parcellation) as the phenotype of interest. Depending on the research focus, other weighted matrices, such as the CSA matrix, can be easily included in this analysis. We fitted an ACE model (Haseman and Elston, 1970; Neale and Cardon, 1992) as follows:

$$y_{\mathit{\text{ij}}}={\mathbf{x}}_{\mathit{\text{ij}}}^T\beta +a_{\mathit{\text{ij}}}+c_i+e_{\mathit{\text{ij}}},$$ (7)

where {y_ij} with j = 1, 2 represent the mean FA measure for the i-th twin pair, a p × 1 vector x_ij is a set of covariates and β represents the vector containing all the coefficients of the effect. There are three variance components in the above model, including the additive genetic variance $a_{\mathit{\text{ij}}}~N(0,{\sigma }_a^2)$, the common environmental variance $c_i~N(0,{\sigma }_c^2)$, and the specific environmental effect $e_{\mathit{\text{ij}}}~N(0,{\sigma }_e^2)$. For the additive genetic effect, it is assumed that cor(a_i1, a_i2) = 1 for the monozygotic twin pairs and cor(a_i1, a_i2) = 0.5 for the dizygotic twin pairs. And $e_{\mathit{\text{ij}}}~N(0,{\sigma }_e^2)$ is assumed to be independent for different subjects. The genetic heritability was calculated as $h^2={\sigma }_a^2/({\sigma }_a^2+{\sigma }_c^2+{\sigma }_e^2)$. To test the significance of the heritability h², we particularly focused on testing whether the genetic variance ${\sigma }_a^2$ equals zero:

$$H_0:{\sigma }_a^2=0\mathrm{v}.\mathrm{s}.H_1:{\sigma }_a^2>0.$$ (8)

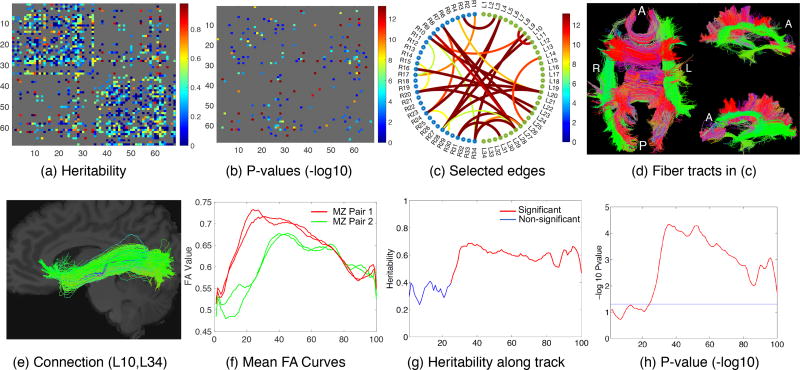
Since a large proportion of connections are zero-inflated where the normal assumption of model (7) is violated, we only kept 672 connections. These connections were selected based on the criterion that each of them has less than 5% of zero weights among all HCP subjects. Based on model (7), the maximum likelihood estimates of $(\beta ,{\sigma }_a^2,{\sigma }_c^2,{\sigma }_e^2)$ were obtained and the log-likelihood ratio test (LRT) was applied to test the significance. The results are presented in Figure 10, in which panel (a) shows the estimated heritability scores for the mean FA weighted matrix, panel (b) shows the p-values of the significant edges (with a threshold of α = 0.05) after Bonferroni correction, panel (c) shows the selected 28 significant connections with heritability scores greater than 0.8, and panel (d) shows the streamlines of the 28 connections. In the Supplementary Table 4, we present the ROI names, heritability scores and adjusted p-values of the 28 selected connections. Our results reveal that some well-known fiber bundles, including the left and right arcuate fasciculus bundles, the right inferior longitudinal fasciculus bundle, the right uncinate fasciculus bundle, the optic radiation bundle, and a large portion of the corpus callosum bundle, are highly heritable. This finding is consistent with the results in the existing literature (Kochunov et al., 2015).

Figure 10.

The top row illustrates the heritability analysis using the mean FA weighted matrix: (a) Estimated heritability scores for each connection based on the mean FA weighted matrix; (b) P-values of the significant edges (with a threshold of α = 0.05) after Bonferroni correction; (c) Selected significant connections with heritability scores greater than 0.8; (d) Corresponding streamlines in the selected connections in (c). The bottom row illustrates the heritability analysis using mean FA curves along streamlines: (e) Selected connection; (f) Mean FA curves along streamlines in this connection for two pairs of monozygotic twins; (g) Heritability score along the curve; and (h) P-value along the curve. A: anterior; P: posterior; R: right; L: left and MZ: monozygotic.

Heritability of streamlines

At the streamline level, we conducted heritability analysis on the mean FA along streamlines in each cell of the SCCS. The same set of subjects from the previous experiment was used here. We fitted a functional version of the ACE model proposed in (Luo et al., 2017):

$$y_{\mathit{\text{ij}}}(s)={\mathbf{x}}_{\mathit{\text{ij}}}^T\beta (s)+a_{\mathit{\text{ij}}}(s)+c_i(s)+e_{\mathit{\text{ij}}}(s),s\in [0,1],$$ (9)

where y_ij(s) with j = 1, 2 represent the mean FA curve for the i-th twin pair at a point s ∈ [0, 1]. Age, gender, handedness and an intercept term were added in x_ij ∈ ℝ⁴ and β(s) is a vector of four functional covariate coefficients. The three variance components a_ij(s) ~ GP(0, Σ_a), c_i(s) ~ GP(0, Σ_c), e_ij(s) ~ GP(0, Σ_e) are Gaussian processes that at a fixed point s ∈ [0, 1] have the same assumptions as in the previous ACE model (7). Then heritability is estimated along each curve as h²(s) = Σ_a(s, s)/[Σ_a(s, s) + Σ_c(s, s) + Σ_e(s, s)] locally. To test the significance of heritability, we performed both local and global tests. For a specific point s₀ ∈ [0, 1], we focused on testing locally whether the genetic variance Σ_a(s₀, s₀) is equal to zero:

$$H_0:{\sum }_a(s_0,s_0)=0\mathrm{v}.\mathrm{s}.H_1:{\sum }_a(s_0,s_0)>0.$$ (10)

The weighted likelihood ratio statistic (WLRS) (Luo et al., 2017) was used to calculate the local p-values. For the global test on the entire curve, we tested whether all the locations have genetic variance equal to zero:

$$H_0:{\sum }_a(s,s)=0,\forall s\in [0,1]\mathrm{v}.\mathrm{s}.H_1:{\sum }_a(s,s)>0,\exists s\in [0,1].$$ (11)

The summation of the local WLRS along the tract curve was taken as a global statistic. We performed a wild bootstrap procedure (Zhu et al., 2012) to efficiently estimate the corresponding global p-value using 10⁶ bootstrap replications. Bonferroni correction was applied to adjust for multiple comparisons of 256 connections under the test. Table 3 shows the top connections with global p-values less than or equal to 2.56 × 10⁻⁴ (the smallest possible p-value based on our bootstrap sampling strategy). Figure 10 panels (e)–(h) present the results for a specific connection (L10, L34), in which panel (e) shows one example of the streamlines in (L10, L34), panel (f) shows one example of the mean FA curves along this connection for two pairs of monozygotic twins, panel (g) shows the heritability score along the curve and panel (h) shows the corresponding local p-values along the curve.

Table 3.

Selected connections with the possible smallest global p-values from streamline-level analysis. The global p-values are evaluated based on 10⁶ bootstrap runs and are adjusted using Bonferroni correction. The heritability scores at the weighted network level (using mean FA values) and the adjusted p-values are also presented for comparison.

ROI1	ROI2	global pval	network-h2	network-pval
L10 (lh-lateraloccipital)	L34 (lh-insula)	≤2.56E−04	0.827	8.34E−07
L10 (lh-lateraloccipital)	R24 (rh-precuneus)	≤2.56E−04	0.417	5.32E−04
L12 (lh-lingual)	L34 (lh-insula)	<2.56E−04	0.622	1.67E−04
L23 (lh-precentral)	R16 (rh-paracentral)	≤2.56E−04	0.311	1.01E−05
L23 (lh-precentral)	R23 (rh-precentral)	≤2.56E−04	0.608	3.08E−05
L24 (lh-precuneus)	R24 (rh-precuneus)	≤2.56E−04	0.241	1.54E−01
L24 (lh-precuneus)	R28 (rh-supparietal)	≤2.56E−04	0.239	1.19E−03
L26 (lh-rostlmidfron)	R26 (rh-rostmidfron)	≤2.56E−04	0.383	7.90E−05
L26 (lh-rostralmidfron)	R25 (rh-supfrontal)	≤2.56E−04	0.745	1.84E−06
L27 (lh-supfrontal)	R25 (rh-supfrontal)	≤2.56E−04	0.767	5.00E−11
L28 (lh-supparietal)	R9 (rh-isthcingulate)	≤2.56E−04	0.37	1.00E+00
L28 (lh-supparietal)	R24 (rh-precuneus)	≤2.56E−04	0.439	1.19E−06
L28 (lh-supparietal)	R28 (rh-supparietal)	≤2.56E−04	0.804	5.99E−06
R10 (rh-lateraloccipital)	R34 (rh-insula)	≤2.56E−04	0.306	2.50E−01
R28 (rh-supparietal)	R34 (rh-insula)	≤2.56E−04	0.436	1.00E+00

4. Discussion

We have developed a powerful PSC mapping framework for performing structural connectome analysis in large-scale neuroimaging studies. The multi-layer representation allows us to explore the brain structural connectome across three different levels. At the streamline level, the geometric information is well preserved, and the developed variance decomposition allows us to separate the streamlines into various components. The shape component usually needs a large number of parameters to represent, but the developed PTCS makes it possible to efficiently represent the shape information using a low-dimensional vector. At the weighted network level, we extract a dozen features from different aspects to better characterize the brain connectivity. Compared to the commonly used count feature, PSC not only provides several novel and robust measures but also describes each connection in a more comprehensive manner. A concatenation of all weighted networks leads to a tensor weighted network representation, which calls for novel statistical methods. At the binary network level, a systematic evaluation of reproducibility helps us to choose optimal thresholds to obtain robust binary networks.

We applied PSC to process both the test-retest dataset and the HCP dataset. The test-retest dataset is crucial for the development of PSC, based on which the reproducibility of the brain’s structural connectomes was evaluated across the three different levels. The tuning parameters of PSC were determined by optimizing the reproducibility results. In our study, we tried to explore some important questions when analyzing the structural connectomes.

Factors that affect connectome reproducibility

Through the newly defined dICC score, we can evaluate the reproducibility of the whole cortical brain connectome at the binary and weighted network levels. From the experimental results, we observe that dilation of the GM ROIs, fiber cutting, and filtering out short streamlines are crucial for improving the reproducibility of the weighted networks. Dilation and fiber cutting can overcome some of the drawbacks of the current tractography algorithms. Specifically, due to low image resolution and noise caused by imaging techniques and tractography algorithms, a decent amount of streamlines are stopped before reaching the GM ROIs. A recent study by Reveley et al. (2015) delineates three major causes of this: the low diffusion anisotropy, dominant superficial WM and sudden propagation changes of small axonal tracts. Dilation and fiber cutting can include pre-stopped and non-stopped fibers, leading to more complete and robust streamlines. However, we note that dilation is only one strategy for reducing the drawbacks of current tractography algorithms. It also has the risk of increasing the false positive rate by introducing false connections. Moreover, the dilation parameter ψ is a key parameter that must be tuned in the PSC framework.

In addition, among all the streamlines in a brain’s tractography data, a large portion are short ones (Girard et al., 2014). These short streamlines tend to be false positives more than the long ones. Thresholding some short streamlines can produce more robust connectomes based on our analyses of the test-retest dataset. To obtain a binary network, our results have shown that using a small threshold for the count matrix will produce much more robust binary networks. In the current setting (with about 10⁶ streamlines in each tractography dataset), a threshold of 20 works well.

Note that the outlier removal strategy we use is relatively simple. The average fiber length between two ROIs can vary. Instead of using a fixed threshold θ_t, an adaptive one can be used to better classify streamlines in a connection and thus remove outliers more effectively. Since we have the test-retest dataset, a future direction will be to utilize these data as a training set and develop a supervised outlier streamline removal method.

Connectomes at different levels

From simple to complex, the developed PSC framework produces binary, weighted and streamline-based connectomes. Each format carries different information. For simplicity, the current literature focuses on the study of binary networks, however, the streamline-based connectome (referred to as the SCCS in this paper) carries much more information. For example, it contains the information carried by the binary network and most of the weighted networks. Our compression method allows us not only to project streamlines into a low-dimensional common space, but also to apply statistical methods to efficiently model them. A study on the shapes of fiber curves (Zhang et al., 2016) has demonstrated that the shape is much more reproducible than the streamline count feature.

Heritability of diffusion profiles

As simple illustrations, we demonstrate the heritability of FA values extracted using the PSC framework. With the weighted mean FA matrix, we observed that many connections are highly heritable (with h² > 0.8). Since PSC preserves the streamline based connectome, we can map the highly heritable connections back to the streamline space using the SCCS and study these streamlines. We found that well-known fiber bundles including the left and right arcuate fasciculus bundles, the right inferior longitudinal fasciculus bundle, the right uncinate fasciculus bundle, the optic radiation bundle, and a large portion of the corpus callosum bundle, are highly heritable. At the streamline level, using the mean FA curves, we can specifically analyze the local and global heritability along the streamlines and achieve results that are consistent with those obtained by using the weighted mean FA matrix.

Although we have demonstrated the use of PSC for groupwise connectome analyses, the power of PSC for groupwise analyses has not been fully explored yet, especially at the streamline level. A low-dimensional representation and the learned common space allow us to build efficient statistical models using the geometric information for the brain structural connectome. The variation decomposition is an alignment process, and shape components from different subjects are in the same coordinate system and can be directly used for modeling. In addition to the extracted features to characterize a particular connection, many other features can be extracted, such as the topologic features generated through persistent homology.