Comparison of cluster-based and source-attribution methods for estimating transmission risk using large HIV sequence databases

Abstract

Phylogenetic clustering of HIV sequences from a random sample of patients can reveal epidemiological transmission patterns, but interpretation is hampered by limited theoretical support and statistical properties of clustering analysis remain poorly understood. Alternatively, source attribution methods allow fitting of HIV transmission models and thereby quantify aspects of disease transmission.

A simulation study was conducted to assess error rates of clustering methods for detecting transmission risk factors. We modeled HIV epidemics among men having sex with men and generated phylogenies comparable to those that can be obtained from HIV surveillance data in the UK. Clustering and source attribution approaches were applied to evaluate their ability to identify patient attributes as transmission risk factors.

We find that commonly used methods show a misleading association between cluster size or odds of clustering and covariates that are correlated with time since infection, regardless of their influence on transmission. Clustering methods usually have higher error rates and lower sensitivity than source attribution method for identifying transmission risk factors. But neither methods provide robust estimates of transmission risk ratios. Source attribution method can alleviate drawbacks from phylogenetic clustering but formal population genetic modeling may be required to estimate quantitative transmission risk factors.

1. Introduction

Phylogenetic clustering of HIV sequences has been commonly used to characterise transmission patterns [1–3]. In developed countries, routine testing for drug resistance mutations has led to the development of large HIV sequence databases. Numerous previous investigations have leveraged such databases along with patients’ clinical and demographic covariates to study clusters of patients with closely related HIV sequences. These clusters can be defined in numerous ways, such as using genetic, evolutionary [4] or phylogeny-based distance criteria [3], or including measures of phylogenetic credibility [5]. The central idea underlying cluster analysis is that patients with similar viruses are likely to be epidemiologically related, such as by direct transmission, or by being infected by a common source or by a short chain of transmissions with potentially unsampled intermediate members [6]. Consequently, individuals who are responsible for more transmissions would likely be in a cluster with more individuals, and patients who transmit at a higher rate would also more likely be in a cluster as opposed to isolated.

The majority of clustering analyses identify transmission risk factors by regressing odds of cluster membership [7, 8] or sometimes cluster size or node degree [2, 9, 10] on patient covariates, although particular statistical models vary greatly. Because HIV evolves rapidly and the rate of mutation has been estimated within hosts, it is possible to quantify the probability of virus lineages diverging over a given range of time, such as the time of diagnosis of a putative donor and recipient of infection [11]. Using information about molecular clock rates and diagnosis dates can be used to refine clustering analyses by excluding pairs which are incompatible with clinical and behavioural histories [12].

Clustering analyses are common, because they are easy to implement and computationally cheap once a phylogeny is estimated. Clustering methods can be applied to sequence databases involving tens of thousands of patients. But despite a long history and numerous published examples, clustering analysis as a statistical methodology has several drawbacks. Most methods rely on a tuneable threshold, such as a cutoff for genetic distance below which samples are considered to be clustered [13]. It is problematic to tune this threshold and most analyses use an ad-hoc threshold or evaluate sensitivity over a range of thresholds. If a panel of known transmission pairs is available, the threshold genetic distance used by clustering methods can be tuned to achieve a desired tradeoff in sensitivity and specificity in classifying transmission pairs [14]. Note however, that a threshold in one setting may not be appropriate in all settings, since optimality will depend on the background genetic diversity of the sample and proportion of hosts sampled [15]. Even with carefully calibrated thresholds to identify transmission pairs, clustering does not exclude the possibility that an unsampled individual is a common source of infection for closely related patients, and potentially informative links with distances above threshold are neglected.

The interpretation of clustering often makes an implicit assumption that clusters form a simple uniform random sample of transmission pairs over the recent epidemic history. But numerous factors influence the probability of a sample appearing in a cluster, foremost the time since infection at the time of sampling [15]. Patients who are early in the course of their infection are likely to be closely related to their donor, and thus cluster membership is not necessarily related to the transmission risk of such patients. Any variable correlated with time since infection is likely to be found associated with clustering. That includes CD4 count, viral load, diagnosis status, treatment status, age of the patient and propensity for early testing [6, 16].

In this study, we use a recently-developed method which is computationally tractable and based on estimating the probability that a given sampled case is the source of infection for another case, called the infector probability [17]. While conceptually similar to clustering, rather than dichotomising all pairs as ‘clustered’ or ‘not clustered’, the source attribution (SA) approach weights each pair in the phylogeny by the estimated probability that the putative donor infected the recipient. These probabilities account for additional epidemiological and clinical data that generic clustering methods neglect. The method can make use of variables that are informative about time since infection, such as CD4, viral load, or incidence assays to account for biased sampling. It also makes use of independent estimates of prevalence and incidence, which yield insight into the proportion of the population sampled and the probability that an unsampled individual is the source of infection. Additionally, the method obviates the need to define arbitrary clustering thresholds, so that patients sampled late in infection and who have correspondingly distant relations in the virus phylogeny can nevertheless be included in the analysis. Finally, the sum of infector probabilities for a given potential donor provides an intuitive statistic to examine individual factors influencing transmission rates.

The aim of our study is to assess how source attribution compares with generic clustering method in detecting heterogeneous transmission according to patients characteristics. This assessment was based on detailed simulations that aim to match on epidemiological and molecular data available in the United Kingdom. We particularly wanted to illustrate how outcomes from the two methods can be informative about transmission risk among men who have sex with men.

2. Materials and methods

In this section, we first describe the source attribution and generic clustering methods used to infer epidemiological quantities from labeled viral sequence data. We then present the simulation experiments used to generate epidemic trajectories and phylogenetic trees taken as input for the above methods. Finally, we describe the statistical tests used to evaluate the ability of both approaches to identify transmission risk factors and to correctly estimate transmission risk ratios assigned in two counterfactual scenarios in the simulations.

2.1. Source attribution method

We applied a phylogenetic source attribution (SA) method that infers the probability of potential transmission between each pair of individuals (infector probability) from a time-scaled phylogeny [17]. The calculation of infector probabilities also uses as inputs additional epidemiological data such as incidence and prevalence of infection. These data inform the proportion of the population sampled, and thus influence the estimated probability that closely related patients have a common source of infection or an unsampled intermediary in a transmission chain. The SA method can also account for the time since infection at the time of sampling, using CD4 counts or incidence assay test results (i.e. in the form recently infected or not).

The calculation detailed in [17] is based on the following rationale: For a sampled individual i to have infected a sampled individual j, the lineages ancestral to i and j must be in patients i and j around the time of transmission (assuming small within-host genetic diversity). This probability is modeled with the survivor function ψ_i(t). Initially, ψ_i(t_i) = 1 at the time t_i that i is sampled. Going backwards in time denoted s (towards the root of the phylogeny), the survivor function is modeled as

$$\frac{d}{ds}{\psi }_i(s)=-{\psi }_i(s)P(i\text{infected}\text{at}s\mid x_i,F(s),Y(s)),$$ (1)

where x_i is a vector of covariates for patient i; Y (s) is a potentially vector-valued function of time that denotes the total number infected in the population of different types corresponding to covariates x_i (demes); and F (s) is a matrix-valued function of time that describes the rate of transmission within and between demes. Note that 1 − ψ_i(s) is the probability that the lineage ancestral to patient i is in a different host who may have been unsampled.

Secondly, conditional on both lineages being hosted by i and j between the time of their most recent common ancestor (MRCA) s_ij and time of sampling, a transmission event must have taken place from a donor characterized by covariates x_i and sampling time t_i to a recipient characterized by x_j and t_j, rather than the opposite. Combining these conditions gives the model for estimated infector probability W_ij that patient i infected j:

$$W_{ij}={\psi }_i(s_{ij}){\psi }_j(s_{ij})P(i\to j\mid i\to j\text{or}j\to i,x_i,t_i,x_j,t_j).$$ (2)

The SA method uses a continuous time Markov chain (CTMC) model to reconstruct the likely state of a lineage at the time of transmission given observed covariates at time of sampling. Rates of the CTMC are derived from an epidemic trajectory summarized by three processes: Y (s), F(s) and G(s) which is a matrix valued function of time that describes migration between demes, including progression of infected hosts through different stages of infection. By solving ordinary differential equations, the model updates the probability ψ (s) as a function of F(s), G(s) and Y (s) that a lineage corresponds to the same host that was sampled while traversing the time-scaled phylogeny backwards in time.

This model is conceptually similar to the coalescent approach used to simulate the trees as described in section 2.3.3. But to account for realistic lack of prior knowledge about the epidemic history, we used a misspecified model for lineage transition rates. The model only accounted for progression between CD4-stages, not on diagnosis, treatment, demographic age or other stages; the generic transmission risk factor was assumed to be unobserved; and the model deliberately misspecified transmission rates by stage of infection as constant. Furthermore, infector probabilities were computed under the approximation that incidence and prevalence were constant over the past 20 years of the epidemic history. With poor prior information about transmission patterns, the analysis procedure offered fewer chances to recover the simulation inputs. Thus we expected that the outcomes provide a conservative picture of the performance of the SA method, that could be improved if more refined surveillance estimates are available.

To estimate relative transmission risk, a summary statistic called out-degree was computed from infector probabilities and used for subsequent statistical analysis. The out-degree for individual i is defined as d_i = Σ_j≠i W_ij, and represents the estimated cumulative number of transmissions that are included in the sample and originate from patient i. We used this quantity to provide estimates of relative transmission risk by stage of infection, accounting for their expected durations. The transmission rate for a patient sampled at a given stage was derived as his out-degree normalised by the cumulative duration of all previous stages. We estimated the difference and ratio in transmission rates between patients in first and last stage of infection.

To study assortative transmission patterns, we also computed the total number of transmissions between groups as A_uv = Σ_i∈Su Σ_j∈Sv W_ij, where S_u is the set of sampled hosts in state u (defined by stage, demographic age, risk factor, and continuum of care).

The algorithm for calculating the matrix of infector probabilities in this study is implemented in function phylo.source.attribution.hiv.msm of the R packagephydynR [18].

2.2. Clustering algorithms

We used three hierarchical clustering algorithms. Firstly, we used the hiv-clustering software [2, 19, 20] on pairwise patristic evolutionary distances derived from coalescent trees (described in section 2.3.3). This approach links individuals within a set such that at least one other individual within the set has a distance less than a pre-specified threshold value (single-linkage algorithm) [21]. Secondly, we computed neighborhood sizes, which we define as the number of individuals within a pre-specified threshold evolutionary distance (complete-linkage algorithm). For these two methods, we varied the thresholds of genetic distance under which cluster membership is de-fined with values 0.5%, 1.5% and 5.0% substitutions per site. Third clustering method (denoted here tMRCA) is another single-linkage algorithm but directly uses the branch lengths from time dated trees. It links two individuals whose nodes have both a time to their MRCA that is less than some threshold, indicating a limited amount of divergence between the respective viruses [22]. We tested threshold values of 2, 5 and 10 years.

Networks were characterized by the odds of clustering, the sizes of clusters or neighborhoods, and assortativity (like-with-like composition of clusters) [23]. Unless otherwise specified (particularly in section 3.4), clustering results in section 3 are those from hivclustering method. To compare transmission networks as described by the SA method and hivclustering method, we represented graphically how individuals from one same cluster selected at threshold 5% are connected by infector probabilities and genetic distance below 1.5% threshold using igraph [24].

2.3. Simulations

Our motivation was to obtain a simple though realistic transmission history in a population that is comparable to men who have sex with men (MSM) in London. Simulations were designed to replicate the sampling proportion, clinical data, and age structure of London MSM in the UK HIV Drug Resistance database [25]. Epidemic simulation was based on a compartmental model which describe the dynamics of the number of infected hosts in different categories. Additionally, genealogical trees were simulated conditioning on the epidemic history, and trees were matched to the real data from the UK pertaining to the number of sequence samples, times of sampling and clinical stage of infection.

2.3.1. Compartmental epidemic model

The epidemic history representing London MSM was modeled with a compartmental model that captures disease progression by a system of ordinary differential equations determining transmission and transition through 5 stages of infection, 4 age groups and 3 diagnosis states (undiagnosed, diagnosed untreated and diagnosed under treatment). The 5 stages of infection corresponded to early HIV infection (stage 1) and 4 stages of declining CD4 as detailed in table 1 [26]. Individuals were further stratified in two risk categories influencing transmission. The population was thus structured in 120 states. Figure S1 shows a subset of the transition flow between stages of infection and diagnosis states, omitting the transition between age groups that similarly affects all compartments and risk categories between which there is no transition. Furthermore, we modeled importation of infections into the population, which can have a dramatic effect on HIV genetic diversity.

Table 1.

Initial parameter values for simulated epidemic model

Notation	Parameter	Value
	Age progression rate a
α1	Group 1 [18–27)	1/9/365 day−1
α2	Group 2 [27–33)	1/6/365 day−1
α3	Group 3 [33–40)	1/7/365 day−1
α4	Group 4 [40–80.5)	1/40.5/365 day−1
	Stage progression rate b
γ1	Stage 2 (CD4 > 500 cells/mm3)	1/3.32/365 day−1
γ2	Stage 3 (350 < CD4 ≤ 500 cells/mm3)	1/2.7/365 day−1
γ3	Stage 4 (200 < CD4 ≤ 350 cells/mm3)	1/5.5/365 day−1
γ4	Stage 5 (CD4 ≤ 200 cells/mm3)	1/5.06/365 day−1
	Fraction of individuals transitioning from b
π1	Stage 1 to stage 2	0.76
π2	Stage 1 to stage 3	0.19
π3	Stage 1 to stage 4	0.05
π4	Stage 1 to stage 5	0
α	Age assortativity factor c	0.5
π	Proportion of individuals in low-risk group	0.8
m	Per lineage rate of migration to source compartment	1/50/365 day−1
g	Rate of growth of source compartment	1/3/365 day−1
s	Initial size of source compartment	1000
i	Incidence scaling factor for London MSM d	0.03
	Diagnosis rate
d85	Fixed rate prior to 1985	1/10 year−1
μd	Maximum value of logistic function after 1985 d	1/3 year−1
kd	Steepness of logistic function after 1985 d	1/7 year−1
	Treatment rate
t95	Fixed rate prior to 1995	0
μt	Maximum value of logistic function after 1995	1
kt	Steepness of logistic function after 1995	0.5
e	Treatment effectiveness	0.95
	Transmission weight conferred to individuals in
ws1	Stage 1	1
ws2 to ws4	Stages 2 to 4 e	0.1
ws5	Stage 5 e	0.3
wa1 to wa4	Age groups 1 to 4	1
wc1	Care status 1 (undiagnosed)	1
wc2	Care status 2 (diagnosed and untreated)	0.5
wc3	Care status 3 (diagnosed and treated)	0.05
wr1	Risk status 1 (low risk)	1
wr2	Risk status 2 (high risk)	10

^aFrom quartiles of age of MSM diagnosed in London reported in UKDRDB

^bFrom Cori et al. [26]

^cFactor raised to the power of age class difference, in the form a^{age_i− age_j}

^dInitial value later calibrated to retrieve the observed number of diagnosed cases from surveillance data

^eCorresponding to baseline scenario where transmission varies by stage. In equal-rates simulation scenario weights w_s1 to w_s5 are all equal to 1

2.3.2. Model parameters

Mean time of progressions to CD4 stages and proportion in each CD4 category after seroconversion were obtained from Cori et al. [26]. Transmission was allowed to vary according to weights provided by risk category, treatment status and according to age assortativity. A proportion of 20% of the population were deemed to be at high risk with a ten-fold increase in transmission than low risk counterparts. Relative to undiagnosed individuals, diagnosed and treated patients had a reduction in transmission by respectively a factor 2 and 20. An age assortativity parameter was introduced in the transmission matrix which caused transmission rates to decrease as a power law function of the difference in age (cf table 1). Age groups were based on quantiles of observed age distribution of MSM diagnosed with HIV in London [27] and transmission rates were independent of age.

Two variations in this simulation were explored in terms of how transmission rate varies with time since infection in order to evaluate rates of false-positive identification of transmission risk factors. In a ’baseline scenario’, we let infection stage influence probability of transmission in early HIV infection (ten-fold increase) and AIDS stage (three-fold increase) relative to chronic infection (stages 2 to 4). In an ’equal-rates scenario’, transmission was independent of infection stage. Expressed mathematically, the total transmission rate of a patient with CD4 stage i, continuum of care status j, and generic risk factor k is λ_ijk(t) ∝ r_ir_jr_k, where r. are risk ratios for each category. Individual transmission rates are normalised so that total incidence is given by ι(t) based on a previous study [28] assuming that dynamics of new infections in MSM was the same at the country level and in London.

Incidence and diagnosis rates were modeled as logistic functions of time and jointly calibrated to match the number of MSM living with diagnosed HIV in London in 2012 [29]. Rates of treatment were modelled as zero before 1995 and then increase according to a logistic function with maximum 1 and steepness 0.5. Parameter values are summarized in table 1.

2.3.3. Coalescent tree simulation

We simulated coalescent trees by conditioning on HIV epidemic histories using the approach described by Volz, 2012 [30]. This method is implemented in the phydynR R package [18]. The simulated tree genealogy assumes that each infected patient corresponds to a single lineage of virus HIV-1 [31], ignoring super-infection, and that the time at which two lineages coalesce corresponds to a transmission event. This approximation is reasonable if within-host evolution generates coalescence time considerably shorter than at the population epidemic level. Coalescent simulation is based on a CTMC model with time-dependent rates which describes the time evolution of the states of lineages. The rate of coalescence for a pair of lineages depends on reconstructed states and underlying transmission rates in the epidemic simulations. Further details can be found in [30] and [17]. Coalescent simulations also condition on the times and states of sample lineages. These were chosen to match the times of sampling in the UK resistance database and associated ages and CD4-stages of patients [25, 29]. Trees comprised 12,164 taxa, corresponding to the number of MSM patients diagnosed with HIV-1 subtype B between 1979 and the end of 2012 in London with at least one partial pol gene sequence available in the database. One hundred trees were simulated for both the baseline and equal-rates scenarios.

Branch lengths for coalescent trees are in calendar year. To apply clustering algorithms based on genetic distance, the number of nucleotide substitutions was simulated with a Langley-Fitch model [32]. Branch lengths in substitution per site were estimated as a Poisson distributed variable centred on branch length estimates in years multiplied by a substitution rate of 1.8 ×10⁻³ per site per year. All code used to simulate epidemic histories and genealogical trees is available online [33].

2.4. Statistical analysis

We used statistical models that have been commonly employed to study how phylogenetic cluster characteristics depend on one or more individuals covariates. We considered both univariate models and multivariate models that adjust for stage of infection at time of sampling using CD4 data. Non-parametric Wilcoxon test was used for univariate comparison of transmission by risk level. Linear regression models were used to examine the association between cluster size or out-degree (as dependent variable Y ) and patient covariates in the form: Y_i = βX_i, with X_i comprising age, risk level, and infection stage as both an independent variable and interaction term with age. Logistic regression models were used to examine how the probability of being into a cluster with at least two members vary by patient covariates, in the form logit(p_i) = βX_i. In regression models, out-degree and cluster sizes were standardized into dimensionless quantities by subtracting population mean and dividing by standard deviation. For each simulation scenario, we quantified the number of simulation replicates where the null hypothesis of no association between covariates and dependent variables was rejected.

The transmission model comprised 4 categories of age determined by quartiles of age at diagnosis of MSM in London with at least one available virus sequence. For each simulation replicate, an age mixing matrix e_ij was computed by cumulating the number of common cluster or neighborhood pairwise memberships for each pair of age categories. For SA statistics, we calculated the sum of infector probabilities from donors of each age category to recipients of each category. Assortativity matrices by age were computed as the difference between these age matrices and a null expectation under random linking. Age assortativity was quantified by Newman’s assortativity coefficient which summarizes the extent to which links between age groups differ from random mixing [23]: r = (Σ_i e_ii − Σ_i a_ib_i)/(1 − Σ_i a_ib_i), where a_i = Σ_j e_ij and b_j = Σ_i e_ij.

Since age is often found associated with cluster characteristics, we studied the association between cluster sizes or out-degrees as dependent variable and age categories as independent variable of a linear regression. We also introduced a variable for stage of infection and its interaction term with age to test if an independent effect of age remained after adjustment. Note that in our simulation model, there is no association between age group and transmission rates. All above analyses were performed using R Statistical Software [34].

3. Results

3.1. Detecting the difference in transmission by risk level

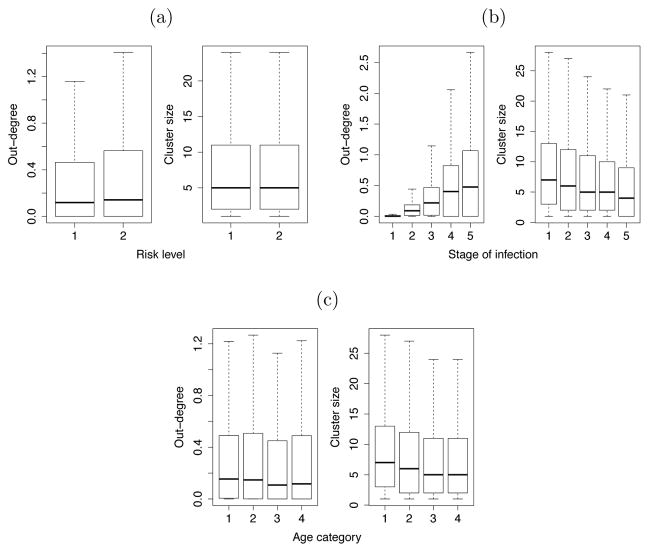
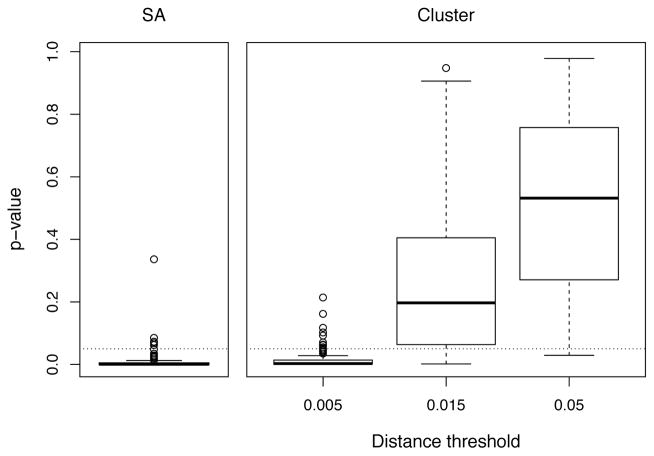
We compared the ability of source attribution and clustering methods to detect the difference in transmission rates by risk level. Figure 1a shows that out-degrees (i.e. estimated number of attributable transmissions) are significantly larger for the high risk category, whereas cluster size is not associated with level of risk. When testing for a difference on each baseline simulation replicate, we found that an univariate analysis would correctly detect significantly larger values of out-degree in 95% of experiments. Analysis of cluster sizes led to the corresponding figures of maximum 89% for the lowest 0.5% threshold and dropping to 17% at 1.5% threshold. These results for respective methods and distance thresholds are illustrated by the distribution of p-values for 100 experiments in figure 2 and percentage of errors in table 2.

Figure 1.

Distribution of out-degrees and cluster sizes by (a) risk level: transmission rate was defined in the model as 10 times higher for risk level 2 relative to risk level 1; (b) stage of infection: relative transmission rates in the model were respectively 10, 1, 1, 1 and 3 for stages 1 to 5 of infection; (c) age category: transmission rates were equal for all 4 age categories in the model. Values are aggregated from 100 simulation replicates. Outliers are not shown. Distance threshold for clustering algorithm is 1.5%.

Figure 2.

Distribution of p-values of univariate test of difference in out-degree or cluster size by risk level. Values are aggregated from 100 simulation replicates. Dotted line indicates p-value = 0.05.

Table 2.

Percentage of error of source attribution (SA) and clustering methods at detecting heterogeneous transmission rates

	Type of error a	SA	Clustering
Analysis			0.5%	1.5%	5.0%
Risk level b
Unadjusted	II	5	11	83	98
Adjusted for stage of infection	II	48	84	86	81
Stage of infection c
Equal-rate scenario	I	17	100	100	100
Baseline scenario	II	19	0	0	0
Age category d
Unadjusted	I	8	75	86	63
Adjusted for stage of infection	I	0	18	25	93

^aType I error corresponds here to falsely associating a variable to an increased transmission (false positive) and type II error corresponds to not detecting a true difference in transmission (false negative). Values reported are % of simulations leading to an erroneous outcome.

^bIndividuals allocated in high-risk category had a ten-fold increase in transmission rate. This allocation was completely random and had no dependance on stage of infection or other clinical variables. Values correspond to the analysis of transmission rate ratio (see section 3.2 in the main text).

^cIn the equal-rate scenario, transmission was independent of infection stage. In the baseline scenario, transmission rates was increased ten-fold in early HIV infection and three-fold in AIDS stage.

^dThere was no association between age category and transmission rates.

When controlling for the stage of infection, the proportion of tests correctly detecting the difference in transmission rates decreased for all methods. Specifically it was 52% when considering out-degrees and a maximum of 16% for cluster sizes at the lowest distance threshold.

In multivariate logistic regressions, cluster membership could be detected as an independent predictor of risk level in respectively 94, 56 and 15% of simulations with threshold 0.5, 1.5 and 5%, with an average odds-ratio of 1.19, 1.10 and 1.06.

3.2. Inferring difference in transmission rates by stage of infection

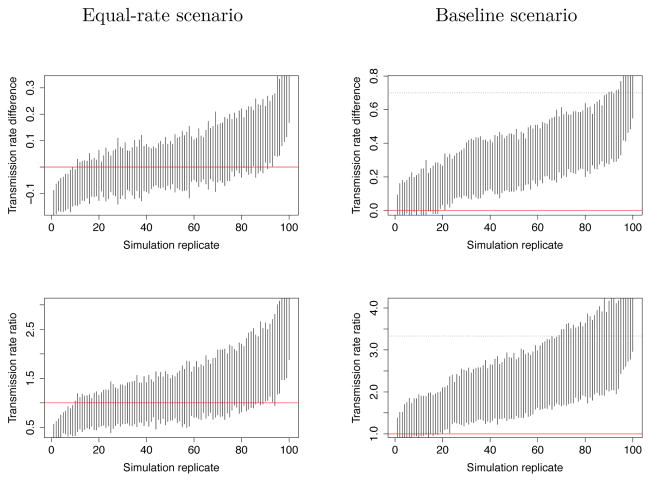
Next, we compared the outcomes of the two methods by stage of infection. For the SA method, figure 3 shows the 95% confidence intervals of relative difference and ratio in transmission rates between early and late stage of infection in 100 simulations of equal-rate scenario (left) and baseline scenario (right). We estimate that the SA method would fail to detect the heterogeneous transmission rates we introduced in the baseline scenario in 19% of the simulations (type II error) and would falsely detect a difference in the equal-rate scenario in 17% of the simulations (type I error) when estimating rate ratio and 19% when estimating rate difference. However, while SA method generally detected the difference in baseline scenario, in figure 3 (right) we see that it underestimates the actual transmission rate difference and ratio between early and late stage of infection.

Figure 3.

Confidence intervals of difference and ratio of transmission rates between early and late stages of infection estimated by source attribution. The results of 100 simulation replicates are sorted in increasing order of the median of rate difference or ratio (x-axis). The red line corresponds to the null-hypothesis of no difference in transmission rate by stage. First row presents estimates of rate difference and second row rate ratio. Left column shows results for the ’equal-rate’ scenario so that confidence intervals crossing the red line indicate true negative results. Right column shows results for the ’baseline’ scenario where confidence intervals not crossing the red line correspond to true positive results. In this ’baseline’ scenario true values of rate difference (top-right) and rate ratio (bottom-right) are indicated by a black dotted line.

For clustering method, since larger cluster sizes were always found in individuals at earlier stages of infection (cf. figure 1b), substituting out-degree by cluster size in all previous analyses led to the same association between earlier stages and increased transmission. This resulted in a 100% type I error in the equal rates scenario, and a 0% type II error in the baseline scenario.

3.3. Age assortativity and relation to cluster characteristics and out-degrees

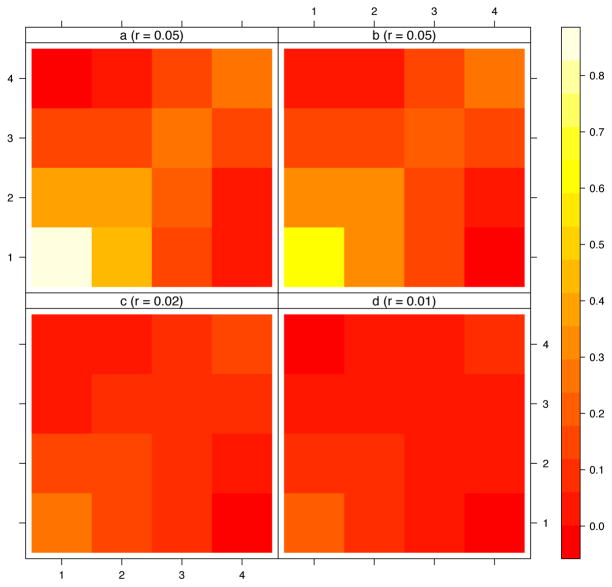
Next, we studied if outcomes of the two methods could reflect the preferential mixing by age and the independence between age and transmission rates. Assortativity matrices in figure 4 show some level of age assortativity both for clustering and source attribution methods. The larger assortativity is seen for the younger category of age. Estimated levels of assortativity are decreasing as increasing distance thresholds are chosen for the clustering method.

Figure 4.

Age assortativity matrices and coefficient from 100 simulations by method. Panel a: infector probabilities; panels b to d: cluster size at 0.5%, 1.5% and 5% thresholds. Labels of x and y axes represent age categories. r values are Newman assortativity coefficients.

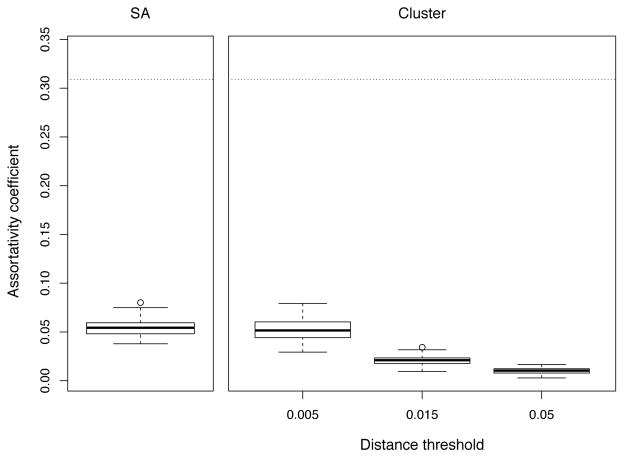
Figure 5 shows the distribution of estimated age assortativity coefficient for respective methods and the true level of the Newman’s coefficient (r = 0.31) as a result of the parameterization in the transmission model. At 0.5% threshold, clustering method allows an estimation slightly closer to the true value and with significantly higher variance than SA. When testing increasingly lower thresholds, we found that estimates became largely imprecise and central value plateaued at r = 0.12 (not shown). Both methods greatly underestimate the true value of the assortativity coefficient.

Figure 5.

Distributions of age assortativity coefficient by method. Values are aggregated from 100 simulation replicates. Dotted line indicates the true level of assortativity coefficient (r = 0.31).

Linear regressions between out-degree and age produced a statistically significant association (type I error) in 8% of analyses using the unadjusted model and in 0% when controlling for stage of infection (cf. table 2). For a typical threshold of 1.5%, we found that cluster size decreased significantly with age in respectively 86% of the simulations for the unadjusted models and 25% for models controlling for the stage of infection.

3.4. Variation of clustering algorithms

In addition to clustering based on patristic distances (with hivclustering), the two other clustering algorithms (neighborhood and tMRCA) gave very similar results. The correlation coefficients between cluster sizes obtained by respective methods were between 77 to 87% but correlation with out-degrees from source attribution was only 9% (figure S2). As in figure 1, figures S3 and S4 show that the same associations between cluster sizes and individuals risk level, stage of infection and age were found for all clustering methods tested.

3.5. Network representations

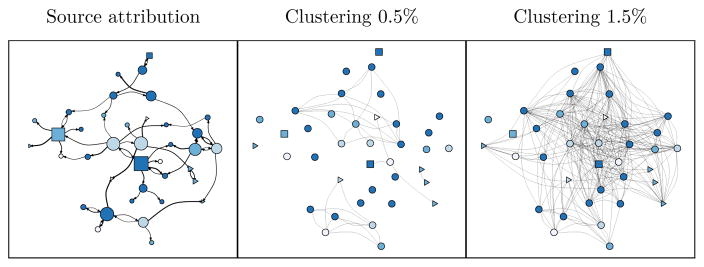
The figure 6 shows the respective transmission networks we obtained in applying source attribution (left panel) and clustering with a 0.5% (middle) and 1.5% threshold (right) to the same simulated sample of patients differentiated by age and stage of infection. This example illustrates the contrasting information provided when considering the probability of potential transmission to others (proportional to the width of the directional links) for any patient and the number of links he has in the cluster, that would correspond to his neighborhood size. The network from source attribution method is also showing that patients in later stages of infection have a larger number of attributable transmissions.

Figure 6.

Comparison of source attribution (left panel) and threshold distance clustering (middle and right panel) applied to one same cluster from simulated coalescent tree. The initial sample comprised 62 individuals forming a cluster at threshold 5%. The node positions, colours, and shapes are the same for all networks. For the SA graph, width of links is proportional to square root of the infector probability. Infector probabilities < 0.1% are not shown. Colour represents age category at time of diagnosis (darker colours represent older patients). Triangle nodes represent patients in early HIV infection, circles represent chronic stages and square nodes represent AIDS stage at time of diagnosis. Node size is proportional to square root of out-degree. For the clustering graphs, the single-linkage algorithm was re-applied to the sample with a genetic distance threshold of 0.5% or 1.5%.

4. Discussion

Our simulation experiments show that detection of heterogeneous transmission is generally estimated with less precision using clustering methods than using source attribution. However, both methods underestimate the true level of assortative mixing.

Our clustering algorithms consistently produce a misleading result in associating younger age categories and cluster sizes when there is no difference in transmission by age. They also indicate a negative correlation between stage of infection and cluster sizes, even though cumulative number of transmissions of a patient is positively related to both its age and its progression in the course of infection. This is because these variables are correlated with the time since infection and clusters are more likely to be observed for recently infected patients. The results of multivariate analyses suggest that even when adjusting for a direct correlates of time since infection like CD4 staging, regression models of phylogenetic cluster characteristics would frequently lead to a false positive association with age. Nevertheless, including CD4 in multivariate analyses improved the performance of clustering analyses. Furthermore, for our purpose of detecting transmission risk factors, we found that much smaller clustering thresholds than are typically used (< 1.5%) minimized the type I error and increased detection power. But this could be only applicable when the sampling fraction of the infected population is sufficiently large to continue to observe related sequences as thresholds are decreased [15, 35].

By studying counterfactual scenarios of transmission variation by stage of infection, we confirm that inferring early stage infectivity from the characteristics of phylogenetic clusters is also potentially misleading [15]. Our results also indicate that source attribution method has a greater power than clustering methods to detect that a characteristic of infected individuals is truly correlated with the risk of transmission. However, the stage of infection is confounding this relation and neither methods are able to capture the magnitude of the actual difference in transmission rates in the risk level variable. Our evaluation of clustering performance leads to the recommendation to always adjust for time since infection when testing for associations with transmission risk factors.

The clustering methods we used and their interpretation do not cover all the range of previous applications such as revealing sexual network structure [13, 22] or detection of outbreaks [36]. In transmission risk analyses, size of clusters has not been frequently used as a continuous value, but there are several published examples where a typology of small, intermediate or large clusters is used to interpret transmission networks [4, 7, 37]. The use of such arbitrary complex cluster definition is questionable as it can force the interpretation of clustering patterns.

Although we used different clustering algorithms, our results may not generalize to all clustering methods. Our simulated genealogies were not obtained by inferring a phylogeny from sequence data, therefore we did not used bootstrap support as a cluster defining factor, as is common in the literature [35]. However, there is no reason why approaches starting by inferring a true genealogy would yield to different clustering patterns in relation to transmission. Indeed the simulation results from Poon [16] indicate that various clustering methods generally failed to identify a subgroup with higher transmission rates. Moreover, methods harnessing bootstrap credibility in tree topology did not performed better than distance-based methods, including the ’patristic’ method that is closely related to the method presented here.

Several alternatives to clustering analysis exist which are theoretically grounded and which have been shown to work well for transmission risk estimation, however their uptake is hampered by their additional complexity and computational cost. One approach is to make use of coalescent theory (e.g. [38]). These models provide a mathematical description of a phylogeny generated by a given epidemiological process. A related approach is the sampling birth-death model which can account for additional stochasticity in the epidemic history if sampling rates are known [39]. Both approaches can provide conditionally unbiased estimates of transmission rates given an exact time-scaled pathogen phylogeny and a correctly-specified epidemiological model. But, such approaches are also more difficult to implement and require additional effort to develop and compare epidemiological models.

The SA method presented has a computational burden similar to that of a tree-based clustering analysis but it accounts for incomplete sampling of infected cases, even with a weak prior epidemiological information. While we show that this SA method has acceptable properties for detecting transmission risk factors, neither clustering nor SA methods provide unbiased estimates of transmission risk ratios. Formal population genetic modeling [38] should be favoured if the aim is to estimate unbiased risk ratios for transmission risk factors.

Phylogenetic clustering analyses has served as a staple method for molecular epidemiological analysis of large pathogen sequence data due to its ease-of-use and computational tractability, but it has numerous shortcomings: clustering analyses rely on ad-hoc distance thresholds that must be chosen by the practitioner and are difficult to calibrate. Because there is no universal standard definition of a cluster, such analyses are prone to misinterpretation, and there is a danger that clustering thresholds will be chosen to demonstrate an effect rather than as a critical test of a hypothesis. Clustering analysis has extremely high type I error rates for any variable correlated with time since infection. And clustering analyses lose power by giving zero weight to all observations above the chosen genetic distance threshold. Recent advances in source attribution methods promise to alleviate these drawbacks, however further progress in this field is also required. Notably, within-host evolution is rarely taken into account, assuming coincidence of coalescent and transmission events. Advances in deep sequencing technologies promise to increase the fidelity of transmission pair identification [40] such as by using minority variants in a putative donor and recipient, but the standard form of data in resistance databases continues to be a single HIV partial pol sequence. To obtain robust estimates of transmission rates in the presence of incomplete sampling, there is currently no shortcut to doing formal population genetic modeling.

Highlights.

• Phylogenetic clustering and source attribution methods are compared in simulations

• Clustering lead to high error rates at detecting difference in HIV transmission

• Source attribution performs better but still underestimate effect sizes