Multiscale mixing patterns in networks

Significance

A central theme of network science is the heterogeneity present in real-life systems, for instance through the absence of a characteristic degree for the nodes. Despite their small-worldness, networks may present other types of heterogeneous patterns, with different parts of the network exhibiting different behaviors. Here we focus on assortativity, a network analogue of correlation used to describe how the presence and absence of edges covaries with the properties of nodes. We design a method to characterize the heterogeneity and local variations of assortativity within a network and exhibit, in a variety of empirical data, rich mixing patterns that would be obscured by summarizing assortativity with a single statistic.

Abstract

Assortative mixing in networks is the tendency for nodes with the same attributes, or metadata, to link to each other. It is a property often found in social networks, manifesting as a higher tendency of links occurring between people of the same age, race, or political belief. Quantifying the level of assortativity or disassortativity (the preference of linking to nodes with different attributes) can shed light on the organization of complex networks. It is common practice to measure the level of assortativity according to the assortativity coefficient, or modularity in the case of categorical metadata. This global value is the average level of assortativity across the network and may not be a representative statistic when mixing patterns are heterogeneous. For example, a social network spanning the globe may exhibit local differences in mixing patterns as a consequence of differences in cultural norms. Here, we introduce an approach to localize this global measure so that we can describe the assortativity, across multiple scales, at the node level. Consequently, we are able to capture and qualitatively evaluate the distribution of mixing patterns in the network. We find that, for many real-world networks, the distribution of assortativity is skewed, overdispersed, and multimodal. Our method provides a clearer lens through which we can more closely examine mixing patterns in networks.

Networks are used as a common representation for a wide variety of complex systems, spanning social (1–3), biological (4, 5), and technological (6, 7) domains. Nodes are used to represent entities or components of the system, and links between them are used to indicate pairwise interactions. The link formation processes in these systems are still largely unknown, but the broad variety of observed structures suggests that they are diverse. One approach to characterize the network structure is based on the correlation, or assortative mixing, of node attributes (or “metadata”) across edges. This analysis allows us to make generalizations about whether we are more likely to observe links between nodes with the same characteristics (assortativity) or between those with different ones (disassortativity). Social networks frequently contain positive correlations of attribute values across connections (8). These correlations occur as a result of the complementary processes of selection (or “homophily”) and influence (or “contagion”) (9). For example, assortativity has frequently been observed with respect to age, race, and social status (10), as well as behavioral patterns such as smoking and drinking habits (11, 12). Examples of disassortative networks include heterosexual dating networks (gender), ecological food webs (metabolic category), and technological and biological networks (node degree) (13). It is important to note that, just as correlation does not imply causation, observations of assortativity are insufficient to imply a specific generative process for the network.

The standard approach to quantifying the level of assortativity in a network is by calculating the assortativity coefficient (13). Such a summary statistic is useful to capture the average mixing pattern across the whole network. However, such a generalization is only really meaningful if it is representative of the population of nodes in the network, i.e., if the assortativity of most individuals is concentrated around the mean. However, when networks are heterogeneous and contain diverse mixing patterns, a single global measure may not present an accurate description. Furthermore, it does not provide a means for quantifying the diversity or identifying anomalous or outlier patterns of interaction.

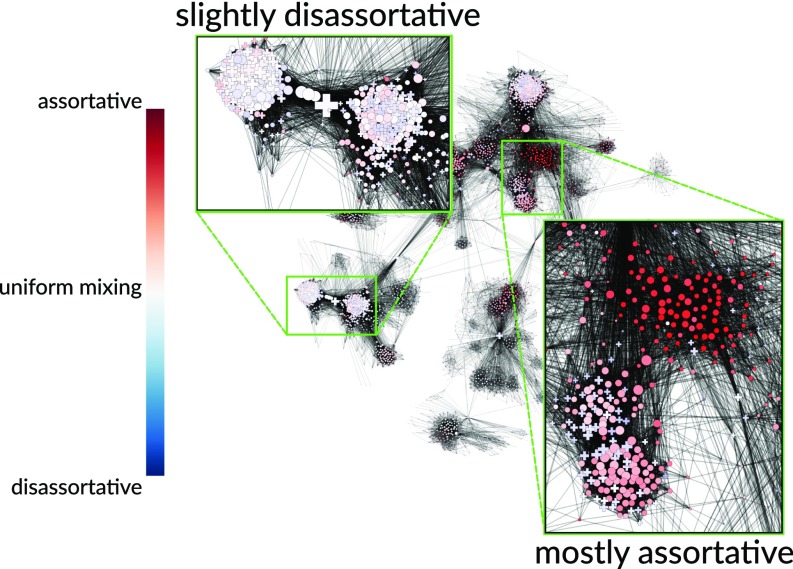
Quantifying diversity and measuring how mixing may vary across a network becomes a particularly pertinent issue with modern advances in technology that have enabled us to capture, store, and process massive-scale networks. Previously, social interaction data were collected via time-consuming manual processes of conducting surveys or observations. For practical reasons, these were often limited to a specific organization or group (1, 2, 15, 16). Summarizing the pattern of assortative mixing as a single value may be reasonable for these small-scale networks that tend to focus on a single social dimension (e.g., a specific working environment or common interest). Now, technology such as online social media platforms allow for the automatic collection of increasingly larger amounts of social interaction data. For instance, the largest connected component of the Facebook network was previously reported to account for ∼10% of the global population (17). These vast multidimensional social networks present more opportunities for heterogeneous mixing patterns, which could conceivably arise, for example, due to differences in demographic and cultural backgrounds. Fig. 1 shows, using the methods we will introduce, an example of this variation in mixing on a subset of nodes in the Facebook social network (14). A high variation in mixing patterns indicates that the global assortativity may be a poor representation of the entire population. To address this issue, we develop a node-centric measure of the assortativity within a local neighborhood. Varying the size of the neighborhood allows us to interpolate from the mixing pattern between an individual node and its neighbors to the global assortativity coefficient. In a number of real-world networks, we find that the global assortativity is not representative of the collective patterns of mixing.

Fig. 1.

Local assortativity of gender in a sample of Facebook friendships (14). Different regions of the graph exhibit strikingly different patterns, suggesting that a single variable, e.g., global assortativity, would provide a poor description of the system.

1. Mixing in Networks

Currently, the standard approach to measure the propensity of links to occur between similar nodes is to use the assortativity coefficient introduced by Newman (13). Here we will focus on undirected networks and categorical node attributes, but assortativity and the methods we propose naturally extend to directed networks and scalar attributes (Supporting Information).

The global assortativity coefficient $r_{\text{global}}$ for categorical attributes compares the proportion of links connecting nodes with same attribute value, or type, relative to the proportion expected if the edges in the network were randomly rewired. The difference between these proportions is commonly known as modularity $Q$, a measure frequently used in the task of community detection (18). The assortativity coefficient is normalized such that $r_{\text{global}}=1$ if all edges only connect nodes of the same type (i.e., maximum modularity $Q_{\text{max}}$) and $r_{\text{global}}=0$ if the number of edges is equal to the expected number for a randomly rewired network in which the total number of edges incident on each type of node is held constant. The global assortativity $r_{\text{global}}$ is given by (13)

$$r_{\text{global}}=\frac{Q}{Q_{\text{max}}}=\frac{{\sum }_g{e}_{gg}-{\sum }_g{a}_g^2}{1-{\sum }_g{a}_g^2},$$ [1]

in which $e_{gh}$ is half the proportion of edges in the network that connect nodes with type $y_i=g$ to nodes with type $y_j=h$ (or the proportion of edges if $g=h$) and $a_g={\sum }_h{e}_{gh}={\sum }_{i\in g}{k}_i/2m$ is the sum of degrees ($k_i$) of nodes with type $g$, normalized by twice the number of edges, $m$. We calculate $e_{gh}$ as

$$e_{gh}=\frac{1}{2m}\sum _{i:y_i=g}\sum _{j:y_j=h}{A}_{ij},$$ [2]

where $A_{ij}$ is an element of the adjacency matrix. The normalization constant $Q_{\text{max}}=\mathrm{\hspace{0.17em}1}-{\sum }_g{a}_g^2$ ensures that the assortativity coefficient lies in the range $-1\le r\le 1$ (see Supporting Information).

Local Patterns of Mixing.

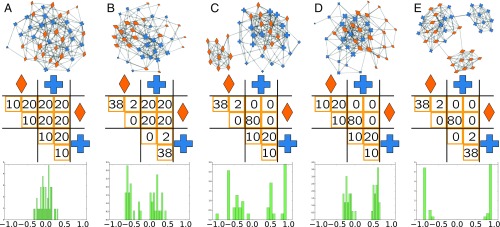
The summary statistic $r_{\text{global}}$ describes the average mixing pattern over the whole network. However, as with all summary statistics, there may be cases where it provides a poor representation of the network, e.g., if the network contains localized heterogeneous patterns. Fig. 2 illustrates an analogy to Anscombe’s quartet of bivariate datasets with identical correlation coefficients (19). Each of the five networks in the top row have the same number of nodes ($n=40$) and edges ($m=160$) and have been constructed to have the same $r_{\text{global}}$ with respect to a binary attribute, indicated by a cross ($c$) or a diamond ($d$). All five networks have $m_{cc}+m_{dd}=80$ edges between nodes of the same type and $m_{cd}=80$ edges between nodes of different types, such that each has $r_{\text{global}}=0$. Local patterns of mixing are formed by splitting each of the types $\{c,d\}$ further into two equally sized subgroups $\{c_1,c_2,d_1,d_2\}$. The middle row depicts the placement of edges within and between the four subgroups. Distributing edges uniformly between subgroups creates a network with homogeneous mixing (Fig. 2A).

Fig. 2.

Five networks (Top) of $n=40$ nodes and $m=160$ edges with the same global assortativity $r_{\text{global}}=0$, but with different local mixing patterns generated by varying how edges are assigned across subgroups of node types (Middle). The different local mixing patterns can be seen by the distributions of $r_{\text{multi}}$ (Bottom). In A, the mixing pattern is homogeneous across all nodes, and this is reflected in the distribution of $r_{\text{multi}}$ by a unimodal distribution that is peaked around 0. In B–E, there are different heterogeneous mixing patterns, with E being the most extreme case in which half the nodes are highly assortative and half the nodes are highly disassortative. These differences can be observed in the different distributions of $r_{\text{multi}}$.

We propose a local measure of assortativity $r(\mathrm{\ell })$ that captures the mixing pattern within the local neighborhood of a given node of interest $\mathrm{\ell }$. Trivially, one could calculate the local assortativity by adjusting Eq. 1 to only consider the immediate neighbors of $\mathrm{\ell }$. However, this approach can encounter problems. For nodes with low degree, we would be calculating assortativity based only on a small sample, providing a potentially poor estimate of the node’s mixing preference. Also, when all of $\mathrm{\ell }$’s neighbors are of the same type, then we would assign $r(\mathrm{\ell })=\mathrm{\infty }$ because $1-{\sum }_g{a}_g^2=0$.

We face similar issues in time series analysis when we wish to interpret how a noisy signal varies over time. Direct analysis of the series may be more descriptive of the noise process than of the underlying signal we are interested in. Averaging over the whole series provides an accurate estimate of the mean, but treats all variation as noise and ignores any important trends. A common solution to this problem is to use a local filter such as the exponential weighted moving average, in which values farther in time from the point of interest are weighted less. We adopt a similar strategy in calculating the local assortativity. To make the connection with time series analysis concrete, we define a random time series where each value is the attribute $y_i$ of a node $i$ visited in a random walk on the graph. A simple random walker at node $i$ jumps to node $j$ by selecting an outgoing edge with equal probability, $A_{ij}/k_i$, and, in an undirected network, the stationary probability ${\pi }_i=k_i/2m$ of being at node $i$ is proportional to its degree. Then, every edge of the network is traversed in each direction with equal probability ${\pi }_i{A}_{ij}/k_i=1/2m$. In this context, a key observation is that we can equivalently rewrite Eq. 2 as

$$e_{gh}=\sum _{i:y_i=g}\sum _{j:y_j=h}{\pi }_i\frac{A_{ij}}{k_i},$$ [3]

which is the total probability that a simple random walker will jump from a node with type $g$ to one with type $h$. We can then interpret the global assortativity of the network as the autocorrelation (with time lag of 1) of this random time series (see SI Text, section D for details).

Global assortativity counts all edges in the network equally, just as the stationary random walker visits all edges with equal probability. To create our local measure of assortativity, we instead reweight the edges in the network based on how local they are to the node of interest, $\mathrm{\ell }$. We do so by replacing the stationary distribution $\pi$ in Eq. 3 with an alternative distribution over the nodes $w(i;\mathrm{\ell })$,

$$e_{gh}(\mathrm{\ell })=\sum _{i:y_i=g}\sum _{j:y_j=h}w(i;\mathrm{\ell })\frac{A_{ij}}{k_i},$$ [4]

and compare the proportion of links between nodes of the same type in the local neighborhood to the global value $\nu (\mathrm{\ell })={\sum }_g(e_{gg}(\mathrm{\ell })-e_{gg})$. Then we can calculate the local assortativity as the deviation from the global assortativity,

$$r(\mathrm{\ell })=\frac{1}{Q_{\text{max}}}\left(\nu (\mathrm{\ell })+\sum _g{e}_{gg}-\sum _g{a}_g^2\right)$$ [5]

$$=\frac{1}{Q_{\text{max}}}\sum _g(e_{gg}(\mathrm{\ell })-a_g^2).$$ [6]

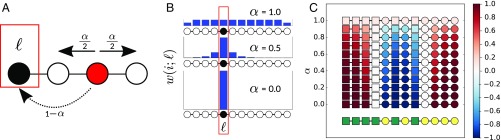
All that remains is to define a distribution $w(i;\mathrm{\ell })$. We choose the well-known personalized PageRank vector, the stationary distribution $w_{\alpha }(i;\mathrm{\ell })$ of a simple random walk, modified so that, at each time step, we return to the node of interest $\mathrm{\ell }$ with probability $(1-\alpha )$ (Fig. 3A). In the special case of a network consisting of nodes linked in a line, $w_{\alpha }(i;\mathrm{\ell })$ corresponds to an exponential distribution (Fig. 3B) and is analogous to the previously mentioned exponential filter commonly used in time series analysis. The personalized PageRank vector is an intuitive choice, given its role in local community detection (20) and connections to the stochastic block model (21). It is, however, not the only way to define a local neighborhood [e.g., a number of graph kernels may be suitable (22)].

Fig. 3.

Example of the local assortativity measure for categorical attributes. (A) Assortativity is calculated (as in Eq. 1) according to the actual proportion of links in the network connecting nodes of the same type relative to the expected proportion of links between nodes of the same type. (B) The nodes in the network are weighted according to a random walk with restart probability of $1-\alpha$. (C) An example of the local assortativity applied to a simple line network with two types of nodes: yellow or green. The blue bars show the stationary distribution ($w(i;\mathrm{\ell })$) of the random walk with restarts at $\mathrm{\ell }$ for different values of $\alpha$. Underneath each distribution, the nodes in the line network are colored according to their local assortativity value.

We can now calculate a local assortativity $r_{\alpha }(\mathrm{\ell })$ for each node and use $\alpha$ to interpolate from the trivial local neighborhood assortativity ($\alpha =0$, the random walker never leaves the initial node) to the global assortativity ($\alpha =1$, the random walker never restarts) $r_1(\mathrm{\ell })=r_{\text{global}}$ (Fig. 3C). We can also view this local assortativity as a (normalized) autocovariance of the random time series of node attributes, defined as before but now generated by a stationary random walker with restarts and only when traversing edges of the original network.

Choice of $𝜶$.

We can use $\alpha$ to interpolate from the global measure at $\alpha =1$ to the local measure based only on the neighbors of $\mathrm{\ell }$ when $\alpha =0$. As previously mentioned, either extreme can be problematic: $r_1$ is uniform across network, while $r_0$ may be based on a small sample (particularly in the case of low degree nodes) and therefore subject to overfitting. Moreover, both extremes are blind to the possible existence of coherent regions of assortativity inside the network, as $r_1$ considers the network as a whole, while $r_0$ considers the local assortativities of the nodes as independent entities.

To circumvent these issues, we consider calculating the assortativity across multiple scales by calculating a “multiscale” distribution $w_{\text{multi}}$ by integrating over all possible values of $\alpha$ (23),

$$w_{\text{multi}}(i;\mathrm{\ell })={\int }_0^1{w}_{\alpha }(i;\mathrm{\ell })\text{d}\alpha ,$$ [7]

which is effectively the same as treating $\alpha$ as an unknown with a uniform prior distribution (see Supporting Information for details). Using this distribution, we can calculate a multiscale measure $r_{\text{multi}}$ that captures the assortativity of a given node across all scales.

As a simple demonstration, we return to Fig. 2 in which the distribution of $r_{\text{multi}}$ for each synthetic network is shown in the bottom row. We see, under homogeneous mixing (Fig. 2A), a unimodal distribution peaked around $0$, confirming that the global measure $r_{\text{global}}$ is representative of the mixing patterns in the network. However, when mixing is heterogeneous (Fig. 2 B–E), we observe multimodal distributions of $r_{\text{multi}}$ that allow us to disambiguate between different local mixing patterns.

2. Real Networks

Next we use $r_{\text{multi}}$ to evaluate the mixing patterns in some real networks: an ecological network and set of online social networks. In both cases, nodes have multiple attributes assigned to them, providing different dimensions of analysis.

Weddell Sea Food Web.

We first examine a network of ecological consumer interactions between species dwelling in the Weddell Sea (4). Fig. 4 shows the distributions (green) of local assortativity for five different categorical node attributes. For comparison, we present a null distribution (black) obtained by randomly rewiring the edges such that the attribute values, degree sequence, and global assortativity are all preserved (see Supporting Information). In each case, we observe skewed and/or multimodal distributions. The empirical distributions appear overdispersed compared with the null distributions.

Fig. 4.

Multiscale assortativity for different attributes in the Weddell Sea Food Web. The observed distribution is depicted by the solid green bars. The black outline shows the null distribution.

It may be surprising to see that, for some attributes, the null distribution appears to be multimodal. Closer inspection reveals that the different modes are correlated with the attribute values and that multimodality arises from the unbalanced distribution of nodes and incident edges across different node types. This effect is particularly pronounced for the attribute “Metabolic Category,” for which we observe two distinct peaks in the distribution. The larger peak that occurs around $r_{\text{multi}}\approx 0$ represents all species that belong to the metabolic category “plant” and accounts for the majority ($348/492$) of the species in the network, upon which approximately two-thirds of the edges are incident. This bias in the distribution of edges across the different node types means that randomly assigned edges are more likely to connect two nodes of the majority class than any other pair of nodes. In fact, it is impossible to assign edges such that nodes in each Metabolic Category exhibit (approximately) the same assortativity as the global value. Specifically, to achieve $r_{\text{global}}=-0.13$, it is necessary that more than half of the edges connect species from different metabolic categories. However, this is impossible for the plant category without changing the distribution of edges over categories.

Facebook 100.

We next consider a set of online social networks collected from the Facebook social media platform at a time when it was only open to 100 US universities (3). The process of incrementally providing these universities access to the platform meant that, at this point in time, very few links existed between each of the universities’ networks, which provides the opportunities to study each of these social systems in a relatively independent manner. One of the original studies on this dataset examined the assortativity of each demographic attribute in each of the networks (3). This study found some common patterns that occurred in many of the networks, such as a tendency to be assortative by matriculation year and dormitory of residence, with some variation around the magnitude of assortativity for each of the attributes across the different universities.

In this case, it makes sense to analyze the universities separately, since it is reasonable to assume that university membership played an important and restricting role in the organization of the network. However, a modern version of this dataset might contain a higher density of interuniversity links, making it less reasonable to treat them independently; in general, partitioning networks based on attributes without careful considerations can be problematic (24).

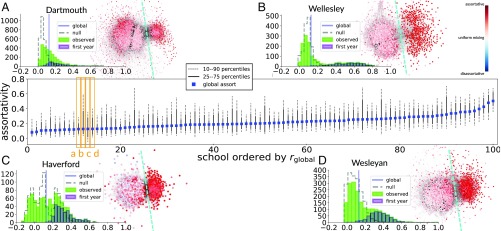
Fig. 5 depicts the distributions of $r_{\text{multi}}$ for each of the 100 networks according to dormitory. For many of the networks, we observe a positively skewed distribution. The surrounding subplots show details for four universities with approximately the same global assortativity $r_{\text{global}}\approx 0.13$, but with qualitatively different distributions of $r_{\text{multi}}$. Common across these distributions is that all of the empirical distributions exhibit a positive skew beyond that of the null distribution. Closer inspection reveals that, in all four networks, the nodes associated with a higher local assortativity belong to a community of nodes more loosely connected to the rest of the network. These nodes also correspond to first-year students, which suggests that residence is more relevant to friendship among new students than it is for the rest of the student body. We see this pattern in many of the other schools too: First-year students are more assortative by year (for all schools except one) and by residence (more than 75% of schools); see Supporting Information for details.

Fig. 5.

Distributions of the local assortativity by residence (dorm) for each of the schools in the Facebook 100 dataset (3). Dotted black lines indicate the 10th and 90th percentiles, while the solid black lines show the interquartile range. The global assortativity is indicated by the blue square markers. (A–D) The distributions for four schools (Dartmouth, Wellesley, Haverford, and Wesleyan) are shown in detail. Each of them has approximately the same global assortativity ($r_{\text{global}}\approx 0.13$), but the distributions indicate different levels of heterogeneity in the pattern of mixing by residence. While the distributions are different, there exists a common trend that the first-year students tend to be more loosely connected to the rest of the network and exhibit higher values of assortativity (nodes to the right of the dashed cyan line).

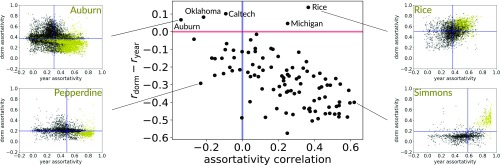
We can also use local assortativity to compare how the mixing of multiple attributes covaries across a network. This may be of interest, as a positive correlation could suggest a relationship between attributes, while a negative correlation indicates that assortativity of one attribute may replace the assortativity of another. Note that differences in normalization between attributes mean that the actual values may not be directly comparable, which is why we focus on correlation. Fig. 6 compares $r_{\text{multi}}$ for year of study and place of residence. The central scatter plot shows, for each university, the correlation between local assortativities of the two attributes (x axis) against the difference in the two global assortativities for each network (y axis), which was previously the only way to compare assortativities (3). The four surrounding subplots show the joint distribution of year and dorm local assortativity for specific universities. The yellow points indicate students in their first year. In most universities, we observed that first-year students were the most assortative by either year, residence, or both. In both Auburn and Pepperdine, there is a negative correlation between year and dorm assortativity, suggesting that many friendships are associated with either being in the same year or sharing a dorm.

Fig. 6.

A scatter plot, in which each school is a point, indicating the correlation of local assortativities by dorm and matriculation year (x axis) and proportion of nodes which are more assortative by dorm than by year (y axis). For reference, the blue vertical line indicates zero assortativity (random mixing), and the red horizontal line indicates zero difference in $r_{\text{global}}$. Joint distributions of the dorm and year assortativities for four of the schools are shown in the surrounding plots, in which each dot represents a student (yellow = first-year; black = others). Blue lines indicate $r_{\text{global}}$.

For Simmons and Rice, we observe a positive correlation between dorm and year local assortativity. However, in Simmons, we see that the first-year students form a separate cluster, while, in Rice, they are much more interspersed. This difference may relate to how students are placed in university dorms. At Simmons, all first-year students live on campus (www.simmons.edu/student-life/life-at-simmons/housing/residence-halls) and form the majority residents in the few dorms they occupy. Rice houses their new intakes according to a different strategy, by placing them evenly spread across all of the available dorms. The fact that students are mixed across years and that the vast majority [almost 78% (campushousing.rice.edu/)] of students reside in university accommodation offers a possible explanation for why we observe a smooth variation in values of assortativity without a distinction between new students and the rest of the population.

3. Discussion

Characterizing the level of assortativity plays an important role in understanding the organization of complex systems. However, the global assortativity may not be representative, given the variation present in the network. We have shown that the distribution of mixing in real networks can be skewed, overdispersed, and possibly multimodal. In fact, for certain network configurations, we have seen that a unimodal distribution may not even be possible.

As network data grow bigger, there is a greater possibility for heterogeneous subgroups to coexist within the overall population. The presence of these subpopulations adds further to the ongoing discussions of the interplay between node metadata and network structure (24) and suggests that, while we may observe a relationship between particular node properties and existence of links in part of a network, it does not imply that this relationship exists across the network as a whole. This heterogeneity has implications for how we make generalizations in network data, as what we observe in a subgraph might not necessarily apply to the rest of the network. However, it may also present new opportunities too. Recent results show that, with an appropriately constructed learning algorithm, it is still possible to make accurate predictions about node attributes in networks with heterogeneous mixing patterns (25) and, in some cases, even utilize the heterogeneity to further improve performance (26). Quantifying local assortativity offers a new dimension to study this predictive performance. Heterogeneous mixing also offers a potential new perspective for the community detection problem (27), i.e., to identify sets of nodes with similar assortativity, which may be useful in the study of “echo chambers” in social networks (28).

Our approach to quantifying local mixing could easily be applied to any global network measure, such as clustering coefficient or mean degree. It may also be used to capture the local correlation between node attributes and their degree, a relationship that plays a definitive role in network phenomena such as the majority illusion (29) and the generalized friendship paradox (30).