Accurate and sensitive quantification of protein-DNA binding affinity

Significance

One-tenth of human genes produce proteins called transcription factors (TFs) that bind to our genome and read the local DNA sequence. They work together to regulate the degree to which each gene is expressed. The affinity with which DNA is bound by a particular TF can vary more than a thousand-fold with different DNA sequences. This study presents the first computational method able to quantify the sequence-affinity relationship almost perfectly over the full affinity range. It achieves this by analyzing data from experiments that use massively parallel DNA sequencing to comprehensively probe protein–DNA interactions. Strikingly, it can accurately predict the effect in vivo of DNA mutations on gene expression levels in fly embryos even for very-low-affinity binding sites.

Abstract

Transcription factors (TFs) control gene expression by binding to genomic DNA in a sequence-specific manner. Mutations in TF binding sites are increasingly found to be associated with human disease, yet we currently lack robust methods to predict these sites. Here, we developed a versatile maximum likelihood framework named No Read Left Behind (NRLB) that infers a biophysical model of protein-DNA recognition across the full affinity range from a library of in vitro selected DNA binding sites. NRLB predicts human Max homodimer binding in near-perfect agreement with existing low-throughput measurements. It can capture the specificity of the p53 tetramer and distinguish multiple binding modes within a single sample. Additionally, we confirm that newly identified low-affinity enhancer binding sites are functional in vivo, and that their contribution to gene expression matches their predicted affinity. Our results establish a powerful paradigm for identifying protein binding sites and interpreting gene regulatory sequences in eukaryotic genomes.

A fundamental goal of genome science is to predict gene expression directly from a DNA sequence, which, in turn, requires identification of all relevant transcription factor (TF) binding sites. This is a challenging problem, in part, because TFs often form multiprotein complexes that interact with DNA over many base pairs. Since favorable molecular contacts accumulate over the entire protein–DNA interface, binding to an optimal DNA sequence can be many orders of magnitude stronger than nonspecific binding. Recent studies have demonstrated that TF binding sites in enhancers can influence gene expression levels in vivo even if their affinity is much lower than optimal (1, 2). Thus, decoding noncoding regulatory sequences requires accurate quantification of TF binding over the entire range of affinities. However, currently available methods fail to identify low-affinity sites from the underlying DNA sequence (1).

How a particular TF is distributed along the genome can be probed using chromatin immunoprecipitation followed by sequencing (3–5). However, the presence of many other chromatin-associated factors in vivo severely complicates the relationship between sequence, affinity, and binding. Binding specificity profiling using in vitro assays has proven to be a fruitful alternative. Although such experiments may not capture the full complexity of the interactions between TFs and DNA that occur in cells, they allow the innate preferences of TFs to be assayed in parallel for a large number of DNA oligomers. Pertinent methods include protein binding microarrays (6, 7), bacterial 1-hybrid assays (8), mechanically induced trapping of molecular interactions [MITOMI (9, 10)], and systematic evolution of ligands by exponential enrichment followed by massively parallel sequencing [SELEX; HT-SELEX/SELEX-seq/SMiLE-seq (11–14)].

Of the existing in vitro protein-DNA recognition profiling technologies, SELEX holds the greatest promise for the full characterization of TF binding specificities. In principle, a single round of affinity-based DNA ligand enrichment should provide optimal information (15), because iterative selection causes exponential suppression of low-affinity ligands and amplifies experimental error. In practice, however, first-round SELEX data are difficult to analyze because the expected number of times a DNA ligand is observed decreases exponentially with its length. As a result, oligomer-based enrichment tables derived from SELEX data selected over multiple rounds (12, 13) have failed to detect functional low-affinity binding sites (1).

Here, we have overcome these limitations by combining a biophysical model of protein–DNA interaction with a statistical model of sequencing read selection within a maximum likelihood framework. This model allows us to define DNA binding specificity across the full range of protein-DNA affinities over arbitrarily large DNA footprints using only a single round of SELEX data. This capability sets it apart from other computational methods that have been proposed for SELEX analysis based on biophysical principles (11, 16). Among the most recent of these, BEESEM (17) relies on enumeration of all possible DNA sequences of a given length for its numerical optimization, which, in practice, limits its application to a 12-bp footprint; SelexGLM (18) overcomes this footprint limitation by ignoring probes that can be bound at multiple offsets, which limits the accurate quantification of low-affinity binding.

We rigorously characterize the performance of our method, which we named No Read Left Behind (NRLB), using both in vitro and in vivo tests and demonstrate that NRLB provides highly accurate estimates of binding affinity and outperforms existing methods on the quantification of low-affinity binding sites. Most significantly, we show that NRLB quantitatively predicts the contribution of ultra-low-affinity binding sites in two Drosophila melanogaster enhancers to gene expression in vivo. Our findings demonstrate that NRLB analysis of SELEX data provides a robust, scalable, and quantitative method for identifying functional in vivo binding sites and for defining relative binding affinities for any TF–DNA complex.

Results

Description of the NRLB Method.

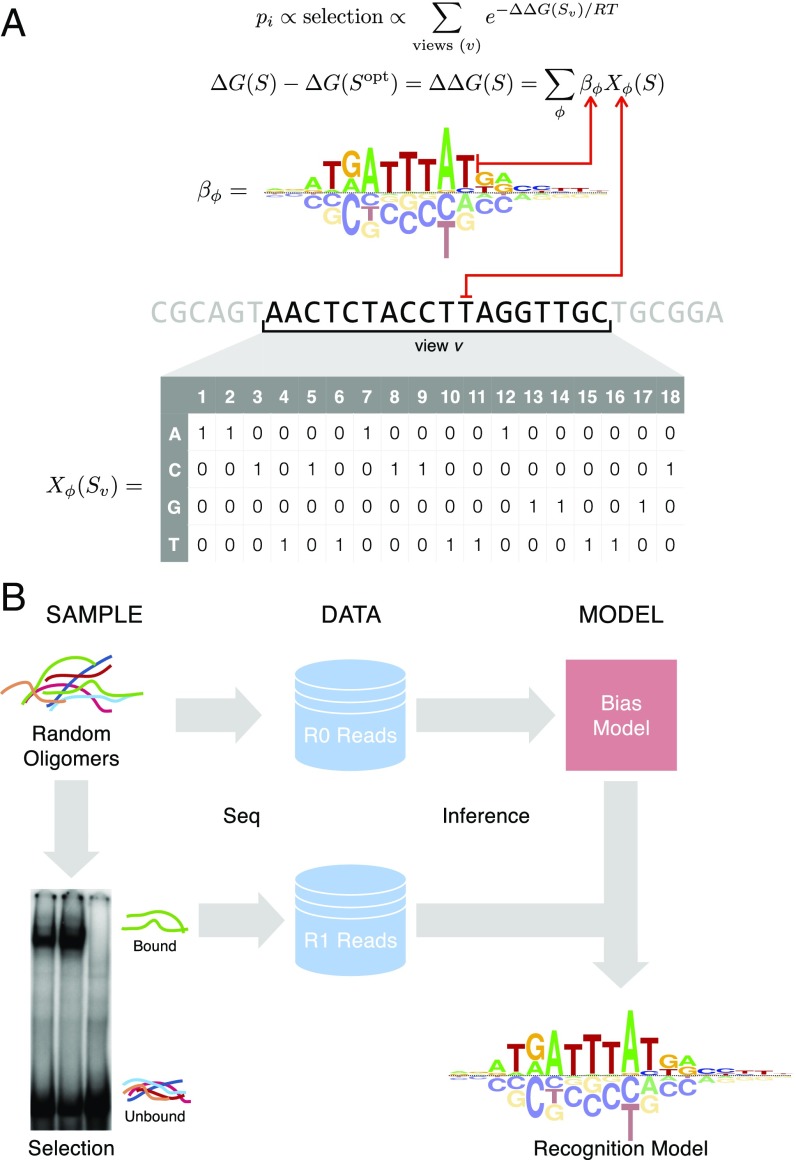
NRLB uses every DNA sequence observed after a single round of SELEX enrichment to characterize the relative affinities of all binding sites, from the optimal site all of the way down to those sites that are bound nonspecifically. At the core of our method is an equilibrium thermodynamics model of protein–DNA interaction (Fig. 1A) used previously to analyze protein binding microarray data (11, 19–21). Assuming that TF binding is affected by a DNA sequence over K base pairs, this model maps each of the 4^K possible bound sequences S to a relative binding free energy $\mathrm{\Delta }\mathrm{\Delta }G\left(S\right)=\mathrm{\Delta }G\left(S\right)-\mathrm{\Delta }G\left(S_0\right)$, where S₀ is a fixed reference sequence usually chosen to be the highest-affinity sequence. The corresponding relative binding affinity is given by $K_{a,\hspace{0.17em}\text{rel}}=\exp (–\mathrm{\Delta }\mathrm{\Delta }G\left(S\right)/RT)$, with R denoting the ideal gas constant and T the absolute temperature. A linear relationship is assumed between the binding free energy and the various sequence features, ϕ, that distinguish sequence S from the reference sequence (usually taken to be the optimal sequence):

$$\frac{\mathrm{\Delta }\mathrm{\Delta }G\left(S\right)}{RT}={\displaystyle \sum _{\varphi }}{\beta }_{\varphi }{X}_{\varphi }\left(S\right).$$

Here, β_ϕ represents the effect of each feature, ϕ, on the binding free energy, as indicated by X_ϕ(S), which equals 1 if S contains the feature and 0 if it does not. The set of features always includes all possible mononucleotide substitutions (“mononucleotide model”). However, dependencies among pairs of adjacent nucleotides can optionally also be taken into account (“dinucleotide model”). The dinucleotide model has the potential to improve prediction, partly because it better captures the effect of variation in DNA shape on binding (22).

Fig. 1.

Overview of the NRLB algorithm for modeling SELEX data. (A) Biophysical model underlying NRLB uses a feature-based representation of binding free energy (Top) and a sliding window sum over all possible binding locations or views v in the probe (Bottom). Mononucleotide free energy parameters β_ϕ can be represented using an energy logo (19). The occurrence of sequence feature ϕ in subsequence S_v is represented by the indicator X_ϕ (gray matrix). (B) Schematic diagram illustrating SELEX-seq library construction and analysis workflow.

The protein–DNA interaction model is embedded in a statistical model of the SELEX method. Each DNA ligand in the initial library of a SELEX experiment consists of a variable region of L base pairs surrounded by constant flanks, resulting in 4^L possible ligands. The input data consist of the complete set of reads sequenced from a random library of DNA ligands at “round zero” (R0) and after one cycle (R1) of affinity-based selection (Fig. 1B). Significantly, the observed distribution of sequences in the initial R0 library f₀(S) is not entirely random; presumably, the processes associated with library generation (probe synthesis, double-stranding, and PCR amplification) introduce sequence-specific biases. We explicitly capture these biases using an oligomer feature-based, log-linear multinomial model (Methods). This is significantly more accurate (SI Appendix, Fig. S1) than the approach we used previously (13).

Binding by the TF complex at various offsets and/or orientations within a probe can contribute to its selection. In the absence of saturation, the frequency f₁(S) of sequence S in the R1 library is proportional both to its frequency f₀(S) in R0 and to the relative affinity with which it is bound:

$$f_1\left(S\right)\propto f_0\left(S\right){\displaystyle \sum _v}\left[{\displaystyle \sum _m}{e}^{\mathrm{\Delta }\mathrm{\Delta }{G}_m\left(S_v\right)/RT}+e^{\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{ns}}/RT}\right].$$

Here, S_v denotes the bound subsequence of length K for “view” v on the probe sequence of length L (Fig. 1A). Explicitly accounting for nonspecific binding ($\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{ns}}/RT$) is essential to achieve accurate prediction of relative affinities. Moreover, since the same TF complex may bind DNA in different configurations, the model can be optionally extended to a weighted sum over multiple binding modes m in parallel (Methods). Finally, a multinomial distribution relates f₁(S) to the observed (and unobserved) R1 counts of all 4^L unique sequences S. In this formalism, every unique sequence S can be considered its own “category.”

The coefficients of the protein-DNA recognition model (β_ϕ and β_ns) are estimated using a likelihood maximization procedure. Despite the conceptual simplicity of our approach, it was necessary to develop tailored dynamic programming techniques and dedicated nonlinear optimization methods to make it feasible to fit the model in an efficient and robust manner. A detailed description is provided in SI Appendix, Supplemental Methods.

Cross-Platform Validation Shows That NRLB Accurately Models Binding Specificity over the Full Affinity Range.

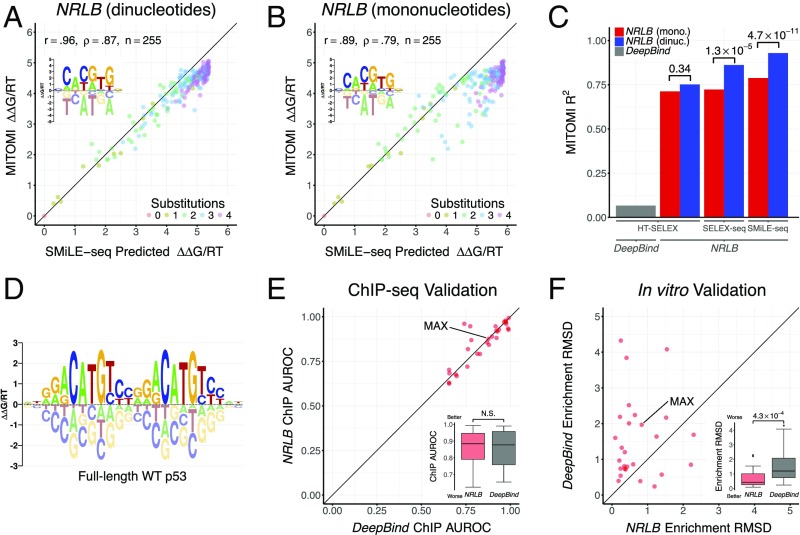
The widely studied human basic helix–loop–helix (bHLH) protein MAX is one of the few TFs whose binding specificity has been simultaneously characterized for many DNA ligands by the “gold-standard” microfluidics-based MITOMI assay (9). It has also been characterized by the bead-based HT-SELEX (23, 24), EMSA-based SELEX-seq [Zhou et al. (22) and this study (Methods)], and microfluidics-based SMiLE-seq (14) platforms. To assess the biophysical accuracy of NRLB predictions, we constructed models on these datasets and compared their predictions for 255 different DNA probes with the observed ∆∆G/RT values obtained from the MITOMI assay. Strikingly, when fit to R1 SMiLE-seq data, an NRLB model with dinucleotide features and a nonspecific binding term (46 independent parameters) achieves near-perfect agreement with MITOMI measurements spanning a 160-fold (∆∆G/RT = 5) range of binding affinity (R² = 0.93; Fig. 2 A and C). This level of agreement is significantly better (Fig. 2C; P = 4.7 × 10⁻¹¹, Fisher’s r-to-z transformation) than for a model with mononucleotide features (13 parameters; R² = 0.79; Fig. 2B) fit to the same data. Importantly, including nonspecific binding is essential to achieve good agreement (SI Appendix, Fig. S2A), because the R1 library is still dominated by low-affinity probes. Models for the same MAX homodimer constructed from the alternative SELEX-seq and HT-SELEX platforms display a slightly lower level of agreement with the MITOMI standard (Fig. 2C and SI Appendix, Fig. S2 B–E). SELEX data can be significantly subsampled before performance degrades, although, as expected, a larger number of reads is required to fit dinucleotide than mononucleotide-only models (SI Appendix, Fig. S3).

Fig. 2.

NRLB models accurately quantify binding affinity over large footprints. (A) Scatterplot comparing the binding energy of human MAX to 255 DNA probes measured using MITOMI (9) (y axis) with the binding energies predicted by an NRLB mononucleotide and dinucleotide model trained on R1 SMiLE-seq data (14) with nonspecific binding (x axis). (Inset) Energy logo representation (19) of the NRLB model. Color denotes the number of substitutions relative to the optimal sequence. Pearson (r) and Spearman rank correlation (ρ), along with the number of data points (n), are indicated. (B) Same as A, but using only mononucleotide features. (C) Bar chart showing the correlation between measured and modeled MAX binding energies, computed as in A, for different models. The NRLB models were trained on HT-SELEX, SELEX-seq, and SMiLE-seq datasets, and the DeepBind (30) model was trained on HT-SELEX data for human MAX (compare SI Appendix, Fig. S2). dinuc., dinucleotide; mono., mononucleotide. (D) Energy logo for an NRLB model with dinucleotide features trained on R1 SELEX-seq data for full-length WT p53. In A, B, and D, the energy logo represents the net effect of each single-base mutation of the optimal sequence. (E) Comparison between NRLB and DeepBind performance when classifying ENCODE ChIP-seq peaks using models trained on HT-SELEX data (23). Each point represents the performance of the respective algorithms for a particular TF in terms of area under the receiver operating characteristic curve (AUROC; Methods). N.S., not significant. (F) Performance comparison for the same NRLB and DeepBind models when predicting the enrichment of probe counts between R0 and R1 in a more deeply sequenced replicate of the same dataset (24). Each point represents the performance of the respective algorithms for a particular TF in terms of root-mean-square deviation (RMSD; Methods). Statistical significance was assessed using a Mann–Whitney U test.

Capturing Specificity over the Full Binding Site of Full-Length p53 Tetramers.

Because NRLB fits ∆∆G/RT coefficients directly to SELEX reads, there is no limit on the size of the footprint over which binding specificity can be modeled. This allows analyses of complexes such as tetramers of tumor suppressor protein p53. A previous study (25) highlighted the role of the C-terminal domain (CTD) of p53 in altering its binding preferences in vivo, although it remained unclear if the CTD impacted the binding preferences of p53’s DNA binding domain (DBD). To further elucidate the CTD’s role in binding, we used SELEX-seq and NRLB to analyze both full-length wild-type (WT) p53 and a version (∆30) from which the CTD has been deleted (26). As expected, WT p53 displayed very poor enrichment after a single round of affinity-based selection: Only 420 of the 16.4 million R1 reads match the binding consensus RRRCATGYYYRRRCATGYYY (R = [A,G], Y = [C,T]) (27). Despite the high degree of nonspecific binding, a dinucleotide-based, multiple-binding mode NRLB model (discussed below) uncovered WT’s specific binding preferences over a 24-bp footprint (Fig. 2D). A direct comparison between the WT and ∆30 models (SI Appendix, Fig. S4A) shows that their coefficients are highly correlated (R² = 0.84; SI Appendix, Fig. S4B), confirming that the CTD does not alter the DBD’s specific binding preferences. In addition, sampling of binding sequences (Methods) indicate that the ratio between nonspecific and optimal binding affinity is nearly two orders of magnitude larger for WT than ∆30, supporting previous conclusions that the CTD enhances nonspecific binding.

Analysis of Exd-Hox Heterodimer Data Uncovers Flanking Specificity.

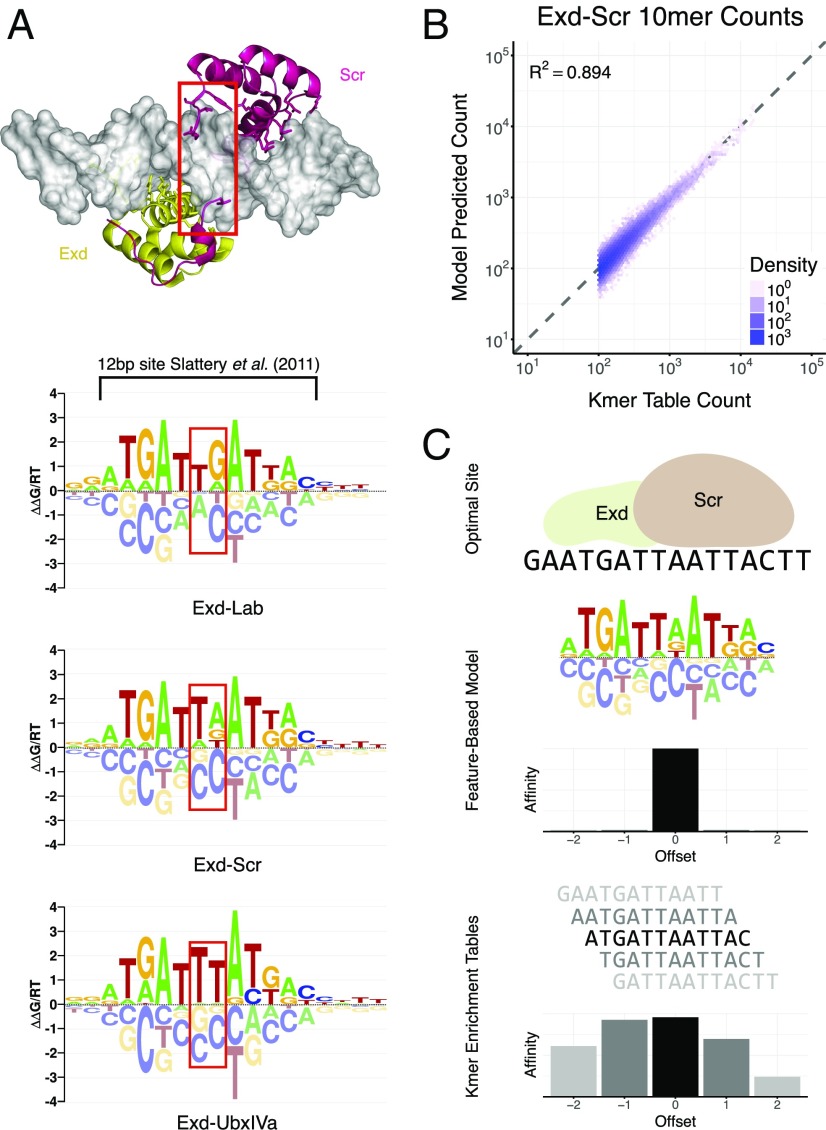
In a previous study, we performed SELEX-seq to probe the binding specificity of D. melanogaster Extradenticle (Exd)-Hox heterodimers (13). Using oligomer enrichment analysis after multiple selection rounds, we uncovered a latent specificity in Hox proteins when they bind in the presence of the cofactor Exd (13). Here, we applied NRLB to the R1 data from the same study and found models that recover this phenomenon (Fig. 3A), including all of the information previously captured using oligomer tables (Fig. 3B and SI Appendix, Figs. S5 and S7). Unlike oligomer enrichment approaches, feature-based model fits select a single “binding frame” among various equivalent (shifted and/or reverse-complemented) representations of the binding site; this has the advantage of yielding a model that is consistently structurally interpretable with reference to the protein–DNA interface (Fig. 3C). In a biological finding, our Exd-Hox models indicate that the sequence specificity extends well outside the previously reported 12-bp footprint (13). We validated this explicitly by performing competitive EMSAs with sequences containing identical 12-bp cores but with different flanks (SI Appendix, Fig. S6). Together, these results show that NRLB models are more sensitive and informative than oligomer enrichment tables.

Fig. 3.

NRLB produces precise, parsimonious, and informative representations of TF behavior. (A) Crystal structure (33) and dinucleotide NRLB models for Exd-Hox heterodimers; red boxes capture previously described differences in spacer preference between Hox proteins from different subclasses, which correspond to differences observed in crystal structures (13). At 18 bp, NRLB models capture a larger footprint than the 12-bp oligomer enrichment tables (black bracket) that were used by Slattery et al. (13). (B) Scatterplot showing the frequencies of observed 10mer counts in R1 Exd-Scr SELEX-seq data versus the frequencies of the same 10mers predicted by the NRLB model in A. Only 10mers with a count of 100 or more were included. (C) Schematic illustrating how oligomer enrichment tables tend to display significant enrichment over multiple offsets, thus confounding structural interpretation, and how feature-based models ensure a consistent definition of the base pair position in the protein–DNA interface. In all panels, Exd-Hox SELEX-seq data from Slattery et al. (13) were used. The Protein Data Bank ID code of the Exd-Scr crystal structure is 2R5Y (33). A truncated version of the Exd-Scr model in B and oligomer enrichment tables for R1 Exd-Scr data from Slattery et al. (13) are used to predict relative affinities.

Identification of Alternative Binding Modes in a Single SELEX Library.

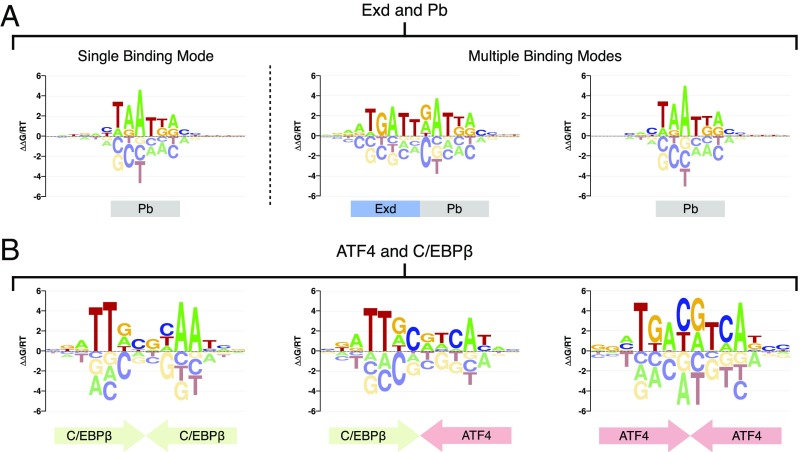
When we used NRLB to reanalyze R1 SELEX-seq libraries (13) where Hox proteins were assayed in the absence of Exd, it yielded the expected monomer motifs (SI Appendix, Fig. S8, Monomer Data). However, a fit to the R1 heterodimer library for Exd-Proboscipedia (Pb) yielded a motif indicative of monomeric rather than heterodimeric binding (Fig. 4A). Indeed, a multiple binding mode fit to the same Exd-Pb data recovers both the Pb monomer motif and the expected Exd-Pb heterodimer motif (Fig. 4A); this yielded a small yet significant increase (P < 1 × 10⁻¹⁶, Fischer’s r-to-z transformation) in the agreement between observed and expected oligomer counts and, at the same time, greatly improved the interpretation of the data (SI Appendix, Fig. S9). Comprehensive multimode analysis of all of the Hox-only and Exd-Hox data yields models with at least two binding modes for each R1 library (SI Appendix, Fig. S8, Heterodimer Data). For some Exd-Hox datasets, NRLB also discovers a motif indicative of Exd monomer binding (SI Appendix, Fig. S8, Bottom). NRLB can also be used to analyze in detail how a TF may dimerize with alternative partners. For example, the basic leucine zipper (bZIP) proteins ATF4 and C/EBPβ can bind either as homodimers or heterodimers (28). We performed SELEX-seq with a mixture of these proteins and generated new R1 libraries. Simultaneously fitting multiple binding modes to these data recovered the heterodimer and both homodimer motifs (Fig. 4B). Moreover, the homodimer models quantitatively agree with NRLB fits to R1 SELEX-seq libraries, where ATF4 and C/EBPβ were assayed separately (R² = 0.735 and R² = 0.476, respectively; SI Appendix, Fig. S10). Together, these results show that NRLB can identify reliable motifs for multiple binding modes in mixtures of two distinct but interacting TFs. It remains to be seen whether NRLB can be applied to even more complex mixtures.

Fig. 4.

NRLB can identify multiple TF complexes in a single sample. (A, Left) Energy logo representation (19) for a single-mode dinucleotide NRLB model fit to R1 SELEX-seq data for Exd-Pb from Slattery et al. (13). (A, Right) Energy logos for two modes from a three-mode dinucleotide NRLB model fit to the same data. (B) Energy logos for all modes from a three-mode dinucleotide NRLB model fit to R1 SELEX-seq data for a mixture of ATF4 and C/EBPβ.

NRLB Enables Improved Quantification of Suboptimal Binding.

It is not yet clear whether the quantitative biophysical models derived from in vitro data are useful for improving predictions of in vivo binding. Recent studies (29, 30) have considered the ability of models to make binary predictions regarding the presence or absence of peaks in ENCODE ChIP-seq data (5) from the underlying DNA sequence (29). By this metric, the “deep learning” algorithm DeepBind (30) was recently shown to outperform both MEME (31) and the method of Jolma et al. (12) when trained on HT-SELEX data for a set of several dozen human TFs (23). We compared NRLB with DeepBind using the same measure of performance (details about the training of NRLB on HT-SELEX data are provided in Methods and SI Appendix, Fig. S11). Comparison of the area under the curve (AUC) for various TFs shows that NRLB does as well as DeepBind [Fig. 2E and SI Appendix, Figs. S12 (overview) and S14 (details)]. However, the binary ChIP-seq peak classification metric may not accurately distinguish between weak and nonspecific binding. To quantitatively assess model performance in this regime, we compared ∆∆G predictions made using models trained on human Max HT-SELEX data with the MITOMI gold standard. Surprisingly, by this metric the DeepBind model showed dramatically poorer agreement with MITOMI (R² = 0.07; Fig. 2C and SI Appendix, Fig. S2F) than did the NRLB model (R² = 0.71; Fig. 2C and SI Appendix, Fig. S2D).

To more comprehensively assess the quantitative performance of DeepBind and NRLB over the full affinity range, we developed in vitro performance metrics to compare the ability of both HT-SELEX trained models to explain R1 probe frequencies from a more deeply sequenced technical replicate of the same dataset (24); details are provided in Methods. Unlike DeepBind, NRLB explicitly accounts for R0 biases; as such, we ignored the contribution of NRLB’s bias model f₀(S) in our predictions to ensure a fair comparison. Even under these constraints, NRLB again significantly outperformed DeepBind when attempting to predict read enrichment between R0 and R1 [Fig. 2F and SI Appendix, Figs. S13A (overview) and S15 (details)] or the observed probe frequency in R1 [SI Appendix, Figs. S13B (overview) and S15 (details)]. The full NRLB model (which accounts for R0 bias) predicts the observed R1 probe frequencies almost perfectly [SI Appendix, Figs. S13C (overview) and S15 (details)].

Identification of Validated D. melanogaster Hox Binding Sites.

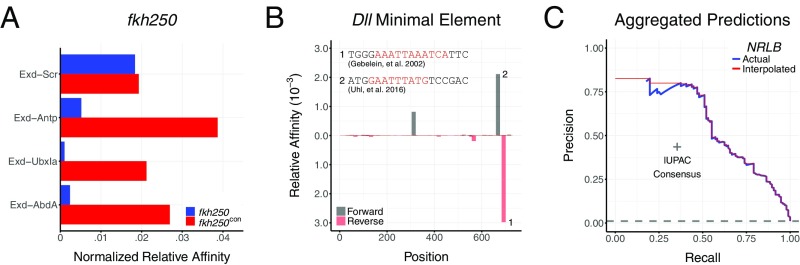
To further test the biological relevance of our NRLB models, we asked how well they detect Exd-Hox binding sites that were previously validated using in vivo reporter assays in D. melanogaster. We started with the well-characterized 37-bp fkh enhancer element, fkh250, which contains a low-affinity Exd-Hox binding site (AGATTAATCG) preferred by Exd-Scr (32). Mutating two base pairs in this element [fkh250^con, AGATTTATGG (mutations underlined)] creates an Exd-Hox consensus site that is also bound by Exd-Antp, Exd-UbxIa, and Exd-AbdA heterodimers (32). NRLB captures these Hox preferences when scoring both fkh250 and fkh250^con (Fig. 5A). Moreover, the relative affinities predicted for Exd-Scr binding to these two sites are similar, consistent with previous K_d measurements (33).

Fig. 5.

NRLB predicts functional binding sites in D. melanogaster enhancers. (A) Relative affinities for the fkh250 and fkh250^con regulatory elements as predicted by NRLB models for four different Exd-Hox heterodimers. (B) Chart showing the relative affinities of Exd-UbxIa as predicted by an NRLB model (y axis) across the DME (x axis). The top binding sites identified by the model (numbered with sequences indicated) have both been verified previously (34, 35). Gray and red indicate forward and reverse strands, respectively. (C) Precision-recall curve for Hox and Exd-Hox models (blue line), consensus matching methods (gray “+”), and a random classifier (gray dashed line) when identifying 96 functionally validated binding sites across 21 curated D. melanogaster enhancer elements. IUPAC, International Union of Pure and Applied Chemistry. For all analyses, NRLB models were trained on R1 SELEX-seq data from Slattery et al. (13) and are shown in SI Appendix, Fig. S8. In A and B, all relative affinities have been rescaled to highest-affinity sequence in the D. melanogaster genome.

Next, we attempted to identify two functionally validated Exd-UbxIa binding sites in the Distalless minimal element (DME): a noncanonical site previously hypothesized to have a 3-bp spacer between the two ATs [AAATTAAATCAT (spacer underlined) (34)] and a second site with a conventional 2-bp spacer located 16 bp upstream [GAATTTATG (spacer underlined) (35)]. The NRLB model for Exd-Ubx consists of only a single binding mode with a 2-bp spacer. Nevertheless, scanning the DME with this model identified both of these sites, along with two previously uncharacterized sites (Fig. 5B). We conclude from this that the Exd-UbxIa heterodimer is likely to bind both sites in the same configuration [AAATTAAATCAT (spacer underlined)], and that it is hard to draw correct conclusions about structural mechanism based only a handful of distinct binding sites.

We extended this analysis to assess how well the Exd-Hox NRLB models (SI Appendix, Fig. S8) identify a total of 96 experimentally validated monomer and heterodimer binding sites for seven Hox factors in 21 enhancer elements reported in the literature (36) (Dataset S3). To account for unobserved variation in local free protein concentration from enhancer to enhancer, we assumed that the highest scoring sequence in any particular enhancer is bound at the same (nonsaturating) level. A site was classified as “bound” whenever its affinity was greater than a certain fraction of the highest-affinity site in the same enhancer; this fraction, in turn, was treated as a variable threshold. According to a precision-recall curve constructed by treating the regions immediately surrounding binding sites as positive and the remaining regions in the elements as negative (Methods, Fig. 5C, and SI Appendix, Fig. S16), NRLB substantially outperforms matches to the Hox consensus site TTWATK distilled from bacterial-one-hybrid assays (37) and the general Exd-Hox consensus TGAYNNAY derived from our previous work (13). Importantly, and as shown for a specific example below, although we treat any binding site predicted by NRLB that was not confirmed in the literature as a false-positive result, these sites might be functional; therefore, the performance shown in Fig. 5C is a lower bound.

Detection and Validation of Ultra-Low-Affinity Binding Sites.

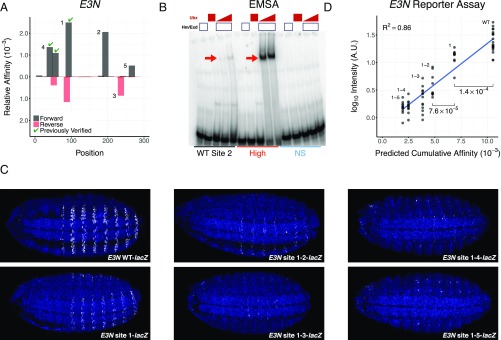
Recent studies have demonstrated that low-affinity binding sites play important roles in vivo in regulating gene expression (1, 2). We hypothesized that other low-affinity sites that cannot be identified using existing approaches and have not been experimentally validated may also contribute to regulation. We therefore reexamined two shavenbaby (svb) enhancers, E3N and 7H, where low-affinity Exd-Ubx binding sites are required to drive robust and specific gene expression in D. melanogaster embryos (1). Significantly, these sites could not be identified using oligomer-enrichment-based affinity tables (1, 13). Using the NRLB model trained on R1 data for Exd-UbxIVa (SI Appendix, Fig. S8), we identified the three previously validated sites in E3N and four additional sites (Fig. 6A); in 7H, we identified two previously validated sites and several additional sites (SI Appendix, Fig. S17A). To verify the newly identified sites, we first used in vitro binding assays to compare the ability of the nonconsensus E3N WT site 2 sequence to bind Exd-UbxIVa with sites that NRLB predicts to be high affinity or to have an affinity in the nonspecific range. As predicted, we found that Exd-UbxIVa binds to both the high-affinity and WT sequences but fails to bind the nonspecific sequence (Fig. 6B).

Fig. 6.

Functional validation of ultra-low-affinity sites predicted by NRLB. (A) Chart showing the relative affinities of Exd-UbxIa as predicted by an NRLB model (y axis) across the shavenbaby (svb) enhancer element E3N in D. melanogaster (x axis). Gray and red indicate forward and reverse strands, respectively. Sites indicated by a green checkmark were functionally validated in a previous study (1). Numbers correspond to the to the order in which sites were mutated. (B) Gel from an EMSA testing the ability of three sequences to bind Exd-UbxIVa (bands indicated by red arrows) in vitro. The WT sequence corresponds to site 2 in A. An NRLB model for Exd-UbxIVa was used to design additional sequences (Dataset S2) that were predicted to have nonspecific (NS) and near-optimal (High) binding affinity. (C) Expression (white) of E3N::lacZ reporter constructs where the binding sites identified in A were sequentially mutated. WT indicates the WT E3N enhancer element, while site 1, site 1-2, etc. indicate the mutations of site 1, sites 1 and 2, etc. (D) Comparison between the NRLB predicted cumulative affinities for Exd-UbxIVa (x axis) and log₁₀ reporter expression level (y axis) for every reporter construct (labels) as quantitated from C. Each point represents the reporter expression level of a single embryo (Methods). The blue line denotes the result of a linear model fit. Mutation of sites 1 and 2 demonstrates statistically significant changes in reporter intensity (Mann–Whitney U test). For all analyses, NRLB models were trained on R1 SELEX-seq data for Exd-UbxIVa from Slattery et al. (13) and are shown in SI Appendix, Fig. S8.

Finally, we tested the contribution of several predicted low-affinity sites in E3N and 7H to enhancer activity by sequentially mutating them and measuring reporter gene expression in vivo (Methods, Fig. 6C, SI Appendix, Fig. S17B, and Dataset S5). These assays confirm that the newly discovered low-affinity binding sites in both the E3N and 7H elements contribute to expression (Fig. 6D and SI Appendix, Fig. S17C; P = 0.001 and P = 0.045, respectively, Mann–Whitney U test). The 7H enhancer shows evidence of saturation (SI Appendix, Fig. S17C), consistent with previous results (1). Despite the demonstrated ultra-low affinity of the individual binding sites in the E3N enhancer, we found a strong quantitative relationship (R² = 0.86, P < 2.2 × 10⁻¹⁶) between expression level as quantified from the 2D embryonic reporter expression pattern and the cumulative binding affinity of the enhancer as predicted by the NRLB model for Exd-Ubx (Fig. 6D). Unlike for E3N, transcriptional activation by the 7H enhancer saturates at high levels of Exd-Ubx binding (1); similarly good predictions from a DNA sequence could be made for 7H using a simple two-parameter model that accounts for this saturation (SI Appendix, Fig. S18).

Assuming clusters of binding sites to contribute additively to enhancer activity was previously successful in predicting how enhancer activity is modified by mutations (38). Significantly, our computational model was able to predict functional ultra-low-affinity binding from a DNA sequence alone and provide an affinity estimate that correlates well with in vivo expression level.

Discussion

We designed NRLB to maximize the amount of information that can be derived from a set of millions of DNA ligands sequenced after a single round of in vitro selection. NRLB estimates model parameters through a maximum likelihood estimation (MLE) approach that considers all possible binding sites within each ligand. This allows sensitive and accurate quantification of DNA binding specificity over the full range (several orders of magnitude) of binding free energy, from optimal to nonspecific, without any prior information. Our MLE framework embeds a biophysically interpretable model of protein–DNA interaction within a statistical model of the complete set of sequencing reads sampled in each experiment. The resulting software tool allows us to perform near-optimal quantification of in vitro protein–DNA interaction specificity for all eight Drosophila Hox proteins and Exd-Hox complexes, as well as dozens of human TFs in the context of this paper, and should facilitate the creation of a comprehensive resource.

Our general methodology can be used to build a sequence-to-affinity model for any TF for which SELEX data are currently available (11–14, 23). Once learned, these models can transform an organism’s genome into a high-resolution (1-bp) affinity landscape to efficiently find biologically relevant binding sites in regulatory DNA. NRLB predictions are sufficiently accurate that further validation of these sites using tedious in vitro binding assays of TF-DNA affinity, such as traditional EMSAs, may no longer be required. It is now possible to imagine accurate quantitative characterization of DNA binding over the full affinity range for all TFs from any organism whenever high-quality SELEX data are available. The fact that we can deal with very large footprint sizes should also make it possible to systematically analyze cooperativity for complexes of two or more TFs for which SELEX libraries are available (14, 39). The multiple binding mode functionality in the current implementation should, in principle, allow NRLB to capture both alternative complexes that can form within the same mixture of TFs and alternative configurations (e.g., relative orientation, internal spacers) with which a given multi-TF complex may bind.

TF-DNA binding models are typically assessed in terms of their ability to predict in vivo ChIP-seq peaks. We believe this is not a sufficiently rigorous test, because peak prediction is a qualitative task and does not account for binding in the low-affinity range. Specifically, NRLB performed similarly to DeepBind on the qualitative task of predicting ChIP-seq binding peaks; by contrast, the NRLB model for the human Max protein dramatically outperformed the corresponding DeepBind model for the quantitative task of predicting MITOMI-derived quantitative measures of affinity. Thus, the ChIP-seq peak classification performance of a model cannot be used to assess how well it quantifies binding affinity. The unprecedented performance of NRLB in predicting functional low-affinity sites in vivo suggests that NRLB will allow the identification of the presence, gain, or loss of binding sites in regulatory DNA with unprecedented sensitivity and accuracy, marking a significant step forward in the identification of noncoding polymorphisms relevant to human disease (40, 41) and evolution (42).

Methods

Protein Expression and Purification.

cDNA clones for human C/EBPβ and ATF4 were obtained from the Dharmacon mammalian clone collection. The full-length protein-coding regions were cloned into pet expression vectors containing a C-terminal His-tag. Proteins were expressed in competent cells supplying additional rare tRNAs (RosettaTM DE3; Novagen) and purified using TALON Metal Affinity Resins (Clontech). For p53, WT (amino acids 1–393) and the C-terminal truncated (∆30, amino acids 1–363) p53 proteins were expressed and purified as previously described (25).

SELEX-Seq and Library Preparation.

EMSAs for the human bZIP proteins and extraction of bound DNA were performed as described previously (13, 21). Purified bound DNA was amplified using a 15-cycle PCR protocol using Phusion polymerase (New England Biolabs) and overhang primers adding the Illumina adapter sites. During each round, a unique Illumina identifier was added in a five-cycle PCR assay, for 20 cycles of PCR in total. The indexed libraries were gel-purified as described previously (13, 21). R0 and R1 indexed experiments were pooled and sequenced using the v2 high-output 75 cycles kit on an Illumina NEXTSeq Series desktop sequencer. R1 SELEX-seq for MAX protein was performed as described previously (22) and sequenced with Illumina’s HiSeq system at the New York Genome Center.

Hox Protein Purification and EMSA Assays.

EMSAs were performed as described previously (13). Proteins were purified as His-tagged fusions from BL21 cells. The UbxIVa isoform was used, and the HM isoform of Hth was copurified in complex with His-tagged Exd protein. Probe sequences used in the assay can be found in Dataset S2. Images were taken using a Typhoon scanner and processed using ImageJ (NIH).

Competitive EMSA.

Binding reactions were performed with 50 nM UbxIVa and 200 nM Hm-Exd protein. ³²P-radiolabeled probe (2 nM) was used in each reaction. The concentrations of low- and high-affinity competitor probes ranged from 2 to 781 nM. Normalized data (fraction bound) from the competition EMSAs (Dataset S2) were fit to competitor concentrations with a sigmoidal dose–response curve using nonlinear least squares with the appropriate start conditions (43). The reported IC₅₀ errors are fit-derived uncertainties. The data and dose–response curves were rescaled such that the parameter b = 1 (compare equation 7 of ref. 43).

E3N WT site 2 EMSA.

Probe (6 nM) was used for the binding reactions. HM-Exd was used at a concentration of 500 nM. UbxIVa concentration ranged from 100 to 500 nM for WT and below nonspecific probes to 30–100 nM for the increased affinity probe.

Fly Strains and Crosses.

D. melanogaster strains were maintained under standard laboratory conditions. All enhancer constructs were cloned into the placZattB expression construct with an hsp70 promoter. Transgenic enhancer constructs were created by Rainbow Transgenic Flies, Inc. and were integrated at the attP2 landing site.

Embryo Manipulations.

Embryos were raised at 25 °C and were fixed and stained according to standard protocols. LacZ protein was detected using an anti–β-Gal antibody (1:1,000; Promega). Detection of primary antibodies was done using secondary antibodies labeled with Alexa Fluor dyes (1:500; Invitrogen).

Microscopy.

Each series of experiments to measure protein levels was performed entirely in parallel. Embryo collections, fixations, staining, and image acquisitions were performed side by side in identical conditions. Confocal exposures were identical for each series and were set to not exceed the 255 maximum level. Series of images were acquired over a 1-d time frame to minimize any signal loss or aberration. Confocal images were obtained on a Leica DM5500 Q Microscope with an ACS APO 20×/0.60 IMM CORR lens and Leica Microsystems LAS AP software. Sum projections of confocal stacks were assembled, embryos were scaled to match sizes, background was subtracted using a 50-pixel rolling-ball radius, and plot profiles of fluorescence intensity were analyzed using ImageJ software (https://imagej.nih.gov/ij/).

NRLB Model of R0 Bias.

To parameterize the biases in the initial (R0) library with probe sequences with an L-bp-long variable region, we maximize the following likelihood function:

$$L={\displaystyle \prod _S}{f}_0{\left(S\right)}^{y_0\left(S\right)}.$$

Here, the product runs over all 4^L possible probes S, while y₀(S) denotes the observed count in R0. The predicted frequency of probe S in R0 is given by $f_0\left(S\right)=w_0\left(S\right)/Z_0$, where $w_0\left(S\right)=\exp \left({\displaystyle {\sum }_{\varphi }{\beta }_{\varphi }{X}_{\varphi }\left(S\right)}\right)$ is the Boltzmann weight and $Z_0={\displaystyle {\sum }_S{w}_0\left(S\right)}$ is the partition function. Our assumption is that the R0 biases are due to an accumulation of processes (oligomer synthesis, Klenow double-stranding, and PCR amplification) that are each translationally invariant within the probe but depend on local sequence context. Assuming independence between the successive positions along the probe in each process leads naturally to the log-linear (i.e., multiplicative) form of the R0 bias model above; this form is also mathematically convenient, as it enables dynamic programming. The set of model features ϕ encompasses all oligomers of length k (or “k-mers”). X_ϕ(S) represents the number of times k-mer ϕ occurs in sequence S, taking into account k − 1 flanking bases up- and downstream of the variable region on the forward strand. Z₀ is computed using dynamic programming techniques. We fit the model parameters β_ϕ by maximizing the multinomial likelihood L(β) using the limited memory Broyden–Fletcher–Goldfarb–Shanno (L-BFGS) algorithm (44). The optimal k is selected using cross-validation. Further information is provided in SI Appendix, Supplemental Methods.

NRLB Model of R1 Probe Selection.

To infer the protein-DNA recognition model based on the trends seen in the selected (R1) library, we maximize the following likelihood function:

$$L={\displaystyle \prod _S}{f}_1{\left(S\right)}^{y_1\left(S\right)}.$$

Again, the product runs over all 4^L possible probes S, while y₁(S) denotes the observed count in R1 (or a later round, if necessary). The predicted frequency of probe S in R1 is given by $f_1\left(S\right)=w_1\left(S\right)/Z_1$, where $w_1\left(S\right)=f_0\left(S\right)\hspace{0.17em}\left({\displaystyle {\sum }_m{\displaystyle {\sum }_v\left[e^{\mathrm{\Delta }\mathrm{\Delta }G\left(S_v\right)/RT}\right]+e^{{\beta }_{ns}}}}\right)$; here, the additional sum is over binding modes m and $Z_1={\displaystyle {\sum }_S{w}_1\left(S\right)}$, the partition function. The views v now include both the forward and reverse orientation and can extend into the up- and downstream regions flanking the variable region. While the combined length of the variable region and relevant flanking regions is unlimited in principle, our current code uses an efficient binary representation of a DNA sequence that limits it to 32 bp. As with NRLB’s R0 bias model, the partition function Z₀ is evaluated using dynamic programming techniques. We fit the model parameters by maximizing the multinomial likelihood L(β) using L-BFGS (44). Due to the redundant parameterization of the model, the likelihood is invariant to changes in the parameters in certain directions (the “null space”). Different model fits can be compared by projecting out components in this null space. Further information is provided in SI Appendix, Supplemental Methods.

NRLB Model Construction.

Various settings were used to construct the NRLB models used in this study; a detailed summary can be found in Dataset S1. All individual NRLB model fits are unseeded and start from all parameters set equal to zero. Further optimization is achieved by shifting the free energy parameters of converged models at all positions by ±1 bp and refitting. Optionally, dinucleotide parameters, initially set to zero, are introduced for the best mononucleotide model fit. When multiple binding modes are used, only a single mode is learned initially and additional modes are added sequentially. Model footprints were increased until the additional parameters were uninformative. In general, models with the highest likelihood were chosen.

Hox data.

For Hox monomers, 13-bp footprints were considered to account for four additional flanking bases on either side of the 5-bp “core” region from Slattery et al. (13). For Exd-Hox heterodimers, 18-bp footprints were considered for the Exd-Hox modes to account for three additional flanking bases on either side of the 12-bp core region defined by Slattery et al. (13). Multimode models were manually selected that contained the largest number of interpretable modes representing Exd monomer, Hox monomer, and Exd-Hox heterodimer binding with the smallest footprint size.

Max data.

Fourteen base pairs was chosen as the footprint size for fits to HT-SELEX and SELEX-seq data, as it appeared to capture all of the specificity. However, for fits to SMiLE-seq data, models with 8-bp footprints have the best likelihood, as the 32-bp limitation of our code prevents fitting more than 1 bp into the flanking regions.

ATF4 and C/EBPβ data.

Fourteen base pairs was chosen for the model footprint size as it appeared to capture most of the specificity. Multimode fits were used on the C/EBPβ dataset to remove additional sequence bias.

p53 data.

Twenty-four base pairs was chosen as the footprint size as it appeared to capture all of the specificity. Fits to the WT p53 dataset required three binding modes to fit to the data and produce a viable motif.

NRLB Model Construction for HT-SELEX Data.

NRLB models were built for 30 of the 35 HT-SELEX datasets used in the DeepBind study (30) (European Nucleotide Archive identifiers ERP001824 and ERP001826). Of the five that were excluded, three did not have R0 data (BHLHE41, CTCF, and PRDM1), while two others used variable regions longer than 32 bp (ELK4 and HNF4A), the limit imposed by our current implementation of NRLB. R0 bias models were built for each unique probe design; we used 2-mer models as these had robust cross-validation performance for most TFs (R0 library size for HT-SELEX is vastly smaller than SELEX-seq libraries). We built selection models with mononucleotide features and nonspecific binding. For all TFs, models were constructed for footprint sizes from 8 to 15 bp and a maximum overlap with the constant flanks of 0–5 bp (a total of 48 hyperparameter combinations). Longer footprints were tested if there appeared to be additional specificity outside the 15-mer (EBF1: 8–16 bp, NFE2: 8–17 bp, PAX5: 8–19 bp, and ZNF143: 8–20 bp). In probes with a 30-bp variable region, the overlap with the flanking regions was restricted to 1 bp. Reverse complement symmetry was enforced only for factors from the following TF families: bHLH (45), bZIP (28), and AP-2 (46) (Dataset S3). Sequence bias frequently produced suboptimal models (compare SI Appendix, Fig. S11A), and it was therefore necessary to employ multiple binding modes; all modes shared the same footprint length and symmetry status. In some cases, contaminants and/or poor enrichment forced the use of later round data (compare SI Appendix, Fig. S11B); in these cases, later rounds were treated in the same way as R1 data. Unlike other factors, Max was fit using criteria designed to align its model with that derived from SELEX-seq data (Dataset S1).

Selection of HT-SELEX Models.

As noted by others (30), HT-SELEX datasets (23) can be subject to contamination and sequence bias (compare SI Appendix, Fig. S11). Consequently, simply using likelihood as the criterion for selecting the best R1 single-mode model from among all footprint and flank hyperparameter combinations discussed above often yields motifs that are incorrect. To automate the selection of an appropriate model for each TF in a way that does not consider classification performance on ChIP-seq data, we settled on the following procedure. First, we defined a “viable” model as one that satisfied these criteria: (i) The highest-affinity sequence matches the relevant consensus sequence found in literature up to a 1-bp mismatch (compare SI Appendix, Fig. S11B and Dataset S3); (ii) the model contains at least three consecutive positions of considerable specificity ([ΔΔG_max − ΔΔG_min]/RT > 3 for mononucleotide features) (compare SI Appendix, Fig. S11C); and (iii) if multiple binding modes were fit simultaneously, only the primary mode (the one with the highest relative affinity) is used. Next, starting with R1 data for a given TF, single-mode models for each footprint size and flank hyperparameter combination that were deemed viable were ranked by likelihood. If no viable models were found, the number of binding modes was incremented by one and the process was repeated. If no viable models were found using three binding modes, the enrichment round was incremented by one and the number of binding modes was reset to one. The first viable motif thus selected for each TF was used in all subsequent analyses.

Visualization of Dinucleotide Models.

Models with dinucleotide features were summarized in terms of the model-predicted relative affinity of all sequences a single point mutation away from the highest-affinity sequence and visualized as an energy logo (19), which was created using the LogoGenerator tool from the REDUCE Suite (reducesuite.bussemakerlab.org). The highest-affinity sequence was determined using a tailor-made dynamic programming algorithm.

Observed and Predicted Sequencing Rate Comparisons.

These comparisons assume that the observed SELEX read counts follow a Poisson distribution whose rate parameter λ (normalized for library size) is determined by the model in question. As such, for a given probe, the predicted sequencing rate and variance are both λ. In practice, there are many more possible SELEX probes than reads, resulting in most reads never being observed (or only once), making it impossible to compute the observed sequencing rate and variance for each probe. To practically compare the observed sequencing rate, we aggregate probes by their model predicted sequencing rates λ. Computing the observed sequencing rate then requires knowledge of the number of probes and their total sequenced count within each bin. Depending on the dataset and model, slight variations in the computation of the observed sequencing rate are required. Once computed, comparing observed and predicted sequencing rates is trivial.

R0 bias models.

Predicted sequencing rates were explicitly computed for the entire universe of 4¹⁶ unique probes for both the NRLB R0 bias model and the Markov model method of Slattery et al. (13). To predict these rates, the Java code underlying the R/Bioconductor package SELEX version 1.6.0 was used to build and run a fifth-order Markov model on R0 SELEX-seq data from Slattery et al. (13). The existing NRLB Java framework was used to do the same. Further analysis computed the the number of probes observed twice (n₂), once (n₁), or not at all (n₀) in each bin and compared the ratios n₁/n₀ and n₂/n₀ with expectation. For Poisson random variables, the expected value of these ratios is equal to λ and λ²/2, respectively.

HT-SELEX R1 comparisons.

In general, the exact enumeration technique used for the R0 analysis described above is not feasible for most widely used SELEX library designs. To avoid the need to explicitly evaluate the sequencing rates of all probes, an adaptive version of the Wang–Landau algorithm (47) was used to compute an approximate density of states (DOS) for NRLB and DeepBind algorithms trained on HT-SELEX data. This allowed us to achieve unbiased estimates of the number of probes in each sequencing rate bin. As inputs, the Wang–Landau algorithm used the raw DeepBind probe scores, the probe binding affinity as estimated only by the raw NRLB binding model, or the overall NRLB probe score f₁(S) (which includes the R0 bias model).

Prediction of R1 Oligomer Counts.

The R/Bioconductor package SELEX version 1.6.0 (bioconductor.org/packages/SELEX) was used to determine the observed R1 count for all 10mers. For each 10mer occurring at least 100 times, a predicted count was computed by summing the predicted frequency of all probes containing it at any offset and then multiplying by the total number of reads in R1. Observed and predicted count values were compared using a linear fit.

Scoring Genomic Sequences with NRLB.

For an NRLB model with footprint K and a target sequence of length L, relative affinity scores were computed at all 2(L − K + 1) views in the forward and reverse directions. If included, the nonspecific binding term inferred on SELEX-seq data was rescaled by explicitly considering the effective length of the DNA ligands in each technology, without adjustable parameters. Total affinity for the target sequence is the sum of all affinity contributions. ΔΔG/RT for the target sequence is the logarithm of this sum.

Exd-Hox analysis.

Dinucleotide NRLB models (18-bp, single-mode) for Exd-UbxIVa and Exd-Scr were truncated to the 12-bp central core region (13), and then used to score all possible 12-mers (compare SI Appendix, Fig. S5).

D. melanogaster enhancer element analysis.

All relative affinity predictions were rescaled by the highest-affinity sequence in the D. melanogaster genome as predicted by the same model (compare Figs. 5 A and B and 6A and SI Appendix, Fig. S17A).

Scoring Sequences with DeepBind.

DNA sequences were scored using the v0.11 scoring tool available at tools.genes.toronto.edu/deepbind/download.html and the interactive database located at tools.genes.toronto.edu/deepbind/. The raw score was used in further analyses, as this value corresponds to ΔΔG/RT. To construct the histograms required for the analysis in SI Appendix, Figs. S13 and S15, we modified the C code of the DeepBind scoring tool to implement the Wang–Landau algorithm (47).

Comparison with MITOMI Binding Free Energy.

MITOMI ligand sequences were scored using NRLB and DeepBind models to obtain predicted ΔΔG/RT values as described above, which were then compared with MITOMI observed ΔΔG/RT values using a linear fit. Scores were shifted such that the target sequence with the highest score was set to ΔΔG/RT = 0.

ChIP-Seq Peak Classification.

NRLB and DeepBind models for 30 TFs in the HT-SELEX dataset (Dataset S3) were compared using AUC metrics. For NRLB, only the primary binding mode was used to score sequences, even if multiple binding modes had been used during the fit to HT-SELEX data. Positive and negative sets were constructed in three different ways: (i) The “DeepBind method” used the same 500 positive and 500 shuffled negative sequences derived from ENCODE ChIP-seq datasets as (30) for each TF, (ii) the “ENCODE Top 500 method” used the same ENCODE ChIP-seq datasets as Alipanahi et al. (30) but restricted the analysis to the 500 highest peaks, and (iii) the “ENCODE Bottom 500 method” used the 500 lowest peaks among those with a significant quality value (qValue). For the last two methods, positive sequences were defined as a 101-bp window centered around the midpoint of each peak; following Bell et al. (48), for each positive sequence, two corresponding negative sequences were defined as a 101-bp window centered exactly one peak’s width upstream or downstream of the peak midpoint. Since this yields 500 positive and 1,000 negative sequences, we use area under the precision-recall curve to quantify classification performance.

Quantitative Validation of HT-SELEX Models.

Quantitative comparisons for 27 of the 30 NRLB and DeepBind models used in the ChIP-seq classification task were run on R1 HT-SELEX data from the more deeply sequenced technical replicate (24) of the original dataset (23) (European Nucleotide Archive identifier PRJEB14744). The three models that were excluded did not have R1 data in this newly sequenced replicate (E2F1, ELF1, and SP1). For the comparisons, it was unknown how much of the flanking regions the DeepBind model was trained on; to account for this, all probe scores were computed, including 10-bp flanking regions. In the analyses below, either the raw DeepBind probe scores or the log of the total probe binding affinity as predicted by the reduced NRLB binding model (no R0 bias) was used.

Density plots.

The predicted DOS was computed using the Wang–Landau algorithm (discussed above). The observed R0 and R1 histograms were computed by binning the observed reads using the score of the respective model.

R0/R1 enrichment.

The binned counts from the density plots were used to compute the log ratio of the R1 and R0 counts (y axis; enrichment) and compared with the expected enrichment (x axis; computed model score). As there is an overall scaling factor between the model scores and the observed enrichment that is unknown, the computed enrichment values are rescaled so as to minimize the root-mean-square deviation between observed and predicted enrichment.

Observed/expected sequencing rate.

The binned counts and the predicted DOS from the density plots were used to compute the observed/exected sequencing rate following the method described above. For the final, optimal (full) NRLB model comparison, the NRLB model with the R0 bias term was used to compute a probe score only over the variable region and the flank length the model was trained on.

Identification of Validated Hox Binding Sites.

We curated 96 functionally validated Hox and Exd-Hox binding sites in 21 different enhancer elements in D. melanogaster based on available reporter data from 31 studies (36) (Dataset S4). The genomic context of a binding site was determined based on the most minimal enhancer element used in the reporter assay, and genomic coordinates were standardized to release 5 (dm3) of the D. melanogaster genome using DNA sequence information reported in the studies. Partial matches to the entire validated binding site sequence were used to identify binding site offsets within the enhancer elements. To account for variation in the position of the 12-bp core binding region within NRLB models, and for experimental error in identifying the true location of the binding site within the enhancer, any model-predicted site overlapping a region extending K − 1 nucleotides up- and downstream of an experimentally validated binding site was considered a match, where K denotes the footprint of the model. Any model-predicted site outside of this extended region was considered a false-positive result.

Enhancer elements were scored using mononucleotide and dinucleotide NRLB models as described above. By default, the appropriate Hox monomer model (SI Appendix, Fig. S8) was used unless the study stated that both Exd and Hox regulated the target; if so, the appropriate Exd-Hox heterodimer model among the multiple binding modes in the model was used (SI Appendix, Fig. S8 and Dataset S4). To account for variations in local protein concentration, all affinities within an enhancer element were normalized to the highest-affinity sequence in the particular enhancer (resulting in the normalized affinities varying between 0 and 1 for all sites in all enhancers). Potential binding windows in the element were considered functionally important if their normalized affinity was at or above a threshold T. Precision and recall were computed for all enhancer elements for all values of T between 0 and 1. A similar analysis was performed to assess the performance of sequence gazing methods. The consensus TTWATK was used for Hox sites, and TGAYNNAY was used for Exd-Hox sites; the former was derived by us from bacterial one-hybrid results (37), and the latter was adopted from the method of Slattery et al. (13). Sites were deemed functional if they matched the consensus. In the absence of a thresholding parameter, only a single precision and recall pair was computed.

Reporter Assay Analysis.

The significance of potential low-affinity sites was established using Mann–Whitney U tests on the recorded intensities (Dataset S5). The cumulative affinity of the various E3N and 7H sequences used in the reporter assays was computed by summing relative affinity over all views on the E3N and 7H genomic regions as scored by the single 18-bp heterodimer mode from a multiple binding mode fit for Exd-UbxIVa (SI Appendix, Fig. S8). The logarithm base 10 of the E3N reporter intensity values was fit to the rescaled total affinities using linear regression. The E3N and 7H reporter intensity values were also fit to a logistic model of expression saturation using nonlinear least squares; parameter values were checked for significance using an F-test.

Data and Software Availability.

SELEX data.

The SELEX-seq data for human Max, ATF4, C/EBPβ, ATF4, and C/EBPβ; full-length WT p53; and ∆30 p53 generated as part of this study will be made available in Gene Expression Omnibus (GEO).

NRLB models.

The NRLB models for more than 50 TFs described here (SI Appendix, Figs. S7, S11, and S12), along with tools for scoring any sequence or genome of interest using an NRLB model, will be made available as an R package via Bioconductor.

NRLB software.

NRLB was implemented entirely in Java. The Java source code and associated R functions for visualizing models and scoring sequences will be made available via GitHub. As designed, NRLB can be run on any machine that has Java installed, but will run slowly unless multithreading is enabled. Runtimes are also highly dependent on the number of reads and the complexity of the model; a single-mode, nucleotide-only model for MAX fit to HT-SELEX data (∼63 thousand reads) can take seconds to fit and uses roughly 2 GB of RAM on a standard MacBook, while a three-mode dinucleotide model for Exd-Pb on SELEX-seq data (∼19 million reads) can take more than 10 h on a server with Dual Xeon Processors and 24 GB of RAM.