Comprehensive, high-resolution binding energy landscapes reveal context dependencies of transcription factor binding

Significance

Transcription factors (TFs) are key proteins that bind DNA targets to coordinate gene expression in cells. Understanding how TFs recognize their DNA targets is essential for predicting how variations in regulatory sequence disrupt transcription to cause disease. Here, we develop a high-throughput assay and analysis pipeline capable of measuring binding energies for over one million sequences with high resolution and apply it toward understanding how nucleotides flanking DNA targets affect binding energies for two model yeast TFs. Through systematic comparisons between models trained on these data, we establish that considering dinucleotide (DN) interactions is sufficient to accurately predict binding and further show that sites used by TFs in vivo are both energetically and mutationally distant from the highest affinity sequence.

Abstract

Transcription factors (TFs) are primary regulators of gene expression in cells, where they bind specific genomic target sites to control transcription. Quantitative measurements of TF–DNA binding energies can improve the accuracy of predictions of TF occupancy and downstream gene expression in vivo and shed light on how transcriptional networks are rewired throughout evolution. Here, we present a sequencing-based TF binding assay and analysis pipeline (BET-seq, for Binding Energy Topography by sequencing) capable of providing quantitative estimates of binding energies for more than one million DNA sequences in parallel at high energetic resolution. Using this platform, we measured the binding energies associated with all possible combinations of 10 nucleotides flanking the known consensus DNA target interacting with two model yeast TFs, Pho4 and Cbf1. A large fraction of these flanking mutations change overall binding energies by an amount equal to or greater than consensus site mutations, suggesting that current definitions of TF binding sites may be too restrictive. By systematically comparing estimates of binding energies output by deep neural networks (NNs) and biophysical models trained on these data, we establish that dinucleotide (DN) specificities are sufficient to explain essentially all variance in observed binding behavior, with Cbf1 binding exhibiting significantly more nonadditivity than Pho4. NN-derived binding energies agree with orthogonal biochemical measurements and reveal that dynamically occupied sites in vivo are both energetically and mutationally distant from the highest affinity sites.

Gene expression is extensively regulated by transcription factors (TFs) that bind genomic sequences to activate or repress transcription of target genes (1). The strength of binding between a TF and a given DNA sequence at equilibrium depends on the change in Gibbs free energy ($\mathrm{\Delta }$G) of the interaction (2–5). Thermodynamic models that explicitly incorporate quantitative binding energies more accurately predict occupancies, rates of transcription, and levels of gene expression in vivo (4, 6–11). In addition, binding energy measurements for TF–DNA interactions can provide insights into the evolution of regulatory networks. Unlike coding sequence variants that manifest at the protein level to influence fitness, noncoding TF target site variants affect phenotype by modulating the binding energies of these interactions to affect gene expression (12–14). Understanding how TFs identify their cognate DNA target sites in vivo and how these interactions change during evolution therefore requires the ability to accurately estimate binding energies for a wide range of sequences.

Most high-throughput efforts to develop accurate models of TF binding specificity have focused on mutations within known TF target sites that dramatically change binding energies. However, even subtle changes in binding energies can have dramatic effects on both occupancy and transcription (15–18). Sequences surprisingly distal from a known consensus motif can affect affinities and levels of transcription (19–22), and genomic variants in regulatory regions outside of known transcription factor binding sites (TFBSs) may be subject to nonneutral evolutionary pressures (23). Therefore, understanding the fundamental mechanisms that regulate transcription requires measurement of binding energies at sufficient resolution to resolve even small effects.

Despite the utility of comprehensive binding energy measurements, existing methods often lack the energetic resolution and scale required to yield such datasets. Currently, three dominant technologies are used to query DNA specificities: methods based on systematic evolution of ligands by exponential enrichment (SELEX) (24–29), protein binding microarrays (PBMs) (30, 31), and mechanically induced trapping of molecular interactions (MITOMI) (32, 33). SELEX-based methods require repeated enrichment and amplification cycles followed by low depth sequencing of the enriched TF-bound material. Thus, these methods are optimized to identify the highest affinity substrates from extremely large random populations but fail to detect weakly bound sequences or measure their affinities. Although PBMs quantify the binding of TFs to DNA microarrays using a fluorometric readout with a broad dynamic range, the precise relationship between measured fluorescence intensities and binding energies is unclear because PBMs require wash steps that disrupt binding equilibrium. In addition, PBM arrays usually contain many replicates for each sequence, limiting the number of distinct sequences probed to $\sim$50,000. The MITOMI platform, based on mechanical trapping by microfluidic valves, enables high-resolution measurements of concentration-dependent binding to yield absolute affinities, but throughput is limited to several hundred sequences. Recent iterations of MITOMI-based assays have addressed throughput limitations by using massively parallel sequencing to increase sequence space coverage but at the cost of resolving binding energies (29, 34). High-throughput sequencing–fluorescent ligand interaction profiling (HiTS-FLIP) couples massively parallel sequencing with the ability to perform concentration-dependent binding measurements; however, adoption of this technology has been limited by the requirement for extensively customized sequencing hardware (35). Taken together, these TF–DNA binding assays can sample vast sequence spaces, but it remains challenging to simultaneously measure binding energies at the scale and resolution necessary to derive complete landscapes.

The most popular and widely used models represent TF specificities as a position weight matrix (PWM), in which each nucleotide at each position contributes additively and independently to overall binding energies (36). These mononucleotide (MN) models are easily implemented, visualized, and interpreted and provide useful approximations of binding specificity for the majority of studied TFs (9, 37–39). However, PWM-based models fail to capture nonadditivity between nucleotides, which can lead to inaccurate predictions, particularly for low-affinity sites (32, 40). This approximation can be refined by including contributions of higher order sequence features, such as dinucleotides (DNs) or longer k-mers (41–50). Recently developed models predict binding based on local DNA shape using structural parameters (e.g., minor groove width, propeller twist, helical twist, and roll) (51–55). However, these biophysical variables are determined by primary sequence, rendering the relationship between the two somewhat degenerate. Deep neural network (NN)-based models can learn complex patterns from large datasets across many applications, including predicting the function of noncoding genomic sequences (56). Training NN models on large sets of binding data therefore has the potential to yield accurate, high-resolution estimates of binding at a per-sequence level, revealing local topography of binding energy landscapes.

To address the need for technologies capable of high-throughput thermodynamic measurements, we developed BET-seq (Binding Energy Topography by sequencing), an integrated sequencing assay and analysis pipeline that yields relative and absolute binding energies ($\mathrm{\Delta }\mathrm{\Delta }$G and $\mathrm{\Delta }$G, respectively) for >1 million sequences in parallel, even for relatively small energetic differences. Using Monte Carlo simulations to mimic the effects of stochastic sampling noise on energetic resolution, we establish guidelines for the sequencing depth required to resolve accurate binding energies for libraries of different sizes and expected energy ranges. We then deployed this assay to measure comprehensive and quantitative binding energy landscapes for >1 million mutations surrounding the known consensus motif for two model yeast TFs (Pho4 and Cbf1). Deep NN models that incorporate all possible higher order, nonadditive contributions were then trained on these large datasets to yield high-resolution estimates of binding energy for each sequence. Comparisons to orthogonal biochemical affinity measurements established that NN predictions are highly quantitative, accurately predicting measured binding energies over a range of 3 kcal/mol. A surprisingly large number of flanking sequences have effects on binding energies as great or greater than mutations in the core, suggesting that current definitions of TFBSs are too restrictive and may limit accurate predictions of TF occupancy in vivo. Comparisons between NN predictions and predictions from a series of biophysically motivated models reveal that DN specificity preferences explain nearly all observed binding behavior, with Cbf1 exhibiting significantly more nonadditivity than Pho4. Strikingly, most dynamically occupied target loci for both Pho4 or Cbf1 are mutationally distant from the energetically optimal flanking sequence, providing evidence of evolutionary molecular selection for near-neutral effects on binding energies. These data demonstrate the utility of our high-throughput approach to measure binding energies and model determinants of substrate specificity required to understand biological behaviors. Furthermore, this assay and analysis pipeline may be extended to a wide variety of TFs, improving predictive models of TF–DNA affinities across species.

Results

A Microfluidic Approach Using High-Throughput Sequencing (HTS) to Derive Comprehensive Binding Affinity Landscapes.

We sought to develop an assay that significantly extends the scale at which TF–DNA interactions can be probed while maintaining the ability to quantitatively measure binding energies at high resolution. TF–DNA interactions can be considered a two-state system, such that the affinity of a given interaction can be determined by the equilibrium partitioning of sequences into bound and unbound states:

$$\mathrm{\Delta }G=-RT\ln \left(\frac{[TF\cdot DN{A}_{bound}]}{[T{F}_{unbound}][DN{A}_{unbound}]}\right).$$

Several groups have established that molecular counting of individual DNA molecules via HTS can reliably measure bound and input concentrations for each species (10, 40, 57). These assays generally use electromobility shift assays (EMSAs) to isolate bound material. However, TF–DNA complexes are not at chemical equilibrium during the electrophoresis step, and complexes with particularly fast dissociation rates may be underrepresented within the bound fraction, leading to a systematic underestimation of weak affinity interactions (58). To address this, we used a microfluidic device incorporating pneumatic valves with fast ($\sim$100 ms) actuation times to mechanically “trap” DNA associated with TF proteins at equilibrium (29, 32–34) (Fig. 1A). This device requires small amounts of DNA substrate and expressed protein, eliminating the need for cell-based protein production. Antibody-patterned surfaces within the device capture monomeric enhanced GFP (meGFP)-tagged TFs produced via in vitro transcription/translation before washing, purifying TFs in situ. After TF capture, libraries of DNA sequences are introduced and allowed to interact with surface-immobilized TFs until equilibrium is reached. Mechanical valves then sequester TF-bound DNA sequences, making it possible to wash out unbound material without loss of weak interactions (32, 33, 59) (Fig. 1B). Bound DNA species can then be eluted from the device and quantified using HTS (Fig. 1C).

Fig. 1.

DNA library design and assay overview. (A) Schematic of flanking sequence library design indicating Illumina sequencing adapters (blue), unique molecular identifiers (UMIs, red), variable flanking regions (orange), and E-box consensus. (B) Photograph of MITOMI device and schematic showing device operation. (C) Schematic showing downstream sample analysis. Counting of individual molecules within bound and input fractions allows calculation of relative binding energies for each sequence (Left and Middle) to yield a comprehensive thermodynamic binding affinity landscape (Pho4 example). Each color-coded point (blue = –$\mathrm{\Delta }\mathrm{\Delta }$G; red = +$\mathrm{\Delta }\mathrm{\Delta }$G) represents a sequence, grouped by Hamming distance from the highest affinity sequence and alphabetically ordered in clockwise polar coordinates.

As a first application of BET-seq, we focused on two model TFs from Saccharomyces cerevisiae, Pho4 and Cbf1. Although Pho4 and Cbf1 bind the same CACGTG variant of the six-nucleotide enhancer-box (E-box) motif both in vitro and in vivo (16, 18, 28, 60–62), they bind largely nonoverlapping sets of genomic loci and regulate distinct target genes (19, 63). To comprehensively probe how flanking nucleotides affect Pho4 and Cbf1 binding affinities, we designed a library of 1,048,576 sequences in which the core E-box sequence was flanked by all possible random combinations of five nucleotides upstream and downstream, embedded within a constant sequence shown to exhibit negligible binding (33) (Fig. 1A). Constant sites at the 5´ and 3´ ends allowed simultaneous PCR amplification and incorporation of Illumina adapters. UMIs included within each sequence allowed accurate counting of library species even in the presence of PCR bias (64). Each UMI barcode was segmented and interspersed along the library sequence to prevent formation of an additional CACGTG consensus site. After sequencing, relative binding affinities ($\mathrm{\Delta }\mathrm{\Delta }$Gs) were calculated for all sequences by considering relative enrichment of individual DNA species, thereby generating a comprehensive binding affinity landscape (example shown in Fig. 1C).

Assay Simulations Determine Sequencing Depth Requirements for Binding Affinity Measurements.

Accurately estimating concentrations of DNA in TF-bound and input samples via sequencing requires that measured read counts reflect true abundances. However, read counts can be distorted by stochastic sampling error, particularly for low read count numbers (65, 66). To understand how stochastic sampling error depends on read depth, library size, and the expected range of binding energies across library sequences, we considered a previously published experiment that quantified interactions between the Escherichia coli LacI repressor and a library of 1,024 binding site variants via deep sequencing (40). Each sequence was sampled with roughly ${10}^3$ reads per species, yielding $\mathrm{\Delta }\mathrm{\Delta }$G measurements with negligible sampling noise. To understand how read depth affects recovery of accurate $\mathrm{\Delta }\mathrm{\Delta }$G measurements, we down-sampled these data to simulate lower sequencing depths of ${10}^2$-${10}^6$ reads, split evenly between bound and input fractions (ca. 0.05–5,000 reads per sequence). We then assessed the accuracy of recovered $\mathrm{\Delta }\mathrm{\Delta }$G values at these lower sequencing depths by calculating the squared Pearson’s correlation coefficient ($r^2$) between $\mathrm{\Delta }\mathrm{\Delta }$G values for each species calculated from down-sampled data and published values calculated from the full dataset. To minimize the effect of a few high accuracy values dominating the correlation statistic, each $r^2$ was normalized by the fraction of observed species (Fig. 2A). For this 1,024-species library with binding energies that span $\sim$3 kcal/mol, $\sim$2 × 10⁵ total reads ($\sim$100 reads per sequence) were sufficient to recover highly accurate $\mathrm{\Delta }\mathrm{\Delta }$G values for every sequence.

Fig. 2.

Probing the relationship between assay accuracy, read depth, library size, and energy range. (A) Normalized median accuracy (Pearson’s $r^2\times f$, where $f$ is the fraction of observed species) comparing results for down-sampled data with “true” values as a function of read depth for MN model coefficients (red) (40) and individual $\mathrm{\Delta }\mathrm{\Delta }$G values (blue). (B) Median squared Pearson’s correlation coefficients between recovered and true values ($r^2$, Left) and median fraction of observed species (Right) as a function of binding affinity range for various library sizes (rows) sequenced to different depths. (C) Median squared Pearson’s correlation coefficient ($r^2$) between recovered and true values (blue) and fraction of observed species (red) as a function of mean reads per sequence for 10 replicate simulations; cyan rectangle denotes flank library assay conditions presented here.

Measuring accurate $\mathrm{\Delta }\mathrm{\Delta }$Gs for a 1,048,576 species library represents a 1,000-fold increase in scale from these prior experiments. To understand more generally the determinants of $\mathrm{\Delta }\mathrm{\Delta }$G measurement accuracy, we generated a simulated test set of true relative binding energies and implemented Monte Carlo simulations to mimic stochastic sampling during HTS. For given library sizes, sequencing depths, and binding energy ranges, we again calculated the correlation coefficient between calculated $\mathrm{\Delta }\mathrm{\Delta }$G values and true values. As expected, accuracy improves and library coverage expands with increasing sequencing depth (Fig. 2B and SI Appendix, Figs. S1 and S2). As the range of expected binding energies increases, accuracy improves but the fraction of sequences observed from the input library decreases. Nearly all existing motif discovery libraries used in SELEX-seq, MITOMI-seq, and SMiLE-seq experiments probe on the order of ${10}^{18}$–${10}^{24}$ species with read depths of several thousand total reads. These simulations establish that such sparse sequencing will sample only the highest affinity sequences, representing an infinitesimal fraction of the input library.

To delineate conditions under which unbound concentrations can be approximated by sequencing the input library, reducing assay cost, we modeled the distribution of “apparent” per-sequence $\mathrm{\Delta }\mathrm{\Delta }$Gs for a given population of sequences under competitive binding conditions in which we explicitly consider effects of ligand depletion. These simulations consider the total number of library sequences, respective concentrations of the TF and the DNA library, and expected range and distribution of $\mathrm{\Delta }\mathrm{\Delta }$G values and return predicted equilibrium concentrations of each species within the bound and unbound fractions (SI Appendix, Fig. S3). To make these simulations computationally feasible, we modeled 100 species uniformly distributed across the $\mathrm{\Delta }\mathrm{\Delta }$G range with a single high concentration “dummy” substrate to represent the majority of species. As the $\mathrm{\Delta }\mathrm{\Delta }$G range and number of species increases, species become depleted from the unbound fraction (SI Appendix, Fig. S3), causing $\mathrm{\Delta }\mathrm{\Delta }$G values estimated from sequencing input to systematically underestimate true $\mathrm{\Delta }\mathrm{\Delta }$G values for high affinity interactions (SI Appendix, Fig. S4). However, under the conditions used here (30 nM and 1 $\mu$M concentrations for TF and DNA libraries, respectively, with 1,048,576 species and a range of $\mathrm{\Delta }\mathrm{\Delta }$Gs $<$ 4kcal/mol), this approximation is justified. Calculated assay accuracies ($r^2\times fractionoflibraryobserved$) for simulated HTS of these distributions reveal two regimes with decreased accuracy (SI Appendix, Fig. S5): Large libraries with small $\mathrm{\Delta }\mathrm{\Delta }$G ranges are subject to sequencing-associated counting error, while libraries with large $\mathrm{\Delta }\mathrm{\Delta }$G ranges are subject to sampling error and effects of ligand depletion.

Previous observations of concentration-dependent Pho4 and Cbf1 binding to E-box motifs with mutations in the first flanking nucleotide revealed differences in affinities spanning $\sim$1 kcal/mol (32). While these observations may not reflect the full energetic range of binding for the larger library queried here, they provide a reasonable initial estimate given that the most proximal flanking nucleotide likely has the largest impact on binding. To guide sequencing assays, we examined in detail simulations sampling a 1,048,576-member library with this energy range at mean read depths per species of ${10}^{-1}$–${10}^3$ (${10}^3$–${10}^8$ total reads) (Fig. 2C). Although 95% of sequences can be recovered from as few as 4–5 reads per species, high read depths of ∼${10}^2$ counts per species (${10}^8$ total reads per TF) are required to yield individual $\mathrm{\Delta }\mathrm{\Delta }$G measurements with accuracies of $\sim$80% and errors of $\sim$0.2 kcal/mol.

Modeling Specificity from Noisy Individual Measurements Improves Assay Resolution.

Very high-depth sequencing may be cost-prohibitive for studies involving many TFs or when considering large DNA libraries. In those scenarios, modeling can be used to infer determinants of binding specificity while minimizing stochastic sampling noise. To illustrate the power of this approach, we again considered the published LacI repressor dataset (40). Although ∼${10}^2$ reads per sequence were required for accurate $\mathrm{\Delta }\mathrm{\Delta }$G estimates, ${10}^1$ to ${10}^2$-fold fewer reads per sequence allowed generation of additive MN PWM models with similar predictive power to those generated from the entire dataset (Fig. 2A). However, while PWMs predict high affinity binding, they fail to explain variance among lower affinity target sites with high sequence diversity (32, 40).

A NN trained on millions of noisy per-sequence measurements can capture all measurable higher order complexity, yielding a high-resolution model capable of accurately predicting binding over a wide range of energies. However, this increased predictive power comes at the cost of interpretability. To improve the accuracy of our energetic estimates while preserving the ability to gain mechanistic insights, we applied an integrated measurement and modeling approach (Fig. 3A). First, we collected millions of sequencing-based estimates of per-sequence $\mathrm{\Delta }\mathrm{\Delta }$Gs. Next, we trained a NN model on these sequencing data to obtain high-resolution energetic predictions for each substrate that capture the effects of all higher order nonadditive interactions among nucleotides. Finally, we parsed and quantified the biophysical mechanisms responsible for observed TF–DNA binding by systematically comparing correlations between predictions made by the NN model and biophysically motivated linear models (MN, nearest neighbor DN, and all DN models). This integrated scheme yielded a binding energy landscape of unprecedented scale and energetic resolution and allowed dissection of the biophysical mechanisms responsible for Pho4 and Cbf1 specificity.

Fig. 3.

Modeling and interpretation of binding specificity based on MN features. (A) Data analysis diagram shows NN modeling from raw data followed by model interpretation. (B) Magnitude of energetic changes ($\mathrm{\Delta }\mathrm{\Delta }$Gs) for core (red) (32) and flanking (blue) mutations for Pho4 and Cbf1. (C) Pho4 and Cbf1 mean MN $\mathrm{\Delta }\mathrm{\Delta }$G values as a function of flanking sequence position (Top), compared with the ScerTF database (67–70) sequence logos (Bottom). Gray boxes show position of core consensus CACGTG. (D) Density scatter plots comparing NN model estimates and MN additive model predictions based on those estimates.

High-Throughput, Comprehensive Estimates of Absolute Binding Affinities for Pho4 and Cbf1.

We used the BET-seq assay and DNA library described above to acquire four replicate measurements of Pho4 and three of Cbf1 at sequencing depths ranging from $\sim$5 to 50 million reads allocated to either bound or input samples (SI Appendix, Table S1). For each experiment, $\mathrm{\Delta }\mathrm{\Delta }$Gs were calculated for each sequence from the measured ratio of bound to input read counts (SI Appendix, Fig. S6). As predicted, measured per-sequence $\mathrm{\Delta }\mathrm{\Delta }$Gs between two experiments at low read depth (ca. 6–8 million limiting counts) show no correlation; at higher read depths ($\sim$24 million limiting counts), this correlation increases to $r^2$ = 0.67 (SI Appendix, Fig. S7 and Table S2). To further improve resolution, we trained a NN regression model that predicted the measured $\mathrm{\Delta }\mathrm{\Delta }$G for each flanking sequence. Accuracy of the NN against observed training data and an unobserved validation dataset was recorded throughout training; training was stopped once accuracy against the validation dataset failed to improve, protecting against overfitting to the training data (SI Appendix, Fig. S8). Predictions from NN models trained on the two high-depth Pho4 replicates showed excellent correlation ($r^2$ = 0.94), validating the ability to apply such models to derive accurate, reproducible estimates of binding energies. For all analyses moving forward, we therefore use per-sequence $\mathrm{\Delta }\mathrm{\Delta }$G estimates output from the NN trained on a composite dataset of all replicates (SI Appendix, Fig. S9).

Absolute binding energies and dissociation constants ($\mathrm{\Delta }$G and K_d, respectively) allow direct comparison between different TFs and across experimental platforms and further enable quantitative predictions of TF occupancy in vivo under known cellular conditions. However, sequencing-based measurements of $\mathrm{\Delta }$Gs from sparse datasets can underestimate the true affinity range due to systematic undersampling of bound reads for low-affinity sequences. In addition, the NN is trained only on relative binding affinities ($\mathrm{\Delta }\mathrm{\Delta }$Gs) and therefore cannot return estimates of absolute energies ($\mathrm{\Delta }$Gs). NN-derived $\mathrm{\Delta }\mathrm{\Delta }$G estimates can be projected onto an absolute scale by calibrating to a set of high-resolution biochemical measurements of $\mathrm{\Delta }$Gs with a linear scaling factor and offset. To generate a set of high-confidence $\mathrm{\Delta }$Gs, we measured concentration-dependent binding for surface-immobilized Pho4 and Cbf1 TFs interacting with all single-nucleotide variants of AGACA_TCGAG, a medium affinity reference flanking sequence (where the underscore indicates the CACGTG core motif), via traditional fluorometric MITOMI (SI Appendix, Figs. S10 and S11). For each sequence, observed binding was globally fit to a single-site binding model, yielding both K_ds and $\mathrm{\Delta }$Gs (SI Appendix, Table S3). All NN values were then scaled by fit parameters returned from a linear regression between NN predictions and experimental measurements for these sequences. Median K_d values for all flanking library sequences were 100 and 63 nM for Pho4 and Cbf1, respectively, in agreement with prior work (32). Strikingly, flanking sequence variation can modulate K_d values by over two orders of magnitude, ranging between 11–1,036 nM and 1–866 nM, respectively. In some cases, the magnitude of these effects exceeds that of mutations within the CACGTG core consensus (Fig. 3B and SI Appendix, Fig. S12), demonstrating the importance of flanking sequences to specificity.

Pho4 and Cbf1 Flanking Preferences Extend Far Beyond the Known Consensus Sequence.

To understand the biophysical features that contribute to the predictive performance of the NN model, we generated PWMs (71), which estimate the mean energetic contribution of each nucleotide at each position, from the full set of scaled NN-predicted $\mathrm{\Delta }\mathrm{\Delta }$G values (Fig. 3C). While the assumption of additivity fails to explain all specificity, these models offer a close approximation (11, 44) and PWMs are easily visualized and interpreted. These MN model results confirm that positions proximal to the E-box core motif exhibit the largest mean effect on binding, in agreement with PWMs generated by orthogonal techniques (67–69) (Fig. 3C). However, nucleotides up to four and five positions from the consensus contribute to specificity for Pho4 and Cbf1, respectively, significantly farther than previously reported.

To quantitatively assess the degree to which MN features dictate binding behavior, we determined the proportion of NN-derived per-sequence $\mathrm{\Delta }\mathrm{\Delta }$G variance explained by a simple PWM (Fig. 3D). If MN models capture all determinants of observed specificity, PWM predictions should explain all of the variance in NN-derived $\mathrm{\Delta }\mathrm{\Delta }$G values; conversely, discrepancies may indicate the presence of higher order interactions. PWMs explained a majority of the variance in NN predictions ($r^2$ = 0.92 and $r^2$ = 0.70 for Pho4 and Cbf1, respectively) (SI Appendix, Table S4), consistent with the prevailing sentiment that PWMs provide good approximations of specificity (9, 11). Intriguingly, PWMs explain a significantly smaller proportion of observed Cbf1 measurement variance, suggesting that Cbf1 recognition may rely on higher order determinants of specificity.

To evaluate BET-seq assay reproducibility, we generated PWMs from each of the Pho4 and Cbf1 technical replicates (SI Appendix, Fig. S13). Linear model coefficients for MNs at each position were strongly correlated between replicates of a TF (Pho4 $r^2$ = 0.95–0.97 and Cbf1 $r^2$ = 0.79–0.87) and uncorrelated between TFs (SI Appendix, Table S5 and Fig. S14); a meGFP negative control protein exhibited no sequence specificity (SI Appendix, Fig. S15). Using the fraction of unexplained variance(1 – $r^2$) as a precision metric, the expected error range in NN-derived mean MN $\mathrm{\Delta }\mathrm{\Delta }$G values for Pho4 is 0.02–0.04 kcal/mol and that of Cbf1 is 0.09–0.16 kcal/mol, highlighting the robustness of binding specificity models derived from the assay and data presented here.

DN Models Reveal that Flanking Nucleotides Exhibit Significant Nonadditivity for Cbf1.

The remaining unexplained variance observed between NN-derived values and PWM-predicted values ($\sim$8% and $\sim$30% for Pho4 and Cbf1, respectively) could indicate higher order nonadditive interactions governing specificity or could simply represent experimental noise (41) (SI Appendix, Table S4). To probe for higher order interactions, we fit two DN models to the NN-derived scaled $\mathrm{\Delta }\mathrm{\Delta }$G values: a nearest neighbor model that considers only contributions from adjacent DNs and a complex model that considers contributions from all DN combinations, including nonadjacent pairs (46).

Comparisons between nearest neighbor DN model-predicted and NN-derived binding energies showed increased correlation for both Pho4 and Cbf1, with $r^2$ values of 0.98 and 0.94 (SI Appendix, Table S4 and Fig. 3 A and B). These improvements, corresponding to $\sim$5% and 24% increases in explanatory power over MN models, are consistent with the potential for physically interacting nucleotides to affect binding energies through local structural distortions. Considering all possible DN features accounts for nearly all of the remaining variance in NN-derived binding energies (improvements of $\sim$1% and 5% for Pho4 and Cbf1, respectively). These findings highlight the differential degree to which nonadditivity defines binding even among structurally related TFs, which ultimately determines the predictive power and accuracy of widely used PWMs.

To visualize and interpret binding energy contributions of DNs alone, we calculated the mean residual $\mathrm{\Delta }\mathrm{\Delta }$G from the linear regression against PWM-predicted $\mathrm{\Delta }\mathrm{\Delta }$G values for all possible DNs within and across flanking sequences (Fig. 4C). Nucleotide interactions with measured $\mathrm{\Delta }\mathrm{\Delta }$Gs lower than expected based on considering the linear combination of individual MNs exhibit cooperativity; conversely, interactions that exhibit negative cooperativity increase measured $\mathrm{\Delta }\mathrm{\Delta }$Gs more than expected. The largest magnitude nonadditivity is observed for DNs immediately upstream or downstream of the E-box (N4/N5 or N6/N7 pairs), with absolute energetic differences among combinations spanning $\sim$0.5 kcal/mol and epistatic interactions occurring primarily within flanks rather than between them. Inter- and intraflank DNs exhibited palindromic arrangements near the core motif, consistent with the expectation of binding site symmetry for homodimeric TFs like Pho4 and Cbf1 (62, 72). For Cbf1, TT and TG DNs upstream of the motif (and the corresponding downstream palindromes) exhibit large positive and negative nonadditivity, respectively. Although the overall magnitude of nonadditivity is significantly smaller for Pho4, a GG DN downstream of CACGTG shows strong synergistic effects. Interestingly, the Pho4 crystal structure reveals direct contacts between the Arg2 and His5 residues and this GG DN, providing a potential structural basis for this observation (62).

Fig. 4.

NN model interpretation using DN features. (A) Density scatter plots of NN model estimates vs. DN (nearest neighbor) additive model predictions based on those estimates. (B) Fraction of variance in Pho4 and Cbf1 NN model estimates explained by MN and DN models. (C) Heatmap of mean residual energetic contributions when MN effects are removed for Cbf1.

Incorporating Weight Constraints into DN Models Confirms that Cbf1 Interactions Are Significantly More Epistatic.

Models that incorporate additional free parameters should always increase explanatory power. While MN models attempt to describe all 1,048,576 observed measurements using only 40 free parameters (4 nucleotides per position across 10 positions), the nearest neighbor DN model adds another 128 free parameters (16 pairs across 8 positions), and the all DNs model includes 720 free parameters [all combinations of nucleotide identities ($4^2$ = 16) and positional pairs ($\left(\begin{array}{c}10\\ 2\end{array}\right)$ = 45)]. In most cases, DN coefficients are near zero (Fig. 4C), meaning they contribute little explanatory power. To identify the minimal set of features that define sequence specificity in an unbiased fashion, we used least absolute shrinkage and selection operator (LASSO) regression to develop parsimonious linear models with weight constraints (73). Nonzero coefficients in the model are penalized, leading to inclusion of only the most explanatory variables with respect to reduction in squared error (SI Appendix, Fig. S16). The regression explores a range of penalization stringencies to distinguish important sequence features based on differential coefficient minimization rates.

From the selected Cbf1 features, four nearest neighbor DNs exhibited large initial coefficient magnitudes and persisted throughout most of the penalization regime [two pairs of palindromic DNs spanning the core motif: (NNNAT_NNNNN, NNNNN_ATNNN) and (NNNGT_NNNNN, NNNNN_ACNNN)]. Strikingly, these DN model coefficients are up to 3-fold larger than that of the most significant MN feature (SI Appendix, Figs. S17 and S18), highlighting the importance of DNs to Cbf1 binding specificity. Among selected DN features for both Pho4 and Cbf1, nearest neighbor pairs exhibited the largest coefficient magnitudes (SI Appendix, Fig. S17).

Orthogonal in Vitro Biochemical Measurements Confirm Results Obtained Via HTS.

To confirm that NN model predictions provide accurate per-sequence estimates of true binding energies, we quantitatively compared titration-based $\mathrm{\Delta }\mathrm{\Delta }$G values with unprocessed measurements and NN predictions. Using traditional fluorometric MITOMI, we determined $\mathrm{\Delta }\mathrm{\Delta }$Gs for Pho4 and Cbf1 binding to single-site variants of the ACAGA_TCGAG flanking sequence (SI Appendix, Table S3 and Figs. S10 and S11). In addition, we compared NN predictions with previously reported $\mathrm{\Delta }\mathrm{\Delta }$G measurements of CACGTG flanking site mutations (18, 32). Consistent with Monte Carlo simulations, $\mathrm{\Delta }\mathrm{\Delta }$G values calculated directly from raw sequencing data showed essentially no correlation to direct measurements, with $r^2$ values ranging between 0.07–0.16 and 0–0.24 for Pho4 and Cbf1, respectively (SI Appendix, Fig. S19). NN-predicted values showed remarkable agreement, with $r^2$ values ranging between 0.76–0.94 and 0.61–0.69 for Pho4 and Cbf1. In all cases, predictions agreed with observations within $\sim$1 kcal/mol. These results establish that the Pho4 and Cbf1 NN models presented here yield accurate measurements of binding energies for >1 million TF–DNA interactions with similar resolution to “gold-standard” biochemical measurements.

High-Resolution in Vitro Affinity Measurements Can Be Used to Identify Biophysical Mechanisms Underlying in Vivo Behavior.

The role of transcriptional activators in vivo is not simply to bind DNA but to bind specific genomic loci and regulate transcription of downstream target genes. The high resolution of these comprehensive binding energy measurements makes it possible to quantitatively estimate the degree to which measured binding affinities explain differences in measured TF occupancies, rates of downstream transcription, and ultimate levels of induction.

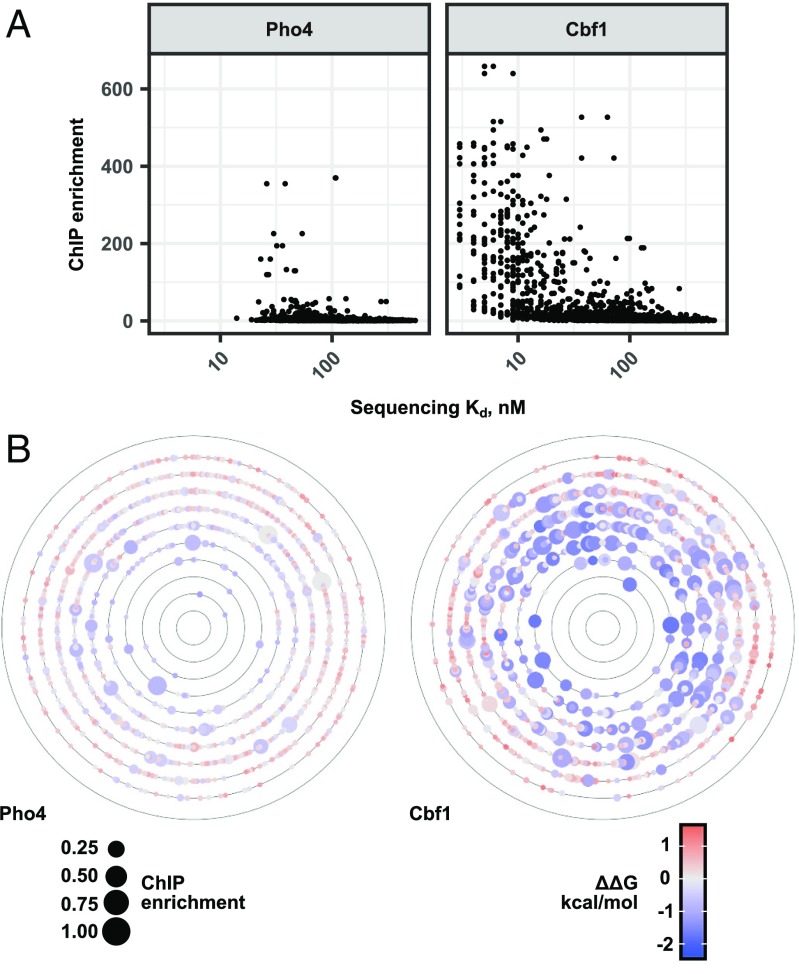
First, we compared NN-modeled $\mathrm{\Delta }$G values with measured rates of transcription and fold change induction for engineered promoters containing CACGTG Pho4 consensus sites with different flanking sequences driving the expression of fluorescent reporter genes (17, 18). As reported previously, rates of transcription and induction scaled with measured $\mathrm{\Delta }$G values (SI Appendix, Fig. S20). Next, we compared NN-derived binding energies with reported levels of TF occupancy in vivo at CACGTG consensus sites in the S. cerevisiae genome for both Pho4 and Cbf1 (63). Large magnitude TF enrichment induced by phosphate starvation was observed at loci with measured K_d values of around 100 nM or lower (Fig. 5A). While TF enrichment roughly correlated with binding energy, very high affinity sequences showed strikingly low enrichment. The observed nonlinearities may indicate the degree to which other regulatory mechanisms, such as cooperation and competition among TFs or changes in DNA accessibility due to nucleosome positioning, contribute to reported TF enrichment (63). Alternatively, these nonlinearities may reveal the need for higher resolution in vivo measurements to test the degree to which binding energies alone dictate occupancies.

Fig. 5.

Pho4 and Cbf1 binding energies and in vivo activity. (A) Pho4 and Cbf1 affinities (K_d, in nM) compared with in vivo ChIP-seq enrichment (63). (B) Functional-energetic landscapes of ChIP enrichment at dynamically regulated loci, relative to the measured highest affinity sequence in Hamming distance space.

Previous analyses of TF binding energies used landscape visualization strategies to identify energy-dependent patterns in the data (74). To better understand the relationship between binding energies and in vivo occupancies, we similarly visualized the binding energy landscapes for both Pho4 and Cbf1 as a function of sequence space (Fig. 5B and SI Appendix, Fig. S21). The highest affinity sequence for each TF was placed at the center of a series of concentric rings, each of which includes all sequences at a given Hamming distance from this sequence. Within each ring, points representing each sequence are arranged alphabetically, with the color of each point reporting the measured $\mathrm{\Delta }\mathrm{\Delta }$G for that sequence. As expected, the landscape forms a somewhat rugged funnel, with binding energies increasing with mutational distance from the highest affinity site (SI Appendix, Fig. S22). Next, we projected flanking site occupancies from ChIP-seq experiments (63) onto these binding affinity landscapes to yield a composite functional-energetic landscape (Fig. 5B). For both Pho4 and Cbf1, the majority of enriched genomic loci are greater than four mutational steps away from the global minimum, corresponding to mean increases in binding energy of approximately 0.8 and 1.5 kcal/mol, respectively (SI Appendix, Fig. S23). These quantitative comparisons between measured affinities and in vivo occupancies establish that even relatively small differences in $\mathrm{\Delta }\mathrm{\Delta }$G are associated with differential TF enrichment.

Discussion

TFs play a central role in regulating gene expression throughout development and allowing organisms to adapt to changing environmental conditions. The ability to quantitatively predict levels of TF occupancy in vivo from DNA sequence would therefore be transformative for our understanding of cellular function. TF binding at a given locus depends on multiple factors, including accessibility of a particular site (75, 76), effects of cooperation and competition with other TFs and nucleosomes (77, 78), the presence of nucleotide modifications (79, 80), and the nuclear concentration of a TF at a given time (81, 82). For accessible, unmodified target sites, the probability of TF occupancy at a given locus includes an exponential dependence on the corresponding TF–DNA binding energy (83); therefore, accurate occupancy predictions require the ability to resolve even small (∼1–2 kcal/mol) changes in binding energies. Toward this goal, we developed an assay to provide comprehensive and quantitative measurements of near-neutral changes in binding energies caused by mutations in the flanking sequences surrounding TF consensus sites. By training a NN on noisy estimates of binding energies for millions of sequences, we obtained a model that incorporates all higher order complex interactions required for accurate binding energy estimates for each sequence. In future work, we anticipate that high-resolution in vitro binding energy landscapes can be combined with genomic [e.g., methylation state (84) and chromatin accessibility data (85, 86)] and mechanistic data (e.g., quantifying cooperation and competition between other TFs and nucleosomes) to yield comprehensive, predictive models of TF binding in vivo.

Many mutations in flanking nucleotides outside of “core” consensus motifs can change binding energies by an amount equal to or greater than mutations within the core. For example, the difference in binding energy between a TCCCCCACGTGCCCCA sequence and a AATTTCACGTGAAAAG sequence is $\sim$2.6 kcal/mol, equivalent to mutating the core motif from CACGTG to CGTGTG. The bold sequence indicates the consensus TF motif ’CACGTG’ that is identical for all sequences within the library, the italics indicate specific upstream and downstream flanking sequences, and the underlined letters highlight a change in the consensus sequence whose effects were previously measured in ref. 32. However, current representations of TFBSs would predict a change in binding energy for only the core mutation. This discrepancy may explain mysteries regarding ChIP data in which some genomic loci are occupied despite an apparent lack of a consensus site while other accessible regions containing consensus sites remain unoccupied. In addition, many current efforts to infer the presence of bound TFs first analyze DNase-seq or ATAC-seq data to identify regions of accessible DNA and then scan these regions for putative bound TFs by searching for sequence similarities to known TFBSs. Failing to consider flanking sequence effects could return a significant number of both false-positives and false-negatives.

In practice, measuring complete binding energy landscapes remains rare, with most assay development focused toward discovery of the highest affinity sequences. The binding energy landscapes presented here provide a unique opportunity to explore the mechanisms that drive evolution of transcriptional regulatory networks. High-affinity, but submaximal, TF binding sites may be evolutionarily favorable due to the potential for greater dynamic transcriptional control (87). Consistent with this, we find that the most highly occupied sites in vivo are mutationally distant from the highest affinity flanking sequences, potentially indicating the existence of an evolutionary buffer used to avoid sequence proximity to a suboptimal binding extreme. In addition, elevated levels of nonadditivity are thought to produce more rugged energetic landscapes compared with those created by additive binding interactions (88). Given that nonadditive DN interactions play a larger role in determining Cbf1 specificity, we speculate that Cbf1 binding sites can traverse fewer nondeleterious evolutionary pathways than Pho4, ultimately rendering Pho4 binding sites more evolutionarily plastic.

Systematic comparisons between per-sequence estimates of binding energies output by a NN and a series of linear models revealed the mechanistic features that drive specificity and quantified their contributions to observed binding energies. These results have relevance to recent debates surrounding the relative utility of DNA sequence-based models (PWMs) and DNA shape-based models representing TF specificity. Both models parameterize DNA binding preferences by a set of four values at each position [nucleotides (A, C, G, and T) for PWMs (36) and structural features (minor groove width, propeller twist, helical twist, and roll) for shape-based models (51–55)]. While these models can extract mechanistic determinants of specificity from sparse data, higher order information is lost in the process. Here, we demonstrate that models based on nearest neighbor DN preferences fully explain observed binding behavior, consistent with biophysical observations that local DNA structure is largely determined by base stacking interactions and interbase pair hydrogen bonds in the major groove between adjacent base pairs (55, 89, 90). Such nearest neighbor DN models require only a modest increase in the number of required free parameters relative to MN models. While the NN’s capacity to incorporate higher order complexity ultimately proved unnecessary for accurately modeling Pho4 and Cbf1 binding specificities, high-resolution predictions output by the NN were essential to quantify the degree to which simpler models could explain observed behavior. The high resolution of these measurements further allows direct quantification of the degree to which thermodynamic models based on binding energies can predict behavior in vivo. The simulation-guided assay design and experimental assay presented here should allow a broader diversity of labs to make comprehensive and high-resolution measurements of binding energy landscapes. While BET-seq was deployed here for a specific use case (measurement of near-neutral effects over a small energy range), these simulations can guide choice of sequencing depths to resolve absolute binding energies across a variety of applications and platforms (9, 11, 29, 91, 92), including target site discovery efforts. The assay further offers the resolution of traditional MITOMI or HiTS-FLIP fluorescence-based assays while requiring significantly less equipment and infrastructure. Traditional MITOMI fluorescence assays require a DNA microarray printer and either a high-cost fluorescence scanner or fully automated microscope capable of imaging a slide with a microfluidic device attached; HiTS-FLIP assays require access to a customized Illumina GAIIx sequencing platform. A sequencing readout eliminates these requirements, allowing any laboratory with access to educational or commercial deep-sequencing services to measure energies at this scale and resolution. Moreover, the microfluidic valving is significantly simpler than for traditional MITOMI assays, reducing the pneumatics infrastructure required. Finally, BET-seq provides unique opportunities in future work to probe additional control mechanisms that influence TF binding in vivo. Introduction of synthesized DNA libraries containing modified bases involved in epigenetic regulation (e.g., 5-methylcytosine, 5-hydroxymethylcytosine) could allow systematic investigation of how these modifications affect TF specificities. In addition, BET-seq should be compatible with DNA libraries assembled into nucleosomal arrays in vitro, facilitating direct and quantitative investigation of how competition between TFs and nucleosomes dictates occupancies and how site-specific histone modifications influence this competition (93–95). The simulations presented here can guide the development of sequencing-based assays to measure binding energies for additional systems, including both protein–RNA and protein–protein interactions. In future work, BET-seq can complement initial SELEX-seq and PBM efforts to probe TF target specificity by providing high-resolution, quantitative mapping of the topography of these binding energy landscapes.

Materials and Methods

NN Binding Models.

NN input was defined as a flattened 4 × 10 one-hot encoded matrix; NN output was the predicted $\mathrm{\Delta }\mathrm{\Delta }$G value for the species of interest. The network consisted of three hidden layers of size 500, 500, and 250 units, respectively. All weights were initialized with Xavier initialization (96), and all layers used batch normalization (97) and ReLU activation. The entire dataset was randomly divided into training (60%), validation (10%), and test (30%) datasets; networks were trained using stochastic gradient descent until the validation set root-mean-squared error failed to decrease for three consecutive epochs. At this point, learning rate (initialized at ${10}^{-3}$) was decreased in 10-fold increments, and training continued until error failed to improve for a further two epochs (SI Appendix, Fig. S8).

Linear Binding Models.

Linear binding models were trained on scaled binding energy estimates output by the NN. The MN model includes sequence features consisting of nucleotide identities at each flanking position; nearest neighbor DN included all MN features plus all possible combinations of adjacent nucleotide pairs. The full DN model adds all nonadjacent (gapped) DN combinations. All linear binding models were trained using the same 60% of the data as the NN; reported accuracies are calculated with respect to the held-out 40% of the data.

Material Availability.

Detailed methods are available in SI Appendix, raw data are available from the Gene Expression Omnibus (accession number GSE111936), processed and intermediate files are available from Figshare (DOI 10.6084/m9.figshare.5728467), and code used for analysis and figure generation is available on GitHub (https://github.com/FordyceLab/BET-seq).