Significance
Soft materials self-assemble into complex structures that can replicate on a larger scale the symmetric arrangements of atomic crystals. Harnessing soft self-assembly for material synthesis requires controlling the symmetries of such structures, a job tailored for group-theoretical methods traditionally used to describe crystal symmetries and their breaking. We illustrate this approach by providing a blueprint for self-assembled materials with an exotic feature of wave propagation known as Weyl points. The presence of such topological objects means that, at certain wavelengths, light or sound can only propagate inside the material in a handful of directions. Most crucially, sound and light waves can propagate on the material surface without backscattering from imperfections.
Keywords: topological matter, metamaterials, polymers, colloids, semimetal
Abstract
Soft materials can self-assemble into highly structured phases that replicate at the mesoscopic scale the symmetry of atomic crystals. As such, they offer an unparalleled platform to design mesostructured materials for light and sound. Here, we present a bottom-up approach based on self-assembly to engineer 3D photonic and phononic crystals with topologically protected Weyl points. In addition to angular and frequency selectivity of their bulk optical response, Weyl materials are endowed with topological surface states, which allow for the existence of one-way channels, even in the presence of time-reversal invariance. Using a combination of group-theoretical methods and numerical simulations, we identify the general symmetry constraints that a self-assembled structure has to satisfy to host Weyl points and describe how to achieve such constraints using a symmetry-driven pipeline for self-assembled material design and discovery. We illustrate our general approach using block copolymer self-assembly as a model system.
The propagation of waves in spatially periodic media is described by band theory, which determines the frequencies that can propagate in a given direction and at a given wavelength. While band theory was first developed to understand the behavior of electrons and phonons in solids, it applies to all kinds of waves. For example, photonic crystals are spatially periodic structures encompassed by such a description (1), which most notably can host a photonic band gap resulting in peculiar optical properties, such as the structural coloration of several butterflies’ wings (2, 3).
A band structure is typically a complicated set of bands, which to a casual observer, seem to cross each other every possible way. This is, in fact, not the case: degeneracies in a band structure mainly appear at highly symmetric points and stem from the existence of additional symmetries (beyond translation invariance). However, so-called accidental degeneracies also exist, which are not enforced by the presence of a particular symmetry (4–6). Accidental degeneracies are generically rare and unstable, as they require a fine tuning of the system parameters to exist. However, such degeneracies may be protected by the existence of a particular singular configuration of the Bloch eigenstates in the neighborhood of the degenerate point (similar to a vortex or a hedgehog), which confers them with a topological character and hence, robustness against certain perturbations.
The simplest of such topological degeneracies are so-called Weyl points, where a 3D band structure locally exhibits a linear band crossing in all directions (7–9). Crucially, such a Weyl point is characterized by a topological charge, which describes the singularity in the Bloch eigenstates near the crossing point. Weyl points are robust against perturbations, which means that they can be moved in momentum space but not made to disappear unless they annihilate with a Weyl point of opposite charge, similar to hedgehog–antihedgehog pairs in real space in liquid crystals (10). Note that the Weyl points that we consider here generically occur at finite frequency and do not require a particular symmetry. In contrast, mechanical symmetry-protected Weyl points (similar to Dirac points in graphene) and Weyl lines occur at zero frequency (11–15). There, a chiral symmetry is essential to define the topological quantities and in turn, reveals a duality between zero-frequency free mechanical motions and so-called self-stress modes (16–21).
Excitations following the Weyl equation (7–9) have been experimentally observed in electronic condensed matter in the so-called Weyl semimetal tantalum arsenide (22–26) as well as in photonic (27–32), phononic, and acoustic (33–36) crystals and in homogeneous magnetized plasma (37). Beyond their fundamental importance, such discoveries may pave the way for multiple applications enabled by the peculiar properties of Weyl points, such as their angular and frequency selective response and the existence of topologically protected arc surface states (called Fermi arcs in the electronic context) that appear at the boundary of finite samples, even when time-reversal invariance is not broken (38–43). This is in sharp contrast with gapped topological materials, where the existence of one-way channels requires breaking time-reversal invariance in some way, such as with external drives (44–47), magnetic or rotation fields (48–51), or active materials (52, 53).
All photonic Weyl materials designed up to now are based on top-down approaches (28–32, 39, 54–59). In this article, we show how soft matter self-assembly (60) provides a viable bottom-up strategy to realize Weyl materials for sound and light. Block copolymers are used as a paradigmatic example of soft materials that self-assemble into a variety of highly structured phases arising from the competition between elastic energy and surface tension (61). However, our strategy is applicable to a wider range of self-assembled materials, because it is rooted in symmetry. In the same way as the arrangement of atoms into various crystalline structures is responsible for the diverse properties of natural materials, the self-assembly of soft mesoscopic structures with various space group symmetries provides an unparalleled platform to synthesize unique materials.
Fully unleashing the potential of soft matter self-assembly in material design involves a constant interplay between the full-wave optical (or acoustic, etc.) equations of motion of the system on one hand and its structural description in terms of free energy minimization subject to external fields and constraints on the other hand. Those problems are generally not analytically tractable and require considerable computational power to be solved numerically for a wide range of parameters. Here, our goal is to design a bottom-up method to create Weyl materials. While self-assembly is a global process taking place in real space, Weyl points exist in reciprocal space, as they are features of the band structure describing wave propagation in the system. Hence, we have to solve an inverse problem involving both descriptions. To shortcut this difficulty, we combine a minimum input of full-wave computations with a comprehensive symmetry analysis that determines analytically the desired symmetry breaking fields without performing heavy numerical simulations.
This article is organized as follows. In the first section, we review the definition of a Weyl point and the properties of band structures with such singularities. This allows us to identify a first set of symmetry constraints on our candidate systems. The second section is devoted to the realization of a self-assembled block copolymer structure that meets this set of minimal requirements, namely breaking inversion symmetry. We then move on to identify what (other) symmetries should be broken to obtain Weyl points and how to do so by applying suitable strains. We then confirm that the designed photonic structure indeed exhibits Weyl points through full-wave computations of Maxwell equations. Simulating the self-assembled structures with broken symmetries is required to determine the quantitative features of the band structure and most crucially, to show our method. However, to predict the existence of Weyl points, our framework only requires the band structure of the unmodified system without symmetry-breaking alterations. This enables the extension of our design to other kinds of waves: from the full-wave band structures of the unperturbed dispersive photonic, phononic, and acoustic systems, we can predict that only the first two will exhibit Weyl points when altered and strained. The last section provides a generic blueprint for mesostructured material design by self-assembly.
Weyl Points and Symmetry Requirements
The 3D band structure of an electronic system possessing Weyl points exhibits linear band crossings locally described by the Hamiltonian (7–9)
| [1] |
where is the wave vector relative to the Weyl point’s position , indicates the Pauli matrices, and is an invertible effective velocity matrix describing the band crossing at first order in . While this description seems at first sight peculiar to quantum mechanical systems, it is also applicable to all kinds of waves, as we will see in the following with the example of light. Crucially, such a Weyl point is characterized by an integer-valued topological charge, which describes the singularity in the eigenstates near the crossing point, and it can be expressed as (8, 9)
| [2] |
Although the existence of such topologically protected Weyl points does not require a particular symmetry, a crucial interplay between such degeneracies and symmetries exists. Notably, Weyl points cannot be obtained when both time-reversal symmetry and space inversion symmetry are present (8, 62), because inversion symmetry requires a Weyl point located at point on the Brillouin zone to have a partner of opposite charge at . Time-reversal symmetry requires a Weyl point located at to have a partner of the same charge at , which implies that this topological charge must be zero and that no Weyl points exist. Hence, either time-reversal or inversion symmetry (or both of them) has to be lifted to allow for Weyl points in the band structure. In a time-reversal invariant system, Weyl points come in pairs of points with identical charge, and the simplest situation then consists of two such pairs with opposite charges (Fig. 1B).
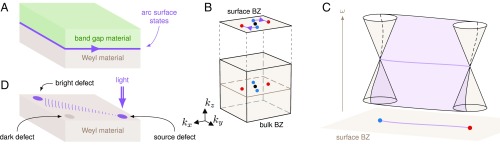
Fig. 1.
Bulk Weyl points and arc surface states. (A) Sketch of an interface between a band gap material and a Weyl material. Arc surface states (purple) appear at this interface. (B) In a time-reversal invariant system, inversion symmetry has to be broken for Weyl points to exist. The simplest situation consists of four Weyl points with charges (red and blue, respectively) in the bulk Brillouin zone (bulk BZ). A plane interface preserves space periodicity in two directions and is hence described by a 2D surface Brillouin zone (surface BZ). Crucially, topological arc surface states (represented in purple) appear between Weyl points of opposite charge on the surface BZs. (C) The surface dispersion relation at the interface between a Weyl material and a gapped system features conical dispersions relations, which are the projections of the Weyl points. In addition, a manifold of topological arc surface states (light purple) appears. The intersection of this manifold with a plane of constant frequency (or energy) is sometimes called a Fermi arc in reference to the situation in electronic solid-state physics, where this plane is set at the Fermi energy. (D) The arc surface states may be observed by creating defects at the interface to couple them with incident waves.
A hallmark of Weyl materials is the existence of topological surface states at the interface with a band gap material. At a plane interface, such as the one pictured in Fig. 1A, the translational invariance is preserved in two directions, and the surface is described by a 2D surface Brillouin zone as represented in Fig. 1B. In addition to conical dispersions stemming from the projection of the bulk Weyl points, the surface band structure features a manifold of arc surface states (represented in purple in Fig. 1C) of topological origin. Let us consider a monochromatic beam of light or sound shone on the system. Depending on the wave frequency and its wave vector, it may be either reflected or transmitted in the bulk material as ruled by the band structure. When the beam hits the interface, it may also excite the arc surface states. At all frequencies close to the Weyl points, there is an arc-shaped curve in momentum space connecting the locations of the Weyl cones, representing the set of wave vectors at which topologically protected surface states are present.
The arc surface states arise from the topology of bulk states: pictorially, they can be seen as the projections of a bulk “Dirac string” connecting the Weyl points.* As the Dirac string is not gauge invariant, however, topology only determines the connectivity of the surface states (i.e., which Weyl points are connected). Beyond their fundamental importance, one of the main interests of arc surface states is the fact that their topological origin confers them a certain robustness to perturbations. Such arc states were experimentally observed in 3D materials both for light (29–32, 58) and for sound (33, 35). Although time-reversal invariance is preserved, unidirectional wave propagation immune to backscattering can be observed at the interface (30, 31, 33). This robustness is, however, not as strong as in a system with broken time-reversal invariance, as a component of the tangent momentum has to be (at least partially) conserved (30, 31, 33).
While the bulk Weyl points are most useful when they are spectrally isolated from other bands (27, 28), the arc surface states do not require such a frequency isolation (31). At microwave frequencies, arc surface states were observed by plugging an antenna into the sample (31). At lower wavelengths, they could be observed as follows: a defect, such as a small hole drilled at the surface of a Weyl material, allows a coupling between the surface states and freely propagating light on the outside. Let us consider several of such holes drilled at different places on the surface of the material as represented in Fig. 1D. In the absence of surface states at the light’s frequencies, a light beam shone on one of such holes propagates in the bulk and quickly disappears from the interface: all of the defects but the source are dark. In contrast, when surface states are present, a sizeable part of the beam intensity propagates at the interface in directions controlled by the positions of the arc states in the surface Brillouin zone. As a consequence, a handful of the holes are illuminated. It is worth noting that the surface of a Weyl metamaterial can only support arc surface modes if the conservation laws prohibit hybridization of such modes with the electromagnetic continuum outside. For the interface between Weyl materials and the vacuum, this requires the Weyl points to be below the light cone in the reciprocal space. When this is not the case, one has to consider an actual interface with a band gap material. In this case, the hole can simply be extended into the band gap material.
Self-Assembling Inversion-Asymmetric Gyroids
In this article, we assume time-reversal invariance and concentrate on inversion symmetry breaking to avoid the need for external drives, magnetic fields, or active materials. However, generically breaking inversion symmetry leads to uninteresting band structures. We adopt the following strategy: (i) start with highly symmetric structures possessing particular degeneracies and (ii) split such degeneracies into Weyl points by applying carefully chosen symmetry-breaking perturbations. Implementing both steps through a bottom-up strategy is very challenging. Our goal is to overcome this difficulty using soft self-assembly.
The first example of a photonic crystal displaying Weyl points was engineered by milling and stacking dielectric layers into a highly symmetric structure called a double gyroid, in which additional holes were deliberately drilled at strategic points to reduce the symmetry of the system (28). A gyroid is an infinitely connected triply periodic surface of zero mean curvature discovered by Alan Schoen (67). The surface of the gyroid divides space into two regions corresponding to the interpenetrating labyrinth structures shown in Fig. 2.
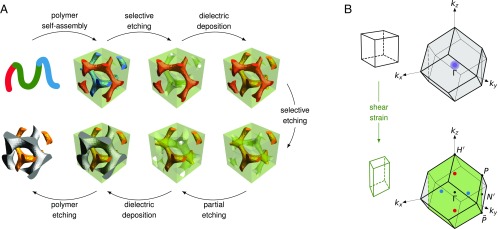
Fig. 2.
Self-assembly process and effect of strain. (A) The self-assembly of triblock terpolymers leads to “colored” double gyroids, where the two minority networks (red and blue) are chemically distinct (68, 69). Starting from the self-assembled structure, a series of selective etching, partial dissolution, and backfilling steps leads to an asymmetric double gyroid made of high dielectric constant materials, which constitute a 3D photonic metacrystal. Crucially, the photonic band structure of such a system has a threefold degeneracy at the center of the Brillouin zone (the point), which is represented in purple in B, Upper Right. This threefold degeneracy can be split into a set of Weyl points by an appropriate strain (in this case, pure shear) represented in red and blue (for Weyl points of charge 1 and , respectively) in B, Lower Right.
A remarkable fact from soft matter science is that double gyroids naturally self-assemble in situations where two or several linked components have repulsive interactions with each other. In such circumstances, the minimization of surface energy constrained by the presence of links between the immiscible components can lead to a variety of minimal surfaces, among which is the gyroid surface. Gyroids generically appear in various soft materials, such as liquid crystals (70–72), amphiphilic surfactants (73, 74), dispersions of anisotropic and patchy colloids (75–79), and block copolymers (61, 80, 81) to name but a few.
AB diblock copolymers are the archetypal example of such a self-assembling soft material. They are composed of two immiscible polymer blocks denoted by A and B glued together by covalent bonds. For a well-chosen set of system parameters (typically the average degree of polymerization, the relative fractions of A and B, and the Flory–Huggins parameter characterizing the interaction energy between the blocks A and B), the constrained minimization of the interface energy leads to a double-gyroid structure, where two minority networks of opposite chirality are interwoven inside a matrix majority network (82, 83). The interface between one of the minority networks and the matrix is a gyroid surface, a triply periodic constant curvature surface (67, 84, 85), which is well-approximated by the isosurface (with ) (86), where , , and are measured in units of the unit cell size . The second minority network is obtained from the first through space inversion. Hence, one of the gyroidal minority networks is described by , while its chiral partner, obtained by space inversion, is described by . Both are composed, say, of the A blocks, while the majority matrix is composed of the B blocks.
Crucially, the resulting structure has inversion symmetry that is almost impossible to get rid of without local modifications. This is certainly possible in engineered structures like the milled structures in ref. 28, where one has direct control on the shape of the unit cell, but it is not compatible with a bottom-up material synthesis scheme. To take advantage of a self-assembly scheme, we instead choose to use ABC triblock terpolymers, which self-assemble in a double gyroid where two chemically distinct gyroid-shaped minority networks of opposite chirality are interwoven inside a matrix majority network (82, 83). For instance, one of the gyroidal labyrinths may be composed of A blocks, but its image by space inversion is then composed of C blocks, and the matrix is still composed of B blocks. The resulting structure is called an asymmetric double gyroid or an alternating double gyroid. After the polymer self-assembly, standard techniques allow us to selectively etch one of the gyroidal minority networks and to replace it with a high-permittivity material (87, 88) [for example, by metal (68, 69) or dielectric (89, 90) deposition]. Crucially, the chemical difference between both gyroidal networks allows us to induce an optical asymmetry between them either by depositing materials of different dielectric constants or through the use of a mild etching agent to tune their respective radii. The last step is to get rid of the majority network matrix. The whole process is summarized pictorially in Fig. 2. After this process is complete, we are left with a structure where the dielectric constant is for , for , and outside of such regions. Similarly, a phononic crystal can be obtained by inducing an asymmetry in the elastic properties of the two gyroidal networks. In the following, we focus on photonic crystals for concreteness, but full details on acoustic and phononic crystals are provided in SI Appendix.
Effective Description of the Band Structure
To obtain Weyl points, the symmetry of the double gyroid must be reduced further. Full-wave numerical simulations reveal that the photonic band structure of a dielectric double gyroid has a threefold quadratic degeneracy at the point (the center of the first Brillouin zone) (91). From the point of view of symmetries, the threefold degeneracy is allowed by the existence of 3D irreducible representations of the subgroup of symmetries leaving the point invariant, namely the irreducible representation T1g of the full octahedral group mm (or Oh in Schoenflies notation) (SI Appendix). This threefold degeneracy can be split into pairs of Weyl points by symmetry-breaking perturbations (27, 39) as represented in Figs. 2B and 3. The systematic description of a band structure near a high-symmetry point of the Brillouin zone as well as the effect of symmetry-breaking perturbations can be obtained from group theory. This approach, known as the method of invariants, originated within condensed matter physics (92–96), but it also applies to photonic systems (97, 98) and more generally, to all kinds of waves in periodic media.
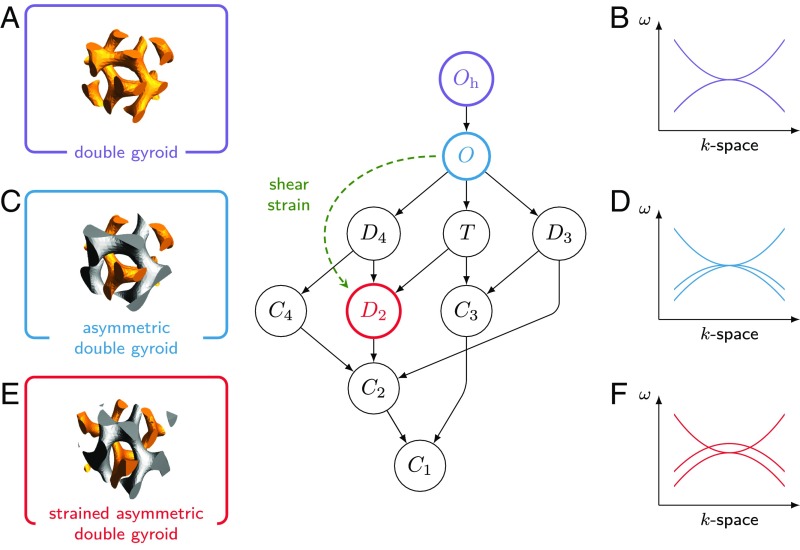
Fig. 3.
Reducing the symmetry. In A–C, we show the various structures of interest: (A) the (symmetric) double gyroid, (B) the asymmetric double gyroid, and (C) the strained asymmetric double gyroid (with shear strain). For the double gyroid, the group of the wave vector is the octahedral group Oh (mm in Hermann–Mauguin notation), while it is the octahedral rotation group O (432) for the asymmetric double gyroid. When strain is applied to the asymmetric double gyroid, its symmetry is reduced, which corresponds at the point to a subgroup of the octahedral rotation group O. Such subgroups are organized in a Hasse diagram. (The octahedral rotation group is indeed a subgroup of the full octahedral group Oh, which has more subgroups that are not relevant here and were not represented. As strain preserves inversion symmetry, any strained symmetric double gyroid still has an inversion center. The point group at is then the product of the inversion group S2 with a subgroup of O. Such situations can be achieved by starting from the symmetric double gyroid. In addition, there are other mixed subgroups of Oh, which cannot be directly realized through our method.) In D–F, the method of invariants predicts the qualitative features of the band structure of the modified double gyroids (B and C).
For example, in the absence of charges and currents, Maxwell equations can be written in a convenient way as
| [3] |
where and are the electric and magnetic fields, respectively, while and are the spatially varying permittivity and permeability of the medium, respectively. In this form, the operator in square brackets, called the Maxwell operator, plays the role of a Hamiltonian† (1, 99, 100). This full-wave Maxwell equation is usually impossible to solve analytically: one has to resort to numerical simulations. However, with minimal input from a numerical full-wave solution complemented with the full knowledge of symmetries in the problem, one can determine an effective Hamiltonian, which is sufficient for perturbative design purposes. Similar considerations apply to other kinds of waves propagating in periodic media (for example, elastic waves) (SI Appendix).
By reducing the full description of the system (contained in the Maxwell operator) to the subspace spanned by a few relevant degrees of freedom, one obtains an effective Hamiltonian describing a few bands in the vicinity of a (usually high-symmetry) point of the Brillouin zone. For example, the eigenstates involved in a degeneracy at can then be used as a basis to describe the effective Hamiltonian operator as a matrix , where . Both the Maxwell operator and the effective Hamiltonian operator are invariant with respect to the symmetries of the group of the wave vector , defined as the subgroup of symmetries that leave invariant. The general idea of the theory of invariants is that symmetries can be used to construct the effective Hamiltonian matrix from scratch by combining a set of basis matrices (which form a basis of, say, the space of Hermitian matrices) and irreducible functions of the wave vector components (like ). The basis matrices represent operators in the basis of eigenstates at . As such, they change when a symmetry operation is applied. This is also the case in irreducible functions as the symmetry operation is applied to the momentum vector. As the effective Hamiltonian operator is invariant when a symmetry is applied, it is possible to determine all terms allowed by symmetry by selecting all combinations of the form , which are left invariant by the action of the symmetries.
More precisely, if the eigenstates at form an irreducible representation , then the matrix representation of the effective Hamiltonian operator describing the corresponding bands will be covariant with respect to the symmetries. Namely, , where is a representation of acting on the effective Hamiltonian by its adjoint action as a representation of . The effective Hamiltonian can then be constructed by combining basis matrices of the irreducible representations appearing in decomposition of this product and irreducible functions of the wave vector components as
| [4] |
where indicates arbitrary constants chosen such that is Hermitian and where labels the basis elements in the same irreducible representation.
Given (i) the input of the space group Iad of the double gyroid and (ii) the fact, known from full-wave computations, that a threefold band crossing transforming according to the 3D irreducible representation T1g exists at the point, the method of invariants yields the following effective Hamiltonian, describing the band structure in the vicinity of this crossing (SI Appendix):
| [5] |
where and c.p. stands for “circular permutation” (of the indices). Matrices are 3 × 3 Hermitian angular momentum matrices satisfying and , and Id is the identity matrix. We also defined and with . In this expansion, the indices of the coefficients refer to the irreducible representation from which the invariant term was constructed and the exponent in parentheses to the order of the irreducible polynomial composed of the wave vector components (at the point, , so that ). Finally, in addition to space symmetries, time-reversal invariance is imposed by considering only time-reversal even combinations.
The main interest of the method of invariants is that it allows us to determine what new terms can be added to the preceding effective Hamiltonian when the symmetry is reduced. This enables us to qualitatively predict the effect of perturbations on the band structure as illustrated in Fig. 3. As we have seen, the very first step toward inducing Weyl points is the removal of inversion symmetry from the structure (Fig. 3C). Hence, the point group at becomes the chiral octahedral group 432 (or O in Schoenflies notation). However, this modification does not allow a constant term in the effective Hamiltonian: only a new linear term of the form appears due to the reduction of the irreducible representation and of Oh to in O. Hence, the quadratic band crossing at cannot be lifted by such a term (Fig. 3D), and a further reduction in symmetry is required.
Strain and Symmetries
The simplest yet global way to reduce the symmetry of a structure is to apply a mechanical strain. The key point is that this strategy is compatible with self-assembly, unlike local modification or patterning of the individual building blocks. The asymmetry between the enantiomeric (i.e., nonidentical mirror images of each other) gyroidal components described in the previous section reduces the space group Iad [International Union of Crystallography (IUC) no. 230] of the symmetric double gyroid to I4132 (IUC no. 214). When strain is applied, this space group is further reduced.
We choose to apply the shear strain
| [6] |
written in the Cartesian coordinates of the standard conventional cell (not the primitive cell). This transformation (illustrated in Fig. 3E) reduces the space group of the asymmetric double gyroid to F222 (IUC no. 22) when is nonzero [the method to compute the space groups of the structures, based on the open source spglib library (101), is detailed in SI Appendix]. Correspondingly, the point group at the point is 222 (or D2 in Schoenflies notation). As we shall see, the effective description of the band structure near the point predicts the appearance of Weyl points in this situation.
The effect of a reduction in symmetry on the effective Hamiltonian can be determined using subduction rules between the original symmetry group and its subgroup, which describe how the original irreducible representations combine into the new ones. In a system with lower symmetry, it is possible to combine some and in a way that was previously not allowed. In our case, going from Oh to D2 allows various new terms in the effective Hamiltonian, which becomes , where
| [7] |
, and while and . Implicit summation over and is assumed. (We imposed, as an additional constraint, that time-reversal symmetry be preserved.) In this expression, , , , and are generically nonvanishing free parameters, which depend on the details of the system. The strained symmetric double gyroid can also be described in such a way: the only difference is that all symmetry groups now include inversion symmetry. Shear strain then reduces the point group at from Oh to D2h, which imposes .
Particularly noteworthy in Eq. 7 are the constant terms with prefactors , which allow the threefold degeneracy at to be lifted. As such constant terms do not break inversion symmetry, they cannot single-handedly lead to the appearance of Weyl points. Instead, they split the threefold degeneracy into an entire nodal line of degeneracies, similar to the one predicted in ref. 27, which is robust against (small) inversion-preserving perturbations. In contrast, a perturbation of the form Eq. 7 generically breaks inversion symmetry and produces Weyl points as observed in Fig. 3F (SI Appendix discusses typical spectra of the effective Hamiltonians with different symmetries). Hence, we can predict that, in a well-chosen parameter range, the strained asymmetric double gyroid will exhibit Weyl points.
Numerical Computation of Photonic Band Structures
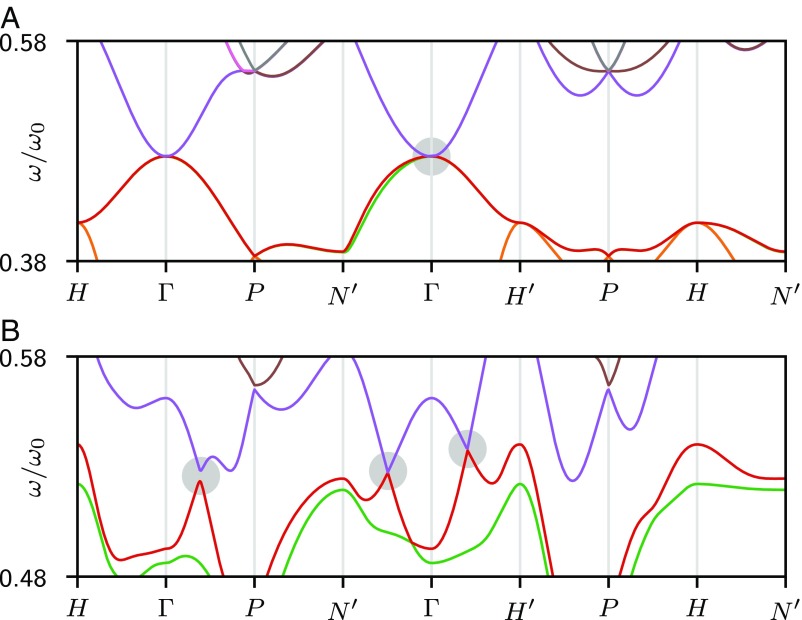
To confirm the existence of Weyl points in the strained asymmetric double gyroid, we proceed to a full-wave computation of the band structure using the well-established open source package MPB, which determines the fully vectorial eigenmodes of Maxwell equations with periodic boundary conditions (102). Linear crossings between the fourth and fifth bands are observed in the situation described in the previous section (in Fig. 4B, the relevant bands are red and purple, and the Weyl points and avoided crossing are marked by gray circles). In this case, the difference between a nodal line and a set of Weyl points has to be searched on the line. In the asymmetric double-gyroid structure, a local gap separates the fourth and fifth bands along this line, which closes in the inversion-symmetric structure. To ensure that such crossings are indeed Weyl points, we compute their topological charge from the numerically computed eigenmodes (SI Appendix). We find that the topological charge of the crossing point on the axis is , while the charge of the crossing point on the axis is (the crossing points on the and axes have the same charge as their time-reversal counterparts).
Fig. 4.
Photonic band structures. Photonic band structures of (A) the symmetric double gyroid and (B) the shear-strained asymmetric double gyroid. The threefold quadratic band crossing at the point of the band structure of the unperturbed double gyroid is split into Weyl points on the and lines (in contrast, there is no crossing on the line, which distinguishes the pair of Weyl points from a nodal line). The first eight bands of the band structures were computed with the MPB package (102) on a grid, with (A) , , and and (B) , , , and . Here, , where is the speed of light in vacuum.
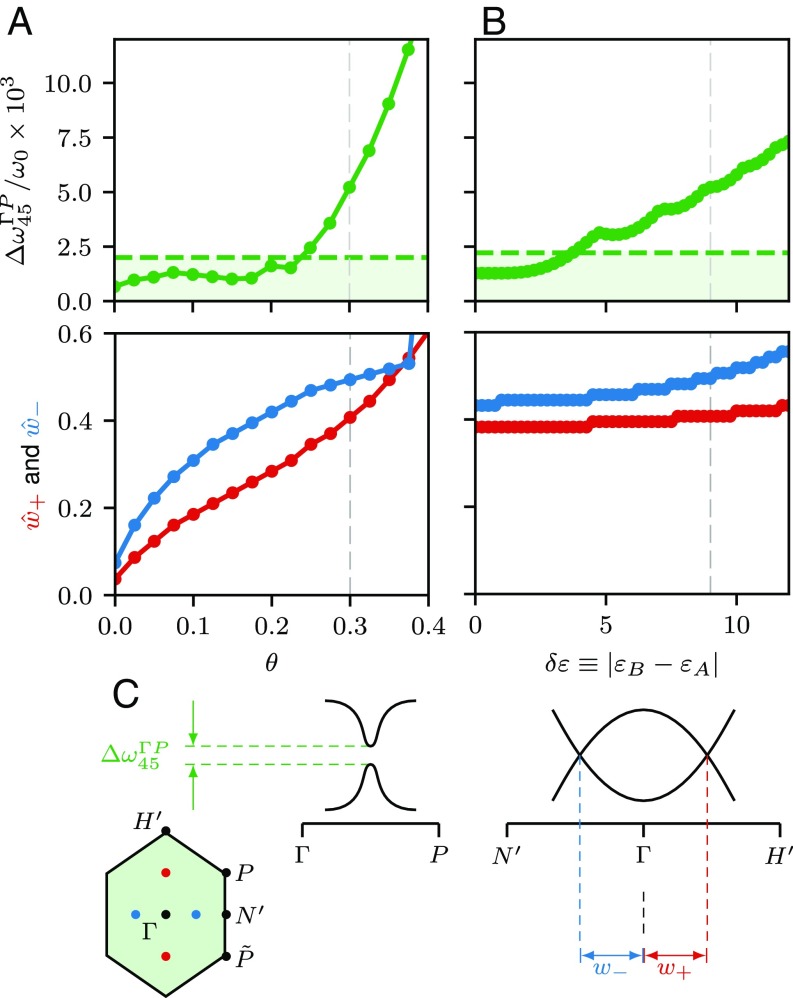
An asymmetry only in either the dielectric constants or the gyroids’ thicknesses is sufficient to obtain photonic Weyl points. The effects of both perturbations are similar but not identical: their combination may allow us to optimize for additional features in the band structure (not necessarily topological; for example, avoiding frequency overlaps) (an example is in SI Appendix). Here, we focus on the Weyl points: the effect of the dielectric constant asymmetry on the local gap on the line and on the positions of the Weyl points is shown in Fig. 5B (the effect of the gyroid thickness asymmetry can be found in SI Appendix). While the strain angle affects both the relative positions of the Weyl points and the gap on (Fig. 5A), the relative positions of the Weyl points are almost not affected by the asymmetry.
Fig. 5.
Evolution of the main features of the photonic band structures. Evolution of characteristic features of the Weyl points, represented in C, with (A) the strain angle and (B) the dielectric asymmetry . Here, the band structures are computed with the set of parameters in Fig. 4B on a grid. We plot both the minimum of the local gap between the fourth and the fifth bands, , and the normalized positions of the two inequivalent Weyl points, and . The gray dashed lines correspond to the value at which each parameter is kept constant in other figures. The abrupt jump in the position of one of the Weyl points near is an artifact: another set of band crossings appears on the and lines near this value (SI Appendix). For the local gap, light green regions delimited by dashed lines correspond to the order of magnitude of symmetry-breaking numerical errors (SI Appendix). The data are not meaningless below this threshold, but the effects of the strain and structural asymmetry are not distinguishable from the spurious numerical reduction of symmetry. Similarly, should both vanish at (which is clearly not the case). This provides an order of magnitude of the uncertainty on both observables.
Additionally, both the dielectric and thickness asymmetries gradually open a complete band gap between the second and third bands. Here, this effect is unwanted, as it reduces the bandwidth available for the Weyl points. It may, however, turn out to be useful in other contexts. As the strain tends to reduce the size of this band gap, we also obtain a 3D strain-tunable photonic band gap material (103, 104), with properties that can be adjusted through the dielectric and thickness asymmetries. Such tunable gap materials have been used to realize strain sensors (105). Here, we can envision a combination of such strain-sensing methods with an optical tracking of the strain-induced Weyl points to achieve a high-precision measure of mechanical properties.
Self-Assembled Weyl Materials for Light and Sound
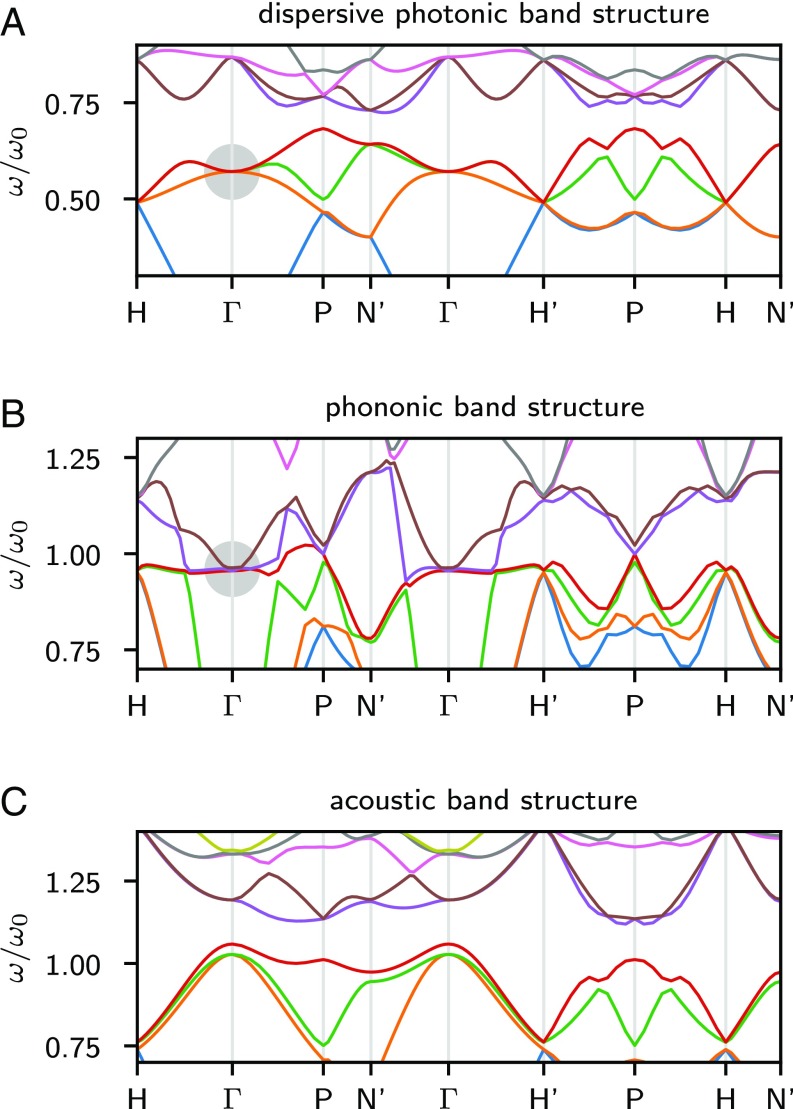
While we focused on photonic systems, the same group-theoretical analysis applies to other kinds of waves. We consider three examples where Weyl points were already shown: (i) dispersive photonic media (37) (i.e., with a frequency-dependent dielectric tensor), (ii) phononic crystals (34), and (iii) acoustic crystals (33, 35, 36). To show the possibility of obtaining a self-assembled Weyl material, we only need to consider the band structure of an unperturbed double gyroid and look for an essential threefold degeneracy at the point. The rest follows from our group-theoretical analysis. As we shall see, such a threefold degeneracy appears in both dispersive photonic and phononic systems but does not seem to arise in the considered acoustic system, at least at reasonably low frequencies.
When light propagates in a structure made of a metal or in a dielectric at high frequency, the plasma oscillations of the electron density couple with the electromagnetic field, leading to a dispersive photonic crystal where the propagation of light is still described by Maxwell equations but with a frequency-dependent dielectric tensor (106, 107). We consider a double gyroid made of a Drude metal with the plasma frequency of gold, the band structure of which is represented in Fig. 6A. In dispersive photonic crystals, the scale invariance of Maxwell equations is not valid anymore, as the plasma frequency provides a length scale. The case of a unit cell of size was previously considered in ref. 68. At such scales, the threefold degeneracy may still be present but is overlapped by highly dense plasma bands, and it cannot be identified. Here, we consider a unit cell of size . A threefold degeneracy appears near . Inspection of the eigenvectors shows that the electric field transforms along the 3D irreducible representations T1u (more details are in SI Appendix). Similarly, in a phononic crystal, elastic waves propagate in a spatially periodic structure. Here, we consider a double gyroid made of steel embedded in an epoxy matrix, which couples elastically the two enantiomeric gyroids (110). As observed in Fig. 6 A and B, a threefold degeneracy is found near . Inspection of the numerical eigenvectors shows that they also transform according to the 3D irreducible representation T1u (more details are in SI Appendix). According to our analysis, such threefold degeneracies will be split into Weyl points by inducing an asymmetry in the enantiomeric gyroid networks and applying an appropriate strain in both the dispersive photonic and phononic systems.
Fig. 6.
Band structures of the unperturbed double gyroid for different waves. (A) Dispersive photonic band structure of a metallic double-gyroid structure made of a Drude metal with the plasma frequency of gold standing in vacuum. (B) Phononic band structure for an elastic double gyroid in steel embedded in an epoxy elastic matrix. (C) Acoustic band structure for sound in air confined outside of a double gyroid with hard wall boundary conditions. In the dispersive photonic and phononic band structures (A and B), a threefold degeneracy (highlighted by gray circles) is found. As such, we expect such systems to exhibit Weyl points when strained. In A, , where is the speed of light in vacuum. We use the plasma frequency of gold, (108), and . The loss term is initially set to 0, and the results show no significant deviations from the case computed with the tabulated value (108). In B, , where is the speed of transverse waves in epoxy. The values assumed for the longitudinal and transverse speeds of sound in steel and epoxy are obtained from the components of elastic tensor as and from the values in refs. 109–111, namely , , and and , , and . In C, , where is the speed of sound in air. All computations are performed with a grid. More details on the model and computation are in SI Appendix.
By contrast, we consider the case of an acoustic system, where sound propagates in air outside a double gyroid-shaped labyrinth. Here, no threefold degeneracy at seems to appear in the band structure (at least below ) (Fig. 6C and SI Appendix) for the values of the parameters we considered. As a consequence, we do not expect Weyl points to appear under strain at those frequencies. Finally, the band structure of electrons constrained to move on gyroid-shaped nanostructured semiconductors displays multiple degeneracies (113, 114), which could also give rise to Weyl points under strain. In this situation, however, one has to take into account the spin degrees of freedom of the electrons, which are also affected by the curvature, and therefore, we can draw no definitive conclusion from our analysis, which would have to be adapted to include double-group representations.
The self-assembly of asymmetric double-gyroid structures has already been shown experimentally in block copolymers (69). Directed self-assembly can induce mechanical strains in the direction of growth (115), which according to our symmetry analysis, would automatically lead to the appearance of Weyl points without the need of applying external perturbations. Moreover, gyroid-based systems appear to be unusually resistant to the appearance of cracks when strained (116–118), possibly as a result of their 3D cocontinuous structure, making them a particularly good fit for our strain-based design. The size of the unit cell of the structures obtained by block polymer self-assembly crucially depends on the blocks’ molar mass. With current experimental techniques, the accessible unit cell sizes range from a few nanometers to a hundred nanometers (83, 119). In photonic crystals, this constraint on the unit cell size means that we can expect Weyl points to appear at wavelengths of order (or smaller), which are at UV wavelength. Depending on the materials used in the process, the light frequency may be high enough for the dielectric function not to be constant anymore, but as we have shown, Weyl points can also occur in dispersive photonic crystals. While the direct observation of a Weyl band structure at such frequencies is challenging, such self-assembled photonic crystals could be used in X-ray/UV optics (for example, to realize Veselago lenses as proposed in ref. 42).
To generate an optical response in the visible spectrum, it would be interesting to explore hierarchical self-assembly of gyroids using soft building blocks larger than standard polymeric monomers, such as superstructures formed by anisotropic colloids (75, 78), or liquid crystalline phases (72).
Symmetry-Driven Discovery of Self-Assembled Materials
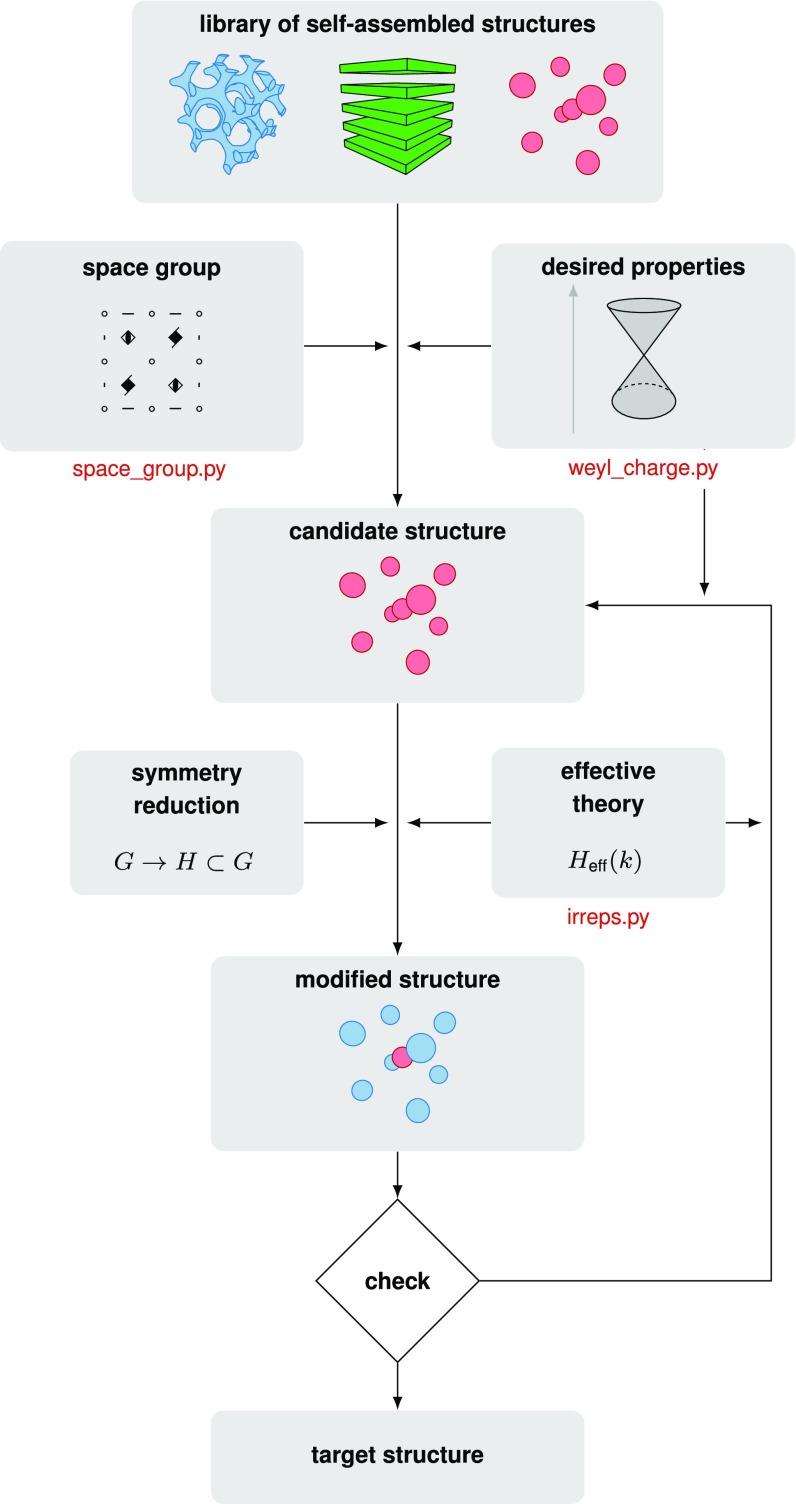
Both the possible existence of a threefold degeneracy and its splitting into Weyl points are predicted by group theory. In this study, we did not need to make an initial guess of a structure leading to a threefold degeneracy at , because we used the well-known example of a double gyroid. Note, however, that symmetry considerations can also guide this first step, as they determine in which structures essential degeneracies can exist (120), such as frequently used both in solid-state physics (121–123) and for classical waves (124, 125). This approach combined with an iterative search through libraries of self-assembled structures could provide an extension of our results to different systems. We developed open source Python packages that perform some of the tasks required (details are in SI Appendix): (i) the script space_group.py numerically determines the space group of a structure represented as a skeletal graph in the presence and absence of mechanical deformations using the open source library spglib (101), (ii) the script irreps.py numerically determines the irreducible representations of the numerical eigenvectors, and (iii) the script weyl_charge.py computes numerically the charges of the Weyl nodes for an arbitrary band structure using a gauge-invariant method (126–132). Fig. 7 provides a schematic representation of an automated self-assembled mesostructured material discovery pipeline, which would blend computationally intensive full-wave simulations and the group theoretical tools used in this study. In such a scheme as well as in our work, symmetries act as a powerful guide in the wealth of self-assembled structures (61, 83, 87, 133) by both identifying candidate systems and determining suitable perturbations to achieve a given response.
Fig. 7.
Symmetry-driven mesostructured material discovery pipeline. To obtain mesostructured materials with a set of desired properties, we suggest the following automated discovery pipeline. We start from a library of self-assembled structures, which is scanned for candidates matching symmetry requirements for a set of target properties. This requires us to automatically determine the space group of each structure: a script space_group.py does this job for structures represented as a skeletal graph (SI Appendix). A best candidate for the initial structure is then selected, and its properties are numerically computed. For example, we compute the band structure, from which the topological charges of the Weyl points (if any) are determined by a script weyl_charge.py. An effective description is then extracted from the numerical data: here, we need to determine the irreducible representations of the numerical eigenvectors, a job performed by the script irreps.py (SI Appendix). The effective description then allows us to determine which modifications should lead to the desired properties (for example, through a symmetry reduction). Here, this step could also be automated using https://github.com/greschd/kdotp-symmetry. Finally, the properties of the modified structure are numerically determined and compared with the desired properties. In case of failure, a new initial structure is selected from the library, and the process is iterated.
Supplementary Material
Acknowledgments
M.F. was supported by the NanoFront Consortium, a program of the Netherlands Organization for Scientific Research that is funded by the Dutch Ministry of Education, Culture and Science. S.-Y.J. and K.H. were supported by National Research Foundation of Korea Grant NRF-2016M3D1A1021142. U.W. thanks National Science Foundation Grant DMR-1707836 for support. V.V. was primarily supported by the University of Chicago Materials Research Science and Engineering Center, which is funded by National Science Foundation Award DMR-1420709.
Footnotes
The authors declare no conflict of interest.
*More precisely, the topology of the band structure is fully characterized not only by the charges of the Weyl points but by weak first Chern numbers (or weak Fu–Kane–Mele invariants) defined on 2D planes or surfaces of the bulk Brillouin zone (63–65). In contrast, the exact shape of the topological surface states is indeed not determined by the topology and depends on the boundary conditions (31). In particular cases, it can, however, be predicted from the bulk through the entire data of the Berry connection (66).
†For normal materials where permittivity and permeability are strictly positive, the Maxwell operator is Hermitian with respect to a relevant scalar product (1, 99). An additional constraint stemming from the source-free equations has to be taken into account, which commutes with the Maxwell operator.
This article is a PNAS Direct Submission.
Data deposition: The code used to compute the photonic band structures, the charges of the Weyl points, the irreducible representations of the numerical eigenvectors, the space group of the structures, and the spectra of the effective Hamiltonians is available on Zenodo at https://doi.org/10.5281/zenodo.1182581.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1720828115/-/DCSupplemental.
References
- 1.Joannopoulos JD, Johnson SG, Winn JN, Meade RD. Photonic Crystals: Molding the Flow of Light. 2nd Ed Princeton Univ Press; Princeton: 2008. [Google Scholar]
- 2.Saranathan V, et al. Structure, function, and self-assembly of single network gyroid (I4132) photonic crystals in butterfly wing scales. Proc Natl Acad Sci USA. 2010;107:11676–11681. doi: 10.1073/pnas.0909616107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Pouya C, Vukusic P. Electromagnetic characterization of millimetre-scale replicas of the gyroid photonic crystal found in the butterfly Parides sesostris. Interface Focus. 2012;2:645–650. doi: 10.1098/rsfs.2011.0091. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Herring C. Effect of time-reversal symmetry on energy bands of crystals. Phys Rev. 1937;52:361–365. [Google Scholar]
- 5.Herring C. Accidental degeneracy in the energy bands of crystals. Phys Rev. 1937;52:365–373. [Google Scholar]
- 6.von Neumann J, Wigner EP. 1929. Über das Verhalten von Eigenwerten bei adiabatischen Prozessen (Physik Z);trans Knox RS, Gold A (1964) Symmetry in the Solid State (Benjamin, New York)
- 7.Weyl H. Elektron und Gravitation. Z für Physik. 1929;56:330–352. [Google Scholar]
- 8.Wan X, Turner AM, Vishwanath A, Savrasov SY. Topological semimetal and fermi-arc surface states in the electronic structure of pyrochlore iridates. Phys Rev B. 2011;83:205101. [Google Scholar]
- 9.Armitage NP, Mele EJ, Vishwanath A. Weyl and Dirac semimetals in three dimensional solids. Rev Mod Phys. 2017;90:015001. [Google Scholar]
- 10.Chaikin PM, Lubensky TC. Principles of Condensed Matter Physics. Cambridge Univ Press; Cambridge, UK: 2000. [Google Scholar]
- 11.Rocklin DZ, Chen BG, Falk M, Vitelli V, Lubensky T. Mechanical Weyl modes in topological Maxwell lattices. Phys Rev Lett. 2016;116:135503. doi: 10.1103/PhysRevLett.116.135503. [DOI] [PubMed] [Google Scholar]
- 12.Po HC, Bahri Y, Vishwanath A. Phonon analog of topological nodal semimetals. Phys Rev B. 2016;93:205158. [Google Scholar]
- 13.Stenull O, Kane C, Lubensky T. Topological phonons and weyl lines in three dimensions. Phys Rev Lett. 2016;117:068001. doi: 10.1103/PhysRevLett.117.068001. [DOI] [PubMed] [Google Scholar]
- 14.Bilal OR, Süsstrunk R, Daraio C, Huber SD. Intrinsically polar elastic metamaterials. Adv Mater. 2017;29:1700540. doi: 10.1002/adma.201700540. [DOI] [PubMed] [Google Scholar]
- 15.Baardink G, Souslov A, Paulose J, Vitelli V. Localizing softness and stress along loops in 3D topological metamaterials. Proc Natl Acad Sci USA. 2017;115:489–494. doi: 10.1073/pnas.1713826115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kane CL, Lubensky TC. Topological boundary modes in isostatic lattices. Nat Phys. 2013;10:39–45. [Google Scholar]
- 17.ge Chen BG, Upadhyaya N, Vitelli V. Nonlinear conduction via solitons in a topological mechanical insulator. Proc Natl Acad Sci USA. 2014;111:13004–13009. doi: 10.1073/pnas.1405969111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Paulose J, ge Chen BG, Vitelli V. Topological modes bound to dislocations in mechanical metamaterials. Nat Phys. 2015;11:153–156. [Google Scholar]
- 19.Paulose J, Meeussen AS, Vitelli V. Selective buckling via states of self-stress in topological metamaterials. Proc Natl Acad Sci USA. 2015;112:7639–7644. doi: 10.1073/pnas.1502939112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Huber SD. Topological mechanics. Nat Phys. 2016;12:621–623. [Google Scholar]
- 21.Süsstrunk R, Huber SD. Classification of topological phonons in linear mechanical metamaterials. Proc Natl Acad Sci USA. 2016;113:E4767–E4775. doi: 10.1073/pnas.1605462113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Yang LX, et al. Weyl semimetal phase in the non-centrosymmetric compound TaAs. Nat Phys. 2015;11:728–732. [Google Scholar]
- 23.Lv BQ, et al. Observation of Weyl nodes in TaAs. Nat Phys. 2015;11:724–727. [Google Scholar]
- 24.Xu SY, et al. Discovery of a Weyl fermion state with Fermi arcs in niobium arsenide. Nat Phys. 2015;11:748–754. [Google Scholar]
- 25.Xu SY, et al. Discovery of a Weyl fermion semimetal and topological Fermi arcs. Science. 2015;349:613–617. doi: 10.1126/science.aaa9297. [DOI] [PubMed] [Google Scholar]
- 26.Lv B, et al. Experimental discovery of Weyl semimetal TaAs. Phys Rev X. 2015;5:031013. [Google Scholar]
- 27.Lu L, Fu L, Joannopoulos JD, Soljačić M. Weyl points and line nodes in gyroid photonic crystals. Nat Photon. 2013;7:294–299. [Google Scholar]
- 28.Lu L, et al. Experimental observation of Weyl points. Science. 2015;349:622–624. doi: 10.1126/science.aaa9273. [DOI] [PubMed] [Google Scholar]
- 29.Noh J, et al. Experimental observation of optical Weyl points and Fermi arc-like surface states. Nat Phys. 2017;13:611–617. [Google Scholar]
- 30.Chen WJ, Xiao M, Chan CT. Photonic crystals possessing multiple Weyl points and the experimental observation of robust surface states. Nat Commun. 2016;7:13038. doi: 10.1038/ncomms13038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Yang B, et al. Direct observation of topological surface-state arcs in photonic metamaterials. Nat Commun. 2017;8:97. doi: 10.1038/s41467-017-00134-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Yang B, et al. Ideal Weyl points and helicoid surface states in artificial photonic crystal structures. Science. 2018;359:1013–1016. doi: 10.1126/science.aaq1221. [DOI] [PubMed] [Google Scholar]
- 33.Li F, Huang X, Lu J, Ma J, Liu Z. Weyl points and Fermi arcs in a chiral phononic crystal. Nat Phys. 2017;14:30–34. [Google Scholar]
- 34.Zhang T, et al. Double-weyl phonons in transition-metal monosilicides. Phys Rev Lett. 2018;120:016401. doi: 10.1103/PhysRevLett.120.016401. [DOI] [PubMed] [Google Scholar]
- 35.Xiao M, Chen WJ, He WY, Chan CT. Synthetic gauge flux and Weyl points in acoustic systems. Nat Phys. 2015;11:920–924. [Google Scholar]
- 36.Yang Z, Zhang B. Acoustic type-II Weyl nodes from stacking dimerized chains. Phys Rev Lett. 2016;117:224301. doi: 10.1103/PhysRevLett.117.224301. [DOI] [PubMed] [Google Scholar]
- 37.Gao W, et al. Photonic Weyl degeneracies in magnetized plasma. Nat Commun. 2016;7:12435. doi: 10.1038/ncomms12435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Lu L, Joannopoulos JD, Soljačić M. Topological states in photonic systems. Nat Phys. 2016;12:626–629. [Google Scholar]
- 39.Wang L, Jian SK, Yao H. Topological photonic crystal with equifrequency Weyl points. Phys Rev A. 2016;93:061801(R). [Google Scholar]
- 40.Bi R, Wang Z. Unidirectional transport in electronic and photonic Weyl materials by Dirac mass engineering. Phys Rev B. 2015;92:241109(R). [Google Scholar]
- 41.Lu L, Wang Z. 2016. Topological one-way fiber of second Chern number. arXiv:1611.01998.
- 42.Hills RDY, Kusmartseva A, Kusmartsev FV. Current-voltage characteristics of Weyl semimetal semiconducting devices, Veselago lenses, and hyperbolic Dirac phase. Phys Rev B. 2017;95:214103. [Google Scholar]
- 43.Zhou M, et al. Electromagnetic scattering laws in Weyl systems. Nat Commun. 2017;8:1388. doi: 10.1038/s41467-017-01533-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Khanikaev AB, Fleury R, Mousavi SH, Alù A. Topologically robust sound propagation in an angular-momentum-biased graphene-like resonator lattice. Nat Commun. 2015;6:8260. doi: 10.1038/ncomms9260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Wang P, Lu L, Bertoldi K. Topological phononic crystals with one-way elastic edge waves. Phys Rev Lett. 2015;115:104302. doi: 10.1103/PhysRevLett.115.104302. [DOI] [PubMed] [Google Scholar]
- 46.Nash LM, et al. Topological mechanics of gyroscopic metamaterials. Proc Natl Acad Sci USA. 2015;112:14495–14500. doi: 10.1073/pnas.1507413112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Fleury R, Khanikaev AB, Alù A. Floquet topological insulators for sound. Nat Commun. 2016;7:11744. doi: 10.1038/ncomms11744. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Wang YT, Luan PG, Zhang S. Coriolis force induced topological order for classical mechanical vibrations. New J Phys. 2015;17:073031. [Google Scholar]
- 49.Swinteck N, et al. Bulk elastic waves with unidirectional backscattering-immune topological states in a time-dependent superlattice. J Appl Phys. 2015;118:063103. [Google Scholar]
- 50.Kariyado T, Hatsugai Y. Manipulation of Dirac cones in mechanical graphene. Sci Rep. 2015;5:18107. doi: 10.1038/srep18107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Delplace P, Marston JB, Venaille A. Topological origin of equatorial waves. Science. 2017;358:1075–1077. doi: 10.1126/science.aan8819. [DOI] [PubMed] [Google Scholar]
- 52.Souslov A, van Zuiden BC, Bartolo D, Vitelli V. Topological sound in active-liquid metamaterials. Nat Phys. 2017;13:1091–1094. [Google Scholar]
- 53.Shankar S, Bowick MJ, Marchetti MC. Topological sound and flocking on curved surfaces. Phys Rev X. 2017;7:031039. [Google Scholar]
- 54.Bravo-Abad J, Lu L, Fu L, Buljan H, Soljačić M. Weyl points in photonic-crystal superlattices. 2D Mater. 2015;2:034013. [Google Scholar]
- 55.Lin Q, Xiao M, Yuan L, Fan S. Photonic Weyl point in a two-dimensional resonator lattice with a synthetic frequency dimension. Nat Commun. 2016;7:13731. doi: 10.1038/ncomms13731. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Xiao M, Lin Q, Fan S. Hyperbolic Weyl point in reciprocal chiral metamaterials. Phys Rev Lett. 2016;117:057401. doi: 10.1103/PhysRevLett.117.057401. [DOI] [PubMed] [Google Scholar]
- 57.Chang ML, Xiao M, Chen WJ, Chan CT. Multiple Weyl points and the sign change of their topological charges in woodpile photonic crystals. Phys Rev B. 2017;95:125136. [Google Scholar]
- 58.Wang Q, Xiao M, Liu H, Zhu S, Chan CT. Optical interface states protected by synthetic weyl points. Phys Rev X. 2017;7:031032. [Google Scholar]
- 59.Yang Z, et al. Weyl points in a magnetic tetrahedral photonic crystal. Opt Express. 2017;25:15772. doi: 10.1364/OE.25.015772. [DOI] [PubMed] [Google Scholar]
- 60.Whitesides GM. Self-assembly at all scales. Science. 2002;295:2418–2421. doi: 10.1126/science.1070821. [DOI] [PubMed] [Google Scholar]
- 61.Bates FS, Fredrickson GH. Block copolymers – designer soft materials. Phys Today. 1999;52:32–38. [Google Scholar]
- 62.Halász GB, Balents L. Time-reversal invariant realization of the Weyl semimetal phase. Phys Rev B. 2012;85:035103. [Google Scholar]
- 63.Mathai V, Thiang GC. Global topology of Weyl semimetals and Fermi arcs. J Phys A Math Theor. 2017;50:11LT01. [Google Scholar]
- 64.Mathai V, Thiang GC. Differential topology of semimetals. Commun Math Phys. 2017;355:561–602. [Google Scholar]
- 65.Thiang GC, Sato K, Gomi K. Fu-Kane-Mele monopoles in semimetals. Nucl Phys B. 2017;923:107–125. [Google Scholar]
- 66.Kim KW, Lee WR, Kim YB, Park K. Surface to bulk Fermi arcs via Weyl nodes as topological defects. Nat Commun. 2016;7:13489. doi: 10.1038/ncomms13489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Schoen AH. 1970. Infinite periodic minimal surfaces without self-intersections (NASA Electronics Research Center, Cambridge, MA), Technical Report NASA-TN-D-5541, C-98.
- 68.Hur K, et al. Three-dimensionally isotropic negative refractive index materials from block copolymer self-assembled chiral gyroid networks. Angew Chem Int Ed Engl. 2011;50:11985–11989. doi: 10.1002/anie.201104888. [DOI] [PubMed] [Google Scholar]
- 69.Cowman CD, et al. Multicomponent nanomaterials with complex networked architectures from orthogonal degradation and binary metal backfilling in ABC triblock terpolymers. J Am Chem Soc. 2015;137:6026–6033. doi: 10.1021/jacs.5b01915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Longley W, McIntosh TJ. A bicontinuous tetrahedral structure in a liquid-crystalline lipid. Nature. 1983;303:612–614. [Google Scholar]
- 71.Mezzenga R, et al. Shear rheology of lyotropic liquid crystals: A case study. Langmuir. 2005;21:3322–3333. doi: 10.1021/la046964b. [DOI] [PubMed] [Google Scholar]
- 72.Aplinc J, Štimulak M, Čopar S, Ravnik M. Nematic liquid crystal gyroids as photonic crystals. Liq Cryst. 2016;43:2320–2331. [Google Scholar]
- 73.Fontell K. Cubic phases in surfactant and surfactant-like lipid systems. Colloid Polym Sci. 1990;268:264–285. [Google Scholar]
- 74.Monnier A, et al. Cooperative formation of inorganic-organic interfaces in the synthesis of silicate mesostructures. Science. 1993;261:1299–1303. doi: 10.1126/science.261.5126.1299. [DOI] [PubMed] [Google Scholar]
- 75.Glotzer SC, Solomon MJ. Anisotropy of building blocks and their assembly into complex structures. Nat Mater. 2007;6:557–562. doi: 10.1038/nmat1949. [DOI] [PubMed] [Google Scholar]
- 76.Sacanna S, Irvine WTM, Chaikin PM, Pine DJ. Lock and key colloids. Nature. 2010;464:575–578. doi: 10.1038/nature08906. [DOI] [PubMed] [Google Scholar]
- 77.Wang Y, et al. Colloids with valence and specific directional bonding. Nature. 2012;491:51–55. doi: 10.1038/nature11564. [DOI] [PubMed] [Google Scholar]
- 78.Phillips CL, Glotzer SC. Effect of nanoparticle polydispersity on the self-assembly of polymer tethered nanospheres. J Chem Phys. 2012;137:104901. doi: 10.1063/1.4748817. [DOI] [PubMed] [Google Scholar]
- 79.Marson RL, Phillips CL, Anderson JA, Glotzer SC. Phase behavior and complex crystal structures of self-assembled tethered nanoparticle telechelics. Nano Lett. 2014;14:2071–2078. doi: 10.1021/nl500236b. [DOI] [PubMed] [Google Scholar]
- 80.Schulz MF, Bates FS, Almdal K, Mortensen K. Epitaxial relationship for hexagonal-to-cubic phase transition in a book copolymer mixture. Phys Rev Lett. 1994;73:86–89. doi: 10.1103/PhysRevLett.73.86. [DOI] [PubMed] [Google Scholar]
- 81.Hajduk DA, et al. The gyroid: A new equilibrium morphology in weakly segregated diblock copolymers. Macromolecules. 1994;27:4063–4075. [Google Scholar]
- 82.Matsen MW. Gyroid versus double-diamond in ABC triblock copolymer melts. J Chem Phys. 1998;108:785–796. [Google Scholar]
- 83.Meuler AJ, Hillmyer MA, Bates FS. Ordered network mesostructures in block polymer materials. Macromolecules. 2009;42:7221–7250. [Google Scholar]
- 84.Karcher H. The triply periodic minimal surfaces of Alan Schoen and their constant mean curvature companions. Manuscripta Mathematica. 1989;64:291–357. [Google Scholar]
- 85.Große-Brauckmann K, Meinhard W. The gyroid is embedded and has constant mean curvature companions. Cal Var Partial Differ Equ. 1996;4:499–523. [Google Scholar]
- 86.Wohlgemuth M, Yufa N, Hoffman J, Thomas EL. Triply periodic bicontinuous cubic microdomain morphologies by symmetries. Macromolecules. 2001;34:6083–6089. [Google Scholar]
- 87.Park C, Yoon J, Thomas EL. Enabling nanotechnology with self assembled block copolymer patterns. Polymer. 2003;44:6725–6760. [Google Scholar]
- 88.Yoon J, Lee W, Thomas EL. Self-assembly of block copolymers for photonic-bandgap materials. MRS Bull. 2005;30:721–726. [Google Scholar]
- 89.Fink Y, Urbas A, Bawendi M, Joannopoulos J, Thomas E. Block copolymers as photonic bandgap materials. J Lightwave Technol. 1999;17:1963–1969. [Google Scholar]
- 90.Urbas A, Maldovan M, DeRege P, Thomas E. Bicontinuous cubic block copolymer photonic crystals. Adv Mater. 2002;14:1850–1853. [Google Scholar]
- 91.Maldovan M, Urbas AM, Yufa N, Carter WC, Thomas EL. Photonic properties of bicontinuous cubic microphases. Phys Rev B. 2002;65:165123. [Google Scholar]
- 92.Luttinger JM. Quantum theory of cyclotron resonance in semiconductors: General theory. Phys Rev. 1956;102:1030–1041. [Google Scholar]
- 93.Pikus GE. A new method of calculating the energy spectrum of carriers in semiconductors. II. Account of spin-orbit interaction. Soviet Phys JETP. 1961;14:1075–1085. [Google Scholar]
- 94.Bir GL, Pikus GE. Symmetry and Strain-induced Effects in Semiconductors. IPST; New York: 1975. [Google Scholar]
- 95.Winkler R. Spin–Orbit Coupling Effects in Two-Dimensional Electron and Hole Systems. Springer; Berlin: 2003. [Google Scholar]
- 96.Willatzen M, Voon LCLY. The K·P Method. Springer; Berlin: 2009. [Google Scholar]
- 97.Sakoda K. Symmetry, degeneracy, and uncoupled modes in two-dimensional photonic lattices. Phys Rev B. 1995;52:7982–7986. doi: 10.1103/physrevb.52.7982. [DOI] [PubMed] [Google Scholar]
- 98.Sakoda K. Optical Properties of Photonic Crystals. 2nd Ed Springer; Berlin: 2004. [Google Scholar]
- 99.Nittis GD, Lein M. On the role of symmetries in the theory of photonic crystals. Ann Phys. 2014;350:568–587. [Google Scholar]
- 100.Nittis GD, Lein M. 2017. The Schrödinger formalism of electromagnetism and other classical waves—How to make quantum-wave analogies rigorous. arXiv:1710.10148.
- 101.Togo A. 2017 Spglib. Available at https://atztogo.github.io/spglib/. Accessed November 29, 2017.
- 102.Johnson S, Joannopoulos J. Block-iterative frequency-domain methods for Maxwell’s equations in a planewave basis. Opt Express. 2001;8:173–190. doi: 10.1364/oe.8.000173. [DOI] [PubMed] [Google Scholar]
- 103.Kim S, Gopalan V. Strain-tunable photonic band gap crystals. Appl Phys Lett. 2001;78:3015–3017. [Google Scholar]
- 104.Li J, et al. Reversibly strain-tunable elastomeric photonic crystals. Chem Phys Lett. 2004;390:285–289. [Google Scholar]
- 105.Fortes LM, Gonçalves MC, Almeida RM. Flexible photonic crystals for strain sensing. Opt Mater. 2011;33:408–412. [Google Scholar]
- 106.Raman A, Fan S. Photonic band structure of dispersive metamaterials formulated as a Hermitian eigenvalue problem. Phys Rev Lett. 2010;104:087401. doi: 10.1103/PhysRevLett.104.087401. [DOI] [PubMed] [Google Scholar]
- 107.Ashcroft NW, Mermin ND. Solid State Physics. Saunders College Publishing; Philadelphia: 1976. [Google Scholar]
- 108.Ordal MA, et al. Optical properties of the metals Al, Co, Cu, Au, Fe, Pb, Ni, Pd, Pt, Ag, Ti, and W in the infrared and far infrared. Appl Opt. 1983;22:1099–1020. doi: 10.1364/ao.22.001099. [DOI] [PubMed] [Google Scholar]
- 109.Vasseur JO, et al. Experimental and theoretical evidence for the existence of absolute acoustic band gaps in two-dimensional solid phononic crystals. Phys Rev Lett. 2001;86:3012–3015. doi: 10.1103/PhysRevLett.86.3012. [DOI] [PubMed] [Google Scholar]
- 110.Sun JH, Wu TT. Analyses of mode coupling in joined parallel phononic crystal waveguides. Phys Rev B. 2005;71:174303. [Google Scholar]
- 111.Hsieh PF, Wu TT, Sun JH. Three-dimensional phononic band gap calculations using the FDTD method and a PC cluster system. IEEE Trans Ultrason Ferroelectrics Frequency Control. 2006;53:148–158. doi: 10.1109/tuffc.2006.1588400. [DOI] [PubMed] [Google Scholar]
- 112.Hur K, Hennig RG, Wiesner U. Exploring periodic bicontinuous cubic network structures with complete phononic bandgaps. J Phys Chem C. 2017;121:22347–22352. [Google Scholar]
- 113.Koshino M, Aoki H. Electronic structure of an electron on the gyroid surface: A helical labyrinth. Phys Rev B. 2005;71:073405. [Google Scholar]
- 114.Khlebnikov S, Hillhouse HW. Electronic structure of double-gyroid nanostructured semiconductors: Perspectives for carrier multiplication solar cells. Phys Rev B. 2009;80:115316. [Google Scholar]
- 115.Darling S. Directing the self-assembly of block copolymers. Prog Polym Sci. 2007;32:1152–1204. [Google Scholar]
- 116.Zhang Q, et al. Pathways to mesoporous resin/carbon thin films with alternating gyroid morphology. ACS Nano. 2017;12:347–358. doi: 10.1021/acsnano.7b06436. [DOI] [PubMed] [Google Scholar]
- 117.Werner JG, Hoheisel TN, Wiesner U. Synthesis and characterization of gyroidal mesoporous carbons and carbon monoliths with tunable ultralarge pore size. ACS Nano. 2013;8:731–743. doi: 10.1021/nn405392t. [DOI] [PubMed] [Google Scholar]
- 118.Robbins SW, Sai H, DiSalvo FJ, Gruner SM, Wiesner U. Monolithic gyroidal mesoporous mixed titanium-niobium nitrides. ACS Nano. 2014;8:8217–8223. doi: 10.1021/nn502548m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 119.Stefik M, Guldin S, Vignolini S, Wiesner U, Steiner U. Block copolymer self-assembly for nanophotonics. Chem Soc Rev. 2015;44:5076–5091. doi: 10.1039/c4cs00517a. [DOI] [PubMed] [Google Scholar]
- 120.Bradley C, Cracknell A. The Mathematical Theory of Symmetry in Solids: Representation Theory for Point Groups and Space Groups. Oxford Univ Press; Oxford: 2010. [Google Scholar]
- 121.Bradlyn B, et al. Topological quantum chemistry. Nature. 2017;547:298–305. doi: 10.1038/nature23268. [DOI] [PubMed] [Google Scholar]
- 122.Bradlyn B, et al. Beyond Dirac and Weyl fermions: Unconventional quasiparticles in conventional crystals. Science. 2016;353:aaf5037. doi: 10.1126/science.aaf5037. [DOI] [PubMed] [Google Scholar]
- 123.Wieder BJ, Kim Y, Rappe AM, Kane CL. Double Dirac semimetals in three dimensions. Phys Rev Lett. 2016;116:186402. doi: 10.1103/PhysRevLett.116.186402. [DOI] [PubMed] [Google Scholar]
- 124.Lu J, et al. Dirac cones in two-dimensional artificial crystals for classical waves. Phys Rev B. 2014;89:134302. [Google Scholar]
- 125.Saba M, Hamm JM, Baumberg JJ, Hess O. Group theoretical route to deterministic weyl points in chiral photonic lattices. Phys Rev Lett. 2017;119:227401. doi: 10.1103/PhysRevLett.119.227401. [DOI] [PubMed] [Google Scholar]
- 126.Lüscher M. Topology of lattice gauge fields. Commun Math Phys. 1982;85:39–48. [Google Scholar]
- 127.Panagiotakopoulos C. Topology of 2D lattice gauge fields. Nucl Phys B. 1985;251:61–76. doi: 10.1103/physrevd.32.1048. [DOI] [PubMed] [Google Scholar]
- 128.Phillips AV, Stone DA. The computation of characteristic classes of lattice gauge fields. Commun Math Phys. 1990;131:255–282. [Google Scholar]
- 129.King-Smith RD, Vanderbilt D. Theory of polarization of crystalline solids. Phys Rev B. 1993;47:1651–1654. doi: 10.1103/physrevb.47.1651. [DOI] [PubMed] [Google Scholar]
- 130.Simon R, Mukunda N. Bargmann invariant and the geometry of the Güoy effect. Phys Rev Lett. 1993;70:880–883. doi: 10.1103/PhysRevLett.70.880. [DOI] [PubMed] [Google Scholar]
- 131.Resta R. Macroscopic polarization in crystalline dielectrics: The geometric phase approach. Rev Mod Phys. 1994;66:899–915. [Google Scholar]
- 132.Fukui T, Hatsugai Y, Suzuki H. Chern numbers in discretized Brillouin zone: Efficient method of computing (spin) hall conductances. J Phys Soc Jpn. 2005;74:1674–1677. [Google Scholar]
- 133.Bates FS, et al. Multiblock polymers: Panacea or Pandora’s box? Science. 2012;336:434–440. doi: 10.1126/science.1215368. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.