Comparing side chain packing in soluble proteins, protein-protein interfaces, and transmembrane proteins

Abstract

We compare side chain prediction and packing of core and non-core regions of soluble proteins, protein-protein interfaces, and transmembrane proteins. We first identified or created comparable databases of high-resolution crystal structures of these three protein classes. We show that the solvent-inaccessible cores of the three classes of proteins are equally densely packed. As a result, the side chains of core residues at protein-protein interfaces and in the membrane-exposed regions of transmembrane proteins can be predicted by the hard-sphere plus stereochemical constraint model with the same high prediction accuracies (> 90%) as core residues in soluble proteins. We also find that for all three classes of proteins, as one moves away from the solvent-inaccessible core, the packing fraction decreases as the solvent accessibility increases. However, the side chain predictability remains high (80% within 30°) up to a relative solvent accessibility, rSASA ≲ 0.3, for all three protein classes. Our results show that ≈ 40% of the interface regions in protein complexes are ‘core’, i.e. densely packed with side chain conformations that can be accurately predicted using the hard-sphere model. We propose packing fraction as a metric that can be used to distinguish real protein-protein interactions from designed, non-binding, decoys. Our results also show that cores of membrane proteins are the same as cores of soluble proteins. Thus, the computational methods we are developing for the analysis of the effect of hydrophobic core mutations in soluble proteins will be equally applicable to analyses of mutations in membrane proteins.

1 Introduction

The computational design of protein-protein interfaces [1–9] and the prediction of the structure of transmembrane proteins [10–12] are still unsolved problems. For example, in a recent Critical Assessment of Prediction of Interactions (CAPRI) competition [4], researchers were given a set of models of 21 protein-protein complexes, 20 of which fail to bind in experiments, and challenged to find the one true protein-protein complex [13]. Only two out of 28 groups correctly identified the pair that binds in experiments. If we are unable to distinguish true complexes from decoys, how can we expect to accurately design new complexes? Several computational designs have been successful, but these have involved testing many of the computational designs experimentally before finding one that works or have used methods that are not effective across different protein design problems [5, 14–18].

Membrane proteins comprise nearly 30% of the proteome. They perform vital functions, including electron transport, ion conductance, and signal transduction. Nevertheless, we currently only have a rudimentary understanding of their structure and thermodynamic stability [19–21]. For example, we do not know whether membrane proteins are fundamentally different from soluble proteins. Specifically, are membrane proteins less, more, or equally well-packed as soluble proteins? One conjecture is that to achieve thermodynamic stability, membrane proteins must be more densely packed than soluble proteins, because the hydrophobic effect does not contribute to their stability [22]. Conversely, others have argued that because many membrane proteins transduce signals across the membrane, they must be more flexible and loosely packed compared to soluble proteins [23–25]. Clearly, to understand their structure, much less to design new membrane proteins, we must answer this question.

We believe that an improved fundamental understanding of protein structure will aid in the development of predictive computational tools for protein design. A defining feature of our strategy is that we start with simple models and test their ability to predict features of protein structure that are seen in high resolution crystal structures. Such predictability is the key metric of success in protein design. In prior work, we investigated the range and limits of the predictability of protein side chain conformations for uncharged amino acids, using a simple repulsive-only hard-sphere plus stereochemical constraint model [26–33]. We showed that the hard-sphere model, when applied to a dipeptide mimetic (Fig. 1), is able to predict the side chain dihedral angle distributions observed in natural proteins for most of the uncharged residues (e.g. Ile, Leu, Val, Thr, Tyr, Trp, Phe, and Cys) [29]. When we consider both intra- and inter-residue atomic interactions, the hard-sphere model is able to predict the specific side chain conformation of each of these amino acids in protein cores [30]. We have shown that Met requires additional attractive interactions for the hard-sphere model predictions to match the observed side chain dihedral angle distributions [32], and that only about 50% of Ser residues can be predicted using the hard-sphere model alone [30, 33]. (We presume that the absence of hydrogen-bonding interactions explains the limited prediction accuracy of Ser using the hard-sphere model.)

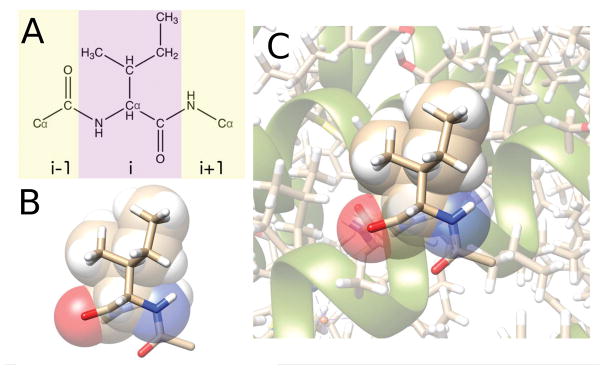
Figure 1.

A) The chemical structure of an Ile dipeptide mimetic. The dipeptide mimetic includes the residue itself (purple), the carboxyl and C_α groups from residue i − 1, and the amine and C_α groups from residue i + 1. B) Stick representation of Ile 135 from 1Q16 as a dipeptide mimetic overlaid on a space-filling representation of the atoms in the purple region of panel A. The atoms are colored beige (carbon), red (oxygen), blue (nitrogen), and white (hydrogen). C) Ile 135 from 1Q16 in its protein environment (shown in stick and ribbon representations)

We have also found that protein cores are as densely packed as jammed packings of residue-shaped particles with explicit hydrogens, which possess a packing fraction ϕ ~ 0.55 [34, 35]. With these data as background, we now seek to investigate to what extent the hard-sphere modeling approach can be applied to contexts other than the cores of soluble proteins–namely non-core residues, protein-protein interfaces, and membrane-embedded regions of transmembrane proteins.

The high accuracy of the hard-sphere model in predicting side chain conformations in protein cores stems from the fact that protein cores are densely random-packed [34] and thus each buried side chain can only exist in a single conformation without having atomic overlaps [33]. We therefore first investigated how the packing fraction varies with solvent accessibility (i.e. relative solvent accessible surface area, rSASA), and performed the same calculations on soluble proteins, protein-protein interfaces (Fig. 2), and the membrane-embedded regions of transmembrane proteins (Fig. 3).

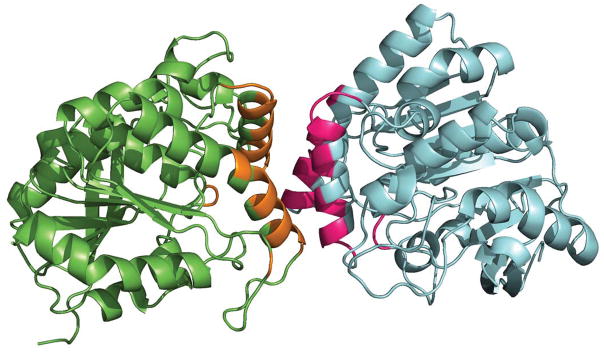
Figure 2.

Ribbon representation of a protein-protein complex (PDB identifier: 1DQZ). The two protein chains are shown in green and blue. The interface residues (displayed in orange and pink) were identified as those residues with a change in SASA, ΔSASA_Res > 0.1 Ų, between the monomer and the complex.

Figure 3.

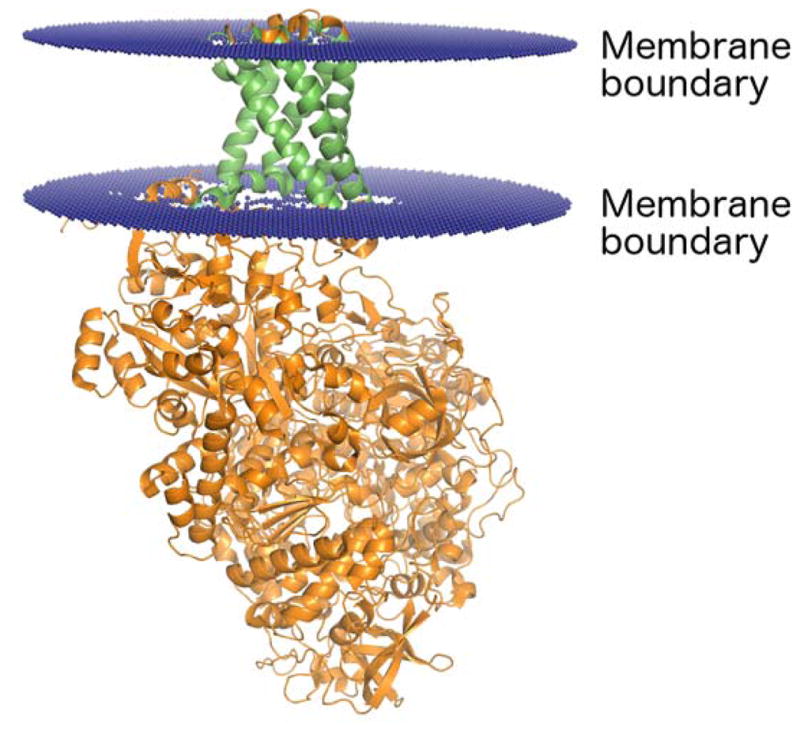
Ribbon representation of a transmembrane protein (PDB identifier: 1Q16). The membrane boundary planes (displayed in blue) were obtained from the Positioning of Proteins in Membranes (PPM) server [52]. The region of the protein that spans the membrane is shown in green, and the portion of the protein that extends beyond the membrane is shown in orange.

We find that for all three types of proteins, rSASA is inversely related to the packing fraction. Importantly, the relationship between packing fraction and rSASA is similar for soluble proteins, protein-protein interfaces, and the membrane-embedded regions of transmembrane proteins. Therefore, we use rSASA as a surrogate for packing fraction. We then calculate the fraction of residues for which the hard-sphere model is able to predict the side chain dihedral angles within 30° of the crystal structure values as a function of rSASA. We find that for soluble proteins, protein-protein interfaces, and membrane proteins, the accuracy of the side chain predictions decreases as solvent accessibility increases. The predictions for soluble proteins, protein-protein interfaces, and transmembrane proteins all show similar behavior as a function of rSASA.

In this article, we provide strong evidence showing that the hydrophobic cores of soluble proteins, solvent inaccessible regions of protein-protein interfaces, and buried residues in the membrane-embedded regions of transmembrane proteins are essentially all the same–i.e. they are all equally well packed. These results are important because they help us identify the key variables that control successful protein-protein interaction designs. Moreover, they show that contrary to the conclusions of several prior studies [22, 23, 36, 37], the buried residues in the membrane-embedded portions of transmembrane proteins are neither more nor less well-packed than the cores of soluble proteins and the side chain conformations are just as predictable as those in soluble proteins using the hard-sphere model.

The remainder of the article is organized into three sections. In the Methods section, we describe the datasets of protein crystal structures that we investigate in this study and details of the hard-sphere model that we employ to predict the side chain conformations of residues. We also explain the methods that we used to calculate the packing fraction and solvent accessibility. In the Results section, we compare the amino acid composition of soluble proteins, protein interfaces, and transmembrane proteins for different values of solvent accessibility. We then show the relationship between packing fraction and solvent accessibility and the accuracy of the predicted side chain conformations as a function of rSASA. In the Discussion section, we argue that the packing fraction can be used as a metric to rank successful computational designs and emphasize that transmembrane proteins possess core regions that are as densely packed as the cores of soluble proteins, and thus their side chain conformations are equally predictable using the hard-sphere model.

2 Methods

2.1 Databases of Protein Crystal Structures

For our studies, we employ three datasets of protein crystal structures: one for soluble proteins (Dun1.0), one for protein-protein interfaces (PPI), and one for transmembrane proteins (TM). The Dunbrack 1.0 Å dataset [38,39] is a collection of 221 high resolution protein crystal structures with resolution ≤ 1.0 Å, R-factor ≤ 0.2, side-chain B-factor per residue ≤ 30 Ų, and sequence identity between proteins in the dataset ≤ 50%. We removed proteins with modified residues, leaving 182 structures, which we refer to as the “Dun1.0” dataset. We created the protein-protein interface dataset (PPI), a collection of 164 homo- and heterodimer protein structures from the Protein Data Bank (PDB). Structures were selected that had exactly 2 chains in the asymmetric and biological unit with no additional ligands or modified residues, a resolution threshold of ≤ 1.5 Å, and sequence identity ≤ 50%. We removed structures for which the biological unit was not assigned as a dimer by the author and for which one chain contained less than five residues, leaving us with 149 structures.

We also created a transmembrane dataset (TM) containing 19 high resolution transmembrane proteins. The structures were obtained from the Protein Data Bank of Transmembrane Proteins [40, 41]. The same criteria for the R-factor, B-factor, and sequence identity used to create the Dun1.0 dataset were applied to select the TM structures. However, since there are very few high-resolution transmembrane crystal structures, the resolution threshold was increased to 2.0 Å. In each dataset, if a protein contained two identical chains, both chains were used when calculating the solvent accessibility, but only one chain was included in all further analyses to avoid double-counting residues. The PDB codes for each dataset are included in the Supporting Information.

2.2 The hard-sphere plus stereochemical constraint model

As described in previous work [29, 33], the hard-sphere plus stereochemical constraint model (i.e. the ‘hard-sphere model’) treats each atom i as a sphere that interacts pairwise with all other non-bonded atoms j via the purely repulsive Lennard-Jones potential:

$$U_{\text{RLJ}}(r_{ij})=\frac{\epsilon }{72}{\left[1-{\left(\frac{{\sigma }_{ij}}{r_{ij}}\right)}^6\right]}^2\mathrm{\Theta }({\sigma }_{ij}-r_{ij}),$$ (1)

where r_ij is the center-to-center separation between atoms i and j, σ_ij = (σ_i +σ_j)/2, σ_i/2 is the radius of atom i, Θ(σ_ij − r_ij) is the Heaviside step function, and ε is the strength of the repulsive interactions. The values for the atomic radii (C_sp3, C_aromatic: 1.5 Å; C_O: 1.3 Å; O: 1.4 Å; N: 1.3 Å; H_C: 1.10 Å; H_O,N: 1.00 Å, and S: 1.75 Å) were obtained in prior work [29] by minimizing the difference between the side chain dihedral angle distributions predicted by the hard-sphere dipeptide mimetic model and those observed in protein crystal structures for a subset of amino acid types. Hydrogen atoms were added using the REDUCE software program [42, 43], which sets the bond lengths for C-H, N-H and S-H to 1.1, 1.0 and 1.3 Å, respectively, and the bond angles to 109.5° and 120° for angles involving C_sp3 and C_sp2 atoms, respectively. Additional dihedral angle degrees of freedom involving hydrogen atoms are chosen to minimize steric clashes [42].

We performed single residue repacking using the hard-sphere model. Predictions of the side chain conformations of single amino acids are obtained by rotating each of the side chain dihedral angles, χ₁, χ₂, …, χ_n (with a fixed backbone conformation [44]), and finding the lowest energy side chain conformations of the residue, where the energy includes both intra- and inter-residue steric repulsive interactions.

We then calculate the Boltzmann weight of the lowest energy side chain conformation of a given residue i, P_i(χ₁, ...., χ_n) ∝ e^{−U(χ₁,…,χ_n/k_BT}, where the small temperature, k_BT/ε=10⁻², approximates hard-sphere-like interactions. To sample bond length and angle fluctuations, we perform side chain dihedral angle rotations with 300 replicas of residue i with different bond length and bond angle combinations that mimic the distributions observed in protein crystal structures. We then randomly select 50 bond length and angle variants (j = 1, …, 50) of the 300 replicas sampled, and for each variant find the lowest energy side chain dihedral angle conformation and corresponding P_ij(χ₁, ...., χ_n) values [33]. We average P_ij over the j = 50 variants to obtain 〈P_i(χ₁, ...., χ_n)〉. We repeat this sampling 50 times, producing 50 different 〈P_i〉_a distributions with a = 1, …, 50. For each 〈P_i〉_a distribution, we select the side chain dihedral angle combination with the highest value as our prediction, giving 50 predicted side chain conformations for each residue i, { ${\chi }_{1,a}^{HS},\dots ,{\chi }_{n,a}^{HS}$}, indexed by a = 1, …, 50. Each of these predictions is then compared to the side chain conformation of the crystal structure { ${\chi }_1^{\mathit{xtal}},\dots ,{\chi }_n^{\mathit{xtal}}$}.

To assess the accuracy of the hard-sphere model in predicting the side chain dihedral angles of residues, we calculated the deviation,

$$\mathrm{\Delta }{\chi }_a=\sqrt{{({\chi }_1^{\mathit{xtal}}-{\chi }_{1,a}^{HS})}^2+\dots +{({\chi }_n^{\mathit{xtal}}-{\chi }_{n,a}^{HS})}^2},$$ (2)

for each set of replicas a for each residue i. We then look at the first Δχ_a value (a = 1) for each instance i of an amino acid type in the dataset and calculate F(Δχ_a), the fraction of residues with Δχ_a < 30°. This is repeated for all a = 50 replicas, producing 50 F(Δχ_a). We then calculate the mean fraction 〈F(Δχ)〉 and use one standard deviation as a measure of the error. (Note that if multiple side chain configurations were reported in the PDB for a given residue, Δχ was only calculated for the conformation labeled ‘A’.)

We have shown that steric interactions between the side chain of a residue and the rest of the protein are necessary to accurately predict the side chain dihedral angles of amino acid residues [30]. However, to obtain a lower bound on the prediction accuracy of the hard-sphere model, we also predicted the side chain conformations for each amino acid without the rest of the protein, i.e. each residue modeled as a dipeptide mimetic (Fig. 1).

2.3 Packing fraction, surface identification, and relative solvent accessible surface area

The packing fraction of each residue in a protein can be calculated using,

$${\varphi }_r=\frac{{\sum }_i{\mathrm{V}}_i}{{\sum }_i{\mathrm{V}}_i^v},$$ (3)

where V_i is the ‘non-overlapping’ volume of atom i, ${\mathrm{V}}_i^v$ is the volume of the Voronoi polyhedron surrounding atom i, and the summations are over all atoms of a particular residue. Voronoi cells were obtained for each atom using Laguerre tessellation, where the placement of each Voronoi face is based on the relative radii of neighboring atoms (which is the same as the location of the plane that separates overlapping atoms) [45]. V_i was calculated by splitting overlapping atoms by the plane of intersection between the two atoms. To study the packing fraction of solvent-exposed atoms, an outer boundary is placed around the protein to terminate some of the Voronoi polyhedra. However, when calculating the packing fraction as a function of rSASA, we only include residues for which the the volumes of the Voronoi polyhedra are independent of the size and placement of the outer boundary.

To investigate the relationship between packing fraction, side chain prediction accuracy, and solvent accessibility, we compute the relative solvent accessible surface area,

$$\text{rSASA}=\frac{{\mathit{SASA}}_{\mathit{Res}}}{{\mathit{SASA}}_{\mathit{Dipep}}},$$ (4)

where SASA_Res is the total solvent accessible surface area of the residue (in Ų) in the context of the protein environment and SASA_Dipep is the solvent accessible surface area of that residue extracted as a dipeptide mimetic (Fig. 1) with the same bond lengths, bond angles, and backbone and side chain dihedral angles. We calculate the SASA of protein structures and dipeptide mimetics using the software program Naccess [46] with a probe size of 1.4 Å and a z-slice of 10⁻³ Å. Naccess uses the method first developed by Lee and Richards [47] to calculate SASA by taking z-slices of the protein, calculating the length of the solvent exposed contours in the slice, and summing over all z-slices. With our choice of parameters for Naccess, the error in the rSASA calculation for a given residue is ≲ 10⁻³, and thus we define core residues as those with rSASA ≤ 10⁻³. Similar rSASA values for each residue are obtained using the software program MSMS, which uses an analytical approach to calculate SASA [48].

Our calculation of the denominator in the definition of rSASA differs from other methods for determining rSASA, which set SASA_Dipep to a constant for each amino acid type. Most methods calculate SASA_Dipep using the tripeptide Gly-X-Gly or Ala-X-Ala, where X is a given residue type. The conformation for the residue X within the tripeptide varies for different methods. For example, some methods choose a particular backbone and side chain dihedral angle conformation across all instances of an amino acid [46, 49, 50]. This approach can lead to an apparent rSASA > 1 since each residue possesses different ϕ, ψ, and χ values than the reference residue used to calculate SASA_Dipep. Other methods instead explore all the possible conformations of backbone and side chains of an amino acid and select the backbone and side chain conformations that yield the maximum SASA_dipep [51]. This method avoids rSASA > 1, but does not allow SASA_Dipep to vary for each instance of a 9 residue of a given type. We have taken a different approach. We compute the maximum SASA (SASA_Dipep) for each residue in its particular ϕ, ψ, and χ conformation. In this way, we are taking into account both backbone and side chain conformations, leading to an accurate normalization of the solvent exposure of a residue and providing a consistent comparison of rSASA between different amino acid types.

2.4 Identification of protein interfaces and transmembrane regions

For the PPI dataset, protein-protein interface residues are identified as those with ΔSASA_Res ≥ 0.1 Ų, where $\mathrm{\Delta }{\mathit{SASA}}_{\mathit{Res}}={\mathit{SASA}}_{\mathit{Res}}^{\mathit{mon}}-{\mathit{SASA}}_{\mathit{Res}}^{\mathit{com}},{\mathit{SASA}}_{\mathit{Res}}^{\mathit{mon}}$ is the SASA of the residue in the monomer created by removing the other chain from the crystal structure, and ${\mathit{SASA}}_{\mathit{Res}}^{\mathit{com}}$ is the SASA of the residue in the complex. In Fig. 4, we show the distribution of the number of interface residues in each complex and ΔSASA_Res for each complex.

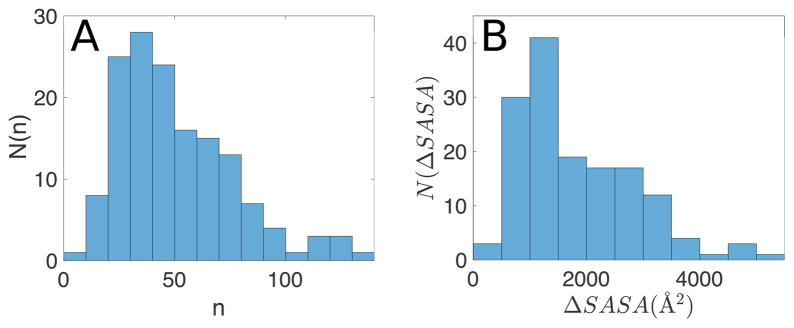
Figure 4.

A) Frequency distribution, N(n), of the number of residues n at each protein-protein interface in the PPI dataset. B) Frequency distribution of the total interface areas (the sum of ΔSASA_res over all interface residues) in the PPI dataset.

For the TM dataset, many entries contain non-membrane regions. (See Fig. 3.) To ensure that our analyses focus on the membrane-embedded region of transmembrane proteins, residues from the soluble protein domains were not considered. Specifically, only residues with one or more atoms predicted to be inside the lipid bilayer were included in this study. The position of the membrane was identified using the Positioning of Proteins in Membranes (PPM) server [52]. The PPM server estimates the location of the lipid bilayer using an approach based on optimizing the free energy of the protein transfer from water to the membrane environment. The residues in the transmembrane region of the protein were then analyzed using the same methods as those for protein-protein interfaces and soluble proteins, where high rSASA values indicate residues that would be exposed to the lipid bilayer.

3 Results

In our studies, we use three high-resolution, non-redundant structural datasets. The details of each dataset are specified in Sec. 2.1. Briefly, Dun1.0 is a dataset of soluble proteins; PPI is a dataset of dimeric protein-protein complexes; and TM is a dataset of transmembrane proteins. For our analyses of the TM dataset, we remove any detergent or lipid molecules and any portion of the protein that is not in the membrane. For protein-protein interfaces, we identify interface residues as those with a change in SASA between the monomer and complex of more than 0.1 Ų and only include these residues in our analyses. When we discuss the PPI and TM datasets, we are only referring to the residues at the interface or in the membrane.

We began by determining the amino acid composition of the PPI and TM databases and then compared the amino acid compositions with that of soluble proteins (Dun1.0). We identify the core residues in each dataset (i.e. those with rSASA < 10⁻³) and calculate the fraction of core residues that are a given amino acid type. In Fig. 5A, we show that the cores of protein-protein interfaces and of membrane proteins have similar amino acid compositions to that of the cores of soluble proteins. Some differences are seen in the composition of TM proteins, which have a higher frequency of Ala and Gly in their cores, which is consistent with the Gly-xxx-Gly motif found in transmembrane helix-helix association [53–59]. Other papers studying transmembrane proteins have also reported a higher frequency of Ala and Gly [36, 60].

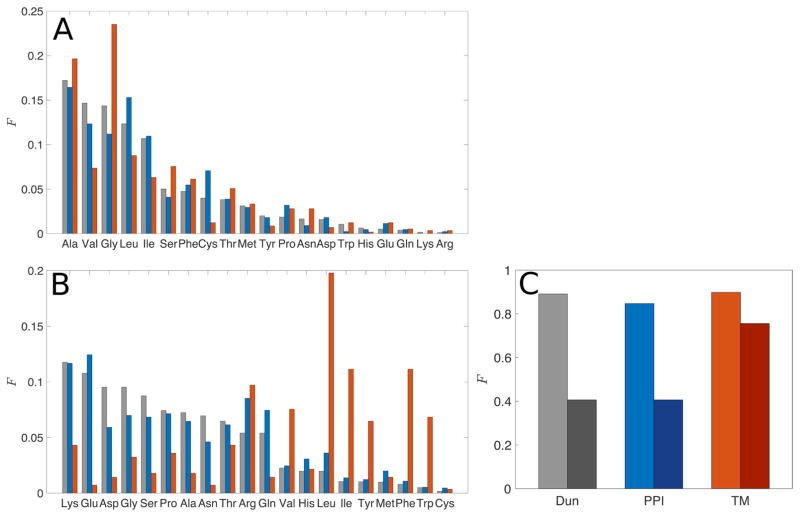
Figure 5.

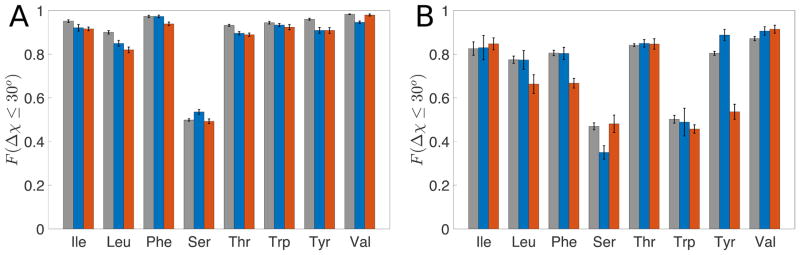
Frequency distribution of amino acids with (A) rSASA ≤ 10⁻³ and (B) rSASA > 0.5 for residues in the Dun1.0 (grey), PPI (blue), and TM (red) datasets. The fractions are defined relative to the total number of residues in each rSASA category. (C) The fractions of core residues (light bars) and non-core residues (rSASA > 0.5, dark bars) among the 11 non-charged residues (Ala, Gly, Ile, Leu, Met, Phe, Ser, Thr, Trp, Tyr, and Val).

In Fig. 5B, we investigate the non-core regions of the proteins (i.e. those residues with rSASA > 0.5) for all three datasets. For TM proteins, where only residues in the membrane are included, residues with high rSASA are membrane-exposed residues, not solvent-exposed. For the PPI dataset, non-core residues are residues at the interface with high rSASA values in the protein complex. We find that proteins in the Dun1.0 and PPI datasets have a similar distribution of non-core residues, with a large fraction of polar and charged residues, while the TM dataset has more hydrophobic residues and a small number of charged residues. This result is further illustrated in Fig. 5C, where we show the fraction of uncharged residues (Ala, Gly, Ile, Leu, Met, Phe, Ser, Thr, Trp, Tyr, and Val) in the core and for rSASA > 0.5 in each dataset. The cores of all three datasets are composed almost entirely of these 11 uncharged residues, while the non-core regions of proteins in the Dun1.0 and PPI datasets only contain ~40% of these residues. In contrast, the non-core regions of TM proteins are highly non-polar, containing ~75% of the 11 uncharged residues, because they are exposed to the membrane, not the aqueous environment.

In earlier studies, other groups have reported similar analyses of amino acid compositions, for different datasets of protein-protein interfaces and membrane proteins [36, 60–66]. We are not reporting any substantial differences from those data. Rather, we performed this tabulation to have these data for the exact datasets that we are studying. Note that our dataset of membrane proteins includes only the transmembrane section, not the whole protein, and our dataset of protein-protein interfaces only considers the interface residues.

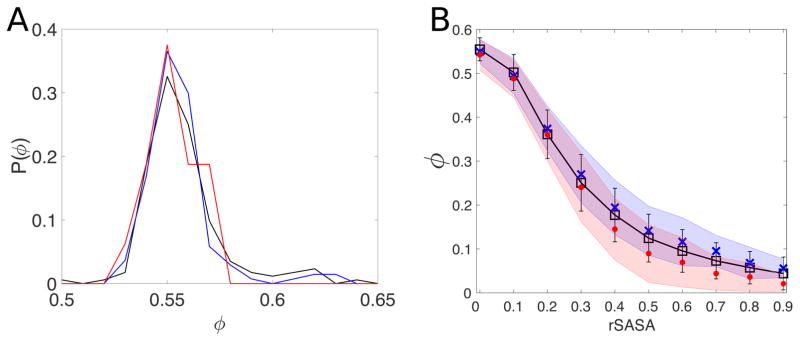
In prior work, we demonstrated that one can repack the side chains of residues in protein cores using only hard-sphere repulsive interactions in the context of a calibrated atomistic model [30, 33]. In this study, we investigate whether the same approach can predict the conformations of amino acid side chains at protein-protein interfaces and in transmembrane proteins. The reason the hard-sphere model can accurately predict side chain conformations in protein cores is because they are densely packed [34, 35]. We therefore first calculated the packing fraction of the cores of protein-protein interfaces and transmembrane proteins, and compared these values with the packing fraction of the cores of soluble proteins. Fig. 6A clearly shows that the distributions P(ϕ) of packing fractions of core residues in the Dun1.0, PPI, and TM datasets are all very similar with mean values, 〈ϕ〉 = 0.56 ± 0.02, 0.56 ± 0.02, and 0.55±0.01, respectively. In prior studies, we showed that this packing fraction matches the value for random close packing of elongated, bumpy particles that match the aspect ratio and surface roughness of core amino acids [35].

Figure 6.

A) Distribution of packing fractions P(ϕ) of core residues in the Dun1.0 (black), PPI (blue), and TM (red) datasets. ϕ is calculated using Eq. 3, where the summation is over all atoms of all core residues in each protein. B) Packing fraction ϕ of residues as a function of the relative solvent accessibility (rSASA) for the Dun1.0 (black line and squares), PPI (blue crosses), and TM (red circles) datasets. The error bars indicate the standard deviation for the Dun1.0 dataset and the blue and red shaded regions indicate the standard deviations for the PPI and TM datasets, respectively.

There have been many studies of the structure of protein-protein interfaces [61, 62, 64, 65, 67–72]. A key observation is that the packing fraction in the core region of protein-protein interfaces is the same as that in the hydrophobic core of soluble proteins, which we is in agreement with our observations [61, 64, 67]. However, there is currently no consensus regarding the packing of core residues in transmembrane proteins. Some groups claim tighter packing in transmembrane proteins than in soluble proteins [22]. embrane proteins even in the absence In contrast, other groups, using different approaches, report that transmembrane proteins pack less efficiently than the cores of soluble proteins [23,24]. Note that some groups studying transmembrane proteins do not limit their studies to residues in the transmembrane region, which makes it difficult to make specific conclusions about transmembrane residues.

The cores of soluble proteins, the cores of protein-protein interfaces, and the cores of transmembrane proteins all have high packing fraction and near-zero solvent accessibility. To study the dependence of the prediction accuracy on packing fraction, we first determined the relationship between packing fraction and solvent accessibility. As anticipated, the packing fraction is inversely proportional to solvent accessibility, because the empty space surrounding residues in the proteins is included in the Voronoi polyhedra for non-core residues, as shown in Fig. 6B. This relationship allows us to use solvent accessibility as a surrogate for packing fraction. Solvent accessibility is preferable because it is relatively straightforward and rapid to calculate, and more importantly, the packing fraction is not well defined for non-core residues because the sizes of the Voronoi polyhedra are not restricted by the surrounding atoms.

We next investigate how our ability to predict side chain conformations depends on solvent accessibility for residues in the Dun1.0, PPI and TM databases. We performed single residue repacking in the protein environment using the hard-sphere plus stereochemical constraint model for all core and solvent-exposed uncharged residues in the datasets. As a ‘lower limit’ of the prediction accuracy, we used the hard-sphere dipeptide model to predict side chain conformations in the absence of neighboring residues. The lower limit represents the minimum prediction accuracy expected for that residue if it had rSASA = 1, allowing us to determine how much the surrounding residues contribute to the repacking prediction accuracy.

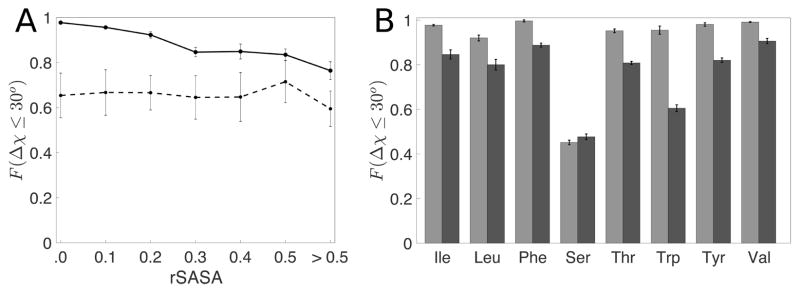
In Fig. 7A, we show the relationship between the prediction accuracy and rSASA for a representative amino acid, Ile. We find that for Ile residues with zero solvent accessibility (rSASA < 10⁻³) we are able to predict over 95% of side chain conformations within 30° of the crystal structure values. As the solvent accessibility increases, the packing fraction decreases and therefore our ability to predict the conformation of the amino acid side chain decreases towards the dipeptide value. In Fig. 7B, we compare the prediction accuracy for core and non-core (0.2 ≤ rSASA < 0.3) uncharged residues in Dun1.0. For all residues, we find a decrease in the prediction accuracy as rSASA increases, except for Ser, which we have mentioned previously [32]. The prediction accuracy versus rSASA plots for each amino acid type are shown in the Supporting Information.

Figure 7.

A) Fraction of residues predicted within 30° (F(Δχ ≤ 30°)) for Ile residues in the Dun1.0 database (solid line) and their corresponding dipeptide mimetics (dotted line) as a function of rSASA values. The dotted line provides lower bounds for the prediction accuracy for the residues in each rSASA bin. Due to the low frequency of uncharged residues in the non-core region, we have combined all residues with rSASA > 0.5 into one bin. B) F(Δχ ≤ 30°) for non-charged amino acids for rSASA < 10⁻³ (light grey) and 0.2 < rSASA ≤ 0.3 (dark grey).

We performed the same calculations for residues in the PPI and TM databases. Data for all amino acids in the Dun1.0, PPI, and TM databases are shown in Fig. 8. For all three datasets, the hard-sphere model gives high prediction accuracy for core residues. A decreased but acceptable predictability (i.e. 80% of residues have Δχ < 30°) is observed for residues with 0.2 ≤ rSASA < 0.3 for all amino acid types (except for Ser and Trp) for all protein classes.

Figure 8.

F(Δχ ≤ 30°) for non-charged amino acids for (A) rSASA < 0.1 and (B) 0.2 < rSASA ≤ 0.3 for the Dun1.0 (grey), PPI (blue) and TM (red) datasets.

Thus, we have identified a crucial parameter that controls the side chain conformation predictability: the packing fraction and its surrogate, solvent accessibility. If the packing fraction is large (i.e. near 0.55–0.56), rSASA is small (i.e. < 10⁻³) and the prediction accuracy is high (> 90%). Conversely, if the packing fraction is small, rSASA is large and the prediction accuracy decreases towards that for an isolated dipeptide mimetic. Moreover, when the packing fraction is large and rSASA is small, the high prediction accuracy is the same in the core of a soluble protein, the core of a protein-protein interface, and the core of the transmembrane region of a membrane protein. As the packing fraction decreases and rSASA increases, the decrease of the prediction accuracy for a given amino acid is slightly different, depending on its protein context. Presumably, this observation implies that forces other than purely repulsive steric interactions come into play at lower packing fractions in the different protein environments.

4 Discussion and Conclusions

We have shown that the packing fraction of the cores of soluble proteins and of the cores of protein-protein interfaces and membrane proteins are the same. We have also studied the relationship between the packing fraction and the prediction accuracy of side chain dihedral angles using the hard-sphere model. The side chain dihedral angle prediction accuracy decreases with decreasing packing fraction (and increasing solvent accessibility).

These results are important for protein-protein interactions because the packing fraction provides a specific metric to assess designed protein-protein interfaces. One of the frequently highlighted issues in computational protein-protein interface design is the difficulty in discriminating between natural protein-protein complexes (i.e. benchmarks) and highly-ranked designed structures that do not bind experimentally. In future studies, we will explore the use of the packing fraction of interfaces to distinguish between protein-protein interaction decoys and true protein-protein interaction pairs. Several experimental studies [73–76] have shown that cavity-forming mutations to protein cores can destabilize proteins. In future work, we will perform studies to understand how packing fraction and interior voids that are caused by mutations affect protein stability and the binding affinity of protein-protein interactions. A similar concept has been successful in discriminating between natural proteins and flawed computational models [77].

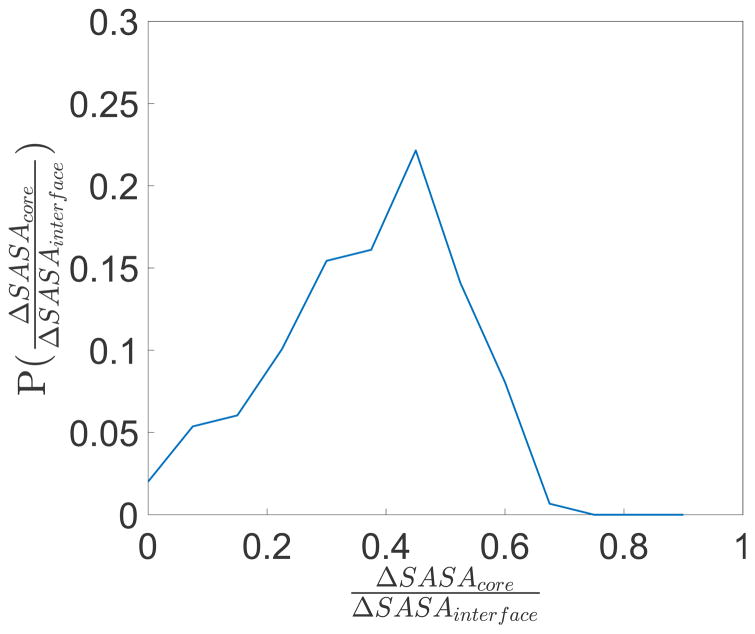
In Fig. 9, we show the distribution of the fraction of each interface in the PPI dataset that is made up of solvent inaccessible residues with rSASA < 0.1. We find that approximately 40% of the surface area of protein-protein interfaces are solvent inaccessible and possess high packing fraction (ϕ > 0.54). Thus, we are able to predict with an accuracy of ~ 90% the conformations of ~ 40% of the total number of residues at protein-protein interfaces. This result holds for protein-protein interfaces ranging in total area up to 6000 Ų.

Figure 9.

Distribution of the fraction of the change in SASA of each interface in the PPI dataset that is due to core residues ΔSASA_core compared to the change in SASA from all residues at the interface ΔSASA_interface. Core residues are defined as those with rSASA < 0.1.

We also showed that the cores of the transmembrane regions of membrane proteins are as well-packed as the cores of soluble proteins, and thus the hard-sphere model can predict the side chain conformations of these core residues with high accuracy. With these results, we can begin to better understand the molecular details of packing in the cores of membrane proteins, and at the interfaces between interacting, membrane embedded regions of membrane proteins [78–83]. In addition to enhancing our fundamental understanding, such knowledge is of significant practical biomedical importance. For example, the oncogenic transformation mediated by the E5 protein of papilloma virus is believed to occur by the interaction of the transmembrane helix of the E5 oncoprotein with the transmembrane region of the Platelet-Derived Growth Factor Receptor (PDGFR) [78, 84]. It has also been demonstrated that certain simple Leu and Ile peptides are also able to activate PDGFR with the resulting oncogenic transformation. The results we present specify the expectations for packing at such helix-helix interfaces. Further analyses may thus enable us to distinguish why some of the Leu/Ile peptides activate PDGFR, whereas others, which may differ by a single residue, do not.

It has been suggested that regions in the protein core with low packing fraction may give rise to large internal motions that are related to a protein’s biological function [23–25, 85, 86]. In future studies, we will correlate core residues with low packing fraction to mobile regions in the protein interior. To do this, we will (1) calculate the vibrational modes for the hard-sphere plus stereochemical constraint model and (2) investigate the residue root-mean-square displacement for proteins where multiple crystal structures are available. We will also calculate the entropy of side chain conformations using the Gibbs entropy. Our current studies considered fixed backbone ϕ and ψ dihedral angles. In future studies, we will investigate whether backbone fluctuations strongly affect the side chain entropy.