ABSTRACT
We performed pharmacokinetic-pharmacodynamic (PK-PD) and simulation analyses to evaluate a standard amikacin dose of 15 mg/kg once daily in children with cancer and to determine an optimal dosing strategy. A population pharmacokinetic model was developed from clinical data collected in 34 pediatric patients and used in a simulation study to predict the population probability of various dosing regimens to achieve accepted safety (steady-state unbound trough plasma concentration [fCmin] of <10 mg/liter)- and efficacy (free, unbound plasma concentration-to-MIC ratio [fCmax/MIC] of ≥8)-linked targets. In addition, an adaptive resistance PD (ARPD) model of Pseudomonas aeruginosa was built based on literature time-kill curve data and linked to the PK model to perform PK-ARPD simulations and compare results with those of the probability approach. Using the probability approach, an amikacin dose of 60 mg/kg administered once daily is expected to achieve the target fCmax/MIC in 80% of pediatric patients weighing 8 to 70 kg with a 97.5% probability, and almost all patients were predicted to have fCmin of <10 mg/liter. However, PK-ARPD simulation predicted that 60 mg/kg/day is unlikely to suppress bacterial resistance with repeated dosing. Furthermore, PK-ARPD simulation suggested that amikacin at 90 mg/kg, given in two divided doses (45 mg/kg twice a day), is expected to hit safety and efficacy targets and is associated with a lower rate of bacterial resistance. The disagreement between the two methods is due to the inability of the probability approach to predict development of drug resistance with repeated dosing. This originates from the use of PK-PD indices based on the MIC that neglects measurement errors, ignores the time course dynamic nature of bacterial growth and killing, and incorrectly assumes the MIC to be constant during treatment.
KEYWORDS: pharmacokinetics, pharmacodynamics, pediatrics, cancer
INTRODUCTION
Bacterial resistance to currently available antibiotics is a growing health problem worldwide, as it compromises the efficacy of modern antibiotic therapies and endangers millions of human lives (1). According to the U.S. Centers for Disease Control and Prevention (CDC), antibiotic-resistant bacteria infect 2 million people in the United States annually and directly cause 23,000 deaths every year (2). Appropriate dosing is a major determinant of successful drug therapy, and for anti-infective medications, suboptimal dosing can lead to greater harm than just therapeutic failure. Considerable evidence from in vitro and in vivo work links antibiotic suboptimal dosing to the emergence of bacterial resistance (3, 4). An inverted U-shaped function is found to describe the relationship between drug exposure and selection of resistant bacteria that initially rises and then declines with increasing exposure until reaching a threshold that prevents amplification of resistant bacteria (4).
The optimization of antibiotic dosing could prevent or at least delay the emergence of resistance. To do so, an understanding of pharmacokinetic-pharmacodynamic (PK-PD) relationships of a drug against a bacterial pathogen is key (5). For example, the licensure of daptomycin, a lipopeptide antibiotic active against Gram-positive bacteria, failed in the 1970s because of poor PK-PD understanding. In 2003, the same drug was approved by the Food and Drug Administration (FDA) for clinical uses after switching from a fixed dose three times a day to weight-based once-daily dosing (3).
Likewise, amikacin, an aminoglycoside antibiotic used either alone or in combination with β-lactams to treat serious Gram-negative infections, was first approved at 15 mg/kg of body weight in 1 to 3 divided doses a day (5–7). Over time, as amikacin PK-PD became better understood, dosing changed to larger once-daily doses in order to maximize efficacy and limit toxicity (7–10). Amikacin is an antibiotic that exhibits a concentration-dependent bactericidal activity, and better clinical outcomes were associated with a high free, unbound plasma concentration-to-MIC ratio (fCmax/MIC). Because a bacterial population is not homogeneous but a mixture of distinct populations having their own MIC levels, a population MIC value, defined as the drug concentration that inhibits the growth of 90% of bacteria (MIC90), is usually used in the fCmax/MIC. Generally, an fCmax/MIC ratio of 8 to 10 has been shown to result in at least a 90% therapeutic success rate and is believed to suppress bacterial resistance (11–14). In addition, amikacin safety was linked to the steady-state unbound trough plasma concentration (fCmin), being below 10 and ideally less than 5 mg/liter (14). Nephrotoxicity is also lower with once-daily administration because it limits repeated exposure of amikacin and provides more time for kidneys to eliminate the drug. There is no doubt that dose optimization of antibiotics is of paramount importance and a promising approach to improve therapeutic outcomes, limit adverse events, and combat bacterial resistance.
Two of several methods are widely used for the selection of optimal dosing: probability of target attainment (PTA) and PK-PD simulation. PTA was first proposed by Drusano's team, in which drug exposure in a virtual patient population of interest was simulated based on a population PK model developed from similar patients (15). The simulated time course PK profiles were then used to compute a PK-PD index of interest (fCmax/MIC; fAUC24/MIC is the ratio of the area under the unbound concentration-time curve over 24 h to MIC, and %fT>MIC is the cumulative percentage of the dosing interval that the unbound concentration is above MIC) and the PTA of achieving the selected PK-PD target within the population for a given dosing regimen. The acceptable PTA level is still subjective and debatable. PTA of 90% or higher is advocated, since it is associated with higher probability to achieve desired clinical outcomes. PK-PD simulation is similar to PTA, except that time-concentration drug profile is linked to a dynamic PD model based on in vitro or in vivo time-kill curve data of a drug-bacterium combination of interest to select a dose that is likely to eradicate bacteria.
The aim of this study was to use a modeling and simulation approach to suggest an optimal dosing regimen of amikacin in pediatric cancer patients through the application of pharmacometric principles. A population pharmacokinetic model was developed from data collected in pediatric cancer patients and used in a simulation study to predict the PTA of various dosing regimens to achieve accepted PK-PD targets for efficacy and safety of an fCmax/MIC of ≥8 and fCmin of <10 mg/liter, respectively. In addition, an adaptive resistance PD (ARPD) model of Pseudomonas aeruginosa was built based on literature time-kill curve data of amikacin and linked to the PK model to perform PK-ARPD simulations of the same dosing regimens explored in the PTA simulations and suggest a regimen associated with maximum bacterial killing and minimum development of resistance.
RESULTS
Pharmacokinetic model.
The PK analysis included 34 Egyptian pediatric patients whose demographics and clinical characteristics are summarized in Table 1. A total of 68 amikacin plasma concentrations (2 samples per subject) were collected for modeling. The data were best fit by a two-compartment PK model with first-order elimination and between-subject variability (BSV) on clearance (CL) and volume distribution of the central compartment (V1). All parameters were allometrically scaled to a 70-kg subject using the following equations:
| (1) |
| (2) |
| (3) |
| (4) |
TABLE 1.
Summary of patient demographic and clinical characteristics
| Characteristic | Value (n = 34) |
|---|---|
| Age, n, median (range) | 34, 9 (1–18) yr |
| Sex, n (%) | |
| Male | 14 (41) |
| Female | 20 (59) |
| Weight, n, median (range) | 34, 25 (8–70) kg |
| Height, n, median (range) | 34, 127.5 (75–169) cm |
| Body surface area, n, median (range) | 34, 0.94 (0.41–1.74) m2 |
| CrCL,a n, median (range) | 34, 207.85 (58.06–418) ml/min |
| BUN, n, median (range) | 31, 21 (7–93) mg/dl |
| Hemoglobin b, n, median (range) | 34, 8.60 (6.23–11.70) mg/dl |
| Albumin, n, median (range) | 19, 3.55 (200–4.30) g/liter |
| ALT, n, median (range) | 17, 22 (5–135) |
| AST, n, median (range) | 17, 23 (9–176) |
| Bilirubin, n, median (range) | 33, 0.44 (0.15–1.50) |
| Concomitant nephrotoxic medication, n (%) | |
| Vancomycin | 12 (35) |
| Amphotericin B | 20 (50) |
| Fever, n (%) | 6 (18) |
| Malignancy, n (%) | |
| Hematological | 26 (76) |
| Solid | 7 (21) |
CrCL is creatinine clearance and is calculated by the Schwartz equation.
Compared to a one-compartment model, the two-compartment model was associated with better diagnostic plots and a reduction in OFV by 19.74 points. No other covariates were found to influence the PK parameters. The adequacy of the final model was supported by diagnostics plots and prediction-corrected visual predictive check (pcVPC) (Fig. 1 and 2). Parameter estimates of the final PK model and their sampling importance resampling (SIR)-based 95% confidence intervals (CI) are presented in Table 2.
FIG 1.
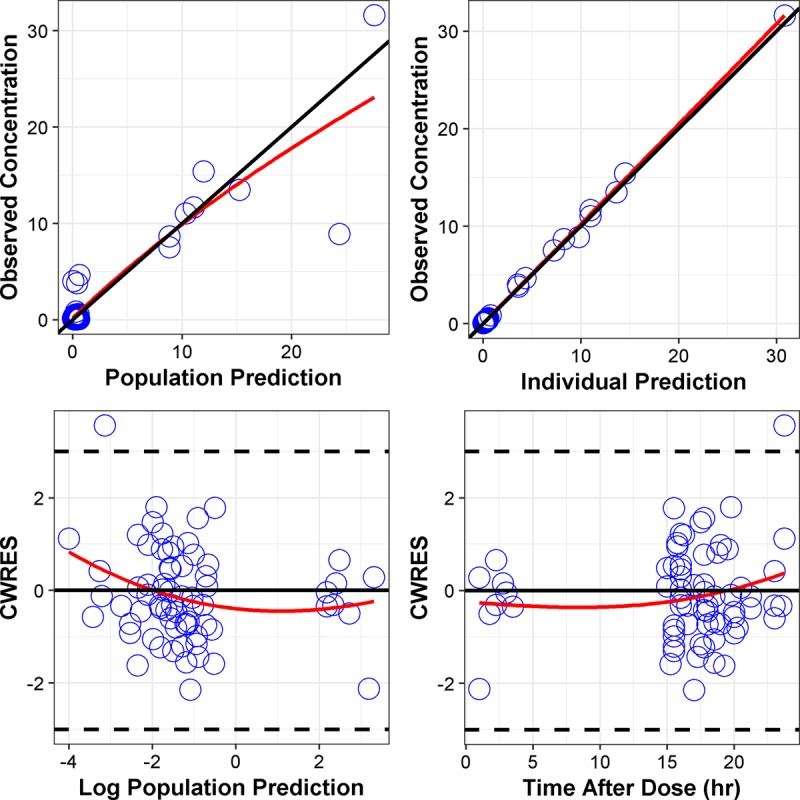
Diagnostic plots for the final PK model. CWRES, conditional weighted residuals.
FIG 2.
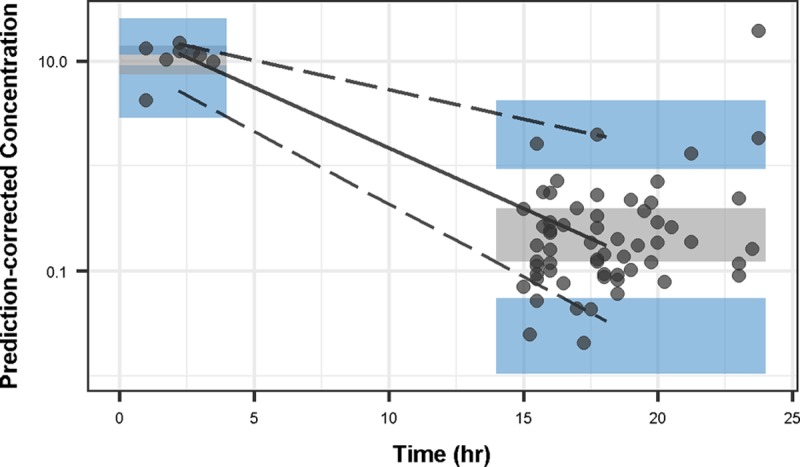
Prediction-corrected visual predictive check for the final PK model. The solid circles represent the prediction-corrected concentrations, and solid and dashed lines represent the median and the 5th and 95th percentiles, respectively. Shaded areas are the simulated 95% CI of each percentile.
TABLE 2.
Parameter estimates for the final PK model
| Parameter (unit) | Definition | Estimate (RSEb, %) | SIR median (95% CI) |
|---|---|---|---|
| CLa (liter/h/70 kg) | Clearance | 11.1 (10) | 11.1 (9.28–13.2) |
| V1a (liter/70 kg) | Central vol of distribution | 30.2 (21) | 30.70 (16.3–43.0) |
| Qa (liter/h/70 kg) | Intercompartmental clearance | 4.26 (42) | 4.48 (2.52–8.81) |
| V2a (liter/70 kg) | Peripheral vol of distribution | 14.9 (13) | 15.41 (12.37–19.80) |
| BSV CL (% CV) | Between subject variability in CL | 33.0 (22) | 33.6 (25.1–46.6) |
| BSV V1 (% CV) | Between subject variability in V1 | 63.1 (22) | 67.7 (35.6–106) |
| RE (% CV) | Proportional residual error | 2.28 (28) | 2.39 (1.37–4.83) |
Parameters are allometrically scaled to a 70-kg person.
RSE, relative standard errors.
PTA.
The single-dose median and range of fCmax and fCmin in Egyptian patients, estimated by empirical Bayesian estimates (EBEs), were 23.7 (8.69 to 27.7) mg/liter and 0.044 (0.0075 to 2.70) mg/liter, respectively. The fCmax was the estimated concentration at the end of infusion, and fCmin was the estimated concentration at 24 h from the start of infusion. The calculated PTA of an fCmax/MIC of ≥8 was zero for MIC90 of 4 and 8 mg/liter (16, 17). All patients had an estimated unbound trough concentration substantially below the target concentration of 10 mg/liter.
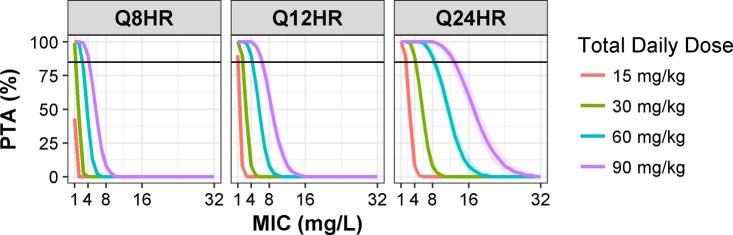
The median and range of simulated weights were 25.5 (8 to 70) kg, and they are similar to the observed values reported in Table 1. The predicted PTA was plotted against MIC values stratified by total daily dose and dosing interval (Fig. 3). PTA of an fCmax/MIC of ≥8 is higher for higher doses of amikacin for any given MIC level and dosing interval. A total daily dose of amikacin given in divided doses resulted in significantly lower PTA than when given once a day. The width of 95% CI around PTA increased with amikacin doses when given at the same frequency. The 95% CI was the widest for 90 mg/kg and the narrowest for 15 mg/kg when given once a day. On the contrary, the width of 95% CI increased as the frequency of dosing (number of doses per day) decreased. The 95% CI of PTA was wider for 90 mg/kg when administered once compared to twice or thrice daily. The overall probability of fCmin being below 10 mg/liter ranged from 95 to 100% for all simulated dosing regimens.
FIG 3.
PTA of achieving an fCmax/MIC of ≥8 versus MIC for amikacin dosing of 15, 30, 60, and 90 mg/kg when given in one (Q24HR) or divided doses (Q8HR or Q12HR). Each PTA line is the median of 500 Monte Carlo simulations from 100 patients with different weights randomly sampled from a truncated log-normal distribution to match the observed weights of patients included in the study. Shaded areas around each PTA line represent the 95% CI. The horizontal line indicates 80% PTA.
In vitro pharmacodynamic model.
The PubMed search identified 10 studies in which in vitro time-kill curve data of amikacin against Pseudomonas aeruginosa were available. Eight studies were included in the development of the in vitro PD model after excluding 2 studies (5, 18–24). One excluded study was an in vivo experiment, and the other study had a design quite different from the others. One included study was static, while the rest were dynamic experiments of single and multiple dosing up to 48 h (Table 3).
TABLE 3.
Summary of in vitro time-kill curve studies included in the final analysis
| Study | Expt | Strain | MIC (mg/liter) | LOD (log10 CFU/ml) | Cmax (mg/liter) | t1/2 (h) | Reference |
|---|---|---|---|---|---|---|---|
| 1 | Static | 27853 | 4 | NRf | 0, 2, 8, 32, 128 | 23 | |
| 2b,e | Dynamic | 27853/16690 | 2/2 | 2 | 0, 80 | 2.1 | 22 |
| 3c,e | Dynamic | 27853/27853R | 2/2 | 2 | 0, 40, 80 | 2.3 | 21 |
| 4c | Dynamic | 27853 | 3.13 | 2 | 0, 80 | 2.35 | 20 |
| 5a,b,e | Dynamic | 64/244 | 8/16 | NR | 24, 72 | 2.2 | 19 |
| 6a,c,d | Dynamic | 27853 | 8 | 1 | 0, 24, 72 | 2 | 18 |
| 7b | Dynamic | 27853 | 3.7 | NR | 10 | 2.4 | 24 |
| 8 | Dynamic | 99063 | NR | NR | 0 | 5 |
Drug was infused over 1 h instead of being given as a bolus.
Single-dose experiment over 24 h.
Multiple-dose experiment up to 48 h.
One-compartment infection model used instead of 2-comparment model.
Studies included more than one strain of Pseudomonas aeruginosa.
NR, not reported.
Overall, there were 302 data points in which 21 observations (6.9%) were at or below the limit of detection (LOD). The final analysis included 281 data points after excluding the below-LOD observations. The final ARPD model included additive interstudy variability (ISV) and inter-arm variability (IAV) on No (initial bacterial count), exponential ISV on Kg (first-order bacterial growth rate constant) and maximal killing effect (Emax), and additive residual unexplained variability (RUV) for static and dynamic experiments separately. Goodness-of-fit plots did not show any model deficiency (Fig. 4). The parameter estimates of the ARPD model and their uncertainty distributions were successfully computed by SIR and are presented in Table 4.
FIG 4.
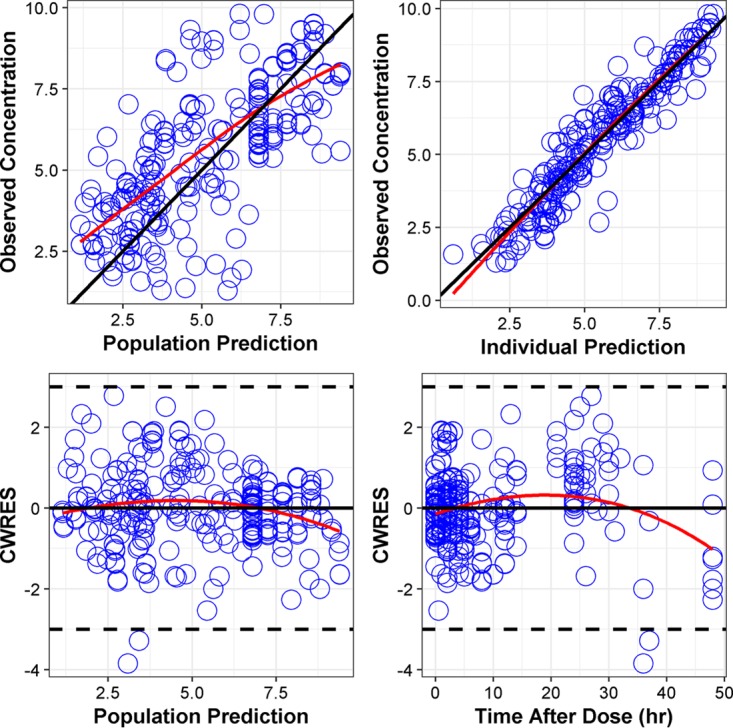
Diagnostic plots for the final PD model.
TABLE 4.
Parameter estimates for the final PD model
| Parameter (unit) | Definition | Estimate | SIR median (95% CI) |
|---|---|---|---|
| N0 (10CFU/ml)a | Initial bacterial count | 6.80 | 6.79 (6.45–7.10) |
| Kg (h−1) | Bacterial growth rate constant | 1.04 | 1.03 (0.89–1.13) |
| Nmax (10CFU/ml)a | Maximum bacterial count | 9.41 | 9.61 (8.96–10.29) |
| Emax (h−1) | Maximum killing rate constant | 9.38 | 9.38 (7.36–11.91) |
| EC50 (mg/liter) | Plasma drug concn to achieve 50% maximum killing rate | 3.49 | 3.46 (2.52–4.79) |
| α (liter/mg · h) | Rate of bacterial adaptation constant | 0.0143 | 0.0143 (0.013–0.016) |
| β | Maximum bacterial adaptation | 29.2 | 30.4 (23.8–38.3) |
| ISV N0 (SD) | Interstudy variability in N0 | 0.91 | 0.914 (0.769–01.018) |
| ISV Kg (% CV) | Interstudy variability in Kg | 23 | 23.0 (217–24.8) |
| ISV Emax (% CV) | Interstudy variability in Emax | 33.9 | 33.9 (31.8–36.2) |
| IAV N0 (SD) | Inter-arm variability in N0 | 0.14 | 0.14 (0.12–0.16) |
| RUVstatic | Log10 residual error for static studies | 0.86 | 0.85 (0.61–1.02) |
| RUVdynamic | Log10 residual error for dynamic studies | 0.57 | 0.58 (0.47–0.67) |
10CFU/ml, 10^estimated parameter (CFU/ml).
PK-ARPD simulations.
Amikacin unbound plasma concentration-time profiles and fCmax and fCmin distributions were similar to those obtained in PTA simulations. In general, the probability of an fCmin of <10 mg/liter decreased when higher amikacin doses were given more frequently, as shown in the top panels of Fig. 5. Significant reduction of bacterial counts occurred with the first dose of amikacin, followed by bacterial regrowth. The magnitude of initial bacterial reduction and time to regrowth were larger and longer with higher doses of amikacin for a given dosing interval. This pattern is clearly evident with the daily dosing, as shown in the bottom right plot of Fig. 5. Administering the same amikacin amount in divided doses was also associated with lower initial bacterial reduction. A reduction in bacterial killing with subsequent doses of the same amount was also observed, indicating development of bacterial resistance. This is a documented phenomenon for aminoglycoside antibiotics, and it is well captured by the ARPD model (3, 25). The loss of bacterial killing is the highest for the dose of 15 mg/kg, and the rate of resistance was faster when the same total daily dose was given more frequently in divided doses. Predicted bacterial counts below the LOD (2 log10 or 102 CFU/ml) were achieved by 90 mg/kg administered either at once or in divided doses. The 60-mg/kg dose also resulted in a bacterial count below the LOD but only when administered daily and not in divided doses. Lower doses (15 to 30 kg/mg) failed to drive bacterial counts to the LOD level.
FIG 5.
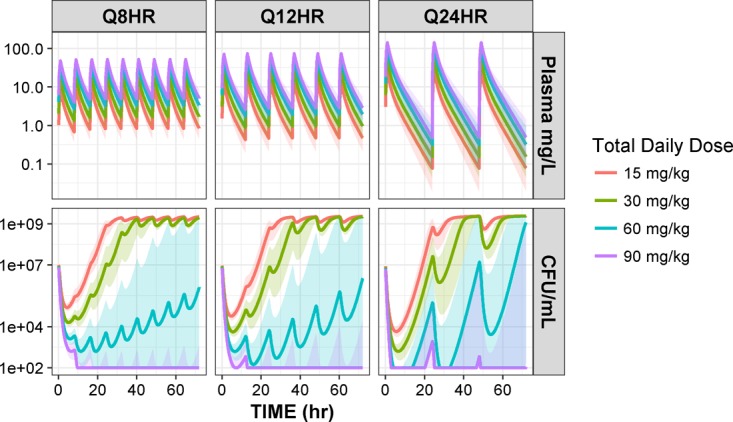
PK-ARPD simulations of 1,000 patients for amikacin dosing of 15, 30, 60, and 90 mg/kg when given in one (Q24HR) or divided doses (Q8HR or Q12HR). Weights of patients were sampled from a truncated log-normal distribution to match the observed weights of patients in the study. (Top) Predicted unbound amikacin plasma concentration-time profiles from the PK model after 1-h infusion. (Bottom) Bacterial time-kill curves predicted by the PD model given the predicted unbound amikacin plasma concentration-time profiles. Lines are the medians and shaded areas are 95% CI.
DISCUSSION
The simulation results suggest that 15 mg/kg/day is a safe but suboptimal dose of amikacin in our pediatric cancer patients. Using the EBEs and percent protein binding, not a single patient in the study was calculated to achieve the target fCmax/MIC of ≥8. The ramification of a low dose is not only limited to high probability of therapeutic failure in a patient but also associated with significant collateral damage that affects our societies through the selection of drug-resistant bacteria (26). Our PTA simulation study suggests that once-daily administration of larger amikacin doses are expected to be associated with higher PTA and lower risk of toxicities overall. The rationale for once-daily dosing is to maximize bactericidal effects driven by fCmax/MIC, prolong postantibiotic effects, and allow a longer time to excrete the drug from the body, leading to lower fCmin. Based on the PTA simulation, a minimum amikacin dose of 60 mg/kg administered once daily is expected to achieve the efficacy target of an fCmax/MIC of ≥8 in 80% of pediatric patients weighing 8 to 70 kg, with a 97.5% probability and a safety target of <10 mg/liter in almost all patients.
This dosing recommendation is consistent with other studies that suggest higher single daily doses of amikacin of ≥40 mg/kg in different patient populations, including pediatric cancer patients (7, 19, 27–29). In 1998, the amikacin dose of 20 mg/kg administered once a day was recommended for immunocompromised pediatric patients, including those with cancer (10). A recent study presented at the 2017 American Society for Clinical Pharmacology and Therapeutics (ASCPT) conference suggested a high dose of 40 mg/kg for a 5-year-old patient weighing 20 kg and having creatinine clearance (CrCL) of 120 ml/min per 1.73 m2 of body surface area (29). The increase in recommended dose from 20 to 40 mg/kg daily is likely due to the documented increase in amikacin MIC90 from 4 to 8 mg/liter against Pseudomonas aeruginosa over the past decades (17, 30). Craig has shown that the magnitude of PK-PD index does not change for resistant bacteria when one corrects for the increase in MIC (31). Higher doses are needed to produce higher exposure and reach the effective PK-PD target as a compensation for the increase in MIC. According to a recent study, the amikacin MIC90 is currently at 16 mg/liter (32). The consistent increase in MIC90 over time is caused at least partly if not entirely by the repeated exposure of suboptimal concentrations of amikacin that selects for the preexisting less-susceptible bacterial populations.
There are several possible explanations for the study findings. Our PK model was based on limited data (64 observations, 2 data points per subject) from Egyptian patients and did not find CrCL and age to be significant covariates, as has been shown previously (29). Despite that, the estimated CL (4.33 liters/h), V1 (8.63 liters), Q (intercompartmental clearance, 1.66 liters/h), V2 (4.26 liters), and half-life (t1/2; 3 h) for a typical patient of 20 kg are similar to reported literature values (10, 29, 33, 34). It is documented that oncology patients do have altered amikacin kinetics characterized by increased clearance and volume of distribution (34–37). This is attributed to the disease condition, severity, and drugs used for treatment. However, the kinetic changes are not uniform and cannot be predicted by a single or combined variables, such as malignancy type, degree of neutropenia, disease state, total exposure, or type of chemotherapy (37). This is in agreement with our results that did not find any influential clinical covariates. It is also important to note that the majority of our patients had hematological malignancy. With that, our results may not apply to children with different types of cancer. The generalization of study findings to other populations is also limited due to the heterogeneity in renal functions.
Another justification for our results is that uncertainty of typical PK parameters, BSV, and variability of body weights were accounted for in the Monte Carlo simulations (MCS) when estimating the mean and 95% CI of PTA to achieve an fCmax/MIC of ≥8 and an fCmin of <10 mg/liter. It is noted that higher uncertainty of and variability in PK parameters generally leads to higher uncertainty of PTA, resulting in higher optimal dose prediction (38). However, this approach is strongly advised by Colin et al. in the support of quality and proper clinical decision-making for anti-infective optimal dosing (38). They stated that the lower boundary of PTA 95% CI can be conservatively used to select an appropriate dosing regimen for a given MIC where there is a 97.5% probability that the unknown PTA exceeds a certain cutoff (e.g., 80% in our case) in a patient population. The high uncertainty in PK parameter estimates caused by the sparse nature of our data, high BSV, high level of confidence (95% versus 90%), and random selection of weight together can explain the higher predicted optimal dose of 60 instead of 40 mg/kg/day, as suggested by Liu et al. (29).
Despite the merits of PTA with the parameter uncertainty approach, it lacks the ability to account for the adaptive resistance of bacteria upon exposure to amikacin (3, 25). The PTA approach is based on MIC, which provides no information about the kinetics of drug action and the persistent activity when drug concentrations are below the MIC, as it is determined at a single time point (39). This is a major limitation that can lead to incorrect dosing recommendation. PK-ARPD simulations show that the 60-mg/kg/day dose suggested by PTA is unlikely to suppress bacterial resistance. Upon repeated dosing, bacterial resistance is expected to dominate over the killing effect that is initially predicted. This is well demonstrated in Fig. 5: after the initial reduction, the predicted median bacterial count at the end of every day increases in a linear fashion. The steepness of slope decreases as the dosing frequency increases, suggesting lower rates of resistance. The predicted increase in bacterial count is driven by both the drop in amikacin concentration with time during long dosing intervals and the loss of amikacin efficacy with repeated exposure. The PK-ARPD simulation shows that safety and development of resistance goes hand in hand, creating a double-edged sword situation. Large single doses are safer for patients with greater initial killing, but they are likely to be selective for the emergence of resistant bacterial populations. When complete bacterial eradication (bacteriological cure) is not achieved, less susceptible bacterial subpopulations with increased MIC will grow and predominate as the amikacin unbound concentration falls below the MIC threshold. A compromise between efficacy on one hand and acceptable safety and less chance of bacterial resistance on the other hand is achieved with twice-daily dosing, where there is enough time between doses for kidneys to excrete amikacin while limiting the amount of time when drug concentrations are below the MIC and maintaining an acceptable fCmax/MIC ratio.
PK-ARPD simulations predicted 90 mg/kg/day given in two divided doses is needed to sustain median bacterial counts below the LOD until the end of day 3. Predicted median bacterial counts remained below the LOD until day 7 (data not shown), but we only presented the results up to day 3, since this is the time it takes to get an informative microbiological report back to adjust therapy accordingly. Taking safety into account, 90 mg/kg administered in two divided doses (45 mg/kg twice a day [BID]) is likely safer for empirical treatment than when given in three divided doses (30 mg/kg three times a day [TID]), which is predicted to have an fCmin of >10 mg/liter. With twice-daily dosing, fCmin is predicted to be <10 mg/liter and provides sufficient time for drug excretion before the next dose to avoid drug accumulation. Furthermore, our stimulation shows that the probability of resistance is lower with twice-daily dosing (45 mg/kg BID) than with a single dose (90 mg/kg four times a day).
PK-ARPD simulation also shows the administration of amikacin in divided doses is generally expected to facilitate bacterial resistance more than killing, unless the divided dose is high enough (≥20 mg/kg TID or ≥40 mg/kg BID) (data not shown). The simulation results (Fig. 5) also show that the bacterial regrowth rate is the same irrespective of dose and peaks at the time of the next dose. This is consistent with amikacin affecting only growing bacteria while leaving less susceptible bacteria in the stationary phase unaffected (40). This may explain the adaptive resistance seen with aminoglycosides despite their bactericidal effect. A limitation of our PK-ARPD simulation is that the in vitro ARPD model does not take into account the role of the immune system of the host. In the antimicrobial world, the observed effect in vivo is a combination of both drug effect and host immune response. With that in mind, it is very possible that even lower doses than what our simulations suggested could be effective.
The disagreement in dose recommendation between PTA and PK-ARPD approaches in our simulations highlights the inability of PTA to predict development of drug resistance. Nielsen and Friberg highlighted several limitations associated with the PTA approach in details which are beyond the scope of the manuscript (41). Importantly, they pointed out that PTA limitations originate from the use of MIC-based PK-PD indices as targets for safety and efficacy. All PK-PD indices rely on the MIC, which is a threshold concentration that neglects measurement errors and ignores the dynamic nature of bacterial growth and killing rates occurring over the incubation period. They also mentioned that MIC is incorrectly assumed to stay constant during the treatment period. In addition, the MIC-based PK-PD indices are surrogate endpoints of the true clinical outcome to achieve the complete eradication of pathogenic bacteria, i.e., bacteriological cure. With that, PK-ARPD modeling and simulation is preferred over the MIC-based PTA. It is a better approach to describe the time course relationships among dose, concentration, bacterial killing, and resistance that happen simultaneously. The PK-ARPD models can also be used to predict the efficacy-linked PK-PD indices (42). However, although PK-ARPD modeling and simulation shows superiority over the MIC-based PTA approach, it remains underused in the development and improvement of antibiotic dosing regimens despite its promising potential (41). When adapted, the PK-ARPD approach could result in more appropriate dosing of antibiotics, which is likely to help in battling growing bacterial resistance.
In conclusion, oncology pediatric patients do have altered amikacin pharmacokinetics which probably necessitate higher doses to achieve therapeutic targets. Based on our simulation findings, daily monodose administration of 15 mg/kg may not be optimal in child patients with cancer. In addition, a dose recommendation suggested by PTA is likely incorrect because it uses surrogate indices of clinical outcomes that are not sufficiently sensitive for determining optimal dosage regimens for total bacteriological cure. We find PK-ARPD modeling and simulation to be superior on a theoretical basis, because it provides deeper insight about the intricate time course relationship among dosing regimens, plasma concentrations, and wanted as well as unwanted outcomes. PK-ARPD simulations suggest that 45 mg/kg BID can achieve safety and efficacy targets and is expected to be associated with lower rates of bacterial resistance. Study results can be used to justify a controlled clinical trial to evaluate suggested doses against current doses used in clinical settings.
MATERIALS AND METHODS
Patients.
This study included children with cancer and suspected or documented Gram-negative bacterial infection admitted to the inpatient ward of the National Cancer Institute (NCI), Cairo, Egypt, during the period of June 2009 to December 2009. Patients were diagnosed with different types of malignancies, broadly categorized into hematological and solid cancers, that were treated with different chemotherapy protocols accordingly. All patients were treated empirically with amikacin at 15 mg/kg once daily infused intravenously over 1 h, which was the standard-of-care dose. Patient demographics and pertinent clinical characteristics were collected and recorded. The study was reviewed and approved by the Hospital Ethical Committee. Parental informed consent and child informed assent, when appropriate, were obtained prior to study inclusion.
Sample collection and analytical assay.
Two blood samples were drawn from a peripheral vein: one was taken at the end of infusion (1 h), while the second sample was drawn at least 2 h after the first sample. Amikacin serum concentrations were measured by amikacin enzyme multiple immunoassay technique (Emit 2008), supplied by Syva Company Co., Dade Behring, Inc. (Cupertino, CA, USA). The assay was linear from 0 to 50 μg/ml, with reported between-run and within-run coefficients of variation (CV) of 3.9% and 5.8%, respectively. Two controls were assayed in every 24-h period, and amikacin serum concentrations were calculated automatically by the Emit 2008 analyzer.
Pharmacokinetic analysis.
Amikacin concentrations from all patients were fitted simultaneously to one- and two-compartment PK models with linear elimination using nonlinear mixed-effects regression analysis. An exponential random-effect model and proportional error model were used to estimate between-subject variability (BSV) and residual unexplained variability (RUV), respectively. To explain variability in model parameters, the effect of patient demographics and clinical characteristics were screened visually as potential covariates, with particular concern for the effects of male versus female, hematological versus solid malignancies, afebrile versus febrile (defined as an oral temperature of >38.5°C or nonoral temperature [axillary or temporal] of 38°C on two separate readings at least 1 h apart) (43), and normal albumin level versus hypoalbuminemia, defined as serum albumin of <3.5 g/dl. The statistical significance of a covariate was tested using a likelihood ratio test (χ2; α = 0.01, df = 1) in which a reduction in objective function value (OFV; a measure of goodness of fits similar to a sum of squares) of 6.63 or greater is observed after the inclusion of a covariate. The final PK model was selected based on the OFV, biological plausibility of parameter estimates, and diagnostics plots. The parameter standard errors and uncertainty distributions were computed by sampling importance resampling (SIR) (44), and model performance was qualified using a prediction-corrected visual predictive check (pcVPC) (45).
PTA calculation.
The empirical Bayesian estimates (EBEs) from the final PK model and amikacin protein binding were used to calculate fCmax and fCmin for a single dose. They consequently were used to estimate the PTA of achieving the efficacy and safety targets of 15-mg/kg/day dosing in study patients.
In addition, the population PK model was used to estimate the population PTA to achieve an fCmax/MIC ratio of ≥8 and an fCmin of less than 10 mg/liter for different amikacin dosing regimens. Monte Carlo simulations (MCS) were used to simulate 500 trials of 100 patients for each combination of amikacin weight-based total daily dose (15, 30, 60, and 90 mg/kg) and dosing interval (every 8 h [q8h], q12h, and q24h). Weights of pediatric patients were simulated from a truncated log-normal distribution (means, 3.23; standard deviations [SD], 0.55) to match the observed weights of patients in the study. To account for parameter uncertainty, BSV, and the extent of correlation among the estimated values of parameters, the full variance-covariance matrix obtained by SIR was incorporated into the MCS. Taking into consideration a fixed 10% protein binding of amikacin, the PTA (expressed as a percentage) of an fCmax/MIC of ≥8 and an fCmin of <10 mg/liter for each trial was calculated for a range of assumed MIC values: 1, 2, 4, 8, 16, and 32 mg/liter. For each of the 500 simulated trials for each dose and dosing interval combination, the median and the 5th and 95th percentiles of PTAs were calculated.
In vitro pharmacodynamic analysis.
A PubMed literature search was performed and identified time-kill curve studies of amikacin against Pseudomonas aeruginosa in which figures were digitized using WebPlotDigitizer (version 3.11) (46). The extracted bacterial counts, measured as CFU per milliliter of medium, from static and dynamic studies were fitted together to a published bacterial dynamic growth model with adaptive resistance (equations 5 to 7) (3).
| (5) |
| (6) |
| (7) |
Bacterial growth (equation 5) follows a logistic model in which N is total bacterial counts at time t, Kg is the first-order bacterial growth rate constant, Nmax is the maximum bacterial count, and DE is the drug effect (it equals 0 when there is no drug). In the presence of amikacin (equation 6), DE was characterized by a maximal killing effect (Emax) and EC50, which is the unbound amikacin plasma concentration (Cp) needed to produce 50% of the Emax. Cp was simulated from a 1-compartment PK model with half-lives (t1/2) and peak concentrations identical to those reported in the in vitro studies. To allow for the development of adaptive resistance, EC50 was multiplied by an adaptation factor (AD) that causes the EC50 to increase with time and Cp. The adaptation factor (equation 7) is a fractional multiplier in which β represents the maximum fractional increase in EC50 when unbound concentration and time become large, and α is the adaptation rate constant that allows adaptation to transition from 1 when drug concentration is zero to 1 + β.
In this meta-analysis of literature data, random-effect terms for interstudy variability (ISV), inter-arm variability (IAV), and log10-based additive RUV were included in the model. The ISV random effect was approximated in NONMEM using $Level and R matrix in the $COVARIANCE record. Below-LOD observations were ignored in the modeling process. The criteria and methods used to develop the PK model were used to select and assess the final ARPD model, except that VPC was not performed due to the sparse nature of extracted literature data.
PK-ARPD simulations.
The literature-based in vitro ARPD model was linked to the final PK model to perform PK-ARPD simulations for the same dosing regimens explored in PTA simulations. A virtual pediatric patient population of 1,000 subjects with different weights sampled from the same truncated log-normal distribution as that mentioned above was generated for each dose and dosing interval combination. In PK-ARPD simulations, parameter uncertainty and BSV were included only in the PK parameters, while typical values were used for the PD model because of the unsuccessful covariance step.
Software.
All nonlinear mixed-effects modeling analyses were performed in NONMEM 7.3 (ICON Development Solutions, Ellicott City, MD) using ADVAN13 and the first-order conditional estimation method with interaction (FOCEI). Data manipulation and plotting were done in R (version 3.2.5). Perl-speaks-NONMEM (PsN) was utilized to perform the VPC and SIR analyses. MCS were performed with the R-based mrgsolve package (version 0.7.1). The Pirana interface was used to maintain and compare NONMEM and PsN runs.
ACKNOWLEDGMENT
This work was supported in part by the Coin Foundation Fellowship, supporting Ph.D. students in experimental and clinical pharmacology conducting research in infectious diseases.
REFERENCES
- 1.Ventola CL. 2015. The antibiotic resistance crisis: part 1: causes and threats. P T 40:277–283. [PMC free article] [PubMed] [Google Scholar]
- 2.Office of Infectious Diseases, Centers for Disease Control and Prevention. 2013. Antibiotic resistance threats in the United States, 2013. Centers for Disease Control and Prevention, Atlanta, GA. [Google Scholar]
- 3.Tam VH, Ledesma KR, Vo G, Kabbara S, Lim TP, Nikolaou M. 2008. Pharmacodynamic modeling of aminoglycosides against Pseudomonas aeruginosa and Acinetobacter baumannii: identifying dosing regimens to suppress resistance development. Antimicrob Agents Chemother 52:3987–3993. doi: 10.1128/AAC.01468-07. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Tam VH, Louie A, Deziel MR, Liu W, Drusano GL. 2007. The relationship between quinolone exposures and resistance amplification is characterized by an inverted U: a new paradigm for optimizing pharmacodynamics to counterselect resistance. Antimicrob Agents Chemother 51:744–747. doi: 10.1128/AAC.00334-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Burgess DS. 2005. Use of pharmacokinetics and pharmacodynamics to optimize antimicrobial treatment of Pseudomonas aeruginosa infections. Clin Infect Dis 40(Suppl 2):S99–S104. doi: 10.1086/426189. [DOI] [PubMed] [Google Scholar]
- 6.Teva Parenteral Medicines, Inc. Amikacin sulfate package insert. Teva Parenteral Medicines, Inc; Irvine, CA. [Google Scholar]
- 7.White BP, Lomaestro B, Pai MP. 2015. Optimizing the initial amikacin dosage in adults. Antimicrob Agents Chemother 59:7094–7096. doi: 10.1128/AAC.01032-15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Murry KR, McKinnon PS, Mitrzyk B, Rybak MJ. 1999. Pharmacodynamic characterization of nephrotoxicity associated with once-daily aminoglycoside. Pharmacotherapy 19:1252–1260. doi: 10.1592/phco.19.16.1252.30876. [DOI] [PubMed] [Google Scholar]
- 9.Nicolau DP, Freeman CD, Belliveau PP, Nightingale CH, Ross JW, Quintiliani R. 1995. Experience with a once-daily aminoglycoside program administered to 2,184 adult patients. Antimicrob Agents Chemother 39:650–655. doi: 10.1128/AAC.39.3.650. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Krivoy N, Postovsky S, Elhasid R, Ben Arush MW. 1998. Pharmacokinetic analysis of amikacin twice and single daily dosage in immunocompromised pediatric patients. Infection 26:396–398. doi: 10.1007/BF02770843. [DOI] [PubMed] [Google Scholar]
- 11.Lacy MK, Nicolau DP, Nightingale CH, Quintiliani R. 1998. The pharmacodynamics of aminoglycosides. Clin Infect Dis 27:23–27. doi: 10.1086/514620. [DOI] [PubMed] [Google Scholar]
- 12.Moore RD, Lietman PS, Smith CR. 1987. Clinical response to aminoglycoside therapy: importance of the ratio of peak concentration to minimal inhibitory concentration. J Infect Dis 155:93–99. doi: 10.1093/infdis/155.1.93. [DOI] [PubMed] [Google Scholar]
- 13.Craig WA. 1998. Pharmacokinetic/pharmacodynamic parameters: rationale for antibacterial dosing of mice and men. Clin Infect Dis 26:1–10. doi: 10.1086/516284. [DOI] [PubMed] [Google Scholar]
- 14.Martínez Illamola S. 2012. Development of a population pharmacokinetic model to determine the optimal doses of amikacin in the treatment of neonatal sepsis. PhD thesis University of Barcelona, Barcelona, Spain, http://diposit.ub.edu/dspace/bitstream/2445/41598/5/01.SMI_PhD_THESIS.pdf. [Google Scholar]
- 15.Drusano GL, Preston SL, Hardalo C, Hare R, Banfield C, Andes D, Vesga O, Craig WA. 2001. Use of preclinical data for selection of a phase II/III dose for evernimicin and identification of a preclinical MIC breakpoint. Antimicrob Agents Chemother 45:13–22. doi: 10.1128/AAC.45.1.13-22.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Zelenitsky SA, Rubinstein E, Ariano RE, Zhanel GG, Zhanel GG, Hoban DJ, Adam HJ, Karlowsky JA, Baxter MR, Nichol KA, Lagace-Wiens PRS, Walkty A. 2013. Integrating pharmacokinetics, pharmacodynamics and MIC distributions to assess changing antimicrobial activity against clinical isolates of Pseudomonas aeruginosa causing infections in Canadian hospitals (CANWARD). J Antimicrob Chemother 68:i67–i72. doi: 10.1093/jac/dkt028. [DOI] [PubMed] [Google Scholar]
- 17.Staneck JL, Glenn S, DiPersio JR, Leist PA. 1989. Wide variability in Pseudomonas aeruginosa aminoglycoside results among seven susceptibility testing procedures. J Clin Microbiol 27:2277–2285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Vergeres P, Blaser J. 2016. Amikacin, ceftazidime, and flucloxacillin against suspended and adherent Pseudomonas aeruginosa and Staphylococcus epidermidis in an in vitro model of infection. J Infect Dis 165:281–289. doi: 10.1093/infdis/165.2.281. [DOI] [PubMed] [Google Scholar]
- 19.Dudley MN, Zinner SH. 1991. Single daily dosing of amikacin in an in-vitro model. J Antimicrob Chemother 27(Suppl C):15–19. doi: 10.1093/jac/27.suppl_C.15. [DOI] [PubMed] [Google Scholar]
- 20.Cappelletty DM, Kang SL, Palmer SM, Rybak MJ. 1995. Pharmacodynamics of ceftazidime administered as continuous infusion or intermittent bolus alone and in combination with single daily-dose amikacin against Pseudomonas aeruginosa in an in vitro infection model. Antimicrob Agents Chemother 39:1797–1801. doi: 10.1128/AAC.39.8.1797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.McGrath BJ, Lamp KC, Rybak MJ. 1993. Pharmacodynamic effects of extended dosing intervals of imipenem alone and in combination with amikacin against Pseudomonas aeruginosa in an in vitro model. Antimicrob Agents Chemother 37:1931–1937. doi: 10.1128/AAC.37.9.1931. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.McGrath BJ, Bailey EM, Lamp KC, Rybak MJ. 1992. Pharmacodynamics of once-daily amikacin in various combinations with cefepime, aztreonam, and ceftazidime against Pseudomonas aeruginosa in an in vitro infection model. Antimicrob Agents Chemother 36:2741–2746. doi: 10.1128/AAC.36.12.2741. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Craig WA, Redington J, Ebert SC. 1991. Pharmacodynamics of amikacin in vitro and in mouse thigh and lung infections. J Antimicrob Chemother 27(Suppl C):29–40. [DOI] [PubMed] [Google Scholar]
- 24.Zinner SH, Blaser J, Stone BB, Groner MC. 1985. Use of an in-vitro kinetic model to study antibiotic combinations. J Antimicrob Chemother 15(Suppl A):221–226. doi: 10.1093/jac/15.suppl_A.221. [DOI] [PubMed] [Google Scholar]
- 25.Barclay ML, Begg EJ, Chambers ST. 1992. Adaptive resistance following single doses of gentamicin in a dynamic in vitro model. Antimicrob Agents Chemother 36:1951–1957. doi: 10.1128/AAC.36.9.1951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Paterson DL. 2004. “Collateral damage” from cephalosporin or quinolone antibiotic therapy. Clin Infect Dis 38:S341–S345. doi: 10.1086/382690. [DOI] [PubMed] [Google Scholar]
- 27.Taccone FS, Laterre P-F, Spapen H, Dugernier T, Delattre I, Layeux B, De Backer D, Wittebole X, Wallemacq P, Vincent J-L, Jacobs F. 2010. Revisiting the loading dose of amikacin for patients with severe sepsis and septic shock. Crit Care 14:R53. doi: 10.1186/cc8945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Burdet C, Pajot O, Couffignal C, Armand-Lefèvre L, Foucrier A, Laouénan C, Wolff M, Massias L, Mentré F. 2015. Population pharmacokinetics of single-dose amikacin in critically ill patients with suspected ventilator-associated pneumonia. Eur J Clin Pharmacol 71:75–83. doi: 10.1007/s00228-014-1766-y. [DOI] [PubMed] [Google Scholar]
- 29.Liu X, Smits A, Wang Y, Wead S, Kagan R, Healy D, De Cock P, Allegaert K, Sherwin C. 2017. Dosing optimization of amikacin in pediatric patients with burn injuries and those with oncology conditions, abstr LB-013. Abstr 118th Annu Meet Am Soc Clin Pharmacol Ther. [Google Scholar]
- 30.Zelenitsky SA, Rubinstein E, Ariano RE, Zhanel GG, Canadian Antimicrobial Resistance Alliance. 2013. Integrating pharmacokinetics, pharmacodynamics and MIC distributions to assess changing antimicrobial activity against clinical isolates of Pseudomonas aeruginosa causing infections in Canadian hospitals (CANWARD). J Antimicrob Chemother 68(Suppl 1):S67–S72. doi: 10.1093/jac/dkt028. [DOI] [PubMed] [Google Scholar]
- 31.Craig WA. 2014. Introduction to pharmacodynamics, p 3–22. In Vinks A, Derendorf H, Mouton J (ed), Fundamentals of antimicrobial pharmacokinetics and pharmacodynamics. Springer New York, New York, NY. [Google Scholar]
- 32.Sutherland CA, Verastegui JE, Nicolau DP. 2016. In vitro potency of amikacin and comparators against E. coli, K pneumoniae and P aeruginosa respiratory and blood isolates. Ann Clin Microbiol Antimicrob 15:39. doi: 10.1186/s12941-016-0155-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Treluyer J, Merle Y, Tonnelier S. 2002. Nonparametric population pharmacokinetic analysis of amikacin in neonates, infants, and children. Antimicrob Agents Chemother 46:1381–1387. doi: 10.1128/AAC.46.5.1381-1387.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Villena R, Rabello M, Pharmd JM, Aravena R, Kopp K, Villarroel M, Santolaya ME. 2011. Pharmacokinetics of amikacin in children with cancer and febrile neutropenia, abstr 903. Abstr 49th Annu Meet Infect Dis Soc Am. [Google Scholar]
- 35.Davis RL, Lehmann D, Stidley CA, Neidhart J. 1991. Amikacin pharmacokinetics in patients receiving high-dose cancer chemotherapy. Antimicrob Agents Chemother 35:944–947. doi: 10.1128/AAC.35.5.944. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Tod M, Lortholary O, Seytre D, Semaoun RM, Uzzan B, Guillevin LC, Casassus P, Petitjean O. 1998. Population pharmacokinetic study of amikacin administered once or twice daily to febrile, severely neutropenic adults. Antimicrob Agents Chemother 42:849–856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Romano S, de Gatta MMF, Calvo MV, Caballero D, Dominguez-Gil A, Lanao JM. 1999. Population pharmacokinetics of amikacin in patients with haematological malignancies. J Antimicrob Chemother 44:235–242. doi: 10.1093/jac/44.2.235. [DOI] [PubMed] [Google Scholar]
- 38.Colin P, Eleveld DJ, Jonckheere S, Van Bocxlaer J, De Waele J, Vermeulen A. 2016. What about confidence intervals? A word of caution when interpreting PTA simulations J Antimicrob Chemother 71:2502–2508. [DOI] [PubMed] [Google Scholar]
- 39.Müller M, Dela Peña A, Derendorf H. 2004. Issues in pharmacokinetics and pharmacodynamics of anti-infective agents: kill curves versus MIC. Antimicrob Agents Chemother 48:1441–1453. doi: 10.1128/AAC.48.5.1441-1453.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Taber HW, Mueller JP, Miller PF, Arrow AS. 1987. Bacterial uptake of aminoglycoside antibiotics. Microbiol Rev 51:439–457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Nielsen EI, Friberg LE. 2013. Pharmacokinetic-pharmacodynamic modeling of antibacterial drugs. Pharmacol Rev 65:1053–1090. doi: 10.1124/pr.111.005769. [DOI] [PubMed] [Google Scholar]
- 42.Nielsen EI, Cars O, Friberg LE. 2011. Pharmacokinetic/pharmacodynamic (PK/PD) indices of antibiotics predicted by a semimechanistic PKPD model: a step toward model-based dose optimization. Antimicrob Agents Chemother 55:4619–4630. doi: 10.1128/AAC.00182-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Newby B, Prevost D, Lotocka-Reysner H. 2009. Assessment of gentamicin 7 mg/kg once daily for pediatric patients with febrile neutropenia: a pilot project. J Oncol Pharm Pract 15:211–216. doi: 10.1177/1078155209102339. [DOI] [PubMed] [Google Scholar]
- 44.Dosne A-G, Bergstrand M, Harling K, Karlsson MO. 2016. Improving the estimation of parameter uncertainty distributions in nonlinear mixed effects models using sampling importance resampling. J Pharmacokinet Pharmacodyn 43:583–596. doi: 10.1007/s10928-016-9487-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Bergstrand M, Hooker AC, Wallin JE, Karlsson MO. 2011. Prediction-corrected visual predictive checks for diagnosing nonlinear mixed-effects models. AAPS J 13:143–151. doi: 10.1208/s12248-011-9255-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Rohatgi A. 2017. WebPlotDigitizer (3.11). https://automeris.io/WebPlotDigitizer.