The delivery of water by impacts from planetary accretion to present

Impact melts and breccias trap surprisingly large quantities of water carried by carbonaceous chondrite–like impactors.

Abstract

Dynamical models and observational evidence indicate that water-rich asteroids and comets deliver water to objects throughout the solar system, but the mechanisms by which this water is captured have been unclear. New experiments reveal that impact melts and breccias capture up to 30% of the water carried by carbonaceous chondrite–like projectiles under impact conditions typical of the main asteroid belt impact and the early phases of planet formation. This impactor-derived water resides in two distinct reservoirs: in impact melts and projectile survivors. Impact melt hosts the bulk of the delivered water. Entrapment of water within impact glasses and melt-bearing breccias is therefore a plausible source of hydration features associated with craters on the Moon and elsewhere in the solar system and likely contributed to the early accretion of water during planet formation.

INTRODUCTION

The timing of volatile delivery to the inner solar system continues to be debated. Some have argued that the terrestrial planets accreted dry and later gained volatiles as part of the “late veneer” (1). Recent Ru isotopic data, however, imply that the late veneer was not the primary source of volatiles on Earth (2). Moreover, data from angrites (3) and eucrites (4) point to the accretion of water in the inner solar system within the first few million years of solar system history. Isotopic evidence (3–5) also indicates that carbonaceous chondrite (CC)–like impactors delivered much of the volatiles in the inner solar system. However, the actual mechanisms that trap this water remain poorly constrained.

The mechanisms for trapping impactor-derived water pertain not only to volatile delivery during the era of planet formation but also to the modern solar system. For example, spacecraft observations made by Dawn at asteroid Vesta reveal that most dark material deposits peppered across its surface are associated with excess hydrogen (6) and a near-infrared hydroxyl absorption (7). Planar impact calculations indicate that CCs should completely devolatize during vertical impacts above ~3.1 km s⁻¹ (8), yet 80% of impacts in the main asteroid belt exceed this speed (9). Previous observations of terrestrial impact melts demonstrated that water can be trapped within impact glasses (10), despite the extreme temperatures and pressures triggered by impacts. Moreover, the same trapping process could account for the presence of volatiles (water and other compounds) at the poles of the Moon (11). Although hydrous anomalies within Bullialdus (12) and in ejecta around the craters Copernicus and Plato (13) on the Moon have previously been attributed to endogenic sources (12, 13), they could also be explained by impact-delivered water. At Giordano Bruno, the spatially heterogeneous hydration signature has recently been interpreted as evidence for exogenic water (14). Thus, mounting observational evidence reveals that water is somehow ferried to and, critically, trapped on asteroids and atmosphere-free bodies not only during planet formation but also in the modern solar system.

Shock physics codes indicate that impacts could deliver water across a range of conditions (15–17). However, these codes cannot yet fully represent material behavior or predict how delivered water is stored. Impact experiments, however, reveal these processes.

This study details the fate of water derived from CC-like impactors. We investigated water delivery using hypervelocity impact experiments at the NASA Ames Vertical Gun Range (AVGR) (see Materials and Methods). Antigorite projectiles, an analog for the CC-like objects thought to have ferried water to the inner solar system, were launched into anhydrous pumice targets, an established proxy for silicate regoliths (18), at ~5 km s⁻¹, a speed comparable to the median impact speed in the main asteroid belt (9) and the median collision speeds during much of solar system formation (19). All impacts are oblique to some degree; hence, experiments were done at 30° and 45° (with respect to horizontal). The latter is the most probable impact angle (20). Figure 1 illustrates the experimental setup. After each experiment, impact products, consisting of impact-generated glasses, antigorite projectile relics, and melt-rich breccias, were recovered (Fig. 2) and analyzed using a broad range of analytical methods (see Materials and Methods).

Fig. 1. Experimental setup.

(A) A Mylar tray was filled with heat-treated powdered pumice. Thick plastic lines the impact chamber to facilitate sample recovery. (B) The tray was centered beneath the impact point, as shown in this pre-impact frame from a high-speed imaging sequence (130,000 frames/s, 3-μs exposure). (C) The same view as (B) but showing a frame 761.5 μs after impact. The Mylar has ruptured, directing most of the luminous melt downward into the well for recovery. White lines mark the extent of the glowing plume; the region outlined in gray contains abundant luminous melt.

Fig. 2. Impact products.

The materials recovered from impact experiments fall into three categories: (A) impact glasses, (B) antigorite relics, and (C and D) breccia pieces. Both impact-generated glasses and melt-bearing breccia pieces contain quenched impact melts. However, the impact-generated glasses have no visible clastic material on their surfaces, whereas the melt-bearing breccias have unmelted, clastic material attached to quenched impact melt. The breccias contain impact-generated glasses, but they also contain comminuted, shock-lithified pumice.

RESULTS

Detailed description of impact products

The impact products recovered from experiments fall into three classes: impact glasses, projectile (antigorite) relics, and breccia pieces. Breccias comprise the bulk of the material [between 53 and 57 weight % (wt %) of the recovered materials]. Impact glasses account for 42 to 43 wt % of the mass of recovered material, with antigorite relics as a minor component (1 to 4 wt %). Table S1 reports the mass of each class of materials recovered from each experiment.

The impact glasses are vesicular pieces of translucent glass with a vitreous luster (Fig. 2A). Occasionally, the glass traps trace amounts of dark flecks of antigorite (for example, upper right corner of Fig. 2A). Antigorite relics consist of small fragments of antigorite found unattached to any other impact materials (Fig. 2B). Breccia pieces are a mixture of shock-compressed pumice and antigorite fragments bound together by impact-generated glasses. In some cases, the breccias are mostly impact-generated glass with a small amount of clastic pumice and a scattering of tiny dark flecks of antigorite within the glass (for example, Fig. 2C). In other cases, thin veins of quenched melt attach larger pieces of antigorite to the breccias (for example, Fig. 2D).

Because of their small sizes, antigorite relics (for example, Fig. 2B) were not powdered and measured using thermogravimetric analysis (TGA) (see Materials and Methods). Instead, samples were studied with the electron microprobe (EMP) (see Materials and Methods). Table S2 summarizes the compositions of antigorite relics from each experiment. Each relic was analyzed in multiple places to assess spatial variation in volatile content. All analyses from antigorite relics have oxide abundances and analytical totals that agree well with the chemical composition of the bulk antigorite projectile as measured by inductively coupled plasma atomic emission spectroscopy (ICP-AES). The similar analytical totals indicate that these isolated antigorite relics retained their original OH inventory.

TG and differential scanning calorimetry results

TGA combined with differential scanning calorimetry (DSC) provided critical information about the amount of water delivered by impact and the reservoirs of that water. TG profiles of the heat-treated pumice target show that the pumice gradually loses mass up to a temperature of 850°C (fig. S1). Mass loss continues above 190°C, which is the temperature at which the silica surface completely dehydrates (21). Therefore, this profile is consistent with diffusive loss of a small amount of OH from within the silicate structure (22). No signals in the TG, derivative TG (DTG), or DSC profiles indicate the presence of other thermally active phases. TG and DTG profiles of replicates are indistinguishable despite the extremely low volatile contents of these samples. The DSC profiles show similar trends but are offset from one another. Between 190° and 850°C, the heat-treated pumice lost 0.13 ± 0.004% of its mass (2σ SD).

Figure S1 also shows TG, DTG, and DSC profiles of three samples of the antigorite projectile. TG profiles show a single mass loss event between ~515° and ~850°C. All three profiles have a DTG maximum at 718°C. DSC profiles show an endothermic reaction between 730° and 770°C, as well as an exothermic reaction near 845°C. The temperature of the DTG maximum, shape of the DTG profile, and endothermic followed by exothermic DSC features are diagnostic of antigorite dehydroxylation (23). The total mass loss between 190° and 850°C was 11.97 ± 0.11 wt % (2σ SD). This mass loss is identical to the mass loss that would be expected for stoichiometric antigorite. The exothermic DSC peak near 845°C likely signals the crystallization of enstatite. The reaction occurs at slightly higher temperatures than the 820° to 826°C reported by Viti (23). However, this difference stems from the higher heating rate used here, which shifts peaks to higher temperatures (22).

Impact glasses begin to lose mass gradually at 50°C (Fig. 3). DTG profiles indicate a maximum rate of mass loss between 145° and 154°C, depending on the sample. DSC curves have minima between 145° and 194°C. Starting between 495° and 600°C (again, depending on the sample), a second mass loss event overprints the ongoing gradual mass loss. This second event lasts to 730° to 750°C (depending on the sample). In impact glasses from experiments 160714 and 160715, this second mass loss is accompanied by W-shaped DTG peaks. The two minima in experiment 160714 occur at 660° and 690°C. In experiment 160715, the minima occur at 530° and 700°C. Overall, impact glasses lost between 0.46 and 0.59% of their mass from 190° to 850°C (table S3).

Fig. 3. TG data.

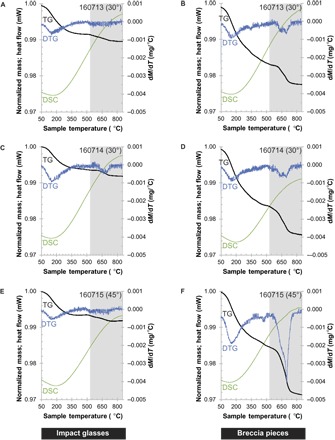
TG, DTG, and DSC profiles for impact glasses (A, C, and E) and melt-bearing breccias (B, D, and F). Each row corresponds to a single experiment. The y axis at left is for both TG and DSC profiles. DSC data have been divided by 7000 and offset by +0.97 to plot on the same axis as TG data. The y axis at right is for the DTG data. The gray rectangle marks the dehydroxylation interval for unshocked antigorite. The profiles reveal that impactor-derived water is stored in an amorphous, glassy component and in crystalline antigorite relics. The glassy reservoir dominates.

Profiles of breccia pieces exhibit many of the same characteristics as impact glasses (Fig. 3). Breccia pieces gradually lose mass beginning at 50°C. DTG profiles indicate a maximum rate of mass loss between 150° and 155°C, depending on the sample. DSC curves have minima between 140° and 149°C. However, breccias lose more of their mass during this portion of the heating routine than the impact glasses lost. In addition, mass loss events that start between 515° and 590°C (depending on the sample) and last until 740°C are more pronounced in the breccias. DTG profiles between ~495° and 750°C also exhibit stronger features than those of the impact glasses. The W-shaped peak in breccias from experiments 160713 and 160714 has two DTG minima at ~645° and 690°C. The DTG peak for breccias from experiment 160715 is highly asymmetric and very deep compared with the DTG peaks in other breccia samples. The DTG maximum in this sample occurs near 695°C. Overall, the breccias lost between 1.49 and 2.19% of their mass between 190° and 850°C (table S3).

The TG/DTG/DSC profiles of impact glasses and breccias are consistent with loss of OH and/or H₂O from an amorphous phase, antigorite, and, in the case of the breccias, an additional thermally active phase(s). In all materials, adsorbed water accounts for most of the mass losses between 50° and 190°C. Between 190° and 500°C, TG and DTG profiles are similar to those of perlite (22), a hydrated volcanic glass. Hence, mass losses between 190° and ~500°C are attributed to diffusive loss of OH and/or H₂O from the glass. The broad, endothermic DSC signal is consistent with removal of OH or H₂O (22).

The temperature range and TG profile shape for mass loss events between ~515° and 740°C are consistent with dehydroxylation of the antigorite projectile (23). The typical dehydroxylation interval for antigorite is shaded gray in Fig. 3. In impact products, this mass loss event occurs over a narrower temperature range, which we attribute to shock damage. The shape of the DTG peak in this temperature range provides even stronger evidence that the mass loss is due to antigorite dehydroxylation: the W-shaped or asymmetric character of DTG profiles (particularly in the impact breccias) is diagnostic and reflects the overlapping reactions that take place during antigorite dehydroxylation (23).

Small DTG peaks in the breccias between ~300° and 450°C indicate the presence of thermally active phases that are not present in the impact glasses. These temperatures may be consistent with brucite (22), a mineral that has been suggested as a decomposition product of shocked antigorite (24). X-ray diffraction (XRD) patterns do not show peaks at 18.53°, 32.88°, 37.98°, 50.79°, and 58.68° 2θ that would demonstrate the presence of brucite. Given the very small mass losses associated with these DTG peaks, brucite, if present, is below the XRD detection limit.

Synthesis of TG data

Impact-generated glasses, melt-bearing breccias, and antigorite relics contain water derived from the projectile. Impact-generated glasses contain 0.46 to 0.59 wt % total water, and melt-bearing breccias contain 1.49 to 2.19 wt % total water. The heat-treated pumice target can contribute no more than 0.13 wt % of this water. The antigorite projectile, with 11.97 wt % OH, provides an ample supply and is the only viable source of enough water to generate the water contents of the impact-generated glasses and melt-bearing breccias (see the Supplementary Materials). After accounting for the potential contribution of water from the target, impact products trap 19 to 22% of the projectile’s water for an impact angle of 30° and 30% of the water for an impact angle of 45° (Table 1).

Table 1. Water delivery during hypervelocity impact experiments.

Experiment number	Angle (°)	Impact product	Amount of water delivered	% of water stored in crystalline antigorite relics	% of water stored in amorphous component
160713	30	Impact glasses	3.3%	8%	92%
		Breccias	13.2%	21%	79%
		Antigorite relics	2.4%	100%	0%
		Total	19%
160714	30	Impact glasses	3.1%	23%	77%
		Breccias	16.2%	11%	89%
		Antigorite relics	3.1%	100%	0%
		Total	22%
160715	45	Impact glasses	2.5%	29%	71%
		Breccias	19.5%	30%	70%
		Antigorite relics	7.9%	100%	0%
		Total	30%

XRD results and FULLPAT modeling

The TG profiles of impact-generated glasses and melt-bearing breccias reveal two distinct reservoirs for projectile-derived water: an amorphous component and crystalline antigorite (see Fig. 3). To constrain the relative importance of these two reservoirs, we complemented the TG data with XRD data.

The XRD pattern of heat-treated pumice shows it to be mostly glass, with small amounts of anorthite, tridymite, quartz, muscovite, and hematite (fig. S2A). The projectile is almost pure antigorite, with a very small amount of calcite (fig. S2B).

XRD data show that all samples of impact glasses and breccias have a significant amorphous component, as indicated by the “amorphous hump” between ~15° and 35° 2θ. In addition, the XRD patterns of impact glasses and breccias have sharp peaks associated with the antigorite (serpentine) projectile and heat-treated pumice target (labeled S and P, respectively, in fig. S3). However, not all samples display every peak. For example, fig. S3B has a peak near 8.8° 2θ attributed to muscovite. Muscovite peaks are present in the target pumice (fig. S2A), but they are not discernible in the other impact materials. Antigorite peaks are more intense in breccias than in impact glasses. Impact glasses, but not breccias, have peaks near 32.2°, 36.4°, and 52.1° 2θ due to forsterite. Enstatite, if present, would have peaks near 28.1° and 31.0° 2θ. These peaks are absent in both impact glasses and breccias. The presence of forsterite in impact glasses is a critical constraint because, as a production of serpentine dehydroxylation (23), it demonstrates that part of the antigorite projectile devolatilized, liberating water vapor that could be captured by other impact products.

On the basis of FULLPAT models (see Materials and Methods), impact glasses contain 0.3 to 2.7 wt % crystalline antigorite. Breccias contain 1.4 to 7.9 wt % crystalline antigorite. Model totals range from 92.7 to 110.8%. Some patterns are modeled quite well (for example, impact breccias from experiment 160713), whereas others exhibit higher misfits. However, the R factors are all less than 0.1, which indicates that all pattern fits are generally good (25). Table S4 lists the results of these models.

Figure S4 compares the observed (blue) and modeled (red) XRD patterns. Small gray plots above each pattern show the misfit. In impact glasses from experiments 160713 and 160714, FULLPAT accurately reproduces the height of the antigorite peak near 12° 2θ. Hence, these antigorite abundances are well constrained. The FULLPAT models overestimate antigorite abundance in impact glasses from experiment 160715 and in breccias from experiments 160713 and 160715. These abundances are therefore upper limits. The modeled peak height, and thus abundance, of antigorite calculated by FULLPAT is too low for breccias from experiment 160714. Hence, this value is a lower bound.

Three factors introduce uncertainty in the models. First, the tektite used as an end-member in the models (see Materials and Methods) is not strictly identical to the impact glasses produced during these experiments; the two glasses formed during different stages of cratering and with different quench histories. Second, the amorphous hump in these XRD patterns is caused by a combination of preexisting amorphous material in the heat-treated pumice and the newly created impact-generated glass. Third, the materials in the impact glasses and breccias have been shocked, an event that strains the lattice and broadens diffraction peaks. The FULLPAT library standards are unshocked and, therefore, have narrower peaks. Much of the model misfit arises because the measured antigorite peaks are broader than the modeled ones.

Given the importance of constraining F_serp, we ran two sets of models: one based on the full diffraction pattern (5° to 70° 2θ) and one that only modeled 12° to 12.4° 2θ, a range that encompasses the strongest antigorite peak (see Materials and Methods). These latter models yielded better fits to the amplitude of the ~12.2° 2θ antigorite peak at the expense of accuracy in modeling the background and amorphous components. For experiment 160715, the models based on the full 2θ range clearly and significantly overestimate the antigorite abundance. For the breccias from 160714, the full-range FULLPAT model underestimates the antigorite abundance. Hence, for these samples, we use antigorite abundances calculated from the peak intensities from 12° to 12.4° 2θ. For all other samples, we use the antigorite abundances from FULLPAT models that used the entire 2θ range. These preferred values are consistent with the results of TG and ICP analyses.

On the basis of these preferred values, impact glasses contain 0.3 to 0.8 wt % crystalline antigorite. Breccias contain 1.4 to 5.2 wt % crystalline antigorite. On the basis of these antigorite abundances, the amorphous component must carry 71 to 92% of the water in impact-generated glasses and 70 to 79% of the water in melt-bearing breccias.

Detailed description of Fourier transform infrared data

Transmission infrared spectra acquired through doubly polished sections of impact glasses show features caused by OH and molecular H₂O (Fig. 4). A broad absorbance peak between ~3200 and 3750 cm⁻¹ is caused by vibrations of molecular H₂O, as well as Si-OH, Al-OH, and an overtone of HOH bending (26–28). The narrower absorbance peaks near 1630 and 5200 cm⁻¹ are caused by molecular water only: the fundamental H₂O bending mode and a combination of the H₂O stretching and bending modes, respectively (26–28). All of the spectra from all impact glasses studied exhibit these three absorbance features. Hence, all of the glasses contain molecular water. An absorbance feature near 4500 cm⁻¹ caused by a combination stretching and bending mode of Al-OH and Si-OH groups (26–28) is present in most, but not all, of the spectra. With the exception of the v2 H₂O bending mode near ~1630 cm⁻¹, absorbance peaks between ~1500 and 2000 cm⁻¹ are due to vibrations of the aluminosilicate glass lattice. A few spectra show features near 3000 cm⁻¹ attributed to C-H surface contamination. These features are very weak (compared to the 3570 cm⁻¹ total water band) and thus do not affect interpretations of bands related to OH and H₂O.

Fig. 4. Transmission spectra of impact glass from experiment 160715.

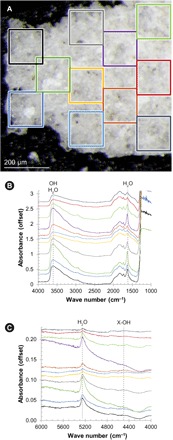
(A) Optical micrograph of a doubly polished piece of impact glass. Colored squares show where spectra were collected. The colors of the squares correspond to the colors of spectra in (B) and (C). (B) Transmission spectra between 1000 and 4000 cm⁻¹. Water-related peaks at both 3570 and 1630 cm⁻¹ are present. Small absorbance peaks near ~2850 and 3000 cm⁻¹ are attributed to C-H surface contamination. (C) Transmission spectra between 4000 and 6000 cm⁻¹. The H₂O feature near 5200 cm⁻¹ is quite strong. The X-OH feature at 4500 cm⁻¹ is small but discernible. Beer-Lambert calculations show that molecular water dominates over hydroxyl.

Total water contents (OH and H₂O) based on the band near 3570 cm⁻¹ range from 190 to 445 parts per million (ppm) in experiment 160713, 1760 to 2140 ppm in experiment 160714, and 1510 to 9330 ppm in experiment 160715. These are likely conservative lower bounds. The highly vesicular nature of these impact glasses complicates the calculations. Vesiculation introduces uncertainty into both sample thickness, d, and density, ρ. For the Beer-Lambert law to yield accurate results, d must be the path length of light through the sample. This is not the case for these samples because of their vesicular nature. The true path length is probably shorter than the measured sample thickness. Scattering, reflection, and refraction through vesicles introduce additional complexities. The highly vesicular nature of the glasses also complicates characterizing the densities of the samples. The densities of the samples reported here were estimated using the Gladstone-Dale rule (27). This approach does not consider the porosity of the samples. Hence, the densities we calculated are too high. Because of these two factors, the use of the Beer-Lambert law to quantify water contents should yield conservative lower bounds.

The calculations reveal that most of the water in the glass is molecular water, not hydroxyl (table S5). The lack of a 4500 cm⁻¹ band in samples from experiment 160713 implies that all of the water in that particular sample is molecular. This result is surprising because Stolper (26) and Mandeville et al. (27) found that, below ~4 wt % H₂O, most of the water in silicate glasses is stored as hydroxyl. Stolper (26) did not detect any molecular water in glasses with <0.2 wt % total water. However, those previous studies dealt with volcanic glasses with much higher total water contents [for example, up to 7 wt % H₂O in the study of Stolper (26)] or glasses produced during petrologic experiments. The glasses analyzed here have lower total water contents and formed during impact, rather than during a volcanic eruption. Higher quench rates may favor molecular water over hydroxyl.

Absorbance maximum position and absorbance depth vary with location in the impact glasses (Fig. 4). Band center varies less than absorbance depth does. For example, in the sample from experiment 160715, the position of the 1630 cm⁻¹ absorbance maximum ranges only from 1627 to 1632 cm⁻¹. However, the molecular water content calculated from this band varies by more than a factor of 8. The position of the broad ~3570 cm⁻¹ feature ranges from 3587 to 3622 cm⁻¹, whereas the total water content varies by a factor of roughly 6. The band center of the 4500 cm⁻¹ feature is the most variable of the three and ranges from 4435 to 4520 cm⁻¹. The calculated hydroxyl content varies only by a factor of 3.5. Variations in peak position likely reflect variations in bonding environment and suggest that these species, particularly the hydroxyl, are bonded to the silicate lattice in diverse ways. Variations in absorbance are tied to either water abundance or path length. Both factors could play a role: The vesicular character of these samples means that path length and scattering effects vary from location to location. However, it is also likely that the water content is spatially heterogeneous.

Two-component chemical mixing model results

Table S6 reports the compositions of the antigorite projectile, heat-treated pumice, impact glasses, and breccias recovered from the experiments (nonvolatile components only). Impact glasses and breccias should be two-component mixtures of the antigorite projectile and heat-treated pumice target. Hence, two-component mixing calculations can quantify how much the projectile and target contribute to the glasses and breccias. This type of model is distinct from the FULLPAT models of XRD patterns: Chemistry, rather than mineralogy, drives the model. Table S7 provides the results of these two-component mixing models.

On the basis of these calculations, the projectile retention efficiency (that is, the mass fraction of the projectile—exclusive of its water—that was recovered in impact products) ranges from 14 to 16% at 30°, up to 19% at 45°. Most of the retained projectile material occurs within breccia fragments. The proportion of antigorite within the other two types of products varies with impact angle. At 30°, antigorite relics account for the least amount of retained projectile material, whereas at 45°, impact glasses carry the least projectile material.

DISCUSSION

Water contents of impact products

Surprisingly, impacts delivered more water than would be expected based on the nonvolatile chemistry of the impact breccias. The two-component mixing models based on the nonvolatile components indicate that impact glasses captured 54 to 80% of the water bound in that part of the projectile that was incorporated into the glasses. Impact breccias, however, trapped up to two and a half times more water than would be expected based on their nonvolatile chemistry. These enhanced water contents are attributed to portions of the projectile that devolatilized but were not ultimately incorporated into the breccias. Alternative water sources cannot account for the measured water contents of the impact glasses and breccias (see the Supplementary Materials).

Mechanisms for capturing water

These enhanced water contents occur as a consequence of the timing of antigorite dehydroxylation and vapor plume evolution. Planar shock experiments predict complete antigorite devolatilization above ~50 to 60 GPa (29). The equation of state for antigorite (30) predicts that symmetric impacts at 5 km s⁻¹ (the impact speed of these experiments) produce a peak pressure of 60.4 GPa in the projectile. Although the oblique nature of these impact experiments reduces peak pressures, frictional heating along the projectile-target interface enhances vaporization (31). The presence of forsterite in impact glasses demonstrates that some of the antigorite completely devolatilized, thereby releasing water vapor into the impact plume. Because these were oblique impacts, some parts of the projectile that devolatilized would have later escaped downrange. The loss of projectile fragments downrange is well established for oblique impacts (32). Some water vapor should be released ~3 μs after impact, by which time the rarefaction wave has reached the front of the projectile. However, devolatilization occurs not only after penetration and decompression but also during further interactions with the target downrange from the point of impact. Water vapor would therefore be available in the impact plume at the time that melts and breccias formed. Because vapor envelopment and melt/breccia production overlap in time, breccias could trap additional water from the water-rich plume. Oblique impacts generate vapor having a wide range of temperatures temporarily contained within the transient cavity (33). These diverse conditions in the impact plume during oblique impacts further facilitate water capture.

The precise mechanisms that trap water vapor within impact products remain unclear. Shock effects (comminution and lattice strain) increase the surface area of pumice grains and strain the molecular structure of the pumice glass. These effects significantly increase defect concentrations, likely enhancing the ability of the breccias to capture water. Similar arguments have been made with respect to shock-comminuted material on the Moon being more receptive to solar wind implantation of hydroxyl (34). The solubility of water in silicate melts depends on temperature and pressure, both of which vary dramatically during the course of impact melt generation and quenching. Although rapid quench rates mean that the water contents of melt-rich impact products are likely not at thermodynamic equilibrium, phase relationships provide useful clues to the process. For example, experimental petrology has shown that the solubility of water in silicate liquids increases with pressure and, above ~0.5 to 1.5 GPa, also increases with temperature (35). Dedicated studies will be needed to detail the individual processes that result in the unexpectedly high water contents of impact products. Nevertheless, these experiments and terrestrial samples (10) demonstrate that these water contents are possible in impact products. In these experiments, the projectile must be the source of the trapped water (see the Supplementary Materials).

Implications

The fact that the amorphous, glassy component—not projectile survivors—constitutes the primary reservoir for impact-delivered water is critical for extrapolating these experiments. Impact melt production increases with impact speed (36). If impact melt derived primarily from the target successfully traps water during collisions among planetary bodies (as it does in experiments), then higher-speed impacts may still deliver significant quantities of water.

These experiments indicate that CC-like objects should be capable of delivering up to 30% of their indigenous water to silicate bodies under impact speeds and impact angles that prevailed during the early phases of planet formation and remain common for collisions in the modern asteroid belt. Isotopic evidence indicates that CC-like objects were the primary carriers of water for Earth (5) and Vesta (4). Even when impact speeds become fast enough to devolatilize CC-like impactors, these experiments indicate that the liberated volatiles could be captured within impact melts and breccias, thereby providing a means for incorporating volatiles into growing planetesimals. On the basis of planar shock experiments, Tyburczy et al. (8) predicted that approximately 99% of Earth’s early volatiles would have existed as recondensed vapor. However, these new experiments raise the possibility that growing terrestrial planets trap water in their interiors as they grow, which would profoundly affect their geodynamical evolution.

These results also have implications for the modern solar system. Many modern-day asteroids—particularly the larger ones—likely bear water (OH + H₂O) delivered by volatile-rich asteroids and meteoroids and subsequently mixed into the regolith by gardening impacts. For example, pitted terrain in craters on Vesta has been interpreted as evidence for subsurface volatile release (37). Water from CC-like impactors trapped in impact melts and later released by meteorite gardening could provide such a source. More generally, impactor-derived water trapped within impact glasses and melt breccias created by the impact of primitive, water-rich impactors may provide an explanation for the D/H values found in lunar agglutinates (38) and account for the elevated hydrous content in certain portions of the distal rays of Tycho (13) in ejecta around certain other craters reported by Bhiravarasu et al. (14) and Li and Milliken (39). Extreme thermal recycling and impact gardening would gradually release glass-trapped OH and H₂O molecules (and other volatiles) that could then gradually migrate to cold polar traps on the Moon. This process seems necessary to account for other volatiles (organics and silver) released during the LCROSS (Lunar CRater Observation and Sensing Satellite) impact experiment and the evidence for both old and new water with different abundances (11) and could be a source for polar ice deposits on Mercury (40).

MATERIALS AND METHODS

Experimental design

This study had two primary objectives: (i) quantify the amount of water captured during impacts by CC-like impactors and (ii) determine how this impact-delivered water is partitioned between various classes of impact products. We achieved these objectives using a combination of hypervelocity impact experiments and detailed sample analyses (see table S1 and Table 2).

Table 2. Analytical methods.

Technique	Abbreviation	Description of data	Data constrain
Inductively coupled plasma atomic emission spectroscopy	ICP-AES	Elemental abundances	How much of the nonvolatile components in the projectile are present in impact glasses and breccias
X-ray diffraction	XRD	Diffraction pattern whose peaks correspond to minerals and amorphous material in impact glasses and breccias	How much crystalline antigorite exists in impact glasses and breccias
Thermogravimetry/derivative thermogravimetry/differential scanning calorimetry	TG/DTG/DSC	Mass loss, rate of mass loss, and heat flow into samples during heating	Bulk water content of impact glasses and breccias; distribution of water between impact glass and antigorite; water delivery efficiency
Fourier transform infrared spectroscopy	FTIR	Absorbance spectrum	Total and molecular water content in field of view; speciation of OH versus H2O in impact glasses
Electron microprobe	EMP	In situ compositions of antigorite relics	Hydration state of antigorite clasts

Hypervelocity impact experiments at the NASA AVGR

Water delivery experiments were performed at the NASA AVGR. The light-gas guns at the AVGR launch projectiles at speeds up to ~6 km s⁻¹ and at a variety of impact angles while keeping the target surface perpendicular to the gravity vector. The AVGR features a large ~2.5-m-diameter impact chamber (31). Hence, volatiles liberated during impact can expand freely in an open system. This capacity sets the AVGR apart from facilities that generate planar shock experiments such as those used by Tyburczy et al. (8, 30) and Lange and Ahrens (29). Although planar shock experiments are necessary to deduce equations of state, shock devolatilization during planar impact experiments can be highly sensitive to capsule design (41). Previous preliminary experiments at the AVGR using serpentine and water-filled projectiles demonstrated that open-system three-dimensional experiments can result in trapped water, although details were not given (10).

Experiments were done at 5 km s⁻¹. The impact angle was either 30° or 45° with respect to horizontal. Cylinders of antigorite served as projectiles. Antigorite projectiles are viable analogs for CC impactors: The shock responses of the two materials are similar (8), the two have similar OH contents (12 and 10 wt %, respectively), and serpentines are among the most abundant water-bearing minerals in CCs (42). However, antigorite is readily available and easier to launch. Airfall pumice with a grain size of <106 μm, an analog for silicate planetary regoliths (18), was used as the target material. Table S1 lists the details for each experiment. Phantom v2512 high-speed color cameras recorded the experiments.

Because this study investigated water delivery, the target needed to be as dry as possible. To drive off volatiles, the pumice was heated at 850°C for 90 min. After heating, the pumice cooled to room temperature in a desiccator. Because of the large volume of heat-treated pumice needed, heat-treated pumice was stored in sealed plastic bags for up to 2 weeks before experiments. Aliquots of heat-treated pumice were powdered to <45 μm and run on a TG analyzer at the completion of the AVGR experiments. The TG data indicate that, at the time of the experiments, the heat-treated pumice contained 0.13 wt % OH + H₂O.

The target was a Mylar tray about 12 cm long, 7 cm wide, and 2 cm deep filled with heat-treated pumice. The pumice-filled tray was suspended over a well inside the impact chamber (Fig. 1). The tray was slightly deeper than three times the projectile diameter, which allowed the projectile to fully coupled to the pumice. However, the Mylar ruptured when the shock reflected from the free surfaces of the tray. This rupture allowed much of the molten impact products to travel into the well, rather than upward and outward, as would happen in a typical half-space target. This approach captured projectile-rich melts and breccias that would otherwise be lost downrange due to the residual projectile momentum and cratering flow field. These tray experiments ensured that the projectile experiences the full range of temperatures and pressures that it would undergo during a half-space experiment while enabling the capture and analysis of impact products that would otherwise have been lost. The well was lined with a thick plastic sheet to facilitate sample recovery.

Analytical methods

After each experiment, impact products were recovered from the plastic-lined well. After an additional step of hand sorting (to remove any extraneous debris, such as bits of Mylar), recovered impact products were weighed and characterized using optical microscopy.

Impact products were then analyzed using a variety of techniques, including ICP-AES, XRD, TGA, Fourier transform infrared (FTIR) spectroscopy, and EMP analysis. Several of these methods provide similar—but not identical—information (see Table 2).

Inductively coupled plasma atomic emission spectroscopy

Major element compositions were determined using ICP-AES. Samples of recovered impact materials, the heat-treated pumice target, and antigorite projectile were powdered to <45 μm in an agate mortar. Aliquots (40 mg) of each homogenized powder were digested using flux fusion and nitric acid digestion (43). A set of U.S. Geological Survey (USGS) rock standards and blanks were processed during the same run. Solutions were analyzed on a JY2000 Ultratrace ICP atomic emission spectrometer at Brown University. After correcting for instrumental drift and blanks, raw intensities were converted to elemental concentrations using the measured intensities and known concentrations of elements in the USGS standards (43). Multiple aliquots of heat-treated pumice were run to assess reproducibility. The reproducibility of each oxide was as follows: 1% Al₂O₃, 17% CaO, 2% FeO_T, 4% K₂O, 3% MgO, 1% MnO, 2% Na₂O, 27% P₂O₅, 1% SiO₂, and 4% TiO₂. However, the average abundance of CaO in the heat-treated pumice was only 0.60 wt % and of P₂O₅ was only 0.01 wt %. A duplicate analysis of the antigorite projectile, which had an average of 2.74 wt % CaO, yielded a reproducibility of 2% for that oxide.

ICP-AES data were used in two-component mixing models to quantify projectile retention efficiency. Using notation based on the study of Cantagrel et al. (44), the following equation describes two-component mixing

$$({\mathit{C}}_{\text{serp}}-{\mathit{C}}_{\text{pum}}){\mathit{X}}_{\text{serp}}=({\mathit{C}}_{\text{br}}-{\mathit{C}}_{\text{pum}})$$

where C_serp, C_pum, and C_br are the concentration of an oxide in the antigorite projectile, heat-treated pumice, and breccias, respectively. An equivalent equation could be written for C_gl, the concentration of an oxide in the impact-generated glasses. X_serp is the mass fraction of the projectile in the impact glasses or breccia, depending on the sample in question. If impact glasses and breccias are two-component mixtures of the target and projectile, then all oxides will plot along a single line that passes through the origin. The slope of that line, calculated from least-squares regression, is X_serp. For all samples analyzed here, the oxides plot along a line passing through the origin, consistent with the impact materials being two-component mixtures. This relationship rules out significant contamination by a third compositional end-member.

Before being used in the mixing model, ICP-AES data were normalized using the method of Allègre et al. (45). After normalizing analytical totals based on the mass lost during TGA, the concentration of each oxide was divided by its SD, multiplied by the concentration range of that oxide among all samples, divided by the analytical error for that oxide, and divided by the mean concentration of the oxide. This method gives the strongest weight to oxides with small analytical errors and large concentration ranges.

The mass fraction of the nonvolatile component of the projectile that was recovered can be calculated from these mixing model results. To do so, the mass of each class of impact materials was multiplied by X_serp and divided by the mass of the projectile. The results from each type of material, along with masses of the antigorite relics, are summed to yield the total projectile retention efficiency for a given experiment (table S7).

Thermogravimetry/differential scanning calorimetry

The volatile contents of impact materials, heat-treated pumice target, and antigorite projectile were measured using TG and DSC. Two samples of heat-treated pumice and three samples of the antigorite projectile were analyzed to assess reproducibility.

Aliquots of homogenized powders (<45 μm) of each sample (21.5 mg, on average) were loosely packed into 70-μl alumina crucibles and analyzed on a Mettler Toledo TGA/DSC-1 STARe system under an N₂ purge at Brown University. The instrument simultaneously measured sample temperature, mass, and heat flow. Sample temperature was increased from 50° to 850°C at a rate of 20 K min⁻¹ to ensure complete antigorite dehydroxylation (23). TG profiles were corrected for buoyancy and convection effects by subtracting the profile of the empty crucible. The Mettler-Toledo instrument accurately measures mass changes as small as 4 μg. The mass losses in even the most volatile-poor samples exceed this limit by a factor of ~15. Thus, all mass changes reported here are meaningful.

Although most adsorbed surface water should be removed by 100°C, the surfaces of amorphous silica samples may not fully dehydrate until 190°C (21). Therefore, using the mass loss between 190° and 850°C yields a conservative lower bound on the total amount of water (OH + H₂O) contained in impact glasses and breccias. Powdering the samples destroyed most of the vesicles. Any water trapped within these broken vesicles would have come off either at the time the vesicles ruptured or at the same time as adsorbed surface water (that is, below 190°C). Consequently, the water contents calculated from the TG data do not include the potential contribution of impact-delivered water stored in vesicles, which could be significant.

The TG profiles of impact glasses and breccias can be used to calculate the amount of antigorite (by mass) that a breccia or glass must have incorporated to explain the water content of that breccia or glass. Before these calculations, mass losses of impact materials were corrected for the 0.13 wt % water that could come from the heat-treated pumice target.

X-ray diffraction

The mineralogy and amorphous content of impact products, heat-treated pumice target, and antigorite samples were constrained using powder XRD. Aliquots of homogenized powders that passed through a 45-μm sieve were loaded into a zero-diffraction plate and analyzed on a Bruker D2 PHASER x-ray diffractometer at Brown University. Each sample was qualitatively assessed based on coupled two θ/θ scans from 8° to 60° 2θ with an increment of 0.02024° 2θ using Cu-α radiation and a count time of 2 s per step. Afterward, powders were mixed with high-purity corundum in a 4:1 ratio (by mass) and analyzed from 5° to 70° 2θ using a coupled two theta/theta scan type, an increment of 0.01826° 2θ, Cu-α radiation, and a count time of 15 s per step.

This second set of scans was resampled to increments of 0.02° 2θ and modeled using the FULLPAT program (25). FULLPAT quantitatively models the abundances of crystalline and amorphous phases in a material using a user-generated library of standards. The models reported here minimized the quantity Σ|Delta|^1/2, where Delta is the difference between the observed intensity and the modeled intensity at each point. This approach yields the best results for samples with a high amorphous component (25), such as those analyzed here. Corundum-spiked patterns of the antigorite projectile, a tektite, and the heat-treated pumice target were used as library standards. The tektite represents glass generated during the impact; none of the impact-generated glasses in these experiments were pure enough to use as an end-member. On the basis of the XRD patterns collected during the faster scans, forsterite abundances in the impact glasses are likely ~1 wt %, which is comparable to the uncertainty in FULLPAT model results. Therefore, forsterite can be omitted without significantly affecting the model results.

The outputs of these FULLPAT models are F_serp, F_targ, and F_glass, which represent the abundances (in wt %) of the antigorite projectile, heat-treated pumice target, and tektite (that is, impact-generated glass). Given the importance of constraining F_serp, a second set of models was run. Instead of modeling the entire pattern between 5° and 70° 2θ, patterns were only modeled from 12° to 12.4° 2θ, a range that encompasses the strongest antigorite peak. Table S4 also lists the results of this second set of models.

EMP analyses

Antigorite relics were embedded in epoxy, polished, carbon-coated, and then analyzed on the Cameca SX 100 EMP at Brown University (15 kV; current, 10 nA; beam diameter, 10 μm). Wavelength dispersive spectroscopy was used for all quantitative analyses. A sodium loss routine (46) corrected for any sodium devolatilized during analysis.

FTIR spectroscopy

The abundance and speciation of water in impact products were determined using transmission FTIR spectroscopy. Samples of impact glass were impregnated with orthodontic resin and sectioned using a low-speed saw. The resulting fillets were mounted on glass slides using additional orthodontic resin and then polished. The final polish was with 1-μm diamond paste. After polishing, the sample was bathed in acetone to remove the orthodontic resin. The sample’s polished side was then placed against the glass slide, and the sample was again embedded in orthodontic resin. The second side was polished exactly like the first. Once fully polished, the sample and slide were soaked in several acetone baths to remove the orthodontic resin. Wafer thickness was then measured using a Mitutoyo micrometer with a resolution of ±1 μm.

Transmission-mode spectra through these polished wafers were acquired using a Bruker LUMOS FTIR microscope at Brown University. Data were acquired between 600 and 6000 cm⁻¹ with 4 cm⁻¹ resolution, with a total of 500 scans per point. The detector was cooled with liquid nitrogen for 1 hour before the start of the analysis and was kept cold throughout the entire analytical run.

The Beer-Lambert law was used to quantify the amount of hydroxyl and molecular water present in the glasses

$$\mathit{C}=(\text{MW}*\text{Abs})/(\mathrm{\rho }\mathit{d}\mathrm{\epsilon })$$

where C is the concentration of the species being measured, MW is the molecular weight of the species, Abs is the height of the absorbance peak above the continuum, ρ is the density in g liter⁻¹, d is the sample thickness in centimeters, and ε is the linear molar absorptivity coefficient in liter mol⁻¹ cm⁻¹.

Total dissolved water was determined using the absorbance band near 3570 cm⁻¹. Water dissolved as molecular H₂O was determined using the band near 1630 cm⁻¹. Water dissolved as OH was computed from the 4500 cm⁻¹ band. The use of these bands is well documented in the literature (26–28). The following values were used for linear molar absorptivities: 1.73 liter mol⁻¹ cm⁻¹ for the OH feature at 4500 cm⁻¹ (28), 75 liter mol⁻¹ cm⁻¹ for the total water feature at 3570 cm⁻¹ (47), and 55 liter mol⁻¹ cm⁻¹ for the molecular water feature at 1630 cm⁻¹ (28). These linear molar absorptivities are for rhyolitic glasses, which is appropriate given the high silica contents of the impact-generated glasses. Densities were estimated from the bulk composition of the samples using the Gladstone-Dale rule (27). The background beneath each absorbance feature was approximated with tangential line segments between 2500 and 3750 cm⁻¹, 4800 and 5400 cm⁻¹, and 1550 and 1690 cm⁻¹, respectively.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/4/eaar2632/DC1

Supplementary Text

fig. S1. TG data for the target and projectile.

fig. S2. XRD data for the target and projectile.

fig. S3. XRD patterns for impact glasses and breccias.

fig. S4. Comparison between observed and modeled XRD patterns.

table S1. Summary of experiments.

table S2. Composition of antigorite relics measured by EMP (wt %).

table S3. Results of TGA analyses.

table S4. Results of FULLPAT modeling.

table S5. Summary of Beer-Lambert results.

table S6. Compositions of projectile, target, and impact products.

table S7. Projectile retention efficiencies.

Reference (48)