Topological Network Analysis of Electroencephalographic Power Maps

Abstract

Meditation practice as a non-pharmacological intervention to provide health related benefits has generated much neuroscientific interest in its effects on brain activity. Electroencephalogram (EEG), an imaging modality known for its inexpensive procedure and excellent temporal resolution, is often utilized to investigate the neuroplastic effects of meditation under various experimental conditions. In these studies, EEG signals are routinely mapped on a topographic layout of channels to visualize variations in spectral powers within certain frequency ranges. Topological data analysis (TDA) of the topographic power maps modeled as graphs can provide different insight to EEG signals than standard statistical methods. A highly effective TDA technique is persistent homology, which reveals topological characteristics of a power map by tracking feature changes throughout a filtration process on the graph structure of the map. In this paper, we propose a novel inference procedure based on filtrations induced by sublevel sets of the power maps of high-density EEG signals. We apply the pipeline to simulated and real data, where we compare the persistent homological features of topographic maps of spectral powers in high-frequency bands of EEG signals recorded on long-term meditators and meditation-naive practitioners.

1 Introduction

Meditation is a set of mental training regimes widely practiced for its claimed benefits to physical and mental health. Over the past decade, neuroscientific research has been accumulating evidence of meditation practice shaping up neuroplasticity, and the investigation of spontaneous brain activity, at rest or during practice, is a sensitive approach to identify neuroplastic changes [3].

Electroencephalogram (EEG) is an important imaging modality for exploring spontaneous human brain activity. EEG signals can be recorded in high temporal resolution on animal or human subjects as a response to an external or internal stimuli. The signals are typically decomposed into frequency components by Fourier transform, and the strengths of the frequency components within a certain range are measured by integrating the power spectral density (PSD) [11]. In practice, PSDs integrated over a frequency range are summarized on a topographic power map of EEG channels to visualize significant changes in spatial patterns of brain activity within the range [10,5]. A practical approach to compare two groups of EEG topographic power maps is to conduct two-sample t-tests at each channel and solve the multiple testing problem by the maximum t-statistic (single-threshold) or cluster-based inference (multi-threshold) methods [9]. These methods depend on the amplitudes of power maps, which do not necessarily correspond to topological difference between the maps. We are thus motivated to develop an inference procedure invariant to continuous amplitude transformations. A promising approach is topological data analysis (TDA) that exploits the robustness of topology [1]. A key TDA technique is persistent homology - an online algorithm tracking topological features through a dynamic thresholding scheme.

In this paper, we develop an inference framework for comparing the persistent homological features of two groups of EEG topographic power maps. Each EEG power map is first modeled as an undirected graph with weights defined from frequency powers on its vertices. We filter through the weights to obtain a sequence of combinatorial structures of vertices, edges and triangles on a triangulation of the graph. The persistent homological features of the filtering process are then incorporated in a permutation test for group difference between the maps. Simulation studies show evidence that the proposed framework is robust to scaling and translation and sensitive to tearing of amplitudes in a power map. The proposed framework is also applied to compare the topographic power maps of long-term meditators and meditation naive practitioners.

2 Background

Suppose v₁,…,v_p are p affinely independent points forming a graph in the Euclidean space ℝ³. Then each of the vertices v_i,i = 1,…, p, is a 0-simplex. A (s − 1)-simplex Δ is the convex hull of a subset $\{v_{i_1},\dots ,v_{i_s}\}$ of the p vertices, e.g. an edge joining two vertices is a 1-simplex, and a triangle formed by three edges is a 2-simplex, and a tetrahedron formed by four triangles is a 3-simplex. A face of Δ is the convex hull of a nonempty subset of $\{v_{i_1},\dots ,v_{i_s}\}$, e.g. the faces of a tetrahedron are its vertices, edges and triangles. A simplicial complex $\mathcal{K}$ on {v₁,…,v_p} is built by attaching its simplices in a certain way: a simplex joins $\mathcal{K}$ when all of its faces have joined and the intersection of two simplices in the complex $\mathcal{K}$ must be a face to each of the simplices. A subcomplex of $\mathcal{K}$ consists of a subcollection of its simplices attached in the same way.

Suppose we have a real-valued monotone function $g:\mathcal{K}\to ℝ$. The monotonicity of g means that g(τ₁) ≤ g(τ₂) when τ₁ is a face of τ₂. It implies that the sublevel set $g^{-1}((-\infty ,\lambda ])$ for an arbitrary λ ∈ ℝ is a subcomplex of $\mathcal{K}$. So the sublevel sets ${\mathcal{K}}_i=g^{-1}((-\infty ,{\lambda }_i])$ with respect to ${\lambda }_1\le \cdots \le {\lambda }_m$ form a nested sequence of subcomplexes of $\mathcal{K}:{\mathcal{K}}_1\subset \cdots \subset {\mathcal{K}}_m$, which is called a filtration of $\mathcal{K}$ and the λ_i are filtration values. The filtration induces a homomorphism chain for each dimension $k:H_k({\mathcal{K}}_1)\to \cdots \to H_k({\mathcal{K}}_m)$, where each arrow indicates a homomorphism $H_k^{i,j}$ between the respective k-dimensional homology groups $H_k({\mathcal{K}}_i)$ and $H_k({\mathcal{K}}_j)$ of ${\mathcal{K}}_i$ and ${\mathcal{K}}_j$. The k-dimensional persistent homology group is the image of the homomorphism $H_k^{i,j}$ for 1 ≤ i ≤ j ≤ m. If a kth homological feature or hole (k = 0: cluster; k =1: loop; k = 2: tunnel, etc.) is born at ${\mathcal{K}}_i$ and dies at ${\mathcal{K}}_j$, then λ_j − λ_i is called the persistence of the feature. A feature that is born at a finite time and never dies is said to have infinite persistence. Longer persistence indicates a more prominent feature and shorter persistence likely corresponds to noise. The k-dimensional Betti number is defined as ${\beta }_k^{i,j}=\mathit{\text{rank}}\left(H_k^{i,j}\right)$, which counts the number of distinct k-dimensional holes that are born before or at ${\mathcal{K}}_i$ and die after ${\mathcal{K}}_j$ [6]. In this paper we define the kth Betti function at ${\lambda }_1\le \cdots \le {\lambda }_m$ as the sequence of k-dimensional Betti numbers $\left({\beta }_k^{1,1},\dots ,{\beta }_k^{m,m}\right)$.

3 Methods

We first compute the power spectral density (PSD) estimation procedure on signals at each EEG channel. The estimated PSDs at all EEG channels are summarized on a spatial map of the channel layout. We denoise the power map with the discrete version of a heat kernel estimator derived from a graph Laplacian L on $\mathcal{G}$, and then obtain PH features of a filtration constructed on the denoised power map.

Power spectral density estimation

The PSD of an EEG signal can be estimated by the periodogram through discrete Fourier transform of the signal. We estimate the PSD of the EEG signal at each channel by Welch’s method of modified periodogram: divide a signal into overlapping segments and then average the modified periodograms computed on all the segments to obtain a PSD estimate with reduced variance than the usual periodogram [11].

Denoising procedure via graph Laplacian

We then spatially filter out noise in the topographic power map f = (f₁,…, f_c) of each subject at a particular frequency band, where c is the number of EEG channels. Each power map is modeled as a graph $\mathcal{G}=\left\{\mathcal{V},\mathcal{E}\right\}$ with the edge set $\mathcal{E}$ from the Delaunay triangulation $\mathcal{T}$ built on the vertex set $\mathcal{V}$ of EEG channels. We denote the vertex set as $\mathcal{V}=\left\{v_1,v_2,\cdots ,v_c\right\}$Two vertices v_i and v_j joined by an edge is denoted v_i ~ v_j. Here we use the most common form of graph Laplacian [2]:

$$l_{ij}=\{\begin{array}{cc}-w_{ij},& v_i\sim v_j\\ {\displaystyle {\sum }_{i\ne j}{w}_{ij},}& v_i=v_j\\ 0,& \text{otherwise}\end{array}$$

with edge weights taken from the adjacency matrix W = (w_ij). There are up to c unique eigenvectors ${\psi }_1,{\psi }_2,\cdots ,{\psi }_c$ satisfying

$$L{\psi }_j={\gamma }_j{\psi }_j$$ (1)

with 0 ≤ γ₁ ≤ γ₂ ≤ … ≤ γ_c. The eigenvectors are orthonormal, i.e., ${\psi }_i^{\prime }{\psi }_j={\delta }_{ij}$- the Kroneker’s delta. The first eigenvector is trivial: ${\psi }_1=1/\sqrt{c}{\left(1,\dots ,1\right)}^{\prime }$. All other eigenvalues and eigenvectors are analytically unknown and need to be numerically computed. Once we obtain eigenvectors ψ_j satisfying (1) on the Delaunay triangulation $\mathcal{T}$, the heat kernel estimate for the power map f is given by

$$\widehat{\mathit{f}}=K_{\sigma }\ast \mathit{f}={\displaystyle \sum _{j=1}^c{e}^{-{\gamma }_{j^{\sigma }}}{\zeta }_j{\psi }_j,}$$ (2)

where $K_{\sigma }={\displaystyle {\sum }_{j=1}^c{e}^{-{\gamma }_{j^{\sigma }}}{\psi }_j{\psi }_j^{\prime },}$ is the discrete heat kernel and ${\zeta }_j={\mathit{f}}^{\prime }{\psi }_j={\psi }_j^{\prime }\mathit{f},j=1,\dots ,c,$ are the Fourier coefficients with respect to the basis {ψ₁,…, ψ}. The parameter σ is the heat kernel bandwidth and it modulates the extent of denoising. In this paper, we use σ = 0.5 for denoising power maps.

Building a sublevel-set filtration on a denoised power map

We now characterize the topology of the denoised power map $\widehat{\mathit{f}}$ by filtering a simplicial complex $\mathcal{K}$ defined on the Delaunay triangulation $\mathcal{T}$ of the vertex set $\mathcal{V}$. The weights on $\mathcal{K}$ are defined through an extension $g:\mathcal{K}\to ℝ$ of $\widehat{\mathit{f}}:\mathcal{V}\to ℝ$: each vertex v_i on $\mathcal{T}$ has the weight ${\widehat{f}}_i$, an edge connecting two adjacent vertices $\left\{v_{i_1},v_{i_2}\right\}$ on $\mathcal{T}$ in $\mathcal{K}$ is assigned the weight max $\left({\widehat{f}}_{i_1},{\widehat{f}}_{i_2}\right)$, and a triangle in $\mathcal{K}$ determined by three pairwise adjacent vertices $\left\{v_{i_1},v_{i_2},v_{i_3}\right\}$ on $\mathcal{T}$ takes the weight max $\left({\widehat{f}}_{i_1},{\widehat{f}}_{i_2},{\widehat{f}}_{i_3}\right)$. It follows that the function g is monotone, i.e. g(τ₁) ≤ g(τ₂) whenever τ₁ is a face of τ₂.

Now we filter $\mathcal{K}$ through the ordered vertex weights of g:

$${\lambda }_1={\widehat{f}}_{(1)}\le \cdots \le {\lambda }_i={\widehat{f}}_{(i)}\le \cdots \le {\lambda }_c={\widehat{f}}_{(c)}.$$

An arbitrary λ < λ₁ induces an empty subcomplex of $\mathcal{K}:{\mathcal{K}}_0=g^{-1}((-\infty ,\lambda ])=Ø.$ We then hit the λ_i, i = 1,…, c, in sequence from the minimum λ₁ up to the maximum λ_c. When we hit a λ_i, the subcomplex of $\mathcal{K}$ is updated to

$${\mathcal{K}}_i=g^{-1}((-\infty ,{\lambda }_i]),$$ (3)

which contains all vertices $v\in \mathcal{T}$ with g(v) ≤ λ_i, all edges whose vertices are in ${\mathcal{K}}_i$ and all triangles whose edges are in ${\mathcal{K}}_i$ We thus obtain the following filtration of $\mathcal{K}$:

$$Ø={\mathcal{K}}_0\subset {\mathcal{K}}_1\subset {\mathcal{K}}_2\subset \cdots \subset {\mathcal{K}}_c=\mathcal{K},$$ (4)

which we call the sublevel-set filtration. Homological features or holes emerge and merge in the filtration by the Elder Rule: older features live on at a merging junction [6].

We illustrate the filtration (4) on a 6-channel EEG layout in the international 10–20 system (Figure 1). We first build up the Delaunay triangulation over the 6-channel layout (Figure 1 (a)). Then a simplicial complex is built on the triangulation and weights of the simplices are defined via vertex values. We then filter the simplicial complex with respect to the filtration values λ = −1, 0, 0.5, 1, 2, 3 (Figure 1 (b)). The connectedness of clusters change as λ increases. The 0th Betti function corresponding to the λ values is (1,1,2,1,1,1).

Fig. 1.

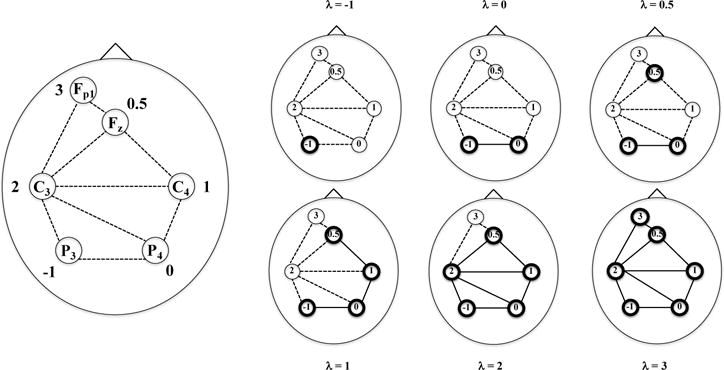
An example of the filtration (4) on 6 weighted EEG channels in the international 10–20 system, (a) The 6-channel layout with the corresponding Delaunay triangulation indicated by dashed lines. A simplicial complex is defined with respect to the triangulation; vertex weights are the weights of the channels and an edge weight is the larger of the weights of the two vertices joined by the edge, (b) At each filtration value λ, we include the vertices and edges with weights less than or equal to λ.

Inference on two groups of sublevel-set filtrations

Utilizing topological information in the data, we test the the null hypothesis that there is no difference between the respective mean 0th Betti functions ${\overline{\beta }}_0^1$ and ${\overline{\beta }}_0^2$ of the sublevel-set filtrations of denoised power maps in Group 1 and Group 2:

$$H_0:{\overline{\beta }}_0^1(\lambda )={\overline{\beta }}_0^2(\lambda ),H_1:{\overline{\beta }}_0^1(\lambda )\ne {\overline{\beta }}_0^2(\lambda ),$$ (5)

at fixed m filtration values $\lambda ={\lambda }_{i_1},\dots ,{\lambda }_{i_m}$. To test the null hypothesis (5), we first compute the ℓ₂ distance

$${\ell }_2\left({\overline{\beta }}_0^1,{\overline{\beta }}_0^2\right)=\sqrt{({\overline{\beta }}_0^1\left({\lambda }_{i_1}\right)-{\overline{\beta }}_0^2{\left({\lambda }_{i_1}\right)}^2+\cdots +{\left({\overline{\beta }}_0^1\left({\lambda }_{i_m}\right)-{\overline{\beta }}_0^2\left({\lambda }_{i_m}\right)\right)}^2},$$ (6)

between the respective means

$${\overline{\beta }}_0^1=\left({\overline{\beta }}_0^1\left({\lambda }_{i_1}\right),\dots ,{\overline{\beta }}_0^1\left({\lambda }_{i_m}\right)\right)\text{and}{\overline{\beta }}_0^2=\left({\overline{\beta }}_0^2\left({\lambda }_{i_1}\right),\dots ,{\overline{\beta }}_0^2\left({\lambda }_{i_m}\right)\right)$$

of the 0th Betti functions of the sublevel-set filtrations characterizing the denoised power maps in Group 1 and 2. Then the labels of the two groups undergo repeated random exchanges. At each label exchange, the ℓ₂ distance between the respective mean Betti functions

$${\overline{\beta }}_0^{1\prime }=\left({\overline{\beta }}_0^{1\prime }\left({\lambda }_{i_1}\right),\dots ,{\overline{\beta }}_0^{1\prime }\left({\lambda }_{i_m}\right)\right)\text{and}{\overline{\beta }}_0^{2\prime }=\left({\overline{\beta }}_0^{2\prime }\left({\lambda }_{i_1}\right),\dots ,{\overline{\beta }}_0^{2\prime }\left({\lambda }_{i_m}\right)\right)$$

of the relabeled power maps is calculated at the same fixed m filtration values:

$${\ell }_2\left({\overline{\beta }}_0^{1\prime },{\overline{\beta }}_0^{2\prime }\right)=\sqrt{{\left({\overline{\beta }}_0^{1\prime }\left({\lambda }_{i_1}\right)-{\overline{\beta }}_0^{2\prime }\left({\lambda }_{i_1}\right)\right)}^2+\cdots +{\left({\overline{\beta }}_0^{1\prime }\left({\lambda }_{i_m}\right)-{\overline{\beta }}_0^{2\prime }\left({\lambda }_{i_m}\right)\right)}^2}$$ (7)

We take the proportion of the distances ${\ell }_2\left({\overline{\beta }}_0^{1\prime },{\overline{\beta }}_0^{2\prime }\right)$ exceeding that of the observed distance ${\ell }_2\left({\overline{\beta }}_0^1,{\overline{\beta }}_0^2\right)$ is taken as the p-value for the permutation test.

4 Simulations

Topology is stable under continuous deformations [7]. It motivates us to test the robustness of the proposed topological inference procedure on a topographic power map undergoing continuous transformations on the amplitude. We are also interested in the sensitivity of the proposed procedure to topology-altering transformations on the amplitude. In other words, we want to control the rate of ’topological false positives’ while maintaining the rate of ’topological true positives’.

We define the power map

$$z_i=3{(1-x_i)}^2{e}^{-(x_i^2+y_i^2)}+3e^{-({(x_i-2)}^2+y_i^2)},i=1,\dots ,100,$$ (8)

with (x₁,y₁),…, (x₁₀₀,y₁₀₀) evenly simulated from the four quadrants of the [−3,3] × [−3,3] grid. We then add independent Gaussian noises N(0, 0.1) to create 5 noisy samples {z₁,…, z₅: z_j = (z_j1,…, z_j100)} of the map (8) and 5 noisy samples $\left\{{\mathit{z}}_1^{\prime },\dots ,{\mathit{z}}_5^{\prime }:{\mathit{z}}_j^{\prime }=\left(z_{j1}^{\prime },\dots ,z_{j100}^{\prime }\right)\right\}$ of each of the following transformation of (8):

1. (scaling) $z_i^{\prime }=2z_i$, scaling preserves the map topology;

2. (translation) $z_i^{\prime }=\left(z_i+5\right)$, translation preserves the map topology;

3. (tearing) $z_i^{\prime }=\left(z_i\pm 5\right)$ (+ for 1 ≤ i ≤ 50 and − for 51 ≤ i ≤ 100), which translates two halves of the map in opposite directions, causing discontinuities or topological tears on the map.

Under each setting, this simulation procedure is repeated 100 times; for each simulation, the null hypothesis (5) is tested on the 2 groups of 5 samples through the proposed inference method with 5000 permutations. We reject the null when a p-value falls below 0.05. The rejection rates are 5%, 4% and 100% in each setting. The results provide numerical evidence that the proposed procedure for testing the difference between topographic maps stays robust under some topology-preserving transformations (scaling and translation) and meanwhile is sensitive to some topology-altering transformations (tearing).

5 Real data application

The aim of this application is to compare topological difference between frequency variations in the EEG signals of 24 meditation-naïve participatns (MNPs) and 24 long-term meditators (LTMs) of Buddhist meditation practices (approximately 8700 mean hours of life practice) during whole-night non-rapid eye movement (NREM) sleep. The EEG signals were recorded with a 256-channel hdEEG system (Electrical Geodesics Inc., Eugene, OR). Data were bandpass filtered (1–50 Hz), and independent component analysis was used to remove ocular and muscle artifacts in the signals. Channels with most of the recording affected by artifacts were removed and spherically interpolated. Data was downsampled to 128Hz and split into six-second epochs with each epoch divided into 8 segments with 50% overlapping for the method of Welch’s averaged modified periodogram with a Hamming window function for PSD estimation at each channel. The participants under 3 sessions of recording: a baseline session, and one session each after two days of Vipassana (mindfulness) and Metta (compassion) meditations. We focused on analyzing the baseline session for unconfounded effect of long-term meditation practice. Also, since existing studies suggested increased parietal-occipital gamma activity during sleep in the LTMs compared to MNPs [4], we only focused on the high-frequency bands of the EEGs.

After heat kernel denoising, we normalized each power map by a z-score transformation across all channels. We then compared the normalized denoised power maps of the LTMs and MNPs in the high-frequency β (15–25 Hz) and γ (25–40 Hz) bands by the proposed permutation test. The sublevel-set filtrations of the average normalized maps in both groups are shown in Figure 2; note the faster closure of clusters in the LTM map as λ increases. The table of p-values in Figure 2 provides comparison between results of the proposed and maximum t-statistic permutation test. The only place where the proposed test shows significant topological difference is the β band in sleep cycle 1, whereas the maximum t-statistic test shows significant difference between LTM and MNP in four out of six categories. It is possible that the maximum t-statistic approach is too sensitive to non-topological differences between two groups of power maps.

Fig. 2.

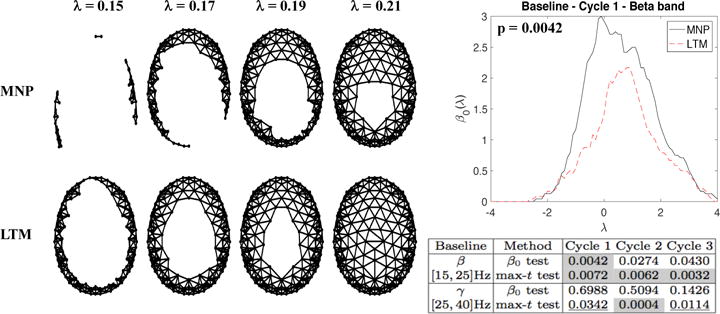
Left: Filtrations of mean normalized power maps in the beta band in sleep cycle 1 under the baseline condition. Right top: Group mean β₀ functions with the p-value from the β₀ permutation test. Right bottom: The p-values of β₀ and maximum t-statistic permutation tests comparing MNPs and LTMs in the baseline session. The p-values below the Bonferonni threshold 0.05/6=0.0083 corrected over 2 (frequency bands) × 3 (sleep cycles) = 6 tests for each method are shaded in gray.

6 Discussion

In this paper, EEG topographic power maps are modeled as graphs with weights defined through the spectral powers on their vertices. The topology of these graphs is studied through persistent homology. A related approach is graph filtration devised to capture the shape of a brain network modeled as graph by filtering a dissimilarity measure between its vertices [8]. The purpose of the two filtration approaches differ in that the former reveals the functional connectivity between channels, whereas the latter aims to reveal the underlying geometric pattern of the power map through topological changes in its sublevel sets.