Significance
Motile cilia are hair-like structures that extend from the surfaces of eukaryotic cells and pump fluid. The motor protein dynein drives the motion of cilia, but it is unclear how the organized beat of a cilium emerges from the combined action of hundreds of dynein molecules. Here, we describe how the molecular architecture of a cilium constrains its possible motion, and we postulate a dynamical law that governs the dynein tensions. Based on this constraint and dynamical law, we construct a model cilium that beats spontaneously. Simulation of multiple copies of this model in fluid reveals that an array of cilia spontaneously breaks synchrony and adopts multiple phases and that such symmetry breaking is helpful in producing net fluid transport.
Keywords: motile cilia, Hopf bifurcation, symmetry breaking, phase desynchronization, fluid transport
Abstract
The exact mechanism to orchestrate the action of hundreds of dynein motor proteins to generate wave-like ciliary beating remains puzzling and has fascinated many scientists. We present a 3D model of a cilium and the simulation of its beating in a fluid environment. The model cilium obeys a simple geometric constraint that arises naturally from the microscopic structure of a real cilium. This constraint allows us to determine the whole 3D structure at any instant in terms of the configuration of a single space curve. The tensions of active links, which model the dynein motor proteins, follow a postulated dynamical law, and together with the passive elasticity of microtubules, this dynamical law is responsible for the ciliary motions. In particular, our postulated tension dynamics lead to the instability of a symmetrical steady state, in which the cilium is straight and its active links are under equal tensions. The result of this instability is a stable, wave-like, limit cycle oscillation. We have also investigated the fluid–structure interaction of cilia using the immersed boundary (IB) method. In this setting, we see not only coordination within a single cilium but also, coordinated motion, in which multiple cilia in an array organize their beating to pump fluid, in particular by breaking phase synchronization.
Motile cilia are hair-like organelles extending from the surfaces of eukaryotic cells and are characterized by their rhythmic wave-like motion. Most motile cilia have a “9 + 2” axoneme architecture, which refers to 9 peripheral doublet “AB” microtubules surrounding a central pair of singlet microtubules. Dynein motor proteins, responsible for force generation, extend from each A tubule of an outer doublet toward the B tubule of the adjacent doublet. Along each A tubule, the dynein motors are regularly spaced in groups with a period of 96 nm (1). The motor proteins generate relative sliding of the adjacent doublets by ATP-fueled cycles of attachment, translocation, and detachment along the B tubule of their target doublet. This active sliding interacts with the passive resistance from the other axonemal components, including the radial spokes and nexin links, and also with the basal body to produce the ciliary beat, yet it is still unclear how the organized motion of a cilium emerges spontaneously from the combined action of the hundreds of individual dynein motor proteins.
This question has been addressed in several different ways. The geometric factors that may regulate the dynein motor proteins include sliding displacement, curvature, and interdoublet distance as reviewed in ref. 2. In curvature-based models, the dynein motors are deactivated when the local curvature exceeds a specified threshold (3–5). In these models, the direction in which the dynein motors move and the sign of curvature are opposite on two sides of the axoneme with respect to the beating plane. In sliding control models, linearity between the sliding displacements and the shear forces is assumed (2, 6–8), and this has been combined with a two-state model of the dynein motor involving strongly and weakly bound states depending on the sliding displacement (8, 9). The geometric clutch model (10, 11) postulates that the interdoublet distance is responsible for the activation of the dynein motors. This distance depends on the transverse force, which develops across the structure in the beating plane when the structure is bent. The active bending and the passive bending of the cilium have an opposite effect on the transverse force, and this antagonism generates the ciliary beating. In another class of models, the cilium is treated as a slender body, and the dynein motors are not modeled in detail. Instead, an internal engine is postulated to generate the beat pattern of the cilium (12–14).
Our model is based on a geometrical constraint that restricts the deformation of the cilium and on a postulated dynamical law for the tension generated by a dynein motor. The geometrical constraint allows us to retain important aspects of the microstructure of the cilium while reducing the dfs of the model to those of a single centerline space curve. The postulated dynamical law allows the tension generated by each dynein motor to evolve independently but in a manner that depends on the length of the link formed by that dynein motor and hence, on the deformation of the structure as a whole. The dynein motors in our model are, therefore, coupled to each other through the structure of the cilium, and this coupling is indirectly responsible for their coordination. The model cilium has an unstable symmetrical steady state, in which the cilium is straight and all motors are under equal tension. The instability of this steady state leads to the emergence of a globally stable limit cycle oscillation, which is the ciliary beat.
The interpretation of ciliary beating as a limit cycle oscillation around an unstable steady state was proposed in ref. 8. The authors presented a local drag model of a 2D cilium driven by two-state molecular motors (9). The instability of the steady state of the model cilium was shown to involve a Hopf bifurcation. Our model is 3D, and our postulated dynamical law governing the tension of an individual dynein motor is continuous rather than discrete.
In ciliary arrays, neighboring cilia interact with each other via surrounding fluid, and this leads to the emergence of phase synchronization and metachronal waves, in which a constant phase difference is maintained between adjacent cilia. The hydrodynamic interactions between cilia have been studied analytically and numerically with various models of cilia from minimal models capturing the essential features of ciliary beating (15–20) to more detailed models to simulate the beating shape of real cilia (12, 14, 21–24). In particular, metachronal coordination of arrays of cilia is believed to be connected to efficient pumping of fluid, which is the principal function of motile cilia. The efficiency of pumping fluid in a ciliary array has been studied by using magnetically actuated artificial cilia (25, 26), a model of cilia with active bending forces (23), or a model with an optimized beat shape for pumping efficiency (21). These studies address the pumping efficiency in relation to phase difference, wave vector, and interciliary spacing. In both studies of 1D (25, 26) and 2D ciliary arrays (21, 23), the metachronal wave pumps fluid more effectively than synchronized ciliary beating, and simplectic metachronal waves, which propagate in the same direction as the power stroke, are generally more efficient in fluid transport than antiplectic waves, which propagate in the opposite direction.
In contrast to previous works focusing on the emergence in phase difference in orthoplectic rows [running in the same or opposite direction as the ciliaty beat (27)], here, we present simulation results showing emergence of multiple phases (i.e., symmetry breaking) in a diaplectic row (which is perpendicular to the beating plane of the cilia) (27). In this simulation, we find that symmetry breaking is essential for effective fluid transport.
Model
According to the 9 + 2 arrangement of the microtubules, we model the configuration of a cilium as 11 discretized space curves in with points each, and , , where corresponds to the nine doublet microtubules at the periphery of the cilium and corresponds to the central pair of microtubules that run along the inside of the cilium. For simplicity of the description of the structure, we introduce the imaginary centerline curve, , defined as , , which we can regard as modeling the central pair of microtubules. Note, in particular, that corresponds to one end of the model cilium anchored at the bottom, and for each , the collection of nine points, with , can be thought of as a cross-section of the model cilium.
Geometric Constraint.
We assume that all of the microtubules are inextensible, so that the distance between adjacent nodes along each microtubule remains constant. That is,
| [1] |
for the centerline (which has no superscript), for the peripheral doublet microtubules , and for all levels . The distance is set equal to 96 nm, which is the periodicity of the dynein motors along the microtubules. Motivated by the microstructure of the cilium, we imposed the minimal additional assumption that, at each cross-section, the point of the centerline, , is the centroid of the nine points of peripheral curves; that is,
| [2] |
This assumption does not, by itself, say anything about the shape or size of the various cross-sections (they might not even be planar). When constraints [1] and [2] are combined, however, it can be shown (Supporting Information) that the configuration of each cross-section is a rigid translation of the base cross-section of the model cilium. We assume, moreover, that the base cross-section of the cilium is planar and has the form of a fixed, regular nonagon. That is, for all s and s,
| [3] |
Note that Eq. 3 allows neither twist nor tilt of the different cross-sections of the cilium and implies that the configuration of the entire cilium is completely determined by that of its centerline. This enables us to retain the detailed structure of the cilium in our model and yet to describe its motion more simply in terms of the motion of the centerline. Since the base cross-section is a planar and regular nonagon, the whole structure can be thought of as a freely jointed chain of regular nonagons. Although the centerline is freely jointed, the nonagons themselves are constrained to move rigidly and by translation only.
In our model, the relative sliding of adjacent peripheral doublet microtubules happens automatically as the local orientation of the centerline changes. This consequence of our geometric constraints is derived in Supporting Information. It is shown there that, as the direction of the centerline changes, its rate of change induces a proportional relative sliding velocity of adjacent peripheral curves of the model. The relative sliding velocity varies sinusoidally around each cross-section, being zero in the direction in which the tangent to the centerline is changing and having the opposite sign on either side of that direction. All of these quantities and therefore, the relative sliding velocities can be different in the different cross-sections of the model cilium.
Forces.
The motion of the cilium is driven by the active dynein motors coupled to the passive elasticity of the structure. We model the dynein motor proteins by active links connected between two points of the adjacent peripheral curves, and , but , with periodic arithmetic on . In most cilia, there is one pair of adjacent peripheral doublet microtubules, conventionally labeled and , which are permanently linked to one another by 5-6 bridges and cannot slide relative to each other (28, 29). The microtubule doublets numbered 5 and 6 are positioned so that a line joining them at their base is nearly parallel to a similar line joining the central microtubules at their base. These nearly parallel lines are approximately perpendicular to the plane in which the cilium beats. Indeed, it is the rigidity of the connections joining the peripheral doublets 5 and 6 and also, the rigidity of the connections between the central microtubules that mechanically restrict the beating to occur in a single plane. We model the 5-6 bridges as stiff linear springs connecting , and , . The passive elasticity of the cilium as a whole is modeled by treating the centerline as an elastic beam. As a consequence of the geometric constraint described above, which restricts the motion of each nonagon to a rigid translation, we find that all forces applied to any node on one of the peripheral doublet microtubules can be applied directly to the centerline node at the same level (30). The model cilium in fluid interacts with the fluid only via its centerline, but the peripheral nine curves of the model still play an important role as a scaffold for the dynein motors (and for the passive 5-6 bridges). The force applied to the fluid by the centerline node may be summarized as
| [4] |
where is the elastic force at node of the centerline generated by the bending and stretching of the centerline beam. Note that the stretching modulus is large enough that the beam is effectively inextensible as assumed in deriving our geometrical constraint. The force is minus the gradient of the elastic energy function
| [5] |
where is the bending modulus and is interpreted as the extension modulus. To simulate the asymmetric beat of a cilium, in which the power stroke is different from the recovery stroke, we have found it necessary to make the bending modulus depend on the direction of curvature as defined by the sign of the triple scalar product of three vectors: the local curvature vector of the centerline, the local tangent vector to the centerline, and a constant reference vector that is orthogonal to the plane of the ciliary beat. Note that the reference vector can be defined in terms of the structure of the cilium (for example, as the vector connecting the base of microtubule doublet number 5 to the base of microtubule doublet number 6). This aspect of the model is discussed in greater detail in Supporting Information.
The active links in our model generate tension governed by the following differential equation:
| [6] |
where is the tension in the link joining nodes and for and with periodic subscript arithmetic. On the right-hand side of this equation, is the instantaneous length of the link, and and are given constants, of which is level-dependent (hence, the subscript ) (Supporting Information). The level dependence of is not essential for spontaneous oscillation, but it is needed to make the time-dependent shape of the cilium realistic. With independent of , the tip of the cilium seems to lead instead of lag, but with decreasing as a function of , the model cilium is driven more from the base, as in reality. The constant has units of , and the constant has units of force per length squared. Note the important point that each active link independently obeys Eq. 6 and that the only information available to any active link about the state of the cilium as a whole at any given time is the instantaneous length of that particular link, . This is not much to go on; nevertheless, it turns out to be enough to tell the link what to do to participate in a coordinated wave-like beating pattern. The motivation for Eq. 6 comes from a toy model, described in Supporting Information, in which a rigid rod hinged at its base is held in the vertical position by two guy wires under tension. The stability of the vertical equilibrium depends on the tension law of the guy wires. If the wires are under constant tension, the vertical equilibrium is unstable; if the tension is proportional to the length of the wire, the vertical equilibrium is neutrally stable, and if the tension is proportional to the square of the length or indeed, to any power of the length greater than one, the vertical equilibrium is stable. Our postulated dynamical law for the tension, [6], contains aspects of the first and third cases. On a fast timescale, Eq. 6 simply asserts that the tension is prescribed (by its instantaneous value, since Eq. 6 requires to be a continuous function of time, even if changes suddenly) regardless of length, but on a slow timescale, it makes the tension proportional to the square of the length. (Any power greater than one could be used here, as shown in Eqs. S32–S36, but we choose the power two for simplicity.) Indeed, when this equation is used to govern the guy wires of the toy model and when the parameters of that model are appropriately chosen, the result is a limit cycle oscillation about the vertical configuration.
Although the detailed mechanism by which dynein generates tension is unknown, the prevailing view (29, 31) is that this process involves cycles of attachment and detachment linked to ATP hydrolysis, like the cross-bridge cycle in muscle (32). We do not attempt to model the details of this process, however, and instead, we consider only the resulting tension, which we model in a phenomenological way, although we do give a possible mechanistic interpretation of Eq. 6 in Supporting Information. In particular, in our model, the whole group of dynein motors within a given 96-nm unit cell of an A tubule is represented by a single link that is permanently attached to the next B tubule in the next lower cross-section of the model (Fig. 1A).
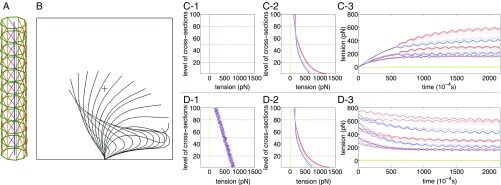
Fig. 1.
(A) Structure of the model cilium showing centerline (blue), peripheral doublet microtubules (green), and dynein links (red). (B) The beating cycle of a single model cilium in fluid. (C and D) Tensions in the passive 5-6 bridges (green) and dynein links (red on one side of the cilium and blue on the other side). C1 and D1 show initial tensions, which are zero in C1 and randomly chosen in D1. C2 and D2 show tensions at a selected time after the limit cycle has been reached. C3 and D3 show the development of tension over time in selected levels (20, 50, and 80 of 100 levels) of the model. In C3, the initial tensions are all zero, and the tensions remain the same as each other within any one level until about s, at which time the symmetry breaks and the ciliary beat begins. In D3, the initial tensions are random, and the beat begins immediately. Despite this transient difference, the eventual beat patterns are the same in the two cases (Movies S1 and S2).
Cilia in Fluid.
We model the fluid–structure interaction of cilia by the immersed boundary (IB) method (33), with the following equations of motion:
| [7] |
| [8] |
| [9] |
| [10] |
| [11] |
| [12] |
Eqs. 7 and 8 are the incompressible time-dependent Stokes equations with fluid velocity , pressure , and applied force per unit volume , which model the influence of the cilia on the fluid. Here, , which we take to be a rectangular box in with periodic boundary conditions, but we break the periodicity in the vertical direction in the manner discussed in Supporting Information. The term has little effect but is included to avoid a technical issue concerning the time-independent Stokes equation in periodic domains (Eqs. S68–S71). Inclusion of this term does not adversely affect the time step restriction for numerical stability, because our implementation is implicit (34) as described in Eqs. S55–S67. Eqs. 11 and 12 define the elastic energy of the model cilia. In these equations, denotes the collection of all of the positions of centerline nodes, any one of which is denoted . (Recall that other nodes of the model cilia have coordinates determined by those of the centerline nodes.) Similarly, denotes the collection of all of the active tensions, any one of which is denoted . The length of the corresponding link in the model is denoted to emphasize that this length is determined by the configuration of the centerline nodes as a consequence of our geometric constraints. In Eq. 11, includes all of the passive contributions to the elastic energy (i.e., the energy defined by Eq. 5 and also, the elastic energy of the 5-6 bridges), and the sum over defines the contributions of the active links. The energy of an active link at any given time is proportional to the length of that link, because the tension is a state variable, which has a particular value at any time , regardless of the length of the link at that time. Thus, the energy function at any particular time is that of a constant tension link. In Supporting Information, Eq. 6 is given a mechanistic interpretation in terms of the making and breaking of constant tension links. Eqs. 9 and 10 are interaction equations that describe the influence of the cilia on the fluid and that of the fluid on the cilia. In Eq. 9, is the gradient of the elastic energy with respect to the position of the point , and is the force applied by node of the model cilium to the surrounding fluid. The function is a regularized version of the Dirac delta function (Eqs. S51–S54). It defines the way in which the force is distributed over the neighborhood of the point . The parameter , which has units of length, determines the size of the region that receives force from any given node. We emphasize that this is a physical parameter of our model related to the physical radius of the cross-section of a cilium (35). In particular, the parameter should be held fixed as the numerical parameters of the model, like mesh width and time step, are refined. In Eq. 10, the velocity of centerline node is defined as a weighted average of the fluid velocity on its neighborhood. Note that the same function is used here as in Eq. 9. This ensures that
| [13] |
(i.e., that the power applied to the fluid by the cilium is correctly accounted for in the fluid equations).
Results
In this section, we report the results of two computer experiments. The first one involves a single model cilium immersed in fluid, and in the second one, we consider the fluid-mediated interaction of multiple cilia.
Single Cilium in Fluid.
We put the cilium in a rectangular box of fluid with periodic boundary conditions, but the periodicity in the direction is broken by a floor/ceiling as explained above. The dimensions of the box are , , and , and the length of the cilium is . The motion of the cilium is in the plane, with the power stroke in the negative direction. Because of the periodicity in the and directions, we can think of the model cilium as one member of an infinite carpet of cilia arranged in a rectangular array, but note that the members of this array are, by definition, synchronized with each other.
In this study, we compare two different initial conditions. In both of them, the initial configuration of the cilium is straight and vertical, but in the first case, the initial tensions of the dynein links are all zero, whereas in the second case, the initial tensions are randomly chosen (Fig. 1 C1 and D1).
Despite this difference in initial conditions, the long-term behavior is the same in both cases (except for phase). Both cilia settle into the same limit cycle oscillation, as shown in Fig. 1 C3 and D3. This limit cycle shows a realistic ciliary beat with clearly distinct power and recovery strokes (Fig. 1B). At early times, however, we see a clear and qualitative distinction between the behaviors of the two model cilia. In the first case, in which the initial tensions are all zero, the system has to break symmetry to move, and this takes some time to occur. Thus, the tensions build up gradually while remaining nearly equal to each other within any given level of the cilium. This is shown in Fig. 1C3 (up to s). During this early time, there is almost no motion of the cilium as a whole. Near s, the symmetry breaks, and the cilium starts to beat. In the second case (Fig. 1D3), there is no need to break symmetry, because the initial tensions are random, and the cilium quickly and smoothly settles into its limit cycle oscillation.
The comparison of these two cases illustrates clearly the self-organizing character of the beat of the model cilium, in which hundreds of dynein motors coordinate successfully without any explicit coordination mechanism.
Multiple Cilia in Fluid.
The computer experiment described in this subsection is similar to those of the previous subsection, but the dimensions of the fluid box are different (), and now, the box contains an array of equally spaced model cilia arranged in a diaplectic row (i.e., a row that runs orthogonal to the beat plane) along the axis of the domain. The distance between adjacent cilia in this row is . Because of the assumed periodicity in the and directions, we can think of this simulation as modeling an infinite carpet of cilia arranged in a rectangular array, just as we could in the previous case. Here, however, there is less enforced synchrony. We still have synchrony by definition among the cilia in every orthoplectic row (parallel to the axis and therefore, to the beat plane), but in a given diaplectic row, there are 16 independent model cilia, which may synchronize or not depending on their own internal dynamics and on their fluid-mediated interaction.
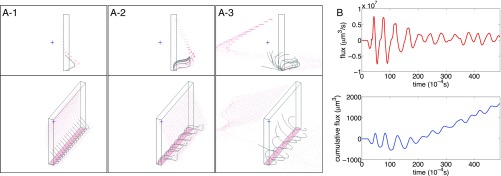
The initial conditions here are the same as those of the first case above: zero initial dynein tension with the cilia straight and vertical. Thus, we expect and find an initial pause after which the cilia start to beat, and we observe that their early beating is synchronized. After a few beats, however, the synchrony spontaneously breaks, and the different cilia adopt different phases.
This symmetry breaking turns out to have an important effect on the ability of the ciliary array to pump fluid. Before the symmetry breaking, the cilia are unable to exhibit a clear distinction between their power and recovery strokes (Fig. 2B). To understand this, note that the asymmetrical beating pattern that pumps fluid requires the tips of the cilia to move down toward the cell boundary to which the cilia are attached (which is a no-slip planar boundary in our simulation) during part of the beat cycle, so that the tips can be closer to the cell boundary during the recovery stroke than during the power stroke. This downward motion is inhibited by fluid incompressibility and viscosity when the cilia are close together and synchronized. Symmetry breaking alleviates this effect.
Fig. 2.
Symmetry breaking in a diaplectic row of cilia. (A) Configuration of cilia (black curved lines) at selected times from two points of view. Red dots are fluid markers, some of which mark the floor (which is also a ceiling of the periodic domain). Rectangular box shows one unit cell of the periodic computation. The cilia (black curved lines) are initially synchronized (A1). The symmetry starts to break in A2, and by the time shown in A3, the cilia have adopted multiple phases (Movie S3). (B) Flux of fluid (positive to the left) generated by the beating cilia. Upper (red curve) shows instantaneous flux, and Lower (black curve) shows cumulative flux. The upward trend in the cumulative flux begins only after the symmetry has broken and the cilia have adopted multiple phases.
Summary and Conclusions
We have introduced a phenomenological model of a motile cilium, in which ciliary beating is driven by actively generated dynein tensions governed by a postulated dynamical law. Under two simple geometric constraints motivated by the inextensibility of microtubules and the centering of the central pair as maintained by the radial spokes of the cilium, we show that the entire configuration of the cilium can be expressed in terms of the configuration of its centerline.
A significant feature of our model is that the hundreds of dynein motors within a single cilium coordinate their tensions spontaneously to produce the ciliary beat as an emergent limit cycle oscillation. To emphasize this, we have shown that the same ciliary beat emerges regardless of initial conditions, in particular starting from zero initial tensions or from random initial tensions of the dynein motors. In the former case, there is a delay before beating starts, during which the dynein links of the model develop tension synchronously and the cilium does not move. The symmetry then breaks suddenly, and the beat is initiated. In the latter case, with random initial tensions, there is no need for symmetry breaking and hence, no delay before the cilium starts to beat.
We have also studied the fluid–structure interaction of multiple cilia by the IB method. In particular, we have considered the interactions that occur within a diaplectic row. In this setting, we see spontaneous symmetry breaking, in which the cilia adopt multiple phases, despite being started in the same initial state. Only after the symmetry breaks are the cilia able to pump fluid.
Supplementary Material
Acknowledgments
We thank David McQueen for helpful advice concerning the computations in this paper and for providing the software that was used to visualize the results. J.H. was supported by the McCracken Fellowship and the Dean’s Dissertation Fellowship of the New York University Graduate School of Arts and Science.
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1712042115/-/DCSupplemental.
References
- 1.Miznuno N, Taschner M, Engel BD, Lorentzen E. Structural studies of ciliary components. J Mol Biol. 2012;422:163–180. doi: 10.1016/j.jmb.2012.05.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Sartori P, Geyer VF, Scholich A, Jülicher F, Howard J. Dynamic curvature regulation accounts for the symmetric and asymmetric beats of Chlamydomonas flagella. Elife. 2016;5:e13258. doi: 10.7554/eLife.13258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Dillon RH, Fauci LJ, Omoto C. Mathematical modeling of axoneme mechanics and fluid dynamics in ciliary and sperm motility. Dyn Contin Discrete Impuls Syst Ser A Math Anal. 2003;10:745–757. [Google Scholar]
- 4.Brokaw CJ. Bend propagation by a sliding filament model for flagella. J Exp Biol. 1971;55:289–304. doi: 10.1242/jeb.55.2.289. [DOI] [PubMed] [Google Scholar]
- 5.Brokaw CJ. Computer simulation of flagellar movement. Biophys J. 1972;12:546–586. doi: 10.1016/S0006-3495(72)86104-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Riedel-Kruse IH, Hilfinger A, Howard J, Jülicher F. How molecular motors shape the flagellar beat. HFSP J. 2007;1:192–208. doi: 10.2976/1.2773861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Hilfinger A, Jülicher F. The chirality of ciliary beats. Phys Biol. 2008;5:016003. doi: 10.1088/1478-3975/5/1/016003. [DOI] [PubMed] [Google Scholar]
- 8.Camalet S, Jülicher F. Generic aspects of axonemal beating. New J Phys. 2000;2:1–23. [Google Scholar]
- 9.Jülicher F, Prost J. Cooperative molecular motors. Phys Rev Lett. 1995;75:2618–2621. doi: 10.1103/PhysRevLett.75.2618. [DOI] [PubMed] [Google Scholar]
- 10.Lindemann CB. A model of flagellar and ciliary functioning which uses the forces transverse to the axoneme as the regulator of dynein activation. Cell Motil Cytoskeleton. 1994;29:141–154. doi: 10.1002/cm.970290206. [DOI] [PubMed] [Google Scholar]
- 11.Lindemann CB. A “geometric clutch” hypothesis to explain oscillations of the axoneme of cilia and flagella. J Theor Biol. 1994;168:175–189. [Google Scholar]
- 12.Gueron S, Levit-Gurevich K, Liron N, Blum JJ. Cilia internal mechanism and metachronal coordination as the result of hydrodynamical coupling. Proc Natl Acad Sci USA. 1997;94:6001–6006. doi: 10.1073/pnas.94.12.6001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Gueron S, Levit-Gurevich K. Computation of the internal forces in cilia: Application to ciliary motion, the effects of viscosity, and cilia interactions. Biophys J. 1998;74:1658–1676. doi: 10.1016/S0006-3495(98)77879-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Gueron S, Levit-Gurevich K. Energetic considerations of ciliary beating and the advantage of metachronal coordination. Proc Natl Acad Sci USA. 1999;96:12240–12245. doi: 10.1073/pnas.96.22.12240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Vilfan A, Jülicher F. Hydrodynamics flow patterns and synchronization of beating cilia. Phys Rev Lett. 2006;96:058102. doi: 10.1103/PhysRevLett.96.058102. [DOI] [PubMed] [Google Scholar]
- 16.Niedermayer T, Eckhardt B, Lenz P. Synchronization, phase locking, and metachronal wave formation in ciliary chains. Chaos. 2008;18:037128. doi: 10.1063/1.2956984. [DOI] [PubMed] [Google Scholar]
- 17.Reichert M, Stark H. Synchronization of rotating helices by hydrodynamic interactions. Eur Phys J E Soft Matter. 2005;17:493–500. doi: 10.1140/epje/i2004-10152-7. [DOI] [PubMed] [Google Scholar]
- 18.Kim MJ, Powers TR. Hydrodynamic interactions between rotating helices. Phys Rev E Stat Nonlin Soft Matter Phys. 2004;69:061910. doi: 10.1103/PhysRevE.69.061910. [DOI] [PubMed] [Google Scholar]
- 19.Uchida N, Golestanian R. Synchronization and collective dynamics in a carpet of microfluidic rotors. Phys Rev Lett. 2010;104:178103. doi: 10.1103/PhysRevLett.104.178103. [DOI] [PubMed] [Google Scholar]
- 20.Cosentino Lagomarsino M, Jona P, Bassetti B. Metachronal waves for deterministic switching two-state oscillators with hydrodynamic interaction. Phys Rev E Stat Nonlin Soft Matter Phys. 2003;68:021908. doi: 10.1103/PhysRevE.68.021908. [DOI] [PubMed] [Google Scholar]
- 21.Osterman N, Vilfan A. Finding the ciliary beating pattern with optimal efficiency. Proc Natl Acad Sci USA. 2011;108:15727–15732. doi: 10.1073/pnas.1107889108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Guirao B, Joanny J-F. Spontaneous creation of macroscopic flow and metachronal waves in an array of cilia. Biophys J. 2007;92:1900–1917. doi: 10.1529/biophysj.106.084897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Elgeti J, Gompper G. Emergence of metachronal waves in cilia arrays. Proc Natl Acad Sci USA. 2013;110:4470–4475. doi: 10.1073/pnas.1218869110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Yang X, Dillon RH, Fauci LJ. An integrative computational model of multiciliary beating. Bull Math Biol. 2008;70:1192–1215. doi: 10.1007/s11538-008-9296-3. [DOI] [PubMed] [Google Scholar]
- 25.Khaderi SN, den Toonder JMJ, Onck PR. Microfluidic propulsion by the metachronal beating of magnetic artificial cilia: A numerical analysis. J Fluid Mech. 2011;688:44–65. [Google Scholar]
- 26.Gauger EM, Downton MT, Stark H. Fluid transport at low Reynolds number with magnetically actuated artificial cilia. Eur Phys J E Soft Matter. 2009;28:231–242. doi: 10.1140/epje/i2008-10388-1. [DOI] [PubMed] [Google Scholar]
- 27.Knight-Jones EW. Relations between metachronism and the direction of ciliary beat in Metazoa. J Cell Sci. 1954;95:503–521. [Google Scholar]
- 28.Afzelius B. Electron microscopy of the sperm tail. J Biophys Biochem Cytol. 1959;5:269–278. doi: 10.1083/jcb.5.2.269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Lindemann CB, Lesich KA. Flagellar and ciliary beating: The proven and the possible. J Cell Sci. 2010;123:519–528. doi: 10.1242/jcs.051326. [DOI] [PubMed] [Google Scholar]
- 30.Han J. 2017. The spontaneous oscillation and fluid-structure interaction of cilia. PhD thesis (Courant Institute of Mathematical Sciences, New York University, New York)
- 31.Summers KE, Gibbons IR. Adenosine triphosphate-induced sliding of tubules in trypsin-treated flagella of sea-urchin sperm. Proc Natl Acad Sci USA. 1971;68:3092–3096. doi: 10.1073/pnas.68.12.3092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Geeves MA, Fedorov R, Manstein DJ. Molecular mechanism of actomyosin-based motility. Cell Mol Life Sci. 2005;62:1462–1477. doi: 10.1007/s00018-005-5015-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Peskin CS. The immersed boundary method. Acta Numer. 2002;11:479–517. [Google Scholar]
- 34.Mori Y, Peskin CS. Implicit second-order immersed boundary methods with boundary mass. Comput Methods Appl Mech Eng. 2008;197:2049–2067. [Google Scholar]
- 35.Lim S, Fernent A, Sheldon Wang X, Peskin CS. Dynamics of closed rod with twist and bend in fluid. SIAM J Sci Comput. 2008;31:273–302. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.