IndeCut evaluates performance of network motif discovery algorithms

Abstract

Motivation

Genomic networks represent a complex map of molecular interactions which are descriptive of the biological processes occurring in living cells. Identifying the small over-represented circuitry patterns in these networks helps generate hypotheses about the functional basis of such complex processes. Network motif discovery is a systematic way of achieving this goal. However, a reliable network motif discovery outcome requires generating random background networks which are the result of a uniform and independent graph sampling method. To date, there has been no method to numerically evaluate whether any network motif discovery algorithm performs as intended on realistically sized datasets—thus it was not possible to assess the validity of resulting network motifs.

Results

In this work, we present IndeCut, the first method to date that characterizes network motif finding algorithm performance in terms of uniform sampling on realistically sized networks. We demonstrate that it is critical to use IndeCut prior to running any network motif finder for two reasons. First, IndeCut indicates the number of samples needed for a tool to produce an outcome that is both reproducible and accurate. Second, IndeCut allows users to choose the tool that generates samples in the most independent fashion for their network of interest among many available options.

Availability and implementation

The open source software package is available at https://github.com/megrawlab/IndeCut.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Genomic networks represent a complex map of molecular interactions which are descriptive of the biological processes occurring in living cells (Gaudinier and Brady, 2016; Milo et al., 2002). Due to the size and complexity of these networks, it is often difficult to infer the physiological function of individual interactions or collections of interactions without additional detailed information about network structure. Because this type of experimentally supported prior information is usually sparse or unavailable, a systematic approach for identifying key sub-components and their functions within a biological system is essential for analysis. From this perspective, it has been shown that the functional essence of a complex genetic network within a cell can often be distilled by thinking of the network as a ‘circuit board’ composed of small, understandable components that work together to carry out higher-order processes (Alon, 2007; Barabasi and Oltvai, 2004; Mangan and Alon, 2003; Megraw et al., 2013; Milo et al., 2002; Ribeiro et al., 2009; Shen-Orr et al., 2002; Wang et al., 2015; Wong et al., 2011). Network motif discovery is a well-established statistical strategy for performing network analysis from this viewpoint. This strategy compares the frequency of observation of a sub-network within the larger original network to its frequencies in many randomized background networks in order to identify network motifs, which are defined as those sub-networks observed at a significantly higher frequency in the original network. In other words, a network motif is an over-represented sub-structure within a larger network.

Network motif discovery tools aid in generating specific testable hypotheses about the behavior and function of a genetic sub-circuit. For example, in the case of a gene regulatory network, a bi-stable switch coupled with a noise-damping circuit may be necessary to tune the expression of developmental transcription factors involved in body-plan patterning at a specific stage of development (Alon, 2007; Megraw et al., 2013; Tran et al., 2015); thus this circuit may appear as a motif in networks constructed from tissue samples in developing organisms. Although such hypotheses are valuable starting points for understanding the underlying mechanisms of a biological process through analysis of genomic networks, the laboratory validation of a predicted network motif is generally a costly and time-consuming endeavor. For example, validating a candidate regulatory sub-network containing a specific transcription factor, a microRNA and a protein coding gene would typically require a series of procedures such as electrophoresis mobility shift assays and generation of reporter constructs, involving months of labor and thousands of dollars in supplies. This highlights the need for accurate network motif discovery procedures in order to acquire a biologically meaningful outcome.

To characterize statistical significance of a given genomic network (here called the ‘original network’), network motif discovery algorithms generate random graphs (here called ‘background network generation’) while striving to satisfy two conditions. (i) Background networks should preserve a sensible set of biological assumptions constrained by the original network. For example, if the original network contains a node type (e.g. transcription factor) that can target itself as well as other genes in the original network, then this property can be preserved in the generated background networks. (ii) The background networks generated should provide a truly representative sample of all possible such networks. That is, for statistical purposes, the generation method should not favor the production of certain types of networks over others. While there are a variety of choices that a researcher may make about network property preservation, it is clearly crucial to generate an unbiased sample of background networks which preserve these properties—thus avoiding inaccuracy resulting from the background network generation procedure itself.

Computationally, the core component of background network generation is the sampling of a number of networks (for example, 1000 networks) from the set of all possible networks (e.g. 1 million networks) having in-degree and out-degree sequences identical to those of the original biological network. Networks are usually thought of as graphs, and this sampling process is known as ‘graph sampling.’ Ideally, graph sampling would be unnecessary; one would simply generate all possible graphs in the sample space, count the number of times a particular sub-graph of interest was observed, and then calculate an exact P-value by comparing this count to the number of times it was observed in the original network. A very small P-value would indicate significant over-representation, and thus a network motif. Unfortunately, for networks of realistic biological size—even a few hundred nodes and edges—the size of the sample space is enormous (over trillions of graphs). Furthermore, there is not even any known closed-form formula for computing just the number of graphs in the sample space. Thus, graph sampling is a practical necessity but presents a challenge in its own right, as one must sample in an unbiased manner from a set of unknown size. To date, no method has been given to estimate even the number of samples required in the background network generation process.

Despite a rich mathematical literature on the subject (Barabási and Albert, 1999; Bezáková et al., 2007; Chatterjee et al., 2011; Chen et al., 2005; Fosdick et al., 2016; Itzkovitz et al., 2003; King, 2004; Miklós et al., 2013; Milo et al., 2003), practical solutions to this problem remain elusive. Even so, several network motif discovery tools with different underlying graph sampling strategies are currently available (Grochow and Kellis, 2007; Kim et al., 2013; Thomas and Bonchev, 2010). Theoretical results that ensure uniformity have been obtained, but only when an arbitrarily large number of samples is allowed (Greenhill, 2015). Practical performance evaluation has been restricted to small ‘test graphs’ where samples spaces can be empirically enumerated by producing all possible graphs in the space. On such graphs, it has been shown that depending on graph topology, the same sampling strategy can have very different performance outcomes in terms of uniform and independent sampling (Megraw et al., 2013). For example, while d-regular graphs rarely pose a problem, small graphs with highly irregular or ‘uneven’ degree sequences frequently cause difficulty (Blitzstein and Diaconis, 2011; Greenhill, 2015; Megraw et al., 2013). This creates a concern for the accurate performance of network motif discovery algorithms on real biological networks, which often contain large source hubs (‘master regulators’) and/or target hubs (heavily regulated nodes) (Sorrells and Johnson, 2015; Winterbach et al., 2013).

To date, no mathematically sound yet computationally practical method is available in order to determine whether a graph sampling method samples uniformly and independently for a large or even moderately sized network of interest. However, relatively recent advances in the enumerative combinatorics literature (Alon and Naor, 2006; Barvinok, 2010) have opened an avenue for the development of solutions to this long-standing problem. In this study we present IndeCut, which assesses the degree of sampling uniformity and independence for network motif discovery algorithms. We also show how IndeCut can provide a way to understand the cause of performance variations among different graph sampling approaches.

2 Materials and methods

2.1 Definitions

A graph $G=(V,E)$ is a structure describing the relationships between elements in a vertex set V through a set of (directed) edges$(v_i,v_j)\in E$ where $v_i,v_j\in V$. In this work, we define a network as a two-layered or bipartite graph G containing m source nodes $\{S_1,\mathrm{..},S_m\}$ and n target nodes $\{T_1,\mathrm{..},T_n\}$ where a single directed edge connects a source node to a target node. The number of edges coming into a node is called its in-degree and the number of edges coming out from a node is called its out-degree. In a bipartite graph G, source nodes and target nodes have zero in-degrees and zero out-degrees, respectively. The structure or topology of a bipartite graph G is described by its in-degree and out-degree sequences.

A bipartite graph G can be represented as a binary matrix $A\in {\{0,1\}}^{m\times n}$. When $A_{i,j}=1$, there is a directed edge from S_i to T_j, and $A_{i,j}=0$ means there is no edge between them. The row sums R = ($r_1,\dots ,r_m$) and column sums C = ($c_1,\dots ,c_n$) of matrix A represent the out-degree and in-degree sequences of G, respectively. Collectively, they are referred to as the degree sequences of a graph. Hence, we have that $\sum _i{A}_{i,j}=C_j$ and $\sum _j{A}_{i,j}=R_i$.

2.2 How does IndeCut work?

This section provides a high-level summary of how IndeCut works, with more mathematical detail contained in Section 2.3 and Supplementary Material Section S1. An ideal graph sampling strategy would produce samples from the set of all possible graphs (the sample space) that are perfectly uniform and independent. In the case of perfect sampling, each sample would have a sample average that is identical to the true average (mean of all elements in the sample space). From this perspective, violation of uniformity and independence can be quantified by measuring how far the sample average is from the true average. Figure 1 provides an abstracted visualization of this concept illustrating how the distance between the sample average A and true average (centroid E) can be used to assess uniform and independent sampling.

Fig. 1.

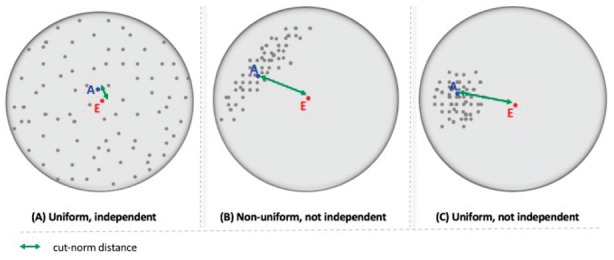
An illustrative view of graph sampling strategy outcomes in terms of uniformity and independence. Each gray circle represents a hypothetical sample space of a graph. Sampled graphs which are the outcome of a hypothetical graph sampling strategy are represented as gray dots inside the sample space of all graphs with the prescribed in and out-degrees. The point A represents the sample average and the point E represents the centroid or true average of sample space. The distance (here characterized with the cut norm) between A and E indicates the degree of uniformity and independence of a produced sample. The further away A is from E, the more confident one can be that points are not sampled uniformly and independently

Computing the exact centroid E by empirically enumerating all graphs in the sample space is generally prohibitive because such spaces are astronomically large (for example, the space of 3-regular bipartite graphs with 10 source nodes and 10 target nodes has more than 10²⁶ elements in it). Therefore instead of computing the exact centroid E, we use a related matrix, called the maximum entropy matrix and denoted by Z, which is known to be close to A in terms of its cut norm distance [Definition (Cut Norm) below] when the sampling regime is uniform and independent [this is proved in Theorem 3 of Barvinok (2010), see Supplementary Material Section S1 for a detailed statement]. Thus, an ideal sampling method will have a zero cut norm for Z − A, the matrix representing the difference between Z and A. Similarly, a cut norm bounded significantly away from zero indicates that sampling is either highly non-uniform, highly non-independent, or both. Unfortunately, computing the cut norm for matrices of realistic size is intractable given today’s computing hardware capability (MAX SNP-hard). We overcome this barrier by using the ideas of Alon and Naor (2006) to create an approximation algorithm that returns an interval in which the distance between Z and A is guaranteed to be contained. Comparing these intervals allows us to compare the uniformity and independence of graph sampling strategies.

In summary, IndeCut, performs the following tasks: the sample average matrix A and maximum entropy matrix Z are computed, and then a (typically small) interval is computed along with a guarantee that the cut norm lies in this interval. As a consequence of Theorem 3 in Barvinok (2010), if the cut norm is large (bounded far from 0), then we can be sure that the sampling was not uniform and independent.

2.3 Mathematical details of IndeCut

Let $\Sigma (R,C)$ be the set of all binary matrices with row-sums $R=(r_1,\dots ,r_m)\in {\mathbb{\mathbb{N}}}^{\mathrm{m}}$ and column-sums $C=(c_1,\dots ,c_n)\in {\mathbb{\mathbb{N}}}^{\mathrm{n}}$. Throughout, we only consider R and C such that for every choice of$1\le i\le m$ and $1\le j\le n$, there exist at least two matrices $L,M\in \Sigma (R,C)$ such that $L_{i,j}=0$ and $M_{i,j}=1$. This condition requires the space $\Sigma (R,C)$ to be reasonably large.

We now recount a pertinent definition from Barvinok (2010).

Definition 1 (Barvinok, 2010, Theorem 1) Let

$$F(\mathbf{x},\mathbf{y})=\left(\prod _{i=1}^m{x}_i^{-r_i}\right)\left(\prod _{j=1}^n{y}_j^{-c_j}\right)\left(\prod _{i,j}(1+x_i{y}_j)\right)$$

for $\mathbf{x}=(x_1,\dots ,x_m)$ and $\mathbf{y}=(y_1,\dots ,y_n)$, and let $\alpha (R,C)=\underset{\mathbf{x},\mathbf{y}>0}{\text{minimum}}\hspace{1em}F(\mathbf{x},\mathbf{y}).$

Taking the logarithm of $F(\mathbf{x},\mathbf{y})$ gives a convex function on ${ℝ}^{m\times n}$, so $\alpha (R,C)$ may be efficiently computed. This allows us to define the maximum entropy matrix:

Definition 2 (Maximum Entropy Matrix (Barvinok, 2010, Lemma 2)) Let${\mathbf{x}}^{*}$and${\mathbf{y}}^{*}$be the vectors that obtain optimality in the definition of$\alpha (R,C)$. Define$Z\in {ℝ}^{m\times n}$as

$$Z_{i,j}=\frac{{\mathbf{x}}_i^{*}{\mathbf{y}}_j^{*}}{1+{\mathbf{x}}_i^{*}{\mathbf{y}}_j^{*}}.$$ (1)

Ideally, we would not need Z and would have access to the true centroid $E_{i,j}=\frac{1}{|\Sigma (R,C\left)\right|}\sum _{M\in \Sigma (R,C)}{M}_{i,j}$ and this would be compared with the sample average of matrices returned by a motif finding algorithm. Unfortunately, the matrix E is computationally intractable to calculate and there appears to be no way to obtain tight estimates of its entries. In contrast, the matrix Z can be computed to arbitrary precision in an efficient fashion, and Theorem 3 of Barvinok (2010) states that the sample averages are close to Z in terms of the cut norm (see the Supplementary Material Section S1, Theorem 3 for a rigorous statement to this effect). We can thus leverage this result to use the cut norm and Z to test for violation of uniform/independent sampling.

Definition 3 Let $A\in {ℝ}^{m\times n}$ . The cut norm is defined by

$$\begin{array}{cccc}\left|\right|A|{|}_{\mathcal{C}}=\hfill & \underset{\begin{array}{l}I\subseteq \{1,\dots ,n\}\\ J\subseteq \{1,\dots ,m\}\end{array}}{\text{maximize}}\hfill & \hfill & \left|\sum _{i\in I,j\in J}{A}_{i,j}\right|\hfill \end{array}$$ (Cut Norm)

Let $\mathcal{A}$ represent a given motif finding algorithm (thought of as a binary matrix valued random variable). Let ${\left(A_i\right)}_{i=1}^N$ be N iterates of this algorithm and define

$$A_{\left(N\right)}=\frac{1}{N}\sum _{i=1}^N{A}_i.$$ (2)

If the sequence ${\left(A_i\right)}_{i\ge 1}$ is a realization of a sequence of independent and uniformly distributed random matrices, then Theorem 3 of Supplementary Material Section S1 implies that, with high probability, the norm $\left|\right|Z-A_{\left(N\right)}|{|}_{\mathcal{C}}$ is small. Arguing contrapositively, a large norm implies too few samples were taken (N is small) or else the sampling was not uniform or not independent. We can thus use $\left|\right|Z-A_{\left(N\right)}|{|}_{\mathcal{C}}$ as a measure of the non-uniformity/independence of a motif finding algorithm $\mathcal{A}$: For large N, if one algorithm outputs matrices whose average is closer in the cut norm to Z than that of another algorithm, then the latter algorithm samples the space $\Sigma (R,C)$ in a less uniform/independent fashion.

Unfortunately, computing the cut norm is MAX SNP-hard. However, it is possible to obtain easy to compute upper and lower bounds on the cut norm and the same logic as above applies when comparing these intervals. In particular, we bound the cut norm above by $\frac{1}{4}\left|\right|·|{|}_{\text{SDR}}$ and below by $\frac{1}{4}\left|\right|·|{|}_{\infty \mapsto 1}^{\text{est}}$ where $\left|\right|A|{|}_{\text{SDR}}=\underset{\left|\right|u_i|{|}_2=|\left|v_j\right|{|}_2=1}{\text{maximize}}\sum _{i,j}{A}_{i,j}(u_i·v_j)$ and $\left|\right|A|{|}_{\infty \mapsto 1}^{\text{est}}$ is the value returned by Algorithm 1 in the Supplementary Material. The Supplementary Material Section S1 contains the proof that these estimates hold. Hence, IndeCut returns an interval estimating the relative cut norm:

$$\text{IndeCut\hspace{0.17em}}(Z,\mathcal{A},N)=\left(\frac{\left|\right|Z-A_{\left(N\right)}|{|}_{\infty \mapsto 1}^{\text{est}}}{4\left|\right|Z|{|}_{\mathcal{C}}},\frac{\left|\right|Z-A_{\left(N\right)}|{|}_{\text{SDR}}}{4\left|\right|Z|{|}_{\mathcal{C}}}\right).$$

Note that $\left|\right|Z|{|}_{\mathcal{C}}$ is straightforward to calculate as all entries of Z are nonnegative.

Finally, while IndeCut uses bipartite graphs to evaluate motif finding algorithm performance, as long as the graphs under consideration can be partitioned into bipartite subgraphs (consisting of layers such as TF→TF, TF→miRNA, etc.) as is typically the case for genomic networks, IndeCut can evaluate the performance on each layer. Non-uniform sampling on any one such layer implies non-uniform sampling overall.

3 Results

As previously described, IndeCut uses the cut norm to assess how uniform and independent a network motif discovery algorithm’s sampling regime is (with larger cut norm values indicating non-uniform or non-independent sampling). In this section, we assess the performance of a selection of such network motif discovery algorithms.

3.1 IndeCut evaluates the performance of network motif discovery algorithms

Two different types of graphs are examined: (i) small graphs with topologies that typically occur in biological networks, and (ii) realistic graphs from the literature with a large number of nodes and edges. We selected four network motif discovery approaches from the recent literature: FANMOD (Fast Network Motif Detection) (Wernicke and Rasche, 2006), DIA-MCIS (Diaconis Monte Carlo Importance Sampling) (Fusco et al., 2007), WaRSwap (Weighted and Reverse Swap sampling) (Megraw et al., 2013) and CoMoFinder (Coregulatory network Motif Finder) (Liang et al., 2015). Each of these algorithms represents a fundamentally different strategy for network motif discovery background network generation. The Supplementary Method Section S2 provides a detailed description of each algorithm and its use in our analysis.

3.1.1 Small graph collection

Three classes of small graphs were created to consider three distinct topological properties: (i) ‘uneven’ (irregular) graphs containing ‘hub’ nodes with large in-degree or out-degree as compared to the other nodes in the graph. (ii) ‘even’ (regular) graphs with even (d-regular) or nearly even degree sequences. (iii) ‘hybrid’ combinations of even and uneven graphs. These graphs mimic the properties of large biological networks on a smaller scale and enable us to examine how IndeCut evaluates the sampling performance of different algorithms on specific graph structures. Supplementary Table S1 shows the degree sequence of each graph examined.

For the uneven class, we created six hub-containing graphs. The first graph (uniFanG1) is an example of a simple hub-containing bipartite graph in which each layer (source and target layers) has a single hub node. We created biFanG1 by duplicating/joining two uniFanG1 graphs. We repeated this process (attaching a uniFanG1 to an existing graph) to generate the ‘Fan’ series of graphs (see Supplementary Fig. S2). These graphs allow us to understand how IndeCut captures the performance of each algorithm on graphs with an increasingly large degree of unevenness, a topology type which is known to pose difficulties to many algorithms (Megraw et al., 2013). For the class of regular graphs, three d-regular and three near d-regular graphs with a different number of nodes and edges were created. Figure 2 and Supplementary Figures S5–S7 show the cut norm estimates for each graph and algorithm within the three classes of small graphs.

Fig. 2.

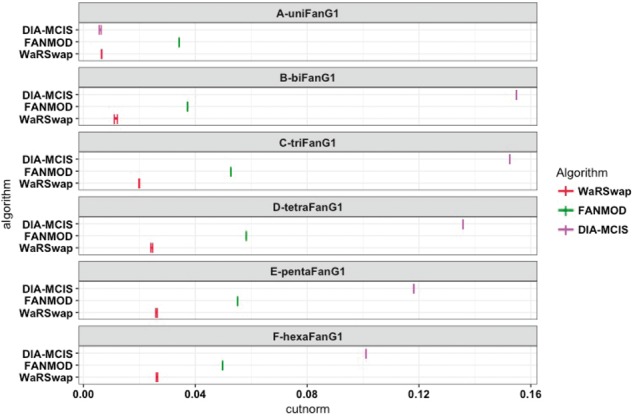
Small uneven graph sampling performance. For each small uneven graph and algorithm, 5000 graphs were generated and the cut norm estimates for each algorithm were computed using IndeCut. The vertical lines represent lower and upper bounds returned by the cut norm estimation with the true (NP-hard) value lying in this interval. A cut norm interval that is far from zero represents less uniform and independent sampling. With the exception of uniFanG1, the cut norm estimates for CoMoFinder were much larger than 0.16, and hence are not shown for ease of comparison (see Supplementary Table S1 and Fig. S3 for detailed results)

In Figure 2, as the degree of unevenness for graphs increases from A to F, one observes decreasing performance (in the case of FANMOD and WaRSwap) or comparatively poor performance (in the case of DIA-MCIS). This is in contrast to the performance on the nearly regular graphs evaluated in Supplementary Figures S4–S5, where most of the methods have comparably strong performance. On the ‘hybrid’ graphs, sampling performance varies widely among the methods. The hybrid graphs highlight the necessity of IndeCut in determining the performance of each algorithm, particularly when the degree sequence of a graph yields no intuition with regard to the anticipated performance of any given method (Supplementary Figs S6 and S7). This is in agreement with the previously observed trend that hub-containing graphs are highly problematic to many algorithms, whereas regular graphs are typically less troublesome (Megraw et al., 2013). We conclude that different graph topologies can produce vast performance differences when using the same algorithm and that there exists a wide variation in performance between algorithms.

3.1.2 Real-world biological networks

In order to understand how these topologies interact in real biological graphs of interest, we examined two published genomic networks with different degree sequences and scales. First, we analyzed a well studied, medium sized E-coli regulatory network ($\approx 400$ nodes and $\approx 600$ edges) with a mixed degree sequence and two node types: transcription factors (TFs) and protein-coding genes (Genes). This network has been used as a case study by several network motif discovery studies including those published in conjunction with the CoMoFinder and FANMOD programs (Liang et al., 2015; Wernicke and Rasche, 2006). Supplementary Figures S8 and S9 show the performance of each algorithm on the E-coli network.

Secondly, we analyzed a large human regulatory network ($\approx 15\hspace{0.17em}000$ nodes and $\approx 150\hspace{0.17em}000$ edges) containing three different node types (TFs, miRNAs and protein-coding genes) that was used as a case study in CoMoFinder’s publication (Liang et al., 2015). This network contains TFs that are ‘master regulators,’ and thus has large source hubs.

As mentioned in Section 2.3, IndeCut uses bipartite graphs as input, so networks were broken into component bipartite graphs (TF→TF, TF→Gene in the Ecoli network and TF→TF, TF→Gene, TF→miRNA, miRNA→TF and miRNA→Gene in the human network). Figure 3 depicts the resulting cut norm estimates for each algorithm on the large human network and demonstrates the variability among the considered algorithms. This highlights the importance of evaluating a network motif discovery algorithm on a network of interest, particularly when considering costly and time-consuming experimental validations.

Fig. 3.

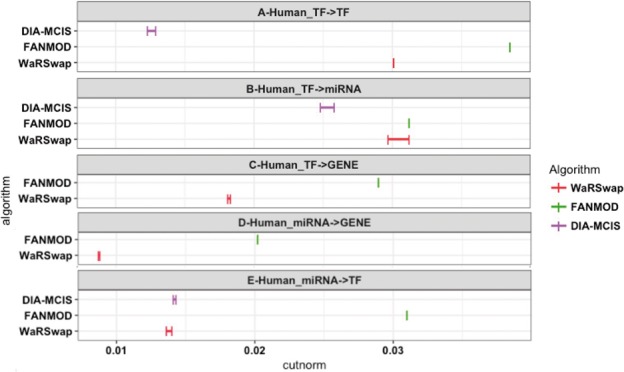
Human TF-miRNA-Gene network sampling performance. A total of 5000 graphs were generated by each algorithm and the cut norm estimates were computed using IndeCut. The vertical lines represent lower and upper bounds returned by the cut norm estimation with the true (NP-hard) value lying in this interval. A cut norm interval that is far from zero represents less uniform and independent sampling. The cut norm estimates for CoMoFinder were much larger than 0.04, and hence were removed for ease of comparison. In panels C and D, results for DIA-MCIS are absent since this algorithm does not operate on graphs with more than 2035 nodes (see Table S1 and Supplementary Fig. S10 for detailed results)

Supplementary Table S2 provides IndeCut's run time on each graph and algorithm, which on smaller networks is no more than 5 minutes but increases considerably as the network size increases.

3.2 IndeCut indicates the number of samples required to achieve reproducible results

For a very large network with hundreds or thousands of nodes and edges, running a network motif discovery program—even with the minimum number of samples recommended in the user manual—generally takes days to month. To date, there has been no method to provide any indication of the number of sample graphs necessary for a reproducible result, but we demonstrate that IndeCut can be used for this purpose.

In general, the larger the number of graphs sampled, the more accurately a program can ‘characterize’ the nature of the entire background network sample space, leading to better performance. Within a certain range of sample sizes, adding more graphs to a sample may result in a large performance increase. However, it is expected that beyond a certain sample size, performance increase per additional graph sampled will start to plateau (reach a point of diminishing returns). Here we use IndeCut to evaluate how the performance of a sampling algorithm improves as the number of graphs in a sample increases. We examine where a performance plateau occurred for each graph and algorithm. Furthermore, we provide an example from the literature that illustrates the advantage of using IndeCut in this fashion. Supplementary Methods Section S3 and Figures S13–S16 describe and depict the performance of all methods on the relevant graphs, and we concentrate on one method and graph here for illustrative purposes. Section S3 also provides some brief practical observations on estimating an appropriate number of iterations given a particular method and graph using a performance curve visualization software plugin to IndeCut.

We selected a published work (Roy et al., 2010) that reports network motifs in a Drosophila regulatory network. The authors have used FANMOD (Wernicke and Rasche, 2006) to detect enriched 3-node network motifs in 100 sampled networks. To examine the reproducibility of the reported motifs, we ran FANMOD on the original network 50 times, where for each time, 5000 samples were generated and the significance of 3-node subgraphs was computed for different subsets of samples (100, 200, 300, $\dots$, 5000 samples). Those 3-node subgraphs with P-value less than 0.01 and Z-score greater than 2.0 were considered in our analysis to be network motifs [thresholds were not reported in the original publication of Roy et al. (2010)]. The performance plot in Figure 4 shows that even for a moderately sized and relatively even graph such as the TF→TF layer extracted from the original network, at least $\approx 1000$ samples are required to reach a performance level that is close to the best possible performance of the algorithm. However, taking only 100 samples as in the original analysis of Roy et al. (2010) can lead to motifs being reported as significant due only to the relatively few number of graphs that were sampled. Indeed, in our results, motif5 in Figure 7B of Roy et al. (2010) (motif c shown here in Fig. 4) was never observed in any iteration. This is likely due to the relatively low number of iterations (100 iterations) that were used to run FANMOD in the original analysis. We also observed two significant network motifs at higher iterations, both of which were missed in the original work. Figure 4 shows that with more than 1000 samples these two motifs are detected consistently, but with a smaller number of samples they do not reliably appear.

Fig. 4.

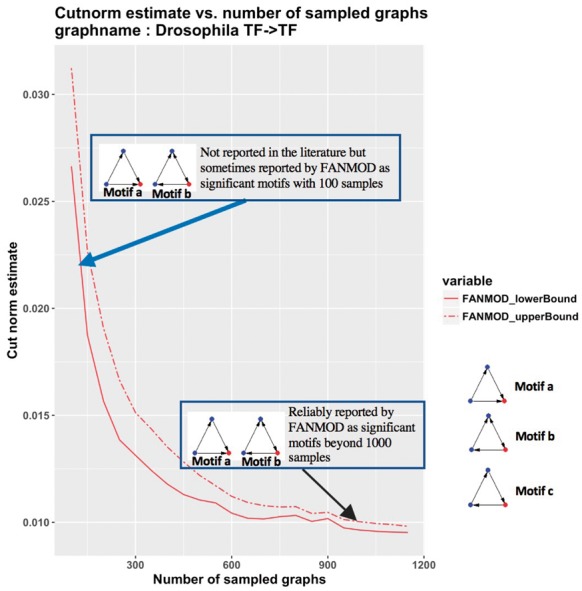
The relationship between cut norm estimates, number of samples and network motif outcome on Drosophila network. FANMOD was run on the Drosophila network (Roy et al., 2010) for 50 iterations. Motifs a and b are not reported in (Roy et al., 2010). These motifs were both found to be significant in a small proportion of trials at 100 sampled graphs (blue arrow). Motifs a and b are reliably detected beyond 1000 samples. Motif c was reported in (Roy et al., 2010) but was never observed as significant in any trials

It is completely understandable that given the long run-times required by many motif finding software implementations and no guidance on sufficient sampling, a relatively small number of samples was chosen by Roy et al. (2010). However, our results show the importance of making an informed choice—enabled now via IndeCut—for the number of background sample graphs required for each algorithm and input network. In large real-world biological networks, we observe that a ‘blanket policy’ of generating a fixed number of graphs may not achieve reasonable performance for a given algorithm and graph topology (for example, FANMOD in its user manual recommends $\approx 1000$ samples whereas Supplementary Figure S13 shows that at least 2000 samples are required to achieve reasonable performance in the considered case).

3.3 Explaining performance differences found by IndeCut

In this section, we aim to explain the performance differences among the motif finding algorithms that we found with IndeCut in Section 3.1. In particular, we use the performance outcomes from IndeCut to analyze why certain graph topologies have been historically challenging for some classes of algorithms. We show that in cases of graphs with uneven degree distributions (characteristic of biological networks), network motif discovery algorithms based on the graph randomization strategy known as ‘edge-switching’ are vulnerable to highly non-uniform and/or non-independent sampling. Thus, this strategy is prone to spurious results on these networks. We use the concept of an edge-switching graph (ESG) to show why this is the case. In essence, edge-switching algorithms produce a sampling bias by spending a majority of time sampling graphs that can be reached from the starting graph via a small number of edge-switches. Figure 5 depicts the construction of a 5-node ESG given a degree sequence of $R=C=\{2,1,1\}$, and Supplementary Method S5 details the construction of an ESG in general.

Fig. 5.

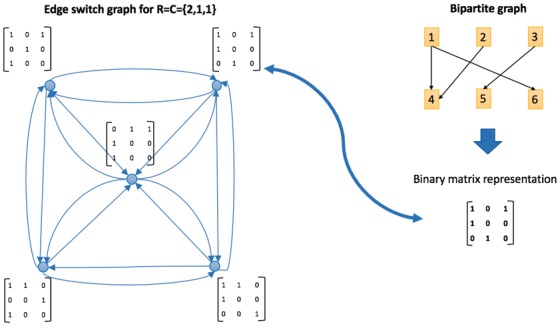
Constructing an ESG. An initial bipartite graph (top right) with degree sequence of $R=C=\{2,1,1\}$ produces a sample space containing five different graphs which are represented as nodes in the ESG (left). The zero-one matrices represent the edge configuration of each node. An edge connects two nodes (graphs) which can be converted to each other by performing one edge switch

Figure 6B shows an ESG constructed from an in-degree sequence of $R=\{2,1,1,2,1,1\}$ and an out-degree sequence of $C=\{2,1,1,2,1,1\}$. The sample space of this graph has 5400 elements. After running a graph clustering algorithm, 10 separate clusters were detected in the ESG. We executed each algorithm on the given degree sequence to produce 10 000 sample graphs per algorithm. We then calculated the number of times each algorithm returned a graph falling within each of the clusters (normalized by cluster size). This indicates how each of the examined algorithms samples its space with respect to these clusters (an equal number of graphs sampled within each cluster indicates a more uniform sampling method). Figure 6C–F shows ‘cluster-time’ diagrams, visualizing how much time each algorithm has spent in each cluster. In a cluster-time diagram, nodes represent clusters (in the ESG) and the size of each node represents the fraction of graphs sampled in the corresponding cluster compared to all graphs sampled (i.e. the total ‘time’ the algorithm spends in a given cluster). The larger a node appears, the more time that has been spent sampling from the associated cluster by a given algorithm. A method that samples uniformly will result in a cluster-time diagram with nearly equal node sizes. We take the fraction of time spent in each cluster and compute the entropy to summarize the ‘evenness’ of the sampling regime (larger numbers are better). The entropy value for each algorithm is noted above the corresponding cluster-time diagram in Figure 6C–F (see Supplementary Figs S11 and S12 for more examples).

Fig. 6.

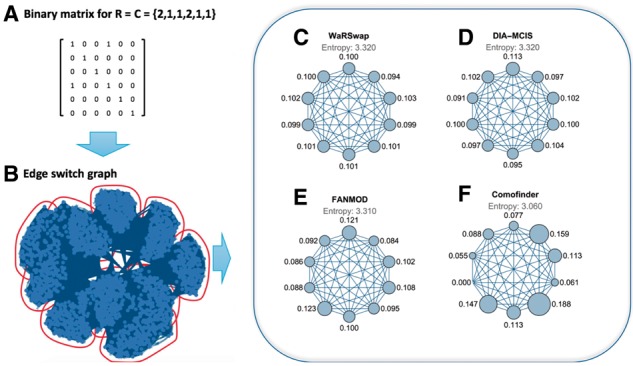
An example ESG for degree sequence $R=C=\{2,1,1,2,1,1\}$. (A) The 0-1 matrix of the initial graph. (B) ESG corresponding to this degree sequence (dots represent graphs in sample space) with detected clusters outlined. (C–F) Cluster-time diagrams for each examined algorithm; nodes represent clusters in the ESG with node size indicating the fraction of times a given algorithm sampled graphs in that cluster

Algorithms based on edge-switching, such as FANMOD and CoMoFinder, generally spend a substantially uneven amount of time in different clusters. Briefly, edge-switching algorithms start with the input graph (the original biological network) and then perform a series of edge-switching operations, resulting in one background graph in the sample. Each series of switching operations corresponds to a path in the ESG. In general, real biological networks have sample spaces in which some graphs in the space are ‘easy’ to reach (few switch operations required) from the initial input network, while others are more ‘difficult’ to reach in the sense that one must select a rare sequence of edge switches in order to reach these graphs.

FANMOD’s strategy selects sequences of edge-switching operations without any condition on the number of times that the same pair of edges can be selected for a switch. CoMoFinder also selects sequences of edge-switching operations, but disallows revisiting the same pair of edges. Effectively, when traversing a path in an ESG away from the initial graph using CoMoFinder’s strategy, the number of paths available to reach a destination graph from the current state is limited as compared to FANMOD’s strategy.

WaRSwap and DIA-MCIS do not use edge-switching, but rather generate each sample graph by placing edges between source and target nodes using a weighted sampling scheme (thus there is no direct relationship between a sampled background graph and the initial input graph in terms of a path in the ESG). In Figure 6, the size of the cluster nodes is nearly even for WaRSwap and DIA-MCIS, and the corresponding entropy values are higher as compared to FANMOD and CoMoFinder; hence the sampling is more uniform. However, there are performance differences between WaRSwap and DIA-MCIS on large hub-containing graphs (Fig. 2) that result from different weighted sampling strategies. In the case of certain highly uneven graphs, the static weighting strategy of DIA-MCIS appears to be susceptible to undersampling of rare graphs (those with few/no hub-hub connections). Overall, either DIA-MCIS or WaRSwap appear preferable to an edge-switching method on graphs containing uneven degree sequences.

4 Discussion

Over the last two decades, network motif discovery algorithms have been proposed that use several different underlying background graph sampling strategies. By all agreement in the literature, a uniform and independent background graph sampling method is fundamental for accurate network motif discovery due to subsequent statistical analysis. Evaluation of this condition on networks beyond tens of nodes was previously not possible because there was no proposed way to perform such an evaluation. Methods originating from the field of mathematical algorithms have been proposed that provably sample uniformly for nearly regular graphs (Bayati et al., 2010; Bezáková et al., 2007), or given an arbitrarily large number of samples (Greenhill, 2015). However, most biological networks of interest contain at least several hundred nodes and one or more ‘hubs’ (for example, a transcription factor that is a master regulator). Thus, these results guaranteeing uniformity are of limited practical value due to very large sample spaces (and subsequently infeasible computation times required) and/or uneven degree sequences seen in practice. Direct uniformity tests were performed in the study of some algorithms by empirically enumerating all the graphs in a very small sample space. This did lead to the understanding that graphs of uneven degree distribution posed problems for most algorithms. However, these small-graph tests left uncertainty as to how these algorithms would perform in the case of larger biological networks. As a result, despite the surge in popularity of network motif finding with the exciting findings reported by Milo et al. (2002) and by Alon (2007), reported laboratory validations of predicted network motif instances were subsequently rare to nonexistent in multicellular organisms. We posit that this may in part be due to unforeseen sampling biases and/or using a low number of samples leading to mis-reporting of motifs (as illustrated in Section 3.2).

In addition, we used IndeCut to show that the same motif finding algorithm can perform very differently depending on the graph topology. We also used IndeCut to show that algorithm performance plateaus often occur at a number of iterations exceeding the number of samples recommended by the program user manuals and/or default settings. Most importantly, IndeCut demonstrates that in cases of graphs with uneven degree distributions that are characteristic of biological networks, algorithms based on the sampling strategy known as ‘edge-switching’ are vulnerable to non-uniform and/or non-independent sampling. In this case, reported P-values may be inaccurate due to sampling biases. For such algorithms, we found that non-uniform sampling biases can be caused by frequently sampling graphs that can be reached in a small number of edge switches from the original graph.

While we observed that DIA-MCIS and WaRSwap (which are not based on edge-switching) maintained relatively strong performance overall, this varied based on the topology of the input graph. Hence, one can use IndeCut to ensure that, for a particular graph of interest, one selects the algorithm offering the most uniform sampling procedure.

Importantly, IndeCut demonstrates that the fast and popular algorithm FANMOD may not uniformly sample graphs when used with uneven degree sequences. This can lead to a bias in the motifs being reported and can confound laboratory validation of motifs. By providing the community with an informed choice of network motif discovery algorithm, we hope that IndeCut will re-ignite interest in laboratory validation of the fascinating hypotheses that result from network motif discovery outcomes.