Hierarchical Nearest-Neighbor Gaussian Process Models for Large Geostatistical Datasets

Abstract

Spatial process models for analyzing geostatistical data entail computations that become prohibitive as the number of spatial locations become large. This article develops a class of highly scalable nearest-neighbor Gaussian process (NNGP) models to provide fully model-based inference for large geostatistical datasets. We establish that the NNGP is a well-defined spatial process providing legitimate finite-dimensional Gaussian densities with sparse precision matrices. We embed the NNGP as a sparsity-inducing prior within a rich hierarchical modeling framework and outline how computationally efficient Markov chain Monte Carlo (MCMC) algorithms can be executed without storing or decomposing large matrices. The floating point operations (flops) per iteration of this algorithm is linear in the number of spatial locations, thereby rendering substantial scalability. We illustrate the computational and inferential benefits of the NNGP over competing methods using simulation studies and also analyze forest biomass from a massive U.S. Forest Inventory dataset at a scale that precludes alternative dimension-reducing methods. Supplementary materials for this article are available online.

1. Introduction

With the growing capabilities of Geographical Information Systems (GIS) and user-friendly software, statisticians today routinely encounter geographically referenced datasets containing a large number of irregularly located observations on multiple variables. This has, in turn, fueled considerable interest in statistical modeling for location-referenced spatial data; see, for example, the books by Stein (1999), Moller and Waagepetersen (2003), Schabenberger and Gotway (2004), and Cressie and Wikle (2011), and Banerjee, Carlin, and Gelfand (2014) for a variety of methods and applications. Spatial process models introduce spatial dependence between observations using an underlying random field, {w(s) : s ∈ 𝒟}, over a region of interest 𝒟, which is endowed with a probability law that specifies the joint distribution for any finite set of random variables. For example, a zero-centered Gaussian process ensures that w = (w(s₁), w(s₂) …, w(s_n))′ ~ N(0, C(θ)), where C(θ) is a family of covariance matrices, indexed by an unknown set of parameters θ. Such processes offer a rich modeling framework and are being widely deployed to help researchers comprehend complex spatial phenomena in the sciences. However, model fitting usually involves the inverse and determinant of C(θ), which typically require ~ n³ floating point operations (flops) and storage of the order of n². These become prohibitive when n is large and C(θ) has no exploitable structure.

Broadly speaking, modeling large spatial datasets proceeds from either exploiting “low-rank” models or using sparsity. The former attempts to construct spatial processes on a lower-dimensional subspace (see, e.g., Higdon 2001; Kammann and Wand 2003; Rasmussen and Williams 2005; Stein 2007, 2008; Banerjee et al. 2008; Crainiceanu et al. 2008; Cressie and Johannesson 2008; Finley, Banerjee, and McRoberts 2009) by regressing the original (parent) process on its realizations over a smaller set of r ≪ n locations (“knots” or “centers”). The algorithmic cost for model fitting typically decreases from O(n³) to O(nr² + r³) ≈ O(nr²) flops since n ≫ r. However, when n is large, empirical investigations suggest that r must be fairly large to adequately approximate the parent process and the nr² flops become exorbitant (see Section 5.1). Furthermore, low-rank models perform poorly when neighboring observations are strongly correlated and the spatial signal dominates the noise (Stein 2014). Although bias-adjusted low-rank models tend to perform better (Finley, Banerjee, and McRoberts 2009; Banerjee et al. 2010; Sang and Huang 2012), they increase the computational burden.

Sparse methods include covariance tapering (see, e.g., Furrer, Genton, and Nychka 2006; Kaufman, Scheverish, and Nychka 2008; Du, Zhang, and Mandrekar 2009; Shaby and Ruppert 2012), which introduces sparsity in C(θ) using compactly supported covariance functions. This is effective for parameter estimation and interpolation of the response (“kriging”), but it has not been fully developed or explored for more general inference on residual or latent processes. Introducing sparsity in C(θ)⁻¹ is prevalent in approximating Gaussian process likelihoods using Markov random fields (e.g., Rue and Held 2005), products of lower-dimensional conditional distributions (Vecchia 1988, 1992; Stein, Chi, and Welty 2004), or composite likelihoods (e.g., Bevilacqua and Gaetan 2014; Eidsvik et al. 2014). However, unlike low-rank processes, these do not, necessarily, extend to new random variables at arbitrary locations. There may not be a corresponding process, which restricts inference to the estimation of spatial covariance parameters. Spatial prediction (“kriging”) at arbitrary locations proceeds by imputing estimates into an interpolator derived from a different process model. This may not reflect accurate estimates of predictive uncertainty and is undesirable.

Our intended inferential contribution is to offer substantial scalability for fully process-based inference on underlying, perhaps completely unobserved, spatial processes. Moving from finite-dimensional sparse likelihoods to sparsity-inducing spatial processes can be complicated. We first introduce sparsity in finite-dimensional probability models using specified neighbor sets constructed from directed acyclic graphs. We use these sets to extend these finite-dimensional models to a valid spatial process over uncountable sets. We call this process a nearest-neighbor Gaussian process (NNGP). Its finite-dimensional realizations have sparse precision matrices available in closed form. While sparsity has been effectively exploited by Vecchia (1988), Stein, Chi, and Welty (2004), Emory (2009), Gramacy and Apley (2014), Gramacy, Niemi, and Weiss (2014), and Stroud, Stein, and Lysen (2014) for approximating expensive likelihoods cheaply, a fully process-based modeling and inferential framework has, hitherto, proven elusive. The NNGP fills this gap and enriches the inferential capabilities of existing methods by subsuming estimation of model parameters, prediction of outcomes, and interpolation of underlying processes into one highly scalable unifying framework.

To demonstrate its full inferential capabilities, we deploy the NNGP as a sparsity-inducing prior for spatial processes in a Bayesian framework. Unlike low-rank processes, the NNGP always specifies nondegenerate finite dimensional distributions making it a legitimate proper prior for random fields and is applicable to any class of distributions that support a spatial stochastic process. It can, therefore, model an underlying process that is never actually observed. The modeling provides structured dependence for random effects, for example, intercepts or coefficients, at a second stage of specification where the first stage need not be Gaussian. We cast a multivariate NNGP within a versatile spatially varying regression framework (Gelfand et al. 2003; Banerjee et al. 2008) and conveniently obtain entire posteriors for all model parameters as well as for the spatial processes at both observed and unobserved locations. Using a forestry example, we show how the NNGP delivers process-based inference for spatially varying regression models at a scale where even low-rank processes, let alone full Gaussian processes, are unimplementable even in high-performance computing environments.

Here is a brief outline. Section 2 formulates the NNGP using multivariate Gaussian processes. Section 3 outlines Bayesian estimation and prediction within a very flexible hierarchical modeling setup. Section 4 discusses alternative NNGP models and algorithms. Section 5 presents simulation studies to highlight the inferential benefits of the NNGP and also analyzes forest biomass from a massive USDA dataset. Finally, Section 6 concludes the article with a brief summary and pointers toward future work.

2. Nearest-Neighbor Gaussian Process

2.1 Gaussian Density on Sparse Directed Acyclic Graphs

We will consider a q-variate spatial process over ℜ^d. Let w(s) ~ GP(0, C(·, · | θ)) denote a zero-centered q-variate Gaussian process, where w(s) ∈ ℜ^q for all s ∈ 𝒟 ⊆ ℜ^d. The process is completely specified by a valid cross-covariance function C(·, · | θ), which maps a pair of locations s and t in 𝒟 × 𝒟 into a q × q real-valued matrix C(s, t) with entries cov{w_i(s), w_j(t)}. Here, θ denotes the parameters associated with the cross-covariance function. Let 𝒮 = {s₁, s₂, …, s_k} be a fixed collection of distinct locations in 𝒟, which we call the reference set. So, w_𝒮 ~ N(0, C_𝒮(θ)), where w_𝒮 = (w(s₁)′, w(s₂)′, …, w(s_k)′)′ and C_𝒮(θ) is a positive definite qk × qk block matrix with C(s_i, s_j) as its blocks. Henceforth, we write C_𝒮(θ) as C_𝒮, the dependence on θ being implicit, with similar notation for all spatial covariance matrices.

The reference set 𝒮 need not coincide with or be a part of the observed locations, so k need not equal n, although we later show that the observed locations are a convenient practical choice for 𝒮. When k is large, parameter estimation becomes computationally cumbersome, perhaps even unfeasible, because it entails the inverse and determinant of C_𝒮. Here, we benefit from expressing the joint density of w_𝒮 as the product of conditional densities, that is,

$$p({\mathbf{w}}_{\mathcal{S}})=p(\mathbf{w}({\mathbf{s}}_1))p(\mathbf{w}({\mathbf{s}}_2)\mid \mathbf{w}({\mathbf{s}}_1))\dots p(\mathbf{w}({\mathbf{s}}_k)\mid \mathbf{w}({\mathbf{s}}_{k-1}),\dots ,\mathbf{w}({\mathbf{s}}_1)),$$ (1)

and replacing the larger conditioning sets on the right-hand side of (1) with smaller, carefully chosen, conditioning sets of size at most m, where m ≪ k (see, e.g., Vecchia 1988; Stein, Chi, and Welty 2004; Gramacy and Apley 2014; Gramacy, Niemi, and Weiss 2014). So, for every s_i ∈ 𝒮, a smaller conditioning set N(s_i) ⊂ 𝒮 \ {s_i} is used to construct

$$\stackrel{\sim }{p}({\mathbf{w}}_{\mathcal{S}})=\prod _{i=1}^{k}p(\mathbf{w}({\mathbf{s}}_i)\mid {\mathbf{w}}_{N({\mathbf{s}}_i)}),$$ (2)

where w_N(si) is the vector formed by stacking the realizations of w(s) over N(s_i).

Let N_𝒮 = {N(s_i); i = 1, 2, …, k} be the collection of all conditioning sets over 𝒮. We can view the pair {𝒮, N_𝒮} as a directed graph 𝒢 with 𝒮 = {s₁, s₂, …, s_k} being the set of nodes and N_𝒮 the set of directed edges. For every two nodes s_i and s_j, we say s_j is a directed neighbor of s_i if there is a directed edge from s_i to s_j. So, N(s_i) denotes the set of directed neighbors of s_i and is, henceforth, referred to as the “neighbor set” for s_i. A “directed cycle” in a directed graph is a chain of nodes s_i1, s_i2, …, s_ib such that s_i1 = s_ib and there is a directed edge between s_ij and s_ij+1 for every j = 1, 2, …, b − 1. A directed graph with no directed cycles is known as a “directed acyclic graph.”

If 𝒢 is a directed acyclic graph, then p̃(w_𝒮), as defined above, is a proper multivariate joint density (see online Appendix A1 or Lauritzen (1996) for a similar result). Starting from a joint multivariate density p(w_𝒮), we derive a new density p̃(w_𝒮) using a directed acyclic graph 𝒢. While this holds for any original density p(w_𝒮), it is especially useful in our context, where p(w_𝒮) is a multivariate Gaussian density and 𝒢 is sufficiently sparse. To be precise, let C_N(si) be the covariance matrix of w_N(si) and let C_siN(si) be the q × mq cross-covariance matrix between the random vectors w(s_i) and w_N(si). Standard distribution theory reveals

$$\stackrel{\sim }{p}({\mathbf{w}}_{\mathcal{S}})=\prod _{i=1}^{k}N(\mathbf{w}({\mathbf{s}}_i)\mid {\mathbf{B}}_{{\mathbf{s}}_i}{\mathbf{w}}_{N({\mathbf{s}}_i)},{\mathbf{F}}_{{\mathbf{s}}_i}),$$ (3)

where ${\mathbf{B}}_{{\mathbf{s}}_i}={\mathbf{C}}_{{\mathbf{s}}_i,N({\mathbf{s}}_i)}{\mathbf{C}}_{N({\mathbf{s}}_i)}^{-1}$ and ${\mathbf{F}}_{{\mathbf{s}}_i}=\mathbf{C}({\mathbf{s}}_i,{\mathbf{s}}_i)-{\mathbf{C}}_{{\mathbf{s}}_i,N({\mathbf{s}}_i)}{\mathbf{C}}_{N({\mathbf{s}}_i)}^{-1}{\mathbf{C}}_{N({\mathbf{s}}_i),{\mathbf{s}}_i}$. Appendix A2 (available online) shows that p̃(w_𝒮) in (3) is a multivariate Gaussian density with covariance matrix C̃_𝒮, which, obviously, is different from C_𝒮. Furthermore, if N(s_i) has at most m members for each s_i in 𝒮, where m ≪ k, then ${\stackrel{\sim }{\mathbf{C}}}_{\mathcal{S}}^{-1}$ is sparse with at most km(m + 1)q²/2 nonzero entries. Thus, for a very general class of neighboring sets, p̃(w_𝒮) defined in (2) is the joint density of a multivariate Gaussian distribution with a sparse precision matrix.

Turning to the neighbor sets, choosing N(s_i) to be any subset of {s₁, s₂, …, s_i−1} ensures an acyclic 𝒢 and, hence, a valid probability density in (3). Several special cases exist in likelihood approximation contexts. For example, Vecchia (1988) and Stroud, Stein, and Lysen (2014) specified N(s_i) to be the m nearest neighbors of s_i among s₁, s₂, …, s_i−1 with respect to Euclidean distance. Stein, Chi, and Welty (2004) considered nearest as well as farthest neighbors from {s₁, s₂, …, s_i−1}. Gramacy and Apley (2014) offered greater flexibility in choosing N(s_i), but may require several approximations to be efficient.

All of the above choices depend upon an ordering of the locations. Spatial locations are not ordered naturally, so one imposes order by, for example, ordering on one of the coordinates. Of course, any other function of the coordinates can be used to impose order. However, the aforementioned authors have cogently demonstrated that the choice of the ordering has no discernible impact on the approximation of (1) by (3). Our own simulation experiments (see Appendix A5, available online) concur with these findings; inference based upon p̃(w_𝒮) is extremely robust to the ordering of the locations. This is not entirely surprising. Clearly, whatever order we choose in (1), p(w_𝒮) produces the full joint density. Note that we reduce (1) to (2) based upon neighbor sets constructed with respect to the specific ordering in (1). A different ordering in (1) will produce a different set of neighbors for (2). Since p̃(w_𝒮) ultimately relies upon the information borrowed from the neighbors, its effectiveness is often determined by the number of neighbors we specify and not the specific ordering.

In the following section, we will extend the density p̃(w_𝒮) to a legitimate spatial process. We remark that our subsequent development holds true for any choice of N(s_i) that ensures an acyclic 𝒢. In general, identifying a “best subset” of m locations for obtaining optimal predictions for s_i is a nonconvex optimization problem, which is difficult to implement and defeats our purpose of using smaller conditioning sets to ease computations. Nevertheless, we have found Vecchia’s choice of m-nearest neighbors from {s₁, s₂, …, s_i−1} to be simple and to perform extremely well for a wide range of simulation experiments. In what ensues, this will be our choice for N(s_i) and the corresponding density p̃(w_𝒮) will be referred to as the “nearest neighbor” density of w_𝒮.

2.2 Extension to a Gaussian Process

Let u be any location in 𝒟 outside 𝒮. Consistent with the definition of N(s_i), let N(u) be the set of m-nearest neighbors of u in 𝒮. Hence, for any finite set 𝒰 = {u₁, u₂, …, u_r} such that 𝒮 ∩ 𝒰 is empty, we define the nearest neighbor density of w_𝒰 conditional on w_𝒮 as

$$\stackrel{\sim }{p}({\mathbf{w}}_{\mathcal{U}}\mid {\mathbf{w}}_{\mathcal{S}})=\prod _{i=1}^{r}p(\mathbf{w}({\mathbf{u}}_i)\mid {\mathbf{w}}_{N({\mathbf{u}}_i)}).$$ (4)

This conditional density is akin to (2) except that all the neighbor sets are subsets of 𝒮. This ensures a proper conditional density. Indeed (2) and (4) are sufficient to describe the joint density of any finite set over the domain 𝒟. More precisely, if 𝒱 = {v₁, v₂, …, v_n} is any finite subset in 𝒟, then, using (4) we obtain the density of w_𝒱 as

$$\begin{gathered} \stackrel{\sim }{p}({\mathbf{w}}_{\mathcal{V}})=\int \stackrel{\sim }{p}({\mathbf{w}}_{\mathcal{U}}\mid {\mathbf{w}}_{\mathcal{S}})\stackrel{\sim }{p}({\mathbf{w}}_{\mathcal{S}})\prod _{\{{\mathbf{s}}_i\in \mathcal{S}\backslash \mathcal{V}\}}d(\mathbf{w}({\mathbf{s}}_i)) \\ \text{where}\mathcal{U}=\mathcal{V}\backslash \mathcal{S}. \end{gathered}$$ (5)

If 𝒰 is empty, then (4) implies that p̃(w_𝒰 | w_𝒮) = 1 in (5). If 𝒮 \ 𝒱 is empty, then the integration in (5) is not needed.

These probability densities, defined on finite topologies, conform to Kolmogorov’s consistency criteria and, hence, correspond to a valid spatial process over 𝒟 (see Appendix A3, available online). So, given any original (parent) spatial process and any fixed reference set 𝒮, we can construct a new process over the domain 𝒟 using a collection of neighbor sets in 𝒮. We refer to this process as the “nearest neighbor process” derived from the original parent process. If the parent process is GP(0, C(·, · | θ)), then

$$\stackrel{\sim }{p}({\mathbf{w}}_{\mathcal{U}}\mid {\mathbf{w}}_{\mathcal{S}})=\prod _{i=1}^{r}N(\mathbf{w}({\mathbf{u}}_i)\mid {\mathbf{B}}_{{\mathbf{u}}_i}{\mathbf{w}}_{N({\mathbf{u}}_i)},{\mathbf{F}}_{{\mathbf{u}}_i})=N({\mathbf{B}}_{\mathcal{U}}{\mathbf{w}}_{\mathcal{S}},{\mathbf{F}}_{\mathcal{U}})$$ (6)

for any finite set 𝒰 = {u₁, u₂, …, u_r} in 𝒟 outside 𝒮, where B_ui and F_ui are defined analogous to (3) based on the neighbor sets N(u_i), F_𝒰 = diag(F_u1, F_u2, …, F_ur), and B_𝒰 is a sparse nq × kq matrix with each row having at most mq nonzero entries (see Appendix A4, available online).

For any finite set 𝒱 in 𝒟, p̃(w_𝒱) is the density of the realizations of a Gaussian process over 𝒱 with cross-covariance function

$$\stackrel{\sim }{\mathbf{C}}({\mathbf{v}}_1,{\mathbf{v}}_2;\mathit{\theta })=\{\begin{array}{l}{\stackrel{\sim }{\mathbf{C}}}_{{\mathbf{s}}_i,{\mathbf{s}}_j},\text{if}{\mathbf{v}}_1={\mathbf{s}}_i\text{and}{\mathbf{v}}_2={\mathbf{s}}_j\text{are}\text{both}\text{in}\mathcal{S},\hfill \\ {\mathbf{B}}_{{\mathbf{v}}_1}{\stackrel{\sim }{\mathbf{C}}}_{N({\mathbf{v}}_1),{\mathbf{s}}_j}\text{if}{\mathbf{v}}_1\notin \mathcal{S}\text{and}{\mathbf{v}}_2={\mathbf{s}}_j\in \mathcal{S},\hfill \\ {\mathbf{B}}_{{\mathbf{v}}_1}{\stackrel{\sim }{\mathbf{C}}}_{N({\mathbf{v}}_1),N({\mathbf{v}}_2)}{\mathbf{B}}_{{\mathbf{v}}_2}^{\prime }+{\delta }_{({\mathbf{v}}_1={\mathbf{v}}_2)}{\mathbf{F}}_{{\mathbf{v}}_1},\text{if}{\mathbf{v}}_1\text{and}{\mathbf{v}}_2\text{are}\text{noth}\text{in}\mathcal{S}\hfill \end{array}$$ (7)

where v₁ and v₂ are any two locations in 𝒟, C̃_A,B denotes submatrices of C̃_𝒮 indexed by the locations in the sets A and B, and δ_(v1=v2) is the Kronecker delta. Appendix A4 (available online) also shows that C̃(v₁, v₂ | θ) is continuous for all pairs (v₁, v₂) outside a set of Lebesgue measure zero.

This completes the construction of a well-defined nearest neighbor Gaussian process, NNGP(0, C̃(·, · | θ)), derived from a parent Gaussian process, GP(0, C(·, · | θ)). In the NNGP, the size of 𝒮, that is, k, can be as large, or even larger than the size of the dataset. The reduction in computational complexity is achieved through sparsity of the NNGP precision matrices. Unlike low-rank processes, the NNGP is not a degenerate process. It is a proper, sparsity-inducing Gaussian process, immediately available as a prior in hierarchical modeling, and, as we show in the next section, delivers massive computational benefits.

3. Bayesian Estimation and Implementation

3.1 A Hierarchical Model

Consider a vector of l dependent variables, say y(t), at location t ∈ 𝒟 ⊆ ℜ^d in a spatially varying regression model,

$$\mathbf{y}(\mathbf{t})=\mathbf{X}{(\mathbf{t})}^{\prime }\mathit{\beta }+\mathbf{Z}{(\mathbf{t})}^{\prime }\mathbf{w}(\mathbf{t})+\mathit{\epsilon }(\mathbf{t}),$$ (8)

where X(t)′ is the l × p matrix of fixed spatially referenced predictors, w(t) is a q × 1 spatial process forming the coefficients of the l × q fixed design matrix Z(t)′, and $\mathit{\epsilon }(\mathbf{t})\stackrel{\mathit{iid}}{\sim }N(\mathbf{0},\mathbf{D})$ is an l × 1 white-noise process capturing measurement error or micro-scale variability with dispersion matrix D, which we assume is diagonal with entries ${\tau }_j^2$, j = 1, 2, …, l. The matrix X(t)′ is block diagonal with $p={\sum }_{i=1}^l{p}_i$, where the 1 × p_i vector x_i(t)′, including perhaps an intercept, is the ith block for each i = 1, 2, …, l. The model in (8) subsumes several specific spatial models. For instance, letting q = l and Z(t)′ = I_l×l leads to a multivariate spatial regression model, where w(t) acts as a spatially varying intercept. On the other hand, we could envision all coefficients to be spatially varying and set q = p with Z(t)′ = X(t)′.

For scalability, instead of a customary Gaussian process prior for w(t) in (8), we assume w(t) ~ NNGP(0, C̃(·, · | θ)) derived from the parent GP(0, C(·, · | θ)). Any valid isotropic cross-covariance function (see, e.g., Gelfand and Banerjee 2010) can be used to construct C(·, · | θ). To elucidate, let 𝒯 = {t₁, t₂, …, t_n} be the set of locations where the outcomes and predictors have been observed. This set may, but need not, intersect with the reference set 𝒮 = {s₁, s₂, …, s_k} for the NNGP. Without loss of generality, we split up 𝒯 into 𝒮^* and 𝒰, where 𝒮^* = 𝒮 ∩ 𝒯 = {s_i1, s_i2, …, s_ir} with s_ij = t_j for j = 1, 2, …, r and 𝒰 = 𝒯 \ 𝒮 = {t_r+1, t_r+2, …, t_n}. Since 𝒮 ∪ 𝒯 = 𝒮 ∪ 𝒰, we can completely specify the realizations of the NNGP in terms of the realizations of the parent process over 𝒮 and 𝒰, hierarchically, as w_𝒰 | w_𝒮 ~ N(B_𝒰w_𝒮, F_𝒰) and w_𝒮 ~ N(0, C̃_𝒮). For a full Bayesian specification, we further specify prior distributions on β, θ, and the ${\tau }_j^2$’s. For example, with customary prior specifications, we obtain the joint distribution

$$p(\mathit{\theta })\times \prod _{j=1}^{l}IG({\tau }_j^2\mid a_{{\tau }_j},b_{{\tau }_j})\times N(\mathit{\beta }\mid {\mathit{\mu }}_{\beta },{\mathbf{V}}_{\beta })\times N({\mathbf{w}}_{\mathcal{U}}\mid {\mathbf{B}}_{\mathcal{U}}{\mathbf{w}}_{\mathcal{S}},{\mathbf{F}}_{\mathcal{U}})\times N({\mathbf{w}}_{\mathcal{S}}\mid \mathbf{0},{\stackrel{\sim }{\mathbf{C}}}_{\mathcal{S}})\times \prod _{i=1}^{n}N(\mathbf{y}({\mathbf{t}}_i)\mid \mathbf{X}{({\mathbf{t}}_i)}^{\prime }\mathit{\beta }+\mathbf{Z}{({\mathbf{t}}_i)}^{\prime }\mathbf{w}({\mathbf{t}}_i),\mathbf{D}),$$ (9)

where p(θ) is the prior on θ and $IG({\tau }_j^2\mid a_{{\tau }_j},b_{{\tau }_j})$ denotes the inverse Gamma density.

3.2 Estimation and Prediction

To describe a Gibbs sampler for estimating (9), we define y = (y(t₁)′, y(t₂)′, …, y(t_n)′)′, and w and ε similarly. Also, we introduce X = [X(t₁) : X(t₂) : …: X(t_n)]′, Z = diag(Z(t₁)′, …, Z(t_n)′), and D_n = Cov(ε) = diag(D, …, D). The full conditional distribution for β is $N({\mathbf{V}}_{\beta }^{\ast }{\mathit{\mu }}_{\beta }^{\ast },{\mathbf{V}}_{\beta }^{\ast })$, where ${\mathbf{V}}_{\beta }^{\ast }={({\mathbf{V}}_{\beta }^{-1}+{\mathbf{X}}^{\prime }{\mathbf{D}}_n^{-1}\mathbf{X})}^{-1},{\mathit{\mu }}_{\beta }^{\ast }=({\mathbf{V}}_{\beta }^{-1}{\mathit{\mu }}_{\beta }+{\mathbf{X}}^{\prime }{\mathbf{D}}_n^{-1}(\mathbf{y}-\mathbf{Zw}))$. Inverse Gamma priors for the ${\tau }_j^2$’s leads to conjugate full conditional distribution $\text{IG}(a_{{\tau }_j}+\frac{n}{2},b_{{\tau }_j}+\frac{1}{2}{({\mathbf{y}}_{\ast j}-{\mathbf{X}}_{\ast j}\mathit{\beta }-{\mathbf{Z}}_{\ast j}\mathbf{w})}^{\prime }({\mathbf{y}}_{\ast j}-{\mathbf{X}}_{\ast j}\mathit{\beta }-{\mathbf{Z}}_{\ast j}\mathbf{w})$, where y_*j refers to the n × 1 vector containing the jth coordinates of the y(t_i)’s, and X_*j and Z_*j are the corresponding fixed and spatial effect covariate matrices, respectively. For updating θ, we use a random walk Metropolis step with target density p(θ) × N(w_𝒮|0, C̃_𝒮) × N(w_𝒰 | B_𝒰w_𝒮, F_𝒰), where

$$\begin{gathered} N({\mathbf{w}}_{\mathcal{S}}\mid \mathbf{0},{\stackrel{\sim }{\mathbf{C}}}_{\mathcal{S}})={\prod }_{i=1}^{k}N(\mathbf{w}({\mathbf{s}}_i)\mid {\mathbf{B}}_{{\mathbf{s}}_i}{\mathbf{w}}_{N({\mathbf{s}}_i)},{\mathbf{F}}_{{\mathbf{s}}_i})\text{and} \\ N({\mathbf{w}}_{\mathcal{U}}\mid {\mathbf{B}}_{\mathcal{U}}{\mathbf{w}}_{\mathcal{S}},{\mathbf{F}}_{\mathcal{U}})={\prod }_{i=r+1}^{n}N(\mathbf{w}({\mathbf{t}}_i)\mid {\mathbf{B}}_{{\mathbf{t}}_i}{\mathbf{w}}_{N({\mathbf{t}}_i)},{\mathbf{F}}_{{\mathbf{t}}_i}). \end{gathered}$$ (10)

Each of the component densities under the product sign on the right-hand side of (10) can be evaluated without any n-dimensional matrix operations.

Since the components of w_𝒰 | w_𝒮 are independent, we can update w(t_i) from its full conditional N(V_tiμ_ti, V_ti) for i = r + 1, r + 2, …, n where ${\mathbf{V}}_{{\mathbf{t}}_i}={(\mathbf{Z}({\mathbf{t}}_i){\mathbf{D}}^{-1}\mathbf{Z}{({\mathbf{t}}_i)}^{\prime }+{\mathbf{F}}_{{\mathbf{t}}_i}^{-1})}^{-1}$ and ${\mathit{\mu }}_{{\mathbf{t}}_i}=\mathbf{Z}({\mathbf{t}}_i){\mathbf{D}}^{-1}(\mathbf{y}({\mathbf{t}}_i)-\mathbf{X}{({\mathbf{t}}_i)}^{\prime }\mathit{\beta })+{\mathbf{F}}_{{\mathbf{t}}_i}^{-1}{\mathbf{B}}_{{\mathbf{t}}_i}{\mathbf{w}}_{N({\mathbf{t}}_i)}$. Finally, we update the components of w_𝒮 individually. For any two locations s and t in 𝒟, if s ∈ N(t) and is the lth component of N(t), that is, say s = N(t)(l), then define B_t,s as the l × l submatrix formed by columns (l − 1)q + 1, (l − 1)q + 2, …, lq of B_t. Let U(s_i) = {t ∈ 𝒮 ∪ 𝒯 | s_i ∈ N(t)} and for every t ∈ U(s_i) define, a_t,si = w(t) − Σ_{s∈N(t),s≠si} B_t,sw(s). Then, for i = 1, 2, …, k, we have the full conditional w_si | · ~ N(V_siμ_si, V_si), where ${\mathbf{V}}_{{\mathbf{s}}_i}={(In({\mathbf{s}}_i\in {\mathcal{S}}^{\ast })\mathbf{Z}({\mathbf{s}}_i){\mathbf{D}}^{-1}\mathbf{Z}{({\mathbf{s}}_i)}^{\prime }+{\mathbf{F}}_{{\mathbf{s}}_i}^{-1}+{\sum }_{\mathbf{t}\in U({\mathbf{s}}_i)}{\mathbf{B}}_{\mathbf{t},{\mathbf{s}}_i}^{\prime }{\mathbf{F}}_{\mathbf{t}}^{-1}{\mathbf{B}}_{\mathbf{t},{\mathbf{s}}_i})}^{-1},{\mathit{\mu }}_{{\mathbf{s}}_i}=In({\mathbf{s}}_i\in {\mathcal{S}}^{\ast })\mathbf{Z}({\mathbf{s}}_i){\mathbf{D}}^{-1}(\mathbf{y}({\mathbf{s}}_i)-\mathbf{X}{({\mathbf{s}}_i)}^{\prime }\mathit{\beta })+{\mathbf{F}}_{{\mathbf{s}}_i}^{-1}{\mathbf{B}}_{{\mathbf{s}}_i}{\mathbf{w}}_{N({\mathbf{s}}_i)}+{\sum }_{\mathbf{t}\in U({\mathbf{s}}_i)}{\mathbf{B}}_{\mathbf{t},{\mathbf{s}}_i}^{\prime }{\mathbf{F}}_{\mathbf{t}}^{-1}{\mathbf{a}}_{\mathbf{t},{\mathbf{s}}_i}$, and In(·) denotes the indicator function. Hence, the w’s can also be updated without requiring storage or factorization of any n × n matrices.

Turning to predictions, let t be a new location where we intend to predict y(t) given X(t) and Z(t). The Gibbs sampler for estimation also generates the posterior samples w_𝒮∪𝒯 | y. So, if t ∈ 𝒮 ∪ 𝒯, then we simply get samples of y(t) | y from N(X(t)′β + Z(t)′w(t), D). If t is outside 𝒮 ∪ 𝒯, then we generate samples of w(t) from its full conditional N(B_tw_𝒮, F_t) and subsequently generate posterior samples of y(t) | y similar to the earlier case.

3.3 Computational Complexity

Implementing the NNGP model in Section 3.2 reveals that one entire pass of the Gibbs sampler can be completed without any large matrix operations. The only difference between (9) and a full geostatistical hierarchical model is that the spatial process is modeled as an NNGP prior as opposed to a standard GP. For comparisons, we offer rough estimates of the flop counts to generate θ and w per iteration of the sampler. We express the computational complexity only in terms of the sample size n, size of the reference set k, and the size of the neighbor sets m as other dimensions are assumed to be small. For all locations, t ∈ 𝒮 ∪ 𝒯, B_t, and F_t can be calculated using O(m³) flops. So, from (10) it is easy to see that p(θ | ·) can be calculated using O((n + k)m³) flops. All subsequent calculations to generate a set of posterior samples for w and θ require around O((n + k)m²) flops.

So, the total flop counts is of the order (n + k)m³ and is, therefore, linear in the total number of locations in 𝒮 ∪ 𝒯. This ensures scalability of the NNGP to large datasets. Compare this with a full GP model with a dense correlation matrix, which requires O(n³) flops for updating w in each iteration. Simulation results in Section 5.1 and online Appendix A6 indicate that NNGP models with usually very small values of m (≈10) provide inference almost indistinguishable to full geostatistical models. Therefore, for large n, this linear flop count is drastically less and linearity with respect to k ensures a feasible implementation even for k ≈ n.

This offers substantial scalability over low-rank models where the computational cost is quadratic in the number of “knots,” limiting the size of the set of knots. Also, the full geostatistical model requires storage of the n × n distance matrix, which can potentially exhaust storage resources for large datasets. An NNGP model only requires the distance matrix between neighbors for every location, thereby storing n + k small matrices, each of order m × m.

3.4 Model Comparison and Choice of 𝒮 and m

As elaborated in Section 2, given any parent Gaussian process and any fixed reference set of locations 𝒮, we can construct a valid NNGP. The resulting finite dimensional likelihoods of the NNGP depend upon the choice of the reference set 𝒮 and the size of each N(s_i), that is, m. Choosing the reference set is similar to selecting the knots for a predictive process. Unlike the number of “knots” in low-rank models, the size of 𝒮 does not thwart computational scalability. Since the flop count in an NNGP model only increases linearly with the size of 𝒮, the number of locations in 𝒮 can be large, with more flexible choices for 𝒮.

Points over a grid across the entire domain seem to be a plausible choice for 𝒮. For example, we can construct a large 𝒮 using a dense grid to improve performance without adversely affecting computational costs. Another, perhaps even simpler, option for large datasets is to simply fix 𝒮 = 𝒯, the set of observed locations. This choice reduces computational costs even further by avoiding additional sampling of w_𝒰 in the Gibbs sampler. Our empirical investigations (see Section 5.1) reveal that choosing 𝒮 = 𝒯 delivers inference almost indistinguishable from choosing 𝒮 to be a grid over the domain for large datasets.

Stein, Chi, and Welty (2004) and Eidsvik et al. (2014) proposed using a sandwich variance estimator for evaluating the inferential abilities of neighbor-based pseudo-likelihoods. Shaby (2012) developed a post-sampling sandwich variance adjustment for posterior credible intervals of the parameters for quasi-Bayesian approaches using pseudo-likelihoods. However, the asymptotic results used to obtain the sandwich variance estimators are based on assumptions that are hard to verify in spatial settings with irregularly placed data points. Moreover, we view the NNGP as an independent model for fitting the data and not as an approximation to the original GP. Hence, we refrain from such sandwich variance adjustments. Instead, we can simply use any standard model comparison metrics such as deviance information criterion (DIC; Spiegelhalter et al. 2002), GPD score (Gelfand and Ghosh 1998), or root mean squared prediction error/root mean square error of coefficient of variation (RMSPE/RMSECV; Yeniay and Goktas 2002) to compare the performance of NNGP and any other candidate model. The same model comparison metrics are also used for selecting m. However, as we illustrate later in Section 5.1, usually a small value of m between 10 and 15 produces performance at par with the full geostatistical model. While larger m may be beneficial for massive datasets, perhaps under a different design scheme, it will be much smaller than the number of knots in low-rank models for comparable inference (see Section 5.1).

4. Alternate NNGP Models and Algorithms

4.1 Block Update of w_𝒮 Using Sparse Cholesky

The Gibbs’ sampling algorithm detailed in Section 3.2 is extremely efficient for large datasets with linear flop counts per iteration. However, it can sometimes experience slow convergence issues due to sequential updating of the elements in w_𝒮. An alternative to sequential updating is to perform block updates of w_𝒮. We choose 𝒮 = 𝒯 so that s_i = t_i for all i = 1, 2, …, n and we denote w_𝒮 = w_𝒯 by w. Then,

$$\begin{gathered} \mathbf{w}\mid ·~N({\mathbf{V}}_{\mathcal{S}}{\mathbf{Z}}^{\prime }{\mathbf{D}}_n^{-1}(\mathbf{y}-\mathbf{X}\mathit{\beta }),{\mathbf{V}}_{\mathcal{S}}), \\ \text{where}{\mathbf{V}}_{\mathcal{S}}={({\mathbf{Z}}^{\prime }{\mathbf{D}}_n^{-1}\mathbf{Z}+{\stackrel{\sim }{\mathbf{C}}}_{\mathcal{S}}^{-1})}^{-1}. \end{gathered}$$ (11)

Recall that ${\stackrel{\sim }{\mathbf{C}}}_{\mathcal{S}}^{-1}$ is sparse. Since Z and D_n are block diagonal, ${\mathbf{V}}_{\mathcal{S}}^{-1}$ retains the sparsity of ${\stackrel{\sim }{\mathbf{C}}}_{\mathcal{S}}^{-1}$. So, a sparse Cholesky factorization of ${\mathbf{V}}_{\mathcal{S}}^{-1}$ will efficiently produce the Cholesky factors of V_𝒮. This will facilitate block updating of w in the Gibbs sampler.

4.2 NNGP Models for the Response

Another possible approach involves NNGP models for the response y(s). If w(s) is a Gaussian process, then so is y(s) = Z(s)′w(s) + ε (without loss of generality we assume β = 0). One can directly use the NNGP specification for y(s) instead of w(s). That is, we derive y(s) ~ NNGP(0, Σ̃(·, ·)) from the parent Gaussian process GP(0, Σ(·, · | θ)). The Gibbs sampler analogous to Section 3 now enjoys the additional advantage of avoiding full conditionals for w. This results in a Bayesian analogue for Vecchia (1988) and Stein, Chi, and Welty (2004) but precludes inference on the spatial residual surface w(s). Modeling w(s) provides additional insight into residual spatial contours and is often important in identifying lurking covariates or eliciting unexplained spatial patterns. Vecchia (1992) used the nearest neighbor approximation on a spatial model for observations (y) with independent measurement error (nuggets) in addition to the usual spatial component (w). However, it may not be possible to recover w using this approach. For example, a univariate stationary process y(s) with a nugget effect can be decomposed as y(s) = w(s) + ε(s) (letting β = 0) for some w(s) ~ GP(0, C(·, · | θ)) and white-noise process ε(s). If y = w + ε, where w ~ N(0, C), ε ~ N(0, τ²I_n), then cov(y) = C + τ²I = Σ, all eigenvalues of Σ are greater than τ², and cov(w | y) = τ²I_n − τ⁴Σ⁻¹. For y(s) ~ NNGP(0, Σ̃(·, ·)), however, the eigenvalues of Σ̃ may be less than τ², so τ²I_n − τ⁴Σ̃⁻¹ need not be positive definite for every τ² > 0 and p(w | y) is no longer well defined.

A different model is obtained by using an NNGP prior for w, as in (9), and then integrating out w. The resulting likelihood is N(y | Xβ, Σ_y), where Σ_y = ZC̃_𝒮Z′ + D_n and the Bayesian specification is completed using priors on β, ${\tau }_j^2$’s, and θ as in (9). This model drastically reduces the number of variables in the Gibbs sampler, while preserving the nugget effect in the parent model. We can generate the full conditionals for the parameters in the marginalized model as follows: $\mathit{\beta }\mid \mathit{y},\mathit{\varphi }~N({({\mathbf{V}}_{\beta }^{-1}+{\mathbf{X}}^{\prime }{\mathbf{\sum }}_y^{-1}\mathbf{X})}^{-1}({\mathbf{V}}_{\beta }^{-1}{\mathit{\mu }}_{\beta }+{\mathbf{X}}^{\prime }{\mathbf{\sum }}_y^{-1}\mathbf{y}),{({\mathbf{V}}_{\beta }^{-1}+{\mathbf{X}}^{\prime }{\mathbf{\sum }}_y^{-1}\mathbf{X})}^{-1})$. It is difficult to factor out ${\tau }_j^2$’s from ${\mathbf{\sum }}_y^{-1}$, so conjugacy is lost with respect to any standard prior. Metropolis block updates for θ are feasible for any tractable prior p(θ). This involves computing ${\mathbf{X}}^{\prime }{\mathbf{\sum }}_y^{-1}\mathbf{X},{\mathbf{X}}^{\prime }{\mathbf{\sum }}_y^{-1}\mathbf{y}$, and ${(\mathbf{y}-\mathbf{X}\mathit{\beta })}^{\prime }{\mathbf{\sum }}_y^{-1}(\mathbf{y}-\mathbf{X}\mathit{\beta })$. Since ${\mathbf{\sum }}_y^{-1}={\mathbf{D}}_n^{-1}-{\mathbf{D}}_n^{-1}\mathbf{Z}{({\stackrel{\sim }{\mathbf{C}}}_{\mathcal{S}}^{-1}+{\mathbf{Z}}^{\prime }{\mathbf{D}}_n^{-1}\mathbf{Z})}^{-1}{\mathbf{Z}}^{\prime }{\mathbf{D}}_n^{-1}={\mathbf{D}}_n^{-1}-{\mathbf{D}}_n^{-1}\mathbf{Z}{\mathbf{V}}_{\mathcal{S}}{\mathbf{Z}}^{\prime }{\mathbf{D}}_n^{-1}$, where V_𝒮 is given by (11), a sparse Cholesky factorization of ${\mathbf{V}}_{\mathcal{S}}^{-1}$ will be beneficial. We draw posterior samples for w from $p(\mathbf{w}\mid \mathbf{y})=\int p(\mathbf{w}\mid \mathit{\theta },\mathit{\beta },\{{\tau }_j^2\},\mathbf{y})p(\mathit{\theta },\mathit{\beta },\{{\tau }_j^2\}\mid \mathbf{y})$ using composition sampling—we draw w^(g) from $p(\mathbf{w}\mid {\mathit{\theta }}^{(g)},{\mathit{\beta }}^{(g)},\{{\tau }_j^{2(g)}\},\mathbf{y})$ one-for-one for each sampled parameter.

Using block updates for w_𝒮 in (9) and fitting the marginalized version of (9) both require an efficient sparse Cholesky solver for ${\mathbf{V}}_{\mathcal{S}}^{-1}$. Note that computational expenses for most sparse Cholesky algorithms depend on the precise nature of the sparse structure (mostly on the bandwidth) of ${\stackrel{\sim }{\mathbf{C}}}_{\mathcal{S}}^{-1}$ (see, e.g., Davis 2006). The number of flops required for Gibbs sampling and prediction in this marginalized model depends upon the sparse structure of ${\stackrel{\sim }{\mathbf{C}}}_{\mathcal{S}}^{-1}$ and may, sometimes, heavily exceed the linear usage achieved by the unmarginalized model with individual updates for w_i. Therefore, a prudent choice of the precise fitting algorithms should be based on the sparsity structure of ${\stackrel{\sim }{\mathbf{C}}}_{\mathcal{S}}^{-1}$ for the given dataset.

4.3 Spatiotemporal and GLM Versions

In spatiotemporal settings where we seek spatial interpolation at discrete time points (e.g., weekly, monthly, or yearly data), we write the response (possibly vector-valued) as y_t(s) and the random effects as w_t(s). Desired inference includes spatial interpolation for each time point. Spatial dynamic models incorporating the NNGP are easily formulated as below:

$$\begin{gathered} {\mathbf{y}}_t(\mathbf{s})={\mathbf{X}}_t{(\mathbf{s})}^{\prime }{\mathit{\beta }}_t+{\mathbf{u}}_t(s)+{\mathit{\epsilon }}_t(\mathbf{s}),{\mathit{\epsilon }}_t(\mathbf{s})\stackrel{\mathit{iid}}{\sim }N(0,D) \\ {\mathit{\beta }}_t={\mathit{\beta }}_{t-1}+{\mathit{\eta }}_t,{\mathit{\eta }}_t\stackrel{\mathit{iid}}{\sim }N(0,{\mathbf{\sum }}_{\eta }),{\mathit{\beta }}_0~N({\mathbf{m}}_0,{\mathbf{\sum }}_0) \\ {\mathbf{u}}_t(\mathbf{s})={\mathbf{u}}_{t-1}(\mathbf{s})+{\mathbf{w}}_t(\mathbf{s}),{\mathbf{w}}_t(\mathbf{s})\stackrel{\mathit{ind}}{\sim }\mathit{NNGP}(\mathbf{0},\stackrel{\sim }{\mathbf{C}}(·,·\mid {\mathit{\theta }}_t)). \end{gathered}$$ (12)

Thus, one retains exactly the same structure of process-based spatial dynamic models, for example, as in Gelfand, Banerjee, and Gamerman (2005), and simply replaces the independent Gaussian process priors for w_t(s) with independent NNGPs to achieve computational tractability.

The above is illustrative of how attractive and extremely convenient the NNGP is for model building. One simply writes down the parent model and subsequently replaces the full GP with an NNGP. Being a well-defined process, the NNGP ensures a valid spatial dynamic model. Similarly NNGP versions of dynamic spatiotemporal Kalman-filtering (as, e.g., in Wikle and Cressie 1999) can be constructed.

Handling non-Gaussian (e.g., binary or count) data is also straightforward using spatial generalized linear models (GLMs; Diggle, Tawn, and Moyeed 1998; Lin et al. 2000; Kammann and Wand 2003; Banerjee, Carlin, and Gelfand 2014). Here, the NNGP provides structured dependence for random effects at the second stage. First, we replace E[y(t)] in (8) with g(E(y(t))), where g(·) is a suitable link function such that η(t) = g(E(y(t))) = X(t)′β + Z(t)′w(t). In the second stage, we model the w(t) as an NNGP. The benefits of the algorithms in Sections 3.2 and 3.3 still hold, but some of the alternative algorithms in Section 4 may not apply. For example, we do obtain tractable marginalized likelihoods by integrating out the spatial effects.

5. Illustrations

We conduct simulation experiments and analyze a large forestry dataset. Additional simulation experiments are detailed in Appendices A5 through A9 (available online). Posterior inference for subsequent analysis were based upon three chains of 25,000 iterations (with a burn-in of 5000 iterations). All the samplers were programmed in C++ and leveraged Intel Math Kernel Library’s (MKL) threaded BLAS and LAPACK routines for matrix computations on a Linux workstation with 384 GB of RAM and two Intel Nehalem quad-Xeon processors.

5.1 Simulation Experiment

We generated observations using 2500 locations within a unit square domain from the model (8) with q = l = 1 (univariate outcome), p = 2, Z(t)′ = 1 (scalar), the spatial covariance matrix C(θ) = σ²R(φ), where R(φ) is a n × n correlation matrix, and D = τ² (scalar). The model included an intercept and a covariate x₁ drawn from N(0, 1). The (i, j)th element of R(φ) was calculated using the Matérn function

$$\rho ({\mathbf{t}}_i,{\mathbf{t}}_j;\mathit{\varphi })=\frac{1}{2^{\nu -1}\mathrm{\Gamma }(\nu )}{(\Vert {\mathbf{t}}_j-{\mathbf{t}}_j\Vert \varphi )}^{\nu }{\mathcal{K}}_v(\Vert {\mathbf{t}}_i-{\mathbf{t}}_j\Vert \varphi );\varphi >0,\nu >0,$$ (13)

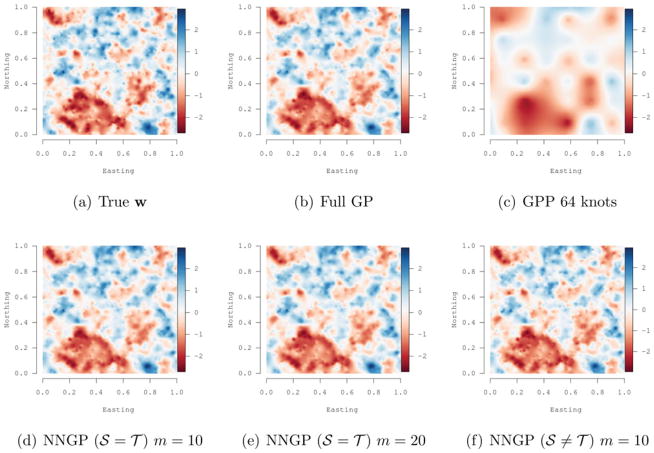
where ||t_i − t_j|| is the Euclidean distance between locations t_i and t_j, φ = (φ, ν) with φ controlling the decay in spatial correlation and ν controlling the process smoothness, Γ is the usual Gamma function, while 𝒦_ν is a modified Bessel function of the second kind with order ν (Stein 1999). Evaluating the Gamma function for each matrix element within each iteration requires substantial computing time and can obscure differences in sampler run times; hence, we fixed ν at 0.5, which reduces (13) to the exponential correlation function. The first column in Table 1 gives the true values used to generate the responses. Figure 2(a) illustrates the w(t) surface interpolated over the domain.

Table 1.

Univariate synthetic data analysis parameter estimates and computing time in minutes for NNGP and full GP models. Parameter posterior summary 50 (2.5, 97.5) percentiles.

		NNGP (𝒮 ≠ 𝒯)		NNGP (𝒮 = 𝒯)
	True	m = 10, k = 2000	m = 20, k = 2000	m = 10	m = 20
β0	1	0.99 (0.71, 1.48)	1.02 (0.73, 1.49)	1.00 (0.62, 1.31)	1.03 (0.65, 1.34)
β1	5	5.00 (4.98, 5.03)	5.01 (4.98, 5.03)	5.01 (4.99, 5.03)	5.01 (4.99, 5.03)
σ2	1	1.09 (0.89, 1.49)	1.04 (0.85, 1.40)	0.96 (0.78, 1.23)	0.94 (0.77, 1.20)
τ2	0.1	0.07 (0.04, 0.10)	0.07 (0.04, 0.10)	0.10 (0.08, 0.13)	0.10 (0.08, 0.13)
φ	12	11.81 (8.18, 15.02)	12.21 (8.83, 15.62)	12.93 (9.70, 16.77)	13.36 (9.99, 17.15)
pD	—	1491.08	1478.61	1243.32	1249.57
DIC	—	1856.85	1901.57	2390.65	2377.51
G	—	33.67	35.68	77.84	76.40
P	—	253.03	259.13	340.40	337.88
D	—	286.70	294.82	418.24	414.28
RMSPE	—	1.22	1.22	1.2	1.2
95% CI cover %	—	97.2	97.2	97.6	97.6
95% CI width	—	2.19	2.18	2.13	2.12
Time	—	14.2	47.08	9.98	33.5
	True	Predictive process 64 knots	Full Gaussian process
β0	1	1.30 (0.54, 2.03)	1.03 (0.69, 1.34)
β1	5	5.03 (4.99, 5.06)	5.01 (4.99, 5.03)
σ2	1	1.29 (0.96, 2.00)	0.94 (0.76, 1.23)
τ2	0.1	0.08 (0.04, 0.13)	0.10 (0.08, 0.12)
φ	12	5.61 (3.48, 8.09)	13.52 (9.92, 17.50)
pD	—	1258.27	1260.68
DIC	—	13677.97	2364.80
G	—	1075.63	74.80
P	—	200.39	333.27
D	—	1276.03	408.08
RMSPE	—	1.68	1.2
95% CI cover %	—	95.6	97.6
95% CI width	—	2.97	2.12
Time	—	43.36	560.31

Figure 2.

Univariate synthetic data analysis: interpolated surfaces of the true spatial random effects and posterior median estimates for different models.

We then estimated the following models from the full data: (i) the full Gaussian process (full GP); (ii) the NNGP with m = {1, 2, …, 25} for 𝒮 ≠ 𝒯 and 𝒮 = 𝒯; and (iii) a Gaussian predictive process (GPP)model (Banerjee et al. 2008) with 64 knots placed on a grid over the domain. For the NNGP with 𝒮 ≠ 𝒯, we considered 2000 randomly placed reference locations within the domain. The 64 knot GPP was chosen because its computing time was comparable to that of NNGP models. We used an efficient marginalized sampling algorithm for the Full GP and GPP models as implemented in the spBayes package in R (Finley, Banerjee, and Gelfand, in press). All the models were trained using 2000 of the 2500 observed locations, while the remaining 500 observations were withheld to assess predictive performance.

For all models, the intercept and slope regression parameters, β₀ and β₁, were given flat prior distributions. The variance components σ² and τ² were assigned inverse Gamma IG(2, 1) and IG(2, 0.1) priors, respectively, and the spatial decay φ received a uniform prior U(3, 30), which corresponds to a spatial range between approximately 0.1 and 1 units.

Parameter estimates and performance metrics for the NNGP (with m = 10 and m = 20), GPP, and the full GP models are provided in Table 1. All model specifications produce similar posterior median and 95% credible intervals estimates, with the exception of φ in the 64 knot GPP model. Larger values of DIC and D suggest that the GPP model does not fit the data as well as the NNGP and full GP models. The NNGP 𝒮 = 𝒯 models provide DIC, GPD scores that are comparable to those of the full GP model. These fit metrics suggest the NNGP 𝒮 ≠ 𝒯 models provide better fit to the data than that achieved by the full GP model, which is probably due to overfitting caused by a very large reference set 𝒮. The last row in Table 1 shows computing times in minutes for one chain of 25,000 iterations reflecting on the enormous computational gains of NNGP models over full GP model.

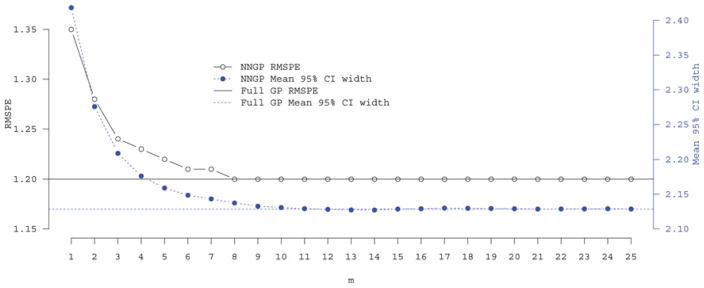
Turning to out-of-sample predictions, the Full model’s RMSPE and mean width between the upper and lower 95% posterior predictive credible interval is 1.2 and 2.12, respectively. As seen in Figure 1, comparable RMSPE and mean interval width for the NNGP 𝒮 = 𝒯 model is achieved within m ≈ 10. There is negligible difference between the predictive performances of the NNGP 𝒮 ≠ 𝒯 and 𝒮 = 𝒯 models. Both the NNGP and full GP model have better predictive performance than the predictive process models when the number of knots is small, for example, 64. All models showed appropriate 95% credible interval coverage rates.

Figure 1.

Choice of m in NNGP models: out-of-sample root mean squared prediction error (RMSPE) and mean width between the upper and lower 95% posterior predictive credible intervals for a range of m for the univariate synthetic data analysis.

Figure 2(b)–2(f) illustrates the posterior median estimates of the spatial random effects from the Full GP, NNGP (𝒮 = 𝒯) with m = 10 and m = 20, NNGP (𝒮 ≠ 𝒯) with m = 10, and GPP models. These surfaces can be compared to the true surface depicted in Figure 2(a). This comparison shows: (i) the NNGP models closely approximates the true surface and that estimated by the full GP model, and (ii) the reduced-rank predictive process model based on 64 knots greatly smooths over small-scale patterns. This last observation highlights one of the major criticisms of reduced-rank models (Stein 2014) and illustrates why these models often provide compromised predictive performance when the true surface has fine spatial resolution details. Overall, we see the clear computational advantage of the NNGP over the full GP model, and both inferential and computational advantage over the GPP model.

5.2 Forest Biomass Data Analysis

Information about the spatial distribution of forest biomass is needed to support global, regional, and local scale decisions, including assessment of current carbon stock and flux, bio-feedstock for emerging bio-economies, and impact of deforestation. In the United States, the Forest Inventory and Analysis (FIA) program of the USDA Forest Service collects the data needed to support these assessments. The program has established field plot centers in permanent locations using a sampling design that produces an equal probability sample (Bechtold and Patterson 2005). Field crews recorded stem measurements for all trees with diameter at breast height (DBH; 1.37 m above the forest floor) of 12.7 cm or greater. Given these data, established allometric equations were used to estimate each plot’s forest biomass. For the subsequent analysis, plot biomass was scaled to metric tons per ha then square root transformed. The transformation ensures that back transformation of subsequent predicted values have support greater than zero and helps to meet basic regression models assumptions.

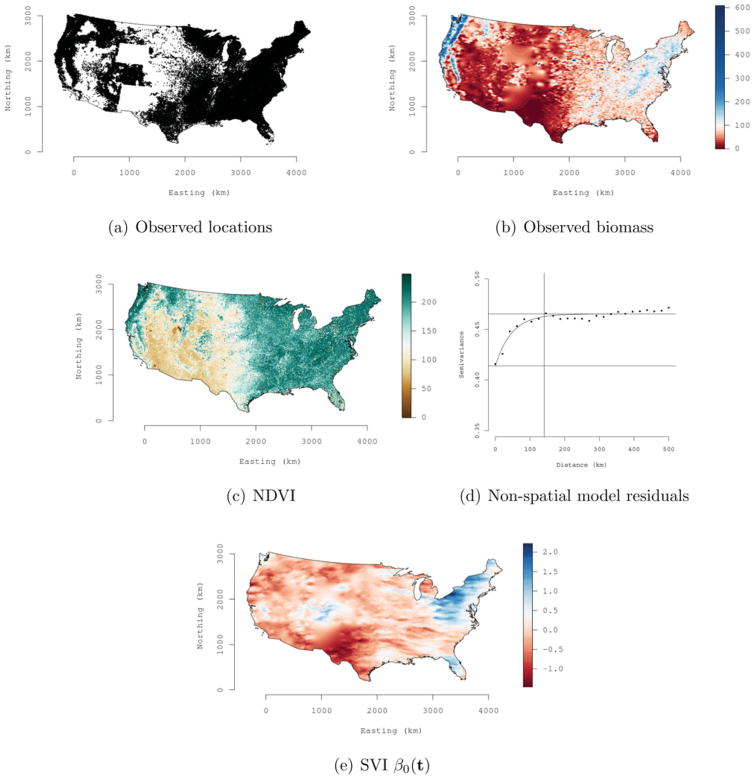
Figure 3(a) illustrates the georeferenced forest inventory data consisting of 114, 371 forested FIA plots measured between 1999 and 2006 across the conterminous United States. The two blocks of missing observations in the Western and Southwestern United States correspond to Wyoming and New Mexico, which have not yet released FIA data. Figure 3(b) shows a deterministic interpolation of forest biomass observed on the FIA plots. Dark blue indicates high forest biomass, which is primarily seen in the Pacific Northwest, Western Coastal ranges, Eastern Appalachian Mountains, and in portions of New England. In contrast, dark red indicates regions where climate or land use limit vegetation growth.

Figure 3.

Forest biomass data analysis: (a) locations of observed biomass, (b) interpolated biomass response variable, (c) NDVI regression covariate, (d) variogram of nonspatial model residuals, and (e) surface of the SVI model random spatial effects posterior medians. Following our FIA data-sharing agreement, plot locations depicted in (a) have been “fuzzed” to hide the true coordinates.

A July 2006 Normalized Difference Vegetation Index (NDVI) image from the MODerate-resolution Imaging Spectroradiometer (MODIS; http://glcf.umd.edu/data/ndvi) sensor was used as a single predictor. NDVI is calculated from the visible and near-infrared light reflected by vegetation, and can be viewed as a measure of greenness. In this image, Figure 3(c), dark green corresponds to dense vegetation whereas brown identifies regions of sparse or no vegetation, for example, in the Southwest. NDVI is commonly used as a covariate in forest biomass regression models; see, for example, Zhang and Kondraguanta (2006). Results from these and similar studies show a positive linear relationship between forest biomass and NDVI. The strength of this relationship, however, varies by forest tree species composition, age, canopy structure, and level of reflectance. We expect a space-varying relationship between biomass and NDVI, given tree species composition and disturbance regimes generally exhibit strong spatial dependence across forested landscapes.

The memory in our workstation was insufficient for storage of distance matrices required to fit a Full GP or GPP model. Subsequently, we explore the relationship between forest biomass and NDVI using a nonspatial model, an NNGP space-varying intercept (SVI) model (i.e., q = l = 1 and Z(t) = 1) in (8), and an NNGP spatially varying coefficients (SVC) regression model with l = 1, q = p = 2, and Z(t) = X(t) in (8). The reference sets for the NNGP models were again the observed locations and m was chosen to be 5 or 10. The parent process w(t) is a bivariate Gaussian process with an isotropic cross-covariance specification C(t_i, t_j | θ) = AΓ(φ)A′, where A is 2 × 2 lower-triangular with positive diagonal elements, Γ is 2 × 2 diagonal with ρ(t_i, t_j; φ_b) (defined in (13)) as the bth diagonal entry, b = 1, 2, and φ_b = (φ_b, ν_b)′ (see, e.g., Gelfand and Banerjee 2010).

For all models, the intercept and slope regression parameters were given flat prior distributions. The variance components τ² and σ² were assigned inverse Gamma IG(2, 1) priors, the SVC model cross-covariance matrix AA′ followed an inverse-Wishart IW(3, 0.1), and the Matérn spatial decay and smoothness parameters received uniform prior supports U (0.01, 3) and U (0.1, 2), respectively. These prior distributions on φ and ν correspond to support between approximately 0.5 and 537 km. Candidate models are assessed using the metrics described in Section 3.4, and inference drawn from mapped estimates of the regression coefficients and out-of-sample prediction.

Parameter estimates and performance metrics for NNGP with m = 5 are shown in Table 2. The corresponding numbers form = 10 were similar. Relative to the spatial models, the nonspatial model has higher values of DIC and D, which suggests NDVI alone does not adequately capture the spatial structure of forest biomass. This observation is corroborated using a variogram fit to the nonspatial model’s residuals; Figure 3(d). The variogram shows a nugget of ~0.42, partial sill of ~0.05, and range of ~150 km. This residual spatial dependence is apparent when we map the SVI model spatial random effects as shown in Figure 3(e). This map, and the estimate of a nonnegligible spatial variance σ² in Table 2, suggests the addition of a spatial random effect was warranted and helps satisfy the model assumption of uncorrelated residuals.

Table 2.

Forest biomass data analysis parameter estimates and computing time in hours for candidate models. Parameter posterior summary 50 (2.5, 97.5) percentiles.

	Nonspatial	NNGP Space-varying intercept	NNGP Space-varying coefficients
β0	1.043 (1.02, 1.065)	1.44 (1.39, 1.48)	1.23 (1.20, 1.26)
βNDVI	0.0093 (0.009, 0.0095)	0.0061 (0.0059, 0.0062)	0.0072 (0.0071, 0.0074)
σ2	—	0.16 (0.15, 0.17)	—
${\mathbf{AA}}_{1,1}^{\prime }$	—	—	0.24 (0.23, 0.24)
${\mathbf{AA}}_{2,1}^{\prime }$	—	—	−0.00088 (−0.00093,−0.00083)
${\mathbf{AA}}_{2,2}^{\prime }$	—	—	0.0000052 (0.0000047, 0.0000056)
τ2	0.52 (0.51, 0.52)	0.39 (0.39, 0.40)	0.39 (0.38, 0.40)
φ1	—	0.016 (0.015, 0.016)	0.022 (0.021, 0.023)
φ2	—	—	0.030 (0.029, 0.031)
ν1	—	0.66 (0.64, 0.67)	0.92 (0.90, 0.93)
ν2	—	—	0.92 (0.89, 0.93)
pD	2.94	6526.95	4976.13
DIC	250137	224484.2	222845.1
G	59765.30	42551.08	43117.37
P	59667.15	47603.47	46946.49
D	119432.45	90154.55	90063.86
Time	—	14.53	41.35

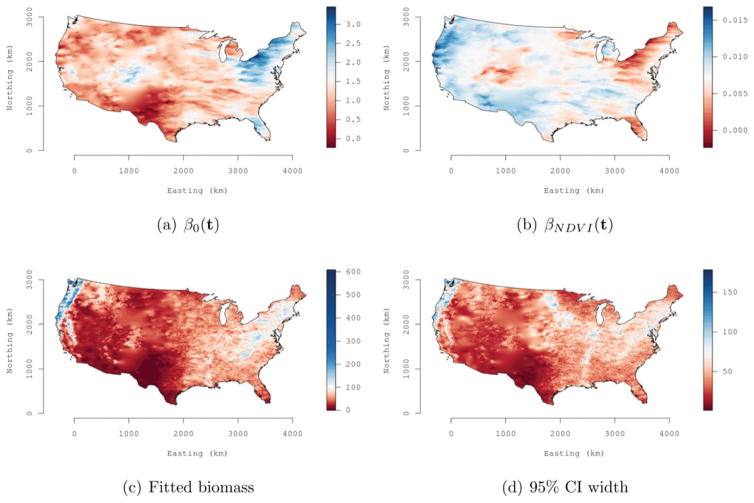
The values of the SVC model’s goodness-of-fit metrics suggest that allowing the NDVI regression coefficient to vary spatially improves model fit over that achieved by the SVI model. Figure 4(a) and 4(b) shows maps of posterior estimates for the spatially varying intercept and NDVI, respectively. The clear regional patterns seen in Figure 4(b) suggest the relationship between NDVI and biomass does vary spatially—with stronger positive regression coefficients in the Pacific Northwest and northern California areas. Forests in the Pacific Northwest and northern California are dominated by conifers and support the greatest range in biomass per unit area within the entire conterminous United States. The other strong regional pattern seen in Figure 4(b) is across western New England, where near zero regression coefficients suggest that NDVI is not as effective at discerning differences in forest biomass. This result is not surprising. For deciduous forests, NDVI can explain variability in low to moderate vegetation density. However, in high biomass deciduous forests, like those found across western New England, NDVI saturates and is no longer sensitive to changes in vegetation structure (Wang et al. 2005). Hence, we see a higher intercept in this region but lower slope coefficient on NDVI.

Figure 4.

Forest biomass data analysis using SVC model: (1) posterior medians of the intercept, (b) NDVI regression coefficients, (c) median of biomass posterior predictive distribution, and (d) range between the upper and lower 95% percentiles of the posterior predictive distribution.

Figure 4(c) and 4(d) maps each location’s posterior predictive median and the range between the upper and lower 95% credible interval, respectively, from the SVC model. Figure 4(c) shows strong correspondence with the deterministic interpolation of biomass in Figure 3(b). The prediction uncertainty in Figure 4(d) provides a realistic depiction of the model’s ability to quantify forest biomass across the United States.

We also used prediction mean squared error (PMSE) to assess predictive performance. We fit the candidate models using 100,000 observations and withheld 14,371 for validation. PMSE for the nonspatial, SVI, and SVC models was 0.52, 0.41, and 0.42, respectively. Lower PMSE for the spatial models, versus the nonspatial model, corroborates the results from the model fit metrics and further supports the need for spatial random effects in the analysis.

6. Summary and Conclusions

We regard the NNGP as a highly scalable model, rather than a likelihood approximation, for large geostatistical datasets. It significantly outperforms competing low-rank processes such as the GPP, in terms of inferential performance and scalability. A reference set 𝒮 and the resulting neighbor sets (of size m) define the NNGP. Larger m’s would increase costs, but there is no apparent benefit to increasing m for larger datasets (see Appendix A6, available online). While some sensitivity to m and the choice of points in 𝒮 is expected, our results indicate that inference is very robust with respect to 𝒮 and very modest values of m (< 20) typically suffice. Larger reference sets may be needed for larger datasets, but its size does not thwart computations. In fact, the observed locations are a convenient choice for the reference set.

A potential concern with this choice is that if the observed locations have large gaps, then the resulting NNGP may be a poor approximation of the full Gaussian process. This arises from the fact that observations at locations outside the reference set are correlated via their respective neighbor sets and large gaps may imply two very near points have very different neighbor sets leading to low correlation. Our simulations in Appendix A7 (available online) indeed reveal that in such a situation, the NNGP covariance field is very flat at points in the gap. However, even with this choice of 𝒮 the NNGP model performs at par with the full GP model as the latter also fails to provide strong information about observations located in large gaps. Of course, one can always choose a grid over the entire domain as 𝒮 to construct an NNGP with covariance function similar to the full GP (see Figure A.5, available online). Another choice for 𝒮 could be based upon configurations for treed Gaussian processes (Gramacy and Lee 2008).

Our simulation experiments revealed that estimation and kriging based on NNGP models closely emulate those from the true Matérn GP models, even for slow decaying covariances (see Appendix A8, available online). The Matérn covariance function is monotonically decreasing with distance and satisfies theoretical screening conditions, that is, the ability to predict accurately based on a few neighbors (Stein 2002). This, perhaps, explains the excellent performance of NNGP models with Matérn covariances. We also investigated the performance of NNGP models using a wave covariance function, which does not satisfy the screening conditions, in a setting where a significant proportion of nearest neighbors had negative correlation with the corresponding locations. The NNGP estimates were still close to the true model parameters and the kriged surface closely resembled the true surface (see Appendix A9, available online).

Most wave covariance functions (like the damped cosine or the cardinal sine function) produce covariance matrices with several small eigenvalues. The full GP model cannot be implemented for such models because the matrix inversion is numerically unstable. The NNGP model involves much smaller matrix inversions and can be implemented in some cases (e.g., for the damped cosine model). However, for the cardinal sine covariance, the NNGP also faces numerical issues as even the small m × m covariance matrices are numerically unstable. Bias-adjusted low-rank GPs (Finley, Banerjee, and McRoberts 2009) possess a certain advantage in this aspect as the covariance matrix is guaranteed to have eigen values bounded away from zero, although stable computations will usually require full Cholesky decompositions.

Apart from being easily extensible to multivariate and spatiotemporal settings with discretized time, the NNGP can fuel interest in process-based modeling over graphs. Examples include networks, where data arising from nodes are posited to be similar to neighboring nodes. It also offers new modeling avenues and alternatives to the highly pervasive Markov random field models for analyzing regionally aggregated spatial data. Also, there is scope for innovation when space and time are jointly modeled as processes using spatiotemporal covariance functions. One will need to construct neighbor sets both in space and time and effective strategies, in terms of scalability and inference, will need to be explored. Comparisons with alternate approaches (see, e.g., Katzfuss and Cressie 2012) will also need to be made. Finally, a more comprehensive study on the alternate algorithms and parameterizations for faster Markov chain Monte Carlo convergence, including direct methods for executing sparse Cholesky factorizations (see Section 4), is being undertaken. More immediately, we plan to migrate our lower-level C++ code to the existing spBayes package (Finley, Banerjee, and Gelfand, in press) in the R statistical environment (http://cran.r-project.org/web/packages/spBayes) to facilitate wider user accessibility to NNGP models.