Association of Pathological Fibrosis With Renal Survival Using Deep Neural Networks

Abstract

Introduction

Chronic kidney damage is routinely assessed semiquantitatively by scoring the amount of fibrosis and tubular atrophy in a renal biopsy sample. Although image digitization and morphometric techniques can better quantify the extent of histologic damage, we need more widely applicable ways to stratify kidney disease severity.

Methods

We leveraged a deep learning architecture to better associate patient-specific histologic images with clinical phenotypes (training classes) including chronic kidney disease (CKD) stage, serum creatinine, and nephrotic-range proteinuria at the time of biopsy, and 1-, 3-, and 5-year renal survival. Trichrome-stained images processed from renal biopsy samples were collected on 171 patients treated at the Boston Medical Center from 2009 to 2012. Six convolutional neural network (CNN) models were trained using these images as inputs and the training classes as outputs, respectively. For comparison, we also trained separate classifiers using the pathologist-estimated fibrosis score (PEFS) as input and the training classes as outputs, respectively.

Results

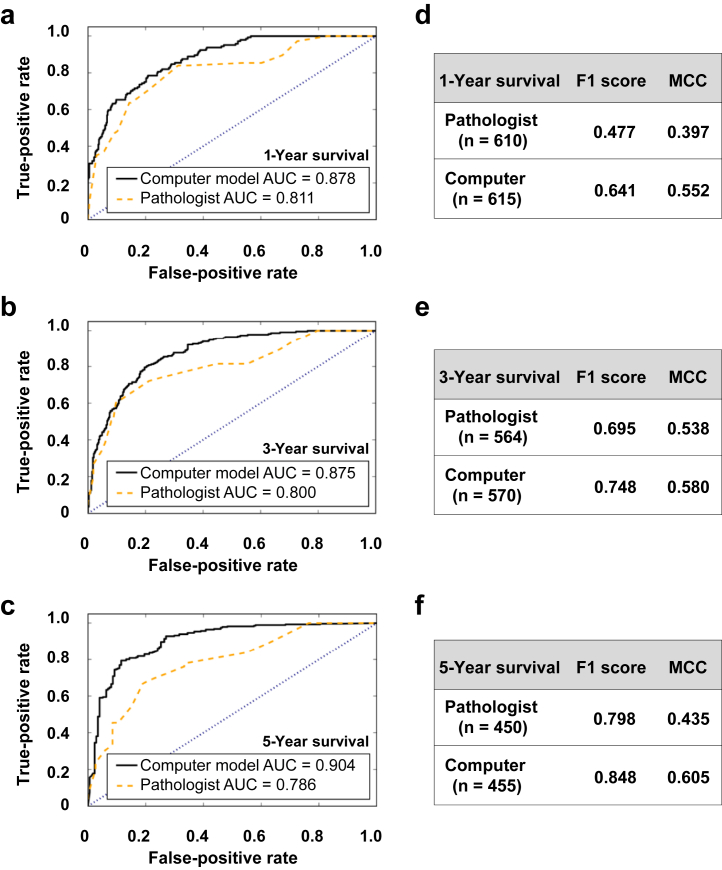
CNN models outperformed PEFS across the classification tasks. Specifically, the CNN model predicted the CKD stage more accurately than the PEFS model (κ = 0.519 vs. 0.051). For creatinine models, the area under curve (AUC) was 0.912 (CNN) versus 0.840 (PEFS). For proteinuria models, AUC was 0.867 (CNN) versus 0.702 (PEFS). AUC values for the CNN models for 1-, 3-, and 5-year renal survival were 0.878, 0.875, and 0.904, respectively, whereas the AUC values for PEFS model were 0.811, 0.800, and 0.786, respectively.

Conclusion

The study demonstrates a proof of principle that deep learning can be applied to routine renal biopsy images.

From self-driving cars to face recognition, artificial intelligence and machine learning (ML) algorithms are being widely applied to enhance human endeavors. Over the last few years, the scientific community has witnessed a rapid increase in the adoption of cutting-edge data analytic tools such as ML to address several questions in clinical medicine.1, 2, 3, 4, 5, 6 ML techniques give computers the ability to integrate discrete sets of data in an agnostic manner to find hidden insights and to generate a disease-specific fingerprint. These tools are now being rapidly adopted in several specialties as unbiased, self-learning approaches for pathologic assessment. Such a framework can leverage hundreds to thousands of images as inputs and allow for objective quantification, followed by their association with several clinical outcomes of interest. ML techniques also have the potential to uncover several nonintuitive features that may be clinically relevant and hypothesis generating, as demonstrated in other disease scenarios.⁷

Although the trained eyes of expert pathologists are able to gauge the severity of disease and to detect nuances of histopathology with remarkable accuracy, such expertise is not available in all locations, especially at a global level. Moreover, there is an urgent need to standardize the quantification of pathological disease severity, such that the efficacy of therapies established in clinical trials can be applied to treat patients with equally severe disease in routine practice. The tools to do this are at hand in the form of digitized images of pathology sections prepared with routine stains and ML algorithms. Such methods have already been tested and shown to be reliable for the analysis of malignancies such as cancer.7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17 The application of deep learning frameworks, such as convolutional neural networks (CNN) for object recognition tasks, is proving to be especially valuable for classification of several diseases.8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29

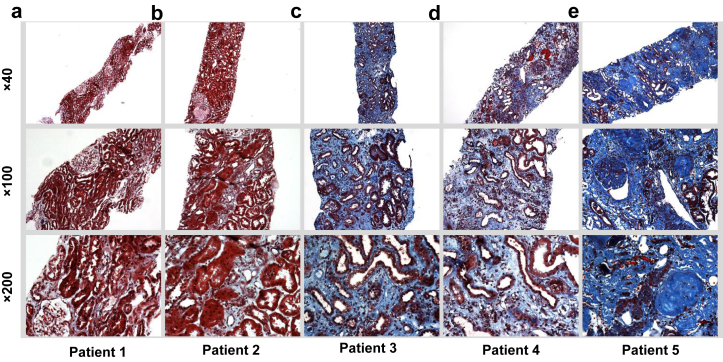
To test the feasibility of applying ML technology to the analysis of routinely obtained kidney biopsy samples, we performed a proof-of-principle study on kidney biopsy sample sections with various amounts of interstitial fibrosis as revealed with Masson trichrome stain (Figure 1). Using an established CNN that relies on pixel density of digitized images,³⁰ we analyzed the ability of the ML technique to quantify the severity of disease as determined by several clinical laboratory measures and renal survival (Supplementary Figure S1). CNN model performance was then compared with that of the models generated, using the amount of fibrosis reported by an expert nephropathologist as the sole input and corresponding laboratory measures and renal survival as the outputs.

Figure 1.

Sample interstitial fibrosis cases from the patient cohort. The trichrome-stained images demonstrate the variability and extent of interstitial fibrosis observed within renal biopsy samples at different magnifications. The in-house nephropathologist−derived fibrosis score was 5% to 10% for (a), 20% for (b), 30% for (c), 50% for (d), and 85% for (e).

Methods

Data Collection

A retrospective analysis of renal biopsy findings was performed on patients treated at the Boston Medical Center (BMC) between January 2009 and December 2012. Reports from all follow-up visits between 2009 and 2016 for these patients were also reviewed. All patient data were collected under protocol H-32289, which was reviewed and approved by the Institutional Review Board at Boston University Medical Campus. More than 300 biopsy samples were processed at BMC, of which 171 biopsy slides were available for subsequent imaging. These biopsy samples were obtained from adult patients who had 1 or more native or renal allograft biopsies, independent of the indication for the biopsy procedure. The only criterion for inclusion was the availability of pathological slides and accompanying clinical data. Several demographic and clinical features (including estimated glomerular filtration rate [eGFR], baseline creatinine, nephrotic-range proteinuria, etc.) were collected on these patients at the time of biopsy (Table 1). The 4-parameter Chronic Kidney Disease Epidemiology Collaboration (CKD-EPI) formula was used to calculate eGFR. A detailed chart review of the patients’ electronic medical record was used to estimate 1-, 3-, and 5-year renal survival (see Supplementary Material for details of clinical data collection). Renal survival was measured as the time from the day of biopsy until the patient had 1 of the following events: initiation of dialysis, renal transplant, or all-cause mortality.

Table 1.

Characteristics of study population^a

Characteristic	Value	Units
Number of patients	171	—
Age, median (range)	52 (19−86)	yr
% Male	59.6	%
Number of patients per race/ethnicity (white, black, Hispanic, other)	46, 79, 24, 22	—
BMI, median (range)	28.94 (15 −56.2)	kg/m2
Native kidney biopsy samples	110
Creatinine, median (range)	2.31 (0.54−13.29)	mg/dl
eGFR, median (range)	30 (5−163)	ml/min per 1.73 m2
Proteinuria, median (range)	1.79 (0.03−20.5)	g/g
Interstitial fibrosis, median (range)	30 (0−90)	%
% Patients with 1-yr renal survival	79.1	%
% Patients with 3-yr renal survival	58.9	%
% Patients with 5-yr renal survival	39.3	%

BMI, body mass index; eGFR, estimated glomerular filtration rate.

^aA team of nephrologists performed a detailed chart review to extract demographic, biopsy, and other clinical data from patients who underwent treatment for chronic kidney disease at the Boston Medical Center between 2009 and 2012. The task also included detailed chart review of follow-up reports between 2009 and 2016 for these patients.

Imaging

Kidney biopsy samples were obtained in the form of individual trichrome-stained slides. Each selected core was imaged at ×40, ×100, and ×200 magnifications using a Nikon Eclipse TE2000 microscope (Melville, NY; http://www.bumc.bu.edu/busm/research/cores/). For ×40 magnifications, images were generated with a special consideration to cover the entirety of the sample. This usually resulted in a minimum of 3 images and a maximum of 14 images, with the majority of the samples requiring 6 images to fully capture the full length of the core. For ×100 and ×200 magnifications, about 5 images per magnification were taken sequentially from 1 end of the sample to the other, with almost no overlapping regions between images. All of the images were manually focused using the NIS-Elements AR software (Nikon, Tokyo, Japan) that was installed on the computer connected to the microscope.

Model Training

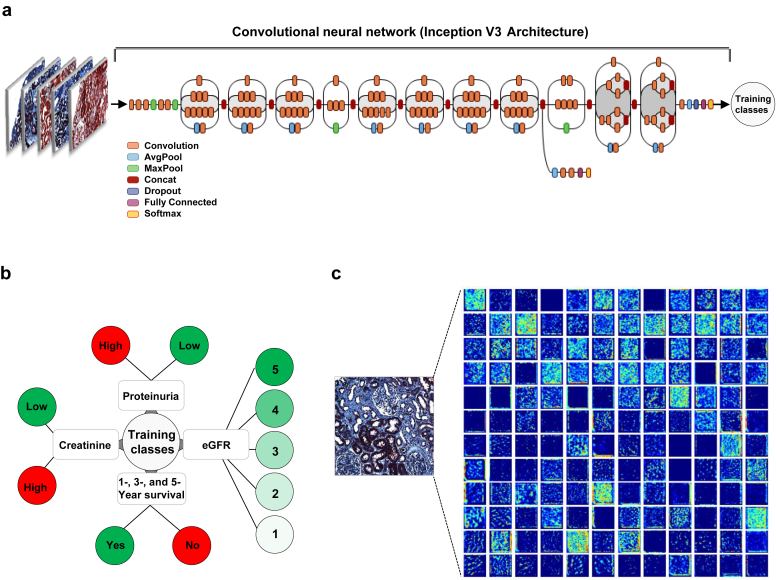
We used Google’s Inception v3 architecture pretrained on millions of images with 1000 object classes by incorporating minor changes to fine-tune the framework and to associate trichrome image features with the clinical phenotypes29, 30 (Figure 2a). Specifically, we removed the final classification layer from the network and retrained it with our dataset using the training classes defined based on the problem of interest (i.e., CKD stage, serum creatinine, and nephrotic-range proteinuria at the time of biopsy, and 1-, 3-, and 5-year renal survival). We then performed fine-tuning of the parameters at all layers. During training, we resized each image to 299 × 299 pixels to make it compatible with the original dimensions of the Inception v3 network architecture and leveraged the image features learned by the ImageNet pretrained network.³⁰ This procedure, known as transfer learning, is optimal, given the amount of data available.

Figure 2.

Deep neural network model. (a) Our classification technique is based on using a transfer learning approach on Google Inception V3 convolutional neural network (CNN) architecture pretrained on the ImageNet dataset (1.28 million images over 1000 generic object classes) and fine-tuned on our dataset (see Methods). Inception v3 CNN architecture reprinted with permission from the Google blog “Train Your Own Image Classifier With Inception in TensorFlow” (https://research.googleblog.com/2016/03/train-your-own-image-classifier-with.html). (b) Using the dataset containing trichrome-stained images from the patients as inputs, several models were constructed with different output classes (chronic kidney disease stage based on estimated glomerular filtration rate [eGFR], binarized serum creatinine and proteinuria, as well as 1-, 3-, and 5-year renal survival). (c) Visualization of filters generated during training. Only 144 of the 256 filters used at the first pooling layer are shown.

Our deep neural network was trained using back-propagation.³¹ Using the framework of transfer learning, we first trained only the top layers that were randomly initialized by freezing all the convolutional layers. We then trained the model using our data for several epochs with the early stopping criteria that monitored the validation loss. We used “rmsprop” with a decay of 0.9, momentum of 0.9, and epsilon of 0.1, along with the use of L1, L2 hybrid regularizers (0.01, 0.01). After the top layers were trained, we performed fine-tuning of the convolutional layers by freezing the bottom (N) layers and training the remaining top layers. Sensitivity analysis was performed to identify the optimal layer (N) for each problem under consideration (Supplementary Figure S2a and b). We then recompiled the model for the above modifications to take into effect. For this task, we used stochastic gradient descent with a learning rate of 0.001 with momentum of 0.9, and L1 and L2 regularizers (0.01, 0.01). We finally trained the model again by fine-tuning the top blocks alongside the top dense layers. We used Google’s TensorFlow (https://www.tensorflow.org) back-end to train, validate, and test our network.

During training, images were augmented by factors of 10 or 100, depending on the problem of interest. Each image was rotated randomly between 0° and 180°, randomly shifted in the horizontal and vertical directions, shifted the channels, sheared, and zoomed, all by a scale of 0.1. Images were also flipped vertically and horizontally, with a probability of 0.5. All these aspects are part of a well-known strategy called data augmentation.32, 33, 34, 35, 36, 37

The first modeling task was a multilabel classification problem in which the resized trichrome images were used as the input and the eGFR-based CKD stage (stages 1−5) defined using the Kidney Disease Outcomes Quality Initiative (KDOQI) guidelines at the time of biopsy was used as the output (Figure 2b). The rest of the tasks were binary classification problems in which the resized trichrome images remained as the input, and binarized values of baseline creatinine >1.3 mg/dl for men and >1.1 mg/dl for women) and nephrotic-range proteinuria (>3.5 g/d), as well as 1-, 3-, and 5-year renal survival values served as outputs, respectively (Figure 2b).

Training and testing of all the models were performed on a 14-core 2.4 GHz Intel Xeon E5-2680v4 processor with Broadwell CPU architecture and an NVIDIA Tesla P100 GPU card with 12 GB of memory that is located on the Boston University’s Shared Computing Cluster (https://www.bu.edu/tech/support/research/computing-resources/scc/).

Performance Metrics

For the binary classification problems (gender-specific high/low creatinine, presence or absence of nephrotic-range proteinuria, and 1-, 3- and 5-year renal survival), the performance of the deep neural network was computed using the c-statistic or area under curve (AUC) computed on the receiver operating characteristic (ROC) curve. We also computed F1 score as a measure of model accuracy that considers both the precision and recall of a test. It is defined as follows:

$$\mathrm{F1=}\mathrm{2}\ast \mathrm{TP}/\left(\mathrm{2}\ast \mathrm{TP}+\mathrm{FP}+\mathrm{FN}\right).$$ (Equation 1)

Here, TP denotes true-positive values, and FP and FN denote false-positive and false-negative cases, respectively (see Supplementary data for more details).

We also computed Matthews correlation coefficient (MCC),³⁸ which is a balanced measure of quality for dataset classes of different sizes of a binary classifier and defined as follows:

$$\mathrm{MCC=}{\left[\left(\mathrm{TP}\ast \mathrm{TN}\right)-\left(\mathrm{FP}\ast \mathrm{FN}\right)\right]/\left[\left(\mathrm{TP}+\mathrm{FP}\right)\ast \left(\mathrm{TP+FN}\right)\ast \left(\mathrm{TN+FP}\right)\ast \left(\mathrm{TN+FN}\right)\right]}^{0.5}.$$ (Equation 2)

Here, TN denotes true negative values. For the multilabel classification problem (i.e., prediction of eGFR-based CKD stage), model accuracy and Cohen’s κ score were computed.39, 40, 41 The κ statistic measures interrater agreement for categorical items. Note that accuracy of 1 is a perfect score, and that a κ score of 1 indicates perfect agreement between the true and predicted labels.

Results

Patient Population

Since this was a retrospective study, we had the advantage of carefully curating all the digital images as well as extracting corresponding baseline characteristics and clinical phenotypes for each patient. The baseline characteristics are representative of a population of patients attended to at a nephrology service at a teaching hospital (Table 1). About 60% patients were male, and about 46% of the overall population was African American. The majority of patients had hypertension (∼84%) and cardiovascular disease (∼75%), and about 43% had diabetes. About 64% of the biopsies were from native kidneys, and the remainder were from transplanted kidneys. About 82% of patients had CKD stage 3 to 5 based on the eGFR using the CKD-EPI formula; 6% had stage 2 CKD, and the rest had stage 1 CKD. About 35% of patients had nephrotic-range proteinuria (>3.5 g/d).

Imaging

Light microscopy images of Masson trichrome−stained sections were captured at 3 different magnifications (×40, ×100, and ×200) and processed in NIS-Elements AR software (Nikon) (Figure 1). In total, we processed kidney biopsy from 171 patients, which resulted in 2255 unique images that were saved in 16-bit TIFF format. These images were then converted to 8-bit red−green−blue (RGB) color images in TIFF format, resized, and subsequently used for training the deep neural network (Figure 2).

Performance Metrics

We developed 6 independent CNN models to better associate information derived from the trichrome images with the clinical phenotypes (CKD stage based on eGFR, creatinine, and nephrotic-range proteinuria, all at the time of biopsy) and renal survival (Figure 2b). For each classification task, we also developed a model to associate pathologist-derived fibrosis score (PEFS) with the output class of interest that served as the baseline for comparison.

For each task, a detailed set of sensitivity analysis was performed, including the layer selection for fine-tuning as well as the impact of batch size on model performance. The CNN model with the best cross-validated performance was selected. For the eGFR model, model accuracy and κ values were computed.⁴² For the binary classification models, area under the curve (AUC or c-statistic), F1 score (Equation 1 in the Methods), and Matthews correlation coefficient (MCC) (Equation 2 in the Methods) were computed (Supplementary Figure S3). Note that the F1 score is a widely used metric in the ML community, as it considers both the precision and the recall of a test, and thus it can be viewed as a weighted average of precision and recall. However, the F1 score does not take the true negatives into account, and therefore composite metrics such as MCC can be considered as more robust measures of performance. In essence, MCC is a correlation coefficient between the observed and predicted binary classifications and a balanced measure that can be used even if the classes are of different sizes.³⁸

Nephropathologist Model Based on Fibrosis Score

Our first goal was to develop baseline models by which to compare the performance of the CNN models. Because PEFS was the input, a linear discriminant classifier was used to associate this score with the respective output class labels (CKD stage, serum creatinine, etc.). Model results indicated that the performance of the pathologist model was remarkably good, considering that only a single scalar value derived from detailed visual assessment by the nephropathologist was used as the input feature (Figure 3, Figure 4, Figure 5). This result underscores the notion that fibrosis score as such is an important predictor of clinical phenotypes including renal survival.

Figure 3.

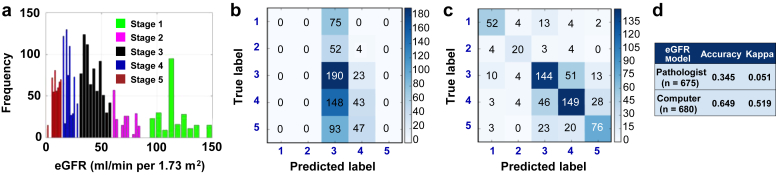
Predictive model of estimated glomerular filtration rate (eGFR) at the time of biopsy. (a) Distribution of eGFR values across the patient cohort. The histogram frequency corresponds to the number of images. (b) A multilabel linear discriminant classifier was trained on the data with pathologist-derived fibrosis as the input and eGFR-based chronic kidney disease (CKD) stage (stages 1−5) at the time of biopsy as the output. Image data were randomly split such that 70% of the data (n = 1512) were reserved for model training and the remaining for testing (n = 648). “True label” denotes the CKD stage derived from calculated eGFR values at the time of biopsy, whereas “Predicted label” indicates the model assessment of the CKD stage. (c) Fine-tuned convolutional neural network (CNN) model was used to predict on test image data (n = 677) not used for training. Performances of the pathologist (b) and the CNN (c) models are shown in the form of confusion matrices. (d) A κ score was computed by comparing model-derived output values with the clinically reported values of eGFR. The CNN model accuracy and κ score indicate the superior performance of the CNN model in comparison to the pathologist model.

Figure 4.

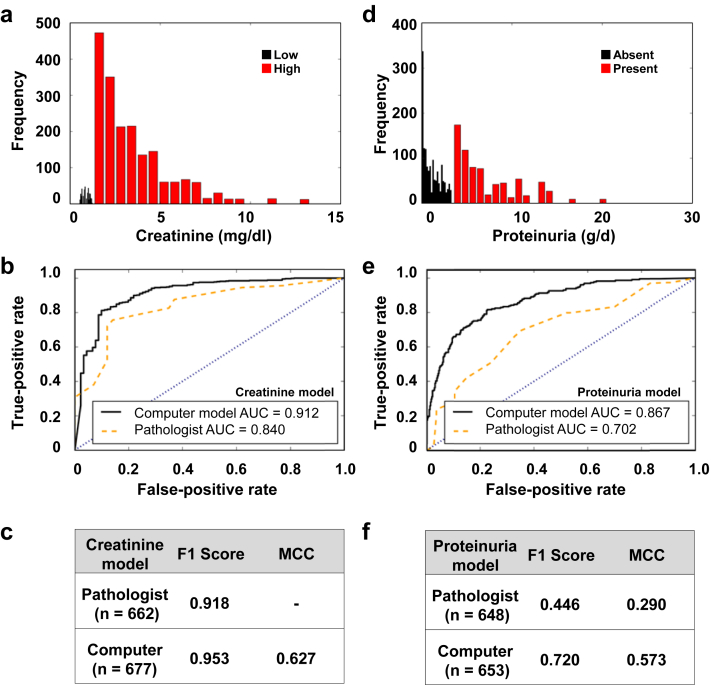
Predictive models of creatinine and nephrotic-range proteinuria at the time of biopsy. (a) Distribution of creatinine values across the patient cohort. The histogram frequency corresponds to the number of images. Color to a set of bars within the histogram was assigned based on the Kidney Disease Outcomes Quality Initiative (KDOQI) guideline−driven cutoff values for high and low creatinine. (b) A binary linear discriminant (BLD) classifier was trained using 70% of the image data (n = 1545), with pathologist-derived fibrosis value as the input and baseline creatinine value at the time of biopsy as the output. Model predictions were performed on the remaining 30% of the data (n = 662), and a receiver operating characteristic (ROC) curve was generated. (c) Both F1 score and Matthews correlation coefficient (MCC) computed using models’ performances on test data indicate superior performance of the convolutional neural network (CNN) model. (d) Distribution of proteinuria values across the patient cohort. Color to a set of bars within the histogram was assigned based on the KDOQI guideline−driven cutoff value for nephrotic-range proteinuria (g/d). (e) A similar BLD classifier was trained using 70% of the image data (n = 1512), with the pathologist-derived fibrosis value as the input and the clinical indication of proteinuria as the output. Model predictions were performed on the remaining 30% of the data (n = 648), and an ROC curve was generated. (f) Both the F1 score and the MCC computed using models’ performances on test data indicate superior performance of the CNN model in comparison to the pathologist model.

Figure 5.

Predictive models of 1-, 3-, and 5-year renal survival. Three separate binary linear discriminant classifiers were trained using 70% of the image data, with pathologist-derived fibrosis value as the input and 1-, 3-, and 5-year renal survival values computed from the clinical reports as the outputs, respectively. The convolutional neural network (CNN) framework was also used to train separate models with the 3 outputs. Predictions of the models were performed on the remaining 30% of the data, denoted as “n” for each case. Receiver operating characteristic curves comparing the pathologist model with the CNN model were generated for each case ([a] 1-year, [b] 3-year, and [c] 5-year renal survival) respectively. F1 score and Matthews correlation coefficient (MCC) values computed for each case ([d] 1-year, [e] 3-year, and [f] 5-year renal survival) on the test data also indicate superior performance of the CNN model.

Also, choosing a different learning algorithm for the classification task of associating PEFS with a clinical phenotype did not alter our overall inferences related to the comparison with the CNN model performance. We used 3 different algorithms—linear discriminant analysis, Naïve Bayes, and support vector machine classifiers—to build several classifiers with PEFS as the input and different clinical phenotypes (serum creatinine and proteinuria at the time of biopsy as well as 1-, 3-, and 5-year renal survival) as the outputs, respectively. Model training, followed by validation on test data that had not been used for training, resulted in similar performances of the binary classifier (Supplementary Figure S4).

CNN Model for Prediction of Clinical Phenotypes at the Time of Biopsy

Our next task was to evaluate the predictive capability of the CNN model. The CNN models developed using the transfer learning approach outperformed the models derived using PEFS on all the classification tasks. Three separate CNN models were trained to associate the images with the stage of kidney disease at the time that the biopsy procedure was performed. The first model was related to predicting CKD stage based on eGFR at the time of biopsy, and our deep learning model resulted in a superior performance (κ = 0.519 [CNN model] vs. κ = 0.051 [pathologist]) (Figure 3b−d). The CNN architecture resulted in superior performance even for models constructed using images processed at only a single magnification. For example, we trained a separate CNN model using images taken at ×100 magnification and predicted on test data of ×100 images not used for training. For comparison purposes, we extracted PEFS from the clinical biopsy reports for these images, and constructed a classifier using linear discriminant analysis. Even for this case, the CNN model outperformed the model derived using PEFS (Supplementary Figure S5).

CNN models used for the binary classification tasks of predicting clinical phenotypes such as gender-specific high/low value of creatinine as well as nephrotic-range proteinuria also outperformed the performance of the models constructed using PEFS. Specifically, for the creatinine CNN model, the c-statistic (or AUC) was 0.912 versus an AUC of 0.840 for the model derived using PEFS (Figure 4b). The superiority of the CNN model is exemplified with the help of other metrics including F1 score (0.918 [pathologist)] and 0.953 [model]), and MCC value of 0.627 for the CNN model (Figure 4c). Note that MCC computation for the case of the pathologist model did not result in a numeric value because both the false-positive and true-negative values were 0 (Equation 2). Similarly, the CNN model predicted the presence of nephrotic-range proteinuria (AUC 0.867) more accurately than the model derived using PEFS (AUC 0.702) (Figure 4e). Other metrics that were computed for this case also showed the superiority of the CNN model (F1 score: 0.446 [pathologist] vs. 0.720 [CNN model]; MCC: 0.290 [pathologist] vs. 0.573 [CNN model]) (Figure 4f). Although we recognize that one does not need a kidney biopsy to determine the stage of CKD, serum creatinine level, or presence of nephrotic-range proteinuria, this exercise allowed us to test the CNN model’s predictive ability against hard numeric (or categorical) values and to proceed with the task of testing its prognostic value.

Prognostic Value of the CNN Model

One of the most interesting aspects of leveraging the CNN model architecture was to evaluate its ability to train the biopsy images for prognostic purposes. Specifically, we trained independent CNN models for 3 binary classification tasks focused on predicting 1-, 3-, and 5-year renal survival, respectively. All patients who underwent a kidney biopsy and were followed up respectively for 1, 3, and 5 years after the biopsy were included in the study. Specifically, kidney biopsy data as well as 1-year renal survival information were available on 158 patients (2050 images), followed by biopsy data and 3-year survival available on 146 patients (1900 images), and finally biopsy data and 5-year survival information available on 117 patients (1517 images). All 3 models resulted in better performance than the respective models developed using the PEFS alone. Specifically, the AUC values for the CNN model for 1-, 3-, and 5-year renal survival were 0.878, 0.875, and 0.904, respectively (Figure 5a−c), whereas the AUC values of the model developed using PEFS for 1-, 3-, and 5-year renal survival were 0.811, 0.800, and 0.786, respectively (Figure 5a−c). Similarly, other metrics such as F1 score and MCC computed for these models also confirmed the superiority of the CNN model over the classification model generated using PEFS (Figure 5d−f). Thus, the CNN architecture accurately reflects the stage of kidney disease as well as renal survival.

Discussion

Renal biopsy is an invasive and yet an invaluable procedure for the diagnosis, prognosis, and treatment of patients with kidney disease.⁴³ Detailed histologic processing of biopsy samples yields important pathologic information, and digitization of these specimens lends itself to the possibility of using computer-based technologies for better quantification. In this study, we chose to apply ML technology to the analysis of interstitial fibrosis, a common manifestation of a wide variety of kidney diseases and a prognostic indicator of chronic kidney disease progression in humans.44, 45, 46, 47 An important strength of the study is that the ML technology was applied to trichrome-stained histologic images of routine kidney biopsy samples without any special processing or manipulation other than digital scanning, which allowed us to directly compare the results of the ML analysis with those derived from the clinical pathological report on the same specimens. Although our results demonstrating the utility of ML are limited to the analysis of interstitial fibrosis, the developed ML framework can be extended to associate other complex renal pathologies with several clinical phenotypes.

Deep learning algorithms such as CNN, powered by advances in hardware as well as software and well-curated datasets, have recently been shown to exceed human performance in visual object recognition tasks.³¹ Although there is an increasing focus on developing these approaches using several modalities of data, such as audio, text, and video, our work focused specifically on image-based classification. The CNN architecture has been shown to be optimal for these tasks, whereas other deep learning methods can be used for applications above and beyond visual object recognition.³¹ Moreover, we are witnessing an increasing interest in image-based classification of a clinical phenotype using deep learning, and it has been shown to be extremely effective in several clinical disciplines such as dermatology, radiology, and oncology.7, 8, 9, 13, 15, 16, 17, 18, 20, 21, 23, 25, 28, 29, 48, 49, 50, 51 To the best of our knowledge, no body of work related to applications of deep learning in nephropathology has been published to date. In this article, we have outlined the development of a CNN that at least matches the performance of a skilled nephropathologist’s ability to quantify the extent of kidney fibrosis as it relates to 6 key classification tasks: determination of CKD stage based on eGFR, baseline serum creatinine and nephrotic-range proteinuria at the time of biopsy, as well as 1-, 3-, and 5-year renal survival. Although the case with eGFR as the output was modeled as a multi-label classification task (CKD stages; 5 labels), the rest were modeled as binary classification tasks.

As part of routine clinical workflow, the expert nephropathologist carefully reviews the trichrome stain−based histological images and assigns a grade of renal fibrosis. Typically, the grading is discrete and ranges from 0 to 100, with 0 assigned to no detectable fibrosis and 100 assigned to the biopsy with complete fibrosis. Such a derived grading process resulting in a single scalar value has shown to have remarkable clinical utility.43, 46, 47 This was confirmed in this study by the models that we developed using the pathological grading as the input and the output classes derived from a detailed chart review of the clinical reports spanning more than several years (Figure 3, Figure 4, Figure 5).

To evaluate the performance of the CNN model on the same biopsy samples, we performed a computer-based analysis of the digitized biopsy images and related the findings to the outcomes of interest. This task resulted in a dataset comprising 171 patients with 2255 images that were subsequently used for model training. As shown in Figure 3, Figure 4, Figure 5, training and testing on these images, followed by predictions on test data, demonstrated superior CNN model performance in comparison to the linear discriminant classifier trained using the pathologist-derived fibrosis score (Supplementary Table S1).

Superiority of the CNN model can be attributed to several factors. First, the concept of transfer learning has boosted the use of CNN models for classification tasks with smaller datasets, as they have begun to single-handedly disconnect the presumed link between larger dataset size and high model accuracy. This is because we can use pretrained CNN models with features that were already learned, using millions of images with different object classes, and that produced outstanding results exceeding human performance.²⁹ Moreover, transfer learning usually results in faster training times than required for constructing a new CNN from scratch, as there is no need to estimate all the parameters in a pretrained CNN. Despite these advantages, we still used a rigorous cross-validation strategy of splitting the dataset into 2 portions and validating our CNN model using the test data that were not used for model training. The transfer learning approach turned out to be very effective, given the number of trichrome images that were generated from 171 patients. Also, to make the most of this dataset, we performed “data augmentation” whereby each image was subjected to random transformations and then fed into the CNN model as multiple images for training.³¹ Moreover, the process of introducing additional variability/noise over that which could possibly be contained within the original images has been shown to limit model overfitting and to increase model generalizability.31, 32, 33, 34, 35, 36, 37

The second reason that explains the superior CNN performance is related to the deep neural network architecture itself. Using operators such as convolution, activation, and pooling (or subsampling), training a CNN model involves performing these operations multiple times in a systematic fashion to transform pixel-level information to high-level features of the input image. These features are then used to perform the classification task using fully connected layers along with training the model using another process called backpropagation, a method that is widely used in the ML community to train artificial neural networks.³¹ Therefore, the CNN model training is in stark contrast to the pathologist model training that was done using a single value (fibrosis score) as an input feature along with corresponding output classes. This aspect underscores the value of leveraging a computer algorithm such as CNN to capture pixel-level information derived from the whole image and to associate it with an outcome of interest but not a fibrosis score per se.

Even though the CNN model outperformed on all the classification tasks, the model derived using PEFS was a close second. This was especially the case with the creatinine, proteinuria, and survival models, as the performances were almost comparable, with the CNN model slightly outperforming the PEFS model each time. However, for predicting the CKD stage, the CNN model resulted in a much better accuracy (Figure 3 and Supplementary Figure S5). One possible explanation is that predicting the CKD stage is a multilabel classification problem with 5 different outcomes, whereas all the other cases are binary classification problems with only 2 different outcomes. Because the PEFS model has only a single scalar value for training, one could argue that CNN model training that involves fine-tuning of several parameters is more suitable for tackling both binary and multilabel classification problems.

Accurate prediction of renal survival and other clinical phenotypes can inform therapeutic interventional strategies. CNN model architectures are beginning to address this aspect with a high level of success, and therefore one can envision the utility of these tools within the daily clinical workflow. A strength of this study is that it demonstrates the ability of an ML algorithm applied to digital images of routinely prepared kidney biopsy slides to assess the severity of pathology and its relationship with clinical measures with accuracy at least equivalent to that of an experienced nephropathologist without the need for labor-intensive morphometric analysis by a skilled observer. Although similar accuracy can be achieved, as recently documented, by meticulous scoring of pathological elements,⁴³ such methods are not applicable to routine anatomic pathology.

If the CNN architecture is embedded in the form of software application (or “app”) within a mobile device or an easily accessible computer, then predictions based on the digitized histologic images can be derived. Using our data as an example, a potential clinical workflow could involve the pathology clinic receiving a kidney biopsy sample, and processing it using trichrome or other staining protocol, followed by sample digitization into a red−green−blue (RGB) color image. If this color image were directly fed into the app containing the trained CNN model installed on the pathologist’s computer, then predictions of 1-, 3-, and 5-year renal survival could be produced as outputs of the model instantaneously. These predictions would provide added value to the biopsy findings and, along with other clinical assessments, would enable a more precise care management and follow-up strategy on the biopsied patient. This technology could become all the more useful in areas where nephropathology expertise is not readily available, so a general pathologist could directly interpret these images using the app and could prepare the clinical reports accordingly to facilitate care management. For all these cases, prospective validation is needed in order for the app to be considered as a clinical tool. One could imagine designing a prospective study in which the app driven by the CNN model predicts the outcome (such as 5-year renal survival) immediately after kidney biopsy is performed on a patient. We can then track the patient over time and check whether the model prediction validates with the actual time of renal survival.

The ML algorithms clearly have limitations and provide incremental value rather than replacing the human factor. We acknowledge that a nephropathologist’s clinical impression and diagnosis is based on contextual factors above and beyond visual and pathologic inspection of a lesion in isolation. Nevertheless, the ability to classify histologic images using a computer with the accuracy of an experienced nephropathologist has the potential to affect renal practice, especially in resource-limited settings.

Another limitation of our study is that we did not consider the possible impact of treatment on renal survival. For example, it is possible that treatment with immunosuppressive drugs might have altered the course and influenced renal survival, which of course, could not have been predicted by ML analysis at the time of the original biopsy. In other words, renal survival might have been better in such cases than our ML model would have predicted. Despite that, the model was remarkably good at predicting survival, and one can only assume that the extent of kidney fibrosis is a major determinant of outcome regardless of treatment. Thus the value of the ML analysis in such cases would be to exclude cases in which treatment would be futile and in which the risks would outweigh the benefits.

Our work relied only on images derived using the Masson trichrome stain, as it has long been used as a standard for quantifying fibrosis not only in renal but in other organ pathologies. Some pathologists, however, rely on other protocols such as Sirius Red staining, and recent work in this area has demonstrated staining protocol−specific accuracies in terms of quantifying fibrosis.⁵¹ The CNN model described here could likely be applied equally well to images generated with Sirius Red or other staining protocols, including periodic acid−Schiff. One could also imagine extending the CNN architecture to model image data derived directly from whole slide imaging. The whole slide imaging−derived images are typically of higher-bit graphics (∼16 bits), and thus require special handling and pre-processing even before they can be used for model construction.⁴³

Although we performed extensive studies to identify the best batch size, learning rate, augmentation factor, and CNN layers for network fine-tuning of images stained to highlight fibrosis, this technology lends itself to the analysis of several other parameters such as glomerular sclerosis and immunohistochemistry of inflammatory cell infiltrates or specific cell types or components. Furthermore, the CNN framework allows for the development of glomerular disease−specific models to evaluate focal segmental glomerulosclerosis and chronic allograft nephropathy, and possibly to identify more accurately those cases in which immunosuppressive therapy is likely to be futile because of the extent of kidney damage.

In conclusion, in this study, we demonstrated the effectiveness of using deep learning architecture in nephropathology, a technique that enabled us to associate trichrome-stained histologic images obtained at the time of biopsy with several clinical phenotypes. Using a single CNN architecture trained on these images, we compared the CNN performance with that of an experienced nephropathologist by testing the model across 6 classification tasks: CKD stage based on eGFR, high/low creatinine and nephrotic-range proteinuria at time-zero biopsy, as well as 1-, 3-, and 5-year renal survival. This rapid, scalable method can be deployable in the form of software at the point of care, and holds the potential for substantial clinical impact, including augmenting clinical decision making for nephrologists. This framework can also be adapted to other organ-specific pathologies focused on evaluating fibrosis, as well as image datasets developed using other histological staining protocols. Further validation of the models across different clinical practices and image datasets is necessary to validate this technique across the full distribution and spectrum of lesions encountered in a typical pathology service.

Disclosure

All the authors declared no competing interests.

Supplementary Material

Supplementary Material

Glossary of technical terms, data collection, performance metrics, and data augmentation.

Figure S1

Flowchart representing the project workflow.

Figure S2

Sensitivity analysis on the convolutional neural network (CNN) model.

Figure S3

Sensitivity analyses performed to determine optimal layer for fine-tuning the convolutional neural network (CNN) model.

Figure S4

Performance of the model developed using pathologist-derived estimate of fibrosis.

Figure S5

Predictive model of eGFR at the time of biopsy using ×100 magnification images.

Figure S6

Performance of the convolutional neural network (CNN) model is a function of data augmentation.

Table S1

Comparison of convolutional neural network (CNN) and pathologist-estimated fibrosis score (PEFS) models.