Using the EM algorithm for Bayesian variable selection in logistic regression models with related covariates

Abstract

We develop a Bayesian variable selection method for logistic regression models that can simultaneously accommodate qualitative covariates and interaction terms under various heredity constraints. We use expectation-maximization variable selection (EMVS) with a deterministic annealing variant as the platform for our method, due to its proven flexibility and efficiency. We propose a variance adjustment of the priors for the coefficients of qualitative covariates, which controls false-positive rates, and a flexible parameterization for interaction terms, which accommodates user-specified heredity constraints. This method can handle all pairwise interaction terms as well as a subset of specific interactions. Using simulation, we show that this method selects associated covariates better than the grouped LASSO and the LASSO with heredity constraints in various exploratory research scenarios encountered in epidemiological studies. We apply our method to identify genetic and non-genetic risk factors associated with smoking experimentation in a cohort of Mexican-heritage adolescents.

1. Introduction

Consider modelling the relation between a binary outcome, Y_i ∈ {0, 1}, and a set of covariates, ${\mathbf{x}}_i^{\prime }=(x_{i1},\dots ,x_{ip})$, with a generalized linear model using the canonical logit link function [1]. Formally, this relation can be modelled as

$$\text{logit}(\omega ({\mathbf{x}}_i))=\log \left[\frac{\omega ({\mathbf{x}}_i)}{1-\omega ({\mathbf{x}}_i)}\right]={\alpha }_0+{\beta }_1{x}_{i1}+{\beta }_2{x}_{i2}+\cdots +{\beta }_p{x}_{ip},$$ (1)

where α₀ is an intercept term, β₁, …, β_p are regression coefficients, and ω(x_i) is the probability that Y_i = 1. There are various other methods for modelling this relation [2–5], including the probit link [6]. However by avoiding the logit link, regression coefficients are no longer interpreted as log odds ratios. For many fields, including epidemiological research, this interpretation is essential to the model’s development and utility.

A critical step in model building is variable selection or determining associated covariates in a regression model [7]. Model misspecification leads to biased parameter estimates [1]. This results in inaccurate model interpretation, a problem when the model’s purpose is to explain, rather than predict. In exploratory epidemiological research, the relation between a set of covariates, or risk factors, and a binary outcome (e.g. death, disease onset, or health behaviour occurrence) is not fully understood. To generate hypotheses then, researchers use variable selection methods to identify associated covariates. Bayesian variable selection methods allow researchers to incorporate prior knowledge of a covariate’s possible association with the outcome. Some of these include Markov Chain Monte Carlo model composition [8], Bayesian model averaging [9], Bayesian LASSO [10], stochastic search variable selection [11], and expectation- maximization variable selection (EMVS) [12]. These methods are attractive because they inherently perform variable selection through the flexibility of a Bayesian hierarchical structure.

In exploratory epidemiological studies, researchers need variable selection methods for binary outcomes that can handle related covariates, such as interaction terms and qualitative covariates. Epidemiological researchers typically reparameterize qualitative covariates, such as race, with indicator variables to simplify interpretation (i.e. an m+1-level qualitative covariate enters the model as m-indicator variables). Often, the indicator variables associated with the qualitative covariate are treated as a group [13–17]. If one member of the group is included in the model as a significant covariate, the entire group is included in the model. By assigning one inclusion parameter to the group, the dimension of the model space is reduced, and the indicator variables associated with the qualitative covariate enter or leave the model together. In practice, this method prevents researchers from having to fit a secondary model that forces in the entire group when at least one but not all of the indicator variables are initially selected. Since only one fit is necessary, this strategy maintains false positive rates while incorporating knowledge of covariates’ relations and preserving interpretation.

In practice, main effects, x_i1, x_i2, …, x_ip, may not fully characterize the complex relation between risk factors and an outcome. For example, in a study investigating risk factors associated with smoking experimentation, it may be of interest to identify gene × gene and gene × environment interactions. Among model selection methods, researchers impose hierarchical structures to constrain the relation between main effects and their interactions [13,18–24]. Constraints, such as strong or weak heredity, follow the inheritance principle (i.e. a higher order term depends on the lower order terms that compose it) [13]. We characterize inheritance by referring to main effects that combine to interact as parents of the interaction. For example, a strong heredity constraint considers an interaction if both parents forming the interaction are included in the model, and a weak heredity constraint implies at least one active parent [13]. Heredity constraints shrink the model space and produce well formulated, interpretable models [25].

While methods for selecting qualitative covariates and interaction terms are well developed separately, researchers require variable selection methods that can handle them simultaneously. Lim and Hastie [22] suggest a method that accommodates both data types but only under a strong heredity constraint. Further, their method does not follow the inheritance principle, since lower order terms’ inclusion can depend on their higher order terms. Our goal is to develop a variable selection method for binary outcomes that can identify interaction terms of continuous and qualitative covariates under the inheritance principle, is generalizable to different types of heredity constraints, and can handle all pairwise interaction terms as well as selected subsets of specific interactions. To achieve this goal, we select EMVS as the platform of our method.

EMVS is a flexible and efficient Bayesian method motivated by stochastic search variable selection. The continuous spike-slab normal mixture model prior framework of stochastic search variable selection shrinks non-associated covariates’ coefficients to zero and allows associated covariates’ coefficients to be freely estimated. Selection is determined by corresponding inclusion parameters. In contrast to stochastic search variable selection, where inference is drawn from the fully sampled posterior distribution using Markov Chain Monte Carlo, EMVS simply estimates the posterior modes with the expectation-maximization (EM) algorithm [26]. This algorithm iteratively estimates the model’s unknown parameters, treating the covariates’ inclusion in the model as missing information, by alternating between an expectation step (E-step) and maximization step (M-step) until convergence. The EM algorithm is sensitive to starting values and is not guaranteed to converge at the global mode, which leads to biased interpretation of the model. To resolve this problem, Ročková and George [12] reinforce EMVS with a deterministic annealing variant. This variation removes the algorithm’s dependence on initial parameterization and increases the probability of finding the true global mode. As a result, EMVS outperforms stochastic search variable selection in a fraction of the time [12]. EMVS’s short runtime allows researchers to tune the model and adjust priors efficiently. By adjusting selection priors, EMVS accommodates dynamic, model-building challenges, such as structured covariates [12]. EMVS was originally shown to perform well selecting covariates associated with continuous outcomes in p > > n settings [12], but it has since been developed for binary outcomes in p > > n settings [27] and quantile regression models in p < n settings [28]. EMVS’s proven flexibility to different data structures and efficiency in practice support its role as the platform of our method.

The remaining sections of this paper are organized as follows. In Section 2, we develop EMVS with a deterministic annealing variant for logistic regression models and propose adjustments to the E-step that accommodate interaction terms and qualitative covariates. In Section 3, we present the results of simulation studies conducted to assess the performance of EMVS for logistic regression models with these accommodations. In Section 4, we briefly discuss the application of this method to identify risk factors associated with smoking experimentation in a cohort of Mexican-heritage adolescents. In Section 5, we provide concluding remarks.

2. Methods

2.1. EMVS logistic

We present EMVS in the context of logistic regression models and then reinforce the method with a deterministic annealing variant. Consider i = 1, …, n, observations of an outcome y_i ∈ {0, 1}, that are potentially related to p covariates, typically centred, through:

$$f(\mathbf{y}|\mathit{\beta })={\displaystyle \prod _{i=1}^n\omega {({\mathbf{x}}_i)}^{y_i}{(1-\omega ({\mathbf{x}}_i))}^{(1-y_i)}},$$ (2)

where ω(x_i) = exp(α₀ + β₁x_i1 + ⋯ + β_px_ip)/(1 + exp(α₀ + β₁x_i1 + ⋯ + β_px_ip)) and ${\mathbf{x}}_i^{\prime }=(x_{i1},\dots ,x_{ip})$ (Note if we use the logit transformation on ω_i, we get Equation (1)). α₀ represents an intercept term whose prior follows a normal distribution with mean zero and diffuse variance, v₁. β is a p-dimensional vector of regression coefficients whose prior regulates the variable selection procedure within EMVS

$$\pi (\mathit{\beta }|\mathit{\gamma },v_0,v_1)=N_p(\mathbf{0},{\mathbf{D}}_{\mathit{\gamma }}),$$ (3)

where D_γ is a p × p diagonal matrix with each D_jj term equal to (1 − γ_j)v₀ + γ_jv₁. Here, v₀ and v₁ are pre-set variances of exclusion and inclusion, similar to the τ and c tuning parameters in stochastic search variable selection [11,12]. By setting v₀ and v₁ to small and large fixed values, respectively, non-associated covariates’ coefficients are shrunk to zero while associated covariates’ coefficients are freely estimated. The p-dimensional inclusion indicators γ = (γ₁, γ₂, …, γ_p), γ_j ∈ {0, 1}, are treated as missing. When the inclusion indicators are considered exchangeable, or there is no known relation between them, π(γ|θ) is given the iid Bernoulli prior

$$\pi (\mathit{\gamma }|\theta )={\theta }^{|\gamma |}{{(1-\theta )}^{p-}}^{|\gamma |},$$ (4)

where $|\gamma |={\displaystyle {\sum }_{j=1}^p{\gamma }_j}$, and γ_j = 1 indicates a covariate’s inclusion in the model. The sparsity θ ∈ [0, 1] completes the model’s formulation. Small values of θ favour sparser models. For illustration, its prior distribution is set to an uninformative, conjugate beta(a, b), where a = b = 1.

To perform EMVS, we iteratively determine the conditional expectation of the log posterior distribution, termed the Q-function, with respect to the missing $\mathit{\gamma }|{\alpha }_0^{(k)}$, β^(k), θ^(k), y (E-step), and then maximize with respect to the parameters α₀, β, and θ (M-step) until convergence.

The Q-function, for iteration k+1, is defined as

$$Q\left[{\alpha }_0,\mathit{\beta },\theta |{\alpha }_0^{(k)},{\mathit{\beta }}^{(k)},{\theta }^{(k)}\right]=E_{\gamma }|\cdot \left[\log (\pi ({\alpha }_0,\mathit{\beta },\theta ,\mathit{\gamma }|\mathbf{y})|{\alpha }_0^{(k)},{\mathit{\beta }}^{(k)},{\theta }^{(k)},\mathbf{y})\right]={\displaystyle \sum _{\mathit{\gamma }}\log \left(\pi ({\alpha }_0,\mathit{\beta },\theta ,\mathit{\gamma }|\mathbf{y})\right)\times \pi (\mathit{\gamma }|{\mathit{\beta }}^{(k)},{\theta }^{(k)})},$$ (5)

where $E_{\gamma |{\alpha }_0^{(k)},{\mathit{\beta }}^{(k)},{\theta }^{(k)},\mathbf{y}}=E_{\gamma |{\mathit{\beta }}^{(k)},{\theta }^{(k)}}$, which we denote as E_γ|·. Here, π(γ | β^(k), θ^(k)) is the posterior probability distribution for inclusion. Equation (5) simplifies into three components,

$$Q\left[{\alpha }_0,\mathit{\beta },\theta |{\alpha }_0^{(k)},{\mathit{\beta }}^{(k)},{\theta }^{(k)}\right]=C+Q_1\left[{\alpha }_0,\mathit{\beta },|{\alpha }_0^{(k)},{\mathit{\beta }}^{(k)},{\theta }^{(k)}\right]+Q_2\left[\theta |{\mathit{\beta }}^{(k)},{\theta }^{(k)}\right],$$ (6)

where C is a constant term,

$$\begin{gathered} Q_1\left[{\alpha }_0,\mathit{\beta }|{\alpha }_0^{(k)},{\mathit{\beta }}^{(k)},{\theta }^{(k)}\right]={\displaystyle \sum _{i=1}^n{y}_i\log (\omega ({\mathbf{x}}_i)) \\ +{\displaystyle \sum _{i=1}^n(1-y_i)\log (1-\omega ({\mathbf{x}}_i))-\frac{1}{2v_1}{\alpha }_0^2-\frac{1}{2}{\displaystyle \sum _{j=1}^p{\beta }_j^2{E}_{\gamma |\cdot }\left[\frac{1}{v_0(1-{\gamma }_j)+v_1{\gamma }_j}\right]}}}, \end{gathered}$$ (7)

and

$$Q_2\left[\theta |{\mathit{\beta }}^{(k)},{\theta }^{(k)}\right]={\displaystyle \sum _{j=1}^p{E_{\gamma }}_{|\cdot }\left[{\gamma }_j\right]\log \left[\frac{\theta }{1-\theta }\right]+(a-1)\log (\theta )+(b+p-1)\log (1-\theta ).}$$ (8)

For the E-step, we evaluate the conditional expectations within the Q-function at the current iteration, k. The conditional expectation of the inclusion parameter, E_γ|·[γ_j], is computed as

$${E_{\gamma }}_{|\cdot }\left[{\gamma }_j\right]=P({\gamma }_j=1|{\mathit{\beta }}^{(k)},{\theta }^{(k)})=\frac{a_j}{a_j+b_j}=p_j^{\ast },$$ (9)

where $a_j=\pi ({\beta }_j^{(k)}|{\gamma }_j=1)P({\gamma }_j=1|{\theta }^{(k)})$, $b_j=\pi ({\beta }_j^{(k)}|{\gamma }_j=0)P({\gamma }_j=0|{\theta }^{(k)})$, and P(γ_j = 1|θ^(k)) = θ^(k). The other conditional expectation is the average of the precisions, 1/v₀ and 1/v₁, weighted by $p_j^{\ast }$, the expected probability of inclusion,

$$E_{\gamma |\cdot }\left[\frac{1}{v_0(1-{\gamma }_j)+v_1{\gamma }_j}\right]=(1-p_j^{\ast })\frac{1}{v_0}+p_j^{\ast }\frac{1}{v_1}.$$ (10)

For the M-step, note that we can maximize Q₁ and Q₂ separately. The maximization of Q₁ does not have a closed-form solution. So, we use the EM gradient method to approximate the M-step of the EM algorithm with one iteration of the Newton–Raphson algorithm [29]. See Appendix 1 for derivations. The closed-form solution of Q₂ remains the same as the original formulation [12]

$${\theta }^{(k+1)}\frac{{\displaystyle {\sum }_{j=1}^p{p}_j^{\ast }+a-1}}{a+b+p-2}.$$ (11)

The algorithm iteratively progresses between the E-step and M-step until convergence. Following [30], convergence is determined when the absolute value of the difference between the log-likelihood distribution evaluated at the current and next step of the EM algorithm is less than a set threshold. See Appendix 2 for the convergence stopping rule. Once the EM algorithm has converged, the final estimates, ${\alpha }_0^{\ast }$, β^∗, and θ^∗, maximize Equation (5). Ročková and George [12] suggest that inclusion in the model is determined if $E_{\mathit{\gamma }|\mathit{\beta }\ast ,\theta \ast }[{\gamma }_j]\ge 0.5$.

2.2. Deterministic annealing variant

In practice, the EM algorithm is not guaranteed to converge to the global mode and may therefore get stuck at a local mode. As a result, the performance of the algorithm is sensitive to initial parameter values. One approach that reduces its dependence on those values is applying a deterministic annealing variant [31]. The deterministic annealing EM algorithm (DAEM) redefines the EM algorithm’s objective based on maximum entropy. Thus, the new objective is to minimize the free-energy function at gradually cooler temperatures. For EMVS, this corresponds to maximizing the negative free-energy function

$$-{\mathcal{F}}_t({\alpha }_0,\mathit{\beta },\theta )=-{\mathcal{U}}_t({\alpha }_0,\mathit{\beta },\theta )+\frac{1}{t}{\mathcal{S}}_t({\alpha }_0,\mathit{\beta },\theta )=\frac{1}{t}{\displaystyle \sum _{\mathit{\gamma }}{\left(\pi ({\alpha }_0,\mathit{\beta },\theta ,\mathit{\gamma }|\mathbf{y})\right)}^t,}$$ (12)

where ${\mathcal{U}}_t({\alpha }_0,\mathit{\beta },\theta )$ is the internal energy, ${\mathcal{S}}_t({\alpha }_0,\mathit{\beta },\theta )$ is the entropy, and 1/t, where 0 < t < 1, is interpreted as the temperature of the annealing process. Following Ueda and Nakano [31], if ${\alpha }_0^{(k+1)},{\mathit{\beta }}^{(k+1)}$, and θ^(k+1) maximize

$$-{\mathcal{U}}_t\left({\alpha }_0,\mathit{\beta },\theta |{\alpha }_0^{(k)},{\mathit{\beta }}^{(k)},{\theta }^{(k)}\right)={\displaystyle \sum _{\mathit{\gamma }}\log \left(\pi ({\alpha }_0,\mathit{\beta },\theta ,\mathit{\gamma }|\mathbf{y})\right)\times \pi {(\mathit{\gamma }|{\mathit{\beta }}^{(k)},{\theta }^{(k)})}^t,}$$ (13)

then $-{\mathcal{F}}_t({\alpha }_0^{(k)},{\mathit{\beta }}^{(k)},{\theta }^{(k)})\le -{\mathcal{F}}_t({\alpha }_0^{(k+1)},{\mathit{\beta }}^{(k+1)},{\theta }^{(k+1)})$. Thus, the DAEM algorithm is viewed as iteratively maximizing the negative internal energy at cooling temperatures.

In application, the annealing process starts with a high temperature (i.e. t close to 0). When the temperature is high, the landscape of $-{\mathcal{F}}_t({\alpha }_0,\mathit{\beta },\theta )$ is smooth, which prevents the EM algorithm from getting stuck in a local mode early in its iterations. As the temperature cools (i.e. t close to 1), the effect of the inclusion posterior is strengthened. As a result, local modes begin to appear and the landscape of $-{\mathcal{F}}_t({\alpha }_0,\mathit{\beta },\theta )$ progressively approaches the true, incomplete posterior.

To formulate EMVS with a deterministic annealing variant, we introduce into EMVS an annealing loop, which regulates the influence of the inclusion posterior, and replace Equation (5) with (13) in the E-step. The algorithm for this method is

• Step 1. Set the initial ${\alpha }_0^{(0)}$, β⁽⁰⁾, θ⁽⁰⁾, and t.

• Step 2. Carry out the EM steps at the current temperature, t, until convergence:

  1. E-Step: Evaluate ${\mathcal{U}}_t({\alpha }_0,\mathit{\beta },\theta |{\alpha }^{(k)},{\mathit{\beta }}^{(k)},{\theta }^{(k)})$
  2. M-Step: ${\alpha }^{(k+1)},{\mathit{\beta }}^{(k+1)},{\theta }^{(k+1)}=\underset{{\alpha }_0,\mathit{\beta },\theta }{\arg max}-{\mathcal{U}}_t({\alpha }_0,\mathit{\beta },\theta |{\alpha }_0^{(k)},{\mathit{\beta }}^{(k)},{\theta }^{(k)})$
  3. Set k ← k + 1

• Step 3. Increase t.

• Step 4. Stop, unless t < 1. Then return to step 2 and use the final estimates given the previous t to initiate at the current t.

Here, the conditional expectation is taken with respect to a tempered inclusion posterior distribution. The tempered probabilities of inclusion are calculated as

$$p_{j,t}^{\ast }=\frac{a_j^t}{a_j^t+b_j^t},$$ (14)

where $a_j=\pi ({\beta }_j^{(k)}|{\gamma }_j=1)P({\gamma }_j=1|{\theta }^{(k)})$, $b_j=\pi ({\beta }_j^{(k)}|{\gamma }_j=0)P({\gamma }_j=0|{\theta }^{(k)})$and P(γ_j = 1 | θ^(k) = θ^(k), each raised to the power t.

At each cooling step, t, we find a global mode that is used to initiate the algorithm at the next temperature thereby finding a new global mode. Assuming that the new global mode is close to the previous, the probability of converging at the true global mode is increased. Note that on the final iteration of the annealing loop (t = 1), Equation (13) matches Equation (5). Thus, the parameter estimates that maximize the negative free-energy function are equivalent to the posterior mode estimates that maximize the log-incomplete posterior.

While convergence at the global mode is still not guaranteed, the variant removes the algorithm’s dependence on initial parameter values and finds the global mode more often than the conventional EM algorithm [31]. Following, we explain our handling of related covariates under the notation of EMVS for clarity of discussion. In practice, it is generalizable to EMVS with a deterministic annealing variant.

2.3. Qualitative covariates

Suppose we are tasked with determining inclusion for an m+1-level qualitative covariate that had been reparameterized with m indicator variables, D_l, l = 1,…,m. Researchers typically assume that an associated indicator variable justifies the other levels’ inclusion [13]. So instead of assigning each indicator variable an inclusion parameter, γ_Dl, we model the group’s inclusion as γ_G. If we ignore this grouping, the inclusion probabilities are no longer considered exchangeable. The conditional expectation of the group’s inclusion is set to

$$p_G^{\ast }=\frac{a_G}{a_G+b_G},$$ (15)

where $a_G=\pi ({\mathit{\beta }}_G^{(k)}|{\gamma }_G=1)P({\gamma }_G=1|{\theta }^{(k)})$, $b_G=\pi ({\mathit{\beta }}_G^{(k)}|{\gamma }_G=0)P({\gamma }_G=0|{\theta }^{(k)})$, and P(γ_G = 1 | θ^(k)) = θ^(k). β_G is the m-dimensional vector of regression coefficients associated with the indicator variables. The indicator variables’ parameters are independent by design, so we replace their joint distribution with the product of their univariate normal distributions.

Since a group is selected when at least one of its indicator variables is selected, there is an increased chance of including the group due to random noise [13]. Suppose an epidemiologist claims that any covariate whose odds ratio falls within a specific range (e.g. [0.95, 1.05]) is clinically irrelevant. To incorporate this intuition into EMVS, the exclusion variance for the prior distribution of β_G is set so that the 95% prior probability of exclusion for the odds ratio covers that range (i.e. υ₀ = 0.00062). If we use this exclusion variance for an indicator variable group, size m = 3, we only achieve an 95%*95%*95% ≈ 85% prior probability that all of the coefficients within β_G exist in the predetermined range. In order to control the false positive rate and achieve the same interpretation for the group’s prior, we suggest adjusting the exclusion variance for the indicator variable group. For this example, we would simply adjust the prior for each of the coefficients within β_G so that the 95% prior probability of exclusion for the odds ratio ranges between [0.942, 1.061]; υ₀,_G = 0.00092. This correction is motivated by Bonferroni’s multiple testing probability theory [32]. We conjecture that the loss in power typically associated with this correction is tolerable for a relatively small number of levels and worth the reduction of false positives. See Appendix 3 for derivations.

2.4. Interaction terms

Suppose for a model similar to Equation (1), we aim to identify associated main effects or parents as well as their pairwise interactions with EMVS. We call an interaction term and its parents a covariate family and assume inclusion indicators between families are independent. To accommodate the inheritance principle within each family, we set their joint prior probability of inclusion similar to [13]

$$P\left({\gamma }_A,{\gamma }_B,{\gamma }_{AB}\right)=P\left({\gamma }_A\right)P\left({\gamma }_B\right)P\left({\gamma }_{AB}|{\gamma }_A,{\gamma }_B\right).$$ (16)

Here, we assume that conditioning an interaction term’s probability of inclusion, γ_AB, on its parents, γ_A and γ_B, achieves independence between family members. Therefore, we can still use an exchangeable inclusion prior (e.g. beta-binomial distribution) in this setting, if we condition interaction terms’ inclusion probabilities accordingly.

The conditional probability of inclusion for an interaction term is parameterized given the values of γ_A and γ_B. Bingham and Chipman [33] suggest a flexible parameterization that uses tuning parameters to impose a specific heredity constraint

$$P\left({\gamma }_{AB}=1|{\gamma }_A,{\gamma }_B\right)=\{\begin{array}{ll}{\pi }_{00}=\pi \ast a_0\hfill & \text{if}({\gamma }_A,{\gamma }_B)=(0,0);\hfill \\ {\pi }_{10}=\pi \ast a_1\hfill & \text{if}({\gamma }_A,{\gamma }_B)=(1,0);\hfill \\ {\pi }_{01}=\pi \ast a_2\hfill & \text{if}({\gamma }_A,{\gamma }_B)=(0,1);\hfill \\ {\pi }_{11}=\pi \ast a_3\hfill & \text{if}({\gamma }_A,{\gamma }_B)=(1,1),\hfill \end{array}$$

where γ_j ∈ {0, 1} indicates a term’s exclusion or inclusion, ∏= (π₀₀, π₁₀, π₀₁, π₁₁) denote inclusion probabilities, π^∗ ∈ [0, 1] is chosen objectively, and a = (a₀, a₁, a₂, a₃) represent tuning parameters. This parameterization supports various research goals [24,34]. For example, an interaction’s inclusion probability is naturally constrained to π₀₀ ≤ π₁₀, π₀₁ ≤ π₁₁, which follows Cox’s intuition that stronger main effects are more likely to suggest associated interactions [35]. Two constraints that characterize this intuition are strong, a = (0, 0, 0, 1), and weak, a = (0, 1, 1, 1), heredities.

Here, we embed into EMVS a heredity constraint that affects the calculation of γ_AB’s conditional expected value in the E-step:

$$E_{\gamma |·}\left[{\gamma }_{AB}\right]=E_{\gamma |·}\left[E_{\gamma |·}\left[{\gamma }_{AB}|{\gamma }_A,{\gamma }_B\right]\right]=p_{ab}^{\ast }={\pi }^{\ast }{a}_3{p}_a^{\ast }{p}_b^{\ast }+{\pi }^{\ast }{a}_2{p}_a^{\ast }(1-p_b^{\ast })+{\pi }^{\ast }{a}_1(1-p_a^{\ast })p_b^{\ast }+{\pi }^{\ast }{a}_0(1-p_a^{\ast })(1-p_b^{\ast }),$$ (17)

where π^∗ = a_AB/(a_AB + b_AB), similar to Equation (9). Note that $p_{ab}^{\ast }$ is simply the product of the parent terms’ and the constrained interaction term’s inclusion probabilities summed over all possible combinations of the parent terms’ inclusion.

We extend this theory to handle a quadratic term, which can be treated as an interaction term from a single parent. We assume that the prior probability of inclusion for a quadratic term, γ_AA, follows

$$P\left({\gamma }_{AA}=1|{\gamma }_A\right)=\{\begin{array}{cc}{\pi }^{\ast \ast }{q}_0& \text{if}({\gamma }_A)=(0);\\ {\pi }^{\ast \ast }{q}_1& \text{if}({\gamma }_A)=(1),\end{array}$$

where q = (q₀, q₁) are tuning parameters and π^∗∗ ∈ [0, 1]. The quadratic term’s conditional expectation, $p_{AA}^{\ast }$, is then formulated as

$$p_{aa}^{\ast }={\pi }^{\ast \ast }{q}_1{p}_a^{\ast }+{\pi }^{\ast \ast }{q}_0(1-p_a^{\ast }),$$ (18)

with π^∗∗ = a_AA/(a_AA + b_AA), similar to Equation (9).

In practice, we recommend following the hierarchical structure when estimating the expected values of inclusion in the E-step. By estimating the parent terms’ inclusion first, their updated values are available to evaluate the conditional expectation of their interaction term’s inclusion. By reformulating an interaction’s expectation, we constrain the model space to interpretable models that are flexible to different heredity constraints and uphold the assumptions needed to use exchangeable priors.

3. Simulations

We conduct a simulation study in R [36] to evaluate the performance of EMVS with a deterministic annealing variant for logistic regression models with qualitative covariates and interaction terms. See Supplement A for simulated data and R code. We simulate multiple exploratory research scenarios motivated by epidemiological data and compare the results to the grouped LASSO and the LASSO with heredity constraints. Multiple models are postulated with true effects set to represent relatively weak effects found in epidemiological research. We restrict our analysis to weaker effects, under the assumption that performance will only improve with larger effects. Our algorithm is initiated at the maximum likelihood estimate for α₀ and β using a logistic regression model, and 0.5 for θ. The inverse temperature is initially set to t = .2 and is increased by .1 until t = 1. Convergence at each temperature level is determined with ε < 0.000001, following A.5.

To assess performance for each simulation, we calculated the average false positive rate (FPR), average false negative rate (FNR), and marginal accuracies (i.e. the percentage of correct inclusion (exclusion) for each covariate over all simulated data sets). We calculate the average false positive and negative rates with

$$\text{FPR}=\text{FP}/(\text{FP}+\text{TN})$$

and

$$\text{FNR}=\text{FN}/(\text{FN}+\text{TP}),$$

where TP(TN) and FP(FN) are the number of true positives(negatives) and false positives(negatives), respectively. To measure the overall performance, we calculate the weighted average correct association percentage [37] with

$$\frac{1}{2}\left[\frac{{\sum }_{\text{associated}}P(\text{selected}|\text{associated})}{\text{Total}\text{number}\text{of}\text{associated}\text{covariates}}+\frac{{\sum }_{\text{unassociated}}1-P(\text{selected}|\text{unassociated})}{\text{Total}\text{number}\text{of}\text{unassociated}\text{covariates}}\right],$$

which is the average of the marginal accuracies, weighted by the true number of associated and unassociated covariates.

Before evaluating the performance of our method to select qualitative covariates and interaction terms simultaneously, we examined its ability to handle them separately. In Supplement B and Supplement C, we compared the ability of EMVS to select qualitative covariates that have various combinations of associated levels with and without the grouping strategy and tested EMVS over multiple simulated models that are not hierarchically well formulated or follow strong(weak) heredity structures with varying heredity constraints assumed. Additionally, we tested the performance of our proposed variance adjustment to reduce the false positive rate in Supplement B, and we applied two different tuning procedures for EMVS (i.e. regularization plots in Supplement B and an intuition-based approach in Supplement C). EMVS’s performance handling quantitative covariates and interaction terms separately in these simulation studies is encouraging for its use to handle them simultaneously.

Then, we examined the ability of our proposed method to select associated covariates in scenarios structured akin to our application in Section 4, which encounters both qualitative covariates and interaction terms. For each model, we simulated 500 data sets with n = 1000 observations from a full model containing, 10 parent terms; 4 two-level qualitative (x_b,1,…,x_b,4), 4 continuous (x_c,5,…,x_c,8), and 1 three-level qualitative (x_d,9, x_d,10). Additionally, the model incorporated all pairwise interactions, including squared terms for continuous covariates, making a total of 58 terms in the full model. Continuous covariates followed a multivariate normal distribution with mean zero, variance one, and an exchangeable covariance structure, parameterized with ρ. We set ρ ∈ {0, 0.4, 0.8}. Qualitative covariates came from a multinomial distribution with equal probabilities set for each of the m+1-levels which sum to one. Qualitative covariates were reparameterized with m indicator variables, D_l, l = 1,…,m. Each indicator variable was set to one if their corresponding covariate was the l+1-level of the qualitative covariate and zero otherwise. For instance a two-level qualitative covariate was reparameterized with one indicator variable D₁ that equals one if the qualitative covariate was equal to the second level and zero otherwise. Interaction terms were equal to their parents’ product. In application, we suggest a tuning procedure that is a compromise between the two methods described in Supplement B and Supplement C. Here, we claimed an odds ratio between [0.95, 1.05] to be clinically irrelevant, and we evaluated the local stability of the regularization plots around our intuition with a 95% prior probability of inclusion for the odds ratio that covers [1/4, 4]. Using this tuning procedure, we set the 95% prior probability of exclusion equivalent to an odds ratio between [0.939, 1.065], υ₀ = 0.001. We applied the variance adjustment to indicator variables, as in Section 2.3. We assumed a strong heredity constraint, a = (0, 0, 0, 1), a weak heredity constraint, a = (0, 1, 1, 1), and no heredity constraint, effectively a = (1, 1, 1, 1). In Supplement D, we also evaluate our method’s performance in the exact same settings, except with n = 120 ≈ p ∗ 2.

We compared the results of our method to the LASSO [38], a popular tool for variable selection, which is extended to model logistic regression [15], handles qualitative covariates [17], and imposes heredity constraints [19]. The grouped LASSO [17] allows researchers to perform LASSO regression on qualitative covariates, similar to our methods in Section 2.3. We compared our method with no heredity constraints to the grouped LASSO for logistic regression models with the gglasso package in R [39]. We chose this package because of its computational efficiency [39]. To compare our method under heredity constraints, we chose the R package hiernet used by [19]. This package allows users to impose a strong or weak heredity constraint and follows the inheritance principle (i.e. only considers interactions if the parents are associated with the outcome). An alternative package, glinternet [22], can handle heredity constraints for qualitative covariates but is only developed for strong heredity constraints and does not follow the inheritance principle. Thus, we find the characteristics of hiernet better for comparison with our method’s approach. Additionally, the hiernet’s inability to accommodate qualitative covariates only affects the inclusion of the non-associated indicator variable, x_d,10, since x_d,9 is associated. We accounted for this in our comparisons. For heirnet and gglasso, we used fivefold cross validation to identify the largest penalty value, λ, that is within one standard error of the minimum [40]. Variable selection was performed on each of the simulated data sets using this penalty on the appropriate models for comparison. We simulated three models from the pool of covariates to evaluate our method’s performance against the LASSO in the following mock research settings:

Model 3.3.1

The true model followed a strong heredity constraint:

$$\text{logit}(\omega ({\mathbf{x}}_i))=-0.65x_{b,1}+0.5x_{b,2}+0.65x_{c,5}-0.5x_{c,6}+0.6x_{d,9}+0.6x_{b,1}{x}_{b,2}-0.6x_{b,1}{x}_{c,5}+0.6x_{c,5}{x}_{c,6}+0.5x_{c,6}^2-0.6x_{d,9}{x}_{b,1}+0.5x_{d,10}{x}_{b,1}-0.6x_{d,9}{x}_{c,5}+0.5x_{d,10}{x}_{c,5}.$$

Model 3.3.2

The true model followed a weak heredity constraint:

$$\text{logit}(\omega ({\mathbf{x}}_i))=0.5x_{b,2}+0.65x_{c,5}-0.5x_{c,6}+0.6x_{d,9}+0.6x_{b,1}{x}_{b,2}-0.6x_{b,1}{x}_{c,5}+0.6x_{c,5}{x}_{c,6}+0.5x_{c,6}^2-0.6x_{d,9}{x}_{b,1}+0.5x_{d,10}{x}_{b,1}-0.6x_{d,9}{x}_{c,5}+0.5x_{d,10}{x}_{c,5}.$$

Model 3.3.3

The true model was not hierarchically well formulated:

$$\text{logit}(\omega ({\mathbf{x}}_i))=0.5x_{b,2}+0.6x_{d,9}+0.6x_{b,1}{x}_{b,2}-0.6x_{b,1}{x}_{c,5}+0.6x_{c,5}{x}_{c,6}+0.5x_{c,6}^2-0.6x_{d,9}{x}_{b,1}+0.5x_{d,10}{x}_{b,1}-0.6x_{d,9}{x}_{c,5}+0.5x_{d,10}{x}_{c,5}.$$

Table 1 presents our method’s overall performance in scenarios that include qualitative covariates and interaction terms. We found that all performance measures were sensitive to correlation structure and that the method detected stronger effects better than weaker effects. Additionally, models under the strong heredity constraint showed a lower average FPR compare to models under a weak heredity constraint or no heredity constraint. As a result, models under the strong heredity constraint experienced a higher average FNR, with the lowest average FNR achieved by models with no heredity constraint. In Figures 1–3, we find that qualitative covariates have higher rates of incorrect association and as result, interaction terms including qualitative covariates had the highest rates of incorrect association. This was expected following the results in Supplement B.

Table 1.

Comparison of EMVS’s and LASSO’s selection performance in simulated application settings: FPR, average false positive rate; FNR, average false negative rate; WACAP, weighted average correct association percentage.

Heredity Constraint	Correlation	Model 3.3.1: True Model Follows Strong Heredity			Model 3.3.2: True Model Follows Weak Heredity			Model 3.3.3: True Model Not Well Formulated
		FPR	FNR	WACAP	FPR	FNR	WACAP	FPR	FNR	WACAP
	0	0.025 (−0.065)	0.164   (0.024)	0.876   (0.008)	0.026 (−0.077)	0.210   (0.111)	0.833 (−0.050)	0.017 (−0.163)	0.263   (0.155)	0.774 (−0.037)
Stronga	0.4	0.028 (−0.074)	0.193   (0.043)	0.846 (−0.004)	0.024 (−0.087)	0.245   (0.123)	0.800 (−0.060)	0.015 (−0.133)	0.264   (0.088)	0.773 (−0.009)
	0.8	0.035 (−0.059)	0.267   (0.012)	0.778   (0.012)	0.029 (−0.085)	0.319   (0.080)	0.728 (−0.037)	0.024 (−0.125)	0.279   (0.095)	0.756 (−0.019)
	0	0.079 (−0.040)	0.094 (−0.007)	0.908   (0.029)	0.082 (−0.027)	0.129 (−0.029)	0.878   (0.036)	0.063 (−0.091)	0.169 (−0.081)	0.836   (0.127)
Weakb	0.4	0.092 (−0.041)	0.115   (0.007)	0.885   (0.020)	0.090 (−0.007)	0.138 (−0.086)	0.866   (0.088)	0.068 (−0.030)	0.180 (−0.180)	0.821   (0.196)
	0.8	0.127   (0.005)	0.177 (−0.031)	0.813   (0.026)	0.126   (0.090)	0.213 (−0.182)	0.779   (0.137)	0.101   (0.047)	0.191 (−0.260)	0.794   (0.244)
	0	0.101 (−0.038)	0.082 (−0.137)	0.903   (0.129)	0.112   (0.015)	0.085 (−0.154)	0.894   (0.108)	0.099   (0.029)	0.082 (−0.208)	0.903   (0.149)
Nonec	0.4	0.119 (−0.020)	0.097 (−0.130)	0.882   (0.115)	0.125   (0.043)	0.097 (−0.183)	0.877   (0.131)	0.113   (0.065)	0.088 (−0.259)	0.889   (0.199)
	0.8	0.176   (0.054)	0.148 (−0.125)	0.806   (0.078)	0.186   (0.148)	0.158 (−0.265)	0.791   (0.210)	0.178   (0.157)	0.135 (−0.306)	0.812   (0.239)

^aDeterministic annealing EMVS (Deterministic annealing EMVS-LASSO with strong heredity constraint).

^bDeterministic annealing EMVS (Deterministic annealing EMVS-LASSO with weak heredity constraint).

^cDeterministic annealing EMVS (Deterministic annealing EMVS-grouped LASSO).

Figure 1.

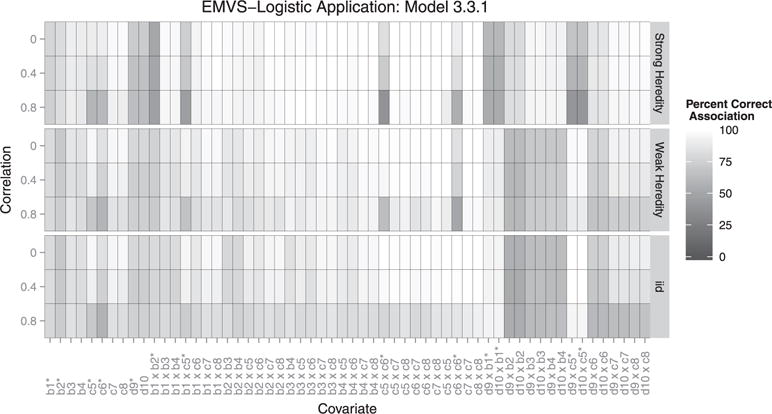
Each box represents the correct association percentage for a covariate. The lighter the box, the better the model performed for that variable, averaged over all simulations. Whether or not a covariate should be included depends on the heredity constraint given. For example: if covariate c₁ is associated with the outcome, but c₂ is not, a strong constraint would exclude their interaction but a weak or no heredity constraint should include it. ∗Covariates existing in the true model.

Figure 3.

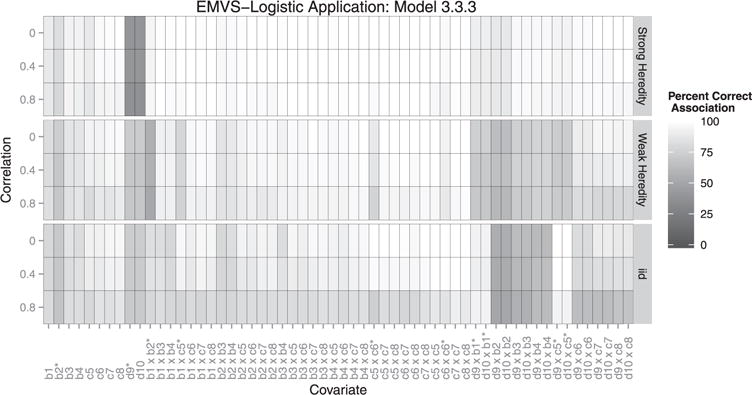
Each box represents the correct association percentage for a covariate. The lighter the box, the better the model performed for that variable, averaged over all simulations. Whether or not a covariate should be included depends on the heredity constraint given. For example: if covariate c₁ is associated with the outcome, but c₂ is not, a strong constraint would exclude their interaction but a weak or no heredity constraint should include it. ∗Covariates existing in the true model.

Overall, our method outperformed the LASSO under a weak heredity constraint and the grouped LASSO for all models (3.3.1–3.3.3), as well as the LASSO under a strong heredity constraint for two of the three correlation structures when the true model followed strong heredity (Table 1). Additionally, our method maintained a lower average FPR under a strong heredity constraint. We found that EMVS was marginally more sensitive to the type of covariate, (e.g. continuous or qualitative), whereas the LASSO was more sensitive to whether or not the covariate is a parent or interaction term (Figures 4–6). The LASSO under heredity constraints showed more false positives for main effects compared with EMVS. Additionally, EMVS performed better in selecting grouped covariates. In results not shown, we also found that EMVS outperformed both the regular LASSO [38] and forward stepwise selection for all performance measures, and the LASSO using a λ that was within one standard error of the minimum performed better than the λ that minimized the cross-validation error for our simulations.

Figure 4.

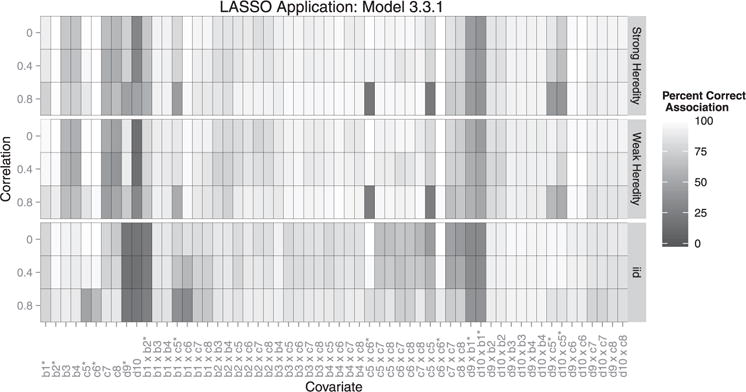
Each box represents the correct association percentage for a covariate. The lighter the box, the better the model performed for that variable, averaged over all simulations. Whether or not a covariate should be included depends on the heredity constraint given. For example: if covariate c₁ is associated with the outcome, but c₂ is not, a strong constraint would exclude their interaction but a weak or no heredity constraint should include it. ∗Covariates existing in the true model.

Figure 6.

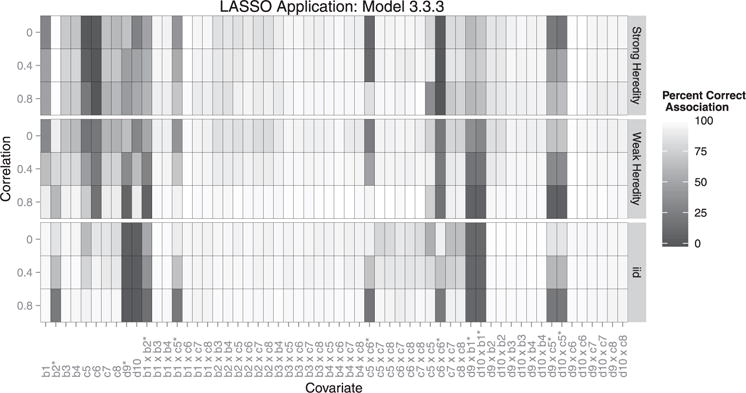
Each box represents the correct association percentage for a covariate. The lighter the box, the better the model performed for that variable, averaged over all simulations. Whether or not a covariate should be included depends on the heredity constraint given. For example: if covariate c₁ is associated with the outcome, but c₂ is not, a strong constraint would exclude their interaction but a weak or no heredity constraint should include it. ∗Covariates existing in the true model.

When the true model followed weak heredity (3.3.2) or the model was not well formulated (3.3.3), the LASSO under a strong heredity constraint outperformed our method overall, with respect to the weighted average correct association percentage. We attest this to the LASSO’s tendency to select a majority of parent terms, regardless of their true influence, and neglect interaction terms, which make up a majority of the full model (Figures 4–6). Additionally, under no heredity constraint, the LASSO had a lower average FPR. This corresponds to EMVS’s tendency to select unassociated interactions involving grouped indicator variables. We find that all LASSO methods were sensitive to correlation structure, similar to EMVS. However, sometimes the LASSO performed better with higher correlations (e.g. average false positives in model 3.3.3). Choi et al. [18] also show that LASSO performed better with correlated data. However, it is worth noting that even though the LASSO outperformed EMVS in some of the simulated scenarios, the two methods are not truly comparable under the strong and weak heredity constraints since the LASSO is unable to simultaneously account for qualitative covariates.

4. Application

In this section, we apply our proposed method to the MATCh data from [41–43] to examine the relation between smoking experimentation and non-genetic (i.e. behavioural, psychosocial, demographic, and contextual) as well as genetic risk factors. Details of the study design are found in [42], and the data collection procedure is described in [41]. Our aim in this exploratory study was to identify which risk factors remained associated when the results of three previously published analyses [41–43] on this cohort are combined to form an aggregated pool of risk factors, while simultaneously evaluating interaction terms. In our analysis, our outcome of interest is ever-experimentation as defined by [41]. They used stepwise logistic regression to determine ever-experimentation’s association with age (continuous), gender (two-level qualitative), social influence of friends (two-level qualitative), social influence of family (two-level qualitative), detentions (two-level qualitative), risk-taking tendencies (continuous), anxiety score (continuous), and exposure to smoking in movies (continuous), while controlling for parental education attainment (three-level qualitative). Country of birth (two-level qualitative) and acculturation (two-level qualitative) were evaluated separately in the model as potential moderators. In a subsequent analysis, Wilkinson et al. [43] also identified the following single nucleotide polymorphisms from the opioid receptor serotonin and dopamine pathways associated with new-experimentation: rs9322451 on OPRM1 (dominant), rs6297 on HTR1B (dominant), on rs8119844 on SNAP25 (recessive), rs9567732 on HTR2A (dominant), rs10052016 on SLC6A3 (dominant), and rs12422191 on DRD2 (dominant) and the psychological factor outcome expectations (continuous). Using our proposed approach, we pooled the risk factors from these two studies and added subjective social status (continuous) [41] to see which remained associated with ever-experimentation. We simultaneously evaluated interactions between exposure to smoking in movies and peers who smoke, as well as between 2 single nucleotide polymorphisms along the dopamine pathway and detention, risk-taking tendencies, and expected positive outcomes. After dropping observations with missing data, this analysis considered 1231 individuals and a pool of potential risk factors that includes 6 continuous, 12 two-level qualitative covariates, 1 three-level qualitative covariate, and 7 interaction terms. For this application, we used the same tuning procedure described in Section 3, with v₁ = 0.5. Using this tuning procedure, we set the 95% prior probability of exclusion equivalent to an odds ratio between [0.956, 1.045], v₀ ≈ 0.0005. We use our proposed variance adjustment for the indicator variables and imposed a strong, weak and no heredity constraint.

Our method identified all of the parent effects in the aggregated pool, excluding anxiety score, subjective social status, country of birth, acculturation, and parental education attainment as associated with ever-experimentation in this cohort. In a previous analysis [42], parental education was forced into the model to control for socioeconomic status. While we allowed for it to be selected in this analysis, its prior could have been adjusted to force it in. Since acculturation and country of birth were highly correlated, their relation, as potential direct effects and moderators on new-experimentation, was examined separately [42]. In that analysis, only country of birth was identified as a moderator for new-experimentation. Additionally, anxiety score was identified as one of the weaker effects associated with ever-experimentation [42]. Among adolescents, ever smoking includes a wide range of smoking levels, from having tried only a puff to daily smoking. This might mask the true relation between anxiety and smoking behaviour, as the experimenter may be qualitatively different than those who increase their level of smoking. Its exclusion could also be the result of parental education attainment neither being forced into the model nor being selected by our method. Only two interaction terms were identified: rs12422191 on DRD2 × detention and rs10052016 on SLC6A3 × detention under a strong, weak, and no heredity constraint.

To our knowledge, no other methods exist that can search through specific interaction terms and impose heredity constraints. Therefore, we compared our results to forward and backward stepwise selection and the LASSO and grouped LASSO. The stepwise methods selected the same parent effects as our method, except they included anxiety score. However, neither identified the two interactions but instead identified a peer and exposure to smoking in movies interaction. The LASSO and grouped LASSO did not select any interaction terms and excluded the same parent terms as the stepwise methods as well as some genetic risk factors. The LASSO only selected rs8119844 on SNAP25 and the grouped LASSO selected rs12422191 on DRD2, rs6297 on HTR1B, as well as rs8119844 on SNAP25. Based on our simulations, it is not surprising that the LASSO methods favoured a more parsimonious model.

5. Discussion

We developed a variable selection method to simultaneously accommodate qualitative covariates and interaction terms using deterministic annealing EMVS for binary outcomes. We offer a variance adjustment for qualitative covariates that controlled the groupwise, false positive rate, and a flexible parameterization for introducing various heredity constraints on interactions. While we did not show it, our method can also apply unique heredity constraints on each family of covariates, similar to [21]. In the majority of our simulations motivated by the application data, we showed that our method tended to outperform the grouped LASSO and the LASSO with heredity constraints in exploratory research settings with the objective of identifying risk factors for an outcome. Particularly, our method was superior overall when the assumption of the model’s heredity structure matched the true model. Unfortunately, we never know the true model in practice. Based on our simulations, we suggest relaxing any heredity constraints or imposing a weak constraint to identify potential risk factors in hypothesis-generating research. We found that our method, under the strong heredity constraint, encouraged effect sparsity, similar to that of [18]. Bien and Tibshirani [19] and Liu et al. [24] also found that implementing strong heredity constraints reduces false positives but consequently limits methods’ ability to detect associated terms. Our method shared this pitfall, which could be marginalized through appropriate tuning. To our knowledge, most of the research on selection methods that accommodate heredity constraints evaluated methods on prediction performance [19,24]. Choi et al. [18] evaluated variable selection, but not marginally. By looking at the performance of the method marginally, we were able to identify underlying strengths and weaknesses of the method that an evaluation of its predictive ability would overlook.

The usefulness of our method is sensitive to tuning parameterization and initialization. While the deterministic annealing variant reduced the method’s sensitivity to initialization, the method still does not guarantee a global mode. Fortunately, the model’s performance could be increased with effective tuning. Sole use of regularization plots for tuning (i.e. without intuition) is useful when the objective of the researcher is to identify large effects, or a prespecified reduction in the size of the full model is sought. For instance, we were interested in identifying the 10 largest effects from a pool of covariates. We found that in application settings, relying solely on regularization plots for tuning can be misleading. Theoretically, as the variance of exclusion increases, more covariates will fall out of the model, ultimately stabilizing at the null model. Since the variance of exclusion could be interpreted as a threshold for clinically meaningful odds ratios, we suggest using this intuition to target local stability in the regularization plots. In practice, the clinical threshold is set a priori, next regularization plots are employed, and then the variance of exclusion is chosen within the range of local stability around the targeted threshold. While this is our suggested tuning method based on our experiences, a more validated approach is justified.

Due to the formation of the likelihood and limitations of the software, our method was sensitive to boundary conditions (i.e. it fails to converge when the null model or full model is selected). For our simulations, if θ, the overall inclusion probability, gets stuck at zero or one (i.e. θ < 1 × 10⁻⁶ or θ > 0.9999), we stopped the method and recorded a null or saturated model. In practice, this limitation is easily circumvented with retuning.

We chose the logit link to model binary data for its familiarity to the field of epidemiology and its interpretability, which we prioritized over any computational difficulties. Within the context of a logit link, future work could improve upon the numerical methods (i.e. EM gradient method) used to remediate these issues in our simulation study. Additionally, researchers could integrate our methods for handling related covariates into other EMVS frameworks [12,27,28]. This would allow researchers to compare our methods for handling related covariates using a logistic regression model to a probit regression model [27]. While the roots of deterministic annealing EMVS are found in p ≫ n research settings, we have shown its usefulness in various other exploratory research scenarios. However, it is of interest to evaluate the performance of our method in p ≫ n settings, as they often arise in epidemiological research, (i.e. genomics, proteomic, and metabolomics). Currently, EMVS has only been evaluated in high dimensional settings with continuous covariates [12,27]. Based on EMVS’s sensitivity to both qualitative covariates and relatively small sample sizes (n ≈ p ∗ 2), extensions of our method to p ≫ n settings may require more efficient optimization methods to facilitate tuning procedures. In some settings, researchers are interested in identifying associated interaction terms and thereafter force in non-associated parent effects to uphold heredity constraints in the model. Our methods could easily be modified to impose this dependency. Lastly, EMVS currently lacks a formal method for estimating parameters’ variance that accommodates estimation as well as selection uncertainty. This addition would prevent researchers from needing to fit a secondary model, including the covariates EMVS selected, that would underestimate parameters’ variances and bias interpretation of the model.

Figure 2.

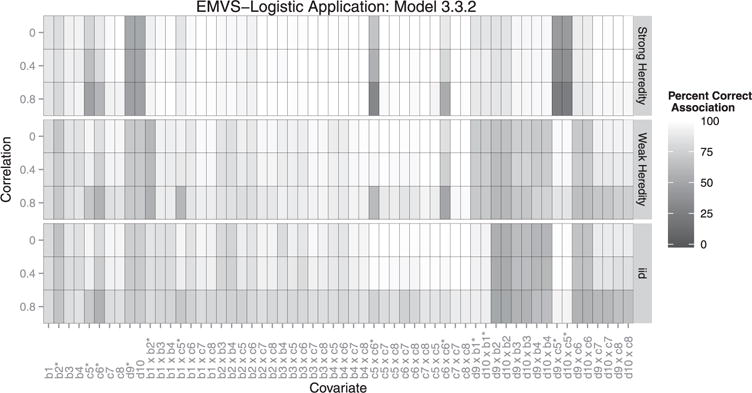
Each box represents the correct association percentage for a covariate. The lighter the box, the better the model performed for that variable, averaged over all simulations. Whether or not a covariate should be included depends on the heredity constraint given. For example: if covariate c₁ is associated with the outcome, but c₂ is not, a strong constraint would exclude their interaction but a weak or no heredity constraint should include it. ∗Covariates existing in the true model.

Figure 5.

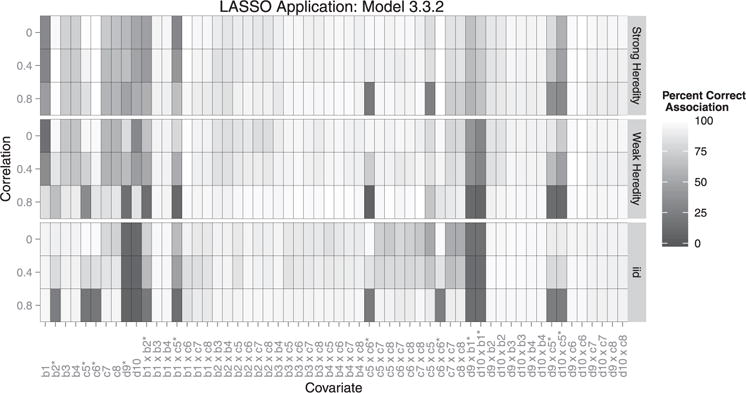
Each box represents the correct association percentage for a covariate. The lighter the box, the better the model performed for that variable, averaged over all simulations. Whether or not a covariate should be included depends on the heredity constraint given. For example: if covariate c₁ is associated with the outcome, but c₂ is not, a strong constraint would exclude their interaction but a weak or no heredity constraint should include it. ∗Covariates existing in the true model.

Appendix 1. Newton–Raphson derivations

Note, we can equivalently maximize Q₁ by letting $\mathrm{\psi }{\prime }_{(1\times p+1)}=({\alpha }_0,\mathit{\beta }\prime ),{\mathit{x}}_i^{\prime }=(x_{i0},x_{i1},\dots ,x_{ip})$ where x_i0 = 1, and ${\mathit{p}}^{\ast }=(p_0^{\ast },p_1^{\ast },\dots ,p_p^{\ast })$ where α₀ is forced into the model by fixing its probability of inclusion, $p_0^{\ast }$, to 1. Then, the next iteration of Ψ is estimated by

$${\mathrm{\Psi }}^{(k+1)}={\mathrm{\Psi }}^{(k)}-{\left[\frac{{\partial }^2{Q}_1}{\partial {\mathrm{\Psi }}^{\prime }\partial \mathrm{\Psi }}\right]}_{\mathrm{\Psi }={\mathrm{\Psi }}^{(k)}}^{-1}{\left[\frac{\partial Q_1}{\partial \mathrm{\Psi }}\right]}_{\mathrm{\Psi }={\mathrm{\Psi }}^{(k)}},$$ (A1)

where the first derivative of the Q₁ function with respect to Ψ is a p+1-dimensional vector with:

$$\frac{\partial Q_1}{\partial {\mathrm{\Psi }}_j}={\displaystyle \sum _{i=1}^n(y_i{x}_{ij}-\omega ({\mathit{x}}_i)x_{ij})-{\mathrm{\Psi }}_j\left[(1-p_j^{\ast })\frac{1}{{\upsilon }_0}+p_j^{\ast }\frac{1}{{\upsilon }_1}\right]}.$$ (A2)

The diagonal elements of the (p + 1) × (p + 1)-dimensional Hessian matrix, [∂²Q₁/∂Ψ′∂Ψ] are formulated as

$$\frac{{\partial }^2{Q}_1}{\partial {\mathrm{\Psi }}^2}=-{\displaystyle \sum _{i=1}^n{x}_{ij}^2\omega ({\mathit{x}}_i)(1-\omega ({\mathit{x}}_i))}-\left[(1-p_j^{\ast })\frac{1}{{\upsilon }_0}+p_j^{\ast }\frac{1}{{\upsilon }_1}\right],$$ (A3)

and the off-diagonals are:

$$\frac{{\partial }^2{Q}_1}{\partial {\mathrm{\Psi }}_j\partial {\mathrm{\Psi }}_k}=-{\displaystyle \sum _{i=1}^n{x}_{ij}\omega ({\mathit{x}}_i)(1-\omega ({\mathit{x}}_i))x_{ik}}.$$ (A4)

Appendix 2. Convergence stopping rule of the EM Algorithm

To determine convergence of this method, we set a stopping rule for the absolute value of the difference between the log-likelihood distribution evaluated at the current and next step of the EM algorithm [30]. Formally, the algorithm stops if:

$$\left|\log L\left({\alpha }_0^{(k+1)},{\mathit{\beta }}^{(k+1)},{\theta }^{(k+1)}|\mathbf{y}\right)-\log L\left({\alpha }_0^{(k)},{\mathit{\beta }}^{(k)},{\theta }^{(k)}|\mathbf{y}\right)\right|=\left|\left[Q\left[{\alpha }_0^{(k+1)},{\mathit{\beta }}^{(k+1)},{\theta }^{(k+1)}|{\alpha }_0^{(k)},{\mathit{\beta }}^{(k)},{\theta }^{(k)}\right]-Q\left[{\alpha }_0^{(k)},{\mathit{\beta }}^{(k)},{\theta }^{(k)}|{\alpha }_0^{(k)},{\mathit{\beta }}^{(k)},{\theta }^{(k)}\right]\right]-\left[R\left[{\mathit{\beta }}^{(k+1)},{\theta }^{(k+1)}|{\mathit{\beta }}^{(k)},{\theta }^{(k)}\right]-R\left[{\mathit{\beta }}^{(k)},{\theta }^{(k)}|{\mathit{\beta }}^{(k)},{\theta }^{(k)}\right]\right]\right|\le \epsilon ,$$ (A5)

where ε is the stopping rule threshold. The Q function is described in Equation (5) and

$$R\left[\mathit{\beta },\theta |{\mathit{\beta }}^{(k)},{\theta }^{(k)}\right]={\displaystyle \sum _{\mathit{\gamma }}\log \left(\pi (\mathit{\gamma }|\mathit{\beta },\theta ,\mathbf{y})\right)}\times \pi (\mathit{\gamma }|{\mathit{\beta }}^{(k)},{\theta }^{(k)},\mathbf{y})=E_{\mathit{\gamma }|·}\left[\log \left(\pi (\mathit{\gamma }|\mathit{\beta },\theta ,\mathbf{y})\right)\right].$$ (A6)

Due to the hierarchical structure of this model, we assume that:

$$\pi (\mathit{\gamma }|\mathit{\beta },\theta ,\mathbf{y})=\pi (\mathit{\gamma }|\mathit{\beta },\theta )={\theta }^{|\gamma |}{(1-\theta )}^{p-|\gamma |},$$ (A7)

where $|\gamma |={\displaystyle {\sum }_{j=1}^p{\gamma }_j}$ and θ ∈ [0, 1], (Similar to 4). Taking the log and conditional expectation, we show:

$$E_{\gamma |·}\left[\log (\pi (\mathit{\gamma }|\mathit{\beta },\theta ))\right]={\displaystyle \sum _{j=1}^p{E}_{\gamma |·}[{\gamma }_j]\log (\theta )+}\left(p-{\displaystyle \sum _{j=1}^p{E}_{\gamma |·}[{\gamma }_j]}\right)\log (1-\theta ).$$ (A8)

Appendix 3. Variance correction for grouped covariates

Determine the variance that places a 95% prior coverage probability (α = 5%, where α = 1 − coverage probability) for β_j between [0.95, 1.05],

$${\mathrm{var}}_{95\mathrm{\%}}={(\log (1.05)/1.96)}^2=0.00062.$$ (A9)

Use var_95% to determine the exclusion threshold for the odds ratio of the grouped covariates, given the adjustment:

$${\mathrm{OR}}_{\text{upper}}=\exp \left(Z_{1-{\alpha }_{\text{adj}}}\sqrt{{\mathrm{var}}_{95\mathrm{\%}}}\right)=1.0614{\mathit{OR}}_{\text{lower}}=\exp \left(-Z_{1-{\alpha }_{\text{adj}}}\sqrt{{\mathrm{var}}_{95\mathrm{\%}}}\right)=0.9421,$$ (A10)

where Z is a z-score, α_adj = 100(1 − α/(2m)) is the new type I error rate, and m represents the number of indicator variable for the group. In this case,

$$1-{\alpha }_{\text{adj}}=1-0.05/(2\ast 3)=99.16\mathrm{\%}.$$ (A11)

Then, solve for an adjusted variance that places a 95% prior coverage probability between the new tolerable range for exclusion, [0.942, 1.061],

$${\text{var}}_{\text{adj}}={(\text{log}(1.061)/1.96)}^2=0.00092.$$ (A12)