Competitive Binding of Mg²⁺ and Na⁺ Ions to Nucleic Acids: From Helices to Tertiary Structures

Abstract

Nucleic acids generally reside in cellular aqueous solutions with mixed divalent/monovalent ions, and the competitive binding of divalent and monovalent ions is critical to the structures of nucleic acids because of their polyanionic nature. In this work, we first proposed a general and effective method for simulating a nucleic acid in mixed divalent/monovalent ion solutions with desired bulk ion concentrations via molecular dynamics (MD) simulations and investigated the competitive binding of Mg²⁺/Na⁺ ions to various nucleic acids by all-atom MD simulations. The extensive MD-based examinations show that single MD simulations conducted using the proposed method can yield desired bulk divalent/monovalent ion concentrations for various nucleic acids, including RNA tertiary structures. Our comprehensive analyses show that the global binding of Mg²⁺/Na⁺ to a nucleic acid is mainly dependent on its structure compactness, as well as Mg²⁺/Na⁺ concentrations, rather than the specific structure of the nucleic acid. Specifically, the relative global binding of Mg²⁺ over Na⁺ is stronger for a nucleic acid with higher effective surface charge density and higher relative Mg²⁺/Na⁺ concentrations. Furthermore, the local binding of Mg²⁺/Na⁺ to a phosphate of a nucleic acid mainly depends on the local phosphate density in addition to Mg²⁺/Na⁺ concentrations.

Introduction

Nucleic acids have important biological functions for genetic storage, expression, and regulation, and their functions are strongly coupled to their structures and structural changes (1, 2). Since nucleic acids are highly charged polyanions, their native structure formation undergoes strong intramolecule Coulombic repulsions (1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26). However, metal ions in the solution can bind to nucleic acids and significantly reduce the Coulombic repulsion, thus favoring the structure folding of nucleic acids (1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 13, 23, 25). Compared with monovalent ions, multivalent ions play a more important and efficient role in structure folding (e.g., Mg²⁺ of millimolar concentration can generally induce RNA folding), whereas Na⁺ can only cause RNA folding at approximately molar concentrations (8, 9, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36). More importantly, a nucleic acid generally resides in mixed divalent/monovalent ion solutions (1, 2, 3, 4, 5, 6, 7). Therefore, the competitive binding of divalent and monovalent ions is critical to the structure folding and stability of nucleic acids (8, 9, 12, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45).

To understand ion-nucleic acid interactions, several classic polyelectrolyte theories have been developed and employed (15, 16, 17, 18, 19, 20, 21, 22, 35, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58). The counterion condensation theory and the Poisson-Boltzmann (PB) theory have been successful in predicting various electrostatic properties of nucleic acids (20, 21, 22, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58). However, the counterion condensation theory was developed for line-charge structure models at very dilute ion concentrations. Thus, it is inapplicable for nucleic acids with complex structures at finite salt concentrations (46, 47). The PB theory ignores the ion-ion correlations and underestimates the role of multivalent ions in stabilizing nucleic acid structures (49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63) and helix assembly (53, 64). The tightly bound ion (TBI) model has recently been developed to account for ion-ion correlation in binding to nucleic acids (52, 53), and the model has been shown to improve predictions regarding the effect of Mg²⁺ in stabilizing RNA/DNA helices/hairpins and tertiary structures (52, 53, 54, 61, 62, 64). However, the TBI model in its present version assumes all the atom charges are distributed in phosphate groups and thus would not result in reliable prediction of detailed ion binding properties in the vicinity of nucleic acids (54, 62, 64).

As an important complementary method to theories and experiments, all-atom molecular dynamics (MD) simulations can offer reliable predictions of the detailed ion-binding properties and dynamics of biomolecules (10, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87). The binding of divalent or monovalent ions to double-stranded (ds) DNA or dsRNA in pure divalent or monovalent ion solutions has been investigated extensively by all-atom MD simulations (27, 28, 66, 72, 74, 75, 82, 85). Recently, all-atom MD simulations have been employed for dsDNA and dsRNA in mixed Mg²⁺/Na⁺ solutions to investigate the competitive binding of Mg²⁺/Na⁺ to dsDNA and dsRNA, and it has been shown that the competitive binding of Mg²⁺ and Na⁺ is strongly dependent on the relative divalent/monovalent ion concentration (27, 28, 66, 82). However, these existing MD-based studies on the binding of divalent/monovalent ions generally involved dsDNA or dsRNA with a given length and seldom covered the competitive binding of divalent/monovalent ions for nucleic acid structures beyond the standard B-form and A-form helical structures (42, 43, 73, 86, 87), although the existing experiments indicate that the global binding of Mg²⁺/Na⁺ (or K⁺) can be strongly dependent on nucleic acid structures (1, 2, 3, 4, 5, 6, 10, 63). Therefore, there is still a lack of comprehensive understanding on the competitive binding of divalent/monovalent ions, especially to various nucleic acid structures.

Furthermore, an important issue in simulating nucleic acids with arbitrary structures in mixed divalent/monovalent ion solutions via MD simulations is to efficiently simulate a nucleic acid solution with desired bulk divalent/monovalent ion concentrations so as to conveniently model experimental systems and analyze ion concentration effects (63, 73, 82, 87). This is challenging, because the competitive binding of divalent/monovalent ions may be sensitive to the structures of nucleic acids as well as the relative divalent/monovalent ion concentrations, and an MD cell generally cannot become very large because of the extremely high computation cost. To simulate a 25-base-pair (bp) dsRNA in various mixed Mg²⁺/Na⁺ solutions, Kirmizialtin and Elber employed a neutralization technique to partition Mg²⁺ and Na⁺ in their MD simulations, although the obtained bulk Mg²⁺/Na⁺ concentrations deviated apparently from the desired concentrations (27, 66). To simulate a 24-bp dsDNA in mixed Mg²⁺/Na⁺ solutions via MD simulations, Yoo and Aksimetiev attempted to obtain the desired bulk Mg²⁺/Na⁺ concentrations through adjusting ion numbers in their MD simulations and repeating the procedure, but the resultant bulk Mg²⁺/Na⁺ concentrations still deviated visibly from the desired concentrations, and such treatment was obviously not efficient (82). To model S-adenosylmethionine (SAM-I) riboswitch in mixed Mg²⁺/K⁺ solution via MD simulations, Hayes et al. also chose the numbers of ions in the MD cell through repeated MD trials to obtain the desired bulk Mg²⁺/K⁺ concentrations (73). Therefore, it is still necessary to obtain a general and efficient method for simulating a nucleic acid with arbitrary structure in a mixed Mg²⁺/Na⁺ solution with desired bulk ion concentrations.

In this work, we first proposed a general and efficient method for simulating a nucleic acid with arbitrary structure in a mixed Mg²⁺/Na⁺ solution with desired bulk ion concentrations and examined the method through extensive MD simulations. Afterward, we investigated the competitive binding of Mg²⁺ and Na⁺ to extensive nucleic acids, including short dsDNA, dsRNAs, and several RNA tertiary structures. Our calculations were compared with available experimental data, and the global and local binding of Mg²⁺ and Na⁺ were analyzed in detail for various nucleic acids. The global binding of ions is characterized as the binding ions in excess of bulk ion concentration (27, 28, 66, 82), and the local binding of ions is characterized by the closely binding of ions near phosphates. Our comprehensive analyses suggest the global binding of Mg²⁺ over Na⁺ to a nucleic acid is mainly dependent on the surface charge density and Mg²⁺/Na⁺ concentrations, and the local binding of Mg²⁺ over Na⁺ to a phosphate of a nucleic acid depends mainly on the local phosphate density (i.e., the number of phosphates around a phosphate) in addition to Mg²⁺/Na⁺ concentrations.

Materials and Methods

Method for simulating a nucleic acid solution with desired bulk divalent/monovalent ion concentrations via MD simulations

Because the competitive binding of divalent/monovalent ions may be strongly dependent on many factors, such as divalent/monovalent ion concentrations and the length and structure of nucleic acids, it is challenging to propose a general and efficient method for simulating a nucleic acid in a mixed divalent/monovalent ion solution with desired bulk ion concentrations via MD simulations (27, 66, 73, 82). The TBI model has been shown to successfully predict the global competitive binding between divalent/monovalent ions to various DNA and RNA structures (54). Through extensive TBI-based calculations for various DNA and RNA structures in mixed Mg²⁺/Na⁺ solutions with wide range of Mg²⁺/Na⁺ concentrations (54), an empirical equivalent formula between divalent and monovalent ions in neutralizing various nucleic acids has been derived (54):

$$\text{l}\text{o}\text{g}{\left[\text{N}{\text{a}}^{+}\right]}_{\text{M}\text{g}}=A\text{log}\left[\text{M}{\text{g}}^{2+}\right]+B,$$ (1)

where [Na⁺]_Mg and [Mg²⁺] are in millimolar and can achieve the equivalent ionic neutralization for a nucleic acid (54). The two parameters A and B in Eq. 1 are dependent on the length and compactness of a nucleic acid (54):

$$A=0.65+\frac{4.2}{N}{\left(\frac{R_g}{R_g^0}\right)}^2;B=1.80-\frac{9.8}{N}{\left(\frac{R_g}{R_g^0}\right)}^2,$$ (2)

where N and R_g represent the number of phosphates and radius of gyration for a nucleic acid. $R_g^0$ is the radius of gyration for the A-form RNA helix with the same length N (–nt), which has been fitted to an empirical formula $R_g^0$ = 0.406N + 130/(N + 11) (54). Based on Eq. 1, for a nucleic acid in a mixed Mg²⁺/Na⁺ solution with desired bulk concentrations [Mg²⁺] and [Na⁺], the numbers $N_{Mg}^c$ and $N_{Na}^c$ of divalent/monovalent counterions for neutralizing the nucleic acid can be given by

$$N_{Mg}^c=N\frac{0.5{\left[\text{N}{\text{a}}^{+}\right]}_{\text{M}\text{g}}}{{\left[{\text{Na}}^{+}\right]}_{\text{M}\text{g}}+\left[\text{N}{\text{a}}^{+}\right]};N_{Na}^c=N\frac{\left[\text{N}{\text{a}}^{+}\right]}{{\left[\text{N}{\text{a}}^{+}\right]}_{\text{M}\text{g}}+\left[\text{N}{\text{a}}^{+}\right]},$$ (3)

respectively. Therefore, the total numbers for divalent/monovalent ions in the simulation cell are given by $N_{Mg}^{}$=$N_{Mg}^c+N_{Mg}^s$ and $N_{Na}^{}$=$N_{Na}^c+N_{Na}^s$, respectively. Here, $N_{Mg}^s$ and $N_{Na}^s$ are the numbers of divalent/monovalent ions dissociated from the added divalent/monovalent salts and can be calculated conveniently with the MD cell size and bulk salt concentrations ([Mg²⁺] and [Na⁺]). Our simulation systems were kept neutral with addition of coions Cl^–.

All-atom MD simulations

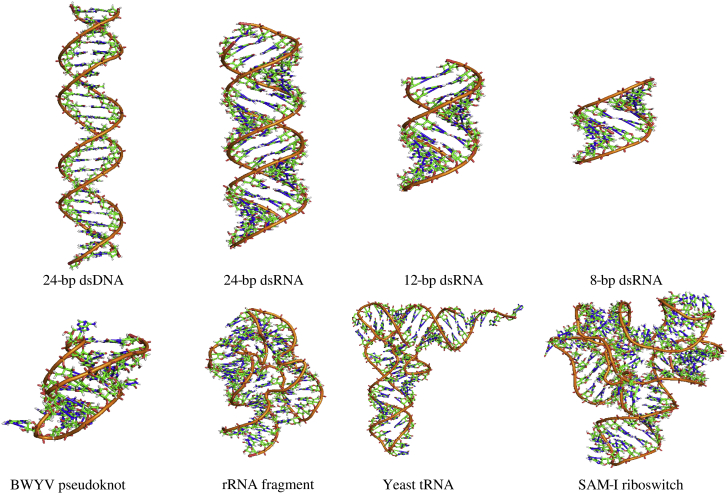
In this work, we performed all-atom MD simulations in mixed Mg²⁺/Na⁺ solutions to 1) examine the method proposed above for simulating nucleic acids in mixed divalent/monovalent ion solutions with desired bulk divalent/monovalent ion concentrations; and 2) perform comprehensive analyses on the competitive binding of divalent/monovalent ions to diverse and representative constructs of nucleic acids (63, 82). The nucleic acids used in our MD simulations include a 24-bp B-form dsDNA, an A-form dsRNA with different lengths (8-, 12-, and 24-bp), and four RNA tertiary structures: 28-nucleotide (nt) beet western yellow virus (BWYV) pseudoknot (Protein Data Bank (PDB): 437D) (88), 58-nt ribosomal RNA (rRNA) fragment (PDB: 1HC8) (89), 76-nt Yeast tRNA^Phe (PDB: 1TRA) (90), and 94-nt SAM-I riboswitch (PDB: 2GIS) (91). The sequences of the dsDNA and dsRNAs are in Table S1. The initial structures of the dsDNA and dsRNA structures were built using the Nucleic Acid Builder of AMBER (AMBER Software, San Francisco, CA) (92), and the initial structures of RNA tertiary structures were taken directly from the PDB (93). The structures of the nucleic acids used in the work are shown in Fig. 1, and the nucleic acids, ion conditions, and the respective simulation cells are listed in Table 1. For the dsDNA and dsRNA structures, the simulation cells were chosen according to the previous simulational work (82) for the convenience of direct comparison, and for the RNA tertiary structures, the simulation cells were selected to ensure the distance between the edge of the cells and the surface of the RNA tertiary structures was larger than two times the Debye-Hückel length. All the details for the numbers of ions (Mg²⁺, Na⁺, and Cl^–) added in the simulation cells were listed in Table S2. In this work, Na⁺ was chosen rather than K⁺ according to the related experimental (63) and simulational works (27, 28, 66, 73, 82), although K⁺ is more prevalent than Na⁺ in intracellular environment.

Figure 1.

The DNA and RNAs used in our simulations, including 24-bp dsDNA; 24-bp, 12-bp, and 8-bp dsRNAs (63); BWYV pseudoknot (88); 58-nt rRNA fragment (89); yeast tRNA^Phe (90); and SAM-I riboswitch (91). The structures for the nucleic acids are displayed with PyMol (http://www.pymol.org). To see this figure in color, go online.

Table 1.

The DNA/RNA Molecules and the Respective MD Simulation Details in the Work

DNA or RNA	Desired Bulk [Mg2+]/[Na+] (mM)	Cell Size (Å 3)	Simulation Time (ns)	Bulk [Mg2+]/[Na+] in Referencea (mM)	Our Bulk [Mg2+]/[Na+]b (mM)
24-bp dsDNA	1/20	150 × 150 × 90	200	–	1.1 ± 0.1/20.2 ± 0.3
	5/20	150 × 150 × 90	200	7/18	5.4 ± 0.1/20.0 ± 0.2
	5/40	150 × 150 × 90	200	8/36	5.3 ± 0.1/40.4 ± 0.3
	5/70	150 × 150 × 90	200	8/72	5.2 ± 0.1/70.3 ± 0.2
	5/240	150 × 150 × 90	200	6/237	5.2 ± 0.2/241.6 ± 0.4
	5/420	150 × 150 × 90	200	7/418	5.3 ± 0.1/421.1 ± 0.3
	10/20	150 × 150 × 90	200	–	10.1 ± 0.1/20.8 ± 0.3
	20/20	150 × 150 × 90	200	–	20.9 ± 0.2/19.7 ± 0.2
	50/20	150 × 150 × 90	200	–	50.8 ± 0.7/20.7 ± 0.5
8-bp dsRNA	1/20	150 × 150 × 48	200	–	1.0 ± 0.1/21.5 ± 0.1
	10/20	150 × 150 × 48	200	–	10.9 ± 0.2/20.4 ± 0.2
12-bp dsRNA	1/20	150 × 150 × 58	200	–	1.0 ± 0.1/21.6 ± 0.8
	10/20	150 × 150 × 58	200	–	10.5 ± 0.3/19.7 ± 0.2
24-bp dsRNA	1/20	150 × 150 × 90	200	–	1.1 ± 0.1/20.2 ± 0.3
	5/20	150 × 150 × 90	200	–	5.1 ± 0.2/21.6 ± 0.3
	10/20	150 × 150 × 90	200	–	10.1 ± 0.1/21.6 ± 0.1
	50/20	150 × 150 × 90	200	–	50.8 ± 0.3/21.7 ± 0.1
28-nt BWYV Pseudoknot	1/20	120 × 110 × 110	200	–	1.0 ± 0.1/20.8 ± 0.2
	10/20	120 × 110 × 110	200	–	10.9 ± 0.2/20.5 ± 0.1
58-nt rRNA Fragment	1/20	130 × 130 × 120	200	–	1.1 ± 0.2/20.5 ± 0.1
	10/20	130 × 130 × 120	200	–	10.2 ± 0.2/19.5 ± 0.1
76-nt Yeast tRNAPhe	1/20	130 × 145 × 160	200	–	1.1 ± 0.1/19.4 ± 0.3
	10/20	130 × 145 × 160	200	–	10.3 ± 0.1/19.1 ± 0.1
94-nt SAM-I Riboswitch	1/20	120 × 145 × 140	200	–	1.0 ± 0.1/21.0 ± 0.2
	10/20	120 × 145 × 140	200	–	10.1 ± 0.1/20.5 ± 0.1

In the table, the sequences of dsDNA and dsRNAs are listed in Table S1, and BWYV pseudoknot, rRNA fragment, Yeast tRNA^Phe, and SAM-I riboswitch represent a 28-nt beet western yellow virus (BWYV) pseudoknot fragment (PDB: 437D) (88), a 58-nt ribosomal RNA fragment (PDB: 1HC8) (89), 76-nt Yeast tRNA^Phe (PDB: 1TRA) (90), and 94-nt S-adenosylmethionine riboswitch mRNA (PDB: 2GIS) (91), respectively.

^aThe bulk [Mg²⁺]/[Na⁺] values are obtained from Yoo and Aksimetiev (82).

^bThe bulk [Mg²⁺]/[Na⁺] values are obtained from our MD simulations.

In our MD simulations, the Amber parmbsc0 force field (92) was employed for DNA and RNA molecules in mixed Mg²⁺/Na⁺ ion solutions, combined with the TIP3P water model and Joung/Cheatham ion model for Na⁺ and Cl^– (94) and Åqvist ion model for Mg²⁺ (95), in which ions were added by replacing the water molecules at least 20 Å away from the surface atom of nucleic acids, i.e., the atoms with the closest distance from the added ions. All the simulation systems were optimized, thermalized (298 K), and equilibrated with the program Gromacs 4.5 (96), with the periodic boundary conditions and particle mesh Ewald method for long-range interaction (97). All atoms in the nucleic acids were restrained by a harmonic potential with force constant 1000 kJ/mol·nm^–2 in x-, y- and z-directions; hence, the effect of nucleic acid flexibility on ion binding was ignored. Each MD simulation was continued for 200 ns in the isothermic-isobaric ensemble (time step = 2 fs, P = 1 atm, and T = 298 K). Generally, our MD simulations for ion binding to various nucleic acids qualitatively nearly reach equilibrium after ∼20 ns, as shown in Figs. S1 and S2. During all our simulations, the change on the box sizes is always less than 0.5 Å in each dimension, and it leads to a change of ∼1.3% on the box volumes; thus, it would only have a slight effect on the calculated bulk ion concentrations. Additionally, we have examined the Mg²⁺ models of Allnér and Villa (98) and Li and Merz (99) for a 12-bp dsDNA (72) and did not find a significant effect of Mg²⁺ models on the Mg²⁺ distribution around the 12-bp dsDNA; see Fig. S3. We have also performed additional simulations for 24-bp dsDNA and 58-nt rRNA fragment in 1 mM Mg²⁺/20 mM Na⁺ solution with different initial positions of ions.

The Poisson-Boltzmann calculations

In addition to the all-atom simulations described above, we also calculated the binding ions in excess of bulk ions and the surface electrostatic potentials for various nucleic acids with the PB theory (52, 53, 54, 59, 60). For calculating the binding ions in excess of bulk ions to nucleic acids, we used the three-dimensional finite-difference algorithm developed in the TBI model for our convenience (52). A three-step focusing process was employed, and the resolutions for the three steps were kept as 2.0, 1.0, and 0.5 Å per grid respectively. The grid size (L_x, L_y, L_z) of the first, second, and third runs were kept larger than 10, 6, and 2 times the Debye-Hückel length from the surface of a nucleic acid and varied with different DNA and RNA molecules. Other details about the solvent have been described in (52, 54). For calculating the surface electrostatic potential for nucleic acids, we used the APBS software (49), since the obtained surface potential can be conveniently displayed with VMD (100). In all the PB calculations, the dielectric constant inside nucleic acids was set to be two, and that of solvent was taken as 78.5. The radii of Mg²⁺ and Na⁺ were taken as 3.0 Å (101) and 2.0 Å (102), respectively.

Results and Discussion

First, we have examined the proposed method for efficiently simulating a nucleic acid in mixed divalent/monovalent solutions with desired bulk ion concentrations via MD simulations. Second, we have performed a detailed comparative analysis on the binding of Mg²⁺ and Na⁺ to dsDNA and dsRNA. Third, we have focused on the binding of Mg²⁺ and Na⁺ to various RNA tertiary structures with different lengths and compactness. Finally, we have summarized what governs the global and local binding of Mg²⁺ and Na⁺ to various nucleic acid structures. In addition, our calculations are compared with the available experimental data and cover the wide ranges of ion concentrations and nucleic acid structures. In our analyses, we will use the binding ions in excess of bulk ions to characterize the global binding of ions to nucleic acids (37, 54) and use detailed ion distributions and closely binding ions near phosphates to characterize the local binding of ions to various nucleic acids.

Simulating a nucleic acid in mixed Mg²⁺/Na⁺ solutions with desired bulk ion concentrations

As described in the Materials and Methods, we proposed a method aiming to efficiently model the system of a nucleic acid in mixed Mg²⁺/Na⁺ solutions with desired bulk ion concentrations via MD simulations. In the following, we have examined whether a one-time MD run with the use of the proposed method can yield the desired bulk ion concentrations for various RNA/DNA molecules in extensively mixed Mg²⁺/Na⁺ conditions. The ion concentration $c_{\alpha }\left(r\right)$ around a nucleic acid can be calculated by

$$c_{\alpha }\left(r\right)=\frac{N_{\alpha }\left(r+dr\right)-N_{\alpha }\left(r\right)}{V\left(r+dr\right)-V\left(r\right)},$$ (4)

where V(r) and N_α(r) denote the volume and the number of ions within a distance r from the nucleic acid, respectively, and α stands for ion species. For dsDNA and dsRNA helices, r is the radial distance from the helical axis that was obtained with the program of Curves+ (103), V(r) stands for the cylinder volume within r without excluding DNA or RNA volume, and c_α(r) was previously used to analyze ion distribution around dsDNA/dsRNA (19, 20, 26, 74, 95). For RNA tertiary structures in which an axis cannot be well defined, r stands for the distance from the surface atoms (the atoms with closest distance from the examined ions), and V(r) excludes the volume of the RNAs. According to Eq. 4, the bulk ion concentrations can be obtained at large r, as shown in Figs. S4–S6. In the following, we have examined the obtained bulk divalent/monovalent ion concentrations for various nucleic acids in comparison with the desired concentrations.

For dsDNA and dsRNA of different lengths, we made extensive examinations on bulk ion concentrations over the wide range of [Mg²⁺] and [Na⁺]. As shown in Table 1, our proposed method can yield the bulk [Mg²⁺] and [Na⁺], which are very close to the desired values. The mean relative deviations of [Mg²⁺] and [Na⁺] from the desired ones are ∼5 and ∼4%, respectively. Here, the mean relative deviation of [Mg²⁺] is slightly larger than that of [Na⁺] because the desired bulk [Mg²⁺] is generally lower (∼mM) than the desired bulk [Na⁺]. Although the largest relative deviation of [Mg²⁺] comes from a mixed solution of 1 mM Mg²⁺ and 20 mM Na⁺, the absolute deviation of [Mg²⁺] is only ∼0.1 mM. Compared with the previous work (e.g., (82)), our obtained bulk [Mg²⁺] and [Na⁺] are much closer to the desired values (e.g., the mean relative deviations of [Mg²⁺] from our MD and (82) for the total cases are ∼5 and ∼44%, respectively), given the same simulation cell (82) (see Table 1). Additionally, our method is much more efficient because only one MD run is required for each case with the proposed method described in the Materials and Methods.

For various RNA tertiary structures ranging from 28-nt BWYV pseudoknot to 94-nt SAM-I riboswitch, the obtained bulk [Mg²⁺]/[Na⁺] in our MD simulations are all close to the desired values, as shown in Table 1. The mean relative deviations of [Mg²⁺] and [Na⁺] from the desired values are rather small (∼5% for [Mg²⁺] and ∼4% for [Na⁺]). In a recent MD simulation of SAM-I riboswitch in mixed Mg²⁺/K⁺ solution, Hayes et al. obtained the desired bulk ion concentrations with the slightly larger mean relative deviations of Mg²⁺ (∼5.1% for [Mg²⁺]) by repeating several MD trials (73), in which the slightly smaller mean relative deviation of [K⁺] (∼2%) may be caused by the high desired bulk concentration (∼100 mM) (73). It should be noted that our proposed method only requires one MD run even for various RNA tertiary structures (see the Materials and Methods) to yield desired bulk ion concentrations for simulating various RNA tertiary structures in mixed Mg²⁺/Na⁺ solutions, although larger RNA tertiary structures (>94 nt) have not been examined here.

Therefore, the above extensive examinations show that our proposed method is effective and efficient for simulating a nucleic acid with arbitrary structure in mixed divalent/monovalent ion solutions with wide ranges of desired bulk ion concentrations. It is encouraging that only a single MD simulation is required for a nucleic acid in a mixed Mg²⁺/Na⁺ solution to yield the desired bulk Mg²⁺/Na⁺ concentrations, and the method is expected to work for other mixed divalent/monovalent ion solutions such as mixed Mg²⁺/K⁺ solutions.

Competitive binding of Mg²⁺/Na⁺ to duplexes: dsDNA versus dsRNA

Global binding of Mg²⁺/Na⁺ and comparison with experiments

Since the global binding of ions is directly coupled to the global stability of nucleic acids (1, 2, 3, 4, 5, 6, 7, 8, 9, 36, 37, 38), we calculated the number of global binding ions for both dsDNA and dsRNA (27, 28, 66). According to (27, 28, 66, 72, 82), the numbers $N_{\alpha }^b$ of global binding ions of species $\alpha$ in excess of bulk ion concentrations can be calculated as those ions:

$$N_{\alpha }^b=\underset{0}{\overset{\infty }{\int }}\left(c_{\alpha }\left(r\right)-c_{\alpha }^0\right)d^{3}r.$$ (5)

Based on the ion concentration distributions and the bulk ion concentrations $c_{\alpha }^0$ shown in Table 1 and Figs. S5 and S6, the numbers $N_{Mg}^b$, $N_{Na}^b$, and $N_{Cl}^b$ of global binding Mg²⁺/Na⁺/Cl^– around the 24-bp dsDNA or dsRNA were calculated through Eq. 5.

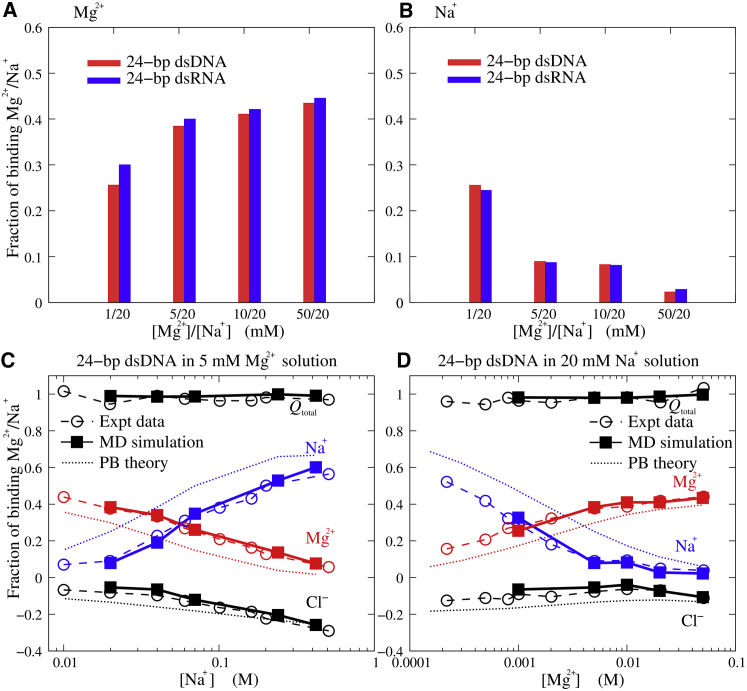
As shown in Fig. 2, A and B and in Table S2, for both dsDNA and dsRNA, with the increase of [Mg²⁺] from 1 to 50 mM, $N_{Mg}^b$ increases apparently and $N_{Na}^b$ decreases simultaneously, suggesting the anticooperative binding between Mg²⁺ and Na⁺. Since the number of negative charges on a nucleic acid is unchanged, the increase of $N_{Mg}^b$ (or $N_{Na}^b$) causes the decrease of $N_{Na}^b$ (or $N_{Mg}^b$). Fig. 2, A and B also show that $N_{Mg}^b$ for dsRNA is always slightly larger than that for dsDNA over the range of [Mg²⁺] from 1 to 50 mM, and correspondingly, $N_{Na}^b$ for dsRNA is slightly smaller than that for dsDNA. The larger number $N_{Mg}^b$ for dsRNA than for dsDNA can be attributed to the more compact structure of dsRNA: A-RNA is slightly shorter than B-DNA, which results in higher charge density and stronger Mg²⁺ binding for dsRNA.

Figure 2.

(A and B) The fractions of binding Mg²⁺ (A) and Na⁺ (B) per nucleotide around the 24-bp dsDNA and dsRNA. (C and D) These panels show the fractions of binding Mg²⁺, Na⁺, and Cl^– per nucleotide and the total charge fraction Q_total of the ion atmosphere (Mg²⁺, Na⁺, and Cl^–) for the 24-bp dsDNA as functions of [Na⁺] (C) and [Mg²⁺] (D). Dashed lines with circles represent experimental data (63); solid lines with squares represent MD simulations; and dotted lines represent PB theory. To see this figure in color, go online.

Fig. 2, C and D show the experimental data (63), our MD calculations, and the PB calculations for $N_{Mg}^b$ and $N_{Na}^b$ around the 24-bp dsDNA. First, the total charge fraction Q_total of binding ions (Mg²⁺, Na⁺, and Cl^–) almost keeps unity, suggesting that the systems are neutral. Second, $N_{Mg}^b$ (or $N_{Na}^b$) increases with the increase of [Mg²⁺] (or [Na⁺]), and the increase (decrease) of $N_{Mg}^b$ is generally accompanied with the decrease (increase) of $N_{Na}^b$. As discussed above, increased ion (Mg²⁺ or Na⁺) concentration reduces the entropic penalty for ion binding and consequently favors the ion (Mg²⁺ or Na⁺) binding, and the interplay between $N_{Mg}^b$ and $N_{Na}^b$ is attributed to the unchanged number of negative charges on a nucleic acid. Third, our MD calculations are in accordance with the experimental data for $N_{Mg}^b$, $N_{Na}^b$, and $N_{Cl}^b$ (55), suggesting that all-atom MD simulations can capture the ion-binding properties despite the computation cost. Fourth, the PB theory apparently underestimates $N_{Mg}^b$ and correspondingly overestimates $N_{Na}^b$, although it predicts the trend of ion binding with ion concentration. Physically, the PB theory assumes the mean fluid-like ion distribution and consequently ignores the discrete properties of ions such as ion correlations, which would allow ions to self-organize to low-energy states and favor the binding of multivalent ions (52, 53, 54, 61, 62). Thus, the PB theory underestimates Mg²⁺ binding and overestimates Na⁺ binding. The systematic deviations of the PB theory were also observed previously in the Monte Carlo simulations and PB calculations for polymeric DNA in mixed salt solutions (20). Our additional calculations show the influence of the choice of dielectric constant of nucleic acids and radii of Mg²⁺ and Na⁺ for the PB results on the numbers of binding ions; see Fig. S7.

Mg²⁺/Na⁺ distributions around duplexes: B-DNA versus A-RNA

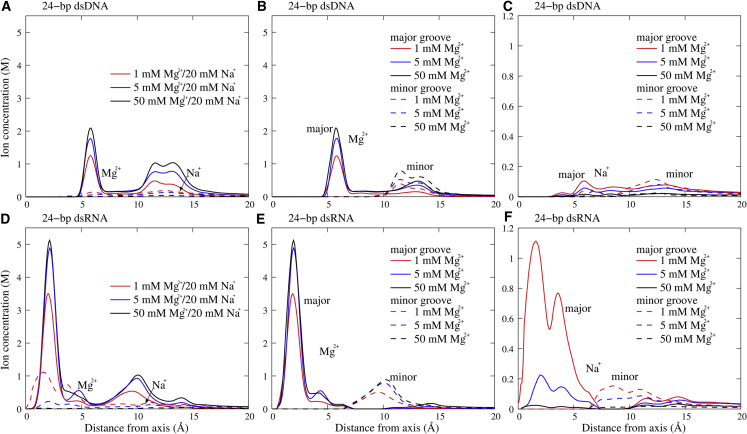
Beyond the above-described global binding, we performed analyses on Mg²⁺/Na⁺ distributions around dsDNA and dsRNA. As shown in Fig. 3, the radial concentration distributions of Mg²⁺ and Na⁺ around dsDNA and dsRNA share the following similar features: 1) there are two major peaks in the radial distributions of Mg²⁺ at two radial locations, and the height of the peaks increases with the increase of bulk [Mg²⁺]; and 2) the radial distribution of Na⁺ appears much lower than that of Mg²⁺ and decreases for higher bulk [Mg²⁺]. The higher peaks of Mg²⁺ and lower peaks of Na⁺ for higher [Mg²⁺] are due to the lowered binding entropy penalty of Mg²⁺, and the overall lower radial concentration of Na⁺ than Mg²⁺ is attributed to the higher charge of Mg²⁺ and the corresponding stronger binding of Mg²⁺. The two major peak locations of Mg²⁺ suggest the two different Mg²⁺ binding modes for dsDNA and dsRNA.

Figure 3.

(A and D) The radial concentration distributions of Mg²⁺ and Na⁺ around 24-bp dsDNA (A) and dsRNA (D) in 20 mM Na⁺ solutions with different [Mg²⁺] values. (B and E) These panels show the Mg²⁺ concentration distributions in/above the minor groove (dashed lines) and the major groove (solid lines) for the 24-bp dsDNA (B) and dsRNA (E). (C and F) These panels show the Na⁺ concentration distributions in/above the minor groove (dashed lines) and the major groove (solid lines) for the 24-bp dsDNA (C) and dsRNA (F). To see this figure in color, go online.

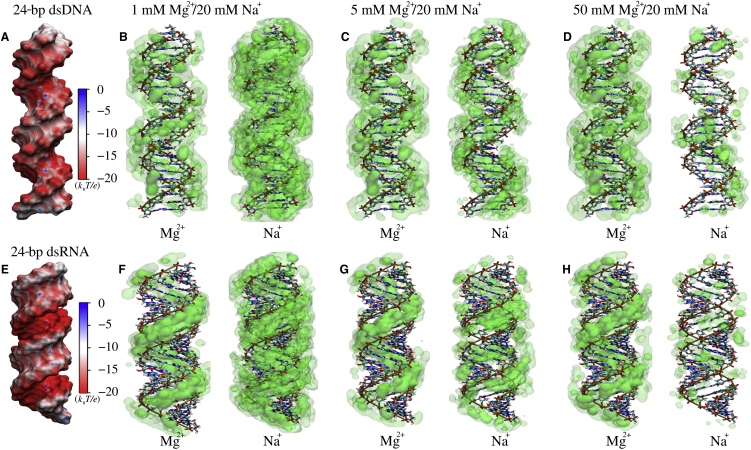
The detailed comparison between dsDNA and dsRNA also shows a distinctive difference in ion binding (e.g., Mg²⁺): the radial locations for two major peaks are apparently different (∼6 and ∼12.5 Å for dsDNA, and ∼2 and ∼10 Å for dsRNA), and the heights of the first peaks of Mg²⁺ and Na⁺ (near-radial distance of ∼2 Å) for dsRNA are much higher than those for dsDNA (near-radial distance of ∼6 Å). To understand this difference, we divided the radial concentration distributions of Mg²⁺ and Na⁺ into those in (or over) major and minor grooves for dsDNA and dsRNA. As shown in Fig. 3, B and C, for dsDNA, Mg²⁺ can bind into the major groove at a radial distance of ∼6 Å, whereas Mg²⁺ can bind more deeply and strongly into the major groove of dsRNA at a radial distance of ∼2 Å. The next preferred binding of Mg²⁺ is above the minor groove (at a radial distance of ∼12.5 Å) for dsDNA, and between phosphate strands in the minor groove (at a radial distance of ∼10 Å) for dsRNA. Na⁺ can also bind more deeply and strongly into the major groove of dsRNA than to dsDNA, although the radial concentration of Na⁺ is much lower than that of Mg²⁺ because of the lower ionic charge, as shown in Fig. 3, E and F. The apparent difference in Mg²⁺ binding between dsDNA and dsRNA is attributed to their different helical structures: A-form dsRNA has a much deeper/narrower major groove and a wider minor groove than B-form dsDNA, which causes very different surface electrostatic potentials for dsDNA and dsRNA (see Figs. 1 and 4). Accordingly, we illustrated the spatial concentration distributions of Mg²⁺ and Na⁺ around dsDNA and dsRNA at different bulk Mg²⁺/Na⁺ concentrations. As shown in Fig. 4, for dsRNA, the deep and narrow major groove is the most preferred binding domain for both Mg²⁺ and Na⁺, and Mg²⁺ binding to the minor groove can become visible at high bulk [Mg²⁺] because the narrow major groove can be almost fulfilled by Mg²⁺. However, for dsDNA, the binding to the major groove and minor groove are both visible, whereas this appears weaker than the binding to the major groove of dsRNA. As [Mg²⁺] increases, Mg²⁺ binding to major and minor grooves becomes stronger for both dsDNA and dsRNA, and simultaneously, Na⁺ binding becomes weaker. Our additional simulations with different initial positions of ions and with longer cell size in the z axis for 24-bp dsDNA yielded similar bulk ion concentrations and ion distributions; see Fig. S8. Additionally, we observed more binding Mg²⁺ ions in the GGG region of the major groove of the 24-bp dsDNA because the guanine bases can hold Mg²⁺ ions more strongly (74); see Fig. S9.

Figure 4.

(A and E) The electrostatic potentials at the Mg²⁺ accessible surface of the 24-bp dsDNA (A) and dsRNA (E) were calculated by APBS (49). Shown is the electrostatic potential computed 3 Å away (the radius of hydrated Mg²⁺ is ∼3 Å (80)) from the surface by VMD (100). (B–D and F–H) The spatial ion concentration distributions of Mg²⁺ and Na⁺ around the surface of 24-bp dsDNA and dsRNA are displayed in green of three-level opacities (0.5 M–5 M, 5 M–10 M, and >10 M for Mg²⁺ and 0.25 M–0.5 M, 0.5 M–2.0 M, and >2.0 M for Na⁺, respectively) by VMD (100). To see this figure in color, go online.

The different ion binding modes for dsDNA and dsRNA have been suggested to be responsible for the different multivalent ion-dependent condensation behaviors (27, 28, 34, 66, 73, 82) and flexibilities for dsDNA and dsRNA (64, 65).

Competitive binding of Mg²⁺/Na⁺ to RNA tertiary structures

Beyond dsDNA and dsRNA helices, we analyzed the competitive binding of Mg²⁺ and Na⁺ to various RNA tertiary structures, including 28-nt BWYV pseudoknot, 58-nt rRNA fragment, 76-nt Yeast tRNA^Phe, and 94-nt SAM-I riboswitch.

Global binding of Mg²⁺ and Na⁺ to RNA tertiary structures

Since numbers of binding Mg²⁺/Na⁺ are associated with the global stability of RNA tertiary structures, we calculated the numbers ($N_{Mg}^b$ and $N_{Na}^b$) of binding Mg²⁺/Na⁺ to various RNA tertiary structures as those in excess of bulk ion concentrations according to Eq. 5. As shown in Fig. 5, A and B and in Table S2, $N_{Mg}^b$ and $N_{Na}^b$ from the MD simulations are in accordance with those from the empirical formula from the TBI model, which has been quantitatively tested by the extensive experimental data for various RNA tertiary structures (54). Fig. 5, A and B also show that for higher bulk [Mg²⁺], $N_{Mg}^b$ increases and $N_{Na}^b$ simultaneously decreases because of the lower entropy penalty of Mg²⁺ at higher [Mg²⁺]. Furthermore, compared with the predictions from the MD simulations and the TBI model, the PB theory significantly underestimates $N_{Mg}^b$ and simultaneously overestimates $N_{Na}^b$. As described above, this is because the PB theory ignores the ion correlation and fluctuation that allow ions to self-organize to low-energy states and favor multivalent ion binding (52, 53, 54, 61, 62).

Figure 5.

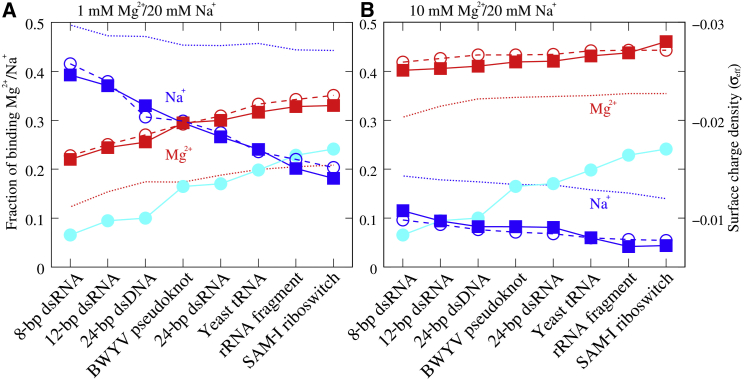
The number fractions of binding Mg²⁺ and Na⁺ per nucleotide for various RNA/DNA molecules in mixed 1 mM Mg²⁺/20 mM Na⁺ (A) and 10 mM Mg²⁺/20 mM Na⁺ (B) ion solutions. Solid lines with squares represent MD simulations; dotted lines represent PB theory; dashed lines with circles represent TBI predictions (Eq. 5 in (54)); and solid lines with spheres represent the effective surface charge density σ_eff. Here, RNA/DNA molecules were listed according to the order of fraction of binding Mg²⁺/Na⁺. The effective surface charge density (in units of e/Ų) was calculated through considering an RNA/DNA as an ellipsoid; see the Supporting Material. To see this figure in color, go online.

For different RNA tertiary structures, $N_{Mg}^b$ exhibits the following order: 94-nt SAM-I riboswitch > 58-nt rRNA fragment > 76-nt Yeast tRNA^Phe > 28-nt BWYV pseudoknot. If we include the DNA/RNA helices, the order of $N_{Mg}^b$ is as follows: 94-nt SAM-I riboswitch > 58-nt rRNA fragment > 76-nt Yeast tRNA^Phe > 24-bp dsRNA > 28-nt BWYV pseudoknot > 24-bp dsDNA > 12-bp dsRNA > 8-bp dsRNA, and $N_{Na}^b$ follows the reversal order. This indicates that the global competitive binding of Mg²⁺/Na⁺ to RNAs may depend not only on RNA length but also structure compactness, and global Mg²⁺ binding appears stronger for RNAs with longer length and more compact structures.

Mg²⁺/Na⁺ distributions around RNA tertiary structures

Beyond the analyses described above on the global binding of Mg²⁺ and Na⁺, we have performed analyses on the detailed binding of Mg²⁺ and Na⁺ to various RNA tertiary structures, including the BWYV pseudoknot, rRNA fragment, yeast tRNA^Phe, and SAM-I riboswitch.

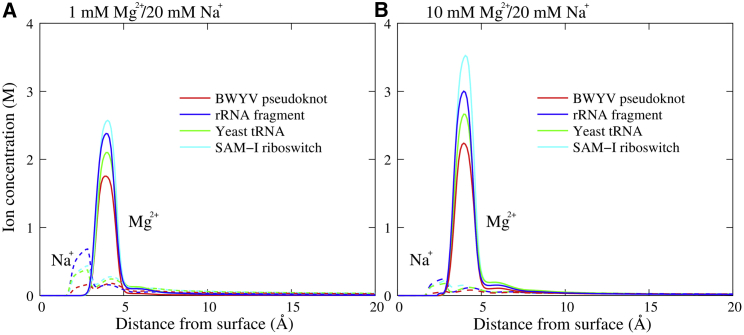
Since RNA tertiary structures are generally more complex than DNA/RNA duplexes and there is no well-defined axis, we calculated the ion concentrations $c\left(r\right)$ from the surface atoms of the RNA tertiary structures according to Eq. 4. As shown in Fig. 6, the concentration distributions of Mg²⁺ and Na⁺ share a similar trend for various RNA tertiary structures: 1) the location of the peaks of Mg²⁺ is ∼4 Å, and the peak heights of Mg²⁺ are apparently higher than those of Na⁺; and 2) with the increase of [Mg²⁺], the peak height of Mg²⁺ increases, and correspondingly, that of Na⁺ decreases. The location of ∼4 Å from surface atoms suggests that Mg²⁺ keeps its hydrated shell in binding to various RNAs because of the very high dehydration penalty for Mg²⁺ (33, 34, 35, 66), and it is hard for Mg²⁺ to become dehydrated within finite MD simulation time (72, 81). However, monovalent ions can become partially dehydrated in binding to RNAs because of the much lower dehydration energy (71, 72, 73). The stronger Mg²⁺ binding and lower Na⁺ binding at higher bulk [Mg²⁺] is attributed to the lowered penalty for Mg²⁺ binding and the anticooperative binding between Mg²⁺ and Na⁺. Despite the above described similarity in ion binding, the peak heights of Mg²⁺ distributions appear different for various RNA tertiary structures and follow the same order as that of $N_{Mg}^b$: 94-nt SAM-I riboswitch > 58-nt rRNA fragment > 76-nt Yeast tRNA^Phe > 28-nt BWYV pseudoknot; see Fig. 5, A and B. This order nearly follows the same order of RNA length except for the 58-nt rRNA fragment, which appears relatively more compact than tRNA^Phe and BWYV pseudoknot (54, 62). This also suggests that Mg²⁺ binding to RNA tertiary structures may be dependent on not only RNA length but also its structural compactness. Compared to Mg²⁺ binding, the difference in Na⁺ binding between different RNA tertiary structures appears relatively slight because of the strong Mg²⁺ binding.

Figure 6.

The ion concentration distributions of Mg²⁺ and Na⁺ around various RNA tertiary structures in mixed 1 mM Mg²⁺/20 mM Na⁺ (A) and 10 mM Mg²⁺/20 mM Na⁺ (B) solutions. The RNA tertiary structures include BWYV pseudoknot (red), 58-nt rRNA fragment (blue), yeast tRNA^Phe (green), and SAM-I riboswitch (cyan), and distance from surface denotes that from surface atoms. To see this figure in color, go online.

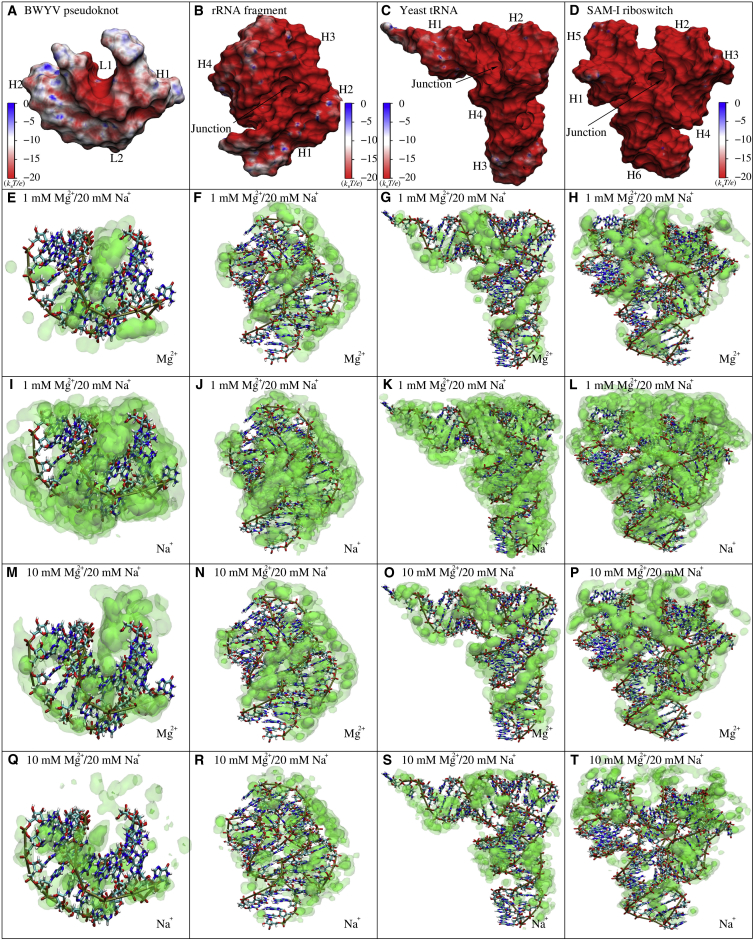
To further reveal the detailed binding of Mg²⁺/Na⁺ to RNA tertiary structures, we have illustrated the surface electrostatic potentials and spatial concentration distributions in Fig. 7. Although the detailed binding of Mg²⁺/Na⁺ exhibits specific patterns for different RNA tertiary structures, the detailed binding of Mg²⁺ and Na⁺ to various RNA tertiary structures share the following similar features: 1) Mg²⁺ prefers to bind deeply into the major groove of A-form helical stems and the junction pocket between helical stems even at low [Mg²⁺]; 2) the binding of Na⁺ into major grooves of helical elements/junction pocket is overwhelmed by Mg²⁺ binding, and Na⁺ prefers to bind relatively loosely around RNA tertiary structures; and 3) the increase of [Mg²⁺] causes more pronounced Mg²⁺ binding in both of the binding locations (to major groove/junction). These features for different RNA tertiary structures are understandable. As shown in Fig. 7 and Fig. S11, there is visible coupling between the local concentration distribution of Mg²⁺ and the local surface electrostatic potential. The surface potential is very negative in major grooves of helical stems and the junction pocket, and these sites are favorable for Mg²⁺ binding rather than Na⁺ binding because of the higher charge of Mg²⁺. Na⁺ can only bind loosely to RNAs because of low ionic charge. The increase of [Mg²⁺] decreases the entropy penalty of Mg²⁺ binding, which would enhance Mg²⁺ binding and more strongly suppress Na⁺ binding. It is noted that the binding of Mg²⁺ to a multibranched junction may be essential in stabilizing specific RNA tertiary structures (1, 5, 6, 7, 8, 9, 10, 12, 37, 38, 39, 42, 43, 44, 73, 86, 87).

Figure 7.

(A–D) The electrostatic potentials at the Mg²⁺ accessible surface of BWYV pseudoknot (A), 58-nt rRNA fragment (B), yeast tRNA^Phe (C), and SAM-I riboswitch (D) were calculated by APBS (49). Shown is the electrostatic potential computed 3 Å away (the radius of hydrated Mg²⁺ is ∼3 Å (80)) from the surface by VMD (100). (E–T) The spatial ion concentration of Mg²⁺ and Na⁺ around BWYV pseudoknot (E, I, M, and Q), 58-nt rRNA fragment (F, J, N, and R), yeast tRNA^Phe (G, K, O, and S), and SAM-I riboswitch (H, L, P, and T) are displayed in green of three-level opacities (0.5 M–5 M, 5 M–10 M, and >10 M for Mg²⁺ and 0.25 M–0.5 M, 0.5 M–2.0 M, and >2.0 M for Na⁺, respectively) by the VMD (100). In panels (A–D), the names of helical stems, loops, and junctions correspond to those in the secondary structures in Fig. S10. The view of the panels in the opposite direction can be found in Fig. S11. To see this figure in color, go online.

What governs the binding of Mg²⁺ and Na⁺ to a nucleic acid?

The global and local binding of Mg²⁺ and Na⁺ to various nucleic acids has been analyzed and discussed extensively. However, the question remains as to whether there is a simple rule that governs the competitive binding of Mg²⁺ and Na⁺ to different nucleic acid structures in addition to Mg²⁺/Na⁺ concentrations. Therefore, in this study, we have attempted to explore such a rule for global binding of Mg²⁺/Na⁺ to various nucleic acid structures. We also attempted to explore the rule for the local binding of Mg²⁺/Na⁺ to various RNA tertiary structures. Here, our analyses cover both ds nucleic acids and RNA tertiary structures to understand the general rule for competitive binding of Mg²⁺/Na⁺, although the binding of Mg²⁺ and a variety of other cationic ligands binding to single-stranded and ds nucleic acids has been reported and discussed previously (6, 15, 16, 17, 18, 19, 20, 21, 22, 23).

Global binding of Mg²⁺/Na⁺ to nucleic acid structures

According to the above analyses, the global binding of Mg²⁺/Na⁺ mainly depends on the length and the compactness of RNA/DNA structures. We investigated whether there is a simple parameter related to RNA/DNA structure for quantifying the global binding of Mg²⁺/Na⁺. Since surface charge density has been previously shown to be a determining parameter for ion binding to spherical and cylindrical polyelectrolytes (47, 48), we calculated the surface charge densities for various RNA/DNA structures (47, 48). Since the surface charge density cannot be clearly defined for a nucleic acid with complex structure, we can approximately model a nucleic acid as an ellipsoid, and the surface charge density σ_eff of the nucleic acid can be estimated as that of the ellipsoid (see the Supporting Material for details).

As shown in Fig. 5, A and B, with the increase of the effective surface charge density σ_eff for various RNA/DNA molecules, the number $N_{Mg}^b$ of binding Mg²⁺ increases monotonously and that of Na⁺ $\left(N_{Na}^b\right)$ decreases monotonously in both 1 mM Mg²⁺/20 mM Na⁺ and 10 mM Mg²⁺/20 mM Na⁺ solutions. Such correlations between $N_{Mg}^b$ (and $N_{Na}^b$) and σ_eff are interesting and reasonable. Physically, Mg²⁺ (Na⁺) binding would become more pronounced (weaker) to a nucleic acid with higher surface charge density because Mg²⁺ with higher ionic charge interacts more strongly with a nucleic acid. Therefore, we propose that the effective surface charge density σ_eff mainly governs the global binding of Mg²⁺/Na⁺ to various nucleic acids, including RNA tertiary structures, in addition to Mg²⁺/Na⁺ concentrations. It is noted that our results in Figs. 5 and S12 are also consistent with the experimental analyses of the interactions of Mg²⁺ and Na⁺ with nucleic acids and the effects of mixtures of these ions on protein-DNA binding (15, 16). Our further analyses suggest that length N may also affect the global binding of Mg²⁺/Na⁺ when nucleic acids are not large, and an empirical linear coupling between the fraction of binding Mg²⁺/Na⁺ and (1 – 3/N)σ_eff has been found for all the nucleic acids we used, as shown in Fig. S12. This Coulombic effect and 1/N dependence of ion accumulation/binding have been previously observed for nucleic acid oligomers in a series of PB- and Monte Carlo-based theoretical studies (17, 18, 19, 21, 22, 23).

Local binding of Mg²⁺/Na⁺ to RNA tertiary structures

Beyond the global binding to a nucleic acid, what governs the local binding of Mg²⁺/Na⁺ to the nucleic acid? Here, we will use the closely binding of ions near phosphates to characterize the local binding of Mg²⁺/Na⁺.

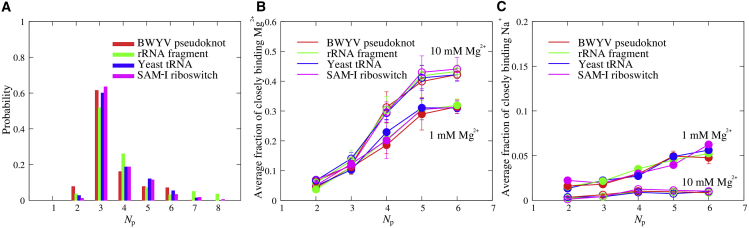
Because the negative charges of a nucleic acid converge on phosphate groups and the local binding of Mg²⁺/Na⁺ is generally around phosphates, we will examine the local competitive binding of Mg²⁺/Na⁺ to phosphates for various RNA tertiary structures. First, we calculated the local phosphate density (i.e., local number N_p of phosphates around a phosphate) within a distance of ∼9 Å, which was taken according to the phosphate-phosphate radial distribution function for various RNA tertiary structures in Fig. S13 A. According to the different number of N_p centered at all phosphates, the phosphates of RNA tertiary structures can be classified into several groups, and the larger N_p represents the more compact domain with higher local charge density as shown in Fig. 8 A. Simultaneously, the fractions f_Mg/f_Na of closely binding Mg²⁺/Na⁺ to phosphates were obtained by calculating the numbers of Mg²⁺/Na⁺ within a small distance around the phosphate atoms, and the small distance was chosen according to the phosphate-Mg²⁺ radial distribution function in Fig. S13 B. The distributions of N_p and f_Mg along phosphate strands for various RNA tertiary structures are shown in Fig. S14, and there is visible correlation between N_p and f_Mg for respective phosphates. Furthermore, we calculated the average number fractions of closely binding Mg²⁺/Na⁺ per phosphate for different N_p. As shown in Fig. 8, B and C and in Table S3, we found that the average number fraction of closely binding Mg²⁺ $\left({\overline{f}}_{Mg}\right)$ increases apparently with the increase of the local phosphate density N_p and becomes saturated at high N_p. Such an increment is more pronounced, and the saturated value of ${\overline{f}}_{Mg}$ is larger for higher [Mg²⁺]. In contrast, the increase of the fraction of closely binding Na⁺ with N_p is weak and appears visible at low (∼1 mM) [Mg²⁺]. This is because the higher charge of Mg²⁺ causes more sensitive binding of Mg²⁺ to the increased local charge density (N_p) of RNAs than that of Na⁺. The increase of [Mg²⁺] enhances the close binding of Mg²⁺ and weakens the close binding of Na⁺ because of the lowered binding entropy penalty and the anticooperative binding between Mg²⁺ and Na⁺. The saturation of ${\overline{f}}_{Mg}$ at large N_p may be attributed to the reduced Mg²⁺-accessible space around a phosphate with the increase of N_p for the phosphate. Our additional simulation with different initial ion positions for 58-nt rRNA fragment shows a similar ion concentration distributions and local binding of ions; see Fig. S16. Additionally, our simulation for 28-nt BWYV pseudoknot without constraint does not show a significant effect of RNA flexibility on bulk ion concentrations and local binding of ions; see Fig. S17. It is interesting that the average number fractions of closely binding Mg²⁺ as functions of N_p converge for different RNA tertiary structures. This is understandable. The local close binding of Mg²⁺/Na⁺ near a site may be mainly dependent on the local charge density around the site rather than the whole RNA structure because ion binding/screening would diminish the electrostatic potential from other phosphates of RNAs beyond the vicinity of the binding site.

Figure 8.

(A) The normalized distribution probability of the local phosphate density N_p for various RNA tertiary structures; N_p for a phosphate denotes the number of phosphates within a distance of 9 Å around the phosphate. (B and C) These show the average number of closely binding Mg²⁺ (B) and Na⁺ (C) around phosphates within a distance of 5 Å for RNA tertiary structures in 1 mM Mg²⁺/20 mM Na⁺ and 10 mM Mg²⁺/20 mM Na⁺ solutions, respectively. The cutoff distances for N_p and for closely binding Mg²⁺/Na⁺ were selected according to the radial distributions of phosphates and Mg²⁺ around phosphates (see Fig. S13). The change of cutoff distance from 5 to 6 Å for phosphate-Mg²⁺ does not significantly change the curves of average fractions of closely binding Mg²⁺ and N_p (see Fig. S15). To see this figure in color, go online.

Conclusions

In this study, we performed all-atom MD simulations for various nucleic acids including dsDNA, dsRNA, and several RNA tertiary structures. A simple and efficient method for partitioning divalent/monovalent ions to simulate a nucleic acid system with desired divalent/monovalent bulk ion concentrations was proposed and validated for extensive nucleic acids in mixed Mg²⁺/Na⁺ solutions. The global binding and local binding of Mg²⁺ and Na⁺ were analyzed for various nucleic acids including several RNA tertiary structures, and our calculations are in accordance with the available experimental data. Through extensive calculations and analyses, we have obtained the following major conclusions:

• 1)We have proposed a simple and efficient method for partitioning divalent/monovalent ions to simulate a nucleic acid in mixed divalent/monovalent ion solutions, and only one MD simulation is required for a nucleic acid with arbitrary structure in a mixed Mg²⁺/Na⁺ solution to obtain desired bulk divalent/monovalent ion concentrations. The method has been tested and validated for extensive nucleic acids and a wide range of mixed divalent/monovalent ion conditions.
• 2)The global binding of Mg²⁺ (Na⁺) to dsRNA is slightly stronger (weaker) than that to dsDNA, and Mg²⁺ binding is much more pronounced than Na⁺ binding for both dsRNA and dsDNA. Furthermore, Mg²⁺ binding to dsRNA is more likely to occur in the deep groove than that to dsDNA. Such difference is attributed to the different helical structures: A-form dsRNA is shorter and has deeper/narrower major grooves and wider/shallower minor grooves in comparison with B-form dsDNA.
• 3)The global binding of Mg²⁺/Na⁺ to RNA tertiary structures depends on the structure compactness and chain length in addition to Mg²⁺/Na⁺ concentrations. Through comprehensive analyses, we found the apparent correlation between global binding of Mg²⁺/Na⁺ and the effective surface charge density for various nucleic acid molecules.
• 4)Local binding of Mg²⁺/Na⁺ near the RNA surface is dependent on the local structures around binding sites, and favorable binding sites are generally in the major grooves of stems and junctions. The local binding of Mg²⁺/Na⁺ near a phosphate is found to be visibly correlated to the local phosphate density for various RNA tertiary structures.

Although our proposed partition formula works very well for extensive nucleic acids over the wide range of mixed divalent/monovalent ion conditions, and our predictions agree well with the available experimental data, there are still some simplifications and limitations in our work. First, we employed the Åqvist force field for Mg²⁺ (95) rather than other Mg²⁺ models (81, 98, 99), such as the NBFIX hydrated Mg²⁺ model (81). However, this treatment should not significantly affect our major analyses and conclusions because previous simulations have shown that Mg²⁺ ions generally become hydrated before accumulating near nucleic acids, and the majority of Mg²⁺ ions would generally keep their hydrated shell (72, 86). The minority of possible chelated Mg²⁺ ions would be somewhat related to the adopted force fields for Mg²⁺ (86). Second, our MD simulations did not cover the salt concentrations below 1 mM [Mg²⁺], since too-low salt concentrations would make the simulation cell too large and bring a huge computation cost. Finally, in our MD simulations, all the nucleic acids are restrained with a strong harmonic potential, and we consequently ignored the effect of flexibility of nucleic acids on ion binding. The interplay of flexibility and ion binding for RNA tertiary structures is an important issue and deserves to be discussed elsewhere. Nevertheless, this work proposed a simple and useful method for simulating a nucleic acid solution with desired mixed divalent/monovalent ion concentrations, and our analyses and results will be helpful for understanding the binding of divalent/monovalent ion to extensive DNAs and RNAs.

Author Contributions

Z.-J.T., K.X., and F.-H.W. designed the research. K.X., F.-H.W., and Z.-L.Z. performed the calculations. Z.-J.T., K.X., F.-H.W., G.X., and Z.-L.Z. analyzed the data. K.X., F.-H.W., and Z.J.T. wrote the manuscript. All authors discussed the results and reviewed the manuscript.

Editor: Nathan Baker.