Ultrasound adds the third dimension to wearable sensors.
Abstract
Ultrasonic imaging has been implemented as a powerful tool for noninvasive subsurface inspections of both structural and biological media. Current ultrasound probes are rigid and bulky and cannot readily image through nonplanar three-dimensional (3D) surfaces. However, imaging through these complicated surfaces is vital because stress concentrations at geometrical discontinuities render these surfaces highly prone to defects. This study reports a stretchable ultrasound probe that can conform to and detect nonplanar complex surfaces. The probe consists of a 10 × 10 array of piezoelectric transducers that exploit an “island-bridge” layout with multilayer electrodes, encapsulated by thin and compliant silicone elastomers. The stretchable probe shows excellent electromechanical coupling, minimal cross-talk, and more than 50% stretchability. Its performance is demonstrated by reconstructing defects in 3D space with high spatial resolution through flat, concave, and convex surfaces. The results hold great implications for applications of ultrasound that require imaging through complex surfaces.
INTRODUCTION
Ultrasound imaging technologies have been widely used to visualize internal discontinuities in objects for nondestructive evaluation, structural health monitoring, and medical diagnosis because of their noninvasiveness, high accuracy, great sensitivity, and strong penetration capabilities (1–3). Ultrasound probes with flat bases have been created to successfully accommodate different components of planar surfaces. However, these rigid probes cannot achieve a solid interfacial contact and therefore good coupling with irregular nonplanar surfaces, which are ubiquitous in real objects. Air gaps at these interfaces lead to large acoustic energy reflections and wave distortions, thereby creating unreliable testing results (fig. S1) (4). Ultrasonic couplants, such as water and gel, are typically used to remove the air gaps. However, an abundant use of the couplants will lead to a high-pass filter effect of the ultrasonic signals, causing significant canceling of small response echoes (5). Furthermore, extensive use of the couplants will bring about an ~80% incident energy transmission loss at the interface between the couplant and the subject because of the significant mismatch of their acoustic impedances (6). In addition, these rigid and bulky probes cannot be applied to hard-to-reach locations such as small cavities and slits. Thus, components at these locations normally have to be disassembled for a reliable diagnosis. At the same time, the stress concentrations present at the geometrical discontinuities of load-bearing objects make these regions particularly prone to defects (7). Although many methods have been reported to solve this interfacial coupling problem (8, 9), a number of disadvantages of the existing approaches remain, such as limited specimen size (10), demanding probe offset (11), and bulky probe housing (12), all of which compromise the feasibility of in situ detection, detection accuracy and sensitivity, and operation convenience of ultrasonic measurements.
Recent efforts have focused on developing flexible ultrasonic probes that can be divided into three main categories: using organic piezoelectric films as transducers, embedding piezoelectric ceramic into polymer substrates, and fabricating capacitive micromachined ultrasonic transducers (CMUTs). The organic piezoelectric films have good flexibility. However, the polymer piezoelectrets, typically polyvinylidene fluoride and its copolymer films (13), are not suitable to serve as transmitters because of their low electromechanical coupling coefficients (a parameter that characterizes the coupling between electrical energy and mechanical energy), low dielectric constants, and high dielectric losses (14). Moreover, their low Curie points make them difficult to process, and high-temperature applications result in phase transformations, which completely degrade the piezoelectric properties (15). The piezoelectric ceramics produce superior electromechanical performance and ease of processing. However, they cannot conform to curved surfaces without external forces because of the large elastic moduli of substrates (4, 15–17). The external force, usually applied manually, is often inconsistent. As a result, noise or even artifacts in the acquired pulse-echo signals can arise because of variations of the coupling conditions at the transducer-specimen interface. Moreover, for some applications related to long-term structural condition monitoring, such as fatigue crack growth at hidden or hard-to-access places of aircrafts and steamboats, the mechanical robot cannot support the testing (18). The CMUTs are fabricated on disjoined silicon wafers, and polydimethylsiloxane (PDMS) refilling the trenches among the elements makes the transducers flexible (17). This passive polymer filler compromises their conformability on curved surfaces. Besides, the silicon substrates are likely to be secondary resonators that generate longitudinal waves with unwanted frequencies and eventually result in artifacts in the images (19). Also, CMUTs generally have a lower electromechanical efficiency than piezoelectric ceramics due to inhomogeneity and parasitic capacitances among the arrayed elements (20, 21). In all cases, these flexible probes can only conform to developable surfaces (such as cylindrical surfaces), not to nondevelopable surfaces (such as spherical surfaces). In addition, the flexible conductive interconnections are subject to breaking or debonding when repeatedly used (22) because being flexible is insufficient to accommodate the sophisticated and time-dynamic motion of the electrodes and the device during the measurements. These drawbacks represent a bottleneck for the development of advanced probes that combine excellent ultrasonic performance with desirable mechanical properties that allow for application to general complex surfaces.
Here, we report a low-profile membrane-based stretchable ultrasonic probe. The probe exploits an array of thin and high-performance 1-3 piezoelectric composites as transducers, multilayered serpentine metal traces as electrical interconnects, and low-modulus elastomer membranes as encapsulation materials. The resulting device has a high electromechanical coupling coefficient (keff ~ 0.60), a high signal-to-noise ratio (SNR; ~20.28 dB), a wide bandwidth (~47.11%), a negligible cross-talk level between adjacent elements (~−70 dB), and a high spatial resolution (~610 μm) at different depths. The “island-bridge” layout offers biaxial stretchability of more than 50% with minimal impact on the transducer performance, which allows the device to work on nonplanar complex surfaces. With these unique properties, the device can obtain three-dimensional (3D) images of complex defects under flat, concave, and convex surfaces.
RESULTS
Design and characterization of the stretchable ultrasonic arrays
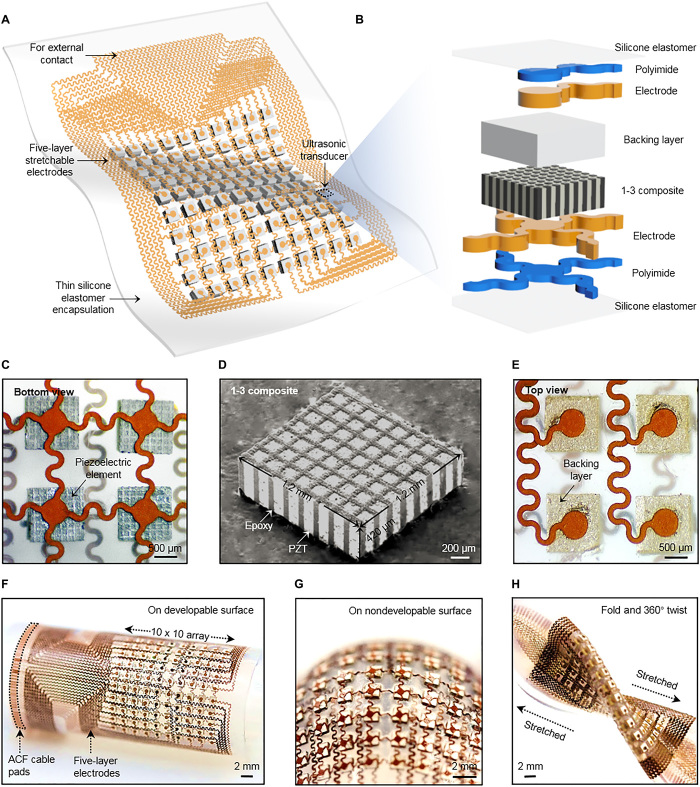
The schematic device structure is shown in Fig. 1A. The piezoelectric transducers are arranged in a 10 × 10 array, connected by an island-bridge structured matrix (the schematic fabrication processes are shown in fig. S2). Each island hosts a rigid element. The wavy bridges can unfold to accommodate the externally applied strain, with limited strain in the components themselves. Therefore, the matrix is rigid locally but soft globally. Each element in the array is individually addressable. The soft probe can consequently reconstruct the target morphology in multisection images. Figure 1B shows the exploded view of one element. Both the substrate and superstrate are silicone elastomer thin films, whose low modulus (~70 kPa) and large stretchability (~900%) offer an extremely compliant platform to accommodate a diverse class of building blocks, such as piezoelectric elements, metal interconnects, backing layers, and solder paste. The thickness of the elastomer substrate and superstrate is 15 μm to provide both high acoustic performance (23) and mechanical robustness of the device (figs. S3 and S4). The islands and bridges are patterned bilayers of Cu (20 μm)/polyimide (PI; 2 μm). The PI layer greatly enhances the bonding strength between the Cu and the elastomer.
Fig. 1. Schematics and design of the stretchable ultrasonic transducer array.
(A) Schematics showing the device structure. (B) Exploded view to illustrate each component in an element. (C) The optical image (bottom view) of four elements, showing the morphology of the piezoelectric material and bottom electrodes. (D) The tilted scanning electron microscopy image of a 1-3 piezoelectric composite. (E) The optical image (top view) of four elements, showing the morphology of the backing layer and top electrodes. (F to H) Optical images of this stretchable device when (F) bent around a developable surface, (G) wrapped on a nondevelopable surface, and (H) in a mixed mode of folding, stretching, and twisting, showing its mechanical robustness.
Piezoelectric 1-3 composites are chosen as the active material of the transducers (Fig. 1, C and D). Compared with an isotropic lead zirconate titanate (PZT), the anisotropic 1-3 composites have superior electromechanical coupling coefficients (thickness mode) that convert the majority of electrical energy to vibrational energy. In addition, the surrounding epoxy filler effectively suppresses transverse vibrations of PZT pillars (fig. S5) (24), leading to enhanced longitudinal waves that go into the targeted objects. Molded blocks of a Ag-epoxy composite serve as the backing layer (Fig. 1E). The backing layer effectively dampens the ringing effects (excessive vibrations) of the piezoelectrics, which shortens the spatial pulse length and broadens the bandwidth (fig. S6) (25) and thus improves the image axial resolution. Ag epoxy and solder paste are used to build robust and electrically conductive 1-3 composite/backing layer and 1-3 composite/metal electrode interfaces, respectively. Because of the close acoustic impedances of the 1-3 composite [~20 megarayleigh (MR)] and the targets to be tested (Al, ~18 MR), the matching layer is not necessary in this study (26, 27).
On one hand, the pitch between adjacent transducer elements should be small to reduce side lobe and grating lobe artifacts in the acquired images (28). On the other hand, sufficient space between the elements should be allocated to the serpentine interconnects for sufficient stretchability. A pitch of 2.0 mm (1.2 mm × 1.2 mm element footprint with a spacing of 0.8 mm) can achieve more than 30% reversible stretchability. The high spatial resolution (~610 μm), negligible cross-talk level between adjacent elements (~−70 dB), and artifact-free images validate this pitch design. Within these limited footprints, the island-bridge electrode layout design is critical, considering the large number of electrical connections needed for wiring the 10 × 10 array. An active multiplexing matrix under the ultrasound transducers could be a potential solution (29). However, the structural support materials introduced by the multiplexing matrix will negatively affect device stretchability. Multilayered electrodes have been demonstrated (30, 31), but the electrode design, passive dielectrics, and the substrate only makes the devices flexible, not stretchable. To individually address the 100 transducer elements, a minimum of 101 electrodes with a common ground electrode is needed. It is very challenging to place this large number of electrodes within limited footprints using conventional single-layer designs.
Thus, we invented a multilayered electrode design based on the “transfer printing” method, which greatly enhanced the level of device integration compared to single-layer designs. This design consists of five layers of “horseshoe”-configured serpentine electrodes. One electrode lies at the bottom of the transducers as the common ground layer (fig. S7). The other 100 electrodes are well aligned and distributed into four layers on top of the transducers as stimulating electrodes (fig. S8). Thin films of silicone elastomer (35 μm thick) provide insulation and adhesion between adjacent layers. The central area of each layer is selectively protected using customized masks during fabrication to allow the islands (bonding pads) to be exposed to the array elements (fig. S9). Laser ablation is used to quickly pattern serpentine structures (figs. S10 and S11). This method has been mostly focused on rigid or flexible substrates, but has been seldom focused on silicone substrates for stretchable electronics. The challenges for using on stretchable substrates are (i) controlling the laser power to fully ablate the pattern while avoiding the pattern delamination from the temporary PDMS substrate and (ii) tuning the surface tackiness of the temporary PDMS substrate to allow the subsequent transfer printing of the patterned electrodes. We solved these challenges and developed a fabrication protocol for stretchable electronics using laser ablation (see Materials and Methods for details). Compared with microfabrication methods by lithography and etching (32, 33), which require sophisticated fabrication processes, chemicals, shadow masks, and a clean room environment, laser ablation is time-efficient, low-cost, and offers high throughput. The as-fabricated final device is seen in Fig. 1 (F to H), which highlights its excellent mechanical properties when conforming to developable (cylindrical) and nondevelopable (spherical) surfaces, and under mixed modes of folding, stretching, and twisting. The device can easily achieve conformal contact with various nonplanar surfaces of real components, such as pipeline elbows, wheel edges, and rail tracks (fig. S12). An anisotropic conductive film (ACF) bonded to the Cu interconnects offers conductive access to external power supplies and data acquisition systems (fig. S13). Details of materials and fabrication processes are provided in Materials and Methods.
Electromechanical characterizations
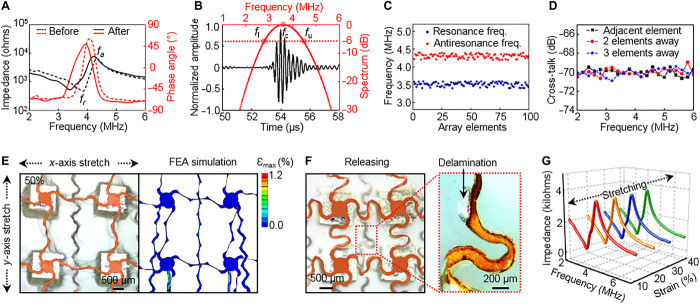
Ultrasound emission and sensing rely on the reversible conversion of mechanical and electrical energy. The electromechanical coupling capability is thus a key metric to evaluate the ultrasound transducer performance. As illustrated in Fig. 2A, the electrical impedance and phase angle spectra of the 1-3 composite before and after fabrication are measured, from which we can obtain the electromechanical coupling coefficient k (kt and keff) and the degree of poling, respectively (34). The black curves show two sets of well-defined peaks, corresponding to the resonance frequency fr and the antiresonance frequency fa. Accordingly, the kt and keff of the 1-3 composite before and after the fabrication are calculated to be ~0.55 and ~0.60, respectively (see Materials and Methods for details). The phase angle of the 1-3 composite at the central frequency slightly dropped from ~60° before fabrication to ~50° after fabrication because of the heat-induced slight depolarization of the 1-3 composite. The final phase angle of ~50°, which significantly exceeds many previous reports in flexible or rigid ultrasound probes, due to the intrinsic properties of the 1-3 composite material and optimized fabrication processes (16, 35), demonstrates that most of the dipoles in the 1-3 composite align during poling, thereby indicating the outstanding electromechanical coupling properties of our device.
Fig. 2. Characterizations of piezoelectric and mechanical properties.
(A) The impedance and phase angle spectra of the 1-3 composite before and after processing, showing good electromechanical coupling of the fabricated transducer (keff, ~0.60; θ, ~50°). (B) Pulse-echo response and frequency spectra, with a short spatial pulse length (~1.94 μs), a high SNR (~20.24 dB), and a wide bandwidth (~47.11%). (C) The resonance and antiresonance frequency variations of the 100 transducer elements. The mean values/SDs are 3.51 MHz/56.8 kHz (resonant) and 4.30 MHz/59.1 kHz (antiresonant), respectively. The 100% yield demonstrates fabrication robustness. (D) Average cross-talk levels between elements that are adjacent, two elements away, and three elements away, showing the outstanding anti-interference capacity of the device. (E) The optical image (left) and corresponding finite element analysis (FEA) simulation (right) of a 2 × 2 array under 50% biaxial tensile strain, showing its excellent stretchability. The local strain level (maximum principal strain) in the interconnects is indicated by the color scale. (F) The optical image after releasing the biaxial strain of 50%. The zoomed-in image highlights plastic deformation and local delamination of the interconnects upon loading/unloading. (G) Electrical impedances of the transducer under different strain levels, showing the mechanical stability of the device.
The Krimholtz-Leedom-Matthaei (KLM) model (36, 37) in MATLAB allows for the prediction of the impulse response of the transducer (see section S1), as a theoretical validation for our device design. The simulated results demonstrate the superb performance of the device in terms of spatial pulse length, bandwidth, and SNR (fig. S14). Figure 2B shows the experimental results of pulse-echo response and its frequency spectrum. The pulse-echo response, with a narrow spatial pulse length (~1.94 μs), a wide bandwidth (~47.11%; see Materials and Methods for details), and a high SNR (~20.24 dB), matches well with the simulation result (fig. S14) and is on par with that of commercial flexible ultrasonic transducers (38). The outstanding transducer performance results from (i) the excellent electromechanical coupling of the transducer and (ii) the optimized backing layer that reduces ringing effects.
The impedance measurements enable extraction of the resonant and antiresonant frequencies of each element in the 10 × 10 array (Fig. 2C). All 100 elements are functional. The mean values are 3.51 MHz (resonant) and 4.30 MHz (antiresonant), with SDs of 56.8 and 59.1 kHz, respectively. The stable capacitance (~37.28 pF) and low dielectric loss (tan δ < 0.02) of the array (figs. S15) further suggest a remarkable uniformity across the array and a reliable fabrication method (fig. S16). Another important metric that assesses the performance of the array is the cross-talk, which indicates the degree of interference between the elements. Figure 2D shows the cross-talk between elements with different spacings. All cross-talk levels are around −70 dB, with slight fluctuations, which is significantly lower than the standard −30 dB in the field (39). The outstanding anti-interference properties arise from the 1-3 composites’ effective suppression of spurious shear and from the silicone elastomer providing effective isolation among the elements. Overall, this combination of properties ensures low levels of noise in the ultrasonic imaging system (25).
Mechanical characterizations
Mechanical properties of conductive interconnects are critical for flexible and stretchable devices (40–42). Experimental results from biaxial stretching of the layered structures of serpentines between 0 and 50% and corresponding 3D finite element analysis (FEA) are shown in Fig. 2E and fig. S17. A 2 × 2 array of elements is selected for visualization of the key mechanics involved (see Materials and Methods for details). Under tensile loading, the horseshoe serpentines undergo an in-plane unraveling process and out-of-plane rotation and twisting, both of which mitigate the level of strain in the islands themselves (43, 44). Specifically, in these ultrasound arrays, 50% biaxial stretching produces a maximum of only ~1.2% tensile strain in the Cu interconnects, as shown in the FEA image of Fig. 2E. After the serpentines have fully unraveled (that is, finished rotating in-plane), the tensile strain in the Cu interconnects increases rapidly, thus defining the stretching limit of the serpentines (43, 45), which is between ~50 and 60% in this case. Going beyond this limit will lead to fracture of the serpentines. In addition, for the reliability of these devices, they must be capable of sustaining mechanical integrity upon repetitive loading. In metals such as Cu, cycling into the plastic regime will cause permanent deformation of the interconnects, which may affect device performance or may eventually produce fatigue cracks (46). According to both the simulations and the experiments, ~30 to 40% biaxial stretching produces irreversible deformation in the serpentines upon releasing (fig. S17) and partial delamination between the serpentines and the silicone elastomer, as highlighted in Fig. 2F. However, below 30 to 40% biaxial stretching, mechanical integrity is maintained. Moreover, mechanical deformations have minimal influence on device performance, which is reflected by the stable impedances of each element (Fig. 2G and figs. S18 and S19) and the resistance of the serpentines (fig. S20) at various levels of tensile strains and bending curvatures.
Spatial resolution characterization
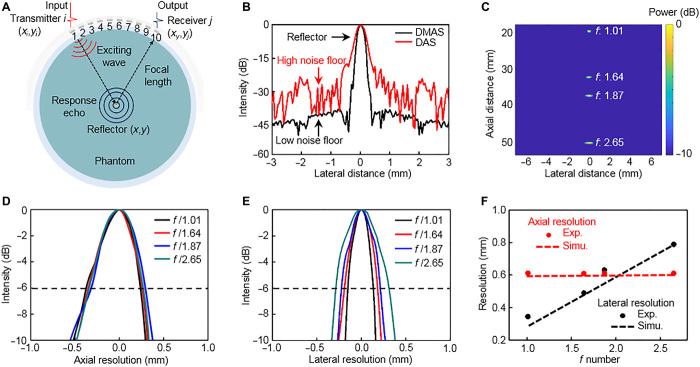
One of the important performance metrics of ultrasound imaging systems is the spatial resolution, in both axial and lateral directions. For the stretchable ultrasound probe, the axial resolution remains constant under different bending curvatures at a defined resonant frequency and bandwidth of the transducer. The lateral resolution is mainly dependent on device geometry, which affects the focal length and aperture size. The f number is used to define the ratio between the focal length and the aperture size (47). To comprehensively explore the lateral resolution of the probe with various f numbers, we performed a series of imaging experiments in which the ultrasonic probe is bent to different curvatures. As shown in Fig. 3A, the spatial resolution was evaluated by focusing the array at focal lengths of 20, 32, 37, and 52 mm, respectively, to image a Cu wire (300 μm in diameter) located at a particular focal point in a phantom sample. The image was reconstructed using the DMAS (delay multiply and sum) algorithm (48), which more effectively suppressed the level of noise floor (~−40 dB, causing the energy ratio of noise to reflector to be only 0.01%) compared with a conventional algorithm such as DAS (delay and sum; Fig. 3B) (49). In light of this metric, the side lobes and grating lobes in images can be greatly reduced by using the DMAS, and the results from these four tests are combined in Fig. 3C. A configuration of −10 dB dynamic range in combination with an image resolution of 20 pixels/mm is applied to highlight the imaging capabilities. The imaging principle of the DMAS algorithm and its detailed comparison with DAS are elaborated on in Materials and Methods and section S2.
Fig. 3. Characterization of spatial resolution.
(A) Schematics of spatial resolution measurement setup, with focal lengths of 20, 32, 37, and 52 mm, respectively. (B) Comparison of noise floors reconstructed by DMAS and DAS algorithms, revealing the benefits of the DMAS algorithm with only 0.01% energy ratio of noise to the reflector. (C) Images of wire phantom combining the four tests with different f numbers, showing the capability of focusing at different depths and obtaining high-resolution images. (D) Axial and (E) lateral line spread functions for the center wire at different focal lengths. Resolution is defined as the linespread function width at an intensity of −6 dB. (F) Experimental (Exp.) and simulation (Simu.) results of lateral and axial resolutions.
Plots of the axial and lateral line spread functions of the obtained images (Fig. 3B) are shown in Fig. 3 (D and E). The measured FWHM (full width at half maximum) resolutions (−6 dB) (47, 50) were calculated for the axial and lateral directions, as indicated by the dashed lines. As the f number decreases, the axial resolution remains relatively constant at around 610 μm, and the lateral resolution improves approximately linearly from 789 to 344 μm. These results are in line with the theoretical results (an axial resolution of around 601 μm; lateral resolutions ranging from 787 to 284 μm) from the MATLAB k-Wave toolbox simulations (Fig. 3F). The fine spatial resolution at the focal point, which is comparable to the 3.5-MHz commercial ultrasound probe resolution of 610 μm (51), is due to the combined effects of the high-performance transducers, a strategic device structural design, and an advanced imaging algorithm.
Multiview imaging on complex surfaces
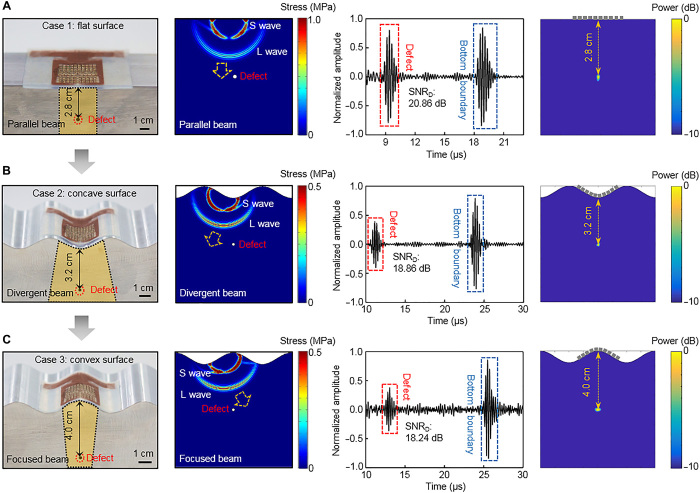
We used the stretchable ultrasonic device to image customized Al work pieces with embedded defects under planar, concave, and convex surfaces. The detailed experimental setup and method are discussed in the Materials and Methods and in figs. S21 and S22. In all cases, a straight defect (2 mm in diameter, orthogonal to the side surface) was created with different distances from the top surface (Fig. 4, A to C, first column). The device was laminated seamlessly on the test surfaces. The synthetic aperture focus (SAF) method was applied to reconstruct the corresponding images (section S2) (50). This method allows a sparse transmitter-receiver scheme that bypasses the need for simultaneous excitations, minimizing the number of simultaneously active elements while preserving the image quality. As indicated by the wave field simulation results, the main lobes of the transducer are parallel, divergent, and focused for the planar, concave, and convex surfaces, respectively (Fig. 4, A to C, second column, and movies S1 to S3). Considering that the central defect acts as a secondary wave source and the transducer is primarily sensitive to out-of-plane motion (direction normal to transducer’s sensing surface), the target surface curvature can greatly influence the captured signal strength. Specifically, for the convex surface, most of the reflected longitudinal wave motion from the defect aligns with the direction perpendicular to the sensing surface; for the concave surface, the reflected wave motion aligns with the in-plane motion (direction parallel to the sensing surface); for the planar surface, which is an intermediate case, the sensitivity of the transducer mainly depends on the component of the reflected wave vector normal to the sensing surface. To acquire the defect signals, for each case, we obtained 90 sets of data. Longitudinal wave reflection signals from the defects and the bottom boundaries, with more than 18 dB SNR, can be collected with predicted times of arrival (Fig. 4, A to C, third column). The obtained full-field images of the defects are shown in the fourth column of Fig. 4 (A to C), which have no artifacts and match the simulation results extremely well (fig. S23). These results suggest that the stretchable ultrasound probe is capable of accurately imaging defects in media of complex surface geometries.
Fig. 4. Two-dimensional images of a linear defect under complex surfaces.
Optical images of experimental setups with the stretchable ultrasonic device tested on (A) planar, (B) concave, and (C) convex surfaces showing the good conformability of the device on these surfaces (first column); simulation results showing the different wave fields and sensing modes (second column); pulse-echo signals from the defects and boundaries with high SNR (third column); and acquired 2D images using DMAS algorithms with accurate and artifact-free positions (fourth column). S wave, shear wave; L wave, longitudinal wave; SNRD, SNR of pulse-echo response from the defect.
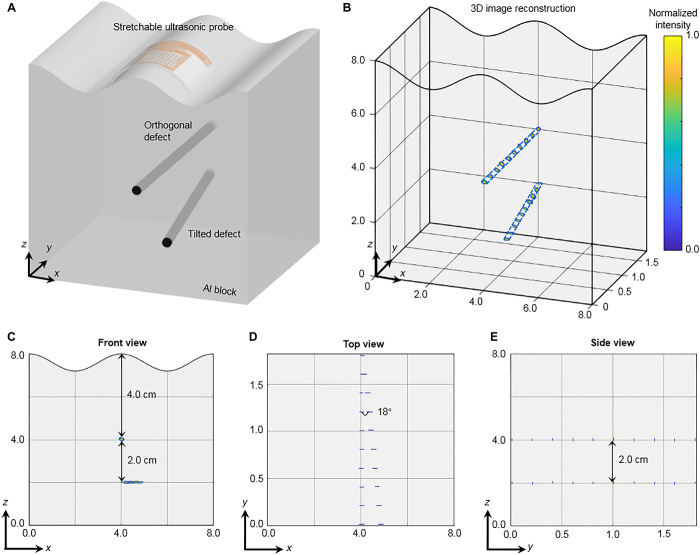
For practical engineering inspections, detection of multiple defects is of particular interest, for example, welding inspection of a pipeline (52) and rail track detection under shelling (53). The stretchable ultrasonic device was used for 3D internal structure visualization by imaging two defects with different depths and orientations under a sinusoidal curved surface. A schematic of the experimental setup is shown in Fig. 5A, with one defect orthogonal to the x-z plane at a depth of 4.0 cm below the top surface, and the other defect 18° tilted away from the y axis at a depth of 6.0 cm below the top surface. Each 1 × 10 linear array in the x-z plane generates a 2D cross-sectional image of the two defects using the DMAS algorithm (fig. S24), similar to Fig. 4. The upper defect reflects part of the wave and reduces the wave energy reaching the lower defect. Thus, it produces a shadowing effect (54), which is exacerbated by the tilted configuration of the lower defect as the array scans from the y = 0 to the y = 1.8 plane. The 3D image can be reconstructed by integrating the 10 slices with a 2-mm pitch along the y axis, as shown in Fig. 5B. The shadowing effect is removed by normalizing against the peak intensity of each defect. The corresponding front, top, and side views are shown in Fig. 5 (C to E), which accurately match the design in Fig. 5A, thereby demonstrating the capability of volumetric imaging using the stretchable ultrasonic probe. Similar protocols of testing and imaging reconstruction can be applied to general and more sophisticated surfaces.
Fig. 5. Three-dimensional image reconstruction of intricate defects under a convex surface.
(A) Schematics of the experimental setup, illustrating the spatial location and relative orientation of the two defects in the test subject. (B) The reconstructed 3D image, showing complete geometries of the two defects. (C to E) The 3D image from different view angles, showing the relative positions and orientations of the two defects to the top surface, which match the design well.
DISCUSSION
The hybridized material integration, electrode design strategies, and imaging algorithm development introduced here provide a foundational basis for stretchable ultrasound imaging arrays that allow nondestructive 3D volumetric inspections under general complex surfaces. The high-performance anisotropic 1-3 piezoelectric composites suppress shear vibrations, reduce cross-talk among the transducer, enhance longitudinal vibrations, and thus improve the overall sensitivity and SNR. Five-layered serpentine electrodes enable a high level of integration and large stretchability of more than 50%. The stretchable ultrasound probe, consisting of a 10 × 10 array of individually addressable transducer elements, can focus at different depths, with comparable spatial resolutions with existing rigid probes. The unique device design, combined with the advanced DMAS imaging algorithms, enables accurate, artifact-free, full-field, and nondestructive examinations underneath general complex surfaces. Future studies will focus on improving the device performance by reducing the pitch between elements and exploring the integration of more active elements, incorporating matching layers, automated sensor positioning systems, and wireless signal actuation and transmission chips, for distributed, mobile, and real-time subsurface health monitoring of infrastructures and the human body.
MATERIALS AND METHODS
Fabrication of the five-layer electrodes
The process began with a coating of PI (2 μm thick) on Cu sheets (20 μm thick). PI [poly(pyromellitic dianhydride-co-4,40-oxydianiline) amic acid solution, PI2545 precursor, HD MicroSystems] was first spin-coated on the Cu sheets (Oak-Mitsui Inc.) at 4000 rpm for 60 s (MicroNano Tools). Then, PI/Cu was baked on a hotplate at 110°C for 3 min and 150°C for 1 min sequentially and then fully cured in a nitrogen oven at 300°C for 1 hour. A glass slide coated with a layer of PDMS (20:1, Sylgard 184 silicone elastomer) served as a substrate for laminating the PI/Cu sheet. The PI and PDMS were activated for bonding by ultraviolet (UV) light (PSD series Digital UV Ozone System, Novascan) for 1.5 min. Five separate pieces of Cu sheets were then patterned in island-bridge–structured geometries (designed by AutoCAD software) by pulsed laser ablation (Laser Mark’s). The laser parameters (central wavelength, 1059 to 1065 nm; power, 0.228 mJ; frequency, 35 kHz; speed, 300 mm/s; and pulse width, 500 ns) were optimized to process Cu with the highest yield. Thin silicone superstrates/substrates of devices (15 μm each; Ecoflex-0030, Smooth-On) were prepared by mixing two precursor components together in a 1:1 ratio, spin-coating at 4000 rpm for 60 s, and curing at room temperature for 2 hours. Here, PDMS was used as a temporary substrate where the PI/Cu sheet was laminated for laser ablation. Compared with the PDMS, Ecoflex has a lower Young’s modulus [Young’s moduli of Ecoflex-0030 (1:1) and PDMS (20:1) are ~60 kPa (55) and ~1 MPa (56), respectively]. Thus, we chose Ecoflex as the substrate, superstrate, and filler in our device to ensure the low modulus of the device that allowed intimately conforming to the highly curved surfaces.
For the first layer, water-soluble tape (3M) was used to transfer-print the patterned Cu electrode to the Ecoflex superstrate after 3 min of UV activation (57). A separate piece of water-soluble tape was used to selectively mask the connect pads at the center and top of the electrode that would be exposed to bond the transducer array and ACF cables (Elform). Next, a 35-μm-thick Ecoflex film was spin-coated at 3000 rpm for 60 s and cured at 80°C for 20 min, forming an insulating layer while the Ecoflex on top of the water-soluble tape mask was removed by dissolving the water-soluble tape. Subsequent layers of electrodes were laminated, with alignment to the previous layer of electrodes, in a similar manner. The integrated four-layer top electrodes are shown in fig. S8. The bottom electrode was fabricated and transfer-printed to a separate Ecoflex substrate (fig. S7). Finally, ACF cables were hot-pressed onto the electrodes to serve as the connection access for data communication and power supply (fig. S13).
Assembling of transducer arrays and their integration with electrodes
As shown in fig. S2, the process began with the fabrication of the backing layer and the 1-3 composite (Smart Material Corp.). The conductive backing layer was prepared by mixing a Ag-epoxy composite with a hardener (E-Solder 3022, Von Roll) in a 12.5:1 ratio and then curing the mixture at 60°C for 8 hours. The backing layer thickness was fixed at 580 μm by mounting the backing layer precursor between two glass slides. The backing layer was then diced into pieces of 1.2 mm × 1.2 mm by a dicing saw (DAD3220, DISCO). The 1-3 composites were fabricated from PZT ceramics and epoxy using the dice-and-fill technique. The size of each PZT pillar was 100 μm × 100 μm with a spacing of 55 μm (Fig. 1D). Each one of the 1-3 composite elements was diced to 1.2 mm × 1.2 mm and bonded with the backing layer via Ag-epoxy (EPO-TEK H20E, Epoxy Technology) at 150°C for 5 min. The single-layer bottom electrode was bonded with the 10 × 10 arrayed 1-3 composite, using a customized scaffold, by solder pastes [Sn42Bi57.6Ag0.4 (melting point, 138°C), Chip Quik Inc.] cured in the oven at 150°C for 6 min. The same approach was used to bond the four-layer top electrode with the backing layer. The gap between the sandwiched device was then filled by Ecoflex and cured at room temperature for 2 hours. Afterward, the glass slides were removed, yielding a free-standing stretchable ultrasound transducer array.
Electromechanical and mechanical testing of the device
A high-voltage power supply (Model 355, Bertan), with a direct voltage output of 52.38 kV/cm, provided a platform to polarize the device for 15 min. The polarization hysteresis loop (fig. S25) was measured to determine the minimal voltage needed to fully polarize the 1-3 composite in the silicone medium without electrical breakdown. A network analyzer (Agilent Technologies) with a scanning range of 2 to 6 MHz under the Smith mode gave the impedance and phase angles of the transducer. Electromechanical efficiency is a parameter that characterizes the degree of energy coupling efficiency between the electrical and mechanical forms. The electromechanical coupling coefficient k is the factor that quantitatively evaluates electromechanical efficiency. The electromechanical coupling coefficients of the 1-3 composite and the transducer (the transducer contains the 1-3 composite and the backing layer, and is processed by heating and poling), kt and keff, were derived from Eqs. 1 and 2, respectively (58)
| (1) |
| (2) |
where the resonant frequency fr and the antiresonant frequency fa were extracted from the impedance and phase angle spectra. An experimental system, including a pulser-receiver (model Panametric 5077PR, Olympus), an oscilloscope (LeCroy WaveJet 314), and a 300-μm-diameter copper wire in the phantom, was used to obtain the pulse-echo signal and frequency spectra. The frequency bandwidth (BW) of the signal at −6 dB was determined by Eq. 3
| (3) |
where fu is the upper frequency, fl is the lower frequency, and fc is the central frequency (47). A function generator (AFG3521, Tektronix) and an oscilloscope (LC534, LeCroy Corp.) were used to assess the cross-talk. The sinusoid burst mode with a peak-to-peak voltage of 5 V was used to excite the elements in the array. The frequency was scanned between 2 and 6 MHz with a step size of 0.2 MHz. The cross-talk level was then defined by counting the ratio of the peak voltages to the reference voltage (the voltage under a 1-megohm coupling on the oscilloscope). The capacitance and dielectric loss of array elements were measured by an inductance-capacitance-resistance (LCR) digital bridge machine (QuadTech).
Mechanical testing of a 2 × 2 transducer array was performed with a customized biaxial stretcher. To accurately evaluate the biaxial stretchability, the strain was quantified based on the distance between the two electrodes. Images of the device under different strain levels were collected with a charge-coupled device (OMAX) on an optical microscope (AmScope). The electric impedance of the transducer under stretching and bending states and the relative resistance change of the Cu serpentines at various tensile strain levels were tested by a network analyzer and a source meter (Keysight Technologies), respectively.
FEA simulations
The commercial software package ABAQUS allowed the simulation of the mechanical response of the transducer arrays. The composite layer (Ecoflex, Cu, and PI) consisted of hybrid hexahedral elements (C3D8H). The simulations used values of the elastic moduli of Ecoflex, PI, and Cu of 0.06, 2300, and 41,500 MPa, respectively. To obtain the yield strength value of the Cu, four pieces of Cu slides with a high aspect ratio (width, 4.18 mm; thickness, 0.02 mm; length, 18.78 mm) were measured by tensile testing. The testing rate was 1% tensile strain per minute, and the load cell was 1 kN (Instron 5965). The stress-strain curves were obtained where the yield strength value of Cu slides (187 MPa) was extracted and used in the simulations.
Noninvasive inspection of the internal defects
To test specimens with planar, concave, and convex surfaces, the coordinate location of each transducer element in the array was determined by aligning the device with a known marker position on the surface. For more complex surfaces, a 3D scanner can be used to locate the exact coordinates of each element. For the specimens whose surfaces were sinusoidal, the amplitude was 4 mm peak to peak, and the wavelength was 40 mm. A data acquisition system, composed of a pulser-receiver, an oscilloscope, a switch controller (NI USB-6008), and high-voltage chips (HV2601), was developed using LabVIEW (National Instruments), as shown in figs. S21 and S22. We used LabVIEW to program the switch controller so that it could turn on and turn off the high-voltage chip. This system allowed the device to automatically transmit and receive ultrasound signals. An electrical impedance matching system between the transducer and the pulser-receiver (50 ohms) was used to minimize power reflection when exciting the transducer. The enhanced power transmission efficiency improved the SNR (fig. S26). A step-pulse excitation (−100 V) was applied on the selected element, and the responses from the other elements were collected. By iterating this procedure over a 1 × 10 linear array, 90 sets of waveform data could be acquired. The received raw signals were first filtered with a band-pass filter based on the continuous wavelet transform to remove the unwanted frequency components and minimize the filter-induced phase shift (fig. S27). Each filtered waveform was decomposed into its in-phase and phase-quadrature components through the Hilbert transform, and an improved SAF algorithm was then applied to each of the Hilbert transformed components separately. Finally, the pixel intensity of the final images was reconstructed by computing the moduli of the two components from the Hilbert transform and converting it to the decibel dynamic range. The image resolution of 20 pixels/mm, which fulfills the half-wavelength spatial sampling of longitudinal waves in the phantom at 3.5 MHz (Nyquist-Shannon sampling theorem), was applied here to completely preserve the information in the signals.
Here, the SAF technique based on DMAS was implemented for image reconstruction (48). To reconstruct an image I(x, y) at each pixel P(x, y) with DMAS, considering a linear array of 1 × M elements, M − 1 ultrasound signals were recorded each time when one element was activated as the transmitter and the remaining M − 1 elements were the receivers. Thus, a total of M ∙ (M − 1) signals were obtained. The amplitudes of the received signals (A) were appropriately backpropagated for each combination of transmitter and receiver. Once all the signals were in phase with regard to pixel P(x, y), they were combinatorially coupled and multiplied. If the number of received signals was N, then the number of multiplications to be performed was given by all the possible signal pair combinations . The backpropagated DMAS algorithm can be written as (48)
| (4) |
where Ai and Aj are the signals received by the ith and jth transmitter-receiver pairs, respectively, and τi,xy and τj,xy are the backpropagation time corresponding to the travel time of the wave from the ith and jth transmitter-receiver pairs, respectively, through the focus point P(x, y). DMAS suppressed the level of noise floor to −40 dB. Thus, the energy ratio of noise to the reflector was 0.01%, which can be calculated by
| (5) |
where P1 and P0 are noise and reflector energies, respectively.
Supplementary Material
Acknowledgments
We thank S. Cai’s group at the University of California San Diego (UCSD) for the Young’s modulus testing, Y. Dai for analyzing the strain distribution of the device in stretching states, and S. Xiang for constructive feedback on the manuscript preparation. Funding: The project described was partially supported by the NIH (grant R21EB025521) and Clinical and Translational Science Awards funding (grant UL1TR001442). Additional partial support was provided by the UCSD Center for Healthy Aging, the U.S. Federal Railroad Administration through grant FR-RRD-0027-11, and the U.S. NSF through grant CMMI-1362144. The content is solely the responsibility of the authors and does not necessarily represent the official views of the NIH or NSF. Author contributions: H.H., X.Z., Chonghe Wang, L.Z., X.L., F.L.d.S., and S.X. designed and executed the experiments, reconstructed images, wrote the paper, and were responsible for Figs. 2 (A, B, F, and G), 3, 4, and 5. S.L. and M.P. carried out FEA simulations and were responsible for Fig. 2E. R.C., Z.C., and Q.Z. characterized the electromechanical coupling performances and were responsible for Fig. 2 (C and D). Z.H., Chunfeng Wang, and Y. Gu edited the manuscript, characterized mechanical properties, and were responsible for Fig. 1 (F to H). Y.C., Y. Lei, and T.Z. were responsible for Fig. 1 (C to E). Chonghe Wang and N.K. were responsible for Fig. 1 (A and B). Y. Guo, W.Z., Y. Li, and A.N. made contributions in device design and fabrication. Y.T. and S.S. made contributions in algorithm development. Competing interests: S.X., L.Z., Chonghe Wang, H.H., and X.L. are inventors on a Patent Cooperation Treaty (PCT) patent application related to this work filed by the Regents of the University of California (PCT/IS18/13116, filed 10 January 2018). The other authors declare that they have no competing interests. Data and materials availability: All data needed to evaluate the conclusions in the article are present in the article and/or the Supplementary Materials. Additional data related to this paper may be requested from the authors upon request.
SUPPLEMENTARY MATERIALS
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/3/eaar3979/DC1
section S1. Piezoelectric transducer design using the KLM model
section S2. SAF imaging and DMAS algorithm
fig. S1. Testing performance of a commercial rigid probe on curved surfaces.
fig. S2. Schematic illustration of the device fabrication process.
fig. S3. Ecoflex thickness as a function of spin coating speed on a glass slide.
fig. S4. Acoustic damping effects of silicone substrates.
fig. S5. The vibration mode comparison between PZT and 1-3 composites.
fig. S6. Pulse-echo response and bandwidth differences of transducers with and without the backing layer (KLM simulation).
fig. S7. Bottom electrode design.
fig. S8. Top electrode design.
fig. S9. Four-layer top electrode fabrication processes.
fig. S10. Optical images of Cu serpentine interconnections under different laser parameters.
fig. S11. Laser ablation resolution experiments.
fig. S12. Photographs of the device seamlessly laminated on different curved surfaces.
fig. S13. ACF cable bonding.
fig. S14. Simulation results from the KLM model.
fig. S15. Dielectric properties of the device.
fig. S16. The phase angle change during the fabrication process and after repetitive testing.
fig. S17. Experimental and simulation of a small array under biaxial tensile strain.
fig. S18. Electric impedances under different bending curvatures.
fig. S19. The real and imaginary parts of electrical impedance under different levels of bending and stretching.
fig. S20. Relative resistance changes of Cu serpentine under stretching.
fig. S21. Instruments for nondestructive evaluation.
fig. S22. Switch circuit of the entire testing system.
fig. S23. Reconstructed images based on simulation under flat, concave, and convex surfaces.
fig. S24. The pulse-echo signal and 2D image of the two defects.
fig. S25. Polarization conditions.
fig. S26. The matching circuit of the ultrasound testing system.
fig. S27. Ultrasound signal filtering.
fig. S28. Simplified schematics of a transducer element.
fig. S29. The electrical model of a transducer.
fig. S30. General diagram showing the transmission line model of a two-port system.
fig. S31. Schematics showing the basic concept of SAF.
fig. S32. Block diagrams for the imaging algorithms.
table S1. Parameters for the 1-3 composite, backing layer, and Ecoflex.
movie S1. Simulation of wave field under a planar surface.
movie S2. Simulation of wave field under a concave surface.
movie S3. Simulation of wave field under a convex surface.
Reference (59)
REFERENCES AND NOTES
- 1.Guemes A., Salowitz N., Chang F.-K., Alfredo G., Salowitz N., Chang F.-K., Trends on research in structural health monitoring. Struct. Health Monit. 13, 579–580 (2014). [Google Scholar]
- 2.Lowe M. J. S., Alleyne D. N., Cawley P., Defect detection in pipes using guided waves. Ultrasonics 36, 147–154 (1998). [Google Scholar]
- 3.Drinkwater B. W., Wilcox P. D., Ultrasonic arrays for non-destructive evaluation: A review. NDT&E Int. 39, 525–541 (2006). [Google Scholar]
- 4.Casula O., Poidevin C., Cattiaux G., Dumas P., Control of complex components with Smart Flexible Phased Arrays. Ultrasonics 44, e647–e651 (2006). [DOI] [PubMed] [Google Scholar]
- 5.Giovagnorio F., Andreoli C., De Cicco M. L., Color Doppler sonography of focal lesions of the skin and subcutaneous tissue. J. Ultrasound Med. 18, 89–93 (1999). [DOI] [PubMed] [Google Scholar]
- 6.L. W. Schmerr Jr., in Fundamentals of Ultrasonic Nondestructive Evaluation, L. W. Schmerr Jr., Ed. (Springer, 2016), pp. 1–13. [Google Scholar]
- 7.W. D. Pilkey, D. F. Pilkey, in Peterson’s Stress Concentration Factors, W. D. Pilkey, D. F. Pilkey, Eds. (John Wiley & Sons, 2008), pp. 1–26. [Google Scholar]
- 8.Xiao H., Sun Y., Chen D., Xu J., Prediction of flat-bottom hole signals received by a spherically focused transducer for an ultrasonic pulse echo immersion testing. Meas. Sci. Technol. 27, 115001 (2016). [Google Scholar]
- 9.R. Long, P. Cawley, in AIP Conference Proceedings (AIP, 2008), pp. 754–761.
- 10.Jasiūnienė E., Raišutis R., Šliteris R., Voleišis A., Jakas M., Ultrasonic NDT of wind turbine blades using contact pulse-echo immersion testing with moving water container. Ultragarsas 63, 28–32 (2008). [Google Scholar]
- 11.Lane C. J. L., The inspection of curved components using flexible ultrasonic arrays and shape sensing fibres. Case Stud. Nondestruct. Test. Eval. 1, 13–18 (2014). [Google Scholar]
- 12.Chatillon S., Cattiaux G., Serre M., Roy O., Ultrasonic non-destructive testing of pieces of complex geometry with a flexible phased array transducer. Ultrasonics 38, 131–134 (2000). [DOI] [PubMed] [Google Scholar]
- 13.Powell D. J., Hayward G., Flexible ultrasonic transducer arrays for nondestructive evaluation applications. II. Performance assessment of different array configurations. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 43, 393–402 (1996). [Google Scholar]
- 14.Qi Y., Jafferis N. T., Lyons K. Jr, Lee C. M., Ahmad H., McAlpine M. C., Piezoelectric ribbons printed onto rubber for flexible energy conversion. Nano Lett. 10, 524–528 (2010). [DOI] [PubMed] [Google Scholar]
- 15.Harvey G., Gachagan A., Mackersie J. W., Mccunnie T., Banks R., Flexible ultrasonic transducers incorporating piezoelectric fibres. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 56, 1999–2009 (2009). [DOI] [PubMed] [Google Scholar]
- 16.Wang Z., Xue Q.-T., Chen Y.-Q., Shu Y., Tian H., Yang Y., Xie D., Luo J.-W., Ren T.-L., A flexible ultrasound transducer array with micro-machined bulk PZT. Sensors 15, 2538–2547 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.X. Zhuang, D.-S. Lin, O. Oralkan, B. T. Khuri-Yakub, Flexible transducer arrays with through-wafer electrical interconnects based on trench refilling with PDMS, in IEEE 20th International Conference on Micro Electro Mechanical Systems (MEMS), Kobe, Japan, 21 to 25 January 2007. [Google Scholar]
- 18.C. Mineo, C. MacLeod, M. Morozov, S. G. Pierce, R. Summan, T. Rodden, D. Kahani, J. Powell, P. McCubbin, C. McCubbin, G. Munro, S. Paton, D. Watson, Flexible integration of robotics, ultrasonics and metrology for the inspection of aerospace components, in AIP Conference Proceedings (AIP Publishing, 2017), pp. 020026.
- 19.E. T. Ong, K. M. Lim, H. P. Lee, in Mems/Nems:(1) Handbook Techniques and Applications Design Methods, (2) Fabrication Techniques, (3) Manufacturing Methods, (4) Sensors and Actuators, (5) Medical Applications and MOEMS, C. T. Leondes, Ed. (Springer Science & Business Media, 2007), pp. 278–288.
- 20.R. S. Singh, M. O. Culjat, M. Lee, D. B. Bennett, S. Natarjan, B. P. Cox, E. R. Brown, W. S. Grundfest, H. Lee, in Acoustical Imaging, M. P. André, Ed. (Springer Science & Business Media, 2007), pp. 211–214.
- 21.Certon D., Teston F., Patat F., A finite difference model for cMUT devices. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 52, 2199–2210 (2005). [DOI] [PubMed] [Google Scholar]
- 22.Bowen C. R., Bradley L. R., Almond D. P., Wilcox P. D., Flexible piezoelectric transducer for ultrasonic inspection of non-planar components. Ultrasonics 48, 367–375 (2008). [DOI] [PubMed] [Google Scholar]
- 23.Ceh D. A., Peters T. M., Chen E. C. S., Acoustic characterization of polyvinyl chloride and self-healing silicone as phantom materials. Proc. SPIE Int. Soc. Opt. Pho. 9412, 94123G (2015). [Google Scholar]
- 24.Gu X., Yang Y., Chen J., Wang Y., Temperature-dependent properties of a 1–3 connectivity piezoelectric ceramic–polymer composite. Energy Harvest. Syst. 2, 107–112 (2015). [Google Scholar]
- 25.K. K. Shung, in Diagnostic Ultrasound: Imaging and Blood Flow Measurements, K. K. Shung, Ed. (CRC Press, 2015), pp. 13–209. [Google Scholar]
- 26.Hatfield J. V., Scales N. R., Armitage A. D., Hicks P. J., Chen Q. X., Payne P. A., An integrated multi-element array transducer for ultrasound imaging. Sens. Actuators A Phys. 41, 167–173 (1994). [Google Scholar]
- 27.P. A. Payne, J. V. Hatfield, A. D. Armitage, Q. X. Chen, P. J. Hicks, N. Scales, Integrated ultrasound transducers, in Proceedings of IEEE Ultrasonics Symposium (IEEE’94), Cannes, France, 31 October to 3 November 1994.
- 28.Liu C., Djuth F., Li X., Chen R., Zhou Q., Shung K. K., Micromachined high frequency PMN-PT/epoxy 1-3 composite ultrasonic annular array. Ultrasonics 52, 497–502 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Kato Y., Sekitani T., Noguchi Y., Yokota T., Takamiya M., Sakurai T., Someya T., Large-area flexible ultrasonic imaging system with an organic transistor active matrix. IEEE Trans. Electron Dev. 57, 995–1002 (2010). [Google Scholar]
- 30.Guo L., DeWeerth S. P., High-density stretchable electronics: Toward an integrated multilayer composite. Adv. Mater. 22, 4030–4033 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Rodger D. C., Fong A. J., Li W., Ameri H., Ahuja A. K., Gutierrez C., Lavrov I., Zhong H., Menon P. R., Meng E., Burdick J. W., Roy R. R., Edgerton V. R., Weiland J. D., Humayun M. S., Tai Y.-C., Flexible parylene-based multielectrode array technology for high-density neural stimulation and recording. Sens. Actuators B 132, 449–460 (2008). [Google Scholar]
- 32.Xu S., Zhang Y., Jia L., Mathewson K. E., Jang K.-I., Kim J., Fu H., Huang X., Chava P., Wang R., Bhole S., Wang L., Na Y. J., Guan Y., Flavin M., Han Z., Huang Y., Rogers J. A., Soft microfluidic assemblies of sensors, circuits, and radios for the skin. Science 344, 70–74 (2014). [DOI] [PubMed] [Google Scholar]
- 33.Kabiri Ameri S., Ho R., Jang H., Tao L., Wang Y., Wang L., Schnyer D. M., Akinwande D., Lu N., Graphene electronic tattoo sensors. ACS Nano 11, 7634–7641 (2017). [DOI] [PubMed] [Google Scholar]
- 34.Zhou Q., Xu X., Gottlieb E. J., Sun L., Cannata J. M., Ameri H., Humayun M. S., Han P., Shung K. K., PMN-PT single crystal, high-frequency ultrasonic needle transducers for pulsed-wave Doppler application. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 54, 668–675 (2007). [DOI] [PubMed] [Google Scholar]
- 35.Y.-F. Wang, T.-L. Ren, Y. Yang, H. Chen, C.-J. Zhou, L.-G. Wang, L.-T. Liu, High-density pMUT array for 3-D ultrasonic imaging based on reverse-bonding structure, in IEEE 24th International Conference on Micro Electro Mechanical Systems (MEMS), Cancun, Mexico, 23 to 27 January 2011.
- 36.S. Cochran, C. E. M. Demore, C. R. P. Courtney, Modelling ultrasonic-transducer performance: One-dimensional models, in Ultrasonic Transducers: Materials and Design for Sensors, Actuators and Medical Applications, K. Nakamura, Ed. (Woodhead Publishing, 2012), pp. 187–219.
- 37.Krimholtz R., Leedom D. A., Matthaei G. L., New equivalent circuits for elementary piezoelectric transducers. Electron. Lett. 6, 398–399 (1970). [Google Scholar]
- 38.Kobayashi M., Jen C.-K., Lévesque D., Flexible ultrasonic transducers. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 53, 1478–1486 (2006). [DOI] [PubMed] [Google Scholar]
- 39.Cannata J. M., Williams J. A., Zhou Q., Ritter T. A., Shung K. K., Development of a 35-MHz piezo-composite ultrasound array for medical imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 53, 224–236 (2006). [DOI] [PubMed] [Google Scholar]
- 40.Secor E. B., Prabhumirashi P. L., Puntambekar K., Geier M. L., Hersam M. C., Inkjet printing of high conductivity, flexible graphene patterns. J. Phys. Chem. Lett. 4, 1347–1351 (2013). [DOI] [PubMed] [Google Scholar]
- 41.Rotenberg M. Y., Tian B., Bioelectronic devices: Long-lived recordings. Nat. Biomed. Eng. 1, 0048 (2017). [Google Scholar]
- 42.Kaltenbrunner M., Sekitani T., Reeder J., Yokota T., Kuribara K., Tokuhara T., Drack M., Schwödiauer R., Graz I., Bauer-Gogonea S., Bauer S., Someya T., An ultra-lightweight design for imperceptible plastic electronics. Nature 499, 458–463 (2013). [DOI] [PubMed] [Google Scholar]
- 43.Xu S., Zhang Y., Cho J., Lee J., Huang X., Jia L., Fan J. A., Su Y., Su J., Zhang H., Cheng H., Lu B., Yu C., Chuang C., Kim T.-i., Song T., Shigeta K., Kang S., Dagdeviren C., Petrov I., Braun P. V., Huang Y., Paik U., Rogers J. A., Stretchable batteries with self-similar serpentine interconnects and integrated wireless recharging systems. Nat. Commun. 4, 1543 (2013). [DOI] [PubMed] [Google Scholar]
- 44.Huang X., Liu Y., Kong G. W., Seo J. H., Ma Y., Jang K.-I., Fan J. A., Mao S., Chen Q., Li D., Liu H., Wang C., Patnaik D., Tian L., Salvatore G. A., Feng X., Ma Z., Huang Y., Rogers J. A., Epidermal radio frequency electronics for wireless power transfer. Microsyst. Nanoeng. 2, 16052 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Hussain A. M., Ghaffar F. A., Park S. I., Rogers J. A., Shamim A., Hussain M. M., Metal/polymer based stretchable antenna for constant frequency far-field communication in wearable electronics. Adv. Funct. Mater. 25, 6565–6575 (2015). [Google Scholar]
- 46.Pan T., Pharr M., Ma Y., Ning R., Yan Z., Xu R., Feng X., Huang Y., Rogers J. A., Experimental and theoretical studies of serpentine interconnects on ultrathin elastomers for stretchable electronics. Adv. Funct. Mater. 27, 1702589 (2017). [Google Scholar]
- 47.Chen Z., Zheng L., Cao W., Chen X., Chen R., Li R., Shung K., Zhou Q., High-frequency ultrasonic imaging with lead-free (Na,K)(Nb,Ta)O3 single crystal. Ultrason. Imaging 39, 348–356 (2017). [DOI] [PubMed] [Google Scholar]
- 48.Matrone G., Ramalli A., Savoia A. S., Tortoli P., Magenes G., High frame-rate, high resolution ultrasound imaging with multi-line transmission and filtered-delay multiply and sum beamforming. IEEE Trans. Med. Imaging 36, 478–486 (2017). [DOI] [PubMed] [Google Scholar]
- 49.Yiu B. Y. S., Tsang I. K. H., Yu A. C. H., GPU-based beamformer: Fast realization of plane wave compounding and synthetic aperture imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 58, 1698–1705 (2011). [DOI] [PubMed] [Google Scholar]
- 50.Frazier C. H., O’Brien W. D., Synthetic aperture techniques with a virtual source element. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 45, 196–207 (1998). [DOI] [PubMed] [Google Scholar]
- 51.Medina-Valdes L., Camacho J., González-Salido N., Cruza J. F., Resolution of image compounding with a ring array transducer. Phys. Procedia 63, 141–146 (2015). [Google Scholar]
- 52.A. J. Hunter, B. W. Drinkwater, P. Wilcox, J. Russell, Automatic image correction for flexible ultrasonic phased array inspection, in 8th International Conference on NDE in Relation to Structural Integrity for Nuclear and Pressurised Components, Berlin, Germany, 9 January 2010.
- 53.Mariani S., Nguyen T., Zhu X., Lanza di Scalea F., Field test performance of noncontact ultrasonic rail inspection system. J. Trans. Eng. A. Syst. 143, 04017007 (2017). [Google Scholar]
- 54.Cruza J. F., Camacho J., Fritsch C., Plane-wave phase-coherence imaging for NDE. NDT&E Int. 87, 31–37 (2017). [Google Scholar]
- 55.Z. Zhang, Y. Xuan, Influence of epithelium and fiber locations on glottal closure and sound production at soft-phonation conditions, in Proceedings of Meetings on Acoustics (ICA2013), Montreal, Canada, 2 to 7 June 2013.
- 56.Wang Z., Volinsky A. A., Gallant N. D., Crosslinking effect on polydimethylsiloxane elastic modulus measured by custom-built compression instrument. J. Appl. Polym. Sci. 131, 41050 (2014). [Google Scholar]
- 57.Lee C. H., Kim D. R., Zheng X., Fabricating nanowire devices on diverse substrates by simple transfer-printing methods. Proc. Natl. Acad. Sci. U.S.A. 107, 9950–9955 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.J. F. Tressler, Piezoelectric transducer designs for SONAR applications, in Piezoelectric and Acoustic Materials for Transducer Applications, A. Safari, E. K. Akdoğan, Eds. (Springer Science & Business Media, 2008), pp. 217–239.
- 59.van Kervel S. J. H., Thijssen J. M., A calculation scheme for the optimum design of ultrasonic transducers. Ultrasonics 21, 134–140 (1983). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/3/eaar3979/DC1
section S1. Piezoelectric transducer design using the KLM model
section S2. SAF imaging and DMAS algorithm
fig. S1. Testing performance of a commercial rigid probe on curved surfaces.
fig. S2. Schematic illustration of the device fabrication process.
fig. S3. Ecoflex thickness as a function of spin coating speed on a glass slide.
fig. S4. Acoustic damping effects of silicone substrates.
fig. S5. The vibration mode comparison between PZT and 1-3 composites.
fig. S6. Pulse-echo response and bandwidth differences of transducers with and without the backing layer (KLM simulation).
fig. S7. Bottom electrode design.
fig. S8. Top electrode design.
fig. S9. Four-layer top electrode fabrication processes.
fig. S10. Optical images of Cu serpentine interconnections under different laser parameters.
fig. S11. Laser ablation resolution experiments.
fig. S12. Photographs of the device seamlessly laminated on different curved surfaces.
fig. S13. ACF cable bonding.
fig. S14. Simulation results from the KLM model.
fig. S15. Dielectric properties of the device.
fig. S16. The phase angle change during the fabrication process and after repetitive testing.
fig. S17. Experimental and simulation of a small array under biaxial tensile strain.
fig. S18. Electric impedances under different bending curvatures.
fig. S19. The real and imaginary parts of electrical impedance under different levels of bending and stretching.
fig. S20. Relative resistance changes of Cu serpentine under stretching.
fig. S21. Instruments for nondestructive evaluation.
fig. S22. Switch circuit of the entire testing system.
fig. S23. Reconstructed images based on simulation under flat, concave, and convex surfaces.
fig. S24. The pulse-echo signal and 2D image of the two defects.
fig. S25. Polarization conditions.
fig. S26. The matching circuit of the ultrasound testing system.
fig. S27. Ultrasound signal filtering.
fig. S28. Simplified schematics of a transducer element.
fig. S29. The electrical model of a transducer.
fig. S30. General diagram showing the transmission line model of a two-port system.
fig. S31. Schematics showing the basic concept of SAF.
fig. S32. Block diagrams for the imaging algorithms.
table S1. Parameters for the 1-3 composite, backing layer, and Ecoflex.
movie S1. Simulation of wave field under a planar surface.
movie S2. Simulation of wave field under a concave surface.
movie S3. Simulation of wave field under a convex surface.
Reference (59)