Abstract
Signal transmission at the molecular level in many biological complexes occurs through allosteric transitions. Allostery describes the responses of a complex to binding of ligands at sites that are spatially well separated from the binding region. We describe the structural perturbation method, based on phonon propagation in solids, which can be used to determine the signal-transmitting allostery wiring diagram (AWD) in large but finite-sized biological complexes. Application to the bacterial chaperonin GroEL–GroES complex shows that the AWD determined from structures also drives the allosteric transitions dynamically. From both a structural and dynamical perspective these transitions are largely determined by formation and rupture of salt-bridges. The molecular description of allostery in GroEL provides insights into its function, which is quantitatively described by the iterative annealing mechanism. Remarkably, in this complex molecular machine, a deep connection is established between the structures, reaction cycle during which GroEL undergoes a sequence of allosteric transitions, and function, in a self-consistent manner.
This article is part of a discussion meeting issue ‘Allostery and molecular machines’.
Keywords: signalling networks, symmetry requirements, structural perturbation method, iterative annealing mechanism, bacterial chaperonin GroEL
1. Introduction
Allosteric transitions, referring to responses at distances several nanometres away from the binding site of ligands to multi-domain proteins, are pervasive in biology and are used as a signalling mechanism at the nanoscale level [1–3]. The classic example is the binding of oxygen to haemoglobin (Hb), which triggers quaternary conformational changes in the latter, as explained in the now classic theory [4,5] due to Monod, Wyman and Changeux (MWC). Since the publication of the MWC theory, there has been growing interest in elucidating the molecular and structural basis of allostery in a large number of signalling molecules, including Hb [6,7]. Achieving this goal has become possible thanks to advances in experimental methods (X-ray crystallography, small-angle X-ray scattering, nuclear magnetic resonance [8,9] and mass spectroscopy [10], and more recently cryo-electron microscopy (cryo-EM) [11]) as well as introduction of a variety of computational models. Several review articles have appeared recently [12–14] showcasing the spectacular impact of the concept of allostery in biology. Although there are arguments that signal transmission could occur without significant conformational changes in the complex [15], in most cases allosteric transitions are accompanied by large structural changes. This is indeed the case in the example we use to illustrate the general concepts of a network of residues involved in signal transmission and the accompanying dynamics of allosteric transitions between two distinct states.
Our focus here is to describe a few concepts associated with transmission of allosteric signals in the bacterial chaperonin GroEL from both a structural and dynamical perspective. Chaperonins, which should be viewed as molecular machines like kinesins or myosins, have evolved to rescue substrate proteins (SPs) that are otherwise destined for aggregation. The GroEL–GroES chaperonin system [16], which functions out of equilibrium by consuming ATP lavishly [17,18], is a promiscuous nanomachine whose spectacular allosteric transitions during its catalytic cycle allow a sufficient number of SPs to reach the folded state in a biologically relevant timescale. Thus, understanding the operation of the chaperonin system in molecular terms is of utmost importance in describing its function both in vitro and in vivo.
GroEL is a homo-oligomer with two heptamers that are stacked back to back. The subunits, which are identical, thus confer GroEL an unusual sevenfold symmetry in the resting (T or taut) state. Large-scale conformational changes between the allosteric states of GroEL,  and
and  transitions (see figure 1 for a schematic of the reaction cycle in a single ring), are triggered solely by ATP binding and hydrolysis. The ATP-binding sites are localized in the equatorial (E) domain in which much of the mass resides. The nature of the reversible
transitions (see figure 1 for a schematic of the reaction cycle in a single ring), are triggered solely by ATP binding and hydrolysis. The ATP-binding sites are localized in the equatorial (E) domain in which much of the mass resides. The nature of the reversible 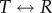 transition was first elucidated in pioneering studies by Yifrach & Horovitz [19,20], who also established an inverse relation, predicted using computations [21], between the extent of cooperativity in this transition and the folding rates of SPs [22]. The irreversible
transition was first elucidated in pioneering studies by Yifrach & Horovitz [19,20], who also established an inverse relation, predicted using computations [21], between the extent of cooperativity in this transition and the folding rates of SPs [22]. The irreversible 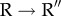 transition is driven by ATP hydrolysis. In both these transitions, strain due to ATP binding and hydrolysis at the catalytic site propagates through a network of inter-residue contacts [23], thus inducing large-scale conformational changes. That such changes must occur during the reaction cycle of GroEL is already evident by comparing the static crystal structures in different allosteric states, such as the T and R″ states [24]. However, the static structures do not provide any information about the network of residues that carry allosteric signals, the dynamics of transition between the key states in the GroEL reaction cycle, and most importantly a link to the function of GroEL.
transition is driven by ATP hydrolysis. In both these transitions, strain due to ATP binding and hydrolysis at the catalytic site propagates through a network of inter-residue contacts [23], thus inducing large-scale conformational changes. That such changes must occur during the reaction cycle of GroEL is already evident by comparing the static crystal structures in different allosteric states, such as the T and R″ states [24]. However, the static structures do not provide any information about the network of residues that carry allosteric signals, the dynamics of transition between the key states in the GroEL reaction cycle, and most importantly a link to the function of GroEL.
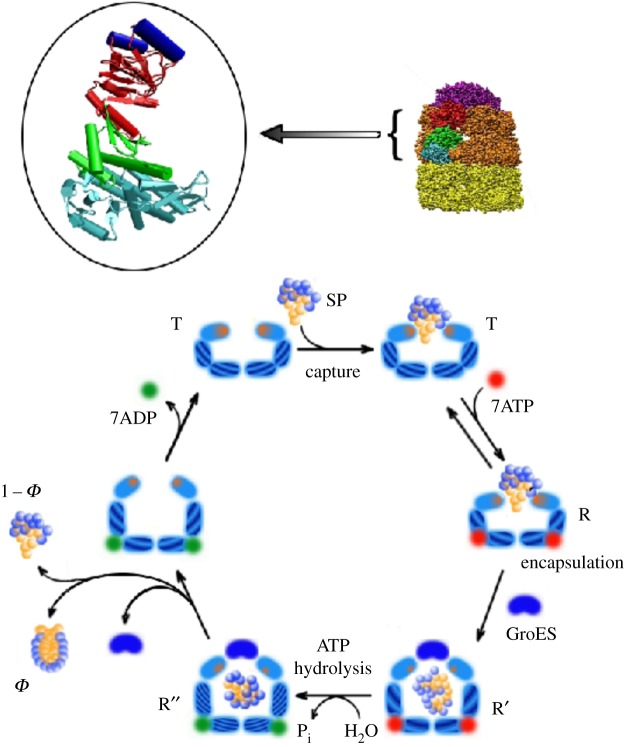
Figure 1.
In the top right corner is the representation of GroEL–GroES in the post-ATP hydrolysis R″ state [19]. The cartoon representation in the oval corresponds to a single subunit of GroEL. The aqua blue, green, and red and blue correspond to E, I and A domains, respectively. The dark blue cylinders, associated with the A domain, are the H and I helices which recognize the substrate proteins when presented in the misfolded form. The bottom panel is a representation of the coupling of the catalytic cycle and the fate of the SP in the cis ring. The various steps are: (i) recognition of the SP when GroEL is in the T state by the helices indicated in dark blue at the top left corner. This is followed by ATP binding, resulting in the  transition. (ii) GroES binding encapsulates the SP in the central cavity for a very short time, during which it can fold with probability Φ (the native state yield in one hemi-cycle). (iii) Following ATP hydrolysis, the
transition. (ii) GroES binding encapsulates the SP in the central cavity for a very short time, during which it can fold with probability Φ (the native state yield in one hemi-cycle). (iii) Following ATP hydrolysis, the 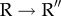 transition occurs. Subsequently, GroES detaches, and inorganic phosphate and ADP are released. In addition, the SP is ejected regardless of whether it has reached the folded state or not, and the cycle begins anew. It should not go unstated that the functional unit is the symmetric complex in which two SP molecules can be processed, one in each ring (see [20,21] for details).
transition occurs. Subsequently, GroES detaches, and inorganic phosphate and ADP are released. In addition, the SP is ejected regardless of whether it has reached the folded state or not, and the cycle begins anew. It should not go unstated that the functional unit is the symmetric complex in which two SP molecules can be processed, one in each ring (see [20,21] for details).
In this perspective, we describe a general computational method, the structural perturbation method (SPM) [25], to determine a network of residues, referred to as the allosteric wiring diagram (AWD), that is largely responsible for transmitting signals between different regions of the protein. The efficacy of the method is illustrated here using GroEL. Applications to other systems such as DNA polymerases and myosin motors can be found in [26,27]. We then show, using a technique for studying the dynamics of allosteric transition between two states [28], that the AWD residues are also involved in the transition between distinct states in GroEL. Finally, we show that the large-scale molecular rearrangements that occur during the reaction cycle are linked, through the iterative annealing mechanism (IAM), to the function of GroEL, which is to assist the folding of SPs. The established connection between the AWD and its role in the dynamics of allosteric transitions and function shows, in a profound way, how the GroEL architecture and non-equilibrium effects that occur during the catalytic cycle are linked to function.
2. Determination of the allostery wiring diagram
We begin by describing the theoretical basis for the SPM [25,26], which hinges on two ideas that are well-known in condensed matter physics dealing with propagation of excitations in ordered solids. In general, transmission of signals across nanoscale structures, such as the GroEL–GroES system, must satisfy two requirements. (i) At least a portion of the complex must be stiff. More precisely, the network of residues that transmits allosteric signals must be capable of bearing ligand-induced strain over almost the length of the complex. The need for this requirement can be explained using an analogy to the transmission of local disturbance in regular solids. In this case, vibrations of atoms in lattice sites are carried along the entire sample by phonons. The propagation of excitation is possible because of the stiffness or rigidity of the solid with long-range order, and cannot occur in liquids. (ii) The presence of stiff regions, linked by the network of residues (AWD) in a biological complex, implies that the regions associated with allosteric signalling have lower symmetry than the disordered regions, permitting them to transmit signals across the complex. Let us explain what is meant by lower symmetry. Consider a protein that is unfolded. This state might be viewed as a high-symmetry state, like a liquid. But in such a state allosteric signals cannot be transmitted because of the absence of persistent order. Folded states are aperiodic with lower symmetry than unfolded states, and hence could act as allosteric states in which binding of a ligand in some part could trigger responses elsewhere. In addition, many of the allosteric proteins contain several domains arranged in a symmetric manner and hence capable of propagating stress. In solids, translational symmetry is broken, for example, thus lowering the symmetry with respect to liquids with short-range order. As a consequence the ordered state is described by elastic constants. In the same vein, in finite-sized biological complexes, the AWD must accommodate excitations across the length scale of the structure, implying that at least a portion of the complex must be structured, which defines the ‘allosteric state’. This implies that the allosteric states must have lower symmetry compared with disordered states bearing higher symmetry, which comports well with the general description that the functional states of biological molecules are aperiodic [29].
In the second requirement above, we are referring to structural symmetry. The complex that carries allosteric signals must be structured, at least in parts. For GroEL, the entire complex has sevenfold symmetry (figure 1). In addition, the subunits also have symmetric arrangements of the individual secondary structural elements, resulting in an aperiodic structure. We should add that the symmetry need not be fully preserved during the allosteric transition. However, all the states involved in signal transmission must be (at least partially) rigid.
We use the analogy to phonon propagation in solids to describe the SPM method, first introduced by Zheng and co-workers [25,26] (see for related ideas in biophysics [32–35] and other areas [36,37]) for determining the network of residues that propagate signals upon ligand (ATP and/or SP) binding to specific regions in the complex of interest. In order to determine the AWD, we represent the structure of a given allosteric state (e.g. the T state in GroEL) as an elastic network of connected springs. Usually in the elastic network model (ENM), the structure is represented as a contact map using the α-carbon of each residue. A contact implies that the Euclidean distance between the α-carbon atoms of two residues is less than a specific distance. We use a generalization of the standard ENM [38,39] by representing each residue by two beads [23], one representing the α-carbon and the other the centre of mass of the side chain (SC), with glycine being an exception. The centre of mass is determined using the side-chain heavy atoms. For glycine, only the α-carbon atom is used.
Following the insightful studies by Bahar and co-workers, who pioneered the applications of ENM to a variety of systems [40–42], we impose a harmonic potential between all the interaction sites (α-carbon atoms and the SCs) that are within a cut-off radius Rc (≈10 Å) in the given allosteric structure. In the structure-based elastic network representation of the protein, the potential energy is
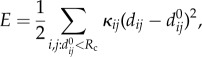 |
2.1 |
where dij is the distance between the interaction centres i and j, d0ij is the corresponding distance in the native structure and κij is the spring constant. The sum is over all the pairs of sites that are in contact in the native conformation. The sites i and j are assumed to be in contact if dij < Rc. The value of Rc is chosen to ensure that the B-factors calculated using equation (2.1) and the measured values are as close as possible [43,44]. The spring constants, κij, are chosen to reflect the strength of inter-residue interaction. In the GroEL application, we choose κij = εij/(σi/2 + σj/2)2 where εij is the Betancourt–Thirumalai statistical potential [45], which is defined based on contact frequencies as in Miyazawa & Zernigan [46], and σi is the van der Waals diameter of the ith residue.
(a). Normal mode spectrum
The first step in the SPM is to perform a normal mode analysis using the energy function in equation (2.1) in order to generate the spectrum of frequencies for the normal modes along with the corresponding eigenvectors. Applications of ENM to a large number of systems including GroEL [26,38,43,47] have shown that typically only a few of the lowest-frequency normal modes are required to characterize the allosteric transitions. In order to identify the modes that best describe the transition between two allosteric states α and β, we compute the overlap between the vector quantifying the change of states from α to β and the Mth normal mode (aM, calculated based on the state α), 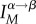 [25]. The function
[25]. The function 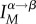 , which quantifies the extent of overlap between the two vectors, is given by
, which quantifies the extent of overlap between the two vectors, is given by
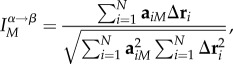 |
2.2 |
where N is the number of residues in the protein and Δri is the change in the position of the ith site between the states α and β. It follows from equation (2.2) that 0 ≤ IM ≤ 1. By evaluating equation (2.2) for a given M, we identify the best overlapping mode that maximizes 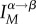 .
.
(b). Structural perturbation method in practice
The extent to which a residue at a given site in a structure responds to a perturbation far away can be used to assess allosteric coupling. The SPM allows us to quantify the strength of such a coupling to a mutation at a particular site. The greater the response (higher δωiM, defined below), the more significant a specific residue is to a given mode.
In practice, the SPM probes the response of a normal mode M to a mutation of a residue i. In the ENM, perturbation of the spring constant around a site mimics the effect of a mutation. The response to such a perturbation is calculated using
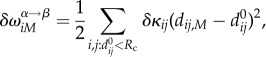 |
2.3 |
where δκij is the perturbed spring constant and dij,M − d0ij is the displacement in residues i and j in the Mth mode. Residues with high δωiM (large stored elastic energy) constitute the AWD or a network of residues that transmit allosteric signals. We have shown that the AWD residues are also strongly conserved [26], thus underscoring their functional importance.
(c). Asymmetry in the response between subdomains in the  transition
transition
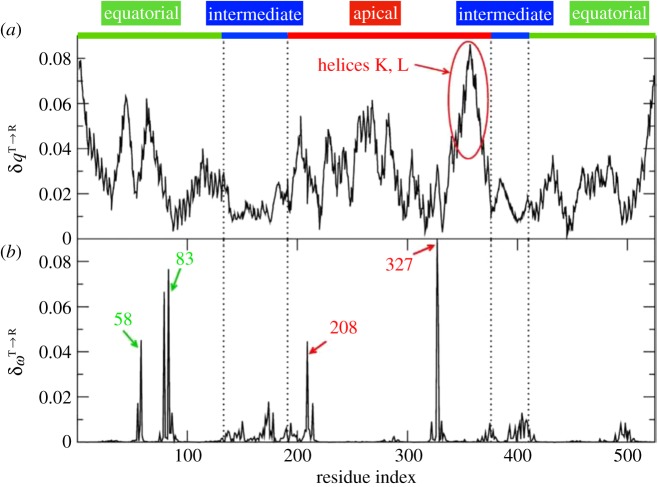
The seven subunits of the oligomer of GroEL are identical. However, it is thought that the allosteric responses of each subunit might be asymmetric in the sense that the amplitude of fluctuations in two E or I domains may be different. As a way of illustrating the application of the SPM and to illustrate the asymmetric response we performed normal mode analysis and estimated the effect of perturbation at a specific site on the whole structure using the procedure outlined above. To identify the most significant residues including those at the interface, we constructed two subunits of GroEL in the T state (figure 1). The  transition of a GroEL model, with two adjacent subunits, is best described by two modes with significant value of the overlap 0.35) (see fig. 4a in [23]). Here a few important points are worth making. (i) The amplitudes of vibration for the two modes, shown in figure 2a, indicate that there is a noticeable reduction in the fluctuations of the intermediate (I) domain residues. (ii) In addition, helices K and L (residues 339–371) show the largest amplitude among the apical (A) domain residues. The SPM result for the modes, displayed in figure 2, shows that residues D83 and K327 have the largest δω values. (iii) Note that this figure also shows the asymmetry in the high δω values between identical subunits. For example, the high values of both the amplitude of fluctuations and δω in one of the E domains (left side in figure 2) are absent in the other domains. (iv) The largest fluctuations in both modes (7 and 13) are localized in the A domain, which, as shown below, is also reflected in the dynamics of the allosteric transitions.
transition of a GroEL model, with two adjacent subunits, is best described by two modes with significant value of the overlap 0.35) (see fig. 4a in [23]). Here a few important points are worth making. (i) The amplitudes of vibration for the two modes, shown in figure 2a, indicate that there is a noticeable reduction in the fluctuations of the intermediate (I) domain residues. (ii) In addition, helices K and L (residues 339–371) show the largest amplitude among the apical (A) domain residues. The SPM result for the modes, displayed in figure 2, shows that residues D83 and K327 have the largest δω values. (iii) Note that this figure also shows the asymmetry in the high δω values between identical subunits. For example, the high values of both the amplitude of fluctuations and δω in one of the E domains (left side in figure 2) are absent in the other domains. (iv) The largest fluctuations in both modes (7 and 13) are localized in the A domain, which, as shown below, is also reflected in the dynamics of the allosteric transitions.
Figure 2.
SPM results for GroEL with two adjacent subunits. (a) The amplitudes of motion in the dominant normal modes. The region with the highest amplitude corresponds to helices K and L. (b) Residue-dependent δω for the dominant modes. The residues with the largest allosteric signal-transmitting values δω are identified. Adapted from Tehver et al. [23].
By mapping the hot spot residues (listed in [23]) onto their structures, we find that 33 of the 85 hot spot residues of chain H (per the chain labelling in the PDB structure 1AON) and 24 of the 62 hot spot residues of chain I belong to the inter-subunit interface. We define interface residues as residues that make at least one contact with a residue in the adjacent subunit. The interface hot spot residues, highlighted in blue and red in figure 3b, show that the large number of interface residues in the AWD is the possible foundation for the strong intra-ring positive cooperativity.
Figure 3.
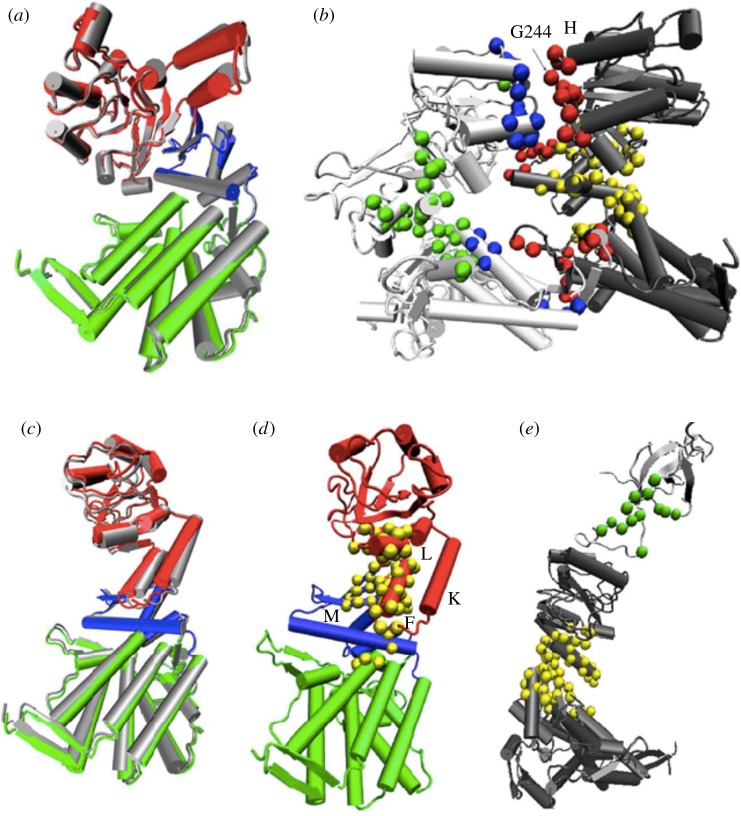
Illustrating the  transition and the associated allostery wiring diagram (AWD) determined using the SPM. (a) Single-subunit structure in the T state. The E, I and A domains are shown in green, blue and red, respectively. The motions of the structural elements due to the dominant mode are in grey. (b) Structure of two adjacent subunits of GroEL (the chains are shown in dark and light grey) in the T state. The residues in the AWD are highlighted in colour. The critical interface residues are in red and blue, and the other hot spot residues are in yellow and green. (c) Same as (a) except this describes the
transition and the associated allostery wiring diagram (AWD) determined using the SPM. (a) Single-subunit structure in the T state. The E, I and A domains are shown in green, blue and red, respectively. The motions of the structural elements due to the dominant mode are in grey. (b) Structure of two adjacent subunits of GroEL (the chains are shown in dark and light grey) in the T state. The residues in the AWD are highlighted in colour. The critical interface residues are in red and blue, and the other hot spot residues are in yellow and green. (c) Same as (a) except this describes the  transition. (d) The AWD for the transition
transition. (d) The AWD for the transition  are in yellow. Helices K, L, F and M are labelled. The domains are coloured as in (c). (e) GroEL (dark grey)–GroES (light grey) model. The AWD is shown in yellow (GroEL) and green (GroES). This figure provides insights into the residues that signal the dissociation of GroES, a key event in the function of the chaperonin.
are in yellow. Helices K, L, F and M are labelled. The domains are coloured as in (c). (e) GroEL (dark grey)–GroES (light grey) model. The AWD is shown in yellow (GroEL) and green (GroES). This figure provides insights into the residues that signal the dissociation of GroES, a key event in the function of the chaperonin.
3. Dynamics of allosteric transitions
The findings based on the SPM highlight the most probable AWD driving the transition between two allosteric states. To better understand the allosteric transitions of the GroEL particle at the microscopic level, we performed multiple sets of Brownian dynamics simulations using the self-organized polymer (SOP) model [48,49]. The SOP model uses a united atom representation lumping the heavy atoms in each amino acid into a single interaction centre. This novel coarse-grained model has been used to make several important contributions to the theoretical biological physics in the area of RNA [48–50] and protein dynamics [28,51–54]. Here, we describe the simulations [28] used to identify key events in the transition between T and R as well as R and R″ states.
(a). Overview of the dynamics of  and
and  transitions
transitions
In the  transition triggered by ATP binding, the A domains undergo counterclockwise motion mediated by a multiple salt-bridge switch mechanism at the interfaces of the seven subunits, where the salt-bridges are defined for the non-covalent contact made between oppositely charged residues, e.g. Arg (R), Lys (K) and Asp (D), Glu (E). The
transition triggered by ATP binding, the A domains undergo counterclockwise motion mediated by a multiple salt-bridge switch mechanism at the interfaces of the seven subunits, where the salt-bridges are defined for the non-covalent contact made between oppositely charged residues, e.g. Arg (R), Lys (K) and Asp (D), Glu (E). The  transition is accompanied by a series of breakage and formation of salt-bridges. The initial event in the
transition is accompanied by a series of breakage and formation of salt-bridges. The initial event in the 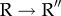 transition, during which GroEL rotates clockwise, involves a dramatic outside-in concerted movement of helices K and L. The outside-in movement of helices K and L, exerting a substantial strain on the GroEL structure, induces 90° clockwise rotation and 40° upward movement of the A domain. Such a large-scale rotation of helices K and L was an entirely new finding using SOP model simulations [28], which provided a basis for understanding the origin of the change in polarity of the GroEL cavity. In both the transitions, considerable heterogeneity is found in the transition pathways, as discussed below. In what follows, we provide further details of the allosteric dynamics of GroEL gleaned from simulations using the SOP model.
transition, during which GroEL rotates clockwise, involves a dramatic outside-in concerted movement of helices K and L. The outside-in movement of helices K and L, exerting a substantial strain on the GroEL structure, induces 90° clockwise rotation and 40° upward movement of the A domain. Such a large-scale rotation of helices K and L was an entirely new finding using SOP model simulations [28], which provided a basis for understanding the origin of the change in polarity of the GroEL cavity. In both the transitions, considerable heterogeneity is found in the transition pathways, as discussed below. In what follows, we provide further details of the allosteric dynamics of GroEL gleaned from simulations using the SOP model.
(b). Global  and
and 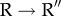 transitions follow two-state kinetics
transitions follow two-state kinetics
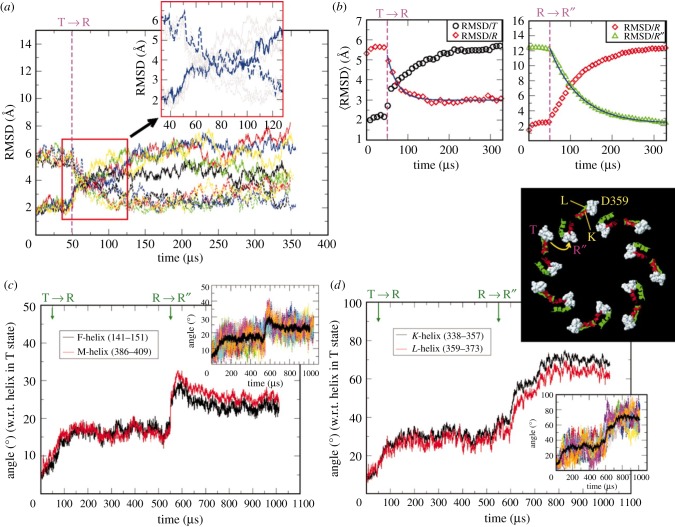
The overall conformational change that occurs during the allosteric transitions can be quantified using a global coordinate characterizing the structural overlap with respect to a reference conformation. Time-dependent changes in the root mean squared distance (RMSD) with respect to a reference state (T, R or R″), from which a specific allosteric transition commences (figure 4), differ from one trajectory to another, reflecting the heterogeneity of the underlying dynamics (figure 4a). Examination of the RMSD for a particular trajectory in the transition region (figure 4a, inset) shows that the GroEL particle recrosses the transition state (TS). Assuming that RMSD is a reasonable representation of the structural changes during the allosteric transitions, we find that GroEL spends a substantial fraction of time (measured with respect to the first passage time for reaching the R state starting from the T state) in the TS region during the  transition. After an initial increase (decrease) with respect to the T (R) state the RMSD changes non-monotonically in the transition region, which suggests that the transition state ensemble (TSE) connecting the two end states is broad (details follow). By averaging over 50 individual trajectories, we find that the ensemble average of the time-dependence of RMSD for both the
transition. After an initial increase (decrease) with respect to the T (R) state the RMSD changes non-monotonically in the transition region, which suggests that the transition state ensemble (TSE) connecting the two end states is broad (details follow). By averaging over 50 individual trajectories, we find that the ensemble average of the time-dependence of RMSD for both the  and
and 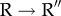 transitions follows single exponential kinetics, which clearly obscures the molecular heterogeneity observed in individual trajectories. Despite such complex dynamics at the individual molecule level, the ensemble average allosteric transition kinetics can be approximately described by a two-state model. Unlike the global dynamics characterizing the overall motion of GroEL, the local dynamics describing the formation and rupture of key interactions associated with GroEL allostery cannot be described by two-state kinetics, which clearly not only reflects the heterogeneity but also shows a certain hierarchy in the dynamics of allosteric signalling at the molecular level (see below).
transitions follows single exponential kinetics, which clearly obscures the molecular heterogeneity observed in individual trajectories. Despite such complex dynamics at the individual molecule level, the ensemble average allosteric transition kinetics can be approximately described by a two-state model. Unlike the global dynamics characterizing the overall motion of GroEL, the local dynamics describing the formation and rupture of key interactions associated with GroEL allostery cannot be described by two-state kinetics, which clearly not only reflects the heterogeneity but also shows a certain hierarchy in the dynamics of allosteric signalling at the molecular level (see below).
Figure 4.
Root mean squared distance (RMSD) as a function of time. (a) Time-dependence of the RMSD of a few individual molecules is shown for the  transition. Solid (dashed) lines are for RMSD/T (RMSD/R) (RMSD calculated with respect to the T (R) state). The enlarged inset gives an example of a trajectory, in blue, that exhibits multiple passages across the transition region. (b) Ensemble averages of the RMSD for the
transition. Solid (dashed) lines are for RMSD/T (RMSD/R) (RMSD calculated with respect to the T (R) state). The enlarged inset gives an example of a trajectory, in blue, that exhibits multiple passages across the transition region. (b) Ensemble averages of the RMSD for the  (left) and
(left) and 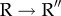 (right) transitions. The solid lines are exponential fits to RMSD/R and RMSD/R″ relaxation kinetics. (c) Time-dependent changes in the angles (measured with respect to the T state) that F, M helices make during the
(right) transitions. The solid lines are exponential fits to RMSD/R and RMSD/R″ relaxation kinetics. (c) Time-dependent changes in the angles (measured with respect to the T state) that F, M helices make during the 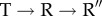 transitions. The inset shows the dispersion of individual trajectories for the F helix, with the black line being the average. (d) Time-dependent changes in the angles (measured with respect to the T state) that K, L helices make during the
transitions. The inset shows the dispersion of individual trajectories for the F helix, with the black line being the average. (d) Time-dependent changes in the angles (measured with respect to the T state) that K, L helices make during the 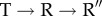 transitions. The inset at the top shows the structural changes in K, L helices during the
transitions. The inset at the top shows the structural changes in K, L helices during the 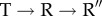 transitions. For clarity, residues 357–360 are displayed in space-filling representation in white. The dispersion of individual trajectories for the K helix is shown in the inset at the bottom. The black line is the average.
transitions. For clarity, residues 357–360 are displayed in space-filling representation in white. The dispersion of individual trajectories for the K helix is shown in the inset at the bottom. The black line is the average.
(c).  transition is triggered by downward tilt of helices F and M followed by a multiple salt-bridge switching mechanism
transition is triggered by downward tilt of helices F and M followed by a multiple salt-bridge switching mechanism
Several residues in helices F and M in the I domain (figure 1) interact with the nucleotide-binding sites in the E domain, thus creating a tight nucleotide-binding pocket. The tilting of F, M helices by approximately 15° closes the nucleotide-binding sites, the residues around which are highly conserved [55,56]. Since the  transition involves the formation and breakage of intra- and inter-subunit contacts, we simulated two adjacent, interacting subunits, which allowed us to dissect the order of events.
transition involves the formation and breakage of intra- and inter-subunit contacts, we simulated two adjacent, interacting subunits, which allowed us to dissect the order of events.
(i) The ATP-binding-induced concerted downward tilt of the F, M helices is the earliest event [57] in the  transition. The changes in the angles that F and M helices make with respect to their orientations in the T state occur in concert (figure 4c). At the end of the
transition. The changes in the angles that F and M helices make with respect to their orientations in the T state occur in concert (figure 4c). At the end of the 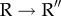 transition the helices have tilted on average by about 25° in all (figure 4c). The downward tilt of the F and M helices narrows the entrance to the ATP-binding pocket, as evidenced by the rapid decrease in the distance between P33 and N153 (figure 5). The contact number of N153 increases substantially as a result of loss in accessible surface area during the
transition the helices have tilted on average by about 25° in all (figure 4c). The downward tilt of the F and M helices narrows the entrance to the ATP-binding pocket, as evidenced by the rapid decrease in the distance between P33 and N153 (figure 5). The contact number of N153 increases substantially as a result of loss in accessible surface area during the 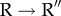 transition [56]. In the T state, E386, at the tip of the M helix, forms inter-subunit salt-bridges with R284, R285 and R197, which are disrupted, and forms a new intra-subunit salt-bridge with K80 (middle panel in figure 5). The tilting of the M helix must precede the formation of the inter-subunit salt-bridge between E386 and K80.
transition [56]. In the T state, E386, at the tip of the M helix, forms inter-subunit salt-bridges with R284, R285 and R197, which are disrupted, and forms a new intra-subunit salt-bridge with K80 (middle panel in figure 5). The tilting of the M helix must precede the formation of the inter-subunit salt-bridge between E386 and K80.
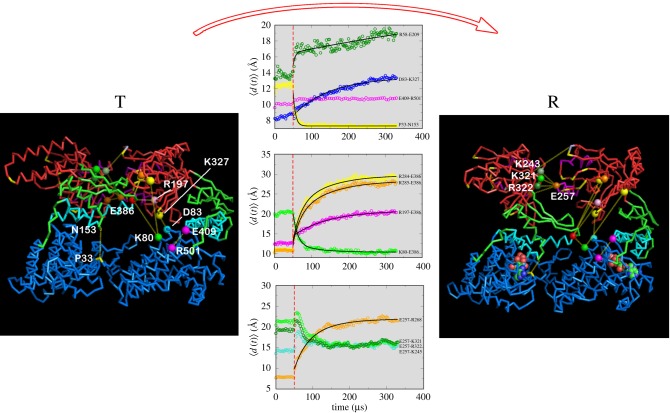
Figure 5.
 GroEL dynamics monitored using two interacting subunits. Side views from the outside to the centre of the GroEL ring and top views are presented for the T (left panel) and R (right panel) states. A few residue pairs are annotated and connected with dotted lines. The ensemble average kinetics of a number of salt-bridges and contacts between a few other residues are shown in the middle panel. Relaxation dynamics of average distance (〈d(t)〉) between some of two residues of interest are fitted to multi-exponential kinetics. The fits for the breakage and formation of the various contacts can be found in [28]. Note that the definition of salt-bridge in the SOP model with a single bead for each residue, located at the α-carbon position, is longer by a few ångströms than it would be in an all-atom representation.
GroEL dynamics monitored using two interacting subunits. Side views from the outside to the centre of the GroEL ring and top views are presented for the T (left panel) and R (right panel) states. A few residue pairs are annotated and connected with dotted lines. The ensemble average kinetics of a number of salt-bridges and contacts between a few other residues are shown in the middle panel. Relaxation dynamics of average distance (〈d(t)〉) between some of two residues of interest are fitted to multi-exponential kinetics. The fits for the breakage and formation of the various contacts can be found in [28]. Note that the definition of salt-bridge in the SOP model with a single bead for each residue, located at the α-carbon position, is longer by a few ångströms than it would be in an all-atom representation.
(ii) The rupture of the intra-subunit salt-bridge D83-K327 occurs nearly simultaneously with the disruption of the E386-R197 inter-subunit interaction with relaxation time in the order of τ ≈ 100 μs (the blue kinetic curve in the top panel in the middle of figure 5). The K80-E386 salt-bridge is formed around the same time as the rupture of the R197-E386 interaction. In the  transition, a network of salt-bridges breaks and new ones form (see below). At the residue level, the reversible formation and disruption of the D83-K327 salt-bridge, in concert with the inter-subunit salt-bridge switch associated with E386 [58] and E257 [59,60], are among the most significant events that dominate the
transition, a network of salt-bridges breaks and new ones form (see below). At the residue level, the reversible formation and disruption of the D83-K327 salt-bridge, in concert with the inter-subunit salt-bridge switch associated with E386 [58] and E257 [59,60], are among the most significant events that dominate the  transition.
transition.
The coordinated global motion is orchestrated by a multiple salt-bridge switching mechanism. The movement of the A domain results in the dispersion of the SP-binding sites and also leads to the rupture of the E257-R268 inter-subunit salt-bridge. The kinetics of breakage of the E257-R268 salt-bridge are distinctly non-exponential (the orange kinetic curve in the bottom panel in the middle of figure 5). It is very likely that the dislocated SP-binding sites maintain their stability through the inter-subunit salt-bridge formation between the A domain residues. To maintain the stable configuration in the R state, E257 engages in salt-bridge formation with positively charged residues that are initially buried at the interface of the inter-A domain in the T state. Three positively charged residues at the interface of the A domain in the R state, namely, K245, K321 and R322, are the potential candidates for the salt-bridge with E257. During the  transition, E257 interacts partially with K245, K321 and R322 as evidenced by the decrease in their separation distances (the last panel in the middle column of figure 5). The length of the E409-R501 salt-bridge, holding the I and E domains together, remains intact at ∼10 Å throughout all the allosteric transitions. This salt-bridge and two others (E408-K498 and E409-K498) might be important for enhancing positive intra-ring cooperativity and for stability of the chaperonins. Indeed, mutations at sites E409 and R501 alter the stability of the various allosteric states [61]. In summary, we find dynamic changes in the network of salt-bridges coordinate the
transition, E257 interacts partially with K245, K321 and R322 as evidenced by the decrease in their separation distances (the last panel in the middle column of figure 5). The length of the E409-R501 salt-bridge, holding the I and E domains together, remains intact at ∼10 Å throughout all the allosteric transitions. This salt-bridge and two others (E408-K498 and E409-K498) might be important for enhancing positive intra-ring cooperativity and for stability of the chaperonins. Indeed, mutations at sites E409 and R501 alter the stability of the various allosteric states [61]. In summary, we find dynamic changes in the network of salt-bridges coordinate the  transition.
transition.
It is worth emphasizing that the order of events described above is not followed in all the trajectories. Each GroEL molecule follows a somewhat different pathway during the allosteric transitions, which is indicated by the considerable dispersion in the dynamics. A recent cryo-EM study [11] has shown that there is considerable heterogeneity in the conformations of the various allosteric states. It therefore stands to reason that the dynamics connecting the allosteric states will be likewise heterogeneous, which would support our findings from over a decade ago [28].
(d). 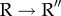 transition involves a spectacular outside-in movement of K and L helices accompanied by inter-domain salt-bridge K80-D359 formation
transition involves a spectacular outside-in movement of K and L helices accompanied by inter-domain salt-bridge K80-D359 formation
The dynamics of the irreversible 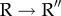 transition are propelled by substantial movements in the A domain helices K and L that drive the dramatic conformational change in GroEL resulting in doubling of the volume of the cavity. The
transition are propelled by substantial movements in the A domain helices K and L that drive the dramatic conformational change in GroEL resulting in doubling of the volume of the cavity. The 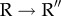 transition also occurs in stages.
transition also occurs in stages.
(i) Upon ATP hydrolysis the F, M helices rapidly tilt by an additional 10° (figure 4c). Nearly simultaneously there is a small reduction in P33–N153 distance (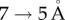 ) (see top panel in figure 6). These relatively small changes are the initial events in the
) (see top panel in figure 6). These relatively small changes are the initial events in the 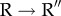 transition.
transition.
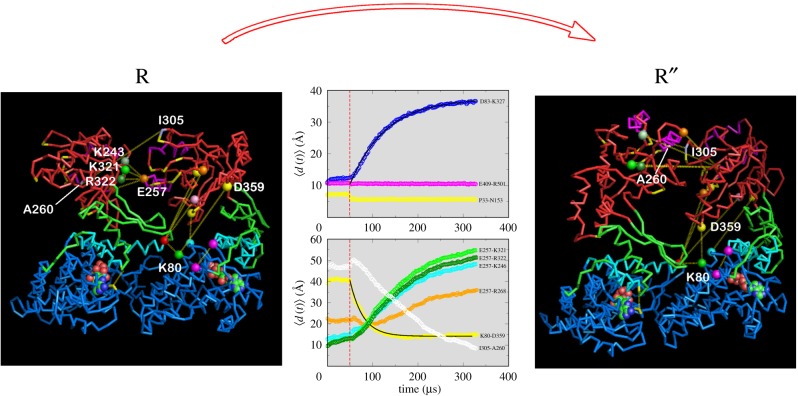
Figure 6.
Dynamics of the 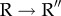 transition using two-subunit SOP model simulations. Intra-subunit salt-bridges (or residue pairs) of interest (D83-K327, E409-R501, P33-N153) are plotted in the top panel, and inter-subunit salt-bridges of interest (E257-K246, E257-R268, E257-K321, E257-R322, I305-A260) are plotted in the bottom panel in the centre of the figure. For emphasis, the dynamics of the K80-D359 salt-bridge, which provides a driving force to other residue dynamics, are highlighted with a black line in the bottom panel.
transition using two-subunit SOP model simulations. Intra-subunit salt-bridges (or residue pairs) of interest (D83-K327, E409-R501, P33-N153) are plotted in the top panel, and inter-subunit salt-bridges of interest (E257-K246, E257-R268, E257-K321, E257-R322, I305-A260) are plotted in the bottom panel in the centre of the figure. For emphasis, the dynamics of the K80-D359 salt-bridge, which provides a driving force to other residue dynamics, are highlighted with a black line in the bottom panel.
(ii) In the subsequent step, the A domain undergoes significant conformational changes that are most vividly captured by the outside-in concerted movement of helices K and L. These two helices, which tilt by about 30° during the  transition, further rotate by an additional 40° when the
transition, further rotate by an additional 40° when the 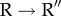 transition occurs (figure 4d). In the process, a number of largely polar and charged residues that are exposed to the exterior in the T state line the inside of the cavity in the R″ state, making the interior of GroEL polar. The outside-in motion of K and L helices leads to an inter-domain salt-bridge K80-D359 whose α-carbon distance changes rapidly from about 40 Å in the R state to about 14 Å in the R″ (figure 6).
transition occurs (figure 4d). In the process, a number of largely polar and charged residues that are exposed to the exterior in the T state line the inside of the cavity in the R″ state, making the interior of GroEL polar. The outside-in motion of K and L helices leads to an inter-domain salt-bridge K80-D359 whose α-carbon distance changes rapidly from about 40 Å in the R state to about 14 Å in the R″ (figure 6).
The wing of the A domain that protrudes outside the GroEL ring in the R state moves inside the cylinder. The outside-in motion facilitates the K80-D359 salt-bridge formation, which in turn orients the position of the wing. The orientation of the A domain's wing inside the cylinder exerts a substantial strain (data not shown) on the GroEL structure. To relieve the strain, the A domain is forced to undergo a dramatic 90° clockwise rotation and 40° upward movement with respect to the R state. As a result, the SP-binding sites (H, I helices, coloured blue in figure 1) are oriented in the upward direction. Before the strain-induced alterations are possible, the distance between K80 and D359 decreases drastically from that in R state (middle panel in figure 6). The clockwise motion of the A domain occurs only after the formation of a salt-bridge between K80 and D359. The formation of the salt-bridge K80-D359 is followed by the disruption of several salt-bridges between the inter-A domain residues, K245, E257, R268, K321 and R322 (figure 6). Formation of contact between I305 and A260 (a binding site for SPs), an inter-subunit residue pair located at the interface of two adjacent A domains in the R″ state, occurs extremely slowly compared with others. The non-monotonic and lag-phase kinetics observed in the rupture and formation of a number of contacts suggests that intermediate states must exist in the pathways connecting the R and R″ states .
The clockwise rotation of the A domain orients the domain in the upward direction so as to permit the binding of the mobile loop of GroES. Hydrophobic interactions between SP-binding sites and GroES drive the 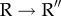 transition. The hydrophilic residues, hidden on the side of the A domain in the T or the R state, are now exposed to form an interior surface of the GroEL. The E409-R501 salt-bridge formed between I and A domains close to the γ-Pi-binding site is maintained throughout the allosteric transitions including in the transition state [61].
transition. The hydrophilic residues, hidden on the side of the A domain in the T or the R state, are now exposed to form an interior surface of the GroEL. The E409-R501 salt-bridge formed between I and A domains close to the γ-Pi-binding site is maintained throughout the allosteric transitions including in the transition state [61].
(e). Transition state ensembles connecting the allosteric states are broad
The structures of the transition state ensembles (TSEs) connecting the T, R and R″ states are obtained using RMSD as a surrogate reaction coordinate. We assume that, for a particular trajectory, the TS location is reached when δ‡ = |(RMSD/T)(tTS) − (RMSD/R)(tTS)| < rc, where rc = 0.2 Å, and tTS is the time during which δ‡ < rc. Letting the value of RMSD at the TS be 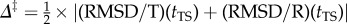 , the distributions Δ‡ for
, the distributions Δ‡ for  and
and 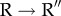 transitions are broad. If Δ‡ is normalized by the RMSD between the two endpoint structures to produce a Tanford β-like parameter q‡ (see caption of figure 7 for definition), we find that the width of the TSE for the
transitions are broad. If Δ‡ is normalized by the RMSD between the two endpoint structures to produce a Tanford β-like parameter q‡ (see caption of figure 7 for definition), we find that the width of the TSE for the 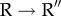 is less than for the
is less than for the  transition (figure 7a). The mean values of q‡ for the two transitions show that the most probable TS is located close to the R states in both
transition (figure 7a). The mean values of q‡ for the two transitions show that the most probable TS is located close to the R states in both  and
and 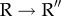 transitions.
transitions.
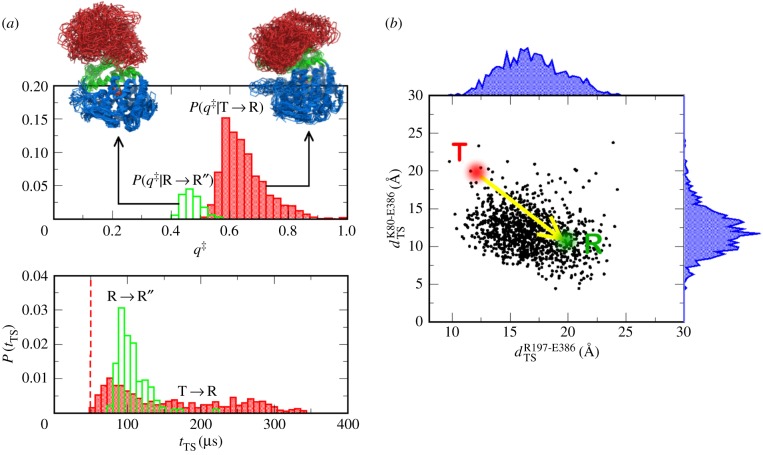
Figure 7.
Transition state ensembles (TSEs). (a) TSEs are represented in terms of distributions P(q‡), where 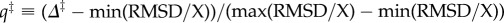 . Histogram in red gives P(q‡) for
. Histogram in red gives P(q‡) for  transition and the data in green are for the
transition and the data in green are for the 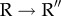 transition. For
transition. For  , X = R,
, X = R, 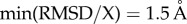 and
and 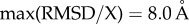 . For
. For 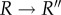 , X = R″,
, X = R″, 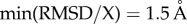 and
and 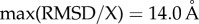 . To satisfy conservation of the number of molecules the distributions are normalized using
. To satisfy conservation of the number of molecules the distributions are normalized using 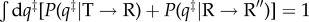 . Twenty overlapped TSE structures for the two transitions are displayed. In the bottom panel, the distributions of tTS that satisfy δ‡ < 0.2 Å are plotted for the
. Twenty overlapped TSE structures for the two transitions are displayed. In the bottom panel, the distributions of tTS that satisfy δ‡ < 0.2 Å are plotted for the  and the
and the  transitions. (b) TSE for the
transitions. (b) TSE for the  transition represented by the pair of two salt-bridge lengths (dR197-E386TS, dK80-E386TS) (black dots). The equilibrium distances (〈dR197-E386TS〉, 〈dK80-E386TS〉) in the T and the R states are shown using red and green dots, respectively. The distance distributions for the TSE are shown in blue.
transition represented by the pair of two salt-bridge lengths (dR197-E386TS, dK80-E386TS) (black dots). The equilibrium distances (〈dR197-E386TS〉, 〈dK80-E386TS〉) in the T and the R states are shown using red and green dots, respectively. The distance distributions for the TSE are shown in blue.
Disorder in the TSE structures (figure 7) is largely localized in the A domain, which once again shows that the substructures in this domain partially unfold as the barrier crossings occur. By comparison, the E domain remains more or less structurally intact even at the transition state, suggesting that the relative immobility of this domain is crucial to the function of this biological nanomachine [16]. It is most likely the case that the E domain is the anchor for force transmission to the SP, thus partially unfolding it, as the reaction cycle proceeds. The dispersions in the TSE are also reflected in the heterogeneity of the lengths of the various salt-bridges in the transition states.
4. Functional implications: iterative annealing mechanism [62]
The dynamics clearly reveal that by breaking a number of salt-bridges, over a hierarchy of timescales, the volume of the central cavity expands dramatically, expanding by twofold. More importantly, in the process the interaction between the SP and GroEL changes drastically. Upon ensnaring the SP the SP–GroEL complex is (marginally) stabilized predominantly by hydrophobic interactions. However, during the subsequent ATP-consuming and irreversible  transition, not only does the volume double but also the microenvironment of the SP is largely polar. This occurs because of the remarkable nearly 180° rotations of helices K and L that result in the inner cavity of the GroEL. Thus, during a single catalytic cycle, the microenvironment that the SP is subject to changes from being hydrophobic to polar. This change is the annealing mechanism of GroEL that moves the SP stochastically from one region, in which the misfolded SP is trapped, to another region from which it could with some probability reach the folded state. The cycle of hydrophobic to polar change takes place with each catalytic cycle, and hence the GroEL–GroES machine iteratively anneals the misfolded SP, enabling it to fold.
transition, not only does the volume double but also the microenvironment of the SP is largely polar. This occurs because of the remarkable nearly 180° rotations of helices K and L that result in the inner cavity of the GroEL. Thus, during a single catalytic cycle, the microenvironment that the SP is subject to changes from being hydrophobic to polar. This change is the annealing mechanism of GroEL that moves the SP stochastically from one region, in which the misfolded SP is trapped, to another region from which it could with some probability reach the folded state. The cycle of hydrophobic to polar change takes place with each catalytic cycle, and hence the GroEL–GroES machine iteratively anneals the misfolded SP, enabling it to fold.
The physical picture of the IAM, described above qualitatively, whose molecular origin is illustrated by the GroEL allostery has been translated into a set of kinetic equations with the express purpose of quantitatively describing the kinetics of chaperonin-assisted folding of stringent in vitro substrates, such as Rubisco [44]. According to theory of IAM (figure 1), in each cycle, corresponding to the completion of  and
and  transitions, the SP folds by the kinetic partitioning mechanism (KPM) [63]. The KPM shows that a fraction, Φ, referred to as the partition factor, reaches the native state. In the context of assisted folding it implies that with each round of folding the fraction of folded molecules is Φ and the remaining fraction gets trapped in one of the many misfolded structures. After n such cycles or iterations, the yield of the native state is
transitions, the SP folds by the kinetic partitioning mechanism (KPM) [63]. The KPM shows that a fraction, Φ, referred to as the partition factor, reaches the native state. In the context of assisted folding it implies that with each round of folding the fraction of folded molecules is Φ and the remaining fraction gets trapped in one of the many misfolded structures. After n such cycles or iterations, the yield of the native state is
| 4.1 |
We illustrate the success of the IAM theory first extracting the key parameters by fitting the kinetic equations to experimental data. The fits at various GroEL concentrations, with a fixed initial concentration of Rubisco, is excellent. Remarkably, for Rubisco the partition factor Φ ≈ 0.02, which means that only about 2% of the SP reaches the folded state in each cycle. The key parameter in the IAM is the rate (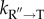 ) of resetting the machine after ATP hydrolysis, which involves release of inorganic phosphate and ADP, to the taut (T) state that can again recognize the SP to start assisted folding. Thus, by maximizing
) of resetting the machine after ATP hydrolysis, which involves release of inorganic phosphate and ADP, to the taut (T) state that can again recognize the SP to start assisted folding. Thus, by maximizing 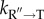 the native state yield can be optimized in a fixed time. It naturally follows that if the wild-type GroEL has evolved to perform optimally then any mutant of GroEL would produce less of the native fold in a specified time. This consequence of the IAM could be tested using data on the ability of GroEL and mutants to rescue the folding of mitochondrial malate dehydrogenase (mtMDH), for which experiments have been carried out by Lund and co-workers [64]. With
the native state yield can be optimized in a fixed time. It naturally follows that if the wild-type GroEL has evolved to perform optimally then any mutant of GroEL would produce less of the native fold in a specified time. This consequence of the IAM could be tested using data on the ability of GroEL and mutants to rescue the folding of mitochondrial malate dehydrogenase (mtMDH), for which experiments have been carried out by Lund and co-workers [64]. With 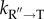 as the only parameter, the IAM predictions match quantitatively with experiments not only for mtMDH but also for citrate synthase [44].
as the only parameter, the IAM predictions match quantitatively with experiments not only for mtMDH but also for citrate synthase [44].
5. Conclusion
From the functional perspective, it is now firmly established that the IAM is the only theory that explains all the available kinetic data quantitatively [44]. The theory mandates that with each cycle only a very small fraction (for a stringent SP such as Rubisco) reaches the native state. As shown here, during each cycle, GroEL and GroES undergo large-scale conformational changes. During each cycle the microenvironment of the inner cavity changes (annealing function), ATP is hydrolysed, and ADP, inorganic phosphate and the SP (folded or not) are ejected. In the process, the machine is reset to the starting taut state for the cycle to begin anew. The release of ADP, which is accelerated by about 100-fold in the presence of SP [31], requires signalling spanning over 100 Å, a remarkable example of allosteric communication! We have argued that transmission of signals across such a large distance requires stiffness in at least certain regions of the GroEL–GroES complex. Interestingly, the SPM predicts the network of most probable residues that carry the signals. The network spans portions of the entire complex, implying that all the regions participate during the mechanics of GroEL function. Interestingly, the residues with large stored elastic energy, which hold the key for allosteric signals, are also involved in the dynamics of allosteric transitions. From both a structural and a dynamic perspective there is an inherent asymmetry in the GroEL allostery, with different subunits exhibiting distinct dynamics even though there is a sevenfold symmetry in the taut state.
We conclude with the following additional remarks.
— There is an inherent asymmetry in the allosteric transitions. The SPM shows that both the fluctuations and the stored elastic energies in residues belonging to adjacent E domains are drastically different. This asymmetry is reflected in the dynamics of transition between distinct allosteric states. There are substantial molecule-to-molecule variations, leading to heterogeneity in the allosteric transitions, which are hidden when ensemble averaging is performed. The implications, if any, of the heterogeneity (found in molecular motors as well [52,65,66]) for GroEL function is unclear. It should be emphasized, however, that the plasticity associated with the A domain [43,67] could be relevant not only for SP recognition but also for ease of inter-domain movement which is crucial in GroEL performing work on the SP [68]. Remarkably, the dispersal in the binding sites in the A domain during the
 transition must occur as a result of the small torque exerted by the movements of key residues in the E domain through the I domain. The molecular basis of this form of allostery is well captured by the SPM and is also reflected in the dynamics. The estimated force experienced by the SP (10–20 pN) is sufficient to partially unfold the SPs, especially considering that the domains move relatively slowly during the ATP-driven
transition must occur as a result of the small torque exerted by the movements of key residues in the E domain through the I domain. The molecular basis of this form of allostery is well captured by the SPM and is also reflected in the dynamics. The estimated force experienced by the SP (10–20 pN) is sufficient to partially unfold the SPs, especially considering that the domains move relatively slowly during the ATP-driven 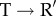 transition.
transition.— Our simulations show that the allosteric transitions are triggered by formation of salt-bridges, which are of both the intra- and inter-subunit varieties. There is a clear hierarchy in the timescales of their rupture and formation [28]. More generally, it appears that in a variety of systems, including molecular switches, salt-bridges collectively drive allosteric transitions.
— We have not discussed the role of the dual cavity in GroEL, whose importance could be understood using the following arguments. In the IAM theory, the larger
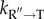 is, the more will be the yield of the native fold in biologically relevant time. A natural question arises: Has the GroEL machine evolved to maximize
is, the more will be the yield of the native fold in biologically relevant time. A natural question arises: Has the GroEL machine evolved to maximize 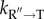 ? This is indeed the case. First, the residence time of a SP in the cavity is drastically smaller when a load, in the form of SP, is present. Second, ADP release from the trans ring in the symmetric complex is greatly accelerated in the presence of SP [31], thus resetting the machine for yet another round of SP processing. This finding shows that when a load (SP) is imposed on GroEL it functions at an accelerated pace by going through the catalytic cycle rapidly (maximizing
? This is indeed the case. First, the residence time of a SP in the cavity is drastically smaller when a load, in the form of SP, is present. Second, ADP release from the trans ring in the symmetric complex is greatly accelerated in the presence of SP [31], thus resetting the machine for yet another round of SP processing. This finding shows that when a load (SP) is imposed on GroEL it functions at an accelerated pace by going through the catalytic cycle rapidly (maximizing 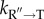 ), as anticipated by the IAM [62] and explicitly shown in [44]. The nearly 100-fold increase in SP-induced ADP release [31] is similar to the nearly 1000-fold enhancement of ADP release from the motor head of kinesin in the presence of microtubule [69]. Thus, just like molecular motors, GroEL functions as a genuine molecular machine, sharing many common functional themes.
), as anticipated by the IAM [62] and explicitly shown in [44]. The nearly 100-fold increase in SP-induced ADP release [31] is similar to the nearly 1000-fold enhancement of ADP release from the motor head of kinesin in the presence of microtubule [69]. Thus, just like molecular motors, GroEL functions as a genuine molecular machine, sharing many common functional themes.-
— A key recent development is that GroEL functions as a parallel processing machine in the sense that it can simultaneously process two SPs, one in each cavity [30,31]. From a structural perspective, the functional state, in the presence of SP, is the symmetric complex, which bears a close resemblance to the American football. Thus, it follows that upon placing a load the GroEL machine turns over as rapidly as possible to maximize yield in a biologically relevant timescale. In other words, it undergoes numerous cycles to achieve the functional objective, as described by the IAM. At the molecular level this requires signal transmission across several nanometres, which is achieved by multiple allosteric transitions.
The transition
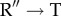 , which involves dissociation of GroES, is required to start a new cycle. If the symmetric complex is the functional state this poses a conundrum: Which of the two GroES particles bound to GroEL would be dislodged first? It appears that the breakage of symmetry [31] in the inherently symmetric functional unit, crucial for maximizing the number of iterations in biologically relevant times, must be a dynamic process related to the differential in the number of ATP molecules hydrolysed in the two rings. It will be most interesting to sort out the molecular basis of the communication that occurs over approximately 16 nm!
, which involves dissociation of GroES, is required to start a new cycle. If the symmetric complex is the functional state this poses a conundrum: Which of the two GroES particles bound to GroEL would be dislodged first? It appears that the breakage of symmetry [31] in the inherently symmetric functional unit, crucial for maximizing the number of iterations in biologically relevant times, must be a dynamic process related to the differential in the number of ATP molecules hydrolysed in the two rings. It will be most interesting to sort out the molecular basis of the communication that occurs over approximately 16 nm!
Acknowledgments
We are grateful to George Lorimer with whom many of the ideas, in particular the IAM, were developed. The contributions of Wenjun Zheng and Riina Tehver are gratefully acknowledged.
Data accessibility
This article has no additional data.
Competing interests
We declare we have no competing interests.
Funding
This work was supported by grants from the National Science Foundation (CHE 16-36424 and 16-32756) and the Collie-Welch Regents Chair (F-0019).
References
- 1.Hynes RO. 2002. Integrins: bidirectional, allosteric signaling machines. Cell 110, 673–687. ( 10.1016/S0092-8674(02)00971-6) [DOI] [PubMed] [Google Scholar]
- 2.Liu J, Nussinov R. 2016. Allostery: an overview of its history, concepts, methods, and applications. PLoS Comp. Biol. 12, e1004966 ( 10.1371/journal.pcbi.1004966) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Motlagh HN, Wrabl JO, Li J, Hilser VJ. 2014. The ensemble nature of allostery. Nature 508, 331–339. ( 10.1038/nature13001) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Monod J, Wyman J, Changeux J-P. 1965. On the nature of allosteric transitions: a plausible model. J. Mol. Biol. 12, 88–118. ( 10.1016/S0022-2836(65)80285-6) [DOI] [PubMed] [Google Scholar]
- 5.Changeux J-P. 2012. Allostery and the Monod-Wyman-Changeux model after 50 years. Annu. Rev. Biophys. 41, 103–133. ( 10.1146/annurev-biophys-050511-102222) [DOI] [PubMed] [Google Scholar]
- 6.Eaton WA, Henry ER, Hofrichter J, Mozzarelli A. 1999. Is cooperative oxygen binding by hemoglobin really understood? Nat. Struct. Biol. 6, 351–358. ( 10.1038/7586) [DOI] [PubMed] [Google Scholar]
- 7.Viappiani C, Abbruzzetti S, Ronda L, Bettati S, Henry ER, Mozzarelli A, Eaton WA. 2014. Experimental basis for a new allosteric model for multisubunit proteins. Proc. Natl Acad. Sci. USA 111, 12 758–12 763. ( 10.1073/pnas.1413566111) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Lukin JA, Kontaxis G, Simplaceanu V, Yuan Y, Bax A, Ho C. 2003. Quaternary structure of hemoglobin in solution. Proc. Natl Acad. Sci. USA 100, 517–520. ( 10.1073/pnas.232715799) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Lisi GP, Loria JP. 2016. Solution NMR spectroscopy for the study of enzyme allostery. Chem. Rev. 116, 6323–6369. ( 10.1021/acs.chemrev.5b00541) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Dyachenko A, Gruber R, Shimon L, Horovitz A, Sharon M. 2013. Allosteric mechanisms can be distinguished using structural mass spectrometry. Proc. Natl Acad. Sci. USA 110, 7235–7239. ( 10.1073/pnas.1302395110) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Roh S-H, Hryc CF, Jeong H-H, Fei X, Jakana J, Lorimer GH, Chiu W. 2017. Subunit conformational variation within individual GroEL oligomers resolved by cryo-EM. Proc. Natl Acad. Sci. USA 114, 8259–8264. ( 10.1073/pnas.1704725114) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Changeux J-P. 2012. 50 years of allosteric interactions: the twists and turns of the models. Nat. Rev. Mol. Cell Biol. 14, 819–829. ( 10.1038/nrm3695) [DOI] [PubMed] [Google Scholar]
- 13.Marzen S, Garcia HG, Phillips R. 2013. Statistical mechanics of Monod–Wyman–Changeux (MWC) models. J. Mol. Biol. 425, 1433–1460. ( 10.1016/j.jmb.2013.03.013) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Gruber R, Horovitz A. 2016. Allosteric mechanisms in chaperonin machines. Chem. Rev. 116, 6588–6606. ( 10.1021/acs.chemrev.5b00556) [DOI] [PubMed] [Google Scholar]
- 15.Cooper A, Dryden DTF. 1984. Allostery without conformational change. Eur. Biophys. J. 11, 103–109. ( 10.1007/BF00276625) [DOI] [PubMed] [Google Scholar]
- 16.Thirumalai D, Lorimer GH. 2001. Chaperonin-mediated protein folding. Annu. Rev. Biophys. Biomol. Struct. 30, 245–269. ( 10.1146/annurev.biophys.30.1.245) [DOI] [PubMed] [Google Scholar]
- 17.Chakrabarti S, Hyeon C, Ye X, Lorimer G, Thirumalai D. 2017. Molecular chaperones maximize the native state yield on biological times by driving substrates out of equilibrium. Proc. Natl Acad. Sci. USA 114, E10 919–E10 927. ( 10.1073/pnas.1712962114) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Goloubinoff P, Sassi A, Fauvet B, Barducci A, De Los Rios P. 2017. Molecular chaperones inject energy from ATP hydrolysis into the non-equilibrium stabilisation of native proteins. bioRxiv, 146852 ( 10.1101/146852) [DOI] [Google Scholar]
- 19.Xu Z, Horwich AL, Sigler PB. 1997. The crystal structure of the asymmetric GroEL-GroES-(ADP)7 chaperonin complex. Nature 388, 741 ( 10.1038/41944) [DOI] [PubMed] [Google Scholar]
- 20.Takei Y, Iizuka R, Ueno T, Funatsu T. 2012. Single-molecule observation of protein folding in symmetric GroEL-(GroES)2 complexes. J. Biol. Chem. 287, 41 118–41 125. ( 10.1074/jbc.M112.398628) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ye X, Lorimer GH. 2013. Substrate protein switches GroE chaperonins from asymmetric to symmetric cycling by catalyzing nucleotide exchange. Proc. Natl Acad. Sci. USA 110, E4289–E4297. ( 10.1073/pnas.1317702110) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Yifrach O, Horovitz A. 1995. Nested cooperativity in the ARPase activity of the oligomeric chaperonin GroEL. Biochemistry 34, 5303–5308. ( 10.1021/bi00016a001) [DOI] [PubMed] [Google Scholar]
- 23.Horovitz A, Fridmann Y, Kafri G, Yifrach O. 2001. Review: allostery in chaperonins. J. Struct. Biol. 135, 104–114. ( 10.1006/jsbi.2001.4377) [DOI] [PubMed] [Google Scholar]
- 24.Betancourt MR, Thirumalai D. 1999. Exploring the kinetic requirements for enhancement of protein folding rates in the GroEL cavity. J. Mol. Biol. 287, 627–644. ( 10.1006/jmbi.1999.2591) [DOI] [PubMed] [Google Scholar]
- 25.Yifrach O, Horovitz A. 2000. Coupling between protein folding and allostery in the GroE chaperonin system. Proc. Natl Acad. Sci. USA 97, 1521–1524. ( 10.1073/pnas.040449997) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Tehver R, Chen J, Thirumalai D. 2009. Allostery wiring diagrams in the transitions that drive the GroEL reaction cycle. J. Mol. Biol. 387, 390–406. ( 10.1016/j.jmb.2008.12.032) [DOI] [PubMed] [Google Scholar]
- 27.Zheng W, Brooks BR, Doniach S, Thirumalai D. 2005. Network of dynamically important residues in the open/closed transition in polymerases is strongly conserved. Structure 13, 565–577. ( 10.1016/j.str.2005.01.017) [DOI] [PubMed] [Google Scholar]
- 28.Zheng W, Brooks BR, Thirumalai D. 2006. Low-frequency normal modes that describe allosteric transitions in biological nanomachines are robust to sequence variations. Proc. Natl Acad. Sci. USA 103, 7664–7669. ( 10.1073/pnas.0510426103) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Zheng W, Thirumalai D. 2009. Coupling between normal modes drives protein conformational dynamics: illustrations using allosteric transitions in myosin II. Biophys. J. 96, 2128–2137. ( 10.1016/j.bpj.2008.12.3897) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Hyeon C, Lorimer GH, Thirumalai D. 2006. Dynamics of allosteric transition in GroEL. Proc. Natl Acad. Sci. USA 103, 18 939–18 944. ( 10.1073/pnas.0608759103) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Schrodinger E. 1943. What is life? Cambridge, UK: Cambridge University Press. [Google Scholar]
- 32.Kumar A, Glembo TJ, Ozkan SB. 2015. The role of conformational dynamics and allostery in the disease development of human ferritin. Biophys. J. 109, 1273–1281. ( 10.1073/pnas.0608759103) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.McLeish TCB, Cann MJ, Rodgers TL. 2015. Dynamic transmission of protein allostery without structural change: spatial pathways or global modes? Biophys. J. 109, 1240–1250. ( 10.1016/j.bpj.2015.08.009) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Townsend PD. et al. 2015. The role of protein-ligand contacts in allosteric regulation of the Escherichia coli catabolite activator protein. J. Biol. Chem. 290, 22 225–22 235. ( 10.1074/jbc.M115.669267) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Flechsig H. 2017. Design of elastic networks with evolutionary optimized long-range communication as mechanical models of allosteric proteins. Biophys. J. 113, 558–571. ( 10.1016/j.bpj.2017.06.043) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Yan L, Ravasio R, Brito C, Wyart M. 2017. Architecture and coevolution of allosteric materials. Proc. Natl Acad. Sci. USA 114, 2526–2531. ( 10.1073/pnas.1615536114) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Rocks JW, Pashine N, Bischofberger I, Goodrich CP, Liu AJ, Nagel SR. 2017. Designing allostery-inspired response in mechanical networks. Proc. Natl Acad. Sci. USA 114, 2520–2525. ( 10.1073/pnas.1612139114) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Bahar I, Chennubhotla C, Tobi D. 2007. Intrinsic dynamics of enzymes in the unbound state and relation to allosteric regulation. Curr. Opin. Struct. Biol. 17, 633–640. ( 10.1016/j.sbi.2007.09.011) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Bahar I, Lezon TR, Yang LW, Eyal E. 2010. Global dynamics of proteins: bridging between structure and function. Annu. Rev. Biophys. 39, 23–42. ( 10.1146/annurev.biophys.093008.131258) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Bahar I, Rader AJ. 2005. Coarse-grained normal mode analysis in structural biology. Curr. Opin. Struct. Biol. 15, 586–592. ( 10.1016/j.sbi.2005.08.007) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Haliloglu T, Bahar I, Erman B. 1997. Gaussian dynamics of folded proteins. Phys. Rev. Lett. 79, 3090–3093. ( 10.1103/PhysRevLett.79.3090) [DOI] [Google Scholar]
- 42.Atilgan AR, Durell SR, Jernigan RL, Demirel MC, Keskin O, Bahar I. 2001. Anisotropy of fluctuation dynamics of proteins with an elastic network model. Biophys. J. 80, 505–515. ( 10.1016/S0006-3495(01)76033-X) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Zheng W, Brooks BR, Thirumalai D. 2007. Allosteric transitions in the chaperonin GroEL are captured by a dominant normal mode that is most robust to sequence variations. Biophys. J. 93, 2289–2299. ( 10.1529/biophysj.107.105270) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Tehver R, Thirumalai D. 2008. Kinetic model for the coupling between allosteric transitions in GroEL and substrate protein folding and aggregation. J. Mol. Biol. 377, 1279–1295. ( 10.1016/j.jmb.2008.01.059) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Betancourt MR, Thirumalai D. 1999. Pair potentials for protein folding: choice of reference states and sensitivity of predicted native states to variations in the interaction schemes. Protein Sci. 8, 361–369. ( 10.1110/ps.8.2.361) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Miyazawa S, Jernigan R. 1996. Residue–residue potentials with a favorable contact pair term and an unfavorable high packing density term, for simulation and threading. J. Mol. Biol. 256, 623–644. ( 10.1006/jmbi.1996.0114) [DOI] [PubMed] [Google Scholar]
- 47.Zheng W, Brooks BR, Thirumalai D. 2009. Allosteric transitions in biological nanomachines are described by robust normal modes of elastic networks. Curr. Protein Pept. Sci. 10, 128–132. ( 10.2174/138920309787847608) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Hyeon C, Thirumalai D. 2007. Mechanical unfolding of RNA: from hairpins to structures with internal multiloops. Biophys. J. 92, 731–743. ( 10.1529/biophysj.106.093062) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Hyeon C, Dima RI, Thirumalai D. 2006. Pathways and kinetic barriers in mechanical unfolding and refolding of RNA and proteins. Structure 14, 1633–1645. ( 10.1016/j.str.2006.09.002) [DOI] [PubMed] [Google Scholar]
- 50.Lin J, Thirumalai D. 2008. Relative stability of helices determines the folding landscape of adenine riboswitch aptamers. J. Am. Chem. Soc. 130, 14 080–14 081. ( 10.1021/ja8063638) [DOI] [PubMed] [Google Scholar]
- 51.Mickler M, Dima RI, Dietz H, Hyeon C, Thirumalai D, Rief M. 2007. Revealing the bifurcation in the unfolding pathways of GFP by using single-molecule experiments and simulations. Proc. Natl Acad. Sci. USA 104, 20 268–20 273. ( 10.1073/pnas.0705458104) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Hyeon C, Onuchic JN. 2007. Internal strain regulates the nucleotide binding site of the kinesin leading head. Proc. Natl Acad. Sci. USA 104, 2175–2180. ( 10.1073/pnas.0610939104) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Hyeon C, Onuchic JN. 2007. Mechanical control of the directional stepping dynamics of the kinesin motor. Proc. Natl Acad. Sci. USA 104, 17 382–17 387. ( 10.1073/pnas.0708828104) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Hyeon C, Jennings PA, Adams JA, Onuchic JN. 2009. Ligand-induced global transition in the catalytic domain of protein kinase A. Proc. Natl Acad. Sci. USA 106, 3023–3028. ( 10.1073/pnas.0813266106) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Brocchieri L, Karlin S. 2000. Conservation among HSP60 sequences in relation to structure, function, and evolution. Protein Sci. 9, 476–486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Stan G, Thirumalai D, Lorimer GH, Brooks BR. 2003. Annealing function of GroEL: structural and bioinformatic analysis. Biophys. Chem. 100, 453–467. ( 10.1016/S0301-4622(02)00298-3) [DOI] [PubMed] [Google Scholar]
- 57.Ma J, Sigler PB, Xu Z, Karplus M. 2000. A dynamic model for the allosteric mechanism of GroEL. J. Mol. Biol. 302, 303–313. ( 10.1006/jmbi.2000.4014) [DOI] [PubMed] [Google Scholar]
- 58.Ranson NA, Farr GW, Roseman AM, Gowen B, Fenton WA, Horwich AL, Saibil HR. 2001. ATP-bound states of GroEL captured by cryo-electron microscopy. Cell 107, 869–879. ( 10.1016/S0092-8674(01)00617-1) [DOI] [PubMed] [Google Scholar]
- 59.Stan G, Brooks BR, Thirumalai D. 2005. Probing the annealing mechanism of GroEL minichaperone using molecular dynamics simulations. J. Mol. Biol. 350, 817–829. ( 10.1016/j.jmb.2005.05.012) [DOI] [PubMed] [Google Scholar]
- 60.Danziger O, Shimon L, Horovitz A. 2006. Glu257 in GroEL is a sensor involved in coupling polypeptide substrate binding to stimulation of ATP hydrolysis. Protein Sci. 15, 1270–1276. ( 10.1110/ps.062100606) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Aharoni A, Horovitz A. 1997. Detection of changes in pairwise interactions during allosteric transitions: coupling between local and global conformational changes in GroEL. Proc. Natl Acad. Sci. USA 94, 1698–1702. ( 10.1073/pnas.94.5.1698) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Todd MJ, Lorimer GH, Thirumalai D. 1996. Chaperonin-facilitated protein folding: optimization of rate and yield by an iterative annealing mechanism. Proc. Natl Acad. Sci. USA 93, 4030–4035. ( 10.1073/pnas.93.9.4030) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Guo Z, Thirumalai D. 1995. Kinetics of protein folding: nucleation mechanism, time scales, and pathways. Biopolymers 36, 83–102. ( 10.1002/bip.360360108) [DOI] [Google Scholar]
- 64.Sun Z, Scott DJ, Lund PA. 2003. Isolation and characterisation of mutants of GroEL that are fully functional as single rings. J. Mol. Biol. 332, 715–728. ( 10.1016/S0022-2836(03)00830-1) [DOI] [PubMed] [Google Scholar]
- 65.Zhang Z, Thirumalai D. 2012. Dissecting the kinematics of the kinesin step. Structure 20, 628–640. ( 10.1016/j.str.2012.02.013) [DOI] [PubMed] [Google Scholar]
- 66.Tehver R, Thirumalai D. 2010. Rigor to post-rigor transition in myosin V: link between the dynamics and the supporting architecture. Structure 18, 471–481. ( 10.1016/j.str.2010.01.019) [DOI] [PubMed] [Google Scholar]
- 67.Fei X, Yang D, LaRonde-LeBlanc N, Lorimer GH. 2013. Crystal structure of a GroEL-ADP complex in the relaxed allosteric state at 2.7 Å resolution. Proc. Natl Acad. Sci. USA 110, E2958–E2966. ( 10.1073/pnas.1311996110) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Corsepius NC, Lorimer GH. 2013. Measuring how much work the chaperone GroEL can do. Proc. Natl Acad. Sci. USA 110, E2451–E2459. ( 10.1073/pnas.1307837110) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Hackney DD. 2005. The tethered motor domain of a kinesin-microtubule complex catalyzes reversible synthesis of bound ATP. Proc. Natl Acad. Sci. USA 102, 18 338–18 343. ( 10.1073/pnas.0505288102) [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
This article has no additional data.