Folding cooperativity and allosteric function in the tandem-repeat protein class

Abstract

The term allostery was originally developed to describe structural changes in one binding site induced by the interaction of a partner molecule with a distant binding site, and it has been studied in depth in the field of enzymology. Here, we discuss the concept of action at a distance in relation to the folding and function of the solenoid class of tandem-repeat proteins such as tetratricopeptide repeats (TPRs) and ankyrin repeats. Distantly located repeats fold cooperatively, even though only nearest-neighbour interactions exist in these proteins. A number of repeat-protein scaffolds have been reported to display allosteric effects, transferred through the repeat array, that enable them to direct the activity of the multi-subunit enzymes within which they reside. We also highlight a recently identified group of tandem-repeat proteins, the RRPNN subclass of TPRs, recent crystal structures of which indicate that they function as allosteric switches to modulate multiple bacterial quorum-sensing mechanisms. We believe that the folding cooperativity of tandem-repeat proteins and the biophysical mechanisms that transform them into allosteric switches are intimately intertwined. This opinion piece aims to combine our understanding of the two areas and develop ideas on their common underlying principles.

This article is part of a discussion meeting issue ‘Allostery and molecular machines’.

1. Tandem-repeat protein: folding for function?

Tandem-repeat domains are one of the most common protein architectures. The frequency of these arrays is probably a result of replication slippage and recombination events on the DNA [1,2]. These mechanisms are considered sources of hypermutability and have given rise to a high polymorphism rate compared with the background rate of point mutations [2–4]. Tandem-repeat proteins have been grouped into different classes according to the size (number of amino acids) of the individual repeats [1,2,5]. In this work, we will focus on the solenoid class comprising repeats of approximately 12–40 amino acids. Individual repeats are not independently stable and a minimum of two or three repeats is required for a stable unit.

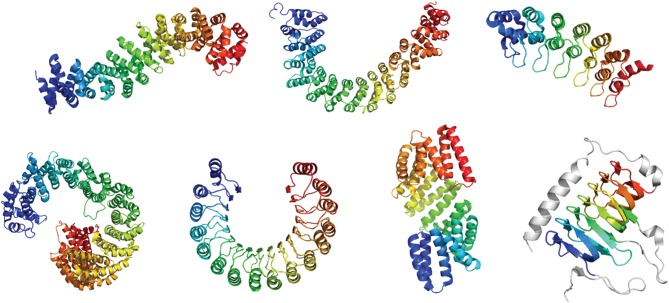
The simplest solenoid proteins contain repeats of two secondary structure elements: α/α, α/β or β/β. More complex repeats have three or four secondary elements [5,6]. In all cases, the secondary structure elements and their relative arrangement give rise to a variety of tertiary structures whose geometries can readily be described using the three angles between the repeat planes: curvature, twist and lateral bending [7,8]. The ‘solenoid’ term originally referred to a coil wound into a tightly packed helix. The repeats pack to form superhelices that differ greatly in their geometries, dependent on the structural class: some fold into planar, horseshoe-like structures, others form spring-like helices and others are very linear (figure 1). All share a common feature in that their architectures create elongated interfaces for molecular recognition, mostly to other proteins but also for some subclasses to DNA and RNA [9–13]. The α-solenoids, the focus of this opinion piece, comprise repeats of a hairpin of antiparallel α-helices [2]. Armadillo repeats [14], HEAT repeats [15,16] and the tetratricopeptide repeats (TPR) [17] are the most common members of this class.

Figure 1.

Secondary structure representations of solenoid tandem-repeat proteins. From top left to bottom right (PDB identifiers in parenthesis): ARM-repeat protein β-catenin (2Z6H), HEAT-repeat protein PR65 (1B3U), Ankyrin-repeat protein gankyrin (1UOH), HEAT-repeat protein Importin-β (3ND2), leucine-rich repeat (LRR) protein Ribonuclease Inhibitor (1BNH), TPR protein RapI (4I1A), β-helical repeat protein carbonic anhydrase (1QRE).

2. Cooperativity in the folding of tandem-repeat proteins: relationship to function?

Tandem-repeat protein structures are stabilized exclusively by local interactions either within a repeat or between adjacent repeats. By contrast, the stability of globular proteins originates from the high cooperativity between sequence-distant interactions and the burial of a large hydrophobic surface area. Nevertheless, small repeat proteins (approx. 100 amino acids) such as p16, myotrophin and the Notch ankyrin domain show two-state unfolding at equilibrium, like globular proteins of similar sizes [18–20]. Protein engineering analysis of p16, myotrophin and gankyrin mapped out their kinetic folding and unfolding pathways and revealed polarized transition states in which structure was localized to a subset of repeats at one end of the protein [21–25], whereas in Notch the central repeats were structured in the transition state [26]. It was shown that the order in which the repeats fold is governed by their relative stabilities, with the most stable repeats folding first, and consequently, the folding pathways can be redirected relatively straightforwardly by manipulating the stability distribution across the repeat array [23,25–27]. It follows also that under any given set of conditions there may be flux through multiple alternative pathways [23], as originally predicted by Wolynes and co-workers [28]. Moreover, the cooperativity of the folding process (both at equilibrium and under kinetic conditions) can also be readily tuned using appropriate mutations [29,30].

High cooperativity is not always desirable, as non-cooperative folding may be important for biological function of some repeat proteins. A striking example is the interaction between the transcription factor NFκB and the 6-ankyrin-repeat protein IκBα, which regulates NFκB by sequestering it in the cytoplasm. The two C-terminal ankyrin repeats of IκBα are intrinsically unfolded and only fold upon binding to NFκB. Not only was the folding process shown to be critical for high-affinity binding, but the large difference in intracellular stability of un-complexed IκBα compared with the NFκB-bound form was also shown to play an essential role in transcriptional regulation. Un-complexed IκBα with its unfolded repeats 5–6 is degraded in a ubiquitin-independent manner with a very short half-life, whereas NFκB-bound IκBα is stable in the cytoplasm and requires triggered ubiquitin-mediated proteolysis for its degradation and the subsequent release of NFκB [31].

Another example of the relationship between folding cooperativity and function is the 15-HEAT repeat protein PR65. PR65 is the scaffold subunit of the heterotrimeric enzyme protein phosphatase 2A (PP2A). The catalytic subunit and the substrate-bound regulatory subunit bind at opposite ends of the PR65 repeat array, and it has been proposed that rather than being a rigid scaffold for these two subunits, PR65 functions as an elastic connector that coordinates cycles of catalysis of multiply phosphorylated substrates [32]. Our analysis suggests that the non-cooperative unfolding of the HEAT repeats, arising from the very heterogeneous distribution of stabilities across the repeat array, might also facilitate PR65's connector function [33].

3. The nearest-neighbour description of repeat protein folding

The simple topology of the repeat-protein architecture has enabled the use of a one-dimensional Ising model description to define the energetic values of each repeat under the assumption of all repeats being coupled. The Ising model was originally developed to describe interactions of atomic dipole spins in ferromagnetic materials. In such a material, the atomic dipoles can adopt one of two states (spin +1 or −1). However, their states are coupled to their nearest neighbours through an exchange interaction, a potential that favours parallel alignment between states [34]. Owing to this coupling, flipping of one spin can result in cascades, or so-called ‘spin-waves’ [35]. In early work on the ankyrin-repeat domain of Notch, Barrick and co-workers [18] recognized that the protein's stability follows a simple additive rule. Regan and co-workers [36] applied the Ising model to so-called ‘consensus-designed repeat proteins’, comprising identical repeats containing the most conserved residues in a protein family. A single value of intrinsic stability of the repeats (ΔG_i) and of interfacial stability between repeats (ΔG_ij) was shown to be sufficient to describe the folding of a series of consensus-designed repeat proteins of increasing size. These energetic values are additive, and the Gibbs free energy of unfolding of a repeat protein comprising identical repeats thus follows the equation:

where n is the number of repeats, κ the intrinsic stability and τ the interfacial stability [36–39]. Several families of repeat proteins have been found to follow the Ising model both at equilibrium and under kinetic conditions [36,40–42]. With this description, one can see that the origin of cooperativity of repeat-protein folding lies in the mismatch between the intrinsic and interfacial repeat stabilities.

Folding cooperativity of repeat proteins breaks down above approximately 100–150 amino acids, similar to the cooperativity limit of globular proteins [43,44]. Moreover, for repeat proteins both large and small, an array with (i) fewer intrinsically stable repeats, (ii) high interfacial stability relative to intrinsic stability and (iii) a more homogeneous distribution of stabilities across the array length will tend to unfold more cooperatively. Indeed, when such conditions are met, the folding of even giant repeat proteins of 300 or more amino acids has, strikingly, been shown to approximate a two-state behaviour [29,45,46].

Hydrogen-exchange experiments have shown that the internal repeats of consensus-designed repeat proteins are more protected from exchange than the terminal repeats [47–49]. That is, even when the repeats are identical in sequence they are not all equally stable. The probabilistic nature of the Ising model and the higher stabilities for a greater number of repeats can be explained in simple terms. For a repeat to unfold, it requires its neighbouring repeats to unfold also. Thus, the terminal repeats of the array are the most likely to unfold, as they have only one neighbour. In natural repeat proteins, however, the simple additivity of internal and interfacial energies becomes more difficult to dissect because repeats have different sequences and therefore different stabilities. For example, analysis of the unfolding pathway of PR65 showed that this giant repeat protein has weak central repeats, which unfold before the N- and C-terminal subdomains [33,50].

We recently showed that extending the length of a single inter-repeat loop in a consensus-designed TPR protein (CTPR) can have a large effect on stability depending on the number of repeats in the array (A.P.-R., L.S.I. et al., under revision). This is in contrast with the small effects observed upon insertion of a long loop into consensus-designed ankyrin-repeat proteins and β-helical repeat proteins [51,52]. Although further investigation is required, there does appear to be a trend of a greater energetic cost of loop extensions when the repeat type has a smaller mismatch between intrinsic and interfacial stability as is the case for TPRs. In other words, short inter-repeat loops are required for a repeat protein that has weak inter-repeat interfaces, possibly because of low enthalpic and high entropic contribution to the overall stability.

In summary, the rules governing the cooperativity of repeat protein structures are now well understood. More and more, we are starting to see that repeat proteins are not static rods and that the natural functions of many repeat proteins require highly dynamic conformational properties. In this opinion piece, we question the relationship between the folding cooperativity and the function of repeat proteins and whether cooperativity plays a role in controlling the transmission of information across the repeat array.

4. The RRNPP family of molecular switches

In recent years, a new family of bacterial regulators has been gaining recognition. Known as the RRNPP family, the name of these cytosolic peptide-sensing regulators refers to the founding members of the family, Rap-Rgg-NprR-PlcR-Prgx [53]. They all have the same domain organization: an N-terminal three-helix bundle, a flexible helical linker and a C-terminal TPR capable of binding short peptides of five to eight residues. Notably, the N-terminal domain and the helical linker form a four-helix bundle that resembles a pair of TPRs. These proteins share the following mechanism: peptide binding to the C-terminal domain triggers a conformational change that propagates to the N-terminal domain. Here, we examine the Rap proteins of Bacillus subtilis, cytosolic aspartate phosphatases that affect downstream gene expression upon binding of the quorum-sensing peptide to their C-terminal TPR domain.

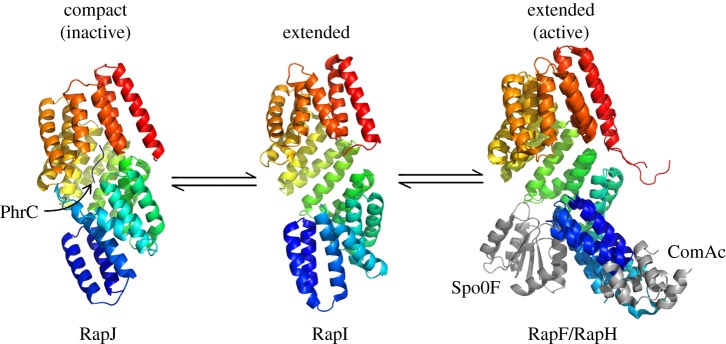
Rap phosphatases and their peptide activators were originally described in B. subtilis by Perego and co-workers [54–59]. There are 16 Rap homologues in B. subtilis. As an example, RapH acts as phosphatase of Spo0F in its Apo form (peptide unbound) and prevents downstream sporulation, whereas RapF binds and inhibits gene regulators such as ComA [53]. RapH and RapF were co-crystallized with Spo0F and ComA, respectively, and both Rap homologues showed the same overall conformation when bound to their partner molecule (figure 2) [61]. In another study, the crystal structure of Apo-RapI was compared with that of RapJ in complex with the PhrC peptide. The solenoid structure of the RapJ–PhrC complex showed a higher degree of compactness relative to Apo-RapI [60] (figure 2).

Figure 2.

Structures of different Rap proteins (C-terminus in red) depicting a possible mode of action. When the TPR domain binds to a signalling peptide, it causes the Rap protein to adopt a compact, or ‘closed’ conformation. Upon binding an interaction partner, however, conformational changes in the TPR domain are minimal, whereas the N-terminal three-helix bundle flips by approximately 180° [60].

Lacking a complete set of crystal structures of the same Rap homologue in three conformational states, Parashar and co-workers [60] used homologous structures to propose a mechanism of action for signal transduction and concluded that quorum-sensing peptides inhibit Rap function via an allosteric mechanism (figure 2). The compact solenoid was described as the inactive configuration and the extended solenoid as the active one. In its active configuration, the N-terminal helix bundle is capable of exposing the Spo0F- or ComA-binding regions of RapF and RapH, respectively. Peptide-bound Rap proteins undergo a conformational change locking the N-terminal domain in a compact configuration in which its binding sites are inaccessible.

Rap proteins are very different from their artificial counterparts, the CTPRs. Both types of TPRs are capable of forming large cooperatively folded repeat arrays, but somehow the amino acid sequence of Rap proteins encodes the additional ability to generate a repeat array with extreme flexibility and consequent dynamic switch-like behaviour capable of transmitting the information of an input to an output across the array. The nearest-neighbour cooperativity between repeats appears to have increased its complexity. Ultimately, allostery necessarily requires a dynamic system, providing further evidence that repeat proteins are not simply rigid rods.

5. Do intrinsic dynamics of Rap proteins form the underlying basis for allostery?

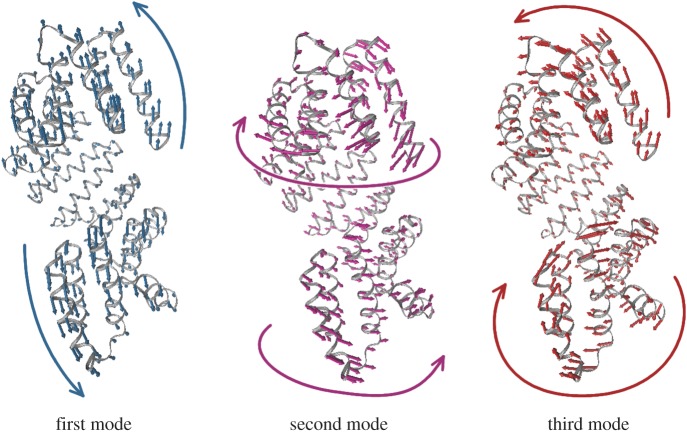
Given the functional relevance of the conformational changes seen for the Rap proteins crystallographically, we have conducted an extensive analysis to investigate whether they arise from the intrinsic dynamics of each protein. To model the vibrational dynamics, we have chosen to use elastic network models (ENMs) for their strong dependence on the shape of the overall structure instead of atomistic detail (see electronic supplementary material, Methods, extensively reviewed in [62] and references therein; [63]). In an ENM, protein dynamics are decomposed into different motions with specific directions, the normal modes. The lowest three normal modes of RapI are shown in figure 3. The predominant motion is that of bending, followed by a screw-like twist of the TPR helix and more localized motions of the N- and C-terminal three-helix bundle and TPR repeats, respectively. We compared normal modes of different Rap configurations using ENMs of a structure-based sequence alignment (electronic supplementary material, figure S1). The dynamics we observe are very similar in all four proteins, and the lowest normal modes tend to involve the collective motion of approximately 40–80% of the protein (electronic supplementary material, figure S2). Owing to the high structural similarity between RapH and RapF, both proteins explore a nearly identical motional space (electronic supplementary material, figure S3). The major difference between the extended conformation, RapI, and the active conformations is the orientation of the N-terminal three-helix bundle, and hence the normal modes of all three proteins are very similar, especially when the TPR domains are modelled independently (electronic supplementary material, figure S3). By contrast, when the Rap protein adopts the compact and inactive conformation, only the motion of a very few of the lowest normal modes remains conserved to some degree, most of which are dominated by the motion of the TPR domain (electronic supplementary material, figure S3). Comparing both peptide-bound and -unbound ENMs of RapJ reveals that most changes in dynamics of the lower modes are not due to the presence of the bound peptide but simply due to the compacted conformation (electronic supplementary material, figure S4).

Figure 3.

The three lowest normal modes of RapI. The first mode (teal) describes a bending motion that alters the distance between the N- and C-termini; the second mode (magenta) tightens the superhelix in a screw-like motion; the third mode (red) twists the N-terminal three-helix bundle and the C-terminal TPR relative to the repeat array superhelix. Models were generated using the NMWIZ plugin for VMD [64]. Movies of these modes can be found with the electronic supplementary material.

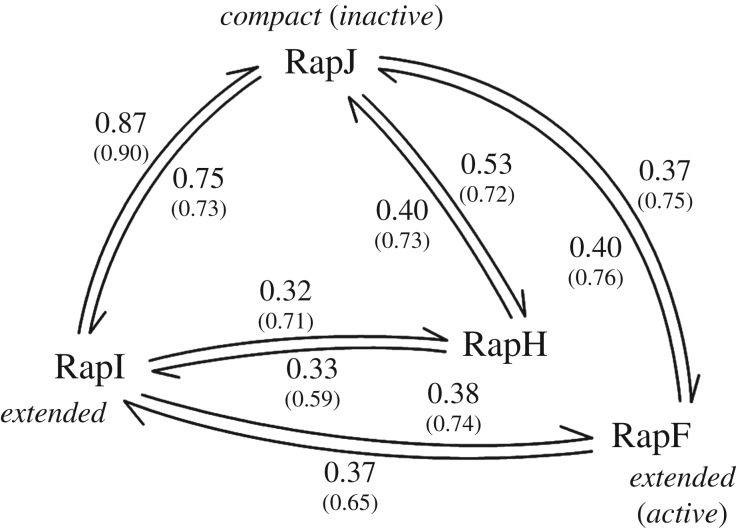
We further examined whether the motions observed in the ENMs can account for some of the conformational changes observed in crystallography by measuring how well the lowest five normal modes of a protein overlap with the conformational transition to another protein (figure 4). The transition between the extended and compact conformations is very well described by the normal modes of either RapI (to 0.87) or RapJ (to 0.75). Transitions between either compact or extended conformation and the active forms (RapH and RapF) are less well described by the lowest five normal modes due to the rotation of the N-terminal three-helix bundle and linker domain (figure 4). This observation is not entirely unexpected, as more localized motions are captured by normal modes of higher order. When mapping the normal modes to the conformational changes seen within the independently modelled TPR domains (small numbers in figure 4), agreements are greater than 0.7 for most.

Figure 4.

Quantitative comparison between the lowest five normal modes and conformational changes between different Rap proteins. The arrows represent the conformational change vector, and the values equal the corresponding cumulative overlap between the vector and the ENM of the starting structure (see electronic supplementary material, Methods). For example, the first five normal modes of RapI can account for 0.87 of the conformational change between RapI and RapJ, while the first five normal modes of RapJ only describe 0.75. Numbers in brackets correspond to the cumulative overlaps between the dynamics of truncated and independently modelled TPR domains and their respective conformational changes (see electronic supplementary material, Methods).

Considering these comparisons, a mechanism emerges by which at least the TPR domain of Rap proteins on its own could potentially explore the different conformations observed. The peptide, substrate or transcription factor could then simply trap the protein energetically in a given conformation. In fact, when considering the entropic contributions of each normal mode (figure 5), the extended conformation is entropically the most favourable. The compact conformation of RapJ comes along with a considerable entropic cost, making it energetically unfavourable (electronic supplementary material, figure S5), for which the enthalpic contributions of multiple contacts between peptide and TPRs need to compensate [60].

Figure 5.

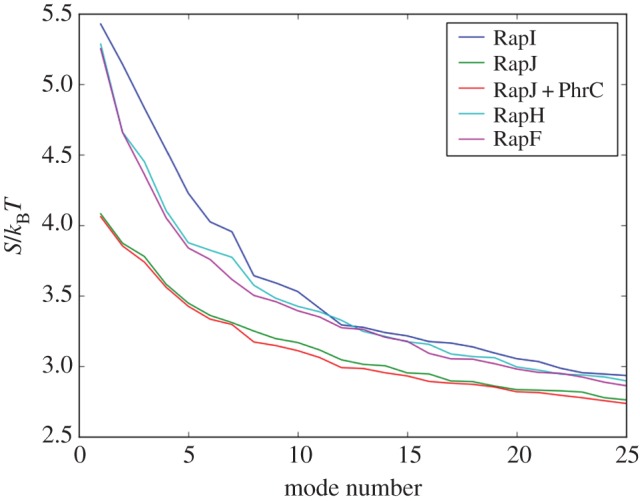
Entropy contributions of each normal mode to the total motion. The closed conformation was modelled both with and without the PhrC peptide. As the differences between both models are only small (electronic supplementary material, figure S5), the effect of peptide binding on the entropy of the system is negligible compared with the entropic cost of the conformational change.

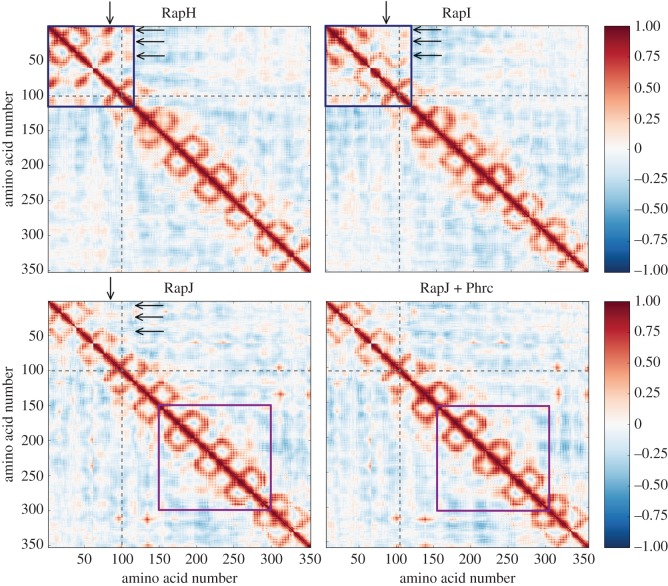
Lastly, by analysing the correlation of motion between different residues (figure 6), we can obtain an insight into why the three-helix bundle in the compact conformation has very little potential for rotating to bind partner proteins. The TPRs exhibit correlated motion only with their nearest neighbours, giving rise to the distinctive pattern of squares along the diagonal [45]. The binding of the peptide marginally increases nearest-neighbour correlation at the centre (purple box in figure 6) which understandably arises from the cross-correlations of higher modes (electronic supplementary material, figures S4 and S6). Movements of the rotated N-terminal three-helix bundle, linker domain and first TPRs repeat (blue box in figure 6) are strongly correlated, suggesting that they form a subdomain relative to the rest of the TPR repeats. Some nearest-neighbour correlations are reduced in the extended conformation of RapI, whereas they are either further reduced or even reversed in the compact conformation (arrows in figure 6). It is notable that the presence of the peptide does not directly influence the correlated motion of the N-terminal domain, indicating that locking of the three-helix bundle to the TPRs is entirely due to the conformational change. However, the peptide could induce indirect or allosteric effects by stabilizing the TPR domain in the compact conformation. These effects could then be ‘transmitted’ through the array via the interaction potential between repeats, that is via the altered cooperativity of individual repeat interfaces due to the TPR rearrangement in the compact conformation.

Figure 6.

Representative cross-correlation maps for the partner-bound, open and peptide-bound conformations. Cross-correlation between residues is a measure of how much these residues move in the same direction, where values of 1 and −1 represent perfectly correlated and anti-correlated motions, respectively [62]. The TPR repeats exhibit correlated motions only with their nearest neighbours, giving rise to the distinctive pattern of squares along the diagonal. Movements of the rotated N-terminal three-helix bundle, linker domain and first TPR motif (blue box) are non-TPR-like, exhibiting non-nearest-neighbour correlations, suggesting that they form a subdomain relative to the rest of the TPR repeats. Some of these correlations are reduced in the open conformation, or even reversed, once a continuous TPR array is formed (arrows) and the distinction of this domain is lost. The global movement of peptide binding TPRs (purple box) and neighbouring repeats is only minimally affected in the presence of the peptide, which only causes a slight increase in the nearest-neighbour correlations. The N-terminal helix bundle and TPR repeats are divided by grey dashed lines and correlations are mirrored across the diagonal for clarity. The cross-correlation was summed over the lowest 25 modes, for correlation maps of lower modes (see electronic supplementary material, figure S6).

In summary, the compact and extended conformations of Rap proteins have different supramolecular geometries, arising from differences in the inter-repeat packing. Consequently, they must have different values of the interfacial repeat stability. The ENMs showed that both conformations are easily accessible through the motions of the TPR domain, albeit that an extended conformation of the array may be preferred owing to the entropic cost of the compact state. Ultimately, the intrinsic flexibility of the TPR array may allow for the existence of two functionally different conformations that can be locked by their respective binding partners.

6. Relating conformational flexibility to the allosteric mechanisms of ‘banana-shaped’ repeat proteins in multi-protein enzyme complexes

When we look across the repeat protein class, the Rap proteins are not the only example where the repeat scaffold may contribute to allosteric mechanisms due to its dynamic flexibility. In quite a few systems, the repeat protein must change its conformation to bind to a variety of partners that all differ in shape and size. We are currently investigating proteins of different repeat types to examine whether their experimentally observed dynamics can also be described by ENM normal modes. As global motions are largely determined by the over-all shape of a molecule [62], one of our leading questions is whether the dynamics of two different proteins with the same tertiary shape will exhibit the same motions, independent of repeat type.

One such protein is PR65, and, as mentioned earlier, we are interested in understanding how it regulates the activity of the heterotrimeric PP2A enzyme (figure 7a). From crystal structures of PR65 in complex with the catalytic C-subunit and different regulatory B-subunits, it is clear that PR65 needs to be highly flexible structurally to be able to form the multitude of PP2A complexes that are present in the cell [66–68]. Biophysical analysis has shown that binding of the catalytic subunit to the C-terminal repeats of PR65 increases by an order of magnitude the affinity of the N-terminal repeats of PR65 for an inhibitor, the SV40 small t antigen [69]. However, there are no obvious direct contacts between the small t antigen and the catalytic subunit [69], suggesting a process by which PR65 functions as an allosteric transmitter of catalytic-subunit binding, though the underlying mechanism involved remains to be resolved.

Figure 7.

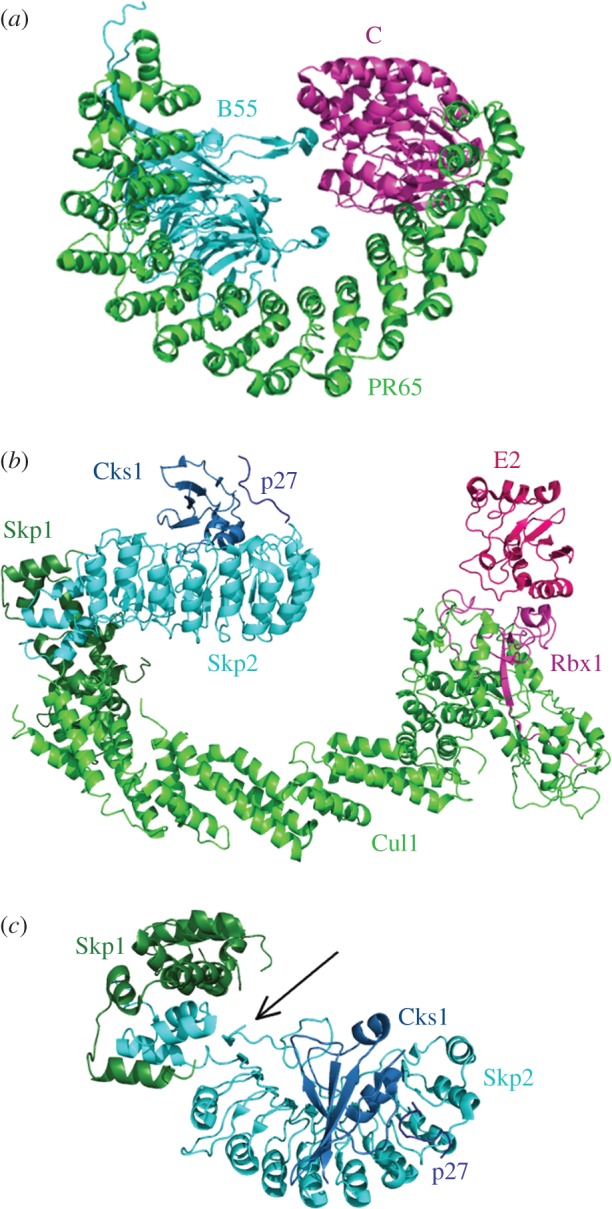
Repeat proteins linking function in multi-protein complexes. (a) PP2A (PDB 3dw8) consisting of the HEAT-repeat scaffold subunit PR65, the catalytic subunit C bound to the C-terminus of PR65, and a regulatory subunit (B55) bound to the N-terminus of PR65. (b) Modelled structure of the SCF^Skp2 ubiquitin ligase consisting of three core subunits Skp1, cullin-repeat containing protein Cul1 and Rbx1, and substrate-recognition subunit Skp2 with accessory protein Cks1, which together recruit the substrate p27. Also shown is the E2 ubiquitin-conjugating enzyme, which is recruited to the SCF by Rbx1, together forming the catalytic entity (PDBs 2AST, 1LDK and 4Q5E [65]). Thus, in both complexes, the substrate-recognition subunit is bound to one end of the repeat protein and the catalytic subunit to the other end. (c) Top view of the Skp2 bound to Skp1, Cks1 and p27, highlighting the insertion of the Skp2 C-terminal tail at its N-terminus.

A number of years ago, we demonstrated such an allosteric effect in the LRR protein Skp2, which is one of many variable substrate-binding subunits of the multi-subunit SCF (Skp1-Cullin-F-box) ubiquitin ligases (figure 7b) [70]. Skp2 has an F-box motif, with which it binds to the Skp1 subunit, thereby connecting it to the Cullin subunit and the rest of the SCF ligase. The C-terminal ‘tail’ of Skp2 is unstructured and folds back onto the concave face of the LRR domain (figure 7c) [65]. Binding of the accessory subunit Cks1 to the C-terminus of the LRR domain results in hydrogen–deuterium exchange protection of the N-terminal LRR repeats without any direct contacts between Cks1 and N-terminal Skp2 repeats [70]. We therefore proposed that binding of Cks1 decreases fluctuations in the C-terminal tail of Skp2, thereby stabilizing residues in the tail that form a β-sheet between the first LRR and the F-box. In the absence of this β-sheet, the linker between the LRR domain and the F-box may constitute a hinge, which could account for deprotection of the N-terminal LRRs when Cks1 is not bound. Thus, the hinge may function as a sensor of substrate binding, tightening of which could reduce the motions of Skp2 and thereby allow for efficient ubiquitination and/or this binding event could be translated allosterically through the Cullin subunit to the E2 ubiquitin-conjugating enzyme. The Cullins themselves are highly flexible repeat proteins, and their ability to change shape is thought to be crucial for orchestrating consecutive cycles of substrate ubiquitination [71]. Considering the similar architectures of the SCF and PP2A enzyme complexes, we hypothesize that there is a common underlying mechanism exploiting flexible repeat-protein scaffolds for such catalytic processes. At this point, it is not clear how exactly this scaffold flexibility arises and how it depends on the repeat types. Moreover, it remains to be seen whether repeat types with different packing interactions, interfacial energies and cooperativities will exhibit correspondingly different dynamics and macromolecular flexibility.

7. Bridging tandem-repeat cooperativity and allosteric transmission

In summary, we have explored the relationship between the stability and cooperativity of repeat arrays and the functional transmission of information along them. For example, Rap proteins are capable of transforming a high concentration of quorum-sensing peptides into a signalling response to downstream effectors [56,61,72,73]. This implies that Rap proteins display higher affinity for their binding partners than for the peptides because the bound conformation is only favoured at the high concentrations associated with quorum-sensing. The Rap proteins are an example of a system where nearest-neighbour interactions in a repeat array can cause allosteric inactivation. Our ENM results showed that the first five normal modes of the extended conformation could account for most of the conformational changes between the extended and compact form, suggesting an equilibrium between the two that favours the extended form in the absence of the peptide. Owing to different packing interactions in the extended and compact conformations, the N-terminal domain displays a varying degree of correlated movement relative to the TPR domain. This observation supports the idea of an N-terminal helix bundle reaching an energy minimum when cooperatively interacting with the compact TPR domain and thus becoming incapable of exploring partner-binding configurations.

In addition to these insights from the Rap ENMs, the examples of banana-shaped proteins discussed here suggest that repeat arrays involved in diverse cellular processes have the potential to function as allosteric modulators in multi-protein complexes and are not simply a molecular-recognition platform for multiple binding partners. In most cases, these repeat proteins are not rigid, rod-like entities, but rather they need to be flexible to function in a biological context. ENMs are a simplistic but efficient way for us to gain insights into the conformational space explored by repeat proteins. Using them, we can identify structural points of allosteric significance, such as hinges or weak points, and design experiments accordingly. Naturally, we think that repeat stability and cooperativity can be linked to distinct mechanical characteristics and therefore function as a transmission pathway for information to travel through the repeat array. Any local event, such as binding of a partner molecule or alterations of repeat packing in TPR arrays, should therefore modulate repeat stability and shape, and this change could be transmitted to nearest neighbours by way of the interaction potential, similar to the mechanism that gives rise to spin-waves in ferromagnets. Hence we suggest that context-dependent changes in cooperativity between repeats must, at least partly, be the basis for allosteric effects in tandem-repeat proteins, and, as such, any repeat protein in itself could function as a switch.

Ultimately, the question of how distantly located repeats can fold cooperatively, how Rap proteins change their superhelical structure upon binding and how information is transmitted through multi-protein complexes via a repeat protein may be different manifestations of the same physical mechanism, namely that underlying the Ising model. The two parameters of intrinsic repeat stability and the interaction potential (i.e. interfacial stability) are straightforward to quantify in consensus repeat arrays but are not easily determined in natural repeat proteins owing to the different sequences of the repeats. Nevertheless, we believe that this parametrization will still hold true but will just result in a model that is mathematically non-trivial. It is crucial to carefully dissect the relationship between repeat protein cooperativity and their ability to function as switches such that we can tune them artificially, thereby translating the peptide-sensing capability to the biotech industry. Last but not least, repeat proteins make up nearly one-third of the human proteome [74], and, given their widespread involvement in key signalling cascades, an understanding of allostery in repeat proteins is also necessary to shed light on the transmission of information in central cellular processes.

Data accessibility

All data presented in this article are based on calculations of data from public repositories, using publicly available software and the methods described in detail in the electronic supplementary material.

Authors' contributions

A.P.-R., M.S. and L.S.I. conceived the opinion piece. M.S. carried out the ENMs. A.P.-R., M.S. and L.S.I. wrote the manuscript.

Competing interests

We declare we have no competing interests. 

Funding

L.S.I. acknowledges the support of a Senior Fellowship from the UK Medical Research Foundation. A.P.-R. was supported by a BBSRC Doctoral Training Programme scholarship and an Oliver Gatty Studentship. M.S. was supported by a BBSRC Doctoral Training Programme scholarship.