Locally Adaptive Smoothing with Markov Random Fields and Shrinkage Priors

Abstract

We present a locally adaptive nonparametric curve fitting method that operates within a fully Bayesian framework. This method uses shrinkage priors to induce sparsity in order-k differences in the latent trend function, providing a combination of local adaptation and global control. Using a scale mixture of normals representation of shrinkage priors, we make explicit connections between our method and kth order Gaussian Markov random field smoothing. We call the resulting processes shrinkage prior Markov random fields (SPMRFs). We use Hamiltonian Monte Carlo to approximate the posterior distribution of model parameters because this method provides superior performance in the presence of the high dimensionality and strong parameter correlations exhibited by our models. We compare the performance of three prior formulations using simulated data and find the horseshoe prior provides the best compromise between bias and precision. We apply SPMRF models to two benchmark data examples frequently used to test nonparametric methods. We find that this method is flexible enough to accommodate a variety of data generating models and offers the adaptive properties and computational tractability to make it a useful addition to the Bayesian nonparametric toolbox.

1 Introduction

Nonparametric curve fitting methods find extensive use in many aspects of statistical modeling such as nonparametric regression, spatial statistics, and survival models, to name a few. Although these methods form a mature area of statistics, many computational and statistical challenges remain when such curve fitting needs to be incorporated into multi-level Bayesian models with complex data generating processes. This work is motivated by the need for a curve fitting method that could adapt to local changes in smoothness of a function, including abrupt changes or jumps, and would not be restricted by the nature of observations and/or their associated likelihood. Our desired method should offer measures of uncertainty for use in inference, should be relatively simple to implement and computationally efficient. There are many methods available for nonparametric curve fitting, but few which meet all of these criteria.

Gaussian process (GP) regression (Neal, 1998; Rasmussen and Williams, 2006) is a popular Bayesian nonparametric approach for functional estimation that places a GP prior on the function of interest. The covariance function must be specified for the GP prior, and the isotropic covariance functions typically used are not locally adaptive. Nonstationary covariance functions have been investigated to make GP regression locally adaptive (Brahim-Belhouari and Bermak, 2004; Paciorek and Schervish, 2004, 2006). Any finite dimensional representation of GPs involves manipulations of, typically high dimensional, Gaussian vectors with mean vector and covariance matrix induced by the GP. Many GPs, including the ones with nonstationary covariance functions, suffer from high computational cost imposed by manipulations (e.g., Cholesky factorization) of the dense covariance matrix in the finite dimensional representation.

Sparsity can be imposed in the precision matrix (inverse covariance matrix) by constraining a finite dimensional representation of a GP to be a Gaussian Markov random field (GMRF), and then computational methods for sparse matrices can be employed to speed computations (Rue, 2001; Rue and Held, 2005). Fitting smooth functions with GMRFs has been practiced widely. These methods use difference equations as approximations to continuous function derivatives to induce smoothing, and have a direct relationship to smoothing splines (Speckman and Sun, 2003). GMRFs have also been used to develop Bayesian adaptive smoothing splines (Lang et al., 2002; Yue et al., 2012, 2014). A similar approach is the nested GP (Zhu and Dunson, 2013), which puts a GP prior on the order-k function derivative, which is in turn centered on another GP. This approach has good adaptive properties but has not been developed for non-Gaussian data.

Differencing has commonly been used as an approach to smoothing and trend estimation in time series analysis, signal processing, and spatial statistics. Its origins go back at least to Whittaker (1922), who suggested a need for a trade off between fidelity to the data and smoothness of the estimated function. This idea is the basis of some frequentist curve-fitting methods based on penalized least squares, such as the smoothing spline (Reinsch, 1967; Wahba, 1975) and the trend filter (Kim et al., 2009; Tibshirani, 2014). These penalized least-squares methods are closely related to regularization methods for high-dimensional regression such as ridge regression (Hoerl and Kennard, 1970) and the lasso (Tibshirani, 1996) due to the form of the penalties imposed.

Bayesian versions of methods like the lasso (Park and Casella, 2008) utilize shrinkage priors in place of penalties. Therefore, it is interesting to investigate how these shrinkage priors (Polson and Scott, 2010; Griffin et al., 2013; Bhattacharya et al., 2015) perform when applied to differencing-based time series smoothing. Although shrinkage priors have been used explicitly in the Bayesian nonparametric regression setting for regularization of wavelet coefficients (Abramovich et al., 1998; Johnstone and Silverman, 2005; Reményi and Vidakovic, 2015) and for shrinkage of order-k differences of basis spline coefficients in adaptive Bayesian P-splines (Scheipl and Kneib, 2009), a Bayesian version of the trend filter and Markov random field (MRF) smoothing with shrinkage priors has not been thoroughly investigated. To our knowledge, only Roualdes (2015), independently from our work, looked at Laplace prior-based Bayesian version of the trend filter in the context of a normal response model. In this paper, we conduct a thorough investigation of smoothing with shrinkage priors applied to MRFs for Gaussian and non-Gaussian data. We call the resulting models shrinkage prior Markov random fields (SPMRFs).

We borrow the idea of shrinkage priors from the sparse regression setting and apply it to the problem of function estimation. We take the perspective that nonparametric curve fitting is essentially a regularization problem where estimation of an unknown function can be achieved by inducing sparsity in its order-k derivatives. We propose a few fully Bayesian variations of the trend filter (Kim et al., 2009; Tibshirani, 2014) which utilize shrinkage priors on the kth-order differences in values of the unknown target function. The shrinkage imposed by the priors induces a locally adaptive smoothing of the trend. The fully Bayesian implementation allows representation of parameter uncertainty through posterior distributions and eliminates the need to specify a single global smoothing parameter by placing a prior distribution on the smoothing parameter, although complete automation is not possible so we offer ways to parameterize the global smoothing prior. In Section 2 we provide a derivation of the models starting from penalized frequentist methods and we show the relationship to GMRF models. In Section 2 we also describe our method of sampling from the posterior distribution of the parameters using Hamiltonian Monte Carlo (HMC), which is efficient and straight forward to implement. In Section 3 we use simulations to investigate performance properties of the SPMRF models under two different prior formulations and we compare results to those for a GMRF with constant precision. We show that the choice of shrinkage prior will affect the smoothness and local adaptive properties. In Section 4 we apply the method to two example data sets which are well known in the nonparametric regression setting.

2 Methods

2.1 Preliminaries

We start by reviewing a locally adaptive penalized least squares approach to nonparametric regression known as the trend filter (Kim et al., 2009; Tibshirani and Taylor, 2011; Tibshirani, 2014) and use that as a basis to motivate a general Bayesian approach that utilizes shrinkage priors in place of roughness penalties. We first consider the standard nonparametric regression problem to estimate the unknown function f. We let θ represent a vector of values of f on a discrete uniform grid t ∈ {1, 2, …, n}, and we assume y = θ + ε, where ε~𝒩(0, Iσ²), and y and ε are vectors of length n. Here all vectors are column vectors. Following Tibshirani (2014) with slight modification, the least squares estimator of the kth order trend filtering estimate θ̂ is

$$\widehat{\mathit{\theta }}=\underset{\mathit{\theta }}{\text{argmin}}{\Vert \mathbf{y}-\mathit{\theta }\Vert }_2^2+\lambda {\Vert {\mathbf{D}}^{(k)}\mathit{\theta }\Vert }_1,$$ (1)

where ||·||_q represents the L_q vector norm, and D^(k) is an (n−k)×n forward difference operator matrix of order k, such that the ith element of the vector Δ^kθ = D^(k)θ is the forward difference ${\mathrm{\Delta }}^k{\theta }_i={(-1)}^k{\mathrm{\sum }}_{j=0}^k{(-1)}^j\left(\begin{array}{l}k\hfill \\ j\hfill \end{array}\right){\theta }_{i+j}$. Note that D^(k) has recursive properties such that ${\mathbf{D}}_n^{(k)}={\mathbf{D}}_{n-k+1}^{(1)}{\mathbf{D}}_n^{(k-1)}$, where ${\mathbf{D}}_m^{(h)}$ has dimensions (m−h)×m. The objective function in equation (1) balances the trade-off between minimizing the squared deviations from the data (the first term in the sum on the right) with minimizing the discretized roughness penalty of the function f (the second term in the sum on the right). The smoothing parameter λ ≥ 0 controls the relative influence of the roughness penalty. Setting λ to 0 we get least squares estimation. As λ gets large, the roughness penalty dominates, resulting in a function with k-th order differences approaching 0 for all t. The trend filter produces a piecewise polynomial function of t₁, …, t_n with degree k − 1 as an estimator of the unknown function f. Increasing the order of the difference operator will enforce a smoother function.

The L₁ penalty in equation (1) results in the trend filter having locally adaptive smoothing properties. Tibshirani (2014) shows that the trend filter is very similar in form and performance to smoothing splines and locally adaptive regression splines, but the trend filter has a finer level of local adaptivity than smoothing splines. A main difference between the trend filter and smoothing splines is that the latter uses a squared L₂ penalty, which is the same penalty used in ridge regression (Hoerl and Kennard, 1970). Note that the L₁ penalty used by the trend filter is also used by the lasso regression (Tibshirani, 1996), and the trend filter is a form of generalized lasso (Tibshirani and Taylor, 2011; Tibshirani, 2014). In the linear regression setting with regression coefficients β_js, the L₁ and L₂ penalties can be represented by the generalized ridge penalty λΣ_j |β_j|^q (Frank and Friedman, 1993), where q = 2 corresponds to the ridge regression penalty, q = 1 to the lasso penalty, and sending q to zero results in all subsets selection regression (Tibshirani, 2011). Based on what we know about lasso regression, subset selection regression, and ridge regression, we expect a penalty closer to subset selection to do better for fitting functions with a small number of large jumps, a trend filter penalty (L₁) to do better for fitting functions with small to moderate deviations from polynomials of degree k−1, and a smoothing spline (squared L₂) penalty to do better for smooth polynomial-like functions with no jumps. This distinction will become important later when we assess the performance of different Bayesian formulations of the trend filter.

One can translate the penalized least squares formulation in equation (1) into either a penalized likelihood formulation or a Bayesian formulation. Penalized least squares can be interpreted as minimizing the penalized negative log-likelihood −l_p(θ | y) = −l(θ | y) + p(θ | λ), where l(θ | y) is the unpenalized log-likelihood and p(θ | λ) is the penalty. It follows that maximization of the penalized log-likelihood is directly comparable to finding the mode of the log-posterior in the Bayesian formulation, where the penalty is represented as a prior. This implies independent Laplace (double-exponential) priors on the Δ^kθ_j, where j = 1, …, n − k, for the trend filter formulation in equation (1). That is, $p({\mathrm{\Delta }}^k{\theta }_j\mid \lambda )=\frac{\lambda }{2}exp\left(-\lambda \mid {\mathrm{\Delta }}^k{\theta }_j\mid \right)$. This is a well-known result that has been used in deriving a Bayesian form of the lasso (Tibshirani, 1996; Figueiredo, 2003; Park and Casella, 2008). Note that putting independent priors on the kth order differences results in improper joint prior p(θ | λ), which can be made proper by including a proper prior on the first k θs.

The Laplace prior falls into a class of priors commonly known as shrinkage priors. An effective shrinkage prior has the ability to shrink noise to zero yet retain and accurately estimate signals (Polson and Scott, 2010). These properties translate into a prior density function that has a combination of high mass near zero and heavy tails. The high density near zero acts to shrink small values close to zero, while the heavy tails allow large signals to be maintained. A simple prior developed for subset selection in Bayesian setting is the spike-and-slab prior, which is a mixture distribution between a point mass at zero and a continuous distribution (Mitchell and Beauchamp, 1988). This prior works well for model selection, but some drawbacks are that it forces small signals to be exactly zero, and computational issues can make it difficult to use (Polson and Scott, 2010). There has been much interest in developing priors with continuous distributions (one group) that retain variable selection properties of the spike-and-slab (two-group) yet do so by introducing sparsity through shrinkage (Polson and Scott, 2010). This approach allows all of the coefficients to be nonzero, but most are small and only some are large. Many such shrinkage priors have been proposed, including the normal-gamma (Griffin et al., 2010), generalized double-Pareto (Armagan et al., 2013), horseshoe (Carvalho et al., 2010), horseshoe+ (Bhadra et al., 2015), and Dirichlet-Laplace (Bhattacharya et al., 2015). The Laplace prior lies somewhere between the normal prior and the spike-and-slab in its shrinkage abilities, yet most shrinkage priors of current research interest have sparsity inducing properties closer to those of the spike-and-slab. Our main interest is in comparing the Laplace prior to other shrinkage priors in the context of nonparametric smoothing.

2.2 Model Formulation

It is clear that shrinkage priors other than the lasso could represent different smoothing penalties and therefore could lead to more desirable smoothing properties. There is a large and growing number of shrinkage priors in the literature. It is not our goal to compare and characterize properties of Bayesian nonparametric function estimation under all of these priors. Instead, we wish to investigate a few well known shrinkage priors and demonstrate as proof of concept that adaptive functional estimation can be achieved with shrinkage priors. Further research can focus on improvements to these methods. What follows is a general description of our modeling approach and the specific prior formulations that will be investigated through the remainder of the paper.

We assume the n observations y_i, where i = 1, …, n, are independent and follow some distribution dependent on the unknown function values θ_i and possibly other parameters ξ at discrete points t. We further assume that the order-k forward differences in the function parameters, Δ^kθ_j, where j = 1, …, n − k, are independent and identically distributed conditional on a global scale parameter which is a function of the smoothing parameter λ. These assumptions result in the following general hierarchical form:

$$y_i\mid {\theta }_i,\mathit{\xi }~p(y_i\mid {\theta }_i,\mathit{\xi }),{\mathrm{\Delta }}^k{\theta }_j\mid \lambda ~p({\mathrm{\Delta }}^k{\theta }_j\mid \lambda ),\lambda ~p(\lambda ),\mathit{\xi }~p(\mathit{\xi }).$$ (2)

One convenient trait of many shrinkage priors, including the Laplace, the logistic, and the t-distribution, is that they can be represented as scale mixtures of normal distributions (Andrews and Mallows, 1974; West, 1987; Polson and Scott, 2010). The conditional form of scale mixture densities leads naturally to hierarchical representations. This can allow some otherwise intractable density functions to be represented hierarchically with standard distributions and can ease computation. To take advantage of this hierarchical structure, we restrict densities p(Δ^kθ_j | λ) to be scale mixtures of normals, which allows us to induce a hierarchical form to our model formulation by introducing latent local scale parameters, τ_j. Here the order-k differences in the function parameters, Δ^kθ_j, are conditionally normally distributed with mean zero and variance ${\tau }_j^2$, and the τ_j are independent and identically distributed with a global scale parameter which is a function of the smoothing parameter λ. The distribution statement for Δ^kθ_j in Equation (2) can then be replaced with the following hierarchical representation:

$${\mathrm{\Delta }}^k{\theta }_j\mid {\tau }_j~\mathrm{N}(0,{\tau }_j^2),{\tau }_j\mid \lambda ~p({\tau }_j\mid \lambda ).$$ (3)

To complete the model specification, we place proper priors on θ₁, …, θ_k. This maintains propriety and can improve computational performance for some Markov chain Monte Carlo (MCMC) samplers. We start by setting θ₁ ~ N(μ,ω²), where μ and ω can be constants or allowed to follow their own distributions. Then for k ≥ 2 and h = 1, …, k − 1, we let ${\mathrm{\Delta }}^h{\theta }_1\mid {\alpha }_h~\mathrm{N}(0,{\alpha }_h^2)$ and α_h | λ ~ p(α_h | λ), where p(α | λ) is the same form as p(τ | λ). That is, we assume the order-h differences are independent with scale parameters that follow the same distribution as the order-k differences. For most situations, the order of k will be less than 4, so issues of scale introduced by assuming the same distribution on the scale parameters for the lower and higher order differences will be minimal. One could alternatively adjust the scale parameter of each p(α_h | λ) to impose smaller variance for lower order differences.

For the remainder of the paper we investigate two specific forms of shrinkage priors: the Laplace and the horseshoe. We later compare the performance of these two priors to the case where the order-k differences follow identical normal distributions. The following provides specific descriptions of our shrinkage prior formulations.

Laplace

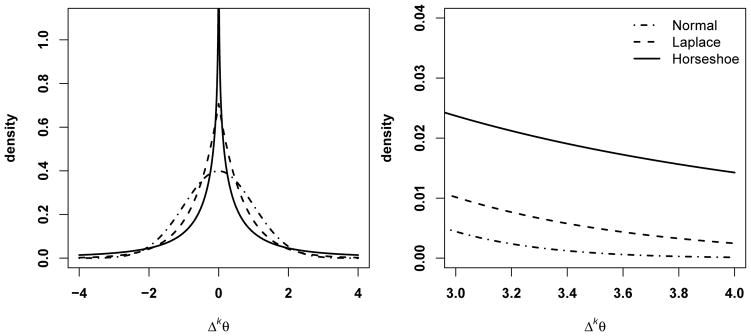
As we showed previously, this prior arises naturally from an L₁ penalty, making it the default prior for Bayesian versions of the lasso (Park and Casella, 2008) and trend filter. The Laplace distribution is leptokurtic and features high mass near zero and exponential tails (Figure 1). Various authors have investigated its shrinkage properties (Griffin et al., 2010; Kyung et al., 2010; Armagan et al., 2013). We allow the order-k differences Δ^kθ_j to follow a Laplace distribution conditional on a global scale parameter γ = 1/λ, and we allow γ to follow a half-Cauchy distribution with scale parameter ζ. That is,

Figure 1.

Shapes of prior distributions (left) and associated tail behavior (right) for priors used for p(Δ^kθ | λ).

$${\mathrm{\Delta }}^k{\theta }_j\mid \gamma ~\text{Laplace}(\gamma ),\gamma ~{\mathrm{C}}^{+}(0,\zeta ).$$ (4)

The use of a half-Cauchy prior on γ is a departure from Park and Casella (2008), who make λ² follow a gamma distribution to induce conjugacy in the Bayesian lasso. We chose to use the half-Cauchy prior on γ because its single parameter simplifies implementation, it has desirable properties as a prior on a scale parameter (Gelman et al., 2006; Polson and Scott, 2012b), and it allowed us to be consistent across methods (see horseshoe specification below). The hierarchical form of the Laplace prior arises when the mixing distribution on the square of the local scale parameter τ_j is an exponential distribution. Specifically, we specify ${\tau }_j^2\mid \lambda ~\text{Exp}({\lambda }^2/2)$ and ${\mathrm{\Delta }}^k{\theta }_j\mid {\tau }_j~\mathrm{N}(0,{\tau }_j^2)$ in the hierarchical representation.

Horseshoe

The horseshoe prior (Carvalho et al., 2010) has an infinite spike in density at zero but also exhibits heavy tails (Figure 1). This combination results in excellent performance as a shrinkage prior (Polson and Scott, 2010), and gives the horseshoe shrinkage properties more similar to the spike-and-slab variable selection prior than those of the Laplace prior. We allow the order-k differences Δ^kθ_j to follow a horseshoe distribution conditional on global scale parameter γ = 1/λ, and allow γ to follow a half-Cauchy distribution with scale parameter ζ. That is,

$${\mathrm{\Delta }}^k{\theta }_j\mid \gamma ~\text{HS}(\gamma ),\gamma ~{\mathrm{C}}^{+}(0,\zeta ).$$ (5)

The horseshoe density function does not exist in closed form, but we have derived an approximate closed-form solution using the known function bounds (see Supplementary Materials), which could be useful for application in some settings. Carvalho et al. (2010) represent the horseshoe density hierarchically as a scale mixture of normals where the local scale parameters τ_j are distributed half-Cauchy. In our hierarchical version, the latent scale parameter τ_j | γ ~ C⁺(0, γ) and then conditional on τ_j the distribution on the order-k differences is ${\mathrm{\Delta }}^k{\theta }_j\mid {\tau }_j~\mathrm{N}(0,{\tau }_j^2)$.

The horseshoe prior arises when the mixing distribution on the local scale parameter τ_j is half-Cauchy, which is a special case of a half-t-distribution where degrees of freedom (df) equal 1. Setting df > 1 would result in a prior with lighter tails than the horseshoe, and setting 0 < df < 1 would result in heavier tails. We tested half-t formulations with df between 1 and 5 in test scenarios, but did not find an appreciable difference in performance relative to the horseshoe. We also attempted to place a prior distribution on the df parameter, but found the data to be insufficient to gain information in the posterior for df in our test scenarios, so we did not pursue this further.

Normal

The normal distribution arises as a prior on the order-k differences when the penalty in the penalized likelihood formulation is a squared L₂ penalty. The normal prior is also the form of prior used in Bayesian smoothing splines. The normal is not considered a shrinkage prior and does not have the flexibility to allow locally adaptive smoothing behavior. We use it for comparison to demonstrate the local adaptivity allowed by the shrinkage priors. For our investigations, the distribution on the order-k differences and associated scale parameter is:

$${\mathrm{\Delta }}^k{\theta }_j\mid \gamma ~\mathrm{N}(0,{\gamma }^2),\gamma ~{\mathrm{C}}^{+}(0,\zeta ).$$ (6)

2.3 Connections to Markov Random Fields

Here we briefly show the models represented by (2) can be expressed with GMRF priors for θ conditional on the local scale parameters τ. It is instructive to start with the normal increments model (6), which belongs to a class of time series models known as autoregressive models of order k. Rue and Held (2005) call this model a k-th order random walk and show that it is a GMRF with respect to a k-th order chain graph — a graph with nodes {1, 2, …, n}, where the nodes i ≠ j are connected by an edge if and only if |i− j| ≤ k. Since the normal model (6) does not fully specify the joint distribution of θ, it is an intrinsic (improper) GMRF. We make it a proper GMRF by specifying a prior density of the first k components of θ, p(θ₁, …, θ_k). The Markov property of the model manifests itself in the following factorization:

$$p(\theta )=p({\theta }_1,\dots ,{\theta }_k)p({\theta }_{k+1}\mid {\theta }_1,\dots ,{\theta }_k)\cdots p({\theta }_n\mid {\theta }_{n-1},\dots ,{\theta }_{n-k}).$$

Equipped with initial distribution p(θ₁, …, θ_k), models (5) and (4) also admit this factorization, so they are kth order Markov, albeit not Gaussian models. However, if we condition on the latent scale parameters τ, both the Laplace and horseshoe models become GMRFs, or more specifically k-th order normal random walks. One important feature of these random walks is that each step in the walk has its own precision. To recap, under prior specifications (5) and (4) p(θ | γ) is a non-Gaussian Markov field, while p(θ | τ, γ) = p(θ | τ) is a GMRF.

Our GMRF point of view is useful in at least three respects. First, GMRFs with constant precision have been used for nonparametric smoothing in many settings (see Rue and Held (2005) for examples). GMRFs with nonconstant precision have been used much less frequently, but one important application is to the development of adaptive smoothing splines by allowing order-k increments to have nonconstant variances (Lang et al., 2002; Yue et al., 2012). The approach of these authors is very similar to our own but differs in at least two important ways. First, we specify the prior distribution on the latent local scale parameters τ_j with the resulting marginal distribution of Δ^kθ_j in mind, such as the Laplace or horseshoe distributions which arise as scale mixtures of normals. This allows a better understanding of the adaptive properties of the resulting marginal prior in advance of implementation. In contrast, Lang et al. (2002) and Yue et al. (2012) appear to choose the distribution on local scale parameters based on conjugacy and do not consider the effect on the marginal distribution of Δ^kθ_j. Second, we allow the local scale parameters τ_j to be independent, whereas Lang et al. (2002) and Yue et al. (2012) impose dependence among the scale (precision) parameters by forcing them to follow another GMRF. Allowing the local scale parameters to be independent allows the model to be more flexible and able to adapt to jumps and sharp local features. We should also note that Rue and Held (2005) in section 4.3 show that the idea of scale mixtures of normal distributions can be used with GMRFs to generate order-k differences which marginally follow a t-distribution by introducing latent local scale parameters. Although they do not pursue this further, we mention it because it bears similarity to our approach.

Second, viewing the SPMRF models as conditional GMRFs allows us to utilize some of the theoretical results and computational methods developed for GMRFs. In particular, one can take advantage of more complex forms of precision matrices such as circulant or seasonal trend matrices (see Rue and Held (2005) for examples). One can also employ the computational methods developed for sparse matrices, which speed computation times (Rue, 2001; Rue and Held, 2005). We note that simple model formulations such as the kth-order random walk models can be coded with state-space formulations based on forward differences, which speed computation times by eliminating the operations on covariance matrices necessary with multivariate Gaussian formulations.

A third advantage of connecting our models to GMRFs is that the GMRF representation allows us to connect our first-order Markov models to subordinated Brownian motion (Bochner, 1955; Clark, 1973), a type of Lévy process recently studied in the context of scale mixture of normal distributions (Polson and Scott, 2012a). Polson and Scott (2012a) use the theory of Lévy processes to develop shrinkage priors and penalty functions. Let us briefly consider a simple example of subordinated Brownian motion. Let W be a Weiner process, so that W(t + s) − W(t) ~ N(0, sσ²), and W has independent increments. Let T be a subordinator, which is a Lévy process that is non-decreasing with probability 1, has independent increments, and is independent of W. The subordinated process Z results from observing W at locations T(t). That is, Z(t) = W[T(t)]. The subordinator essentially generates a random set of irregular locations over which the Brownian motion is observed, which results in a new process. In our hierarchical representation of Laplace and horseshoe priors for the first order differences, we can define a subordinator process $T_j={\mathrm{\sum }}_{i=1}^j{\tau }_i^2$, so that the GMRF p(θ | τ) can be thought of as a subordinated Brownian motion or as a realization of a Brownian motion with unit variance on the random latent irregular grid T₁, …, T_n. The subordinated Brownian motion interpretation is not so straight forward when applied to higher-order increments, but we think this interpretation will be fruitful for extending our SPMRF models in the future. One example where this interpretation is useful is when observations occur on an irregularly spaced grid, which we explore in the following section.

2.4 Extension to Irregular Grids

So far we have restricted our model formulation to the case where data are observed at equally-spaced locations. Here we generalize the model formulation to allow for data observed at locations with irregular spacing. This situation arises with continuous measurements over time, space, or some covariate, or when gaps are left by missing observations.

For a GMRF with constant precision (normally distributed kth-order differences), we can use integrated Wiener processes to obtain the precision matrix (see Rue and Held (2005) and Lindgren and Rue (2008) for details). However, properly accounting for irregular spacing in our models with Laplace or horseshoe kth-order differences is more difficult. To use tools similar to those for integrated Wiener processes we would need to show that the processes built on Laplace and horseshoe increments maintain their distributional properties over any subinterval of a continuous measure. Polson and Scott (2012a) show that processes with Laplace or horseshoe first-order increments can be represented as subordinated Brownian motion. However, to meet the necessary condition of an infinitely divisible subordinator, the subordinator for the Laplace process needs to be on the precision scale and the subordinator for the horseshoe process needs to be on the log-variance scale. Both resulting processes are Lévy process, which means they have independent and stationary increments, but the increments are no longer over the continuous measure of interest. This makes representation of these processes over continuous time difficult and development of the necessary theory is out of the scope of this paper.

Absent theory to properly address this problem, we instead start with our hierarchical model formulations and assume that conditional on a set of local variance parameters τ, we can use methods based on integratedWiener processes to obtain the precision matrices for the latent GMRFs. This requires the assumption that local variances are constant within respective intervals between observations. Let s₁ < s₂ < … < s_n be a set of locations of observations, and let δ_j = s_j+1 − s_j be the distance between adjacent locations. We assume we have a discretely observed continuous process and denote by θ(s_j) the value of the process at location s_j. For the first-order model and some interval [s_j, s_j+1], we assume that conditional on local variance τ_j, θ(s) follows a Wiener process where $\theta (s_j+h)-\theta (s_j)\mid {\tau }_j~\mathrm{N}(0,h{\tau }_j^2)$ for all 0 ≤ h ≤ δ_j. If we let Δθ_j = θ(s_j+1) − θ(s_j), the resulting variance of Δθ_j is

$$\text{Var}(\mathrm{\Delta }{\theta }_j)={\delta }_j{\tau }_j^2.$$

Note that the resulting marginal distribution of θ(s_j +h)−θ(s_j) after integrating over τ_j is therefore assumed to be Laplace or horseshoe for all h, with the form of the marginal distribution dependent on the distribution of τ_j. We know this cannot be true in general given the properties of these distributions, but we assume it approximately holds for h ≤ δ.

The situation becomes more complex for higher order models. We restrict our investigations to the second-order model and follow the methods of Lindgren and Rue (2008), who use a Galerkin approximation to the stochastic differential equation representing the continuous process. The resulting formula for a second-order increment becomes

$${\mathrm{\Delta }}^2{\theta }_j=\theta (s_{j+2})-\left(1+\frac{{\delta }_{j+1}}{{\delta }_j}\right)\theta (s_{j+1})+\frac{{\delta }_{j+1}}{{\delta }_j}\theta (s_j),$$

and the variance of a second-order increment conditional on τ_j is

$$\text{Var}({\mathrm{\Delta }}^2{\theta }_j)=\frac{{\delta }_{j+1}^2({\delta }_j+{\delta }_{j+1})}{2}{\tau }_j^2.$$

This adjustment of the variance results in good consistency properties for GMRFs with constant precision (Lindgren and Rue, 2008), so should also perform well over intervals with locally constant precision. We show in the Supplementary Materials that integrating over the local scale parameter τ_j maintains the distance correction as a multiplicative factor on the scale of the resulting marginal distribution. We also provide a data example involving a continuous covariate in the Supplementary Materials where we apply the methods above for irregular grids.

2.5 Posterior Computation

Since we have two general model formulations, marginal and hierarchical, we could use MCMC to approximate the posterior distribution of heights of our piecewise step functions, θ, by working with either one of the two corresponding posterior distributions. The first one corresponds to the marginal model formulation:

$$p(\mathit{\theta },\gamma ,\mathit{\xi }\mid \mathbf{y})\propto \prod _{i=1}^{n}p(y_i\mid {\theta }_i,\mathit{\xi })p(\mathit{\theta }\mid \gamma )p(\mathit{\xi })p(\gamma ),$$ (7)

where p(θ | γ) is a Markov field induced by the normal, Laplace, or horseshoe densities, and p(γ) is a half-Cauchy density. Note that a closed-form approximation to the density function for the horseshoe prior (see Supplementary Materials) is needed for the marginal formulation using the horseshoe. The second posterior corresponds to the hierarchical model with latent scale parameters τ:

$$p(\mathit{\theta },\tau ,\gamma ,\mathit{\xi }\mid \mathbf{y})\propto \prod _{i=1}^{n}p(y_i\mid {\theta }_i,\mathit{\xi })p(\mathit{\theta }\mid \mathit{\tau })\prod _{j=1}^{n-k}p({\tau }_j\mid \gamma )p(\mathit{\xi })p(\gamma ),$$ (8)

where p(θ | τ) is a GMRF and the choice of p(τ_j | γ) makes the marginal prior specification for θ correspond either to a Laplace or to a horseshoe Markov random field. Notice that the unconditional GMRF (normal prior) has only the marginal specification.

Both of the above model classes are highly parameterized with dependencies among parameters induced by differencing and the model hierarchy. It is well known that high-dimensional, hierarchical models with strong correlations among parameters can create challenges for standard MCMC samplers, such as component-wise random walk Metropolis or Gibbs updates. When faced with these challenges, random walk behavior can result in inefficient exploration of the parameter space, which can lead to poor mixing and prohibitively long convergence times. Many approaches have been proposed to deal with these issues, including block updating (Knorr-Held and Rue, 2002), elliptical slice sampling (Murray et al., 2010; Murray and Adams, 2010), the Metropolis adjusted Langevin algorithm (MALA) (Roberts and Stramer, 2002), and Hamiltonian Monte Carlo (HMC) (Duane et al., 1987; Neal, 1993, 2011). All of these approaches jointly update some or all of the parameters at each MCMC iteration, which usually improves mixing and speeds up convergence of MCMC. Among these methods, HMC offered the most practical choice due to its ability to handle a wide variety of models and its relative ease in implementation via readily availble software such as stan (Carpenter et al., 2016). We used a modification of HMC proposed by Hoffman and Gelman (2014) which automatically adjusts HMC tuning parameters. We used the open source package rstan (Stan Development Team, 2015a), which provides a platform for fitting models using HMC in the R computing environment (R Core Team, 2014).

Even with HMC, slow mixing can still arise with hierarchical models and heavy-tailed distributions due to the inability of a single set of HMC tuning parameter values to be effective across the entire model parameter space. Fortunately this problem can often be remedied by model reparameterizations that change the geometry of the sampled parameter space. For hierarchical models, the non-centered parameterization methods described by Papaspiliopoulos et al. (2003, 2007) and Betancourt and Girolami (2015) can be useful. Non-centered parameterizations break the dependencies among parameters by introducing deterministic transformations of the parameters. The MCMC algorithm then operates directly on the independent parameters. Betancourt and Girolami (2015) discuss non-centered parameterizations in the context of HMC, and further examples of these and other reparameterization methods that target heavy-tailed distributions are provided in the documentation for stan (Stan Development Team, 2015b).

We note that after employing reparameterizations, HMC with stationary distribution equal to the hierarchical model posterior (8) had good convergence and mixing properties for each of our models and in nearly all of our numerical experiments. HMC that targeted the marginal model posterior (7) had fast run times and good mixing for the normal and Laplace formulations, but we could not effectively reparameterize the (approximate) marginal horseshoe distribution to remove the effects of its heavy tails, which resulted in severe mixing problems for the marginal horseshoe-based model. Therefore, in the rest of the manuscript we work with the hierarchical model posterior distribution (8) for all models.

For SPMRF and GMRF models, the computation time needed to evaluate the log-posterior and its gradient scales as 𝒪(n), where n is the grid size. However, the hierarchical SPMRF models have approximately twice as many parameters as the GMRF or marginal SPMRF models. These hierarchical SPMRF methods are therefore slower than their GMRF counterparts. Since the computational cost of evaluating the log-posterior is only one factor determining the MCMC speed, we compared run times of the SPMRF and GMRF models on simulated and real data (see Supplementary Materials). Our results show that SPMRF models are slower than GMRFs, but not prohibitively so.

We developed an R package titled spmrf which allows for easy implementation of our models via a wrapper to the rstan tools. The package code is publicly available at https://github.com/jrfaulkner/spmrf.

3 Simulation Study

3.1 Simulation Protocol

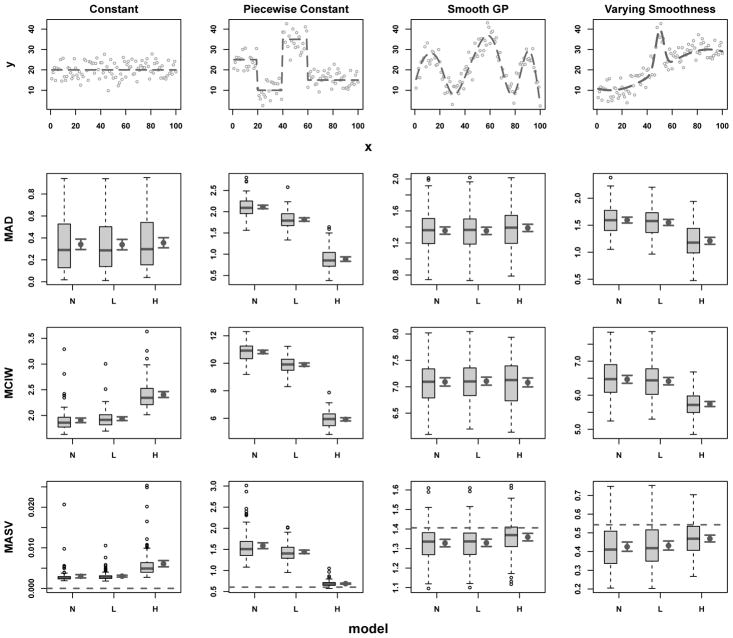
We use simulations to investigate the performance of two SPMRF formulations using the Laplace and horseshoe shrinkage priors described in section (2.2) and compare results to those using a normal distribution on the order-k differences. We refer to the shrinkage prior methods as adaptive due to the local scale parameters, and the method with normal prior as non-adaptive due to the use of a single scale parameter. We constructed underlying trends with a variety of characteristics following approaches similar to those of other authors (Scheipl and Kneib, 2009; Yue et al., 2012; Zhu and Dunson, 2013). We investigated four different types of underlying trend (constant, piecewise constant, smooth function, and function with varying smoothness). The first row of Figure 2 shows examples of the trend functions, each illustrated with simulated normal observations centered at the function values over a regular grid. We used three observation types for each trend type where the observations were conditionally independent given the trend function values θ_i, where i = 1, …, n. The observation distributions investigated were 1) normal: y_i | θ_i ~ N(θ_i, σ²), where σ = 1.5 or σ = 4.5; 2) Poisson: y_i | θ_i ~ Pois(exp(θ_i)); and 3) binomial: y_i | θ_i ~ Binom(m, (1 + exp(−θ_i))⁻¹), where m = 20 for all scenarios.

Figure 2.

Functions used in simulations and simulation results by model (N=normal, L=Laplace, H=horseshoe) and function type for normally distributed data with σ = 4.5. Top row shows true functions (dashed lines) with example simulated data. Remaining rows show mean absolute deviation (MAD), mean credible interval width (MCIW), and mean absolute sequential variation (MASV). Horizontal dashed line in plots on bottom row is the true mean absolute sequential variation (TMASV). Shown for each model are standard boxplots of simulation results (left) and mean values with 95% frequentist confidence intervals (right).

Note that we constructed the function values for the scenarios with normally distributed observations so that each function would have approximately the same mean and variance, where the mean and variance were calculated across the function values realized at the discrete time points. This allowed us to specify observation variances which resulted in the same signal-to-noise ratio for each function, where signal-tonoise ratio is defined as the standard deviation of function values divided by the standard deviation of observations. The signal-to-noise ratios for our scenarios with normal observations were 6 for σ = 1.5 and 2 for σ = 4.5. We chose the mean sizes for the Poisson scenarios and sample sizes for the binomial scenarios so that the resulting signal-to-noise ratios would be similar to those for the normal scenarios with σ = 4.5. These levels allowed us to assess the ability of the models to adapt to local features when the signal is not overwhelmed by noise. We describe the trend functions further in what follows.

Constant

This scenario uses a constant mean across all points. We use this scenario to investigate the ability of each method to find a straight horizontal line in the presence of noisy data. The values used for the constant mean were 20 for normal and Poisson observations, and 0.5 for binomial observations.

Piecewise constant

This type of function has been used by Tibshirani (2014) and others such as Scheipl and Kneib (2009) and Zhu and Dunson (2013). The horizontal trends combined with sharp breaks offer a difficult challenge for all methods. For the scenarios with normal or Poisson observations, the function values were 25, 10, 35, and 15 with break points at t ∈ {20, 40, 60}. For the binomial observations the function values on the probability scale were 0.65, 0.25, 0.85, and 0.45 with the same break points as the other observation types.

Smooth trend

We use this as an example to test the ability of the adaptive methods to handle a smoothly varying function. We generated the function f as a GP with squared exponential covariance function. That is, f ~ GP(μ, Σ), ${\mathrm{\sum }}_{i,j}={\sigma }_f^{2}exp\left[-{(t_j-t_i)}^2/(2{\rho }^2)\right]$, where Σ_{i, j} is the covariance between points i and j, ${\sigma }_f^2>0$ is the signal variance and ρ > 0 is the length scale. We set μ = 10, ${\sigma }_f^2=430$, and ρ = 10 for the scenarios with normal or Poisson observations. For binomial observations, f was generated in logit space with μ = −0.5, ${\sigma }_f^2=3$, and ρ = 10 and then back-transformed to probability space. For all scenarios the function was generated with the same random number seed.

Varying smoothness

This function with varying smoothness was initially presented by DiMatteo et al. (2001) and later used by others, including Yue et al. (2012). We adapted the function to a uniform grid, t ∈ [1, n], where n = 100 in our case, resulting in the function

$$g(t)=sin\left(\frac{4t}{n}-2\right)+2exp\left(-30{\left(\frac{4t}{n}-2\right)}^2\right).$$

For the normal and Poisson observations we made the transformation f (t) = 20 + 10g(t). For binomial observations we used f (t) = 1.25g(t) on the logit scale.

We generated 100 datasets for each combination of trend and observation type. This number of simulations was sufficient to identify meaningful differences between models without excessive computation time. Each dataset had 100 equally-spaced sample points over the interval [1, 100]. For each dataset we fit models representing three different prior formulations for the order-k differences, which were 1) normal, 2) Laplace, and 3) horseshoe. We used the hierarchical prior representations for these models given in Section 2.2. We selected the degree of k-th order differences for each model based on knowledge of the shape of the underlying function. We fit first-order models for the constant and piecewise constant functions, and we fit second-order models for the smooth and varying smooth functions. For the scenarios with normal observations, we set σ ~ C⁺ (0, 5). In all cases, θ₁ ~ N(μ,ω²), where μ is set to the sample mean and ω is two times the sample standard deviation of the observed data transformed to match the scale of θ. We also set γ ~ C⁺ (0, 0.01) for all models.

We used HMC to approximate the posterior distributions. For each model we ran four independent chains with different randomly generated starting parameter values and initial burn-in of 500 iterations. For all scenarios except for normal observations with σ = 1.5, each chain had 2,500 posterior draws post-burn-in that were thinned to keep every 5th draw. For scenarios with normal observations with σ = 1.5, chains with 10,000 iterations post-burn-in were necessary, with additional thinning to every 20th draw. In all cases, these settings resulted in 2,000 posterior draws retained per model. We found that these settings consistently resulted in good convergence properties, where convergence and mixing were assessed with a combination of trace plots, autocorrelation values, effective sample sizes, and potential scale reduction statistics (Gelman and Rubin, 1992).

We assessed the relative performance of each model using three different summary statistics. We compared the posterior medians of the trend parameters (θ̂_i) to the true trend values (θ_i) using the mean absolute deviation (MAD):

$$\text{MAD}=\frac{1}{n}\sum _{i=1}^n\mid {\widehat{\theta }}_i-{\theta }_i\mid .$$ (9)

We assessed the width of the 95% Bayesian credible intervals (BCIs) using the mean credible interval width (MCIW):

$$\text{MCIW}=\frac{1}{n}\sum _{i=1}^n{\widehat{\theta }}_{97.5,i}-{\widehat{\theta }}_{2.5,i},$$ (10)

where θ̂_97.5,i and θ̂_2.5,i are the 97.5% and 2.5% quantiles of the posterior distribution for θ_i. We also computed the mean absolute sequential variation (MASV) of θ̂ as

$$\text{MASV}=\frac{1}{n-1}\sum _{i=1}^{n-1}\mid {\widehat{\theta }}_{i+1}-{\widehat{\theta }}_i\mid .$$ (11)

We compared the observed MASV to the true MASV (TMASV) in the underlying trend function, which is calculated by substituting true θ’s into equation for MASV.

3.2 Simulation Results

In the interest of space, we emphasize results for the scenarios with normally distributed observations with σ = 4.5 here. This level of observation variance was similar to that for Poisson and binomial observations and therefore offered results similar to those scenarios. We follow these results with a brief summary of results for the other observation types, and we provide further summary of other results in the Supplementary Materials.

Constant

The three models performed similarly in terms of absolute value of all the metrics (Table 1 and Figure 2), but the Laplace and normal models were slightly better at fitting straight lines than the horseshoe. This is evidenced by the fact that the horseshoe had larger MCIW and larger MASV than the other methods. The first column of plots in Figure 3 provides a visual example of the extra variation exhibited by the horseshoe.

Table 1.

Mean values of performance measures across 100 simulations for normal observations (σ = 4.5) for each model and trend function type.

Function	Model	MAD	MCIW	MASV	TMASV
Constant	Normal	0.341	1.904	0.003	0.000
	Laplace	0.339	1.937	0.003	0.000
	Horseshoe	0.356	2.406	0.006	0.000
Piecewise Const.	Normal	2.112	10.826	1.587	0.606
	Laplace	1.816	9.899	1.441	0.606
	Horseshoe	0.886	5.919	0.689	0.606
Smooth	Normal	1.355	7.092	1.328	1.406
	Laplace	1.352	7.106	1.329	1.406
	Horseshoe	1.389	7.081	1.359	1.406
Varying Smooth	Normal	1.596	6.467	0.426	0.543
	Laplace	1.552	6.413	0.432	0.543
	Horseshoe	1.211	5.743	0.470	0.543

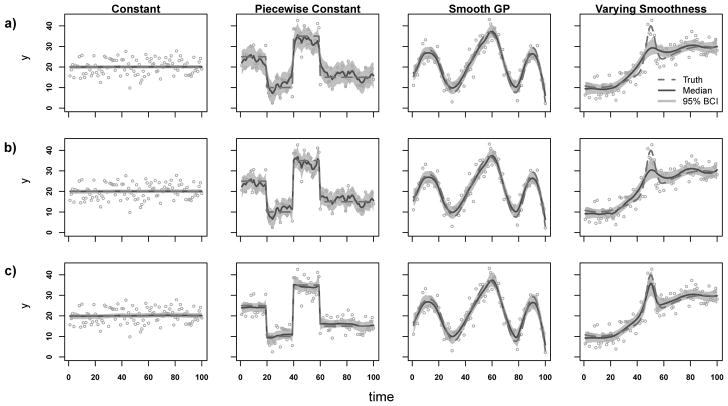
Figure 3.

Example fits for models using a) normal, b) Laplace, and c) horseshoe priors where observations are drawn from normal distributions with SD = 4.5. Plots show true functions (dashed gray lines), posterior medians (solid dark gray lines), and associated 95% Bayesian credible intervals (BCI; gray bands) for each θ. Values between observed locations are interpolated for plotting.

Piecewise constant

The horseshoe model performed the best in all categories for this scenario and the normal model performed the worst (Table 1 and Figure 2). The Laplace model was closer to the normal model in performance. The horseshoe was flexible enough to account for the large function breaks yet still able to limit variation in the constant segments. Example fits for the piecewise constant function are shown in the second column of plots in Figure 3.

Smooth trend

The different models were all close in value of the performance metrics for the smooth trend scenario (Table 1 and Figure 2). The normal and Laplace models had smallest MAD, but the horseshoe had MSAV closer to the true MSAV. The fact that the values of the metrics were similar for all models suggests that not much performance is lost in fitting a smooth trend with the adaptive methods in comparison to non-adaptive.

Varying Smoothness

Again the models all performed similarly in terms of absolute value of the metrics, but there was a clear ordering among models in relative performance (Table 1 and Figure 2). The horseshoe model performed the best relative to the other models on all metrics. This function forces a compromise between having large enough local variance to capture the spike and small enough local variance to remain smooth through the rest of the function. The horseshoe was more adaptive than the other two methods and therefore better able to meet the compromise. The plots in the last column of Figure 3 provide example fits for this function.

The results for the scenarios with normal observations with σ = 1.5 and Poisson and binomial observations (see Supplementary Materials) showed similar patterns to those with normal observations and σ = 4.5. For the constant function, the normal prior performed the best and the horseshoe prior the worst, although differences in terms of absolute values of the performance metrics were small. The relative differences were more pronounced with the scenarios with normal observations with σ = 1.5. For the piecewise constant function, the horseshoe prior performed the best for all scenarios and the normal prior the worst. All methods performed similarly for the smooth function, with the normal and Laplace generally performing a little better than the horseshoe. For the function with varying smoothness, the horseshoe performed the best and the normal the worst for all scenarios.

4 Data Examples

Here we provide two examples of fitting SPMRF models to real data. Each example uses a different probability distribution for the observations. The first example exhibits a change point, which makes it amenable to adaptive smoothing methods. The second example has a more uniformly smooth trend but also shows a period of rapid change, so represents a test for all methods. First we address the issue of setting the hyperparameter for the global smoothing parameter.

4.1 Parameterizing the Global Smoothing Prior

The value of the global smoothing parameter λ determines the precision of the marginal distributions of the order-k differences, which influences the smoothness of the estimated trend. Selection of the global smoothing parameter in penalized regression models is typically done via cross-validation in the frequentist setting (Tibshirani, 1996) or marginal maximum likelihood in the empirical Bayes setting (Park and Casella, 2008). Our fully Bayesian formulation eliminates the need for these additional steps, but in turn requires selection of the hyperparameter controlling the scale of the prior on the smoothing parameter. The value of this hyperparameter will depend on the order of the model, the grid resolution, and the variability in the latent trend parameters. Therefore, a single hyperparameter value cannot be used in all situations. Some recent studies have focused on methods for more careful and principled specification of priors for complex hierarchical models (Fong et al., 2010; Simpson et al., 2014; Sørbye and Rue, 2014). The method of Sørbye and Rue (2014) was developed for intrinsic GMRF priors and we adapt their approach to our specific models in what follows.

We wish to specify values of the hyperparameter ζ for various situations, where the global scale parameter γ ~ C⁺ (0, ζ). Let Q be the precision matrix for the Markov random field corresponding to the model of interest (see Supplementary Materials for examples), and Σ = Q⁻¹ be the covariance matrix with diagonal elements Σ_ii. The marginal standard deviation of all components of θ for a fixed value of γ is σ_γ(θ_i) = γσ_ref(θ), where σ_ref(θ) is the geometric mean of the individual marginal standard deviations when γ = 1 (Sørbye and Rue, 2014). We want to set an upper bound U on the average marginal standard deviation of θ_i, such that Pr(σ_γ(θ_i) > U) = α, where α is some small probability. Using the cumulative probability function for a half-Cauchy distribution, we can find a value of ζ for a given value of σ_ref(θ) specific to a model of interest and given common values of U and α by:

$$\zeta =\frac{U}{{\sigma }_{\text{ref}}(\mathit{\theta })tan\left(\frac{\pi }{2}(1-\alpha )\right)}.$$ (12)

By standardizing calculations to be relative to the average marginal standard deviation, the methods of Sørbye and Rue (2014) allow us to easily calculate ζ for a model of different order or a model with a different density of grid points. For practical purposes we apply the same method to the normal and SPMRF models. This is not ideal in terms of theory, however, since the horseshoe distribution has infinite variance and the corresponding SPMRF will clearly not have the same marginal variance as a GMRF. This is not necessarily problematic since GMRF approximation will result in an estimate of ζ under the horseshoe SPMRF which is less informative than would result under similar methods derived specifically for the horseshoe SPMRF, and could therefore be seen as more conservative in terms of guarding against over smoothing. In contrast, the Laplace SPMRF has finite marginal variance that is well approximated by the GMRF methods. We apply these methods in the data examples that follow.

4.2 Coal Mining Disasters

This is an example of estimating the time-varying intensity of an inhomogeneous Poisson process that exhibits a relatively rapid period of change. The data are on the time intervals between successive coal-mining disasters, and were originally presented by Maguire et al. (1952), with later corrections given by Jarrett (1979) and Raftery and Akman (1986). We use the data format presented by Raftery and Akman (1986). A disaster is defined as an accident involving 10 or more deaths. The first disaster was recorded in March of 1851 and the last in March of 1962, with 191 total event times during the period 1 January, 1851 through 31 December, 1962. Visual inspection of the data suggests a decrease in rate of disasters over time, but it is unclear by eye alone whether this change is abrupt or gradual. The decrease in disasters is associated with a few changes in the coal industry at the time. A sharp decline in labor productivity at the end of the 1880’s is thought to have decreased the opportunity for disasters, and the formation of the Miner’s Federation, a labor union, in late 1889 brought added safety and protection to the workers (Raftery and Akman, 1986).

This data set has been of interest to various authors due to uncertainty in the timing and rate of decline in disasters and the computational challenge presented by the discrete nature of the observations. Some authors have fit smooth curves exhibiting gradual change (Adams et al., 2009; Teh and Rao, 2011) and others have fit change-point models with abrupt, instantaneous change (Raftery and Akman, 1986; Carlin et al., 1992; Green, 1995). An ideal model would provide the flexibility to automatically adapt to either scenario.

We assumed an inhomogeneous Poisson process for the disaster events and binned the event counts by year. We fit first-order models using the normal, Laplace, and horseshoe prior formulations. We assumed the event counts, y_i, were distributed Poisson conditional on the θ_i: y_i | θ_i ~ Pois (exp(θ_i)). The marginal prior distributions for the first-order increments were Δθ_j ~ N(0, γ²) for the Normal, Δθ_j ~ Laplace(γ) for the Laplace, and Δθ_j ~ HS(γ) for the horseshoe. We used the same prior specifications as those used in the simulations for the remaining parameters, except we used the guidelines in Section 4.1 to set the hyperparameter on the global scale prior. Using calculations outlined in the Supplementary Materials, we set σ_ref(θ) = 6.47 and U = 0.860. Setting α = 0.05 and substituting into Equation (12) results in ζ = 0.0105, so γ ~ C⁺(0, 0.0105) for each model. We used HMC for approximating the posterior distributions. For each model we ran four independent chains, each with a burn-in of 500 followed by 6,250 iterations thinned at every 5. This resulted in a total of 5,000 posterior samples for each model. We were interested in finding the best representation of the process over time as well as finding the most likely set of years associated with the apparent change point. For this exercise we arbitrarily defined a change point as the maximum drop in rate between two consecutive time points.

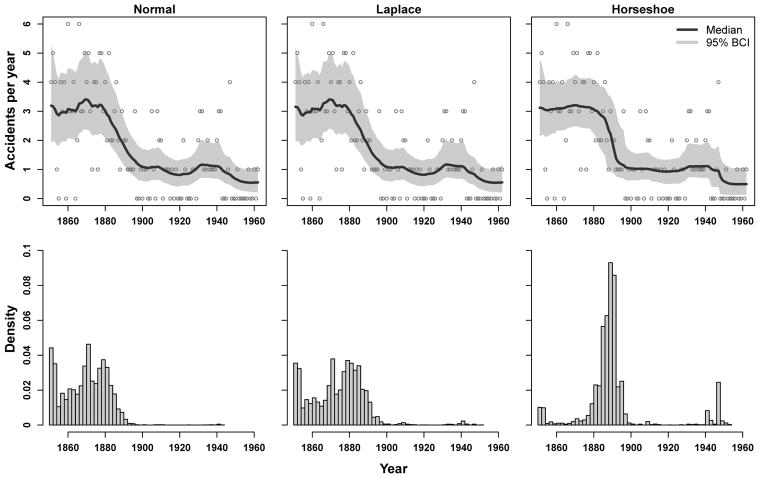
Plots of the fitted trends (Figure 4) indicate that the horseshoe model picked up a sharper change in trend and had narrower BCIs than the other models. The normal and Laplace models did not have sufficient flexibility to allow large jumps and produced a gradual decline in accidents rate, which is less plausible than a sharp decline in light of the additional information about change in coal mining industry safety regulations. The relative qualitative performance of the normal, Laplace, and horseshoe densities is similar to that for the piecewise constant scenario from our simulation study. The posterior distributions of the change point times are shown in Figure 4. The horseshoe model clearly shows a more concentrated posterior for the break points, and that distribution is centered near the late 1880’s, which corresponds to the period of change in the coal industry. Therefore, we think the Bayesian trend filter with the horseshoe prior is a better default model in cases where sharp change points are expected.

Figure 4.

Top row: fits to coal mining disaster data for different prior distributions. Posterior medians (lines), 95% credible intervals (shaded regions), and data points are shown. Bottom row: associated posterior distributions for change points.

It is important to point out that we tried other values for the scale parameter (ζ) in the prior distribution for γ and found that the models were somewhat sensitive to that hyperparameter for this data set. In particular, the horseshoe results for ζ = 1 looked more like those for the other two models in Figure 4, but when ζ = 0.0001, the horseshoe produced more defined break points and straighter lines with narrower BCIs compared to the results with ζ = 0.01 (see Supplementary Materials).

4.3 Tokyo Rainfall

This problem concerns the estimation of the time-varying mean of an inhomogeneous binomial process. We are interested in estimating the seasonal trend in daily probability of rainfall. The data are binary indicators of when daily rainfall exceeded 1 mm in Tokyo, Japan, over the course of 39 consecutive years (1951–1989). The indicators were combined by day of year across years, resulting in a sample size of m = 39 for each of 365 out of 366 possible days, and a size of m = 10 for the additional day that occurred in each of the 10 leap years. The observation variable y is therefore a count, where y ∈ {0, 1, …, 39}. Data were obtained from the NOAA’s National Center for Climate Information (https://www.ncdc.noaa.gov). A smaller subset of these data (1983–1984) was initially analyzed by Kitagawa (1987) and later by several others, including Rue and Held (2005).

We fit SPMRF models with Laplace and horseshoe priors and a GMRF model (normal prior). All models were based on second-order differences. The observation model was

$$y_i\mid {\theta }_i~\text{Bin}\left(m_i,\frac{1}{1+exp(-{\theta }_i)}\right),$$

and the marginal prior distributions for the second-order differences were Δ²θ_j ~ N(0, γ²) for the normal prior, Δ²θ_j ~ Laplace(γ) for the Laplace, and Δ²θ_j ~ HS(γ) for the horseshoe. We used the same prior specifications as those used in the simulations for the remaining parameters, except we used the guidelines in Section 4.1 to set the hyperparameter on the global scale prior. Using calculations outlined in the Supplementary Materials, we set σ_ref(θ) = 906.7 and U = 0.679. Setting α = 0.05 and substituting into Equation (12) results in ζ = 5.89 × 10⁻⁵, so γ ~ C⁺ (0, 5.89 × 10⁻⁵) for each model. We ran four independent chains for each model, each with a burn-in of 500 followed by 6,250 draws thinned at every 5. This resulted in a total of 5,000 MCMC samples retained for each model.

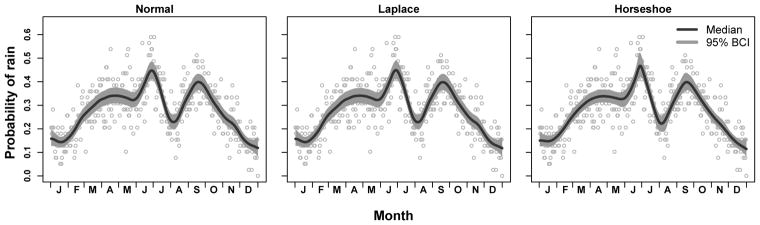
The resulting function estimates for all models reveal a sharp increase in probability of rain in June followed by a sharp decrease through July and early August and a subsequent sharp increase in late August and September (Figure 5). Changes through the rest of the months were relatively smooth. The estimated function displays some variations in smoothness similar to the function with varying smoothness used in our simulations. All methods resulted in a similar estimated function, but the horseshoe prior resulted in a smoother function that displayed sharper features at transition points in late June and early August, yet also had narrower credible intervals over most of the function. The normal and Laplace models resulted in a little more variability in the trend in January-April and in November. In their analysis of a subset of these data, Rue and Held (2005) used a circular constraint to tie together the endpoints of the function at the beginning and end of the year. We did not use such a constraint here, although it is possible with the SPMRF models. Even so, it is evident that the horseshoe model resulted in more similar function estimates at the endpoints than did the other two models.

Figure 5.

Fits to Tokyo rainfall data for different prior distributions. Posterior medians (lines), 95% credible intervals (shaded regions), and empirical probabilities (y_i/n_i) are shown.

5 Discussion

We presented a method for curve fitting in a Bayesian context that achieves locally adaptive smoothing by exploiting the sparsity-inducing properties of shrinkage priors and the smoothing properties of GMRFs. We compared the performance of the Laplace prior, which simply reformulates the frequentist trend filter to a Bayesian analog, to a more aggressive horseshoe shrinkage prior by using simulations and found that the horseshoe provided the best balance between bias and precision. The horseshoe prior has the greatest concentration of density near zero and the heaviest tails among the priors we investigated. This combination allows smooth functions to be fit in regions with weak signals or noisy data while still allowing for recovery of sharp functional changes when supported by informative data. The Laplace prior allowed more functional changes of moderate value to be retained and could not accommodate large changes without compromising the ability to shrink the noisy and smaller functional changes. This resulted in greater variability in the estimated functions and wider associated credible intervals for the models with the Laplace prior in comparison to those with the horseshoe prior when the underlying true functions had jumps or varying smoothness. The Laplace prior did have adaptive ability not possessed by the normal prior, but the horseshoe prior clearly had the best adaptive properties among the priors we investigated.

The Laplace prior performed better than the horseshoe for the constant and smooth functions in our simulations, with results closer to those of the normal prior, although the differences in performance among the three methods were relatively small. These functions do not have large deviations in order-k differences, and so there are many small or medium sized values for the estimated Δ^kθ. This situation is reflective of cases described by Tibshirani (1996) where the lasso and ridge regression perform best, which helps explain why the analogous SPMRF models with Laplace or normal prior distributions do better here. We expect that non-adaptive or mildly adaptive methods will perform better when used on functions which do not exhibit jumps or varying smoothness. However, it is reassuring that an adaptive method does nearly as well as a non-adaptive method for these functions. This allows an adaptive model such as that using the horseshoe to be applied to a variety of functions with minimal risk of performance loss.

Our fully Bayesian implementation of the SPMRF models eliminates the need to explicitly select the global smoothing parameter λ, either directly or through selection methods such as cross-validation (e.g., Tibshirani (1996)) or marginal maximum likelihood (e.g., Park and Casella (2008)). However, the fully Bayesian approach does still require attention to the selection of the hyperparameter that controls the prior distribution on the smoothing parameter. We found the methods of Sørbye and Rue (2014) to offer practical guidelines for selecting this hyperparameter, and we successfully applied a modification of those methods in our data examples. A highly informative prior on the global smoothing parameter can result in over-smoothing if the prior overwhelms the information in the data, while a diffuse prior may result in a rougher function with insufficient smoothing. Noisier data are therefore more sensitive to choice of parameterization of the prior on the global smoothing parameter. We tested prior sensitivity in the coal mining example and found that the horseshoe prior was more responsive to changes in hyperparmeter values than the normal and Laplace priors (see Supplementary Materials). However, the results for the simulations and for the Tokyo rainfall example were much more robust to the value of the hyperparameter on the global scale due to the information in the data. As a precaution, we recommend first applying methods such as those by Sørbye and Rue (2014) to set the hyperparameter, but then also paying attention to prior sensitivity when analyzing noisy data with the SPMRF models.

We only addressed one-dimensional problems here, but we think the GMRF representation of these models can allow extension to higher dimensions such as the spatial setting by incorporating methods used by Rue and Held (2005) and others. We also plan to extend these methods to semi-parametric models that allow additional covariates.