Spin- and valley-polarized one-way Klein tunneling in photonic topological insulators

We demonstrate a robust pseudospin- and valley-polarized one-way Klein tunneling and topological edge states.

Abstract

Recent advances in condensed matter physics have shown that the spin degree of freedom of electrons can be efficiently exploited in the emergent field of spintronics, offering unique opportunities for efficient data transfer, computing, and storage (1–3). These concepts have been inspiring analogous approaches in photonics, where the manipulation of an artificially engineered pseudospin degree of freedom can be enabled by synthetic gauge fields acting on light (4–6). The ability to control these degrees of freedom significantly expands the landscape of available optical responses, which may revolutionize optical computing and the basic means of controlling light in photonic devices across the entire electromagnetic spectrum. We demonstrate a new class of photonic systems, described by effective Hamiltonians in which competing synthetic gauge fields, engineered in pseudospin, chirality/sublattice, and valley subspaces, result in bandgap opening at one of the valleys, whereas the other valley exhibits Dirac-like conical dispersion. We show that this effective response has marked implications on photon transport, among which are as follows: (i) a robust pseudospin- and valley-polarized one-way Klein tunneling and (ii) topological edge states that coexist within the Dirac continuum for opposite valley and pseudospin polarizations. These phenomena offer new ways to control light in photonics, in particular, for on-chip optical isolation, filtering, and wave-division multiplexing by selective action on their pseudospin and valley degrees of freedom.

INTRODUCTION

The rich physics of electromagnetic phenomena facilitated by the internal degrees of freedom of light (for example, polarization and angular momentum) has enabled a multitude of applications, from multimode optical fibers and holography to tractor beams and topologically robust propagation (7–9). This plethora of opportunities for optical manipulation is enabled by the use of synthetic photonic potentials implemented via engineered light-matter interactions in structured materials, which allow imprinting of a specific structure to light. Periodically patterned optical media, such as photonic crystals and metamaterials (10, 11), play an important role here, allowing the emulation of a wide range of condensed matter phenomena. Suitably tailored periodicity has enabled the emergence of photonic bandgaps and, most recently, led to the discovery of photonic topological insulators (4–6, 12–27), enabling parallels with condensed matter physics that have been an inspirational driving force for photonics research.

Recent progress in spintronics has opened markedly new opportunities to manipulate spin-polarized carriers and serves as an additional example of this analogy. Engineered pseudospin in photonics has inspired significant interest as an additional degree of freedom in the context of topological electromagnetic states (4–6, 12–27). Photonic structures biased by synthetic gauge potentials selectively acting on the polarization of light, its angular momentum, or valley degrees of freedom have been used to engineer symmetry-protected topological order for photons and topologically robust pseudospin-polarized transport (24–27). More recently, coupling of pseudospin and valley degrees of freedom has been used to create spin-polarized bandgaps at the two valleys of a photonic analog of graphene (27).

To engage the full potential of spin-valley photonics, we should design a special class of materials exhibiting conducting versus insulating states for opposite photonic pseudospins and valleys. Even more intriguing properties can be achieved if the conduction takes place via photonic modes with relativistic-like Dirac spectrum. Here, we achieve, for the first time, this selectivity in systems with Dirac spectrum with respect to both pseudospin and valley degrees of freedom. In turn, this discovery allows us to nontrivially extend the space of available effective photonic potentials by coupling pseudospin, valley, and sublattice (chiral) degrees of freedom. We demonstrate these phenomena in systems with and without time-reversal symmetry (TRS), proving the existence of valley- and spin-valley–polarized one-way Dirac spectra in both circumstances. The proposed structures behave effectively as Dirac semimetals and insulators for opposite pseudospin and/or valley polarizations. These exotic optical responses emerge at the crossover between distinct topological photonic phases: (i) quantum Hall and valley Hall and (ii) quantum spin Hall and valley Hall phases. The critical points of topological transitions exhibit unusual properties at topological domain walls, where the pseudospin- and valley-polarized edge states coexist within the continuum associated with opposite polarizations.

The proposed systems to realize these effects are shown in Fig. 1 (A and B), which emulate two different scenarios without and with TRS, and represent photonic crystals with hexagonal and triangular lattices, respectively. The degeneracies with crossed linear Dirac-like dispersion in honeycomb crystals are protected by both spatial inversion symmetry (SIS) and TRS. In photonic lattices, these Dirac cones necessarily appear in pairs, unless TRS is broken. For this reason, photonic graphene exhibits a pair of Dirac cones at each valley of its Brillouin zone (28). Provided that the intervalley scattering is absent, the valleys can be used as a new degree of freedom, offering the opportunity to engineer and control electrons and photons (29–36). In particular, coupling of valley and pseudospin degrees of freedom has been proposed to generate spin-valley–coupled currents and spin-valley filtering in condensed matter physics. In photonics, the valley degree of freedom has been used to emulate spin in photonic topological insulators (6) and to separate pseudospin flows in metamaterials (27).

Fig. 1. Schematic geometries and corresponding band structures.

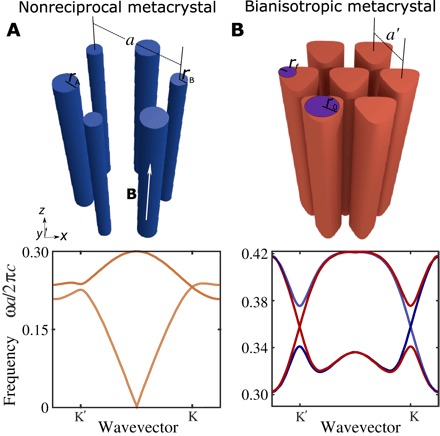
(A) Nonreciprocal two-dimensional (2D) photonic crystal composed of ferromagnetic rods arranged in a honeycomb lattice with magnetic bias applied along the z direction. (B) Topological 2D photonic crystal made of bianisotropic triangulated rods arranged in a triangular array in air. Dimensionless (normalized to lattice constants a and a′) geometric parameters of the rods are r_A = 0.191, δ = r_A − r_B = 0.01, μ = 2, κ = 0.6, ϵ_A = ϵ_B = 14 (A) and r₀ = 0.34, r_f = 0.27, ϵ_|| = μ_|| = 14, ϵ_z = μ_z = 1 (B). A bianisotropic response ξ_xy = 0.2 is introduced in the background. In (B), red bands correspond to (pseudo)spin-up states, whereas blue bands correspond to (pseudo)spin-down states.

RESULTS

Topological photonic crystals with one-way Dirac spectra

We first consider the simpler case of photonic graphene (Fig. 1A) with broken TRS—a honeycomb array of high-index ferromagnetic rods magnetized along their axes. The bipartite unit cell consists of cylinders with radii r_A and r_B with scalar permittivity ϵ in a lattice with lattice constant a. The gyromagnetic response of the ferromagnetic material is induced by a static magnetic field B₀ along the z axis, and it is described by a magnetic permeability tensor with diagonal components μ_xx = μ_yy = μ and off-diagonal components μ_xy = −μ_yx = iκ. Two types of symmetry reduction can be introduced to this system, resulting in two distinct quantum Hall–like (12, 13, 15) and valley Hall topological phases (12, 35). In the photonic graphene, the valley Hall phase is induced by the reduction of the sublattice symmetry due to the dimerization of A and B sites, that is, by making the radii unequal. The quantum Hall–like phase is attained by breaking of TRS due to magnetization. For the photonic crystals with hexagonal symmetry considered here, the spectrum hosts a pair of Dirac points at K and K′ valleys of the Brillouin zone. Both symmetry reductions induce synthetic gauge fields, leading to the inversion of bands touching at the Dirac points. As a result, the bands ascribed to nonvanishing Berry curvature and can ascribe an appropriate topological invariant—Chern or valley Chern number for magnetized and dimerized lattices, respectively (12, 35).

The effective Hamiltonian describing both states can be obtained from Maxwell’s equations using the plane-wave expansion (PWE) method (4, 11) and the k·p approximation in the vicinity of the Dirac points. Including the valley degree of freedom, the effective Hamiltonian then assumes the form (section S1.1)

$$\widehat{\mathcal{H}}={\mathit{v}}_{\mathrm{D}}{\widehat{\mathrm{\sigma }}}_{\mathit{x}}{\widehat{\mathrm{\tau }}}_{\mathit{z}}\mathrm{\delta }{\mathit{k}}_{\mathit{x}}+{\mathit{v}}_{\mathrm{D}}{\widehat{\mathrm{\sigma }}}_{\mathit{y}}{\widehat{\mathrm{\tau }}}_0\mathrm{\delta }{\mathit{k}}_{\mathit{y}}+{\widehat{\mathrm{\sigma }}}_{\mathit{z}}({\widehat{\mathrm{\tau }}}_{\mathit{z}}{\mathit{m}}_{\mathrm{T}}-{\widehat{\mathrm{\tau }}}_0{\mathit{m}}_{\mathrm{I}})$$ (1)

where ${\widehat{\mathrm{\tau }}}_{\mathit{i}}$ and ${\widehat{\mathrm{\sigma }}}_{\mathit{i}}$ are Pauli matrices in valley and sublattice degrees of freedom, δk is a deviation of the wavevector from Dirac points, and m_T and m_I are mass terms induced by TRS and SIS reductions, respectively.

The form of Hamiltonian (Eq. 1) reveals that the effective mass due to TRS breaking (m_T-term) has opposite signs at the two valleys. On the other hand, the effective mass due to SIS breaking (m_I-term) has the same sign at both valleys. This implies that one can artificially tune the structure parameters to make the masses equal m_T = m_I, thus closing the bandgap at the K point and, at the same time, doubling it at the K′ point. As a result, the dispersion at the K′ valley exhibits locally quadratic (parabolic) dispersion ${\mathrm{\Omega }}_{\pm }(\mathrm{\delta }\mathbf{k})=\pm \sqrt{{\mathit{v}}_{\mathrm{D}}^2(\mathrm{\delta }{\mathit{k}}_{\mathit{x}}^2+{\mathrm{\delta }\mathit{k}}_{\mathit{y}}^2)+{\mathit{m}}^2}$, with m = m_T + m_I, whereas the dispersion at the K valley exhibits gapless linear Dirac-like dispersion.

The second model we consider implements TRS-preserving scenario with a pseudospin degree of freedom. It represents a triangular array of triangulated bianisotropic rods. The pseudospin degree of freedom is introduced by the duality symmetry, ensured by equal electric permittivity $\widehat{\mathrm{ϵ}}$ and permeability $\widehat{\mathrm{\mu }}$ of the rods (5). The dual crystals have been shown to emulate a quantum spin Hall state for the pseudospins ψ^↑(↓) = E_z ± H_z when the bianisotropic response is introduced. The bianisotropy is described by the effective constitutive relations with magnetoelectric coupling $\mathbf{D}=\widehat{\mathrm{ϵ}}\mathbf{E}+\widehat{\mathrm{\xi }}\mathbf{H}$ and $\mathbf{B}=\widehat{\mathrm{\mu }}\mathbf{H}+{\widehat{\mathrm{\xi }}}^{†}\mathbf{E}$, where the only nonvanishing elements of the bianisotropy parameter $\widehat{\mathrm{\xi }}$ are ξ_xy = −ξ_yx = iΔ.

The duality of the crystal provides double degeneracy of the spectrum with respect to transverse electric (TE) and transverse magnetic (TM) modes, whereas its triangular symmetry ensures the presence of two overlaid Dirac points for dipolar (orbital number l = ±1) bands at each valley. The bianisotropic response has an effect analogous to spin-orbit coupling in electronic systems, and it results in band crossing of TE and TM bands and opening of topological bandgaps for both pseudospins and valleys (5). In addition, the Dirac points can be gapped by the reduction of spatial symmetry by triangulation of the rods, which has an effect analogous to the dimerization of a honeycomb (graphene) lattice, giving rise to a valley Hall photonic state (24, 35).

The effective Hamiltonian describing this structure can be again obtained from Maxwell’s equations (see section S1.2) and has the form

$$\widehat{\mathcal{H}}={\mathit{v}}_{\mathrm{D}}{\widehat{\mathrm{\sigma }}}_{\mathit{x}}{\widehat{\mathrm{\tau }}}_{\mathit{z}}{\widehat{\mathit{s}}}_0\mathrm{\delta }{\mathit{k}}_{\mathit{x}}+{\mathit{v}}_{\mathrm{D}}{\widehat{\mathrm{\sigma }}}_{\mathit{y}}{\widehat{\mathrm{\tau }}}_0{\widehat{\mathit{s}}}_0\mathrm{\delta }{\mathit{k}}_{\mathit{y}}+{\widehat{\mathrm{\sigma }}}_{\mathit{z}}({\widehat{\mathrm{\tau }}}_{\mathit{z}}{\widehat{\mathit{s}}}_{\mathit{z}}{\mathit{m}}_{\mathrm{B}}-{\widehat{\mathrm{\tau }}}_0{\widehat{\mathit{s}}}_0{\mathit{m}}_{\mathrm{I}})$$ (2)

where an additional set of Pauli matrices ${\widehat{\mathit{s}}}_{\mathrm{i}}$ corresponding to the pseudospin degree of freedom is introduced, and m_B and m_I are mass terms induced by the bianisotropy and SIS reductions, respectively.

The form of Hamiltonian (Eq. 2) suggests that the two mass terms exhibit different behaviors at the two valleys, implying that one can again artificially tune the structure parameters to equate the effective masses m_B = m_I, thus closing (doubling) the bandgap at the K point while doubling (closing) it at the K′ point for the pseudospin-up (spin-down) state. Thus, for this system, TRS invariance ensures that opposite spins exhibit Dirac-like dispersion at the two opposite valleys. As a result, the dispersion for the pseudospin-up (spin-down) state is quadratic at the K′ (K) valley, with effective mass m = m_B + m_I. Both proposed systems therefore exhibit valley-selective linear Dirac-like dispersions, which should manifest itself in peculiar wave transport properties both in the bulk and on the edges.

One-way Klein tunneling

Klein tunneling is a fascinating phenomenon in quantum mechanics, consisting in the unimpeded penetration of particles through potential barriers. It was first envisioned in relativistic quantum physics of high-energy spin-1/2 fermions (36). More recently, a prediction of this exotic chiral transport found experimental confirmation (37, 38) in junctions of graphene (39), which exhibits quasi-relativistic carrier dynamics described by the effective massless Dirac equation (40–43). The optical analog of this unique 2D material, referred to as photonic graphene, also shows unprecedented optical characteristics, and it is of eminent research interest in photonics (28, 44–46).

In the systems under investigation, Klein tunneling is expected to assume an even more exotic form—consisting in valley- and pseudospin-polarized uniform transmission through the Dirac bands. To illustrate this behavior, we performed analytical (section S2) and first-principle numerical studies of wave transmission through a photonic potential barrier introduced in the middle of a larger domain. To describe the transmission analytically, we use the description based on the effective photonic Hamiltonian obtained directly from Maxwell’s equations by applying the PWE method, along with the continuity boundary conditions across the interfaces. We consider a geometry sequence 1/2/1, where domains (1) and (2) are characterized by total masses m_1,2 and homogeneous photonic potentials u_1,2, which essentially represent unit-cell averaged dielectric parameters (see section S1 for the details). We assume the case of normal incidence k_y = 0 of the propagating wave (|Ω| > m₁) from region 1 along the x axis onto the photonic “potential barrier” of height (u₂ − u₁) and width L located in domain (2), which is assumed to be infinitely long in the y direction. The difference in effective dielectric parameters would typically give rise to impedance mismatch and reflection from such a barrier, but similar to the electronic case, the physics of Dirac bands redefines the way photons scatter in our systems. By solving for the photonic eigenmodes in each region described by the respective effective Hamiltonians and then by applying the continuity boundary conditions, we obtain the transmittance

$$\mathit{T}=\frac{4{\mathit{s}}_1^2{|{\mathit{s}}_2|}^2}{{|2{\mathit{s}}_1{\mathit{s}}_2\text{cos}(\mathrm{\delta }{\mathit{k}}_{2\mathit{x}}\mathit{L})-\mathit{i}({\mathit{s}}_1^2+{\mathit{s}}_2^2)\text{sin}(\mathrm{\delta }{\mathit{k}}_{2\mathit{x}}\mathit{L})|}^2}$$ (3)

where ${\mathit{s}}_{1,2}=\sqrt{{(\mathrm{\Omega }-{\mathit{u}}_{1,2})}^2-{\mathit{m}}_{1,2}^2}∕(\mathrm{\Omega }-{\mathit{u}}_{1,2}-{\mathit{m}}_{1,2})$ and $\mathrm{\delta }{\mathit{k}}_{2\mathit{x}}=\sqrt{{(\mathrm{\Omega }-{\mathit{u}}_2)}^2-{\mathit{m}}_2^2}/{\mathit{v}}_{\mathrm{D}}$. Assuming linear dispersion for the K valley, the well appears to be perfectly transparent in the K valley for all frequencies for any width of the barrier, which is a direct manifestation of Klein tunneling. In contrast, for the K′ valley, where the spectrum is parabolic, total transmission takes place only within the passband when the resonant condition, δk_2xL = Nπ, $\mathit{N}\in \mathbb{Z}$, is satisfied. As expected for the gap at the K′ valley, the transmittance T decreases exponentially with the depth (and width) of the well (section S2). To verify these analytical predictions, we modeled the electromagnetic response of the two proposed crystals in Fig. 1 using the finite element method solver in COMSOL Multiphysics.

Valley-polarized Klein tunneling in photonic topological crystal with broken TRS

In Fig. 2A (top), we show the two lowest TM bands of the honeycomb crystal of Fig. 1A for the case when the magnetic field is absent and the rods in the unit cell are identical. Because time and space inversion symmetries are preserved, the band structure is reciprocal with respect to the wavevector k_x, and the band diagram features a pair of Dirac bands with nearly linear dispersion crossing at $\mathrm{K}(\frac{4\mathrm{\pi }}{3\mathit{a}},0)$ and $\mathrm{K}\prime (-\frac{4\mathrm{\pi }}{3\mathit{a}},0)$ points. In Fig. 2A (middle), we show the dispersion of the same structure with TRS and SIS broken by applying opposite magnetization in the two cylinders of each unit cell. In this case, the dispersion exhibits two slightly nonreciprocal Dirac cones with slightly detuned frequencies, due to the applied magnetic bias. This magnetization preserves parity-time (PT) symmetry so that Dirac-like dispersion is maintained.

Fig. 2. One-way Klein tunneling in nonreciprocal photonic topological insulator.

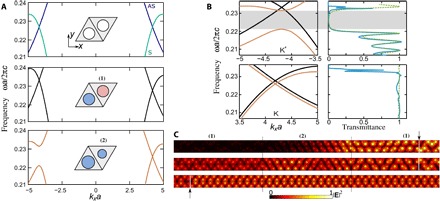
(A) Dispersion bands for a symmetric (nondimerized) structure of nonmagnetized rods (μ = 2, κ = 0) (top), a nonreciprocal PT-preserving crystal where cylinders of equal radii are magnetized in opposite directions (μ = 2, κ = 0.6) (middle), and a nonreciprocal PT-violating crystal where cylinders of slightly detuned radii are magnetized in the same direction (parameters are as in Fig. 1) (bottom). (B) Photonic bands near K and K′ points (left) and transmission coefficients (right). Top and bottom panels correspond to the backward and forward wave propagation, respectively. Numerically calculated transmission is plotted with a blue line. The analytically retrieved dependence with second-order correction in k·p method is shown with a green dashed line. The fitting parameters of the spectra extracted from the numerically calculated band diagrams are as follows: At the top (K′ valley), the frequency of the Dirac crossing at the K′ point ω₀a/2πc = 0.233, and Fermi velocity v_D/2πc = 0.020. In domain (1), u₁ = 0, m₁ = 0, α₁ = −0.12v_D, β₁ = 0.54v_D; in domain (2), u₂a/2πc = −0.007, m₂a/2πc = 0.005, α₂ = −0.005v_D, β₂ = 0.06v_D;. At the bottom (K valley), parameters are the same as those in domain (1) at the K′ valley, except that the frequency of the Dirac crossing at the K point becomes ω₀a/2πc = 0.228, and in domain (2), m₂ = 0, u₂a/2πc = −0.004. α_i, β_i are the coefficients of ${\mathrm{\sigma }}_0{\mathrm{\delta }\mathit{k}}_{\mathit{x}}^2,{\mathrm{\sigma }}_{\mathit{x}}{\mathrm{\delta }\mathit{k}}_{\mathit{x}}^2$ in the effective Hamiltonian with their numerical values expressed in term of v_D. (C) Simulated electric field intensity |E|² distributions in the strip for backward (top and middle) and forward (bottom) wave propagation. The strip consists of three domains: Domain (1) is the nonreciprocal PT-preserving honeycomb lattices and separated by domain (2), which is composed of the inequivalent-sites lattice with magnetic field applied perpendicular to the lattice, and domains (1) and (2) contain 2 × 42 and 2 × 12 unit cells, respectively. The boundaries of three crystal regions are marked by black vertical lines. The modes are excited by current sheets at cuts indicated by the arrows and white lines.

Finally, we introduce valley-chirality coupling in the system (Fig. 2A, bottom). First, we dimerize the structure by applying a small detuning in the cylinders with radii r_A(B) = r ± δ/2, therefore breaking SIS and inducing a valley Hall state. Second, we break TRS by magnetizing both A and B sites in the same direction, which drives the system in a quantum Hall–like state. We now observe nonreciprocal Dirac spectra ω(k) ≠ ω(−k). Next, we tune the parameter δ such that the effects of magnetization and dimerization cancel out for positive values of k_x (K-valley), thus closing the gap but amplifying the bandgap for negative values of k_x (K′ valley). This one-way nonreciprocal response is shown in the photonic band structure in Fig. 2A (bottom), and it reveals the presence of a one-way Dirac cone.

For the band structures at the K′ valley (k_x < 0) of two nonreciprocal crystals, plotted in Fig. 2B (upper left), we observe an overlay of the Dirac and gapped bands, whereas for the ones at the K valley (k_x > 0), plotted in Fig. 2B (lower left), two nearly overlapping Dirac cones appear in the spectrum. We use these nonreciprocal photonic band structures to design a large-scale photonic transport, an analog of Klein tunneling, in a supercell that consists of three adjacent domains separated by zigzag cuts. The two side domains are constructed from the nonreciprocal PT-preserved crystal (gapless spectrum at both K and K′ valleys). The middle domain is made of the nonreciprocal PT-violating crystal exhibiting a one-way Dirac cone, and it also effectively behaves as a potential well for propagating waves due to the spectral shift of the photonic bands between the domains (Fig. 2B, bottom). To calculate the transmission through the potential well, we use a pair of current sheets located in the side regions, which selectively excite modes with positive and negative group velocities at K and K′ valleys, respectively. As expected for Klein tunneling, the calculated transmission is close to unity for the K valley (forward propagation) across a wide frequency range, as illustrated in Fig. 2B (lower right). Only at higher frequencies, where the band becomes parabolic due to the presence of the higher-order bandgap, the transmission starts to fall off. In contrast, we see that for the K′ valley (backward propagation), Klein tunneling is not observed, and the transmission rapidly drops to zero in the bandgap region, which is consistent with the band structure in Fig. 2B (upper left). At the same time, transmission through the parabolic passband at the K′ valley exhibits numerous resonances, intermitted by regions of low transmission. These first-principle results were subsequently fitted with the use of Eq. 3 by assuming m₁ = u₁ = 0 (and optimizing other fitting parameters), with the result plotted in Fig. 2B (green dashed line). Analytical and numerical results are in excellent qualitative agreement, confirming the origin of the observed valley-polarized one-way Klein tunneling.

Inspection of the field profiles in Fig. 2C, obtained by first-principle simulations at different frequencies, provides additional details explaining the markedly different wave transport behavior at the two valleys. Thus, when the structure is excited from the right edge (K′-valley case) of the domain (as indicated by a black arrow), at the frequency within the bandgap, the excited wave experiences an exponential decay in the middle region (Fig. 2C, top). At the lower frequency, a standing wave pattern is formed in the middle region (Fig. 2C, middle), explaining the resonant transmission at certain frequencies. Conversely, when the system is excited from the left (K-valley case), a uniform field distribution is observed over the whole structure (Fig. 2C, bottom). The wave travels toward the right without decay, featuring the analog of one-way Klein tunneling in this magneto-optical photonic crystal.

Spin-valley–polarized one-way Klein tunneling in TRS-invariant photonic topological insulator

We switch now to the TRS-invariant photonic crystal in Fig. 1B. We calculate the photonic band structure of a triangular lattice of circular rods preserving the duality ϵ = μ, which exhibits a pair of overlaid Dirac spectra at both K and K′ valleys, plotted in Fig. 3A (top). The inversion symmetry reduction is achieved, triangulating the rods, which leads to the lifting of the degeneracy at the Dirac points. Bianisotropic response is also introduced to mix TE and TM modes, effectively creating gauge fields with opposite signs for pseudospin-up and pseudospin-down states. These two mechanisms of bandgap opening are tuned by changing the parameters of triangulation and bianisotropy in such a way that for the pseudospin-up state, plotted as a red line in Fig. 3A (bottom), the bandgap closes at the K valley and doubles at the K′ valley, thus exhibiting valley-dependent Dirac-like and parabolic dispersions, respectively. For the pseudospin-down state, shown with blue lines, the situation is reversed, and the linear dispersion appears at the K′ valley instead. One can regard this scenario as the two copies, essentially time-reversal pairs, of the one-way Dirac cones described above for the magnetic crystal with broken TRS. Therefore, the TRS-invariant system should also exhibit one-way Klein tunneling, with an additional selection rule with respect to the pseudospin degree of freedom, thus exhibiting spin-valley–dependent transport.

Fig. 3. Spin-valley–coupled Klein tunneling in bianisotropic photonic topological insulator.

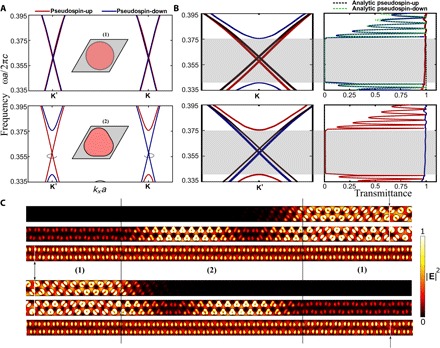
(A) Photonic band diagrams for dual triangular lattice without any symmetry reduction and with ϵ_|| = μ_|| = 14 (top) and triangulated triangular lattice with ϵ_|| = μ_|| = 14 with bianisotropic response ξ_xy = 0.2 introduced along with fillet of radius r_f = 0.27 at each vertex (other parameters are the same as before) (bottom). Red bands correspond to the states of (pseudo)spin-up, and blue lines correspond to the states of (pseudo)spin-down. (B) Photonic band diagrams of the symmetric triangular lattice (black lines) overlapped with the triangulated rods and bianisotropy introduced. Numerically calculated transmittance for the spin-polarized source generating selectively (pseudo)spin-up or (pseudo)spin-down state for the transport at K (K′) valleys, as shown in the upper (lower) right panel. The analytically retrieved transmittance with second-order correction in k·p method at the K valley for pseudospin-down (spin up) is shown with a green (black) dashed line. The fitting parameters of the spectra extracted from the numerically calculated band diagrams are as follows: In the case of pseudospin-down, the frequency of the Dirac crossing at K point ω₀a/2πc = 0.358, and Fermi velocity v_D/2πc = 0.039. In domain (1), u₁ = 0, m₁ = 0, α₁ = −0.05v_D, β₁ = −0.4v_D; in domain (2), u₂a/2πc = −0.003, m₂a/2πc = 0.018, α₂ = −0.001v_D, β₂ = −0.07v_D;. In the case of pseudospin-up, parameters are the same as those in pseudospin-down, except m₂ = 0, α₂ = −0.04v_D, β₂ = −0.25v_D. α_i and β_i are the coefficients of ${\mathrm{\sigma }}_0{\mathrm{\delta }\mathit{k}}_{\mathit{x}}^2,{\mathrm{\sigma }}_{\mathit{z}}\mathrm{\delta }{\mathit{k}}_{\mathit{x}}^2$ in effective Hamiltonian with their numerical values expressed in term of v_D. (C) Simulated electric field intensity |E|² distributions along the strip excited by the sources containing only one pseudospin component. The upper (lower) three panels correspond to pseudospin-down (spin-up) excitation. The strip consists of two domains of the first type on the left and right (1), which represent triangular lattices of circular rods with ϵ = μ, separated by domain type (2), in the middle, which is composed of the triangulated rods with bianisotropy. The domains (1) and (2) contain 2 × 25 and 2 × 20 unit cells, respectively. Black dashed lines denote the boundaries between domains. The source is placed in the right domain (1) in the upper panel and in the left domain (1) in the lower panel, as indicated by black arrows and white lines.

Turning to first-principle simulations of spin-valley–polarized transmission, in Fig. 3B (left), we plot alongside the band structure for (i) the crystals without either gap-opening mechanisms (black lines) and (ii) the optimized spin-valley–coupled structure with the Dirac cone for pseudospin-up (down) state at one of the valleys. The Dirac cones largely overlap, with a slight shift in frequency, sufficient to provide a potential barrier and coexist with the gapped spectrum for the opposite pseudospin. Note that the flip of valley from K to K′ results in the reversed situation for the pseudospin states. Large-scale simulations were carried out for the supercell consisting of three domains, with the middle domain made of the triangulated rods with the bianisotropic response and the two side domains made of nontriangulated and nonbianisotropic rods. Periodic boundary conditions are imposed along the top and bottom boundaries, and matching layers are implemented on the sides. To ensure both pseudospin- and valley-polarized excitation, we constructed the field source from a pair of current sheets located at right (left) side domains, as indicated by arrows and white lines in Fig. 3C. The symmetric current distribution again ensures that we always excite the mode with positive (negative) group velocity at the K (K′) valley. Transmission spectra for left (right) to right (left) excitation calculated for each pseudospin are shown in Fig. 3B (right). For the Dirac bands, the Klein tunneling is observed, and a perfect uniform transmission from the left (right) to right (left) is observed for the pseudospin-up (spin-down) state, whereas for the opposite pseudospin, which perceives the gapped spectrum at the particular valley, the transmission is suppressed because of exponential decay. In addition, as expected for the parabolic bands, the transmission exhibits oscillatory behavior at frequencies outside the bandgap region.

The electric field distributions corresponding to the cases of forward (K valley) and backward (K′ valley) valley- and pseudospin-polarized excitations are plotted along the supercell strip. When the excitation frequency is chosen inside the bandgap, the pseudospin-up (spin-down) state transmitted from the left (right) to the right (left), that is, at the K-valley (K′-valley), we observe uniform field intensity distribution, as shown in Fig. 3C (bottom). At the same time, for opposite pseudospin polarizations excited at the same valleys within the gapped frequency band, the field undergoes exponential decay, as seen in Fig. 3C (top). For the frequency chosen within the parabolic dispersion outside the bandgap, the field exhibits a clear standing wave pattern, as shown in Fig. 3C (middle), which complies with the transmission spectra in Fig. 3B.

The analytical expression of Eq. 3 implies that the Klein tunneling will appear for any width of the barrier, and therefore, the transmission should be uniform as long as the bands remain linear. To confirm this, we performed numerical calculations of the transmittance as a function of the barrier for the two pseudospin states at the same valley. The results, shown in Fig. 4A, prove that the transmission is uniform and close to unity for the pseudospin-up state, exhibiting Klein tunneling through the Dirac cone at this valley. In contrast, the pseudospin-down state exhibits vanishingly small transmission within the bandgap due to the exponential decay. Right outside the bandgap region, where the corresponding bands are parabolic, we observe strong oscillatory behavior due to standing waves. Very small oscillations can also be seen for the pseudospin-up state due to slight parabolicity of the bands (described by the second-order corrections in k·p theory), but they do not exceed 3% in magnitude. The corresponding numerical results were successfully fitted by Eq. 3, with second-order corrections included, which, once again, confirms the adequacy of the effective photonic Hamiltonian description. Therefore, the numerical results demonstrate the most extreme case of spin-valley–polarized transport in the form of spin-polarized one-way Klein tunneling.

Fig. 4. Robustness of transmission through bulk Dirac bands.

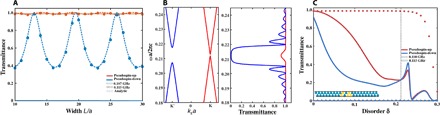
(A) Transmittance as a function of the width of the photonic potential barrier for the case of TR-invariant spin-valley–polarized bulk transport at the K-valley. Numerical and fitted analytical results are shown by dotted and dashed lines, respectively, for the case outside the bandgap region for the pseudospin-down and for the same frequencies for pseudospin-up polarizations (ν = 0.115 GHz). Solid lines correspond to numerical results within the bandgap (for pseudospin-down polarization) and at the same frequency for pseudospin-up polarization, which lies near the Dirac point (ν = 0.107 GHz). Fitting parameters are the same as ones in Fig. 3. (B) Band structure (left) for the case of 10% imbalance of mass terms (m_I = 1.1m_T) and transmission (right) through the structure for K and K′ valleys. Narrowband and limited in magnitude effect of imbalance is evidenced by nearly unity transmission over the most frequencies. The frequency of the Dirac crossing at the K′ point ω₀a/2πc = 0.233, and Fermi velocity v_D/2πc = 0.0227. In domain (1), u₁ = 0, m₁ = 0.0052; in domain (2), u₂a/2πc = −0.021, m₂a/2πc = m₁/10, and the potential barrier length is 13a₀. (C) Effect of disorder (δ variation in ϵ = μ) introduced at sites indicated by yellow color. Red dotted line shows the persistence of Klein tunneling of pseudospin-up state even for strong disorder for frequencies close to Dirac point. Blue dotted line is the complete reflection of pseudospin-down due to bandgap. The cases of frequencies remote from Dirac frequency are shown by solid lines. Note that in this case, the parabolicity of the pseudospin-up band leads to the destruction of Klein tunneling for weaker disorders.

Robustness against structural imperfections

In the presented designs, the occurrence of one-way Dirac degeneracies was dictated by the precise balance of the two mass terms, m_I and m_T. However, small deviations from this condition can arise in any realistic structure due to fabrication imperfections. In general, two scenarios can be considered: (i) uniform (global) mismatch of mass terms and (ii) nonuniform (local) disorder.

In the first scenario, we argue that these imperfections and the resultant mass imbalance do not significantly affect the Klein tunneling because the gap at one of the valleys is always expected to be significantly narrower than that at the opposite valley. The latter fact directly stems from the inequality $|{\mathit{m}}_{\mathrm{K}\prime }|=|{\mathit{m}}_{\mathrm{I}}+{\mathit{m}}_{\mathrm{T}}|\approx 2|{\mathit{m}}_{\mathrm{I}}|\gg |{\mathit{m}}_{\mathrm{I}}-{\mathit{m}}_{\mathrm{T}}|=|{\mathit{m}}_{\mathrm{K}}|$, which is always satisfied for relatively weak imbalance of the mass terms across the structure. Consequently, even if the Dirac cone at one valley (for example, K) is not perfectly induced, the unimpeded transmission due to Klein tunneling will still be observed at almost all frequencies. The exception is only a narrow frequency range near the bandgap induced by this imbalance. These conclusions are confirmed by the results in Fig. 4B, where the band structure and transmittance are presented for the case of uniform mass imbalance (m_I ≠ m_T). One can see that the Klein tunneling prevails at almost all frequencies. Moreover, even within the narrow gap due to the imbalance of mass terms, the transmission remains very high (for finite structures of width L) because the localization length l ~ 1/|m_I − m_T| is very long (l ≫ L). This phenomenon can be simply explained by the fact that a tiny bandgap open at the Dirac point leads to mixing of chiral states close to the Dirac point, giving rise to mixing between different chiral states and backscattering. However, far from this narrowband gapped region, within the region of linear dispersion, this perturbation is negligible, the chirality is preserved, and backscattering does not occur.

In the second, and more likely, scenario, the structural imperfections and defects will be randomly distributed over the structure, which leads to a different mechanism of backscattering due to disorder-induced diffusion and localization. We note that, although these isolated defects can lead to the appearance of localized resonant states, which may potentially appear within the spectrum of the bulk crystal, these localized states still will be embedded within the Dirac continuum. However, in this case, we also expect that the chiral nature of the modes of this continuum will lead to suppression of the effects of disorder. It has already been shown that Dirac and other pseudospin systems are protected to some degree against disorder, and these anomalous localization regimes have been reported (44). Our numerical simulations confirm that in this scenario, the transmission is quite insensitive to the pseudospin-preserving disorder.

To confirm the robustness of modes in our structure, we performed numerical simulations and calculated transmission through the TRS crystal, with (pseudospin-preserving) disorder deliberately introduced at randomly selected sites (Fig. 4C, inset). The strength of defects was gradually increased until the regime of Klein tunneling recedes and localization occurs. The simulation results, shown in Fig. 4C, show that the system demonstrates significant robustness against disorder, and spin-polarized one-way Klein tunneling survives moderate levels of disorder. It is only for large values of disorder that spins and valleys start to mix intensely, leading to the collapse of Klein tunneling.

Edge states in the continuum at critical points of topological transitions

Although the observed one-way Klein tunneling appears at the crossover between two topological phases, (i) quantum Hall–like and valley Hall phases and (ii) quantum spin Hall and valley Hall phases, respectively, it is important to assess whether the structures under investigation can host topological surface states. To address this question, we performed first-principle numerical studies of the edge states residing in the bandgaps for both TRS-breaking and TRS-preserving scenarios.

In our simulations for the nonreciprocal crystal, the supercell was chosen to contain a domain wall between two domains with mass terms of opposite signs due to simultaneous TRS and SIS reduction. In that case, the bandgaps and the Dirac cones for the two domains appeared at the same valleys. We found that the edge mode does occur within the gap at the K′ valley, and it coexists spectrally with the gapless bulk continuum at the K valley, as shown in Fig. 5A.

Fig. 5. Edge states in the continuum.

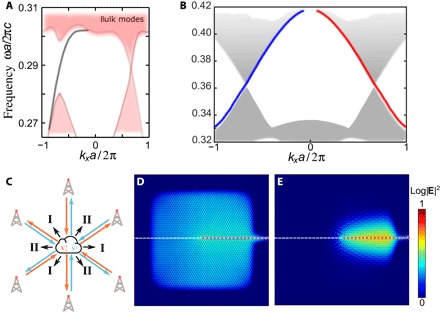
(A and B) Band diagram of a supercell consisting of two domains, which have opposite signs of mass terms for TRS and SIS reduction (A) and bianisotropy and SIS reduction (B). (A) The continuum of bulk modes is shown by red-shaded area, and a dispersion branch of the edge mode supported by the domain wall is depicted by a black line. (B) Gray- and color-shaded regions show dispersion for the continuum of bulk modes. Color shading indicates (pseudo)spin states of the continuum: blue for spin-down and red for spin-up. Red and blue solid lines are the bands corresponding to the edge states supported by domain wall for (pseudo)spin-up and (pseudo)spin-down states, respectively. (C to E) Numerically calculated field distributions in the crystal illustrating the excitation of the one-way edge mode at the domain wall. (C) Schematic of spin- and valley-controlled selection of peer-to-peer or broadcast communication between receivers/transmitters performed over edge and bulk states, respectively. Photonic states excited by K-valley–polarized (D) and K′ valley–polarized (E) pseudospin-up source. The source represents spatially modulated [as exp(ik_xx)] spin-polarized current line placed at the right half of the domain wall and is shown by red dotted lines. The excitation frequency is $\mathrm{\omega }\mathit{a}/2\mathrm{\pi }\mathit{c}=0.358$. The quadratic growth of energy density of the edge state occurs because of the one-way buildup of the field along the edge. To ensure reflectionless propagation of the waves at outer boundaries, we add progressively increasing material losses in the background in the region, enclosing the entire simulated structure. Accordingly, darker blue color closer to the boundaries in (D) and (E) implies exponential decay of the fields due to these custom-built crystalline perfectly matched layers.

Similarly, for the TRS-invariant bianisotropic crystal of triangulated rods, we calculated the band diagram of a supercell made of two domains with mass terms of opposite signs. The latter was achieved by inverting both the orientation of triangulated rods and their bianisotropy, and the band structures found from the first-principle simulation are shown in Fig. 5B. Edge states supported by the domain wall for the pseudospin-up and spin-down states appear at different valleys, and they coexist with the corresponding bulk continuum of opposite pseudospin state at the same valley.

Large-scale simulations enable the observation of this one-way propagation of spin-valley–locked edge modes. A spatially modulated current line source containing both electric and magnetic dipole components j_e = j_m = j₀ exp[ik_xx] was placed at the domain wall to excite only the pseudospin-up mode at the K-valley (k_x = 4π/3a₀). As seen in Fig. 5E, the pseudospin-up edge state excited by the source propagates to the right along the domain wall (indicated by the red line), in the direction that corresponds to the K-valley. At the same time, reversal of excited valley (k_x = −4π/3a₀) for the same pseudospin-state leads to the excitation of bulk modes propagating in all directions away from the source (as in Fig. 5D), as expected for the bulk Dirac spectrum. The edge mode in our simulations (Fig. 5E) experiences a quadratic growth of energy density as it propagates away from the center of the structure. This growth occurs because of the one-way nature of the edge mode that is generated by a continuous current line placed along the domain wall starting at the center (red dotted line in Fig. 5E). This specific excitation geometry yields a linear buildup of the field along the edge and therefore, a quadratic growth of the energy density. This effect creates an illusion of field spreading into the bulk. However, we confirmed that the excited fields have the same exponential decay rate in the direction perpendicular to the domain wall at all locations, which proves the fact that only the edge mode is excited. Our simulation results for both TRS-breaking and TRS-preserving structures therefore unambiguously show that the combined action of gauge fields in sublattice and valley and in pseudospin and valley subspaces leads to the appearance of one-way topological edge states that are polarized with respect to both degrees of freedom.

We believe that the new physics reported in this study will enable a new class of nonreciprocal and pseudospin-controlled devices. For example, we envision a new class of devices where one-way peer-to-peer communications over the edge states can be performed for one of spin and/or valley polarizations. At the same time, the opposite polarizations can be used to broadcast signals over bulk states to multiple indiscriminate receivers. A conceptual functionality of this device is plotted in Fig. 5C, where a set of transmitters and receivers (shown as antennas) can communicate unidirectionally peer-to-peer via spin-valley–polarized edge states (indicated by blue and red arrows) and, at the same time, can broadcast bidirectionally to all receivers via bulk modes (shown by small black arrows).

Proposed experimental design

Both suggested systems in Fig. 1 can be readily implemented in practice. Topological states and robust transport have been successfully demonstrated experimentally in the recent past for both systems with and without TRS. In particular, a graphene-like photonic crystal with ferrite rods was used to demonstrate edge states confined at the interface with free space (38). This system would need only a minor modification, the dimerization of ferrite posts, to introduce the effective valley gauge field that can couple to chiral states induced by the magnetization. To realize the spin-valley–polarized analog of Klein tunneling, we propose a design that is amenable to a physical implementation in the microwave domain, with details summarized in section S3.

DISCUSSION

Synthetic gauge fields acting on either natural or engineered degrees of freedom of light, such as chirality/sublattice, polarization, pseudospin, and valley, offer an unprecedented degree of control of electromagnetic fields and have recently been proven to be of great potential in photonics. Combining the effects of these gauge fields, acting in synergy on different synthetic dimensions, may significantly expand the space of possible optical responses, pushing forward the field of topological photonics. In particular, co-acting gauge fields effectively increase the dimensionality of synthetic photonic potentials, thus enabling a much broader degree of control of electromagnetic radiation. On the basis of this idea, we introduced topological TRS-violating and TRS-preserving optical systems, showing how the combined action of sublattice-valley and spin-valley potentials enables valley- and spin-valley–polarized one-way transport, respectively. We demonstrated sublattice-valley– and spin-valley–polarized one-way Klein tunneling, which represents the extreme case of selective action of these hybrid photonic potentials, enabling efficient filtering of bulk modes by either of the degrees of freedom used, as well as a new class of valley-polarized one-way and spin-locked edge states. An increasingly large domain of synthetic degrees of freedom engineered in photonics, from quasicrystals (17, 21) to synthetic dimensions in multispectral Floquet systems (22, 23), makes it even more interesting to investigate the effects of coactive gauge potentials in these complex, higher-dimensional systems. To the best of our knowledge, the classification of topological orders in systems with several gauge fields acting on orthogonal internal degrees of freedom is not well understood, and it may require the use of non-Abelian gauge field theory methods (23), which makes it of special fundamental and practical interest.

MATERIALS AND METHODS

Methods

The full-wave numerical modeling of electrodynamic response of photonic structures was performed with a finite element method solver COMSOL Multiphysics, radio frequency module (version 5.2a).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/5/eaap8802/DC1

section S1. Low-energy effective Hamiltonians

section S2. Nonreciprocal tunneling in photonic graphene with a single potential barrier

section S3. Specific designs of spin-valley–coupled metacrystals with one-way Dirac cones

fig. S1. Photonic bands and transmission spectra.

fig. S2. Schematics of the meta-waveguide design and band structures.