Covariate-Adjusted Spearman’s Rank Correlation with Probability-Scale Residuals

Summary

It is desirable to adjust Spearman’s rank correlation for covariates, yet existing approaches have limitations. For example, the traditionally defined partial Spearman’s correlation does not have a sensible population parameter, and the conditional Spearman’s correlation defined with copulas cannot be easily generalized to discrete variables. We define population parameters for both partial and conditional Spearman’s correlation through concordance-discordance probabilities. The definitions are natural extensions of Spearman’s rank correlation in the presence of covariates and are general for any orderable random variables. We show that they can be neatly expressed using probability-scale residuals (PSRs). This connection allows us to derive simple estimators. Our partial estimator for Spearman’s correlation between X and Y adjusted for Z is the correlation of PSRs from models of X on Z and of Y on Z, which is analogous to the partial Pearson’s correlation derived as the correlation of observed-minus-expected residuals. Our conditional estimator is the conditional correlation of PSRs. We describe estimation and inference, and highlight the use of semiparametric cumulative probability models, which allow preservation of the rank-based nature of Spearman’s correlation. We conduct simulations to evaluate the performance of our estimators and compare them with other popular measures of association, demonstrating their robustness and efficiency. We illustrate our method in two applications, a biomarker study and a large survey.

1. Introduction

It is often of interest to summarize the degree of association between two variables using a single number. To this end, associations are frequently described using correlation coefficients, which, well over a century after their introduction, remain popular in practice. Although correlation coefficients have limitations (e.g., an inability to accurately describe non-monotonic relationships), their continued popularity is due in part to their simplicity and interpretability. For symmetrically distributed continuous variables, a common choice is Pearson’s correlation coefficient. When dealing with ordered categorical data, nonlinear relationships, skewed distributions, and extreme values, rank correlation coefficients such as Spearman’s rho or Kendall’s tau are preferred. For example, many studies investigate pairwise associations between large numbers of biomarkers to better understand biological processes. The distributions of these biomarkers may be very heterogeneous with high skewness for some and assay detection limits for others. Biomarkers’ scales often vary, their relationships are frequently non-linear, and there may be little interest in obtaining, at least at a first pass, regression coefficients to describe pairwise associations. For these reasons, Spearman’s rank correlations are often presented (e.g., Andrade et al. (2014)).

In many applications, it is desirable to adjust the correlation coefficients for the influence of other variables. For example, when quantifying the association between biomarkers, investigators may want to adjust for demographic variables such as age, sex, and weight. In general, there are two approaches to adjusting the correlation for covariates. One is to obtain a partial correlation, i.e., removing the effect of covariates and then summarizing the relationship with a single number. The other is to obtain conditional correlations, i.e., assessing the correlation at various levels of the covariates. For example, a conditional correlation might look at the association between two biomarkers as a function of age, so that for different ages, the correlation may differ. One could also consider partial correlations conditional on specific covariates; for example, the correlation between two biomarkers conditional on age after adjusting for sex and weight.

The partial Pearson’s correlation coefficient between X and Y controlling for Z, denoted as ρ_XY·Z, is the correlation between residuals from linear regression models of X on Z and of Y on Z. When Z is a single variable,

$${\rho }_{XY\cdot Z}=\left({\rho }_{XY}-{\rho }_{XZ}{\rho }_{YZ}\right)/\sqrt{\left(1-{\rho }_{XY}^2\right)\left(1-{\rho }_{YZ}^2\right)},$$ (1)

where ρ_AB represents the Pearson’s correlation between A and B. Partial Spearman’s and partial Kendall’s correlations have also been proposed with the same formula: substituting ρ_AB with corresponding rank correlations (Kendall, 1942). If Z is more than a single covariate, the traditional forms of these partial correlations are computed recursively using a similar expression. However, they have limitations. The partial Kendall’s correlation can be far from 0 even under conditional independence, and therefore, is generally not useful (Korn, 1984). The partial Spearman’s correlation is ad hoc, has little theoretical justification, and does not correspond with a sensible population parameter (Kendall, 1942; Gripenberg, 1992).

Conditional rank correlations have been studied for continuous data with copulas. For continuous variables, Spearman’s correlation and Kendall’s correlation can be expressed as functions of copulas (Nelsen, 2006). Gijbels et al. (2011) proposed a kernel-based method to estimate the conditional copula and the associated conditional Spearman’s and Kendall’s correlations. However, their approach cannot be directly extended to discrete data because rank correlations between discrete variables cannot be easily described with copulas (see the discussions in Genest and Nešlehová (2007); Nešlehová (2007)).

In this paper, we define population parameters for both partial and conditional Spearman’s correlations through concordance-discordance probabilities, and show that they can be expressed using probability-scale residuals (PSRs; Li and Shepherd, 2012; Shepherd et al., 2016) to derive simple estimators. Our estimator of partial Spearman’s correlation is the correlation of PSRs from models of X on Z and of Y on Z, which is analogous to the partial Pearson’s correlation derived as the correlation of observed-minus-expected residuals. Our conditional estimator is the conditional correlation of PSRs. In the absence of covariates, our partial Spearman’s correlation reduces to the usual sample Spearman’s correlation; in the presence of covariates, it averages the conditional Spearman’s correlation across covariate values. Since PSRs are widely defined for orderable variables (Shepherd et al., 2016), our estimators are quite general.

The paper is organized as follows. In Section 2, we review PSRs, illustrate their connection with Spearman’s correlation, and derive expressions for population parameters of conditional and partial Spearman’s correlation using PSRs. In Section 3, we discuss estimation and inference, highlighting the use of semiparametric cumulative probability models. In Sections 4 and 5, we provide numerical illustrations and conduct simulations to evaluate the performance of our estimators. In Section 6, we illustrate our approach in two applications. Section 7 contains a discussion. Additional information is in the Supplementary Material.

2. Population Parameters of Covariate-adjusted Spearman’s Rank Correlations

2.1 Spearman’s Rank Correlation and PSRs

Fundamentally, Spearman’s rank correlation is a scale-invariant concordance measure (Kruskal, 1958). Its population parameter, the rank correlation between the random variables X and Y, denoted as γ_XY, can be interpreted as the scaled difference between the probability of concordance and the probability of discordance between (X, Y) and (X₀, Y₀), where X₀ and Y₀ have the same marginal distributions as X and Y, respectively, but X₀ is independent of Y₀, and (X₀, Y₀) are independent of (X, Y) (Kruskal, 1958). That is,

$${\gamma }_{XY}=c\left(P_c-P_d\right),$$

where P_c = P {sign(X, X₀)sign(Y, Y₀) = 1}; P_d = P {sign(X, X₀)sign(Y, Y₀) = −1}; sign(a, b) is −1, 0, and 1 for a < b, a = b, and a > b, respectively; and c is a scaling factor so that −1 ≤ γ_XY ≤ 1 and the bounds can be reached. For continuous X and Y, c = 3. For noncontinuous X and/or Y, c is a function of the marginal distributions (Nešlehová, 2007). Let F and G be the marginal distributions of X and Y, respectively, and F (x−) = lim_t↑xF (t). With an infinite sample, Spearman’s rank correlation equals corr[{F (X) + F (X−)}/2, {G(Y) + G(Y −)}/2], the correlation of ridits (Bross, 1958; Kendall, 1970), which for continuous X and Y is corr{F (X), G(Y)}, the grade correlation (Kruskal, 1958).

We express γ_XY in terms of a new type of residual: the probability-scale residual (PSR). For an orderable random variable X from distribution F, the PSR of X = x is

$$r\left(x,F\right)=E\left\{\text{sign}\left(x,X_0\right)\right\}=P\left(X_0<x\right)-P\left(X_0>x\right)=F\left(x-\right)+F\left(x\right)-1,$$

where X₀ is a random variable with distribution F (Li and Shepherd, 2012; Shepherd et al., 2016). We sometimes use X_res = r(X, F) to denote the corresponding random variable. In practice, F is replaced by F^∗, an assumed or fitted distribution of X. As shown in Shepherd et al. (2016), E{r(X, F)} = 0, and var{r(X, F)} = 1/3 if X is continuous or $\left(1-{\displaystyle \sum f_x^3}\right)/3$ if X is discrete, where f_x = P(X = x). Following arguments similar to those of Kruskal (1958), it can be shown that

$$P_c-P_d=E\left\{\text{sign}\left(X,X_0\right)\text{sign}\left(Y,Y_0\right)\right\}=E_{\left(X,Y\right)}\left[E\left\{\text{sign}\left(X,X_0\right)\text{sign}\left(Y,Y_0\right)|\left(X,Y\right)\right\}\right]=E_{\left(X,Y\right)}\left[E\left\{\text{sign}\left(X,X_0\right)|X\right\}E\left\{\text{sign}\left(Y,Y_0\right)|Y\right\}\right]=E_{\left(X,Y\right)}\left\{r\left(X,F\right)r\left(Y,G\right)\right\}=\text{cov}\left\{r\left(X,F\right),r\left(Y,G\right)\right\},$$

with the last equality holding because E{r(X, F)} = E{r(Y, G)} = 0. Let the scaling factor be c = [var{r(X, F)}var{r(Y, G)}]^−1/2; e.g., c = 3 when both X and Y are continuous. Then,

$${\gamma }_{XY}=\text{corr}\left\{r\left(X,F\right),r\left(Y,G\right)\right\}.$$

This expression suggests that Spearman’s rank correlation can be estimated with PSRs, i.e., with observed data {(x_i, y_i); i = 1, 2, …, n}, γ_XY is estimated as the sample correlation between {r(x₁, F^∗), …, r(x_n, F^∗)} and {r(y₁, G^∗), …, r(y_n, G^∗)}. In the absence of covariates, F^∗ and G^∗ are often estimated with empirical distribution functions, and r(x_i, F^∗) and r(y_i, G^∗) are linear functions of the ranks of x_i and y_i (Shepherd et al., 2016). Therefore, the estimate obtained above with PSRs equals the sample Spearman’s rank correlation.

2.2 Conditional Spearman’s Rank Correlation

In the presence of covariates Z, let F_X|Z be the conditional distribution of X given Z and G_Y|Z be that of Y given Z. The PSRs given Z are r(X, F_X|Z) and r(Y, G_Y|Z). Then, E{r(X, F_X|Z)|Z} = 0 and var{r(X, F_X|Z)|Z} = 1/3 for continuous X or $\text{var}\left\{r\left(X,F_{X|Z}\right)|Z\right\}=\left(1-{\displaystyle {\sum }_x{f}_{x|Z}^3}\right)/3$ for discrete X, where f_x|Z = P(X = x|Z).

We define the population version of the conditional Spearman’s rank correlation as

$${\gamma }_{XY|Z}=c_Z\left(P_{c|Z}-P_{d|Z}\right),$$

with P_c|Z = P {sign(X, X₀)sign(Y, Y₀) = 1|Z} and P_d|Z = P {sign(X, X₀)sign(Y, Y₀) = −1|Z}, where X₀|Z ∼ F_X|Z, Y₀|Z ∼ G_Y|Z, and conditional on Z, X₀ is independent of Y₀ and (X₀, Y₀) are independent of (X, Y). Note that γ_XY|Z is a function of Z. As shown in the unconditional case, P_c|Z − P_d|Z = cov{r(X, F_X|Z), r(Y, G_Y|Z)|Z}. With the scaling factor c_Z = [var{r(X, F_X|Z)|Z}var{r(Y, G_Y|Z)|Z}]^−1/2, γ_XY|Z can be expressed as

$${\gamma }_{XY|Z}=\text{corr}\left\{r\left(X,F_{X|Z}\right),r\left(Y,G_{Y|Z}\right)|Z\right\}.$$

In general, c_Z ⩾ 3. When both X and Y are continuous, c_Z = 3, and this expression is equivalent to the definition in Gijbels et al. (2011) using conditional copulas. However, since PSRs are well defined for any orderable random variable, including discrete random variables (Shepherd et al., 2016), our expression of γ_XY|Z with PSRs is quite general.

2.3 Partial Spearman’s Rank Correlation

Partial Spearman’s rank correlation can be defined in two equivalent ways. One is

$${\gamma }_{XY\cdot Z}=\text{corr}\left\{r\left(X,F_{X|Z}\right),r\left(Y,G_{Y|Z}\right)\right\}.$$

This is analogous to the partial Pearson’s correlation, which is the correlation of observed-minus-expected residuals. Another definition is as a rescaled average of conditional concordance-discordance probabilities,

$${\gamma }_{XY\cdot Z}=c^{\ast }{E}_Z\left(P_{c|Z}-P_{d|Z}\right),$$

where the scaling factor c^∗ = [var{r(X, F_X|Z)} var{r(Y, G_Y|Z)}]⁻¹ ⩾ 3. The equivalence of these two definitions is shown in Supplementary Material S.1. Note that γ_XY·Z is not a function of Z.

When both X and Y are continuous, γ_XY·Z = 3E_Z(P_c|Z − P_d|Z) = E(γ_XY|Z). Otherwise, γ_XY·Z is a weighted average of γ_XY|Z where the weights are a function of covariates Z (Supplementary Material S.1). For example, if both X and Y are discrete, γ_XY·Z = E(w_Zγ_XY|Z), where $w_Z=\sqrt{\left(1-{\displaystyle {\sum }_x{f}_{x|Z}^3}\right)\left(1-{\displaystyle {\sum }_y{g}_{y|Z}^3}\right)}/\sqrt{\left\{1-{\displaystyle {\sum }_x{E}_Z\left(f_{x|Z}^3\right)}\right\}\left\{1-{\displaystyle {\sum }_y{E}_Z\left(g_{y|Z}^3\right)}\right\}}$, f_x|Z = P (X = x|Z), and g_y|Z = P (Y = y|Z). Note that the denominator of w_Z is fixed for all values of Z, and that larger weights are assigned to the values of Z at which the discrete variables X and Y are less likely to have ties (e.g., have more categories or are more evenly distributed).

2.4 Partial Spearman’s Rank Correlation Conditional on Covariates

When covariates are multidimensional, it may be useful to condition the partial Spearman’s rank correlation on one or a subset of covariates. For example, suppose Z can be divided into two (potentially multidimensional) components, i.e., Z = (Z₁, Z₂). To describe the rank correlation between X and Y at a specific level of Z₁ while adjusting for the other covariates, we can define the partial Spearman’s rank correlation conditional on Z₁ as

$${\gamma }_{XY\cdot Z|Z_1}=\text{corr}\left\{r\left(X,F_{X|Z}\right),r\left(Y,G_{Y|Z}\right)|Z_1\right\}.$$

It can be shown that ${\gamma }_{XY\cdot Z|Z_1}=c_{Z_1}^{\ast }{E}_{Z_2|Z_1}\left(P_{c|Z}-P_{d|Z}\right)=E_{Z_2|Z_1}\left(w_{Z_1}^{\ast }{\gamma }_{XY|Z}\right)$ (derivation and expressions of $c_{Z_1}^{\ast }$ and $w_{Z_1}^{\ast }$ are in Supplementary Material S.2). For continuous X and Y, $c_{Z_1}^{\ast }=3$ and $w_{Z_1}^{\ast }=1$, and therefore, ${\gamma }_{XY\cdot Z|Z_1}=3E_{Z_2|Z_1}\left(P_{c|Z}-P_{d|Z}\right)=E_{Z_2|Z_1}\left({\gamma }_{XY|Z}\right)$ and ${\gamma }_{XY\cdot Z}=E_{Z_1}\left({\gamma }_{XY\cdot Z|Z_1}\right)$.

Notice that both γ_XY·Z and γ_XY|Z are special cases of ${\gamma }_{XY\cdot Z|Z_1}$; specifically, if Z₁ is the empty set (∅), then ${\gamma }_{XY\cdot Z|Z_1}={\gamma }_{XY\cdot Z}$, and if Z₂ = ∅, then ${\gamma }_{XY\cdot Z|Z_1}={\gamma }_{XY|Z}$.

3. Estimation and Inference

3.1 Modeling Strategies and Calculation of PSRs

The definitions in the previous section allow estimation of partial and conditional Spearman’s correlation using PSRs. First, we need to fit models for X on Z and for Y on Z, and then compute the two sets of PSRs. As shown in Section 2.1, PSRs are well defined as long as the underlying cumulative distribution functions are estimable at the observed values of x and y. We consider nonparametric, parametric, and semiparametric models.

Since Spearman’s rank correlation is a nonparametric statistic, it is natural to consider obtaining the PSRs using nonparametric models. For example, given a dataset {(x_i, y_i, z_i); i = 1, 2, …, n}, a kernel estimator for the conditional distribution could be ${\widehat{F}}_{X|Z=z}\left(x\right)={\displaystyle {\sum }_{i=1}^n{w}_i\left(z\right)I\left(x_i\le x\right)}$, where the kernel weight w_i(z) is given by $K\left\{d\left(z_i,z\right)/h\right\}/{\displaystyle {\sum }_{i=1}^{n}K\left\{d\left(z_i,z\right)/h\right\}}$ with kernel function K(·), distance metric d(·), and bandwidth h (Gijbels et al., 2011). Similarly, ${\widehat{F}}_{X|Z=z}\left(x-\right)={\displaystyle {\sum }_{i=1}^n{w}_i\left(z\right)I\left(x_i<x\right)}$. Then, the PSR for x_i can be calculated as $x_{i,\mathit{res}}={\widehat{F}}_{X|Z=z_i}\left(x_i-\right)+{\widehat{F}}_{X|Z=z_i}\left(x_i\right)-1$. The PSR for y_i can be calculated similarly. Although feasible, there are challenges to incorporating such nonparametric models to real data. One challenge is that the fitted models can be highly dependent on the selected bandwidth. Additional challenges arise with multidimensional covariates due to the curse of dimensionality. Also, nonparametric estimators are often inefficient and do not have analytic expressions of their variance.

One could instead fit parametric models for X on Z and Y on Z. Parametric models are usually easier to fit than nonparametric models, are more convenient for obtaining PSRs, and yield more efficient estimators when correctly specified. However, estimators from parametric models are less robust to outliers and are generally sensitive to model misspecification. Using PSRs derived from parametric models for estimation seems contrary to the robust nature of Spearman’s rank correlation.

To balance robustness and efficiency, we consider semiparametric models that only use the order information of the outcomes, thereby allowing us to include covariates while preserving the rank-based nature of Spearman’s correlation. Specifically, we focus on the semiparametric transformation model X = H(βZ + ε), where H(·) is an unspecified monotonic increasing transformation and ε is random error with a specified parametric distribution F_ε (Zeng and Lin, 2007; Liu et al., 2017). Since the transformation H(·) is not specified and only needs to be monotonic, this model only depends on the order of X. Note that

$$F_{X|Z}\left(x\right)\equiv P\left(X\le x|Z\right)=P\left\{H\left(\beta Z+\epsilon \right)\le x|Z\right\}=F_{\epsilon }\left\{H^{-1}\left(x\right)-\beta Z\right\}.$$

Therefore, this semiparametric transformation model can be written in the form of the ordinal cumulative probability model (CPM) (Walker and Duncan, 1967; McCullagh, 1980):

$$g\left\{F_{X|Z}\left(x\right)\right\}=\alpha \left(x\right)-\beta Z,$$

with link function $g(\cdot )=F_{\epsilon }^{-1}(\cdot )$ and the intercept α(x) = H⁻¹(x). Based on this fact, Harrell (2015a) proposed an estimating procedure that maximizes an approximated multinomial likelihood of the CPM. This maximum likelihood estimation procedure treats a continuous response variable as an ordered categorical variable, and results in estimators that are very similar to the nonparametric maximum likelihood estimators proposed by Zeng and Lin (2007), whose asymptotic properties have been well studied for right censored data (Murphy et al., 1997; Zeng and Lin, 2007). In practice, this ordinal estimation procedure is easy to implement; estimation is efficiently executed with the orm() function in the rms package of R (Harrell, 2015b). These models are also widely applicable to any orderable outcome. For example, with the logit link function, the CPM is the commonly used proportional odds model when the outcome is ordered categorical and the logistic regression model when the outcome is binary. Computation of PSRs from CPMs is straightforward (Shepherd et al., 2016). For a more detailed description and illustrations of CPMs, we refer the reader to Liu et al. (2017).

3.2 Partial Correlation Estimators

After obtaining PSRs from models of X on Z and of Y on Z, we estimate γ_XY·Z simply as the sample correlation of PSRs. In the special case where X and Y are both ordered categorical variables, Li and Shepherd (2010) described two approaches for obtaining the distribution of the correlation of PSRs, a bootstrap method and a large sample approximation, both of which can be applied with more general X and Y. We focus here on the large sample approach using M-estimation for approximate inference (Stefanski and Boos, 2002).

Let Ψ_x(·) denote estimating functions for the model of X on Z with parameter θ_x, and Ψ_y(·) denote estimating functions for the model of Y on Z with parameter θ_y. Ψ_x(·) and Ψ_y(·) can be stacked together with the components necessary for computing the correlation of PSRs, resulting in the following estimating function:

$$\mathrm{\Psi }\left(X_i,Y_i,Z_i;\theta \right)={\left\{{\mathrm{\Psi }}_x\left(X_i,Z_i;{\theta }_x\right),{\mathrm{\Psi }}_y\left(Y_i,Z_i;{\theta }_y\right),X_{i,\mathit{res}}-{\theta }_1,Y_{i,\mathit{res}}-{\theta }_2,X_{i,\mathit{res}}{Y}_{i,\mathit{res}}-{\theta }_3,X_{i,\mathit{res}}^2-{\theta }_4,Y_{i,\mathit{res}}^2-{\theta }_5\right\}}^T,$$

where θ = (θ_x, θ_y, θ₁, θ₂, θ₃, θ₄, θ₅), with θ₁ = E(X_i,res), θ₂ = E(Y_i,res), θ₃ = E(X_i,resY_i,res), ${\theta }_4=E(X_{i,\mathit{res}}^2)$ and ${\theta }_4=E(Y_{i,\mathit{res}}^2)$, and ${\displaystyle {\sum }_{i=1}^n\mathrm{\Psi }\left(X_i,Y_i,Z_i;\widehat{\theta }\right)}=0$. Under standard regularity conditions (Stefanski and Boos, 2002), $\sqrt{n}\left(\widehat{\theta }-\theta \right)\stackrel{d}{\to }N\left\{0,V\left(\theta \right)\right\}$, where V (θ) = A(θ)⁻¹B(θ){A(θ)⁻¹}′, A(θ) = E{−∂Ψ_i(θ)/∂θ}, and B(θ) = E{Ψ_i(θ)Ψ_i(θ)′}. Since ${\widehat{\gamma }}_{XY\cdot Z}=\left({\widehat{\theta }}_3-{\widehat{\theta }}_1{\widehat{\theta }}_2\right)/\sqrt{\left({\widehat{\theta }}_4-{\widehat{\theta }}_1^2\right)\left({\widehat{\theta }}_5-{\widehat{\theta }}_2^2\right)}$, the delta-method can be employed to obtain the large sample distribution of ${\widehat{\gamma }}_{XY\cdot Z}$. In practice, estimating the large sample distribution of the Fisher transformation of ${\widehat{\gamma }}_{XY\cdot Z}$, i.e., $\text{log}\left\{\left(1+{\widehat{\gamma }}_{XY\cdot Z}\right)/\left(1-{\widehat{\gamma }}_{XY\cdot Z}\right)\right\}/2$, typically results in more rapid convergence to normality, and is therefore preferable for constructing confidence intervals. Some parameters may have known values and can be removed. For example, if F^∗ and G^∗ are continuous and correctly specified, then θ₁ = θ₂ = 0 and θ₄ = θ₅ = 1/3. In our experience, however, estimating these parameters has little impact on resulting confidence intervals.

With parametric models of X and Y, implementation is straightforward; e.g., with maximum likelihood estimation, Ψ_x and Ψ_y are simply the score functions. When modeling X and Y using semiparametric CPMs, we also advocate using the score functions from the approximated multinomial likelihoods for Ψ_x and Ψ_y. Notice that with continuous data, as n increases, the number of parameters (specifically the intercept parameters α(x)) in these models also increases. Therefore, standard large sample theory for M-estimation no longer holds. More generally, the large sample distribution of nonparametric maximum likelihood estimators of semiparametric transformation models with uncensored, continuous data have not been fully developed, and are quite challenging (Zeng and Lin, 2007; Zeng, Kosorok, and Lin, personal communication). However, based on fairly extensive simulations and heuristic arguments by us and others (Zeng and Lin, 2007; Liu et al., 2017; Zeng, Kosorok, and Lin, personal communication), standard functions of the estimated parameters (e.g., conditional expectations or quantiles) appear to be consistent and asymptotically normal. As illustrated in Section 5, our simulations also demonstrate that the large sample distribution of the partial Spearman’s rank correlation with these semiparametric models is well approximated using M-estimation techniques.

3.3 Conditional Correlation Estimators

To estimate γ_XY|Z, we calculate the correlation of PSRs as a function of covariate values. Again, let Z be a vector of covariates, such that Z = (Z₁, Z₂). Since conditional rank correlations can be viewed as a special case of partial rank correlations conditional on Z₁ (see Section 2.4), we focus on the more general case in this section. To obtain ${\widehat{\gamma }}_{XY\cdot Z|Z_1}$ we compute the correlation of PSRs as a function of Z₁. If Z₁ is a categorical variable with sufficient numbers per category, one can compute the correlation of PSRs within each level of Z₁. If Z₁ is continuous or multidimensional, smoothing is often needed. It should be noted that smoothing approaches will only work well with low-dimensional Z₁, which is typically what is desired in practice.

We consider two ways to smooth estimators of the conditional correlation. A nonparametric kernel smoother for estimating the conditional correlation at Z₁ = v is to weight the observations by their Z₁ values, the farther from v the smaller the weight. Specifically,

$${\widehat{\gamma }}_{XY\cdot Z|Z_1}\left(v\right)=\frac{{\displaystyle \sum w_i\left(v\right)x_{i,\mathit{res}}{y}_{i,\mathit{res}}}-{\displaystyle \sum w_i\left(v\right)x_{i,\mathit{res}}}{\displaystyle \sum w_i\left(v\right)y_{i,\mathit{res}}}}{\sqrt{{\displaystyle \sum w_i\left(v\right)x_{i,\mathit{res}}^2}-{\left\{{\displaystyle \sum w_i\left(v\right)x_{i,\mathit{res}}}\right\}}^2}\sqrt{{\displaystyle \sum w_i\left(v\right)y_{i,\mathit{res}}^2-{\left\{{\displaystyle \sum w_i\left(v\right)y_{i,\mathit{res}}}\right\}}^2}}},$$

where $w_i\left(v\right)=K\left\{d\left(z_{1i},v\right)/h\right\}/{\displaystyle {\sum }_{i=1}^{n}K\left\{d\left(z_{1i},v\right)/h\right\}}$ and z_1i is the value of Z₁ for subject i.

Alternatively, we can estimate conditional rank correlations using parametric smoothing. For example, since under correctly specified models, E(X_res|Z₁) = E(Y_res|Z₁) = 0, then cov(X_res, Y_res|Z₁) = E(X_resY_res|Z₁), $\text{var}\left(X_{\mathit{res}}|Z_1\right)=E\left(X_{\mathit{res}}^2|Z_1\right)$, and $\text{var}\left(Y_{\mathit{res}}|Z_1\right)=E\left(Y_{\mathit{res}}^2|Z_1\right)$. Therefore, ${\widehat{\gamma }}_{XY\cdot Z|Z_1}$ can be approximated with $\widehat{E}\left(X_{\mathit{res}}{Y}_{\mathit{res}}|Z_1\right)/\sqrt{\widehat{E}\left(X_{\mathit{res}}^2|Z_1\right)\widehat{E}\left(Y_{\mathit{res}}^2|Z_1\right)}$, where $\widehat{E}\left(\cdot |Z_1\right)$ designates an estimator of a conditional expectation. To obtain $\widehat{E}\left(X_{\mathit{res}}{Y}_{\mathit{res}}|Z_1\right)$, $\widehat{E}\left(X_{\mathit{res}}^2|Z_1\right)$, and $\widehat{E}\left(Y_{\mathit{res}}^2|Z_1\right)$, one might fit regression models of X_resY_res on Z₁, $X_{\mathit{res}}^2$ on Z₁, and $Y_{\mathit{res}}^2$ on Z₁, using natural spline functions to allow flexible modeling. When X and Y are continuous variables, $\widehat{E}\left(X_{\mathit{res}}^2|Z_1\right)$ and $\widehat{E}\left(Y_{\mathit{res}}^2|Z_1\right)$ converge to 1/3 under correctly specified models; plugging in 1/3 could further simplify estimation and inference because then only $\widehat{E}\left(X_{\mathit{res}}{Y}_{\mathit{res}}|Z_1\right)$ needs to be estimated. For these parametric smoothing techniques, standard errors and confidence intervals can be estimated using the bootstrap or large sample approximation techniques similar to those described in Section 3.2; details are in Supplementary Material S.3.

4. Numerical Illustrations

To illustrate our definitions, let Z ~ N(0, 1) and $\left(\begin{array}{c}{X}_1\\ Y_1\end{array}\right)|Z\sim N\left\{\left(\begin{array}{c}Z\\ -Z\end{array}\right),\left(\begin{array}{cc}1& \rho \\ \rho & 1\end{array}\right)\right\}$, with ρ varying over a fine grid over [0, 1]. We consider four scenarios: (I) Y = Y₁ and X = X₁; (II) Y = exp(Y₁) and X = X₁; (III) Y = Y₁ and X is generated by discretizing X₁ with cut-offs at the 0.2, 0.4, 0.6, 0.8 quantiles of the standard normal distribution; (IV) Y = exp(Y₁) and X is the discretized version of X₁ as in (III).

In Scenarios I and II, since (X₁, Y₁) conditional on Z is normally distributed, γ_XY|Z = 6 arcsin(ρ/2)/π (Pearson, 1907). Thus, for any fixed ρ, γ_XY|Z is a constant function of Z. In this case, it is desirable for a partial rank correlation to have the same value, which is true for our definition: γ_XY·Z = E(γ_XY|Z) = γ_XY|Z. Figure 1 (left panel) compares γ_XY·Z with the traditional partial Pearson’s $\left({\rho }_{XY\cdot Z}^{\ast }\right)$, Spearman’s $\left({\gamma }_{XY\cdot Z}^{\ast }\right)$, and Kendall’s $\left({\tau }_{XY\cdot Z}^{\ast }\right)$ correlations obtained by plugging corresponding parameters into (1). Under scenario I, γ_XY·Z and ${\rho }_{XY\cdot Z}^{\ast }$ are very close with $max\left|{\gamma }_{XY\cdot Z}-{\rho }_{XY\cdot Z}^{\ast }\right|<0.02$, whereas ${\rho }_{XY\cdot Z}^{\ast }$ is not a suitable measure of correlation after the exponential transformation of Y (scenario II). In contrast, all rank based correlations, including ours, are unchanged between scenarios I and II. As expected, ${\tau }_{XY\cdot Z}^{\ast }$ has poor performance: its value departs from 0 even under conditional independence (ρ = 0). ${\gamma }_{XY\cdot Z}^{\ast }$ is fairly similar to γ_XY·Z, but its difference is more pronounced when ρ is close to one.

Figure 1.

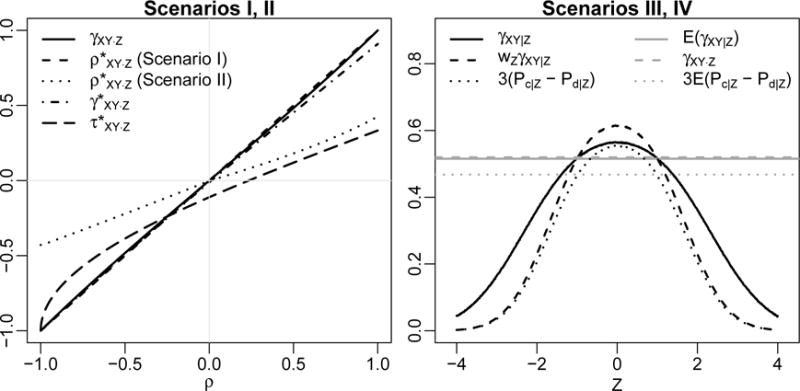
Correlation parameters in Scenarios I, II (left panel) and III, IV (right panel). In the left panel, γ_XY·Z is the population parameter of our partial Spearman’s rank correlation; ${\rho }_{XY\cdot Z}^{\ast }$, ${\gamma }_{XY\cdot Z}^{\ast }$, and ${\tau }_{XY\cdot Z}^{\ast }$ are traditional partial Pearson’s, Spearman’s, and Kendall’s correlations based on (1), respectively. In the right panel, γ_XY|Z is the population parameter of our conditional Spearman’s rank correlation as a function of Z, and γ_XY·Z = E(w_Zγ_XY|Z) is the population parameter of our partial Spearman’s rank correlation, which is constant over Z. For comparison with γ_XY|Z, we also show w_Zγ_XY|Z and 3(P_c|Z − P_d|Z), i.e., 3 times the difference between the probability of concordance and the probability of discordance conditional on Z, which is what γ_XY|Z would be if X and Y were both continuous. For comparison with γ_XY·Z, we also show E(γ_XY|Z) and 3E(P_c|Z − P_d|Z).

In Scenarios III and IV, X is discrete and has, when Z = 0, five evenly distributed categories. As Z departs from 0, the conditional distribution of X becomes skewed, and the conditional correlation between X and Y is expected to become weaker. Figure 1 (right panel) plots γ_XY|Z as a function of Z at ρ = 0.6, showing this trend. Our partial correlation γ_XY·Z (≈ 0.520) differs, although only slightly in this example, from E(γ_XY|Z). Since γ_XY·Z = E(w_Zγ_XY|Z) = c^∗E(P_c|Z − P_d|Z), we also plot w_Zγ_XY|Z and 3(P_c|Z − P_d|Z) for comparison. As shown in Figure 1, the scaling factor c^∗ is larger than 3, and the weight w_Z is bigger when the distribution of X given Z is more dispersed (i.e., Z is closer to 0).

5. Simulations

We first evaluated the performance of our estimator of γ_XY·Z using PSRs derived from parametric, nonparametric, and semiparametric models in finite samples (n = 200) under the four scenarios described in Section 4. In this set of simulations, we set ρ = 0.6; therefore, γ_XY·Z ≈ 0.582 in Scenarios I and II, and γ_XY·Z ≈ 0.520 in Scenarios III and IV. Our parametric models are linear regression models (LM), and we computed two sets of PSRs: 1) assuming normality of the error distribution, and 2) empirically, assuming a constant variance of the error distribution (Shepherd et al., 2016). For our nonparametric models, we used Gaussian kernels to estimate F_X|Z and G_Y|Z, and chose the bandwidth based on Silverman’s rule of thumb (Wand and Jones, 1995). We also fit semiparametric CPMs using the approximated maximum likelihood procedure described in Section 3.1 as implemented in the R function orm(). When fitting CPM, we used both the properly specified link function (probit) and misspecified link functions (logit, loglog, and cloglog). In all simulations, we used large sample approximations with Fisher’s transformation to compute confidence intervals. The results based on 10,000 simulation replications are shown in Table 1.

Table 1.

Simulation results for our estimator of γ_XY·Z with PSRs derived from linear models (LM), kernel estimation (kernel), and semiparametric cumulative probability models (CPM) with n=200 and 10,000 simulation replicates

Scenarios			truth	est	% bias	est.SE	emp.SE	MSE	coverage
I
	LM
		normality	0.582	0.582	0.01	0.048	0.049	0.0024	0.946
		empirically	0.582	0.580	−0.35	0.048	0.049	0.0024	0.945
	kernel
		Silverman	0.582	0.552	−5.10	—	0.050	0.0034	—
	CPM
		probit	0.582	0.577	−0.92	0.050	0.049	0.0025	0.950
		logit	0.582	0.573	−1.59	0.050	0.050	0.0026	0.948
		loglog	0.582	0.565	−2.85	0.050	0.049	0.0027	0.942
		cloglog	0.582	0.565	−2.88	0.050	0.049	0.0027	0.941
II
	LM
		normality	0.582	0.394	−32.33	0.058	0.063	0.0393	0.057
		empirically	0.582	0.386	−33.68	0.060	0.063	0.0424	0.051
	kernel
		Silverman	0.582	0.552	−5.10	—	0.050	0.0034	—
	CPM
		probit	0.582	0.577	−0.92	0.050	0.049	0.0025	0.950
		logit	0.582	0.573	−1.59	0.050	0.050	0.0026	0.948
		loglog	0.582	0.565	−2.85	0.050	0.049	0.0027	0.942
		cloglog	0.582	0.565	−2.88	0.050	0.049	0.0027	0.941
III
	LM
		normality	0.520	0.499	−3.86	0.054	0.055	0.0034	0.931
		empirically	0.520	0.500	−3.72	0.054	0.055	0.0034	0.930
	kernel
		Silverman	0.520	0.499	−3.92	—	0.053	0.0032	—
	CPM
		probit	0.520	0.517	−0.52	0.053	0.053	0.0028	0.945
		logit	0.520	0.514	−1.02	0.053	0.053	0.0029	0.945
		loglog	0.520	0.505	−2.84	0.053	0.053	0.0030	0.943
		cloglog	0.520	0.504	−2.90	0.053	0.053	0.0030	0.939
IV
	LM
		normality	0.520	0.361	−30.52	0.054	0.056	0.0283	0.144
		empirically	0.520	0.382	−26.50	0.053	0.055	0.0219	0.226
	kernel
		Silverman	0.520	0.499	−3.92	—	0.053	0.0032	—
	CPM
		probit	0.520	0.517	−0.52	0.053	0.053	0.0028	0.945
		logit	0.520	0.514	−1.02	0.053	0.053	0.0029	0.945
		loglog	0.520	0.505	−2.84	0.053	0.053	0.0030	0.943
		cloglog	0.520	0.504	−2.90	0.053	0.053	0.0030	0.939

est is the mean of the point estimates.

est.SE is the mean of the standard error estimates.

emp.SE is the standard deviation of the point estimates

In summary, our estimators of γ_XY·Z using PSRs from CPMs had minimal bias, good coverage, and low mean squared error (MSE) across all scenarios we considered. In Scenario I, estimators using CPMs properly specified with the probit link performed similarly to fully parametric estimators correctly assuming normality. However, because of their invariance to the exponential transformation of Y, in Scenarios II and IV, estimators using PSRs from CPMs easily out-performed those using PSRs from linear models. The bias and MSE of our estimators using CPMs were also generally smaller than those using kernel smoothers. Surprisingly, our estimators using PSRs from CPMs were robust to link function misspecification, with only slight increases in bias. However, especially poor models of Y and X on Z can lead to poor estimation (e.g., linear models, Scenarios II and IV). This is further illustrated with simulations in Supplementary Material S.4, which show that failure to include a quadratic term in models of Y and X on Z leads to biased estimates of γ_XY·Z. Additional simulations reported in Supplementary Material S.5 show that ${\widehat{\gamma }}_{XY\cdot Z}$ tends to be biased towards zero with especially small sample sizes.

We next investigated the performance of our estimator of γ_XY·Z using PSRs from CPMs for testing covariate-adjusted association, and compared them with tests based on traditionally defined Pearson, Spearman, and Kendall partial correlation coefficients using (1). We set ρ = 0 under the null hypothesis (H₀) and ρ = 0.2 under the alternative hypothesis (H₁) (Table 2). For tests based on the traditional partial correlation coefficients, p-values were obtained based on large sample approximations using the R package ppcor (Kim, 2012). Consistent with the observation in Figure 1, tests based on partial Kendall’s correlations had poor performance: high type I error rate and almost no power at ρ = 0.2. Compared with the partial Pearson’s correlation, our estimators were slightly less efficient when the relationships were linear or approximately linear (Scenarios I and III), but much more robust in the presence of nonlinearity and extreme values (Scenarios II and IV). Also, our estimators had better performance than the traditional ad hoc partial Spearman’s correlation: type I error rate closer to 5% and generally higher power.

Table 2.

Type I error rate and power (%) for testing covariate-adjusted association using our estimator of γ_XY·Z and the traditional partial correlation coefficients with n=200 and 10,000 simulation replicates

Scenarios		our estimator of γXY·Z				traditional partial coefficients
		probit	logit	loglog	cloglog	Pearson	Spearman	Kendall
I
	H0	4.96	4.97	5.11	5.04	4.83	6.22	67.42
	H1	77.47	76.62	76.44	76.86	81.55	68.68	1.77
II
	H0	4.96	4.97	5.11	5.04	5.10	6.22	67.42
	H1	77.47	76.62	76.44	76.86	33.36	68.68	1.77
III
	H0	5.12	5.12	5.29	5.29	4.99	6.51	72.04
	H1	67.19	66.81	64.79	65.02	67.87	65.20	4.49
IV
	H0	5.12	5.12	5.29	5.29	2.76	6.51	72.04
	H1	67.19	66.81	64.79	65.02	26.32	65.20	4.49

We also performed an additional set of simulations investigating the finite sample performance of ${\widehat{\gamma }}_{XY|Z}$ under correct model specification. We considered scenarios conditioning on a continuous covariate and conditioning on a discrete covariate. Results were similar to those for the partial rank correlation under correctly specified models. Bias was small and slightly towards zero, Type I error rates were conserved under the null, and 95% confidence intervals covered close to their nominal level. Details are in Supplementary Material S.6.

6. Application Examples

6.1 HIV Biomarker Data

HIV-positive persons who have been on antiretroviral therapy (ART) for a long time tend to be at higher risk of diabetes and other cardiometabolic diseases than those who are HIV-negative. An increasing number of studies are examining biomarkers related to inflammation, metabolism, and immune cell activation, to better understand and prevent cardiometabolic diseases in HIV-positive patients. Here we pool biomarker data from HIV-positive adults on ART with an undetectable viral load (≤ 400 copies/mL) and no history of diabetes or myocardial infarction from two studies: the Vanderbilt Lipoatrophy and Neuropathy Cohort (LiNC; n=147; Koethe et al. (2012)) and the Adiposity and Immune Activation Cohort (AIAC; n=69; Koethe et al. (2016)). We are interested in assessing the pairwise association between five biomarkers: high sensitivity C-reactive protein (hsCRP), interleuken 6 (IL-6), interleuken 1 β (IL-1-β), soluble CD14 (sCD14), and leptin. The first three biomarkers are measures of inflammation, sCD14 is a marker of monocyte activation, and leptin is a hormone that regulates energy balance. These biomarkers are likely influenced by other patient characteristics, and it is possible that some biomarker associations are due to common causes, not to intrinsic relationships between the biomarkers. Hence, we adjusted for patient characteristics that could potentially affect these biomarkers: age, sex, race, body mass index (BMI), CD4 cell count, and smoking status. In addition, we adjusted for study cohort to account for potential differences between measurements across cohorts.

Figure 2 shows pairwise rank correlations between the 5 biomarkers. The upper-left region of the plot shows unadjusted Spearman correlations; the lower-right region shows covariate-adjusted partial Spearman correlations using the methods described earlier. The covariate-adjusted correlations were obtained by fitting CPMs with the logit link for each biomarker, computing PSRs, and then calculating the sample correlation between the PSRs.

Figure 2.

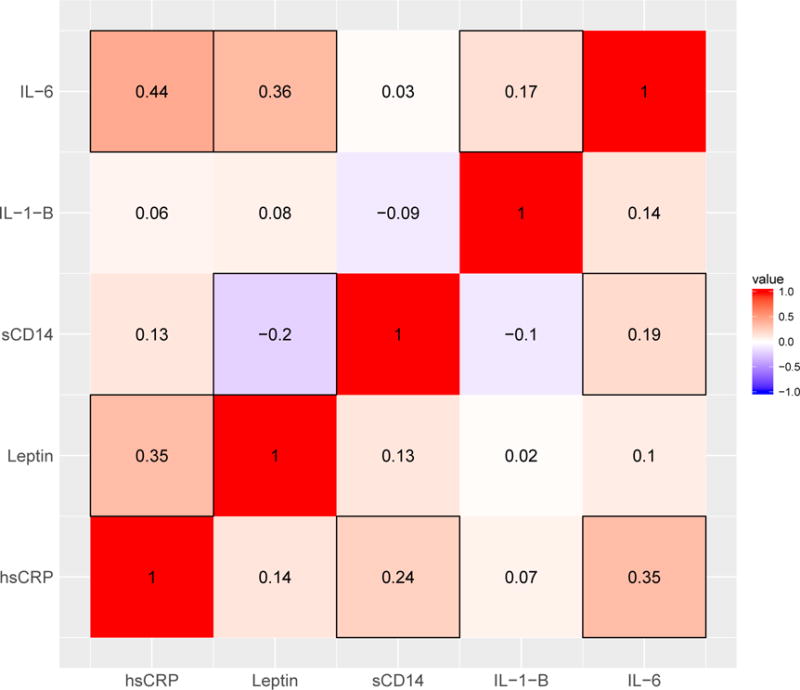
Heat map showing the pairwise Spearman’s rank correlations between 5 biomarkers. The upper-left correlations are unadjusted, the lower-right correlations are partial correlations adjusted for age, sex, race, BMI, CD4 cell count, smoking status, and study cohort. Shading denotes the strength of the correlation with those closer to −1 and 1 being darker. Boxes are placed around correlations whose 95% confidence intervals do not contain zero. This figure appears in color in the electronic version of this article.

Adjusting for covariates had a large impact on some of the rank correlations. For example, the unadjusted rank correlation between IL-6 and sCD14 was close to zero (0.03; 95% confidence interval [CI] −0.11, 0.16), whereas after adjusting for the covariates, the partial rank correlation was significantly positive (0.19; 95% CI 0.04, 0.33). For some other correlations, adjusting for covariates had less of an impact. For example, the association between IL-6 and hsCRP, both markers of inflammation, was strong both before (0.44; 95% CI 0.32, 0.55) and after (0.35; 95% CI 0.22, 0.46) adjusting for covariates.

The association between leptin and sCD14 is interesting because their unadjusted rank correlation was negative, −0.20 (95% CI −0.32, −0.06), whereas the adjusted rank correlation was positive, 0.13 (95% CI −0.01, 0.27). Leptin is known to be positively associated with BMI while sCD14 is negatively associated with BMI (in our data, unadjusted rank correlations were 0.66 and −0.41, respectively). Hence, it is reasonable that after adjusting for BMI and other covariates, the rank correlation changed. It is also of interest to see if this correlation varies as a function of BMI. Obese patients were over-sampled in these studies: nearly half of the patients were obese (BMI > 30 kg/m²), and 20% were severely obese (> 35 kg/m²). The left panel of Figure 3 shows the partial rank correlation between leptin and sCD14 conditional on patient BMI. Again, PSRs from the CPMs described above were used to estimate partial rank correlations as a function of BMI. This was done parametrically using splines (solid line) and non-parametrically using Gaussian kernel smoothers (dashed line) as described in Section 3.3. This figure suggests that the partial rank correlation between leptin and sCD14 varies as a function of BMI, with p-value = 0.024. (This p-value was computed by setting $\widehat{E}\left(X_{\mathit{res}}^2|Z_1\right)=\widehat{E}\left(Y_{\mathit{res}}^2|Z_1\right)=1/3$; estimating ${\gamma }_{XY\cdot Z|Z_1}$ as $3\widehat{E}\left(X_{\mathit{res}}{Y}_{\mathit{res}}|Z_1\right)$, with $\widehat{E}\left(X_{\mathit{res}}{Y}_{\mathit{res}}|Z_1\right)$ modeled using linear regression with BMI expanded using natural splines with 2 degrees of freedom; and applying a Wald-test with variance estimated through M-estimation as motivated in Section 3.3.) In contrast, the partial rank correlation between leptin and sCD14 appears to be fairly stable across age (right panel of Figure 3; p=0.91).

Figure 3.

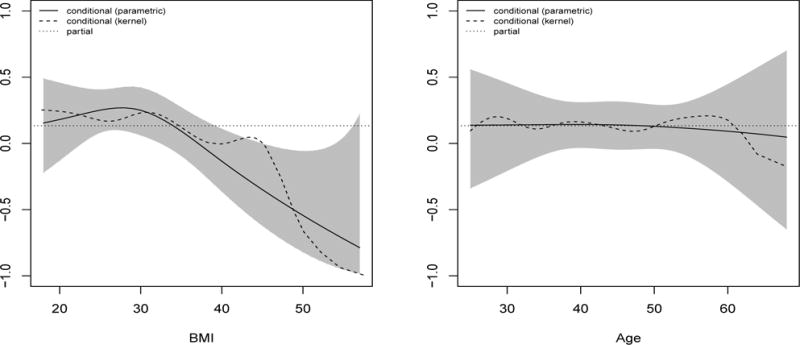
Partial Spearman’s rank correlations between leptin and sCD14 conditional on BMI (left panel) and age (right panel). The solid curve (and shaded region) represent estimates (and pointwise 95% confidence intervals) using a parametric estimation procedure. Specifically, the parametric estimate fit separate ordinary least squares models to the product of the residuals and the square of each set of residuals, including BMI in the models using natural splines with 2 degrees of freedom. The dashed curve represents estimates using a Gaussian kernel smoother, using Silverman’s rule of thumb to select the bandwidth (h = 2.7).

6.2 SCIP Survey Data

In a second example, we use our partial estimator as a quick and robust tool to summarize a large number of covariate-adjusted associations with survey data from the Strengthening Communities through Integrated Programming (SCIP) project. In this survey, 3,892 female heads of household in Mozambique were asked to give opinions on their quality of life, health care, nutrition, education, and other aspects of livelihood. The investigators were interested in the correlations among the participants’ responses to different questions while adjusting for relevant demographic factors. The purpose of such an analysis is largely exploratory, and can be used to focus on particular sets of questions for further study.

We included all 171 questions with orderable responses from 13 modules of the survey, including 54 questions with binary responses, 106 with ordinal responses, and 11 with continuous responses. We fit 171 CPMs using the logit link function and the covariates age, language, marital status, religion, region (urban or rural), and district. The pairwise correlation of PSRs from these models were computed among participants who responded to both questions. A heatmap of our partial Spearman’s correlation matrix is shown in Figure 4. To better visualize the results, we developed a web application (https://scip.shinyapps.io/scip_app) to allow investigators to zoom into any specific area in the heatmap and check the detailed information about the questionnaire and responses. The web application includes 95% confidence intervals and compares results with the unadjusted Spearman’s correlation. More details are given in Supplementary Material S.7.

Figure 4.

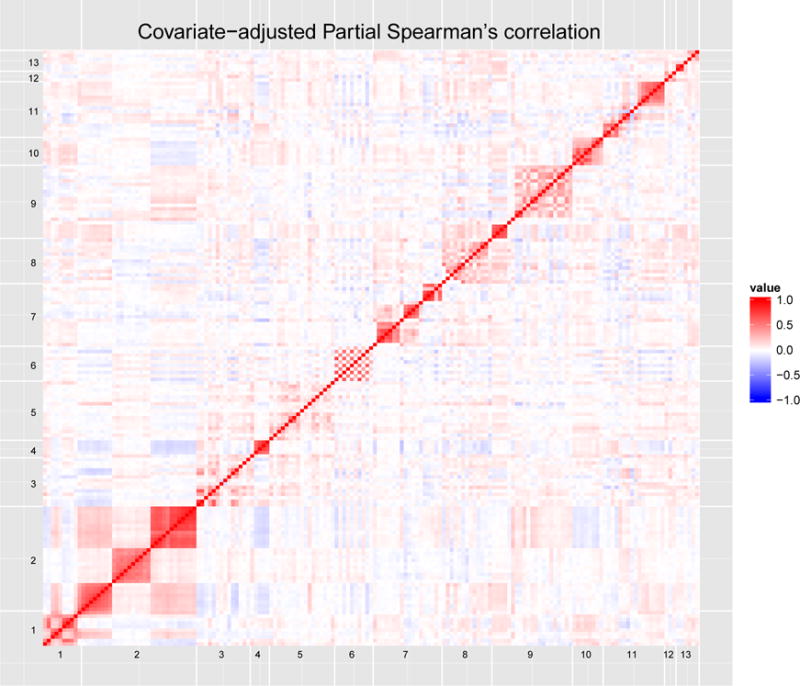
The heatmap of our partial estimators for pairwise Spearman’s rank correlation adjusting for demographic factors for responses to 171 questions from 13 modules of the SCIP survey labeled as 1: overall quality of life, 2: mental health, 3: income, 4: food and nutrition, 5: material goods, 6: transportation, 7: health care, 8: voluntary counseling and testing (VCT) services, 9: HIV prevention, 10: social support, 11: community service, 12: education test result, and 13: perception of education. This figure appears in color in the electronic version of this article. An interactive figure of results is at https://scip.shinyapps.io/scip_app.

7. Discussion

In this work, we express the population parameters of unadjusted, partial, and conditional Spearman’s correlations in terms of probability-scale residuals, which allows us to connect these nonparametric statistics to a variety of regression models. Our methods therefore permit the adjustment of Spearman’s correlation for multidimensional covariates. Similar to Pearson’s partial correlation, Spearman’s partial correlation can now be written as a correlation of residuals. Our framework is very general, applicable to any orderable variables modeled with estimable fitted distributions. Our method requires initially fitting models for the distributions of X and Y given Z, which need to be approximately correct to get unbiased estimates of rank correlations. We suggest fitting semiparametric cumulative probability models to preserve the rank-based nature of Spearman’s correlation while allowing flexible modeling of covariates. The broad applicability, robustness, and computational simplicity of our estimators make them very useful, as illustrated in our HIV biomarker and survey examples.

Since PSRs are widely defined (Shepherd et al., 2016), our framework has the potential to be extended to more complicated settings, such as censored outcomes in which fitted distributions are not completely determined and longitudinal data in which the observations are not independent. We are studying extensions in these settings.

We have developed an R package, PResiduals, that implements the new methods.