Cross-Validation of a Glucose-Insulin-Glucagon Pharmacodynamics Model for Simulation Using Data From Patients With Type 1 Diabetes

Abstract

Background:

Currently, no consensus exists on a model describing endogenous glucose production (EGP) as a function of glucagon concentrations. Reliable simulations to determine the glucagon dose preventing or treating hypoglycemia or to tune a dual-hormone artificial pancreas control algorithm need a validated glucoregulatory model including the effect of glucagon.

Methods:

Eight type 1 diabetes (T1D) patients each received a subcutaneous (SC) bolus of insulin on four study days to induce mild hypoglycemia followed by a SC bolus of saline or 100, 200, or 300 µg of glucagon. Blood samples were analyzed for concentrations of glucagon, insulin, and glucose. We fitted pharmacokinetic (PK) models to insulin and glucagon data using maximum likelihood and maximum a posteriori estimation methods. Similarly, we fitted a pharmacodynamic (PD) model to glucose data. The PD model included multiplicative effects of insulin and glucagon on EGP. Bias and precision of PD model test fits were assessed by mean predictive error (MPE) and mean absolute predictive error (MAPE).

Results:

Assuming constant variables in a subject across nonoutlier visits and using thresholds of ±15% MPE and 20% MAPE, we accepted at least one and at most three PD model test fits in each of the seven subjects. Thus, we successfully validated the PD model by leave-one-out cross-validation in seven out of eight T1D patients.

Conclusions:

The PD model accurately simulates glucose excursions based on plasma insulin and glucagon concentrations. The reported PK/PD model including equations and fitted parameters allows for in silico experiments that may help improve diabetes treatment involving glucagon for prevention of hypoglycemia.

The treatment goal for patients with type 1 diabetes is near-normalization of plasma glucose levels. Few patients achieve this even with intensive insulin treatment.¹ New approaches with automatic glucose controlled insulin and glucagon delivery, known as a dual-hormone artificial pancreas (AP), may offer a solution to improve glycemic control.^2-6 To design and tune control algorithms for AP devices prior to in vivo tests, a validated simulation model capturing the dynamics between glucose, insulin and glucagon is needed to perform helpful in silico experiments.^7-9

Glucagon primarily affects hepatic glucose production by increasing glycogenolysis, while the rate of gluconeogenesis seems less affected by changes in both insulin and glucagon concentrations.¹⁰ Currently marketed glucagon is approved as a 1 mg rescue-treatment for severe hypoglycemia, although the interest in mini-dose glucagon is increasing.^11,12 Recent studies proved that the glycemic response to low-dose glucagon is dependent on ambient insulin levels,¹³ but neither on plasma glucose level^14,15 nor on prior glucagon dosing.¹⁶ At high circulating insulin concentrations (50-60 mU/l), the endogenous glucose production (EGP) is completely inhibited,¹⁷ and at insulin levels exceeding ~40 mU/l the EGP cannot be stimulated by glucagon.¹³

The ability of insulin to suppress the glycogenolytic response to glucagon at high insulin concentration is not reflected in previously published models of glucose-glucagon dynamics.^18-20 A comparative study found that a multiplicative relationship was needed to describe insulin’s inhibitory effect and glucagon’s stimulating effect on glycogenolysis with insulin overriding the effect of glucagon at high concentrations of both hormones.²¹ Recently, we extended the multiplicative model by incorporating the interaction between insulin and glucagon on glycogenolysis.^13,22 The model extension was developed using preclinical data from dogs and was fitted to clinical human data in previous studies.^23,24 In this article, we aim to validate the multiplicative glucose-insulin-glucagon model for simulation studies in humans using data from eight patients with type 1 diabetes.

Methods

Data Collection

Clinical data originated from a glucagon dose-finding study in eight well-controlled patients with type 1 diabetes (5 females, age range: 19-64 years, BMI range: 20.0-25.4 kg/m², HbA1c range: 6.1-7.4%), who were insulin pump-treated and had no endogenous production of insulin.²⁵ Table S1 summarizes the patient characteristics. In brief, the patients completed four similar study days in random order. On each study day, patients arrived at the research facility in the morning in a fasting state. A subcutaneous (SC) insulin bolus (NovoRapid®, Novo Nordisk A/S, Bagsværd, Denmark) was administered via the patient’s insulin pump, aiming to lower plasma glucose to 54 mg/dl if no interventions were made. The insulin bolus was calculated based on each patient’s individual sensitivity factor, which was determined prior to the first study visit using a standard procedure.²⁶ When plasma glucose reached ≤70 mg/dl, a single SC bolus of either 100 µg (visit B), 200 µg (visit C), 300 µg (visit D) glucagon (GlucaGen®, Novo Nordisk A/S, Bagsværd, Denmark), or saline (visit A) was administered (see Figure 1). Blood was sampled and analyzed for plasma glucose (YSI 2300 STAT Plus, Yellow Springs Instrument, Yellow Springs, OH), plasma glucagon²⁷ and serum insulin aspart (Mercodia AB, Uppsala, Sweden). The insulin pump continuously infused insulin as a basal rate during the study days. The insulin infusion rate was adjusted before the first study day, to keep near constant blood glucose values in the fasting and resting condition. The individual insulin infusion basal rates were similar between study visits.

Figure 1.

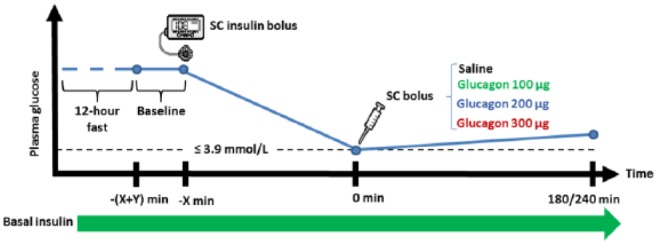
Schematic design of the study days. Baseline blood samples were taken at time –(X+Y). An insulin bolus was given after Y minutes. In a few cases, multiple insulin boluses had to be administered to lower the plasma glucose sufficiently. When the plasma glucose measured below 70 mg/dl, a saline or glucagon bolus was given depending on the study day. At 180 or 240 minutes after the saline/glucagon bolus the experiment was stopped. Basal insulin infusion continued throughout the experiment. From t = –x to t = 0, plasma glucose was measured every 15-30 minutes, while plasma glucagon and serum insulin were measured every 60 minutes. Plasma glucose was measured every 5 minutes from t = 0 to t = 60, every 10 minutes from t = 60 to t=120 and then every 15 minutes. Plasma glucagon and serum insulin were measured every 5 minutes from t = 0 to t = 15, every 15 minutes from t = 15 to t = 60, every 30 minutes from t = 60 to t = 120, and then every 60 minutes.

Models

When applying a pharmacokinetic (PK) model, we assume that all increases in insulin and glucagon concentrations are due to exogenously dosed drugs so that endogenous production is constant or negligible.

Insulin Pharmacokinetic Model

Previous studies showed that a simple two-state model with identical time constants for absorption and elimination could be used to describe the PK of insulin aspart after SC dosing.²⁸

$$\frac{d{X}_1\left(t\right)}{dt}=u_I\left(t\right)-\frac{X_1\left(t\right)}{t_{max}}$$

$$\frac{d{X}_2\left(t\right)}{dt}=\frac{X_1\left(t\right)}{t_{max}}-\frac{X_2\left(t\right)}{t_{max}}$$

$$I\left(t\right)=\frac{1}{t_{max}}\frac{X_2\left(t\right)}{W\cdot C{l}_{F,I}}{10}^6+I_b$$

Table 1 lists the interpretations of the insulin PK model parameters and their units. The insulin concentration in serum is the sum of external rapid acting insulin dosage and basal infusion. The model assumes steady state insulin concentration, I_b, maintained by the basal infusion when no exogenous rapid acting insulin is dosed.

Table 1.

Interpretation of Insulin PK (Top Rows), Glucagon PK (Middle Rows), and Glucose PD (Bottom Rows) Model Parameters and Their Units.

Parameter	Unit	Interpretation
X1(t)	U	Insulin mass due to exogenous dosing, in SC tissue
X2(t)	U	Insulin mass due to exogenous dosing, in serum
uI(t)	U/minute	Insulin dose
tmax	minutes	Time from dose to maximum serum concentration
W	kg	Body weight
ClF,I	ml/kg/minute	Apparent insulin clearance
Ib	mU/l	Steady state insulin concentration
I(t)	mU/l	Insulin concentration in serum
Z1(t)	pg	Glucagon mass due to exogenous dosing, in SC tissue
Z2(t)	pg	Glucagon mass due to exogenous dosing, in plasma
uC(t)	pg/minute	Glucagon dose
k1	minute-1	Absorption rate constant
k2	minute-1	Elimination rate constant
ClF,C	ml/kg/minute	Apparent glucagon clearance
Cb	pg/ml	Steady state glucagon concentration
C(t)	pg/ml	Glucagon concentration in plasma
Q1(t)	µmol/kg	Glucose mass per W in the accessible compartment
Q2(t)	µmol/kg	Glucose mass per W in the nonaccessible compartment
x1(t)	mU/l	Remote effects of insulin on glucose transport
x2(t)	mU/l	Remote effects of insulin on glucose disposal
x3(t)	mU/l	Remote effects of insulin on glycogenolysis
G(t)	mmol/l	Glucose concentration in plasma
GGG(t)	µmol/kg/minute	Glucose production due to glycogenolysis
GGNG	µmol/kg/minute	Glucose production due to gluconeogenesis
F01	µmol/kg/minute	Insulin independent glucose flux
FR	µmol/kg/minute	Renal glucose clearance
ST	minute-1/(mU/l)	Insulin sensitivity of glucose transport
SD	minute-1/(mU/l)	Insulin sensitivity of glucose disposal
SE	l/mU	Insulin sensitivity on glycogenolysis
k12	minute-1	Transfer rate constant from the nonaccessible to the accessible compartment
ka1	minute-1	Insulin deactivation rate constant
ka2	minute-1	Insulin deactivation rate constant
ka3	minute-1	Insulin deactivation rate constant
Emax	µmol/kg/minute	Maximum EGP at basal insulin concentration
CE50	pg/ml	Glucagon concentration yielding half of maximum EGP
V	ml/kg	Glucose volume of distribution

Glucagon Pharmacokinetic Model

A two-state model with different absorption and elimination rate constants can describe glucagon PK after SC dosing.²³

$$\frac{d{Z}_1\left(t\right)}{dt}=u_C\left(t\right)-k_1{Z}_1\left(t\right)$$

$$\frac{d{Z}_2\left(t\right)}{dt}=k_1{Z}_1\left(t\right)-k_2{Z}_2\left(t\right)$$

$$C\left(t\right)=\frac{k_2{Z}_2\left(t\right)}{W\cdot C{l}_{F,C}}+C_b$$

Table 1 lists the interpretations of the glucagon PK model parameters and their units. The glucagon concentration in plasma is the sum of constant endogenous glucagon, C_b, and external glucagon dosage. The model does not include an endogenous response to hypoglycemia.

Glucose Pharmacodynamic Model

The glucose PD model was originally derived by Hovorka et al^29,30 and further extended by Wendt et al.²³

$$\begin{array}{l}\frac{d{Q}_1\left(t\right)}{dt}=-F_{01}-F_R-S_T{x}_1\left(t\right)Q_1\left(t\right)\\ +k_{12}{Q}_2\left(t\right)+G_{GG}\left(t\right)+G_{GNG}\end{array}$$

$$\frac{d{Q}_2\left(t\right)}{dt}=S_T{x}_1\left(t\right)Q_1\left(t\right)-\left[k_{12}+S_D{x}_2\left(t\right)\right]Q_2\left(t\right)$$

$$G_{GG}\left(t\right)=\frac{1-S_E{x}_3\left(t\right)}{1-S_E{I}_b}\left(\left(E_{max}-G_{GNG}\right)\frac{C\left(t\right)}{C_{E50}+C\left(t\right)}\right)$$

$$G\left(t\right)=\frac{Q_1\left(t\right)}{V}$$

$$\frac{d{x}_1\left(t\right)}{dt}=k_{a1}\left[I\left(t\right)-x_1\left(t\right)\right]$$

$$\frac{d{x}_2\left(t\right)}{dt}=k_{a2}\left[I\left(t\right)-x_2\left(t\right)\right]$$

$$\frac{d{x}_3\left(t\right)}{dt}=k_{a3}\left[I\left(t\right)-x_3\left(t\right)\right]$$

Table 1 lists the interpretations of the glucose PD model parameters and their units. The endogenous glucose production is the sum of glycogenolysis, G_GG, and gluconeogenesis, G_GNG. The gluconeogenesis is fixed at 6 µmol/kg/minute.¹⁰ F₀₁ is constant when plasma glucose concentration exceeds 81 mg/dl.³⁰ The renal glucose clearance is zero when plasma glucose concentrations do not exceed 162 mg/dl.³⁰ The glucose volume of distribution is fixed at 160 ml/kg.²⁹

Model Fitting

All model fitting was executed in R version 3.1.0 Spring Dance using the additional packages CTSM-R and numDeriv.³¹ Additional data handling was carried out using Microsoft Excel 2013. Unless stated otherwise, the results are reported as means with 95% Wald confidence intervals (CIs) derived from the inverse Hessian, which provides the curvature of the log-likelihood function.³²

We fitted the insulin PK model using ordinary differential equations (ODEs) and estimated the log-normally distributed observation noise variance using maximum likelihood (ML).³³ Due to missing insulin data around the expected time of maximum insulin concentration both t_max and Cl_F,I were estimated using maximum a posteriori (MAP) while I_b was estimated using ML. Prior distributions of t_max and Cl_F,I were reported in Haidar et al²⁸ and further information regarding t_max was extracted from the product monograph on insulin aspart.³⁴ Table S2 lists the prior parameter distributions. No prior correlation between t_max and Cl_F,I was assumed.

Insulin PK parameters were optimized on a subject basis to datasets from all four visits (8 parameter sets reported). Despite SC infusion rates of short acting insulin (ie, the basal rates) were similar per subject for all study visits, the baseline insulin concentration varied as evident from the raw data plotted in Figures S1-S7. Therefore, the parameter describing the steady state insulin level was estimated separately for each visit. Using the subject specific optimized parameters, the insulin PK was simulated every minute and used as input to the PD model.

We fitted the glucagon PK model for visits B, C, and D using ODEs and estimated the log-normally distributed observation noise variance using ML. Plasma glucagon was sampled adequately to perform ML estimation of all parameters in the glucagon PK model. There was some uncertainty regarding the exact dosing time of the glucagon bolus, which was given after the blood sampling at time zero but before the next blood sampling five minutes after. Due to this uncertainty, we estimated the dosing time by choosing the discrete dosing time within the five-minute interval yielding the fit with the highest likelihood value and kept this updated dosing time throughout the data fitting and handling.

As the absolute elimination rate of glucagon is limited by the absorption rate, glucagon exerts flip-flop kinetics.³⁵ To avoid the flip-flop phenomenon and to reduce the population variation in the two time constants, k₂ was parameterized such that it was greater than k₁ in all datasets.

The glucagon PK parameters were estimated to the datasets from visits with glucagon dosing (24 parameter sets, data not shown) and the PK simulated every minute to be used as input when fitting the PD model. On a subject basis, the glucagon PK parameters were optimized to datasets from all three glucagon visits (8 parameter sets reported). Due to the limited amount of data, we assumed the parameters did not differ between the visits.

The data following administration of saline (visit A) were not fitted to the glucagon PK model but described using linear interpolation between measurements. These interpolated data were used as inputs to the PD model.

The PD model was fitted using ODEs and the log-normally distributed observation noise variance estimated using ML. The remaining parameters (E_max, C_E50, F₀₁, k₁₂, k_a1, k_a2, k_a3, S_D, S_E, S_T) were estimated using MAP with priors inspired by literature.^22,29 We used priors for the time constants rather than fixing the four parameters.³⁰ The time constants and the insulin sensitivities were log-transformed during the parameter estimation. Table S2 lists the prior PD model parameter distributions. The PD model parameters have units yielding a glucose output measured in mmol/l, but the output is converted and graphically displayed with units of mg/dl. We assumed no prior correlation between parameters. As previously mentioned, glucose volume of distribution and gluconeogenesis were both fixed based on literature.^10,29 I_b was fixed for each subject based on their average steady state insulin concentration. The final PD model parameters were obtained by optimizing the fit to all nonoutlier visits by each subject (8 parameter sets reported).

Pharmacodynamic Model Validation

To quantify the simulation accuracy of the model on datasets not used for parameter optimization, the bias was calculated by the mean prediction error (MPE) and the precision calculated by the mean absolute prediction error (MAPE). MPE and MAPE were calculated as percentages.³⁶

$$MPE=\frac{1}{N}{\displaystyle \sum }_{j=1}^N\left[\left(\frac{pre{d}_j-ob{s}_j}{ob{s}_j}\right)\times 100\right]$$

$$MAPE=\frac{1}{N}{\displaystyle \sum }_{j=1}^N\left[\left(\frac{\left|pre{d}_j-ob{s}_j\right|}{ob{s}_j}\right)\times 100\right]$$

The variables pred_j and obs_j are the jth predicted and observed value, respectively of a total of N observations. If the MPE is less than ±15% and the MAPE is less than 20%, we regard the model fit as accurate, precise and suitable for simulations. Cut-off limits were based on categorizing some fits as “good,” “medium,” and “bad” prior to knowledge of those fits’ MPE and MAPE values by two independent raters. The limits were chosen so that all fits categorized as “good” by both raters would be accepted and all fits categorized as “bad” by both raters would not meet the acceptance criteria.

The PD model validation was carried out as a fourfold leave-one-out cross-validation leaving all data from one visit out per fold. As each subject participated in four visits, each subject had four training datasets comprised of data from three visits and four corresponding test datasets with data from one visit:

• Training: B-C-D, Test: A

• Training: A-C-D, Test: B

• Training: A-B-D, Test: C

• Training: A-B-C, Test: D

Thus, all four visits were used for testing once without being used for optimization during that fold. If the MAPE of a test fit exceeded 50%, the test visit was considered an outlier and removed from further analysis. After removal of the outlier dataset another round of leave-one-out was performed on the remaining three datasets. To validate the PD model in a subject, we required that at least one PD model test fit of a dataset from a glucagon visit (B, C or D) was accepted.

Results

Table 2 lists the estimated insulin PK model parameters. The fasting steady state insulin concentration had day-to-day variation within patients of up to 6 mU/l and ranged from 3.0 mU/l to 22.6 mU/l between subjects. The mean of all steady state insulin concentrations was 9.7 mU/l. The time to maximum concentration ranged from 40.8 to 68.5 minutes and the apparent clearance ranged from 14.8 to 26.8 ml/kg/minute.

Table 2.

Summary of Insulin PK Model Parameters for Simulation With Range of Means and 95% CI or Mean and 95% CI.

Patient	Ib (mU/l)	tmax (min)	ClF,I (ml/kg/min)
1	6.6-7.8 (6.0-8.3)	57.6 (50.9-64.3)	18.9 (17.3-20.6)
2	10.0-11.2 (9.1-12.0)	57.3 (48.8-65.9)	18.5 (16.1-21.2)
3	10.3-13.4 (9.7-14.0)	40.8 (37.6-44.0)	14.8 (13.6-16.1)
4	7.8-9.4 (7.4-9.9)	67.9 (63.5-72.2)	17.4 (16.6-18.3)
5	5.2-8.2 (4.8-8.8)	48.5 (44.7-52.4)	17.3 (15.7-19.0)
6	3.0-8.5 (2.3-9.4)	46.5 (41.7-51.3)	24.6 (22.9-26.3)
7	16.8-22.6 (15.6-23.6)	68.5 (60.6-76.4)	23.7 (21.3-26.4)
8	4.7-9.1 (4.4-9.6)	55.4 (49.6-61.2)	26.8 (24.8-29.0)

Table 3 lists the estimated glucagon PK model parameters and the calculated time to maximum concentration. The fasting steady state glucagon concentrations were similar in the range 7.6-11.6 pg/ml for all patients except patient 8 who had a concentration of 19.0 pg/ml. The absorption and elimination time constants ranged from 0.022 to 0.058 minute^-1 and 0.058 to 0.28 minute^-1, yielding a calculated time to maximum concentration of 7.5-19.1 minutes. The apparent clearance ranged from 91 to 200 ml/kg/minute.

Table 3.

Summary of Glucagon PK Model Parameters for Simulation With Mean and 95% CI.

Patient	Cb (pg/ml)	k1 (min-1)	k2 (min-1)	ClF,C (ml/kg/min)	tmax (min)
1	10.7 (9.4-12.0)	0.042 (0.036-0.048)	0.14 (0.10-0.22)	94 (83-105)	12.2
2	7.6 (6.9-8.3)	0.056 (0.052-0.062)	0.26 (0.18-0.38)	106 (96-116)	7.5
3	7.6 (5.9-9.3)	0.022 (0.018-0.028)	0.10 (0.06-0.17)	114 (96-132)	19.1
4	10.9 (9.2-12.6)	0.058 (0.011-0.313)	0.058 (NA)	159 (133-184)	17.3
5	8.7 (7.7-9.8)	0.038 (0.032-0.044)	0.19 (0.13-0.29)	200 (176-223)	10.7
6	8.9 (7.8-10.0)	0.035 (0.031-0.040)	0.28 (0.19-0.41)	125 (111-138)	8.6
7	11.6 (10.1-13.0)	0.035 (0.030-0.041)	0.25 (0.16-0.39)	136 (120-152)	9.2
8	19.0 (16.1-22.0)	0.052 (0.037-0.072)	0.090 (0.04-0.26)	91 (78-105)	14.5

Table 4 provides an overview of the leave-one-out cross-validation procedure of the PD model. The MPE and MAPE for the test fits are listed together with a dichotomous decision of acceptance or not using the criteria outlined in the “Pharmacodynamic Model Validation” section. Based on the MAPE during leave-one-out, we excluded four outlier datasets from further analysis and these four patients had a second round of leave-one-out including the remaining three datasets. Overall, the test fit was accepted two to three times out of three in three patients, and one to two times out of four in four patients. In patient 8 we did not accept any of the test fits even after removal of an outlier dataset. Figure 2 presents examples of PD model test fits and corresponding MPE and MAPE values of the test fits both passing and violating the acceptance criteria. In summary, the PD model successfully predicted unseen glucose data at least once in seven patients and therefore we regard the PD model as validated and suitable for simulation studies of these seven type 1 diabetes patients.

Table 4.

PD Model Validation Using Leave-One-Out Cross-Validation.

Patient	Training visits	Test visit	MPE (%)	MAPE (%)	Accept? (Y/N)
1	BCD	A	–25.0	25.0	N
	ACD	B	–11.3	13.7	Y
	ABD	C	78.8	78.8	Na
	ABC	D	3.3	25.5	N
	BD	A	–10.3	11.1	Y
	AD	B	10.4	13.1	Y
	AB	D	4.0	21.3	N
2	BCD	A	29.1	29.8	N
	ACD	B	–18.2	18.7	N
	ABD	C	–6.3	7.5	Y
	ABC	D	6.3	10.0	Y
3	BCD	A	10.3	17.4	Y
	ACD	B	–2.3	8.6	Y
	ABD	C	23.4	24.6	N
	ABC	D	–20.1	20.1	N
4	BCD	A	–17.3	18.9	N
	ACD	B	–9.4	11.1	Y
	ABD	C	–23.6	23.7	N
	ABC	D	38.2	38.4	N
5	BCD	A	–13.4	13.4	Y
	ACD	B	–30.0	30.4	N
	ABD	C	–16.3	21.3	N
	ABC	D	74.6	74.6	Na
	BC	A	–1.7	4.5	Y
	AC	B	–9.8	14.1	Y
	AB	C	–7.5	17.4	Y
6	BCD	A	–23.5	24.2	N
	ACD	B	–4.5	12.0	Y
	ABD	C	59.0	59.0	Na
	ABC	D	–8.6	16.3	Y
	BD	A	–13.7	16.9	Y
	AD	B	16.7	17.5	N
	AB	D	4.7	15.8	Y
7	BCD	A	43.0	43.3	N
	ACD	B	–19.0	19.0	N
	ABD	C	–2.9	19.0	Y
	ABC	D	6.0	8.0	Y
8	BCD	A	–8.0	12.4	Y
	ACD	B	–32.9	33.0	N
	ABD	C	–14.5	24.2	N
	ABC	D	174.1	174.1	Na
	BC	A	–26.2	26.2	N
	AC	B	–24.6	24.6	N
	AB	C	42.5	42.5	N

Initially, data from three visits are used for training the model, ie, optimizing model parameters, and data from the fourth visit are used for testing the model with the optimized parameters.

^aA test fit with MPE or MAPE exceeding 50% is considered an outlier. The outlier dataset is removed and another round of leave-one-out cross-validation is performed on the remaining three visits.

Figure 2.

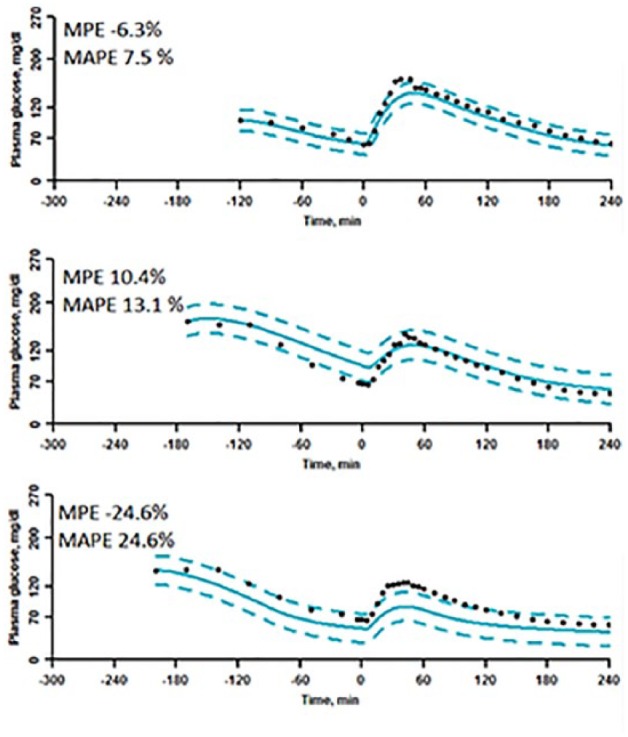
Examples of validation PD model fits with “good,” “medium,” and “bad” MPE and MAPE. Top graph is test of patient 2’s visit C (accepted). Middle graph is test of patient 1’s visit B (accepted). Bottom graph is test of patient 8’s visit B (not accepted).

Table 5 lists the PD model parameters optimized to all nonoutlier visits in each patient with mean parameter values and 95% CI. The parameter describing the maximum EGP at steady state insulin concentration, E_max, ranged from 56 to 84 µmol/kg/minute. The glucagon concentration at which the effect is half maximum, C_E50, ranged from 141 to 436 pg/ml. Extrapolated to zero insulin and at basal glucagon concentration, the EGP ranged from 7 to 13.3 µmol/kg/minute. According to the inverse of the parameter describing the insulin sensitivity to EGP, S_E, the calculated insulin concentration at which the effect of glucagon shuts off ranged from 22 to 71 mU/l. Figures 3 and S1-S7 provide simulations of patient optimized PD model fits and data.

Table 5.

Summary of PD Model Parameters for Simulation With Mean and 95% CI.

ID	Data	CE50 (pg/ml)	Emax (µmol/kg/min)	F01 (µmol/kg/min)	k12*10-4 (min-1)	ka1*10-4 (min-1)	ka2*10-4 (min-1)	ka3*10-4 (min-1)	SD*10-4 (min-1/(mU/l))	SE*10-4 ((mU/l)-1)	ST*10-4 (min-1/(mU/l))
1	ABD	436 (355-517)	56.4 (51.1-61.8)	14.2 (12.9-15.5)	244 (181-330)	16 (7-35)	522 (221-1233)	215 (59-778)	1.5 (0.6-3.3)	155 (83-289)	23 (16-31)
2	ABCD	405 (339-471)	67.4 (59.3-75.5)	13.8 (12.8-14.7)	285 (223-363)	15 (7-35)	495 (236-1039)	231 (137-389)	1.2 (0.6-2.3)	334 (232-481)	19 (15-25)
3	ABCD	401 (327-475)	57.4 (49.8-65.0)	15.5 (14.2-16.8)	397 (277-568)	18 (8-42)	548 (268-1121)	327 (168-638)	1.4 (0.7-2.5)	237 (183-308)	25 (17-36)
4	ABCD	285 (226-344)	84.4 (73.9-94.8)	12.8 (11.3-14.4)	213 (157-289)	18 (9-36)	437 (183-1044)	68 (42-113)	2.0 (1.0-3.8)	415 (347-496)	18 (13-25)
5	ABC	339 (251-427)	65.4 (53.8-77.1)	12.0 (10.6-13.5)	281 (194-406)	15 (7-32)	517 (223-1201)	235 (95-586)	1.1 (0.4-2.6)	229 (127-415)	31 (20-47)
6	ABD	424 (333-515)	60.1 (46.3-74.0)	13.1 (11.7-14.5)	238 (172-330)	10 (4-22)	353 (102-1221)	74 (23-232)	2.6 (1.1-6.2)	404 (185-882)	21 (14-32)
7	ABCD	141 (96-187)	78.0 (68.9-87.1)	14.2 (12.2-16.1)	358 (252-509)	49 (23-105)	624 (319-1221)	178 (69-459)	4.4 (3.2-6.0)	140 (99-199)	21 (16-29)
8	ABC	307 (228-386)	75.3 (61.5-89.1)	13.4 (11.4-15.4)	289 (197-424)	37 (18-75)	518 (203-1324)	154 (68-348)	4.2 (2.8-6.5)	463 (377-569)	29 (20-42)

Figure 3.

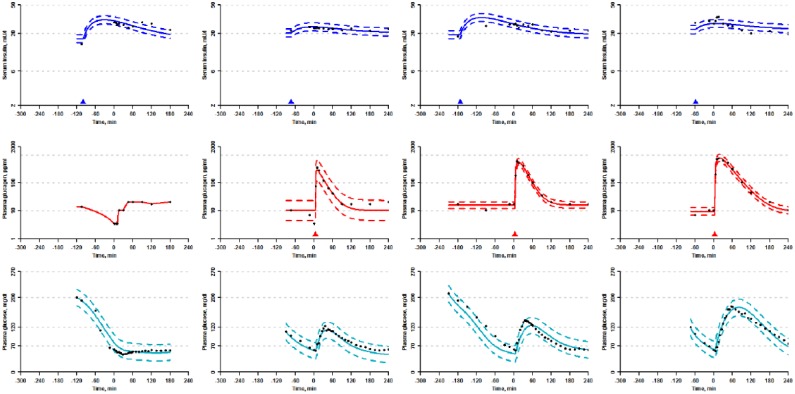
Data from all of patient 7’s visits (left to right: visit A to D) with insulin PK model fits (top row, logarithmic y-axes) and glucagon linear interpolation or PK model fits (middle row, logarithmic y-axes) both used as inputs to the glucose PD model for simulation built with data from all four visits (bottom row). The triangles indicate dose time of the insulin and glucagon boluses, respectively.

Discussion

We fitted simple PK models of serum insulin and plasma glucagon after SC bolus administrations of the hormones. The simulated concentrations of insulin and glucagon were used as inputs to the PD model. We sought to validate the PD model for simulations in eight type 1 diabetes patients and succeeded in seven. Finally, we estimated the patient’s individual PD model parameters.

The fitted insulin PK model assumes that all changes in serum insulin concentration are due to SC insulin dosing. This is a valid assumption as no patients had measureable endogenous insulin secretion after glucagon stimulation.²⁵ Patients’ insulin levels are at steady state when no insulin bolus is administered.

The clinical study focused on generating data describing the effect of glucagon on glucose, and therefore only few data points describing the insulin PK were obtained. The insulin PK data were sampled very sparsely around the expected time of maximum concentration. The missing data did not allow for ML estimation of the insulin PK model. However, using literature informed prior distributions of both t_max and Cl_F,I and optimizing for all four visits simultaneously we obtained reasonable fits by MAP estimation.^28,34

As the insulin PK model was fitted to in-hospital sedentary patients, its application in patients with type 1 diabetes outside the hospital setting may be limited due to numerous factors affecting insulin absorption rate, sensitivity and bioavailability. Such factors could be accounted for by introducing time-variant model parameters, which was beyond the scope of this work.^9,37,38 Especially, differences in insulin absorption could explain the observed intrapatient variation in steady state insulin concentration despite equal basal rates at all four visits.

Patients with type 1 diabetes have a blunted glucagon response to hypoglycemia compared to healthy subjects.³⁹ The fitted glucagon PK model assumes that all changes in plasma glucagon concentration are due to SC dosing and that the endogenous production is constant or negligible. To verify this assumption, we determined the size of the endogenous glucagon response to hypoglycemia during the saline day and compared it to simulations of glucagon PK in each of the eight subjects (data not shown). We found that exogenous glucagon doses of 1-10 µg would equal the plasma glucagon increase to hypoglycemia. Since the endogenous glucagon response to hypoglycemia was at most one tenth of the administered dose during the glucagon days, this confirmed that the endogenous response during these days was negligible compared to the exogenous dosed glucagon. However, the endogenous response was not negligible during the saline day and therefore the glucagon PK model was not applicable to those datasets.

The glucagon PK fit was challenged by the short time to maximum concentration combined with the uncertainty of the exact dosing time of glucagon. This could potentially result in an error in time to maximum concentration of up to ±4 minutes. However, this possible deviation has minor impact on the PD model fit when the glucagon PK fit is used as an input. Despite the dosing time uncertainty, the calculated times to maximum concentration are within reasonable range of population averages reported in the literature.^28,40 In the model by Haidar et al,²⁸ the glucagon absorption rate and elimination rate were identical which we only observed in patient 4. In the remaining seven patients, the elimination rate was significantly higher than the absorption rate. Moreover, having different absorption and elimination rate constants we observed a higher clearance rate. Compared to Haidar et al, we found lower basal concentration of glucagon, which could be attributed to differences in the assays for analysis of plasma glucagon concentration.²⁶

Despite using informed priors for all PD model parameters, some optimized parameters are very different from the population mean and vary considerably more than originally listed in Hovorka et al.²⁹ However, the original reference is based on a population of only six subjects, which makes it unlikely that all true population variations were captured, and we believe, therefore, that our parameter estimates are still valid. Similarly, with a population of eight subjects, we did not fit a population model but focused on estimating parameters for each subject individually.

The limited human data on EGP response to glucagon are consistent with data from dogs.²² As the human response to high glucagon concentrations has not been thoroughly investigated, the dog data provide best guesses of the human values. The maximum EGP due to glucagon and glucagon concentration at half-maximum effect at basal insulin average around 60 µmol/kg/minute and 300 pg/ml in dogs.²² Our results match the reference values and therefore seem plausible.

We found that EGP at zero insulin and basal glucagon is somewhat lower than previous publications, which state 10-20 µmol/kg/minute²⁹ and ~30 µmol/kg/minute.²² This might be due to the fixation of gluconeogenesis at 6 µmol/kg/minute,¹⁰ which is increased in subjects with poorly controlled type 1 diabetes compared to the present well-controlled patients or healthy subjects.^25,41 Assuming the proposed model of EGP is correct, the insulin concentration at which the glycogenolysis, hence the effect of glucagon, shuts off is reasonable compared to the limited publications showing glycogenolysis at various insulin concentrations.^22,42 Rizza et al found that the glucose production was suppressed by insulin beyond approximately 60 mU/l.¹⁷ El Youssef et al found that at serum insulin concentrations beyond 40 mU/l glucagon concentrations below 450 pg/ml did not stimulate EGP.¹³ Further clinical studies are needed to investigate whether high insulin concentrations completely suppress the effect of glucagon or whether the maximum EGP is still attainable though at higher glucagon concentrations.

A major limitation to some of the previously published models describing the effect of glucagon on glucose production is lack of validation.^18,21 We were able to mimic never-before-seen glucose data at least once and at most three times in seven of the eight subjects using the presented glucose PD model. We did not expect to accept the test fit of all nonoutlier datasets in each subject as the visits often described complimentary dynamics of the glucose-insulin-glucagon relationship; for instance the placebo day had very limited information on how different glucagon concentrations affects EGP as glucagon levels were changing very little. On the contrary, the placebo datasets were rich in information about the effects of insulin on plasma glucose. Some glucagon datasets had few observations of the effects of insulin on EGP as the plasma glucose some days reached the bolus threshold of 70 mg/dl quickly, for example, in subjects 2 and 7 shown in Figure S2 and Figure 3, respectively. As an example, this difference in data sampling can explain why it was not possible to validate the model using subject 2’s visit B as the test dataset. For this particular patient, the placebo visit was stopped early and therefore does not contain much information about the insulin dynamics. Moreover, the insulin only phase of visit B lasted nearly five hours and only two hours during visits C and D. Leaving visit B out of the training dataset does not provide the model with enough information to predict the insulin dynamics present in visit B. We noted that in most cases when the test fit was not accepted there was a monotone bias in the residuals yielding almost equal values of absolute MPE and MAPE (see Table 4). This bias indicates that the test fit would either over- or undershoot compared to data and thus both insulin and glucagon dynamics of the test dataset were not well described by the training datasets. Analyzing the PD model parameters during leave-one-out in Tables S3-S10, we observed that when a test fit could not be accepted, usually one or more parameters were outside the CI obtained when fitting to all nonoutlier data. Therefore, failing to accept the test fit during a fold is not necessarily a sign of an incorrect model structure. Rather it could emphasize that the test dataset contains unique information about the dynamics, which are not present in any of the training datasets.⁴³ However, in four patients one dataset was so different from the other three datasets that it had to be excluded from the final PD model estimation as it would otherwise affect the parameters and yield bad fits for all four study days.

Simulation models are rarely validated on unseen data. The only glucose model including glucagon that is currently validated and FDA approved has undisclosed parameter values and can only be accessed by payment.^19,44 We believe that this article is a step toward more openly sharing simulation models that will allow more research groups to test dual-hormone dosing strategies and control algorithms for managing diabetes before carrying out expensive simulations or clinical trials.

Conclusion

We have successfully validated a model describing the glucose-insulin-glucagon dynamics in seven type 1 diabetes subjects using leave-one-out cross-validation. We have reported model parameter sets with uncertainties for each subject, which could be used for in silico experiments. Simulations could also aid in optimizing treatment for type 1 diabetes patients such as glucagon dosing strategies for preventing hypoglycemia and tuning control strategies for an AP.