Experimental comparison of forces resisting viral DNA packaging and driving DNA ejection

Abstract

We compare forces resisting DNA packaging in bacteriophage phi29 inferred from optical tweezers studies with forces driving DNA ejection inferred from osmotic pressure studies. Ejection forces from 0–80% filling are consistent with a model that assumes a repulsive DNA-DNA interaction potential derived from DNA condensation studies and predicts an inverse spool DNA conformation. Forces resisting packaging from ~80–100% filling are also consistent with this model. However, that electron microscopy does not reveal a spool conformation suggests that this model overestimates bending rigidity and underestimates repulsion. Below 80% filling, inferred ejection forces are higher than those resisting packaging. Although unexpected, this suggests that most force that builds during packaging is available to drive DNA ejection.

Two critical steps in the life cycle of many viruses are the packaging of double-stranded DNA during assembly and the subsequent ejection of DNA during the infection of a host cell. Many DNA viruses follow a remarkable assembly process during which viral capsid shells are assembled first and a single DNA molecule (the viral genome) is translocated into the capsid via a portal nanochannel by an ATP-powered molecular motor [1–4]. DNA in these viruses is packed extremely tightly, reaching nearly crystalline densities of ~0.5 g/ml, resulting in an average inter-axial separation between hexagonally packed DNA strands of only ~25–30 Å [5–8]. This tight confinement is highly energetically unfavorable due to electrostatic self-repulsion of charged DNA segments, entropy loss, and DNA bending rigidity [9–15].

We have previously shown via single molecule optical tweezers measurements of packaging in bacteriophages phi29, lambda, and T4, that the packaging motors are very powerful, capable of exerting forces of >60 pN [16–22]. It is widely assumed that the forces resisting DNA confinement that build during packaging play an important role in driving the later ejection of the DNA [10–15]. The simplest models assume that the DNA is in a free energy minimum conformation and that the ejection force at a particular capsid filling level is equal to the force resisting DNA confinement [10–12]. However, recent experiments show that the DNA undergoes nonequilibrium dynamics during packaging [23], suggesting that ejection forces could be lower than forces resisting packaging if significant energy dissipation occurs during packaging or prior to ejection.

Ejection forces in bacteriophage lambda were inferred via osmotic pressure experiments to be ~14 pN at 100% capsid filling (with 100% of the wildtype genome length packaged) [24,25]. In comparison, forces resisting packaging in bacteriophage phi29 have been inferred via optical tweezers experiments to rise to a maximum of ~20–25 pN [26,27]. However, ejection forces for lambda could be different than phi29 because lambda and phi29 have different capsid sizes and shapes and possibly slightly different packaging densities, and the lambda measurements were done under different ionic conditions [12,14]. There has not been a direct experimental comparison of packaging and ejection forces for the same virus under the same conditions. In this Letter, we report experimental determinations of DNA ejection forces for phage phi29 and a direct comparison with determinations of forces resisting packaging under the same ionic conditions. We compare both measurements with theoretical models [12,15].

To study phi29 ejection, we adapted a technique established by Evilevitch, Lavelle, Knobler, Raspaud, and Gelbart [24,28]. They showed that DNA ejection from phage lambda is inhibited when external osmotic pressure is applied using high-molecular weight polyethylene glycol (PEG). The viral capsids are permeable to water and ions but not PEG, thus creating an external osmotic pressure that opposes DNA ejection. The fraction of the DNA length ejected decreases progressively with increasing osmotic pressure. After a long incubation thermodynamic equilibrium is presumed to be reached between forces driving ejection and forces resisting ejection.

Ejection with phage lambda into a solution containing 10 mM Mg²⁺ at 37°C was found to be completely suppressed by ~25 atm of applied osmotic pressure, corresponding to ~14 pN of force opposing ejection [25]. Only roughly half of the genome was ejected when 3 atm of osmotic pressure was applied. This technique has further been applied to phages T5 and SPP1, which contain similar DNA packing densities, and roughly similar pressures were found to be needed to inhibit ejection [29,30].

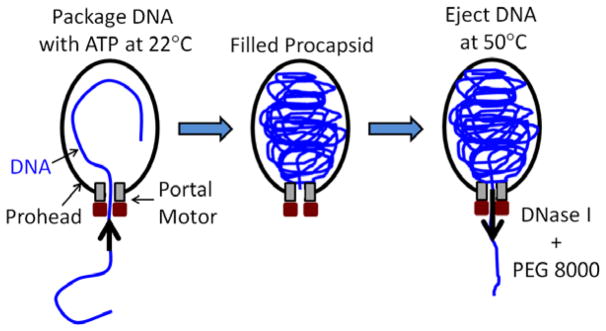
Phi29 is one of the smallest well-characterized phages, having a 19.3 kbp genome length and a prolate icosahedral capsid ~42 nm in diameter and ~54 nm in height [31]. The dynamics of phi29 DNA packaging has been extensively studied through the use of a highly efficient system in which packaging activity is reconstituted in vitro using purified DNA, procapsids, and recombinant motor ATPase [32]. To study DNA ejection we first carried out packaging reactions (Fig. 1) as described previously [33], at room temperature (~22°C) in a solution containing 25 mM Tris-HCl, pH 7.5, 5 mM MgCl₂, 50 mM NaCl, and 0.5 mM ATP for 15 minutes, more than enough time for the whole genome to be packaged. Typically ~50% of the added molecules are packaged in a bulk reaction, and DNAse I (1 unit/μg of DNA; NEB, Inc.) is added to digest any unpackaged DNA.

FIG. 1.

Schematic illustration of the experiment. The phi29 genome is packaged by the portal motor complex into the viral procapsid (left). After packaging is completed (middle) the DNA is ejected by heating to 50°C (right). DNase is added to digest the DNA as it is ejected. External osmotic pressure is applied by adding an osmolyte, PEG 8000, which does not permeate the capsid.

We found that DNA ejection can then be triggered by heating the complexes to 50°C (we note that 45°C did not trigger measurable ejection). As in previous ejection experiments, not all capsids eject their DNA [28–30]. This is advantageous as it provides an internal control for each reaction to confirm that a majority of complexes packaged the full genome length. The efficiency of packaging and ejection are unimportant as long as a sufficient number of DNAs are packaged and subsequently ejected, permitting quantitative assessment of the partly ejected DNA.

To apply osmotic pressure, various quantities of PEG 8000 (Fluka, Inc.) were added prior to triggering ejection. Additional DNase was also added to completely digest the ejected DNA (3 units/μg of input DNA). As in prior studies [28], samples were incubated for 30 min. EDTA was then added to 20 mM to inhibit the DNase. To rupture the capsids and release the unejected DNA 20 units of Proteinase K was then added and the sample was heated to 65°C for 30 min. The extracted DNA was analyzed by electrophoresis on 0.5–0.8% agarose gels in 40 mM Tris-Acetate, pH 8.3, 1 mM EDTA at 3.3 volts/cm for 3 hr. with ethidium bromide staining.

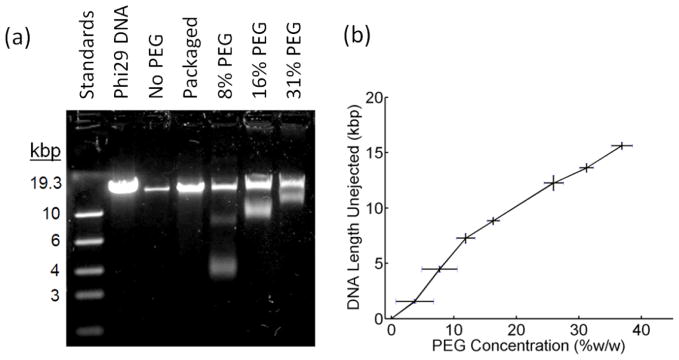
When ejection was triggered in PEG solutions, we measured unejected DNA lengths less than the full genome length (Fig. 2(a)), indicating that less than the full genome length was ejected. As expected, the unejected length increased with increasing PEG concentration, indicating that ejected DNA length decreases with increasing osmotic pressure (Fig. 2(b)). In all experiments the full genome length is also detected because, as mentioned above, heating does not trigger ejection from all capsids.

FIG. 2.

(a) Gel electrophoresis of DNA remaining unejected with varying PEG concentrations (%w/w). Also shown are DNA length standards, full length phi29 DNA, and packaged phi29 DNA extracted from capsids. (b) Length of unejected DNA vs. PEG concentration. Each measurement was repeated ≥3×. Error bars in the length measurements indicate standard deviation and errors in the PEG concentration were determined by weighing the PEG solutions.

For most of the PEG concentrations used only two bands were detected on the gel. The top band, which is the full genome length, corresponds to complexes that did not eject and the bottom band corresponds to complexes that ejected a fraction of the full length (Fig. 2(a)). Consistent with recent ejection studies with phage lambda [34], the bottom band is significantly broader than bands having a similar quantity of fixed-length DNA standards, indicating that there is variability in the lengths of DNA ejected from different individual capsids. This has been interpreted as indicating that there is heterogeneity in the ejection forces in individual phage particles due to heterogeneity in the DNA conformations [34,35], consistent with our finding that the DNA undergoes nonequilibrium dynamics during packaging [23].

Three control experiments are shown in Fig. 2(a). First, when proteinase-treated phi29 DNA is run on the gel directly, the expected full genome length is seen. Second, when the DNA is packaged with ATP but not heated to induce ejection, the packaged full genome is seen (less bright than the input DNA since in-vitro packaging is not 100% efficient). Third, when no PEG is added, no partly unejected DNA is seen, indicating that complexes that eject DNA eject the full genome (and only a small quantity of full length DNA is seen, corresponding to a small fraction of complexes that did not eject).

In all experiments with 8% PEG (e.g., Fig. 2(a)) and some experiments with 12% PEG, we observed a faint middle band on the gel, indicating that a small fraction of individual complexes eject shorter lengths of DNA. A similar effect was observed in ejection studies with phage T5 with similar PEG concentrations, suggesting that ejection does not reach equilibrium in a small fraction of complexes [30]. It was proposed this is due to kinetic trapping of the DNA in nonequilibrium conformations [30]. In Fig. 2(b) we plot the shortest unejected DNA length, corresponding to the dominant gel band and maximum DNA length ejected, vs. PEG concentration.

At the highest PEG concentration used (31.2%) the observed unejected length is still slightly below the full genome length, indicating ejection was not completely inhibited, as was observed in similar studies of phage SPP1 [29]. As in those studies, we could not test higher PEG concentrations because the solutions became too viscous for accurate pipetting.

We determine osmotic pressure as described previously [25], using an empirical formula derived based on experimental measurements: Π(atm) = −1.29 G²T + 140 G² + 4G, where T is the temperature (°C) and G = w/(100-w), where w is the %(w/w) of PEG. This allows us to replot the data in terms of DNA length ejected vs. osmotic pressure (Fig. 3(a)). As expected, the length of DNA ejected decreases monotonically with increasing osmotic pressure.

FIG. 3.

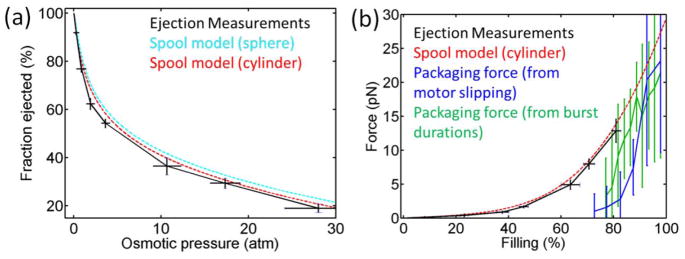
(a) Fraction of phi29 genome length ejected vs. applied osmotic pressure (black points). Error bars were determined as in Fig. 2. Shown for comparison are predictions of the inverse spool model assuming a cylindrical capsid (dashed red line) and spherical capsid (dashed cyan line), as described in the text. (b) Comparison of internal force vs. capsid filling (% of genome length packaged) inferred from the ejection measurements (black points), predicted by the spool model assuming a cylindrical capsid (dashed red line), inferred from motor slipping measurements during packaging [27] (blue points; error bars show standard error in the mean), and inferred from motor burst duration measurements [26] (green points).

Fig. 3(a) also shows a comparison of the data with quantitative predictions made by the inverse DNA spool model [12]. This model predicts that the DNA inside the viral capsid is arranged as a spool coaxial with the portal channel with hoops of DNA arranged in a hexagonal lattice filling inward from the outermost radii; this is proposed to be the equilibrium conformation. Free energy is calculated as the sum of the DNA bending energy and DNA-DNA intra-strand interaction energy. The energy is minimized by balancing these two terms to determine force resisting packaging or ejection force as a function of DNA length inside the capsid.

Analytic results have been derived for spherical and cylindrical capsid geometries [12]. Although the phi29 capsid is actually a prolate icosahedral shape, it does not have a large aspect ratio (being ~42 nm in maximum diameter and ~54 nm in maximum height), and it was thus proposed that it could be well modeled as either a sphere or cylinder since the predicted forces were found to be insensitive to changes in geometry [12]. Fig. 3(a) shows calculations for both geometries. Cryo-electron microscopy (cryoEM) studies indicate that the volume occupied by DNA is ~4 × 10⁻²³ m³, and the maximum diameter (perpendicular to the portal axis) occupied by the DNA is 35 nm [31]. We therefore assumed a cylinder of diameter 35 nm and height 41 nm and a sphere of radius 21 nm, where both volumes were constrained to equal the DNA volume determined from the cryoEM measurements.

As in previous studies, we assumed 50 nm for the DNA persistence length, based on experimental data [12]. We note that in the spool model there is only a small predicted temperature dependence associated with the bending energy [12]. The predicted forces resisting packaging at 50°C (where ejection measurements were done) vs. 22°C (where packaging measurements were done) differ by <2%. We determined parameters describing the DNA-DNA interaction potential based on measurements of spacing between DNA segments condensed by osmotic pressure [11,36]. Pressure (Π) vs. spacing (d) follows Π=F₀ exp(-d/c) [11,12]. We fit this equation to measurements by Donald Rau, described in [15], for a solution containing 100 mM Na⁺ and 10 mM Mg²⁺ and obtained c=0.28 nm and F₀=44,615 pN/nm²ⁱ At these concentrations DNA is expected to be saturated with counterions [37] and the ratio of mono- to divalent ions is the same as in our studies. When these parameters are used in the spool model we observe good agreement with our measurements for both geometries (Fig. 3(a)).

On the other hand, cryoEM studies of phi29 capsids packaged to 32%, 51%, and 78% filling did not find evidence for an inverse-spool DNA conformation [31]. In this filling range the model predicts that the DNA will preferentially spool on the periphery, with the first segments to be packaged lying against the inner walls of the capsid and subsequent layers spooling inwards, leaving a void in the center of the capsid [12]. The cryoEM studies observed uniform average DNA density across the full volume of the capsid with no central void, suggesting that bending energy plays a smaller role than assumed in the model. Our present finding of pressure values that agree with the model predictions despite this discrepancy further supports the conclusion that the model overestimates the role of bending rigidity and underestimates intra-strand repulsion.

Phi29 DNA packaging has also been investigated via molecular dynamics simulations, also assuming a DNA-DNA interaction potential derived in similar fashion from the DNA condensation data [12]. Consistent with the cryoEM findings these simulations did not predict a spool conformation. Rather, they observed a partially-disordered folded toroid. The predicted resistance forces were somewhat higher than those predicted by the spool model: ~25 pN at 80% filling and ~57 pN at 100% filling.

We estimate force resisting DNA ejection as described previously [25]. Specifically, F=ΠπR_DNA², where Π is osmotic pressure and R_DNA ≅ 1.2 nm is the effective radius of the approximately cylindrical volume of PEG displaced by the ejected DNA. We plot this in Fig. 3(b) along with theoretical predictions of the spool model and forces resisting packaging inferred from optical tweezers measurements. Again, good agreement is found between ejection force over the measured range from 0–80% filling and the prediction of the inverse spool model. Good agreement is also observed between the model prediction and the forces resisting packaging in the high filling limit (~90–100% filling). This comparison suggests that most of the force that builds during packaging is available to drive DNA ejection.

However, unexpectedly, the inferred ejection force at each filling level <80% is higher than the force resisting packaging. At 80% filling, the two measurements agree to within errors, but at lower filling levels they diverge. Theoretically, one would not expect the ejection force to be higher because the potential energy available to drive ejection cannot be higher than work done by the motor on the DNA (energy transferred to the DNA) during packaging [14]. We note that the inverse spool model predicts only a weak temperature dependence due to the bending energy [12]. The predicted resisting forces at 80% filling at 50°C (where the ejection measurements were done) vs. 22 °C (where the packaging measurements were done) differ by <2%.

The discrepancy suggests that methods by which ejection forces and/or packaging forces are inferred from the measurements are not completely accurate. However, we note that the estimated uncertainties do not include potential systematic errors that are presently difficult to quantify. In the determination of packaging forces from motor slipping measurements, slipping is very infrequent at low force and becomes subject to large measurement error [27]. The analysis also relies on an assumption that the dependence of slipping frequency on force is independent of capsid filling. Determining the force via measurements of motor burst duration also becomes difficult below 5 pN because the durations become very short (<20 ms) [26]. The analysis also relies on an assumption that the dependence of burst duration on force is independent of capsid filling.

There are also potential additional sources of error in the inference of ejection forces from the osmotic pressure experiments. First, conversion of PEG concentration to osmotic pressure relies on an empirical relationship based on experiments, but the absolute certainty is unclear [25]. Second, the conversion of osmotic pressure to force resisting DNA ejection is based on an approximate scaling description suggested to only be accurate to within a factor of ~2 [38].

Despite these caveats, we have shown that the ejection force inferred from the osmotic pressure experiments fits the inverse-spool model prediction very well over the measurable range from 0–80% filling, and the model also agrees very well with the inferred packaging force in the high filling limit. The finding that ejection force is not significantly lower than force resisting packaging suggests that most of the force that builds up during DNA packaging is available to drive ejection.