Coexistence and Pattern Formation in Bacterial Mixtures with Contact-Dependent Killing

Abstract

Multistrain microbial communities often exhibit complex spatial organization that emerges because of the interplay of various cooperative and competitive interaction mechanisms. One strong competitive mechanism is contact-dependent neighbor killing enabled by the type VI secretion system. It has been previously shown that contact-dependent killing can result in bistability of bacterial mixtures so that only one strain survives and displaces the other. However, it remains unclear whether stable coexistence is possible in such mixtures. Using a population dynamics model for two interacting bacterial strains, we found that coexistence can be made possible by the interplay of contact-dependent killing and long-range growth inhibition, leading to the formation of various cellular patterns. These patterns emerge in a much broader parameter range than that required for the linear Turing-like instability, suggesting this may be a robust mechanism for pattern formation.

Introduction

In natural habitats, microorganisms often form multispecies communities with intricate social organization and complex spatial structures (1). The repertoire of interactions among microorganisms is very diverse and includes cooperation (2, 3), competition for common resources (4, 5), and predation (6, 7, 8). One major question drawing significant interest is how different microbial species may stably coexist within a common environment in the presence of competition and predation (4, 9). In this work, we address this question theoretically, focusing on one ubiquitous mechanism of bacterial predation: contact-dependent killing of neighboring cells by direct injection of lethal toxins via the type VI secretion system (T6SS) (10, 11, 12, 13, 14, 15, 16). The T6SS has been found in many genera of bacteria, including Vibrio, Pseudomonas, and Acinetobacter.

In a recent work, Borenstein et al. (17) demonstrated that although small micro-colonies of T6SS-sensitive cells are quickly eliminated by surrounding T6SS-active cells, sufficiently large micro-colonies can survive the assault and expand. They explained this size-dependent bifurcation with a purely geometric mechanism. Since the killing occurs on the perimeter of the colony and the growth is in the bulk, the overall balance between killing and growth depends on the colony size. However, these theoretical results predicted no stable coexistence; rather, T6SS inhibition was expected to lead to bistability. Depending on initial conditions, either the T6SS-sensitive or T6SS-active bacteria outcompete the other strain and asymptotically approach a spatially uniform state. The experiments with mixtures of Escherichia coli (T6SS-sensitive strain) and Vibrio cholerae (T6SS-active strain) indeed showed either growth or shrinkage of localized domains of E. coli depending on their initial size. However, the finite time span of the experiments did not allow the authors to see complete elimination of one strain, and thus the question of possible coexistence remained open. McNally et al. (18) also recently studied phase separation in a system of two mutually antagonistic T6SS-active strains of V. cholerae and found persistent domain coarsening, which indicates that the stronger strain would eventually win the competition.

In another recent work, Blanchard et al. (19) computationally studied the dynamics of a bacterial population with contact-dependent inhibition such as that mediated by the T6SS. In the well-mixed case, they also found bistability leading to extinction of one strain or the other. On the other hand, they reported that in spatiotemporal simulations, if the diffusion of bacteria was sufficiently slow, two strains could coexist separated by stationary interfaces in a finite parameter domain. However, this effect in their two-component model with bistability could have been a consequence of front pinning that may sometimes occur in coarse finite-difference numerical simulations (20) (see more on this in the Discussion).

Although local antagonistic interactions generally lead to phase separation and coarsening via front propagation and thus cannot sustain stable strain coexistence, additional long-range interactions may potentially change this outcome and lead to stable coexistence. In this article, we revisit the possibility of stable coexistence in a binary mixture of T6SS-active and T6SS-sensitive bacteria, taking into consideration the potential effects of long-range growth inhibition. We demonstrate theoretically and numerically, using both continuous deterministic and discrete stochastic models, that the interplay of short-range killing and long-range growth inhibition can indeed stabilize the system in a bimodal state with well-separated patches of different bacterial strains. Furthermore, when diffusion of the inhibitor is fast but finite, stable patterns with a characteristic spatial scale can emerge. Such long-range growth inhibition can plausibly arise in natural settings, since a number of factors that limit colony growth, including resource availability, waste accumulation, and quorum sensing, are mediated by fast-diffusing small molecules (21, 22, 23). Long-range growth inhibition can also be forward-engineered using the tools of modern synthetic biology (24), for example, by placing an antibiotic resistance gene under the control of a promoter that is repressed by a fast-diffusing quorum-sensing signal (e.g., N-acyl homoserine lactones (AHL)).

Methods

Continuum deterministic model

We developed a continuum population dynamics model for a binary mixture of two strains of bacteria that grow on a two-dimensional (2D) surface and interact via both short-range contact-dependent killing and long-range growth inhibition. The model is based on the partial differential equations for the area densities of T6SS-sensitive bacteria $n_1\left(\mathbf{r},t\right)$ and T6SS-active bacteria $n_2\left(\mathbf{r},t\right)$, and on the reaction-diffusion equation for the density of the growth inhibitor $A\left(\mathbf{r},t\right)$ in a 2D space, $\mathbf{r}\in {\mathbf{R}}^2$:

$$\frac{\partial n_1}{\partial t}=\frac{{\gamma }_1}{1+A}{n}_1\left(1-n_1-n_2\right)-\delta n_1-\kappa n_1{n}_2+{\nabla }^2{n}_1,$$ (1)

$$\frac{\partial n_2}{\partial t}=n_2\left(1-n_1-n_2\right)-\delta n_2+{\nabla }^2{n}_2,$$ (2)

and

$$\frac{\partial A}{\partial t}={\gamma }_A{n}_1-{\delta }_{A}A+D_A{\nabla }^{2}A.$$ (3)

The first equation describes the logistic growth of the T6SS-sensitive cells, their spontaneous death, killing by colocated T6SS-active cells, and diffusion. Note that the growth rate of T6SS-sensitive strain 1 is reduced by the local concentration of inhibitor $A\left(\mathbf{r},t\right)$. We use a simple Hill-like function for the inhibition since the specific form is not qualitatively important. The second equation describes the logistic growth of T6SS-active cells, their spontaneous death, and diffusion. The death rates of both strains are small, and if they move on solid agar, their diffusion rates are also small. Although these parameters can be different for the two strains, that difference is not essential, and we assume them to be equal for simplicity. The third equation describes synthesis, decay, and diffusion of the inhibitor A that reduces the growth rate of species $n_1$. This model has a typical structure of a reaction-diffusion system. Strictly speaking, bacterial communities are not reaction-diffusion systems since they do not “react” with each other as chemical species, and their motility is often quite different from simple linear diffusion. However, such simplified description of their collective dynamics (growth, death, interactions, and motility) is convenient and may serve as a reasonable first approximation to more realistic models of multistrain bacterial communities.

Here, we assume that A is only produced by $n_1$ and only inhibits growth of $n_1$. This interaction of A only with $n_1$ can be realized in synthetic biology as discussed later. However, in natural environments, it might also be produced by $n_2$ and inhibit growth of $n_2$. The analysis of a more general model with A produced by and inhibiting growth of both strains is discussed in the Supporting Material, in which we also allow for different death rates of the two strains. In the analysis and simulations described below, we use Eqs. 1, 2, and 3 for simplicity, but our main conclusions are general. In these equations, all variables and parameters are scaled by the growth rate of species 2, the diffusion constant of both strains, and the maximal total density of bacteria at which the logistic growth saturates. Note that in our model the cell growth saturates in the bulk at sufficiently large density, whereas Borenstein et al. (17) assumed that growth was continuous, with new cells pushing old cells out of the simulation domain once the maximal density was reached. This is an important difference since in the latter case, the faster-growing strain always wins for sufficiently large initial domains, whereas in our system, the outcome is more complex and parameter dependent.

Discrete stochastic model

We also developed a lattice-based, discrete-element model to study the effects of stochasticity on the population dynamics of two bacterial strains. We assume that each site of a square lattice may contain an integer number of T6SS-sensitive and T6SS-active cells ($n_1$ and $n_2$, respectively). At every time step, each cell can divide with a probability that is proportional to its growth rate (${\gamma }_1$ or ${\gamma }_2$, respectively), thereby increasing the occupancy number of the corresponding cell type in that lattice site by one. We assume that each lattice site can only accommodate no more than $n_0$ cells, so once the total number of cells $n_1+n_2$ at a certain lattice site reaches $n_0$, cell division at that site is suspended. To model the short-range cell motility, we allow cells to hop to any of four neighboring lattice sites with rates $P_n$ if that neighboring site has a vacancy. A cell can also spontaneously die with probability proportional to δ, thus reducing the number of cells of its type in its lattice site by one. Finally, type-2 cells can kill type-1 cells with probability proportional to κ if they occupy the same site, thus reducing the occupancy number $n_1$ by one. All these processes are simulated as independent Markovian events. We also introduce a real-valued inhibitor field A that is defined on the same lattice. It is produced at each lattice site in proportion to the corresponding $n_1$ value, degrades with rate ${\delta }_A$, and diffuses with the diffusion constant $D_A$. The spatiotemporal evolution of A was simulated deterministically using the first-order split-step pseudospectral method. We employed 256 × 256 or 512 × 512 lattices with periodic boundary conditions.

Results

Continuum deterministic theory

Population dynamics without long-range inhibition

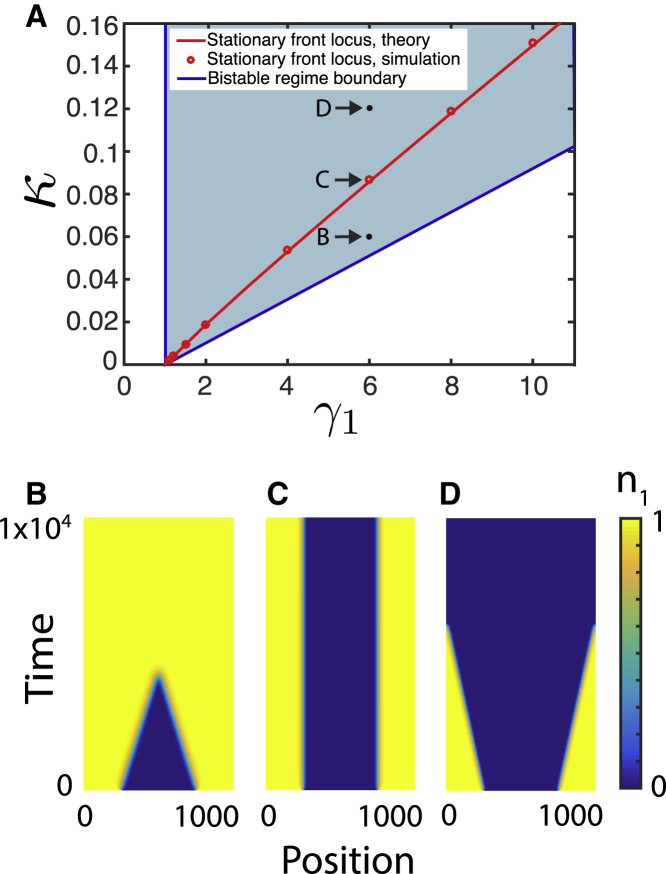
Let us first consider the two-species population dynamics without long-range inhibition by assuming ${\gamma }_A=0$ and imposing the initial condition $A\left(\mathbf{r},0\right)=0$. Clearly, $A\left(\mathbf{r},t\right)$ will then remain zero at all times and can be omitted from consideration. The set of two Eqs. 1 and 2 possesses at most four fixed points, including the trivial fixed point $n_{\mathrm{1,2}}=0$, two “pure” states in which either $n_1=0,n_2\ne 0$ or $n_1\ne 0,n_2=0$, and a mixed state where both $n_{\mathrm{1,2}}\ne 0$. The linear stability analysis (see Supporting Material) shows that if $\delta <1,{\gamma }_1$, the trivial state is always unstable, and pure $n_1$ and $n_2$ states are stable for sufficiently large and small ${\gamma }_1$, respectively. For intermediate ${\gamma }_1$, at $1<{\gamma }_1<1\text{+}\kappa \left(1\text{−}\delta \right)/\delta$, the system is bistable (see Fig. 1 A, blue wedge). In the following, we will always assume ${\gamma }_1>1$, since the most interesting dynamics occur within this regime. For nonzero ${\gamma }_A$, the bifurcation analysis can be carried out as well (Supporting Material).

Figure 1.

(A) The blue-shaded wedge in the parameter plane $\left({\gamma }_1,\kappa \right)$ for $\delta =0.01$ shows the region of bistability in which both pure states are stable and may transiently coexist in space; however, the fronts separating them would generally move in either direction when diffusion is not zero. (B–D) demonstrate how one-dimensional fronts reverse direction when κ is increased from 0.06 (B) to 0.087 (C) to 0.12 (D) for ${\gamma }_1=6$ (direct numerical integration of Eqs. 1 and 2). Only the dynamics of $n_1$ are shown here. In the region where $n_1$ is high, $n_2$ is low and vice versa. The red solid line in (A), which is plotted according to formula (4), corresponds to the stationary front solution. It separates the parameter regions in which either $n_1$ or $n_2$ win the competition. The symbols show the parameter values for which the fronts were indeed found to be stationary in direct simulations. To see this figure in color, go online.

In the bistable regime, two subcolonies dominated by species 1 and 2 can coexist by occupying different spatial domains. If these domains contact each other and the diffusion coefficients of the two species are nonzero, smooth fronts will form, separating the domains of different species. These fronts will generally move in either direction depending on the system parameters ${\gamma }_1,\delta ,\kappa$. Generally, since ${\gamma }_1>1$ for small killing rate κ, the front propagates in the direction of species 2 and species 1 wins, whereas for sufficiently large κ the front reverses and T6SS-active species 2 wins. For given ${\gamma }_1$ and δ, there is a unique value of ${\kappa }_s$ at which the front is stationary. For $\delta ,\kappa \ll 1$ it can be found analytically using the so-called Maxwell rule (25) (see Supporting Material for details),

$${\kappa }_s=\frac{3\delta {\left({\gamma }_1-1\right)}^2\left({\gamma }_1^2-1-2{\gamma }_1\text{ln}{\gamma }_1\right)}{2{\gamma }_1^3+3{\gamma }_1^2-6{\gamma }_1+1-6{\gamma }_1^2\text{ln}{\gamma }_1}.$$ (4)

For small ${\gamma }_1\text{−}1$, this expression simplifies to ${\kappa }_s=2\delta \left({\gamma }_1-1\right)$. Direct numerical simulations of Eqs. 1 and 2 agree well with this formula (Fig. 1).

Infinitely fast inhibitor diffusion

In the limit of infinitely fast inhibitor diffusion $\left(D_A\to \infty \right)$, A is spatially uniform, with a magnitude that is dependent on the average concentration of type-1 bacteria over the entire domain: $N_1\left(t\right)={\int }_C{n}_1\left(\mathbf{r},t\right)d\mathbf{r}/\text{Area}\left(C\right)$. For ${\delta }_A\gg \delta$, after the initial transient, the magnitude of the inhibitor A becomes slaved to the current value of $N_1$: $A\left(t\right)={\gamma }_A{N}_1\left(t\right)/{\delta }_A$. In the bistable regime, after the phase separation has occurred, $N_1\approx n_1^{\text{∗}}{s}_1$, where $s_1$ is the surface area fraction occupied by the type-1 strain and $n_1^{\text{∗}}=1-\delta \left(1+A\right)/{\gamma }_1$ is at the local fixed point. This yields the self-consistency condition resulting in the relation between $s_1$ and A:

$$A=\frac{{\gamma }_1-\delta }{\frac{{\delta }_A{\gamma }_1}{{\gamma }_A{s}_1}+\delta }.$$ (5)

Now we can use the results of the analysis of the two-variable model with renormalized

$${\gamma }_1^{\text{∗}}={\gamma }_1/\left(1+A\right)=\left({\delta }_A{\gamma }_1+\delta {\gamma }_A{s}_1\right)/\left({\delta }_A+{\gamma }_A{s}_1\right)$$ (6)

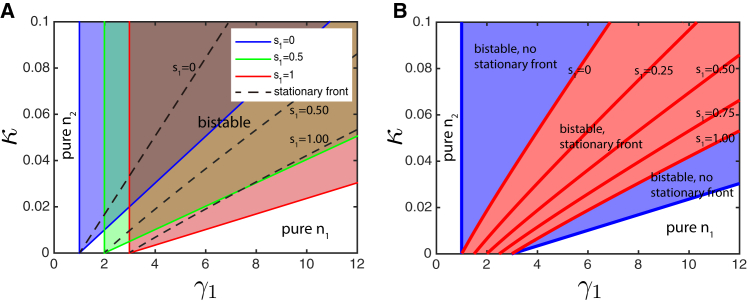
instead of ${\gamma }_1$ and determine how the region of bistability will depend on $s_1$ (see Fig. 2 A). The bistability region for arbitrary $0<s_1<1$ is the wedge $1<{\gamma }_1^{\text{∗}}<1+\kappa \left(1-\delta \right)/\delta$ (Fig. 2 A). Since for each $s_1$ there is a unique line corresponding to a stationary front, we can also plot a union of all lines $\kappa \left({\gamma }_1\right)$ by using Eq. 4 with ${\gamma }_1$ replaced by ${\gamma }_1^{\text{∗}}$ for arbitrary $0<s_1<1$; this union forms a wedge shown in Fig. 2 B. Thus, any combination of κ and ${\gamma }_1$ within this wedge can yield a stationary, phase-separated structure with a particular area fraction $s_1^{\text{∗}}$, for which κ and ${\gamma }_1^{\text{∗}}\left(s_1^{\text{∗}}\right)$ satisfy Eq. 4. Similar results can be obtained in the dual-inhibition model in which both species produce and are inhibited by the same inhibitor (see Supporting Material).

Figure 2.

(A) shows the regions for bistability on $\left(\kappa ,{\gamma }_1\right)$ plane for three different values of strain 1 area fraction $s_1$. The blue wedge $\left(s_1=0\right)$ that corresponds to $s_1=0$ and $A=0$ is the same as the one for the two-variable model shown in Fig. 1. (B) shows the region of bistability for all values $0<s_1<1$ (blue wedge) and the region where fronts would become stationary at specific values of $s_1$ (red region). Parameters are $\delta =0.01,{\gamma }_A/{\delta }_A=2$. To see this figure in color, go online.

Dynamically, if the parameters κ and ${\gamma }_1$ fall within the domain allowing a stationary front for a certain area fraction $s_1^{\text{∗}}$ given by Eqs. (4), (6), but the initial area fraction of species 1 is smaller than $s_1^{\text{∗}}$, then $n_1$-domains will expand, and $s_1$ will increase until it becomes equal to $s_1^{\text{∗}}$, at which time the expansion terminates. Conversely, if $s_1\left(t=0\right)>s_1^{\text{∗}}$, domains of $n_1$ will shrink until $s_1\to s_1^{\text{∗}}$. This phase separation with subsequent stabilization of the total area fractions occupied by $n_1$ and $n_2$ is easily seen even when ${\delta }_A/\delta =O\left(1\right)$ in numerical simulations of a 2D version of this model starting from random initial conditions (Fig. S5). Fig. S6 shows a comparison of the stationary state of a one-dimensional (1D) system as predicted either analytically using Eqs. 4 and 6 or with direct 1D numerical simulations of the continuum model.

Finite inhibitor diffusion

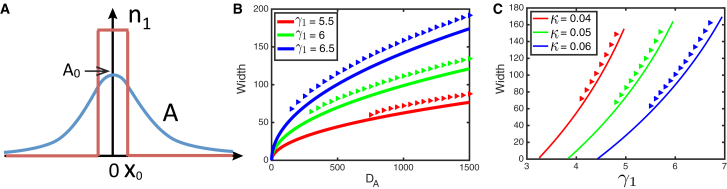
For large but finite diffusion rate $D_A$, the approximation of spatially uniform A is only applicable for a sufficiently small system size $L\ll q\equiv \sqrt{D_A/{\delta }_A}$. In larger systems, the spatial variability of A becomes essential. Furthermore, a finite diffusion rate $D_A$ imposes a characteristic scale for isolated domains of $n_1$ and $n_2$. Indeed, consider an isolated island of $n_1$ in an infinite “sea” of $n_2$ in 1D (Fig. 3 A). This island is a source of inhibitor A that gradually dissipates in the surrounding area. Thus, an island of $n_1$ generates a localized bump of A, of which the amplitude $A_0$ depends on the size of the island. If the halfwidth of the island $x_0$ is much smaller than the inhibitor diffusion scale q, we can neglect the variation of A across the island and obtain the following approximate expression for $A_0$ valid for small $q{x}_0$ (see Supporting Material),

$$A_0=\frac{{\gamma }_A}{{\delta }_A}\left(1-\delta /{\gamma }_1^{\text{∗}}\right)q{x}_0.$$ (7)

The value of $A_0$ depends on the size $2x_0$ of the island of $n_1$. For a very small island, the value of $A_0$ is also small, ${\gamma }_1^{\text{∗}}$ is large, and the island will be expanding. For a sufficiently large island, the value of $A_0$ is also large, the effective growth rate of $n_1$, ${\gamma }_1^{\text{∗}}$ will be small, and the island will shrink. The island will neither expand nor shrink if the value of ${\gamma }_1^{\text{∗}}={\gamma }_1/\left(1+A_0\right)$ satisfies Eq. 4, which in turn yields a solution for $x_0$. Comparisons between the width of an isolated spot of $n_1$ given by this calculation and the direct simulation are illustrated in Fig. 3, B and C (for these plots, we used a more accurate expression for $A_0$ than Eq. 7; see Supporting Material). The simulation results are generally consistent with the theory; the slight deviation is because we neglected the variation of A and $n_1$ across the island. Also, in the simulations, there is a minimal size for stable stationary islands—very small islands shrink and disappear. Reference (17) also pointed out the existence of a critical minimal size of a T6SS-sensitive domain surrounded by T6SS-active cells, but in that work, the mechanism behind it was related to the balance between the bulk growth and perimeter killing, so the bigger the domain, the greater the ratio between the area and the surrounding perimeter. In our model, the bulk growth is saturated at the maximal local density, so the balance between killing and growth is weakly dependent on the area. The existence of the critical minimal domain size is not seen in the analytical results because we neglected the width of the front between $n_1$ and $n_2$ in the theory (Fig. 3 A). However, in our simulations, for a finite diffusion of $n_1$ and $n_2$, the interfaces have a finite width. When the size of an island becomes so small that the two finite-width fronts of the island between $n_1$ and $n_2$ overlap and annihilate each other, the island collapses.

Figure 3.

(A) is a sketch showing the distribution of A produced by a spot of $n_1$ surrounded by the sea of $n_2$. (B and C) show the width of an isolated spot of $n_1$ as a function of $D_A$ (B) and ${\gamma }_1$ (C). The curves show the results from theory, and the symbols are from simulations. Parameters are $\delta =0.01$, ${\delta }_A=0.02$, and ${\gamma }_A=0.04$. $\kappa =0.06$ in (B), and $D_A=800$ in (C). To see this figure in color, go online.

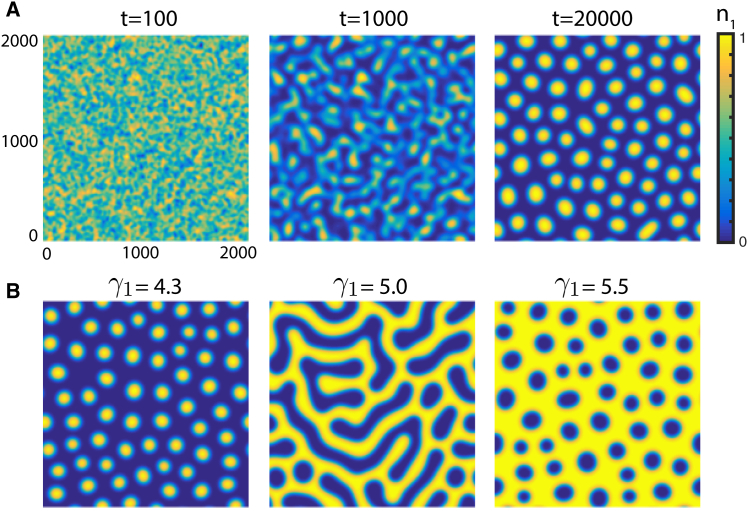
We also performed simulations of the full three-component deterministic model in 2D, starting from random initial conditions, and observed the formation of quasi-regular patterns of a characteristic size (see Fig. 4). Depending on the parameters, such as the strain-1 growth advantage ${\gamma }_1$ in the case of Fig. 4 B, the patterns can manifest as strain-1 islands surrounded by strain 2 or vice versa. For intermediate values of ${\gamma }_1$, labyrinthine patterns are observed.

Figure 4.

Pattern formation in a deterministic model with finite $D_A=80$ and random initial conditions. (A) shows three snapshots of $n_1$. (B) shows snapshots at time $t=40000$ for different ${\gamma }_1$. ${\gamma }_1=4.5$ in (A), and the other parameters are as follows: $\delta =0.01$, $\kappa =0.03$, ${\gamma }_A=0.04$, and ${\delta }_A=0.02$. To see this figure in color, go online.

Turing-like instability

It is well known that an interplay of short-range activation and long-range inhibition is responsible for the onset of the Turing instability (26). We wondered if pattern formation in our system was also the result of a Turing-like instability. Here, indeed, slowly diffusing bacteria $n_1$ effectively play the role of self-activator by shielding interior cells from the killer strain $n_2$ and thus promoting their own growth. At the same time, the fast-diffusing field A produced by $n_1$ acts as an inhibitor for the growth of $n_1$. When the diffusion constants of activator and inhibitor are sufficiently different, the Turing mechanism manifests itself in the linear instability of a uniform state with respect to small spatially periodic perturbations with finite wavenumbers. To test whether our system indeed exhibits Turing-like instability, we linearized the full model Eqs. 1, 2, and 3 near the mixed state and computed the eigenvalues of spatially periodic perturbations. We indeed found that for certain parameter values, the mixed state is linearly unstable with respect to finite-wavenumber perturbations (Supporting Material).

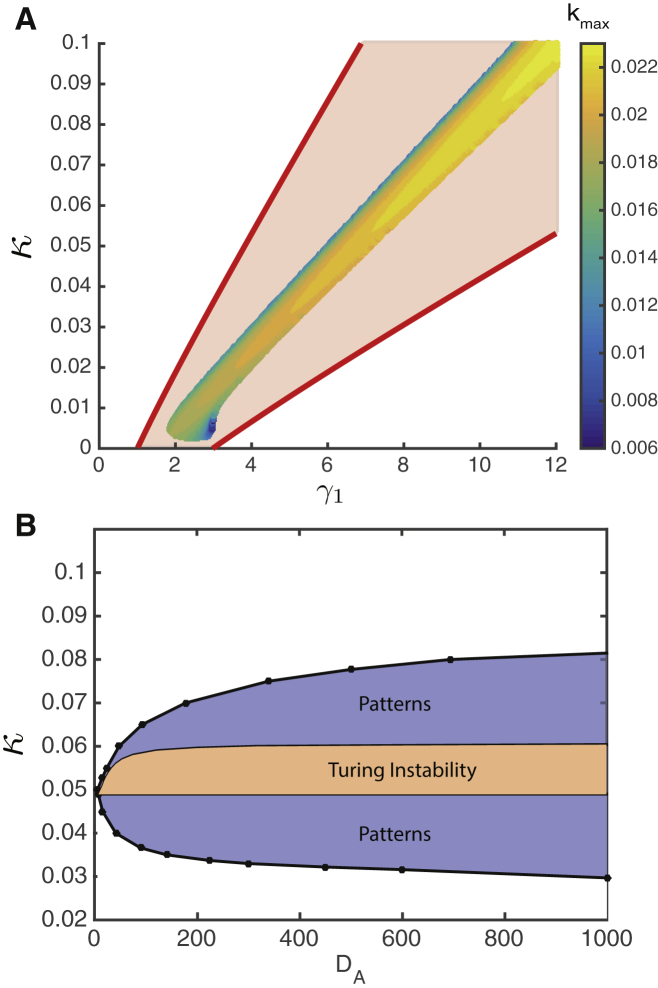
Fig. 5 A shows the region corresponding to the Turing-like instability in the $\left(\kappa ,{\gamma }_1\right)$ plane for fixed $\delta ,{\gamma }_A,{\delta }_A$ and finite $D_A$, along with the theoretical lines limiting the region for stationary fronts in the case of infinite $D_A$, as shown as the red sector in Fig. 2 B. As explained above, the existence of such fronts leads to stable pattern formation. The heatmap indicates the values of the wavenumber corresponding to the maximal positive eigenvalue. The Turing-like instability region lies inside the domain allowing stationary fronts, but it is much narrower. Similarly, the region for stable pattern formation obtained numerically from the full nonlinear model Eqs. 1, 2, and 3 for finite inhibitor diffusion is significantly wider than the corresponding Turing-like instability domain (Fig. 5 B). These results suggest that pattern formation in this system is a more robust and easily observable phenomenon than linear Turing-like instability of a well-mixed state. Although the Turing-like instability can indeed initiate morphogenesis in this system, the patterns can emerge and stabilize in a much broader range of system parameters because of the nonlinearity of the system. In fact, our numerical simulations show that patterns emerge spontaneously if the two strains are initially well-separated (i.e., there are sufficiently large regions where $n_1\gg n_2$ or $n_2\gg n_1$).

Figure 5.

The region of the linear Turing-like instability in the $\kappa -{\gamma }_1$ (A) and $\kappa -D_A$ (B) parameter planes. (A) The heatmap depicts the wavenumber $k_{max}$ corresponding to the maximal positive eigenvalue for the Turing-like instability for $D_A=500$. The red lines limit the region with stationary fronts and pattern. The parameter values are as follows: (A) $D_A=500$ and (B) ${\gamma }_1=7$. Other parameters ($\delta =0.01,{\gamma }_A=0.04,{\delta }_A=0.02$) are the same for both panels. To see this figure in color, go online.

Discrete stochastic model

As described in the previous section, the three-component continuum model for the two slowly diffusing bacterial densities and one fast-diffusing growth inhibitor exhibits a pattern-forming Turing-like instability. However, numerical simulations show that stable patterns can exist in a much wider parameter range. We identified a nonlinear mechanism of pattern formation that is based on interface stabilization because of the self-consistent changes in the growth caused by the fast-diffusing inhibitor. This raises the question of how such well-separated states can emerge from an unpatterned initial condition if it is linearly stable. We note, however, that in an actual experiment, dilute inoculated mixtures would initially grow in conditions that are actually very different from the spatially uniform, well-mixed state that is typically assumed in deterministic reaction-diffusion models. If a mixture was inoculated as a smattering of isolated bacteria that initially have no direct contact, then bacteria of both types would grow for some time, unimpeded by interaction with bacteria of the other type so by the time they begin contacting each other, they would form sufficiently large micro-colonies. This scenario can lead to pattern formation even when the uniformly mixed state is linearly stable.

We used a lattice-based discrete-element model introduced in Methods to simulate this scenario. The simulation results from this model are illustrated by three snapshots of $n_1$ and $n_2$ in Fig. S7 A. The initial condition for this simulation was a “dilute mixture” of both strains, so on average only 10% of lattice sites were occupied and typically by no more than a single cell of either type. As seen from the figure, this initial condition eventually gives rise to a patterned state in which spots of $n_1$ are surrounded by a “sea” of $n_2$. A characteristic size of the pattern emerges, as evidenced by the narrow-peaked area distribution of $n_1$ spots (Fig. S7 B). If either inhibitor production is disabled $\left({\gamma }_A=0\right)$ or neighbor-killing is turned off $\left(\kappa =0\right)$, patterns do not form, and either $n_1$ or $n_2$ takes over the whole system as the other species is driven to extinction, unless the system parameters are tuned precisely to satisfy the balance condition similar to Eq. 4 (data not shown).

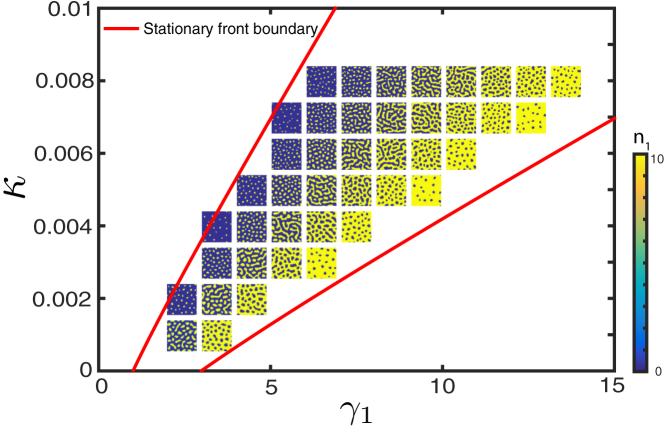
To evaluate the range of parameters in which patterns spontaneously emerge from a dilute initial state, we ran a series of discrete stochastic simulations with a range of values of ${\gamma }_1$ and κ. Again, the initial condition was randomly distributed $n_1$ and $n_2$ cells at low concentration. In agreement with the continuum theory, in the bulk of the region where the existence of stable patterns was expected, the patterns indeed spontaneously emerged (see Fig. 6). As seen from this figure, depending on the relative growth advantage of the type-1 strain and the killing efficiency of the type-2 strain, the patterns change their structure: for smaller ${\gamma }_1/{\gamma }_2$ or larger κ, they appear as isolated islands of $n_1$ surrounded by $n_2$. For large growth advantage of the type-1 strain or small κ, the patterns are reversed: the islands of $n_2$ are surrounded by the sea of $n_1$. In the intermediate range, we found more symmetric labyrinthine patterns. We also characterized the observed patterns by the average fraction of $n_1$ vs. $n_2$ and the power spectrum of the spatial distribution of $n_1$ (Fig. S8).

Figure 6.

Typical patterns emerging from random initial conditions in stochastic simulations for different values of parameters κ and ${\gamma }_1$. Other parameters are as follows: ${\gamma }_2=1,n_0=10,\delta =0.01,{\delta }_A=0.02,{\gamma }_A=0.004,P_n=0.1,D_A=12.5$. The system size is 256 × 256. Because the number of cells must be integers in stochastic simulations, we use unscaled parameters here. To see this figure in color, go online.

Discussion

Ecological diversity is ubiquitous in nature, ranging in scale from the ecosystems that cover our planet to the microbiome that inhabits our gut. Diversity plays an important role in maintaining the functions of an ecosystem; e.g., the gut microbiome provides many health benefits to its host (27, 28, 29, 30). However, the conditions and mechanisms that robustly stabilize this biodiversity are still unclear. To study and explain the coexistence of different species within a community, several models have been proposed, such as the rock-paper-scissors game models (31, 32, 33, 34). On the other hand, in synthetic biology, stabilization of multistrain microbial communities has proven to be a challenge (35). One recent example of ongoing efforts in this direction is a stable coculture of two different strains with different growth rates in microfluidic chips using a synthetic population control gene circuit (36).

Previous modeling studies of multistrain coexistence used population dynamics equations similar to our work. Frank (37) studied the co-dynamics of bacteriocin-producing strain with bacteriocin-susceptible strain and found that the two species could coexist only when the habitat was spatially heterogeneous. His results can also be readily applied to other mechanisms of contact-dependent killing. In another work, Durrett and Levin (31) studied two-species interactions via colicins and showed that despite the bistability of well-mixed populations, in a spatially structured population only one “stronger” strain will eventually win, depending on system parameters; i.e. neither bistability nor coexistence occurs. This was consistent with previous experimental results (38). On the other hand, Iwasa et al. (39) showed that in relatively small stochastic lattice-type models, a narrow parameter region of bistability may exist, but still without coexistence. Blanchard et al. (19) studied the interaction of two bacterial strains in the presence of contact-dependent killing using a reaction-diffusion-type model and correctly predicted the emergence of bistability that may in principle lead to coexistence of the strains. They also showed through numerical simulations that fronts separating two strains can remain static in a finite parameter range if the diffusion of bacteria is slow enough. However, this latter result has to be taken with the grain of salt because front stabilization in finite-difference simulations may come from pinning. The phenomenon of front pinning in systems with periodic or random inhomogeneities has been studied previously (40, 41, 42, 43, 44). Discretization of a continuous reaction-diffusion model in finite-difference numerical integration provides such a periodic structure, which can stop slowly moving fronts (45, 46). In our simulations, to minimize pinning artifacts, we used high spatial resolution (512–1024 nodes) and relatively large diffusion constant for bacteria $D_n=1$. We also verified our simulations by increasing spatial resolution and comparing the results to analytical predictions. The results shown in Fig. 1 demonstrate that our simulations are indeed consistent with continuum theory. However, if we artificially decrease spatial resolution and reduce the diffusion constant in our simulations, we immediately begin to see prominent pinning effects. We performed numerical simulations of the two-variable model without long-range inhibition for small bacterial diffusion $D_n=0.01$ and different numbers of grid points $N_g$. Some results of these simulations are shown in Fig. S9. For example, for $N_g=128$ nodes and a certain value of ${\gamma }_1$, there is a large finite range of κ at which the fronts are stationary, but this range becomes progressively smaller as the number of nodes increases toward the values used in our work.

The coexistence of different species creates the possibility of the emergence of regular patterns. One example is a spiral pattern in the rock-paper-scissors model (34). The balance of local activation and global inhibition has been used to explain many forms of pattern formation, such as self-organized patchiness in ecosystems (47). In another study, nutrient competition and mechanical pushing can drive the occurrence of spatial patterns that can also cycle through hole, labyrinth, and spot patterns (48). The mechanical pushing plays the role of local activation, and nutrient competition assumes the task of global inhibition.

In this article, we demonstrated that a combination of short-range killing with long-range growth inhibition may lead to stable coexistence and pattern formation in mixtures of T6SS-sensitive and T6SS-active bacteria. In the absence of either one of these two mechanisms, one of the two strains eventually takes over, and no stable spatial patterns form. Although the mechanism of pattern formation is similar to the Turing instability, the parameter region for stable coexistence and pattern formation is much broader than the range of the linear Turing-like instability of the uniform mixed state. Thus, in a broad parameter range, the stable patterns may coexist with stable uniform states, and the final outcome depends on the initial conditions. If cells of both types are initially well separated, the system evolves toward stable patterns. In experiments, this would correspond to an initially dilute bacterial inoculum where individual cells are not in direct contact, allowing them to develop into patches (micro-colonies) before making contact with each other. We performed simulations of a lattice-based discrete stochastic model that incorporates cell growth, death, diffusion, neighbor killing, and growth inhibition, and indeed found that patterns emerge spontaneously from an initially dilute state for a broad range of parameters, as predicted by the theory.

In our continuous model, the motion of bacterial cells is described by diffusion terms. In reality, bacterial cells do not simply diffuse like Brownian particles. For example, T6SS-sensitive motile E. coli cells perform a run-and-tumble random walk, and T6SS-active bacteria Acinetobacter baylyi move on agar surface through twitching using their pili (49). Furthermore, when bacteria form dense communities such as biofilms, cells push each other, and so mechanical stress plays an important role in cell motility and overall colony organization (50, 51, 52). In addition, cell motion and growth of real biofilms are affected by cell-cell adhesion and secretion of extracellular matrix (53). None of these factors are included explicitly in our model. Instead, we use diffusion as a simple but reasonable approximation of the cell motility as many researchers have done previously (54, 55, 56, 57). In our stochastic lattice model, the cells can jump to neighboring sites only if there is room there. Still, the results of our stochastic simulations are consistent with the theory and simulations of the deterministic continuum model.

Although we only presented theoretical results here, we anticipate that the mechanism of pattern formation described in this article operates in nature and can be observed in the laboratory. Compared to the Turing instability, this mechanism can produce stable patterns in a much wider parameter range, likely making it easier for experimental verification. In our system, it requires that the T6SS-sensitive bacteria grow faster than T6SS-active ones (${\gamma }_1>1$) and that the killing rate κ is small. These conditions are not difficult to fulfill. Different bacteria exhibit vastly different growth rates and abilities to metabolize different carbon sources (58, 59, 60). For example, in our preliminary experiments, the growth rate of T6SS-sensitive E. coli was found to be significantly faster than T6SS-active A. baylyi. In the laboratory, we can also vary growth rates by changing carbon sources and/or adding sublethal amounts of antibiotics that selectively slow down growth of different species. The ability of T6SS-active bacteria to kill their neighbors also varies greatly by both the predator and the prey. For example, of three T6SS-active species, A. baylyi can kill V. cholerae, whereas A. baylyi itself succumbs to Pseudomonas aeruginosa (61). According to the same study, the T6SS killing rates of these strains are comparable to their division rates if predator and prey cells maintain prolonged contact. However, motile cells are unlikely to have prolonged contacts, so the effective killing rate may be significantly smaller. Furthermore, in laboratory environments, one could tune killing rates in a broad range by knocking out certain T6SS toxic effectors (62), placing key components of the T6SS under an inducible promoter in the predator, or by placing an immunity gene under an inducible promoter in the prey. The death rate used in our model is of the order of 0.01 compared with the growth rate, which is typical in reality (63).

Our model also requires bacteria to produce a long-range inhibitor. As mentioned above, production of fast-diffusing waste or consumption of fast-diffusing nutrients could provide a native mechanism of long-range inhibition. Since bacteria vary in their ability to utilize different carbon sources, it is likely that the degree of growth inhibition within a pair of strains would also differ. However, long-range inhibition could be also forward-engineered using synthetic biology (24). For example, E. coli could be endowed with an antibiotic resistance gene controlled by a promoter repressed by a quorum-sensing signal, such as AHL produced by a constitutively expressed AHL-synthase LuxI (64, 65). If we add that antibiotic to the media, then as E. coli grow and produce more and more AHL, which represses the antibiotic resistance gene, the growth of E. coli colonies would gradually slow down. The T6SS-active strain (A. baylyi) could be made immune to this antibiotic by constitutively expressing the same resistance gene. Another possible candidate for such long-range inhibitor is colicin, a type of bacteriocin. Some wild-type E. coli can produce colicins against closely related bacteria (66, 67, 68), but they themselves are usually not affected by their own colicin so long as they express an immunity gene (67). If that immunity gene was knocked out, fast-diffusing colicins would inhibit the growth of E. coli. We plan to explore these different possibilities in our future work.

Author Contributions

L.S.T. designed research. L.X. and L.S.T. performed analytical and numerical calculations. R.C. contributed biological background and expertise. L.X., R.C., and L.S.T. analyzed results and wrote the manuscript.

Editor: Zemer Gitai.

Supporting Material

Movie S1. Two-Dimensional Simulations of the Deterministic Continuum Model with Spatially Uniform Inhibitor A and Random Initial Conditions

The parameters are as follows: γ₁ = 4.5, δ = 0.01, κ = 0.03, γ_A = 0.04, and δ_A = 0.02.

Movie S2. Two-Dimensional Simulations of the Deterministic Continuum Model with Finite D_A = 80 and Random Initial Conditions

The parameters are as follows: γ₁ = 4.5, δ = 0.01, κ = 0.03, γ_A = 0.04, and δ_A = 0.02.

Movie S3. Two-Dimensional Stochastic Simulations with Random Initial Conditions

The parameters are as follows: γ₁ = 3.5, γ₂ = 1, n₀ = 10, δ = 0.01, κ = 0.003, γ_A = 0.004, δ_A = 0.02, P_n = 0.1, and D_A = 12.5.

Movie S4. Two-Dimensional Stochastic Simulations of Dual-Inhibition Model with Random Initial Conditions

The parameters are as follows: γ₁ = 6, γ₂ = 1, n₀ = 10, δ₁ = 0.01, δ₂ = 0.005, α = 0.1, κ = 0.001, γ_A1 = 0.004, γ_A2 = 0.001, δ_A = 0.02, P_n1 = 0.1, P_n2 = 0.5, and D_A = 12.5.