Nonvolatile infrared memory in MoS₂/PbS van der Waals heterostructures

Researchers demonstrate a nonvolatile infrared memory cell operating in the optical communication wavebands.

Abstract

Optoelectronic devices for information storage and processing are at the heart of optical communication technology due to their significant applications in optical recording and computing. The infrared radiations of 850, 1310, and 1550 nm with low energy dissipation in optical fibers are typical optical communication wavebands. However, optoelectronic devices that could convert and store the infrared data into electrical signals, thereby enabling optical data communications, have not yet been realized. We report an infrared memory device using MoS₂/PbS van der Waals heterostructures, in which the infrared pulse intrigues a persistent resistance state that hardly relaxes within our experimental time scales (more than 10⁴ s). The device fully retrieves the memory state even after powering off for 3 hours, indicating its potential for nonvolatile storage devices. Furthermore, the device presents a reconfigurable switch of 2000 stable cycles. Supported by a theoretical model with quantitative analysis, we propose that the optical memory and the electrical erasing phenomenon, respectively, originate from the localization of infrared-induced holes in PbS and gate voltage pulse-enhanced tunneling of electrons from MoS₂ to PbS. The demonstrated MoS₂ heterostructure–based memory devices open up an exciting field for optoelectronic infrared memory and programmable logic devices.

INTRODUCTION

Memory devices constitute the basis of modern electronic information industries (1, 2). However, their operation principles focus on electrical or magnetic manipulation, and the optoelectronic devices (3, 4) for information storage and processing have received far less attention. The optoelectronic storage devices (3–6), which could capture and deposit electromagnetic radiation of matter and function as light-activated logic gates, are of central importance for the development of optical communication, recording, and computing.

The infrared spectra (7) are used as a communication medium for night vision, military communication, object inspection, and medical diagnosis. Specifically, 850, 1310, and 1550 nm are typical optical communication wavebands (8) due to their low energy dissipation in the optical fiber. Therefore, the optoelectronic devices that would convert and store infrared information into electrical signals are highly pursued.

Two-dimensional (2D) materials with gate tunability provide an excellent platform for constructing optoelectronic nonvolatile memory devices. Graphene (9) and monolayer MoS₂ (10) have demonstrated a photo-intrigued memory via the persistent photoconductivity (PPC) due to a light-induced metastable resistance state. However, this technology suffers from uncontrollable environmental factors because the materials’ PPC results from charge trapping of disorders or impurities. Recently, the gate voltage–controlled programmable storage of light-induced carriers has been reported in 2D materials (11) and their heterostructures (12). However, the charge storage in these hybrid structures depends on an external negative back gate voltage, which creates the charge trap. Although 2D materials and their mixed van der Waals heterostructures (13, 14) have enabled versatile electronic and optoelectronic functions (15, 16), so far, the study of optical memory using 2D materials is still limited to the visible spectrum. 2D materials, including their heterostructures, cannot simultaneously satisfy efficient infrared absorption and suitable band alignments that can govern the photoexcited carriers. It remains a big challenge to produce optical memory devices operating in the wavebands of infrared radiation (0.76 to 3.0 μm) (17).

Herein, we exploit an infrared memory device using few-layer MoS₂-PbS heterostructures with the back gate (V_g) (Fig. 1A). The device shows nonvolatile features, in which an infrared pulse intrigues a persistent resistance, and presents a reconfigurable switch of 2000 stable cycles. We demonstrate a physical model using simulations and quantitative analysis that explains the mechanism of the optical memory and the electrical erasing behavior and that proposes potential applications of our device in the optoelectronic memory and programmable logic.

Fig. 1. Schematic and optoelectronic transport of infrared memory device.

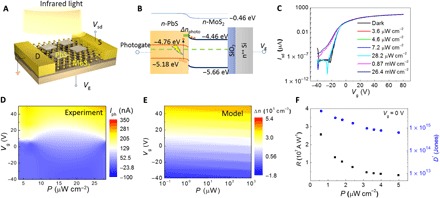
(A) Schematic of infrared memory device, showing few-layer MoS₂-PbS nanoplates heterostructure connected to source (S) and drain (D) electrodes. Infrared light entirely illuminates the device. (B) Band alignment of heterostructure. The photogate effect is schematically presented on the PbS side. (C) Transfer characteristic curves of I_sd versus V_g under infrared illumination with variable light power density P. (D) V_g- and P-dependent photocurrent I_ph extracted from transfer characteristic curves in (C). (E) Numerical simulation of carriers density (Δn) in MoS₂ channel via photo injection and V_g injection. (F) Dependence of responsivity and specific detectivity on power density shows maximum R of 2.6 × 10⁷ A/W and D* of 5.5 × 10¹⁵ Jones at P = 0.6 mW cm⁻².

RESULTS

Device structure and operation principle

The few-layer MoS₂ flakes were mechanically exfoliated from MoS₂ bulk crystals and transferred to SiO₂ (280 nm)/n⁺⁺-Si substrates. Then, infrared-sensitive PbS nanoplates were grown on top of few-layer MoS₂ flakes by chemical vapor deposition. The crystallinity quality and chemical composition were examined by a high-resolution transmission electron microscope (HRTEM) with selected-area electron diffraction (SAED) and x-ray photoelectron spectroscopy (XPS), respectively. The HRTEM image (fig. S1) shows distinct crystal fringes with a lattice distance of 0.29 nm in (200) planes. The clear square SAED pattern reveals that PbS nanoplates are of cubic symmetry. The element ratio of Mo to S (~1.0:2.1) is estimated from the XPS spectra area ratio of Mo 4d to S 2p, which is very close to the chemical stoichiometry of MoS₂. We also obtain an almost perfect element ratio of Pb to S (1.1 to 1.0) in PbS nanoplates from the XPS spectra area ratio of Pb 4f to S 2p.

The carrier transport channel of MoS₂ was connected to a Ti (10 nm)/Au (40 nm) source and drain electrodes. To clarify the optical memory properties, we measured five devices labeled as nos. 1 to 5. All five devices presented similar physical behaviors of optoelectronic transports, optical memory, and electrical erasing, except some difference of memory performance. The main text data were based on the experimental results from device no. 1 unless specified. Figure 1B shows the schematic of band alignment at the interface of MoS₂-PbS heterostructure. Because of the build-in electrical field, the PbS energy band (18) bends upward, whereas that of MoS₂ (19) bends downward, which creates the holes trap below the valence band of PbS near the interface.

The infrared (808, 1340, 1550, and 1940 nm) illumination-induced electrons in PbS nanoplates are injected into the transport channel of MoS₂. There are a few possible mechanisms for electron injection over the barrier from PbS to MoS₂. First, the energy scales of 808 nm (1.53 eV), 1340 nm (0.9 eV), and 1540 nm (0.81 eV) are larger than the bandgap of PbS (0.42 eV) and higher than the barrier height (~0.76 eV). The injection of electrons into MoS₂ is possible because of photoexcitation of electrons from the valance band or free electrons in the conduction band (20). The photon-enhanced thermionic emission (21) can also induce the carrier injection from the conduction band of PbS to MoS₂. For 1940-nm (0.6 eV) illumination, because its energy scale is smaller than the barrier height, the photo-generated electrons possibly inject into MoS₂ by photon-enhanced thermionic emission or the photo-thermionic effect (20). However, infrared-excited holes are localized in PbS due to charge traps, which modulates the conductivity of MoS₂ via electrostatic interaction (the photogate effect).

Optoelectronic transport

We first investigated the optoelectronic transport in the devices. Figure 1C shows the transfer characteristic curves (I_sd versus V_g) under infrared illumination (808 nm) with various light power densities (P). With a low power density (P ≤ 28.2 μW cm⁻²), the photocurrent I_ph, defined as the change of I_sd due to light excitation, varies from positive to negative as V_g decreases from 50 to −40 V (Fig. 1D). Unless otherwise stated, all the measurements were carried out at 80 K with the bias voltage of V_sd = 2 V in a high-vacuum (10⁻⁶ torr) chamber of four-probe station. By contrast, at a high power density (P ≥ 0.87 mW cm⁻²), I_ph changes from negative to positive with decreasing V_g (fig. S2D). Control experiments (fig. S3) show that pure few-layer MoS₂ does not respond to 808-nm laser pulses, until the laser power density increases to 0.25 mW cm⁻², and is completely insensitive to 1940-nm laser pulses. This is consistent with the band structure of MoS₂ that the direct optical transition occurs at ~680 nm (22). For a fair comparison, the few-layer MoS₂ was treated by the similar conditions as the few-layer MoS₂ used in the heterostructure. Thus, the photoconductivity of MoS₂-PbS heterostructures arises from the injection of infrared-induced electrons in PbS to MoS₂.

We now analyze the physical process of carrier injection into MoS₂ at a low power density. The field effect mobility (μ) of the device is ~147 cm² V⁻¹ s⁻¹, which is independent of P (fig. S2F). Thus, the photocurrent I_ph solely depends on the total change of carrier density Δn in MoS₂. Δn is the sum of the change in photo-injected (Δn_photo) carriers and back gate voltage (V_g)–accumulated carriers (Δn_gate). Δn is expressed as $\mathrm{\Delta }\mathit{n}=\mathrm{\eta }\mathit{P}\mathit{t}/{\mathit{V}}_{{\text{MoS}}_2}\mathit{h}\mathrm{\upsilon }+{\mathrm{\epsilon }}_0{\mathrm{\epsilon }}_{\mathit{r}}\mathrm{\Delta }{\mathit{V}}_{\mathrm{g}}/\mathit{T}\mathit{d}\mathit{e}$ (see note S1), where η describes the photoelectric conversion efficiency determined by the absorption coefficient of PbS and injection efficiency of infrared-excited electrons from PbS to MoS₂, t represents the duration of infrared illumination, h denotes the Plank constant, υ is the infrared frequency, ΔV_g = V_g − V_T, V_T is the threshold voltage of transfer characteristic curves (Fig. 1C), ε₀ and ε_r are the vacuum permittivity and relative permittivity of SiO₂, respectively, T is the thickness of MoS₂, ${\mathit{V}}_{{\text{MoS}}_2}$ is the volume of the MoS₂ nanosheet, d is the thickness of SiO₂, and e is the elementary charge. The first term of Δn describes Δn_photo by photo-injected electrons from PbS to MoS₂, and the second term displays Δn_gate, which is hole-dominant when ΔV_g < 0 and electron-dominant in the case of ΔV_g > 0. As shown in Fig. 1E, Δn is positive when ΔV_g > 0 because both Δn_photo and Δn_gate are electron-dominated. When ΔV_g moves toward negative values, Δn becomes negative because the net injections of carriers change from electrons to holes. This is consistent with the sign change of photocurrents from positive to negative with decreasing V_g (Fig. 1D). In Fig. 1E, Δn > 0 and Δn < 0, respectively, indicate that electrons and holes dominate the photocurrent.

In contrast to the low P, at a high P of 0.87 and 26.4 mW cm⁻², the mobility decreases to 140.8 and 131.8 cm² V⁻¹ s⁻¹, respectively, leading to a downward shift of I_sd-V_g curves. Consequently, we observe a negative-to-positive transition of photoresponse as V_g drops (fig. S2D). As presented in fig. S2E, the V_T gradually decreases from −21.8 to −38.0 V as P increases from 3.6 to 26.4 mW cm⁻², implying a larger injection of photo-induced electrons into MoS₂ with increasing P. The μ decreases at a high P, which can be attributed to the increased Coulomb scattering in MoS₂ due to positively charged PbS nanoplates (23, 24).

Reconfigurable optical memory

With the injection of photo-induced electrons into MoS₂, the infrared-generated holes are localized at traps (Fig. 1B), behaving as the positive gate voltage. This positive photogate effect generates an interesting physical effect of the PPC as shown in Fig. 2A. The device is applied by the infrared pulses (808 nm) with a duration of 5 s and P of 0.55 mW cm⁻². As the laser pulse switches on, the I_sd sharply increases to a finite value (${\mathit{I}}_{\mathit{P}}^{\text{on}}$). Even if the laser pulse switches off, ${\mathit{I}}_{\mathit{P}}^{\text{on}}$ hardly relaxes within our measurement duration of 1500 s. The exponential fitting of exp(−t/τ_l) leads to the lifetime τ_l = 5125 s of localized holes in the MoS₂/PbS heterostructure, which is two orders of magnitude larger than that of localized carriers in pure MoS₂ (τ_l = 17 s) (Fig. 2B). The PPC can be removed by V_g = 40 V with a duration of 100 ms (Fig. 2C). The above process is highly repeatable at various V_g. The photocurrent is positive at −10 and 0 V but negative at 10 and 20 V, which is consistent with the photoresponse under 808-nm infrared illumination with a high power density.

Fig. 2. PPC and rewritable memory.

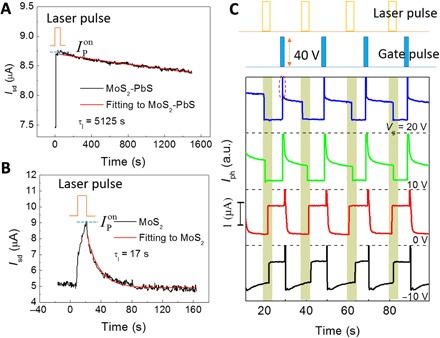
(A and B) Time evolution of I_sd in MoS₂-PbS heterostructure and pure MoS₂, respectively. The blue dashed line labels the source-drain current under a radiation of laser pulse (${\mathit{I}}_{\mathit{P}}^{\text{on}}$). (C) Writing and erasing of a memory using infrared laser pulses and gate voltage pulses, respectively. A gate voltage pulse of 40 V with a duration of 100 ms is applied to reset the system. The infrared pulse power density is 0.55 mW cm⁻² with a duration of 5 s. The red dashed circle indicates an instant increase of source-drain current when the gate voltage pulse is applied. a.u., arbitrary units.

Mechanism of infrared memory

We now discuss the mechanism of infrared pulse-intrigued memory and V_g pulse–induced erasing. Figure 3 (A to C) displays the time evolution of carrier density distribution in the system, time-dependent magnitude of laser pulses and V_g pulses, and time evolution of the carrier density change Δn in MoS₂, respectively. At t = t₀, when a laser pulse is applied (Fig. 3B), the infrared-excited holes (black pocket in Fig. 3A) are localized in the charge traps of PbS nanoplates with a potential barrier ΔE_v = 0.48 eV (Fig. 4A). The Δn in MoS₂ instantly raises because of the injection of photo-induced electrons (red pocket in Fig. 3A) from PbS to MoS₂ (see Δn_photo in Fig. 1B). When switching off the laser pulse at t = t₁, an interface barrier (Φ_R) prevents the reversed diffusion of electrons from MoS₂ to PbS (Fig. 4A). The localized holes cannot be recombined and, hence, induce electrons in MoS₂ via the photogate field effect.

Fig. 3. Physical principle of infrared memory and V_g pulse erasing.

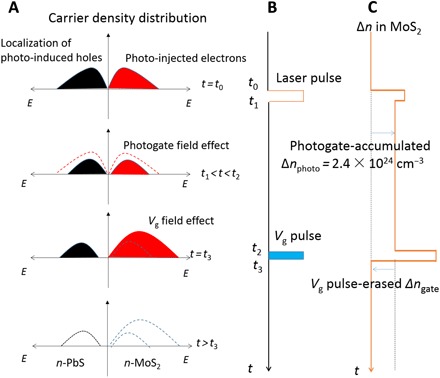
(A) Schematic illustration of time evolution of carrier distribution in MoS₂-PbS heterostructure. (B) Magnitude of infrared laser pulses and V_g pulses as a function of time. The laser pulse and V_g pulse switch on at t₀ and t₂, respectively. (C) Change of carrier density Δn versus time in MoS₂. The photogate-accumulated electron density Δn_photo in MoS₂ is estimated to be 2.4 × 10²⁴ cm⁻³ between t₁ and t₂ in device no. 3.

Fig. 4. Quantitative analysis of charge storage.

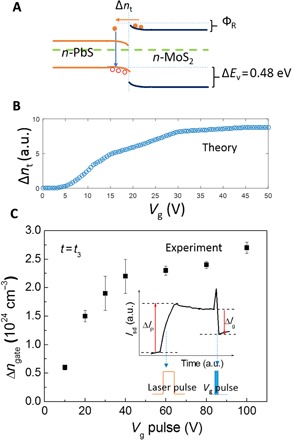
(A) Schematic of electron transfer at the interface of MoS₂-PbS heterostructure by tunneling or thermionic emission. Δn_t shows the number of transferred electrons from MoS₂ to PbS. (B) Simulated Δn_t as a function of back gate V_g. (C) Quantitative analysis of V_g pulse–erased electron density Δn in MoS₂. Inset shows infrared pulse– and V_g pulse–intrigued change of I_sd. The ΔI_p and ΔI_g, respectively, represent infrared pulse–induced increase of I_sd and V_g pulse–induced decrease of I_sd.

At t = t₂, a positive V_g pulse instantaneously increases the electron density due to the back gate capacitance effect (Fig. 4C). Thus, we see an immediate rise of photocurrent when V_g pulse is applied as shown by red dashed circle in Fig. 2C. Our dynamics analysis (see note S2) points out that back gate voltage pulse increases the numbers of transferred electrons (Δn_t) from MoS₂ to PbS (Fig. 4B). The simulation simultaneously considers the quantum tunneling and thermionic emission. We find that electron transferring from MoS₂ to PbS (Δn_t (R→L) is far larger than that from PbS to MoS₂ [Δn_t (L→R)] (fig. S11). In addition, Δn_t (R→L) is dominated by quantum tunneling. The localized holes in PbS are eventually recombined by tunneling electrons from MoS₂ due to the downward shift of the conduction band of MoS₂, which eliminates the optical memory effect.

To verify the proposed mechanism, we conducted a set of V_g pulse–induced erasing in the heterostructure with writing by 1940-nm pulses. Figure 5A shows the optical memory and electrical erasing effects at various V_g pulses from device no. 3. The laser pulse intrigues an increase of photocurrents in MoS₂. As mentioned above, the trapped holes in PbS behave as a positive voltage (photogate), which induces electrons in MoS₂. The photogate-accumulated electron density Δn_photo in MoS₂ is highly stable and maintains the memory state. The inset of Fig. 4C shows a single cycle of laser pulse writing and V_g pulse erasing. The photogate-induced increase of I_sd is labeled by ΔI_p. The photogate-accumulated Δn_photo is estimated to be 2.4 × 10²⁴ cm⁻³ from ΔI = Δn_photoeμES, where E = 3.2 × 10³ V cm⁻¹ represents the electric field, S = 7.9 × 10⁻⁸ cm² is the cross-section area of MoS₂, and μ = 0.53 cm² V⁻¹ s⁻¹. The decrease of I_sd due to V_g erasing is indicated as ΔI_g, which gradually increases as V_g increases from 10 to 100 V and approaches ΔI_p (fig. S7B). Correspondingly, the removed electron Δn_gate in MoS₂ increases from 0.6 × 10²⁴ to 2.2 × 10²⁴ cm⁻³ and then saturates at ~2.5 × 10²⁴ cm⁻³ (Fig. 4C), which is close to photogate-induced Δn_photo (2.4 × 10²⁴ cm⁻³) in MoS₂. The above observation is consistent with our theoretical simulation that the transferred electrons from MoS₂ to PbS increase with increasing V_g (Fig. 4B). Then, the localized holes gradually recombine with the electrons from MoS₂ to PbS. Thus, we find that I_sd fully recovers its preillumination state (${\mathit{I}}_{\mathrm{P}}^0$) using a large V_g pulse.

Fig. 5. V_g pulse– and temperature-dependent optical memory.

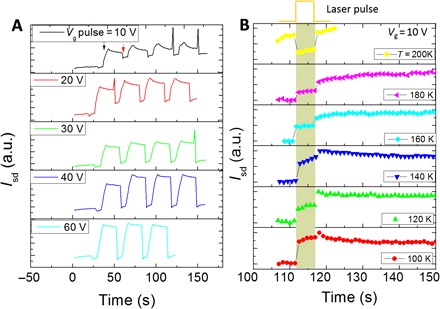
(A) Time evolution of I_sd with a 1940-nm laser pulse–intrigued writing and V_g pulse–induced erasing. The black and red arrows indicate when the laser pulse and V_g pulse are applied, respectively. The power density of laser pulse is fixed to 5.24 mW cm⁻². (B) Temperature dependence of PPC, which gradually disappears as the temperature increases to 200 from 100 K.

The temperature (T)–dependent PPC (Fig. 5B) in device no. 4 becomes weaker as T increases from 100 to 180 K, and it disappears at 200 K. All other devices also present significant persistent photoconductances at low temperatures. However, no PPC is observed at room temperature. The localized holes can escape from the traps due to strong thermal fluctuations at high temperatures. This excludes the mechanism of random local potential fluctuations due to intrinsic defect and charged impurities states. The PPC of random local potential fluctuations (25) should be obvious at high temperatures because the localized trap centers release and play the role at high temperatures (26). The limitation of the operating temperature can be improved by interface engineering (27). For example, inserting a passivating buffer layer TiO₂ at the interface of PbS and MoS₂ (28) significantly increases the potential barrier height of trapped holes in PbS₂, which makes the localized holes robust against thermal fluctuations. However, the thickness of a buffer layer should be carefully chosen to ensure the tunneling of electrons from MoS₂ to PbS for erasing process. We further discuss the roles of disorder states on the optical memory in note S3. We also exclude the photothermal effect or Schottky barrier effect from physical origins of optical memory (note S4).

Nonvolatile operation of optical memory

The charge storage stability is an important parameter to characterize the optical memory. Figure 6A presents the retention performance of laser pulse–intrigued persistent photocurrents with a measurement range of ~1.7 × 10⁴ s. The light power density is 27 μW cm⁻² with a pulse width of 5 s. The readout current almost fully retrieves the original state even if the device is powered off for 10 min and 1 and 3 hours. The readout current hardly decays during the entire experimental range, indicating the potential of nonvolatile charge storage. The endurance of optical writing and electrical erasing is another critical factor for practical applications. As demonstrated in Fig. 6B, on and off states are hardly changed during the entire 2000 cycles of writing and erasing operations. We further demonstrate a multilevel memory in device no. 3, which can lead to an optoelectronic arithmetic function. Figure 6C shows four distinct resistance states, which are programed by three continuous laser pulses with 1-s duration. The readout current gradually increases with the application of three laser pulses. The readout charge is nearly linearly dependent on the number of optical states before saturation, in which each state captures ~8.1 nC on average (Fig. 6D).

Fig. 6. Performance evaluation of infrared memory.

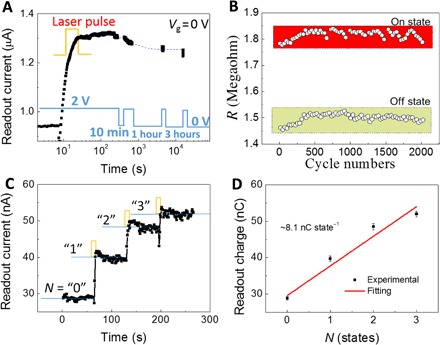
(A) Charge storage stability. The infrared pulse intrigues a persistent photocurrent state. The readout current fully retains its original state even if the device is powered off for 10 min and 1 or 3 hours. The inset at the bottom of (A) shows time-dependent bias voltage V_sd for reading the states. (B) Endurance of optical writing and electrical erasing operation. The on and off states are hardly changed during the entire 2000 cycles. (C) Four states are continuously programed by multiple laser pulses with a wavelength of 1940 nm, laser pulse intensity of 27 μW cm⁻², and duration of 1 s. The readout current increases with the number of laser pulses. Four resistance states are numbered as “0,” “1,” “2,” and “3.” (D) The readout charge collected for 1 s is nearly linearly dependent on the resistance states.

DISCUSSION

In our devices, the lifetime of localized holes is as large as 5125 s. However, the transit time of the photoexcited electrons in MoS₂ is only 2.9 ns. As a result, the photoexcited electrons cycle multiple times in the transport channel before recombination with trapped holes, resulting in the multiplication of photocurrent. This leads to a huge optical gain (G) and ultrahigh external responsivity (R), which is important for memory applications. G = τ_l/τ_t = τ_lμV_sd/L² is estimated (29) to be 1.8 × 10¹² electrons per photon with a channel length L = 9.33 μm, V_sd = 2 V, and μ = 147.8 cm² V⁻¹ s⁻¹, where τ_t is the carrier transit time in MoS₂. This G is six and three orders of magnitude higher than quantum dots/Si heterostructures (30) and hybrid graphene (31), respectively. Our device shows a longer lifetime of localized carriers compared with hybrid graphene (20 ms or 1 s) (31), which explains the huge optical gain of ~10¹² in our device. R = I_ph/P_in reaches 2.6 × 10⁷ A/W for 808 nm (Fig. 1F), 3.6 × 10⁵ A/W for 1340 nm (fig. S6A), and 1.2 × 10⁴ A/W for 1940 nm (fig. S6C), where P_in = PA is the incident light power with the effective radiation area A. The largest R value is comparable with hybrid graphene (31), graphene-MoS₂ heterostructures (12), and three orders of magnitude greater than that of quantum dots/Si heterostructures (30). In addition, our memory devices are highly sensitive to ultraweak signals. When the shot noise of dark currents is considered (32, 33), the specific detectivity D* = RA^1/2/(2eI_dark)^1/2, a figure of merit that evaluates the sensitivity, achieves 5.5 × 10¹⁵, 2.7 × 10¹³, and 4.4 × 10¹² Jones (1 Jones = 1 cm Hz^1/2 W⁻¹) for 808 nm (Fig. 1F), 1340 nm (fig. S6B), and 1940 nm (fig. S6D), respectively, which is comparable to conventional infrared materials (34).

The optical energy used for laser pulse writing is given by the product of the device area A, light power density P, and laser pulse duration t. The memory performance of five devices is listed in table S1, and device no. 1 displays the lowest energy dissipation. Device no. 1 consumes an energy of ~420 pJ during the writing. The energy consumption for V_g pulse erasing is roughly estimated by C_iAU²/2, where C_i is the capacitance per unit area of the SiO₂ dielectric layer with a thickness of 280 nm and U is the V_g pulse magnitude. The electric energy consumption for erasing is 1.5 pJ in device no. 1. The power consumption can be further decreased by optimizing the pulse width, pulse magnitude, and device quality.

We further evaluate the on/off ratio and operation speed. The highest on/off ratio among five devices is obtained from device no. 4 (table S1) with a low noise level (dark current ~ 0.1 pA at V_g < 0 V) (fig. S8). The on/off ratio is 150 at V_g = −1 V. With V_g in the depletion region (V_g = −3 V), we would expect an on/off ratio of ~600 due to the decrease of dark currents. However, if V_g further decreases, then the signal also drops, resulting in a reduction of the on/off ratio. We then analyze the writing (τ_writing) and erasing (τ_erasing) time in five devices. The optimal τ_writing of 15.7 ms and τ_erasing of 0.17 s are observed in device no. 1 (inset of fig. S2F). The τ_writing describes the optical memory speed, which is affected by the light power density, carrier mobility in PbS and MoS₂, surface or interface disorders (26), thickness of PbS nanoplates, and channel length of MoS₂. τ_erasing relates to the recombination speed of electrons in MoS₂ with trapped holes in PbS. τ_erasing can be improved by optimizing the interface potential width with the buffer layer. In addition, the surface or interface treatments (35), to vanish the influence from the surface or interface disorders states, are possible routes to improve the memory speed and increase the on/off ratio while decreasing the background noise.

We proposed a nonvolatile optical memory cell of MoS₂-PbS heterostructures that efficiently works in the optical communication wavebands. The devices operate via the photogate effect, which leads to the persistent retention of charges without any external voltage bias. The readout current fully retrieves memory states, even if the device is powered off for 3 hours, and hardly decays within our measurement range (more than 10⁴ s), suggesting a promising nonvolatile charge storage device. The buffer layer can further improve the charge storage stability by increasing the width of charge-free region. Our devices are robust to uncontrolled environmental factors such as surface and interface impurities or defects. However, the devices have the temperature limitation of memory effect disappearing above 200 K, which can be improved by inserting the buffer layer. Nevertheless, the demonstrated devices show a long-term stability (2000 cycles), signifying their promise in the infrared memory, optoelectronic arithmetic, and logic circuit.

MATERIALS AND METHODS

Synthesis and characterization

Few-layer MoS₂ flakes were mechanically exfoliated from MoS₂ bulk crystals and were transferred to SiO₂ (300 nm)/n⁺⁺-Si substrates. The substrates with few-layer MoS₂ flakes were cleaned by hot acetone (100°C) for removing surface residues. Then, the samples were placed in the downstream of quartz tube of a high-temperature furnace. The quartz tube was pumped to 20 Pa, and the exfoliated few-layer MoS₂ was annealed in a vacuum for half an hour at 650°C. During the annealing, the tube was fed by hydrogen gas with a flow rate of 20 standard cubic centimeters per minute. Subsequently, PbS nanoplates were grown on the few-layer MoS₂ via thermal evaporation of PbS powder (99.99%; Alfa Aesar). The source and substrate temperatures were set to 750° and 550°C for 2 min, respectively. The furnace was then naturally cooled down after the growth. The materials were characterized by HRTEM in FEI Tecnai F20 with SAED and XPS (ESCALAB 250 Xi).

Device fabrication

The electrodes were fabricated by standard electron beam lithography (Nova 200 NanoLab). The defined pattern was successively coated by 10-nm Ti and 40-nm Au thin films via a magnetron sputtering system. Then, the pattern was lifted off using acetone. The device morphology and dimensions were characterized by scanning electron microscopy (Zeiss) and atomic force microscopy (Dimension 3100, Veeco).

Optoelectronic characterization

All optoelectronic transport was performed on a manual probe station (TTP4, Lakeshore) equipped with a vacuum chamber and temperature control system. Keithley 4200 semiconductor parameter analyzer was used to collect the data. The focused infrared lasers with wavelengths of 808, 1340, 1550, and 1940 nm were applied to illuminate the samples. The laser pulses were produced by a chopper. The back gate voltage pulses were generated by a wave generator. The spot size was obtained by shining the infrared laser on the detector cards (THORLABS VRC4 and VRC6S). The VRC4 converted 808-, 1340-, and 1550-nm lasers to visible light. VRC6S changed color when it was excited by a 1940-nm laser. Taking a 1550-nm laser as an example, we used the camera to record the image of laser spot on a detector card. The vernier caliper was placed nearby the laser spot to identify the diameter of laser spot.

Numerical simulation

The physical model of light illumination- and gate voltage–modulated current density and V_g pulse–induced erasing in MoS₂ was derived from the theory of thermionic emission, quantum tunneling, and diffusion transport (see notes S1 and S2). Simulations for the change of carrier density induced by photo injection and V_g injection were based on the capacitance effect of back gate voltages.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/4/eaap7916/DC1

fig. S1. Chemical and structural characterization.

fig. S2. Device morphology and optoelectronic transport.

fig. S3. Control experiments on few-layer MoS₂.

fig. S4. Photoresponse in PbS nanoplate with an 808-nm laser illumination.

fig. S5. The optoelectronic transport and optical memory.

fig. S6. Photoresponse performance.

fig. S7. V_g pulse–dependent erasing current.

fig. S8. Optoelectronic transport and on/off ratio.

fig. S9. Persistent photocurrent as a function of time after the laser pulse switches off.

fig. S10. Optoelectronic transport and optical memory.

fig. S11. Number of transferred electrons as a function of the Fermi level shift.

table S1. Memory performance of five devices.

note S1. Theoretical simulation of carrier injection to MoS₂.

note S2. Dynamics analysis of V_g pulse erasing.

note S3. Roles of disorder states on the optical memory.

note S4. Photothermal effect or Schottky barrier effect.

References (36–43)