Spike-Centered Jitter Can Mistake Temporal Structure

Abstract

Jitter-type spike resampling methods are routinely applied in neurophysiology for detecting temporal structure in spike trains (point processes). Several variations have been proposed. The concern has been raised, based on numerical experiments involving Poisson spike processes, that such procedures can be conservative. We study the issue and find it can be resolved by reemphasizing the distinction between spike-centered (basic) jitter and interval jitter. Focusing on spiking processes with no temporal structure, interval jitter generates an exact hypothesis test, guaranteeing valid conclusions. In contrast, such a guarantee is not available for spike-centered jitter. We construct explicit examples in which spike-centered jitter hallucinates temporal structure, in the sense of exaggerated false-positive rates. Finally, we illustrate numerically that Poisson approximations to jitter computations, while computationally efficient, can also result in inaccurate hypothesis tests. We highlight the value of classical statistical frameworks for guiding the design and interpretation of spike resampling methods.

1. Introduction

Jitter procedures have been developed to detect and quantify the presence of fine temporal structure in point processes (see Amarasingham, Harrison, Hatsopoulos, & Geman, 2012, for an overview) and have been applied extensively to analyze spike trains (see Amarasingham, Geman, & Harrison, 2015, for broader motivation). Loosely, the idea is to locally “jitter” the locations of observed spikes to generate surrogate data sets and then to ask whether the original spike train data set can be distinguished from the jitter surrogates. The amount of jitter specifies a hypothesized timescale of temporal structure. There are many variations in theme and terminology—for example: basic jitter in Amarasingham et al. (2012), dithering in Gerstein (2004), Grün (2009), and Louis, Gerstein, Grün, and Diesmann (2010); teetering in Shmiel et al. (2006); the convolution method in Stark and Abeles (2009); interval jitter in Amarasingham et al. (2012) and Date, Bienenstock, and Geman (1998); pattern jitter in Harrison and Geman (2009) and Amarasingham et al. (2012); and tilted jitter in Amarasingham et al. (2012).

This basic idea is intuitively compelling in neurophysiology. The point of this letter is to emphasize that subtleties arise in translating this intuition into data-analytic procedures. We provide several constructive examples, based on the classical theory of statistical hypothesis testing, to make this point. The examples are deliberately simple, involving either single or paired spike trains, but the issues they raise are amplified in large-scale settings and confirm previous cautions about heuristic methods (Amarasingham et al., 2012).

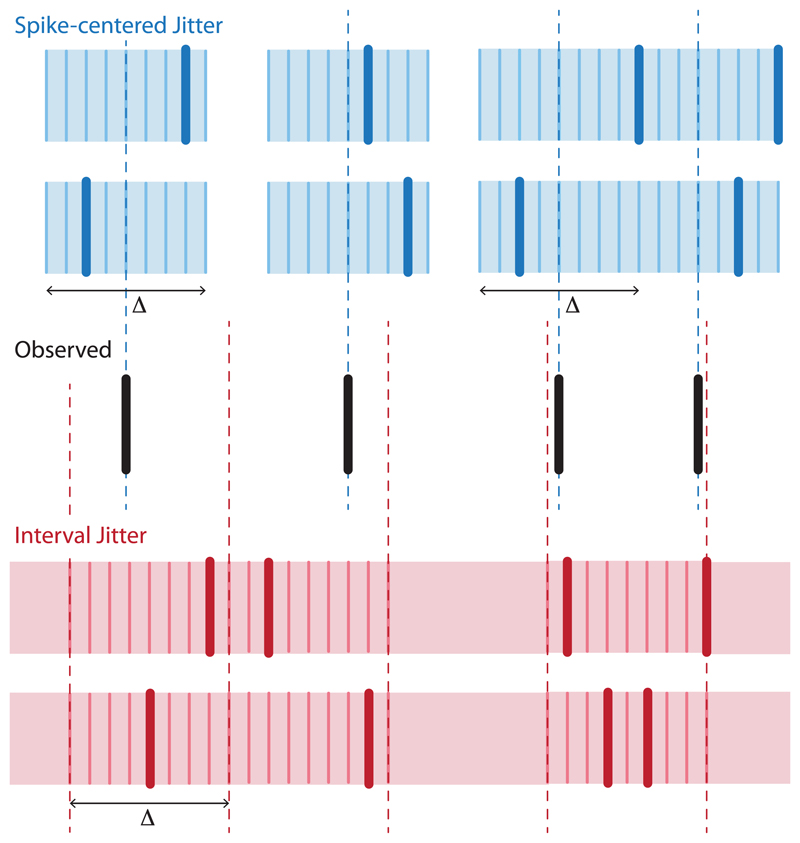
In the first example, we discuss a concern raised by a numerical experiment of Stark and Abeles (2009). In essence, the concern is that a jitter procedure applied to analyze synchrony in a pair of independent, homogeneous Poisson processes is conservative (“biased,” in the terminology of Stark & Abeles, 2009). We review the distinction between spike-centered (basic) jitter procedures and interval jitter procedures (Amarasingham et al., 2012). In spike-centered jitter, jitter surrogates are formed by jittering spikes within an interval centered at their location in the original spike train; in interval jitter, surrogates are formed by jittering spikes in intervals that are chosen independently of the original spike train (see Figure 1). Interval jitter is derived from an exact test of a null hypothesis that contains homogeneous Poisson processes (Amarasingham et al., 2012), whereas spike-centered jitter is not. We conclude that this accounts for the concern that motivates Stark and Abeles (2009).

Figure 1.

Two prototypical spike resampling methods. In spike-centered (basic) jitter (blue), each spike is resampled in an interval centered at its original location (black). In interval jitter (red), each spike is resampled in an interval whose location is specified independent of the original spike train. The thick colored lines represent the surrogate spike trains, whereas the thin colored lines represent the potential locations of a resampled spike. For illustration purposes, only two surrogate trains are shown for each jitter type. The actual computation involves many surrogates.

A source of intuition is the following. Intuitively, resampling can be understood here as a way of removing structure from the data. Differences between the resamples and the observed trains thus provide statistical evidence for structure. However, the original spike trains can be exactly reconstructed from a sufficiently large ensemble of spike-centered jitter surrogates. The same does not hold for interval jitter surrogates. This observation makes clear that spike-centered jitter does not actually remove temporal structure and provides one informal way to distinguish the two procedures.

Motivated in part by the above observations, we then seek more extreme examples of the discrepancy between spike-centered and interval jitter. We focus on examples of spike processes that unambiguously contain no temporal structure. In such a setting, interval jitter procedures are guaranteed to function properly, regardless of the choice of test statistic. In contrast, we construct test statistics and unstructured spike processes for which spike-centered jitter generates more exaggerated examples of conservatism. More striking, we construct examples in which spike-centered jitter even hallucinates temporal structure in the sense of exaggerated false-positive rates. The effect of the hallucination can be arbitrarily large.

As a third class of example, we show that the natural, and computationally compelling, idea of approximating a jitter technique with a Poisson approximation (Abeles & Gat, 2001) can also have practical consequences. The latter is shown with a demonstration of conservative as well as invalid procedures in a numerical example involving an analytical version of an interval jitter experiment.

2. Spike-Centered Jitter Can Be Conservative with Structureless Spike Processes

The problem that Stark and Abeles (2009) examined can be summarized by describing a numerical experiment as follows. Generate two independent, homogeneous Poisson spike trains with identical rates λ. We represent a spike train as a list of spike times. For example, denote t₁ = (t_1,1, t_1,2, … , t_1,N1) as the first spike train, and denote t₂ = (t_2,1, t_2,2, … , t_2,N2) as the second spike train (t_{i, j} is the jth spike time in spike train i, and N_i is the number of spikes in the spike train i). (A glossary of mathematical terms is provided at the end of the letter.) Then the Monte Carlo–resampled train ${\mathit{\text{t}}}_i^{\left(k\right)}$ is generated from the assignment $t_{i,j}^k=t_{i,j}+{ϵ}_{i,j,k},$ where ϵ_{i, j,k} is a random variable uniformly distributed on the interval [−Δ/2, Δ/2], and all ϵ_{i, j,k} terms are drawn independently. (Alternatively, when spike times are discretized, ϵ_{i, j, k} is distributed uniformly on {−Δ/2, −Δ + 1, … , Δ/2}.) Following Amarasingham et al. (2012), we will refer to this resampling technique as spike-centered, or basic, jitter (“dithering” in Grün, 2009; “teetering” in Shmiel et al., 2006; “artificial jitter” in Rokem et al., 2006; “jittering” in Stark & Abeles, 2009). The intuition, which turns out to be incorrect, is that the resamples and the original data should be indistinguishable because a homogeneous Poisson spike train has no temporal structure. To quantify indistinguishability, choose a statistic f (s₁, s₂) that converts a spike train pair (s₁, s₂) into a number and compute S₀ = f (t₁, t₂), and $S_k=f({\mathit{\text{t}}}_1^{\left(k\right)},{\mathit{\text{t}}}_2^{\left(k\right)})$ for k ∈ {1, 2, … , K}. For shorthand, we use X = (t₁, t₂) and $R=({\mathit{\text{t}}}_1^{\left(1\right)},{\mathit{\text{t}}}_2^{\left(1\right)},\dots ,{\mathit{\text{t}}}_1^{\left(K\right)},{\mathit{\text{t}}}_2^{\left(K\right)}),$ so that X represents the data and R the Monte Carlo resamples. Then compute

$$p\left(X,R\right)=\frac{1+{\displaystyle {\sum }_{i=1}^K𝟙\left\{S_i\ge S_0\right\}}}{K+1},$$ (2.1)

where 𝟙 represents the indicator function, so that 𝟙 {S_i ≥ S₀} takes the value 1 if S_i ≥ S₀ and 0 otherwise.

Thus, p(X, R) measures, in some sense, how unusual the original data are with respect to the surrogate spike trains, in terms of the statistic f(s₁, s₂). Can p(X, R) be interpreted as a p-value for a statistical hypothesis of “no temporal structure”?

For example, taking f (t₁, t₂) to be synchrony, with synchrony width δ,

$$f\left({\mathit{\text{t}}}_1,{\mathit{\text{t}}}_2\right)≔{\displaystyle \sum _{i=1}^{N_1}{\displaystyle \sum _{j=1}^{N_2}𝟙\left\{\left|t_{1,i}-t_{2,j}\right|<\delta \right\}}},$$ (2.2)

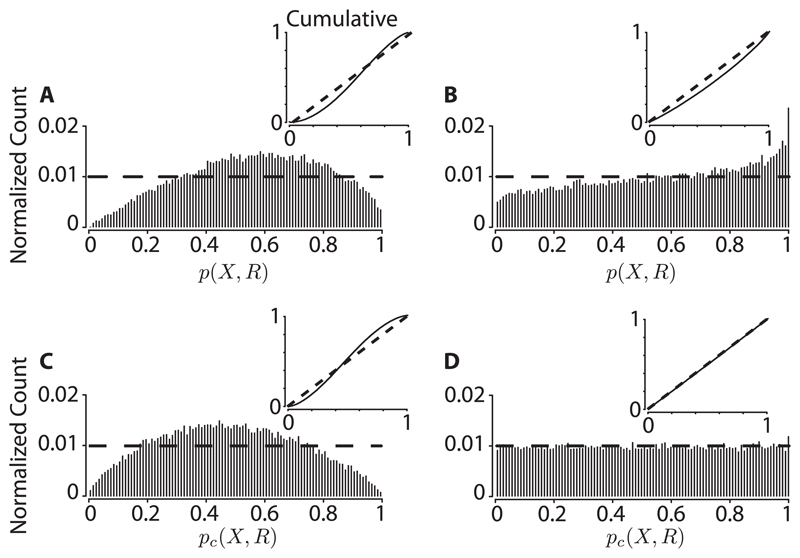
and implementing the experiment numerically, we find that the empirical distribution of p(X, R) does not look uniform (see Figure 2A). This is, in essence, the motivating observation of Stark and Abeles (2009). A standard property of exact p-values that are absolutely continuous is that they are uniformly distributed. Thus, the discreteness of the test statistic S₀ = f (s₁, s2) could be the underlying source of the nonuniformity. However, the same phenomenon occurs when we impose absolute continuity by further randomizing the number S_k. That is, let $S_k^{\prime }=S_k+{\delta }_k,$ where δ₀, δ₁, … , δ_K are independently drawn and uniformly distributed on [−1/2, 1/2], and define

$$p_c\left(X,R\right)=\frac{1+{\displaystyle {\sum }_{i=1}^K𝟙\left\{S_i^{\prime }\ge S_0^{\prime }\right\}}}{K+1}.$$ (2.3)

p_c (X, R) is absolutely continuous. Nevertheless, it is evidently nonuniform (see Figure 2C). Therefore p_c (X, R) cannot be a p-value for any null hypothesis (H₀) that includes independent Poisson spike trains.

Figure 2.

A numerical demonstration of the distribution of p(X, R) (see equation 2.1) and p_c(X, R) (see equation 2.3), generated by both the spike-jittered and interval jitter procedures. Data are taken from pairs of homogeneous (20 spikes/s) Poisson-generated artificial spike trains, and synchrony is used as a test statistic. Details of the experiment are described in the text. Here δ = 30 ms, K = 500, Δ = 20 ms, and trial lengths are 1 s. Each trial provides a single value of p(X, R) (resp., p_c(X, R)). Fifty thousand trials were generated to produce 50,000 such values. The histograms were computed using a 0.01 bin width. (A, C) The respective distributions, using the spike-centered jitter procedure. The horizontal dashed line in all panels represents the theoretical limit (as the number of samples/trials goes to ∞) if the distribution is truly uniform. (B, D) The respective distributions, using the interval jitter procedure. In all panels, the inset represents the respective cumulative distribution, Pr(p(X, R) ≤ α) or Pr(p_c(X, R) ≤ α) (as appropriate). Note that the test is invalid for sufficiently large α with spike-centered jitter. Code is available at https://github.com/aamarasingham/bjitter.

One way to get a proper hypothesis test is to use interval jitter in place of basic jitter (see Amarasingham et al., 2012, for a complete treatment). To summarize, the interval jitter null hypothesis associated with parameter Δ is as follows (Date et al., 1998; Amarasingham et al., 2012). Partition the time interval into disjoint subintervals of length Δ. Let the sequence C_Δ(t₁, t₂) represent the counts in the subintervals. (We conceptualize C_Δ(t₁, t₂) as a Δ-coarsening of spike trains t₁ and t₂.) The null hypothesis is that the conditional distribution of t₁ and t₂, conditioned on C_Δ(t₁, t₂), is uniform (see section A.1 and Amarasingham et al., 2012, for a detailed review of the concept of conditional uniformity).

To generate surrogates, instead of the assignment $t_{i,j}^{\left(k\right)}=t_{i,j}^{\left(k\right)}+{ϵ}_{i,j,k}$ above, use

$$t_{i,j}^{\left(k\right)}=\Delta \lfloor t_{i,j}/\Delta \rfloor +{ϵ}_{i,j,k}^{\prime },$$ (2.4)

where ⌊x⌋ denotes the floor of x (round down) and ${ϵ}_{i,j,k}^{\prime }$ are uniformly distributed on [0, Δ] and drawn independently. With these surrogates, p(X, R) and p_c(X, R) are (both) now proper p-values for the interval jitter null hypothesis. (The reasoning is reviewed in section A.2; see Amarasingham et al., 2012, for explicit statements and demonstrations.) To illustrate one implication of this, we repeat the same numerical experiment with interval jitter: p_c(X, R) indeed appears uniformly distributed (see Figure 2D). This is a corollary of the theory, as independent homogeneous Poisson spike trains are in the null hypothesis for interval jitter, for any Δ (Amarasingham et al., 2012). Independent homogeneous Poisson spike trains are indeed conditionally uniform, conditioned on C_Δ(t₁, t₂), for any Δ. Another implication is that the interval jitter procedure has greater sensitivity toward detecting “nonaccidental” synchronous events, when they are present (see section A.3 in the appendix).

This provides a theoretical account of the observation motivating Stark and Abeles (2009).

3. Spike-Centered Jitter Can Make Mistakes with Structureless Spike Processes

The key general requirement of a p-value is not uniformity; rather the typical implication of hypothesis testing is that, under a null hypothesis H₀, the p-value is subuniform (Casella & Berger, 2001), meaning that

$$\text{Pr}\left(\widehat{p}\le \alpha \right)\le \alpha ,\text{for}\text{all}\alpha >0.$$ (3.1)

In some sense, subuniformity of p-values is a necessary and sufficient condition for hypothesis testing of H₀. (A technical explanation of this equivalence is provided in section A.4 in the appendix.) In contrast, uniformity is a stronger requirement that, under H₀, a p-value p̂ satisfies Pr(p̂ ≤ α) = α for all α. The difference is that the hypothesis tests associated with subuniform p-values are valid but conservative, whereas the tests associated with uniform p-values are valid and nonconservative. For these reasons, our opinion is that conservatism, while certainly sensible to avoid when possible, is a lesser concern and not particularly dangerous, if it is properly interpreted (see section 5). As a familiar example of conservatism, any discrete-level α test is conservative for most values of α.

On the other hand, misconstruing a statistic as a p-value in such a way that, under the null hypothesis of no temporal structure, rejection of the null occurs more often than one expects by chance, will lead to substantially misleading conclusions (i.e., an excess of false positives). This is exactly what happens when random variables that are not subuniform are treated as p-values. That is, we are concerned about the situation in which we treat p(X, R) as a p-value despite the fact of examples, which clearly belong in H₀, for which Pr(p(X, R) ≤ α) = κα, with κ > 1. The higher the value of κ, the greater the concern; thus, the ratio κ(α) = Pr(p(X, R) ≤ α)/α can be viewed as a kind of hallucination factor. (Henceforth, we will write κ(α) simply as κ, bearing in mind that κ depends on α.) Such a decision-making procedure is invalid as a hypothesis test (Stark & Abeles, 2009, refers to the case κ > 1 as permissive).

For example, consider a pair of spike processes such that the spike trains are conditionally uniform and independent, conditioned on (N₁, N₂), for each neuron (see section A.1 for definitions of conditional uniformity in specific settings). Regardless of the many subtleties involved in constructing a quantitative definition of temporal structure for a point process (spike train), it is sufficient here to work with the conditionally uniform example because it is a prototypical example of a point process with no temporal structure. Because such a process is in the interval jitter null hypothesis (Amarasingham et al., 2012) for any Δ, p-values from interval jitter are guaranteed to be subuniform and the tests are guaranteed to be valid. Furthermore, if the p-value p(X, R) is (absolutely) continuous, then interval jitter p-values are guaranteed to be uniform.

Interval and basic jitter are intuitively similar procedures. To what degree is it appropriate to suppose that properties of interval jitter, such as sub-uniformity with respect to conditionally uniform processes, approximately extend to basic jitter? Previously, Amarasingham et al. (2012) emphasized that the basic jitter procedure did not have a clearly defined null hypothesis, cautioning against its unaccompanied use. One aspect of this is that the mathematical logic that justifies interval jitter does not necessarily apply when basic jitter is used to generate surrogates (see section A.2 and Amarasingham, Harrison, Hatsopoulos, & Geman, 2011, for more details).

Continuing to focus on conditionally uniform processes, we sought a more refined look at this question. We examined the implications of using spike-centered jitter surrogates to calculate equation 2.1, and then interpreting the result as a p-value. We find that it is possible for the resulting decision procedure to be conservative (κ < 1) or invalid (κ > 1). The latter case (κ > 1) conclusively establishes that the spike-centered jitter procedure cannot be justified in general; loosely, we refer to this as hallucination of temporal structure. The possibility of both κ > 1 and κ < 1 is independent of the discreteness or continuity of the test statistics. Moreover, there is no upper bound on κ, even focusing only on small α. The range of these possibilities is demonstrated below.

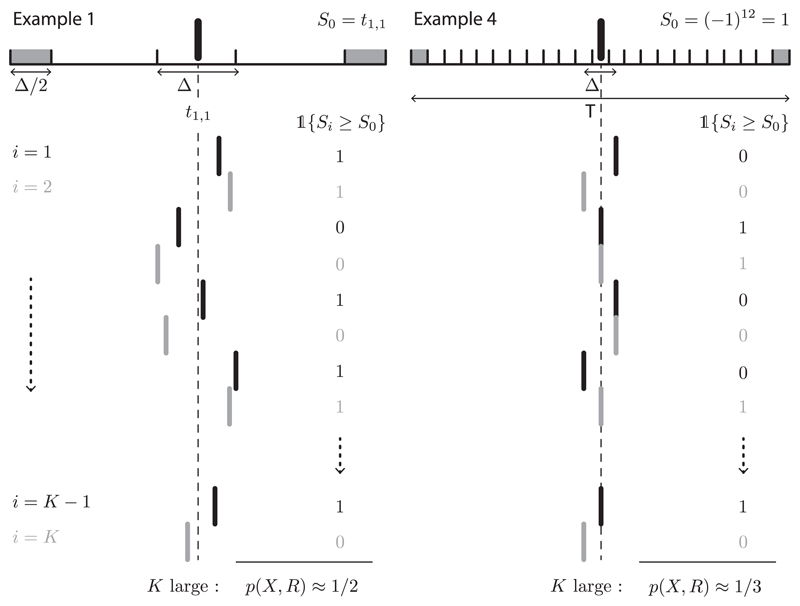
The examples are all of the following common form, involving at most two spike trains, t₁ and t₂, in a single trial. Let N_i be the total number of spikes in the trial for neuron i. N₁ and N₂ are deterministic. t₁ and t₂ are uniformly distributed on the space of all possible (consistent) outcomes. All such examples are conditionally uniform by definition, conditioned on any Δ-coarsening. Thus, they are in (any) interval jitter null hypothesis. A visual representation of the key idea in examples 1 and 4 is provided in Figure 3.

Figure 3.

Illustration of examples 1 and 4. The top spike trains represent the observed data, where the spike-centered jitter window length is indicated. The shaded areas correspond to the edges. The collection of spikes below represents the surrogate data. The gray color and the dashed line are only for visual clarity.

Example 1: A Conservative Spike-Centered Jitter Test (α < 1/2). Consider the example of a single spike: suppose N₁ = 1 with probability 1. The spike train is specified by t_1,1, which is uniformly distributed on the interval [0, 1]. Let 0 < Δ < 1. (It does not matter how edge effects are handled in this example.) Let the statistic f (t₁, t₂) = t_1,1. Conditioned on {Δ/2 <t_1,1 < 1 − Δ/2}, the law of large numbers (LLN) implies that p(X, R) → 1/2, as K → ∞. Thus, for any α < 1/2, we have inf_K,Δ Pr(p(X, R) ≤ α) = 0, demonstrating conservatism. A generalization of this example is implicit in Amarasingham et al. (2011).

Example 2: An Invalid Spike-Centered Jitter Test (1/2 < α < 1). Repeat example 1, except now consider α > 1/2. By the same reasoning, sup_K,Δ Pr(p(X, R) ≤ α) = 1 > α, so the test is invalid (κ = α⁻¹ > 1).

Example 3: A Conservative Spike-Centered Jitter Test (α < 1/2). For another (somewhat more natural) example, consider N₁ = N₂ = 1. Let f (t₁, t₂) = |t_1,1 − t_2,1|, or consider N₁ = 2 and let f (t₁, t₂) = |t_1,2 − t_1,1|. In either case, conditioned on {Δ/2 < t_{i, j} < 1 − Δ/2 ∀i, j, |t_{i, j} − t_{i′, j′} | > Δ/2 ∀(i, j) ≠ (i′, j′)}, p(X, R) → 1/2 as K → ∞ (LLN). Thus, as in example 1, for any α < 1/2, we have inf_K,Δ Pr(p(X, R) ≤ α) = 0, demonstrating conservatism. Note also that p(X, R) is (absolutely) continuous in this example as well as example 1, so the exhibited conservatism is not a consequence of discreteness.

Example 3a: Synchronization. Sticking to the spike process of example 3, use f (t₁, t₂) = −|t_1,1 − t_2,1| (analogous to a left-tailed test). The conclusion is the same. With respect to interval jitter, the statistic implies power toward alternatives that favor spike synchronization, though in a different sense from equation 2.2. The example has natural generalizations to physiological settings, including multiple-spike, multiple-trial versions. The qualitative conclusion is the same. Similarly, f (t₁, t₂) = −|t_1,1 − t_2,1 − j| targets lagged synchronization at time lag j. (Think of cross-correlogram analysis.) Note the implications for sensitivity.

Example 4: An Invalid Spike-Centered Jitter Test, α (Arbitrarily) Close to 1/3, κ (Arbitrarily) Close to 3/2. A relatively simple example can be constructed with discrete (binary) spike trains. For example, consider a 1 ms discretization, with time specified in ms units. Suppose again that N₁ = 1 with probability one and also that Δ = 2. In this case, t_1,1 takes values in {1, 2, … , T}, where T is the length of a trial in ms (for simplicity, suppose T is even). Let f (t₁, t₂) = (−1)^t_1,1. It follows that P(S₀ = 1) = P(S₀ = −1) = 1/2. Conditioned on {S₀ = 1, 2 < t_1,1 < T − 1}, p(X, R) converges to 1/3 as K → ∞. Conditioned on {S₀ = −1, 2 < t_1,1 < T − 1}, p(X, R) = 1 (for all K). Thus, ${\text{sup}}_{T,K}\text{Pr}(p(X,R)\le \frac{1}{3}+ϵ)=\frac{1}{2},$ for sufficiently small ϵ > 0, which demonstrates a permissive procedure with α arbitrarily close to 1/3. (Moreover, this gives ${\text{sup}}_{T,K}\text{Pr}(p(X,R)\le \frac{1}{3}+ϵ)/(\frac{1}{3}+ϵ)=\frac{3}{2}+O(ϵ),$ for sufficiently small ϵ > 0, as well.)

Example 5: An Invalid Spike-Centered Jitter Test, α Arbitrarily Small, κ Arbitarily Large. Expanding on example 4, take discretized binary spike trains (e.g., with 1 ms bins), and let N₁ = m with probability one (m an arbitrary natural number) and Δ = 2. Let $f(t_1,t_2)={\displaystyle {\sum }_{k=1}^{N_1}{(-1)}^{t_{1,k}}},$ and let A be the event {|t_1,i − t_{1, j}| > 2 ∀i ≠ j, 2 ≤ t_1,i ≤ T − 1 ∀1 ≤ i ≤ N₁}. We note that:

1. Pr(A, S₀ = m) → 2^−m as T → ∞.

2. Conditioned on {S₀ = m, A}, p(X, R) → 3^−m as K → ∞ (LLN).

Consequently,

$${\text{sup}}_{T,K}\text{Pr}(p(X,R)\le 3^{-m}+ϵ)\ge 2^{-m},$$

and

$${\text{sup}}_{T,K,m}\text{Pr}(p(X,R)\le 3^{-m}+ϵ)/(3^{-m}+ϵ)=\infty ,$$

for all sufficiently small ϵ > 0. Thus, there is no upper bound on κ in the sense that sup_H0 κ(α) = ∞ (H₀ here is the interval jitter null hypothesis). A related relevant implication is that lim sup_α↓0 sup_H0 κ(α) = ∞.

Remark 1: Edge Effects. In example 1, edge effects are sidestepped by conditioning on the event that t_1,1 is not near the edge. This event can be made arbitrarily unlikely by taking Δ small (alternatively, make the interval arbitarily long). Thus, edge effects do not underlie the phenomena we highlight. The same idea is used in the other examples, as well as the analogous idea to preserve a minimum distance between spikes. This is all that is needed because here we are only seeking counterexamples (see section 5). Another way to understand the irrelevance of edge effects is to construct the examples directly on the circle, generalizing the test statistics as appropriate. Then there are no edge effects by definition, but the identical phenomena occur.

Remark 2: Symmetry of the Jitter Distribution. The uniformity of the jitter distribution does not play an important role either, as all the effects will persist if the jitter distribution is nonuniform yet symmetrical. For example, it is clear in the first three examples that the main phenomenon is simply due to the fact that spike-centered jitter is equally likely to move a spike forward as backward.

As a final remark, we note that the physiological relevance of the examples is besides the point. Rather, the goal is to clarify the concerns with respect to spike-centered jitter hypothesis tests using examples in which the relevant probabilities can be easily computed. At the least, they demonstrate that some restriction on the class of statistics is a requirement to avoiding hallucinations with spike-centered jitter. This is in contrast to interval jitter, where p(X, R) is a proper p-value for the null hypothesis (of conditional uniformity), regardless of the test statistic. Even these relatively simple examples hint that using more physiologically motivated statistics with spike-centered jitter should immediately warrant concern, particularly for complex test statistics (Shmiel et al., 2006). However, the examples may not be altogether pathological. Example 3a is relevant to synchronization studies. Also, the statistic f in examples 4 and 5 essentially quantifies phase locking of spikes or spike bursts to an (extremely smoothed, coarsened) oscillating field (Jones, 2016). The latter examples can be rescaled to correspond to a synchronization example involving physiologically relevant oscillation frequencies as follows. Generate and then coarsen and threshold an oscillatory inhomogeneous Poisson train and a homogeneous Poisson train, both of them independent. With appropriate choices for relevant parameters (period of oscillation, constants of coarsening and thresholding, and firing rates), a stochastic version of examples 4 and 5 can be reproduced with realistic firing rates, employing the identical statistic f. In effect, synchronization is measured with respect to an oscillating spike train rather than an external oscillation. As expected, the result in numerical experiments is an excess of small p-values, in the sense of hallucination (results not shown).

Analogous but more complex versions of examples 1 to 5 can also be constructed from homogeneous Poisson processes.

4. Poisson Approximations of Interval Jitter Can Produce Nonuniform Approximate p-Values

It is natural to use a Poisson approximation to facilitate jitter computations (Abeles & Gat, 2001), as in the convolution method (Stark & Abeles, 2009). What is the effect of such an approximation? Here we illustrate that Poisson approximation errors can have practical consequences. A single numerical example suffices to make the point. We will work here with a simplified interval jitter example, using synchrony as a test statistic. The interval jitter null hypothesis is that spike times are conditionally uniform, conditioned on C_Δ(t₁, t₂) (see above). In the simplest case, consider a spike process such that the spike count in each interval is at most one (for both spike trains). Synchrony is the test statistic (see equation 2.2). Under the null, conditioned on C_Δ(t₁, t₂), the synchrony test statistic is binomially distributed with parameters N and q, by which we mean $\text{Pr}\left(S_0=s|C_{\Delta }\left({\mathit{\text{t}}}_1,{\mathit{\text{t}}}_2\right)\right)=\left(\begin{array}{c}N\\ s\end{array}\right)q^s{\left(1-q\right)}^{N-s}$ (the parameters N and q depend on C_Δ(t₁, t₂); N is the number of intervals with spikes in both trains; q = 1/Δ). This binomial distribution can be approximated as Poisson with parameter N_q. This suggests two ways to compute a p-value for this null hypothesis. In the first, an exactly valid p-value is given by Pr(X ≥ S₀|S₀), where X is distributed as a binomial random variable with parameters (N, q), and independent of S₀. In the second, an approximately valid p-value is given by Pr(ϒ ≥ S₀|S₀), where ϒ is distributed as a Poisson random variable with parameter Nq, independent of S₀.

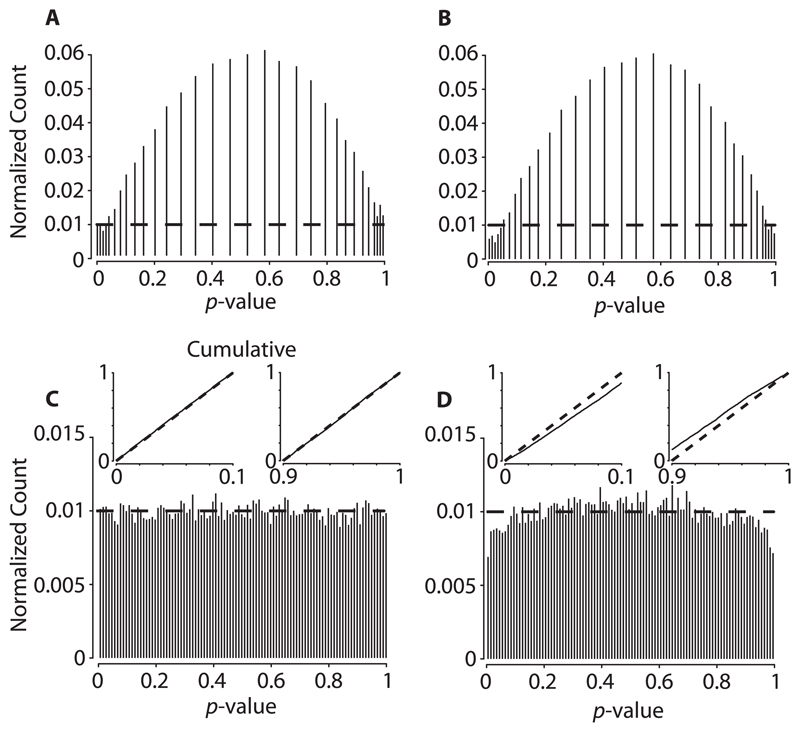
The p-values, resulting from either the original binomial distribution or the Poisson approximation, cannot be uniformly distributed because in both cases, the synchrony statistic is discrete. (The exactly valid method will give subuniform p-values.) Abeles and Gat (2001) used a randomization technique to generate strictly uniform p-values. The technique can be described as follows. Sample U independently and uniformly from the interval [0, 1], and then compute

$$p^{\prime }\left(X\right)=U\cdot \text{Pr}\left(\Upsilon =X|X\right)+\text{Pr}\left(\Upsilon >X|X\right).$$ (4.1)

Then p′ (X) will be strictly uniform. (See the appendix for an intuitive derivation of this formula.) In the example discussed above, the (conditional) distribution of synchrony, under the (conditional) null hypothesis, is exactly binomial. (Note that there is no need for Monte Carlo surrogates in this example.) A numerical example, using N = 500, q = .1 is provided in Figure 4A. Thus, use of this technique produces uniformly-distributed p-values (Figure 4C). However, the technique depends on the fact that the conditional distribution is known exactly. If an approximation of the conditional distribution, such as a Poisson approximation, is used instead, there are no corresponding guarantees of uniformity. The randomized approximate p-values, computed from the Poisson distribution, are visibly nonuniform (see Figure 4D), suggesting conservative tests for small α (invalid tests, for sufficiently large α).

Figure 4.

Nonuniformity of randomized p-values induced by Poisson approximation. Fifty thousand binomial random variables were independently drawn with parameters N = 500 and q = .1, to construct 50,000 p-values. The histograms were computed using a 0.01 bin width. p-Values were constructed by (A) using the exact binomial distribution without randomization, (B) Poisson approximation without randomization, (C) using the exact binomial distribution with randomization, and (D) Poisson approximation with randomization. In all panels, the horizontal dashed line represents the theoretical limit (as the number of samples goes to ∞) if the p-value distribution is truly uniform. Compare panels C and D to notice the nonuniformity induced by Poisson approximation alone. In panels C and D, the insets represent the respective cumulative distribution, Pr(p(X, R) ≤ α) or Pr(p_c(X, R) ≤ α) (as appropriate). Note in panel D that the test is conservative for small α and invalid for sufficiently large values. Code is available at https://github.com/aamarasingham/bjitter.

5. Discussion

The distinction between spike-centered and interval jitter might appear esoteric to some readers. Nevertheless, these results indicate that it is not as mild as it appears. For example, even in the prototypical case of analyzing synchrony between independent homogeneous Poisson processes, the spike-centered jitter procedure can be surprisingly more conservative than interval jitter. This insensitivity is not simply an artifact of discrete statistics. More striking, we show with relatively simple examples that spike-centered jitter can even hallucinate temporal structure to an arbitrary extent. Thus, we caution the use of spike-centered jitter as a rigorous test of hypotheses regarding temporal structure.

It is worth emphasizing that these issues clearly generalize beyond isolated pairs of spike trains and will scale up when applied to large data sets involving multiple neurons, test statistics, and periods of analysis. Such settings amplify the dangers of invalid tests. Correspondingly, multiple testing corrections constructed in such situations will generally require that they are built out of hypothesis tests that are valid in isolation.

In reviewing the literature on these topics, a common theme in these discrepancies is a lack of a well-specified null hypothesis. We wondered whether this has practical implications. The subtleties reported here indeed make a case for rigorous treatment (i.e., precise specification of null hypotheses, in the classical sense). Our conclusions are largely consistent with the overview in Amarasingham et al. (2012).

Once oriented in this direction, other issues arise. As an example, interval jitter has more degrees of freedom than spike-centered jitter, associated with the selection of an interval’s location. This arbitrariness can make practitioners uneasy. Here two points bear considering. The first is that the issue is essentially identical to the arbitrariness associated with rounding (discretizing) measurements. When rounding, we anchor a discretization grid on the origin (zero), but the choice of the origin is arbitrary. Second, there are occasions when one can anchor the interval in an intuitively satisfying way. In the case of synchrony or other cross-correlogram analyses, one can choose to anchor intervals with respect to a reference train (Hatsopoulos, Geman, Amarasingham, & Bienenstock, 2003). For example, in a synchrony analysis, center the intervals around the spikes in a reference train; then jitter the spikes in the target train, respecting the intervals.

More fundamentally, however, the arbitrariness of interval locations is a symptom of the broader problem that the (conditional) uniformity assumption is an approximation. A more precise null hypothesis would accommodate relative variations in the conditional likelihood of spike placement (cf. tilted jitter: Amarasingham et al., 2012), patterned structures such as bursts and refractory periods (cf., pattern jitter: Harrison & Geman, 2009; Amarasingham et al., 2012), multiple comparisons corrections (Amarasingham et al., 2012; Harrison, Amarasingham, & Truccolo, 2015), and quantitative measures of effect size (Amarasingham et al., 2012). With respect to technique, it seems reasonable to expect that statistical precision ought to be applied in proportion to the subtlety of observed effects. In scenarios involving strong effects, this may justify a conservative approach (Fujisawa, Amarasingham, Harrison, & Buzsáki, 2008). In more subtle scenarios, it underscores the need for finely grained analysis.

Related to the above comments, our purpose in using processes with no temporal structure in these examples was to clarify these issues in the simplest setting. For the same reasons, we focused on examples (i.e., sparse firing) where refractory and bursting phenomena, as well as edge effects and firing rate inhomogeneities, are irrelevant to probability computations. Here, these complications were avoided only for clarity of exposition. The issues we have discussed will remain essentially the same embedded in more complicated structures. The same motivations led us to use the randomization approach to handling discretization artifacts. There are procedures for multiple hypothesis testing corrections that do not rely on randomization (see Amarasingham, Chen, Geman, Harrison, & Sheinberg, 2006, for an example in a neurophysiology setting), which we anticipate to be more powerful (data efficient).

Finally, we have largely ignored the inconvenience of excessively time-consuming computation, which in day-to-day work is a major motivation for using approximate methods. We hope that the observations highlighted here will encourage further development of computationally efficient procedures that can be rigorously understood or rigorously calibrated (Harrison, 2013; Jeck & Niebur, 2015).

Glossary

C_Δ(t₁, t₂)

Δ-coarsening of spike trains t₁ and t₂

Δ

jitter window width

δ

synchrony window width

f

function to compute the test statistic

K

number of surrogate spike trains

N_i

number of spikes in the spike train i

R

$=({\mathit{\text{t}}}_1^{\left(1\right)},{\mathit{\text{t}}}_2^{\left(1\right)},\dots ,{\mathit{\text{t}}}_1^{\left(K\right)},{\mathit{\text{t}}}_2^{\left(K\right)})$

S₀

test statistic derived from the original spike train pair

S_k

test statistic derived from surrogate spike train pair k

$S_k^{\prime }:$

randomized S_k

t₁

spike train 1

$t_i^{(k)}$

Monte Carlo resampled spike train i, surrogate k

X

= (t₁, t₂)