Selection on skewed characters and the paradox of stasis

Abstract

Observed phenotypic responses to selection in the wild often differ from predictions based on measurements of selection and genetic variance. An overlooked hypothesis to explain this paradox of stasis is that a skewed phenotypic distribution affects natural selection and evolution. We show through mathematical modelling that, when a trait selected for an optimum phenotype has a skewed distribution, directional selection is detected even at evolutionary equilibrium, where it causes no change in the mean phenotype. When environmental effects are skewed, Lande and Arnold’s (1983) directional gradient is in the direction opposite to the skew. In contrast, skewed breeding values can displace the mean phenotype from the optimum, causing directional selection in the direction of the skew. These effects can be partitioned out using alternative selection estimates based on average derivatives of individual relative fitness, or additive genetic covariances between relative fitness and trait (Robertson-Price identity). We assess the validity of these predictions using simulations of selection estimation under moderate samples size. Ecologically relevant traits may commonly have skewed distributions, as we here exemplify with avian laying date – repeatedly described as more evolutionarily stable than expected –, so this skewness should be accounted for when investigating evolutionary dynamics in the wild.

One of the most striking facts revealed by studies of evolutionary dynamics and natural selection on wild organisms over the past fifty years is the relative temporal stability of heritable phenotypes, despite the detection of directional selection with rather consistent direction in time (Kingsolver, 2001; Kingsolver and Pfennig, 2007; Merilä et al. 2001; Morrissey and Hadfield, 2011). Such absence of evolution of heritable traits under apparent directional selection constitutes the so-called “paradox of stasis” at the micro-evolutionary scale (the macro-evolutionary paradox of stasis involves absence of long-term change despite the possibility of rapid evolution, Estes and Arnold 2007; Gingerich 2009).

Several non-exclusive hypotheses have been formulated to explain this paradox (Merilä et al. 2001; Morrissey et al. 2010; Stinchcombe and Kirkpatrick, 2012; Walsh and Blows, 2009). For instance, the multivariate nature of phenotypes under selection may induce an over-estimation of heritability by non-multivariate approaches (due to genetic correlations between traits, Hansen and Houle, 2004; Teplitsky et al. 2014), or spurious estimates of selection may be caused by purely environmental covariances between phenotypes and fitness (Rausher 1992; Morrissey et al. 2010; Bonnet et al. 2017). At present, there is no consensus as to the origin of this evolutionary paradox (Estes and Arnold, 2007; Haller and Hendry, 2013; Hansen and Houle, 2004; Kaplan, 2009; Merilä et al. 2001; Rollinson and Rowe, 2015), and while several processes are most probably involved, there is insufficient empirical evidence to conclude on their relative importance.

One phenomenon that could contribute to the paradox of stasis but has so far been largely neglected is skewness in phenotypic distributions. Quantitative genetics theory and statistical analyses mostly rest on the assumption of Gaussian distributions of phenotypes, breeding values, and environmental effects (e.g. Lynch and Walsh 1998; Falconer and MacKay 1996). This assumption is commonly made for mathematical convenience, but is also biologically justified when variation in a quantitative trait is determined by a large number of loci with infinitesimal effects (Falconer and MacKay, 1996; Fisher, 1918; Turelli and Barton, 1994), or by a balance between stabilizing selection and high mutation rates even at a few loci (Kimura, 1965; Lande, 1976b). However, phenotype distributions are not always Gaussian in the wild; in particular, they may be skewed (asymmetric). Formally, skewed distributions have a non-zero third central moment µ₃, and skewness can be measured by scaling this moment by the standard deviation, α = µ₃/σ³. As an example, in Table 1 we report phenotype distributions and phenotypic skewnesses for avian breeding phenology (i.e. date of first egg laid), a textbook example of phenotypic responses to climate change (Bradshaw and Holzapfel, 2008; Gienapp et al. 2014), which also includes several examples of the paradox of stasis in wild populations (Charmantier and Gienapp, 2014). We found a positive mean phenotypic skewness (across multiple years) in all seven populations of six bird species explored (see Table 1; skewness ranging from 0.40 in the Savanah Sparrow Passerculus sandwichensis to 1.37 in the Common Tern Sterna hirundo).

Table 1.

Skewness of laying date in seven wild bird populations. Datasets are from the references listed in the last column, apart from the Kent Island Savannah sparrow data provided by Nathaniel T. Wheelwright. Laying date was annually standardised by the mean (i.e. laying date minus the annual mean laying date), in order to estimate the mean skewness of the laying date distribution on the entire dataset. Skewness was estimated with the function skewness from the R package Moment, and its significance tested using an Agostino test (function agostino.test of the same package). In the histograms, laying dates were binned by intervals of two days.

Species	Population	Date (number of years)	Number of measures (number of females)	Laying date Distribution (full line: mean, dotted line: median)	Skewness	Variance of skewness between years	References
Passerculus sandwichensis	Kent Island (Canada)	1987-2004 (18)	772 (NA)		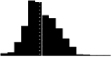0.40***	0.24	https://www.bowdoin.edu/kent-island/datasets/index.shtml
Uria aalge	Isle of May (Scotland)	1982-2005 (24)	2594 (NA)		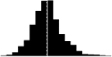0.40***	NA	Reed et al. 2006
Strix uralensis	Päijät-Häme (Finland)	1978-2008 (31)	1115 (361)		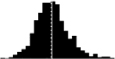0.44***	NA	Brommer et al. 2012
Cyanistes caeruleus	Pirio (Corsica)	1980-2009 (30)	781 (489)		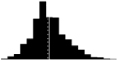0.44***	0.33	Porlier et al. 2012
Uria aalge	Farallon Island (California)	1986-2005 (20)	583 (NA)		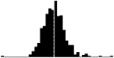0.50***	NA	Reed et al. 2009; Schroeder et al. 2009
Parus major	Wytham, Oxford (England)	1961-2004 (44)	7784 (5068)		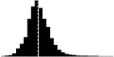0.83***	0.48	Charmantier et al. 2008
Sterna hirundo	Wilhelmshaven (Germany)	1993-2008 (16)	1390 (294)		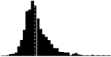1.39***	0.40	Dobson et al. 2017

Several non-exclusive processes may lead to a skewed phenotypic distribution, including: i) a sustained directional displacement of the adaptive optimum in time (Jones et al. 2012), such as the advancement of phenology with global warming (e.g. Visser et al. 2010); ii) migration between two populations with different adaptive optima (Débarre et al. 2015); iii) a skewed stabilizing fitness function (Urban et al. 2013).When phenotype distribution is skewed, it is sometimes possible to transform the trait to a scale that makes it close to Gaussian, for instance by log transformation, as is commonly done for morphological traits, notably when investigating allometry (e.g. Pélabon et al. 2013; Bolstad et al. 2015). However, transformation is not always recommended, as it may violate the natural scale allowing trait comparison, or lead to wrong biological interpretations (Houle et al. 2011). For some traits with specific non-normal distributions (e.g. Poisson), the response to selection may be analysed using the generalized linear model framework (de Villemereuil et al. 2016), but this is not applicable to traits with arbitrary distributions.

Previous theoretical work has explored the general response to selection of non-Gaussian traits (Burger, 1991; Turelli and Barton, 1990, 1994), and shown that a skewed distribution of breeding values can modify the expected response to selection. However, these studies did not consider a skewed distribution of environmental effects, and more generally did not address how phenotypic skewness affects empirical estimates of natural selection. We here investigate how skewed phenotype distributions affect natural selection and its estimation in wild populations. Specifically, we aim to understand whether the genetic versus environmental origin of phenotypic skewness has different effects on measurements of selection, and how these effects are captured by different metrics that reflect different strategies for quantifying selection. Our theoretical analysis, combined with simulations of empirical estimation with limited sample size, indicate that phenotypic skewness may have substantial effects on measurements of selection, and that the direction and magnitude of these effects depend on whether they concern the heritable or environmental components of phenotypic variation.

Model

Generalized Response to Selection

We focus on a quantitative trait, for which the phenotypic value z can be partitioned as

$$z=g+e$$ (1)

with g the breeding value contributing to parent-offspring resemblance – and hence to responses to selection – and e a residual component of variation (with mean 0) caused by environmental variation and developmental noise, as well as by non-additive genetic effects. Contrary to classical quantitative genetics (e.g. Lynch and Walsh 1998; Falconer and MacKay 1996), we do not assume that all components of the phenotype (z, g, and e) are normally distributed. In particular, we allow for non-zero third central moment µ₃, and hence for skewness. The response to selection for a trait with arbitrary distribution of breeding values has been investigated by several authors (Burger, 1991; Turelli and Barton, 1990, 1994), who have shown that, up to third order,

$$\Delta \overline{z}={\sigma }_g^2\frac{\partial \mathit{\text{ln}}(\overline{W})}{\partial \overline{z}}+{\mu }_{3g}\frac{\partial \mathit{\text{ln}}(\overline{W})}{\partial {\sigma }_g^2},$$ (2)

where µ_3g is the genetic third central moment. The first term in the right-hand side of eq. (2) is the product of the directional selection gradient (defined as the derivative of log-mean fitness relative to the mean trait, see Table 2) by the additive genetic variance, as appears in the selection response of Gaussian traits (Lande, 1976a). In contrast, the second term only exists when the breeding value distribution is asymmetric, as it depends on µ_3g. The related component of selection is the partial derivative of natural logarithm mean fitness with respect to genetic variance.

Table 2.

Definitions of selection gradients. We here summarize alternative ways to conceptualize selection gradients, respectively as derivatives of (log) mean fitness with respect to mean phenotype (theoretical perspective, from Lande’s extension of Wright’s mean fitness landscape to quantitative traits), as average derivatives of individual relative fitness with respect to individual phenotype, or as Ordinary Least-Square (OLS) regression slopes of individual relative fitness on individual phenotype. For directional selection, these expressions are all equivalent if the trait is normally distributed. Furthermore, the response to selection by the mean phenotype is proportional to these directional gradients only for a normally distributed trait.

	Derivative of mean fitness	Average Derivative of Individual Relative Fitness (ADIRF)	Regression slope (OLS)
Directional selection (Selection on trait mean)	$\frac{\partial ln\overline{W}}{\partial \overline{z}}=\frac{1}{\overline{W}}\frac{\partial \overline{W}}{\partial \overline{z}}=\beta$	$\frac{1}{\overline{W}}E\left(\frac{\partial W}{\partial z}\right)=\beta$	$\frac{1}{\overline{W}}\frac{Cov(z,W)}{{\sigma }_z^2}$ (= β when z is Gaussian)
Stabilizing/disruptive selection (Selection on trait variance)	$\frac{{\partial }^{2}ln\overline{W}}{\partial {\overline{z}}^2}=\frac{1}{\overline{W}}\frac{{\partial }^2\overline{W}}{\partial {\overline{z}}^2}-{\left(\frac{1}{\overline{W}}\frac{\partial \overline{W}}{\partial \overline{z}}\right)}^2=\gamma -{\beta }^2$	$\frac{1}{\overline{W}}E\left(\frac{{\partial }^{2}W}{\partial z^2}\right)=\gamma$	$\frac{1}{\overline{W}}\frac{Cov({(z-\overline{z})}^2,W)}{{\sigma }_z^4}$ (= γ when z is Gaussian)

Equilibrium Mismatch with Optimum

Here we are interested in modelling an evolutionary equilibrium caused by stabilizing selection, as often invoked to explain stasis in the long run (Arnold et al. 2001; Estes and Arnold, 2007; Hansen, 1997; Hansen and Houle, 2004). We model stabilizing selection using a quadratic function, where the absolute fitness W(z) of an individual with phenotype z is

$$W\left(z\right)=W_{\mathit{\text{max}}}\left(1-\frac{{\left(z-\theta \right)}^2}{2{\omega }^2}\right)$$ (3)

with W_max the maximal fitness values for an optimal phenotype θ, and ω the width of the fitness peak (stabilizing selection is stronger for smaller ω). This function is such that fitness declines with increasing distance between phenotype z and optimal values θ. A quadratic function is chosen here for mathematical convenience and because it is a good approximation to any form of stabilizing selection under weak directional and quadratic selections, i.e when the mean phenotype is close to the optimum and the phenotypic variance is smaller than the squared peak width.

With this fitness function, the mean fitness of individuals with breeding values g, averaged over all possible phenotypic values accounting for environmental effects e, is

$$\tilde{W}\left(g\right)=W_{\mathit{\text{max}}}\left(1-\frac{{\sigma }_e^2}{2{\omega }^2}-\frac{{\left(g-\theta \right)}^2}{2{\omega }^2}\right)$$ (4)

Hence with this fitness function, environmental effects affect the fitness of individuals with breeding value g only through their variance, but not their higher moments, including the environmental third order moment µ_3e. Averaging W̃(g) over the distribution of breeding values g in the population, the mean fitness in the population is

$$\overline{W}=W_{\mathit{\text{max}}}\left(1-\frac{{\sigma }_z^2}{2{\omega }^2}-\frac{{\left(\overline{z}-\theta \right)}^2}{2{\omega }^2}\right),$$ (5)

where ${\sigma }_z^2={\sigma }_g^2+{\sigma }_e^2$ is the total phenotypic variance of the population, and ḡ = z̄. Here again, the population mean fitness depends on the mean and variance of the phenotype, but not on the third central moment (or any higher moment) of the phenotypic distribution.

From eq. (5), the directional selection gradient appearing in eq. (2) (as derivative of mean fitness relative to mean phenotype, Table 2 and Lande 1976a) is

$$\frac{\partial \mathit{\text{ln}}\left(\overline{W}\right)}{\partial \overline{z}}=-S\left(\overline{z}-\theta \right),$$ (6)

where

$$S={\left({\omega }^2-\frac{{\sigma }_z^2+{\left(\overline{z}-\theta \right)}^2}{2}\right)}^{-1}.$$ (7a)

The parameter S is positive under weak stabilizing and directional selection $({\omega }^2>\frac{{\sigma }_z^2+{(\overline{z}-\theta )}^2}{2}),$ as required in the first place by the use of a quadratic fitness function. Eq. (6) shows that directional selection acts as a restoring force towards the optimum (i.e. is in opposite direction to the deviation from the optimum z̄ – θ), with a strength S that increases when the fitness peak is narrower (small ω), as shown by Lande (1976a). Furthermore, if the squared deviation from the optimum (z̄ – θ)² is much smaller than phenotypic variance ${\sigma }_z^2$ (directional selection weaker than stabilizing selection), then

$$S\approx \frac{1}{{\omega }^2-\frac{{\sigma }_z^2}{2}},$$ (7b)

such that directional selection is proportional to the deviation of the mean phenotype from the optimum in this model (since S no longer depends on z̄ – θ).

The selection gradient on genetic variance appearing in eq. (2) is, from eq. (5),

$$\frac{\partial \mathit{\text{ln}}(\overline{W})}{\partial {\sigma }_g^2}=-S/2.$$ (8)

This gradient is negative when selection is stabilizing (because stabilizing selection reduces genetic variance). Then combining eq. (6) and (8) with eq. (2), the response to selection under skewed phenotypic distribution and quadratic stabilizing selection is

$$\Delta \overline{z}=-S\left[\left(\overline{z}-\theta \right){\sigma }_g^2+\frac{{\mu }_{3g}}{2}\right].$$ (9)

Note that eq. (9) is exact, such that no higher-order term exists in the response to selection with this fitness function (Burger 1991). Assuming that the genetic variance and third central moment are maintained at an equilibrium between selection and other evolutionary forces including mutation, recombination, and possibly migration (see Introduction), the evolutionary equilibrium for the mean phenotype is obtained by setting ∆z̄ = 0 in eq. (9), leading to an equilibrium deviation from the optimum

$${\left(\overline{z}-\theta \right)}_{eq}=-\frac{{\mu }_{3g}}{2{\sigma }_g^2}.$$ (10)

Hence, at the evolutionary equilibrium, when breeding values are skewed, the mean phenotype is not at the adaptive optimum. The distance between the mean phenotype and the optimum increases with the skewness of breeding values (eq. 10). Importantly, even though there is a difference between the mean phenotype and the optimum, there is no response to selection since the population is at equilibrium.

Equilibrium Selection Gradient

Empirical estimates of directional selection gradients from finite population samples are generally not based on the relationship between population mean fitness and mean phenotype (as used above), but instead use regression of individual fitness on individual phenotype. For normally distributed traits, the linear version of the Ordinary Least-Square (OLS) regression of relative fitness (i.e. individual fitness divided by mean fitness) on individual phenotype directly yields the slope of the natural log-mean fitness function (∂ln (W̄)/∂ z̄), that is, the selection gradient used to predict the response to selection (Lande, 1976a; Lande and Arnold, 1983, and see Table 2). This is no longer true when phenotype distributions are non-Gaussian, notably when they are skewed (as discussed in the Appendix of Lande and Arnold 1983, where a special rescaling of traits is introduced to correct for the effect of skewness). For instance, with a quadratic fitness function as modelled in eq. (3), and using the fact that, from eqs (1), (3) and (7), $W/\overline{W}-1=\left(S/2\right)\left[{\sigma }_z^2-2\left(\overline{z}-\theta \right)\left(z-\overline{z}\right)-{\left(z-\overline{z}\right)}^2\right],$ the selection gradient estimated by the OLS method is

$${\widehat{\beta }}_{OLS}={\sigma }_z^{-2}\text{E}\left[(z-\overline{z})(\frac{W}{\overline{W}}-1)\right]=-S\left[(\overline{z}-\theta )+\frac{{\mu }_{3z}}{2{\sigma }_z^2}\right],$$ (11)

where E[] denotes an expectation over the phenotypic distribution. Note that the gradient in eq. (11) includes a contribution from phenotypic skewness (through the third central moment µ_3z). This shows that, if the phenotype distribution is skewed due to skewness in environmental effects distribution (i.e. µ_3g = 0 but µ_3e ≠ 0, leading to µ_3z ≠ 0), the selection gradient β̂_OLS estimated by the Lande and Arnold (1983) method does not vanish when the mean phenotype is at the optimum (i.e. even if z̄ = θ at equilibrium because µ_3g = 0). This occurs because the asymmetry in the phenotype distribution causes individuals to lie farther on one side of the optimum than on the other side, resulting in a non-zero directional gradient, when the fitness function is symmetric around the optimum (Fig. 1a). Note also the striking similarity between the response to selection in eq. (9) and the measured selection gradient using OLS method in eq. (11). The difference is that the former depends on the additive genetic variance and third central moment, while the latter depends on the phenotypic moments.

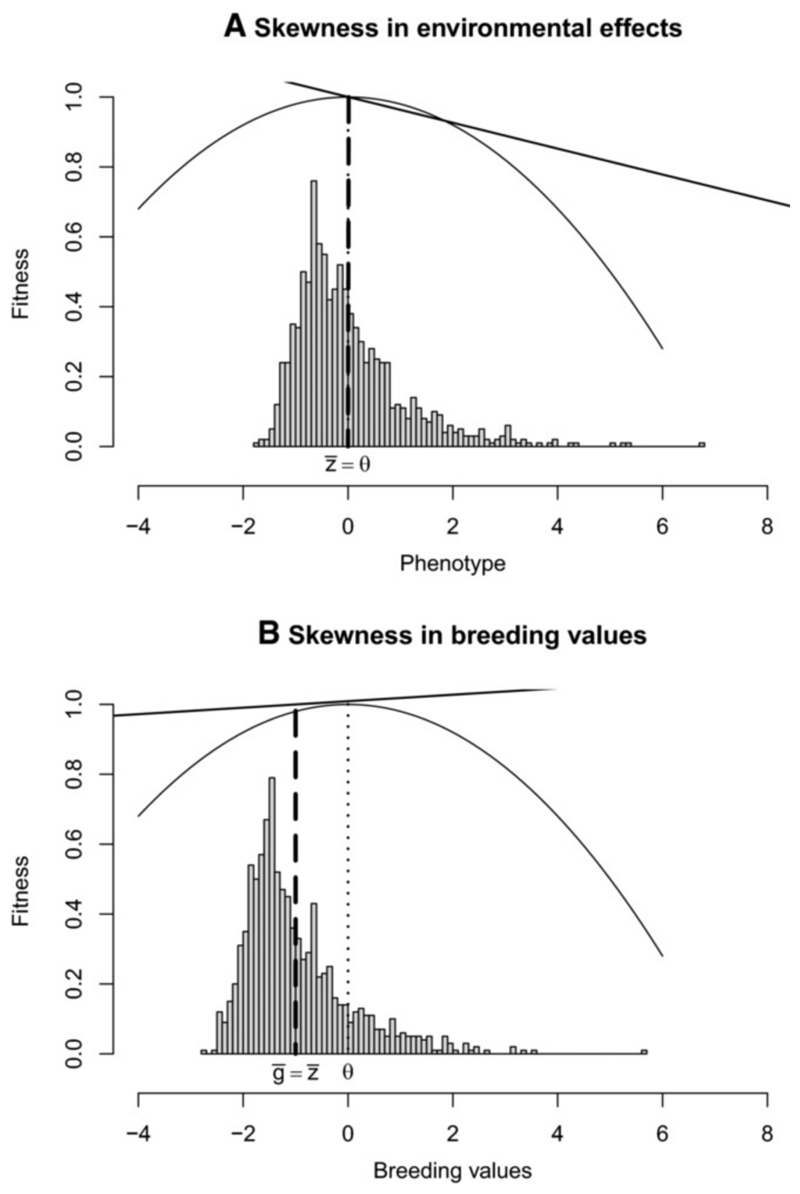
Figure 1.

Influence of phenotypic skewness on estimates of directional selection. The histograms show phenotype distributions under skewed environmental effects (a) (skewness α_e = 2, heritability h² = 0.1), or skewed breeding values (b) (skewness α_g = 2, heritability h² = 0.9). The dotted line represents the optimum phenotype θ for the stabilizing fitness function (solid curve, eq. (3)). The dashed line shows the mean phenotype. The solid straight line has a slope equal to the directional gradient estimated by OLS regression (as in Lande and Arnold (1983)).

Eq. (11) can be used to predict the response to selection that would be estimated from a selection gradient estimated by OLS method, which is simply $\Delta {\overline{z}}_{OLS}={\widehat{\beta }}_{OLS}{\sigma }_g^2.$ Comparison with the actual response to selection in eq. (9) shows that

$$\Delta {\overline{z}}_{OLS}-\Delta \overline{z}=-\frac{s}{2}(h^2{\mu }_{3z}-{\mu }_{3g}).$$ (12)

Hence, the error made by ignoring phenotypic skewness when computing the response to selection as ∆z̄_OLS is all the more important as the third central moment of breeding values µ_3g differs from the phenotypic third central moment µ_3z multiplied by the heritability h². Finally, at evolutionary equilibrium, the selection gradient estimated by the OLS method according to Lande and Arnold (1983) is

$${\widehat{\beta }}_{OLS,eq}=-\frac{s}{2}\left(\frac{{\mu }_{3z}}{{\sigma }_z^2}-\frac{{\mu }_{3g}}{{\sigma }_g^2}\right).$$ (13)

Eq. (13) shows that even at evolutionary equilibrium, where the mean phenotype no longer evolves in response to selection, the selection gradient measured by the OLS method (that is, using the classic Lande and Arnold (1983) approach) on a character with skewed phenotypic distribution is likely to be non-zero. The sign of the measured selection gradient depends on the origin of the phenotypic skewness: at evolutionary equilibrium, with environmental skewness, the selection gradient is of the opposite sign to the phenotypic skewness (Fig. 1a), while with genetic skewness, the selection gradient is of the same sign as phenotypic skewness (Fig. 1b). This occurs because phenotypic skewness affects the selection gradient by itself, but skewness of breeding values also affects the response to selection, displacing the mean phenotype from the optimum in the opposite direction.

Alternative Measurements of Selection

When phenotype distributions are skewed, the response to selection may still be correctly predicted empirically by using methods that do not assume normality. For instance, the Robertson–Price identity (Price, 1970; Robertson, 1966, 1968) states that the response to selection equals the additive genetic covariance between a trait z and relative fitness w, regardless of the phenotype distribution, that is, ∆z̄ = σ_a(z,w). Expanding terms in the covariance, using W̃(g)/W̄ (from eqs. (4) and (5)) as the additive genetic relative fitness associated with genotypes with breeding value g, after some simple algebra we recover the correct response to selection in eq. (9).

A complementary approach would be to use a method that directly computes the theoretical selection gradients based on mean fitness. This strategy, originally introduced by Janzen and Stern (1998) for the specific case of logistic regression in viability selection, has recently been extended by Morrissey and Sakrejda (2013), who advocated its use in general, and proposed a framework based on Generalized Additive Model (Wood, 2006, GAM, R package mgcv, function gam) to directly estimate the theoretical selection gradient that appears in eq. (2). More precisely, this method estimates the individual fitness landscape (relationship between individual traits and relative fitness), and uses it to compute the Average Derivative of Individual Relative Fitness (i.e. the mean slope of the individual fitness landscape, ADIRF method hereafter), which is equivalent to the derivative of mean fitness for the linear selection gradient (for the quadratic selection gradient, a correction term is added, Lande and Arnold, 1983 and Table 2). This is implemented as gam.gradient in the gsg R package by Morrissey and Sakrejda (2013).

These alternative measurements of selection can be used in combination, in order to partition out the contribution of phenotypic skewness to selection and the response to selection. For instance, the part of the observed phenotypic selection attributable to skewness in phenotypes is provided by the difference between the selection gradients estimated by the OLS and ADIRF methods,

$${\widehat{\beta }}_{OLS}-{\widehat{\beta }}_{\mathit{\text{ADIRF}}}=-\frac{s}{2}\frac{{\mu }_{3z}}{{\sigma }_z^2}$$ (14)

Similarly, the part of the response to the selection attributable to skewness in breeding values is provided by the difference between the Robertson-Price identity and the response to selection predicted with the ADIRF method,

$$\Delta {\overline{z}}_{R-P}-\Delta {\overline{z}}_{ADIRF}={\sigma }_a\left(z,w\right)-{\sigma }_g^2{\widehat{\beta }}_{\mathit{\text{ADIRF}}}=-\frac{s}{2}{\mu }_{3g}.$$ (15)

Eq. (15) holds even when the population is not at evolutionary equilibrium, but at equilibrium this term exactly cancels out the selective effect of the mismatch between z̄ and θ (eq. 10). Note also that the component of the selection response in eq. (15) depends on the genetic third central moment µ_3g, but not on heritability.

Simulation of selection estimation

To assess the relevance of these theoretical predictions for empirical estimates of selection with moderate sample sizes, we simulated data sets of skewed phenotypic distributions and associated fitness based on an adaptive landscape with a fitness optimum.

Simulation Procedure

All simulations were performed in the R environment (R 3.2.4 version). Each individual phenotype was the sum of a breeding value and an environmental effect. Because skewness in phenotype distribution can have genetic or environmental origins, simulations were performed under two scenarios: i) skewed breeding values but normally distributed environmental effects; and ii) normally distributed breeding values but skewed environmental effects.

To explore a range of parameter values, we used a distribution that allows modifying skewness while controlling for mean and variance. We chose the Gamma distribution Г(k,h) with shape and scale parameters k and h respectively, because its skewness is simply $\alpha =\frac{2}{\sqrt{k}}.$ We made use of the properties relating the shape and scale parameters of a Gamma to its mean µ = kh and variance σ² = kh². Specifically, we chose the scale parameter as $h=\frac{\sigma }{\sqrt{k}}$ with σ the standard-deviation of the distribution, such that changing k changed skewness without changing the variance. Finally, adding –kh to the variable (leading to a displaced Gamma distribution) allowed controlling for the mean.

In each simulation, the breeding value and environmental effect of each individual were drawn from distributions with the required moments. In particular, the distribution of environmental effects had mean zero in all simulations. The distribution of breeding values had mean zero in simulations with skewed environmental effects, while in simulations with skewed breeding values, the mean was displaced from the optimum according to eq. (10). We used distributions with several theoretical values of skewness in breeding values or environmental effects: α = 0, 0.5, 1, 2, 3, 4 or 5. We only considered positive skewness, but all results can be transposed to negative phenotypic skewness, simply with opposite signs. When skewness was caused by the environmental effects, the latter had an expected variance ${\sigma }_e^2=1$, and we tested several variances of breeding values: ${\sigma }_g^2=1,1/2,1/5\text{or}0,$ leading to heritabilities $h^2=\frac{{\sigma }_g^2}{{\sigma }_g^2+{\sigma }_e^2}=\frac{1}{2},\frac{1}{3},\frac{1}{6}\text{or}0,$ respectively. Conversely, when skewness was due to breeding values, the genetic variance was set to ${\sigma }_g^2=1$, and the environmental variance varied: ${\sigma }_e^2=0,1,2\text{or}5,$ leading to heritability $h^2=1,\frac{1}{2},\frac{1}{3}\text{or}\frac{1}{6}$ respectively. Because the phenotype distribution is a mixture between the distributions of breeding values and environmental effects (one of which is Gaussian by assumption), its skewness is necessarily smaller (in absolute value) than the skewness of breeding values or environmental effects, and increases with increasing (respectively, decreasing) heritability (Fig. S1).

Selection was implemented using the quadratic fitness function in eq. (3), with optimum θ = 0, fitness maximum W_max = 10 and peak width ω = 5. These values were chosen to be consistent with recent estimates for laying date in a wild great tit population (Chevin et al. 2015), so fitness W corresponded to the expected number of offspring per female reproductive event (i.e. selection on reproductive success). The actual offspring number for a female with phenotype z was randomly drawn from a Poisson distribution with mean W(z), thus accounting for demographic stochasticity. Relative fitness was obtained by dividing absolute realized fitness (number of offspring) by the mean fitness in the population.

Directional and quadratic selection gradients were estimated in each simulation using the two methods described in the Model section: i) the classical OLS method of Lande and Arnold (1983), and ii) the ADIRF method, as implemented in the gsg R package by Morrissey and Sakrejda (2013). All selection gradients were standardized by variance – by multiplication by standard deviation or by variance, for directional or quadratic gradient respectively – in order to compare our results across parameter values, and with empirical studies. For every set of parameters, 100 replicates were performed and selection estimates obtained with both methods of estimation. We also estimated the expected response to selection using the Robertson-Price identity (Robertson, 1968). For this purpose, we estimated the additive genetic values of fitness by calculating the mean expected fitness associated with each bin of breeding values of width 0.1. Note that knowing the exact breeding values of fitness and traits in our simulations allows for a much more accurate estimation of the Robertson-Price identity than would be possible in the wild, where these have to be estimated. We investigated two sample sizes frequently typically found in the literature: 200 (e.g. annual selection estimation, such as Reed et al. 2009) and 1000 individuals (e.g. long-term studies, such as Pelletier et al. 2007). However, because results were qualitatively similar, only results for the largest sample size (1000 individuals) are presented here.

Skewed Environmental Effects

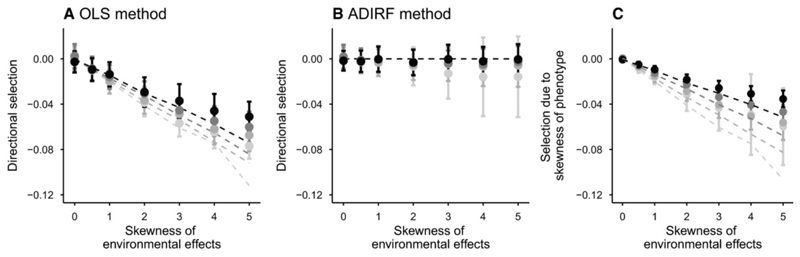
When positive phenotypic skewness is only due to skewed environmental effects, the OLS method detects negative directional selection (Fig. 2a), that is, selection in the opposite direction to the skew, as predicted by our analytical developments. The strength of selection estimated by β̂_OLS increases with skewness in environmental effects, but decreases with increasing heritability (Fig. 2a). Directional selection gradients are detected with high power for moderate and high skewness (Fig. S2a). In contrast, the ADIRF method detects little or no directional selection (Fig. 2b and Fig. S2b for the power analysis), as expected because the mean phenotype is at the adaptive optimum in this case (since µ_3g = 0), so the ADIRF estimation should be close to zero (eq. 6). The part of selection detected by the OLS method that is attributable to phenotypic skewness (β̂_OLS – β̂_ADIRF, eq. 14) is thus negative, with a magnitude that increases with increased skewness of environmental effects and decreased heritability (Fig. 2c), similar to β̂_OLS. Estimates of quadratic selection are negative, as expected because of stabilizing selection, weakly sensitive to the skewness in environmental effects (Fig. S3), and quadratic selection is detected with high power (Fig. S4).

Figure 2.

Estimated directional selection gradients with skewed environmental effects. Standardized directional selection gradient (mean ± se) estimated by the OLS method (a) or the ADIRF method (b), and the contribution of phenotypic skewness to estimated selection with the OLS method (c), are represented against the skewness of environmental effects, for variable heritabilities (${\mathit{h}}^{\mathbf{2}}=\frac{\mathbf{1}}{\mathbf{2}}\mathbf{;}\frac{\mathbf{1}}{\mathbf{3}}\mathbf{;}\frac{\mathbf{1}}{\mathbf{6}}\text{or}\mathbf{0}$ from black to light grey). Dotted lines show predictions from the model, eq. (13) for (a), 6-7 for (b), and (14) for (c).

Skewed Breeding Values

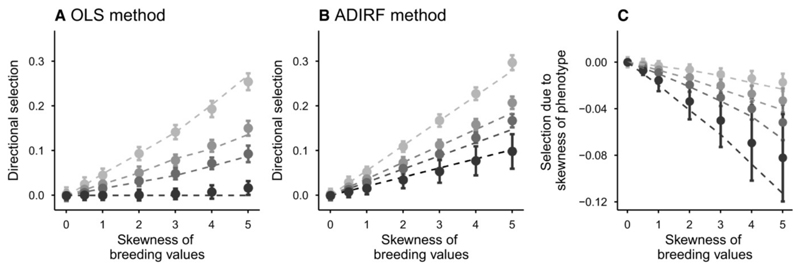
When phenotypic skewness is caused by skewed breeding values, both the OLS method and the ADIRF estimate positive selection gradients, that is, selection in the same direction as the phenotypic skew. This effect, which increases in magnitude when genetic skewness increases, is well predicted by our theoretical analysis (dashed lines in Fig. 3), and occurs because skewed breeding values cause a mismatch (z̄ – θ) between the mean phenotype and the optimum at evolutionary equilibrium (eqs. 10-11). Selection is efficiently detected, including for magnitudes of skewness comparable to our estimates from wild populations (Table 1), and relatively small heritability (Fig. S5). Selection gradients estimated by the OLS method are smaller than those estimated using ADIRF (Fig. 3a,b), as a consequence of the contribution of phenotypic skewness to OLS gradients, in the direction opposite to the phenotypic skew. Indeed, the difference between the OLS and ADIRF estimates of directional selection are similar to that under environmental skewness (compare Fig. 2c and 3c). However, under skewed breeding value distribution, this component increases in absolute value with increasing heritability (Fig. 3c), since this causes larger phenotypic skewness (for a given skewness in breeding values).

Figure 3.

Estimated directional selection gradients with skewed breeding values. Standardized directional selection gradient (mean ± se) estimated by the OLS method (a) or the ADIRF method (b), and the contribution of phenotypic skewness to estimated selection (c), are represented against the skewness of breeding values, for variable heritabilities (${\mathit{h}}^{\mathbf{2}}=\mathbf{1}\mathbf{;}\frac{\mathbf{1}}{\mathbf{2}}\mathbf{;}\frac{\mathbf{1}}{\mathbf{3}}\text{or}\frac{\mathbf{1}}{\mathbf{6}}$ from black to light grey). Dotted lines show, eq. (13) for (a), 6-7 for (b), and (14) for (c).

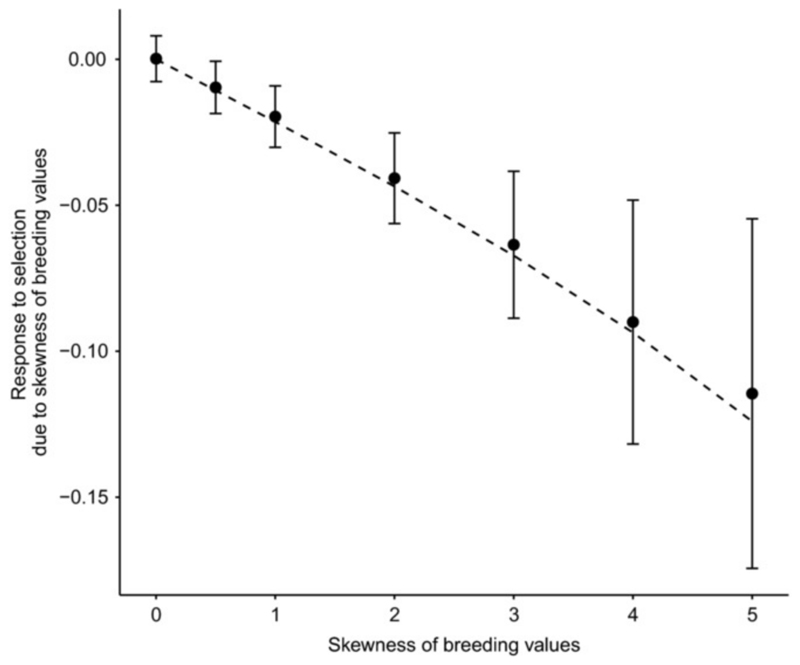
The contribution of skewness in breeding values to the response to selection, as quantified by the difference between the Robertson-Price identity and the response to selection predicted by the ADIRF estimation (∆z̄_R–P – ∆z̄_ADIRF), is negative (i.e. opposite to the genetic skew), and increases in magnitude with increasing genetic skewness (Fig. 4). Note that at evolutionary equilibrium, this effect precisely cancels out the deviation of the mean phenotype from the optimum, and is in the opposite direction to the measured selection gradient in Fig. 3. As expected, the contribution of genetic skewness to the response to selection is well predicted by our model. Finally, the quadratic selection gradient depends little on skewness of breeding values distribution (Fig. S6), and is also significantly detected (Fig. S7).

Figure 4.

Contribution of skewed breeding values to the selection response. The difference between the response to selection predicted by the Robertson-Price identity versus using the selection gradient estimated by the ADIRF method is shown for simulations (mean ± se), together with the theoretical prediction in eq. (15) in dashed lines, for the same simulations as used in Fig. 3.

Discussion and Conclusion

We show that skewness in phenotype distributions for a trait under selection for an optimum phenotype can have substantial impacts on natural selection and its estimation in the wild. With skewed environmental effects, the OLS method (i.e. the classic Lande and Arnold (1983) method) detects directional selection (in the opposite direction to the skew), even when the mean phenotype is at the optimum. In contrast, if phenotypic skewness is due, at least in part, to a skewed distribution of breeding values, the mean phenotype is displaced from the optimum at evolutionary equilibrium, because the curvature of the fitness function contributes to evolution of the mean phenotype when breeding values are skewed (Burger, 1991; Turelli and Barton, 1990, 1994). This displacement from the optimum contributes an additional term to the estimated directional selection, in the direction of the skew. In both cases (genetic or environmental skew), because the population is at equilibrium, there is no response to selection (i.e. the mean phenotype of the population does not evolve). Hence, selection would be detected on a heritable trait, but without any evolutionary response, so skewness in environmental effects (using OLS regression as in the Lande and Arnold (1983) method), and/or breeding values would contribute to the paradox of stasis.

According to classic meta-analyses (Hoekstra et al. 2001; Kingsolver et al. 2001; Kingsolver and Pfennig, 2007), estimates of standardized directional selection gradients are exponentially distributed with mean magnitude 0.23, which was recently re-evaluated to about 0.1 in a re-analysis of the same dataset by Morrissey (2016), taking into account standard-error of estimates. Hence, estimated directional selection gradients in natural populations are of the same order of magnitude as directional selection generated by genetic or environmental skewness in our analysis (Fig. 2a,b and 3a,b). However, genetic (respectively, environmental) skewness can only contribute to an observed paradox of stasis when directional selection and genetic (respectively, environmental) skewness are of the same sign (respectively, of opposite signs).

For laying date, negative directional selection is generally detected in wild populations (i.e. selection for earlier breeding, e.g. Sheldon et al. 2003; Porlier et al. 2012), while mean skewness tends to be positive (Table 1). If phenotypic skewness of laying date is due to a skewed genetic values distribution, a positive (rather than negative) selection gradient will ensue at evolutionary equilibrium, so correcting for this effect would accentuate (rather than alleviate) the paradox of stasis. Conversely, if phenotypic skewness is mostly due to skewed environmental effects, it will contribute negatively to the selection gradient commonly estimated using Ordinary Least Square regression (OLS, i.e. Lande and Arnold 1983), such that correcting for this effect would alleviate the paradox of stasis. However, the strength of selection would only slightly decrease: for a skewness of environmental effects of 1.5 – as can be observed in wild populations, Table 1 – the strength of selection estimated by the OLS method would be around 0.03 (Fig. 2a,c), which is lower than the average estimate of selection gradients from meta-analyses (Kingsolver et al. 2001, Morrissey 2016).

Phenotypic distributions are a mixture of genetic and environmental effects, and it is empirically difficult to attribute phenotypic skewness to any of these sources using current quantitative genetic methods. Indeed, quantitative genetic methods, such as the ‘animal model’ that is commonly used for natural populations (Kruuk, 2004), were designed to partition phenotypic variance into various genetic and non-genetic components, under the assumption of normally distributed traits (i.e. without skewness). It is unclear whether such methods can accurately partition genetic from non-genetic components of higher moments (such as the third central moment, contributing to skewness) for traits with non-Gaussian distributions. Nevertheless, phenotypic skewness and heritability could already be informative about the origin of the skew. For heritabilities of 1/3 or less (as often reported for phenological traits), a phenotypic distribution with skewness α = 1 (as seen in some wild populations, see Table 1), if of genetic origin only, requires a skewness of breeding values distribution of about 10 (Fig. S1). This kind of distribution is probably unlikely in nature, and such a trait would perhaps not even be analysed using quantitative genetics, because of the extreme prevalence of genotypes with phenotypes near the mode. It is thus more likely that phenotypic skewness results from environmental effects, or a mixture of genetic and environmental skewness. This implies that skewness of laying date is more probably of environmental origin, and would thus have a contribution (albeit modest) to the paradox of stasis for this trait. A related crucial point is that when heritability is low, a strong skewness of breeding values can result in vanishingly weak skewness of phenotypic distribution (Fig. S1). Hence, even when skewness is essentially undetectable at the phenotypic level, the population mean phenotype can be displaced from the adaptive optimum at evolutionary equilibrium, thereby generating directional selection.

We have shown that taking into account the skewness in the distributions of phenotypic components of quantitative traits can help understand evolutionary dynamics in the wild, and could partially alleviate the paradox of stasis in some cases. Because the OLS method by Lande and Arnold (1983), when applied in its classic form, does not necessarily predict the correct response to selection for characters with a skewed distribution (as indeed highlighted by Lande and Arnold (1983), who proposed a possible correction in their Appendix), we encourage the use of a combination of approaches, including the Robertson-Price identity and methods based on derivatives of mean fitness derived from the individual fitness function, when investigating natural selection on skewed phenotypic traits.