Abstract
Histotripsy is a form of therapeutic ultrasound that liquefies tissue mechanically via acoustic cavitation. Bubble expansion is paramount in the efficacy of histotripsy therapy, and the cavitation dynamics are strongly influenced by the medium elasticity. In this study, an analytic model to predict histotripsy-induced bubble expansion in a fluid was extended to include the effects of medium elasticity. Good agreement was observed between the predictions of the analytic model and numerical computations utilizing highly nonlinear excitations (shock-scattering histotripsy) and purely tensile pulses (microtripsy). No bubble expansion was computed for either form of histotripsy when the elastic modulus was greater than 20 MPa and the peak negative pressure was less than 50 MPa. Strain in the medium due to the expansion of a single bubble was also tabulated. The viability of red blood cells was calculated as a function of distance from the bubble wall based on empirical data of impulsive stretching of erythrocytes. Red blood cells remained viability at distances further than 44 μm from the bubble wall. As the medium elasticity increased, the distance over which bubble expansion-induced strain influenced red blood cells was found to decrease sigmoidally. These results highlight the relationship between tissue elasticity and the efficacy of histotripsy. In addition, an upper medium elasticity limit was identified, above which histotripsy may not be effective for tissue liquefaction.
Keywords: histotripsy, cavitation, mechanical ablation, elasticity
1. Introduction
Histotripsy is an ultrasound therapy under development for the treatment of deep vein thrombosis (Maxwell et al 2011a, Bader et al 2016, Zhang et al 2017), prostate pathologies (Hall et al 2008, Darnell et al 2015), intracerebral hemorrhage (Gerhardson et al 2017), fetal septal defects (Xu et al 2010), and liver cancer (Vlaisavljevich et al 2013a, 2017). Tissue liquefaction is induced through the strain of nanoscale cavitation nuclei expansion to microbubbles (Maxwell et al 2011b, Vlaisavljevich et al 2015b). The method by which histotripsy induces bubble expansion depends on the insonation scheme (Khokhlova et al 2015). Microtripsy utilizes single-cycle pulses with peak negative pressure in excess of 25 MPa to nucleate individual bubbles within the focal zone (Maxwell et al 2013). Shock-scattering histotripsy employs highly asymmetric, nonlinear pulses 3–20 μs in duration with peak negative pressures of 15–25 MPa, and peak positive pressures in excess of 80 MPa (Maxwell et al 2012). The tensile phase of the pulse causes the expansion of a single bubble within the focal zone. The bubble scatters the incident shock wave geometrically, and a bubble cloud forms in the regions of constructive interference between the incident and scattered waves (Maxwell et al 2011b). Cavitation can also be nucleated via shock-induced heating from millisecond-long pulses (Khokhlova et al 2006).
The dynamics of histotripsy-induced cavitation and the resultant strain fields have been assessed with numerical computations (Maxwell et al 2013, Mancia et al 2017). An analytic model based on the mechanical index for diagnostic ultrasound (Apfel and Holland 1991) was shown to have high accuracy in comparison to numerical computations and experimental observations of histotripsy cavitation (Bader and Holland 2016). The analytic formulation assumed the bubble was immersed in a fluid (Apfel 1981a, Holland and Apfel 1989), and did not model elasticity. Elasticity can significantly influence the bubble dynamics (Vlaisavljevich et al 2015b), and be a determining factor in the efficacy of histotripsy (Vlaisavljevich et al 2013b). The formation of an analytic model of histotripsy-induced bubble dynamics in an elastic medium would aid in the understanding of the physical processes of the tissues most resistant to mechanical liquefaction, thereby aiding in improved histotripsy treatment strategies.
In this study, medium elasticity will be incorporated into an analytic model to investigate the dominant mechanisms of the suppression of histotripsy-induced bubble expansion. The predictions of the analytic model will be compared to numerical computations of the maximum bubble diameter for both shock scattering histotripsy and microtripsy pulses, as well as experimental observations. Strain fields surrounding the expanded bubble will also be computed. Red blood cells are a primary component of a deep vein thrombus (Mewissen et al 1999, Gagne et al 2015), a primary target for histotripsy. The viability of red blood cells will be computed as a function of distance from the bubble based on empirical observation (Li et al 2013).
Methods
2.1. Numeric model
The radial oscillations of cavitation nuclei in soft tissue were calculated by numerical integration of the Yang/Church model (2005). An adaptive fourth-order Runga-Kutta algorithm was implemented in MATLAB® (The Mathworks, Natick, MA, USA), employing the function ‘ode15s’ to carry out the integration. The Yang/Church model has the form:
| (1) |
where R is the time dependent bubble radius, the diacritic dot denotes the temporal derivative, c is the sound speed of the viscoelastic medium (1540 m/s), and ρ is the medium density (1000 kg/m3). The pressure at the bubble wall, pw, is defined in terms of the properties of the viscoelastic medium (Yang and Church 2005):
| (2) |
where P0 is the ambient pressure (0.1 MPa), R0 is the initial radius of the air-filled cavitation nucleus, κ is the ratio of specific heats (1.4), and pAC is the time-dependent source term. The following values were used for the medium properties: surface tension, σ = 0.056 N/m (Church et al 2015, Holland and Apfel 1989), and dynamic viscosity, μ = 0.005 kg/m•s (Church et al 2015, Holland and Apfel 1989). Medium viscoelasticity was computed via the Kelvin-Voight model assuming an isotropic medium, which has been validated for soft tissues in the 3–13 MHz range (Madsen et al 1983). Bubble expansion during histotripsy is slow compared to the sound speed (Bader and Holland 2016), and the shear modulus G can be expressed in terms of the elastic modulus E for incompressible media as G ≈ 3E. Elastic moduli between 1 kPa and 20 GPa were considered in this study, which spans the properties of soft and mineralized tissues (Duck 1990).
Shock-scattering histotripsy and microtripsy excitations were considered in this study. The maximum bubble diameter is independent of the nucleus diameter for cavitation nuclei larger than 5 nm (microtripsy) or 20 nm (shock-scattering histotripsy) (Bader and Holland 2016). Calculations in this study utilized these nuclei sizes for each respective form of histotripsy to provide an upper estimate to the maximum bubble size. The time-dependent source term in (2), pAC, was approximated as a half cycle, peak negative only pulse for microtripsy excitations (Vlaisavljevich et al 2015b, Mancia et al 2017), with peak negative pressures of 25–50 MPa, and fundamental frequencies of 0.1–3 MHz. Shock-scattering histotripsy pulses were implemented with pressure waveforms measured experimentally of 1-MHz fundamental frequency source as described previously (Bader and Holland 2016).
2.2. Analytic model to predict maximum bubble size for single-cycle excitation
The maximum size of a cavitation nucleus exposed to a single-cycle excitation was derived analytically via Holland and Apfel (1989):
| (3) |
where ξ and τ are defined in Holland and Apfel (1989), and P0, R0, and ρ are as defined in section 2.1. The effective pressure, pEFF, acts as a “Blake brake” to arrest bubble expansion (Bader and Holland 2016), and depends on the histotripsy insonation scheme. Microtripsy pulses do not have an appreciable compressional phase (Maxwell et al 2013, Lin et al 2014, Vlaisavljevich et al 2015a), and the effective pressure can be set to the ambient pressure, pEFF = P0 (Bader and Holland 2016). For shocked pulses, the bubble wall velocity is maximized at the shock front, and the effective pressure can be approximated as the magnitude of the negative pressure, pEFF = |pN|.
Incorporation of elasticity into the analytic model requires two modifications: 1) a delay to bubble expansion (Apfel 1986, Holland and Apfel 1989), and 2) an additional overpressure as the bubble expands (Gent and Lindley 1959). Bubble expansion will lag behind the onset of tension due to conformational changes of the elastic medium (Vincent 2012). Following Apfel (1981b) and Holland and Apfel (1989), the delay to bubble expansion due to elasticity, τG, can be estimated by equating the elastic and driving terms in the Yang/Church model (fourth and sixth term in (2)):
| (4) |
Delays in bubble expansion due to elasticity can be integrated into the analytic model through modifying the term τ in (3) as:
| (5) |
where τHA is as defined by equation (9) in Holland and Apfel (1989), which includes the effects of surface tension, viscosity, and inertia.
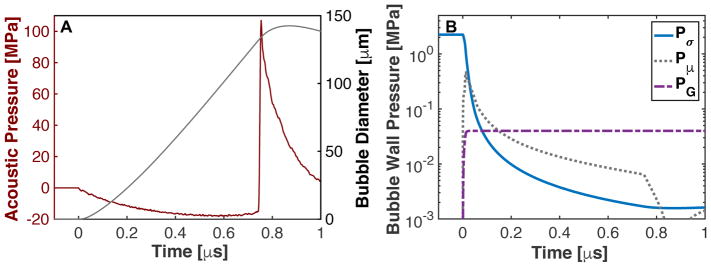
Elasticity also modifies the effective pressure (Gent and Lindley 1959). This is denoted in Fig. 1, where the pressure terms due to surface tension, viscosity, and elasticity are plotted below for a bubble exposed to the first cycle of a shocked histotripsy pulse (second, third, and fourth terms, respectively, in (2)). As noted in Fig. 1B, the pressure contributions from surface tension and viscosity decrease rapidly during bubble expansion. The elastic pressure contribution asymptotes to a fixed value of 4G/3 for the finite-strain Kelvin-Voight elastic model (the limit of R0/R ≪ 1 for the fourth term in (2))
Fig. 1.
(A) Expansion of a 20-nm cavitation nucleus to a shock-scattering histotripsy pulse. (B) Pressure components due to surface tension (Pσ), viscosity (Pμ), and elasticity (PG), corresponding to the second, third, and forth terms in (2).
The additional overpressure modifies the parameters ξ and pEFF in the analytic model. The former represents the time-averaged pressure as the bubble undergoes expansion. Substituting P0 + 4G/3 for P0 into equation 4 of Holland and Apfel (Holland and Apfel 1989), ξ can be estimated to second order as:
| (6) |
where ξHA is as defined by equation 6 in Holland and Apfel (1989). Modification to the effective pressure term depends on the insonation type (Bader and Holland 2016). The elastic pressure term acts to increase the overall ambient pressure (Fig. 1B). For a microtripsy excitation, the additional overpressure acts to increase the effective pressure (pEM):
| (7) |
For a shock-scattering histotripsy excitation, the elastic pressure acts to decrease the overall wall velocity and the effective pressure takes the form (pES):
| (8) |
2.3. Analytic prediction of shock scattering-induced bubble cloud extent
The analytic model (3) predicts the bubble size after a single-cycle excitation. A shock-scattering histotripsy pulse is 3–20 cycles in duration (Maxwell et al 2012), during which time the bubble undergoes continuous expansion (Maxwell et al 2011b). The bubble expansion rate is largest during the first cycle of the histotripsy pulse. Beyond the first cycle, the expansion rate slows due to the shocked compressional pressure. The slowed bubble expansion rate after the first cycle of the histotripsy pulse 〈Ṙs〉 can be approximated as:
| (9) |
The value 〈pAC〉 is the pressure of the histotripsy pulse, time-averaged from the second cycle to the end of the pulse. Equation (9) is the same form as equation 9 in Bader and Holland (2016), with the addition of an elastic term. The final extent of the bubble cloud, LAX, can be computed utilizing (3) and (9) following Bader and Holland (2016).
2.4. Alternative elastic model formation
The functional form of tissue elasticity is an active area of research (Schmitt et al 2011). For the massive bubble expansion characteristic of histotripsy-induced cavitation (RMAX ≫ R0), alternative forms of finite-strain elastic models can readily be incorporated into the analytic model using the same formalism described by (4)–(9). Table 1 denotes modifications to the effective pressure, ξ, and the time-averaged bubble wall velocity for Kelvin-Voight, linear, and neo-Hookean elastic models (Gent 2005b, Gaudron et al 2015).
Table 1.
Modifications for the parameter ξ, the effective pressure for microtripsy (pEM) and shock scattering histotripsy (pES), and bubble expansion rate (〈Ṙ〉) based on form of the elastic model.
| Elasticity Model | ξ | pEM | pES | 〈Ṙ〉 | |||
|---|---|---|---|---|---|---|---|
| Linear | ξHA−6G/P0 |
|
|Pr|−2G |
|
|||
| Kelvin-Voight | ξHA−4G/P0 |
|
|
|
|||
| Neo-Hookean | ξHA−15G/2P0 |
|
|
|
|||
| Fung+ | ξHA−58.2G/P0 |
|
|Pr|−58.15G |
|
|||
| Gent* | ξHA−17.5G/P0 |
|
|Pr|−17.5G |
|
The solution for the Fung model was computing assuming fracture of an agar medium beyond an expansion ratio of 2.2 (i.e. solution of (10) for λ = 2.2) (Movahed et al 2016).
The solution for the Gent model was computed assuming fracture of an agar medium beyond an expansion ratio of 2.93 (i.e. solution of (11) for λ = 2.93).
In addition to the consideration of bubble behavior in soft tissues, in vitro studies describing histotripsy-induced bubble behavior are frequently conducted in agar-based phantoms (Maxwell et al 2010, Vlaisavljevich et al 2013b, Bader et al 2018). Agar behaves as a strain-hardening material (Barrangou et al 2006), and the elastic behavior can be modeled via Fung (Fung et al 1979, Movahed et al 2016) or Gent (Gent 1996). In the Fung model, the elastic pressure term (fourth term in (2)) can be computed as:
| (10) |
where λ = R/R0, and α ~ 1 (Movahed et al 2016). Gent elasticity can be expressed as (Gent 2005a):
| (11) |
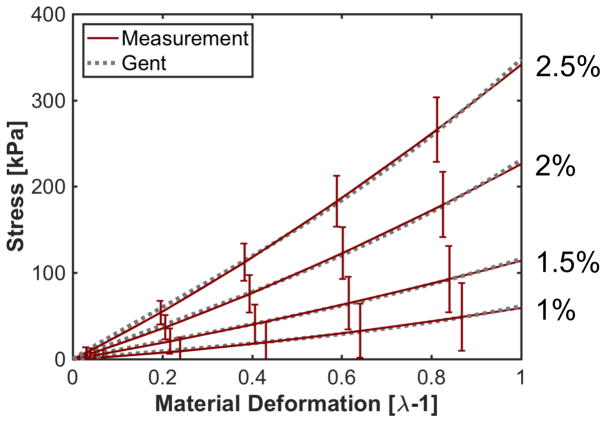
The term JM in (11) represents the effect of finite chain extensibility (Roland 2011). For agar phantoms, the Gent model accurately predicts pure strain measurements of agar phantoms (1–2.5% w/v) when JM ~ 17.5 (Appendix A) (Barrangou et al 2006).
Unlike finite-strain elastic models, the elastic pressure contribution for a strain-hardening elastic model does not asymptote to a fixed value for massive bubble expansion (Fig. 2). Agar is a brittle material, and will fracture under sufficient strain (Madsen et al 2003, Wilks et al 2015). The elastic energy released by bubble expansion will then equate to the fracture energy required for the increased bubble size (Gent 1999). Thus, PG will not increase beyond a critical fracture expansion λF for strain-hardening elastic models (Griffith 1921, Hutchens et al 2016). The onset of medium fracture depends on the form of the elastic model, and can be estimated using Griffith’s criterion (Gent and Wang 1991). For the Fung elastic model, Griffith’s criterion is satisfied when λF ~2.2 (Movahed et al 2016), or PG ~ 58.2G as calculated via (10). Griffith’s criterion is satisfied when λF~2.93, or PG ~ 17.5G for the Gent elastic model (Horgan and Saccomandi 1999).
Fig. 2.
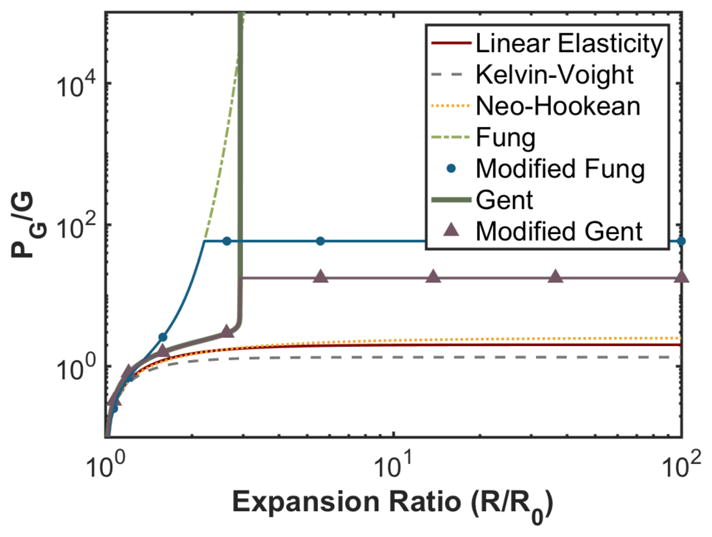
Elastic pressure contribution as a function of the bubble expansion ratio for elastic models described in Table 1.
2.5. Red blood cell viability surrounding histotripsy-induced cavitation
The viability of red blood cells due to transient strain from laser-induced cavitation can be expressed as (Li et al 2013):
| (12) |
where S is the stain (%), S0 = 105.8%, and S1 = 0.18% (Li et al 2013). The normal Hencky (or true) strain in an isotropic medium surrounding an expanded or collapsed bubble was computed in these studies as (Mancia et al 2017):
| (13) |
where r is the radial distance from the center of the bubble and Ri corresponds to the maximum or minimum bubble radius. The maximum bubble radius was computed analytically via (3) for a Kelvin-Voight elastic medium (Table 1). The minimum bubble size was computed assuming the bubble behaved as a Rayleigh cavity (Rayleigh 1917, Leighton 1994) with an addition contribution due to Kelvin-Voight elasticity:
| (14) |
Histotripsy-induced cavitation expands to sizes much larger than that of the original nucleus (Maxwell et al 2013, Bader and Holland 2016), meaning the bubble will behave as a Rayleigh cavity until the final stages of bubble collapse (Lastman and Wentzell 1981). Dampening will soften the bubble collapse, and the predictions of minimum bubble radius by (14) will be an underestimate compared to the true size (Prosperetti and Lezzi 1986). The large bubble expansion induced by histotripsy pulses necessitates that the bubble size at the completion of the collapse will be much smaller than the size of the initial nucleus (Gaudron et al 2015). Errors in the strain surrounding the bubble at its minimum radius as calculated via (13) will be less than 0.1%.
3. Results
3.1. Analytic prediction in delays to the onset of bubble expansion
Delays to bubble expansion due to surface tension, viscosity, elasticity, and medium inertia are shown in Fig. 3. Surface tension dominated the onset of bubble expansion for nuclei smaller than 5 nm (Fig. 3A) and for peak negative pressures less than 8 MPa (Fig. 3B). For the operational range of histotripsy (peak negative pressures greater than 15 MPa) in soft tissues (elastic modulus less than 1 MPa (Duck 1990)), viscous and inertial effects dominated bubble expansion (Fig. 3B). As the elastic modulus increased beyond 105 MPa, medium elasticity was the largest contributor to delaying bubble expansion (Fig 3C).
Fig. 3.
Bubble expansion delays due to surface tension (τσ), fluid inertia ( τI), viscosity (τμ), and tissue elasticity (τG) as a function of (A) initial bubble diameter with peak negative pressure (23 MPa) and elastic modulus (90 kPa), (B) peak negative pressure with fixed initial bubble diameter (20 nm) and elastic modulus (90 kPa), and (C) elastic modulus with fixed initial bubble diameter (20 nm) and peak negative pressure (23 MPa). The legend for each component of time delay is shown in panel A.
3.2. Comparison of analytic and numerical models for single-cycle excitation
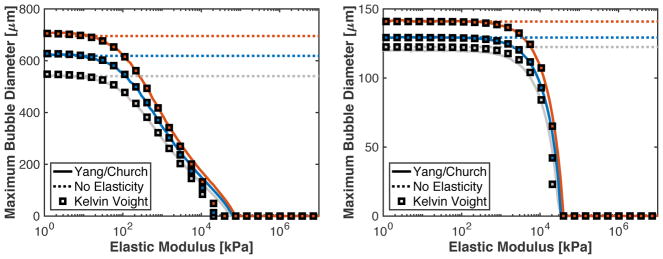
Maximum bubble sizes based on numerical computations (Yang/Church model) and analytic calculations are shown in Fig. 4 as a function of the medium elasticity. Numerical computations were conducted with microtripsy or single-cycle shock-scattering histotripsy excitations, and a Kelvin-Voight elastic model. Analytic calculations were conducted without the contribution of elasticity (i.e. G = 0), and with Kelvin-Voight elasticity incorporated into the analytic model (Table 1). For elastic moduli less than 1 MPa, the numeric and analytic calculations agreed within 1.5% for shock-scattering histotripsy and microtripsy excitations. The analytic model underestimated the maximum bubble size relative to the numerical computation over the elastic modulus range of 1.8 and 20 MPa for microtripsy excitations.
Fig. 4.
(A) Predicted maximum bubble size as a function of elastic modulus for microtripsy pulses with 24.9 (gray), 29.3 (blue), and 33.6 MPa (red) peak negative pressures. (B) Predicted maximum bubble size as a function of elastic modulus for a single cycle shock-scattering histotripsy pulse with peak negative/peak positive pressures of 14.5/88.9 (gray), 15.8/98.8 (blue), and 18.3/107.0 MPa (red) peak negative/peak positive pressures. For both panels, the solid line is the numerical computations with the Yang/Church model with Kelvin-Vought elasticity, the dotted line is the analytic model without elasticity incorporated, and squares are the analytic theory with Kelvin-Voight elasticity incorporated.
The parameters ξ and pES become negative when the elastic moduli exceeds approximately 20 MPa for both shock-scattering histotripsy and microtripsy. Mathematically, this means that the predictions of the analytic model were complex. Physically, this means the tension of the histotripsy pulse is insufficient to cause expansion of the cavitation nucleus.
3.3. Bubble expansion during a shock-scattering histotripsy pulse
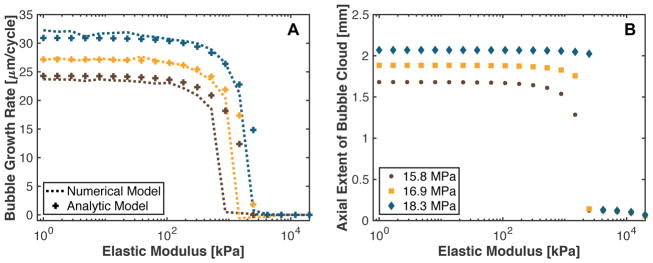
The analytic prediction for the bubble expansion rate over the duration of a shock-scattering histotripsy pulse is shown in comparison the numerical computation in Fig. 5A. The analytic model agreed within 2.5% of the numerical computations for tissue with an elastic modulus less than 875 kPa and greater than 2.5 MPa. For tissue with an elastic modulus between 875 kPa and 2.5 MPa, the analytic model overestimated the bubble expansion rate compared to estimates based on numerical computations. The bubble expansion rate was only weakly dependent on medium elasticity when the elastic modulus was less than 115 kPa for both numeric and analytic calculations. For stiffer media, the bubble grow rate decreased rapidly to 0 μm/cycle.
Fig. 5.
(A) Bubble expansion rate over the course of a shock-scattering histotripsy pulse based on the numerical integration of the Yang/Church model (dashed line) and the analytic prediction via (9) (crosses). The peak positive/peak negative pressures were 98.8/15.8 MPa for the brown symbols, 102.8/16.9 MPa for the yellow symbols, and 107/18.3 MPa for the blue symbols. (B) Predicted axial extent of the bubble cloud initiated with a 5-μs shock-scattering histotripsy pulse as a function of the elastic modulus of the medium. The fundamental frequency of the shock scattering pulse was 1 MHz. Kelvin-Voight elasticity was used in the calculation.
The analytic computation of the bubble cloud axial length is shown in Fig. 5B for a 5-μs duration shock-scattering histotripsy pulse (1-MHz fundamental frequency). For elastic moduli less than 1.5 – 2.5 MPa, the axial extent of the bubble cloud was found to depend weakly on the medium elasticity. In stiffer media, the incidental nucleus did not grow sufficiently large over the duration of the histotripsy pulse to initiate shock scattering. Consequently, bubble cloud formation was suppressed and cavitation activity was limited to the expansion of the initial nucleus.
3.4. Dependence of maximum bubble size on elastic model
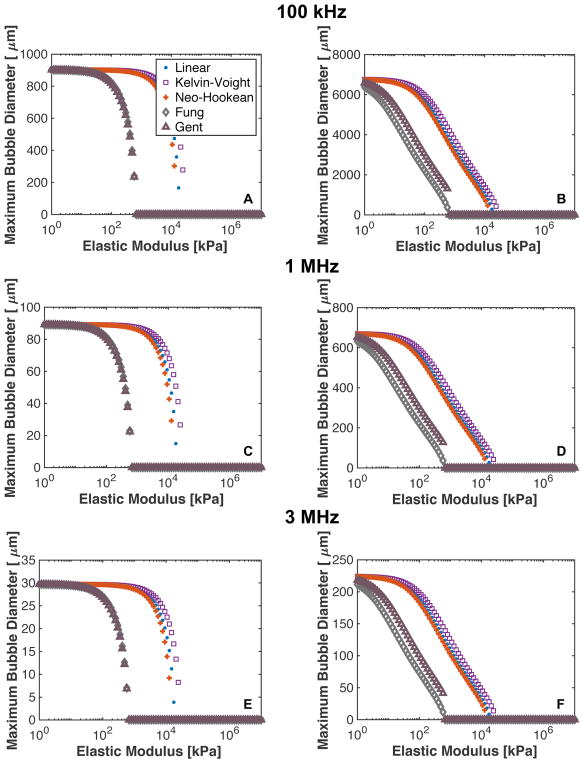
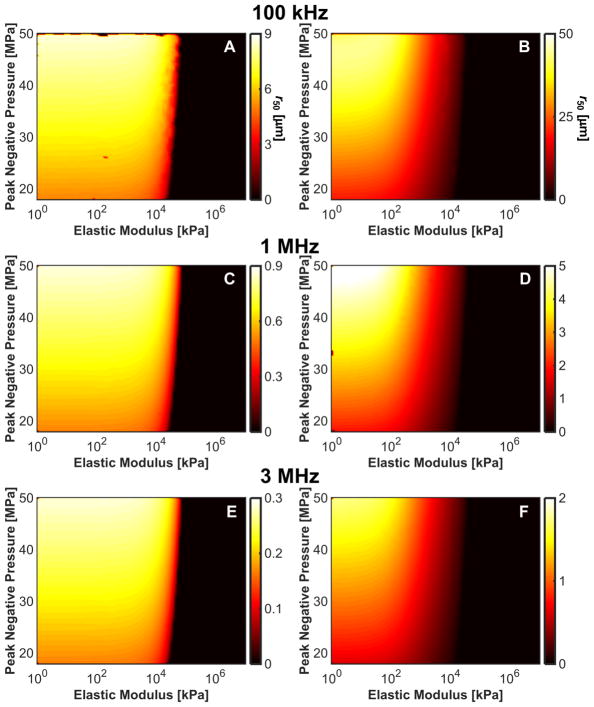
The dependence of the maximum bubble size on the elastic model is shown in Fig. 6. For shock-scattering histotripsy excitations, predictions of bubble expansion based on finite-strain elastic models (classical, Kelvin-Voight, and neo-Hookean) agreed within 11.9% when the medium elastic modulus was less than 1 MPa. Predictions of the maximum bubble size for strain-hardening elasticity (modified Fung and Gent) and Kelvin-Voight elasticity were within 10% when the elastic modulus was less than 100 kPa. Beyond 100 kPa, bubble expansion was suppressed in strain-hardening media compared to finite-strain elasticity.
Fig. 6.
Predicted maximum bubble diameter for linear, Kelvin-Voight, Neo-Hookean, and Fung elasticity for a single cycle shock-scattering histotripsy excitation (left column) and microtripsy excitation (right column). The fundamental frequency of the excitation was 100 kHz for panels A and B, 1 MHz for panels C and D, and 3 MHz for panels E and F. The initial nucleus for the shock scattering histotripsy excitation was 20 nm, and the peak negative pressure was 17.4 MPa. The initial nucleus size for the microtripsy pulse was 5 nm, and the peak negative pressure was 33.8 MPa.
For microtripsy excitations, the predicted maximum bubble size was within 18.8% for finite-strain elastic modulus when the elastic modulus was less than 1 MPa. The predicted maximum bubble size was on average 62% smaller for the strain-hardening models compared to the Kelvin-Voight model when the elastic modulus was less than 100 kPa. For all the elastic models and insonation schemes (frequency and peak negative pressure), bubble expansion was suppressed in a medium with an elastic modulus greater than 20 MPa.
3.5. Microtripsy: Comparison with experimental data
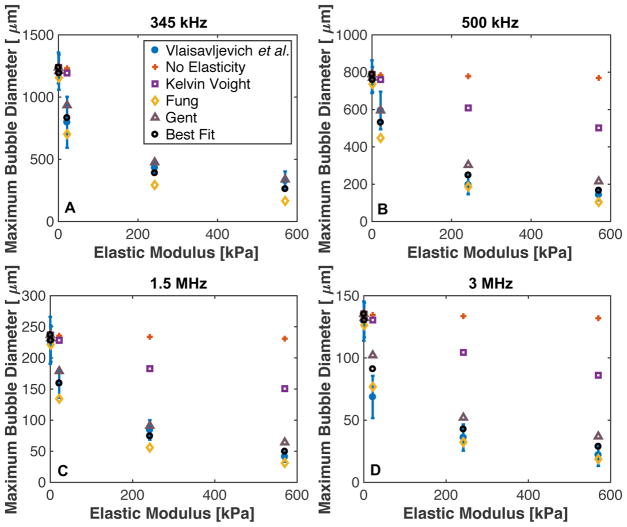
Previous measurements of the maximum size of microtripsy induced cavitation as a function of frequency and elastic modulus dependence in agar phantoms (Vlaisavljevich et al 2015b) and predictions of the analytic model are shown in Fig. 7. Kelvin-Voight, modified Fung, modified Gent, or no elastic model (i.e. G = 0) were considered in the analytic calculations (Table 1). A comparison of the measured bubble size and predictions of the analytic model with Kelvin-Voight elasticity agreed within 9.4 ± 6.3 μm (3.8% ± 1.4%) when the elastic modulus was 1.13 kPa. With increasing elastic modulus, the predictions of the model with Kelvin-Voight elasticity and the measurements diverged, with a 123.9 ± 95.7 μm (236.6% ± 66.5%) difference at 570 kPa. Over the same range of elasticities, the analytic model prediction agreed with the measured bubble diameter within 38.8 ± 52.4 μm (14.3% ± 13.0%) for modified Fung elasticity, and within 27.1 ± 36.6 μm (19.4% ± 23.6%) for modified Gent elasticity. The modified Gent model appeared to be accurate within the standard deviation of the experimental measurements for frequencies 345 kHz and 1.5 MHz. The modified Fung model under predicted the maximum bubble size for frequencies 345 kHz and 1.5 MHz, but was within experimental error for 500 kHz and 3 MHz.
Fig. 7.
Maximum size of cavitation nuclei excited by microtripsy pulse as a function of medium elasticity at (A) 345 kHz, (B) 500 kHz, (C) 1.5 MHz, and (D) 3 MHz. Blue dots are measured values (table 2 from Vlaisavljevich et al. (2013b)). Analytic calculations were computed via (3), with constants acquired from Table 1. The “Best Fit” elastic model conditions utilized the constants ξ = ξHA − 30G/P0 and in the analytic calculation. The legend shown in panel A labeling the elastic models used in the analytic calculation is the same for the remaining panels.
In addition to the elastic models in Table 1, an elastic model optimized to the experimental data was also utilized in the analytic calculation. The optimized elastic model denoted that the elastic pressure contribution approached 30G for large bubble expansion, or ξ = ξHA − 30G/P0 and . Predictions of the maximum bubble size with the optimized elastic model were within experimental error for all conditions considered, except for 3 MHz insonation of agar phantoms with an elastic modulus of 21.7 kPa (Fig. 8). For all conditions, the predicted maximum bubble diameter based on the best fit elastic model was within 9.5 ± 11.0 μm (10.2% ± 10.0%) of the measured maximum bubble diameter.
Fig. 8.
Predicted maximum bubble diameter for a single cycle shock-scattering histotripsy excitation (left column) and microtripsy excitation (right column). The fundamental frequency of the insonation was 100 kHz for panels A and B, and 3 MHz for panels C and D. The initial nucleus for the shock scattering histotripsy excitation was 20 nm, and initial nucleus size for the microtripsy pulse was 5 nm. Kelvin-Voight elasticity was used in the calculation.
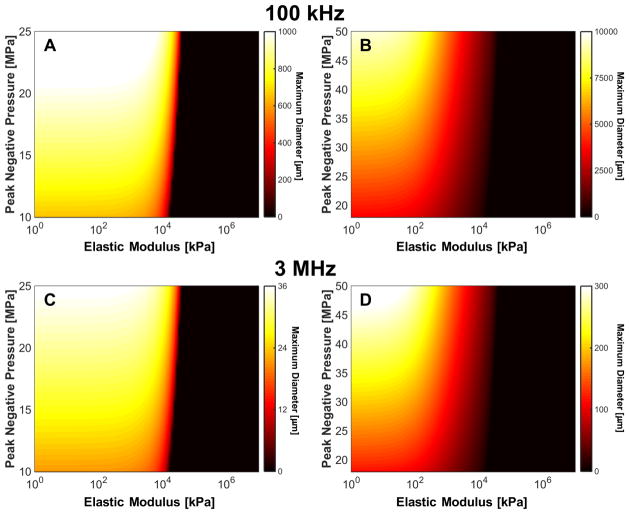
3.6. Metric to predict maximum bubble diameter based on elasticity and insonation parameters
The analytic prediction of the maximum bubble size appeared to be a well-behaved function of the medium elasticity and the histotripsy insonation parameters (Fig. 8). For a given set of insonation conditions (microtripsy vs. shock-scattering histotripsy, fundamental frequency, and peak negative pressure), a critical elastic modulus was observed. For tissues stiffer than the critical elastic modulus, the maximum bubble diameter decreased exponentially with increasing medium elasticity. To reflect this critical elastic behavior, the maximum bubble size predicted by the analytic model was fit in the least squares sense to a function of the form:
| (15) |
using the ‘nlinfit’ function in MATLAB, where the maximum bubble diameter in micrometers is denoted by DMAX, |pN| is the magnitude of the peak negative pressure in MPa, f is the fundamental frequency of the histotripsy pulse in MHz, E is the elastic modulus in kPa, and a1, a2, a3, a4, and a5 are fitting parameters. The critical elastic modulus is modeled in (15) via the parameter a4, and the exponential decay via parameter a5. The fitting parameters are listed in Table 2 in terms of the type of histotripsy excitation, along with mean square error of the fit.
Table 2.
Coefficients of five-parameter fit (15) of the fit for the frequency, pressure, and elastic modulus dependence of the maximum bubble diameter for shock scattering histotripsy and microtripsy. The goodness-of-fit parameter mean square error (MSE) is also shown.
| Histotripsy Type | a1 [μm] | a2 | a3 | a4 [kPa] | a5 [kPa] | MSE [μm] |
|---|---|---|---|---|---|---|
| Shock Scattering | 17.06 | 0.56 | −1.00 | 2951.10 | 51324 | 0.30 |
| Microtripsy | 14.56 | 0.93 | −1.00 | 425.74 | 769.23 | 65.07 |
The maximum bubble diameter was inversely proportional to frequency (a3 = −1 for both shock scattering and microtripsy) and directly proportional to the peak negative pressure (a2 = 0.56 for shock scattering histotripsy and 0.93 for microtripsy). The parameters a4 and a5 indicate tissue elasticity has a stronger influence on microtripsy excitation of cavitation nuclei compared to shock-scattering histotripsy when the elastic modulus is less than 2.95 MPa. Beyond 2.95 MPa, shock scattering histotripsy-induced cavitation will be more strongly influenced by the tissue elasticity compared to microtripsy.
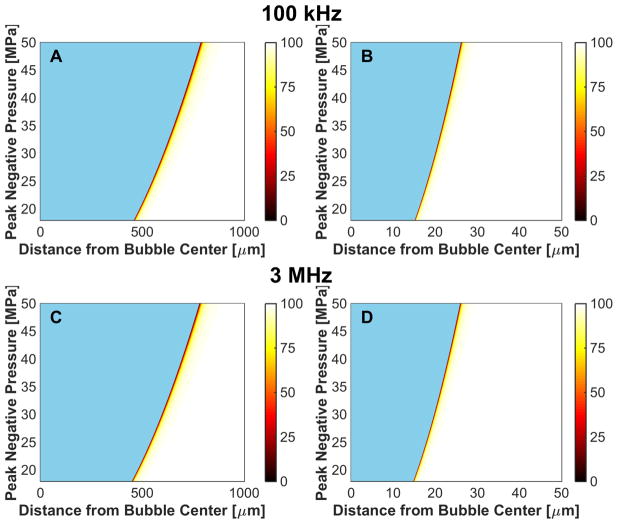
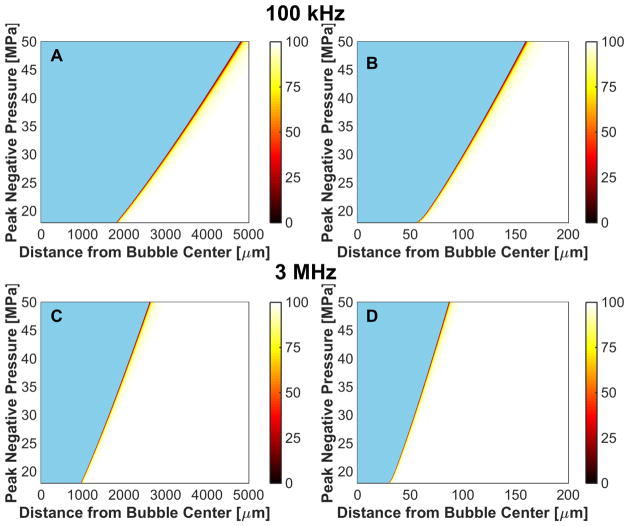
3.7. Red blood cell viability surrounding histotripsy-induced cavitation
The viability of red blood cells is shown as a function of distance from the bubble wall for microtripsy excitations in Fig. 9, and for a single-cycle shock-scattering histotripsy excitation in Fig. 10. Strains were computed analytically at the maximum bubble diameter for Kelvin-Voight elasticity. The red blood cell viability increased rapidly from 0% at the bubble wall to 100% within 50 μm for all insonation conditions. The red blood cell viability increased sigmoidally as a function of distance away from the bubble wall, and was fit to a function of the form:
| (16) |
where d is the distance from the center of the bubble, and d0 and ds are fitting parameters. The parameter d0 was used to express the distance from the bubble wall over which the predicted red blood cell viability decreased by 50%:
| (17) |
Fig. 9.
Microtripsy-induced reduction in red blood cell viability due to bubble expansion, reported in terms of percent viability in the colorbar. The fundamental frequency of the insonation was 100 kHz for the left column, and 3 MHz for the right column. The elastic modulus was 1 kPa for panels A and B, and 1 MPa for panels C and D. The initial bubble diameter was 5 nm. The regions in blue represent the extent of the bubble.
Fig. 10.
Shock-scattering histotripsy-induced reduction in red blood cell viability due to bubble expansion, reported in terms of percent viability in the colorbar. The fundamental frequency of the insonation was 100 kHz for the left column, and 3 MHz for the right column. The elastic modulus was 1 kPa for panels A and B, and 1 MPa for panels C and D. The initial bubble diameter was 20 nm. The regions in blue represent the extent of the bubble.
The frequency, pressure, and elasticity dependence of r50 had a similar form to that for the maximum bubble size, as indicated in Fig. 11. For a medium with elastic modulus greater than 20 MPa, r50 approached 0 μm as bubble expansion was completely suppressed. For fixed medium elasticity and insonation conditions (peak negative pressure and fundamental frequency), r50 was greater for microtripsy pulses than shock scattering histotripsy pulses (Table 3). Thus, the distance over which bubble expansion effects red blood cell viability is greater for microtripsy compared to shock scattering histotripsy. For fundamental frequencies greater than 1 MHz, changes in red blood cell viability did not extend beyond 5 μm, roughly the size of a red blood cell (Lewis 1996).
Fig. 11.
Distance from bubble wall to 50% reduction in red blood cell viability, r50, induced by bubble expansion as a function of elastic modulus and peak negative pressure for shock-scattering histotripsy (left column) and microtripsy (right column) excitations. (A), (B) 100-kHz fundamental frequency. (C), (D) 1-MHz fundamental frequency. (E), (F), 3-MHz fundamental frequency.
Table 3.
The maximum and mean values for r50 as a function of frequency and insonation type. Here, the average value is tabulated over the peak negative pressures and elastic moduli considered in the study.
| Histotripsy Type | Max r50 [μm] | Mean r50 [μm] |
|---|---|---|
| Microtripsy | ||
| 100 kHz | 44.3 | 11.15 |
| 1 MHz | 5.22 | 1.70 |
| 3 MHz | 1.75 | 0.55 |
|
| ||
| Shock Scattering | ||
| 100 kHz | 8.60 | 4.37 |
| 1 MHz | 0.86 | 0.45 |
| 3 MHz | 0.29 | 0.15 |
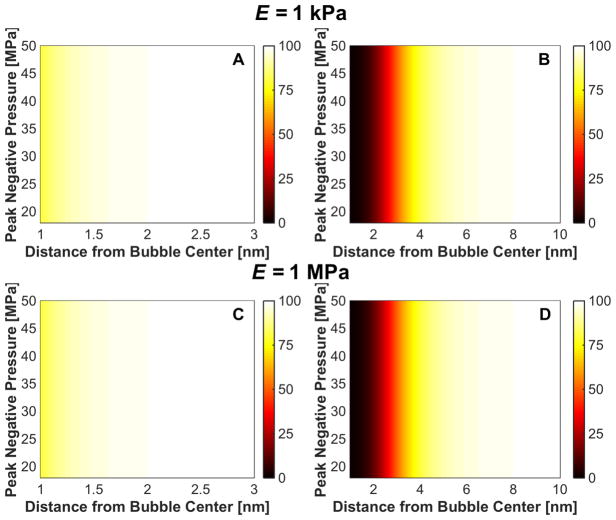
Changes in cell viability induced by strain from the bubble collapse are shown in Fig. 12. While strain during the expansion pushes red blood cells away from the bubble, strain during collapse pulls the red blood cells toward the bubble. For conditions of massive bubble expansion (i.e. medium elasticity less than 20 MPa), the cell viability at a fixed distance from the bubble varied by less than 0.1% over the range of media elasticity or insonation conditions considered in this study. Bubble collapse-induced changes in cell viability appear to be restricted within 2 nm for microtripsy excitations, and 10 nm for shock scattering histotripsy.
Fig. 12.
Change in cell viability, expressed in terms of percent in the colorbar, due to strain at minimum bubble radius for microtripsy insonation (left column) and shock-scattering histotripsy insonation (right column) for medium elastic modulus of 1 kPa (panels A and B) and 1 MPa (panels C and D). The fundamental frequency of the insonation was 1 MHz for both calculations, and the initial bubble diameter was 5 nm for the microtripsy excitation and 20 nm for the shock scattering histotripsy excitation.
Discussion
4.1. Validity of analytic model
An analytic model to predict histotripsy-induced bubble expansion (Bader and Holland 2016) was extended to include the effects of medium elasticity. Good agreement was observed between the predictions of the analytic model and numerical calculations based on integration of the Yang/Church model (Yang and Church 2005) for medium elasticities that span soft tissue (elastic modulus less than 1 MPa (Duck 1990)), Fig. 4. For a medium with an elastic modulus between 1.8 and 20 MPa, the analytic model underestimates the maximum bubble size compared to numerical computations for microtripsy excitations. For a medium with an elastic modulus less than 1.8 MPa, the analytic model and numerical computations agree within 1.5 % for both forms of histotripsy considered in this study.
The maximum size of a nucleus in a viscoelastic medium exposed to a single-cycle excitation can be computed analytically via (3) in combination with Table 1. Microtripsy insonations rely on a single tensile pulse, and bubble expansion is sufficiently described by the analytic model (3). For shock scattering histotripsy, bubble clouds are generated over the course of several cycles (Maxwell et al 2012). The onset of bubble cloud formation occurs once the initial bubble grows sufficiently large to scatter the incident shock wave geometrically (Maxwell et al 2011b, Bader and Holland 2016). Analytic predictions of bubble expansion over the duration of the shock scattering histotripsy pulse are in good agreement with numerical computations for mediums with an elastic modulus less than 875 kPa, as shown in Fig. 5. The analytic model overestimates bubble expansion in a medium with elastic modulus between 875 kPa and 2.5 MPa. For tissues over this range of stiffness, the axial extent of the bubble cloud, and therefore the extent of tissue liquefaction, will be overestimated for the analytic formulation.
Analytic predictions of maximum bubble size were also compared to experimental measurements of microtripsy-induced cavitation (Fig. 7). Analytic predictions based on strain-hardening elastic models (Fung and Gent) were the closest to measured bubble sizes in agar phantoms, consistent with the observation that agar is a strain-hardening medium (Erkamp et al 2000, Hall et al 1997). While there was some discrepancy between the measured values and the strain-hardening models, incorporation of a “best-fit” elastic model improved the accuracy of the analytic predictions 8.7% and 3.3% compared to the use of the Gent and Fung models, respectively. The agreement between the analytic prediction and measured bubble sizes indicates the analytic model captures the behavior of histotripsy-induced cavitation, but requires the proper medium-dependent elastic model for accurate prediction of the bubble size (Schmitt et al 2011). Alternatively, there may be a strain rate dependence (and therefore frequency dependence) contribution to the bubble dynamics not properly modeled here.
4.2. Influence of medium elasticity on maximum bubble size
Medium elasticity was found to influence the cavitation dynamics through two mechanisms: a retardation to the onset of bubble expansion, and a modification to the effective pressure that halts bubble expansion. The longest delays in bubble expansion are dictated by surface tension compare to other mechanisms for peak negative pressures less than 5 MPa (Fig. 3B). Histotripsy operates at peak negative pressures greater than 15 MPa (Maxwell et al 2012), where inertial and viscous effects are the major retarding effects to bubble expansion for soft tissues and muscle (Fig. 3B). As the elastic modulus exceeds 105 MPa, bubble expansion will be dictated by the medium elasticity (Fig. 3C). Thus, histotripsy-induced bubble dynamics in tissues such as hair, nail, collagen, and mineralized tissue (e.g. bone, tooth, kidney stones, etc.) will be dictated by the medium elasticity (Duck 1990). This also has interesting implications for histotripsy studies with fixed tissues. Fixation of tissues in formalin has been shown to increase the elastic modulus by two orders of magnitude compared to fresh tissues (Braun et al 2017). Such stiffening effects of the tissue will cause additional delay to the onset of bubble expansion compared to fresh tissue, potentially altering the dominate mechanisms of bubble dynamics (Hoffmeister et al 1996).
The medium elasticity also influences the effective pressure, or “Blake brake” (equations 7 and 8). The form of the effective pressure depends on the insonation type (Bader and Holland 2016), and therefore the means by which elasticity effects the maximum bubble diameter. A critical elastic modulus was identified for both forms of histotripsy, a4 in Table 3. For a given set of insonation conditions, the maximum bubble size was found to decrease exponentially for an elastic modulus greater than the critical modulus. For shock-scattering histotripsy, which has a large compressional component in the excitation waveform, the best-fit for a4 was found to be 2.95 MPa. The critical elastic modulus for microtripsy, which has no compressional component, was found to be reduced by a factor of seven compared to shock-scattering histotripsy (425 kPa). The best-fit values for a4 indicate bubble expansion is more resistant to tissue elasticity for shock-scattering histotripsy compared to microtripsy over the elastic modulus range 425 kPa to 2.95 MPa.
The axial extent of the bubble cloud induced by shock-scattering histotripsy also has a critical elastic modulus, decreasing rapidly for a medium stiffness greater than 1.5–2.5 MPa (Fig. 5B). Beyond the critical elastic modulus, the initial cavitation nucleus does not expand sufficiently to scatter the incident shock wave geometrically. Consequently, the efficacy of shock-scattering histotripsy will be significantly reduced for a medium with elasticity greater than 2.5 MPa. The erosion of tissue via shock-scattering histotripsy has been demonstrated to be significantly reduced for tissues with elastic moduli ranging from several MPa to GPa (Duck 1990), including vascular adventitia, skin, cartilage, tendon, bone, and tooth (Vlaisavljevich et al 2013b).
The critical elastic moduli denoted in these studies suggest the choice of insonation scheme should be chosen to induce a specific bubble dynamics (shock-induced bubble cloud or microtripsy bubble expansion) based on a priori knowledge of the tissue elasticity. Microtripsy can nucleate cavitation in a medium with elasticity up to 425 kPa, beyond which the efficacy of the therapy will be reduced. The formation of shock-scattering bubble clouds is impervious to the medium elasticity up to 2.95 MPa, beyond which the cloud expansion is suppressed and the efficacy of shock-scattering histotripsy is mitigated. The explosive bubble expansion necessary for microtripsy tissue liquefaction can still be nucleated in a medium with elasticity greater than 2.95 MPa (Fig. 4), but at a reduced efficacy.
For both forms of histotripsy, bubble expansion was completely suppressed for a medium with elastic modulus greater than 20 MPa (figures 9 and 10). The elastic modulus for arterial tissue can reach 20 MPa under systolic pressure (Nichol et al 2011), indicating histotripsy liquefaction would be suppressed. Histotripsy has been noted to act as a vessel sparing therapy (Vlaisavljevich et al 2013a, 2013b, 2017, Zhang et al 2017), consistent with this conclusion. Bubble expansion was also suppressed for the largest elastic moduli considered in this study, which are representative of mineralized tissues such as cortical bone and kidney stones (5–80 GPa), enamel (20–80 GPa), and dentine (11–21 GPa) (Duck 1990, Heimback et al 2000). The largest tension considered in this study was based on the current state of histotripsy technology (Sukovich et al 2016). In order to generate cavitation in mineralized tissue (elastic modulus ~ 10 GPa), a peak negative pressure in excess of 1 TPa would be required based on analytic model predictions. For perspective, the side lobes of a highly focused source (f-number of 0.5, 6.5-cm focal length and 10-cm diameter, 1-MHz fundamental frequency) would be in excess of 2 GPa to generate 1 TPa in the focal zone (Mast et al 2005). Surface erosion thus appears the most feasible means for histotripsy treatment of mineralized tissue (Xu et al 2005, Duryea et al 2015), restricting the targets to superficial disease.
4.3. Influence of elastic model on prediction of bubble expansion
These studies focused primarily on the use of the Kelvin-Voight elastic model because of its applicability for soft tissues (Frizzell et al 1976, Madsen et al 1983). The predicted maximum bubble size was similar for all the finite-strain models (Kelvin-Voight, linear, and Neo-Hookean in Fig. 6), indicating that the large bubble expansion for soft tissues is only mildly dependent on the form of the elastic model. The best agreement between measured bubble sizes in an agar phantom and the analytic model were for strain-hardening elastic models (Fung and Gent models in Fig. 7). Agar displays behaviors similar to a strain hardening medium, with a stronger increase in elasticity with strains than ex vivo soft tissue (Erkamp et al 2000, Hall et al 1997) and fracturing at moderate strain (Madsen et al 2003). Strain-hardening models were developed to capture the response of tissue with high content of collagen fibers, such as skin and arterial walls (Tong and Fung 1976, Deng et al 1994, Horgan and Saccomandi 2003). Interestingly, this suggests that bubble behavior observed in agar phantoms may not be totally reflective of that occurring in soft tissues, but in tissue that derives its structure from extracellular components (i.e. collagen).
4.4. Prediction of red blood cell viability
Red blood cell viability surrounding histotripsy cavitation activity was modeled based on measurements of impulsive stretching of erythrocytes (Li et al 2013). Strain fields surrounding the bubble were rapidly attenuated within 50 μm from the bubble wall, consistent with previous calculations of histotripsy-induced cavitation (Mancia et al 2017). Only red blood cells within a few micrometers from the bubble wall experienced lethal strain (Table 3), and the erythrocyte viability increased sigmoidally with distance away from the bubble. On a macroscopic level, the limited distance over which red blood cell viability is reduced observed in this study is consistent with the sharp boundaries observed in histotripsy lesions (Vlaisavljevich et al 2013a, Parsons et al 2006, Kieran et al 2007, Darnell et al 2015). In vitro studies have demonstrated histotripsy-induced breast cancer cell bisection occur only within a few micrometers to a nucleated bubble (Vlaisavljevich et al 2016). Under the similar insonation conditions, the calculations in this study indicate changes in red blood cell viability would be restricted within 1 μm of the bubble (Fig. 11C and 11E).
Tissue elasticity was observed to influence the degree of bubble expansion, and the subsequent strain surrounding the bubble. Erythrocyte viability for a given histotripsy exposure will be restricted to the bubble wall in highly elastic tissue, reducing the volume of red blood cell lysis. This has implications for the age of histotripsy-treated thrombus. Retraction of the thrombus over time changes its elasticity (Xie et al 2005) and composition (Sutton et al 2013). Zhang et al (2016) noted a change in in elastic modulus from 2.31 kPa for unretracted clots to 11.12 kPa for retracted clots, with a significant reduction in the efficacy of 1-MHz microtripsy pulses. Interestingly, the calculations here suggest a 1.1% decrease in bubble expansion and 3.5% reduction in red blood cell lysis over the same range of elastic moduli. The change in thrombus structure may alter the acousto-mechanical properties, increasing the attenuation of the histotripsy field (Nahirnyak et al 2006). Alternatively, anisotropies in fibrin-rich clot may not be properly modeled by the normal strains computed in this study (Weiss et al 2013). Up to 43% of thrombi are multifaceted, with both acute and chronic portions (Mewissen et al 1999, Gagne et al 2015). To ensure sufficient mechanical action throughout the thrombus, histotripsy image guidance should thus focus on not only qualifying the presence of cavitation, but also spatially quantifying the degree of cavitation activity (Bader et al 2018, Macoskey et al 2017).
In media stiffer than 20 MPa, calculations indicate the strain on erythrocytes is insufficient to induce lysis for the histotripsy insonation parameters considered (Fig. 11). In softer media, the extent of damage beyond the bubble volume was found to depend on the insonation type. Microtripsy-nucleated bubbles induce larger strains at greater distances from the bubble compared to shock scattering cavitation for a given set of insonation parameters. Depending on the necessity for precision relative to the observed spatial location of the bubble cloud, the choice of insonation scheme should be considered.
4.5. Limitations of the study
There are several aspects of this study that limit the generalizability of these findings. The amplitude of the measured shock scattering histotripsy pulses used as the source term in (1) may be underestimated due to spatial averaging of the fiber width and the bandwidth of the system (Canney et al 2008). The size of the bubble is assumed to be much smaller than the wavelength of the excitation pressure for the Yang/Church model, which is not the case for shockwave excitation. The analytic model does not consider the effects of bubble-bubble interactions, which are likely for a highly dense bubble cloud. Tissue damage was modeled here due purely to strain in the medium surrounding the bubble (Li et al 2013), but the type of cell death can be dictated by the strain rate (Bar-Kochba et al 2016). The strain-dependent cell viability was based on impulsive measurements of erythrocyte stretching (Li et al 2013), and may not be applicable across all cell types (Ofek et al 2009, Barbee 2005). The use of (17) to predict the minimum bubble radius is based on the collapse of a Rayleigh cavity in an elastic medium, and will underestimate the actual minimum bubble size due to damping (Gaudron et al 2015) and gas diffusion (Church 1989). The goal of this study was to estimate the strain during collapse, which depends on the difference in the cube of the minimum bubble size and the size of the initial bubble nucleus via (16). For large bubble expansion, such as histotripsy-induced cavitation (Bader and Holland 2016, Mancia et al 2017), the minimum bubble size will be much smaller than the size of the nucleus, (13) will be largely independent of the minimum bubble size. Normal strains were computed in this study, which would be indicative of isotropic tissues. The strain will have an angular dependence in anisotropic tissues such as tendon and myocardium (Hoffmeister et al 1996). The analytic model does not include the contribution of gas diffusion in the prediction of the maximum bubble size. Bubble expansion is controlled by the inertia of the medium, with minimal contributions from diffusion (Church 1989).
5. Summary
Histotripsy-induced tissue liquefaction relies on the expansion of nanoscale nuclei in an elastic medium. An analytic model was extended to include finite-strain (linear, neo-Hookean, and Kelvin-Voight) and strain-hardening (modified Fung and Gent) elastic models. The extended analytic model was used in these studies to predict the maximum size of a nucleus exposed to microtripsy or shock-scattering histotripsy pulses. The influence of medium elasticity on bubble expansion depended on the insonation type. However, bubble expansion was completely suppressed in media with elastic modulus greater than 20 MPa for both forms of histotripsy. The predicted maximum bubble size was similar for finite-strain elastic models. A strong decrease in the maximum bubble size was observed when comparing the strain-hardening and finite-strain elastic models. Strain-induced changes in red blood cell viability surrounding an expanded cavitation nucleus were also assessed, and found to be restricted within a few micrometers from the bubble wall.
Acknowledgments
The author gratefully acknowledges discussion of this topic with members of the Image-guided Therapeutic Laboratories at the University of Cincinnati, Dr. Charles Church of the University of Mississippi, and for Dr. Adam Maxwell of the University of Washington. This work was funded in part by the National Institutes of Health, Grant K12CA139160, Grant R01HL13334, Grant T32EB002103, and Grant UL1TR000430.
Appendix
For pure strain conditions, the stress for Gent elasticity (σ) can be written in the form:
| (A1) |
Equation A1 was fit in the least-squares sense to large strain rheologic measurements of agar phantoms (1–2.5 % w/v) (Barrangou et al 2006) to determine the fitting parameter JM (Fig. A1).
Fig. A1.
Measured stress versus material deformation in agar phantoms (Table 1 in (Barrangou et al 2006)) and least-squares fits of the Gent model, A1, to the measured stress to determine parameter JM. The concentration of agar is noted along the side of the figure.
References
- Apfel RE. Acoustic cavitation prediction. J Acoust Soc Am. 1981a;69:1624–33. [Google Scholar]
- Apfel RE. Methods in Experimental Physics. Vol. 19. New York: Academic Press, Inc; 1981b. Acoustic Cavitation; pp. 355–411. [Google Scholar]
- Apfel RE. Possibility of microcavitation from diagnostic ultrasound. IEEE Trans Ultrason Ferro Freq Control. 1986;33:139–42. doi: 10.1109/t-uffc.1986.26805. [DOI] [PubMed] [Google Scholar]
- Apfel RE, Holland CK. Gauging the likelihood of cavitation from short-pulse, low-duty cycle diagnostic ultrasound. Ultrasound Med Biol. 1991;17:179–85. doi: 10.1016/0301-5629(91)90125-g. [DOI] [PubMed] [Google Scholar]
- Bader KB, Holland CK. Predicting the growth of nanoscale nuclei by histotripsy pulses. Phys Med Biol. 2016:2947–66. doi: 10.1088/0031-9155/61/7/2947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bader KB, Haworth KJ, Maxwell AD, Holland CK. Post hoc analysis of passive cavitation imaging for classification of histotripsy-induced liquefaction in vitro. IEEE Trans Med Imaging. 37:106–115. doi: 10.1109/TMI.2017.2735238. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bader KB, Haworth KJ, Shekhar H, Maxwell AD, Peng T, McPherson DD, Holland CK. Efficacy of histotripsy combined with rt-PA in vitro. Phys Med Biol. 2016b;61:5253–74. doi: 10.1088/0031-9155/61/14/5253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bar-Kochba E, Scimone MT, Estrada JB, Franck C. Strain and rate-dependent neuronal injury in a 3D in vitro compression model of traumatic brain injury. Sci Rep. 2016;6:1–11. doi: 10.1038/srep30550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barbee KA. Mechanical Cell Injury. Ann NY Acad Sci. 2005;1066:67–84. doi: 10.1196/annals.1363.006. [DOI] [PubMed] [Google Scholar]
- Barrangou LM, Daubert CR, Allen Foegeding E. Textural properties of agarose gels. I. Rheological and fracture properties. Food Hydrocol. 2006;20:184–95. [Google Scholar]
- Braun J, Tzschatzsch H, Korting C, Ariza de Schellenberger A, Jenderka M, Driesle T, Ledwig M, Sack I. A compact 0.5 T MR elastography device and its application for studying viscoelasticity changes in biological tissues during progressive formalin fixation. Magn Reson Med. 2017;79:470–8. doi: 10.1002/mrm.26659. [DOI] [PubMed] [Google Scholar]
- Canney MS, Bailey MR, Crum LA, Khokhlova VA, Sapozhnikov OA. Acoustic characterization of high intensity focused ultrasound fields: A combined measurement and modeling approach. J Acoust Soc Am. 2008;124:2406. doi: 10.1121/1.2967836. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Church CC. A theoretical study of cavitation generated by an extracorporeal shock wave lithotripter. J Acoust Soc Am. 1989;86:215. doi: 10.1121/1.398328. [DOI] [PubMed] [Google Scholar]
- Church CC, Labuda C, Nightingale K. A Theoretical Study of Inertial Cavitation from Acoustic Radiation Force Impulse Imaging and Implications for the Mechanical Index. Ultrasound Med Biol. 2015;41:472–85. doi: 10.1016/j.ultrasmedbio.2014.09.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Darnell SE, Hall TL, Tomlins SA, Cheng X, Ives KA, Roberts WW. Histotripsy of the Prostate in a Canine Model: Characterization of Post-Therapy Inflammation and Fibrosis. J Endourol. 2015;29:810–5. doi: 10.1089/end.2014.0585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deng SX, Tomioka J, Debes JC, Fung Y-C. New experiments on shear modulus of elasticity of arteries. Am J Physiol. 1994;266:H1–10. doi: 10.1152/ajpheart.1994.266.1.H1. [DOI] [PubMed] [Google Scholar]
- Duck FA. Physical properties of tissue: A comprehensive reference book. Academic Press, Inc; 1990. [Google Scholar]
- Duryea AP, Roberts WW, Cain CA, Hall TL. Removal of residual cavitation nuclei to enhance histotripsy erosion of model urinary stones. IEEE Trans Ultrason Ferroelect Freq Contr. 2015;62:896–904. doi: 10.1109/TUFFC.2015.7001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Erkamp RQ, Emelianov SY, Skovoroda AR, Chen X, O’Donnell M. Exploiting strain-hardening of tissue to increase contrast in elasticity imaging. IEEE Ultrasonics Symposium. 2000;2:1833–6. [Google Scholar]
- Frizzell LA, Carstensen EL, Dyro JF. Shear properties of mammalian tissues at low megahertz frequencies. J Acoust Soc Am. 1976;60:1409–11. doi: 10.1121/1.381236. [DOI] [PubMed] [Google Scholar]
- Fung YC, Fronek K, Patitucci P. Pseudoelasticity of arteries and the choice of its mathematical expression. Am J Physiol. 1979;237:H620–31. doi: 10.1152/ajpheart.1979.237.5.H620. [DOI] [PubMed] [Google Scholar]
- Gagne P, Khoury T, Zadeh BJ, Rajasinghe HA. A Multicenter, Retrospective Study of the Effectiveness of the Trellis-8 System in the Treatment of Proximal Lower-Extremity Deep Vein Thrombosis. Ann Vasc Surg. 2015;29:1633–41. doi: 10.1016/j.avsg.2015.05.029. [DOI] [PubMed] [Google Scholar]
- Gaudron R, Warnez MT, Johnsen E. Bubble dynamics in a viscoelastic medium with nonlinear elasticity. J Fluid Mech. 2015;766:54–75. [Google Scholar]
- Gent AN. A New Constitutive Relation for Rubber. Rub Chem Technol. 1996;69:59–61. [Google Scholar]
- Gent AN. Elastic instabilities in rubber. Int J Non-Linear Mech. 2005a;40:165–75. [Google Scholar]
- Gent AN. Elastic Instabilities of Inflated Rubber Shells. Rub Chem Technol. 1999;72:263–8. [Google Scholar]
- Gent AN. Extensibility of rubber under different types of deformation. J Rheol. 2005b;49:271–5. [Google Scholar]
- Gent AN, Lindley PB. Internal Rupture of Bonded Rubber Cylinders in Tension. Proc Roy Soc London. 1959;249:195–205. [Google Scholar]
- Gent AN, Wang C. Fracture mechanics and cavitation in rubber-like solids. J Mat Sci. 1991;26:3392–5. [Google Scholar]
- Gerhardson T, Sukovich JR, Pandey AS, Hall TL, Cain CA, Xu Z. Catheter Hydrophone Aberration Correction for Transcranial Histotripsy Treatment of Intracerebral Hemorrhage (ICH): Proof-of-Concept. IEEE Trans Ultrason Ferroelect Freq Contr. 2017;64:1684–1697. doi: 10.1109/TUFFC.2017.2748050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Griffith AA. The phenomena of rupture and flow in solids. Proc Roy Soc London. 1921;221:163–98. [Google Scholar]
- Hall TJ, Bilgen M, Insana MF, Krouskop TA. Phantom materials for elastography. IEEE Trans Ultrason Ferroelect Freq Contr. 1997;44:1355–65. [Google Scholar]
- Hall TL, Hempel CR, Lake AM, Kieran K, Ives K, Fowlkes JB, Cain CA, Roberts WW. Histotripsy for the treatment of BPH: evaluation in a chronic canine model. IEEE Ultrasonics Symposium. 2008:765–767. [Google Scholar]
- Heimbach D, Munver R, Zhong P, Jacobs J, Hesse A, Ller SCM, Preminger GM. Acoustic and mechanical properties of artificial kidney stones in comparison to natural kidney stones. J Urol. 2000;164:537–44. [PubMed] [Google Scholar]
- Hoffmeister BK, Handley SM, Wickline SA, Miller JG. Ultrasonic determination of the anisotropy of Young’s modulus of fixed tendon and fixed myocardium. J Acoust Soc Am. 1996;100:3933–40. doi: 10.1121/1.417246. [DOI] [PubMed] [Google Scholar]
- Holland CK, Apfel RE. Improved Theory for the Prediction of Microcavitation Thresholds. IEEE Trans Ultrason Ferroelect Freq Contr. 1989;36:204–8. doi: 10.1109/58.19152. [DOI] [PubMed] [Google Scholar]
- Horgan CO, Saccomandi G. A description of arterial wall mechanics using limiting chain extensibility constitutive models. Biomech Model Mechanobiol. 2003;1:251–66. doi: 10.1007/s10237-002-0022-z. [DOI] [PubMed] [Google Scholar]
- Horgan CO, Saccomandi G. Simple Torsion of Isotropic, Hyperelastic, Incompressible Materials with Limiting Chain Extensibility. J Elasticity. 1999;56:159–70. [Google Scholar]
- Hutchens SB, Fakhouri S, Crosby AJ. Elastic cavitation and fracture via injection. Soft Matter. 2016;12:2557–66. doi: 10.1039/c5sm02055g. [DOI] [PubMed] [Google Scholar]
- Khokhlova VA, Bailey MR, Reed JA, Cunitz BW, Kaczkowski PJ, Crum LA. Effects of nonlinear propagation, cavitation, and boiling in lesion formation by high intensity focused ultrasound in a gel phantom. J Acoust Soc Am. 2006;119:1834. doi: 10.1121/1.2161440. [DOI] [PubMed] [Google Scholar]
- Khokhlova VA, Fowlkes JB, Roberts WW, Schade GR, Xu Z, Khokhlova TD, Hall TL, Maxwell AD, Wang Y-N, Cain CA. Histotripsy methods in mechanical disintegration of tissue: Towards clinical applications. Int J Hyperthermia. 2015;31:145–62. doi: 10.3109/02656736.2015.1007538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kieran K, Hall TL, Parsons JE, Wolf JS, Jr, Fowlkes JB, Cain CA, Roberts WW. Refining Histotripsy: Defining the Parameter Space for the Creation of Nonthermal Lesions With High Intensity, Pulsed Focused Ultrasound of the In Vitro Kidney. J Urol. 2007;178:672–6. doi: 10.1016/j.juro.2007.03.093. [DOI] [PubMed] [Google Scholar]
- Lastman GJ, Wentzell RA. Comparison of five models of spherical bubble response in an inviscid compressible liquid. J Acoust Soc Am. 1981;69:638–42. [Google Scholar]
- Leighton TG. The Acoustic Bubble. London: Academic Press; 1994. [Google Scholar]
- Lewis JH. Comparative Hemostasis in Vertebrates. New York: Plenum Press; 1996. [Google Scholar]
- Li F, Chan CU, Ohl C-D. Yield Strength of Human Erythrocyte Membranes to Impulsive Stretching. Biophys J. 2013;105:872–9. doi: 10.1016/j.bpj.2013.06.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin KW, Kim Y, Maxwell A, Wang TY, Hall T. Histotripsy beyond the intrinsic cavitation threshold using very short ultrasound pulses: microtripsy. IEEE Trans Ultrason Ferroelect Freq Contr. 2014;61:251–65. doi: 10.1109/TUFFC.2014.6722611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Macoskey JJ, Sukovich JR, Hall TL, Cain CA, Xu Z. Acoustic cavitation emission feedback to monitor tissue fractionation during histotripsy. J Acoust Soc Am. 2017;141:3551–1. [Google Scholar]
- Madsen EL, Frank GR, KROUSKOP TA, Varghese T, Kallel F, Ophir J. Tissue-Mimicking Oil-in-Gelatin Dispersions for Use in Heterogeneous Elastography Phantoms. Ultrasonic Im. 2003;25:17–38. doi: 10.1177/016173460302500102. [DOI] [PubMed] [Google Scholar]
- Madsen EL, Sathoff HJ, Zagzebski JA. Ultrasonic shear wave properties of soft tissues and tissuelike materials. J Acoust Soc Am. 1983;74:1346–55. doi: 10.1121/1.390158. [DOI] [PubMed] [Google Scholar]
- Mancia L, Vlaisavljevich E, Xu Z, Johnsen E. Predicting Tissue Susceptibility to Mechanical Cavitation Damage in Therapeutic Ultrasound. Ultrasound Med Biol. 2017;43:1421–40. doi: 10.1016/j.ultrasmedbio.2017.02.020. [DOI] [PubMed] [Google Scholar]
- Mast TD, Makin IRS, Faidi W, Runk MM, Barthe PG, Slayton MH. Bulk ablation of soft tissue with intense ultrasound: Modeling and experiments. J Acoust Soc Am. 2005;118:2715–24. doi: 10.1121/1.2011157. [DOI] [PubMed] [Google Scholar]
- Maxwell AD, Cain CA, Hall TL, Fowlkes JB, Xu Z. Probability of Cavitation for Single Ultrasound Pulses Applied to Tissues and Tissue-Mimicking Materials. Ultrasound Med Biol. 2013;39:449–65. doi: 10.1016/j.ultrasmedbio.2012.09.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maxwell AD, Owens G, Gurm HS, Ives K, Myers DD, Jr, Xu Z. Noninvasive Treatment of Deep Venous Thrombosis Using Pulsed Ultrasound Cavitation Therapy (Histotripsy) in a Porcine Model. J Vasc Intervent Radiol. 2011a;22:369–77. doi: 10.1016/j.jvir.2010.10.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maxwell AD, Wang TY, Yuan L, Duryea AP, Xu Z. A tissue phantom for visualization and measurement of ultrasound-induced cavitation damage. Ultrasound Med Biol. 2010;36:2132–43. doi: 10.1016/j.ultrasmedbio.2010.08.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maxwell AD, Wang T-Y, Cain CA, Fowlkes JB, Sapozhnikov OA, Bailey MR, Xu Z. Cavitation clouds created by shock scattering from bubbles during histotripsy. J Acoust Soc Am. 2011b;130:1888. doi: 10.1121/1.3625239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maxwell A, Sapozhnikov O, Bailey M, Crum L, Xu Z, Fowlkes B, Cain C, Khokhlova V. Disintegration of tissue using high intensity focused ultrasound: two approaches that utilize shock waves. Acoust Today. 2012;8:24–37. [Google Scholar]
- Mewissen MW, Seabrook GR, Meissner MH, Cynamon J, Labropoulos N, Haughton SH. Catheter-directed thrombolysis for lower extremity deep venous thrombosis: report of a national multicenter registry. Radiol. 1999;211:39–49. doi: 10.1148/radiology.211.1.r99ap4739. [DOI] [PubMed] [Google Scholar]
- Movahed P, Kreider W, Maxwell AD, Hutchens SB, Freund JB. Cavitation-induced damage of soft materials by focused ultrasound bursts: A fracture-based bubble dynamics model. J Acoust Soc Am. 2016;140:1374–86. doi: 10.1121/1.4961364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nahirnyak VM, Yoon SW, Holland CK. Acousto-mechanical and thermal properties of clotted blood. J Acoust Soc Am. 2006;119:3766. doi: 10.1121/1.2201251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nichol WW, ORouke MF, Viachopoulos C. McDonald’s Blood Flow in Arteries: Theoretical, Experimental and Clinical Principles. Boca Raton: 2011. [Google Scholar]
- Ofek G, Dowling EP, Raphael RM, McGarry JP, Athanasiou KA. Biomechanics of single chondrocytes under direct shear. Biomech Model Mechanobiol. 2009;9:153–62. doi: 10.1007/s10237-009-0166-1. [DOI] [PubMed] [Google Scholar]
- Parsons JE, Cain CA, Abrams GD, Fowlkes JB. Pulsed cavitational ultrasound therapy for controlled tissue homogenization. Ultrasound Med Biol. 2006;32:115–29. doi: 10.1016/j.ultrasmedbio.2005.09.005. [DOI] [PubMed] [Google Scholar]
- Prosperetti A, Lezzi A. Bubble dynamics in a compressible liquid. J Fluid Mech. 1986;168:457–7478. [Google Scholar]
- Rayleigh L. VIII. On the pressure developed in a liquid during the collapse of a spherical cavity. Phil Mag. 1917;34:94–8. [Google Scholar]
- Roland CM. Viscoelastic Behavior of Rubbery Materials. Oxford University Press; 2011. [Google Scholar]
- Schmitt C, Henni AH, Cloutier G. Characterization of blood clot viscoelasticity by dynamic ultrasound elastography and modeling of the rheological behavior. J Biomech. 2011;44:622–9. doi: 10.1016/j.jbiomech.2010.11.015. [DOI] [PubMed] [Google Scholar]
- Sukovich JR, Xu Z, Kim Y, Cao H, Nguyen T-S, Pandey AS, Hall TL, Cain CA. Targeted Lesion Generation Through the Skull Without Aberration Correction Using Histotripsy. IEEE Trans Ultrason Ferroelect Freq Contr. 2016;63:671–82. doi: 10.1109/TUFFC.2016.2531504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sutton JT, Ivancevich NM, Perrin SR, Jr, Vela DC, Holland CK. Clot Retraction Affects the Extent of Ultrasound-Enhanced Thrombolysis in an Ex Vivo Porcine Thrombosis Model. Ultrasound Med Biol. 2013;39:813–24. doi: 10.1016/j.ultrasmedbio.2012.12.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tong P, Fung Y-C. The stress-strain relationship for the skin. J Biomech. 1976;9:649–57. doi: 10.1016/0021-9290(76)90107-x. [DOI] [PubMed] [Google Scholar]
- Vincent J. Structural Biomaterials. Princeton University Press; 2012. [Google Scholar]
- Vlaisavljevich E, Kim Y, Allen S, Owens G, Pelletier S, Cain C, Ives K, Xu Z. Image-guided non-invasive ultrasound liver ablation using histotripsy. Ultrasound Med Biol. 2013a;39:1398–409. doi: 10.1016/j.ultrasmedbio.2013.02.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vlaisavljevich E, Kim Y, Owens G, Roberts W, Cain C, Xu Z. Effects of tissue mechanical properties on susceptibility to histotripsy-induced tissue damage. Phys Med Biol. 2013b;59:253–70. doi: 10.1088/0031-9155/59/2/253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vlaisavljevich E, Lin K-W, Maxwell A, Warnez MT, Mancia L, Singh R, Putnam AJ, Fowlkes B, Johnsen E, Cain C, Xu Z. Effects of ultrasound frequency and tissue stiffness on the histotripsy intrinsic threshold for cavitation. Ultrasound Med Biol. 2015a;41:1651–67. doi: 10.1016/j.ultrasmedbio.2015.01.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vlaisavljevich E, Lin K-W, Warnez MT, Singh R, Mancia L, Putnam AJ, Johnsen E, Cain C, Xu Z. Effects of tissue stiffness, ultrasound frequency, and pressure on histotripsy-induced cavitation bubble behavior. Phys Med Biol. 2015b:2271–92. doi: 10.1088/0031-9155/60/6/2271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vlaisavljevich E, Maxwell A, Mancia L, Johnsen E, Cain C, Xu Z. Visualizing the Histotripsy Process: Bubble Cloud-Cancer Cell Interactions in a Tissue-Mimicking Environment. Ultrasound Med Biol. 2016;42:2466–77. doi: 10.1016/j.ultrasmedbio.2016.05.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vlaisavljevich E, Owens G, Lundt J, Teofilovic D, Ives K, Duryea A, Bertolina J, Welling TH, Xu Z. Non-Invasive Liver Ablation Using Histotripsy: Preclinical Safety Study in an In Vivo Porcine Model. Ultrasound Med Biol. 2017;43:1237–51. doi: 10.1016/j.ultrasmedbio.2017.01.016. [DOI] [PubMed] [Google Scholar]
- Weiss HL, Selvaraj P, Okita K, Matsumoto Y, Voie A, Hoelscher T, Szeri AJ. Mechanical clot damage from cavitation during sonothrombolysis. J Acoust Soc Am. 2013;133:3159. doi: 10.1121/1.4795774. [DOI] [PubMed] [Google Scholar]
- Wilks AM, Rabice SR, Garbacz HS, Harro CC, Smith AM. Double-network gels and the toughness of terrestrial slug glue. J Ex Biol. 2015;218:3128–37. doi: 10.1242/jeb.128991. [DOI] [PubMed] [Google Scholar]
- Xie H, Kim K, Aglyamov SR, Emelianov SY, O’Donnell M, Weitzel WF, Wrobleski SK, Myers DD, Wakefield TW, Rubin JM. Correspondence of ultrasound elasticity imaging to direct mechanical measurement in aging DVT in rats. Ultrasound Med Biol. 2005;31:1351–9. doi: 10.1016/j.ultrasmedbio.2005.06.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu Z, Fowlkes JB, Rothman ED, Levin AM, Cain CA. Controlled ultrasound tissue erosion: The role of dynamic interaction between insonation and microbubble activity. J Acoust Soc Am. 2005;117:424. doi: 10.1121/1.1828551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu Z, Owens G, Gordon D, Cain C, Ludomirsky A. Noninvasive Creation of an Atrial Septal Defect by Histotripsy in a Canine Model. Circulation. 2010;121:742–9. doi: 10.1161/CIRCULATIONAHA.109.889071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang X, Church CC. A model for the dynamics of gas bubbles in soft tissue. J Acoust Soc Am. 2005;118:3595. doi: 10.1121/1.2118307. [DOI] [PubMed] [Google Scholar]
- Zhang X, Macoskey JJ, Ives K, Owens GE, Gurm HS, Shi J, Pizzuto M, Cain CA, Xu Z. Non-Invasive Thrombolysis Using Microtripsy in a Porcine Deep Vein Thrombosis Model. Ultrasound Med Biol. 2017;43:1378–90. doi: 10.1016/j.ultrasmedbio.2017.01.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang X, Owens GE, Cain CA, Gurm HS, Macoskey J, Xu Z. Histotripsy Thrombolysis on Retracted Clots. Ultrasound Med Biol. 2016;42:1903–18. doi: 10.1016/j.ultrasmedbio.2016.03.027. [DOI] [PMC free article] [PubMed] [Google Scholar]