Distribution of Initiation Times Reveals Mechanisms of Transcriptional Regulation in Single Cells

Abstract

Transcription is the dominant point of control of gene expression. Biochemical studies have revealed key molecular components of transcription and their interactions, but the dynamics of transcription initiation in cells is still poorly understood. This state of affairs is being remedied with experiments that observe transcriptional dynamics in single cells using fluorescent reporters. Quantitative information about transcription initiation dynamics can also be extracted from experiments that use electron micrographs of RNA polymerases caught in the act of transcribing a gene (Miller spreads). Inspired by these data, we analyze a general stochastic model of transcription initiation and elongation and compute the distribution of transcription initiation times. We show that different mechanisms of initiation leave distinct signatures in the distribution of initiation times that can be compared to experiments. We analyze published data from micrographs of RNA polymerases transcribing ribosomal RNA genes in Escherichia coli and compare the observed distributions of interpolymerase distances with the predictions from previously hypothesized mechanisms for the regulation of these genes. Our analysis demonstrates the potential of measuring the distribution of time intervals between initiation events as a probe for dissecting mechanisms of transcription initiation in live cells.

Introduction

One of the key findings of the genomic era is the unexpectedly high similarity between the genomes of different organisms (1). As the number of genomes being sequenced is increasing, it is becoming clear that the biggest difference among organisms is not to be found in their protein-coding sequences, but in the ways in which their genes are regulated (2, 3, 4, 5). This is putting the spotlight on the parts of the genome that are responsible for gene regulation and prompting the question: how do changes in regulatory sequences alter the way in which cells respond to intra- and extracellular signals (6)?

More often than not, genetic regulation occurs at the level of transcription, by which cells control the amount of messenger RNA of each gene they express (7). Regulation of transcription is commonly achieved by the integration of multiple intracellular signals at the regions of DNA upstream from and in proximity to the gene’s coding region. This “promoter region” consists of a collection of transcription factor binding sites and, in eukaryotes, nucleosome positioning sites. Together, these binding sites dictate the binding and unbinding of specific transcription factors, cofactors, and chromatin remodeling factors, which, in turn, either promote or inhibit the assembly of the transcriptional machinery at the gene.

The collection of transcription factor binding sites (which includes enhancer regions in eukaryotes), their position, and affinity for transcription factor proteins constitutes the promoter architecture. Considerable effort has been directed to elucidating how promoter architecture determines measurable quantities like the average transcriptional response (8, 9, 10, 11) of cells to a given stimulus, as well as the population-wide fluctuations of that response (12, 13, 14, 15). Although we have witnessed considerable progress on this front in recent years, many mysteries remain even in simple organisms such as bacteria. In particular, how promoter architecture affects the dynamics of transcription initiation in single cells remains poorly understood. To answer this question, experiments are being done in which the number of RNA molecules from a gene of interest is measured at a single-cell level in a population of isogenic cells (12, 16, 17, 18). The measured distribution of mRNA numbers in the cell population can then be used to test the predictions of different models of transcription initiation in the hope that some of these are supported by the data (19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30). This approach has led to the discovery of bursty mechanisms of transcription initiation (12, 16). However, this method of inferring the kinetics of transcription is limited by the fact that the mRNA copy number reflects additional processes downstream of transcription, such as the nonlinear degradation of mRNA and proteins (31), maturation time of fluorescent reporters (32), mRNA transport (33), mRNA splicing (34), and small RNA regulation (35). The stochastic nature of these processes may introduce fluctuations in the number of mRNAs that masks the contribution of the transcriptional dynamics (36, 37, 38).

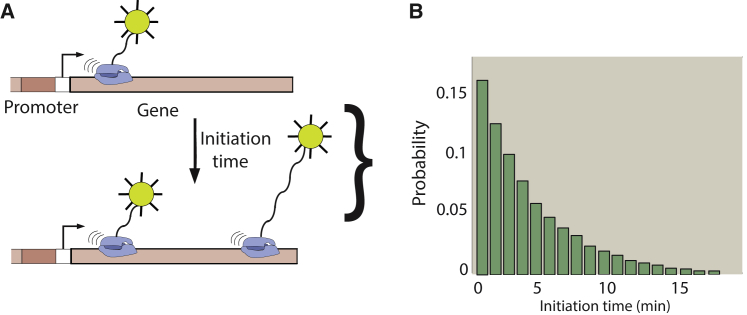
In contrast, experiments that catch RNA polymerase (RNAP) molecules in the process of transcribing a gene provide a more direct readout of transcription initiation dynamics. Techniques developed by Miller and his group in a series of landmark papers over several decades rely on imaging actively transcribed genes in recently lysed cells by electron microscopy (39, 40, 41, 42, 43, 44). In these images, the positions of transcribing polymerases along a gene can be determined (Fig. 1 A). Interpolymerase distance distributions can be extracted from these positions, and, with a few reasonable assumptions (36), these can be used to extract information about the distribution of times between successive initiation events (Fig. 1 B). The information contained in these distributions of interpolymerase distances is akin to that obtained in live cells by fluorescently labeling nascent RNAs to observe transcription initiation events in real time at the single-cell level (19, 20, 45, 46, 47, 48, 49), as illustrated in Fig. 1 B.

Figure 1.

Positions of transcribing RNAP carry the signature of transcription initiation dynamics. A schematic of the key idea of this work is shown. (A) The times between successive transcription initiation events (“initiation time”) can be extracted at the single-cell level using fluorescent reporters for nascent RNA molecules (19, 20, 45, 46, 47, 48, 49), or from electron micrograph (EM) images of RNAP caught in the process of transcribing a gene (39, 40, 41, 42, 43, 44). Native elongating transcript sequencing (85) can obtain the same quantitative information as EM images. (B) The distribution of times between individual transcription initiation events can be extracted from experiments and compared to theoretical predictions based on stochastic models of transcription initiation. To see this figure in color, go online.

Here, we calculate the distribution of times between successive initiation events to quantitatively test mechanistic models of transcription initiation in cells. To accomplish this, we introduce a stochastic model of transcription that incorporates both initiation and elongation kinetics. Using the derived analytical results in conjunction with simulations, we show that the kinetics of initiation leaves a signature in the distribution of transcription initiation times that can be used to discern different models of transcription initiation. To showcase the power of this approach, we have reanalyzed a set of micrographs of Escherichia coli genomic DNA that provided evidence of transcriptional bursting, a phenomenon that was later found to be widespread across all organisms (50). In fact, to our knowledge, McKnight et al. used Miller spreads to provide the first evidence of transcriptional bursting (51). We show that by filtering the information contained in these micrographs through our theoretical framework, we can test different models of regulation of ribosomal promoters in E. coli that have been proposed to account for the cell’s response to an increase in rrn operon copy number. We find that some of these previously proposed models produce distributions of interpolymerase distances that are inconsistent with the Miller spread data, whereas others are in excellent agreement.

Methods

Data analysis and parameter estimation

We evaluate the utility of our theoretical framework by employing it to gain mechanistic insights into the regulation of ribosomal genes in E. coli. To this end, we have reanalyzed data obtained from images of elongating RNAP molecules on ribosomal RNA (rRNA) genes in E. coli. Images of RNAPs were obtained from electron micrographs of fixed cells using the Miller spread technique by Voulgaris et al. (39), and the distances between neighboring RNAPs were measured by them. To extract the data from the published interpolymerase distance distribution plots in Fig. 3 B of (39), we used DigitizeIt, a free online tool for digitizing data plots.

Voulgaris et al. (39) increased the number of rrn operons in E. coli cells by inserting an rrn operon on a multicopy plasmid. They observed that the rate of rRNA transcription per operon is reduced to maintain a constant number of rRNA in the cell. In fact, electron micrograph (EM) images showed that fewer RNAP molecules were engaged in transcribing each rrn gene, consistent with previous studies (52). Moreover, RNAP molecules formed bunches separated by gaps along the genes. Although the authors ruled out transcription elongation or termination as origins of these bunches, they suggested that the bunches are caused by stochastic interruptions of initiation, or promoter-proximal elongation events. Using our theory, we analyze the distributions of intrabunch distances between RNAP.

In this study, we consider three models of transcriptional regulation of ribosomal genes: the dead-end complex model, the cooperative recruitment model, and the “ppGpp” model. For the dead-end complex model, after the loading of polymerase molecules to the promoter at a rate k_LOAD, each RNAP molecule either escapes the promoter at a rate k_ESC and starts transcribing the gene or forms a dead-end complex at the promoter at a rate k_DEAD. These dead-end complexes are unproductive and are removed at a rate k_OFF.

For the cooperative recruitment of RNAP by DNA supercoiling, RNAP molecules are loaded onto the promoter at a rate k_LOAD^LOW. After RNAP initiates transcription at a rate k_ESC, it leaves the promoter DNA in a supercoiled state, and subsequent loading of polymerases occurs at the promoter at a faster rate, k_LOAD^HIGH. The rate of relaxation of the supercoiled state is k_RELAX.

For the third model, the production of “control molecules” (e.g., ppGpp) reduces the initiation rate by regulating the initiation process by converting the active promoter-RNAP complexes into inactive ones. It is described by the same kinetic scheme as the dead-end complex model. However, the rate of inactivation of RNAP-DNA complex is given by k_ON, with every other rate remaining the same. Each of the three models considered above has five parameters.

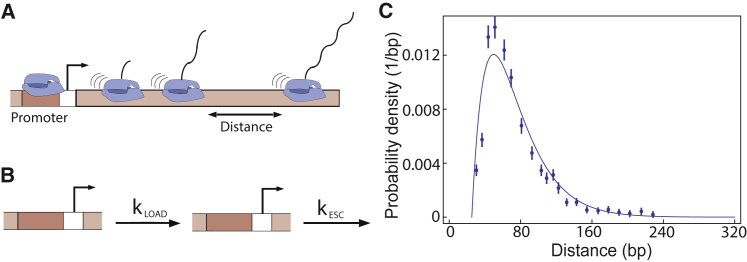
To test these proposed models based on the experimentally observed transcriptional bunching data for rrn genes, we first extract all the model parameters by fitting the predicted inter-RNAP distance distributions to the data from wild-type E. coli cells with seven rrn operons, as reported in (39). The authors in (39) analyzed the interpolymerase distance distributions extracted from the micrograph images by defining a “transcriptional bunch” as a group of RNAPs separated by less than 240 bp from each other (39). The distribution of distances greater than 240 bp is referred to as interbunch distribution. Evidently, the intrabunch distribution is dictated by the biochemical rates k_ESC (rate of promoter escape), k_LOAD (rate of RNAP loading onto the promoter, which is called k_LOAD^HIGH for the supercoiling mediated recruitment model), and τ_clear (time for an RNAP to clear the promoter). In Fig. 3 C, we show the interpolymerase distribution for the seven rrn promoters for the ribosomal genes in wild-type E. coli cells. Using Eq. 4 we find the probability distribution of interpolymerase distances as a function of these different rates is given by

$$p_1\left(x\right)=\frac{1}{v}\frac{k_{LOAD}{k}_{ESC}}{k_{LOAD}+k_{ESC}}\left[\exp \left(-k_{ESC}\left(\frac{x}{v}-\frac{30}{v}\right)\right)-\exp \left(-k_{LOAD}\left(\frac{x}{v}-\frac{30}{v}\right)\right)\right].$$ (1)

Figure 3.

Initiation of transcription of ribosomal genes in E. coli. (A) The positions of RNAP molecules transcribing a gene at a given instant in time can be obtained from electron microscopy images or native elongating transcript sequencing (85). (B) The two-step model of transcription initiation is shown. (C) The fit (line) of the two-step model to the interpolymerase distance distribution data (points) obtained by Voulgaris et al. (39) for ribosomal genes in E. coli is given. The different biochemical rates we extract from the fit are as follows: k_ESC (rate of promoter escape) ≈ 3/s, k_LOAD (rate of RNAP loading onto the promoter) ≈ 3/s, and τ_clear (time for an RNAP to clear the promoter) ≈ 0.3 s, taking the elongation speed v = 78 bps/s, as reported in experiments (39). To see this figure in color, go online.

Here, 30 bps is roughly the size of an RNAP molecule, and v is the rate of transcription elongation of the RNAP molecules along a gene. By comparing the data from the experiments for interpolymerase distances within a bunch and the prediction from the model, we extract k_LOAD, k_ESC, and τ_CLEAR. By fitting the model (see Fig. 3 C), we extract the rates k_ESC ≈ 3/s, k_LOAD ≈ 3/s, and τ_clear ≈ 0.3 s (τ_clear = $\left(30/\mathit{v}\right)$); v is the rate of elongation, which we take to be 78 bps/s (39). These three parameters are common to all three models examined.

Next, we extract the remaining two parameters for each of these three models (see Fig. 4, A–C) by making use of the intrabunch distances (39). The mean intrabunch distance allows us to extract the average time the promoter spends in the inactive state, which does not lead to initiation. From Fig. 3 A of (39), we extract the mean gap between RNAP bunches to be ∼5 s. Hence, for the three bursting models, we take k_OFF (dead-end complex model) = k_OFF (ppGpp model) = k_LOAD^LOW (cooperative recruitment model) ≈ 0.2/s. To obtain the fifth parameter of these models, we assume that the addition of extra copies of ribosomal genes to the E. coli cell reduces the average transcription rate per gene to keep the level of rRNA in the cell constant. In other words, for the models considered above, the total initiation rate remains constant, or nI = Constant, where n is the number of ribosomal genes and I is the initiation rate on one of the genes. The initiation rate for a wild-type strain with n = 7 genes is I = 1 initiation/s (39). Using the formulas for the rate of average initiation for each of the models of transcription initiation (see the Supporting Material), we find for the cooperative recruitment model k_RELAX ≈ 0.055/s and for the k_DEAD (dead-end complex) = k_ON (ppGpp model) ≈ 0.047/s.

Figure 4.

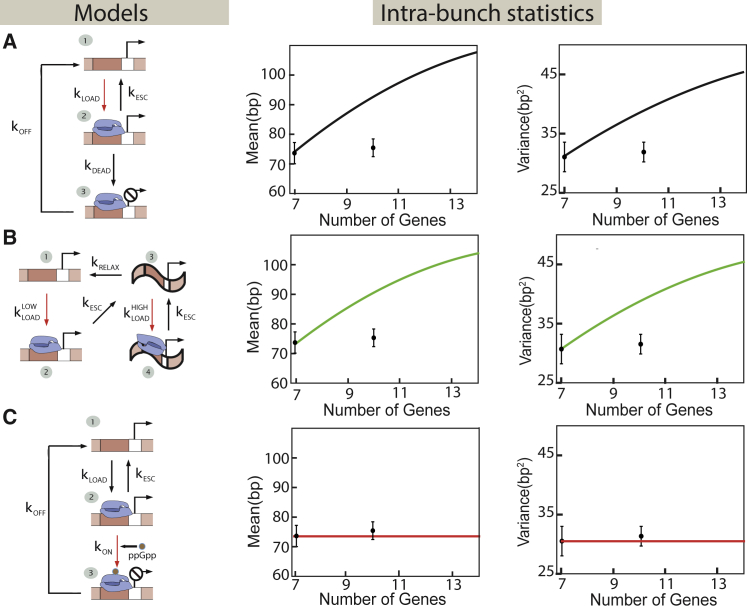
Different models of transcriptional regulation of ribosomal genes can be tested by tuning the gene-copy number. (A and B) Models of transcription initiation that rely solely on the interaction of RNAP with promoter DNA are shown. (A) This class of model considers the formation of long-lived nonproductive initiation complexes at the promoter by RNAP molecules (25, 70). After binding the promoter at a rate k_LOAD, each RNAP can initiate transcription at a rate k_ESC or make a dead-end complex at the promoter at a rate k_DEAD. These dead-end complexes are unproductive and are removed at a rate k_OFF. The change in gene-copy number affects the binding rate of RNAP molecules to the promoter because of a change in the free RNAP concentration, as indicated by the red arrow. Theory predicts that the mean and variance of distances between RNAPs within a bunch increase with the gene number, contrary to experiments on ribosomal genes in E. coli. (B) The cooperative recruitment of RNAP by DNA supercoiling is shown. RNAP molecules are loaded onto the promoter at a rate k_LOAD^LOW. After RNAP initiates transcription at a rate k_ESC, it leaves the promoter DNA in a supercoiled state, and subsequent loading of RNAP polymerases at the promoter happens at a faster rate, k_LOAD^HIGH. The rate of relaxation of the supercoiled state is k_RELAX. The change in gene-copy number affects both polymerase loading rates (red arrows) because of the change in free RNAP concentration. The model predicts that the mean and variance of the intrabunch RNAP distances increase with the gene-copy number, contrary to measurements in E. coli. (C) As the number of genes increases, the rate of rRNA production increases. This triggers the production of control molecules (e.g., ppGpp), which then reduce the initiation rate by modulating the promoter-RNAP interactions. ppGpp regulates the initiation process by converting the active promoter-RNAP complexes into inactive ones. It is described by the same kinetic scheme as the dead-end complex model (A) with a critical difference: in this case, it is the rate of inactivation of RNAP-promoter complex (k_ON) because of ppGpp binding to the complex that is tuned as the copy number of ribosomal genes is increased (red arrow), whereas the rate of RNAP loading onto the promoter is unchanged. The mean and variance of distances between RNAPs within a bunch are predicted to remain constant, as observed in experiments. In all the plots, the two data points shown are taken from (39). To see this figure in color, go online.

Estimate of error bars

In the published data plots that were digitized to obtain our Fig. 3 C, no error bars were given. To obtain estimates for error bars on the measured frequencies of interpolymerase distances for ribosomal genes in wild-type E. coli cells (Fig. 3 C), we consider the binomial counting error. Let i ∈1,…,I be the histogram bins that the measured distances fall in. The probability (frequency) of a distance measurement falling in bin i is p_i. This is just a binomial trial, i.e., the data point is either in the bin or not, and therefore the variance of the measured frequency for this bin is p_i (1−p_i)/N, where N is the total number of distance measurements. The error bars in Fig. 3 C are the standard deviations, i.e., square root of the variance, for each bin. Based on the total number of distance measurements reported, which is roughly 1000, the relative errors on the data points are around 10%.

Limitations of the EM data

Interpolymerase distances extracted from EM images of RNAP molecules transcribing a gene have known limitations. The possibility of RNAP molecules bound to the gene of interest being lost during preparation of samples for EM imaging cannot be ruled out (53). This does open up the possibility that the observed fluctuation in the interpolymerase distances is an artifact of the experiment. Furthermore, the resolution of the EM images is typically 1.8 nm/pixel, and therefore any distance less than 5 bps cannot be resolved (54).

Limitations of the modeling framework

A crucial assumption our model makes is that interpolymerase distances along a gene of interest are governed by the initiation dynamics and not the elongation dynamics. Although for the data set analyzed in this study, this assumption is valid (as outlined in the Discussion; also see the Supporting Material), one needs to be cautious when using this assumption for other genes. Ideally, any kind of analysis of interpolymerase distances should to be done on a gene-by-gene basis. However, because of the simplicity of our modeling framework, we believe it serves as a good starting point for analyzing interpolymerase distance distribution data. Deviations from the model predictions could point to other transcriptional processes such as elongation and termination.

Results

Distribution of initiation times for an arbitrary mechanism of transcription initiation can be computed from a master equation

Transcription initiation is typically regulated by transcription factors and cofactors that bind to the regulatory DNA sequences and either inhibit or aid the binding of RNAP molecules to the promoter. To connect mechanisms of transcription initiation with measured times between successive initiation events, we consider a stochastic model of transcription with a general initiation mechanism, in which the promoter can be in an arbitrary number of states defined by different constellations of bound transcription factors and cofactors. Using a chemical master equation approach (22, 55, 56), we show that the distribution of times between two initiation events and its moments can be computed analytically for any mechanism of transcription initiation. These equations allow us to discriminate between different mechanisms of initiation by comparing the predicted distributions to experimental distributions of transcription initiation times.

To compute the distribution of times between successive initiation events, we assume that the promoter can be in N different discrete biochemical states and that transitions between different states occur as different transcription factors bind and fall off their respective binding sites. The rate of transition from the m-th to the n-th promoter state is k_m,n, and the rate at which an RNAP molecule initiates transcription from the m-th promoter state is k_m,esc. The assumption that the transitions between these states are random Poisson processes characterized by rate constants leads to a chemical master equation that describes the time evolution of P_m(t), the probability that the promoter is in the m-th state (m = 1, 2,.., N) at time t:

$$\frac{d{P}_m}{dt}=\sum _{n=1}^N\left[k_{\text{n},\text{m}}{P}_n-k_{\text{m},\text{n}}{P}_m\right]-k_{m,esc}{P}_m.$$ (2)

Solving this chemical master equation for all the states m from which the promoter initiates transcription with rate k_m,esc, leads to a general formula for the probability distribution q₁(t) of the time intervals between successive transcription initiation events (details of the calculation can be found in the Supporting Material):

$$q_1\left(t\right)=\sum _{m=1}^N{k}_{m,esc}{P}_m\left(t\right).$$ (3)

Assuming a uniform elongation rate v (37, 57) along the gene, the distribution q₁(t) of time intervals between successive initiation events directly translates into a distribution of distances p₁(x) between RNAPs along the gene. In other words, the interpolymerase distance distribution along a gene is given by

$$p_1\left(x\right)=q_1\left(\frac{x}{v}\right)\frac{1}{v}.$$ (4)

In the ensuing investigation of regulation of ribosomal genes, Eq. 4 forms the basis of our analysis of positions of RNAP molecules along a gene at a given moment in time, which provides a quantitative test for different models of transcription initiation. Although transcription elongation of ribosomal genes is typically more complicated and involves pausing and backtracking of polymerases along the gene (58), here we assume that transcriptional pausing happens on timescales that are negligible compared to the times between transcription initiation events (59). For a detailed discussion of this model assumption, see the Supporting Material.

The distribution of transcription initiation times can be used to discern between different models of initiation

To illustrate how the distribution of times between successive initiation events can be used to extract mechanistic insights about the process of transcription initiation, we consider three different models of initiation as case studies (see Fig. 2).

Figure 2.

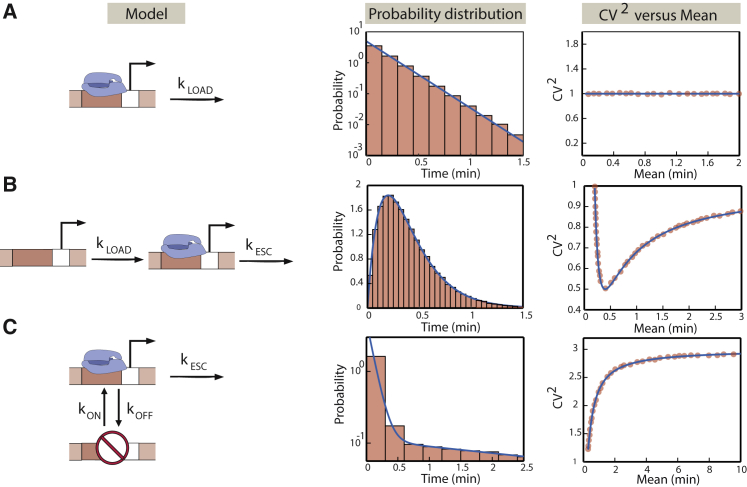
Different models of transcriptional regulation lead to distinct signatures in the initiation times. (A) The one-step model of transcription initiation is depicted. Initiation happens at a constant rate k_LOAD. The times between successive initiation events are exponentially distributed. The square of the coefficient of variation is plotted as a function of the mean, in which we change the mean by changing the rate of initiation, k_LOAD. We confirm the analytical results using Gillespie simulations (65). The histograms and closed circles represent simulation results. (B) The two-step model of transcription initiation is depicted. Initiation happens in two sequential steps: the rate of RNAP loading onto the promoter occurs with rate k_LOAD, followed by RNAP escaping the promoter, leading to transcript elongation at a rate k_ESC. The distribution of times between successive initiation events and the square of the coefficient of variation of the distribution as a function of the mean are shown. To change the mean, we change the rate of loading of RNAP polymerase molecules on the promoter, k_LOAD. As in (A), simulation results are compared to the analytical results. (C) The ON-OFF model is depicted. The promoter switches between two states: an active and an inactive one. The rate of switching from the active state to the inactive state is k_OFF and from the inactive to the active state is k_ON. From the active state, transcription initiation proceeds with a probability per unit time, k_ESC. The distribution of times between initiation events and the square of the coefficient of variation as a function of the mean are shown. Results from Gillespie simulations (65) are shown for comparison. To change the mean, we tune the rate k_ON of switching from the inactive to the active state. To illustrate the distinctive impact of the different initiation models on the distribution and moments of the times between successive initiation events, we use the following parameters: k_OFF = 5/min, k_ON = 0.435/min, k_LOAD= 0.14/min, and k_ESC= 0.14/min, which are characteristic of yeast promoters (36). To see this figure in color, go online.

Poisson (single rate-limiting step) model

The Poisson model is the null model of initiation, which is usually associated with constitutive promoters (12). In this model, initiation happens with a constant probability of k_LOAD per unit time, as shown in Fig. 2 A. In bacteria, this step could, at the molecular scale, represent the rate of loading of RNAP molecules to the promoter DNA, whereas for eukaryotes, this step could correspond to the formation of the preinitiation complex. As obtained from Eq. 3, the one-state model is characterized by exponentially distributed times between successive initiation events. One of the key properties of an exponential distribution is that its mean and standard deviation are equal. Therefore, the CV² (defined as the ratio of the variance to the square of the mean) is always equal to one, independent of the rate k_LOAD, as shown in Fig. 2 A.

Two-limiting-steps model

Next, we consider a model in which initiation happens in two sequential rate-limiting steps. This is the situation in which two steps in the sequence of events leading to initiation are of comparable duration. For example, in bacteria, the first step could correspond to an RNAP molecule binding to the promoter with a rate k_LOAD. In eukaryotes, this step could represent the loading of the transcriptional machinery at the promoter (23, 48). In the second step, the promoter-bound RNAP molecule escapes the promoter at a rate k_ESC and starts transcribing the gene. For several promoters in yeast (36) and E. coli (60), it has been reported that initiation proceeds through two sequential steps.

For this case, using Eq. 3, we find that the waiting-time distribution between successive initiation events is gamma distributed. This result agrees with previous theoretical studies (25) and leads to the following relationships between the kinetic rates associated with this mechanism (k_LOAD and k_ESC) and the mean and the coefficient of variation of the waiting-time distribution:

$$\begin{array}{c}Mean=\frac{k_{ESC}+k_{LOAD}}{k_{ESC}{k}_{LOAD}},\\ C{V}^2=\frac{k_{ESC}^2+k_{LOAD}^2}{{\left(k_{ESC}+k_{LOAD}\right)}^2}.\end{array}$$ (5)

As shown in Fig. 2 B, when we tune either one of the two rates of the model while keeping the other one constant, the coefficient of variation initially decreases as a function of the mean, develops a minimum when the two rates become equal, and then asymptotically goes to one. In the limit of one rate being much slower than the other one, the waiting-time distribution becomes exponential, leading to a coefficient of variation of one.

ON-OFF promoter

The third scenario we consider is the ON-OFF model of initiation. This model of initiation has been established as the canonical model of transcriptional regulation for both bacteria (19) and eukaryotes (17, 21, 61, 62, 63, 64). In this model, the promoter switches between two states: an active state from which transcription initiation can occur, and an inactive state from which initiation does not occur. The two states might correspond to a free promoter and one bound by a repressor protein, or a promoter covered by nucleosomes. The rate of switching from the active to the inactive state is k_OFF and from inactive to the active state is k_ON. The rate of initiation from the active state is k_ESC.

In this case, we find that the waiting-time distribution between successive initiation events is given by a sum of two exponentials, as shown in Fig. 2 C. Thus, it can be distinguished from a single exponential expected from the one-state promoter on the condition that the decay constants of the two exponentials are well-separated in magnitude. The mean and the coefficient of variation as functions of the different biochemical rates are given by

$$\begin{array}{l}Mean=\frac{k_{ON}+k_{OFF}}{k_{ON}{k}_{ESC}},\hfill \\ C{V}^2=1+\frac{2k_{OFF}{k}_{ESC}}{{\left(k_{ON}+k_{OFF}\right)}^2}.\hfill \end{array}$$ (6)

When we tune the rate k_ON, the CV² increases as a function of the mean and eventually saturates, as shown in Fig. 2 C.

We compare our analytical results for the three models described above against Gillespie simulations (65). This allows us to numerically generate multiple time traces of initiation events. From these different time traces, we obtain the distribution of initiation times as well as the corresponding values of the mean and variance. The histograms for the times between initiation events for all the three models are shown in Fig. 2, A–C. We also show the coefficient of variation as a function of the mean for these models as we tune the relevant rates in Fig. 2, A–C. These results imply that we can discern these three different models of initiation based on the predictions they make for the waiting-time distribution of consecutive initiation events as a function of the different experimentally tunable parameters.

The dynamics of transcription initiation of ribosomal genes in E. coli can be extracted from images of transcribing polymerases in fixed cells

To demonstrate how the distribution of interpolymerase distances along a gene can be used to extract dynamical information about the process of transcription initiation in vivo, we have reanalyzed data obtained from images of elongating RNAP molecules on rRNA genes in E. coli, which were obtained using the Miller spread technique by Voulgaris et al. (39). In Fig. 3 C, we reproduce the interpolymerase distance distribution for the seven ribosomal genes in wild-type E. coli cells (39). A remarkable feature of this distribution is the presence of a peak at small distances. This is inconsistent with a Poisson initiation mechanism (19) described above. Indeed, the presence of a maximum in the probability at intermediate distances suggests the two-limiting-steps model of initiation (Fig. 3 B), in which, for example, the polymerase first binds to the promoter and then escapes the promoter, leading to elongation, and in which the two steps occur with comparable rates. Recent in vivo studies in yeast have shown that initiation can proceed in multiple sequential steps, in which the rates involving these steps have comparable magnitude (36). In addition, when analyzing this data, we consider the time it takes for the polymerase to clear the promoter by elongating through it.

To test the hypothesis of two sequential steps leading to initiation, we fit Eq. 4 to the experimental distribution obtained from the images and assume an elongation speed of 78 bp/s (as measured elsewhere (39)). We find that the two-limiting-steps model is in good agreement with the data. Furthermore, the fit provides estimates for the rates of promoter escape, the rate of RNAP loading onto the promoter, and time to clear the promoter (k_LOAD ≈ 3/s, k_ESC ≈ 3/s, and τ_CLEAR ≈ 0.3 s), all of which are in good agreement with previous measurements (66) (see the Methods).

Bursting accompanies the downregulation of the transcription of rrn operons in the presence of additional copies of the rrn genes

In a second set of experiments, EM images were used to shed light on a previously reported effect (52), namely that the transcriptional activity of individual rrn genes is inversely proportional to the copy number of these genes in such a way that the net transcriptional output of rrn genes in the cell is kept constant. Surprisingly, the EM showed that when the copy number of ribosomal genes was altered by placing extra rrn genes on plasmids, a very different pattern of polymerase occupancy of the rrn genes emerged. Besides the mean number of RNAP molecules along each gene decreasing with increased gene-copy number, it was also observed that RNAP molecules were then grouped in bunches along the gene, which is indicative of transcriptional bursting. Moreover, it was observed that the mean and the variance of the interpolymerase distances within a bunch remained unchanged as the copy number varied (39). To explain the observed reduction in the mean number of RNAP molecules along each gene, Bremer et al. (67) focused on the fact that a significant fraction of RNAPs in the cell are engaged in transcribing the ribosomal genes. In that case, changing the gene-copy number will significantly alter the concentration of free polymerases available for transcription initiation. This will, in turn, decrease the rate of transcription initiation, which is assumed to be proportional to the free RNAP concentration. This “free RNAP hypothesis” (67), along with the two-step model of transcription initiation (Fig. 1 B), predicts that the mean number of RNAPs per gene will decrease in response to an increase in the number of genes, as observed experimentally, but it cannot account for the observed bunching of polymerases, as was shown in a previous theoretical study (25). Therefore, to account for the bunching of RNAPs seen in experiments by Voulgaris et al. (39), it is necessary to consider models of initiation with promoter states that are off-pathway to elongation. Indeed, several such models have been proposed to explain the downregulation of individual rrn genes in response to an increase in the gene-copy number (39). These models can be broadly classified into three different classes. Using our mathematical framework, we put to the test these different classes of models with the goal of gaining insight into the unresolved question of how the transcription of ribosomal genes is regulated in response to an increase in the gene-copy number.

The first proposed class of models considers the formation of long-lived, nonproductive initiation complexes at the promoter (68, 69, 70). For example, nonproductive complexes that cannot exit the abortive initiation state into productive elongation have been observed in vitro (25). The second class of models assumes cooperative recruitment of RNAP molecules to the promoter by an RNAP molecule already present on the promoter (71, 72, 73). For instance, when an RNAP molecule initiates transcription, it can leave the promoter DNA in a supercoiled state, as illustrated in Fig. 3 B. In the supercoiled state, the energy barrier for melting a strand of DNA to make a transcriptional bubble is lowered, leading to an increased rate of RNAP loading onto the promoter (25). Both these classes of models can lead to bunching of RNAP molecules on the gene, as observed in the experiments (39). However, a common feature of both classes of models is that they incorporate the “free RNAP” hypothesis, in that an increase in the number of rrn genes in the cells leads to a lower concentration of free RNAP and thus to a reduction in the rate of RNAP loading onto the promoter (red arrows in Fig. 4, A and B). Consequently, for both classes of models, the mean and variance of the intrapolymerase distance distribution within a bunch will increase as the rrn gene-copy number is increased, which is in contrast to the experimental observations as shown in Fig. 4, A and B. It must be noted that the interpolymerase distance distribution within a bunch is dictated by the biochemical rates k_ESC (rate of promoter escape), k_LOAD (rate of RNAP loading onto the promoter, which we denote as k_LOAD^HIGH in the supercoiling mediated recruitment model), and τ_clear (time for an RNAP to clear the promoter). Hence, any change in one of these rates would lead to a change in the interpolymerase distance distribution within a bunch, contrary to what is seen in experiments.

The third proposed class of regulatory models for the transcription of ribosomal genes considers a secondary molecular messenger, the abundance of which in the cell is regulated in response to the changing number of ribosomal genes. These molecules either inhibit or activate the transcription of rrn genes (Fig. 3 C) (74). One such model is based on the alarmone nucleotide molecule ppGpp, which is capable of inactivating the promoter-RNAP complex upon binding to the polymerase (74, 75). Formation of such inactive complexes can lead to bursty transcription initiation dynamics caused by the inactivated polymerase blocking the promoter. Another set of experiments has shown that the number of ppGpp molecules increases with increasing ribosomal gene-copy number (76). Consistent with these observations, we propose a kinetic model of transcriptional regulation of ribosomal genes in which RNAP-promoter complexes are inactivated by ppGpp molecules that increase in concentration as the rrn gene-copy number is increased (shown in Fig. 4 C). The key assumption of this class of models that distinguishes it from the first two is that an increase in the number of rrn genes does not significantly change the number of free RNAPs in the cell (74, 75).

The mean and variance of the interpolymerase distance distributions within a bunch for the secondary messenger mechanism are consistent with the experimental results. Because the key assumption of this model is that an increase in the number of genes does not significantly change the number of free RNAPs in the cell (74, 75), the rate of RNAP loading onto the promoter remains unchanged. This has the effect of keeping the distribution of distances between RNAPs within the bunch unchanged (Fig. 4 C). At the same time, the proposed mechanism generates the bursting kinetics that is observed in EM, suggesting that it may be a candidate mechanism for regulating the transcription of rrn genes. We note that any mechanism based on stochastically and transiently preventing promoter escape by a bound polymerase would have the same outcome. Although ppGpp-based mechanism is a plausible candidate, as this mode of its action has been documented before, whether it is in fact responsible for the changes in transcription initiation that accompany the increase in rrn gene-copy number is still an open question.

Discussion

The dynamics of transcription in live cells is poorly understood. Because of the difficulties in directly imaging the process of transcription (19, 47, 48, 50, 77), experimental methods for counting the products of transcription (such as RNA and protein molecules) in single cells have been developed over the past years. The protein and mRNA distributions carry the signature of the dynamics of transcription and hence can be exploited to decipher the underlying mechanisms of transcriptional regulation (12, 16, 47, 78). However, both mRNA and protein counts are affected by noisy processes other than transcription, such as mRNA processing, binomial partitioning, nonlinear degradation of mRNA molecules, etc (31, 33, 34, 79, 80, 81, 82), which can potentially mask the signature of transcription on protein and mRNA distributions.

EM images of RNAP molecules engaged in the process of transcribing a gene at a given instant in time (also known as “Miller spreads”) provide information about the position of polymerase molecules on the gene (39, 40, 41, 42, 43, 44). Similar information can be extracted by observing transcription initiation events in real time using fluorescent reporters (19, 20, 45, 46, 47, 48, 49). These measurements are not affected by posttranscriptional processes and are therefore more direct readouts of transcription compared to mRNA and protein counting (83). In this study, we have derived mathematical equations that allow us to interpret and analyze the interpolymerase distance distribution, or equivalently, the waiting-time distribution between successive initiation events across a population of isogenic cells. To demonstrate the potential utility of our analytical results, we fit the interpolymerase distance distribution for ribosomal genes in E. coli (acquired from EM) to a theoretical distribution computed for a two-step model of initiation. The model fits the data well, allowing us to extract the rates that characterize transcription initiation dynamics.

It must be noted that other mechanisms, like fluctuations in the promoter clearing time, could also generate a peaked distribution of interpolymerase distances in Fig. 3 C. A multistep initiation model, in which initiation happens in more than two sequential steps, could also account for a peaked interpolymerase distribution. Although we cannot rule out these and other possibilities, we make use of the two-step initiation model as a simple scenario that explains the data well and provides mechanistic insight into the dynamics of initiation that leads to experimentally testable predictions.

We also reanalyze data from images of RNAP transcribing ribosomal genes in wild-type and mutant strains of E. coli. We show that previously proposed mechanisms, based on the effect that extra rrn gene copies might have on the concentration of free RNAPs in the cell, are inconsistent with the observed interpolymerase distance distributions. In contrast, we find that an alternative possibility (74), in which the alarmone nucleotide ppGpp may interact with promoter-bound RNAP and prevent promoter escape, produces bursting transcription initiation kinetics that is consistent with experimental observations.

Our model assumes that interpolymerase distance distributions are governed by transcription initiation dynamics. However, stochastic transcription elongation dynamics can also impact interpolymerase distances. Depending on the timescales of the two processes, they will affect the distribution differently (see Supporting Material for details). If the initiation timescales are much longer than the elongation timescales, the distribution of RNAP distances will remain largely unaffected by the elongation dynamics, as in the case of most of the mRNA promoters in E. coli (36). Because the ribosomal genes are very highly transcribed, the initiation and elongation timescales become comparable, and hence the effect of elongation on the RNAP distance distributions can be significant (58). To better understand this interplay of the two, we use a model of initiation and elongation proposed by Klumpp et al. (58) that incorporates ubiquitous pauses on the elongating RNAPs. Using stochastic simulations (65, 84), we explore the effect of elongation dynamics on the interpolymerase distance distributions for ribosomal genes (for a detailed discussion, see the Supporting Material). We find that the interpolymerase distribution, for rate parameters that are pertinent to experiments on rrn genes (39), is solely a result of the transcription initiation dynamics, and that elongation has little impact on it.

We believe that the approach and ideas presented here will be helpful to uncovering detailed kinetic information about the process of transcription initiation in live cells.

Author Contributions

S.C., J.K., and A.S. designed and performed the research. S.C. analyzed data. S.C., J.K., and A.S. wrote the manuscript.

Editor: Anatoly Kolomeisky.