Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2018 Apr 11;7(5):1406–1412. doi: 10.1021/acssynbio.8b00016

An Automated Design Framework for Multicellular Recombinase Logic

Sarah Guiziou †, Federico Ulliana ‡, Violaine Moreau †, Michel Leclere ‡, Jerome Bonnet †,*
PMCID: PMC5962929  PMID: 29641183

Abstract

graphic file with name sb-2018-000169_0005.jpg

Tools to systematically reprogram cellular behavior are crucial to address pressing challenges in manufacturing, environment, or healthcare. Recombinases can very efficiently encode Boolean and history-dependent logic in many species, yet current designs are performed on a case-by-case basis, limiting their scalability and requiring time-consuming optimization. Here we present an automated workflow for designing recombinase logic devices executing Boolean functions. Our theoretical framework uses a reduced library of computational devices distributed into different cellular subpopulations, which are then composed in various manners to implement all desired logic functions at the multicellular level. Our design platform called CALIN (Composable Asynchronous Logic using Integrase Networks) is broadly accessible via a web server, taking truth tables as inputs and providing corresponding DNA designs and sequences as outputs (available at http://synbio.cbs.cnrs.fr/calin). We anticipate that this automated design workflow will streamline the implementation of Boolean functions in many organisms and for various applications.

Keywords: synthetic biology, biological computing, recombinases, logic gates, automated genetic design, distributed multicellular computing

Reprogramming the response of living cells to chemical or physical signals is a key goal of synthetic biology and would support the development of complex manufacturing processes, sophisticated diagnostics, or cellular therapies.1 In order to control cellular behavior, researchers have engineered many types of Boolean logic gates operating in single cells by using transcriptional regulators,2−8 RNA molecules,9−11 or site-specific recombinases.12−14 However, scaling-up single-cell logic systems requires solving multiple engineering challenges. First, when program complexity increases (number of inputs ≥3), the high number of parts needed can cause metabolic burden and affect cellular viability. Second, current design methods are mostly ad-hoc, and each Boolean function is implemented using a different genetic architecture that needs to be fully characterized and optimized. Despite recent progress toward predictable gate design,7 some gates simply do not work or are too complex to be implemented within a single cell. Finally, in order to avoid cross-talk, single-cell logic systems need to use different components for every novel signal to be detected. While library of orthogonal regulatory components have greatly expanded,3,6,15,16 their deployment can be challenging and requires time-consuming optimization.

In nature, division of labor between cellular subpopulations is a ubiquitous mechanism allowing cellular communities to accomplish complex functions.17,18 Early efforts to engineer synthetic multicellular systems led to the construction of pattern-forming communities,19 predator–prey ecosystems,20 synchronized oscillators,21,22 or distributed metabolic pathways.23 Researchers also realized that problems faced by logic circuits operating in single cells could be addressed by distributing the logic program between different cells.24 Because of the spatial separation allowed by cellular compartments, optimized regulatory components can be reused in different subpopulations. As the circuit is divided into smaller subcircuits, metabolic burden is reduced. Finally, simple cellular computing modules can be composed in different manners and wired via cell–cell communication channels to obtain different logic functions. For example, Tamsir et al. used multilayered circuit designs inspired from electronics to construct all 2-input logic gates by combining spatially separated E. coli colonies encoding NOR gates wired via quorum-sensing molecules.25 Specific features of biology can also be used to our advantage to engineer logic systems in a more efficient manner than by strictly transposing electronic designs.12,24,26 One particularly promising approach is distributed multicellular computation (DMC).24,27−29 DMC is based on the decomposition of a Boolean function into various subfunctions, each performed by a particular subpopulation of cells. Different subpopulations can then be combined in different manners to realize any given Boolean function of interest. Importantly, multiple cells are capable of producing the output which is therefore distributed among the cellular subpopulations. Recently, Macia and colleagues implemented DMC within a multicellular consortium by using cellular computing units performing elementary IDENTITY or NOT operations.30 While highly scalable, the need for spatial separation between each subpopulation prevents these systems from operating autonomously.

Here we present a composable framework enabling the systematic design of logic gates performing Boolean logic within an autonomous multicellular consortium.

We designed our system to operate using site-specific recombinases, more specifically serine integrases, which allow robust and flexible engineering of complex logic gates.12,13 Serine integrases are members of the large serine recombinase family31 and catalyze site-specific recombination between attachment sites attB and attP. Recombination operates via double-strand breaks located at the central dinucleotides followed by the generation of hybrid sites attL and attR. Depending on the relative orientation of attB and attP, the recombination reaction leads to excision (parallel orientation) or inversion (antiparallel orientation) of the DNA sequence flanked by the attachment sites.32 Recombinase devices can implement complex logic functions without the need of cascading multiple logic gates like in electronics.12,13,26 Integrase recombination is irreversible in the absence of cofactors, so that recombinase logic gates exhibit memory, are single use (one-shot), and therefore belong to the family of asynchronous logic devices (i.e., the system can respond to multiple signals even if they are not present simultaneously).

Our design for Boolean logic is based on a reduced library of cellular computing units responding to one or multiple inputs that can be composed at will to implement all desired Boolean functions (Figure 1). Our logic system is single layer, does not require cell–cell communication nor spatial separation, greatly facilitating its implementation. In order to make our design framework broadly accessible, we provide a fully automated web platform called CALIN (Composable Asynchronous Logic using Integrase Networks) taking truth tables as inputs and providing corresponding DNA designs and sequences as outputs.

Figure 1.

Figure 1

Open in a new tab

Distribution of a Boolean function within a multicellular consortium. The Boolean function of interest is decomposed as a disjunction (i.e., sum) of subfunctions (or clauses). Here, as an example, a given function, f, is decomposed into functions f1, f2, and f3. The strains performing f1, f2 and f3 are selected from the strain library to assemble a multicellular consortium computing the desired Boolean function.

Results

A Hierarchical Composition Framework for Multicellular Boolean Logic Using Integrase Switches

In order to implement a Boolean function within a multicellular consortium, we decomposed the function into several independent subfunctions, or clauses,30 executed by a different cellular subpopulation, chosen from a library containing a reduced number of cellular computing units (Figure 1). To facilitate multicellular system composition, we designed our system so that each cellular subpopulation computes independently of the others, without cell–cell communication needed. As a consequence, if one cellular subpopulation is ON (expression of the output gene), the global output of the system is considered to be ON. Because of their reduced number and of the absence of cell–cell communication, cellular computing units can be extensively characterized and optimized to predictably implement all Boolean functions at the multicellular level.

Boolean functions encode the output state of the logic gate. The variables of the function are the inputs of the gate which are equal to 1 if the signal has been present and otherwise to 0. We express Boolean functions using the disjunctive normal form.33

The Boolean function f is a disjunction: f = β1 OR...OR βM, where M is the number of clauses present in f, and each βi is a conjunctive clause: βi = θi,1 AND...AND θi,ni, where each θi,j is a literal of the variable xj (either the identity of the variable or its negation), with j being an integer between 1 and ni. ni corresponds to the number of variables in this conjunction (an integer between 1 and N). N is the number of variables in the function f.

Each cellular computing unit executes a particular “subfunction” corresponding to a conjunctive clause. Then, the full function is performed by combining multiple cellular computing units (Figure 2A).

Figure 2.

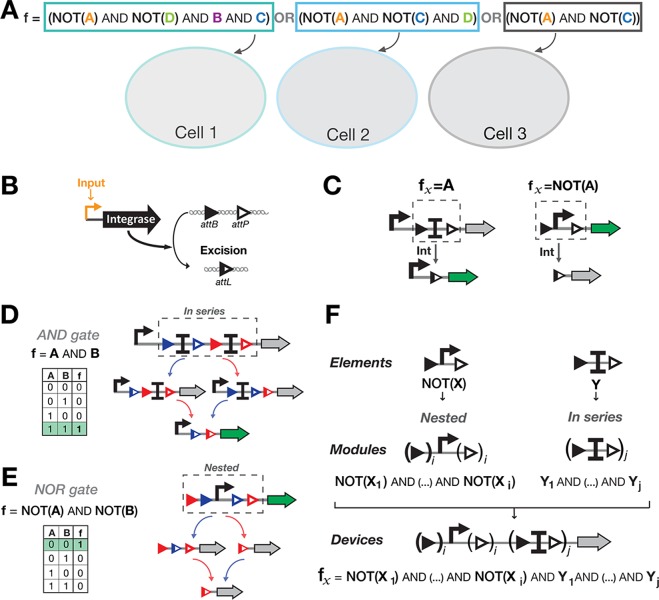
Figure 2

Open in a new tab

A hierarchical composition framework for asynchronous Boolean recombinase logic. (A) Distribution of a Boolean function within a multicellular consortium by decomposition into conjunctions of literals (variables or their negations). Here an example is depicted in which a Boolean function is decomposed into three subfunctions and implemented in three separate cellular computing units. (B) attB and attP disposed in parallel orientation. (C) Elements implementing IDENTITY and NOT functions. To obtain an IDENTITY function, a transcriptional terminator is flanked by parallel attachment sites, blocking transcription of the gene of interest. When the signal is present, the terminator is excised and the output gene is expressed. To obtain a NOT function, a promoter is flanked by parallel attachment sites. When the signal is present, the promoter is excised, and the gene is no longer expressed. (D) Functional composition of ID-elements into ID-modules, by placing elements in series to obtain the conjunction of IDENTITY functions. For a 2-input ID-module, the output gene is expressed only when both inputs have been present, both terminators excised (corresponding to an AND gate (A AND B)). (E) Functional composition of NOT-elements into NOT-modules, by nesting elements to obtain conjunction of NOT functions. For a 2-input NOT-module, the output gene is expressed only when none of the inputs has been present (corresponding to a NOR gate: NOT(A) AND NOT(B)). (F) Hierarchical composition framework for Boolean recombinase logic. ID- and NOT-modules are composed in series, following a priority rule in which the NOT-module is placed upstream the ID-module. The device shown here can be scaled to perform all functions based on conjunction of NOT and IDENTITY functions.

We designed a hierarchical composition framework in which two elements encoding the NOT and IDENTITY functions (called ID-element and NOT-element) are composed into computational modules which are then combined to generate computational devices executing a particular clause within a cellular subpopulation.

For the sake of simplicity and robustness, we designed switches controlled by integrase-mediated excision (Figure 2B). Excision-based design reduces the distance between gate promoter and the gene of interest. Moreover, as no asymmetric terminator is needed, this design might be easier to deploy into many organisms.14

The ID-element consists of a transcriptional terminator flanked by recombination sites and placed between the promoter and the output gene. In presence of the signal, the terminator is excised and the output gene is expressed (Figure 2C, left panel). The NOT-element consists of a promoter driving the output gene and flanked by recombination sites. In presence of the signal, the promoter is excised and the gene is not expressed anymore (Figure 2C, right panel). Computational modules performing conjunctions of NOT or conjunctions of IDENTITY functions are respectively realized by nesting NOT-elements or by placing ID-elements in series (Figure 2D,E). Finally, NOT- and ID-modules are composed in series to obtain the final computational devices: in this case the NOT-module containing the promoter is positioned in 5′ of the ID-module, with the output gene positioned downstream (Figure 2F). Following this hierarchical composition framework, all conjunctive clauses are implementable within a cellular computing unit. The full Boolean function is then executed by a multicellular consortium containing different cellular computing units.

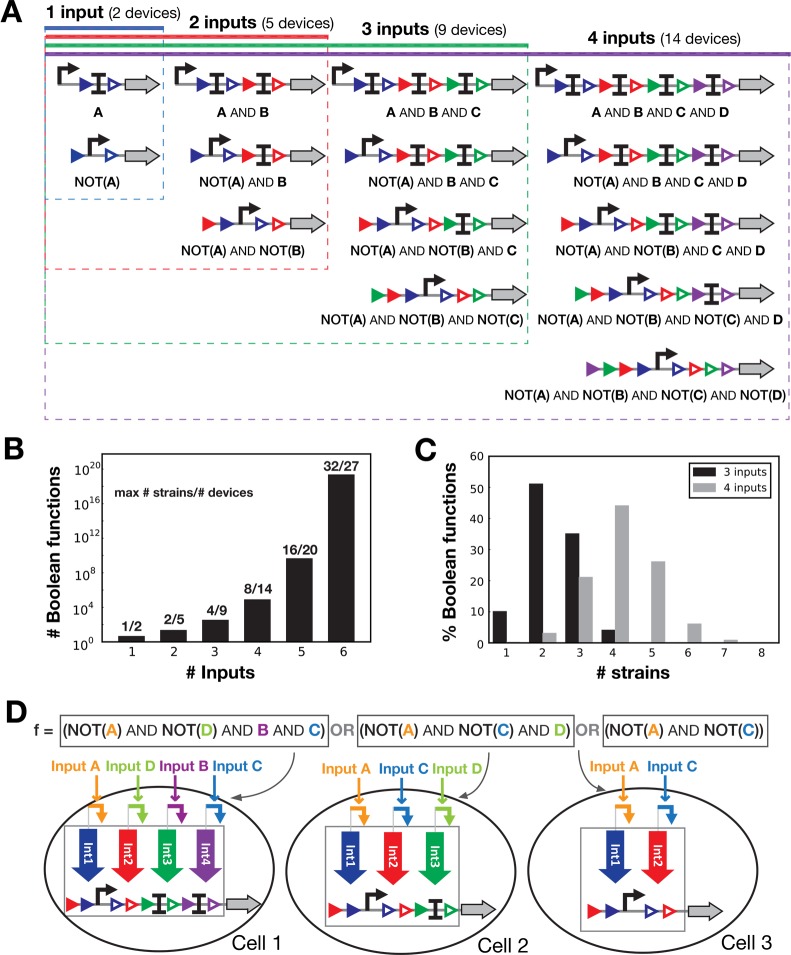
To reduce the number of computational devices, we implemented only one computational device per set of symmetric Boolean functions and interchanged connection between integrases and control signals. For example, the two Boolean functions: NOT(A) AND B; B AND NOT(A) are executed using the same computational device (Figure S1). Consequently, only 14 computational devices are needed to realize all 4-input Boolean functions (65 536 functions) (Figure 3A). For every additional input (from N – 1 to N), only N + 1 novel computational devices are needed while the number of Boolean functions increases drastically. For example, 7 additional devices are needed to transition from 5 to 6 inputs (27 devices in total), enabling a 1010 fold increase in the number of Boolean functions (for a total of ∼1019) (Figure 3B). Of note, the different cellular computing units do not always include N integrases and computational devices responding to N inputs. As an example, the 4-input Boolean equation shown in Figure 3D can be executed using 3 strains containing respectively 4, 3, and 2 integrases and with different signal-integrase connectivities.

Figure 3.

Figure 3

Open in a new tab

Implementing all Boolean logic functions using a reduced number of computational devices. (A) Schematics of all devices needed to implement up to 4-input functions. (B) Maximum number of strains and number of computational devices needed to compute all Boolean functions for a given number of inputs. See Methods for details. (C) Proportion of Boolean functions implementable with a specific number of strains for 3 and 4 inputs (obtained by generating all the biological designs for 3 and 4-input Boolean functions, see Table S1 for numbers). (D) Example of a biological implementation for a 4-input Boolean function. The function shown here is divided into a disjunction of conjunctive clauses (see Figure 2A). Each conjunctive clause is executed using a particular computational device (defined in panel A) each placed into a separate cellular computing unit. By combining the different units, the full logic function is obtained. If at least one of the cellular units is ON, the output is considered to be ON. Of note, inputs are not always connected to the same integrase (as for input D in Cell 1 and Cell 2), and all integrases and inputs are not present in all cells.

To implement a N-input Boolean function, a maximum of 2N–1 different cellular computing units have to be composed, corresponding to a culture of 2N–1 different strains: 4 for 3 inputs and 8 for 4 inputs (Figure 3B). However, most logic functions can be performed using less cellular computing units (an average of 2.3 strains for 3-input and 3.6 strains for 4-input Boolean functions, Figure 3C).

In summary, we provide a hierarchical composition framework using a reduced library of computational devices to systematically implement all N-input Boolean logic functions within a multicellular consortium.

An Automated Design Platform for Recombinase Logic

We then aimed at generating a software for automating the design of cellular consortia performing asynchronous Boolean logic. Softwares enabling such automated genetic circuit design are necessary and extremely useful when the design space becomes too large for humans to explore it efficiently.7,34−36

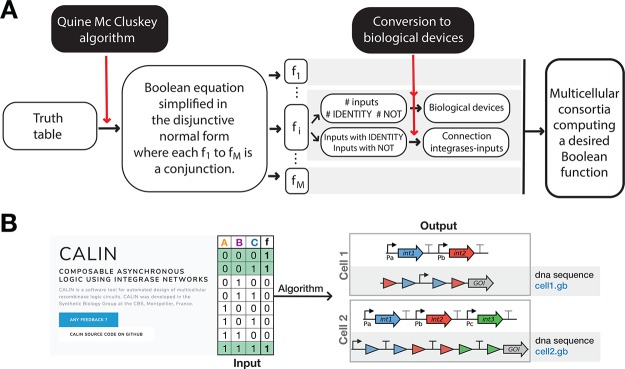
We thus designed an algorithm called CALIN (Composable Asynchronous Logic using Integrase Networks) based on two main steps (Figure 4A). First, the Boolean function of interest is decomposed into a disjunction of conjunctive clauses using the Quine–McCluskey algorithm (see Methods). Then, each clause is converted into a given computational device for which particular connections between integrases and inputs are generated.

Figure 4.

Figure 4

Open in a new tab

Automated design of multicellular recombinase logic. (A) The CALIN algorithm enables the systematic design of Asynchronous Boolean logic. (B) CALIN web-interface takes as an entry a Boolean truth table and generates as outputs: the connection map between inputs and integrases, the DNA architectures of the computational devices and the corresponding DNA sequences.

The CALIN script written in Python is available on Github and can be directly used for high-throughput generation of biological designs. Furthermore, the CALIN python script can design logic devices customized for specific organisms (E. coli, B. subtilis and S. cerevisiae) and can be tailored by the user to generate devices using fully customized DNA sequences.

In order to enable broader access to our design framework, we also provide a Web site of CALIN accessible at http://synbio.cbs.cnrs.fr/calin.

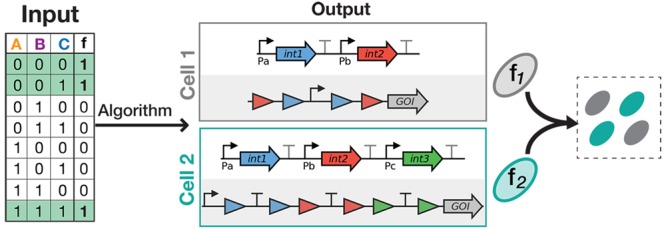
In the CALIN web-interface, the user fills the number of inputs to process (up to 5) and the desired Boolean truth table or corresponding binary number. The Web site provides as outputs the DNA architectures of the computational devices, the connection map between signals and integrases, and the corresponding DNA sequences (Figure 4B).

Discussion

In this work we present a scalable composition framework for implementing asynchronous Boolean logic within a multicellular consortium. We provide an online design tool for the systematic design of recombinase logic circuits called CALIN (Composable Asynchronous Logic using Integrase Networks). While these designs are currently theoretical, the robustness of integrase-mediated recombination against various site permutations and orientations12,13,34,37 should support straightforward experimental implementation.

By taking advantage of the single-layer architecture of recombinase logic, we encapsulated complex Boolean functions into various subcellular populations. Because of its compact architecture, our design exhibit two significant improvements over previous DMC systems: (i) no cell–cell communication channels are needed, and (ii) cells do not need to be spatially separated, thereby supporting the implementation of fully autonomous multicellular consortia operating without an external physical device.

Another difference between our system and other DMC is the use of recombinase switches that provide memory.34,38,39 Recombinase mediated data-storage could be useful for applications requiring endpoint measurements, or delayed readout, like diagnostics. Also, because the state of the logic system is written within DNA, it can be addressed via PCR or DNA sequencing,13,38,40 even if the cells die, providing other robust readout modalities.

As with others DMC systems, for a given number of inputs, the number of elementary computational devices needed to compose all logic functions compares very favorably with the number of possible functions. For example, implementing all 65 536 4-input, or all ∼4.3 × 109 5-input Boolean functions only requires respectively 14 and 20 computational modules.

As serine recombinases do not require host-specific cofactors and can operate in several species, the designs presented here could be implemented in many organisms. Logicfunctions could also be distributed between different species operating in concert. In such schemes, researchers could take advantage of the particular capacities of different organisms to detect different signals and/or perform specific tasks. Examples of applications include environmental remediation41,42 or microbiome engineering for therapeutic applications.43

A possible challenge for our system is the high number of strains that have to operate together when the number of inputs increases (Figure 3B). Cultivating many strains together could lead to counter selection of some subpopulations, but this problem could be addressed by encapsulating the different strains into hydrogel beads.40 Also, as the number of strains increases, the output of one subpopulation representing a small fraction of the whole consortia could become difficult to measure. The output level in the ON state will also be different if one or multiple cellular subpopulations are turned ON. However, adding a single cell–cell communication channel could address this problem by propagating the output to the whole-population (Figure S2).

Finally, for some applications, “real-time” response could be achieved via a similar composition framework using synchronous recombinase logic gates based on reversible recombination reactions performed by integrases coupled with recombination directionality factors (RDFs) (Figure S3).12,26

Methods

Equations for Determining of Numbers of Functions/Strains/Devices

The number of Boolean functions corresponds to 2 to the power of the number of possible states. As each state can be equal to 1 or to 0, the number of possible states is equal to 2 to the power of N where N is the number of inputs. Consequently, the number of Boolean functions is equal to eq 1.

graphic file with name sb-2018-000169_m001.jpg 1

The maximum number of strains needed to implement any Boolean logic function with N inputs is equal to eq 2, as all N-input Boolean equations can be written in the disjunctive normal form, then as a disjunction of a maximum of 2N–1 conjunctive clauses.33

graphic file with name sb-2018-000169_m002.jpg 2

The number of different conjunctive clauses (corresponding to a conjunction of literals) is equal to eq 3.

graphic file with name sb-2018-000169_m003.jpg 3

If we implement all these functions within cells, the number of standard devices needed is equal to the number of conjunctive clauses (eq 4).

graphic file with name sb-2018-000169_m004.jpg 4

This method leads to a high number of devices. Therefore, we decided to construct only one device per set of symmetric Boolean functions (e.g., A AND NOT(B) is the symmetric function of NOT(A) AND B). This approach reduces the number of standard devices. In consequence, for an N-input Boolean function, devices computing from 1 to N inputs are needed and k + 1 nonsymmetric Boolean functions computing the conjunction of k literals exist:

graphic file with name sb-2018-000169_m005.jpg 5

Of note, the number of devices follows the arithmetic series: 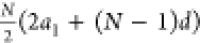Inline graphic where a1 = 2, d = 1, and N is the number of inputs.

In a first approximation, N sensor-modules in which a control signal (i.e., a sensor device responding to an input of interest) is connected to an integrase are needed for the construction of an N-input system. However, as we reduced the number of devices to a set composed of nonsymmetric Boolean functions, we need to connect all control signals to all integrases to compute all Boolean functions. Therefore, N2 sensor-modules are needed.

Automated Generation of Genetic Designs

We encoded an algorithm generating genetic designs executing N-input Boolean functions using Python (Figure S4). The algorithm takes as input a Boolean truth table or the binary number corresponding to the function. The output corresponds to the biological implementation of the Boolean function, such as for each strain: a graphical representation of the genetic circuit and its associated DNA sequences.

The truth table is transformed into a Boolean function in the disjunctive normal form using the Quine–McCluskey algorithm33 (Figure 4A). The Boolean function is decomposed into conjunctive clauses (conjunction of literals). In this scheme, each clause can be regarded as a “subfunction”. From each conjunctive clause, we extract two types of information. First, based on the number of IDENTITY and NOT functions, we identify which logic device is needed. Second, based on the association of inputs to either IDENTITY and NOT functions, we identify which sensor-modules are needed among the different connection possibilities between control signals and integrases. Finally, we combine the designs executing the different conjunctive clauses to obtain the global design for implementing the desired truth table.

To simplify the construction process, the DNA sequence of the computational devices is generated by our Python code. In CALIN, sequences are adapted for E. coli, but sequence generation can be adapted to other organisms (database available for B. subtilis and Saccharomyces cerevisiae) or customized using the source Python code available on github.

Acknowledgments

We thank L. Ciandrini, G. Cambray, G. Labesse, members of the synthetic biology group and of the CBS, P. Lemaire and P. Hersen for fruitful discussions, J. L. Pons and L. Bonnet for help with the CALIN website. Support was provided by an ERC Starting Grant “COMPUCELL”, the CNRS/INSERM Atip-Avenir program and the Bettencourt-Schueller Foundation to J.B. S.G. was supported by Ph.D. fellowships from the French Ministry of Research and from the FRM: Fondation pour la Recherche Medicale (FDT20170437282). The CBS acknowledges support from the French Infrastructure for Integrated Structural Biology (FRISBI) ANR-10-INSB-05-01.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acssynbio.8b00016.

  • Figures S1–S3; Table S1 (PDF)

The authors declare no competing financial interest.

Notes

The CALIN Web server can be found at http://synbio.cbs.cnrs.fr/calin. CALIN source code is available at https://github.com/sguiz/calin.

Supplementary Material

sb8b00016_si_001.pdf (3.1MB, pdf)

References

  1. Endy D. (2005) Foundations for engineering biology. Nature 438, 449–453. 10.1038/nature04342. [DOI] [PubMed] [Google Scholar]
  2. Fischer C.; Fussenegger M. (2004) BioLogic gates enable logical transcription control in mammalian cells. Biotechnol. Bioeng. 87, 478. 10.1002/bit.20142. [DOI] [PubMed] [Google Scholar]
  3. Stanton B. C.; Nielsen A. A. K.; Tamsir A.; Clancy K.; Peterson T.; Voigt C. A. (2014) Genomic mining of prokaryotic repressors for orthogonal logic gates. Nat. Chem. Biol. 10, 99–105. 10.1038/nchembio.1411. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Anderson J. C.; Voigt C. A.; Arkin A. P. (2007) Environmental signal integration by a modular AND gate. Mol. Syst. Biol. 10.1038/msb4100173. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Wang B.; Kitney R. I.; Joly N.; Buck M. (2011) Engineering modular and orthogonal genetic logic gates for robust digital-like synthetic biology. Nat. Commun. 2, 508. 10.1038/ncomms1516. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Moon T. S.; Lou C.; Tamsir A.; Stanton B. C.; Voigt C. A. (2012) Genetic programs constructed from layered logic gates in single cells. Nature 491, 249–253. 10.1038/nature11516. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Nielsen A. A. K.; Der B. S.; Shin J.; Vaidyanathan P.; Paralanov V.; Strychalski E. A.; Ross D.; Densmore D.; Voigt C. A. (2016) Genetic circuit design automation. Science 352, aac7341. 10.1126/science.aac7341. [DOI] [PubMed] [Google Scholar]
  8. Ausländer S.; Ausländer D.; Müller M.; Wieland M.; Fussenegger M. (2012) Programmable single-cell mammalian biocomputers. Nature 487, 123–127. 10.1038/nature11149. [DOI] [PubMed] [Google Scholar]
  9. Rinaudo K.; Bleris L.; Maddamsetti R.; Subramanian S.; Weiss R.; Benenson Y. (2007) A universal RNAi-based logic evaluator that operates in mammalian cells. Nat. Biotechnol. 25, 795–801. 10.1038/nbt1307. [DOI] [PubMed] [Google Scholar]
  10. Win M. N.; Smolke C. D. (2008) Higher-Order Cellular Information Processing with Synthetic RNA Devices. Science 322, 456–460. 10.1126/science.1160311. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Lucks J. B.; Qi L.; Mutalik V. K.; Wang D.; Arkin A. P. (2011) Versatile RNA-sensing transcriptional regulators for engineering genetic networks. Proc. Natl. Acad. Sci. U. S. A. 108, 8617–8622. 10.1073/pnas.1015741108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Bonnet J.; Yin P.; Ortiz M. E.; Subsoontorn P.; Endy D. (2013) Amplifying genetic logic gates. Science 340, 599–603. 10.1126/science.1232758. [DOI] [PubMed] [Google Scholar]
  13. Siuti P.; Yazbek J.; Lu T. K. (2013) Synthetic circuits integrating logic and memory in living cells. Nat. Biotechnol. 31, 448–452. 10.1038/nbt.2510. [DOI] [PubMed] [Google Scholar]
  14. Weinberg B. H.; Pham N. T. H.; Caraballo L. D.; Lozanoski T.; Engel A.; Bhatia S.; Wong W. W. (2017) Large-scale design of robust genetic circuits with multiple inputs and outputs for mammalian cells. Nat. Biotechnol. 35, 453–462. 10.1038/nbt.3805. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Rhodius V. A.; Segall-Shapiro T. H.; Sharon B. D.; Ghodasara A.; Orlova E.; Tabakh H.; Burkhardt D. H.; Clancy K.; Peterson T. C.; Gross C. A.; Voigt C. A. (2013) Design of orthogonal genetic switches based on a crosstalk map of σs, anti-σs, and promoters. Mol. Syst. Biol. 9, 702. 10.1038/msb.2013.58. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Yang L.; Nielsen A. A. K.; Fernandez-Rodriguez J.; McClune C. J.; Laub M. T.; Lu T. K.; Voigt C. A. (2014) Permanent genetic memory with > 1-byte capacity. Nat. Methods 11, 1261–1266. 10.1038/nmeth.3147. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Hays S. G.; Patrick W. G.; Ziesack M.; Oxman N.; Silver P. A. (2015) Better together: engineering and application of microbial symbioses. Curr. Opin. Biotechnol. 36, 40–49. 10.1016/j.copbio.2015.08.008. [DOI] [PubMed] [Google Scholar]
  18. Wintermute E. H.; Silver P. A. (2010) Dynamics in the mixed microbial concourse. Genes Dev. 24, 2603–2614. 10.1101/gad.1985210. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Basu S.; Gerchman Y.; Collins C. H.; Arnold F. H.; Weiss R. (2005) A synthetic multicellular system for programmed pattern formation. Nature 434, 1130–1134. 10.1038/nature03461. [DOI] [PubMed] [Google Scholar]
  20. Balagaddé F. K.; Song H.; Ozaki J.; Collins C. H.; Barnet M.; Arnold F. H.; Quake S. R.; You L. (2008) A synthetic Escherichia coli predator-prey ecosystem. Mol. Syst. Biol. 4, 187. 10.1038/msb.2008.24. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Danino T.; Mondragón-Palomino O.; Tsimring L.; Hasty J. (2010) A synchronized quorum of genetic clocks. Nature 463, 326–330. 10.1038/nature08753. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Prindle A.; Samayoa P.; Razinkov I.; Danino T.; Tsimring L. S.; Hasty J. (2012) A sensing array of radically coupled genetic ’biopixels’. Nature 481, 39–44. 10.1038/nature10722. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Shong J.; Jimenez Diaz M. R.; Collins C. H. (2012) Towards synthetic microbial consortia for bioprocessing. Curr. Opin. Biotechnol. 23, 798–802. 10.1016/j.copbio.2012.02.001. [DOI] [PubMed] [Google Scholar]
  24. Macía J.; Posas F.; Solé R. V. (2012) Distributed computation: the new wave of synthetic biology devices. Trends Biotechnol. 30, 342–349. 10.1016/j.tibtech.2012.03.006. [DOI] [PubMed] [Google Scholar]
  25. Tamsir A.; Tabor J. J.; Voigt C. a. (2011) Robust multicellular computing using genetically encoded NOR gates and chemical ’wires’. Nature 469, 212–215. 10.1038/nature09565. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Subsoontorn P. (2014) Reliable Functional Composition of a Recombinase Device Family, Ph.D. thesis, https://purl.stanford.edu/sm186rb9123.
  27. Regot S.; Macía J.; Conde N.; Furukawa K.; Kjellén J.; Peeters T.; Hohmann S.; de Nadal E.; Posas F.; Solé R. (2011) Distributed biological computation with multicellular engineered networks. Nature 469, 207–211. 10.1038/nature09679. [DOI] [PubMed] [Google Scholar]
  28. Macia J.; Sole R. (2014) How to make a synthetic multicellular computer. PLoS One 9, e81248. 10.1371/journal.pone.0081248. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Goñi-Moreno A.; Amos M.; de la Cruz F. (2013) Multicellular Computing Using Conjugation for Wiring. PLoS One 8, e65986. 10.1371/journal.pone.0065986. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Macia J.; Manzoni R.; Conde N.; Urrios A.; de Nadal E.; Solé R.; Posas F. (2016) Implementation of Complex Biological Logic Circuits Using Spatially Distributed Multicellular Consortia. PLoS Comput. Biol. 12, e1004685. 10.1371/journal.pcbi.1004685. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Groth A. C.; Calos M. P. (2004) Phage integrases: biology and applications. J. Mol. Biol. 335, 667–678. 10.1016/j.jmb.2003.09.082. [DOI] [PubMed] [Google Scholar]
  32. Grindley N. D. F.; Whiteson K. L.; Rice P. A. (2006) Mechanisms of site-specific recombination. Annu. Rev. Biochem. 75, 567–605. 10.1146/annurev.biochem.73.011303.073908. [DOI] [PubMed] [Google Scholar]
  33. Enderton H., and Enderton H. B. (2001) A Mathematical Introduction to Logic, Academic Press. [Google Scholar]
  34. Roquet N.; Soleimany A. P.; Ferris A. C.; Aaronson S.; Lu T. K. (2016) Synthetic recombinase-based state machines in living cells. Science 353, aad8559. 10.1126/science.aad8559. [DOI] [PubMed] [Google Scholar]
  35. Marchisio M. A.; Stelling J. (2011) Automatic design of digital synthetic gene circuits. PLoS Comput. Biol. 7, e1001083. 10.1371/journal.pcbi.1001083. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Otero-Muras I.; Henriques D.; Banga J. R. (2016) SYNBADm: a tool for optimization-based automated design of synthetic gene circuits. Bioinformatics 32, 3360–3362. 10.1093/bioinformatics/btw415. [DOI] [PubMed] [Google Scholar]
  37. Rubens J. R.; Selvaggio G.; Lu T. K. (2016) Synthetic mixed-signal computation in living cells. Nat. Commun. 7, 11658. 10.1038/ncomms11658. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Ham T. S.; Lee S. K.; Keasling J. D.; Arkin A. P. (2008) Design and Construction of a Double Inversion Recombination Switch for Heritable Sequential Genetic Memory. PLoS One 3, e2815. 10.1371/journal.pone.0002815. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Hsiao V.; Hori Y.; Rothemund P. W.; Murray R. M. (2016) A population-based temporal logic gate for timing and recording chemical events. Mol. Syst. Biol. 12, 869. 10.15252/msb.20156663. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Courbet A.; Endy D.; Renard E.; Molina F.; Bonnet J. (2015) Detection of pathological biomarkers in human clinical samples via amplifying genetic switches and logic gates. Sci. Transl. Med. 7, 289ra83. 10.1126/scitranslmed.aaa3601. [DOI] [PubMed] [Google Scholar]
  41. Li L.; Yang C.; Lan W.; Xie S.; Qiao C.; Liu J. (2008) Removal of methyl parathion from artificial off-gas using a bioreactor containing a constructed microbial consortium. Environ. Sci. Technol. 42, 2136–2141. 10.1021/es702631x. [DOI] [PubMed] [Google Scholar]
  42. De Lorenzo V. (2008) Systems biology approaches to bioremediation. Curr. Opin. Biotechnol. 19, 579–589. 10.1016/j.copbio.2008.10.004. [DOI] [PubMed] [Google Scholar]
  43. Mimee M.; Citorik R. J.; Lu T. K. (2016) Microbiome therapeutics - Advances and challenges. Adv. Drug Delivery Rev. 105, 44–54. 10.1016/j.addr.2016.04.032. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

sb8b00016_si_001.pdf (3.1MB, pdf)

Articles from ACS Synthetic Biology are provided here courtesy of American Chemical Society

RESOURCES