Shell feature: a new radiomics descriptor for predicting distant failure after radiotherapy in non-small cell lung cancer and cervix cancer

Abstract

Distant failure is the main cause for human cancer-related mortalities. To develop a model for predicting distant failure in non-small cell lung cancer (NSCLC) and cervix caner (CC) patients, a shell feature, consisting of outer voxels around the tumor boundary, was constructed using pre-treatment positron emission tomography (PET) images from 48 NSCLC patients received stereotactic body radiation therapy (SBRT) and 52 CC patients underwent external beam radiation therapy and concurrent chemotherapy followed with high-dose-rate intracavitary brachytherapy. The hypothesis behind this feature is that non-invasive and invasive tumors may have different morphologic patterns in the tumor periphery, in turn reflecting the differences in radiological presentations in the PET images. The utility of the shell was evaluated by the support vector machine (SVM) classifier in comparison with intensity, geometry, gray level co-occurrence matrix (GLCM)-based texture, neighborhood gray tone difference matrix (NGTDM)-based texture, and a combination of these four features. The results were assessed in terms of accuracy, sensitivity, specificity, and AUC. Collectively, the shell feature showed better predictive performance than all the other features for distant failure prediction in both NSCLC and CC cohorts.

1. Introduction

Distant failure, the spread of cancer cells from the primary tumor to any site of distant organs without loco-regional failure, occurs when malignant tumor cells metastasize to distant organs, causing up to 90% human cancers-associated deaths (Mehlen and Puisieux, 2006). Stereotactic body radiation therapy (SBRT) is widely used in patients with early stage medically inoperable non-small cell lung cancer (NSCLC), achieving 85–95% local control rates (Chetty et al., 2013). Despite the high local control rates, distant failure is still common, with 3-year and 5-year distant relapse rates of 22% and 31%, respectively (Zhou et al., 2017; Timmerman et al., 2010). Similarly, in patients with locally advanced cervical cancer (CC), even receiving external beam radiation therapy (EBRT) with concurrent chemotherapy and intracavitary brachytherapy (ICBT) as the recommended therapy, at least 20% of them still develop distant metastases (Whitney et al., 1999; Rose et al., 2007); and in the patients with positive para-aortic involvement, the rate is more than 40% (Schmid et al., 2014). Therefore, predicting distant failure in high risk patients is essential to achieve better treatment outcomes with intensified treatment modalities.

Although many of the mechanisms that govern metastasis are still unclear, the tumor microenvironment is known to regulate tumor evolution toward metastasis (Quail and Joyce, 2013), as shown for cervix (Braumann et al., 2005), lung (Wood et al., 2014), colon cancer among other cancer types (Koelzer et al., 2016; Koelzer and Lugli, 2014). A correlation was found between the microenvironment and distant failure (Valastyan and Weinberg, 2011), typically exemplified by the theory of epithelial-to-mesenchymal transition (EMT). In this process, a portion of cancer cells located at the tumor edges may acquire cancer stem cell (CSC)-like traits typical of metastasis, including self-renewal, tumor-originating, invasiveness, and elevated apoptosis resistance; these cancer cells depart from the main tumor and initiate metastasis, leading to junctional alterations and spatial heterogeneity (Chaffer and Weinberg, 2011; Plaks et al., 2013). This cellular invasion process was simulated by a hybrid multiscale mathematical model, showing that invasive tumor cells first developed within the tumor and later penetrated the tumor edge to form metastases (Robertsontessi et al., 2015).

In addition to EMT and CSCs, tumor budding is another factor contributing to invasion and correlating with worse outcomes in colon cancer (Lugli et al., 2017), lung cancer (Yamaguchi et al., 2010; Taira et al., 2012), cervix cancer among others (Huang et al., 2016; Alhadi et al., 2014). In tumor budding, isolated or clustered small malignant cells are close to the tumor edge. Literature reviews have reported that tumor buds can be a realization of CSC and an exhibition of the EMT process (Dan et al., 2016), suggesting tumor budding as an independent prognostic factor (Huang et al., 2016; Kadota et al., 2014).

Tumor islands were also observed on tumor edges. In lung cancer, tumor islands are large nests of malignant cells connected with one another and with primary tumors in alveolar spaces, slightly near the tumor border; they also have been associated with poor prognosis (Onozato et al., 2013). Studies were expanded by discovering spread through air space (STAS), a phenomenon of aggressive cells within air spaces closely beyond the edge of the tumor. STAS has been recognized an important pattern of invasion (Lu et al., 2017), and was approved by the 2015 World Health Organization as an independent metastatic predictor of lung cancer within the lung classification system (Travis et al., 2015).

These findings suggest that the appearance of the interface between tumor and normal tissue may provide phenotypic information related to metastatic potential that would enable the development of prognostic and predictive models. This application is enabled by radiomics, which can extract quantitative radiologic imaging features related to the aforesaid cellular phenotype, i.e., EMT-induced CSC changes, tumor budding, tumor islands, and STAS. Furthermore, because of its potential correlation with pathologic morphology (Cook et al., 2014; Baardwijk et al., 2008), positron emission tomography (PET) has been studied to predict the pathologic outcome of therapy in various cancers, including lung (Wu et al., 2016; Tan et al., 2013), cervix (Kidd et al., 2010), and other cancers (Nogami et al., 2014). These studies have revealed PET as a promising quantitative reflection of the pathologic heterogeneity at the tumor edges.

In this pilot study, we developed the tumor shell, a radiomics feature that characterizes the tumor periphery and its correlation with distant failure. We demonstrated its ability in predicting treatment response for patients receiving SBRT for early stage NSCLC and for patients receiving EBRT and concurrent chemotherapy followed by high-dose-rate ICBT in stage IB-IVA CC.

2. Material and Method

2.1. Patients

Our study was conducted at our institution, on two cohorts of patients approved by Institutional Review Board: (1) 48 early stage IA and IB NSCLC patients treated with SBRT from 2006 to 2012 (28 males and 20 females; mean age, 70.58 ± 9.84 years; range, 54 to 90 years); (2) 52 stage IB-IVA cervix cancer patients without para-aortic node involvement, treated with EBRT and concurrent chemotherapy followed by high-dose-rate ICBT from 2009 to 2012 (mean age, 47.10 ± 11.82 years; range, 26 to 72 years). The gold standard of this study is the state whether the patient developed distant failure after the treatment, which is represented as a binary outcome: the number 0 denotes not having distant failure while 1 denotes having distant failure. In the NSCLC dataset, the total number of PET slices for each patient varied from 274 to 355, with 2.00 to 5.00-mm slice thickness and 4.0×4.0-mm or 5.0×5.0-mm pixel spatial resolution. Spline-based interpolation has continuous first and second order derivatives and has been shown to generate more accurate and smooth results over several other methods for medical imaging (Meijering et al., 2001; Saha et al., 2015). Therefore, to achieve a consistent resolution, all slices were interpolated with the smallest slice thickness of 2.0 mm by spline interpolation along the axial dimension for 1D interpolation and spatial resolution of 4.0×4.0 mm by bicubic spline algorithm in the axial plane for 2D interpolation. Detailed information about the interpolation is described in the Appendix A. In the CC dataset, all slices were used directly without interpolation since they had the same 5.00-mm slice thickness and 4.0×4.0-mm pixel spatial resolution. Before tumor analysis, the raw PET data were converted to standard uptake values (SUV).

2.2. Tumor Analysis

For each patient, slices containing primary tumors were selected for analysis. In the NSCLC cohort, tumors were segmented automatically, with the middle location slice segmented by the object information based interactive segmentation method (OIIS) (Zhou et al., 2013) and other slices segmented by the OTSU method. In the CC cohort, the region of interest that incorporated the entire tumor was delineated manually by a radiation oncologist with 4 years’ experience and reviewed by another radiation oncologist with 19 years’ experience. In the NSCLC cohort, the number of selected slices originally ranged from 5 to 17, and zero padding was used for patients with slice numbers less than 17. Therefore, after interpolation to the smallest slice thickness of 2.0 mm, all patients had 42 slices. Meanwhile, because the greatest in-plane tumor diameter in all the patients’ slices was 13 pixels, a patch of 17 × 17 pixels was cropped around the tumor center in each slice, resulting in a cube size of 17 × 17 × 42 for each patient. A volume size of 29 × 29 × 40 was used for each patient in the CC cohort. All features were computed on cropped PET cubes.

2.3. Tumor Shell Feature Construction

The shell feature was extracted from the voxels around the tumor boundaries in a series of axial PET slices. The workflow of the shell feature construction is illustrated in Figure 1. The top row shows slices of the tumor (outlined in the red windows) in axial sequence (Figure 1(a)). First, as displayed in the second row (Figure 1(b)), the patches that include the delineated tumor were cropped from the corresponding slices above. The PET intensity values in the delineated tumor were remained while the pixels outside the tumor contour were set to be zero. Furthermore, binary mask images were obtained to represent the specific tumor region by setting inside tumor region as 1 and outside tumor region as 0. A number of grayscale sub-shells Ψ (t) (outlined in yellow, blue and green squares in Figure 1(c)) were derived by calculating the difference images between every two adjacent grayscale patches P (t) (outlined in yellow, blue and green rectangles in Figure 1(b)) and their corresponding binary masks M (t). As formulated in Equation (1), the sub-shell was then obtained by combining the two difference images together through the Hadamard product. As expected, the sub-shell image was generally the outer region of the tumor. Finally, by adding up the sub-shells Ψ (t) together shown in Equation (2), the shell S (k) (Figure 1(d)) was formed and used to represent the holistic heterogeneity of voxels in the boundary of the entire tumor volume.

Figure 1.

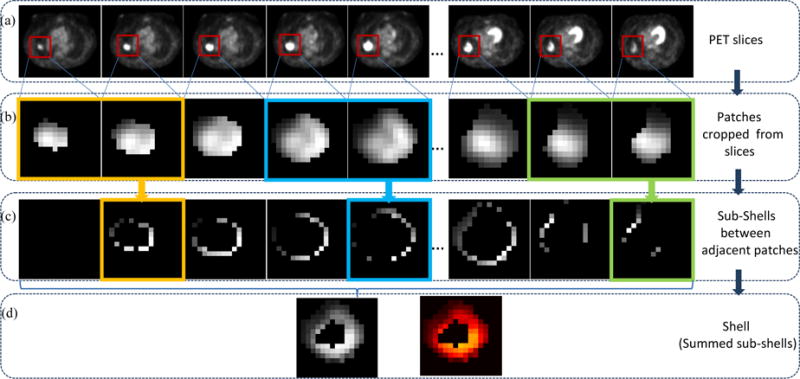
Shell feature extraction workflow. (a) Series of axial PET slices of one patient, (b) Series of patches (red windows in (a)) including tumors are cropped from each slice in (a), (c) Series of sub-shells derived from adjacent two patches in (b), (d) Shell feature, with grayscale image left and Heatmap image right.

The sub-shell sequence Ψ (t) in Figure 1(c) is defined as:

$$\Psi (t)\{\begin{array}{ll}\left(M(t)-M(t-1)\right)\circ \left(P(t)-P(t-1)\right),\hfill & t\ge 2\hfill \\ \mathbf{0},\hfill & t=1\hfill \end{array},$$ (1)

where P(t) denotes a grayscale patch sequence shown in Figure 1(b) and M (t) is the matching binary mask image sequence that indicates the region of the tumor, the symbol ° indicates the Hadamard product and t is the patch (slice) number. When t = 1,Ψ(t) is a zero matrix 0. The element in Ψ(t) is either greater than (when corresponding elements in M(t) and M(t − 1) are 0, 1 or 1, 0) or equal to zero (when corresponding elements in M(t) and M(t − 1) are 0, 0 or 1, 1). Thus, each sub-shell partially describes the heterogeneous architecture of the tumor edge in an image where the higher SUV value pixels appear brighter. Examples of sub-shells are presented in Figure 1.

To represent the heterogeneity of the whole tumor border, for each patient k the shell feature S(k) is constructed by successively accumulating sub-shells together and can be written as:

$$S(k)={\sum }_{t=2}^n\Psi (t).$$ (2)

where n is the total slice amount with n = 42 in the NSCLC cohort and n = 40 in the CC cohort. The strength of the shell feature is the use of a compact, yet comprehensive description that captures a sequence of morphologic patterns across the tumor boundary, such as shape, size, SUV values, and heterogeneities in a simple 2D map (Figure 1, bottom row). It is noted that this 2D map as a whole is considered as a shell feature in this work. The vectorized shell (e.g., 1D vector converted from the 2D map) is then used as the input for a support vector machine (SVM) based classifier (Section 2.5). This approach is along the same line of voxel/pixel-based methods (Huang et al., 2017; Khamis et al., 2017; Zuluaga et al., 2015) without further explicit calculating handcrafted features as those in a typical radiomics-based method.

2.4. Handcrafted Feature

Our proposed shell feature was compared with the following five groups of handcrafted features extracted from the whole delineated tumor region: 9 intensity features, 8 geometry features, 12 second order gray level co-occurrence matrix (GLCM) features, 5 high order neighborhood gray tone difference matrix (NGTDM) texture features, and a combination of these four types, for a total of 34. The features are described in Table 1 and calculation functions are provided in the Appendix B.

Table 1.

Types of handcrafted features

Histogram based image intensity	Geometry	GLCM based texture	NGTDM based texture
Minimum	Volume	Energy	Coarseness
Maximum	Major diameter	Entropy	Contrast*
Mean	Minor diameter	Correlation	Busyness
Stand deviation	Eccentricity	Contrast*	Complexity
Sum	Elongation	Texture Variance	Texture Strength
Median	Orientation	Sum-Mean
Skewness	Bounding Box Volume	Inertia
Kurtosis	Perimeter	Cluster Shade
Variance		Cluster tendency
		Homogeneity
		Max-Probability
		Inverse Variance

NOTE.

^*Contrast: Different calculation methods were employed in GLCM and NGTDM, though the same names are indicated.

Abbreviations: GLCM, Gray level co-occurrence matrix; NGTDM, Neighborhood gray tone difference matrix.

2.5. Prediction Model Development

To develop our prediction model, a supervised learning method support vector machine (SVM) with Gaussian radial basis function (RBF) is employed to classify the patients with and without distant failure into two categories. SVM is a discriminative model that can classify data through a separating hyperplane representing the largest separation margin between two classes and having two parameters penalty factor C and gamma (Suykens and Vandewalle, 1999). We used the procedure in the LIBSVM toolbox (Chang and Lin, 2011) and conducted the grid search to find the best parameters by minimizing the classification error of SVM as illustrated in literature (Hsu, 2010). Before being fed to SVM, the vectorized shell was applied by principal component analysis (PCA) to reduce the feature dimension. The reduction process is described in the Appendix C. The predictive ability of the shell feature was compared with that of the other five features using ten random trails of 5-fold cross validation on both NSCLC and CC cohorts. Meanwhile, to handle the class imbalance problem, the synthetic minority over-sampling technique (SMOTE) is applied to augment the minority (samples with distant failure) category by creating synthetic examples on the basis of minority class neighborhood distribution (Chawla et al., 2002). In this study, 24 (the difference between 12 distant failure positive and 36 distant failure negative) synthetic samples are generated in the NSCLC cohort and 24 (the difference between 14 distant failure positive and 38 distant failure negative) new samples were created in the CC cohort. Accuracy, sensitivity, specificity, and area under the receiver operating characteristic curve (AUC) were used as evaluation metrics. The code was implemented in Matlab (version R2016a).

2.6. Statistical Analysis

The difference in AUC performance between the shell feature and the other features was assessed by the Student’s t-test. The difference was considered statistically significant with a P value less than 0.05. The receiver operating characteristic (ROC) curve with 95% confidence interval is presented in Figure 2. Statistical analysis was performed with the Matlab statistical toolbox (version R2016a).

Figure 2.

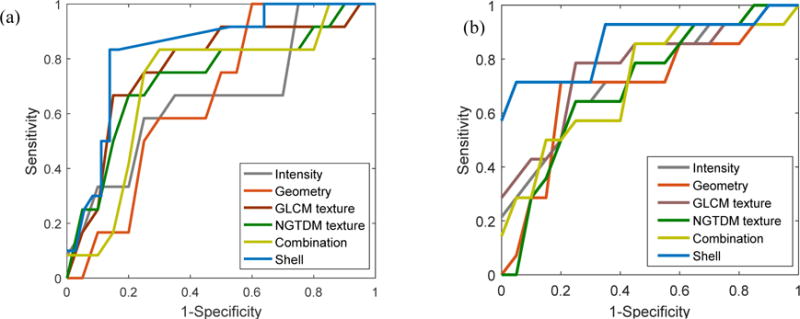
Receiver operating characteristic (ROC) curves of shell feature and other five groups of handcrafted features. (a) NSCLC cohort. (b) CC cohort. ROC curves depict the classification ability of the binary SVM model in terms of predictive feature and observed outcome of distant failure under varied discrimination threshold. The x-axis represents the false positive rate and is calculated as (1-specificity). The y-axis represents the true positive rate by sensitivity. A larger area under the curve indicates better prediction.

3. Results

3.1. Clinical Characteristics

The demographic and clinical characteristics of patients in the NSCLC and CC cohorts are listed in Table 2. No significant difference in distant failure prevalence was observed between the two trials (P = 0.917). During follow-up time, distant metastases were observed in 25% (12 of 48) of patients in the NSCLC cohort and 26.9% (14 of 52) in the CC cohort after radiotherapy.

Table 2.

Characteristics of two cohorts of patients

Characteristics	NSCLC Cohort		CC Cohort
	Distant failure (+)	Distant failure (−)	Distant failure (+)	Distant failure (−)
Age, years
mean ± SD	69.9 ± 9.2	70.2 ± 10.2	41.6 ± 11.7	49.1 ± 11.3
Median (range)	69.0 (57.0–89.0)	71.0 (54.0–90.0)	38.0 (29.0–70.0)	49.0 (26.0–72)
Ethnicity, No. (%)
Caucasian	9 (75.0)	27 (75.0)	6 (42.9)	12 (31.6)
Hispanic	0 (0)	1 (1.3)	2 (14.3)	15 (39.5)
African American	3 (25.0)	7 (19.4)	5 (35.7)	10 (26.3)
Asian	0 (0)	1 (1.3)	1 (7.1)	0 (0)
Other	0 (0)	0 (0)	0 (0)	1 (2.6)
Clinical tumor size, mm, No. (%)
≤ 10	1 (8.3)	0 (0)	0 (0)	1 (2.6)
11-30	6 (50.0)	26 (72.2)	2 (14.3)	4 (10.6)
31-50	5 (41.7)	9 (25.0)	9 (64.3)	20 (52.6)
51-70	0 (0)	1 (1.3)	2 (14.3)	9 (23.6)
> 71	0 (0)	0 (0)	1 (7.1)	4 (10.6)
Histology, No. (%)
Adenocarcinoma	6 (50.0)	17 (47.3)	1 (7.1)	4 (10.6)
Squamous cell carcinoma	5 (41.7)	12 (33.3)	11 (78.6)	33 (86.8)
Other	1 (8.3)	7 (19.4)	2 (14.3)	1 (2.6)
Stage, No. (%)
IA	5 (41.7)	30 (83.3)	0 (0)	0 (0)
IB	7 (58.3)	6 (16.7)	4 (28.6)	12 (31.6)
IIA	0 (0)	0 (0)	1 (7.1)	3 (7.9)
IIB	0 (0)	0 (0)	7 (50.0)	15 (39.5)
IIIB	0 (0)	0 (0)	0 (0)	6 (15.8)
IVA	0 (0)	0 (0)	2 (14.3)	2 (5.2)

NOTE. Stages in NSCLC and CC are determined by the TNM and Federation of Gynecology and Obstetrics (FIGO) staging system, respectively.

Abbreviations: NSCLC, non-small cell lung cancer; CC: cervix cancer; SD: standard deviation.

3.2. Comparison of Predictive Performance

The comparison between the shell feature and other features was performed on both NSCLC and CC cohorts through quantitative analysis (Table 3) and ROC graphing (Figure 2). AUC, sensitivity, specificity, and accuracy were the criteria used in the study. Definitions are given in the Appendix D.

Table 3.

Prediction performance of features with respect to distant failure on CC and primary NSCLC cohort

cohort	features	Accuracy	Sensitivity	Specificity	AUC	95% CI	P value
NSCLC	Intensity	0.70 ± 0.01	0.70 ± 0.02	0.69 ± 0.01	0.73 ± 0.02	[0.5615,0.8613]	.0002
	Geometry	0.68 ± 0.01	0.65 ± 0.06	0.70 ± 0.04	0.65 ± 0.01	[0.4861,0.8009]	.0001
	GLCM texture	0.75 ± 0.03	0.75 ± 0.03	0.74 ± 0.03	0.76 ± 0.02	[0.5528,0.8905]	.0044
	NGTDM texture	0.68 ± 0.03	0.70 ± 0.06	0.65 ± 0.02	0.73 ± 0.03	[0.5139,0.8783]	.0015
	Combination	0.73 ± 0.04	0.72 ± 0.02	0.71 ± 0.03	0.76 ± 0.02	[0.5887,0.8796]	.0025
	Shell	0.81 ± 0.03	0.81 ± 0.02	0.80 ± 0.03	0.82 ± 0.03	[0.6632,0.9247]	–
CC	Intensity	0.72 ± 0.02	0.71 ± 0.03	0.75 ± 0.03	0.69 ± 0.01	[0.4743,0.8533]	.0003
	Geometry	0.71 ± 0.04	0.71 ± 0.01	0.71 ± 0.04	0.71 ± 0.01	[0.4891,0.8590]	.0006
	GLCM texture	0.75 ± 0.02	0.80 ± 0.02	0.73 ± 0.02	0.76 ± 0.04	[0.5427,0.8981]	.0015
	NGTDM texture	0.72 ± 0.04	0.71 ± 0.02	0.74 ± 0.04	0.74 ± 0.03	[0.5396,0.8524]	.0002
	Combination	0.72 ± 0.03	0.75 ± 0.05	0.73 ± 0.03	0.73 ± 0.02	[0.5519,0.8813]	< .0001
	Shell	0.80 ± 0.04	0.81 ± 0.02	0.80 ± 0.04	0.83 ± 0.02	[0.6559,0.9212]	–

NOTE. “Combination” refers to the combined four types of features, i.e., intensity, geometry, GLCM texture and NGTDM texture; 95% CI and P value are both derived from values of AUC; P value measures the statistical AUC difference between each group of handcrafted features and shell feature.

Abbreviations: AUC, the area under a characteristic operation curve; CI, confidence interval.

The shell feature showed the highest accuracy in predicting distant failure (Table 3). In the NSCLC cohort, the shell feature achieved an AUC of 0.82 (95% CI, 0.6632 to 0.9247) with 0.81 sensitivity, 0.80 specificity, and 0.81 accuracy. For the other five features, the best result was observed for the GLCM texture as shown by 0.76 AUC (95% CI, 0.5528 to 0.8905), 0.75 sensitivity, 0.74 specificity, and 0.75 accuracy. Similarly, in the CC cohort the shell feature still achieved the best performance for all metrics, with 0.83 AUC (95% CI, 0.6559 to 0.9212), 0.81 sensitivity, 0.80 specificity, and 0.80 accuracy. These results revealed that the shell feature had more discriminative capacity than the other features. Also, the difference in AUC performance between the shell feature and the other features was found to be significant (P < 0.005 for both features in both cohorts).

The ROC curves for different feature sets are illustrated in Figure 2. Similar results were obtained for NSCLC (Figure 2(a)) and CC (Figure 2(b)). The proposed shell feature, represented by the upper blue curve, is located close to the top left corner of the chart, indicating on average a greater discriminative ability than the other methods.

The discriminative ability is indicated by representative 2D shell maps (Figure 3(a) and 3(b)). The top row shows tumors without distant failure (Figure 3(a)) and the bottom row reports those with distant failure (Figure 3(b)). Pixels with higher SUV values are indicated in brighter colors, while lower values are shown in darker colors. As evident from the shell maps, distant failure-positive tumors show more heterogeneous boundary expression than the distant failure-negative ones. This finding may be attributed to the more active, varied, and potentially invasive cellular behavior of the tumor in the barrier microenvironment.

Figure 3.

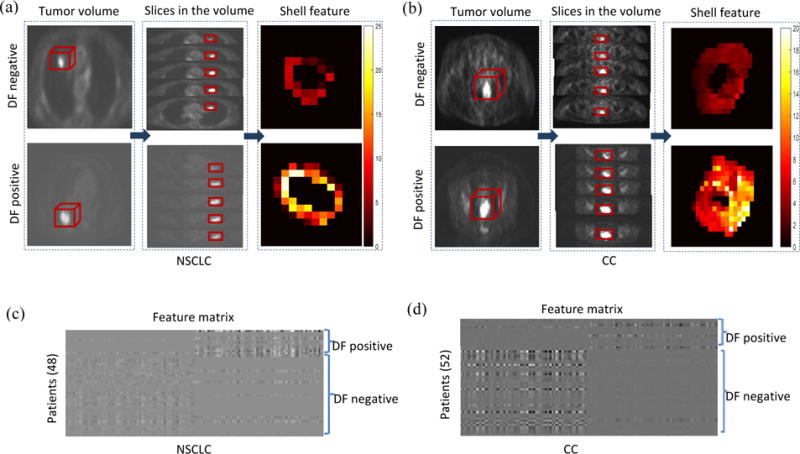
The shell feature has the discriminative ability to detect distant failure (DF)-negative and -positive tumors. (a) (b) are representative examples of 2D shell in terms of structure heterogeneity. (a) NSCLC cases. (b) CC cases. In each cohort, the shell feature (third column) is computed from a series of slices (second column) in the tumor volume (first column), with the top row showing tumors without distant failure and the bottom row showing tumors with distant failure. As shown, tumors with distant failure present more complicated morphologic patterns. (c) (d) are feature matrices of the whole patients, where each row refers to sparse coefficient of the vectorized shell from one patient, and each column corresponds to an element of the feature. (c) NSCLC cases. (d) CC cases. These features are sparse coefficients learned from the original vectorized shells by dictionary learning method. These feature matrices exhibit clustering characteristics for (DF)-positive and -negative tumors.

The overall capability of the shell’s classification for the NSCLC and CC cohorts is further illustrated in Figure 3(c) and 3(d), where the rows in the matrices are the vectorized shell’s sparse coefficients learned by the dictionary learning method (Gu et al., 2014). Given the matrix X (each column is a vectorized shell and the number of the rows is the length of the shell) with class label Y (the binary outcome 0/1 of distant failure state), the task of dictionary learning under the framework of sparse representation is to solve the optimization problem $\{D^{\ast },Q^{\ast }\}=\arg \underset{D,Q}{min}||X-\mathit{DQX}|{|}_{\mathrm{F}}^2+\text{φ(}D,Q,X,Y\text{)}$, where φ(D, Q, X, Y) is a discrimination function, D is the synthesis dictionary utilized to reconstruct X, Q is the analysis dictionary applied to encode X. Using the solved D and Q, the sparse coefficient matrix can be obtained by W = QX with each column being a sparse coefficient corresponding to its vectored shell of a patient, which is a projection of the original training data (the input vectorized shell) to the learned dictionary that includes the discriminative information. Clustering characteristics can be seen on both cohorts, with features of the same class showing similar representation and features of different classes displaying distinct representations. In the horizon row of Figures 3(c) and 3(d), the sparse coefficients in DF-negative has higher values in the first half and lower values in the second half, while the sparse coefficients in DF-positive has lower values in the first half and higher values in the second half.

3.3. Independent validation on NSCLC patients

To further evaluate the shell’s predictive ability, another cohort of 23 early stage IA and IB NSCLC inoperable patients underwent SBRT from 2012 to 2016 (12 males and 11 females; mean age, 73.30 ± 9.58 years; range, 55 to 91 years) in our institution was used for an independent validation. The distant metastasis was observed in 30.4% (7 of 23) of patients. The demographic and clinical characteristics of patients are listed in Table 4. There are no significant differences between the validation and primary cohorts (the cohort of 48 patients) in the characteristics (P = 0.320), either within the distant failure positive cohort (P = 0.336) or in the distant failure negative cohort (P = 0.792), which justified its use as a validation cohort. The primary cohort of 48 NSCLC patients with 5-fold cross validation were used for training and the trained model was then applied on the validation cohort.

Table 4.

Characteristics of patients in the validation cohort

Characteristics	Validation NSCLC Cohort
	Distant failure (+)	Distant failure (−)
Age, years
mean ± SD	70.9 ± 9.4	75.4 ± 10.0
Median (range)	74.0 (55.0–85.0)	74.0 (64.0–91.0)
Ethnicity, No. (%)
Caucasian	10 (62.5)	6 (85.8)
Hispanic	0 (0)	1 (14.2)
African American	6 (37.5)	0 (0)
Asian	0 (0)	0 (0)
Other	0 (0)	0 (0)
Clinical tumor size, mm, No. (%)
≤ 10	0 (0)	0 (0)
11–30	13 (81.2)	5 (71.6)
31–50	3 (18.8)	1 (14.2)
51–70	0 (0)	1 (14.2)
> 71	0 (0)	0 (0)
Histology, No. (%)
Adenocarcinoma	9 (56.2)	4 (57.1)
Squamous cell carcinoma	6 (37.5)	3 (42.9)
Other	1 (6.3)	0 (0)
Stage, No. (%)
IA	15 (93.7)	7 (100.0)
IB	1 (6.3)	0 (0)
IIA	0 (0)	0 (0)
IIB	0 (0)	0 (0)
IIIB	0 (0)	0 (0)
IVA	0 (0)	0 (0)

NOTE. Stage in NSCLC is determined by the TNM.

Abbreviations: NSCLC, non-small cell lung cancer; SD: standard deviation.

The performance of shell feature in the validation set was also compared with other features. The experiment results are shown in Table 5. The shell feature still outperformed the other features for distant failure prediction in the validation cohort. The AUC achieved by the shell feature was 0.79 (95% CI, 0.6559 to 0.9212) with 0.71 sensitivity, 0.87 specificity, and 0.83 accuracy, while the highest AUC achieved by the other features was 0.70 (95% CI, 0.4079 to 0.8442) with 0.71 sensitivity, 0.62 specificity, and 0.65 accuracy, respectively.

Table 5.

Prediction performance of features with respect to distant failure on validation NSCLC cohort

cohort	features	Accuracy	Sensitivity	Specificity	AUC	95% CI
Validation NSCLC	Intensity	0.65	0.71	0.62	0.70	[0.4079,0.8442]
	Geometry	0.65	0.71	0.62	0.69	[0.4616,0.8413]
	GLCM texture	0.61	0.57	0.61	0.64	[0.3304,0.8466]
	NGTDM texture	0.65	0.57	0.69	0.65	[0.3447,0.8415]
	Combination	0.70	0.71	0.69	0.66	[0.4236,0.8634]
	Shell	0.83	0.71	0.87	0.79	[0.6559,0.9212]

4. Discussion and Conclusion

The potential of tumor boundary as a predictive factor for distant failure was evaluated by the tumor shell, a PET-derived feature that allows us to detect its associations with metastasis within the microenvironment. The shell feature can be used to predict the outcome of SBRT for NSCLC patients and EBRT and concurrent chemotherapy followed with high-dose-rate ICBT for CC patients.

The tumor-host interface has been associated with metastasis because interactions between tumor cells and their microenvironment play an active part in tumor invasion and metastasis. However, to the best of our knowledge, few studies have targeted tumor boundaries in medical imaging for constructing risk models of metastasis (Mezheyeuski et al., 2016; Lennon et al., 2015). A recent study linked the morphology at the tumor-stroma interface to a multifractal metric, which derived from tumor outlines (excluding tumor internal tissue) on pathological images. The outline-based metric was found to be associated significantly (P < 0.001) with metastasis-related features, such as tumor border configuration and tumor budding grade, thereby verifying its prognostic and predictive efficacy for treatment response in colon cancer (Mezheyeuski et al., 2016). Similarly, in a lung cancer review, a fractal dimension of the tumor-stroma interface was used to measure tumor progression (Mezheyeuski et al., 2016). The study highlighted the use of radiological imaging, and found that the derived metric correlated with tumor growth and predicted treatment response (Lennon et al., 2015). Notably, the predictors in these studies were scores calculated from the contour lines of the tumor edge, whereas our method used the areas of the tumor boundary, where more minable information may be included. Besides, the calculation of the scores is a handcrafted processing, which is subject to human inconsistency and operator dependence.

Since the shell is built from the periphery pixels around tumor edge and the shell feature is constructed by simply vectorization of the pixel intensity values of PET at the shell region, the shell feature is fixed once the PET image is reconstructed. Compared to handcrafted feature based methods that require further feature extraction/calculation from reconstructed PET, the shell feature may be less dependent on voxel related factors as it considers the whole vectorized shell as a feature directly. On the other hand, the noise level and image resolution of reconstructed PET are affected by reconstruction algorithms as well as parameters selected during reconstruction. In this preliminary study, PET images were reconstructed at different resolutions, where spline based interpolation was employed to overcome inhomogeneous resolutions of PET images due to its superior performance. As shown in Appendix A, different interpolation schemes will generate different interpolated results. Thus the reconstruction parameters may still affect the performance of the shell feature. Due to relatively small samples we currently have, we are not able to quantify the influence of PET reconstruction parameters to the performance of the shell feature by further grouping patients according to reconstruction parameters. If the reconstruction parameters are harmonized, the performance of the shell feature could be further improved.

The correlation between distant failure and radiomics features of the tumor edge is based on known biological processes that are associated with metastatic potential such as EMT and tumor budding. On the assumption that these findings are located at the tumor boundary, the shell feature was proposed to describe spatial morphology of the tumor periphery in relation to the likelihood of metastasis. Moreover, to the extent that these processes are present in other tumor types, it is likely that the shell feature may be used to predict the outcomes for other cancers.

Our study presents a few limitations, including the use of a small patient. Also, accumulating a serial of sub-shells (3D) into a 2D shell feature may lead to a loss of spatial complexity in the axial perspective. We only used vectorized shell as the input as we mainly aim to assess the shell’s ability for predicting distant failure. When combining with other features such as intensity, geometry and texture features, shell needs additional process to have a more concise and effective description, which could lead to better predictive power. Finally, the influence of tumor boundary extension is not investigated in this paper.

In conclusion, the PET-derived shell feature revealed a relationship between tumor edge and distant failure, and could be used to facilitate early prediction of the radiotherapeutic response in NSCLC and CC patients.

APPENDIX

Appendix A: Interpolation methods comparison

We used the spline interpolation along the axial dimension for 1D interpolation and bicubic spline algorithm in the axial plane for 2D interpolation due to the spline-based interpolation’s superior performance over other methods.

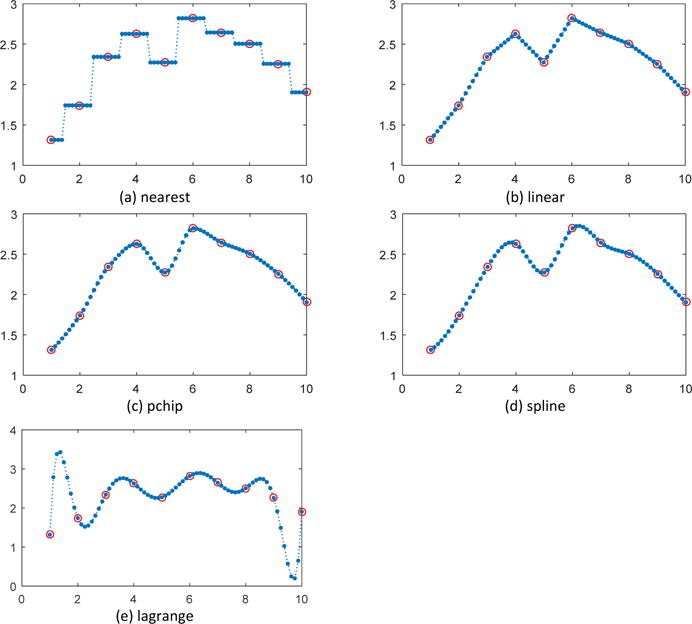
For the axial dimension, five commonly used 1-D interpolation methods, nearest, linear, pchip, spline and lagrange polynomial were employed for comparison in two experiments. As shown in Figure 1(a) and Figure 2(a), nearest interpolation takes the value of nearest neighboring pixel as those of the new data points, introducing piecewise constant interpolated result and sharp discontinuities between each piece. Linear interpolation in Figure 1(b) and Figure 2(b) uses linear polynomials to construct interpolated data within the range of sampled data points and is piecewise linear, but still exhibits sharp discontinuity in the intersections of pieces. Pchip interpolation demonstrated in Figure 1(c) and Figure 2(c) uses piecewise cubic hermite interpolating polynomial and can obtain more favorable interpolations than nearest and linear methods. Spline interpolation in Figure 1(d) and Figure 2(d) is implemented by piecewise polynomial called spline and guarantees the continuity of the first and second function derivative, thus yields the smoothest interpolant compared with the previous three methods. In Figure 1(e), lagrange polynomial also achieved a smooth fitting curve as spline method but in Figure 1(e) oscillation can been seen at the two ends of the concerned points. While spline interpolation avoids the problem of Runge's phenomenon, in which oscillation can occur between points when interpolating using high degree polynomials. In addition, if considering the computational cost, spline interpolation can make theinterpolated data converge most rapidly to the original sample since it has the highest order of approximation, which makes the spline interpolation a good choice.

Figure 1.

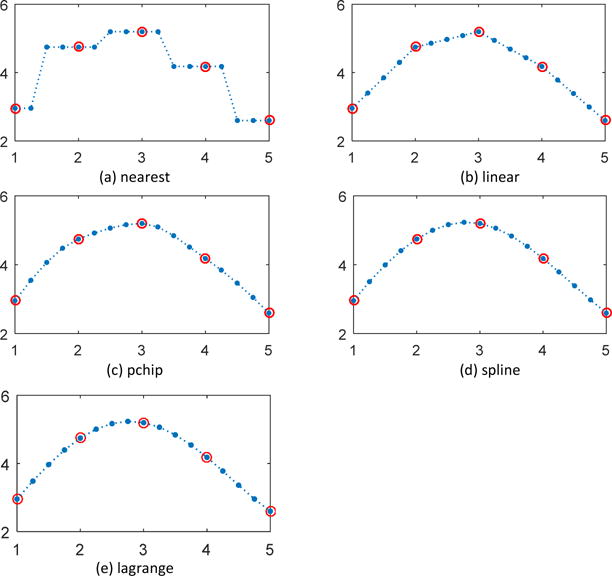
1-D interplolation along the axial dimension (example 1)

Figure 2.

1-D interplolation along the axial dimension (example 2)

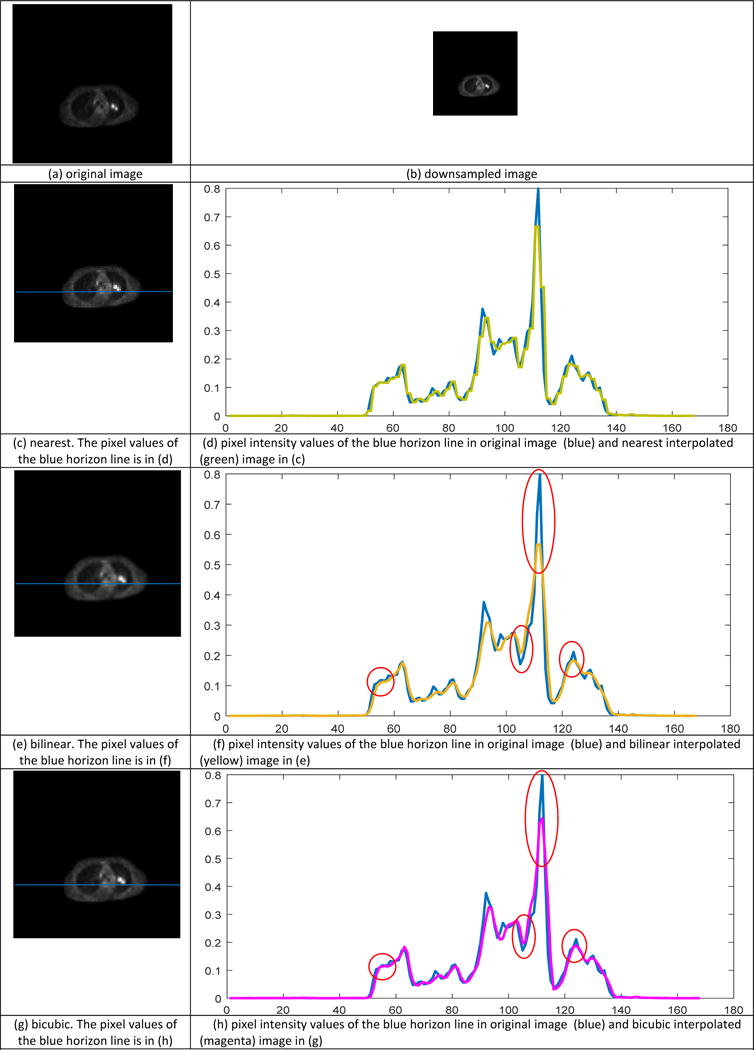
For the axial plane image, i.e., the 2-D slice, three generally used 2-D interpolation methods, nearest, bilinear and bicubic interpolation are utilized for comparison. To demonstrate the interpolation performance, the original slice (in Figure 3(a)) was down sampled to the half-sized image in each direction (Figure 3(b)) and then interpolated with nearest, bilinear and bicubic methods. The results were shown in Figure 3(c) and (d), Figure 3(e) and (f), Figure 3(g) and (h) respectively. Nearest interpolation in Figure 3(c) introduce aliasing artifact due to the neighboring interpolated pixels sharing same value as the sample data. Figure 3(d) is the pixel intensity values of the blue horizon line in Figure 3(c), with blue and green curve representing the values in original image and interpolated image by nearest method respectively. As shown in Figure 3(c), the interpolated curve is constant over small intervals and poorly continuous. The bilinear interpolation is an implementation of linear interpolation on a rectilinear 2D grid, but as a whole is not linear but rather quadratic in the sample location. In this method, output pixel value is a weighted average of pixels in the nearest 2 × 2 neighborhood and can produces much smoother interpolated image in Figure 3(e). In contrast to bilinear method, bicubic interpolation consider the nearest 4 × 4 neighborhood of sample pixel values surrounding the unknown pixel and take a weighted average of these 4 pixels to yield the interpolated value, thus has smoother surface and fewer interpolation artifacts in Figure 3(g). Comparing Figure 3(f) with Figure 3(h), the value difference along the blue horizon line between original image and interpolated image by bilinear interpolation is larger than by bicubic spline interpolation, especially in the peaks and troughs illustrated in red circles. The bicubic spline interpolation can achieve a more accurate fitting with the original one. In addition to the visual comparison, performance was quantitatively evaluated by metrics in terms of mean square error (MSE), peak signal to noise ratio (PSNR) and Structural Similarity Index (SSIM). In Table 1, the bicubic spline interpolation achieved the lowest error with the smallest MSE of 1.8820 and highest interpolation accuracy with the highest PSNR of 41.7600 and the premier similarity with the original image with the top SSIM of 0.9895.

Figure 3.

2-D image interpolation

Table 1.

Prediction performance of features with respect to distant failure

Interpolation method	MSE	PSNR	SSIM
nearest	3.1935	39.4635	0.9829
bilinear	2.0177	41.4576	0.9885
bicubic	1.8820	41.7600	0.9895

Appendix B: Handcrafted feature calculation

In this work, four types of handcrafted features extracted from the whole tumor, i.e., 9 intensity features, 8 geometry features, 12 GLCM (second order) texture features and 5 NGTDM (high order) texture features, as well as a combination of the four type features, 34 in total, were used for comparison with the proposed shell feature. The calculations of these handcrafted features were as follows.

1. Intensity features

Intensity features were calculated on the intensity histogram of SUV value and include 9 features:

1. Minimum;

2. Maximum;

3. Mean;

4. Stand deviation;

5. Sum;

6. Median;

7. Skewness describes the degree of distribution asymmetry around its mean:

   $$\mathit{Skewness}=E\left[{\left(\frac{X-\mu }{\sigma }\right)}^3\right],$$ (1)

   Where X denotes SUV value, μ is the mean and σ is the stand deviation.
8. Kurtosis describes the flatness or the spikiness of the signal:

   $$\mathit{Kurtosis}=E\left[{\left(\frac{X-\mu }{\sigma }\right)}^4\right].$$ (2)

   Where X denotes SUV value, μ is the mean and σ is the stand deviation.

9. Variance;

2. Geometry features

Geometry features describe the shape, size, or relative position of the tumor. The major diameter is defined as the major axis length or longest diameter, while the minor diameter is the shortest diameter. Eccentricity is the aspect ratio, defined as the ratio of the length between the major and the minor axis. These features are calculated by the regionprops function in Matlab.

1. Volume;

2. Major diameter is the major axis length or longest diameter;

3. Minor diameter the shortest diameter;

4. Eccentricity is the ratio of the length between the major and the minor axis;

5. Elongation;

6. Orientation the angle between the x-axis and the major axis of the ellipse that has the same second moments as the region;

7. Bounding Box Volume the smallest rectangle containing the region;

8. Perimeter the distance around the boundary of the region;

3. GLCM texture feature

The gray level co-occurrence matrix (GLCM) is a square matrix with the number of rows and columns equaling the quantized gray level denoted by N_g. Each element p(i,j) in GLCM represents the number of times a pixel of gray level i occurs with a neighbor pixel of gray level j in the image at a particular displacement distance and angle. We used histograms with 64 bins and constructed GLCM using 3D analysis of the tumor region with 26 neighboring voxels and 13 directions of the 3D space.

1. Energy describes image homogeneity and a higher energy value indicates a more homogeneous image,

   $$\mathit{Energy}={\sum }_{i=0}^{N_g-1}{\sum }_{j=0}^{N_g-1}p{(i,j)}^2,$$ (3)
2. Entropy describes the randomness of the image intensity distribution,

   $$\mathit{Entropy}=-{\sum }_{i=0}^{N_g-1}{\sum }_{j=0}^{N_g-1}p(i,j)\mathit{log}\left(p(i,j)\right)$$ (4)
3. Correlation measures the linear dependency of gray levels on those of either neighboring voxels or specified points,

   $$\mathit{Correlation}=\frac{{\sum }_{i=0}^{N_g-1}{\sum }_{j=0}^{N_g-1}(ij)\cdot p(i,j)-{\mu }_x{\mu }_y}{{\sigma }_x{\sigma }_y},$$ (5)
4. Contrast is the local variations within an image,

   $$\mathit{Contrast}={\sum }_{k=0}^{N_g-1}{k}^2\left\{{\sum }_{i=0}^{N_g-1}{\sum }_{j=0}^{N_g-1}p(i,j)|i-j|=k\right\},$$ (6)
5. Texture Variance the variation around the mean value,

   $$\mathit{Variance}={\sum }_{i=0}^{N_g-1}{\sum }_{j=0}^{N_g-1}{(i-u_x)}^2\cdot p(i,j)+{\sum }_{i=0}^{N_g-1}{\sum }_{j=0}^{N_g-1}{(i-u_y)}^2\cdot p(i,j),$$ (7)
6. Sum-Mean is defined as,

   $$\mathit{Sum}-\mathit{Mean}={\sum }_{i=0}^{N_g-1}{\sum }_{j=0}^{N_g-1}(i+j)\cdot p(i,j),$$ (8)
7. Inertia measures the local variation between a voxel and its neighbors,

   $$\mathit{Inertia}={\sum }_{i=0}^{N_g-1}{\sum }_{j=0}^{N_g-1}{(i-j)}^2\cdot p(i,j),$$ (9)
8. Cluster Shade measures matrix skewness,

   $$\mathit{Cluster}\mathit{Shade}={\sum }_{i=0}^{N_g-1}{\sum }_{j=0}^{N_g-1}{(i+j-u_x-u_y)}^{3}p(i,j),$$ (10)
9. Cluster tendency describes asymmetry,

   $$\mathit{Cluster}\mathit{Tendency}={\sum }_{i=0}^{N_g-1}{\sum }_{j=0}^{N_g-1}{(i+j-u_x-u_y)}^{4}p(i,j),$$ (11)
10. Homogeneity describes closeness of the elements in p(i,j) to the diagonal,

    $$\mathit{Homogeneity}={\sum }_{i=0}^{N_g-1}{\sum }_{j=0}^{N_g-1}\frac{p(i,j)}{1+|i-j|\prime }$$ (12)
11. Max-Probability is defined as,

    $$\mathit{Max}-\mathit{Probability}={max}_{i,j}p(i,j),$$ (13)
12. Inverse Variance is defined as,

    $$\mathit{Inverse}\mathit{Variance}={\sum }_{i=0}^{N_g-1}{\sum }_{j=0}^{N_g-1}\frac{p(i,j)}{1+{(i-j)}^2}.$$ (14)

4. NGTDM texture feature

The neighborhood gray tone difference matrix (NGTDM) is a high order texture and which related to human perception. It represents a difference in grayscale between pixels with a certain gray scale and the neighboring pixels. Let P(i) represents the summation of the gray-level differences between all voxels with gray level i and the average gray level of their 26 neighbors in 3D space. N_g represents the quantized gray level in V, and (N_g)_eff is the effective number of gray-level in V.

1. Coarseness is defined as,

   $$\mathit{coarseness}={\sum }_{i=0}^{N_g-1}{n}_{i}P(i),$$ (15)

   Where $n_i=\frac{N_i}{N}$, N_i is the number of voxels with gray level i in V and N is the total number of voxels in V.
2. Contrast is defined as,

   $$\mathit{contrast}=\left[\frac{1}{N_g(N_{g-1})}{\sum }_{i=0}^{N_g-1}{\sum }_0^{N_g-1}{n}_i{n}_j{(i-j)}^2][\frac{1}{N}{\sum }_{i=0}^{N_g-1}P(i)\right],$$ (16)

   Where $n_i=\frac{N_i}{N}$, $n_j=\frac{N_j}{N}$, N_i, N_j are the number of voxels with gray level i and j in V and N is the total number of voxels in V.
3. Busyness is defined as,

   $$\mathit{busyness}=\frac{{\sum }_{i=0}^{N_g-1}{n}_{i}P(i)}{{\sum }_{i=0}^{N_g-1}{\sum }_0^{N_g-1}(i{n}_i-j{n}_j)]},$$ (17)
4. Complexity is defined as,

   $$\mathit{complexity}={\sum }_{i=0}^{N_g-1}{\sum }_{i=0}^{N_g-1}\frac{|i-j|[n_{i}P(i)+n_{j}P(j)]}{N(n_i+n_j)}$$ (18)
5. Texture Strength is defined as,

   $$\mathit{strength}=\frac{{\sum }_{i=0}^{N_g-1}{\sum }_0^{N_g-1}(n_i+n_j){(i-j)}^2]}{{\sum }_{i=0}^{N_g-1}P(i)}.$$ (19)

Appendix C: PCA dimension reduction

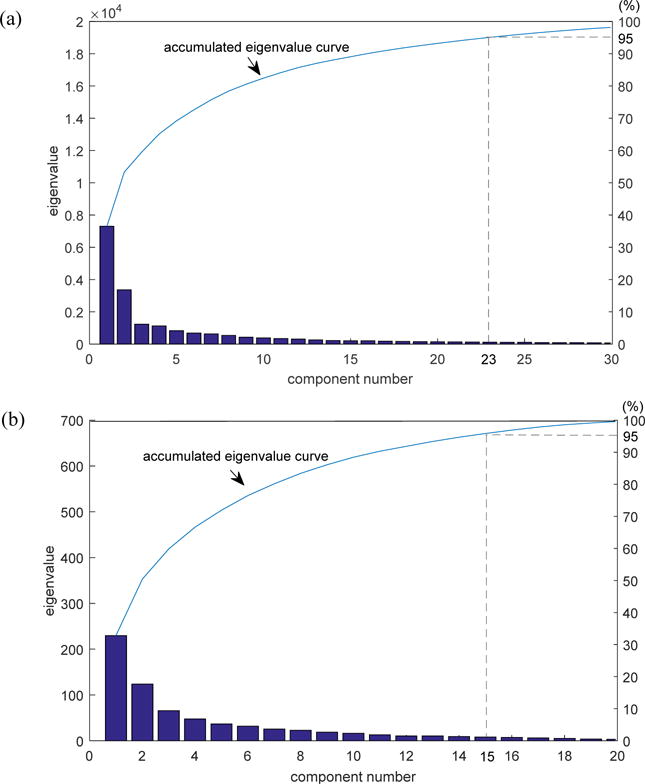
The image size of shell feature for each patient in non-small cell lung cancer (NSCLC) and cervix cancer (CC) cohorts were 17×17 and 29×29, resulting vectors of 289 and 841 lengths, respectively. Before inputting them to support vector machine (SVM), principal component analysis (PCA) was performed to reduce the dimensionality. The component number was chosen as the number of components account for 95% of the variance. Accordingly, the chosen component number for NSCLC and CC were 23 and 17, as shown in Figure 4 (a) and (b).

Figure 4.

Component number chosen for each cohort. (a) NSCLC cohort; (b) CC cohort.

Appendix D: Performance criteria

Assume TP and TN denote the number of true positives and true negatives; FP and FN indicate the number of false positives and false negatives. The criteria used in this work are as follows:

1. Accuracy = (TP + TN)/(TP + FN + FP + TN) is an common metric used for classification performance over all classes;

2. Sensitivity = TP/(TP + FN) represents true positive rate and is the percentage of positives correctly classified;

3. Specificity = TN⁄(TN + FP) corresponds to true negative rate and is the percentage of negatives correctly classified;

4. AUC is a single measure derived from the area under the ROC curve and a trade-off between sensitivity and specificity, thus an average evaluation for features’ performance.