Current methods and limitations for longitudinal fMRI analysis across development

Abstract

The human brain is remarkably plastic. The brain changes dramatically across development, with ongoing functional development continuing well into the third decade of life and substantial changes occurring again in older age. Dynamic changes in brain function are thought to underlie the innumerable changes in cognition, emotion, and behavior that occur across development. The brain also changes in response to experience, which raises important questions about how the environment influences the developing brain. Longitudinal functional magnetic resonance imaging (fMRI) studies are an essential means of understanding these developmental changes and their cognitive, emotional, and behavioral correlates. This paper provides an overview of common statistical models of longitudinal change applicable to developmental cognitive neuroscience, and a review of the functionality provided by major software packages for longitudinal fMRI analysis. We demonstrate that there are important developmental questions that cannot be answered using available software. We propose alternative approaches for addressing problems that are commonly faced in modeling developmental change with fMRI data.

1. Introduction

Developmental science is concerned with understanding systematic changes over time and characterizing the underlying dynamics that produce those changes (Ford and Lerner, 1992). Variability in emotion, cognition, behavior and neurobiology over time is thought to reflect maturational processes that unfold as a result of ongoing interactions between people and environmental context across development that reflect fluctuations in the relationships among factors occurring at multiple levels of organization (Lerner, 2001, Lerner and Castellino, 2002). Central goals in studies of development are to understand how a particular process or characteristic changes over time within individuals and to identify factors that predict variation, or individual differences, in that change process. In developmental cognitive neuroscience, the questions of interest typically focus on changes in neural structure or neural function over time and how those neural changes influence developmental change in other domains, including behavior, cognition, emotion, or health. These questions are inherently multivariate in nature—in other words, they involve processes that involve multiple systems or levels of organization. To date, however, the models available to the neuroimaging community have been limited in the range of questions to which they can be applied regarding how changes in neural function relate to development in other domains. In this paper, we review current methods for examining longitudinal change in fMRI data and describe a novel approach we are developing to allow more complex multivariate growth models to be applied to questions in developmental cognitive neuroscience.

Longitudinal studies that involve the collection of MRI data at several time points have become increasingly popular in developmental cognitive neuroscience because they allow researchers to study and track changes in brain structure and function over time within individuals. Longitudinal designs provide numerous advantages over cross-sectional studies for estimating changes over time and identifying predictors of change, including greater ability to distinguish between and within-individual variation(Rogosa et al., 1982). However, analysis of individual differences in longitudinal data can be challenging, particularly in studies involving three or more time points of data collection. For instance, researchers may be interested in modeling multiple forms of change (e.g., linear, quadratic, logarithmic, etc.), or in applying more exploratory, non-polynomial models of change (such as latent basis models; Grimm et al., 2011) while accounting for substantial individual variation in change between individuals (Dean et al., 2009). Often, procedures are required to address missing data that commonly result from subject dropouts (e.g., Matta et al., in this issue), and to include sources of measurement error in models (e.g. caused by differential subject motion across time, changes in data processing methods, scanner upgrades or hardware changes) that can bias estimates of expected change. Changes in task performance extraneous to neural development, such as practice effects, can also be associated with time (Salthouse, 2014), and it can be challenging to disentangle the effects of interest from these confounding factors. Taken together, the analysis of longitudinal fMRI data is more complex than typical cross-sectional analyses, and requires more advanced methods to effectively model processes involving change over time.

To date, the implementation of these more advanced approaches has been limited by the lack of available programs to model longitudinal fMRI data. At present, widely-used software programs for processing task-related fMRI data rely predominantly on the general linear model (GLM) approach to analyze data (Poline and Brett, 2012). The GLM is a broad class of models that assumes a linear relationship between one (or more) dependent variables and one (or more) independent variables. In fMRI analyses, the GLM estimates the BOLD time series as a linear combination of several signal components and tests whether activity in a voxel is linked to any known input function or stimuli (Lindquist, 2008). The GLM framework can be used to conduct analysis of variance (ANOVA), analysis of covariance (ANCOVA), multiple ANOVA and ANCOVA, and ordinary least squares (OLS) regression. Although each of these approaches have been developed and adopted in parallel to address distinct research questions (e.g., ANOVA-based methods are typically used in experimental designs with categorical predictors and regression in designs with continuous predictors), these methods are computationally equivalent (Howell and Lacroix, 2012) and have similar limitations in modeling longitudinal data.

In this paper, we provide an overview of major statistical models of longitudinal change that would be useful to apply to research questions in developmental cognitive neuroscience to evaluate changes in brain structure and function over time, identify predictors of those developmental trajectories, and to use change over time itself as a predictor of behavioral outcomes. We review functionality provided by major software packages for longitudinal fMRI analysis and describe what questions can and cannot be answered by these packages. Finally, we describe a novel approach to voxel-wise modeling that can facilitate iterative model experimentation and demonstrate its use on an example longitudinal fMRI data set.

2. Developmental questions of interest in cognitive neuroscience

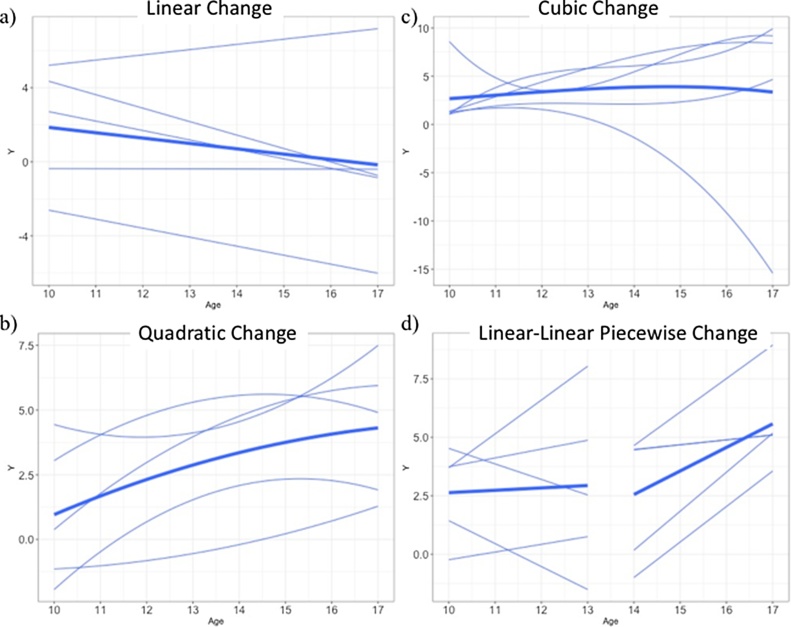
Developmental changes in neural and behavioral processes can unfold in a variety of different ways (Ram and Grimm, 2015), and the pattern of these changes may vary across different metrics of neural development, including measures of brain structure, task-based functional activation and connectivity, and functional connectivity measured at rest. Initially, much developmental cognitive neuroscience research examined developmental differences in these metrics using cross-sectional samples that spanned a wide age range, but more recently the field has begun systematic examination of how these aspects of neural structure and function change across development using longitudinal data. These changes can take a variety of forms (Kail and Ferrer, 2007). Change can occur as linear increases or decreases, a pattern frequently described, for example, in theoretical models of the development of cognitive control and maturation of prefrontal cortex (PFC) regions that support these control processes (Steinberg, 2010). Evidence from recent longitudinal studies, however, suggests that the developmental trajectory of activation during an inhibitory control task is non-linear and varies across regions of the PFC, with decreases in activation observed into adolescence that level off by early adulthood in dorsolateral PFC regions involved in executive control and increasing activation in error processing regions, including dorsal anterior cingulate, across adolescence that levels off in early adulthood (Luna et al., 2015, Ordaz et al., 2013a, Ordaz et al., 2013b). Indeed, developmental change in neural structure and function in other domains frequently follows a variety of non-linear patterns. These can include, among other forms: 1) quadratic patterns of growth, where a behavior or pattern of neural activity either emerges during a specific developmental period and then declines, or disappears during a specific period and then reappears later; 2) logarithmic changes that reflect more rapid developmental change at earlier ages that slow and level off at later ages; 3) cubic patterns, characterized by growth followed by decline (or vice versa) that occur at unequal rates; and a variety of other non-linear patterns (e.g., transition models, where a linear slope changes in magnitude at a discrete point in development) (see Fig. 1 for examples) (Kail and Ferrer, 2007). Quadratic patterns have been described in task-based fMRI studies for neural and behavioral processes that are at their greatest level in adolescence, and are either at much lower levels or not observable at all in childhood and adulthood. One example of this pattern is reward sensitivity and ventral striatum activation to reward, each of which are higher during adolescence than either childhood or adulthood, and have been observed in both cross-sectional and longitudinal studies (Braams et al., 2015a, Galvan et al., 2007). Logarithmic patterns have been documented in developmental studies of white matter microstructure, particularly for association fibers (e.g., fronto-temporal tracts including the cingulum and uncinate fasciculus), where growth is more rapid earlier in development and levels off in late adolescence and early adulthood (Lebel and Beaulieu, 2011). Finally, cubic patterns have been observed in longitudinal studies of cortical structure, whereby cortical thinning is present during childhood, accelerates during adolescence, and stabilizes by early adulthood (Tamnes et al., 2017). A variety of more complex patterns are also possible; for example, rapid development in neural circuits can produce relatively rapid changes in functioning, where there is a sudden shift in ability or behavior (Ram and Grimm, 2015). Such patterns might be expected, for example, for domains that exhibit critical periods of development where environmental input plays a strong role in shaping skill acquisition during circumscribed windows of time (e.g., phoneme discrimination; Kuhl et al., 2003). However, few longitudinal neuroimaging studies have examined the developmental changes in neural circuitry that underlie these patterns of sudden developmental change.

Fig. 1.

Examples of growth models showing inter-individual variability in growth: a) linear, b) quadratic, c) cubic and d) piecewise growth.

Longitudinal methods can also address a variety of questions about atypical patterns of developmental change that result, for example, from environmental experiences (e.g., exposure to toxins or to early-life stress), neurodevelopmental disorders, or psychopathology. Although atypical neural development can take a variety of forms, patterns of particular interest in developmental cognitive neuroscience include precocious development, where development occurs more rapidly than average for some individuals; delayed development, where developmental processes occur more slowly than expected; halted development, which involves maturation that stops after a period of typical development; failure to mature, reflecting an absence of developmental change; and ectopic development, where maturation occurs but is unexpected (Di Martino et al., 2014). Finally, the implications of developmental trajectories of neural structure, function, and connectivity for behavior and adaptive functioning are of central interest to the field. Exploring these questions introduces a variety of statistical challenges (e.g., examining relative model fit across groups; examining parallel or sequential longitudinal changes in brain and behavioral measures) that have yet to be resolved in standard neuroimaging software packages.

3. Statistical models that can be applied to these developmental questions

There are many statistical approaches that can be used to model within and between individual differences in change over time, which have arisen from distinct statistical traditions. Most longitudinal models may be classified as deriving from either the generalized mixed linear modeling (GMLM) framework or the structural equation modeling (SEM) framework. The GMLM is an extension of the GLM (described above), with the generalized referring to a broader class of models that all retain the same form of the linear model (i.e. Y = b0 + b1 * X + r_i) but allow for dependent variables with non-linear distributions (such as counts, binomial, and exponential distributions, among others) (see McCulloch, 2003). The mixed refers to the inclusion of random effects, which model variances and covariances among the coefficients in the linear model according to some unit of clustering (such as repeated observations clustered within individuals). There is also a broad class of longitudinal models that rely on the SEM framework that model latent (i.e. unobserved) variables as arising from common covariances between observed variables, as well as the structural relations between them. Both SEM and GMLM models are typically estimated using maximum likelihood. Table 1 provides an overview of some commonly used models and their capabilities as described in this section. Given that extensive scholarship has examined the relative merits and weaknesses of each of the modeling approaches we review here, we provide a brief summary of each approach, illustrations for how each type of model can be applied to longitudinal data, and point readers to seminal papers and reviews of each model where applicable.

Table 1.

Capabilities of different statistical models.

Statistical Model	Between-group mean differences	Rank-order change	Between individual change	Within individual change	Predictors of within-individual change over time	Correlations between growth processes	Latent Groups	Change as a predictor
Independent Samples T-test	X
ANOVA	X
(Multiple) Regression, General Linear Modeling	X	X
Repeated Measures ANOVA	X	X	X
Auto-regressive panel models	X	X	X
Latent change score	X	X	X	X	X	X		X
Multilevel growth models	X	X	X	X	X
Latent growth curve	X	X	X	X	X	X		X
Growth mixture model	X	X	X	X	X	X	X	X

To date, the vast majority of studies examining longitudinal change in developmental cognitive neuroscience have relied on GLM or GMLM-based models. GLM-based models, which estimate changes over time in the mean level of a particular behavior or neural process, have been used to determine whether changes in neural structure—modeled as difference scores from one time point to another—predict changes in working memory (Tamnes et al., 2013); or to determine if brain connectivity at one time point can predict alcohol use at a later time point (Peters et al., 2016a). These and other GLM-based methods (e.g., independent samples t-tests and ANOVA) may be appropriate for assessing mean level or rank order (i.e., between-individual) changes, and for identifying average developmental patterns of change over time. In longitudinal studies with two time points, GLM-based methods can also be used to address how an individual’s rank order changes between time points (i.e. how their level on a variable might change relative to others in the sample) by treating the initial measurement occasion as a covariate (e.g., regressing time 2 on time 1 and additional covariates of interest). Repeated-measures ANOVA is one example of how this type of GLM approach can be applied to longitudinal data. In developmental cognitive neuroscience, this method has been used, for example, to identify predictors of change in reward sensitivity across two time points (Urošević et al., 2012). Related SEM approaches such as auto-regressive and cross-lagged models can estimate rank-order changes and reciprocal associations between variables across time (Selig and Little, 2012). Collectively, GLM and their SEM-based equivalents support inferences about either cross-sectional differences in the mean of an outcome over time, or rank-order change between two time points (i.e., between-individual change), but are not appropriate for estimating within-individual changes, or between-individual differences in change over time. A general shortcoming of these approaches is that they conflate within and between-person associations (such as in cross-lagged panel models; Berry and Willoughby, 2016, Hamaker et al., 2015), and as such can provide misleading information about change. This results in a more general tendency to ignore common correlates of between-person differences, and to obtain misleading information about the directionality of associations (for an excellent illustration of this problem see Bailey and Littlefield (2016).

Increasingly, GMLM methods are being used to estimate within-individual change over time in developmental cognitive neuroscience. Multilevel growth models (also referred to as hierarchical linear growth models), probably the most common variant of GMLM, can estimate within-individual change over time, along with between-individual differences in mean levels over time and the predictors of these differences (Curran, 2003; for a general overview of multilevel models see Snijders and Bosker, 2011) Such models have been used, for example, to examine developmental changes in cortical thickness among children with and without attention-deficit/hyperactivity disorder (Shaw et al., 2006) and to evaluate whether brain activation during a cognitive control task is associated with developmental change in behavioral performance on the task over time (Ordaz et al., 2013a, Ordaz et al., 2013b). They have also been used to analyze developmental change in neural activity over multiple longitudinal assessments during a narrative comprehension task, and to determine whether reading comprehension is associated with these neural changes (Szaflarski et al., 2012). In short, GMLM methods allow researchers to characterize average changes in brain structure and function over time, and to predict between- and within-individual differences in those patterns. These models are particularly useful for estimating change across three or more measurement occasions.

Numerous other analytic approaches exist for analyzing longitudinal developmental data, though these have yet to be applied systematically to research questions in developmental cognitive neuroscience (see King et al. (under review) this issue). These are largely based in SEM, and allow researchers to test hypotheses that are unavailable in the GMLM framework. A variety of terms have been used to describe these SEM-based approaches, but most include the terms “latent” and “growth model.” There are some similarities between GMLM approaches and latent variable growth models (Curran, 2003), but SEM-based approaches allow a much broader array of models (and thus hypotheses) to be tested. The most critical difference is that latent variable growth models estimate change over time as a latent variable, which allows individual differences in growth to be correlated with (or predict) other variables. A broad overview of the types of longitudinal models available in the SEM framework is provided by Newsom (2015).

For example, in SEM-based models growth can be modeled not only as an outcome but also as a predictor of other processes, as in parallel process latent growth models (Cheong et al., 2003). Such a model could be used, for example, to examine not only how changes in exposure to stressful experiences over time predict changes in brain structure and function, but also to determine whether those changes in neural processes predict subsequent increases in symptoms of anxiety or depression. Neural changes across numerous time points could be examined as outcomes, predictors, correlates of other change processes, moderators, or mediators in SEM-based latent growth models. Other forms of longitudinal SEM-based models can be applied to determine whether there are discrete sub-groups that display different kinds of change over time, such as latent trajectory, growth mixture models, and latent transition models. Such models could be used to determine whether different underlying trajectories of development exist within a sample, reflecting various patterns of typical and atypical development (Di Martino et al., 2014), whether different trajectories of improvement following an insult or injury occur, or to characterize how individuals move between latent subgroups over time (Chow et al., 2013, Dolan et al., 2005); critically, such models can also be used to identify predictors of those disparate patterns over time. There are many other types of change models that rely on SEM-based approaches (see Ram and Grimm, 2015 or King et al. (under review) for a thorough discussion of SEM based models for longitudinal change). It is worth noting, however, that none of these models can be estimated in any of the widely used fMRI analysis software packages.

Analytic strategies using multilevel growth models frequently rely on model comparison to test hypotheses; in other words, two or more models that represent hypotheses of interest are estimated and compared to determine which model best describes the data. There is no universal generally accepted method for comparing models, and numerous types of model fit statistics can be computed to do so. Dozens of model fit statistics have been developed for making these types of comparisons. Each of these fit statistics varies in the underlying statistical approach for estimating fit and the types of penalties applied for increasing the number of terms in the model, among many other differences. Commonly used fit statistics include the Bayesian information criterion (BIC; Kass and Wasserman, 1995) and the Akaike information criterion (AIC; Akaike, 1973) each of which take into account the number of parameters in the model when assessing model fit (Braams et al., 2015b, Ordaz et al., 2013b, Peters et al., 2016b). These fit statistics can be compared across models to identify the model that provides the best fit to the data. Nested models form a particular class of models where the first (nested) model can be obtained from the second model by constraining parameters of the second model (e.g., a model estimating a linear effect of time is nested within a model that includes both linear and quadratic effect of time; as a result, the relative fit of these models can statistically compared). Likelihood ratio tests between nested models can be used to determine if one model provides a significantly better fit to the data than another model. In addition to these types of tests, researchers often use the heuristic of parsimony in order to select the best fitting model that is not over-fitted to the specific dataset. Because of the complexity of performing model comparison over tens of thousands of voxels representing different regions of the brain, neuroimaging software does not generally support these types of model fit statistics.

4. Review of existing fMRI longitudinal analysis software

Following pre-processing and pre-whitening to remove noise and autocorrelation (Huettel et al., 2014, Poldrack et al., 2011), common software packages such as the FMRIB Software Library (FSL), Statistical Parametric Modeling (SPM), and Analysis of Functional Neuroimages (AFNI) rely predominantly on a GLM approach, albeit with some extensions, to model brain responses over time. This approach allows for the estimation of t-tests, ANOVA, ANCOVA, and multiple regression. A simple single-parameter GLM can be modeled by the following equation:

$$y\left(t\right)=a*x\left(t\right)+b+e\left(t\right)$$

Here, the data from each voxel y(t) is modeled as a linear function of a stimulus being presented across a given voxel timecourse x(t), as well as an intercept b and a residual error (noise) term e(t). Because the BOLD response occurs after the presented stimuli and is nonlinear, the stimulus is convolved with a hemodynamic response function. Note that the shape of this function itself may vary across individuals. The GLM estimates the effect of the stimulus condition a on the BOLD response by minimizing e(t). Multiple stimuli timecourses can be modeled simultaneously. Because each voxel’s timecourse is modeled independently, this approach is vulnerable to type I errors introduced due to multiple comparison. Therefore, correction for multiple comparisons is typically performed following model estimation by analyzing clusters of voxels which are activated beyond a predetermined threshold using statistical testing derived from Gaussian random field theory (Friston et al., 1994, Hayasaka and Nichols, 2003), although recent simulations suggest that this approach can inflate false positives, particularly in some software packages, as compared to permutation testing approaches (Eklund et al., 2016).

The major software packages implement voxel-wise univariate modeling of the BOLD signal using a multi-stage process. The first-level models, executed on each individual run for each participant, assume fixed effects only − that is, the parameter of interest a is assumed to be the same for every participant. This approach provides the analyst with a single fixed effect estimate of a stimulus condition on BOLD response for each subject, above and beyond the noise included in the BOLD signal. The estimates derived from the first-level models are then “carried up” to higher-level models in subsequent mixed-effects analyses (Holmes and Friston, 1998). Modeling the random effect of intercept (i.e., the average task-related effect for each participant) is an extension to the GLM framework in fMRI analysis that is necessary to be able to extrapolate results beyond the study sample (Mumford and Poldrack, 2007). In this two-stage estimation procedure, subjects can be added to the analysis without having to re-run all the first level analyses, reducing execution time. This approach is often more practical than running a single multilevel model and has been shown to be statistically equivalent (Friston et al., 2005).

Although the GLM framework has been instrumental in the analysis of fMRI task data to date, it imposes numerous assumptions about the data structure and therefore limits the developmental questions that can be addressed. These limitations, reviewed in depth in a more general context by Chen et al. (2013), are as follows:

• 1.From ANCOVA, these models hold an assumption of sphericity, which requires that the variances of the differences between time points be equal across all pairwise combinations. Correspondingly, more flexible, alternative covariance matrices, such as autoregressive, compound, and fully unstructured covariance, cannot be specified. These covariance structures are frequently used in longitudinal models of behavioral factors (Raudenbush and Bryk, 2002).
• 2.While random intercepts are necessary for generalizability, it is not possible to specify random slopes (i.e., individual differences in change over time across multiple measurement occasions). Accordingly, meaningful residual variance cannot be modeled, which limits the capacity of GLM for addressing questions of change over time. More specifically, it is not possible to model multiple continuous within- and between-individual predictors, nor specify within-level and cross-level interactions to explain patterns of change over time (i.e., a random slope of time).
• 3.It is difficult to deal with missing data. This may require that imputation of the data be performed before model fitting, although this functionality is not available in most fMRI software packages.

These assumptions limit the flexibility of the GLM in developmental research. The first assumption of sphericity stems from the multi-level estimation procedure. If this assumption is not met, this can lead to inflation of both Type I and Type II errors (e.g., Chen et al., 2013). This means that estimates may be biased, although the degree to which they are biased depends on how auto-correlated the data actually are. In other words, when within-individual values are correlated more strongly with values at time points that are closer in time as opposed to farther away in time (i.e., auto-correlation), numerous assumptions are violated that can introduce bias into estimates that varies in magnitude depending on the magnitude of auto-correlation. The second assumption makes the GLM unsuitable for estimating variance in trajectories of change (such as rates of growth, or differences in the shape of growth curves over time), which are important outcomes in developmental processes (see Section 2). The third assumption is problematic in longitudinal research; as the number of scheduled scans per subject increases, it becomes highly likely that some scans will be unusable or be missed, necessitating modeling approaches that are robust to missing data.

Given these limitations in existing software packages, longitudinal fMRI studies that have used more complex longitudinal models have typically done so by modeling the BOLD signal using some non-fMRI statistical analysis package in one or more regions of interest (ROIs). For example, Ordaz et al., 2013a, Ordaz et al., 2013b used R to model developmental trajectories in brain regions within known circuits involved in aspects of inhibitory control (Ordaz et al., 2013a, Ordaz et al., 2013b). This ROI approach limits analysis to specific regions rather than taking a whole brain voxel-wise approach (as with a GLM). The advantage of this approach is that it is easier to apply more sophisticated methods; the parameter estimates from a first level analysis can be extracted and used more generally in higher-level models. The problem of correcting for multiple comparisons is greatly diminished because the number of regions is controlled, and the statistical power of the experiment is greater. The disadvantage of the approach is that one loses the ability to conduct exploratory analysis of the whole brain, producing an incomplete picture of how brain function is changing over time. Using parameter estimates derived from a single contrast of interest in a higher-level model might fail to fully account for correlated random effects. To address these challenges with ROI-based approaches, Ordaz et al., 2013a, Ordaz et al., 2013b expanded their ROI analysis to conduct a voxel-wise analysis in R as verification of their findings. The field would benefit from a tool that would allow these types of voxel-wise analyses using more advanced growth modeling to be applied more easily to fMRI data. Before describing such a tool, we first review the functionality for longitudinal analyses available in each of the three commonly used fMRI analysis software packages.

4.1. FSL

FSL is a library of neuroimaging analysis tools, written primarily in C/C++ with Tcl graphical front-ends. FSL implements a univariate voxel-wise approach to fMRI analysis, taking a multi-level modeling approach for within-subject data that can estimate random intercepts (Beckmann et al., 2003). Specifically, FSL utilizes a three-stage modeling approach. First, person-level statistics are calculated (i.e., task effects) for each run of data acquired. Second, these person-level estimates are combined to estimate a mean effect for each participant—these estimates are allowed to vary across participants in a study. Third, these person-level estimates are used in group-level analysis of various kinds (e.g., t-tests comparing two groups on a contrast of interest, or linear regression to examine a continuous predictor of a contrast of interest). FLAME (FMRIB's Local Analysis of Mixed Effects) (Woolrich et al., 2004) is used to specify GMLM models in FSL that can estimate a random intercept for each individual based on multiple runs of data. This has advantages in modeling group/person-level differences (equivalent to specifying random intercepts in multilevel models) because it does not need the same number of time points for all subjects or require the same number of subjects across groups. The estimation is achieved using a Bayesian method. One key limitation is that FLAME does not model within-individual variance across multiple distinct measurement occasions (i.e., random slopes). This is because there are usually not many sessions per subject, which can cause convergence problems associated with estimating session-to-session variance. Moreover, as described above, models are conducted using repeated measures ANOVA, meaning that explanatory variables in person-level models are necessarily categorical rather than continuous (see above limitations).

4.2. SPM

The Statistical Parametric Mapping (SPM) software suite is a toolbox based in MATLAB (MathWorks, Inc.). Like most neuroimaging software, SPM is massively univariate, treating each voxel independently, with support for cluster-level significance testing based on random field theory. Underlying statistical models in SPM are based on the GLM with additional support for limited Bayesian inference using the same sets of models that can be specified in the GLM component. Factorial designs can be specified at both the individual level and group level, and this procedure allows estimation of t-tests, linear models, and ANCOVA when certain assumptions are met. However, as described above, longitudinal data often have many properties that violate assumptions of, or that are burdensome to encode in these models. There is support for estimating simple repeated measures ANOVA using a within-subjects factor, either by using the so called “Flexible Factorial” design or doing much of the estimation at the individual level (Henson and Penny, 2003). SPM tools are thus not well-suited for unbiased estimation for longitudinal studies with missing data. Relating changes in neural data over time with changes in other time-varying covariates is not possible. GLM Flex Fast2 (Schultz, 2017) does provide some extended capabilities to SPM’s implementation of the GLM, but it still does not address several of the situations indicated above.

4.3. AFNI

The Analysis of Functional NeuroImages (AFNI) is suite of programs written in multiple languages—mainly C, but also Python (van Rossum, 2001) and R (R Core Team, 2014)—for the analysis of fMRI data. Like SPM, AFNI relies on a two stage analysis approach in which individual level statistics are calculated and used as the raw data for the group-level analysis. Similar to SPM and FSL, AFNI is massively univariate, and includes support for non-parametric estimation of cluster-wise significance values, although the estimates of spatial smoothness are parametric. In addition to providing similar functionality to SPM (and FSL, though without accounting for first-level variance), AFNI has recently added a component, 3dLME, that implements a maximum-likelihood, multi-level (i.e., linear mixed effects, or hierarchical linear) modeling approach to group level data. This component was written to address the above limitations of the GLM approach (Chen et al., 2013). 3dLME is built around the nlme and the lme4 mixed effects modeling packages (Bates et al., 2015; Pinheiro et al., 2017) in R (R Core Team, 2014), and so can encode and analyze nearly any single model allowable in either package, even ones that include auto-correlated error structures. Missing data is handled by the underlying R packages. However, variance-covariance structures cannot be customized. The output of this program are 3D images of voxel-wise F-statistics for all model terms (main and interaction effects), t-tests for quantitative (continuous) variables, as well custom general linear t and F tests. It is also possible to generate per-voxel intra-class correlation estimates. 3dLME is a fixed framework in which the BOLD signal in a single voxel is always the dependent variable, and the return values are fixed in the way described above, so it does not allow the flexibility one would have by using R directly. Despite these limitations, 3dLME remains the most sophisticated tool among the regularly used neuroimaging analysis suites available for analyzing longitudinal fMRI data.

5. A new approach for longitudinal fMRI analysis

As shown in Table 2, existing packages for fMRI analysis fall well short of being able to fit the spectrum of models that are of interest in developmental research. The most flexible major software package is AFNI, which passes through features of mixed effects models as implemented by R in the packages nlme and lme4. However, other major packages do not have this flexibility and have serious limitations when applied to longitudinal fMRI data. The most obvious limitation with current fMRI software is an inability to model the types of changes that longitudinal studies are designed to characterize. In particular, it is currently impossible to answer questions that require modeling change as a latent variable. This is required for questions that involve using changes in brain structure, function, and connectivity as a predictor of other factors (e.g., behavior, health), or to examine brain changes over time as mediators or moderators of other associations. Importantly, because of the complexity of aspects of fMRI processing that are unrelated to statistical modeling, and the multi-level analysis approach adopted by commonly used packages, it is difficult to bridge modeling methods used in developmental science with fMRI analysis. Below, we present a novel approach that would allow the most current statistical models of developmental change to be applied to fMRI data.

Table 2.

Capabilities of commonly used neuroimaging statistical software.

fMRI Analysis Software	Missing Data	Voxel-wise model comparison	Between-group mean differences	Rank-order change	Between individual change	Within individual change	Predictors of within-individual change over time	Correlations between growth processes	Latent Groups	Change as a predictor
FSL			x	x	x
SPM			x	x	x
AFNI			x	x	x
AFNI (3dNLME)	x	x	x	x	x	x	x			x

Recent developments in scientific computing can be exploited to address the lack of flexibility of current fMRI modeling. We are currently developing a package called Neuropointillist that allows a model to be run on each voxel, for each participant, at each time point of the study using any type of model that can be specified in R, including GMLM and SEM-based models. Neuropointillist assembles longitudinal pre-processed and spatially normalized fMRI data into a long-form data set (i.e., where each row represents data from a particular voxel from a particular subject at a particular time) suitable for analysis in R (Madhyastha et al., in prep). The specified model is applied to every voxel, for every subject in the dataset, and each measurement occasion. The program then assembles the outputs into statistical parameter maps. Because of the lack of consensus in best practices for pre-processing neuroimaging data, we have separated the tools used for statistical modeling from those involved in preprocessing, following a growing trend for interchangeability within neuroimaging workflows (Askren et al., 2016, Gorgolewski et al., 2011). The only additional step that would normally be performed by fMRI software is pre-whitening, an approach to correcting for autocorrelation of the BOLD signal; autocorrelation needs to be handled by the model.

However, one can also use the parameter estimates obtained from first-level analyses with standard fMRI packages. This affords complete flexibility to evaluate any statistical model of interest for voxel-wise analysis, particularly those that are more commonly used in psychology and behavioral sciences (i.e., latent growth curve models that estimate growth as a latent factor).

Neuropointillist was designed to address the computing challenges inherent in estimating complex models that are slow to converge in fMRI data, where these models must be estimated thousands of times (i.e., at every voxel in the brain). This is particularly important for estimating more complex longitudinal models. In rapidly developing fields such as cognitive neuroscience, where it is important to quickly develop, evaluate, and reject or refine new models, ease of programming is key. Scripted languages such as R or Python are easier to program and more widely used in the behavioral sciences than compiled languages like C or C++, and are therefore more likely to be used. R is of particular interest because it is the lingua franca of statisticians—most of the newest statistical techniques are first implemented in R before they reach other statistical packages. This decreases the barriers to collaboration with developmental researchers and statisticians who may be familiar with longitudinal modeling, but not with the syntax and restrictions of model specification in fMRI analysis packages.

A caveat, however, is that scripted languages, such as R, are much slower than compiled code. This means that computation time in R on standard desktop computers may be intractable for certain voxel-wise models. An important observation is that analyses applied to tens of thousands of voxels in the brain can be split so that each voxel runs independently of the others. Neuropointillist exploits this parallelism. Specifically, it splits all voxels in the brain and allows them each to be sent to different processing units to be run in parallel, reassembling them upon completion. Although most universities facilitate access to parallel computing clusters, parallel computing resources are now generally accessible for an hourly fee through cloud service providers such as Amazon, Google and Microsoft. Use of parallelism can dramatically minimize the amount of time needed to run a complex voxel-wise model. Reducing execution time in this way makes it feasible to perform the iterative model testing that is required when estimating latent growth models or other more complex longitudinal models in a voxel-wise analysis. Cost optimization strategies (e.g., spot pricing available through Amazon) bring the cost to the user below that of purchasing and maintaining dedicated hardware. By separating parallelism and cloud services development from statistical modeling, we hope to make it easier to conduct voxel-wise exploratory modeling without advanced computational expertise.

To illustrate the flexibility of Neuropointillist, we provide three modeling examples using a longitudinal developmental data set with three time points. These examples are not intended to test or evaluate actual developmental processes or effects, and we refrain from interpretation of specific contrasts. These examples are provided simply to illustrate the functionality of Neuropointillist and demonstrate that these types of analyses are possible on an actual longitudinal task-based fMRI data set. The first example uses fit statistics to evaluate where in the brain two task-related predictors interacted in a model that included random effects for both intercept and time (i.e., slope). The second example determines the best functional form for time by comparing model fit statistics for linear fixed, linear random, and fixed quadratic and logarithmic forms of growth. Although these types of model comparisons are common in developmental research, the only neuroimaging package that currently outputs model fit statistics is AFNI 3dLME—a feature that was recently added as of this writing. However, fit statistics are limited to those that are passed through from the underlying R packages to the AFNI output. In contrast, numerous types of model fit statistics can easily be estimated in R in a general framework. The third example uses a parallel growth model to explore the correlation between of linear growth in pubertal development with linear growth in neural activation (i.e., BOLD signal) over time. This type of SEM analysis is currently not possible with current neuroimaging software, but could be used to address numerous questions of interest, particularly regarding brain-behavior associations over time.

The longitudinal dataset comprises adolescents who were scanned at 3 waves (N1 = 78, N2 = 49, N3 = 35) at ages 10–16 while making evaluations of target ‘self’ and ‘other’ in both social and academic domains (see Pfeifer et al. (2013) and Pfeifer et al. (2007) for a description of the task and subsets of the data; the data set used in these demonstrations of Neuropointillist is larger than previously described). The Pubertal Development Scale (PDS; Petersen et al., 1988) was administered at each measurement occasion. We estimated and compared mixed effects models in a voxel-wise analysis using t-statistics from a first level analysis where each voxel represented the degree of association between the BOLD response time course and the model-expected time course for each cell of this 2 × 2 experiment (target [self vs. other] and domain [social vs. academic]). All coordinates are reported in MNI space. R code for the analyses described below are in Supplemental Materials.

For greater details about the Neuropointillist package and its use, please see http://github.com/IBIC/neuropointillist, the software repository for the code. Documentation on the use of the software, and a worked tutorial, is included in this repository and is hosted on http://ibic.github.io/neuropointillist. Currently the package parallelizes execution in shared memory and Son of Grid Engine (SGE) cluster environments. To use Amazon Web Services (AWS) one creates a temporary cluster using an AWS account to run neuropointillist as on a local cluster. This means that data needs to be copied to the cluster and back. We are working on improving the integration of AWS with neuropointillist to make remote execution easier and more transparent.

5.1. Example 1: identifying where an interaction exists using model fit statistics

The base model included fixed effects of age, time, domain and target and a random intercept and slope, while the extended model included an additional interaction between target and domain. The relative fit of the base and extended models were then compared using the AIC. In all examples, where there was an error in model fit or in convergence, a missing data code was returned to exclude the voxel from analysis.

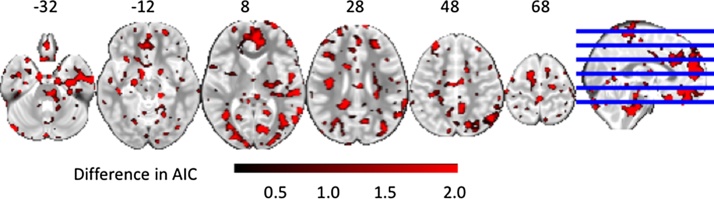
Fig. 2 shows areas of the brain where there is evidence based on the AIC for the extended model, supporting an interaction between target and domain. Evidence for an interaction is strong in areas that we expect to be activated by the task (e.g., medial prefrontal cortex). This simple example demonstrates the importance of model testing for identifying the best-fitting model. Inferences from a model that did not properly specify the presence of an interaction between task conditions might be incorrect in areas where the extended model was superior.

Fig. 2.

Neuropointillist results: Evaluating where there is a significant interaction. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

5.2. Example 2: determining the best functional form for time

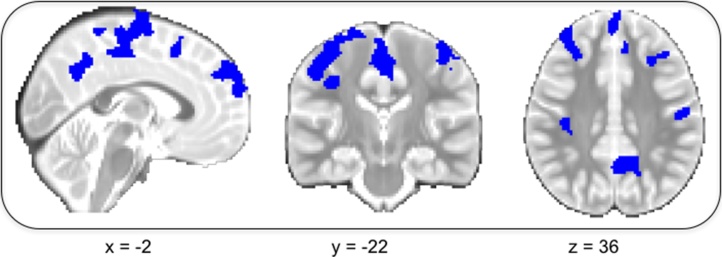
Our second example determines the best functional form for time − a standard step in model fitting for longitudinal data analysis. Here, we include fixed effects of target and domain, and compare linear fixed, linear random, quadratic fixed, and logarithmic fixed effects of time. Linear fixed models were nested within linear random and quadratic fixed effects models and so could be statistically compared using a log-likelihood ratio test; all models were compared using the AIC and BIC. After running all models, we identified masks for the best models (as indicated by all available fit statistics). With these masks, we identified clusters of voxels for each model that were significantly associated with time, cluster-corrected for multiple comparisons at p < 0.05, alpha = 0.05.

We found that inclusion of a random effect of time improved model fit over nearly all voxels in the brain as compared to a fixed effect of time. Similarly, we found that the logarithmic model was best only where the effect of time was non-significant or within white matter (not shown). Fig. 3 shows areas (in blue) where the quadratic model for time was best. It is important to note that estimating functional forms that are non-linear would ideally be done in data with more than three time points, particularly as random effects can only be tested for a linear slope with three time points (King et al., this issue).

Fig. 3.

Neuropointillist results: Determining the best functional form for time. Blue regions are areas where there is a quadratic effect of time. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

5.3. Example 3: correlating growth curves

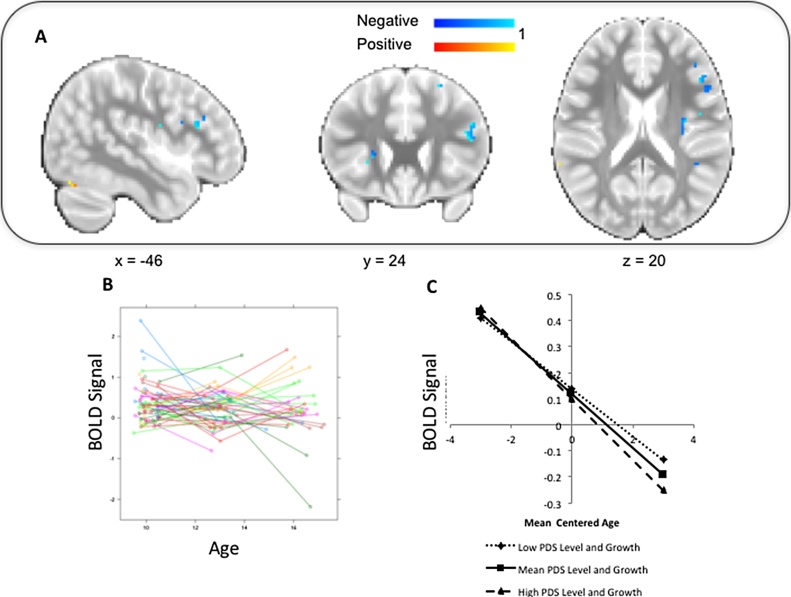
Our third example used the SEM package lavaan (Rosseel, 2012) to identify areas in the brain where the slope of pubertal development (measured by the PDS) was correlated with the slope of mean BOLD signal (averaged across all four task conditions). Although the analysis approach is of interest for many questions in developmental cognitive neuroscience (i.e., questions of how change in brain function correlates with change in behavior or other characteristics), in this example, the signal we are modeling is of no particular interest (i.e., we averaged BOLD signal across all conditions rather than using a particular contrast). Fig. 4A shows areas in the brain where the estimated correlation of the slopes is significantly positive or negative, uncorrected for multiple comparisons at p < 0.05.

Fig. 4.

Neuropointillist results: Correlating growth curves. A. Regions where there is evidence for positive or negative correlation between slopes of pubertal development and BOLD signal. B. Individual growth curves for BOLD signal. C. Illustration of the relationship between BOLD signal and mean centered age for different initial levels and growth of PDS. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

We extracted the parameter estimates from a single voxel (−46, 24, 20) in the inferior frontal gyrus, with negative linear growth, to illustrate how to interpret correlated growth. Fig. 4B shows individual change in activation by age. Although the mean BOLD signal in this voxel is not statistically different from zero, there is substantial individual variability in the slope of the growth curves. This growth is systematically related to pubertal development. Fig. 4C shows average growth curves in activation at this voxel for a hypothetical individual who had low initial levels of the PDS and exhibited low growth over time (1 SD below the mean), compared to an individual who exhibited both average initial levels on the PDS and exhibited average growth in the PDS over time, and an individual who showed high initial levels of the PDS and grew at a higher rate over time (1 SD above the mean). Both level and slope of PDS must be incorporated to show how they are associated with trajectories of BOLD signal, because both level and slope define the trajectory in a parallel process model. At low PDS slope and intercept, pubertal development is unfolding relatively slowly, and the decrease in BOLD signal is shallow. At a high PDS slope and intercept, puberty is advancing more rapidly, and there is a much steeper decrease in BOLD signal.

6. Summary of examples

As demonstrated in these examples, Neuropointillist is a parallelizable framework that permits the use of any model to be applied to voxel-wise fMRI data. The flexibility of the framework we propose is extremely general, allowing any model callable from R to be run on a voxel. This helps to address some of the limitations of existing neuroimaging software, such as missing data. There are many strategies for dealing with missing data, such as imputation or using statistical models to allow for missing data, that are easy to implement in R and could easily be applied within Neuropointillist. Another problem inherent in longitudinal studies is practice effects. Flexibility in modeling growth curves using SEM models for change is helpful in modeling practice effects; for example, developmental effects can be estimated separately from practice effects (Ferrer et al., 2005).

The R package OpenMX, which supports mixture growth modeling, may be used instead of lavaan. Mplus (Muthén and Muthén, 1998), a powerful commercial latent variable modeling program, can also be invoked from R using the MplusAutomation package. These SEM options allow the use of a wide range of SEM-based longitudinal growth and latent variable models, none of which are currently available to the neuroimaging community.

Although this framework makes it easier to execute and compare voxel-wise models in R, there are still many challenges that will need to be addressed. Perhaps the biggest challenge is that model building is often an iterative process. Practically, this is challenging to do with tens of thousands of voxels. We will need to be able to program iterative strategies for testing and modifying models at each voxel. Then, we will need tools for visualizing and interpreting complex results. As our examples above show, it is not clear whether the same model will be accurate in all parts of the brain. However, there is currently no consensus on how to best compare methods in the spatially extended context of the brain. Although our software exploits parallelism to improve performance, there are still models that will be intractable and improvements that will need to be made to increase computational speed. This will require programming optimization and/or the development of new, more efficient statistical approaches.

fMRI pre-processing steps can have an impact on subsequent statistics. For example, larger spatial smoothing kernels affect the size of a cluster that is statistically significant. Moving away from program defaults means that scientists need to be aware of statistical assumptions throughout the analysis pipeline. Finally, these approaches are limited only to voxel-based analyses. Multivariate approaches are clearly important to understanding both task activation and longitudinal analysis and will ultimately need to be supported within this framework. This is functionality we hope to incorporate in the future.

7. Discussion

There is a wide gap between the modeling capabilities of current neuroimaging software and the models that are necessary to answer developmental questions. Most neuroimaging software is based on the GLM model, which supports inferences about either cross-sectional differences in the mean of an outcome over time, or between-individual change. However, GLM-based models are not appropriate for estimating within-individual changes, or between-individual differences in change over time. These types of questions require multilevel growth models, which are currently only implemented in AFNI 3dnlme. Many types of questions about growth cannot be answered in the multilevel growth model framework, however. For example, questions about how growth predicts other processes, whether there are discrete sub-groups that display different types of change over time, and whether neural changes are moderators or mediators of other processes require the use of SEM-based models and are currently impossible to answer in neuroimaging software in a whole-brain analysis framework.

We propose a flexible framework called Neuropointillist, which allows one to use R to describe a model that can be applied to pre-processed fMRI data. Voxel-wise models are executed in parallel and reassembled to create a spatial statistical map. Rather than wrapping specific functions, we permit any code to be executed on each voxel. This approach has the advantage of allowing experimentation with any growth model, including SEM-based models, that can be described in R (or in software that can be called from R). We demonstrate this approach to compare fit statistics for various model specifications in a longitudinal fMRI data set.

The power to model longitudinal fMRI data more flexibly introduces new challenges. First, there is no guarantee that the same model will describe change in all areas of the brain, and there are currently no accepted methods for selecting a best-fitting model or summarizing this type of complexity. As it is generally not of interest to make inferences at the level of voxels but at the level of meaningful clusters of voxels, it is likely that principles drawn from cluster-level inference could be applied to issues of model fit. But these methods will require ongoing refinement and debate. Second, building and testing SEM-based growth models is often an iterative procedure that will need to be automated to conduct such modeling at a voxel-wise scale in longitudinal fMRI data. Third, this paper has focused on voxel-wise analyses only, despite the fact that there is much interest in development of connections between regions in the brain, both at task and at rest. Multivariate longitudinal analysis of the development of networks remains relatively unexplored. Finally, no statistical method can compensate for the lack of a good theory to help understand how to interpret complex patterns of growth across the brain.

These challenges are welcome, because the ability to apply state-of-the-art longitudinal models is necessary to advance our understanding of how the brain changes across development, allowing us to study individual change in brain structure and function in relation to the environment and experience and in relation to changes in behavior. This understanding is key to developmental cognitive neuroscience and presents the field with innumerable challenges to tackle in the years to come as we develop more sophisticated approaches for modeling dynamic changes in the brain across time.

Conflict of Interest

None

Appendix A. Supplementary data

The following is Supplementary data to this article: