Locally stable brain states predict suppression of epileptic activity by enhanced cognitive effort

Abstract

Cognitive effort is known to play a role in healthy brain state organization, but little is known about its effects on pathological brain dynamics. When cortical stimulation is used to map functional brain areas prior to surgery, a common unwanted side effect is the appearance of afterdischarges (ADs), epileptiform and potentially epileptogenic discharges that can progress to a clinical seizure. It is therefore desirable to suppress this activity. Here, we analyze electrocorticography recordings from 15 patients with epilepsy. We show that a cognitive intervention in the form of asking an arithmetic question can be effective in suppressing ADs, but that its effectiveness is dependent upon the brain state at the time of intervention. By applying novel techniques from network analysis to quantify brain states, we find that the spatial organization of ADs with respect to coherent brain regions relates to the success of the cognitive intervention: if ADs are mainly localized within a single stable brain region, a cognitive intervention is likely to suppress the ADs. These findings show that cognitive effort is a useful tactic to modify unstable pathological activity associated with epilepsy, and suggest that the success of therapeutic interventions to alter activity may depend on an individual's brain state at the time of intervention.

Highlights

• •Cognitive intervention in the form of an arithmetic question can sometimes stop epileptic afterdischarges
• •Brain states are measured through community structure of functional brain networks
• •Success of intervention depends on spatial relationship between afterdischarge network and brain state
• •Dynamic community detection is used to assess community stability
• •If the afterdischarge network is in a strong, stable community, the cognitive intervention likely stops the afterdischarges

1. Introduction

The healthy human brain is a dynamic system of connected elements whose state is constantly changing over time and with behavior. However, in diseased patients, it is sometimes the case that brain activity becomes altered. Suppressing unwanted brain activity through applied perturbations is possible, and brain stimulation has demonstrated success in treating pathological brain activity associated with a multitude of disorders such as tremor (Elias and Shah, 2014; Fasano and Lozano, 2015), Parkinson's disease (Grafton et al., 2006; Hess, 2013), and epilepsy (Fisher and Velasco, 2014). However, much remains unknown about the mechanisms of such interventions, making it difficult to direct and improve treatment strategies (Johnson et al., 2013).

This is particularly true in the case of epilepsy, a highly diverse spectrum of disorders characterized by the presence of recurrent seizures (England et al., 2012). Because approximately 1/3 of epilepsy patients will develop a drug resistant form of the disorder (Laxer et al., 2014), the development of alternative methods to suppress and/or modify the unwanted brain activity are essential, and recent advances in the ability to selectively modify brain circuits makes this kind of intervention an attractive option (Krook-Magnuson and Soltesz, 2015). Such interventions can be achieved by electrical stimulation through implanted electrodes that target specific anatomical regions (Fisher and Velasco, 2014; Fridley et al., 2012; Schulze-Bonhage, 2017), or in rodent models, by optical stimulation (Ewell et al., 2015; Krook-Magnuson et al., 2013; Paz et al., 2013), targeting genetically defined subpopulations of neurons. However, it is known that certain subnetworks of brain regions become engaged during task performance (Davison et al., 2015; Kirschner et al., 2012), and thus an alternative and non-invasive option is the modification of brain activity through the activation or inactivation of a subnetwork associated with the performance of a task.

Much work has focused on altering epileptiform activity associated with seizures (Fisher and Velasco, 2014; Fridley et al., 2012; Schulze-Bonhage, 2017), but epileptiform afterdischarges (ADs) present another form of undesirable brain activity associated with epilepsy. These short spike and wave events visible in electrocorticography recordings can appear after electrical stimulation in patients undergoing functional brain mapping for surgical evaluation (Lee et al., 2010; Lesser et al., 1999). Brief pulse stimulation (BPS) has been shown to sometimes be successful in aborting ADs when applied through the same stimulating electrodes (Lesser et al., 1999; Mizuno-Matsumoto et al., 2002; Ren et al., 2017), but if this intervention is not effective, the ADs can progress to a clinical seizure, interfering with clinical testing and placing the patient at risk. Because BPS is only partially effective in aborting AD, it is especially important to investigate alternative methods of intervention, such as task circuit activation, in order to suppress the AD and prevent seizures.

While targeted stimulation or task network activation provide efficient means to alter brain activity, it is also known that the current state of the brain can also play a role in the efficacy of the intervention (Alagapan et al., 2016; Gharabaghi et al., 2014; Silvanto et al., 2008, Silvanto et al., 2007). It is therefore necessary to develop methods to quantify and classify brain state evolution. Here, network science provides the necessary tools to map the brain to a graph and measure brain states by quantifying network structure over time (Bassett and Sporns, 2017; Muldoon and Bassett, 2016). Functional brain networks can be derived in which recording electrodes are network nodes and connections between nodes (electrodes) are given by statistical relationships such as synchronization between brain activity recorded by two electrodes. It is then possible to quantify brain states over time using techniques from network theory to measure dynamic properties of the network structure.

In this study, we use network neuroscience to characterize electrocorticography recordings from 15 patients with epilepsy who display ADs resulting from stimulation during functional brain mapping. Each patient's data is mapped to a functional brain network by measuring the pairwise coherence between electrodes. We then quantify the brain state using community detection techniques to identify the presence and spatial location of coherent communities of electrodes. We additionally measure the spatial interaction between detected communities and the AD subnetwork and further characterize the brain state by measuring community strength and stability. Finally, we show that a cognitive intervention (in the form of an arithmetic question) can be successful in stopping unstable brain activity characterized by epileptiform ADs, but that the success of the intervention hinges on the brain state immediately prior to the intervention.

2. Materials and methods

2.1. Patient data and experimental design

Electrocorticographic activity was continuously recorded from 15 patients in their hospital rooms in the Epilepsy Monitoring Unit at Johns Hopkins Hospital. Patients were awaiting surgical resection for intractable epilepsy and had been previously implanted with grid, strip, or depth electrodes. Placement and locations of electrodes were determined solely on clinical grounds. Implantations and surgeries on a given patient were always done by the same surgeon. One surgeon performed ten cases, another performed four, and another performed one. See Table 1 for details of patient information and recording sites. Patients underwent continuous video-electrocorticographic monitoring. Electrocorticography (ECoG) was recorded at 1000 samples/s using Schwarzer EEG Amplifiers Model 210033 (Natus Europe GmbH, Robert-Koch-Str. 1, Planegg, Germany). The machines used 16 bit A-D converters (gain 1408, range 4.5 V, noise referred to input 1.5 mV). Recordings had a high linear frequency setting of 300 Hz with a 20 dB/octave slope and a low linear frequency setting of 0.0016 Hz, slope 6 dB/octave. During recordings, patients were awake and comfortable, lying in bed with the head of the bed elevated. Stimulation for clinical testing was delivered to pairs of implanted electrodes, using 50 Hz, 0.3-millisecond-duration biphasic square wave pulse pairs, delivered in trains lasting up to 5 s, with intensities gradually increased from 1 up to as high as 15 mA, depending upon clinical findings. ADs appeared with intensities of 7–15 mA (11.5 ± 1.8). If ADs occurred, brief pulse stimulation (BPS; (Lesser et al., 1999)) was used in an attempt to stop the ADs. Decisions to use BPS, or to subsequently use a cognitive task in an effort to abort the ADs, were determined solely on clinical grounds. We reviewed 58 consecutive patients who underwent cortical stimulation via subdural electrodes over a 4 year period. Of these, 15 were found to have been asked arithmetic questions in an effort to abort ADs, and this 15 patient subgroup is presented in this study. The analysis of the recordings was approved by the Institutional Review Board of the Johns Hopkins Medical Institutions.

Table 1.

Patient information. Patient information for the 15 subjects analyzed.

Patient	Gender	Age		AC Rx	SZ type*	Surgery type	Pathology	Electrodes		Number of trials
		Onset	Surgery					Monitored	Implanted	ADs stop	ADs cont
S1	f	21 y	41 y	OXC	1,2	L F res	Reactive changes only	86	91	12	10
S2	m	16 y	30 y	LTG	1,2,3	R P les	Cortical dysplasia/balloon cells	77	81	3	3
S3	f	3 m	20 y	LTG ZNS	1	R F les	Cortical dysplasia	81	88	4	1
S4	m	10 y	16 y	VPA	1,2	L T les	Low grade glioma GFAP+, synaptophysin −, EMU staining for microlumens neg, no mitoses, MIB-1 index overall low focally somewhat high (6%)	56	61	0	1
S5	m	8 h	12 y	VPA LOR	1,2,3	rt post F les	No specific findings	75	81	2	0
S6	m	46 y	50 y	CBZ	2,3	L B res, leave H	Neocortex with Chaslin's subplial gliosis	91	97	1	0
S7	f	10 y	27 y	LTG	1,3	Ant RF re-res	Balloon cells, abnormal distribution of pyramidal neurons	99	110	1	2
S8	f	7 y	53 y	LEV CBZ	1,2,3	R T re-res	Neuronal loss, gliosis	59	62	0	3
S9	f	12 y	32 y	PHN	2,3	Extend RT res	Reactive changes only	79	83	1	0
S10	m	“Childhood”	48 y	LTG	1,3	rt F	No specific changes	109	113	0	3
S11	m	32 y	41 y	VPA CBZ	1,2	L T Lob sparing H	Reactive changes only	77	81	2	1
S12	f	47 y	50 y	OXC PGB	2	L T Lob sparing base & H	Oligodendroglioma grade 2	107	108	0	1
S13	f	13 y	20 y	LEV CBZ	2	R T re-res	Reactive changes only	80	86	1	3
S14	m	8 y	14 y	OXC RUF LCM VNS	2	Deferred. Subsequent les	Left occipital dysembryoplastic neuroepithelial tumours (DNET)	88	96	0	1
S15	f	15 y	29 y	LCM LEV	2	No surgery - risk to language	No surgery	105	115	1	0
Sum	7 m 8f	0–46 y	12–53 y					1269	1353	27	30

Gender: f = female m = male.

Age: h = hours, m = months, y = years, m = month.

AC RX = anticonvulsant treatment at time of surgery: CBZ = carbamazepine; LCM = lacosamide; LEV = levetiracetam; LOR = lorazepam; LTG = lamotrigine; OXC = oxcarbazepine; PGB = pregabalin; PHN = phenytoin; RUF = rufinamide; VNS = vagal nerve stimulator; VPA = divalproex; ZNS = zonisamide.

Surgery type = surgery performed consequent to this evaluation: Ant = anterior; Post = posterior; L = left; R = right; B = temporal base; F = frontal; mes = mesial; P = parietal; T = temporal; H = hippocampus; Les = lesionectomy; Lob = lobectomy; Res = resection; Re-res = re-resection.

SZ type = seizure type: *using recent International League Against Epilepsy Classification (Fisher et al., 2017); 1 = focal aware; 2 = focal impaired awareness; 3 = focal to bilateral tonic-clonic.

2.2. Cognitive task

When BPS was unsuccessful in terminating ADs, patients were next given a cognitive task: they were asked to answer an arithmetic question using mental calculation. The calculation involved addition to, subtraction from, or multiplication of a two-digit number, each chosen at random from the set of real numbers between 10 and 99.

2.3. Selection of analysis windows

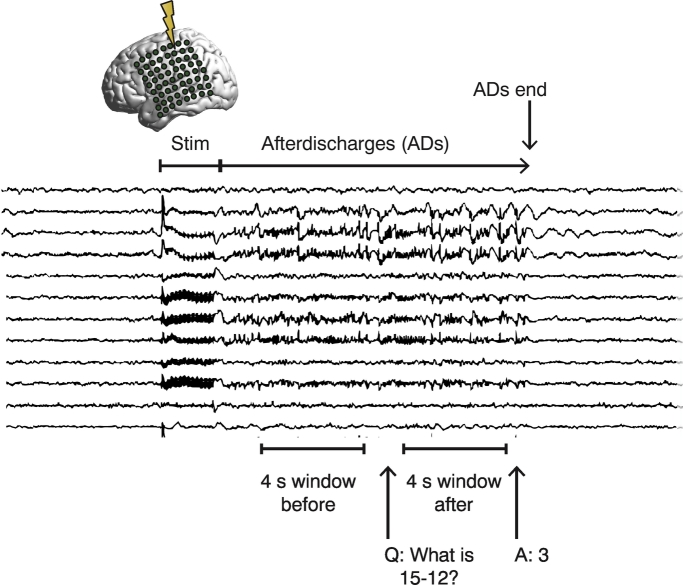
The data were analyzed for two artifact free 4.096 s windows. The first was during ADs but before the arithmetic question was asked. The second window was after the question was asked but before the ADs stopped. Because ADs could end quickly after the question was asked, the second 4.096 s window might include the time when the question was asked, or might be after the question ended but include the time when the answer was given. If the initial question did not stop the ADs, in some cases, subsequent questions were asked in an attempt to stop the ADs. However, in this paper, only the data associated with the first question was analyzed for comparison to the brain state before questions were asked (57 total trials across the 15 patients; 27 trials in which ADs stopped; 30 trials in which ADs continued). The times of the stimulations, BPS, onset of the questions and answers, and timing of the 4.096 s windows were marked to a precision of 10 ms using a locally developed software program (written by one of the co-authors W.R.S. Webber), called VZ. The software tool is an EEG review program similar to clinical EEG viewers with added tools for precision marking and selecting segments of EEG for import into analysis programs such as MATLAB.

2.4. Quantifying functional brain states

To assess functional brain connectivity, we examined pairwise relationships between the time series of ECoG signals. To decrease the impact of the reference electrode on subsequent calculations, we first subtracted the average reference from each electrode in the ECoG time series (Kramer et al., 2011). Although common in the analysis of scalp EEG data, a spatial Laplacian was not applied, as theoretical calculations predict that spatial spreading between electrode contacts is not expected in ECoG data (Zaveri et al., 2009). In our study, the electrode edges were 7.7 mm apart, and we observed distinct patterns of both AD and non-AD activity on adjacent electrodes further indicating that spatial spreading was not observed in our data (Supplementary Fig. 1). We then calculated the pairwise magnitude-squared coherence to determine the interactions (edge weights) between electrodes. The magnitude-squared coherence operates in the frequency domain and is defined as

$$\mathit{MSC}\left(f\right)=\frac{{\left|S_{\mathit{ij}}\left(f\right)\right|}^2}{S_{\mathit{ii}}\left(f\right)S_{\mathit{jj}}\left(f\right)},$$

where S_ii(f) is the power spectral density of node i, S_jj(f) is the power spectral density of node j, and S_ij(f) is the cross-power spectral density between node i and node j. The pairwise coherence between electrode channels was computed using the multitaper method (time-bandwidth product of 5 and 9 tapers) (Kramer et al., 2011). We examined the difference in average pairwise connectivity strength after the arithmetic question was asked between electrodes that expressed AD and those that did not across a range of frequency bands (5–15 Hz, 15–30 Hz, 30–50 Hz, 70–110 Hz). Because we observed the greatest changes in functional connectivity between electrodes that expressed ADs and those that did not in a frequency range of 70–110 Hz corresponding to high gamma band, all further analysis was performed only for this frequency band (5–15 Hz: median AD = 0.35, median no AD = 0.31, p = 2.96; 15–30 Hz: median AD = 0.26, median no AD = 0.30, p = 0.64; 30–50 Hz: median AD = 0.23, median no AD = 0.30, p = 2.5 × 10⁻³; 70–110 Hz: median AD = 0.20, median no AD = 0.33, p = 7.1 × 10⁻⁷; two-sample Kolmogorov-Smirnov test; N = 57 trials from 15 patients). This frequency band has also previously been shown to display time specific task-related cortical activation in ECoG recordings at 1000 Hz (Crone et al., 2006).

Supplementary Fig. 1.

Adjacent ECoG channels record unique signals. Data from four adjacent electrodes. In our study the electrodes centers were 1 cm apart, with 2.3 mm in diameter exposed to the cortical surface (i.e. 1.15 mm radius). Thus the electrode edges were 7.7 mm apart. We see distinct activity patterns in both channels that do and do not display AD.

2.5. Static community detection

To detect static communities, functional connectivity was first calculated between all pairs of electrodes in the 4.096 s window immediately preceding the cognitive intervention. Within this NxN matrix A, we searched for groups of electrodes that were more densely and strongly interconnected to one another than expected by chance. Specifically, we employed a commonly used community detection algorithm based on optimizing the following modularity quality function:

$$Q=\sum \left[A_{\mathit{ij}}-\mathrm{\gamma }{P}_{\mathit{ij}}\right]\delta \left(g_i,g_j\right),$$

where A_ij represents the strength of a connection (in this case, the pairwise coherence) from node i to node j, node i is assigned to community g_i, node j is assigned to community g_j, the Kronecker delta δ (g_i,g_j) is 0 unless g_i = g_j, in which case it is 1, γ is the structural resolution parameter, and P_ij is the expected strength of the connection between node i and node j under the Newman-Girvan null model (also called the configuration model: a random graph model that gives the probability of node i and node j being connected by chance while maintaining the expected strengths of all nodes) (Blondel et al., 2008; Newman, 2006). We then used a Louvain-like (Blondel et al., 2008) locally greedy algorithm to maximize Q to identify a partition of nodes into communities, where nodes within a community share the greatest possible total edge weight (Jutla et al., n.d.).

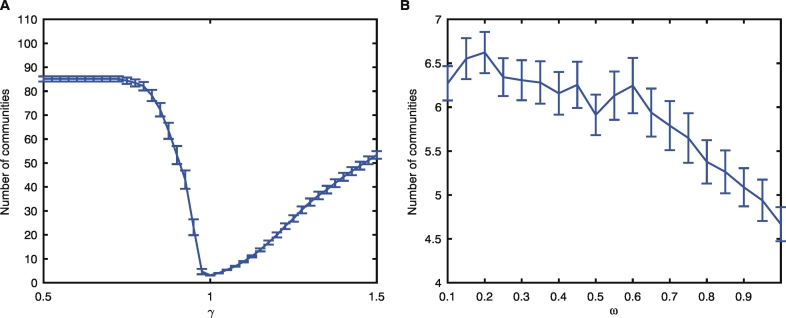
To assess the robustness of the partitions identified with the community detection algorithm, we varied the value of the structural resolution parameter, γ, in the modularity quality function and examined the number of resultant communities with γ = 0.5–1.5 (stepsize of 0.1). We determined that setting γ = 1 resulted in a stable community structure over iterative optimizations of the quality function across subjects, resulting in the detection of 3.14 ± 0.08 communities on average (Supplementary Fig. 2A). Therefore all subsequent analysis was performed using this value.

Due to the many near-degeneracies in the modularity quality function (Good et al., 2010), each run of the community-detection algorithm returns similar yet not identical community assignments. Thus, to determine a robust representative community partition, we followed the nodal association method (Bassett et al., 2013a). For this process, we ran static community detection 100 times with γ = 1 on the nodal association matrix and used a consensus partition approach to identify consistent communities (Chai et al., 2016).

2.6. Dynamic community detection

While static community detection over the 4.096 s window gives an average account of the community structure during this time, it is also possible to calculate fluctuations in the community structure over time using dynamic community detection applied over the same window of data (Bassett et al., 2011, Bassett et al., 2013b; Chai et al., 2016; Mattar et al., 2015). To do so, we split the window before the ADs into seven, 1 s time windows with 50% overlap. A window size of 1 s was chosen to balance stationarity and sufficient data length for functional connectivity calculations (Kramer et al., 2011). For each window, we calculated the functional connectivity as previously described. We then linked the seven resultant networks to form a temporal network through the addition of interlayer self-identity links connecting nodes in adjacent temporal windows (Bassett et al., 2013a).

To determine the dynamic community structure in these temporal networks, we maximized a multilayer extension of the previously described modularity quality function:

$$Q=\frac{1}{2\mu }\sum _{\mathit{ijlr}}\left\{\left(A_{\mathit{ijl}}-{\gamma }_l{P}_{\mathit{ijl}}\right){\delta }_{\mathit{lr}}+{\delta }_{\mathit{ij}}{\omega }_{\mathit{jlr}}\right\}\delta \left(g_{\mathit{il}},g_{\mathit{jr}}\right),$$

where in layer l, A_ijl is the adjacency matrix, P_ijl is the corresponding component in the Newman-Girvan null model, γ_l is the structural resolution parameter, node i is assigned to community g_il, κ_jl = k_jl + c_jl is the strength of node j, k_jl = ∑_iA_ijl is the intra-layer strength of node j, and c_jl = ∑_rω_jlr is the inter-layer strength of node j. In addition, node j in layer r is assigned to community g_jr, ω_jlr is the temporal resolution parameter from node j in layer r to node j in layer l, and $\mu =\frac{1}{2}{\sum }_{\mathit{jr}}{\kappa }_{\mathit{jr}}$ is the total edge weight of the temporal network (Bassett et al., 2013a; Mucha et al., 2010).

As in static community detection, we used a value of γ = 1 and varied ω between ω = 0.1–0.6 (step size of 0.05). We determined that ω = 0.45 resulted in a stable regime across subjects, detecting on average 6.3 ± 0.3 communities overall and 3.70 ± 0.08 communities per layer (Supplementary Fig. 2B). To determine robust representative community partitions for each time slice, we again followed the nodal association method (Bassett et al., 2013a).

2.7. Stability and strength

To quantify the stability of a community, we first calculated the flexibility (Bassett et al., 2011) of each node (electrode), f_i, defined to be the number of times a single node changes module allegiance in the dynamic community structure, normalized by the total number of possible changes. We defined the community stability to be.

$$S_C=1-\frac{1}{N_C}\sum _{i=1}^{N_C}{f}_i,$$

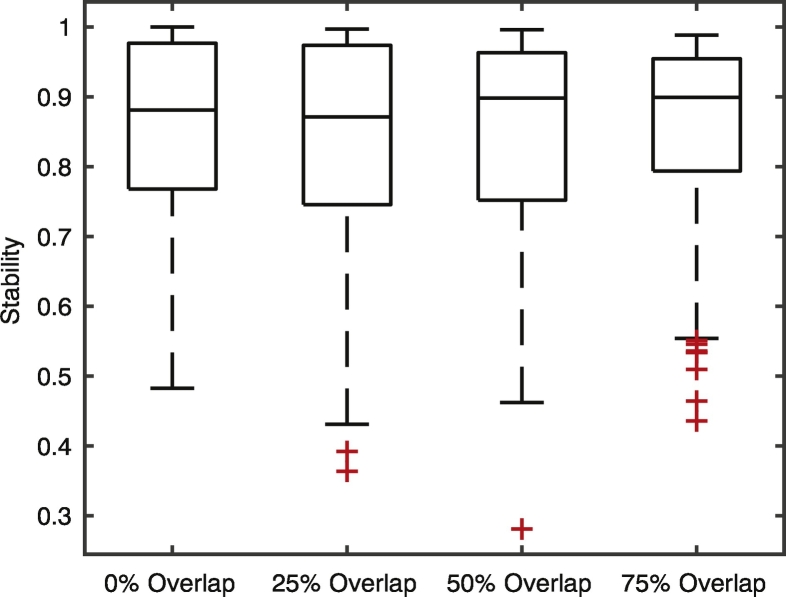
where N_C is the total number of nodes in a static community. This measure is bounded between 0 and 1 with higher values representing a more stable structure over time. Note that the average community stability was consistent across varying choices of the amount of window overlap used to created temporal networks (Supplementary Fig. 3). The strength of a static community was calculated as the average strength of connections between nodes within the community.

Supplementary Fig. 3.

Community stability calculated for four different amounts of window overlap. The amount of window overlap determines the number of layers in the corresponding temporal network. Results are robust over a range of different overlap values.

2.8. Classification of trial groups

When classifying trials into “high” and “low” groups with respect to the percentage of AD channels within a community and with respect to community stability, we calculated the median value of these measures during the window of data immediately preceding the intervention (median percentage AD channels = 73.86%; median stability = 0.89). Trials were classified as “high” if above the median and “low” if below the median.

2.9. Statistical analysis

We used a permutation test to determine whether our observed result occurs more frequently than expected by chance. First, we constructed a random sampling distribution for each possible population by permuting successful and unsuccessful trials into possible populations 1000 times. Next, we determined each population's p-value by locating its observed statistic on its corresponding distribution. All reported p-values were adjusted using a Bonferroni correction for multiple comparisons when necessary.

3. Results

We analyzed ECoG recordings from fifteen patients at Johns Hopkins Hospital undergoing clinical evaluation for medically refractory focal epilepsy. Before surgical resections, these patients underwent extraoperative cortical stimulation to localize regions of the brain critical for motor, sensory, or language function (Jayakar and Lesser, 2008). As a result of the electrical stimulation, ADs sometimes occurred in the cortex underlying a subset of their electrodes (Supplementary Fig. 1). Brief pulse stimulation (BPS) applied to the same electrodes has been shown to sometimes abort ADs, but is only successful approximately half of the time (Lesser et al., 1999). Because BPS can fail, we explored other options for intervention and observed that a cognitive intervention – specifically, having patients answer an arithmetic question in the form of adding to or subtracting from, or multiplying by a two digit number – often could suppress a patient's ADs. To understand the role of the brain state in the efficacy of the cognitive intervention, we analyzed two separate 4.096-s intervals: (i) the patient's initial brain state while the ADs were present, but before the arithmetic question was asked, and (ii) the patient's resultant brain state after the question at the end of the ADs (Fig. 1, Materials and methods).

Fig. 1.

Experimental design. Stimulation is applied to the implanted electrodes during testing, resulting in the appearance of ADs in some (but not all) ECoG channels. The patient is asked to answer an arithmetic question, which sometimes causes the ADs to stop. We analyze the approximately 4-second window of brain activity before the arithmetic question is asked as well as an approximately 4-second window after the question has been asked but before the ADs stop.

Brain states were quantified by assessing the functional connectivity of brain dynamics based on the pairwise magnitude-squared coherence in the high gamma band (70–110 Hz) between electrode channels. This method involves modeling the brain as a network, where the electrodes represent network nodes and the strength of connections between nodes is assigned based on the pairwise coherence of their recorded activity (Fig. 2A). We chose the high gamma band based on previous reports of the sensitivity of gamma to mental arithmetic (Kissler et al., 2000; Umeno et al., 2003), and based on the fact that the frequency range of 70–110 Hz showed the greatest differences in functional connectivity between electrodes that expressed ADs and those that did not (see Materials and methods).

Fig. 2.

Brain states and lobar brain structure. (A) Brain state networks are quantified by calculating the functional connectivity between electrodes based on the pairwise mean-squared coherence (MSC) between recorded activity. (B) No differences are observed in the average connectivity strength of full brain state networks before and after the cognitive intervention. (C) Average connectivity strength of AD and non-AD subnetworks before and after the cognitive intervention. In both cases, the AD subnetwork shows a significantly weaker connectivity than its non-AD counterpart. (D) Percentage of AD subnetwork contained in the frontal (left column), parietal (middle column), and temporal (right column) lobes for trials where the majority of the AD subnetwork is located within the frontal (top row), parietal (middle row), or temporal (bottom row) lobe. No significant differences are observed between spatial relationships in trials where ADs stopped or continued.

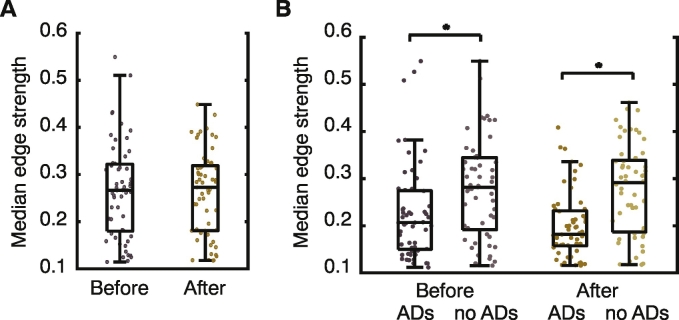
In our data, ECoG networks displayed similar values of edge strength (coherence) both before and after the cognitive intervention (mean edge strength - Fig. 2B; before: median = 0.30, after: median = 0.30, p = 0.74; two-sample Kolmogorov-Smirnov test; N = 57 trials from 15 patients; and median edge strength - Supplementary Fig. 5; before: median = 0.27, after: median = 0.27, =0.85; two-sample Kolmogorov-Smirnov test; N = 57 trials from 15 patients). However, when examining subnetworks composed of only electrodes that displayed (or did not display) ADs, we observe a weakened average connectivity among the electrodes that displayed ADs, which becomes statistically significant after the cognitive intervention (Fig. 2C; before: median ADs = 0.23, median no ADs = 0.32, p = 9.5 × 10⁻⁵, after: median ADs = 0.20, median no ADs = 0.33, p = 7.1 × 10⁻⁷; two-sample Kolmogorov-Smirnov test; N = 57 trials from 15 patients), indicating that subnetworks of AD electrodes are not as coherent as their non-AD counterparts. This weakened coherence was observed in both trials in which the ADs continued and trials in which the ADs stopped.

Supplementary Fig. 5.

Median edge strengths. Same as Fig. 2B–C but with median edge strengths as opposed to mean. (A) No differences are observed in the median connectivity strength of full brain state networks before and after the cognitive intervention. (B) Median connectivity strength of AD and non-AD subnetworks before and after the cognitive intervention. In both cases, the AD subnetwork shows a significantly weaker connectivity than its non-AD counterpart.

We next asked if the interplay between the spatial arrangement of the AD subnetworks and the lobar structure of the brain was related to the success of the cognitive intervention given that both frontal and parietal regions have been implicated in the cognitive processes supporting mental arithmetic (Fehr et al., 2008; Vansteensel et al., 2014). Electrode channels were classified as frontal, parietal, or temporal, based upon their location on the brain. Due to the variability in electrode location among patients, we additionally classified each trial as having the majority of AD electrodes in the frontal, parietal, or temporal lobe. As seen in Fig. 2D, we observed some weak trends in the data: in trials with a majority of AD electrodes in the frontal lobe, ADs seemed more likely to stop if a lower percentage of AD electrodes were located in the parietal lobe, while in trials with a majority of AD electrodes in the temporal lobe, ADs seemed more likely to stop if a higher percentage of AD electrodes were located in the frontal lobe. However, none of these observations were statistically significant.

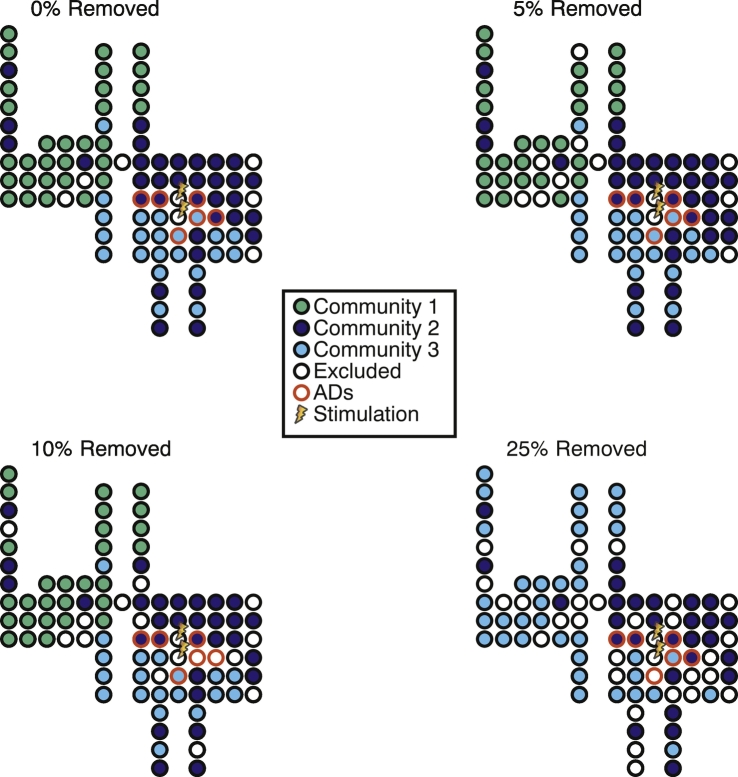
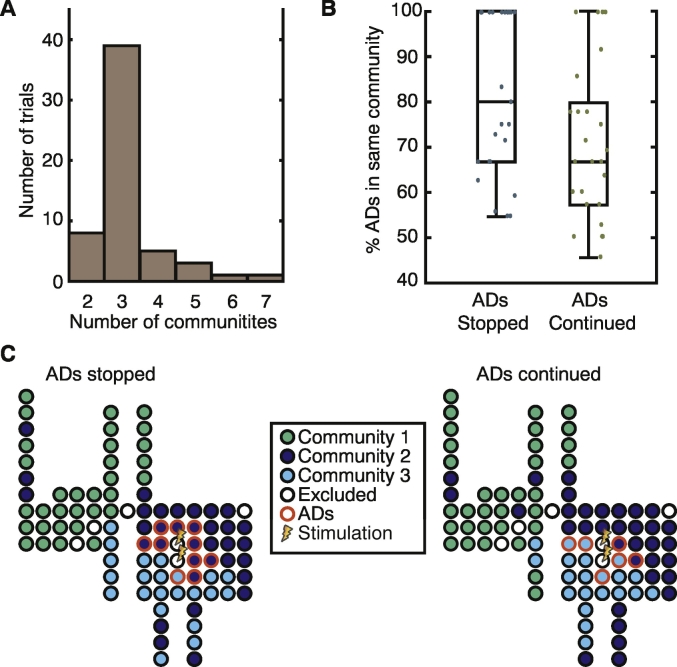
Given that we did not observe a link between the arrangement of AD subnetworks and lobar brain structure with respect to the success of the intervention, we next asked how the location of AD channels related to the functional brain state immediately before patients were asked arithmetic questions. To quantify the spatial properties of the functional brain state, we employed static community detection to parse the functional brain network into communities in which electrodes within a given community displayed coherent activity, but activity between two electrodes in different communities was not coherent. (Note that the community detection algorithm does not depend on the presence or lack of ADs in a channel, and additionally was found to be robust to random removal of electrodes from the data as shown in Supplementary Fig. 6) In almost all cases, we observed that the community detection algorithm found 2–4 communities (Fig. 3A) of coherent brain activity. In trials with greater than 4 communities (7 trials), patients possessed brain state that was not comparable to that observed in the trials with 4 or fewer communities due to the spatial size and arrangement of community partitions, and therefore in the remaining analysis, we analyze only trials with less than 5 communities (N = 50 total trials from 14 patients).

Supplementary Fig. 6.

Robustness of static community detection. Spatial distributions of detected static communities when electrodes are randomly removed from the analysis. Detected communities are the same for 0%, 5%, and 10% random removal of electrodes. Although only two communities are detected when 25% of the electrodes are removed, the distribution of AD channels between the communities is not altered.

Fig. 3.

Static communities and AD subnetworks. (A) Histogram of the number of detected static communities across all trials. (B) The largest percentage of electrodes in the same communities for trials in which the cognitive intervention either stopped the ADs or the ADs continued. In trials in which the cognitive intervention stopped the AD, we tend to see a higher percentage of the AD subnetwork contained in a single functional community. (C) Schematic examples of the spatial layout of electrode channels, color coded by community assignment and AD location for a trial in which the cognitive intervention stopped the ADs (left: 90% AD in same community) and one where it did not (right: 66% AD in same community). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

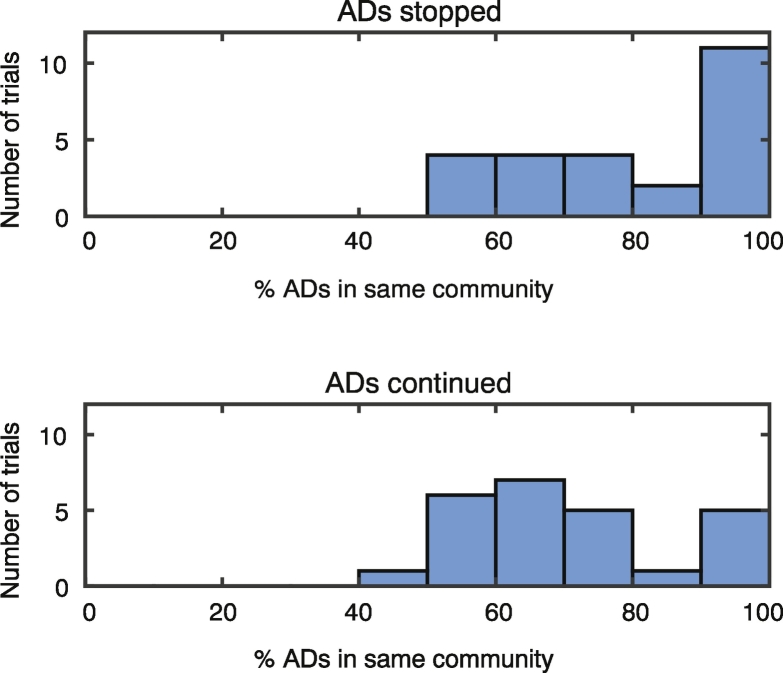
To determine how AD electrodes were distributed within these functional communities, we extracted the community containing the highest percentage of AD electrodes and compared this value between trials in which the intervention successfully stopped the ADs and those in which it did not. We observed a trend that in trials where the act of answering the arithmetic question stopped the ADs, a higher percentage of the AD subnetwork was located within a single community (Fig. 3B and Supplementary Fig. 7; median ADs stopped = 80, median ADs continued = 67; two-sample Kolmogorov-Smirnov test, p = 0.12, N = 50 trials from 14 patients). An example of the spatial distribution of the AD subnetwork with regard to the functional brain state can be seen in Fig. 3C for a trial in which the intervention stopped the ADs and one in which the ADs continued. Note that when the arithmetic question stopped the ADs, most of the AD subnetwork is contained in the dark blue community, whereas when the arithmetic question did not stop the ADs, this network spans both the light and dark blue communities.

Supplementary Fig. 7.

Spatial overlap of AD and communities. A histogram representation of the data presented as boxplots in Fig. 3B. The largest percentage of electrodes in the same communities for trials in which the cognitive intervention either stopped the ADs (upper) or the ADs continued (lower). In trials in which the cognitive intervention stopped the AD, we tend to see a higher percentage of the AD subnetwork contained in a single functional community.

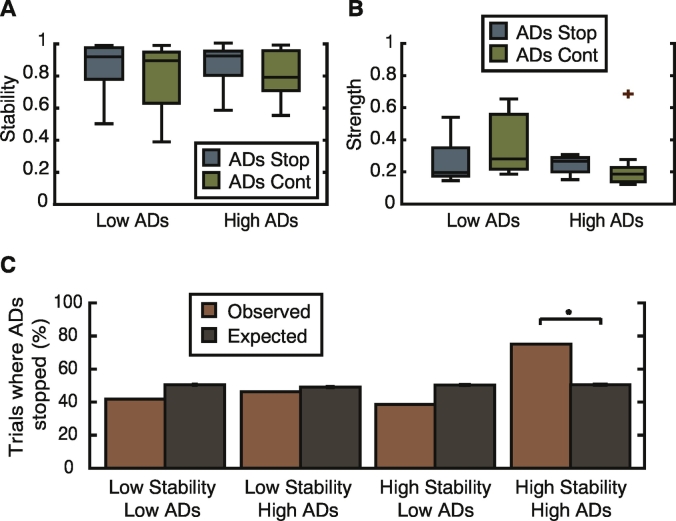
While this finding could indicate a link between the functional brain state and ability of the intervention to stop the ADs, our observation was only that of a trend and not statistically significant. We therefore further investigated the properties of the brain state by quantifying its stability and strength. For each of the detected static communities previously analyzed, we calculated the community stability using a dynamic community detection technique, and additionally, classified communities as having a high or low percentage of AD channels. In communities classified as having a low percentage of AD channels, we saw no differences in the community strength or stability. However, in communities with a high percentage of ADs, we again noted a trend of a higher community stability in trials where the intervention stopped the ADs (Fig. 4A; median ADs stopped = 0.92, median ADs continued = 0.79; two-sample Kolmogorov-Smirnov test, p = 0.15) as well as an increased strength of coherence (Fig. 4B; median ADs stopped = 0.26, median ADs continued = 0.18; two-sample Kolmogorov-Smirnov test, p = 0.15).

Fig. 4.

Strong stable communities predict success of cognitive intervention. (A) Community stability and (B) average strength in trials classified as having either a low or high percentage of the AD subnetwork within a single functional community. In trials where a high percentage of the AD subnetwork is contained within a single functional community, the stability and strength of the community are higher in trials where the cognitive intervention was successful in stopping the ADs. (C) Comparison between observed success of cognitive intervention and chance when data is classified into 4 groups based upon a low/high community stability and low/high overlap between the AD subnetwork and a single community. Comparison to chance was performed using permutation testing and only the group of trials containing a highly stable community with a high overlap with the AD subnetwork were found to be significantly more likely to cause ADs to stop as a result of cognitive intervention.

The presence of a strong and stable local community that encompasses the majority of the AD subnetwork is therefore linked to the success of the cognitive effort in suppressing the ADs. To demonstrate this, we divided the communities into four groups based upon their classification as having a high or low stability, and a high or low percentage of AD electrodes (Materials and methods). This sorting partitioned trials into 4 groups: low stability/low percentage ADs (12 trials), low stability/high percentage ADs (13 trials), high stability/low percentage ADs (13 trials), high stability/high percentage ADs (12 trials). By comparison to a permutation test, we observed that only the group with a high percentage of ADs and high stability was more likely to result in an effective intervention that stopped the ADs more often than would be expected by chance (Fig. 4C; group permutation test, p = 0.05, N = 1000 permutations).

4. Discussion

We conclude that the ability of the cognitive intervention – answering an arithmetic question – to suppress the unstable AD activity, was enhanced upon the spatial co-localization of the AD subnetwork and a strong, stable coherent community in the functional brain state. While we can currently only speculate on the mechanisms of the cognitive intervention, it is plausible that the presence of a highly coherent, stable functional community aides in the suppression of ADs because if a portion of the AD subnetwork is positively affected by the cognitive intervention, the entire functional community follows suit, and the ADs cease. However, in instances where the AD subnetwork is split between functional communities and/or the communities are less coherent, the individual dynamics of the AD subnetwork are less linked and the suppression of ADs in a few channels is not sufficient to abort ADs across the entire network. These data motivate the future examination of cognitive interventions to suppress other forms of pathological neural activity, including seizures.

Our findings indicate that it is important to observe the functional brain state at the time of intervention to achieve optimal success in mitigating unstable or unwanted brain activity. The influence of the brain state on epileptiform activity has been observed previously in the context of sleep versus awake states (Ewell et al., 2015; Sedigh-Sarvestani et al., 2014; Sinha, 2011) and it has been shown in rat models of epilepsy that optogenetic stimulation of a subset of interneurons could shorten the duration of seizures that originated from non-theta (but not theta) states (Ewell et al., 2015). However, here, we define a more subtle classification of brain states based on the observed patterns of functional brain connectivity recorded during seemingly similar awake behavioral states. The fact that such subtle, yet quantifiable, differences in brain states can influence the effect of the intervention has important implications for the development of individualized therapies to treat pathological brain activity. Given that seizures themselves have been shown to evolve through a sequence of states, (Burns et al., 2014; Khambhati et al., 2015), our analysis suggests that methods for on-demand seizure control will likely benefit from careful consideration of real-time brain state evolution.

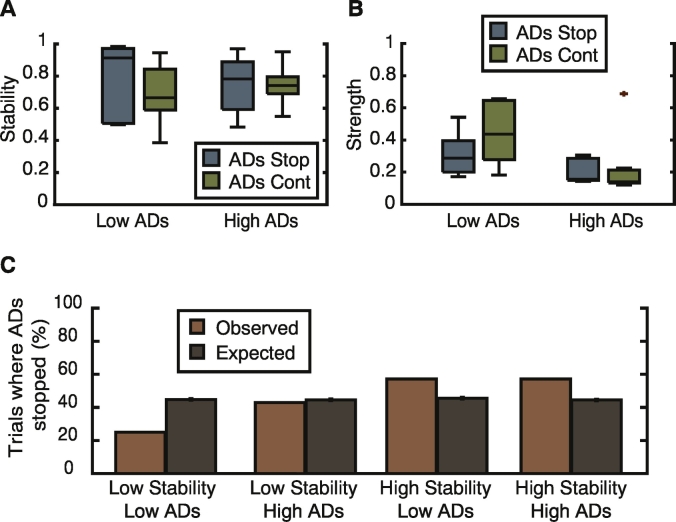
While our results present promising new avenues for suppressing epileptiform activity, the current study does suffer from a few limitations. Given the clinical nature of the data, the placement of electrodes varied from patient to patient. Although we used techniques from network theory that were agnostic to spatial locations of electrodes to define network communities and measure brain states, we cannot control for the impact of specific brain regions on the underlying dynamics that could influence the detected network structure, nor could we control for differences in the severity of the epilepsy between patients. Future studies could examine the relationship between the AD subnetwork and the specific brain regions implicated the performance of mental arithmetic, although one would also need to control for the complexity and type of calculation as these factors can influence the specific networks activated by the calculation (Fehr et al., 2008). The heterogeneity of anti-epileptic drugs used to treat the patients and their potential modulatory effects could also introduce noise into the data. Finally, the study was limited by its small sample size. Due to the fact that much of the data was obtained from subject 1, we also analyzed the data in the absence of this subject. As seen in Supplementary Fig. 8, while we cannot achieve statistical significance due to the reduced number of trials, we see similar trends to those reported in the main manuscript. Future studies with a larger sample size should further examine the impact of these important issues and their relationship to the quantification of brain states and impact on the AD subnetwork.

Supplementary Fig. 8.

Excluding subject 1. The same as the results presented in Fig. 4, but with subject 1 removed from the analysis. (A) Community stability and (B) average strength in trials classified as having either a low or high percentage of the AD subnetwork within a single functional community. (C) Comparison between observed success of cognitive intervention and chance when data is classified into 4 groups based upon a low/high community stability and low/high overlap between the AD subnetwork and a single community. No results are statistically significant, but we observe similar trends to the data presented in Fig. 4.

The results presented in this study also only focused on one form of cognitive intervention in the form of answering an arithmetic question. Preliminary findings suggest that other types of cognitive intervention (such as spelling a word) can also be effective in suppressing ADs. Different types of cognitive effort (i.e., different tasks) invoke different subnetworks (Collard et al., 2016; Korzeniewska et al., 2011; Roux et al., 2008), and therefore it could be true that if one type of cognitive intervention is unsuccessful in suppressing epileptiform activity during a specific brain state, that a different type of cognitive intervention could still prove successful. We therefore encourage future studies to explore this interaction between brain state and task subnetwork activation as a promising new avenue for altering brain states and we further encourage future work to take these findings into account when using brain computer interfaces to develop therapeutic protocols.

The following are the supplementary data related to this article.

Supplementary Fig. 2.

Determination of parameters for community detection. (A) Number of total detected communities as a function of varying γ in static community detection averaged across all subjects. The choice of γ = 1 resulted in a stable regime with 3.14 ± 0.08 communities on average. (B) Number of total communities detected averaged across subjects when using γ = 1 and varying ω in dynamic community detection. The choice of ω = 0.45 used in the paper lies in the middle of the stable regime and resulted in 6.3 ± 0.3 overall communities with 3.70 ± 0.08 communities per layer. Error bars represent standard error.

Supplementary Fig. 4.

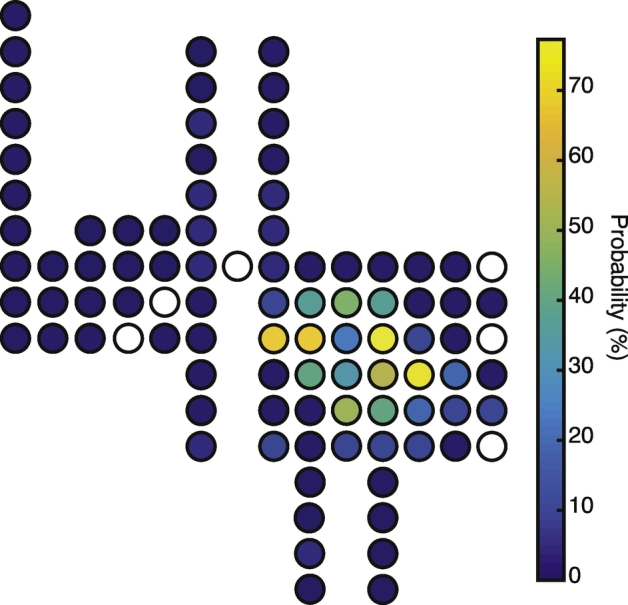
Spatial distribution and probability of ADs. Schematic depicting the spatial layout and probability of individual electrode channels displaying ADs for Subject 1.