Anchor Selection Strategies for DIF Analysis

Abstract

Differential item functioning (DIF) indicates the violation of the invariance assumption, for instance, in models based on item response theory (IRT). For item-wise DIF analysis using IRT, a common metric for the item parameters of the groups that are to be compared (e.g., for the reference and the focal group) is necessary. In the Rasch model, therefore, the same linear restriction is imposed in both groups. Items in the restriction are termed the ``anchor items''. Ideally, these items are DIF-free to avoid artificially augmented false alarm rates. However, the question how DIF-free anchor items are selected appropriately is still a major challenge. Furthermore, various authors point out the lack of new anchor selection strategies and the lack of a comprehensive study especially for dichotomous IRT models. This article reviews existing anchor selection strategies that do not require any knowledge prior to DIF analysis, offers a straightforward notation, and proposes three new anchor selection strategies. An extensive simulation study is conducted to compare the performance of the anchor selection strategies. The results show that an appropriate anchor selection is crucial for suitable item-wise DIF analysis. The newly suggested anchor selection strategies outperform the existing strategies and can reliably locate a suitable anchor when the sample sizes are large enough.

Introduction

Differential item functioning (DIF) is present if test-takers from different groups—such as male and female test-takers—display different probabilities of solving an item even if they have the same latent trait. In this case, the test results no longer represent the ability alone and the groups of test-takers cannot be compared in an objective, fair way.

Various methods have been suggested to analyze item-wise DIF (see Millsap & Everson, 1993, for an overview). DIF tests based on item response theory (IRT) such as the item-wise Wald test (see, e.g., Glas & Verhelst, 1995) rely on the comparison of the estimated item parameters of the underlying IRT model. For this purpose, anchor methods are employed to place the estimated item parameters onto a common scale.

Previous studies showed that a careful consideration of the anchor method is crucial for suitable DIF analysis: If the anchor contains DIF items, which is referred to as contamination (see, e.g., Finch, 2005; Wang, Shih, & Sun, 2012; Woods, 2009), the construction of a common scale for the item parameters may fail and seriously increased false alarm rates can result (see, e.g., Finch, 2005; Kopf, Zeileis, & Strobl, 2013; Stark, Chernyshenko, & Drasgow, 2006; Wang & Su, 2004; Wang & Yeh, 2003; Wang, 2004; Woods, 2009). This means that items truly free of DIF may appear to have DIF and jeopardize the results of the DIF analysis as well as the associated investigation of the causes of DIF (Jodoin & Gierl, 2001). One alternative to reduce the risk of a contaminated anchor is to employ a short anchor that should be easier to find from the set of DIF-free items. However, the statistical power to detect DIF increases with the length of the (DIF-free) anchor (Kopf et al., 2013; Shih & Wang, 2009; Thissen, Steinberg, & Wainer, 1988; Wang & Yeh, 2003; Wang, 2004; Woods, 2009).

In the literature, one can find both methods that do and methods that do not require an explicit anchor selection. While at first sight it may seem that methods that do not require an anchor selection strategy have an advantage, it has been shown that there are situations where these methods are not suitable for DIF detection. The all-other anchor method, for example, uses all items except for the currently studied item as anchor (see, e.g., Cohen, Kim, & Wollack, 1996; Kim & Cohen, 1998) and requires no anchor selection strategy. However, the method was shown to be inadvisable for DIF detection when the test contains DIF items that favor one group (Wang, 2004; Wang & Yeh, 2003). Excluding DIF items from the anchor by using iterative steps may not solve the problem when the test contains many DIF items (Wang et al., 2012). In practice, there is usually no prior knowledge about the exact composition of the DIF effects, and thus, it is advisable to use an anchor method that relies on an explicit anchor selection strategy such as an anchor of the constant length of four items (used, e.g., by Shih & Wang, 2009; Thissen et al., 1988; Wang, 2004). An anchor selection strategy then guides the decision which particular items are used as anchor items.

Several anchor selection strategies have already been proposed, some of which rely on prior knowledge of a set of DIF-free items or on the advice of content experts, while others are based on preliminary item analysis (for an overview, see Woods, 2009). Here, only those strategies that do not require any information prior to data analysis, such as the knowledge of certain DIF-free items, will be reviewed and presented in a straightforward notation. The reason for excluding strategies that require prior knowledge about DIF-free items from this review is that in practical testing situations sets of truly DIF-free items are most likely unknown (as opposed to simulation analysis, where the true DIF pattern is known) and even the judgment of content experts is unreliable (for a literature overview where this approach fails, see Frederickx, Tuerlinckx, De Boeck, & Magis, 2010). New suggestions of anchor selection strategies are often only compared to few alternative strategies or in situations of only a limited range of the sample size and “have not been exhaustively compared for the dichotomous case” (González-Betanzos & Abad, 2012, p. 135). In this article, we systematically evaluate the performance of the existing anchor selection strategies for DIF analysis in the Rasch model by conducting an extensive simulation study.

Furthermore, we assess the appropriateness of the anchor selection strategies to find a suitable short anchor (of four anchor items) and also their ability to select a suitable longer anchor, which “is a challenging question for researchers and practitioners” (Wang et al., 2012, p. 705). For practical research, recommendations how anchor items can be found appropriately are still required (Lopez Rivas, Stark, & Chernyshenko, 2009, p. 252). We also provide guidelines how to choose anchor items for the Rasch model when no prior knowledge of DIF-free items is at hand.

In addition to the existing strategies, new developments of anchor selection strategies have also been encouraged (Wang et al., 2012). Here, we also suggest three new anchor selection strategies. The new anchor selection strategies are implemented and the results show an improvement of the classification accuracy in the analysis of DIF in the Rasch model.

The article is organized as follows. The technical aspects of the anchoring process in the Rasch model are introduced in the next section. Details of the anchor classes and of the existing as well as of the newly suggested anchor selection strategies are given in the third section. The simulation design is addressed in the fourth section, and the results are discussed in the fifth section. Finally, a concluding summary and practical recommendations are presented.

Model and Notation

In this section, the model and notation are introduced along with some technical statistical details about the anchoring process that provide all information necessary for the implementation of the anchor methods discussed in this article: (a) how parameter estimates under certain restrictions can be obtained and (b) how the associated item-wise parameter differences between a focal and reference group can be assessed given a selection of anchor items. In the next section, we provide the information about the model estimation and the required restrictions for the Rasch model. In addition, the equations to transform the restrictions, which represent the core of the anchor methods, are given so that the entire procedure how to assess item-wise parameter differences can be outlined in section “Item-Wise Parameter Differences.”

Based on the resulting item-wise tests, the subsequent sections will then discuss how the tests can be combined employing a wide range of classes of anchors and different strategies for selecting the anchor items. In our discussion, we focus on the Rasch model but the underlying ideas can also be applied to other IRT models.

Model Estimation and Scale Indeterminacy

To fix notation, we employ the widely used (Wang, 2004) Rasch model with item parameter vector $\beta ={({\beta }_1,\dots ,{\beta }_k)}^T\in {ℝ}^k$ (where k denotes the number of items in the test). It is estimated here using the conditional maximum likelihood (CML) approach, because of its desirable statistical properties and the fact that it does not rely on the person parameters (Molenaar, 1995).

To overcome the scale indeterminacy (Fischer, 1995) of the item parameters β, one linear restriction is typically imposed on them. Hence, only k− 1 parameters can be freely estimated and the remaining one parameter is determined by the restriction. Commonly used approaches restrict a set $\mathcal{A}\subseteq \{1,\dots ,k\}$ of one or more (or even all) item parameters to sum to zero $\sum _{\ell \in \mathcal{A}}{\beta }_{\ell }=0$ (Eggen & Verhelst, 2006). Conveniently, the item parameter estimates $\hat{\beta }$ under any such restriction can be easily obtained from any other set of parameter estimates $\tilde{\beta }$ fulfilling another restriction. Without loss of generality we employ the restriction ${\tilde{\beta }}_1=0$ for the initial CML parameter estimates and also obtain the corresponding covariance matrix $\widehat{\mathrm{Var}}(\tilde{\beta }),$ which consequently has zero entries in the first row and in the first column. To obtain any other restriction of the sum type above, the item parameter estimates $\hat{\beta }$ and corresponding covariance matrix estimate can be obtained as follows:

$$\hat{\beta }=A\tilde{\beta },$$

$$\widehat{\mathrm{Var}}\left(\hat{\beta }\right)=A\widehat{\mathrm{Var}}\left(\tilde{\beta }\right)A^T,$$

where $A={\text{I}}_k-\frac{1}{\sum _{\ell =1}^k{a}_{\ell }}{1}_k·a^T$ is the contrast matrix corresponding to an indicator vector $a$ of elements $a_{\ell }$, such as $a={(0,1,0,0,0,\dots )}^T$ for item 2, with ${\text{I}}_k$ denoting the identity matrix and $1_k={(1,1,\dots ,1)}^T$ a vector of one entries of length k. To emphasize that the parameter estimates $\hat{\beta }$ depend on the set of restricted item parameters, we sometimes employ the notation $\hat{\beta }(\mathcal{A})$ in the following (although the dependence on $\mathcal{A}$ is mostly suppressed).

Item-Wise Parameter Differences

In DIF analysis using IRT models, groups are to be compared regarding their item parameters. We focus here on the situation of item-wise comparisons between two groups (reference and focal). To establish a common scale for the item parameters the same linear restriction

$$\sum _{\ell \in \mathcal{A}}{\hat{\beta }}_{\ell }^g=0(g\in \{\mathrm{ref},\mathrm{foc}\})$$

has to be imposed on the item parameters in both groups (Glas & Verhelst, 1995). Thus, $\mathcal{A}$ is the set of anchor items employed to align the scales between the two groups $g$.

More specifically, to assess differences between the two groups for the jth item parameter ${\beta }_j(j=1,\dots ,k)$, the following steps are carried out:

1. Obtain the initial CML estimates ${\tilde{\beta }}^g$ in both groups $g$ (i.e., using the restriction ${\tilde{\beta }}_1^g=0$).

2. Based on the same set of anchor items $\mathcal{A}$, compute ${\hat{\beta }}^g={\hat{\beta }}^g(\mathcal{A})$ and corresponding $\widehat{\mathrm{Var}}({\hat{\beta }}^g)$ using Equations 1 and 2 so that Equation 3 holds in both groups $g$.

3. Carry out an item-wise Wald test (see, e.g., Glas & Verhelst, 1995) for the jth item with test statistic $t_j=t_j(\mathcal{A})$ given by

$$t_j=\frac{{\hat{\beta }}_j^{\mathrm{ref}}-{\hat{\beta }}_j^{\mathrm{foc}}}{\sqrt{\widehat{\mathrm{Var}}({\hat{\beta }}_j^{\mathrm{ref}}-{\hat{\beta }}_j^{\mathrm{foc}})}}=\frac{{\hat{\beta }}_j^{\mathrm{ref}}-{\hat{\beta }}_j^{\mathrm{foc}}}{\sqrt{\widehat{\mathrm{Var}}{({\hat{\beta }}^{\mathrm{ref}})}_{j,j}+\widehat{\mathrm{Var}}{({\hat{\beta }}^{\mathrm{foc}})}_{j,j}}}.$$

Either the test statistic $t_j$ or the associated p-value $p_j$ can then be employed as a DIF index because under the null hypothesis of no DIF the item parameters from both groups should be equal: ${\beta }_j^{\mathrm{ref}}={\beta }_j^{\mathrm{foc}}.$

Note that this item-wise Wald test is applied to the CML estimates (as in Glas & Verhelst, 1995) and not the joint maximum likelihood (JML) estimates (as in Lord, 1980). The inconsistency of the JML estimates leads to highly inflated false alarm rates (Lim & Drasgow, 1990; McLaughlin & Drasgow, 1987). In case other IRT models are regarded, the recent work of Woods, Cai, and Wang (2013) showed that an improved version of the Wald test, termed Wald-1 (see Paek & Han, 2013, and the references therein), also displayed well-controlled false alarm rates if the anchor items were DIF-free. Since the Wald-1 test also requires anchor items, it can in principle be combined with the anchor methods discussed here as well.

Anchor Methods

Under this null hypothesis of equality between all item parameters, in principle any set of items could be chosen for the anchor $\mathcal{A}$. However, under the alternative that some of the k item parameters are actually affected by DIF, the results of the analysis strongly depend on the choice of the anchor items, as previous studies illustrated. If the anchor contains at least one DIF item, it is referred to as contaminated (see, e.g., Finch, 2005; Wang et al., 2012; Woods, 2009). The scales may then be artificially shifted apart and the false alarm rates of the DIF tests may be seriously inflated (see, e.g., Finch, 2005; Stark et al., 2006; Wang & Su, 2004; Wang, 2004; Wang & Yeh, 2003; Woods, 2009). Instructive examples that illustrate the artificial scale shift are provided by Wang (2004) and Kopf et al. (2013).

For distinguishing between the different approaches, we employ a framework for anchor methods previously used in Kopf et al. (2013) where the anchor class determines characteristics of the anchor methods, such as a predefined anchor length, and the anchor selection strategy guides the decision which items are used as anchor items. The combination of an anchor class together with an anchor selection strategy is then termed an anchor method. Different anchor classes are now briefly reviewed.

Anchor Classes

The constant anchor class consists of an anchor with a predefined, constant length. Usually, it is claimed that a constant anchor of four items assures sufficient power (cf., e.g., Shih & Wang, 2009; Wang et al., 2012). An anchor selection strategy is needed to guide the decision which items are used as anchor items. The all-other anchor class uses all items except for the currently studied item as anchor and the equal-mean difficulty anchor class uses all items as anchor (see, e.g., Wang, 2004, and the references therein). These latter two anchor classes do not require an additional anchor selection strategy. Furthermore, iterative anchor classes build the anchor in an iterative manner. The iterative backward class (used, e.g., by Candell & Drasgow, 1988; Drasgow, 1987; Hidalgo-Montesinos & Lopez-Pina, 2002) starts with all other items as anchor and excludes DIF items from the anchor, whereas the iterative forward anchor class starts with a single anchor item and then, iteratively, includes items in the anchor (Kopf et al., 2013). The latter anchor class also requires an explicit anchor selection strategy.

Wang (2004), Wang and Yeh (2003), and González-Betanzos and Abad (2012) compared the all-other and the equal-mean difficulty anchor class to different versions of the constant anchor class regarding various IRT models. All methods from the constant anchor class were built using prior knowledge about the set of DIF-free items to locate the anchor items. Methods from the constant anchor class yielded well-controlled false alarm rates, whereas methods from the all-other and the equal-mean difficulty anchor class displayed seriously inflated false alarm rates when the direction of DIF was unbalanced (i.e., the DIF effects did not cancel out between groups and one group was favored in the test) and it is doubtful whether the situation of balanced DIF (i.e., no group has an advantage in the test) is met in practice (Wang et al., 2012; Wang & Yeh, 2003). This is of utmost importance for practical testing situations, since items truly free of DIF can display artificial DIF and may be eliminated by mistake.

As a result, all three studies showed that the direction of DIF has a major impact on the results of the DIF analysis for the all-other and the equal-mean difficulty anchor class as opposed to the constant anchor class based on DIF-free anchor items. The constant anchor class is in principle able to yield appropriate results for the DIF analysis even if DIF is unbalanced. However, since Wang and Yeh (2003), Wang (2004), and González-Betanzos and Abad (2012) used prior knowledge of the set of DIF-free items to select the constant anchor items, no information is yet available on how well anchor selection strategies without prior knowledge perform and “[f]urther research is needed to investigate how to locate anchor items correctly and efficiently” (Wang & Yeh, 2003, p. 496).

Another anchor class was recently suggested by Kopf et al. (2013). Instead of a predefined anchor length, the iterative forward anchor class builds the anchor in a step-by-step procedure. First, one anchor item is used for the initial DIF test. As long as the current anchor length is shorter than the number of items currently not displaying statistically significant DIF (termed the presumed DIF-free items in the following), one item is added to the current anchor and DIF analysis is conducted using the new current anchor. The sequence which item is first included and which items are added to the anchor is determined by an anchor selection strategy. In a simulation study, the iterative forward anchor class and the constant anchor class were combined with two different anchor selection strategies and compared to the all-other class and the iterative backward anchor class. The iterative forward anchor class was found to be superior since it yielded high hit rates and, simultaneously, low false alarm rates for sufficiently large sample sizes in any studied condition of balanced or unbalanced DIF if the number of significant threshold anchor selection strategy (see section “Anchor Selection Strategies”) was employed (Kopf et al., 2013).

To assess the appropriateness of the anchor selection strategies in this article, we combine them with the constant four anchor class and the iterative forward anchor class. The reason for this is that both classes require an anchor selection strategy and it is claimed in the literature that they have a high power when the anchor selection works adequately (cf., e.g., Shih & Wang, 2009, for an literature overview regarding the constant four anchor class; Kopf et al., 2013, for the iterative forward anchor class). Furthermore, both classes are structurally different. The constant four anchor class always includes four anchor items and, thus, leads to a short anchor, whereas the iterative forward class allows for a longer anchor that is built in an iterative way. For a comparison with an anchor class that does not rely on an explicit anchor selection strategy, the all-other anchor class is included in the simulation as well, even though it can display seriously inflated false alarm rates when the direction of DIF is unbalanced (González-Betanzos & Abad, 2012; Kopf et al., 2013; Wang, 2004; Wang & Yeh, 2003).

Anchor Selection Strategies

Anchor selection strategies determine a ranking order of candidate anchor items. We focus on those strategies that are based on preliminary item analysis since these strategies are most common in practice. This approach has been referred to as the DIF-free-then-DIF strategy by Wang et al. (2012) because auxiliary DIF tests are conducted to locate (ideally DIF-free) anchor items before the final DIF tests are carried out.

Auxiliary DIF Tests

For each item $j=1,\dots ,k,$ auxiliary DIF tests are conducted using Steps 1 to 3 in section “Item-Wise Parameter Differences.” Typically, there are two alternative ways to conduct auxiliary DIF tests, which will be referred to as tests of Type (I) or of Type (II) in the following:

• (I) The auxiliary DIF tests of Type (I) are conducted using all-other items $\{1,\dots ,k\}\setminus j$ as anchor. This yields one observed test statistic $t_j(\{1,\dots ,k\}\setminus j)$ for every currently studied item $j$.

• (II)  The auxiliary DIF tests of Type (II) are conducted using every other item $\ell \ne j$ as constant single anchor. This results in $(k-1)$ test statistics per item $t_j(\{\ell \})$ with the corresponding p-values $p_j(\{\ell \}).$ Anchor selection strategies decide how all tests are aggregated to obtain the ranking order of candidate anchor items. Note that the test statistics and p-values display the following symmetry properties $|t_j\left(\left\{\ell \right\}\right)|=\left|t_{\ell }\left(\left\{j\right\}\right)\right|$ and $p_j\left(\left\{\ell \right\}\right)=p_{\ell }\left(\left\{j\right\}\right)$ since the constant scale shift of one single anchor item is reflected in the test statistic of the item currently investigated and vice versa. Even though the p-values represent a monotone decreasing transformation of the absolute test statistics, the aggregations of both measures may yield different ranking orders.

Rank-Based Approach

Anchor selection strategies use the information from the auxiliary DIF tests of Type (I) or of Type (II) to define a criterion $c_j$ for each item $j$ that ideally reflects how strong the item is affected by DIF. All anchor selection strategies that are regarded in this article follow a rank-based approach that was first suggested together with auxiliary tests of Type (I) by Woods (2009). The ranking order of candidate anchor items is defined by the ranks of the criterion values rank ($c_j)$. The item displaying the lowest rank is the first candidate anchor item, whereas the item corresponding to the highest rank is the last candidate anchor item.

The ranking order resulting from the anchor selection strategies is used within the anchor classes to conduct the final DIF analysis. For the constant four anchor class, the items with the lowest four ranks are selected as the final anchor set ${\mathcal{A}}_{\mathrm{final}}.$ For the iterative forward anchor class, items are selected into the anchor as long as the anchor is shorter than the number of currently presumed DIF-free items. In this anchor class, anchor items are selected in a step-by-step procedure following the ranking order that results from the anchor selection. When the stopping criterion is reached, the final anchor set ${\mathcal{A}}_{\mathrm{final}}$ is found.

Final DIF Analysis

The final DIF tests are carried out using the anchor set ${\mathcal{A}}_{\mathrm{final}}$. Since $k-1$ parameters are free in the estimation, only $k-1$ estimated standard errors result (Molenaar, 1995), the kth standard error is determined by the restriction and, hence, only $k-1$ tests can be carried out. To overcome the problem that the classification of an item as a DIF or a DIF-free item is intended for each of the $k$ items, we classify the first final anchor item with the lowest rank to be DIF-free—a decision that may be false if even the item with the lowest rank does indeed have DIF, but in this case this would be noticeable in the final test results.

The decision to classify the first anchor item as DIF-free is applied only to those methods that rely on an anchor selection strategy. In the simulation study, the all-other method will be included as well, for which the anchor varies for each test conducted and we report $k$ test results.

Note that classifying the first anchor item as DIF-free is by no means as drastic as testing only those items for DIF that have not been selected as anchor, as was done, for example, by Woods (2009), or as choosing the anchor items only from the set of items that are known to be DIF-free in a simulation, as was done by Wang and Yeh (2003) and Wang (2004), but cannot be done in any real study where the true DIF and DIF-free items are unknown.

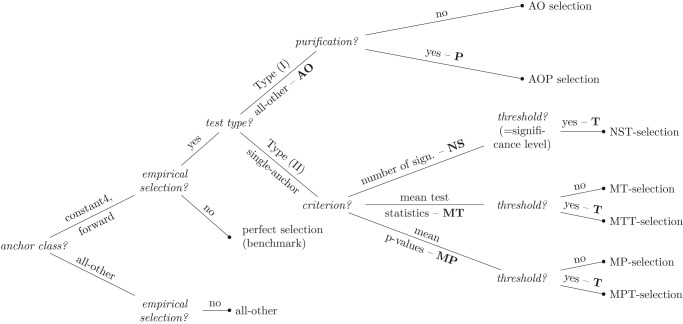
In the following, first, the selection strategies that are built on auxiliary DIF tests of Type (I) are reviewed. Second, the selection strategies that rely on auxiliary DIF tests of Type (II) are discussed. Third, three new selection strategies are suggested that also rely on auxiliary DIF tests of Type (II). A summary of all anchor selection strategies discussed in this article is provided in Figure 1 and in Table 1. Note that the DIF tests mentioned in the next paragraphs are only used as preliminary steps to assess the criterion values that determine the ranking order of candidate anchor items.

Figure 1.

Summary of the characteristics of the anchor selection strategies that are investigated in this article.

Table 1.

A Short Summary of the Anchor Selection Strategies That Are Investigated in This Article.

Selection	Description
AO	The items are ranked according to the lowest absolute test statistics $\left|t_j(\{1,\dots ,k\}\setminus j)\right|.$
AOP	Beginning with all other items as anchor, DIF items are iteratively excluded from the anchor until the purified anchor set ${\mathcal{A}}_{\mathrm{purified}}$ is reached; the items are ranked according to the lowest absolute test statistics $\left|t_j\left({\mathcal{A}}_{\mathrm{purified}}\right)\right|.$
NST	The items are ranked according to the lowest number of significant test statistics $t_j(\{\ell \}).$
MT	The items are ranked according to the lowest mean absolute test statistics $\frac{1}{k-1}{\displaystyle \sum _{\ell \in \{1,\dots ,k\}\setminus j}}|t_j(\{\ell \})|.$
MP	The items are ranked according to the largest mean p-values $\frac{1}{k-1}{\displaystyle \sum _{\ell \in \{1,\dots ,k\}\setminus j}}{p}_j(\{\ell \}).$
MTT	The items are ranked according to the smallest number of test statistics $|t_j(\{\ell \})|$ exceeding the $\left(\lceil 0.5\cdot k\rceil \right)$-th ordered absolute mean test statistic $\left|\frac{1}{k-1}{\displaystyle \sum _{\ell \in \{1,\dots ,k\}\setminus j}}{t}_j\left(\left\{\ell \right\}\right)\right|.$
MPT	The items are ranked according to the largest number of p-values $p_j(\{\ell \})$ exceeding the $\left(\lceil 0.5\cdot k\rceil \right)$-th ordered mean p-value $\frac{1}{k-1}{\displaystyle \sum _{\ell \in \{1,\dots ,k\}\setminus j}}{p}_j\left(\left\{\ell \right\}\right).$
perfect	The perfect ranking consists of randomly permuted DIF-free items followed by randomly permuted DIF items.

All-Other Selection

The all-other selection strategy (AO-selection) was proposed by Woods (2009) as what she called the rank-based strategy. For this strategy a predefined number of anchor items is chosen according to the lowest ranks of the absolute DIF test statistics resulting from the auxiliary DIF tests of Type (I):

$$c_j^{\text{AO}}=\left|t_j(\{1,\dots ,k\}\setminus j)\right|.$$

(Note that, originally, Woods, 2009, suggested to use the ratios of the test statistics and the degrees of freedom, that may vary across items if the items display a different number of response categories. However, this is not discussed here since the responses are always dichotomous in the Rasch model that we focus on here.)

The constant anchor method of 20% of the items based on the AO-selection was found to be superior compared to the all-other anchor method in the majority of the simulated settings and compared to the constant single anchor method based on the AO-selection (Woods, 2009). Nevertheless, the author claimed that “[a] study comparing the strategy proposed here to the various other suggestions for empirically selecting anchors is needed” (Woods, 2009, p. 53).

All-Other Purified Selection

Recently, Wang et al. (2012) suggested a modification (here referred to as AOP-selection for all-other purified selection) of the all-other anchor selection strategy proposed by Woods (2009) by adding a scale purification procedure. First, auxiliary DIF tests of Type (I) are carried out. Similar to the iterative procedures (used, e.g., by Candell & Drasgow, 1988; Drasgow, 1987; Hidalgo-Montesinos & Lopez-Pina, 2002), those items displaying DIF are excluded from the set of anchor items and DIF tests are conducted using the new anchor set. These steps are repeated until two successive steps reach the same results. In the next step, DIF tests are conducted using the purified anchor ${\mathcal{A}}_{\mathrm{purified}}.$ Here, the first anchor item obtains no DIF test statistic, since only $k-1$ test statistics are available, and is omitted in the ranking of candidate anchor items. The criterion values of the remaining $k-1$ items are defined by

$$c_j^{\mathrm{AOP}}=\left|t_j\left({\mathcal{A}}_{\mathrm{purified}}\right)\right|.$$

In a simulation study, Wang et al. (2012) found the modified AOP-selection to be superior to the AO-selection since both methods displayed comparable results when DIF was balanced but the AOP-selection yielded more often a DIF-free anchor set when DIF was unbalanced. Still, there were conditions where the proportions of replications yielding a DIF-free anchor set were far away from 100%, for example, 13% for the AO- and 17% for the AOP-selection when the sample size was small (i.e., 250 observations in each group in their most difficult scenarios).

Number of Significant Threshold Selection

An anchor selection strategy that is a simplified version of the proposition of Wang (2004) is called number of significant threshold (NST) selection strategy here. Now, auxiliary DIF tests of Type (II) are carried out and the number of significant DIF tests defines the criterion values

$$c_j^{\text{NST}}=\sum _{\ell \in \{1,\dots ,k\}\setminus j}\mathbb{I}\{p_j\left(\left\{\ell \right\}\right)\le \alpha \}$$

that is written as the number of p-values that do not exceed the threshold α, for example, α = .05. $\mathbb{I}$ denotes the indicator function. The item displaying the least number of significant DIF tests is chosen as the first anchor item. If more than one item displays the same number of significant results, one of the corresponding items is selected randomly.

Originally, Wang (2004) suggested the next candidate (NC) modification: The item that was selected by the NST-selection strategy functions as the current single anchor item and DIF tests are again carried out (see Wang, 2004). The next candidate is then included in the anchor if it displays “the least magnitude” (Wang, 2004, p. 250) of (non-significant) DIF and the steps are repeated until either the predefined anchor length is reached or the candidate item displays significant DIF. Since Kopf et al. (2013) found the NST-selection superior to the original NC-strategy, only the former is investigated in this article.

Mean Test Statistic Selection

To reach an ideally pure set of anchor items, Shih and Wang (2009) introduced the following anchor selection procedure: Every item is assigned the mean absolute DIF test statistic from the auxiliary DIF tests of Type (II)

$$c_j^{\mathrm{MT}}=\frac{1}{k-1}\sum _{\ell \in \{1,\dots ,k\}\setminus j}|t_j(\{\ell \})|.$$

We abbreviate this method MT-selection (for mean test statistic selection). Shih and Wang (2009) found high rates of correctly locating one or four DIF-free anchor items when the sample size was high (i.e., 1,500 observations in each group in their most difficult scenarios).

Mean p-Value Selection

In addition to the existing approaches described above, we propose three new anchor selection strategies. First, we suggest an idea similar to the MT-strategy of Shih and Wang (2009) (see Equation 8) that we abbreviate MP-strategy (for mean p-value selection). Instead of the lowest mean absolute DIF test statistic, items are here chosen that display the highest mean p-value from the auxiliary tests of Type (II) and, for easier comparability with the previous methods, the criterion is defined by negative mean p-values

$$c_j^{\mathrm{MP}}=-\frac{1}{k-1}\sum _{\ell \in \{1,\dots ,k\}\setminus j}{p}_j\left(\left\{\ell \right\}\right).$$

The next two suggestions were inspired by the threshold approach of the NST-selection (see Equation 7) where those items are chosen as anchor items that display the least number of significant DIF test results. Kopf et al. (2013) showed that this strategy was superior to the AO-selection when the DIF direction was unbalanced. The major drawback using the NST-selection was that it was strongly affected by the sample size. The reason for this is that the selection is based on the decisions of statistical significance tests which are strongly influenced by the sample size. The next two newly suggested anchor selection strategies rely on a different criterion and both methods assume—similar to the MT- and the MP-selection—that the majority of items is DIF-free, an assumption that is often found in the construction of anchor or DIF methods (see, e.g., Magis & De Boeck, 2011; Shih & Wang, 2009).

Mean Test Statistic Threshold Selection

Our second suggestion is the following: For every item the absolute mean of the test statistics resulting from the auxiliary tests of Type (II) is calculated and the resulting values are ordered. The threshold for the MTT-selection (for mean test statistic threshold) is the $\left(\lceil 0.5\cdot k\rceil \right)$-th ordered value, which is indicated by the index in parenthesis, for an even number of items or the next larger whole number in case of an odd number of items (indicated by the ceiling function $\lceil \rceil$). The number of absolute test statistics exceeding this threshold determines the criterion value:

$$c_j^{\mathrm{MTT}}=\sum _{\ell \in \{1,\dots ,k\}\setminus j}\mathbb{I}\{\left|t_j\left(\left\{\ell \right\}\right)\right|>{\left(\left|\frac{1}{k-1}\sum _{\ell \in \{1,\dots ,k\}\setminus j}{t}_j\left(\left\{\ell \right\}\right)\right|\right)}_{(\lceil 0.5·k\rceil )}\}.$$

The items corresponding to the lowest number of test statistics above the threshold are chosen as anchor items. Here, we follow an argumentation similar to the argumentation of Shih and Wang (2009). When the anchor item is DIF-free, which is assumed to be the case for the majority of the items, the DIF tests work appropriately. On the other hand, if a DIF item functions as the anchor, those items with the same direction of DIF display less DIF (or even no DIF in the most indistinct situation when the magnitude of DIF is approximately the same for the respective items), those items with the opposite direction of DIF display on average their original magnitude of DIF plus the artificial magnitude of DIF of the anchor item and the items truly free of DIF display on average the artificial DIF magnitude of the anchor item.

Thus, those DIF tests where the anchor is truly DIF-free should display the least absolute mean test statistics. Since the majority of items—that is, at least 50% of all k items—is assumed to be DIF-free, the $(\lceil 0.5·k\rceil )$-th mean test statistic should correspond to a DIF-free item. In order to use the information of every single test statistic as opposed to the mere mean values, we use the indicator function to provide the information whether the single test statistics exceed the $(\lceil 0.5·k\rceil )$-th ordered absolute mean test statistic. Furthermore, in case of unbalanced DIF, the absolute mean test statistics may be very similar, when the DIF proportion is close to 0.5. The binary decisions are assumed to yield more accurate classifications of the truly DIF-free items. The selection strategy is designed for all directions of DIF and intended for all sample sizes. In contrast to the MT-selection proposed by Shih and Wang (2009), we use the absolute mean test statistics instead of the mean absolute test statistics. The reason for this is that all item parameters vary slightly between reference and focal group due to sampling fluctuation. These differences are expected to cancel out when the absolute values are taken after the mean statistic and, hence, should yield a better threshold.

Mean p-Value Threshold Selection

In our third suggestion, similar to the MTT-selection in Equation 10, the threshold of the MPT-selection (for mean p-value threshold) relies again on auxiliary DIF tests of Type (II). Now, the $\left(\lceil 0.5\cdot k\rceil \right)$-th ordered (from large to small) value of the mean of the resulting p-values $p_j(\{\ell \})$ is used as the threshold. The criterion value is defined by the number of tests per item that yield p-values exceeding the threshold p-value

$$c_j^{\mathrm{MPT}}=-\sum _{\ell \in \{1,\dots ,k\}\setminus j}\mathbb{I}\{p_j\left(\left\{\ell \right\}\right)>{\left(\frac{1}{k-1}\sum _{\ell \in \{1,\dots ,k\}\setminus j}{p}_j\left(\left\{\ell \right\}\right)\right)}_{(\lceil 0.5·k\rceil )}\}.$$

In summary, the newly suggested methods (see again Table 1 and Figure 1) are developed for balanced and unbalanced DIF situations and should outperform not only the AO-selection that initiates with the potentially biased DIF test results using the all-other method but also the AOP-selection that may not be able to exclude all DIF items from the anchor set when the proportion of DIF items is high (Wang et al., 2012). In comparison with the NST-selection, which uses the binary decisions of the significance tests (Woods, 2009), the newly suggested methods should be less affected by sample size. While the MT- and the MP-selection use mere mean values, the MPT- and the MTT-selection use all individual test results and are, therefore, expected to better distinguish between DIF and DIF-free anchor items. By employing a threshold, the new methods should select those items as anchor that display little artificial DIF which can be caused by contamination (see, e.g., Finch, 2005; Woods, 2009) or by random sampling fluctuation (Kopf et al., 2013).

Simulation Study

To evaluate the performance of the newly suggested anchor selection strategies, we conducted an extensive simulation study in the free R system for statistical computing (R Development Core Team, 2013). Parts of the simulation design were inspired by the settings used by Wang et al. (2012). Each setting from the simulation study is replicated 1,000 times to ensure reliable results.

Data Generating Processes

One replication corresponds to a data set that contains the information of the test including the item responses, the group membership and the ability variable.

Test Characteristics

Here, we consider a test length of $k$ = 40 items.

IRT Model

The responses follow the Rasch model

$$P(U_{\mathrm{ij}}=1|{\theta }_i,{\beta }_j)=\frac{\exp ({\theta }_i-{\beta }_j)}{1+\exp ({\theta }_i-{\beta }_j)},$$

with the difficulty parameters β = (−2.522, −1.902, −1.351, −1.092, −0.234, −0.317, 0.037, 0.268, −0.571, 0.317, 0.295, 0.778, 1.514, 1.744, 1.951, −1.152, −0.526, 1.104, 0.961, 1.314, −2.198, −1.621, −0.761, −1.179, −0.610, −0.291, 0.067, 0.706, −2.713, 0.213, 0.116, 0.273, 0.840, 0.745, 1.485, −1.208, 0.189, 0.345, 0.962, 1.592)^T used by Wang et al. (2012). The first 10%, 25%, or 40% of the items are simulated as the DIF items (see section DIF Proportion and DIF Direction below).

Ability Distribution

In the following simulation study, ability differences are simulated since this case is often found to be more challenging for the methods than a situation where no ability differences are present (see, e.g., Penfield, 2001). The ability parameters ${\theta }_i$ follow a standard normal distribution for the reference group ${\theta }^{\mathrm{ref}}~N(0,1)$ and a normal distribution with a lower mean for the focal group ${\theta }^{\mathrm{foc}}~N(-1,1)$ similar to Wang et al. (2012).

DIF Magnitude

For those items j affected by DIF, the magnitude of DIF as simulated is set to the constant value of ${\text{Δ}}_j^{\mathrm{DIF}}={\beta }_j^{\mathrm{ref}}-{\beta }_j^{\mathrm{foc}}=0.4.$ This magnitude has previously been used by Rogers and Swaminathan (1993).

Manipulated Variables

In addition to the selection strategies investigated by Wang et al. (2012), namely, the AO- and the AOP-selection, five other empirical anchor selection strategies, the perfect selection of DIF-free items that serves as a benchmark method and the all-other method without an explicit anchor selection strategy are included (for a summary see again Table 1 and Figure 1).

Sample Size

The sample size is defined by the following pairs of reference and focal group sizes: $(n^{\mathrm{ref}},n^{\mathrm{foc}})\in$ {(250, 250), (500, 500), (750, 750), (1,000, 1,000), (1,250, 1,250), (1,500, 1,500)}.

DIF Proportion and DIF Direction

The proportion of simulated DIF items is varied from 0% DIF items—representing the null hypothesis of no DIF—to 10%, 25%, or 40% DIF items (such high proportions of DIF items may actually occur in practical research; Allalouf, Hambleton, & Sireci, 1999, for example, found 45% DIF items in their study, and Shih & Wang, 2009, listed further examples of 40% or more DIF items).

The sign of ${\text{Δ}}_j^{\mathrm{DIF}}$ is set consistent with the intended direction of DIF. The direction of DIF is either balanced or unbalanced. In case of balanced DIF, the DIF items either favor the focal or the reference group, and on average, no group has an advantage in the test. In case of unbalanced DIF, all items favor the reference group.

Anchor Methods

Anchor classes

All anchor selection strategies are combined with two anchor classes, the constant four anchor class (abbreviated constant4) and the iterative forward class (abbreviated forward). As an example of an anchor class without an explicit anchor selection strategy the all-other class (abbreviated all-other) is included as well.

Anchor selections

Eight different anchor selection strategies (for a brief summary see again Table 1 and Figure 1) are compared across the simulated settings: The AO-, AOP-, NST-, and MT-selection as well as the newly suggested MP-, MTT-, and MPT-selection and the perfect-selection that serves as the benchmark condition: The perfect selection for the four anchor class includes four randomly chosen DIF-free items. For the iterative forward anchor class, a random ranking order that includes the DIF-free items first, followed by the DIF items is handed to the procedure. The remaining steps of the iterative procedure are carried out as usual. Thus, for the “perfect” forward method, it may happen that DIF items occur in the anchor because the length of the iteratively selected anchor may exceed the length of the sequence of DIF-free items, which is not the case for the perfect four anchor method.

Anchor methods

Seventeen anchor methods result from the combination of the eight anchor selection strategies with the two anchor classes together with the all-other method. Their names (constant4-AO, constant4-AOP, constant4-NST, constant4-MT, constant4-MP, constant4-MTT, constant4-MPT, constant4-perfect, forward-AO, forward-AOP, forward-NST, forward-MT, forward-MP, forward-MTT, forward-MPT, forward-perfect, all-other) include the anchor class (all-other, constant4 or forward) together with the abbreviation of the anchor selection (in cases where the latter is necessary).

Outcome Variables

In order to evaluate whether the anchor selection strategies locate anchor items that allow to correctly classify DIF and DIF-free items, the following outcome variables are recorded in each of the 1,000 replications of one simulated setting:

False Alarm Rate

For a single replication the false alarm rate is defined as the proportion of DIF-free items that are (erroneously) diagnosed with DIF in the final DIF test. The estimated false alarm rate for each simulated setting is computed as the mean over all 1,000 replications and represents the type one error rate of the final DIF test.

Hit Rate

The hit rate for a single replication is computed as the proportion of DIF items that are (correctly) diagnosed with DIF in the final DIF test. Analogously, the estimated hit rate is again computed as the mean over all 1,000 replications and corresponds to the statistical power of the final DIF test.

Average Mean Bias

The recovery of the item parameter differences between the reference and the focal groups is evaluated by means of the average mean bias. For a single replication the mean bias is calculated as the mean of the differences ${\widehat{\text{Δ}}}_j^{\mathrm{DIF}}-{\text{Δ}}_j^{\mathrm{DIF}}$ over all $j$ items that are tested for DIF. Here, ${\widehat{\text{Δ}}}_j^{\mathrm{DIF}}={\hat{\beta }}_j^{\mathrm{ref}}-{\hat{\beta }}_j^{\mathrm{foc}}$ denotes the estimated DIF-effect measured as the difference between the estimated item parameter of the reference and of the focal group, whereas ${\text{Δ}}_j^{\mathrm{DIF}}$ represents the simulated DIF-effect that is either 0.4, if item $j$ is a DIF item, or 0 otherwise. The average mean bias is computed as the mean over all 1000 replications. This measure identifies how well effect sizes, such as Raju’s area (Raju, 1988), are expected to cover the true DIF effects.

Results

In the following, we present the results of our simulation study. First, the selection of a short anchor of four anchor items is regarded in the next section. Then, the selection of a longer anchor by means of the iterative forward anchor class is addressed. Finally, the best performing anchor selection strategies are compared.

Anchor Selection for the Constant Four Anchor Class

In this section, the anchor selection strategies combined with the constant anchor class are regarded. Consequently, four anchor items were selected by the respective strategy, and the results of the final DIF tests are discussed and compared to the all-other method.

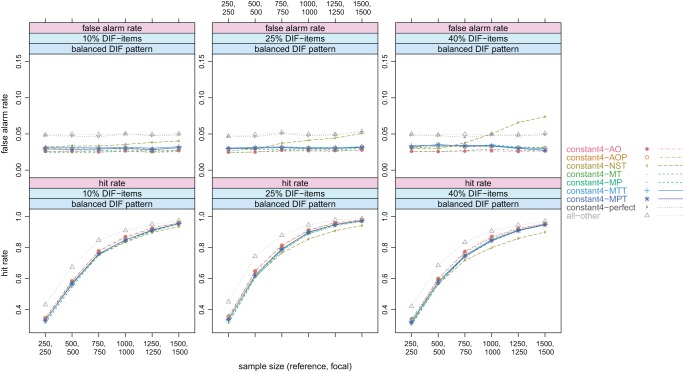
Figure 2 depicts the false alarm rates under the null hypothesis of no DIF. Under the no DIF condition, all items were truly DIF-free and only the false alarm rate was calculated. All methods based on empirical anchor selection strategies remained below the significance level of 5% and were even overconservative. This fact was also found by Kopf et al. (2013) and is not surprising, since the selection strategies were designed to select anchor items in a way such that the other items display little DIF. The all-other method and the benchmark constant4-perfect method (that artificially selected items from the set of DIF-free items) yielded false alarm rates close to the significance level.

Figure 2.

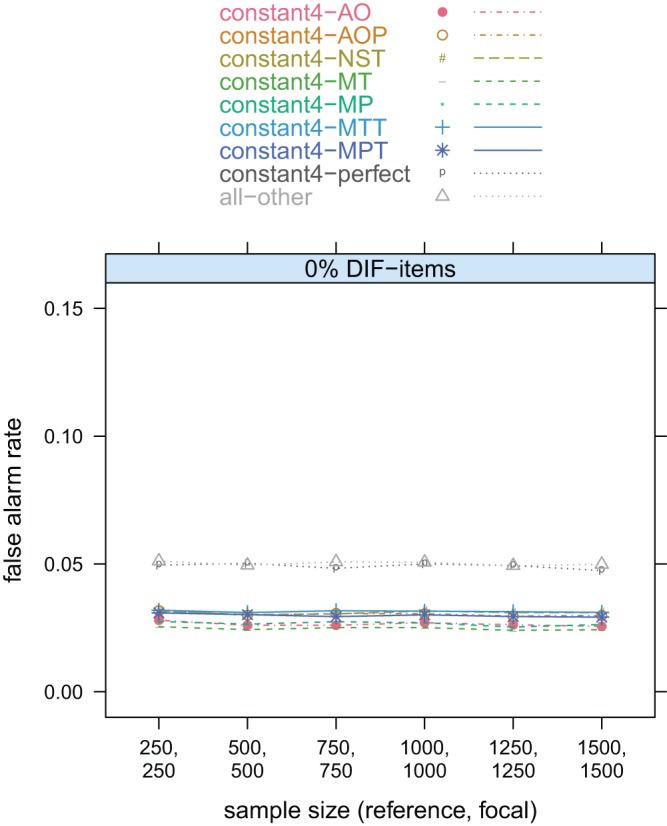
Constant4 class; no DIF condition: 0% DIF items; sample size varied from (250; 250) up to (1,500; 1,500); false alarm rates.

Figure 3 contains the results of the false alarm rates (top row) and the hit rates (bottom row) in case of 10%, 25%, or 40% DIF items (from left to right) that did not systematically favor one group. In this balanced condition, again, the empirical anchor selection strategies were overconservative and almost all methods displayed false alarm rates below the 5% level in the observed range of the sample size. The only exception was the method relying on the NST-selection with the maximum observed false alarm rate of 0.074, which occurred at the sample size of 1,500 observations in each group and 40% DIF items. This method also displayed a lower hit rate compared to the other anchor selection strategies in regions of medium to large sample sizes. Surprisingly, the perfect anchor selection did not display a substantially higher hit rate compared to the methods based on empirical anchor selection strategies. In contrast to this, the all-other method (not relying on an explicit anchor selection) showed a higher hit rate. This reflects the fact that the all-other method uses all but the studied item as anchor and allows for a higher power due to a longer anchor. In summary, four anchor items were selected appropriately in the balanced condition by all selection strategies except for the NST-selection strategy in regions of large sample sizes.

Figure 3.

Constant4 class; balanced condition: 10%, 25% and 40% DIF items with no systematic advantage for one group; sample size varied from (250; 250) up to (1,500; 1,500); top row: false alarm rates; bottom row: hit rates.

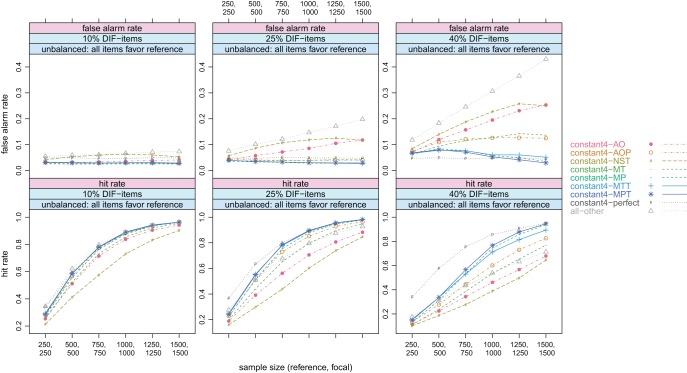
In the unbalanced condition where all DIF items systematically favored the reference group (see Figure 4 ¹), all previously suggested methods (the constant4-AO, the constant4-AOP, the constant4-NST, the constant4-MT, and the all-other method) displayed several weaknesses: In case of a moderate DIF proportion of 25%, the false alarm rates of the constant4-AO, the constant4-NST, and the all-other method, that was—in accordance with previous results (González-Betanzos & Abad, 2012; Kopf et al., 2013; Wang, 2004; Wang & Yeh, 2003)—inadvisable in case of unbalanced DIF, showed inflated false alarm rates. The hit rates of all previously suggested methods were lower compared to those of the new suggestions (the constant4-MP, the constant4-MTT, and the constant4-MPT method) when 25% DIF items were present. In case of 40% DIF items, the false alarm rates of the previously suggested methods were strongly inflated and even (at least partly) increasing with the sample size, whereas the new suggestions displayed false alarm rates decreasing with the sample size as well as higher hit rates and outperformed the previous suggestions. In case of 40% DIF items, the MPT-selection was the best performing method to select four anchor items empirically.

Figure 4.

Constant4 class; unbalanced condition: 10%, 25%, and 40% DIF items favoring the reference group; sample size varied from (250; 250) up to (1,500; 1,500); top row: false alarm rates; bottom row: hit rates.

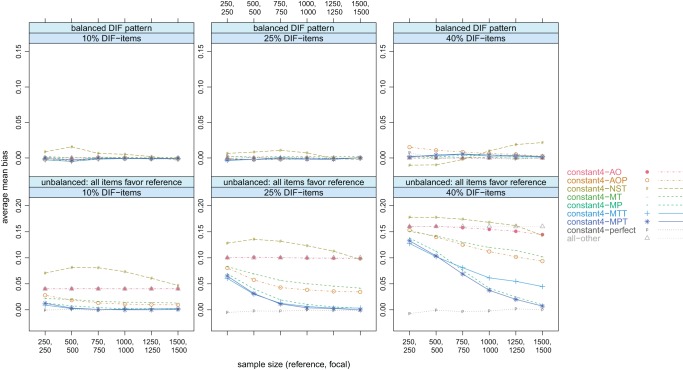
The bias in the estimation of the item parameter differences is illustrated in Figure 5 for the balanced condition (top row) and for the unbalanced condition (bottom row). In the balanced condition, no method showed considerable bias except for the constant anchor found by the NST-selection and by the AOP-selection when the DIF proportion was high and the sample sizes were small. In all unbalanced conditions, the superiority of the new anchor selection strategies (the MP-, the MTT-, and the MPT-selection) is visible at first sight, since these methods showed a lower and more rapidly decreasing bias compared to the previously suggested selection strategies and compared to the all-other method.

Figure 5.

Constant4 class; balanced condition: 10%, 25%, and 40% DIF items with no systematic advantage for one group; unbalanced condition: 10%, 25%, and 40% DIF items favoring the reference group; sample size varied from (250; 250) up to (1,500; 1,500); average mean bias.

In summary, the MPT-selection outperformed the other suggestions in selecting four anchor items by yielding a low false alarm rate while simultaneously achieving a high hit rate in any regarded condition. The newly suggested MP-selection yielded clearly better results than the MT-selection even though both methods were structurally very similar and the MPT-selection slightly outperformed the MTT-selection when the DIF proportion was high. For this reason, an anchor selection based on mean p-values instead of mean test statistics is advisable for selecting an anchor of constant length four in our simulated settings. As expected, the methods based on threshold comparisons (MPT- and MTT-selection) improved the final DIF test results in our study compared to the corresponding strategies based on mere mean values (MP- and MT-selection).

Anchor Selection for the Iterative Forward Anchor Class

In this section, we investigate the combination of the anchor selection strategies with the iterative forward anchor class, which was designed to specify a longer anchor (Kopf et al., 2013).

Similar to that in section “Anchor Selection for the Constant Four Anchor Class,”Figure 6 includes the false alarm rates under the null hypothesis of no DIF. Here, all empirical anchor selection strategies, the perfect selection, and also the all-other method yielded similar false alarm rates near the significance level of 5%. The iterative forward anchor class allowed for a longer anchor, while the constant four anchor class consisted of a short anchor what led to overconservative test results in the previous section (see again Figure 2).

Figure 6.

Forward class; no DIF condition: 0% DIF items; sample size varied from (250; 250) up to (1,500; 1,500); false alarm rates.

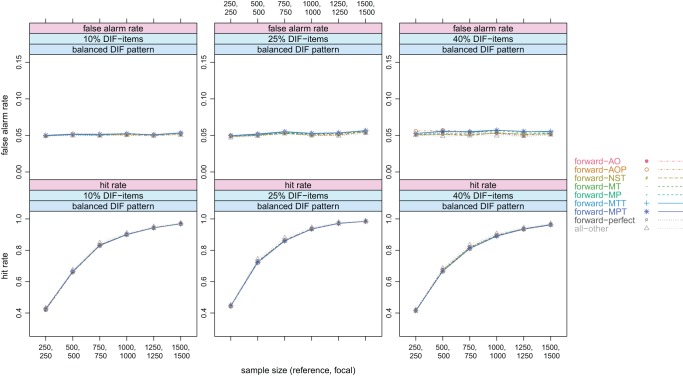
Figure 7 includes the results for the false alarm rates (top row) and the hit rates (bottom row) in the balanced condition (i.e., the items affected by DIF did not systematically favor one group). In contrast to the results of the previous section where the all-other method was superior in case of balanced DIF (see again Figure 3), there was neither a visible difference in the false alarm rates nor in the hit rates for any of the investigated methods. Again, all empirical selection strategies yielded test results similar to the iterative method based on the perfect selection. Hence, all empirical selection strategies were advisable and the iterative forward anchor class was robust against the anchor selection strategy employed in this case. Furthermore, the iterative forward anchor class (see Figure 7) allowed for a higher hit rate compared to the constant four anchor class (see Figure 3).

Figure 7.

Forward class; balanced condition: 10%, 25%, and 40% DIF items with no systematic advantage for one group; sample size varied from (250; 250) up to (1,500; 1,500); top row: false alarm rates; bottom row: hit rates.

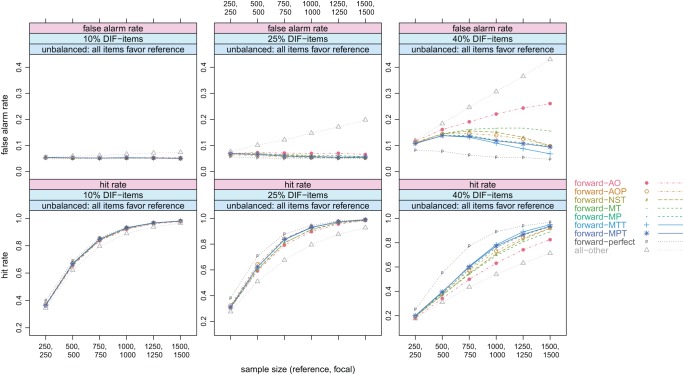
Figure 8² includes the results for the false alarm rates (top row) and the hit rates (bottom row) in the unbalanced condition (i.e., the items affected by DIF systematically favored the reference group). The differences in this condition were smaller and the results of the final DIF tests varied notably with the anchor selection strategies only for 40% unbalanced DIF items. This condition will now be regarded in detail. Here, the previously suggested methods (the forward-AO, the forward-AOP, the forward-NST, the forward-MT, and the all-other method) were outperformed by the new suggestions (the forward-MP, the forward-MTT, and the forward-MPT method) that showed lower false alarm rates and simultaneously reached higher hit rates. Except for the perfect forward method, the newly suggested forward-MTT method yielded the lowest false alarm rate together with the highest hit rate.

Figure 8.

Forward class; unbalanced condition: 10%, 25%, and 40% DIF items favoring the reference group; sample size varied from (250; 250) up to (1,500; 1,500); top row: false alarm rates; bottom row: hit rates.

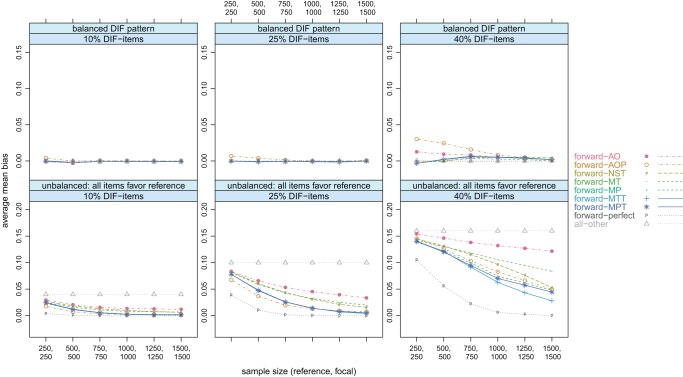
The bias is indicated in Figure 9. In the balanced condition (top row), only the AO- and the AOP-selection relying on DIF-tests using all other items as anchor yielded a slightly higher bias when the sample sizes were low and the DIF-proportion was high. In case of 10% or 25% unbalanced DIF items (bottom row), the AOP-selection yielded a slightly lower bias when the sample sizes were small, followed by the new suggestions. Still, large differences occurred only in case of 40% unbalanced DIF items, where the new suggestions—especially the MTT-selection—performed best. Note, however, that the benchmark method based on the perfect selection performed far worse here compared to the previous section, since it was possible that it included DIF items (see again section “Manipulated Variables”).

Figure 9.

Forward class; balanced condition: 10%, 25%, and 40% DIF items with no systematic advantage for one group; unbalanced condition: 10%, 25%, and 40% DIF items favoring the reference group; sample size varied from (250; 250) up to (1,500; 1,500); average mean bias.

In summary, the iterative forward anchor class was less affected by the anchor selection strategy compared to the constant four anchor class. Furthermore, it allowed for a higher hit rate, but at the expense of a higher false alarm rate. Even though the AOP-selection had a slight advantage in case of 10% or 25% unbalanced DIF items when small sample sizes were present, the iterative anchor class is ideally combined with the newly suggested MTT-selection under similar conditions, because this combination allowed for a low bias and a low false alarm rate together with a high hit rate in any regarded condition. The forward-MTT method performed well also in the extreme setting of 40% unbalanced DIF items, where the differences between the methods were rather large. Compared to the selection of an anchor of constant length four, where the MPT-selection based on p-values reached the best final DIF test results, for the longer, iteratively selected anchor the MTT-selection that is built on mean test statistics is advisable in case of a high number of DIF items. A detailed explanation for this finding will be given in the next section. Again, the methods based on threshold comparisons (MPT- and MTT-selection) outperformed the corresponding strategies based on mere mean values (MP- and MT-selection).

Comparison of the Mean Test Statistic and Mean p-Value Threshold Selection

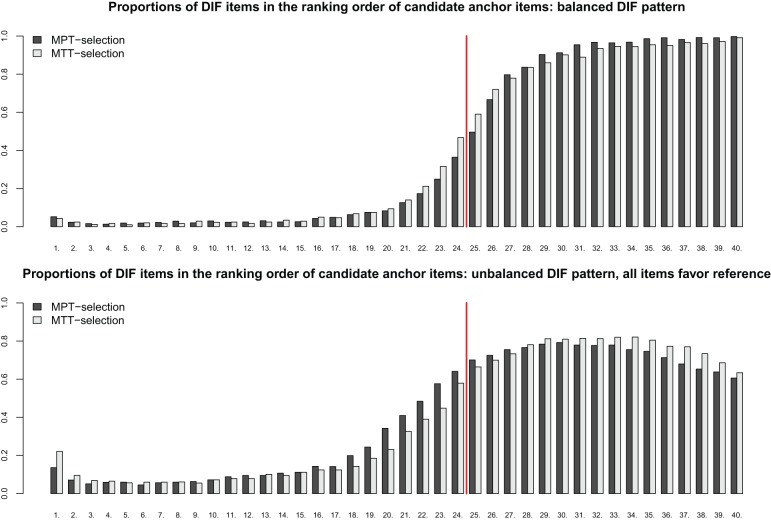
To explain the fact that the MPT-selection yielded better results when it was combined with the constant four anchor class, whereas the MTT-selection performed better combined with the iterative forward anchor class, the ranking order of candidate anchor items is now regarded in detail for one balanced and one unbalanced setting (with 40% DIF items and 1,000 observations in each group). Figure 10 contains the proportions of DIF items in the ranking order of candidate anchor items. In the regarded setting, 24 items were DIF-free and, ideally, the 24 lowest ranks (from left to the vertical line) should display low proportions of DIF items.

Figure 10.

Top row: proportion of DIF items in the ranking order of anchor candidates in the balanced condition: 40% DIF items with no systematic advantage for one group; bottom row: proportion of DIF items in the ranking order of anchor candidates in the unbalanced condition: 40% DIF items favoring the reference group; sample size was set to 1,000 observations in each group.

In the balanced condition (Figure 10, top panel), the first items of the sequence of anchor candidates—that is, the items to the left of the vertical line—displayed low proportions of DIF items over the simulation runs for both the MPT-selection (black bars) and the MTT-selection (gray bars). In contrast to this, the items that were assigned the highest ranks—that is, the items to the right of the vertical line—displayed large proportions of DIF items. Thus, both anchor selection strategies yielded appropriate ranking orders that clearly separated DIF and DIF-free items: The first candidates displayed low proportions of DIF items, whereas the last candidates displayed large proportions of DIF items as intended for all ranks above 24.

In the unbalanced condition (Figure 10, bottom panel), the separation of candidates with low proportions of DIF items for the first ranks and high proportions for the last ranks was harder for both methods. Now the first anchor candidates displayed higher proportions of DIF items. Generally, the MTT-selection (gray) yielded lower DIF proportions for items up to the vertical line compared to the MPT-selection (black) and was, in consequence, better suited to locate a longer anchor. However, when an anchor of constant length four was intended, only the first four candidates were included in the anchor. The first four ranks selected by the MPT-selection displayed lower proportions of DIF items compared to the MTT-selection (see very left of Figure 10, bottom panel). As a result, the MPT-selection was better suited to locate four anchor items.

Now the question addressed is which of the methods—the constant4-MPT or the forward-MTT method—can be considered as overall superior. Therefore, we review the results from section “Anchor Selection for the Constant Four Anchor Class” and “Anchor Selection for the Iterative Forward Anchor Class” where 40% DIF items were present together with information about the variation of the false alarm and the hit rate (not shown).

In the balanced and also in the unbalanced condition, the constant4-MPT method led to a lower false alarm rate compared to the forward-MTT method. The false alarm rate also fluctuated less when the sample sizes were large. Consequently, the constant4-MPT method should be preferred with respect to the false alarm rate. In contrast to this, the forward-MTT method achieved a higher and—for large sample sizes simultaneously less fluctuating—hit rate and was, accordingly, superior regarding the hit rate.

In summary, the first anchor candidates were more likely found from the set of DIF-free items by the MPT-selection, whereas the MTT-selection was better suited for longer anchors. However, first results show that neither the constant4-MPT nor the forward-MTT method was clearly superior in the 40% DIF items setting regarding a strictly smaller and less fluctuating false alarm rate and a higher and less fluctuating hit rate.

Discussion and Practical Recommendations

In this article, we introduced three new anchor selection strategies and compared them to existing methods that do not rely on any prior knowledge of DIF-free items. Moreover, we introduced a straightforward notation of the anchor selection strategies to facilitate the implementation and the usage of the newly suggested anchor selection strategies. An extensive simulation study was conducted to evaluate the performance of the anchor selection strategies in combination with the constant four anchor class and the iterative forward anchor class for the Rasch model. The two anchor classes are structurally different, since the constant four anchor class always uses a short anchor of constant length four, whereas the iterative forward class determines the anchor length in an iterative way and usually yields a longer anchor.

To allow for a comparison with an anchor method that does not rely on an explicit anchor selection, the all-other method was included in our simulation as well. Our results were in accordance with previous research, as the all-other method heavily suffered from an inflated false alarm rate when a large proportion of unbalanced DIF items was present (González-Betanzos & Abad, 2012; Kopf et al., 2013; Wang, 2004; Wang & Yeh, 2003) and discourage from the usage of the all-other method.

Our analysis was limited to the analysis of differential item functioning in the dichotomous Rasch model. In our investigated settings, the results of the DIF tests—evaluated by means of the false alarm rate, the hit rate, and the average mean bias—strongly depended on the anchor selection strategies employed, when four anchor items were intended. This highlights the importance of a suitable anchor selection strategy that allows the researcher to correctly classify DIF and DIF-free items and to study the underlying causes of DIF (Jodoin & Gierl, 2001). Consistent with previous results (see, e.g., González-Betanzos & Abad, 2012; Kopf et al., 2013; Wang & Yeh, 2003; Wang, 2004), seriously inflated false alarm rates occurred if the anchor method did not work appropriately, especially when DIF was unbalanced and the DIF proportion was high. This was the case for several existing anchor selection strategies in our simulation study. Anchor selections based on the all-other anchor method (the AO- and the AOP-selection) are inadvisable to select four anchor items, since the estimated item parameter differences were biased in the unbalanced DIF condition and even additional purification steps included in the AOP-selection were not able to completely reduce the bias when the DIF proportion was high. For this reason, we advise against constructing new anchor selection strategies for the constant four anchor class that use all other items as anchor. Unsatisfactory results were also found for the MT-selection that is based on mean absolute test statistics resulting from DIF tests for every item using every other item as single anchor and the NST-selection that counts the number of significant results in those particular tests. As a result, the newly suggested anchor selection strategies based on a threshold criterion clearly outperformed the existing suggestions. Four anchor items were ideally selected using the MPT-selection in our simulated settings.

In our study, the iterative forward anchor class was relatively robust against the anchor selection strategy employed. Only in the case of 40% unbalanced DIF items, the effects of the anchor selection strategies were clearly visible. In the remaining investigated settings, all anchor selection strategies performed quite well and achieved results similar to the benchmark method of the perfect anchor selection. However, in the case of 40% unbalanced DIF items, all three new anchor selection strategies outperformed the previously suggested anchor selection strategies by yielding a lower false alarm rate, a higher hit rate, and less biased estimates of the item parameter differences. Still, since the perfect selection reached better results, the selection strategies can be further improved.

Altogether, our results showed that the appropriateness of the anchor selection not only depended on the sample size, the proportion of DIF items, and the direction of DIF but also on the intended anchor length.

In case a short anchor of length four is intended, the MPT-selection outperformed all other investigated empirical anchor selection strategies by yielding a low false alarm rate and simultaneously reaching a high hit rate in all regarded conditions. As a result, we recommend using the MPT-selection if a short constant anchor length is intended under similar conditions.

When the selection strategies were combined with the iterative forward anchor class, the newly suggested MTT-selection reached the best results in our extreme setting of 40% DIF items. It is recommended for DIF analysis when the iterative forward anchor class is used, as well as in general when a longer anchor length is intended under conditions similar to those investigated in this article.

Nevertheless, the benchmark method of the perfect anchor selection still reached lower false alarm rates and higher hit rates in regions of small to medium sample sizes when DIF was simulated unbalanced. Hence, new developments for anchor selection strategies that ideally follow the threshold approach are needed to further improve the classification of DIF and DIF-free items when the sample sizes are small. When the sample sizes are large, the newly suggested constant4-MPT and the forward-MTT method reached satisfying results in our simulation study.

Future research may investigate the adaption of our anchor selection strategies to other DIF tests and may evaluate modifications of the iterative anchor method, such as the exclusion of a certain percentage of the first anchor candidates that we found more likely to have DIF. Moreover, future research may evaluate the performance of these methods when the data are generated from other IRT models. In the Rasch model, the items are assumed to have the same discriminatory power. The items are, thus, characterized by the item difficulty parameters only. Other IRT models include further parameters for the discriminatory power (2 parameter logistic, 2PL, model) or for guessing behavior (3 parameter logistic, 3PL, model) or allow for more than two response categories. For the 2PL or the 3PL model, anchor items that displayed high discrimination parameters were found to be better suited as anchor items (González-Betanzos & Abad, 2012; Lopez Rivas et al., 2009). Future research may combine the strategies introduced in this article with new requirements and other underlying IRT models. The ranking order of candidate anchor items could, for example, be modified in a way such that items with a low discriminatory power are less likely to be selected as anchor candidates.